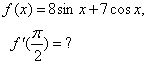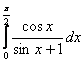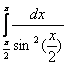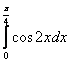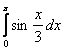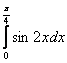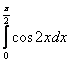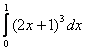Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра высшей математики
МАТЕМАТИКА В ЭКОНОМИКЕ
Методические указания и задания к расчетно-графическим работам
для студентов специальности 5В050600-«Экономика»
Часть 2
Алматы 2011
Составители: С.А. Нурпеисов, Ж.С. Абдулланова. Математика в экономике. Методические указания и задания к расчетно-графическим работам. Часть 2.-Алматы: АУЭС, 2011-23 с.
Методическое указание подготовлено в соответствии с типовой прог- раммой по курсу «Математика для экономистов» по всем направлениям эко- номических специальностей.
Методические указания и задания к РГР содержат задачи курса матема- тики для экономических специальностей дневного отделения АУЭС: введение в анализ, дифференциальное исчисление функции одной переменной, диффе- ренциальное исчисление функции двух переменных, интегральное исчисле- ние. Даны основные теоретические вопросы программы и решение типового варианта.
Рецензент: канд. физ.-мат. наук, проф. С.Е. Базарбаева.
Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2011 г.
ã НАО «Алматинский университет энергетики и связи», 2011 г.
Сводный план 2011 г., поз.
Типовой расчет 2
Введение в анализ, дифференциальное исчисление функции одной
переменной и двух переменных, интегральное исчисление
Теоретические вопросы
1. Раскрытие неопределенностей.
2. Точки разрыва, асимптоты.
3. Производная функции.
4. Геометрический смысл производной
5. Производная сложной функции.
6. Дифференциал. Производная второго порядка.
7. Экстремум. Выпуклость. Точки перегиба.
8. Частные производные первого и второго порядка.
9. Дифференциал функции двух переменных. Градиент.
10. Экстремум функции двух переменных.
11. Первообразная функция.
12. Неопределенный интеграл.
13. Определенный интеграл.
14. Площадь плоской фигуры
1.Вычислить пределы.
|
1. |
|
2. |
|
3. |
|
|
4. |
|
5. |
|
6. |
|
|
7. |
|
8. |
|
9. |
|
|
10. |
|
11. |
|
12. |
|
|
13. |
|
14. |
|
15. |
|
|
16. |
|
17. |
|
18. |
|
|
19. |
|
20. |
|
21. |
|
|
22. |
|
23. |
|
24. |
|
|
25. |
|
26. |
|
27. |
|
|
28. |
|
29. |
|
30. |
|
2.Найти точки разрыва функции и асимптоты
кривой ![]() .
.
|
1.
|
2.
|
3.
|
4.
|
|
5.
|
6.
|
7.
|
8.
|
|
9. |
10.
|
11.
|
12. |
|
13.
|
14.
|
15.
|
16.
|
|
17.
|
18.
|
19.
|
20.
|
|
21.
|
22.
|
23.
|
24.
|
|
25.
|
26.
|
27.
|
28.
|
|
29.
|
30.
|
||
3. Найти производную функции в заданной точке.
|
1.
|
2.
|
3. |
|
4.
|
5.
|
6.
|
|
7.
|
8.
|
9.
|
|
10.
|
11.
|
12.
|
|
13.
|
14.
|
15.
|
|
16.
|
17.
|
18.
|
|
19.
|
20.
|
21.
|
|
22.
|
23.
|
24.
|
|
25.
|
26.
|
27.
|
|
28.
|
29.
|
30.
|
4.Найти угловой коэффициент касательной,
проведенной к графику функции
![]() .
.
|
1.Найти угловой коэффициент касательной,
проведенной к графику функции |
|
2. Найти угловой коэффициент касательной,
проведенной к графику функции |
|
3. Найти угловой коэффициент касательной,
проведенной к графику функции |
|
4. Под каким углом к оси Ох наклонена
касательная, проведенная к графику функции |
|
5. Под каким углом к оси Ох наклонена
касательная, проведенная к графику функции |
|
6. Под каким углом к оси Ох наклонена
касательная, проведенная к графику функции |
|
7. Под каким углом к оси Ох наклонена
касательная, проведенная к графику функции |
|
8. Под каким углом к оси Ох наклонена
касательная, проведенная к графику функции |
|
9. Под каким углом к оси Ох наклонена
касательная, проведенная к графику функции |
|
10.Найти точку графика функции
|
|
11. Найти точку графика функции
|
|
12. В какой точке касательная к
графику функции
|
|
13. В какой точке касательная к
графику
функции
|
|
14. Найти точку графика функции
|
|
15. Найти точку графика функции
|
|
16. Составить уравнение касательной,
проведенной к графику функции |
|
17. Составить уравнение касательной,
проведенной к графику функции |
|
18. Составить уравнение касательной,
проведенной к графику функции |
|
19. Составить уравнение касательной, проведенной
к графику функции |
|
20. Составить уравнение касательной,
проведенной к графику функции |
|
21.Составить уравнение касательной,
проведенной к графику функции |
|
22. Какие углы |
|
23. Составить равнение касательной к графику
функции |
|
24. Написать уравнение касательной к параболе
|
|
25. Написать уравнение касательной к параболе
|
|
26. На графике функции |
|
27. В каких точках касательная к графику
функции |
|
28.Найти угловой коэффициент касательной,
проведенной к графику функции |
|
29. Найти угловой коэффициент касательной,
проведенной к графику функции |
|
30. Найти угловой коэффициент касательной,
проведенной к графику функции |
5. Найти значение производной сложной функции в указанной точке.
|
1.
|
2.
|
3.
|
|
4.
|
5.
|
6.
|
|
7.
|
8.
|
9.
|
|
10.
|
11.
|
12.
|
|
13.
|
14.
|
15.
|
|
16.
|
17.
|
18.
|
|
19.
|
20.
|
21.
|
|
22.
|
23.
|
24.
|
|
25.
|
26.
|
27.
|
|
28.
|
29.
|
30.
|
6. Найти производную второго порядка и дифференциал данной функции.
|
1.
|
2.
|
3.
|
|
4.
|
5.
|
6.
|
|
7.
|
8.
|
9.
|
|
10.
|
11.
|
12.
|
|
13.
|
14.
|
15.
|
|
16.
|
17.
|
18.
|
|
19.
|
20.
|
21.
|
|
22.
|
23.
|
24.
|
|
25.
|
26.
|
27.
|
|
28.
|
29.
|
30.
|
7. Выполнить указанные задания.
|
1. Найти точку перегиба кривой
|
2. Найти точку перегиба кривой
|
|
3. Найти точку перегиба кривой
|
4. Найти точку перегиба кривой
|
|
5.Найти интервалы выпуклости вверх кривой
|
6. Найти интервалы выпуклости вниз кривой
|
|
7. Найти интервалы выпуклости вверх кривой
|
8. Найти точку перегиба кривой
|
|
9.Найти минимум функции
|
10.Найти максимум функции
|
|
11.Найти экстремум функции
|
12. Найти экстремум функции
|
|
13. Найти экстремум функции |
14.Найти интервалы возрастания функции
|
|
15. Найти интервалы убывания функции
|
16. Найти экстремум функции
|
|
17. Найти экстремум функции
|
18. Найти экстремум функции
|
|
19. Найти экстремум функции
|
20. Найти точку перегиба кривой
|
|
21. Найти точку перегиба кривой
|
22. Найти точку перегиба кривой
|
|
23.Найти точку перегиба кривой |
24.
|
|
25.
|
26.Исследовать на
экстремум функцию |
|
27. Исследовать на экстремум функцию
|
28. Исследовать на экстремум функцию
|
|
29. Исследовать на экстремум функцию |
30.Определить промежутки возрастания и
убывания функции |
8-15.
Дана функция ![]() и точка
и точка
![]() .
.
Требуется:
8)
найти частные производные ![]() ;
;
9) найти частные производные второго порядка;
10) найти дифференциал функции;
11)
найти линию уровня функции ![]() , проходящей через точку
, проходящей через точку
![]() и построить ее
градиент;
и построить ее
градиент;
12) найти
![]() и
построить его;
и
построить его;
13)
вычислить в точке
![]() производную
функции
производную
функции
![]() по направлению
по направлению ![]() ;
;
14)
вычислить в точке
![]() производную
функции
производную
функции
![]() по направлению
по направлению
вектора ![]() где
где
![]() ;
;
15)
найти и построить линию уровня функции ![]() проходящую через точку
проходящую через точку
![]() ,где
,где ![]() указать какое свойство
градиента здесь иллюстрируется.
указать какое свойство
градиента здесь иллюстрируется.
|
1. |
2.
|
|
3.
|
4.
|
|
5. |
6.
|
|
7.
|
8.
|
|
9.
|
10.
|
|
11.
|
12.
|
|
13.
|
14.
|
|
15.
|
16.
|
|
17.
|
18.
|
|
19.
|
20.
|
|
21.
|
22.
|
|
23.
|
24.
|
|
25.
|
26.
|
|
27.
|
28.
|
|
29.
|
30.
|
16. Исследовать функцию на экстремум .
|
1.
|
2.
|
|
3. |
4.
|
|
5.
|
6.
|
|
7.
|
8. |
|
9. |
10. |
|
11. |
12. |
|
13. |
14. |
|
15.
|
16.
|
|
17.
|
18.
|
|
19.
|
20.
|
|
21.
|
22. |
|
23. |
24.
|
|
25.
|
26.
|
|
27. |
28. |
|
29.
|
30.
|
17.
Найти первообразную
![]() для функции
для функции ![]() , если
, если ![]() .
.
|
1.
|
2.
|
|
3.
|
4. |
|
5.
|
6.
|
|
7.
|
8. |
|
9.
|
10.
|
|
11.
|
12.
|
|
13.
|
14.
|
|
15.
|
16.
|
|
17.
|
18.
|
|
19. |
20.
|
|
21.
|
22.
|
|
23. |
24.
|
|
25. |
26. |
|
27. |
28.
|
|
29. |
30.
|
18. Найти неопределенный
интеграл ![]() .
.
|
1. |
2. |
3. |
4. |
5.
|
|
6. |
7. |
8. |
9. |
10.
|
|
11. |
12. |
13. |
14. |
15. |
|
16. |
17.
|
18. |
19. |
20. |
|
21.
|
22. |
23. |
24. |
25.
|
|
26. |
27. |
28. |
29. |
30.
|
19. Вычислить определенный интеграл.
|
1. |
2. |
3. |
4.
|
|
5. |
6. |
7. |
8.
|
|
9. |
10. |
11. |
12. |
|
13. |
14. |
15. |
16.
|
|
17. |
18. |
19. |
20.
|
|
21. |
22. |
23. |
24. |
|
25. |
26. |
27. |
28.
|
|
29. |
30.
|
||
20. Вычислить площадь плоской фигуры, ограниченной линиями:
|
1. |
2.
|
|
3. |
4. |
|
5. |
6.
|
|
7. |
8.
|
|
9. |
10.
|
|
11. |
12. |
|
13. |
14.
|
|
15. |
16.
|
|
17. |
18.
|
|
19. |
20. |
|
21. |
22. |
|
23. |
24. |
|
25. |
26.
|
|
27. |
28. |
|
29. |
30. |
Решение типового варианта
1. Вычислить пределы
а)![]() в)
в)![]() с)
с)![]()
д)![]() е)
е)![]() ж)
ж)![]()
Решение: для вычисления пределов а), в), с) воспользуемся таблицей №1.
Если
а)степенные показатели многочленов в числителе и в знаменателе одина- ковые (m=n=2),то предел будет
равен отношению коэффициентов при наивыс- ших степенях этих многочленов:
![]()
в) степенной показатель
многочлена в числителе больше степени многочлена в знаменателе (3>2), то
![]() с)
степенной показатель многочлена в знаменателе
больше степени многочлена в числителе (4>3), то
с)
степенной показатель многочлена в знаменателе
больше степени многочлена в числителе (4>3), то ![]()
Для вычисления пределов д) и е) разложим числитель и знаменатель на мно- жители, чтобы сократить дробь на общий множитель, стремящийся к нулю. По определению предела функции аргумент х стремится к своему предельно- му значению, никогда не принимая это значение; поэтому до перехода к пре- делу можно произвести сокращение на множитель, стремящийся к нулю. Имеем:
д) ![]() .
.
е) ![]() .
.
Для вычисления предела ж)
умножим числитель и знаменатель на сопряжен- ный знаменателю множитель ![]() и затем, сократив дробь на (х-3), полу- чим: ж)
и затем, сократив дробь на (х-3), полу- чим: ж)![]() .
.
2. а) показать, что при
х=3 функция ![]() имеет
разрыв.
имеет
разрыв.
Решение: находим ![]()
![]() .Таким образом, функция при
.Таким образом, функция при ![]() не имеет ни левого, ни
правого конечного предела. Следовательно, х=3 является точкой разрыва 2 рода;
не имеет ни левого, ни
правого конечного предела. Следовательно, х=3 является точкой разрыва 2 рода;
б) показать, что при х=2
функция ![]() имеет
разрыв.
имеет
разрыв.
Решение:
если ![]() то
то ![]() ,
,
если ![]() то
то ![]() .
.
Итак, при ![]() функция имеет левый и
правый конечные пределы, причем эти пределы различны. Следовательно, х=2
является точкой разрыва 1 рода. В данном примере скачок равен
функция имеет левый и
правый конечные пределы, причем эти пределы различны. Следовательно, х=2
является точкой разрыва 1 рода. В данном примере скачок равен
![]()
в) найти асимптоты
кривой ![]() .
.
Решение: кривая имеет
вертикальную асимптоту х=1, так как ![]() . Ищем наклонные асимптоты:
. Ищем наклонные асимптоты:
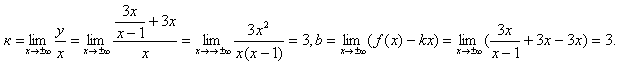 Итак, прямая
Итак, прямая ![]() является наклонной асимптотой.
Горизонтальную асимптоту можно рассматривать как частный случай наклонной
асимптоты при к=0. Различают три вида асимптот: вертикальные, горизонтальные,
нак- лонные. Если хотя бы один из пределов функции
является наклонной асимптотой.
Горизонтальную асимптоту можно рассматривать как частный случай наклонной
асимптоты при к=0. Различают три вида асимптот: вертикальные, горизонтальные,
нак- лонные. Если хотя бы один из пределов функции ![]() в точке а справа и слева равен
бесконечности, то прямая х=а – вертикальная асимптота. Если
в точке а справа и слева равен
бесконечности, то прямая х=а – вертикальная асимптота. Если ![]() , то прямая у=А – горизонтальная
асимптота (правая при
, то прямая у=А – горизонтальная
асимптота (правая при ![]() и левая при
и левая при ![]() ). Если
). Если ![]() , то прямая
, то прямая ![]() - наклонная асимптота (правая). Если
существуют пределы
- наклонная асимптота (правая). Если
существуют пределы ![]()
![]() то прямая
то прямая ![]() - наклонная асимптота
(левая).
- наклонная асимптота
(левая).
3. Найти производную функции в заданной точке.
![]()
Решение:
![]()
4.а)
найти угловой коэффициент касательной, проведенной к графику функции ![]()
Решение:
уравнение касательной к графику функции, проведенный в точке ![]() , имеет вид
, имеет вид ![]() где угловым
коэффициентом касатель-ной является
где угловым
коэффициентом касатель-ной является ![]() . Итак, находим значение производной
функции в задан- ной точке:
. Итак, находим значение производной
функции в задан- ной точке: ![]() ;
;
б) составить уравнение
касательной к графику функции ![]() в точках пересечения его с осью Ох.
в точках пересечения его с осью Ох.
Решение:
![]()
Уравнение
касательной к графику функции ![]() в точке с абсциссой
в точке с абсциссой ![]() имеет вид:
имеет вид:![]() . Так как
. Так как ![]() .
.
Уравнения
касательной в точках А и В соответственно имеют вид ![]() .
.
Ответ:
![]() .
.
в)
в каких точках касательная к графику функции ![]() образует с осью Ох угол в
образует с осью Ох угол в
![]()
Решение: координаты
точек касания найдем, решив уравнение: ![]() абсцисса точки касания.
абсцисса точки касания.
Имеем: 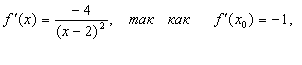
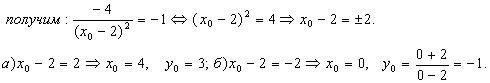
Ответ (4; 3) и (0; -1).
5.Найти значение производной сложной функции в указанной точке
![]() .
.
Решение:
![]()
6.Найти производную второго порядка и дифференциал данной функции
![]()
Решение:
чтобы найти производную второго порядка, нужно найти произ- водную первого
порядка: ![]() и
далее
и
далее
![]() Теперь найдем
дифференциал функции по формуле
Теперь найдем
дифференциал функции по формуле
![]()
7. Выполнить указанные задания:
а)
найти
промежутки возрастания и убывания функции
![]() .
.
Решение:
![]() .
Если
.
Если ![]() и
и
следовательно,
функция ![]() убывает
в промежутке
убывает
в промежутке ![]() если
если
![]() и
следовательно, функция
и
следовательно, функция ![]() возрастает в про- межутке
возрастает в про- межутке
![]()
б)
найти
промежутки возрастания и убывания функции
![]() .
.
Решение:
здесь х=3-точка разрыва функции и![]()
Следовательно, функция ![]() убывает в промежутке
убывает в промежутке
![]()
в) найти экстремум функции
![]()
Решение:
![]() Далее
найдем вторую производную:
Далее
найдем вторую производную: ![]() Определим знак второй производной в каждой
ста- ционарной точке. Имеем:
Определим знак второй производной в каждой
ста- ционарной точке. Имеем: ![]()
![]() следовательно, х=-2 есть точка максимума, а
х=2- точка минимума функции;
следовательно, х=-2 есть точка максимума, а
х=2- точка минимума функции;
г)
определить участки выпуклости вверх и вниз кривой ![]() и точку перегиба.
и точку перегиба.
Решение:![]() , отсюда
, отсюда ![]() ,
,
![]() . Следовательно, при
любом
. Следовательно, при
любом ![]() кривая
кривая ![]() выпукла вверх
выпукла вверх ![]() а при
а при ![]() кривая
кривая ![]() выпукла вниз
выпукла вниз
![]()
Абсцисса
точки перегиба ![]() .
Отсюда ордината точки перегиба
.
Отсюда ордината точки перегиба
![]() Таким образом, точкой
перегиба кривой
Таким образом, точкой
перегиба кривой ![]() будет
будет
![]()
8-15.
Дана функция ![]() и точка
и точка
![]() .
.
Требуется:
8) Найти
частные производные ![]() ;
;
9) Найти частные производные второго порядка;
10) Найти дифференциал функции;
11) Найти линию
уровня функции ![]() ,
проходящей через точку
,
проходящей через точку
![]() и
построить ее градиент;
и
построить ее градиент;
12) Найти
![]() и
построить его;
и
построить его;
13)
Вычислить в точке
![]() производную
функции
производную
функции
![]() по направлению
по направлению ![]() ;
;
14)
Вычислить в точке
![]() производную
функции
производную
функции
![]() по направлению
по направлению
вектора ![]() где
где
![]() ;
;
15)
Найти и построить линию уровня функции ![]() проходящую через точку
проходящую через точку
![]() ,где
,где ![]() указать какое свойство
градиента здесь иллюстрируется.
указать какое свойство
градиента здесь иллюстрируется.
Решение:
8) частная производная ![]() находится дифференцированием функции
находится дифференцированием функции ![]() по х, при этом у
считается постоянным, а
по х, при этом у
считается постоянным, а ![]() находится дифференциро- ванием функции
находится дифференциро- ванием функции ![]() по у, при этом х
считается постоянным.
по у, при этом х
считается постоянным.
Итак,
![]() ,
, ![]() ;
;
9) ![]()
![]() ,
, ![]() .
.
10) Полным
дифференциалом называется выражение ![]()
11)
Линия уровня данной функции, проходящая через точку
![]() , имеет уравнение
, имеет уравнение
![]() . Вычислим
. Вычислим ![]() . Отсюда
. Отсюда ![]() - уравнение искомой линии уровня.
Выделив полный квадрат, приведем уравнение к виду
- уравнение искомой линии уровня.
Выделив полный квадрат, приведем уравнение к виду 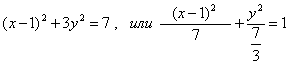 . Это канони- ческое уравнение
эллипса с центром в точке О(1; 0) и полуосями
. Это канони- ческое уравнение
эллипса с центром в точке О(1; 0) и полуосями ![]() . График изображен на рисунке1.
. График изображен на рисунке1.
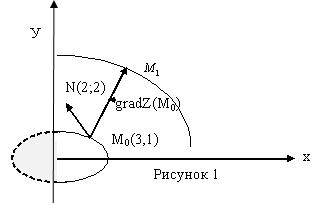
12) ![]() -это вектор, координатами
которого являются частные произ- водные, вычисленные в точке
-это вектор, координатами
которого являются частные произ- водные, вычисленные в точке![]() , т.е.
, т.е.
![]() ;
;
Следовательно,
![]() .
.
13)
Вычисляем в точке
![]() производную
функции
производную
функции
![]() по направлению
по направлению ![]() . Обозначим
. Обозначим ![]() . По свойствам градиента
. По свойствам градиента
![]() ;
;
14)
Вычисляем
в точке
![]() производную функции
производную функции
![]() по направлению
по направлению
вектора
![]() .Обозначим
.Обозначим ![]() ,
по условию
,
по условию
![]() , поэтому
, поэтому ![]() . Итак,
. Итак, ![]() , тогда орт этого вектора
, тогда орт этого вектора ![]() . По свойствам гради- ента
. По свойствам гради- ента
![]() . В данной задаче
. В данной задаче
![]() . Найдем
скалярное произведение этих векторов. Тогда
. Найдем
скалярное произведение этих векторов. Тогда ![]() . Следовательно,
. Следовательно,![]() . Это естественно, так как в
точке
. Это естественно, так как в
точке
![]() производная по направлению градиента имеет
наибольшее значение, равное
производная по направлению градиента имеет
наибольшее значение, равное ![]() .
.
15)
Найдем и построим линию уровня функции ![]() проходящую через точку
проходящую через точку
![]() ,где
,где ![]() указать какое свойство градиента
здесь иллюс- трируется. Для этого найдем сначала координаты точки
указать какое свойство градиента
здесь иллюс- трируется. Для этого найдем сначала координаты точки
![]() . Так как вектор
. Так как вектор
![]() и
и
![]() , то точка
, то точка ![]() имеет координаты х=7, у=7. Линия
уровня, проходящая через точку
имеет координаты х=7, у=7. Линия
уровня, проходящая через точку ![]() , имеет уравнение
, имеет уравнение
![]() .
.
Отсюда
![]() . Это эллипс
с центром в точке О (1; 0) и полуосями
. Это эллипс
с центром в точке О (1; 0) и полуосями ![]() . Дуга этого эллипса, лежащая в первой четверти,
изображена схематически на рисунке1.
. Дуга этого эллипса, лежащая в первой четверти,
изображена схематически на рисунке1.
Итак,
при переходе от точки
![]() к
точке
к
точке ![]() по направлению гради-
ента функции
по направлению гради-
ента функции
![]() значение этой функции
возрастает от 6 до 182. Это иллюстрирует свойство градиента, состоящего
в том, что направление градиента является направлением наискорейшего
возрастания функции.
значение этой функции
возрастает от 6 до 182. Это иллюстрирует свойство градиента, состоящего
в том, что направление градиента является направлением наискорейшего
возрастания функции.
16.
Исследовать на экстремум функцию ![]() .
.
Решение: находим частные производные и приравниваем их к нулю,
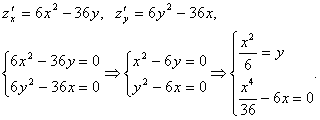
(Здесь комплексные корни не рассматриваются).
Таким
образом, имеем две критические точки: ![]() .
.
Теперь найдем производные второго порядка
![]()
![]()
![]() и вычислим их значения в критических
точках:
и вычислим их значения в критических
точках: ![]()
![]()
![]() , тогда
, тогда ![]() , поэтому в этой точке экстремума
нет.
, поэтому в этой точке экстремума
нет.
![]()
![]()
![]() ,тогда
,тогда ![]() , поэтому
, поэтому ![]() .
.
17.
Найти первообразную функцию ![]() для функции
для функции
![]() , если
, если ![]() :
:
![]()
Решение:
если функция имеет первообразную функцию ![]() , то она имеет бесконечное множество
первообразных функции, причем все первообразные функции содержатся в выражении
, то она имеет бесконечное множество
первообразных функции, причем все первообразные функции содержатся в выражении ![]() , где С-постоянная. Найдем
перво- образную для нашей функции
, где С-постоянная. Найдем
перво- образную для нашей функции![]() По условию задачи
По условию задачи
![]() Теперь найдем значение
С:
Теперь найдем значение
С: ![]() Итак,
искомое выражение
Итак,
искомое выражение ![]()
18. Найти неопределенные интегралы
а) ![]() б)
б) ![]() в)
в) ![]() ; г)
; г)![]()
Решение: 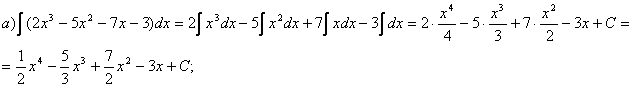
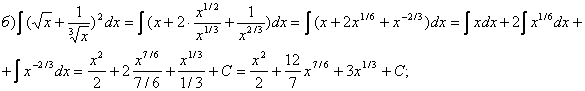
в) это интеграл вычислим путем подведения функции под знак дифферен- циала:
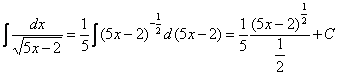 ;
;
г)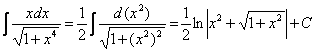 .
.
19.Вычислить определенные интегралы.
1.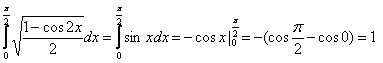 .
.
2.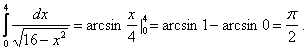
3.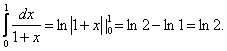
4.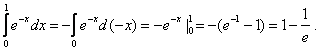
5.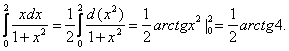
6.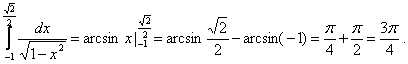
20.а)
вычислить площадь, ограниченную параболой ![]() , прямыми х=1 и х=3 и осью абсцисс.
, прямыми х=1 и х=3 и осью абсцисс.
Решение:
искомая площадь выражается интегралом ![]() ;
;
б)
вычислить площадь, ограниченную кривой![]() и осью ординат.
и осью ординат.
Решение:
здесь изменены роли осей координат и поэтому искомая площадь выражается
интегралом ![]() ,
где пределы интегрирования у=-2 и у=1 найдены как ординаты точек пересечения
данной кривой с осью ординат;
,
где пределы интегрирования у=-2 и у=1 найдены как ординаты точек пересечения
данной кривой с осью ординат;
в)
вычислить площадь
S,
заключенную между кривыми:![]() (*).
(*).
Решение:
решая совместно систему уравнений (*), находим пределы интегрирования: х=-1 и
х=1. Тогда ![]() .
.
В
более общем случае, если площадь
S ограничена двумя непрерывными кри- выми ![]() и двумя вертикалями х=а
и х=в, где
и двумя вертикалями х=а
и х=в, где ![]() при
при
![]() , то будем
иметь:
, то будем
иметь: 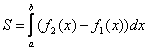 .
.
Таблица №1
|
Виды пределов |
Результат в предельных точках |
Результат вычисления пределов |
|
|
1)
|
Неопределенность |
|
2)
|
Неопределенность |
|
|
3)
|
|
|
|
4)
|
0 |
|
|
5)
|
|
|
|
|
6)
|
0 |
|
7)
|
|
|
|
0, если m<n |
||
|
|
Список литературы
1. Данко П.Е., Попов А.Г. и др. «Высшая математика в упражнениях и задачах» : В24.-М.:Высш.шк. 1986.-ч.1-352 с.
2 А.К Казешев, С.А. Нурпеисов «Математика для экономистов» учебное
пособие ./-Алматы:«Экономика» баспасы.2009.-450 с.
3. Кузнецов А.А. Сборник заданий по высшей математике: типовые расчеты.
- М.:Высш. шк.,1983.-176 с.
Содержание
Типовой расчет 2 3
Теоретические вопросы 3
Расчетные задания 3
Решение типового варианта 13
Список литературы 23