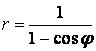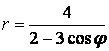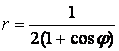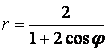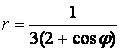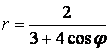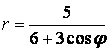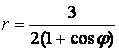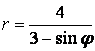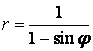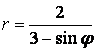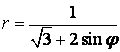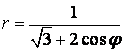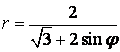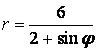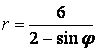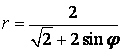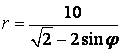Некоммерческое акционерное общество

АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра высшей математики

 

 

 

ГЕОМЕТРИЯ

Методические указания и задания

к выполнению расчетно-графических работ

(для студентов очной формы обучения специальности

5В060200 – Информатика)

Часть 1

 

 

 

Алматы 2011  

СОСТАВИТЕЛИ: М.Ж.Байсалова, Д.Т.Жанузакова. Геометрия. Методические   указания  и задания к   выполнению расчетно-графической работы для студентов очной  формы обучения специальности 5В060200     – Информатика. -Алматы:  АУЭС, 2011.- 18 с.

 

Методические указания и задания к расчетно-графической работе содержат типовой расчет №1 дисциплины «Геометрия» для студентов очной формы обучения специальности 5В060200 – Информатика. Приведены основные теоретические вопросы программы. Дано решение типового варианта.

          Табл. 9, библиогр. – 4 назв.

 

Рецензент: канд.физ.-мат.наук, доцент Л.Н.Астраханцева.

 

Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2011 г.

 

 

ã НАО «Алматинский университет энергетики и связи», 2011

 

1 Типовой  расчёт 1. Векторная алгебра

 

1.1 Теоретические вопросы

 

1 Векторы, их длина, линейные операции над векторами

2 Линейная зависимость и независимость векторов. Геометрический смысл  линейной зависимости векторов.

4 Коллинеарность, компланарность, ортогональность векторов, угол между векторами.

4 Базис, координаты векторов относительно базиса. Преобразование базиса. Матрица перехода. Проекция вектора.

5 Скалярное произведение векторов, его приложения.

6 Векторное произведение векторов, его приложения.

7 Смешанное произведение векторов, его приложения.

8 Общие аффинные и декартовы прямоугольные координаты. Понятие алгебраической линии и поверхности.

9 Преобразование координат при переходе от одной системы координат к другой.

10 Ортогональные матрицы.

11 Полярные, цилиндрические и сферические координаты.

1.2 Расчётные  задания

 

1 Даны точки А и В. Найти:

а) найти координаты векторов  и ;

б) найти длину вектора  (или расстояние между точками А и В);

в) найти середину отрезка АВ:

г) координаты точки М, делящей отрезок АВ в отношений .

Т а б л и ц а 1

1.1 А(9, -1,7), В(4, 4,-6) , =4

1.2 А(-4, 1, 0), В(5, 1, -4)

=4

1.4 А(1, 4, 5), В(7, 4,-1)

=5

1.4 А(6, -2, 5), В(1, 5, 7)

=5

1.5 А(1, -3, 7), В(4, 2, 6)

=4

1.6   А(2, -1, 7), В(6, 2, 4)

=2

1.7  А(-9 1, 7), В(2, 8, 5)

=4

1.8  А(7, 1, -2), В(1, 4, 8)

=5

1.9   А(3, -4, 8), В(5, 4, 7)

=2

1.10 А(5 2, 3, В(4,1, -4)

=4

1.11А(5, 4, -1),В(-6, 1, 2)

=5

1.12А(-4, 2, 4),В(8, 7, -2)

=4

1.14 А(3 4, 6), В(-1, 4, 5)

=2

1.14 А(2, 6, 0), В(6, 4, -4)

=6

1.15 А(5, 2, 0), В(1, -7, 8)

=4

1.16 А(6 2, 5), В(-1,3, 6)

=5

1.17 А(3,-1, 0), В(6,4, -1)

=4

1.18А(6, 2, 2),В(-5, 7, -7)

=4

1.19 А(1 -4,1), В(2,4, -2)

=4

1.20А(5,-6, 4),В(10, 5, 0)

=2

1.21 А(7, 5,-8), В(8, 12,7)

=5

 

продолжение таблицы 1

1.22 А(5 -1, 4), В(4, 5, 8)

=4

1.24 А(2, 5,-7), В(2, 4, 1)

=4

1.24 А(8, -6, 5), В(4, 9, 5)

=4

1.25А(8,6, 11),В(2, 4, -4)

=6

1.26 А(5, 9, 4),В(4,-10, 7)

=5

1.27 А(-9, 8, 9),В(7, 1,-2)

=4

1.28 А(9 2, 6), В(5, 8, -2)

=4

1.29 А(2, 8, -9),В(2, 5,-5)

=2

1.40 А(-1, 7, 0), В(8, 4, 5)

=5

 

 

2  Даны векторы , , :

а) найти модуль (длину) вектора ;

б) найти скалярное произведение векторов  и . Будут ли эти векторы ортогональны?

в) найти векторное произведение векторов  и ;

г) найти смешанное произведение векторов , , . Будут ли эти векторы   компланарны?

д) проверить, будут ли векторы   и  коллинеарны?

е) найти косинус угла между векторами  и ;

ж) найти проекцию вектора   на вектор .

 

Т а б л и ц а 2

2.1 =(7, -4, 1),=(2,3, 4), =(6,5, -1)

2.2 =(6, -4, -1),=(2, 1, 4),=(3, 8, -4)

 

2.4 =(-1, -4, 0),=(2, 4, 4),=(3,0, -2)

2.4 =(3, -5, 4),=(5, 1, 4),=(5, -4, -4)

 

2.5 =(1, -5, 0),=(3, 4, 6), =(0, 6, -2)

2.6 =(2, -7, 0), =(4, 5, 4), =(7, 8, 5)

 

2.7 =(4, -7, 1),=(9, 1, 4), =(8, 2, -4)

2.8 =(4, -6, 4),=(1, 1, 8), =(5, -4, 9)

 

2.9 =(-8, 5, 0), =(6, 4, 4),=(7, 2, -2)

2.10 =(5, -4, 1), =(7, 2, 4),=(5, 8, 4)

 

2.11 =(7, -5, 0), =(2, 9, 6),=(0, 6, 4)

2.12 =(9, -5, 4), =(5, 4, 4),=(5, 4, 4)

 

2.14 =(-1,5, 0),=(6, 2, 4), =(7, 2, -7)

2.14 =(8, -7, 0),=(8, 5, 4), =(7, 8, 7)

 

2.15 =(6,-5, 0),=(2, 8, 6), =(0, 6, 4)

2.16 =(-1, -5, 4), =(2, 1, 8), =(5, 9, 9)

2.17 =(2, 6, 8), =(7, 4, 4),=(4, 2, -2)

2.18 =(2, -7, 1), =(6, 1, 4), =(1, 8, 7)

2.19 =(4, -5, 0),=(2, 7, 6), =(7, 6, 4)

2.20 =(4, -5, 4), =(9, 1, 8), =(4, 9, 1)

2.21 =(2, 6, 7),=(1, 4, 4), =(4, 6, -2)

2.22 =(0, -7, 1), =(7, 8, 4), =(1, 8, 9)

2.24 =(3, -5, 0),=(2, 5, 6), =(7, 6, 8)

2.24 =(2, -5, 2), =(6, 1, 4), =(0, 9, 1)

2.25 =(4, -5, 0),=(4, 7, 6), =(8, 6, 4)

2.26 =(3, -5, 4), =(8, 1, 7), =(4, 5, 1)

2.27 =(9, 6, 8), =(7, 2, 4),=(5, 2, -1)

2.28 =(6, -7, 1), =(4, 2, 4), =(2, 4, 7)

2.29 =(5, -5, 6), =(8, 1, 6),=(6, 1, 4)

2.40 =(8, 6, 4), =(2, -4, 8), =(4, 9, 2)

3 Даны векторы  и , где , , . Найти:

а) скалярное произведение ;

б) ;

в) 

Т а б л и ц а 3

 

3.1

-4

5

2

8

2

5

-4

1/4

1

4

3.2

3

3

3

7

1

9

/4

-2

1/3

2

6

3.3

2

4

5

4

3

2

-3

1/5

4

3

3.4

1

6

4

5

8

1

-5

1/7

3

2

3.5

-1

2

9

7

7

5

-6

1/9

5

1

3.6

5

1

3

2

6

4

/3

-1

1/8

9

6

3.7

6

2

1

5

4

3

2/3

-2

1/3

7

1

3.8

7

3

5

1

2

7

/6

-3

1/6

1

4

3.9

1

4

7

3

2

1

5/4

-5

1/7

2

6

3.10

-2

1

6

5

1

4

9/4

-6

1/2

8

3

3.11

4

7

2

5

7

6

7/6

3

1/4

3

2

3.12

-3

9

1

9

5

9

/6

-4

1/3

5

1

3.13

6

2

4

8

4

2

/3

-2

1/5

3

6

3.14

2

3

5

7

3

1

/6

-3

1/7

4

7

3.15

4

1

8

6

2

3

/3

-5

1/9

6

1

3.16

-1

5

4

8

2

6

-4

1/4

1

4

3.17

2

3

3

7

1

9

/4

-2

1/3

2

6

3.18

9

4

5

4

3

2

-3

1/5

4

3

3.19

4

5

1

3

7

9

-5

1/7

7

2

3.20

5

2

8

7

3

5

-6

1/9

5

1

3.21

7

1

3

2

6

4

/3

-1

1/8

9

6

3.22

6

2

1

3

4

8

2/3

-2

1/3

7

1

3.23

2

3

5

1

2

7

/6

-3

1/6

1

4

3.24

3

4

7

3

2

1

5/4

-5

1/7

5

6

3.25

4

1

6

5

1

7

9/4

-6

1/2

8

3

3.26

1

7

2

5

7

6

7/6

3

1/4

3

2

3.27

-5

9

1

2

5

3

/6

-4

1/3

5

4

3.28

4

2

4

8

6

2

/3

-2

1/5

3

6

3.29

-1

3

5

7

3

1

/6

-3

1/7

2

7

3.30

2

1

8

5

2

3

/3

-5

1/9

3

1

 

 

4  Вычислить площадь параллелограмма, построенного на векторах  и , если даны разложения этих векторов по базису , длины векторов ,  угол   между векторами  -  .

Т а б л и ц а 4

4.1

3

5

4.16

4

1

4.2

4

2

4.17

1

3

 

продолжение таблицы 4

4.4

3

5

4.18

5

1

4.4 

5

3

4.19 

8

6

4.5 

2

7

4.20 

5

8

4.6 

6

1

4.21 

1

7

4.7

7

8

4.22 

3

6

4.8 

8

3

4.24 

7

9

4.9 

6

3

4.24 

3

8

4.10

5

2

4.25 

2

3

4.11

9

3

4.26 

4

7

4.12

1

8

4.27 

5

4

4.14

3

8

4.28  

6

8

4.14

2

5

4.29 

7

2

4.15

7

1

4.40  

5

1

 

 

5 Даны вершины А, В, С, D пирамиды:

а) найти площадь указанной грани;

б) найти площадь сечения, проходящего через середину указанного ребра и две вершины пирамиды;

 в) найти объём пирамиды;

г) найти высоту пирамиды, опущенной из вершины А на грань ВС D.

Т а б л и ц а 5

5.1 A(3, 1,7), B(-1,4,6), C(2,-1,7),

D(1, 2, 8); АСD; l=BC, A, D

5.2 A(3, -1, 7), B(5, 4, 1), C(9, 2, 8),

D(7, -4, 7); ABD; l=AD, B, C

5.4 A(2, 4, 5), B(1, 8, 7), C(8, 2, 0), D(3, 4, 10); ACD; l=BD, A, C

5.4 A(7, 2, 5), B(8, 0, 6), C(9, 6, 5),

D(1, 4, -1); BCD; l=CD, A, B

5.5 A(8, 2, 10), B(1, 2, 0), C(4, 5,7),  D(1, -4, 5); ACD; l=AB, C, D

5.6 A(6, 4, 5),  B(5, 4, -7), C(1, 2, 7),

D(3, 2, 0); ACD; l=AD, B, C

5.7 A(9, -6, 4), B(1, 5, 5), C(5, 6, 8), D(7, 10, 7); ABD; l=BD, A, C

5.8 A(7, -1, 4), B(6, 5, 8), C(4, 5,8),     D(5, 4, 1); ACD; l=BC, A, D

5.9A(1, 4, 5), B(4, -2, 1), C(4, 5, 6), D(0, 4, 2); BCD; l=BC, A, D

5.10 A(6, 1, 6), B(1, 4, 7), C(2, -5,8),      D(6, 4, 2); ABD; l=AB, C, D

5.11 A(8, 1, 4), B(-1, 6,1), C(2,1,6), D(5, 4, -1); ACD; l=BD, A, C

5.12 A(4,-1,2), B(-1,0,1), C(1,1,4),       D(9, 5, 8); BCD; l=AD, B, C

5.14 A(9, 4, 4), B(1,1,5), C(4,9, 5), D(5, 6, 7); ABD; l=BD, A, C

5.14 A(-1, 5,5), B(2, 7,1), C(5, 7, 8),     D(1, 9, 2); BCD; l=BC, A, D

5.15 A(8,-5, 4), B(4,-1,4),C(1, 5,1), D(4, 8, -1); ACD; l=AD, B, C

5.16 A(5,1, 1), B(4, 6,6), C(4,2,0),       D(4, 2, 6); ABD; l=BD, A, C

 

 

продолжение таблицы 5

5.17 A(3, 8, 2), B(2, 4,7),C(2, 4, 7), D(5, 4, 7); ACD; l=BC, A, D

5.18 A(3, 2, 5), B(0, 7,1), C(0, 4, 7),     D(2, 5, 0); BCD; l=BC, A, D

5.19 A(1,6,5), B(6,9,4), C(1,10,10), D(4, 5, 9); ABD; l=AB, C, D

5.20 A(8, 5,4), B(8, 7,4), C(5,10,4),      D(3, 7, 8); ACD; l=BD, A, C

5.21 A(4, 8, 2), B(5,2, 6), C(5,7,4), D(5, 10, 9); BCD; l=AD, B, C

5.22 A(1, 6,5), B(4, 9,5), C(4,6,11),     D(5, 9, 4); ABD; l=BD, A, C

5.24 A(1, 7,1), B(2,-1,5), C(1, 6,4), D(2, -9, 8); BCD; l=BC, A, D

5.24 A(1, 5,4), B(9,4,4), C(4, 5,7),

D(5, 9, 6); ACD; l=AD, B, C

5.25 A(8,4,10), B(7, 9,2), C(2,8, 4), D(1, 6, 9); ABD; l=BD, A, C

5.26 A(0, 4,7), B(-2,4,5), C(4,2,10),     D(3, 2, 7); ACD; l=BC, A, D

5.27 A(2,-2,7). B(4, 2, 1), C(2, 4,5), D(9, 4, 7); ABD; l=AC, B, D

5.28 A(9, 2,2), B(-5,7,7), C(5,-4,1),      D(5, 4, 7); ACD; l=BC, A, D

5.29 A(4,9, 6), B(2,68,2), C(9,8,9),

D(1, 10, 4); BCD; l=CD, A, B

5.40 A(8, 5,4), B(5, 8,4), C(1, 2,-1),       D(-3, 0, 2); ACD; l=AB, C, D

 

6 Сила F приложена к точке А. Вычислить:

а) работу силы F в случае, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку В;

б) модуль момента силы F относительно точки В.

Т а б л и ц а 6

6.1  F(6, -4, 7), A(5, 2, 4), B(4, 6, -5)

6.2  F(8, 5, 2), A(7, 2, 6), B(4, -1, -5)

6.3  F(3, -1, 6), A(1, 7,3), B(9,0, -2)

6.4  F(2, -2, 6), A(3, 0, 4), B(1, 2, -3)

6.5  F(5,2, 9), A(3, 1, 1), B(2, 6, 8)

6.6  F(5, -8, 1), A(1, 2, 1), B(2, 7, 1)

6.7  F(6, -8, 5), A(1, 2,3), B(3, 6, -5)

6.8  F(9, -4, 2), A(8, 2, 1), B(1, 5, 4)

6.9  F(6, -1, 6), A(4, 2, 8), B(1, 6, -5)

6.10  F(1, -4, 5), A(9, -1, 4), B(1, 6, 8)

6.11  F(6, 3, 2), A(3, 2, 6), B(7, 6, -5)

6.12  F(5,2 , 3), A(5, 3, 8), B(0, 1, -2)

6.13  F(6, -2, 1), A(8, 2, 5), B(6, 1, 2)

6.14  F(3, -1, 0), A(9, 5, 4), B(3, 2, 1)

6.15  F(6, -5, 4), A(9, 2, 1), B(1, 6, 3)

6.16  F(4, -5, 1), A(-1, 2, 4), B(6, 1, 3)

6.17  F(6, -8, 5), A(7, 2, 3), B(2, 6, 2)

6.18  F(8, 3, 5), A(0, 2, 4), B(7, 0, 2)

6.19  F(6, -1, 4), A(1, 2, 3), B(3, 6, 1)

6.20  F(5, -4, 8), A(7, 0, 4), B(8, 9, -4)

6.21  F(6, 4, 1), A(8, 2, 4), B(9, 6, 0)

6.22  F(1, -4, 7), A(3, -1, 4), B(5, 6, 0)

6.23  F(6, 7, 5), A(3, 2, 5), B(8, 6, -2)

6.24  F(2, -4, 7), A(9, 3, 4), B(2, 4, 7)

6.25  F(6, 0, 2), A(1, 2, 6), B(1, 6, -3)

6.26  F(3, -4, 7), A(1, 7, 4), B(8, 5, -1)

6.27  F(6, 2, 1), A(2, 9, 4), B(2, 6, -1)

6.28  F(7, -4, 7), A(8, 9, 4), B(1, 4, 3)

6.29  F(6, 3, 0), A(1, 2, 4), B(3, 6, -7)

6.30  F(8, -4, 7), A(-2, 5, 4), B(0, 2, -5)

 

         7 Доказать, что векторы a, b, c   образуют  базис, и найти координаты вектора в этом базисе.

 

Т а б л и ц а 7

7.1 a=(5,4,1), b=(-3,5, 2), c=(2,-1, 3),

d=(7,23, 4)

7.2 a=(2, -1,4), b=(-3, 0, -2), c=(4, 5, -3),

d=(0,11, -14)

 

продолжение таблицы 7

7.3 a=(-1,1,2), b=(-3,5, 2), c=(2,-1, 3),

d=(28,-19, -7)

7.4 a=(1,3,4), b=(-2,5,0), c=(3,-2, -4),

d=(13,-5, -4)

7.5 a=(1,-1,1), b=(-5,-3,1), c=(2,-1,0),

d=(-15,-10,5)

7.6 a=(3,1,2), b=(-7,-2, -4), c=(-4, 0, 3)

d=(16,6,15)

7.7 a=(-3,0,1), b=(2,7,-3), c=(-4,3,5),

d=(-16,33, 13)

7.8 a=(5,1,2), b=(-2, 1, -3), c=(4,-3,5),

d=(-45,15, -66)

7.9 a=(0,2,-3), b=(4,-3,-2), c=(-5,-4,0)

d=(-19,-5,-4)

7.10 a=(3, -1,2), b=(-2,3,1), c=(4,-5, -3),

d=(-3,2, -3)

7.11 a=(5,3,1), b=(-1,2,-3), c=(3,-4,2),

d=(-9,34,-20)

7.12 a=(3,1,-3), b=(-2,4,1), c=(1,-2,5),

d=(1,12, -20)

7.13 a=(6,1,-3), b=(-3,2,1), c=(-1,-3,4),

d=(15,6,-17)

7.14 a=(4, 2,3), b=(-3,1, -8), c=(2,-4, 5),

d=(-12,14, -31)

7.15 a=(-2,1,3), b=(3,-6,2),c=(-5,-3,-1),

d=(31,-6,22)

7.16 a=(1,3,6), b=(-3,4, -5),c=(1,-7,2), d=(8,47, 65)

7.17 a=(7,2,1), b=(5,1,-2), c=(-3,4, 5),

d=(26,11,1)

7.18 a=(3,5,4), b=(-2,7, -5), c=(6,-2, 1),

d=(6,-9, 22)

7.19 a=(5,3,2), b=(2,-5,1), c=(-7,4, -3),

d=(36,1,15)

7.20 a=(11,1,2), b=(-3,3,4), c=(-4,-2, 7),

d=(-5,11, -15)

7.21 a=(9,5,3), b=(-3,2,1), c=(4,-7, 4),

d=(-10,-13, 8)

7.22 a=(7, 2,1), b=(3,-5 ,6), c=(-4,3 , -4),

d=(-1,18, -16)

7.23 a=(1,2,3), b=(-5,3,-1), c=(-6,4, 5),

d=(-4,11,20)

7.24 a=(-2,5,1), b=(3,2,-7), c=(4, -3,2),

d=(-4,22, -13)

7.25 a=(3,1,2), b=(-4,3,-1), c=(2,3,4),

d=(14,14,0)

7.26 a=(3,-1,2), b=(-2,4,1), c=(4,-5, -1),

d=(-5,11, 1)

7.27 a=(4,5,1), b=(1,3,1), c=(-3,-6,7),

d=(19,33,0)

7.28 a=(1, -3,1), b=(-2,-4, 3), c=(0,-2,3),

d=(-8,-10, 13)

7.29 a=(5,7,-2), b=(-3,1,3), c=(1,-4, 6),

d=(14,9,-1)

7.30 a=(-1,4,3), b=(3,2, -4), c=(-2,-7,1),

d=(6,20, -3)

 

8 Твердое тело вращается с постоянной угловой скоростью  вокруг оси, проходящей через начало координат. Найти вектор  поля линейных скоростей точек этого поля

Т а б л и ц а  8

8.1     

8.2   

8.3     

8.4     

8.5   

8.6    

8.7          

8.8    

8.9    

8.10 

8.11   

8.12  

8.13     

8.14   

8.15  

 

продолжение таблицы 8

8.16  

8.17  

8.18   

8.19  

8.20 

8.21   

8.22  

8.23 

8.24   

8.25  

8.26  

8.27   

8.28  

8.29   

8.30 

 

9 Линия задана уравнением  в полярной системе координат. Требуется:

а)  построить линию по точкам, начиная с   до , придавая  значения через промежуток ;

б) найти уравнение данной линии в прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс с полярной осью.

Т а б л и ц а  9

9.1     

9.2   

9.3    

9.4     

9.5   

9.6    

9.7          

9.8    

9.9    

9.10       

9.11   

9.12  

9.13  

9.14   

9.15  

9.16  

9.17  

9.18   

9.19  

9.20 

9.21   

9.22  

9.23 

9.24   

9.25  

9.26  

9.27   

 

 

 

продолжение таблицы 8

9.28  

9.29  

9.30 

 

         1.4 Решение типового варианта

 

1 Даны точки А(6, -5, 3) и  В(4, 1, 2):

а) найти координаты векторов  и ;

б) найти длину вектора  (или расстояние между точками А и В);

в) найти середину отрезка АВ.

Решение:

а) координаты вектора  по координатам начала А() и конца

В() находят по формуле = (). Таким образом, = (4-6, 1-(-5), 2-3) = (-2, 6, -1); = (6-4, -5-1, 3-2) = (2, -6, 1) или

= - = - (-2, 6, -1) = (2, -6, 1);

б) длина (модуль) вектора  или расстояние между точками А и В обозначается  и находится по формуле

= .

Значит,  в нашем случае == ;

в) середина  С отрезка АВ имеет координаты С.

У нас С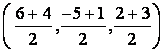= С( 5, -2, 5/2 ).

2  Даны векторы :

а) найти модуль (длину) вектора ;

б) найти скалярное произведение векторов  и . Будут ли эти векторы ортогональны?

 в) найти векторное произведение векторов  и ;

 г) найти смешанное произведение векторов , , . Будут ли эти векторы  компланарны?

д) проверить, будут ли векторы   и  коллинеарны?

е) найти косинус угла между векторами  и ;

ж) найти проекцию вектора   на вектор .

Решение:

для векторов  имеют место формулы:

а) модуль (длина) вектора : ;

б) скалярное произведение векторов  и : . Если векторы ортогональны, то ;

в) векторное произведение векторов  и

 ;

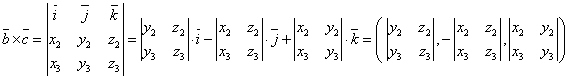г)  смешанное произведение векторов , , : 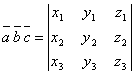, если эти векторы компланарны, то ;

д) если векторы  и  коллинеарны, то  или ;

е) косинус угла  между векторами  и

 ;

ж) проекция вектора   на вектор    .

По этим формулам в нашем варианте мы получим:

а) ;

б) , так как , то векторы  и  не ортогональны;

в) ;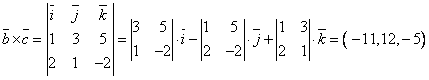

г) 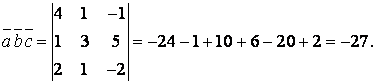 Так как , то векторы не компланарны;

д) для векторов  и :  и , следовательно векторы   и  не коллинеарны;

е) ;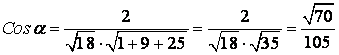

ж) .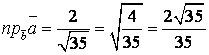

 

4 Вычислить площадь параллелограмма, построенного на векторах  и , если длины векторов равны , ,  угол   между векторами равен .

Решение:

по свойствам векторного произведения имеем: . Площадь параллелограмма, построенного на векторах  и  равна .

5 Даны вершины пирамиды А(5,1,0), В(7,2,-1), С(3,1,5), D(2,4,-1):

а) найти площадь указанной грани АВD;

б) найти площадь сечения, проходящего через середину указанного ребра ВD  и вершины А и С;

 в) найти объём пирамиды.

Решение:

сделаем схематический чертеж

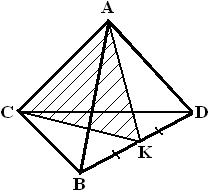
                                                          Рисунок 1

а) так как площадь треугольника, построенного на векторах  и , равна , то . Найдем координаты векторов

, =(-3,3,-1). .

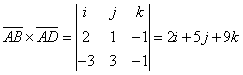 (кв.ед.);

           б) К(4,5;3;-1) – середина ВD. , . .

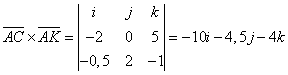 (кв.ед.);

           в) объем пирамиды, построенной на векторах , ,  равен . Поэтому .

.

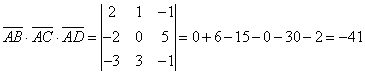           Таким образом   (куб.ед.).

6 Сила  (3,2,4)  приложена к точке А(2,-1,3). Вычислить:

а) работу силы F в случае, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку В(3,4,2);

           б) модуль момента силы  относительно точки В.

           Решение: а) так как , , то

, ;

           б) момент силы ,     ,

.

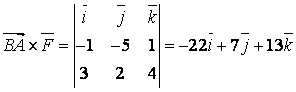Следовательно, .

           7 Доказать, что векторы =(4,2,1), =(1,-1,1), =(4,2,2) образуют базис, и найти координаты вектора =(19,11,8) в этом базисе.

Решение: вычисляем

 

Следовательно, векторы , ,  образуют базис, и вектор  линейно выражается через базисные векторы:  или в координатной форме   .

Решим полученную систему по формулам Крамера. Находим: ,

,      ,    ,

,   ,  .

 

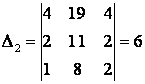Поэтому  =(1,-1,4)= – +4.

8 Твердое тело вращается с постоянной угловой скоростью  вокруг оси, проходящей через начало координат. Найти вектор  поля линейных скоростей точек этого тела.

Решение: Как известно, линейная скорость  равна векторному произведению  , где - вектор угловой скорости (т.е. вектор, отложенный на оси вращения и численно равный величине угловой скорости; этот вектор направлен так, что, если смотреть из его конца, вращение кажется происходящим против часовой стрелки). Пусть ось вращения тела принята за ось Oz, а - радиус-вектор точки М вращающегося тела относительно начала координат. Найдем вектор .

Имеем     .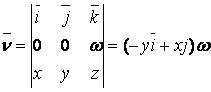

9 Линия задана уравнением 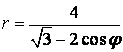 в полярной системе координат. Требуется:

а)  построить линию по точкам, начиная с   до , придавая  значения через промежуток ;

б) найти уравнение данной линии в прямоугольной системе координат, у которой ось абсцисс cовпадает с полярной осью.

Решение: а) так как  есть расстояние от точки до полюса, то нужно рассматривать те значения , при которых . Сделаем таблицу.

От 0 до

…

9,43

3,10

1,73

1,20

1,23

1,13

1,1

 

В силу четности  кривая будет симметрична относительно полярной оси (оси абсцисс). Построим полученные точки и соединяем их плавной кривой;

 

 

а) Заданное уравнение представляет собой уравнение кривых второго порядка с эксцентриситетом е=1 и с фокальным параметром р=1/2. Оно определяет параболу, у которой вершина совпадает с началом декартовой системы координат, а фокус F(1|4; 0)  служит полюсом в полярной системе координат.

б)  из чертежа

 

 

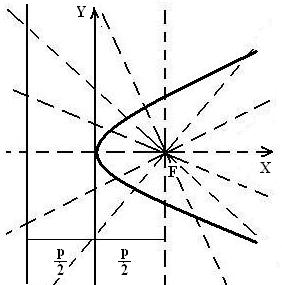
Рисунок 1

 

  .

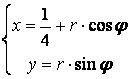
По условию:

,

,

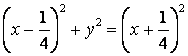 (парабола с ветвями, направленными вправо).

 

Список литературы 

       1. Апатенок Р.Ф., Маркина А.М. Сборник задач по линейной алгебре. - Мн.: Выш. Школа, 1980. – 192 с.

       2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: в 2 ч. – М.: Высшая школа, 2004. – ч. 1,2.-452 с.

       4. Сборник индивидуальных заданий по высшей математике: в 4 ч. (Рябушко А.П., Бархатов В.В. и др.). Под ред. Рябушко А.П. – Минск: Высш. школа, 2000.-ч.1.-496 с.

       4. Хасеинов К.А. Каноны математики: Учебник. – Алматы, 2004.-686 с.

 

Содержание 

1 Теоретические вопросы                                                                                     3

2 Расчётные задания                                                                                             3

4 Решение типового варианта                                                                            10

5 Список литературы                                                                                          15

                                                                                      

                                                          Сводный план 2011 г., поз.  225