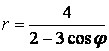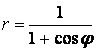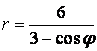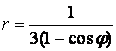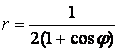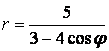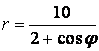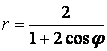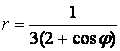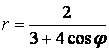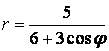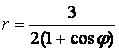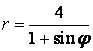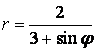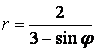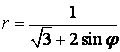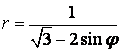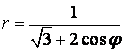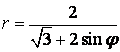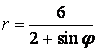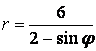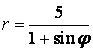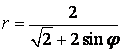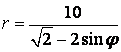Коммерциялық емес акционерлік қоғам
АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ
Жоғары математика кафедрасы
ГЕОМЕТРИЯ
5В060200 – Информатика мамандығы бойынша оқитын барлық
бөлім студенттері үшін есептеу-графикалық жұмыстарды
орындауға арналған әдістемелік нұсқаулар мен тапсырмалар
1 - бөлім
Алматы 2011
ҚҰРАСТЫРУШЫЛАР: М.Ж.Байсалова, Д.Т.Жанузакова. Геометрия. 5В060200 – Информатика мамандығы бойынша оқитын барлық бөлім стуенттері үшін есептеу-графикалық жұмыстарды орындауға арналған әдістемелік нұсқаулар мен тапсырмалар. 1- бөлім - Алматы: АЭжБУ, 2011. - 20 б.
«Информатика» мамандығы бойынша оқитын барлық бөлім студенттеріне арналған есептеу-графикалық жұмыстарды орындауға арналған әдістемелік нұсқаулар мен тапсырмалар. «Геометрия» пәнінің № 1 типтік есептеулерінен тұрады. Бағдарламаның теориялық сұрақтары енгізілген. Типтік нұсқаның шешімі келтірілген.
Кесте 9, әдеб. көрсеткіші 5 атау.
Пікір беруші: физ.-мат.ғыл. канд., доцент К.М.Мұстахишев.
“Алматы энергетика және байланыс университетінің” коммерциялық емес акционерлік қоғамының 2011 ж. баспа жоспары бойынша басылады.
ã “Алматы энергетика және байланыс университетінің ” КЕАҚ, 2011 ж.
1 Есептік-графикалық жұмыс 1. Векторлық алгебра
1.1 Теориялық сұрақтар
1 Векторлар, олардың ұзындығы, векторларға қолданылатын сызықты қисаптар.
4 Векторлардың сызықты тәуелділігі мен тәуелсіздігі. Векторлардың сызықты тәуелділігінің геометриялық мағынасы.
5 Векторлардың коллинеарлығы, компланарлығы, ортогоналдығы, векторлар арасындағы бұрыш.
6 Базис, векторлардың базиске қатысты координаталары. Базисті түрлендіру. Ауысу матрицасы. Вектордың проекциясы.
7 Векторлардың скаляр көбейтіндісі, олардың қолданылуы.
8 Векторлардың векторлық көбейтіндісі, олардың қолданылуы.
9 Векторлардың аралас көбейтіндісі, олардың қолданылуы.
10 Жалпы аффиндік және декарттық тікбұрышты координаталары. Алгебралық сызық пен беттің ұғымы.
11 Бір жүйеден екінші жүйеге көшкенде координаталардың түрлендіруі.
12 Ортогоналды матрицалар.
13 Полярлық, цилиндрлік және сфералық координаталар.
1.2 Есептік тапсырмалар
1 А және В нүктелері берілген:
а) 
және 
векторларының координаталарын табу
керек;
б) векторының ұзындығын
(немесе А және В нүктелерінің арасындағы ара
қашықтығын) табу керек;
в) АВ кесіндісін 
қатынасында бөлетін
М-ның координатасын табу керек
1 К е с т е
|
1.1 А(9, -1,7), В(4, 4,-6) , |
1.2 А(-4, 1, 0), В(5, 1, -4)
|
1.4 А(1, 4, 5), В(7, 4,-1)
|
|
1.4 А(6, -2, 5), В(1, 5, 7)
|
1.5 А(1, -3, 7), В(4, 2, 6)
|
1.6 А(2, -1, 7), В(6, 2, 4)
|
|
1.7 А(-9 1, 7), В(2, 8, 5)
|
1.8 А(7, 1, -2), В(1, 4, 8)
|
1.9 А(3, -4, 8), В(5, 4, 7)
|
|
1.10 А(5 2, 3, В(4,1, -4)
|
1.11А(5, 4, -1),В(-6, 1, 2)
|
1.12А(-4, 2, 4),В(8, 7, -2)
|
1 Кестенің соңы
|
1.14 А(3 4, 6), В(-1, 4, 5)
|
1.14 А(2, 6, 0), В(6, 4, -4)
|
1.15 А(5, 2, 0), В(1, -7, 8)
|
|
1.16 А(6 2, 5), В(-1,3, 6)
|
1.17 А(3,-1, 0), В(6,4, -1)
|
1.18А(6, 2, 2),В(-5, 7, -7)
|
|
1.19 А(1 -4,1), В(2,4, -2)
|
1.20А(5,-6, 4),В(10, 5, 0)
|
1.21 А(7, 5,-8), В(8, 12,7)
|
|
1.22 А(5 -1, 4), В(4, 5, 8)
|
1.24 А(2, 5,-7), В(2, 4, 1)
|
1.24 А(8, -6, 5), В(4, 9, 5)
|
|
1.25А(8,6, 11),В(2, 4, -4)
|
1.26 А(5, 9, 4),В(4,-10, 7)
|
1.27 А(-9, 8, 9),В(7, 1,-2)
|
|
1.28 А(9 2, 6), В(5, 8, -2)
|
1.29 А(2, 8, -9),В(2, 5,-5)
|
1.40 А(-1, 7, 0), В(8, 4, 5)
|
2 
, 
, 
векторлары берілген:
а) векторының модулін
(ұзындығын) табу керек;
б) және векторларының скаляр
көбейтіндісін табу керек. Бұл векторлар ортогональ бола ма?
в) және векторларының векторлық
көбейтіндісін табу керек;
г) , , векторларының аралас
көбейтіндісін табу керек. Бұл векторлар компланар бола ма?
д) және
векторлары коллинеар бола ма?
е) және векторларының арасындағы
бұрыштың косинусын табу керек;
ж) векторының векторына проекциясын табу
керек;
К е с т е 2
|
2.1 |
2.2 |
|
2.4 |
2.4 |
|
2.5 |
2.6 |
|
2.7 |
2.8 |
|
2.9 |
2.10 |
|
2.11 |
2.12 |
|
2.14 |
2.14 |
2 Кестенің соңы
|
2.15 |
2.16 |
|
2.17 |
2.18 |
|
2.19 |
2.20 |
|
2.21 |
2.22 |
|
2.24 |
2.24 |
|
2.25 |
2.26 |
|
2.27 |
2.28 |
|
2.29 |
2.40 |
3 
және 
векторлары берілген, мұндағы 
, 
, 
. Табу керек:
а) 
скаляр көбейтіндісін;
б) 
;
в) 
К е с т е 3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.1 |
-4 |
5 |
2 |
8 |
2 |
5 |
|
-4 |
1/4 |
1 |
4 |
|
3.2 |
3 |
3 |
3 |
7 |
1 |
9 |
|
-2 |
1/3 |
2 |
6 |
|
3.3 |
2 |
4 |
5 |
4 |
3 |
2 |
|
-3 |
1/5 |
4 |
3 |
|
3.4 |
1 |
6 |
4 |
5 |
8 |
1 |
|
-5 |
1/7 |
3 |
2 |
|
3.5 |
-1 |
2 |
9 |
7 |
7 |
5 |
|
-6 |
1/9 |
5 |
1 |
|
3.6 |
5 |
1 |
3 |
2 |
6 |
4 |
|
-1 |
1/8 |
9 |
6 |
|
3.7 |
6 |
2 |
1 |
5 |
4 |
3 |
2 |
-2 |
1/3 |
7 |
1 |
|
3.8 |
7 |
3 |
5 |
1 |
2 |
7 |
|
-3 |
1/6 |
1 |
4 |
|
3.9 |
1 |
4 |
7 |
3 |
2 |
1 |
5 |
-5 |
1/7 |
2 |
6 |
|
3.10 |
-2 |
1 |
6 |
5 |
1 |
4 |
9 |
-6 |
1/2 |
8 |
3 |
|
3.11 |
4 |
7 |
2 |
5 |
7 |
6 |
7 |
3 |
1/4 |
3 |
2 |
|
3.12 |
-3 |
9 |
1 |
9 |
5 |
9 |
|
-4 |
1/3 |
5 |
1 |
|
3.13 |
6 |
2 |
4 |
8 |
4 |
2 |
|
-2 |
1/5 |
3 |
6 |
|
3.14 |
2 |
3 |
5 |
7 |
3 |
1 |
|
-3 |
1/7 |
4 |
7 |
|
3.15 |
4 |
1 |
8 |
6 |
2 |
3 |
|
-5 |
1/9 |
6 |
1 |
|
3.16 |
-1 |
5 |
4 |
8 |
2 |
6 |
|
-4 |
1/4 |
1 |
4 |
|
3.17 |
2 |
3 |
3 |
7 |
1 |
9 |
|
-2 |
1/3 |
2 |
6 |
|
3.18 |
9 |
4 |
5 |
4 |
3 |
2 |
|
-3 |
1/5 |
4 |
3 |
|
3.19 |
4 |
5 |
1 |
3 |
7 |
9 |
|
-5 |
1/7 |
7 |
2 |
|
3.20 |
5 |
2 |
8 |
7 |
3 |
5 |
|
-6 |
1/9 |
5 |
1 |
|
3.21 |
7 |
1 |
3 |
2 |
6 |
4 |
|
-1 |
1/8 |
9 |
6 |
3 Кестенің соңы
|
3.22 |
6 |
2 |
1 |
3 |
4 |
8 |
2 |
-2 |
1/3 |
7 |
1 |
|
3.23 |
2 |
3 |
5 |
1 |
2 |
7 |
|
-3 |
1/6 |
1 |
4 |
|
3.24 |
3 |
4 |
7 |
3 |
2 |
1 |
5 |
-5 |
1/7 |
5 |
6 |
|
3.25 |
4 |
1 |
6 |
5 |
1 |
7 |
9 |
-6 |
1/2 |
8 |
3 |
|
3.26 |
1 |
7 |
2 |
5 |
7 |
6 |
7 |
3 |
1/4 |
3 |
2 |
|
3.27 |
-5 |
9 |
1 |
2 |
5 |
3 |
|
-4 |
1/3 |
5 |
4 |
|
3.28 |
4 |
2 |
4 |
8 |
6 |
2 |
|
-2 |
1/5 |
3 |
6 |
|
3.29 |
-1 |
3 |
5 |
7 |
3 |
1 |
|
-3 |
1/7 |
2 |
7 |
|
3.30 |
2 |
1 |
8 |
5 |
2 |
3 |
|
-5 |
1/9 |
3 |
1 |
4 
және 
векторларынан құрылған
параллелограммның ауданын табу керек. Бұл векторлардың
базисі
бойынша жіктелуі, 
векторларының
ұзындығы, векторларының арасындағы бұрыш
берілген.
К е с т е 4
|
|
|
|
|
|
|
|
|
|
|
|
|
4.1
|
|
3 |
5 |
|
4.16
|
|
4 |
1 |
|
|
|
4.2
|
|
4 |
2 |
|
4.17
|
|
1 |
3 |
|
|
|
4.4
|
|
3 |
5 |
|
4.18
|
|
5 |
1 |
|
|
|
4.4
|
|
5 |
3 |
|
4.19
|
|
8 |
6 |
|
|
|
4.5
|
|
2 |
7 |
|
4.20
|
|
5 |
8 |
|
|
|
4.6
|
|
6 |
1 |
|
4.21
|
|
1 |
7 |
|
|
|
4.7
|
|
7 |
8 |
|
4.22
|
|
3 |
6 |
|
|
|
4.8
|
|
8 |
3 |
|
4.24
|
|
7 |
9 |
|
|
|
4.9
|
|
6 |
3 |
|
4.24
|
|
3 |
8 |
|
|
|
4.10 |
|
5 |
2 |
|
4.25
|
|
2 |
3 |
|
|
|
4.11
|
|
9 |
3 |
|
4.26
|
|
4 |
7 |
|
|
|
4.12
|
|
1 |
8 |
|
4.27
|
|
5 |
4 |
|
|
|
4.14
|
|
3 |
8 |
|
4.28
|
|
6 |
8 |
|
|
|
4.14
|
|
2 |
5 |
|
4.29
|
|
7 |
2 |
|
|
4 Кестенің соңы
|
4.15
|
|
7 |
1 |
|
4.30
|
|
5 |
1 |
|
5 Пирамиданың А, В, С, D төбелерінің координаталары берілген:
а) берілген жақтың ауданын табу керек;
б) берілген қабырғаның ортасы мен пирамиданың екі төбесі арқылы өтетін қиманың ауданын табу керек;
в) пирамиданың көлемін табу керек;
г) ВС D жағына А төбесінен түсірілген пирамиданың биіктігін.
К е с т е 5
|
5.1 A(3, 1,7), B(-1,4,6), C(2,-1,7), D(1, 2, 8); АСD; l=BC, A, D |
5.2 A(3, -1, 7), B(5, 4, 1), C(9, 2, 8), D(7, -4, 7); ABD; l=AD, B, C |
|
5.4 A(2, 4, 5), B(1, 8, 7), C(8, 2, 0), D(3, 4, 10); ACD; l=BD, A, C |
5.4 A(7, 2, 5), B(8, 0, 6), C(9, 6, 5), D(1, 4, -1); BCD; l=CD, A, B |
|
5.5 A(8, 2, 10), B(1, 2, 0), C(4, 5,7), D(1, -4, 5); ACD; l=AB, C, D |
5.6 A(6, 4, 5), B(5, 4, -7), C(1, 2, 7), D(3, 2, 0); ACD; l=AD, B, C |
|
5.7 A(9, -6, 4), B(1, 5, 5), C(5, 6, 8), D(7, 10, 7); ABD; l=BD, A, C |
5.8 A(7, -1, 4), B(6, 5, 8), C(4, 5,8), D(5, 4, 1); ACD; l=BC, A, D |
|
5.9A(1, 4, 5), B(4, -2, 1), C(4, 5, 6), D(0, 4, 2); BCD; l=BC, A, D |
5.10 A(6, 1, 6), B(1, 4, 7), C(2, -5,8), D(6, 4, 2); ABD; l=AB, C, D |
|
5.11 A(8, 1, 4), B(-1, 6,1), C(2,1,6), D(5, 4, -1); ACD; l=BD, A, C |
5.12 A(4,-1,2), B(-1,0,1), C(1,1,4), D(9, 5, 8); BCD; l=AD, B, C |
|
5.14 A(9, 4, 4), B(1,1,5), C(4,9, 5), D(5, 6, 7); ABD; l=BD, A, C |
5.14 A(-1, 5,5), B(2, 7,1), C(5, 7, 8), D(1, 9, 2); BCD; l=BC, A, D |
|
5.15 A(8,-5, 4), B(4,-1,4),C(1, 5,1), D(4, 8, -1); ACD; l=AD, B, C |
5.16 A(5,1, 1), B(4, 6,6), C(4,2,0), D(4, 2, 6); ABD; l=BD, A, C |
|
5.17 A(3, 8, 2), B(2, 4,7),C(2, 4, 7), D(5, 4, 7); ACD; l=BC, A, D |
5.18 A(3, 2, 5), B(0, 7,1), C(0, 4, 7), D(2, 5, 0); BCD; l=BC, A, D |
|
5.19 A(1,6,5), B(6,9,4), C(1,10,10), D(4, 5, 9); ABD; l=AB, C, D |
5.20 A(8, 5,4), B(8, 7,4), C(5,10,4), D(3, 7, 8); ACD; l=BD, A, C |
|
5.21 A(4, 8, 2), B(5,2, 6), C(5,7,4), D(5, 10, 9); BCD; l=AD, B, C |
5.22 A(1, 6,5), B(4, 9,5), C(4,6,11), D(5, 9, 4); ABD; l=BD, A, C |
5 Кестенің соңы
|
5.24 A(1, 7,1), B(2,-1,5), C(1, 6,4), D(2, -9, 8); BCD; l=BC, A, D |
5.24 A(1, 5,4), B(9,4,4), C(4, 5,7), D(5, 9, 6); ACD; l=AD, B, C |
|
5.25 A(8,4,10), B(7, 9,2), C(2,8, 4), D(1, 6, 9); ABD; l=BD, A, C |
5.26 A(0, 4,7), B(-2,4,5), C(4,2,10), D(3, 2, 7); ACD; l=BC, A, D |
|
5.27 A(2,-2,7). B(4, 2, 1), C(2, 4,5), D(9, 4, 7); ABD; l=AC, B, D |
5.28 A(9, 2,2), B(-5,7,7), C(5,-4,1), D(5, 4, 7); ACD; l=BC, A, D |
|
5.29 A(4,9, 6), B(2,68,2), C(9,8,9), D(1, 10, 4); BCD; l=CD, A, B |
5.40 A(8, 5,4), B(5, 8,4), C(1, 2,-1), D(-3, 0, 2); ACD; l=AB, C, D |
6 F күші А нүктесіне қарай бекітілген.
а) F күшінің бекітілген нүктесі тік сызық бойымен В нүктесіне жылжығандағы жұмысын табу керек;
б) В нүктесіне қатысты F күш моментінің модулін табыңдар.
К е с т е 6
|
6.1 F(6, -4, 7), A(5, 2, 4), B(4, 6, -5) |
6.2 F(8, 5, 2), A(7, 2, 6), B(4, -1, -5) |
|
6.3 F(3, -1, 6), A(1, 7,3), B(9,0, -2) |
6.4 F(2, -2, 6), A(3, 0, 4), B(1, 2, -3) |
|
6.5 F(5,2, 9), A(3, 1, 1), B(2, 6, 8) |
6.6 F(5, -8, 1), A(1, 2, 1), B(2, 7, 1) |
|
6.7 F(6, -8, 5), A(1, 2,3), B(3, 6, -5) |
6.8 F(9, -4, 2), A(8, 2, 1), B(1, 5, 4) |
|
6.9 F(6, -1, 6), A(4, 2, 8), B(1, 6, -5) |
6.10 F(1, -4, 5), A(9, -1, 4), B(1, 6, 8) |
|
6.11 F(6, 3, 2), A(3, 2, 6), B(7, 6, -5) |
6.12 F(5,2 , 3), A(5, 3, 8), B(0, 1, -2) |
|
6.13 F(6, -2, 1), A(8, 2, 5), B(6, 1, 2) |
6.14 F(3, -1, 0), A(9, 5, 4), B(3, 2, 1) |
|
6.15 F(6, -5, 4), A(9, 2, 1), B(1, 6, 3) |
6.16 F(4, -5, 1), A(-1, 2, 4), B(6, 1, 3) |
|
6.17 F(6, -8, 5), A(7, 2, 3), B(2, 6, 2) |
6.18 F(8, 3, 5), A(0, 2, 4), B(7, 0, 2) |
|
6.19 F(6, -1, 4), A(1, 2, 3), B(3, 6, 1) |
6.20 F(5, -4, 8), A(7, 0, 4), B(8, 9, -4) |
|
6.21 F(6, 4, 1), A(8, 2, 4), B(9, 6, 0) |
6.22 F(1, -4, 7), A(3, -1, 4), B(5, 6, 0) |
|
6.23 F(6, 7, 5), A(3, 2, 5), B(8, 6, -2) |
6.24 F(2, -4, 7), A(9, 3, 4), B(2, 4, 7) |
|
6.25 F(6, 0, 2), A(1, 2, 6), B(1, 6, -3) |
6.26 F(3, -4, 7), A(1, 7, 4), B(8, 5, -1) |
|
6.27 F(6, 2, 1), A(2, 9, 4), B(2, 6, -1) |
6.28 F(7, -4, 7), A(8, 9, 4), B(1, 4, 3) |
|
6.29 F(6, 3, 0), A(1, 2, 4), B(3, 6, -7) |
6.30 F(8, -4, 7), A(-2, 5, 4), B(0, 2, -5) |
7 a, b, c векторларының базис құрайтындығын дәлелдеңдер және d векторының осы базистегі координатасын табыңдар.
К е с т е 7
|
7.1 a=(5,4,1), b=(-3,5, 2), c=(2,-1, 3), d=(7,23, 4) |
7.2 a=(2, -1,4), b=(-3, 0, -2), c=(4, 5, -3), d=(0,11, -14) |
|
7.3 a=(-1,1,2), b=(-3,5, 2), c=(2,-1, 3), d=(28,-19, -7) |
7.4 a=(1,3,4), b=(-2,5,0), c=(3,-2, -4), d=(13,-5, -4) |
7 Кестенің соңы
|
7.5 a=(1,-1,1), b=(-5,-3,1), c=(2,-1,0), d=(-15,-10,5) |
7.6 a=(3,1,2), b=(-7,-2, -4), c=(-4, 0, 3) d=(16,6,15) |
|
7.7 a=(-3,0,1), b=(2,7,-3), c=(-4,3,5), d=(-16,33, 13) |
7.8 a=(5,1,2), b=(-2, 1, -3), c=(4,-3,5), d=(-45,15, -66) |
|
7.9 a=(0,2,-3), b=(4,-3,-2), c=(-5,-4,0) d=(-19,-5,-4) |
7.10 a=(3, -1,2), b=(-2,3,1), c=(4,-5, -3), d=(-3,2, -3) |
|
7.11 a=(5,3,1), b=(-1,2,-3), c=(3,-4,2), d=(-9,34,-20) |
7.12 a=(3,1,-3), b=(-2,4,1), c=(1,-2,5), d=(1,12, -20) |
|
7.13 a=(6,1,-3), b=(-3,2,1), c=(-1,-3,4), d=(15,6,-17) |
7.14 a=(4, 2,3), b=(-3,1, -8), c=(2,-4, 5), d=(-12,14, -31) |
|
7.15 a=(-2,1,3), b=(3,-6,2),c=(-5,-3,-1), d=(31,-6,22) |
7.16 a=(1,3,6), b=(-3,4, -5),c=(1,-7,2), d=(8,47, 65) |
|
7.17 a=(7,2,1), b=(5,1,-2), c=(-3,4, 5), d=(26,11,1) |
7.18 a=(3,5,4), b=(-2,7, -5), c=(6,-2, 1), d=(6,-9, 22) |
|
7.19 a=(5,3,2), b=(2,-5,1), c=(-7,4, -3), d=(36,1,15) |
7.20 a=(11,1,2), b=(-3,3,4), c=(-4,-2, 7), d=(-5,11, -15) |
|
7.21 a=(9,5,3), b=(-3,2,1), c=(4,-7, 4), d=(-10,-13, 8) |
7.22 a=(7, 2,1), b=(3,-5 ,6), c=(-4,3 , -4), d=(-1,18, -16) |
|
7.23 a=(1,2,3), b=(-5,3,-1), c=(-6,4, 5), d=(-4,11,20) |
7.24 a=(-2,5,1), b=(3,2,-7), c=(4, -3,2), d=(-4,22, -13) |
|
7.25 a=(3,1,2), b=(-4,3,-1), c=(2,3,4), d=(14,14,0) |
7.26 a=(3,-1,2), b=(-2,4,1), c=(4,-5, -1), d=(-5,11, 1) |
|
7.27 a=(4,5,1), b=(1,3,1), c=(-3,-6,7), d=(19,33,0) |
7.28 a=(1, -3,1), b=(-2,-4, 3), c=(0,-2,3), d=(-8,-10, 13) |
|
7.29 a=(5,7,-2), b=(-3,1,3), c=(1,-4, 6), d=(14,9,-1) |
7.30 a=(-1,4,3), b=(3,2, -4), c=(-2,-7,1), d=(6,20, -3) |
8 Координаттар басынан өтетін тұрақты
бұрыштық
жылдамдықпен осьтің айналасымен қатты дене айналады. Осы
өрістегі сызықты жылдамдықтар нүктесінің
өрісіндегі 
векторын
табыңдар.
К е с т е 8
|
8.1
|
8.2
|
8.3
|
|
8.4
|
8.5
|
8.6
|
|
8.7
|
8.8
|
8.9
|
|
8.10
|
8.11
|
8.12
|
|
8.13
|
8.14
|
8.15
|
|
8.16
|
8.17
|
8.18
|
|
8.19
|
8.20
|
8.21
|
8 Кестенің соңы
|
8.22
|
8.23
|
8.24
|
|
8.25
|
8.26
|
8.27
|
|
8.28
|
8.29
|
8.30
|
9 Сызық 
теңдеуі арқылы полярлық координат
жүйесінде берілген. Табу керек:
а) 
аралығы арқылы 
бастап 
дейін 
-ге мән беріп, осы
нүктелер арқылы сызық тұрғызамыз;
б) тік бұрышты координат жүйесінде басы полюспен, ал абсциссаның оң жарты осі полярлық осьпен дәл келетіндей етіп берілген сызықтың теңдеуін табу керек.
К е с т е 9
|
9.1
|
9.2
|
9.3
|
|
9.4
|
9.5
|
9.6
|
|
9.7
|
9.8
|
9.9
|
|
9.10
|
9.11
|
9.12
|
|
9.13
|
9.14
|
9.15
|
|
9.16
|
9.17
|
9.18
|
|
9.19
|
9.20
|
9.21
|
|
9.22
|
9.23
|
9.24
|
|
9.25
|
9.26
|
9.27
|
|
9.28
|
9.29
|
9.30
|
1.4 Типтік нұсқаның шешуі
1 5 А(6, -5, 3) және В(4, 1, 2) нүктелері берілген:
а) және векторларының координаталарын табу
керек;
б) векторының ұзындығын
(немесе А және В нүктелерінің арасындағы ара
қашықтығын) табу керек;
в) АВ кесіндісінің ортасын табу керек.
Шешуі:
а) басы А(
) және ұшы В(
) нүктелері
болатын векторының
координаталары келесі формула бойынша табылады = (
). Сонымен, = (4-6, 1-(-5), 2-3) = (-2, 6, -1); = (6-4, -5-1, 3-2) = (2,
-6, 1) немесе =
- = - (-2, 6,
-1) = (2, -6, 1);
б) векторының ұзындығы
немесе А және В нүктелерінің арасындағы ара
қашықтығы 
деп белгіленеді және = 
формуласы бойынша есептелінеді.
Біздің жағдайда =
= 
;
в) АВ кесіндісінің ортасының координаталары
С
. Біздің есеп
үшін С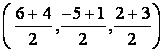
=
С( 5, -2, 5/2 ).
2 
векторлары берілген:
а) векторының модулін
(ұзындығын) табу керек;
б) және векторларының скаляр
көбейтіндісін табу керек. Бұл векторлар ортогональ бола ма?
в) және векторларының векторлық
көбейтіндісін табу керек;
г) , , векторларының аралас
көбейтіндісін табу керек. Бұл векторлар компланар бола ма?
д) және
векторлары коллинеар бола ма?
е) және векторларының арасындағы
бұрыштың косинусын табу керек;
ж) векторының векторына проекциясын табу
керек.
Шешуі:
векторлары үшін келесі формулалар
орын алады:
а) векторының модулі
(ұзындығы) 
;
б) және векторларының скаляр
көбейтіндісі: 
. Егер векторлар ортогональ болса, онда 
;
в) және векторларының векторлық
көбейтіндісін
;
г) , , векторларының аралас
көбейтіндісі 
. Егер бұл
векторлар компланар болса, онда 
;
д) егер векторлар және
коллинеарлы
болса, онда 
немесе
;
е) және векторларының арасындағы
бұрыштың косинусы
;
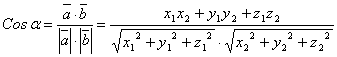ж) векторының векторына проекциясы:
.
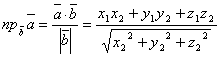Біздің вариантымыз үшін
а) 
;
б) 
, сонымен
болғандықтан, және векторлар ортогональ емес;
в)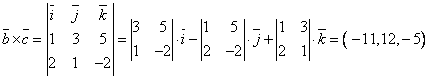 
;
г)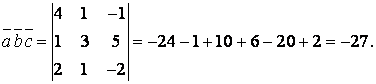 
Сонымен 
болғандықтан,
векторлар компланарлы емес;
д) және
векторлары үшін:
және
, олай болса
және
коллинеарлы
емес;
е)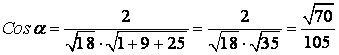 
;
ж)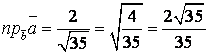 
.
4 
және 
векторларынан құралған параллелограммның ауданын табу керек. Бұл
векторлардың базисі бойынша жіктелуі, 
, 
,
векторларының ұзындығы,
векторларының арасындағы бұрыш 
берілген.
Шешуі: векторлық көбейтіндінің қасиеті бойынша
.
және
векторларынан
құрылған параллелограммның ауданы
.
5 Пирамиданың А(5,1,0), В(7,2,-1), С(3,1,5), D(2,4,-1) төбелерінің координаталары берілген:
а) берілген АВD жақтың ауданын табу керек;
б) берілген ВD қабырғаның ортасы мен пирамиданың А, С төбесі арқылы өтетін қиманың ауданын табу керек;
в) пирамиданың көлемін табу керек
Шешуі:
схемалық сүлбесін салайық
1 Сурет
а) және 
векторларында
тұрғызылған үшбұрыштың ауданы 
, онда 
. Векторлардың
координаталарын табайық
, 
=(-3,3,-1). 
.
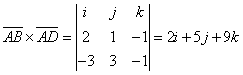(кв.ед.);
б)
К(1;1;-1,5) – ВD-ның ортасы.
, 
. 
.
(кв.ед.);
в)
, , векторларында
тұрғызылған пирамиданың көлемі 
. Сондықтан 
.
.
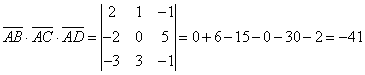Сонымен
(куб.бірлік).
6 
(3,2,4) күші
А(2,-1,3) нүктесіне қарай бекітілген.
а) F күшінің бекітілген нүктесі тік сызық бойымен В(3,4,2) нүктесіне жылжыған жағдайдағы жұмысын табу керек;
б)
В нүктесіне қатысты 
күш моментінің модулін
табыңдар
Шешуі:
а)
,
, болғандықтан,
онда
, 
;
б)
Күш моменті 
,
.
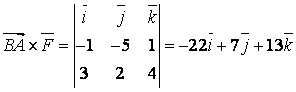Сондықтан,
.
7
=(4,2,1), 
=(1,-1,1), 
=(4,2,2) векторларының
базис кұрайтындығын дәлелдеңдер және 
=(19,11,8) векторынын
осы базисте координатасын
табыңдар.
Шешуі:
,
,
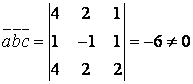
векторларынын
аралас көбейтіндісі нөлден өзгеше болгандықтан олар
базис құрайды. векторы
базистық векторы арқылы
сызықты түрде алынады немесе координталық түрде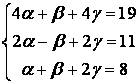
.
Алынған жүйені Крамер формуласы арқылы шығарамыз.
,
,
,
,
, 
,
.
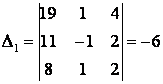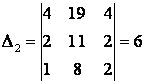Сондықтан
=(1,-1,4)=
–
+4.
8 Координаттар басынан өтетін
тұрақты бұрыштық жылдамдықпен осьтің
айналасымен қатты дене айналады. Осы өрістегі сызықты
жылдамдықтар нүктесінің өрісіндегі
векторын
табыңдар
Шешуі:
Сызықтық
жылдамдықтың 
векторлық көбейтіндісіне тең
екендігі белгілі. Мұнда - бұрыштық жылдамдық векторы. Ол
дененің айналу осі бойында орналасқан және оның
оң бағытынан қарағанда айналу сағат тілінің
жүрісіне қарсы бағытта орындалады. Енді айналу осін Oz осі ретінде
қабылдап, дененің кез келген M(x,y,z) нүктесінің
координаталардың бас нүктесіне қарағандағы радиус-вкторы
болатынын ескеріп, нүктенің сызықтық
жылдамдығын табайық:
.
9 Сызық теңдеуі арқылы полярлық координат
жүйесінде берілген. Табу керек:
а) аралығы арқылы
бастап
дейін
-ге
мән беріп, осы нүктелер арқылы сызық
тұрғызамыз;
б) тік бұрышты координат жүйесінде басы полюспен, ал абсциссаның оң жарты осі полярлық осьпен дәл келетіндей етіп берілген сызықтың теңдеуін табу керек.
Шешуі:
а)
нүктеден полюске дейінгі ара
қашықтық болғандықтан, -ң мәнін 
жағдайында
қарастыруымыз қажет.Таблица құраймыз:
|
|
|
|
|
|
|
|
|
|
|
|
6,57 |
1,7 |
0,81 |
0,5 |
0,36 |
0,29 |
0,26 |
0,25 |
жұптығына байланысты
қисық полярлық оське (абсцисса осіне) қатысты
симметриялы болады. Нүктелерді белгілеп, оларды қисықпен
біріктіреміз.
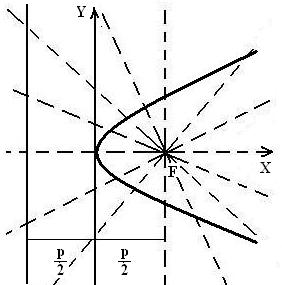
Сурет 1
а) Берілген теңдеу эксцентриситеті е=1 және фокалдық параметрі р=1/2 болатын екінші ретті қисықтықтың теңдеуі. Ол төбесі декарттық координаталар жүйесінің төбесімен беттесетін, ал фокусы F(1/4; 0) полярлық координаталар жүйесінде полюс болатын параболаны анықтайды.
б) сызбадан
.
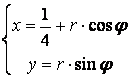
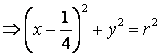Шарт бойынша:
,
,
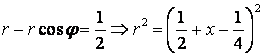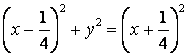(тармағы оңға
бағытталған парабола).
Әдебиеттер тізімі
1. Клетеник Д.В. Сборник задач по аналитической геометрии.-СПб., 2007. – 192 бет.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: 2 томдық. – М.: Высшая школа, 2004. – 1,2 том.-452 бет.
3. Сборник индивидуальных заданий по высшей математике: в 4 томдық. (Рябушко А.П., Бархатов В.В. және т.б.). Рябушко А.П.ред. бойынша – Минск: Высш. школа, 2000.-1 том.-496 бет.
4. Хасеинов К.А. Математика канондары: Оқулық. – Алматы, 2003.-686 бет.
5. Мустахишев К.М., Ералиев С. Атабай Б.Ж. Математика. (Толық курс) А.; «TST-company». 2009 ж., 410 бет
Мазмұны
1 Теориялық сұрақтар 3
2 Есептеу-графикалық жұмыстар 3
3 Типтік нұсқаның шығарылуы 10
4 Әдебиеттер тізімі 17
2011 ж. жинтық жоспары, реті 226