ГЕОМЕТРИЯ

Некоммерческое акционерное общество

АЛМАТИНСКИЙ  УНИВЕРСИТЕТ  ЭНЕРГЕТИКИИ СВЯЗИ

Кафедра высшей математики

 

 

ГЕОМЕТРИЯ

Методические указания к расчетно-графической работе и задания
для студентов специальности 5В060200 –Информатика 2-часть

 

Алматы 2013

 

СОСТАВИТЕЛИ: Толеуова Б.Ж., АбдуллановаЖ.С. Геометрия. Методические указания к расчетно-графической работе и задания для студентов специальности 5В060200 – Информатика. 2-часть - Алматы: АУЭС, 2013.- 17 стр.

 

Настоящие методические указания  к расчетно-графической работе для студентов специальности 5В060200 – Информатика составлены в соответствии с программой дисциплины «Геометрия» по разделу «Плоскости и прямые».

Содержатся варианты заданий, приведены необходимые теоретические сведения. Типовые задачи даются с подробными решениями.

Табл. 6, библиогр. – 5 назв.

Рецензент: канд.физ.-мат.наук, доцент Нурпеисов С.А.

 

Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2012 г.

 

 

НАО «Алматинский университет энергетики и связи», 2013г.

 

 Сводный план  2012 г., поз.182 

 

1 Расчетно-графической работа №2. Прямая на плоскости. Плоскость и прямая в пространтстве

 

Цель расчетно-графической работы №2: усвоение студентами материала из раздела «Прямая на плоскости. Плоскость и прямая в пространстве» из курса аналитической геометрии, содержащегося в работе. Привить умение использовать знания и навыки, которыми студент овладевает в процессе изучения раздела, в прикладных задачах математики. А также выявить отлично успевающих студентов с помощью более сложных заданий, приведенных в разделе «Задания второго уровня».

                   

2 Теоретические вопросы

 

1.         Различные виды уравнений прямой: общее уравнение, уравнение в отрезках, уравнение с угловым коэффициентом, каноническое уравнение, параметрическое уравнение.

2.         Взаимное расположение двух прямых: параллельность и перпендикулярность. Угол между прямыми.

3.         Расстояние от точки до прямой.

4.         Различные виды уравнений плоскости: общее уравнение, уравнение

в отрезках, уравнение плоскости, проходящей через заданную точку и перпендикулярной к заданному вектору, уравнение плоскости, проходящей через три точки.

5.         Взаимное расположение двух плоскостей: параллельность и перпендикулярность. Угол между плоскостями.

6.         Расстояние от точки до плоскости.

7.         Уравнение прямой в пространстве.

8.         Взаимное расположение двух прямых в пространстве: параллельность и перпендикулярность. Угол между прямыми.

9.         Взаимное расположение прямой и плоскости: угол между прямой и плоскости.

10.          Расстояние между прямыми.

 

3 Задания первого уровня

 

1-задание. Найти угловой коэффициент данной прямой  и отрезки, отсекаемые ею на осях координат

№

№

№

1.1

1.11

1.21

1.2

1.12

1.22

1.3

1.13

1.23

1.4

1.14

1.24

1.5

4

1.15

1.25

1.6

1.16

1.26

1.7

1.17

1.27

1.8

1.18

1.28

1.9

1.19

1.29

1.10

1.20

1.30

    

2-задание. Написать уравнение прямой c угловым коэффициентом  , проходящей через точку  

№

№

№

2.1

2

2.11

6

2.21

3

2.2

-3

2.12

-8

2.22

-9

2.3

4

22.13

2

2.23

8

2.4

8

2.14

0,25

2.24

2

2.5

0,5

2.15

-6

2.25

1,25

2.6

-4

2.16

1

2.26

-2.2

2.7

3

2.17

5

2.27

4

2.8

5

2.18

-7

2.28

6

2.9

-2

2.19

0,2

2.29

3,4

2.10

-1

2.20

5

2.30

5

 

3-задание. Написать уравнение прямой, проходящей через точки  и

№

№

3.1

3.16

3.2

3.17

3.3

3.18

3.4

3.19

3.5

3.20

3.6

3.21

3.7

3.22

3.8

3.23

3.9

3.24

3.10

3.25

3.11

3.26

3.12

3.27

3.13

3.28

3.14

3.29

3.15

3.30

 

4-задание. Даны вершины треугольника . Написать уравнение медианы  

№

№

4.1

4.16

4.2

4.17

4.3

4.18

4.4

4.19

4.5

4.20

4.6

4.21

4.7

4.22

4.8

4.23

4.9

4.24

4.10

4.25

4.11

4.26

4.12

4.27

4.13

4.28

4.14

4.29

4.15

4.30

 

5-задание. Найти уравнение высоты  треугольника  из задания 4.

 

6-задание. Написать уравнение прямой, проходящей через вершину  треугольника , параллельно стороне  из задания 4.

 

7-задание. Найти расстояние от точки  до прямой   из задания 4.

 

8-задание. Найти угол между прямыми  и  из задания 4.

 

9-задание. Даны точки , , . Составить уравнение плоскости  

№

№

9.1

9.16

9.2

9.17

9.3

9.18

9.4

9.19

9.5

9.20

9.6

9.21

9.7

9.22

9.8

9.23

9.9

9.24

9.10

9.25

9.11

9.26

9.12

9.27

9.13

9.28

9.14

9.29

9.15

9.30

 

10-задание. Составить уравнение прямой   из задания 9.

 

11-задание. Даны точки , ,  и . Найти расстояние от точки  до плоскости  

№

 

 

 

 

 

11.1

11.2

11.3

11.4

11.5

11.6

11.7

11.8

11.9

11.10

11.11

11.12

11.13

11.14

11.15

11.16

11.17

11.18

11.19

11.20

11.21

11.22

11.23

11.24

11.25

11.26

11.27

11.28

11.29

11.30

 

12-задание. Найти синус угла между прямой  и плоскостью  из задания 11.

 

13-задание. Найти косинус угла между прямыми    и     из задания 1

 

4 Задания второго уровня

 

14-задание. Решить следующие задачи.

14.1  Найти уравнение прямой, проходящей через точку пересечения прямых   и    и отсекающей на оси абсцисс отрезок, равный 3.

14.2  Найти проекцию точки   на прямую, проходящую через точки    и  .

14.3 Даны две вершины треугольника :   ,    и точка пересечения его высот. Найти вершину .

14.4 Найти уравнение прямой, проходящей параллельно прямой   и отсекающей на оси ординат отрезок, равный 2.

14.5 Найти уравнение прямой, проходящей через точку  и точку пересечения прямых       и    .

14.6 Доказать, что четырехугольник  – трапеция, если   , ,     и   .

14.7. Найти уравнение прямой, проходящей через точку перпендикулярно прямой , если  ,  .

14.8 Найти уравнение прямой, проходящей через точку параллельно прямой , если  ,  .

14.9 Найти точку, симметричную точке относительно прямой .

14.10 Найти точку  пересечения диагоналей четырехугольника , если   , ,     и   .

14.11 Через  точку пересечения прямых  , 2 провести прямую, параллельную оси абсцисс.

14.12  Известны уравнения стороны  треугольника   4, его высот    2  и     2. Найти уравнения двух других сторон треугольника .     

14.13  Даны две вершины треугольника   ,  и точка пересечения его высот . Найти координаты точки  пересечения стороны   и высоты .

14.14 Найти уравнения высот треугольника , проходящих через вершины  и , если   , ,  .

14.15 Вычислить координаты точки пересечения перпендикуляров, проведенных через середины сторон угольника, вершинами которого служат точки   , ,  .

14.16 Составить уравнение высоты, проведенной через вершину   треугольника , зная уравнения его сторон:    ,

  ,    .

14.17 Даны треугольник  вершинами  ,  и . Найти уравнение медианы, проведенной из вершины , и вычислить ее длину.

14.18 Составить уравнение прямой, проходящей через начало координат и точку пересечения прямых   и   2.

14.19 Найти уравнения перпендикуляров к прямой 3, проведенных через точки пересечения данной прямой с осями координат.

14.20 Даны стороны четырехугольника   ,    , ,  3. Найти уравнения его диагоналей.

14.21 Составить уравнения медианы  и высоты   треугольника , если   , ,     и   .

14.22 Через  точку  провести прямую: а) отсекающую равные отрезки на осях координат,  б) параллельную оси ординат.

14.23 Записать уравнение прямой, проходящей через точку и составляющей с осью  угол:  а) ,   б) ,  в) .

14.24 Какую ординату имеет точка , лежащая на одной прямой с точками    и   и имеющая абсциссу, равную 3.

14.25 Через точку пересечения прямых       и   провести прямую,  делящую отрезок между точками    и   в отношении   .

14.26 Известны уравнения двух сторон ромба  4, 2  и  уравнение одной из его диагоналей   . Найти уравнение второй диагонали.    

14.27 Найти точку   пересечения медиан треугольника, вершинами которого являются точки   ,  ,  .

14.28 Записать уравнения прямых, проходящих через точку под углом    к прямой .

 14.29 Даны уравнения высот треугольника   2,    и  координаты его вершины  . Найти уравнения сторон  и  треугольника .

14.30 Даны уравнения двух сторон параллелограмма   ,      и точка пересечения  его диагоналей. Найти уравнения двух других сторон.

 

15-задание. Решить следующие задачи.

15.1 Найти величины отрезков, отсекаемых на осях координат плоскостью, проходящей через точку  параллельно плоскости .

15.2 Составить уравнение плоскости, проходящей через середину отрезка    перпендикулярно к этому отрезку,  , .

15.3 Найти расстояние от точки     до плоскости . 

15.4 Составить уравнение плоскости, проходящей через   параллельно плоскости .

15.5  Составить уравнение плоскости, проходящей через ось   и точку .

15.6 Составить уравнение плоскости, проходящей через точки ,   параллельно оси .

15.7  Составить уравнение плоскости, проходящей через точку    и  прямую .

15.8 Составить уравнение плоскости, проходящей через две параллельные прямые         и       .

15.9 Составить общие уравнения прямой, образованной пересечением плоскости   с плоскостью, проходящей через ось   и точку .

15.10 Составить уравнение плоскости в отрезках, если она проходит через точку    и отсекает на оси  отрезок, равный , а на оси   – отрезок  .

15.11 Составить уравнение плоскости, проходящей через точку   параллельно двум векторам   и .

15.12 Составить уравнение плоскости, проходящей через точки ,  перпендикулярно к плоскости .  

15.13 Составить уравнение плоскости, проходящей через начало координат перпендикулярно к двум плоскостям    и .

15.14 Составить уравнение плоскости, проходящей через точки ,   параллельно вектору  .

15.15 Составить уравнение плоскости, проходящей через начало координатперпендикулярно к вектору  , если ,  .      

15.16 Найти величины отрезков, отсекаемых на осях координат плоскостью, проходящей через точку    параллельно плоскости .

15.17 Составить уравнение плоскости, проходящей через точку   перпендикулярно к отрезку ,  , .

15.18 Показать, что прямая    параллельна плоскости , а прямая , ,   лежит в этой плоскости.

15.19 Составить общее уравнение плоскости, проходящей через точку   параллельно координатной плоскости.

15.20 Составить уравнение плоскости, проходящей через ось  и точку  .

15.21 Составить уравнение плоскости, проходящей через точки   и   параллельно оси .

15.22 Составить уравнение плоскости, проходящей через точку   и прямую , , .

15.23 Найти проекцию точки  на плоскость .

15.24 Определить, при каком значении  плоскости  и    будут перпендикулярны.

15.25 Составить уравнение плоскости, проходящей через точку   и отсекает на осях координат отличные от нуля отрезки одинаковой величины.

15.26 При каких значениях   и    прямая     перпендикулярна к плоскости?

15.27. Составить уравнение плоскости, проходящей через точки ,   перпендикулярно к плоскости.

15.28. Составить уравнение плоскости, проходящей через начало координат перпендикулярно к плоскостям   и  .

15.29. Составить уравнение плоскости, проходящей через точки   и   параллельно вектору  .    

15.30. Определить, при каком значении   плоскости  и    будут перпендикулярны.

 

 

5    Методические указания к разделу «Прямая на плоскости. Плоскость и прямая в пространстве». Решение типового варианта

 

1. Найти угловой коэффициент прямой :  4 и отрезки, отсекаемые ею на осях координат.

Решение. Т.к. уравнение прямой с угловым коэффициентом имеет вид , то разрешив уравнение относительно , получаем:

,   где    .

Уравнение вида 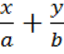          является уравнением прямой в отрезках.

Перенесем свободный член общего уравнения в правую часть и разделим обе части на  -15; имеем  -. Переписав последнее уравнение в виде

,

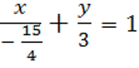получим уравнение данной прямой в отрезках.

2. Написать уравнение прямой c угловым коэффициентом  , проходящей через точку .

  Решение. Воспользуемся уравнением прямой , проходящей через точку    с угловым коэффициентом  :

  Þ    Þ  .

3.    Написать уравнение прямой, проходящей через точки     и  .

  Решение. Уравнение прямой, проходящей через точку   и   записывается в виде

 

 

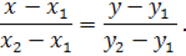
  Полагая  ,    ,  ,   в данном уравнении, получаем

или 

 

 

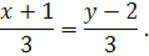
Итак, искомое уравнение имеет вид    .

 

          Даны вершины треугольника : , , . Написать уравнение медианы . 

          Решение. Т.к. медиана  делит сторону  на две равные части, то сначала найдем по формулам     ,       координаты середины отрезка :

,     .

 

Теперь по известным точкам   и   составляем уравнение медианы:

 

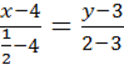    или     .

 

Отсюда получаем искомое уравнение  2.

          1. Даны вершины треугольника : , , . Написать уравнение высоты  треугольника .

Решение. Воспользовавшись уравнением прямой, проходящей через две точки, получим уравнение стороны  с угловым коэффициентом:

 

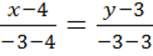   или 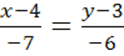  ,  т.е.   ,   где    .

 

 Известно, что высота  треугольника  перпендикулярна стороне . С учетом условия  перпендикулярности (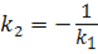)  двух прямых  и  угловой коэффициент высоты   . По точке  и угловому  коэффициенту    составляем уравнение высоты : 

  или    7.

 

2.      Даны вершины треугольника : , , . Написать уравнение прямой, проходящей через вершину  треугольника , параллельно стороне .

Решение. Прямая, проходящая через вершину , параллельна стороне . Зная угловой коэффициент   стороны  и используя условие параллельности двух прямых (), получим угловой коэффициент для этой прямой: .  Тогда уравнение прямой, проходящей через вершину , параллельно стороне  имеет вид:

 

  или  6.

 

3.              Найти расстояние от точки  до прямой  4.

Решение. Расстояние от точки  до прямой  A вычисляется по формуле

 

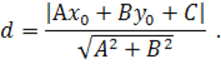
Тогда по этой формуле найдем искомое расстояние:

 

                      

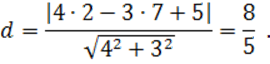
4. Найти угол между прямыми       и    .

Решение. Острый угол между прямыми определяется по формуле

 

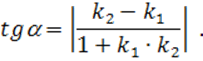
  Определим угловые коэффициенты этих прямых:

 ,       ,     ,   .

  Тогда подставляя найденные значения в формулу, получим

 

          5. Даны точки , , . Составить уравнение плоскости   

Решение. Уравнение плоскости, проходящей через три заданные точки , ,  можно записать в координатной форме:

 

 

 

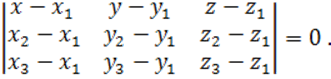
Подставляя координаты точек в формулу, получим:

 

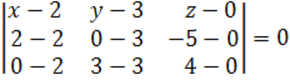     или      

 

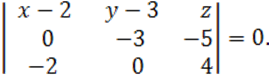
Отсюда получим     .

 

6.      Даны точки   и  . Написать уравнение прямой в пространстве, проходящей через точки   и  .

Решение. Учитывая уравнение прямой, проходящей через две точки

 

 

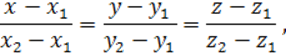
уравнение прямой    можно записать в виде

 

 

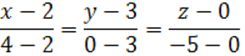
или

 

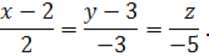
7.      Даны точки , ,  и . Найти расстояние от точки  до плоскости  

Решение. Как известно из задания 9, уравнение плоскости, проходящей через три заданные точки :

 

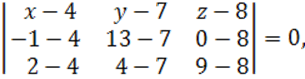    или  

 

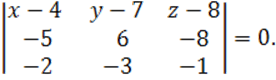
Отсюда получим  уравнение плоскости  :   

 

.

 

Расстояние    от точки     до плоскости, заданной уравнением  , вычисляется по формуле

 

 

Таким образом, имеем

 

 

8.      Даны точки , ,  и . Найти синус угла между прямой  и плоскостью .

Решение. Как известно из задания 11, уравнение плоскости  имеет вид

Составим уравнение прямой :

 

 

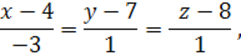
откуда видно, что ее направляющий вектор   .

Величина угла j  между прямой

 

 

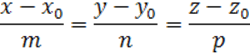
 и плоскостью    вычисляется по формуле

 

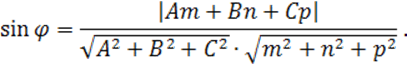
Подставляя данные в последнюю формулу, имеем

 

 

9.      Даны точки , , . Найти косинус угла между прямыми    и   .

Решение. Если прямые заданы каноническими уравнениями:

 

 

то величина угла j  между ними определяется из формулы

 

 

Напишем канонические уравнения прямых  ,   : 

 

 

 

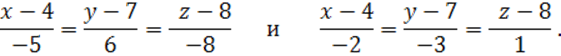
Подставляя данные в последнюю формулу, получим: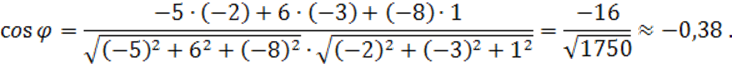

 

 

Список литературы

 

1.    Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1980.

2.    Бугров Я.С., Никольский С.М. Элементы  линейной алгебры и аналитической геометрии. – М.: Наука, 1980.

3.    Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 3 ч. Ч.1– М.: Высш. школа, 1986.

4.    Апатенок Р.Ф., Маркина А.М., Попова Н.В., Хейнман В.Б. Сборник задач по линейной алгебре. – Мн.: Выш. школа, 1980.

5.    Ильин В.А., Позняк В.Г. Линейная алгебра. – М.: Наука, 1974.

 

 

Содержание

 

Теоретические вопросы

3

Задания первого уровня

3

Задания второго уровня

7

Методические указания к разделу «Прямая на плоскости. Плоскость и прямая в пространстве». Решение типового варианта

11

Список литературы

17