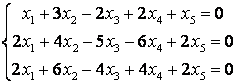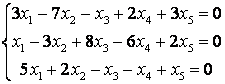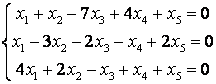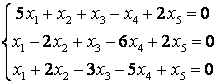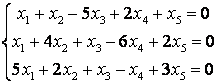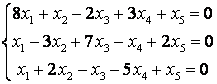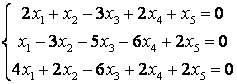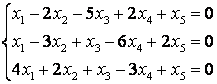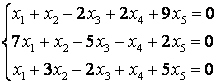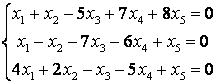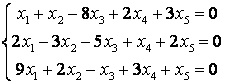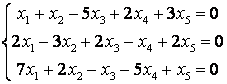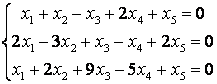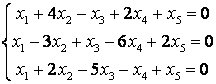Некоммерческое акционерное общество

АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра высшей математики

 

 

 

АЛГЕБРА

Методические указания и задания

к выполнению расчетно-графических работ

(для студентов очной формы обучения специальности

5В060200 – Информатика)

Часть 1

 

 

 

Алматы 2011 

          СОСТАВИТЕЛИ:  Т.Каирбеков,  Л.Н.Астраханцева,  М.Ж.Байсалова. лгебра. Методические указания и задания к  выполнению расчетно-графической  работы  для  студентов  очной  формы обучения  специальности 5В060200 – Информатика. -Алматы:  АУЭС, 2011.- 18 с.

 

Методические указания и задания к расчетно-графической работе содержат типовой расчет №1 дисциплины «Алгебра» для студентов очной формы обучения специальности 5В060200 – Информатика. Приведены основные теоретические вопросы программы. Дано решение типового варианта.

          Табл. 9, библиогр. – 4 назв.

 

Рецензент: канд.физ.-мат.наук, доцент Р.Е.Ким

 

Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2011 г.

 

 ã НАО «Алматинский университет энергетики и связи», 2011 г.

 

1 Типовой  расчёт 1. Элементы линейной алгебры

 

1.1 Теоретические вопросы

 

1  Определители, их свойства, вычисление.

2 Матрицы, действия над ними, обратная матрица.

3 Ранг матрицы и его вычисление.

          4 Системы линейных уравнений. Правило Крамера. Матричный метод  

решения систем.

         5 Метод Гаусса решения неоднородных систем линейных уравнений.

         6 Решение однородных систем линейных уравнений. Фундаментальная  система решений.

 

1.2 Расчётные  задания

 

1 Вычислить определитель второго порядка

Т а б л и ц а 1

1.1

1.2

1.3

1.4

1.5

1.6

1.7

1.8

1.9

1.10 

1.11

1.12

1.13

1.14

1.15  

1.16

1.17

1.18

1.19 

1.20 

1.21

1.22

1.23

1.24

1.25

1.26

1.27  

1.28

1.29

1.30

 

2  Дан определитель третьего порядка:

а) найти минор M и алгебраическое дополнение A элемента a;

б) разложить определитель по i-ой строке;

в) вычислить определитель, разложив его по j-му столбцу;

г) вычислить по правилу треугольника (правилу Саррюса). 

 

Т а б л и ц а 2

2.1

2.2 

2.3

2.4

2.5

2.6

2.7

2.8

2.9

2.10

2.11

2.12

2.13

2.14

2.15

2.16

2.17

2.18

2.19 

2.20

2.21

2.22 

2.23

2.24

2.25

2.26

2.27 

 

продолжение таблицы 2

2.28

2.29

2.30

  

3 Даны матрицы  А, В, С, Д:

а) найти матрицы 3С+2Д, С-4Д;

б) найти матрицу  В, транспонированную матрице В.

Т а б л и ц а 3

3.1     ,  .

3.2        

3.3    ,    .

3.4        .

3.5

  .

3.6

        .

 

продолжение таблицы 3

3.7 

       

3.8

       .

3.9 

      

3.10  ,    .

3.11   

3.12        

3.13

      

3.14  

      

3.15 

              

продолжение таблицы 3

3.16

            , 

3.17

             

3.18

              

3.19

             

3.20 

              

3.21 

               

3.22

               

  

продолжение таблицы 3

3.23

     

3.24

              

3.25

                      

3.26

                     

3.27

                     

3.28

                         

3.29 

         

 

продолжение таблицы 3

3.30       

  

4  Даны матрицы  А, В, С   (в задании 3):

а) возможно ли произведение матриц АВ, ВС ? Объяснить почему, если невозможно; найти произведение, если возможно;

б) найти матрицу , обратную матрице  А.

 

5 Вычислить определитель четвёртого порядка

 

Т а б л и ц а 4

4.1

 

4.2

 

4.3

4.4

 

4.5

4.6

4.7

 

4.8

 

4.9

4.10

 

4.11

4.12

 

4.13

4.14

4.15

4.16

 

  

продолжение таблицы 4

4.17

4.18

4.19

4.20

4.21

4.22

4.23

 

4.24

 

4.25

4.26

 

4.27

4.28

 

4.29

 

4.30

4.31

4.32

 

  

6 Вычислить ранг матрицы двумя способами:

а) методом окаймляющих миноров;

б) методом  элементарных преобразований.

Указать базисный минор.

Т а б л и ц а  5

5.1

5.2

 

5.3

 

  

продолжение таблицы 5

5.4 

5.5

 

5.6

 

5.7

 

5.8 

5.9 

5.10

 

5.11

5.12

5.13

  

5.14

5.14

 

5.16

5.17

5.18

5.19

5.20

 

5.21

 

  

продолжение таблицы 5

5.22

 

5.23

 

5.24

 

5.25

 

5.26

 

5.27

5.28

5.29

5.30

 

          7 Решить систему:

          а) по правилу Крамера;

          б) матричным методом (с помощью обратной матрицы).

Т а б л и ц а  6

6.1

6.2

6.3

6.4

6.5

6.6

6.7

6.8

6.9

6.10

6.11

6.12

6.13

6.14

6.15

6.16

6.17

6.18

продолжение таблицы 6

6.19

6.20

6.21

6.22

6.23

6.24

6.25

6.26

6.26

6.28

6.29

6.30

6.31

6.32

 

 8  Проверить совместность систем уравнений; определить количество решений; в случае совместности решить методом Гаусса

 

Т а б л и ц а  7

7.1

7.2

7.3

  

продолжение таблицы 7

7.3

7.4

7.5

7.6

 

7.7

7.8

7.9

 

 

7.10

7.11

7.12

продолжение таблицы 7

7.11

7.12    

7.13

7.14

 

7.15

7.16

7.17

7.18

  продолжение таблицы 7

7.19

7.20

7.21

7.22

7.23

7.24

 

7.25

7.26

  продолжение таблицы 7

7.25

7.26

7.27

7.28

 

7.27

7.28

7.29

7.30

 

9  Решить однородную систему линейных уравнений

 

  Т а б л и ц а  8

8.1 а) ,                                    

8.2 a),                                  

8.3 a)  ,                                    

продолжение таблицы 8

8.4 a)  ,                                  

8.5 a) ,                                

8.6  a) ,                                 

8.7  a) ,                                   

8.8  a) ,                                 

8.9  a) ,                                   

8.10 a) ,                                 

8.11 a) ,                                   

8.12 a) ,                                 

8.13 a) ,                                

8.14 a)  ,                               

8.15 a)  ,                               

8.16 a) ,                                 

8.17 a)  ,                                

8.18 a)  ,                                

8.19 a)  ,                                   

продолжение таблицы 8

8.20 a) ,                                

8.21 a) ,                                   

8.22 a) ,                                   

8.23 a) ,                                     

8.28 a) ,                                   

8.29 a) ,                                     

8.30 a) ,                                   

 

10 Решить однородную систему линейных уравнений. Найти нормированную фундаментальную систему решений

 

Т а б л и ц а  9

9.1

9.2

9.3

9.4

9.5

9.6

9.7

9.8

  

 продолжение таблицы 9

9.9

9.10

9.11

9.12

9.13

9.14

9.15

9.16

9.17

9.18

9.19

9.20

9.21

9.22

9.23

9.24

9.25

9.26

9.27

9.28

  

продолжение таблицы 9

9.29

9.30

 

1.3 Решение типового варианта

1        Вычислить определитель второго порядка .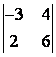

Решение:

по формуле  имеем .

2  Дан определитель третьего порядка  , i=2, j=3:

а) найти минор M и алгебраическое дополнение  элемента a;

б) разложить определитель по i-ой строке;

в) вычислить определитель, разложив его по j-му столбцу;

г) вычислить по правилу треугольника (правилу Саррюса).

Решение: 

a) минор Mэлемента aравен определителю, полученному из данного после вычёркивания i-ой строки и j-го столбца. Таким образом, вычёркиваем в нашем определителе вторую строку и третий столбец, получаем  . Алгебраическое дополнение элемента aвычисляем по формуле  A=(-1)M. Значит ;

б)  формула разложения определителя по i-ой строке для определителя n - го порядка имеет вид 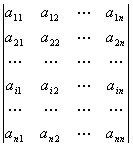= ,где A алгебраическое дополнение элемента a. Так как i = 2, j = 3, то формула перепишется так 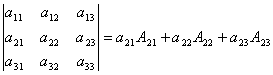. Искомое разложение имеет вид  ;

в) j = 3. Формула разложения по третьему столбцу имеет вид 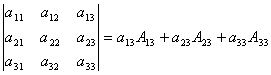. Таким образом,

;

г) правило треугольника: определитель третьего порядка равен сумме шести членов; члены со знаком плюс получают при перемножении по три элемента определителя, взятых по схеме 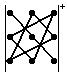, члены со знаком минус – по схеме. Поэтому

 

 

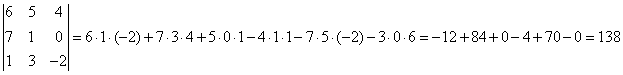
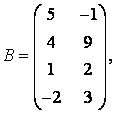
3-4. Даны матрицы  , , ,: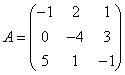     

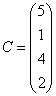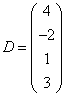а) найти матрицы , ;

б) найти матрицу  В, транспонированную матрице В;

в) возможно ли произведение матриц АВ, ВС ? Объяснить почему, если невозможно; найти произведение, если возможно;

г) найти матрицу А, обратную для матрицы А.

Решение:

а)  .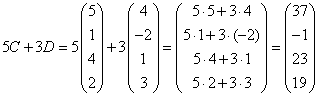

;

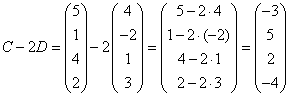б)  матрица, транспонированная матрице В, получается заменой строк матрицы В её столбцами с теми же номерами:  ;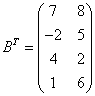

в)  произведение матриц АВ возможно, если число столбцов матрицы А равно числу строк матрицы В. Размеры матриц: А, В, С, Д. Таким образом,  АВ=  – произведение невозможно.    ВС=  – произведение возможно.

Произведением матриц АВ является матрица С, число строк которой равно числу строк матрицы А, число столбцов равно числу столбцов матрицы В: . Элемент матрицы С равен сумме произведений i–ой строки матрицы А на j–ый столбец матрицы В. Таким образом, .         .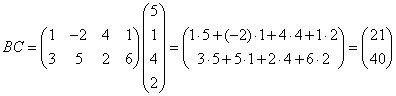

Итак, ;

г) обратная матрица для квадратной матрицы существует, если определитель матрицы не равен нулю; не существует, если – равен нулю. Обратная матрица А для матрицы

А =  находится по формуле 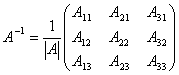 где  – определитель матрицы А;  – алгебраические дополнения элементов . Найдём определитель матрицы А: 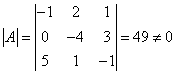, следовательно А существует. Определим алгебраические дополнения всех элементов матрицы А

,         ,        ,

,        ,  ,

,         ,      .

Составим А по вышеуказанной формуле

 

 

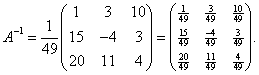
5 Вычислить определитель четвёртого порядка .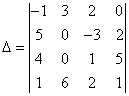

Решение:

используя свойства определителей получим в одной из его строк  или столбцов нули. Выберем второй столбец, где уже есть два нуля: умножим первую строку на (-2) и прибавим к последней, получим 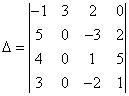 . Теперь разложим определитель по второму столбцу

.

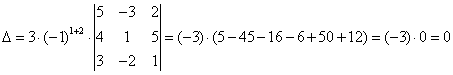6 Вычислить ранг матрицы 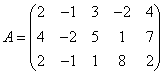 двумя способами:

а) методом окаймляющих миноров;

б) элементарных преобразований.

Указать базисный минор.

Решение:

а) начнем с левого верхнего угла. Минор второго порядка , поэтому возьмем другой . Рассмотрим миноры, окаймляющие ,  (т.е. содержащие в себе ):

.

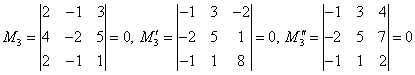Так как все окаймляющие миноры третьего порядка равны нулю, то ранг матрицы равен 2 (, ранг – наибольший порядок не равного нулю минора). Базисный минор ;

б) с помощью элементарных преобразований будем приводить матрицу к ступенчатому виду

~~.

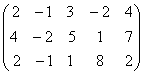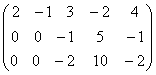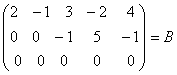На первом шаге первая строка была умножена на (-2) и прибавлена ко второй, затем умножена на (-1) и прибавлена к третьей, получены нули в первом столбце ниже первой строки. На втором шаге вторую строку умножили на (-2) и прибавили к третьей. Получена ступенчатая матрица . В ней две ненулевые строки или существует минор второго порядка, например, . Поэтому . Так как матрицы  и  эквивалентны, то их ранги равны . За базисный минор можно взять .

7 Решить систему 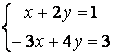 а) по правилу Крамера; б) матричным методом (т.е. с помощью обратной матрицы).

         Решение:

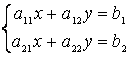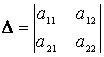         а) решение системы  по правилу Крамера имеет вид , где - определитель системы, 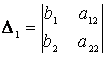, 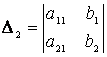- вспомогательные определители, полученные из определителя системы заменой первого и второго столбцов столбцом свободных членов.

         В нашем случае 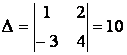, , 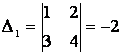. Таким образом, х = -1/5, у =3/5. Ответ можно записать в виде вектора:

(-1/5; 3/5);

         б)  в матричном виде решение системы 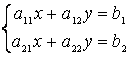записывается так:,  где   - матрица–столбец неизвестных, - матрица-столбец свободных членов,  – матрица, обратная для матрицы системы .

Найдём обратную матрицу для матрицы 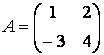системы . Так как определитель системы , то обратная матрица существует и  равна 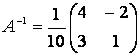. Тогда 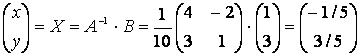. Ответ в обычном виде: .

         8   Проверить совместность систем; определить количество решений; в случае совместности решить методом Гаусса.

         а), b) , c)

Решение:

         а) по теореме Кронекера-Капелли система совместна (т.е. имеет хотя бы одно решение), если ранг матрицы системы равен рангу расширенной матрицы ; система не совместна (т.е. не имеет решений), если . Матрица системы 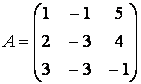, расширенная матрица – .

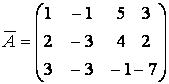         Определим ранги матриц методом элементарных преобразований. Так как матрица  содержится в матрице , то достаточно производить элементарные преобразования только над строками матрицы : умножим первую строку на -2 и прибавим ко второй,  затем умножим первую строку на -3 и прибавим к третьей. Получим, что матрица, а вместе с ней и матрица, приводится к ступенчатой матрице, имеющей три ненулевые строки: .

Значит,   и система совместна. Так как число неизвестных n равно 3 и равно рангу (n=r), то система имеет одно решение.

         Метод Гаусса заключается в последовательном исключении неизвестных из уравнений системы с помощью элементарных преобразований и приведении её к ступенчатому виду. Так как элементарные преобразования систем аналогичны элементарным преобразованиям матриц, то на практике заменяют первые вторыми, проводимыми над строками расширенной матрицы системы. Выше эти преобразования были проделаны. Таким образом, данная система сводится к системе, соответствующей последней матрице: .

Поднимаясь по этой системе снизу вверх, найдём из последнего уравнения ; из предпоследнего ; из первого . Ответ: (-4; -2; 1);

       б) выпишем расширенную матрицу системы и найдём ранги матриц и :

.

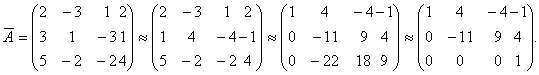Проделаны следующие преобразования: сначала первая строка умножена на -1, прибавлена ко второй, и они переставлены местами, затем первая строка умножена на-2, прибавлена ко второй и умножена на -5 и прибавлена к третьей, и, наконец, вторая строка умножена на -2 и прибавлена к третьей. Матрица  приведена к ступенчатой матрице с тремя ненулевыми строками, поэтому её ранг равен 3 (). Матрица  одновременно приведена к матрице , у которой две ненулевые строки, поэтому её ранг равен 2  (). Итак,  и система несовместна;

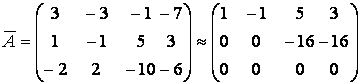     в) выпишем расширенную матрицу системы и найдём ранги матриц   и : . Так как  , то система совместна. Так как число неизвестных n=3 и , то система имеет бесчисленное множество решений. Выберем базисный минор . В базисный минор вошли коэффициенты при неизвестных , поэтому эти неизвестные будут базисными, а - свободным. Последней матрице соответствует система, поднимаясь по которой снизу вверх, найдём выражение базисных неизвестных через свободное, т.е. найдём общее решение: 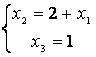. Общее решение можно записать в другом виде. Обозначим через с (с – произвольное число), тогда общее решение, записанное в виде вектора, будет . Проверить правильность результата можно с помощью частного решения, которое получается из общего при определённом значении с. Пусть, например, с=1, тогда– частное решение. Подстановка частного решения в уравнения системы обращает их в тождества.

         9   Решить однородную систему линейных уравнений.

          a) 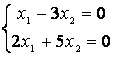 ,       б) .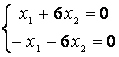

Решение.

         Поскольку число неизвестных равно числу уравнений, то судить о количестве решений можно по определителю системы : если , то система имеет бесчисленное множество решений, если , то система имеет одно нулевое решение:

         а) , следовательно, система имеет одно нулевое решение ;

         б) 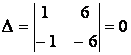, значит, система имеет бесчисленное множество решений. Так как , то ранг матрицы системы равен 1, и система равносильна одному уравнению, например, , одно неизвестное будет базисным, другое - свободным. Пусть - свободное неизвестное. Выразим базисное неизвестное через свободное  и придадим свободному неизвестному произвольное значение , тогда . Получим общее решение системы ,  или в векторной форме . Частные решения можно получать из общего, давая с различные значения. Например, пусть с=1, тогда , – частное решение.

10 Решить однородную систему линейных уравнений  

;  найти нормированную фундаментальную систему решений.

Решение.

         Выпишем матрицу системы и приведём её к ступенчатому виду, проводя элементарные преобразования над строками матрицы:

.

, n=4: r<n, значит, система имеет  бесчисленное множество решений. 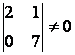– базисный минор, - базисные неизвестные, – свободные неизвестные. Составим систему по последней матрице и выразим базисные неизвестные через свободные: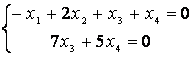

–общее решение. Пространство решений имеет размерность n-r = 4-2 = 2, поэтому фундаментальная система решений состоит из двух векторов.

         Будем придавать свободным неизвестным значения, равные строкам определителя , получим два решения, образующие фундаментальную систему решений:

         а) , тогда из общего решения .– первый вектор фундаментальной системы;

         б) , тогда . – второй вектор фундаментальной системы.

         Так как фундаментальная система решений является базисом пространства решений однородной системы линейных уравнений, то любое решение этой системы будет линейной комбинацией векторов фундаментальной системы, т.е.  (– произвольные числа), и формула   также представляет общее решение системы. 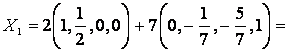Чтобы получить частное решение, придадим  и произвольные значения, например, пусть =2, =7, тогда    – частное решение.

 

Список литературы

 

       1. Апатенок Р.Ф., Маркина А.М. Сборник задач по линейной алгебре. - Мн.: Выш. Школа, 1980. – 192 с.

       2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: в 2 ч. – М.: Высшая школа, 2003. – ч. 1,2.-352 с.

       3. Сборник индивидуальных заданий по высшей математике: в 3 ч. (Рябушко А.П., Бархатов В.В. и др.). Под ред. Рябушко А.П. – Минск: Высш. школа, 2000.-ч.1.-396 с.

       4. Хасеинов К.А. Каноны математики: Учебник. – Алматы, 2003.-686 с.

 

Содержание

 

1 Теоретические вопросы                                                                                   3

2 Расчётные задания                                                                                            3

3 Решение типового варианта                                                                            20

Список литературы                                                                                             30

 

                                                         Сводный план 2011 г., поз.  223
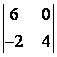
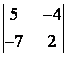
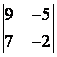
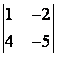
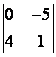
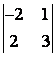
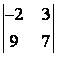
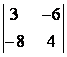
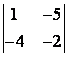
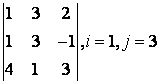
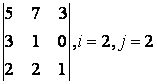
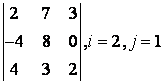
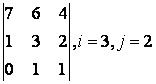
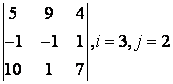
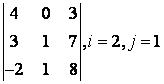
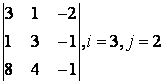
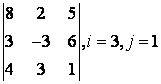
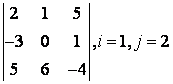
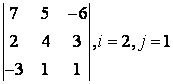
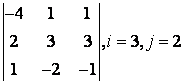
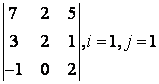
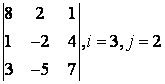
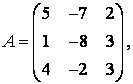
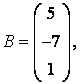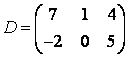
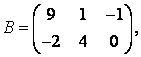
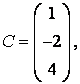
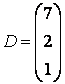
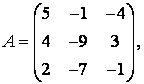
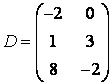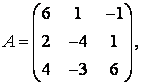
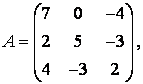
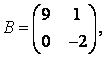
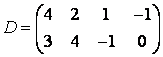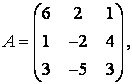
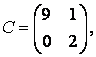
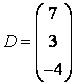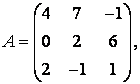
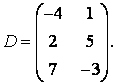
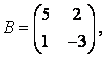
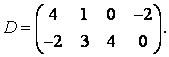
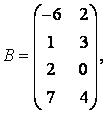
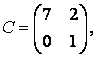
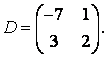
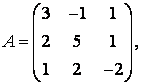
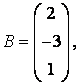
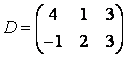
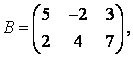
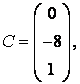
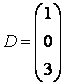
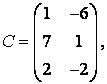
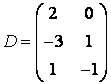
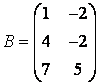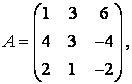
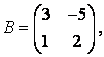
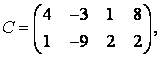
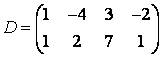
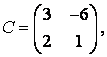
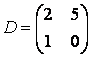
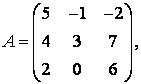
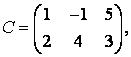
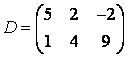
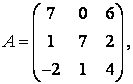
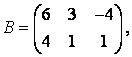
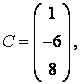
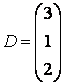
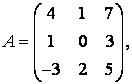
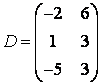
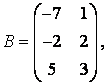
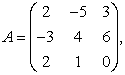
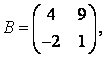
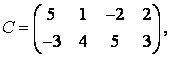
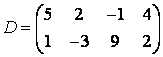
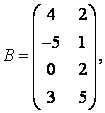
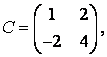
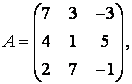
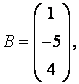
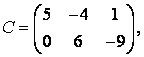
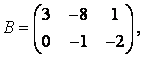
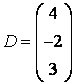
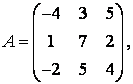
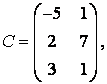
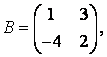
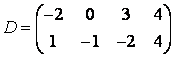
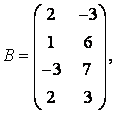
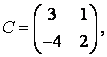
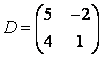
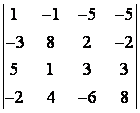
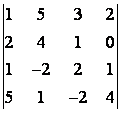
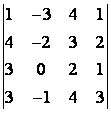
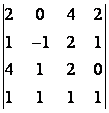
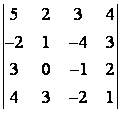
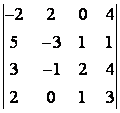
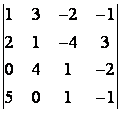
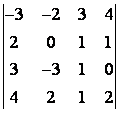
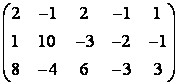
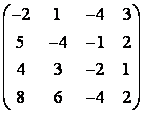
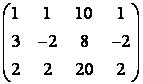
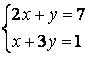
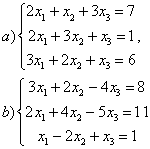
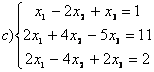
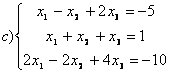
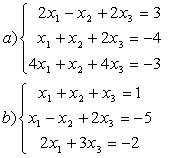
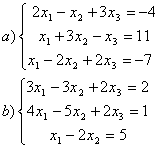
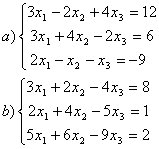
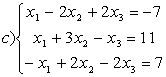
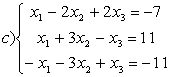
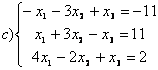
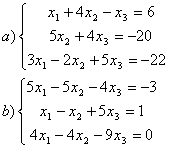
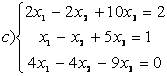
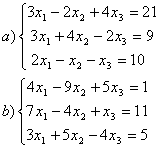
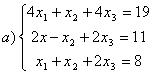
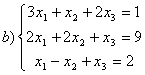
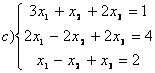
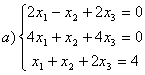
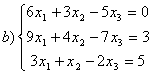
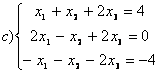
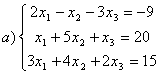
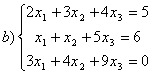
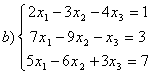
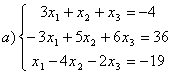
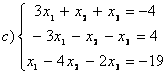
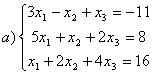
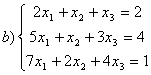
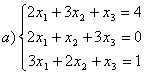
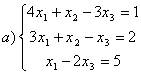
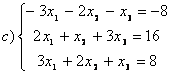
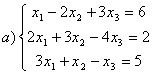
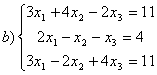
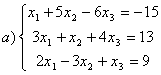
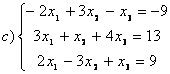
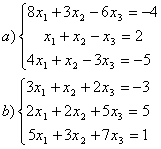
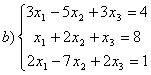
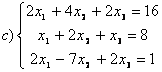
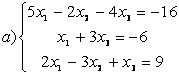
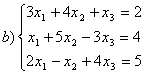
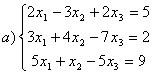
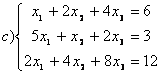
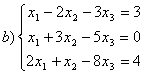
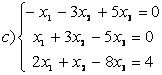
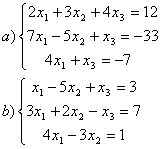
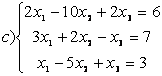
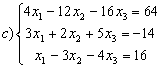
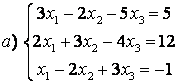
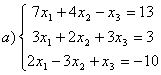
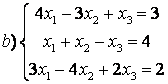
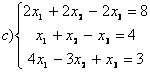
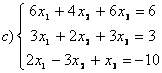
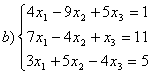
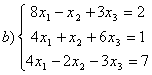
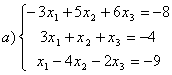
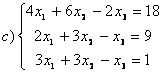
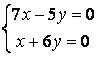
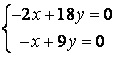
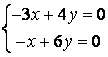
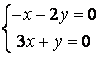
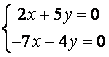
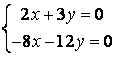
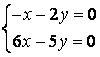
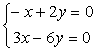
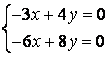
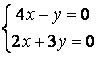
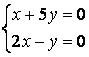
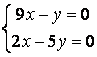
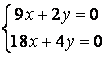
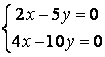
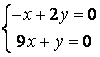
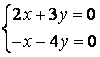
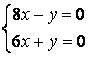
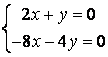
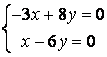
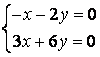
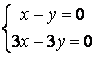
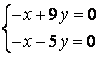
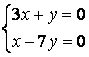
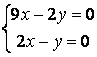
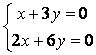