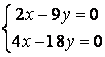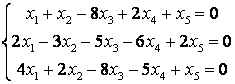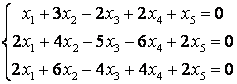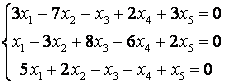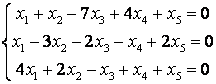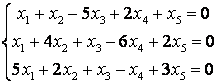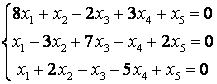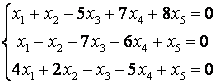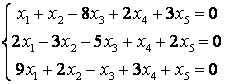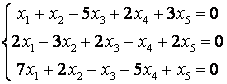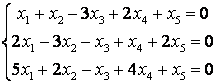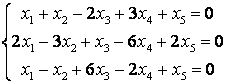Коммерциялық емес акционерлік қоғам
АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ
Жоғары математика кафедрасы
АЛГЕБРА
5В060200 – Информатика мамандығы бойынша оқитын барлық
бөлім студенттері үшін есептеу-графикалық жұмыстарды
орындауға арналған әдістемелік нұсқаулар мен тапсырмалар
1 - бөлім
Алматы 2011
ҚҰРАСТЫРУШЫЛАР: Т.Каирбеков, Л.Н.Астраханцева, М.Ж.Байса- лова. Алгебра. 5В060200 – Информатика мамандығы бойынша оқитын барлық бөлім стуенттері үшін есептеу-графикалық жұмыстарды орындауға арналған әдістемелік нұсқаулар мен тапсырмалар. 1- бөлім - Алматы: АЭжБУ, 2011. - 30 б.
«Информатика» мамандығы бойынша оқитын барлық бөлім студенттеріне арналған есептеу-графикалық жұмыстарды орындауға арналған әдістемелік нұсқаулар мен тапсырмалар. «Алгебра» пәнінің № 1 типтік есептеулерінен тұрады. Бағдарламаның теориялық сұрақтары енгізілген. Типтік нұсқаның шешімі келтірілген.
Кесте 9, әдеб. көрсеткіші 4 атау.![]()
Пікір беруші: аға оқытуы Б.Ж.Толеуова
“Алматы энергетика және байланыс университетінің” коммерциялық емес акционерлік қоғамының 2011 ж. баспа жоспары бойынша басылады.
ã “Алматы энергетика және байланыс университеті” КЕАҚ, 2011 ж.
1 Есептік-графикалық жұмыс 1. Сызықты алгебра элементтері
1.1 Теориялық сұрақтар
1 Анықтауыштар, олардың қасиеттері, есептеуі.
2 Матрицалар, оларға қолданылатын амалдар, кері матрица.
3 Матрицаның рангы және оны есептеу.
4 Сызықты теңдеулер жүйесі. Крамер ережесі. Жүйелерді матрицалық әдіспен шешу.
5 Біртекті емес теңдеулер жүйесін Гаусс әдісімен шешу.
6 Біртекті теңдеулер жүйесін шешу. Шешімдердің іргелі жүйесі.
1.2 Есептік тапсырмалар
1 Екінші ретті анықтауышты есептеу керек
1 к е с т е
|
1.1
|
1.2
|
1.3
|
1.4
|
1.5
|
|
|
1.6
|
1.7
|
1.8
|
1.9
|
1.10
|
|
|
1.11
|
1.12 |
1.13
|
1.14
|
1.15
|
|
|
1.16 |
1.17
|
1.18
|
1.19
|
1.20
|
|
|
1.21
|
1.22 |
1.23
|
1.24
|
1.25
|
|
|
1.26 |
1.27
|
1.28
|
1.29
|
1.30
|
|
2 Үшінші ретті анықтауыш берілген:
а) a![]() элементінің
M
элементінің
M![]() миноры мен
A
миноры мен
A![]() алгебралық
толықтауышын табу керек;
алгебралық
толықтауышын табу керек;
б) анықтауышты i-ші жол бойынша жіктеу керек;
в) анықтауышты j-ші баған бойынша жіктеу арқылы есептеу керек;
г) анықтауышты үшбұрыш ережесі бойынша есептеу керек (Саррюс ережесі).
2 к е с т е
|
2.1
|
2.2
|
2.3
|
|
2.4
|
2.5
|
2.6 |
|
2.7
|
2.8
|
2.9
|
|
2.10
|
2.11 |
2.12 |
|
2.13
|
2.14 |
2.15 |
|
2.16
|
2.17
|
2.18
|
|
2.19
|
2.20
|
2.21 |
|
2.22
|
2.23
|
2.24
|
2 кестенің соңы
|
2.25 |
2.26 |
2.27
|
|
2.28
|
2.29
|
2.30
|
3 А, В, С, Д матрицалары берілген:
а) 3С+2Д, С-4Д матрицаларын табу керек;![]()
б) В матрицасының транспонирленген В![]() матрицасын табу керек.
матрицасын табу керек.
3 к е с т е
|
3.1
|
|
3.2
|
|
3.3
|
|
3.4
|
|
3.5
|
|
3.6
|
3 кестенің жалғасы
|
3.7
|
|
3.8
|
|
3.9
|
|
3.10
|
|
3.11
|
|
3.12
|
|
3.13 |
|
3.14
|
|
3.15
|
3 кестенің жалғасы
|
3.16
|
|
3.17
|
|
3.18
|
|
3.19
|
|
3.20
|
|
3.21
|
|
3.22
|
|
3.23
|
3 кестенің соңы
|
3.24
|
|
3.25
|
|
3.26
|
|
3.27
|
|
3.28
|
|
3.29
|
|
3.30
|
4 А, В, С (3 тапсырмадан) матрицалары берілген:
а) АВ, ВС матрицаларын көбейтуге бола ма? Егер көбейту мүмкін болмаса, себебін түсіндіру керек; көбейту мүмкін жағдайда екі матрицаның көбейтіндісін жазу керек;
б) А матрицасына кері
![]() матрицасын
табу керек.
матрицасын
табу керек.
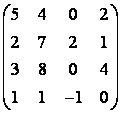
5 Төртінші ретті анықтауышты есептеу керек
4 к е с т е
|
4.1 |
4.2 |
4.3
|
4.4 |
|
4.5
|
4.6
|
4.7 |
4.8 |
|
4.9
|
4.10 |
4.11
|
4.12 |
|
4.13
|
4.14
|
4.15
|
4.16 |
|
4.17 |
4.18
|
4.19 |
4.20
|
|
4.21 |
4.22
|
4.23 |
4.24 |
4 кестенің соңы
|
4.25
|
4.26 |
4.27
|
4.28 |
|
4.29 |
4.30
|
4.31
|
4.32 |
6
а) минорларды жиектеу әдісі;
б) элементар түрлендірулер арқылы
Матрицаның рангын табу керек. Базисті минорды көрсету керек.
5 к е с т е
|
5.1
|
5.2
|
5.3
|
|
5.4
|
5.5 |
5.6 |
|
5.7
|
5.8
|
5.9
|
|
5.10 |
5.11
|
5.12
|
5 кестенің жалғасы
|
5.13
|
5.14
|
5.15 |
|
5.10 |
5.11
|
5.12
|
|
5.13
|
5.14
|
5.15 |
|
5.16
|
5.17
|
5.18
|
|
5.19
|
5.20 |
5.21 |
|
5.22 |
5.23 |
5.24 |
|
5.25 |
5.26 |
5.27
|
5 кестенің соңы
|
5.28
|
5.29
|
5.30
|
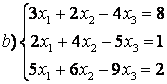
7 а) Крамер әдісімен; ә) матрицалық әдіспен (кері матрица көмегімен) жүйені шешу керек
6 к е с т е
|
6.1
|
6.2
|
|
6.3
|
6.4
|
|
6.5
|
6.6
|
|
6.7
|
6.8
|
|
6.9
|
6.10
|
|
6.11
|
6.12
|
|
6.13
|
6.14
|
|
6.15
|
6.16
|
|
6.17
|
6.18
|
|
6.19
|
6.20
|
|
6.21
|
6.22
|
|
6.23
|
6.24
|
|
6.25
|
6.26 |
|
6.27
|
6.28
|
|
6.29
|
6.30
|
6 кестенің соңы
|
6.31
|
6.32
|
8 Теңдеулер жүйесінің үйлесімділігін тексеріп, шешімдер санын анықтау керек. Үйлесімді болған жағдайда Гаусс әдісімен шешу керек
7 к е с т е
|
7.1 |
7.2
|
|
7.3 |
7.4
|
|
7.5
|
7.6
|
7 кестенің жалғасы
|
7.7
|
7.8
|
|
7.9
|
7.10
|
|
7.11
|
7.12
|
7 кестенің жалғасы
|
7.13
|
7.14
|
|
7.15
|
7.16
|
|
7.17
|
7.18
|
7 кестенің жалғасы
|
7.19
|
7.20
|
|
7.21
|
7.22
|
|
7.23
|
7.24
|
7 кестенің соңы
|
7.25
|
7.26
|
|
7.27
|
7.28
|
|
7.29
|
7.30
|
9 Біртекті сызықты теңдеулер жүйесін шешу керек
8 к е с т е
|
8.1
а) |
|
8.2
a) |
|
8.3 a) |
|
8.4 a) |
|
8.5
a) |
|
8.6
a) |
|
8.7
a) |
|
8.8
a) |
|
8.9
a) |
|
8.10 a) |
|
8.11 a) |
|
8.12 a) |
|
8.13 a) |
|
8.14 a) |
|
8.15 a) |
8 кестенің соңы
|
8.16 a)
|
|
8.17 a) |
|
8.18 a) |
|
8.19 a) |
|
8.20 a) |
|
8.21 a) |
|
8.22 a) |
|
8.23 a) |
|
8.24 a) |
|
8.25 a) |
|
8.26 a) |
|
8.27 a) |
|
8.28 a) |
|
8.29 a) |
|
8.30 a)
|
10 Біртекті сызықты теңдеулер жүйесін шешу керек. Нормаланған іргелі шешімдер жүйесін табу керек
9 к е с т е
|
9.1
|
9.2
|
|
9.3
|
9.4
|
|
9.5
|
9.6
|
|
9.7
|
9.8
|
|
9.9
|
9.10
|
|
9.11
|
9.12
|
|
9.13
|
9.14
|
|
9.15
|
9.16
|
|
9.17
|
9.18
|
|
9.19
|
9.20
|
9 кестенің соңы
|
9.21
|
9.22
|
|
9.23
|
9.24
|
|
9.25
|
9.26
|
|
9.27
|
9.28
|
|
9.29
|
9.30
|
1.3 Типтік варианттың шешуі
1
 екінші ретті анықтауышты есептеу керек.
екінші ретті анықтауышты есептеу керек.
Шешуі:
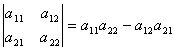 формуласы бойынша
формуласы бойынша
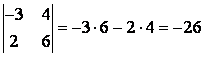 .
.
2 Үшінші ретті анықтауыш берілген
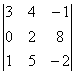 ,
i=2, j=3.
,
i=2, j=3.
а) a![]() элементінің M
элементінің M![]() миноры мен A
миноры мен A![]() алгебралық толықтауышын табу керек;
алгебралық толықтауышын табу керек;
б) анықтауышты i-ші жол бойынша жіктеу керек;
в) анықтауышты j-ші баған бойынша жіктеу арқылы есептеу керек;
г) анықтауышты үшбұрыш ережесі бойынша есептеу керек (Саррюс ережесі).
Шешуі:
a) a![]() элементінің M
элементінің M![]() миноры осы элемент тұрған i-ші жол мен j-ші
бағанды сызып тастағанда алынған анықтауышқа
тең. Сонымен екінші жол мен үшінші бағанды сызып
тастасақ,
миноры осы элемент тұрған i-ші жол мен j-ші
бағанды сызып тастағанда алынған анықтауышқа
тең. Сонымен екінші жол мен үшінші бағанды сызып
тастасақ, 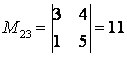 минорын аламыз. Осы элементтің алгебралық
толықтауышын келесі формуламен есептейміз
минорын аламыз. Осы элементтің алгебралық
толықтауышын келесі формуламен есептейміз
A![]() =(-1)
=(-1)![]() M
M![]() , яғни А
, яғни А![]() =(-1)
=(-1)![]() 11= -11;
11= -11;
б) n-ші ретті анықтауышты i-ші жол
бойынша жіктеу формуласы 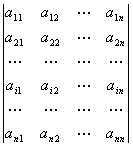 =
=
![]() , мұндағы A
, мұндағы A![]() –
a
–
a![]() элементінің
алгебралық толықтауышы. i = 2, j = 3 болғандықтан,
формула мына түрде жазылады
элементінің
алгебралық толықтауышы. i = 2, j = 3 болғандықтан,
формула мына түрде жазылады
 . Біздің жағдайдағы жіктеу
. Біздің жағдайдағы жіктеу
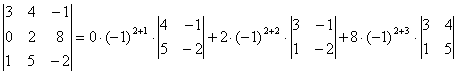 ;
;
в) ![]() . Үшінші баған бойынша жіктеу формуласы
. Үшінші баған бойынша жіктеу формуласы
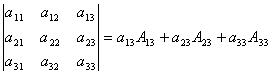 .
Сонымен,
.
Сонымен,
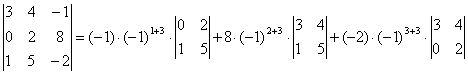 =
2 – 88 – 12 = - 98;
=
2 – 88 – 12 = - 98;
г) үшбұрыш ережесі: үшінші ретті
анықтауыш алты мүшенің қосындысына тең; плюс
таңбамен алынатын мүше
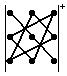 сұлбасы бойынша анықтауыштың
мүшелерін үш-үштен көбейткенде алынады, ал минус
таңбамен –
сұлбасы бойынша анықтауыштың
мүшелерін үш-үштен көбейткенде алынады, ал минус
таңбамен – 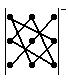 сұлбасы
бойынша.
сұлбасы
бойынша.
Сондықтан,
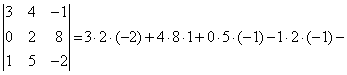
![]()
3-4. 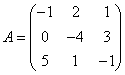 ,
, ![]() ,
, 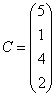 ,
, матрицалары берілген:
матрицалары берілген:
а) ![]() ,
, ![]() матрицаларын табу керек;
матрицаларын табу керек;![]()
б) В матрицасының транспонирленген В![]() матрицасын табу керек;
матрицасын табу керек;
в) АВ, ВС матрицаларын көбейтуге бола ма? Егер көбейту мүмкін болмаса, себебін түсіндіру керек; көбейту мүмкін жағдайда екі матрицаның көбейтіндісін жазу керек;
г) А матрицасына кері
![]() матрицасын
табу керек.
матрицасын
табу керек.
Шешуі:
а) 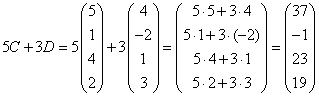 ,
,
 ;
;
б) В матрицасының транспонирленген
матрицасы оның жолын сол нөмірлі бағанмен ауыстырғанда
алынады:  ;
;
в) егер А матрицасының жол саны В
матрицасының баған санына тең болса, онда А, В матрицаларын
көбейтуге болады. Матрицалар өлшемі: А![]() , В
, В![]() , С
, С![]() , Д
, Д![]() . Сонымен, А
. Сонымен, А![]() В
В![]() =
= ![]() – көбейту мүмкін емес. В
– көбейту мүмкін емес. В![]() С
С![]() =
= ![]() – көбейту мүмкін. АВ
матрицаларының көбейтіндісі С матрицасы болады, оның жол саны
А матрицасының жол санына тең, ал баған саны В
матрицасының баған санына тең:
– көбейту мүмкін. АВ
матрицаларының көбейтіндісі С матрицасы болады, оның жол саны
А матрицасының жол санына тең, ал баған саны В
матрицасының баған санына тең:
![]() . С
матрицасының
. С
матрицасының ![]() элементі
А матрицасының i–ші жолы мен В матрицасының
j–ші
бағанына көбейткенде алынады. Сондықтан,
элементі
А матрицасының i–ші жолы мен В матрицасының
j–ші
бағанына көбейткенде алынады. Сондықтан,
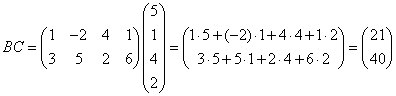 .
. ![]() .
.
Сонымен,
![]() ;
;
г) егер шаршы матрицаның анықтауышы нөлден өзге болса, онда оның кері матрицасы бар болады. Егер анықтауыш нөлге тең болса, кері матрицасы болмайды.
А
=  матрицасының
кері матрицасы келесі формула бойынша есептелінеді
матрицасының
кері матрицасы келесі формула бойынша есептелінеді 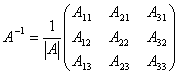 мұндағы
мұндағы ![]() –А матрицасының
анықтауышы,
–А матрицасының
анықтауышы, ![]() –
a
–
a![]() элементінің
алгебралық толықтауышы. А матрицасының
анықтауышын табайық:
элементінің
алгебралық толықтауышы. А матрицасының
анықтауышын табайық: 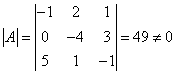 , олай болса А
, олай болса А![]() бар болады. А матрицасының
барлық элементтері үшін алгебралық
толықтауышын анықтайық
бар болады. А матрицасының
барлық элементтері үшін алгебралық
толықтауышын анықтайық
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Жоғарыдағы
формула бойынша А![]() :
:
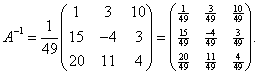
5 Төртінші ретті анықтауышты есептеу керек
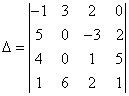 .
.
Шешуі:
анықтауыштың қасиеттерін
қолданып, берілген анықтауыштың бір жолында не бір
бағанында нөлдер алуымыз керек.
Екі нөлі бар екінші бағанды таңдап аламыз: бірінші жолды
(-2)-ге көбейтіп, соңғы жолға қоссақ
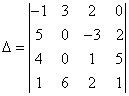 анықтауышын аламыз. Енді
анықтауышты екінші
баған бойынша жіктейміз
анықтауышын аламыз. Енді
анықтауышты екінші
баған бойынша жіктейміз
 .
.
6 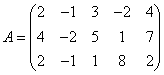 матрицаның рангын екі әдіспен
есептеу керек:
матрицаның рангын екі әдіспен
есептеу керек:
а) минорларды жиектеу әдісі;
б) элементар түрлендірулер арқылы.
Базисті минорды көрсету керек.
Шешуі:
а) жоғарғы сол бұрыштан
бастайық. Екінші ретті ![]() минор аламыз, ол нөлге тең
болғандықтан, басқасын аламыз
минор аламыз, ол нөлге тең
болғандықтан, басқасын аламыз ![]() .
. ![]() – ге жиектеліп шыққан минорларды
қарастырамыз (яғни
– ге жиектеліп шыққан минорларды
қарастырамыз (яғни ![]() миноры енетін)
миноры енетін)
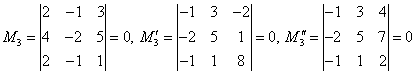 .
.
Үшінші ретті жиектеліп шыққан
минорлардың барлығы нөлге тең болғандықтан,
матрицаның рангы 2-ге тең (![]() , ранг – нөлге тең емес
минордың ең үлкен реті). Базистік минор
, ранг – нөлге тең емес
минордың ең үлкен реті). Базистік минор ![]() ;
;
б) элементар түрлендірулер көмегімен матрицаны сатылы түрге келтіреміз
 ~
~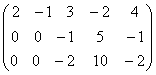 ~
~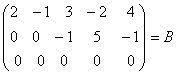 .
.
Алдымен бірінші жолды (-2)-ге көбейтіп, екінші
жолға қостық (алынған нәтиже екінші жолға
жазылып, бірінші жол өзгеріссіз тұрады). Содан соң бірінші
жолды (-1)-ге көбейтіп үшінші жолға қостық, сонда
бірінші бағанның бірінші жолынан төмен нөлдер пайда
болды. Енді екінші жолды (-2) (-1)-ге көбейтіп үшінші жолға
қостық. Сатылы ![]() матрицасын алдық. Бұл
матрицаның нөлден өзге екі жолы бар, бұл дегеніміз
екінші ретті минор бар екендігін білдіреді, мысалы,
матрицасын алдық. Бұл
матрицаның нөлден өзге екі жолы бар, бұл дегеніміз
екінші ретті минор бар екендігін білдіреді, мысалы, ![]() . Сондықтан
. Сондықтан ![]() .
. ![]() және
және ![]() матрицалары эквивалентті
болғандықтан, олардың рангтары тең
матрицалары эквивалентті
болғандықтан, олардың рангтары тең ![]() . Базистік минор ретінде
. Базистік минор ретінде ![]() алуға болады.
алуға болады.
7  жүйесін а) Крамер әдісімен; ә) матрицалық
әдіспен
жүйесін а) Крамер әдісімен; ә) матрицалық
әдіспен
(кері матрица көмегімен) шешу керек.
Шешуі:
а)
 жүйесін Крамер әдісімен шешкенде, шешім
келесі түрде жазылады
жүйесін Крамер әдісімен шешкенде, шешім
келесі түрде жазылады ![]() , мұндағы
, мұндағы
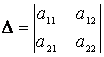 –
жүйенің анықтауышы,
–
жүйенің анықтауышы,  ,
,
 - жүйенің анықтауышындағы
бірінші және екінші бағандарды бос мүшелермен
алмастырғандағы қосалқы анықтауыштар. Біздің
жағдайда
- жүйенің анықтауышындағы
бірінші және екінші бағандарды бос мүшелермен
алмастырғандағы қосалқы анықтауыштар. Біздің
жағдайда 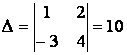 ,
, 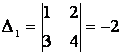 ,
,  . Сонымен, х = -1/5, у =3/5.
Жауапты вектор түрінде жазуға
болады: (-1/5; 3/5).
. Сонымен, х = -1/5, у =3/5.
Жауапты вектор түрінде жазуға
болады: (-1/5; 3/5).
ә)
 жүйенің шешімі матрицалық
түрде былай жазылады:
жүйенің шешімі матрицалық
түрде былай жазылады: ![]() ,
мұндағы
,
мұндағы
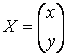 – белгісіздердің баған-матрицасы,
– белгісіздердің баған-матрицасы,
 – бос
мүшелердің баған-матрицасы,
– бос
мүшелердің баған-матрицасы,
![]() – жүйенің
– жүйенің  матрицасына
кері матрица.
матрицасына
кері матрица.
Жүйенің  матрицасының кері матрицасын табамыз.
Жүйенің
анықтауышы
матрицасының кері матрицасын табамыз.
Жүйенің
анықтауышы ![]() нөлден өзге болған соң, кері
матрицасы бар болады және ол
нөлден өзге болған соң, кері
матрицасы бар болады және ол  .
.
Онда 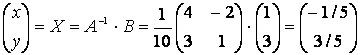 . Жауабын қарапайым түрде жазуға
болады:
. Жауабын қарапайым түрде жазуға
болады: ![]() .
.
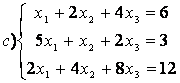
8 Теңдеулер жүйесінің үйлесімділігін тексеріп, шешімдер санын анықтау керек. Үйлесімді болған жағдайда Гаусс әдісімен шешу керек
а) , ә)
, ә)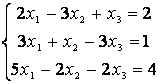 ,б)
,б) .
.
Шешуі:
а) Кронекер-Капелли теоремасы бойынша, егер матрицаның
рангы жүйенің кеңейтілген жүйесінің рангысына
тең ![]() болса,
онда жүйе үйлесімді (яғни ең болмағанда
жалғыз шешімі болады), ал егер
болса,
онда жүйе үйлесімді (яғни ең болмағанда
жалғыз шешімі болады), ал егер ![]() , онда жүйе үйлесімді емес (яғни
шешімі жоқ). Жүйенің матрицасы –
, онда жүйе үйлесімді емес (яғни
шешімі жоқ). Жүйенің матрицасы –
 ,
кеңейтілген матрица –
,
кеңейтілген матрица –  .
.
Матрицалардың рангын қарапайым түрлендірулер
арқылы анықтаймыз. ![]() матрицасы
матрицасы
![]() матрицасының құрамында
болғандықтан, онда
матрицасының құрамында
болғандықтан, онда ![]() матрицасының жолдарына элементар
түрлендіру жасаған жеткілікті: бірінші жолды -2-ге көбейтіп,
екінші жолға қосамыз, содан соң бірінші жолды -3-ге
көбейтіп, үшінші жолға қосамыз.
матрицасының жолдарына элементар
түрлендіру жасаған жеткілікті: бірінші жолды -2-ге көбейтіп,
екінші жолға қосамыз, содан соң бірінші жолды -3-ге
көбейтіп, үшінші жолға қосамыз.
![]() матрицасы,
сонымен қатар
матрицасы,
сонымен қатар ![]() матрицасы да сатылы түрге келтірілетінін
көреміз:
матрицасы да сатылы түрге келтірілетінін
көреміз:  .
.
Олай болса
![]() және жүйе үйлесімді. Белгісіздер саны
n=3 және ол рангке тең болғандықтан (n=r), онда
жүйенің жалғыз шешімі болады.
және жүйе үйлесімді. Белгісіздер саны
n=3 және ол рангке тең болғандықтан (n=r), онда
жүйенің жалғыз шешімі болады.
Гаусс әдісі қарапайым түрлендірулер
арқылы жүйенің теңдеулеріндегі белгісіздерді біртіндеп
жою арқылы сатылы түрге келтіруді көздейді. Жүйелердің
қарапайым түрлендірулері матрицалардың қарапайым түрлендірулері
сияқты болғандықтан, практикада жүйенің
кеңейтілген матрицасының бірінші жолын екіншісімен орын ауыстыра
береді. Жоғарыда бұл түрлендірулер жасалынды. Сонымен, берілген
жүйе соңғы матрицаға сәйкес келетін жүйеге
келтіріледі:  .
.
Осы жүйеде төменнен жоғарыға
көтеріле отырып, соңғы теңдіктен
![]() ;
екінші теңдіктен
;
екінші теңдіктен ![]() ; біріншіден
; біріншіден
![]() аламыз. Жауабы: (-4; -2; 1);
аламыз. Жауабы: (-4; -2; 1);
ә) жүйенің кеңейтілген матрицасын
жазып, ![]() және
және ![]() матрицаларының рангыларын табамыз:
матрицаларының рангыларын табамыз:

Келесі түрлендірулер жасалынды: алдымен бірінші
жол -1-ге көбейтіліп, екінші жолға қосылды, содан соң
олардың орнын ауыстырып жаздық. Сосын бірінші жол -2-ге
көбейтіліп, екінші жолға қосылды, Бірінші жол -5-ке
көбейтіліп, үшінші жолға қосылды. Екінші жол -2-ге
көбейтіліп, үшінші жолға қосылды.
![]() матрицасы
нөлден өзге үш жолда сатылы түрге келтірілді, сондықтан
оның рангы 3-ке тең (
матрицасы
нөлден өзге үш жолда сатылы түрге келтірілді, сондықтан
оның рангы 3-ке тең (![]() ).
).
![]() матрицасы бір мезгілде
матрицасы бір мезгілде
 матрицасына келтірілді, соңғы
матрицаның екі нөлден өзге жолы бар болғандықтан,
оның рангы 2-ге тең (
матрицасына келтірілді, соңғы
матрицаның екі нөлден өзге жолы бар болғандықтан,
оның рангы 2-ге тең (![]() ). Сонымен,
). Сонымен,
![]() және жүйе
үйлесімсіз;
және жүйе
үйлесімсіз;
б) жүйенің кеңейтілген матрицасын жазып
алып, ![]() және
және ![]() матрицаларының рангтарын табамыз:
матрицаларының рангтарын табамыз:
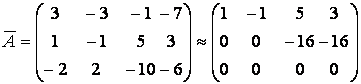 .
.
![]() болғандықтан, жүйе үйлесімді.
Белгісіздер саны n=3 және
болғандықтан, жүйе үйлесімді.
Белгісіздер саны n=3 және ![]() болғандықтан, жүйенің шексіз
көп шешімдер жиыны болады.
болғандықтан, жүйенің шексіз
көп шешімдер жиыны болады. ![]() базистік минорын таңдап аламыз. Базистік
минорға
базистік минорын таңдап аламыз. Базистік
минорға ![]() белгісіздер алдындағы коэффициенттер енді, сондықтан
бұл белгісіздер базисті, ал
белгісіздер алдындағы коэффициенттер енді, сондықтан
бұл белгісіздер базисті, ал ![]() - бос белгісіз болады. Соңғы матрицаға
- бос белгісіз болады. Соңғы матрицаға
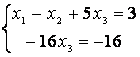 жүйесі
сәйкес келеді. Төменнен жоғарыға көтерілу
арқылы базисті белгісіздердің бос белгісіздер арқылы
өрнегін алуға болады, яғни жалпы шешімді табамыз:
жүйесі
сәйкес келеді. Төменнен жоғарыға көтерілу
арқылы базисті белгісіздердің бос белгісіздер арқылы
өрнегін алуға болады, яғни жалпы шешімді табамыз:
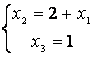 .
Жалпы шешімді басқаша жазуға болады.
.
Жалпы шешімді басқаша жазуға болады.
![]() -ді с арқылы белгілейік (с – кез-келген
сан), онда жалпы шешімнің векторлық түрі
-ді с арқылы белгілейік (с – кез-келген
сан), онда жалпы шешімнің векторлық түрі
![]() .
Нәтиженің дұрыстығын дербес шешім арқылы
тексеруге болады, ал дербес шешім жалпы шешімдегі с-ға қандай-да
бір мәнді беру арқылы табылады. Мысалы, с=1 болсын, онда
.
Нәтиженің дұрыстығын дербес шешім арқылы
тексеруге болады, ал дербес шешім жалпы шешімдегі с-ға қандай-да
бір мәнді беру арқылы табылады. Мысалы, с=1 болсын, онда
![]() -дербес
шешім. Дербес шешімдер жүйедегі теңдеулерді тепе-теңдікке
айналдырады.
-дербес
шешім. Дербес шешімдер жүйедегі теңдеулерді тепе-теңдікке
айналдырады.
9 Біртекті сызықты теңдеулер жүйесін шешу керек
a) ; ә)
; ә)
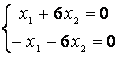 .
.
Шешуі:
Белгісіздер саны теңдеулер санына тең
болғандықтан, шешімдер саны туралы жүйенің
анықтауышы ![]() бойынша айтуға болады: егер
бойынша айтуға болады: егер
![]() ,
онда олай болса жүйенің шексіз шешімі болады, егер
,
онда олай болса жүйенің шексіз шешімі болады, егер
![]() ,
онда жүйенің жалғыз нөлдік шешімі болады:
,
онда жүйенің жалғыз нөлдік шешімі болады:
а)
 , олай болса, онда жүйенің жалғыз
нөлдік шешімі болады
, олай болса, онда жүйенің жалғыз
нөлдік шешімі болады ![]() ;
;
ә)
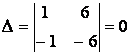 , олай болса, онда жүйенің шексіз шешімі
болады.
, олай болса, онда жүйенің шексіз шешімі
болады. ![]() болғандықтан,
жүйенің матрицаның рангы 1-ге тең және де
жүйе, мысалы,
болғандықтан,
жүйенің матрицаның рангы 1-ге тең және де
жүйе, мысалы, ![]() теңдеуіне мәндес. Бір белгісіз базисті, қалғаны
бос белгісіз болады.
теңдеуіне мәндес. Бір белгісіз базисті, қалғаны
бос белгісіз болады. ![]() - бос белгісіз болсын. Базисті белгісізді бос белгісіз
арқылы өрнектейік
- бос белгісіз болсын. Базисті белгісізді бос белгісіз
арқылы өрнектейік ![]() . Бос белгісізге кез келген мән берсек
. Бос белгісізге кез келген мән берсек
![]() ,
онда
,
онда ![]() .
Жүйенің жалпы шешімін аламыз
.
Жүйенің жалпы шешімін аламыз ![]() ,
,
![]() немесе векторлы түрде
немесе векторлы түрде
![]() .
с-ға әртүрлі мәндер беру арқылы жалпыдан дербес
шешімдерді алуға болады. Мысалы, с=1 болсын, онда
.
с-ға әртүрлі мәндер беру арқылы жалпыдан дербес
шешімдерді алуға болады. Мысалы, с=1 болсын, онда
![]() ,
,
![]() -
дербес шешім.
-
дербес шешім.
10 Біртекті сызықты теңдеулер жүйесін шешу керек
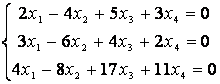 ; шешімдердің нормаланған іргелі
жүйесін табу керек.
; шешімдердің нормаланған іргелі
жүйесін табу керек.
Шешуі:
Жүйенің матрицасын жазып алып сатылы түрге келтіреміз, ол үшін жолдарына қарапайым түрлендірулер жүргіземіз:
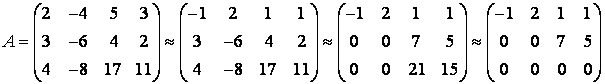 .
.
![]() , n=4: r < n, олай болса жүйенің шексіз
шешімі болады.
, n=4: r < n, олай болса жүйенің шексіз
шешімі болады. 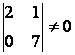 - базисті минор,
- базисті минор,
![]() – базисті белгісіздер,
– базисті белгісіздер, ![]() -
бос белгісіздер. Соңғы
матрица бойынша жүйе құрамыз, содан соң
базисті
белгісіздерді бос белгісіздер арқылы өрнектейміз:
-
бос белгісіздер. Соңғы
матрица бойынша жүйе құрамыз, содан соң
базисті
белгісіздерді бос белгісіздер арқылы өрнектейміз: 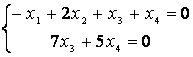
![]()
 –
жалпы шешім.
Шешімдер
кеңістігінің өлшемі
–
жалпы шешім.
Шешімдер
кеңістігінің өлшемі ![]() ,
сондықтан шешімдердің іргелі жүйесі екі вектордан
тұрады.
,
сондықтан шешімдердің іргелі жүйесі екі вектордан
тұрады.
Бос белгісіздерге ![]() анықтауыштың
жолына тең мәндер бере бастаймыз,
шешімдердің іргелі
жүйесін құрайтын екі шешім аламыз:
анықтауыштың
жолына тең мәндер бере бастаймыз,
шешімдердің іргелі
жүйесін құрайтын екі шешім аламыз:
а)
![]() ,
онда жалпы шешімнен
,
онда жалпы шешімнен ![]() .
.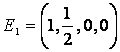 -
іргелі жүйенің бірінші векторы;
-
іргелі жүйенің бірінші векторы;
ә)
![]() ,
онда
,
онда ![]() .
.
 –
іргелі
жүйенің екінші векторы.
–
іргелі
жүйенің екінші векторы.
Іргелі жүйе біртекті сызықты
теңдеулер жүйесінің шешімінің кеңістігінің
базисі болғандықтан,
бұл жүйенің кез келген
шешімі іргелі жүйенің векторларының
сызықты комбинациясы болады,
яғни
![]() (
(![]() -
кез-келген сандар).
-
кез-келген сандар). ![]() жүйенің жалпы шешімі формуласымен
беріледі. Дербес шешімдерді алу үшін
жүйенің жалпы шешімі формуласымен
беріледі. Дербес шешімдерді алу үшін ![]() және
және![]() –
ге кез келген мәндер береміз,
мысалы,
–
ге кез келген мәндер береміз,
мысалы, ![]() =2,
=2, ![]() =7 болса, онда
=7 болса, онда  =
=![]() -
дербес шешімдері.
-
дербес шешімдері.
Әдебиеттер тізімі
1. Апатенок Р.Ф., Маркина А.М. Сборник задач по линейной алгебре.- Мн.: Выш. Школа, 1980. – 192 с.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: в 2 ч. – М.: Высшая школа, 2003. – ч. 1,2.-352 с.
3. Сборник индивидуальных заданий по высшей математике: в 3 ч. (Рябушко А.П., Бархатов В.В. и др.). Под ред. Рябушко А.П. – Минск: Высш. школа, 2000.-ч.1.-396 с.
4. Дүйсек А.К., Қасымбеков С.К. Жоғары математика (оқу құралы) - Алматы: ҚБТУ, 2004. - 440 б.
Мазмұны
1 Теориялық сұрақтар 3
2 Есептік тапсырмалар 3
3 Типтік варианттың шешуі 21
Әдебиеттер тізімі 31
2011 ж. жинт. жоспары, реті 224


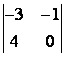
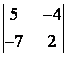





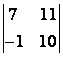

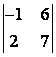
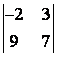

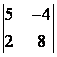
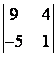
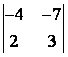
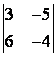
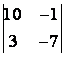


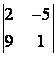
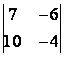


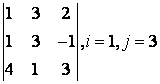
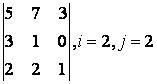
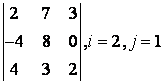
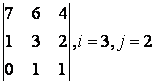
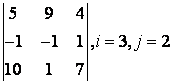
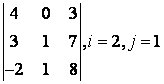



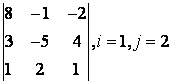
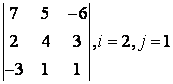
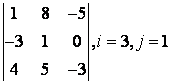


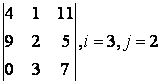
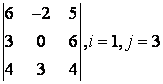



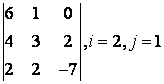

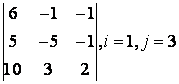



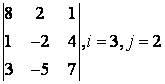

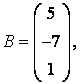
 ,
, 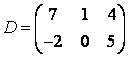

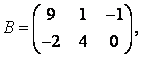
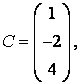



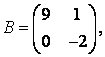
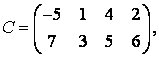
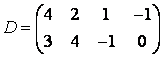

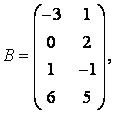
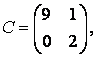
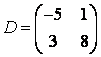
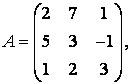
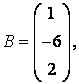

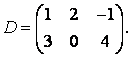




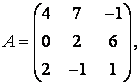
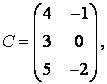
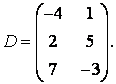
 ,
, 

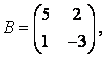

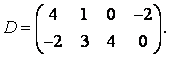

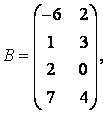


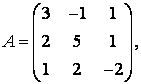
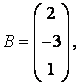
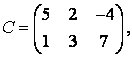


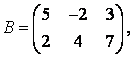
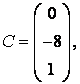



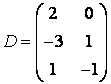

 ,
, 


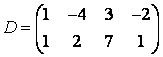


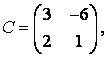

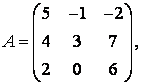

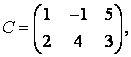

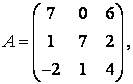
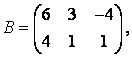
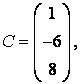
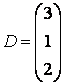


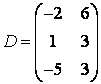
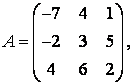
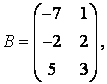

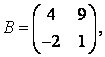
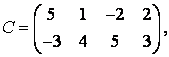

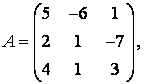
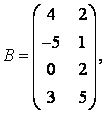

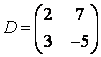
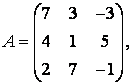
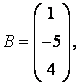
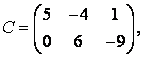
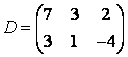
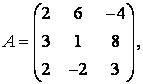
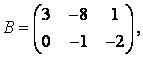

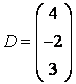

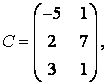
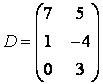


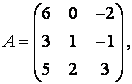
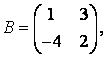
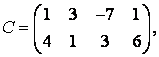
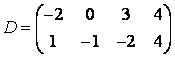

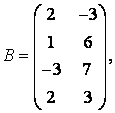
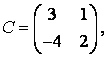
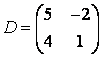




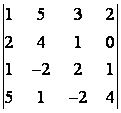

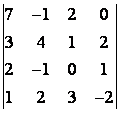





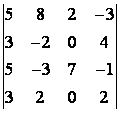
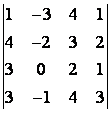




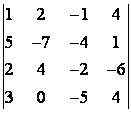





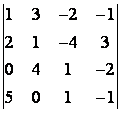
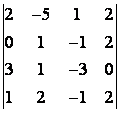


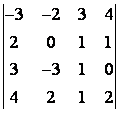





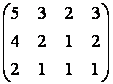

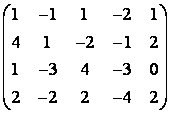
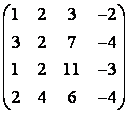
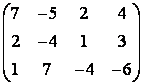

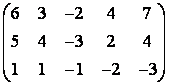




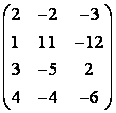


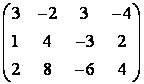

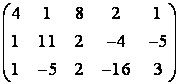


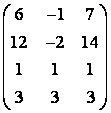
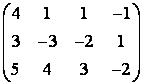
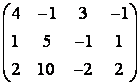
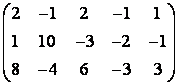



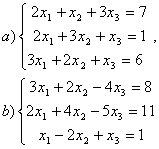

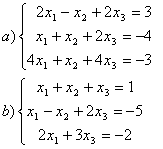
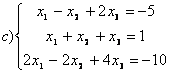
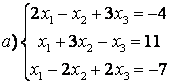
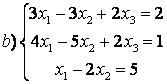





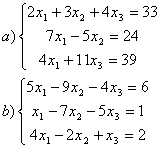
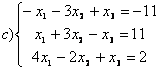
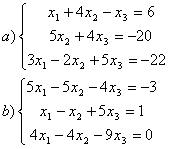
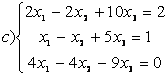
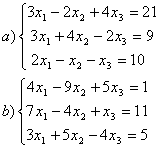


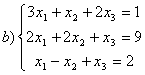
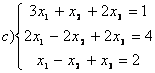


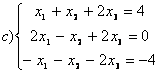

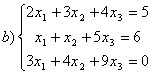

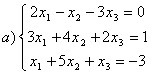
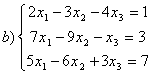

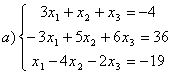

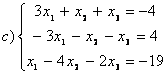
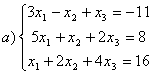
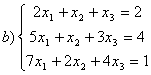


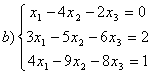
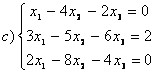
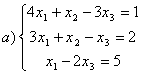



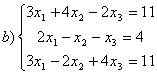

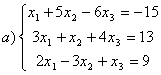
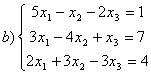

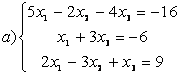
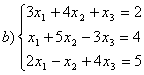
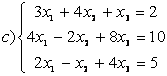
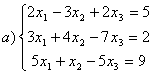
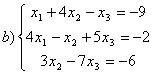
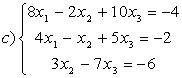
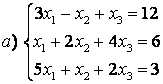
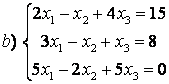
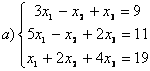

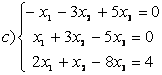


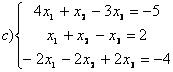


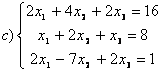
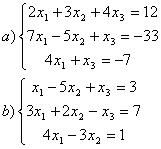
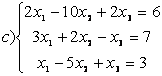
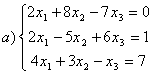


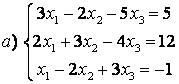



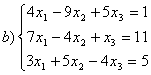
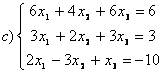
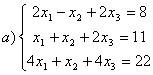


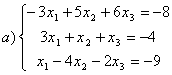
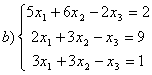
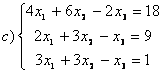

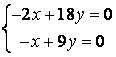
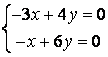
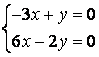
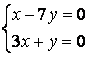
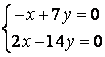
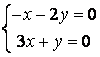
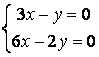

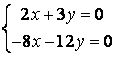
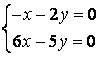
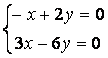
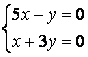
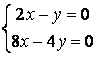
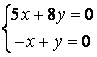
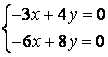
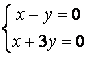
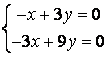
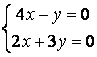
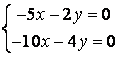
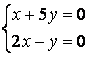
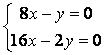
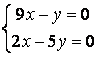

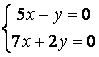

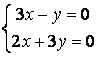
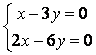
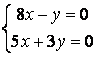
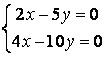

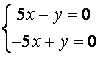

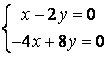
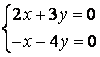

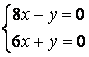

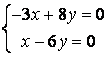





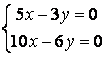








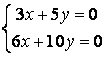

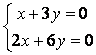
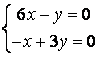 ,
,