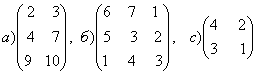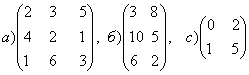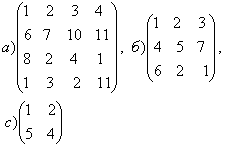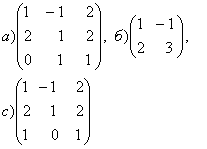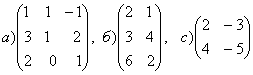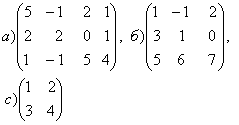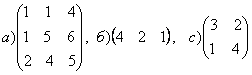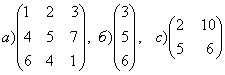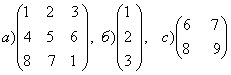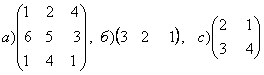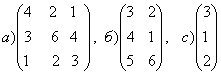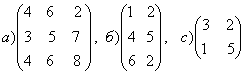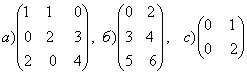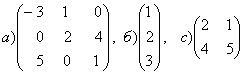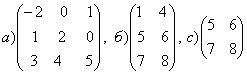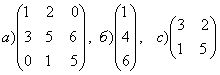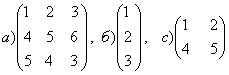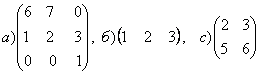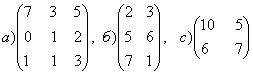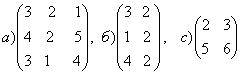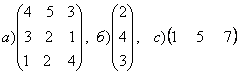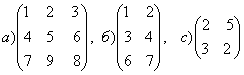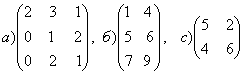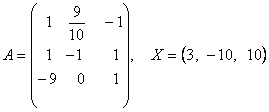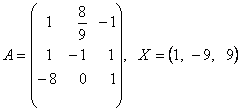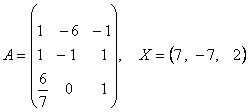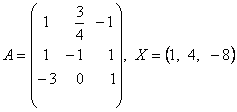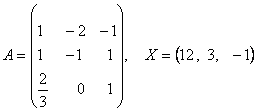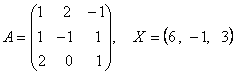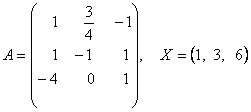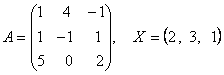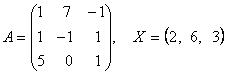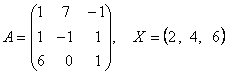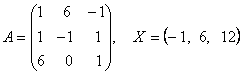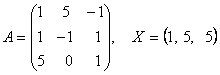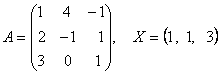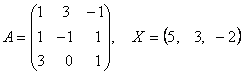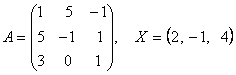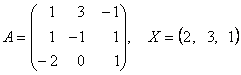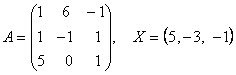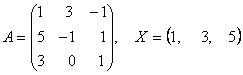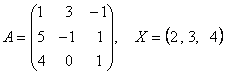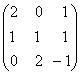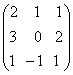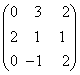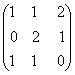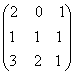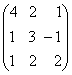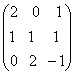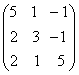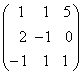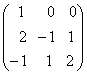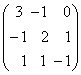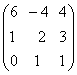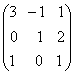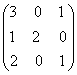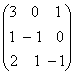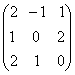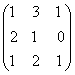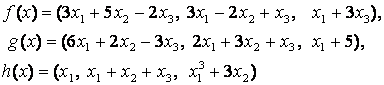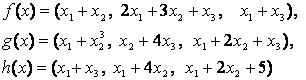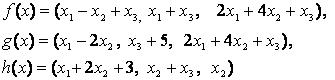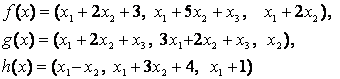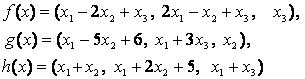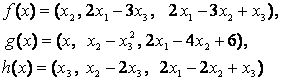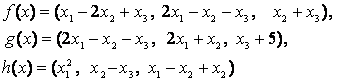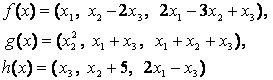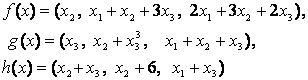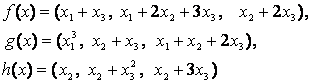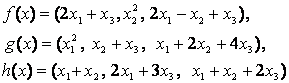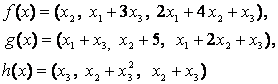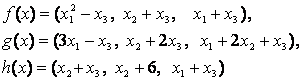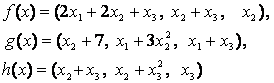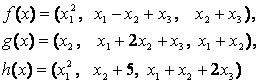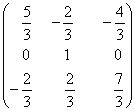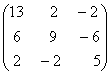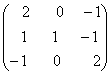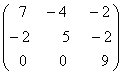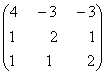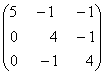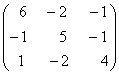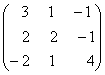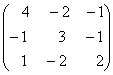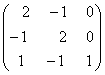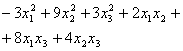Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ СВЯЗИ
Кафедра высшей математики
АЛГЕБРА
Методические указания и задания к расчетно-графическим работам
для студентов специальности 5В060200-«Информатика»
Часть 3
Алматы 2012
Составители: Т. Кайырбеков, Ж.С. Абдулланова, Б.Ж. Толеуова.Алгебра. Методические указания и задания к расчетно-графическим работам. Часть 3.-Алматы: АУЭС, 2012.-21с.
Методическое указание подготовлено в соответствии с типовой программой по курсу «Алгебра» для специальности «Информатика».
Методические указания и задания к РГР содержат задачи курса алгебры для специальности «Информатика» АУЭС: «Линейные преобразования пространства. Квадратичные формы линейного отображения».
Даны основные теоретические вопросы программы и решение типового варианта.
Введение
Это методическое указание представляет собой 3-ю часть расчетно-графической работы по курсу «Алгебра», который изучается студентами специальности «Информатика» на первом семестре.
Так как были изданы 1 и 2-е части этого курса, которые охватили курс высшей алгебры, называемые линейной алгеброй с элементами аналитической геометрии и алгебры многочленов, появилась необходимость выпуска 3-ей части.
Расчетно-графическая работа написана в соответствии с действующей программой по курсу «Алгебра» для студентов специальности «Информатика». Настоящее методическое указание адресовано преподавателям и студентам и предназначено для проведения самостоятельной работы во время аудиторных занятий и выдачи индивидуальных домашних заданий. Здесь содержится материал по линейным преобразованиям пространства, по основным характеристикам линейного оператора и квадратичным формам.
Данный РГР состоит из 12 заданий (10 заданий 1-го уровня сложности и 2 задания 2-го уровня сложности) по 30 вариантов каждый. В конце приведено решение типового варианта, где дано подробное решение каждого задания
1-го уровня сложности. Решение заданий 2-го уровня сложности предоставляется для самостоятельного решения студентам. Также приводятся основные теоретические вопросы, которые должны освоить студенты по этому разделу высшей алгебры.
Расчетно-графическая работа №3
Тема: Линейные преобразования пространства. Квадратичные формы.
Цель: научить студентов применять теоретические знания для определения матрицы, характеристического уравнения, собственных зачений и собственных векторов линейного преобразования пространства, а также привить навыки нахождения матрицы и ранга квадратичной формы и приведения ее к каноническому виду с помощью ортогонального преобразования и метода Лагранжа.
Задания первого уровня
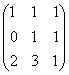
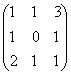
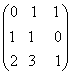
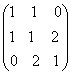
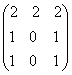
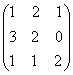
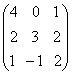
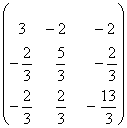
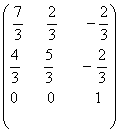
1-задание. Какими матрицами определяется линейное преобразование в трехмерном пространстве?
|
№ |
Матрицы |
№ |
Матрицы |
||
|
1 |
|
2 |
|
||
|
3 |
|
4 |
|
||
|
5 |
|
6 |
|
||
|
7 |
|
8 |
|
||
|
9 |
|
10 |
|
||
|
11 |
|
12 |
|
||
|
13 |
|
14 |
|
||
|
15 |
|
16 |
|
||
|
17 |
|
18 |
|
||
|
19 |
|
20 |
|
||
|
21 |
|
22 |
|
||
|
23 |
|
24 |
|
||
|
25 |
|
26 |
|
||
|
27 |
|
28 |
|
||
|
29 |
|
30 |
|
||
2-задание. В трехмерном пространстве линейное преобразование 
задано в базисе 
вектором 
и матрицей 
.
Найти 
?
(
).
|
№ |
Матрица |
№ |
Матрица |
|
1 |
|
2 |
|
|
3 |
|
4 |
|
|
5 |
|
6 |
|
|
7 |
|
8 |
|
|
9 |
|
10 |
|
|
11
|
|
12 |
|
|
13 |
|
14 |
|
|
15 |
|
16 |
|
|
17 |
|
18 |
|
|
19 |
|
20 |
|
|
21 |
|
22 |
|
|
23 |
|
24 |
|
|
25 |
|
26 |
|
|
27 |
|
28 |
|
|
29 |
|
30 |
|
3-задание. Линейное
преобразование пространства в базисе задано матрицей . Найти матрицу
(
) линейного преобразования в базисе 
(для всех вариантов
матрица перехода Т находится из следующего разложения:
.
|
№ |
|
№ |
|
№ |
|
№ |
|
|
|
1 |
|
2 |
|
3 |
|
4 |
|
|
|
5 |
|
6 |
|
7 |
|
8 |
|
|
|
9 |
|
10 |
|
11 |
|
12 |
|
|
|
13 |
|
14 |
|
15 |
|
16 |
|
|
|
17 |
|
18 |
|
19 |
|
20 |
|
|
|
21 |
|
22 |
|
23 |
|
24 |
|
|
|
25 |
|
26 |
|
27 |
|
28 |
|
|
|
29 |
|
30 |
|
31 |
|
32 |
|
|
4-задание. В трехмерном пространстве заданы линейные
преобразования
.
Определить, какое из этих преобразований будет линейным.
|
№ |
Линейные преобразования |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10
|
|
|
11 |
|
|
12 |
|
|
13 |
|
|
15 |
|
|
16 |
|
|
17
|
|
|
18 |
|
|
19 |
|
|
20 |
|
|
21 |
|
|
22 |
|
|
23 |
|
|
24 |
|
|
25 |
|
|
26 |
|
|
27 |
|
|
28 |
|
|
29 |
|
|
30 |
|
5-задание. В трехмерном пространстве линейное преобразование в
определенном базисе задано матрицей . Найти собственные значения этой матрицы.
|
№ |
|
№ |
|
№ |
|
|
1 |
|
2 |
|
3 |
|
|
4 |
|
5 |
|
6 |
|
|
7 |
|
8 |
|
9 |
|
|
10 |
|
11 |
|
12 |
|
|
13 |
|
14 |
|
15 |
|
|
16 |
|
17 |
|
18 |
|
|
19 |
|
20 |
|
21 |
|
|
22 |
|
23 |
|
24. |
|
|
25 |
|
26 |
|
27 |
|
|
28 |
|
29 |
|
30 |
|
6-задание. Найти собственные векторы соответствующих собственных значений матриц из задания 5.
7-задание. Найти матрицу С, приводящую к диагональному виду
матрицу линейного
преобразования пространства . Матрица 
является диагональной матрицей.
|
№ |
|
№ |
|
№ |
|
№ |
|
№ |
|
||||
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
||||
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
||||
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
||||
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
||||
|
21 |
|
22 |
|
23 |
|
24 |
|
25 |
|
||||
|
26 |
|
27 |
|
28 |
|
29 |
|
30 |
|
||||
8-задание.Записать квадратичные формы в матричном виде.
|
№ |
|
№ |
|
|
1 |
|
2 |
|
|
3 |
|
4 |
|
|
5 |
|
6 |
|
|
7 |
|
8 |
|
|
9 |
|
10 |
|
|
11 |
|
12 |
|
|
13 |
|
14 |
|
|
15 |
|
16 |
|
|
17 |
|
18 |
|
|
19 |
|
20 |
|
|
21 |
|
22 |
|
|
23 |
|
24 |
|
|
25 |
|
26 |
|
|
27 |
|
28 |
|
|
29 |
|
30 |
|
9-задание. Найти ранг квадратичной формы из задания 8.
10-задание. Исследовать на знакоопределенность квадратичную форму из задания 8.
Задания второго уровня
11-задание. Привести к каноническому виду по методу Лагранжа квадратичную форму из задания 8.
12-задание. Привести к каноническому виду с помощью ортогонального преобразования квадратичную форму из задания 8.
|
№ |
|
№ |
|
||
|
1 |
|
2 |
|
||
|
3 |
|
4 |
|
||
|
5 |
|
6 |
|
||
|
7 |
|
8 |
|
||
|
9 |
|
10
|
|
||
|
11
|
|
12
|
|
||
|
13
|
|
14
|
|
||
|
15
|
|
16
|
|
||
|
17
|
|
18
|
|
||
|
19
|
|
20
|
|
||
|
21
|
|
22
|
|
||
|
23
|
|
24
|
|
||
|
25
|
|
26
|
|
||
|
27
|
|
28
|
|
||
|
29 |
|
30
|
|
||
Решение типового варианта
1-задание. Какими матрицами определяется линейное преобразование в трехмерном пространстве?
.
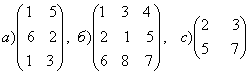Решение. В n-мерном пространстве линейному преобразованию соответствует квадратная
матрица n-го порядка. В нашей задаче линейное преобразование отображает
трехмерное пространство. Поэтому ему соответствует квадратная матрица 3-го
порядка, т.е. ответом является вариант б).
2-задание. В трехмерном пространстве линейное преобразование задано в базисе вектором векторы и матрицей .
.
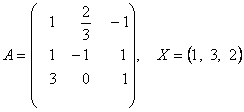Найти ?
().
Решение. В этом заданий мы найдем связь между координатами
образа и оригинала, т.е. . Пространство является трехмерным, поэтому
.
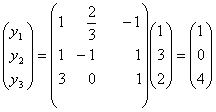Отсюда 
.
Поэтому 
.
3-задание. Линейное преобразование пространства в базисе задано матрицей . Найти матрицу () линейного преобразования в базисе (для всех вариантов
матрица перехода Т находится из следующего разложения: .
Решение.Из заданного разложения найдем матрицу перехода Т:
.
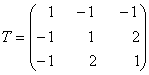Определитель этой матрицы не равен нулю, поэтому она будет матрицей
перехода. В базисе 
матрицу
линейного
проебразования можно
вычислить с помощью следующей формулы: . Из этой формулы следует, что надо сперва
найти обратную матрицу для матрицы перехода Т. Обратная матрица Т будет равна
.
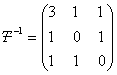Матрица линейного преобразования в базисе задана следующей
матрицей
.
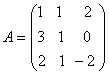Теперь
вычислим искомую матрицу: 
.
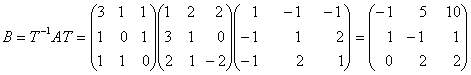4-задание. В трехмерном пространстве заданы линейные
преобразования 
.Определить,
какое из этих преобразований будет линейным
Решение. Для того, чтобы определить, какое из них линейное, достаточно проверить следующие два условия:
Сначала проверим условие 1) для преобразования f(x).
Положим 
.Тогда 
, и отсюда
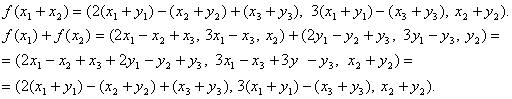
Из этого выражения очевидно, что 
.
Проверим 2)
условие для преобразования f(x). 
Итак, выполняются два условия линейности преобразования. Отсюда следует, что преобразование f(x) линейное.
Теперь проверим эти условия для преобразования g(x).
Положим .
Тогда
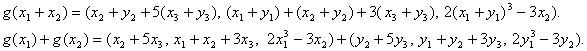
Отсюда 
Тогда получается, что
, т.е. не выполняется
условие 1).
Итак, преобразование g(x) не является линейным.
5-задание. В трехмерном пространстве линейное преобразование в
определенном базисе задано матрицей А
.
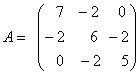Найти собственные значения этой матрицы.
Решение. Только действительные корни характеристического уравнения могут быть собственными числами линейного преобразования.
Составим характеристическое
уравнение
для матрицы
:
.
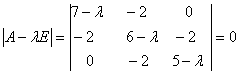Вычислив этот определитель, найдем такое уравнение:
.
Чтобы решить это уравнение, нужно его разложить на множители:
.
Отсюда 
. Решая уравнение 
, получим корни 
. Итак, собственными
значениями матрицы будут
следующие числа: 
.
6-задание. Найти собственные векторы соответствующих собственных значений матриц из задания 5.
Решение. Любой ненулевой вектор х линейного преобразования называется собственным
вектором линейного преобразования, если существует действительное число 
, для которой выполняется
следующее условие 
Или
это равенство можно записать в таком виде
.
Раскрывая это матричное уравнение, получим следующую систему:
.
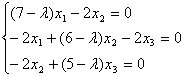Теперь найдем собственные векторы, соответствующие собственным
значениям .Для этого каждое
собственное значение подставим в систему (1) :
.
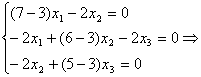
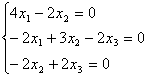Ранг матрицы этой системы будет равен 
. Из первых двух уравнений
системы получим 
.
Теперь, положив , что 
,
получим следующий собственный вектор 
. Это собственный вектор соответсвующий
собственному значению 
.
Далее
.
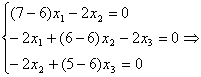
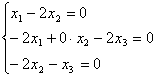Ранг матрицы этой системы равен . Решив систему, получим собственный вектор
, который
соответствует собственному значению 
.
Аналогичным образом найдем собственный
вектор для собственного значения 
, который будет равен 
.
7-задание. Найти матрицу С, приводящую к диагональному виду
матрицу линейного
преобразования пространства . Матрица является диагональной матрицей.
.
Решение. Сначала напишем характеристическое уравнение для матрицы :
.
Решая это уравнение, получим : 
, 
.
Теперь найдем собственные векторы, соответствующие
собственным значениям 
. Для этого рассмотрим
следующую систему:
.
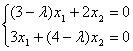Положим 
.
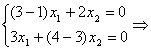
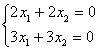Решив эту систему, получим 
. Итак, собственному значению 
соответствует
собственный вектор 
;
собственному значению 
соответствует
собственный вектор 
.
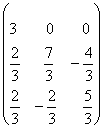
Таким образом, составим матрицу С, приводящую матрицу к диагональному виду:
.
Обратная матрица для этой матрицы будет равна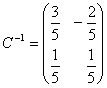 
.
Матрица
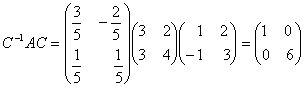будет
диагональной матрицей.
8-задание.Записать квадратичную форму в матричном виде.
.
Решение. Матрицу этой квадратичной формы запишем в таком виде
.
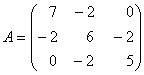Если обозначим неизвестные через матрицу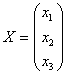 
, а ее транспонированную матрицу обозначим
через 
, то
данную квадратичную форму можно заисать и в такой матричной форме:
.
Или 
.
9-задание. Найти ранг квадратичной формы из задания 8.
.
Решение. Рангом квадратичной формы называется ранг ее матрицы.
Чтобы найти ранг данной квадратичной формы, нужно записать ее матрицу
.
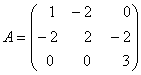Ранг этой матрицы равен 
. Поэтому и ранг квадратичной формы тоже
будет равен 3.
10-задание. Исследовать на знакоопределенность квадратичную форму из задания 8.
.
Решение. Действительная квадратичная форма положительно определена тогда и только тогда, когда главные миноры положительны .
Действительная квадратичная форма отрицательно определена тогда и только тогда, когда главные миноры четного порядка ее матрицы были положительны, а нечетного порядка-отрицательны.
Напишем матрицу данной квадратичной формы:
.
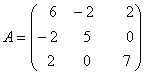Теперь будем вычислять главные миноры:
.
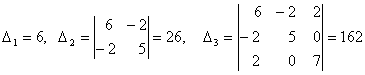Все главные миноры положительны, следовательно данная квадратичная форма является положительно определенной.
Теоретические вопросы
1. Линейные преобразования пространства и его матрица.
2. Связь между матрицами в различных базисах. Подобные матрицы.
3. Число и характеристическое уравнение линейного преобразования.
4. Собственный вектор линейного преобразования.
5. Ортогональная матрица.
6. Квадратичная форма, ее матрица и ранг.
7. Матричная форма квадратичной формы.
8. Знакоопределенные квадратичные формы.
9. Приведение квадратичной формы к каноническому и нормальному виду.
Список литературы
1. Апатенок Р.Ф., Маркина А.М. и др. Сборник задач по линейной алгебре. -Мн.:Высш. шк.,1980.-192 с.
2. Мантуров О.В., Матвеев Н.А. «Курс высшей математики»-М.:Высш.шк., 1986.-480 с.
3. Апатенок Р.Ф., Маркина А.М. и др. Элементы линейной алгебры и аналитической геометрии.-Мн.:Высш. шк.,1986.-272 с.
4. Кузнецов А.А. Сборник заданий по высшей математике: типовые расчеты. - М.:Высш. шк.,1983.-176 с.
5. Письменный Д.Т. Конспект лекций по высшей математике.-М.:Айрис- пресс, 2010.-608 с.
6. Письменный Д.Т. Сборник задач по курсу высшей математики.- М.:Айрис- пресс, 2009.-592 с.
Содержание
Введение 3
Расчетно-графическая работа № 3 4
Задания первого уровня 4
Задания второго уровня 14
Решение типового варианта 15
Теоретические вопросы 20
Список литературы 21