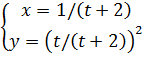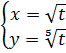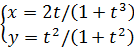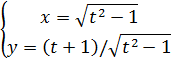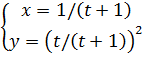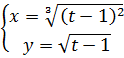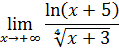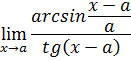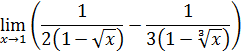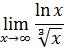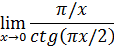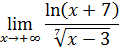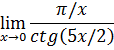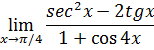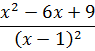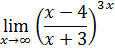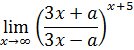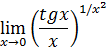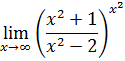Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра высшей математики
ВВЕДЕНИЕ В АНАЛИЗ
Методические указания к расчетно-графической работе
для студентов специальности 5В060200 – Информатика всех форм обучения
3-часть
Алматы 2012
СОСТАВИТЕЛИ: Толеуова Б.Ж., Кушербаева У. Введение в анализ. Методические указания к расчетно-графическим работам для студентов специальности 5В060200 – Информатика всех форм обучения. 3-часть -Алматы: АУЭС, 2011.- 17 стр.
Настоящие методические указания к расчетно-графическим работам для студентов специальности 5В060200 – Информатика всех форм обучения составлены в соответствии с программой дисциплины «Введение в анализ» по разделу «Производные и дифференциалы высших порядков. Применение
дифференциального исчисления к исследованию функции».
Содержатся варианты заданий, приведены необходимые теоретические сведения. Типовые задачи даются с подробными решениями.
Ил. 1, табл. 13, библиогр. – 5 назв.
![]()
Рецензент: доцент Койлышев У.К.
Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2011 г.
ã НАО «Алматинский университет энергетики и связи», 2012 г.
Теоретические вопросы
1. Производные и дифференциалы высших порядков.
2. Дифференцирование параметрически заданной функции.
3. Основные теоремы дифференциального исчисления.
4. Раскрытие неопределенностей. Правило Лопиталя.
5. Формула Тейлора. Разложение некоторых функций по формуле
Маклорена.
6. Признаки монотонности функции. Экстремумы функции.
7. Выпуклость, вогнутость графика функции. Точки перегиба.
8. Асимптоты графика функции. Исследование функции с помощью
производной. Построение графика функции.
Задания первого уровня
1-задание. Для данной функции ![]() и аргумента
и аргумента ![]() вычислить
вычислить ![]()
|
№ |
|
|
№ |
|
|
|
1.1 |
|
|
1.2 |
|
1 |
|
1.3 |
|
0 |
1.4 |
|
0 |
|
1.5 |
|
0 |
1.6 |
|
0 |
|
1.7 |
|
π |
1.8 |
|
1 |
|
1.9 |
|
2 |
1.10 |
|
0 |
|
1.11 |
|
0 |
1.12 |
|
2 |
|
1.13 |
|
|
1.14 |
|
|
|
1.15 |
|
|
1.16 |
|
|
|
1.17 |
|
1 |
1.18 |
|
1 |
|
1.19 |
|
|
1.20 |
|
3 |
|
1.21 |
|
|
1.22 |
|
|
|
1.23 |
|
|
1.24 |
|
1 |
|
1.25 |
|
|
1.26 |
|
1 |
|
1.27 |
|
|
1.28 |
|
1 |
|
1.29 |
|
|
1.30 |
|
|
2-задание.
Записать формулу
![]() для функции из задания 1
для функции из задания 1
3-задание. Найти ![]() функции, заданной параметрически
функции, заданной параметрически
|
№ |
Функция |
№ |
Функция |
|
3.1 |
|
3.2 |
|
|
3.3 |
|
3.4 |
|
|
3.5 |
|
3.6 |
|
|
3.7 |
|
3.8 |
|
|
3.9 |
|
3.10 |
|
|
3.11 |
|
3.12 |
|
|
3.13 |
|
3.14 |
|
|
3.15 |
|
3.16 |
|
|
3.17 |
|
3.18 |
|
|
3.19 |
|
3.20 |
|
|
3.21 |
|
3.22 |
|
|
3.23 |
|
3.24 |
|
|
3.25 |
|
3.26 |
|
|
3.27 |
|
3.28 |
|
|
3.29 |
|
3.30 |
|
4-задание. Найти указанные пределы, используя правило Лопиталя
|
№ |
а) |
б) |
|
4.1 |
|
|
|
4.2 |
|
|
|
4.3 |
|
|
|
4.4 |
|
|
|
4.5 |
|
|
|
4.6 |
|
|
|
4.7 |
|
|
|
4.8 |
|
|
|
4.9 |
|
|
|
4.10 |
|
|
|
4.11 |
|
|
|
4.12 |
|
|
|
4.13 |
|
|
|
4.14 |
|
|
|
4.15 |
|
|
|
4.16 |
|
|
|
4.17 |
|
|
|
4.18 |
|
|
|
4.19 |
|
|
|
4.20 |
|
|
|
4.21 |
|
|
|
4.22 |
|
|
|
4.23 |
|
|
|
4.24 |
|
|
|
4.25 |
|
|
|
4.26 |
|
|
|
4.27 |
|
|
|
4.28 |
|
|
|
4.29 |
|
|
|
4.30 |
|
|
5-задание.
С помощью
дифференциала приближенно вычислить
данную величину
|
№ |
Величина |
№ |
Величина |
№ |
Величина |
|
5.1 |
|
5.2 |
|
5.3 |
|
|
5.4 |
|
5.5 |
|
5.6 |
|
|
5.7 |
|
5.8 |
|
5.9 |
|
|
5.10 |
|
5.11 |
|
5.12 |
|
|
5.13 |
|
5.14 |
|
5.15 |
|
|
5.16 |
|
5.17 |
|
5.18 |
|
|
5.19 |
|
5.20 |
|
5.21 |
|
|
5.22 |
|
5.23 |
|
5.24 |
|
|
5.25 |
|
5.26 |
|
5.27 |
|
|
5.28 |
|
5.29 |
|
5.30 |
|
6-задание. Разложить по формуле Маклорена данную функцию до члена
с
![]() с остаточным членом в форме Лагранжа
с остаточным членом в форме Лагранжа
|
№ |
|
№ |
|
№ |
|
|
6.1 |
|
6.2 |
|
6.3 |
|
|
6.4 |
|
6.5 |
|
6.6 |
|
|
6.7 |
|
6.8 |
|
6.9 |
|
|
6.10 |
|
6.11 |
|
6.12 |
|
|
6.13 |
|
6.14 |
|
6.15 |
|
|
6.16 |
|
6.17 |
|
6.18 |
|
|
6.19 |
|
6.20 |
|
6.21 |
|
|
6.22 |
|
6.23 |
|
6.24 |
|
|
6.25 |
|
6.26 |
|
6.27 |
|
|
6.28 |
|
6.29 |
|
6.30 |
|
7-задание . Найти интервалы монотонности и экстремумы заданной функции
|
№ |
|
№ |
|
№ |
|
|
7.1 |
|
7.2 |
|
7.3 |
|
|
7.4 |
|
7.5 |
|
7.6 |
|
|
7.7 |
|
7.8 |
|
7.9 |
|
|
7.10 |
|
7.11 |
|
7.12 |
|
|
7.13 |
|
7.14 |
|
7.15 |
|
|
7.16 |
|
7.17 |
|
7.18 |
|
|
7.19 |
|
7.20 |
|
7.21 |
|
|
7.22 |
|
7.23 |
|
7.24 |
|
|
7.25 |
|
7.26 |
|
7.27 |
|
|
7.28 |
|
7.29 |
|
7.30 |
|
8-задание. Найти интервалы выпуклости, вогнутости и точки перегиба кривой
из задания 7
9-задание. Провести полное исследование и построить график функции
из задания 7
Задания второго уровня
10-задание.
Записать формулу для производной ![]() -го порядка указанной
-го порядка указанной
функции
|
№ |
|
№ |
|
№ |
|
|
10.1 |
|
10.2 |
|
10.3 |
|
|
10.4 |
|
10.5 |
|
10.6 |
|
|
10.7 |
|
10.8 |
|
10.9 |
|
|
10.10 |
|
10.11 |
|
10.12 |
|
|
10.13 |
|
10.14 |
|
10.15 |
|
|
10.16 |
|
10.17 |
|
10.18 |
|
|
10.19 |
|
10.20 |
|
10.21 |
|
|
10.22 |
|
10.23 |
|
10.24 |
|
|
10.25 |
|
10.26 |
|
10.27 |
|
|
10.28 |
|
10.29 |
|
10.30 |
|
11-задание. Найти указанные пределы, используя правило Лопиталя
|
№ |
а) |
б) |
|
11.1 |
|
|
|
11.2 |
|
|
|
11.3 |
|
|
|
11.4 |
|
|
|
11.5 |
|
|
|
11.6 |
|
|
|
11.7 |
|
|
|
11.8 |
|
|
|
11.9 |
|
|
|
11.10 |
|
|
|
11.11 |
|
|
|
11.12 |
|
|
|
11.13 |
|
|
|
11.14 |
|
|
|
11.15 |
|
|
|
11.16 |
|
|
|
11.17 |
|
|
|
11.18 |
|
|
|
11.19 |
|
|
|
11.20 |
|
|
|
11.21 |
|
|
|
11.22 |
|
|
|
11.23 |
|
|
|
11.24 |
|
|
|
11.25 |
|
|
|
11.26 |
|
|
|
11.27 |
|
|
|
11.28 |
|
|
|
11.29 |
|
|
|
11.30 |
|
|
12-задание. Используя разложение соответствующей функции по формуле Маклорена, вычислить указанную величину приближенно с заданной
степенью
точности ![]() , используя разложение в степенной ряд
, используя разложение в степенной ряд
|
№ |
|
|
№ |
|
|
|
12.1 |
|
0,0001 |
12.2 |
|
0,01 |
|
12.3 |
|
0,00001 |
12.4 |
|
0,001 |
|
12.5 |
|
0,001 |
12.6 |
|
0,0001 |
|
12.7 |
|
0,0001 |
12.8 |
|
0,0001 |
|
12.9 |
|
0,00001 |
12.10 |
|
0,001 |
|
12.11 |
|
0,001 |
12.12 |
|
0,001 |
|
12.3 |
|
0,001 |
12.14 |
|
0,001 |
|
12.15 |
|
0,001 |
12.16 |
|
0,00001 |
|
12.17 |
|
0,0001 |
12.18 |
|
0,001 |
|
12.19 |
|
0,0001 |
12.20 |
|
0,001 |
|
12.21 |
|
0,001 |
12.22 |
|
0,0001 |
|
12.23 |
|
0,0001 |
12.24 |
|
0,001 |
|
12.25 |
|
0,001 |
12.26 |
|
0,0001 |
|
12.27 |
|
0,0001 |
12.28 |
|
0,001 |
|
12.29 |
|
0,001 |
12.30 |
|
0,001 |
Методические указания к разделу «Производные и дифференциалы высших порядков. Применение дифференциального исчисления к исследованию функции». Решение типового варианта
1.
Дана функция ![]() . Найти
. Найти ![]()
Решение. Последовательно находим:
![]() ,
, 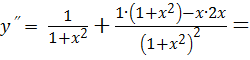
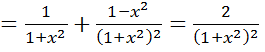 ,
, 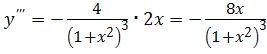 ,
,
![]()
2.
Записать формулу ![]() для функции из задания 1.
для функции из задания 1.
Решение. В
предыдущем примере была найдена ![]() . Так как
. Так как
![]() , то
, то ![]() . Значит,
. Значит, 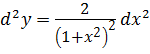 .
.
3.
Найти ![]() ,
если
,
если ![]() .
.
Решение. Производные функций, заданной параметрически, вычисляются по формулам
![]() ,
, 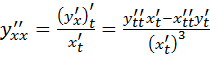 .
.
Тогда
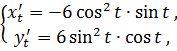
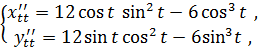
отсюда
![]() ,
,
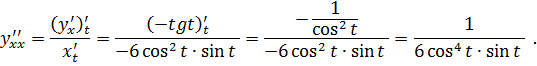
4. Найти указанные пределы, используя правило Лопиталя.
а) 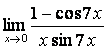 .
.
Решение. 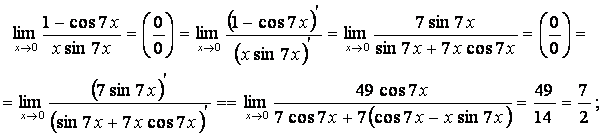
б) 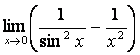 .
.
Решение. При значении ![]() получаем неопределенность вида
получаем неопределенность вида
![]() . Т.к
правило Лопиталя применяется для непределенностей вида
. Т.к
правило Лопиталя применяется для непределенностей вида ![]() или
или
![]() ,
то приведем дроби к общему знаменателю и воспользуемся эквивалентностью
бесконечно малых величин:
,
то приведем дроби к общему знаменателю и воспользуемся эквивалентностью
бесконечно малых величин: 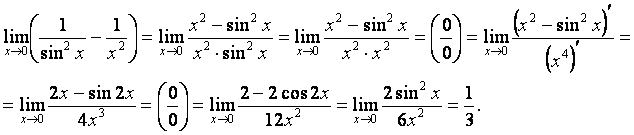
5. С помощью дифференциала приближенно
вычислить![]() .
.
Решение. Если
приращение аргумента ![]() по абсолютной величине достаточно мало, то дифференциал
функции в
точке
по абсолютной величине достаточно мало, то дифференциал
функции в
точке ![]() и ее приращение в этой точке будут приближенно
равны:
и ее приращение в этой точке будут приближенно
равны:
![]() ,
,
т.е. ![]() , откуда
, откуда ![]() . Введем функцию
. Введем функцию ![]() , где
, где ![]() ,
, ![]() ,
, ![]() .
.
Тогда
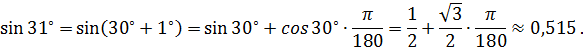
6.
Разложить
по формуле Маклорена функцию ![]() до члена с
до члена с ![]() с остаточным членом в форме Лагранжа.
с остаточным членом в форме Лагранжа.
Решение.![]() – целое положительное число. Пусть функция
– целое положительное число. Пусть функция ![]() определена
на сегменте
определена
на сегменте ![]() , дифференцируема
, дифференцируема
![]() раз
на этом сегменте и существует конечная производная
раз
на этом сегменте и существует конечная производная ![]() в
интервале
в
интервале ![]() . Тогда
для
. Тогда
для ![]() верна
формула Тейлора:
верна
формула Тейлора:
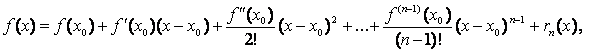
где ![]() ,
, ![]() ,
–– остаточный
член в форме Лагранжа.
,
–– остаточный
член в форме Лагранжа.
При ![]() получаем формулу Маклорена:
получаем формулу Маклорена:
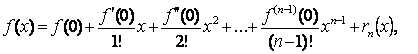
где ![]() ,
, ![]() .
.
Находим
![]()
![]()
![]() ...
... ![]()
![]() .
.
Соответственно,
![]()
![]()
![]()
![]()
![]()
Подставляя полученные значения в формулу Маклорена, получаем разложение данной функции в следующем виде:
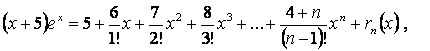
где ![]() ,
, ![]() .
.
Отсюда разложение функции до члена с ![]() имеет вид
имеет вид
![]()
где ![]() – остаточный член в форме Лагранжа.
– остаточный член в форме Лагранжа.
7.
Найти интервалы монотонности и
экстремумы функции 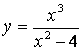 .
.
Решение. Находим производную:
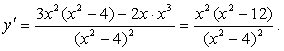
Приравниваем ее нулю и находим стационарные точки:
![]()
![]()
![]()
![]()
![]() ,
, ![]()
Результаты
исследования введем в таблицу:![]()
|
|
|
|
|
|
0 |
|
|
|
|
|
|
+ |
0 |
– |
– |
0 |
– |
– |
0 |
+ |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
возр |
|
убыв |
убыв |
нет экстр. |
убыв |
убыв |
|
возр |
8.
Найти интервалы выпуклости,
вогнутости и точки перегиба кривой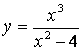 .
.
Решение. Имеем
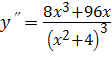 ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Результаты
исследования введем в таблицу:![]()
|
|
|
|
0 |
|
|
|
|
– |
+ |
0 |
– |
+ |
|
|
|
|
0 |
|
|
|
|
выпукла |
вогнута |
точка перегиба |
выпукла |
вогнута |
(0;0) – точка перегиба.
9.
Провести полное исследование и
построить график функции ![]() .
.
Решение. Полное исследование функции проведем по следующей схеме:
а) область определения функции и точки разрыва;
б) асимптоты графика функции;
в) точки пересечения графика функции с осями координат;
г) четность, нечетность функции;
д) интервалы монотонности, точки экстремума;
е) выпуклость, вогнутость кривой и точки перегиба;
ж) построение графика функции.
а) область определения функции ![]()
В точках ![]() находим односторонние
пределы:
находим односторонние
пределы:
![]() ,
, ![]() .
.
Итак, ![]()
![]() –
точки разрыва второго рода, а прямые
–
точки разрыва второго рода, а прямые ![]() и
и ![]() являются вертикальными асимптотами;
являются вертикальными асимптотами;
б) прямая ![]() , где
, где ![]()
![]()
является наклонной асимптотой. Определим, существуют ли для данной кривой наклонные асимптоты. Находим:
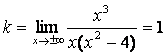 ,
, 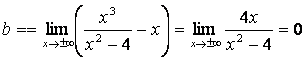 .
.
Таким образом, существует наклонная асимптота ![]()
в) точки пересечения с осями координат: если ![]()
![]()
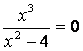
![]()
![]() ; если
; если ![]()
![]()
![]() .
Итак, точка пересечения с осями координат (0;0);
.
Итак, точка пересечения с осями координат (0;0);
г) т.к. 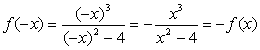 , функция нечетная,
т.е. график симметричен относительно начала координат;
, функция нечетная,
т.е. график симметричен относительно начала координат;
д) исследуем функцию на экстремум:
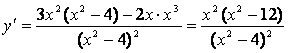 ,
,![]()
![]()
![]()
![]()
![]() ,
, ![]() - критические точки, точки
- критические точки, точки ![]() не входят в
область определения, поэтому они не являются критическими точками.
не входят в
область определения, поэтому они не являются критическими точками.
|
|
|
|
|
|
0 |
|
|
|
|
|
|
+ |
0 |
– |
– |
0 |
– |
– |
0 |
+ |
|
|
|
- |
|
|
0 |
|
|
|
|
|
|
возр |
|
убыв |
убыв |
нет экстр |
убыв |
убыв |
|
возр |
е) исследуем график функции на выпуклость, вогнутость и найдем точки перегиба:
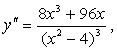
![]()
![]()
![]()
![]()
![]() .
.
|
|
|
|
0 |
|
|
|
|
– |
+ |
0 |
– |
+ |
|
|
|
|
0 |
|
|
|
|
выпукла |
вогнута |
точка перегиба |
выпукла |
вогнута |
(0;0) – точка перегиба;
ж) используя полученные данные, строим график функции:
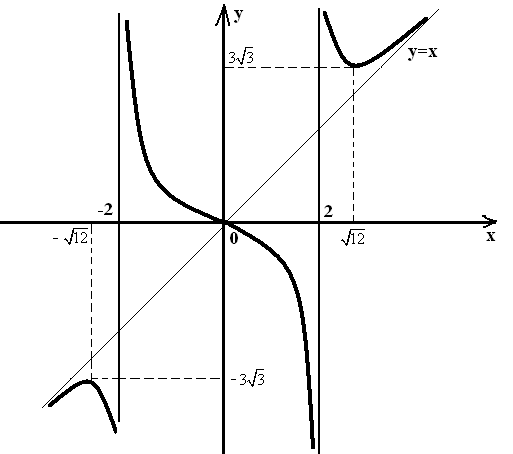
Замечание: используя нечетность функции, таблицу достаточно заполнить
на множестве ![]() .
.
Список литературы
1. Болгов В.А, Демидович Б.П., Ефимов А.В. и др. Сборник задач по математике. – М.: Наука, 1986.
2. Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. – М.: Наука, 1977.
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2 ч. Ч.1– М.: Издательский дом «ОНИКС 21 век»: Мир и Образование, 2003.
4. Апатенок Р.Ф., Маркина А.М., Попова Н.В., Хейнман В.Б. Сборник задач по линейной алгебре. – Мн.: Выш. школа, 1980.
5. Рябушко А.П., Бархатов В.В., Державец В.В., Юруть И. Е. Индивидуальные задания по высшей математике. – Мн.: Выш. школа, 1980.
Содержание
|
Теоретические вопросы |
3 |
|
Задания первого уровня |
3 |
|
Задания второго уровня |
8 |
|
Методические указания к разделу «Производные и дифференциалы высших порядков. Применение дифференциального исчисления к исследованию функции». Решение типового варианта |
10 |
|
Список литературы |
17 |
Сводный план 2011 г., поз. 231