Некоммерческое акционерное общество

АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра высшей математики

 

 

ДИСКРЕТНАЯ МАТЕМАТИКА И МАТЕМАТИЧЕСКАЯ ЛОГИКА

КОМБИНАТОРИКА

Методические указания и задания к расчетно-графическим работам

(для специальности 5В060200 – Информатика)

  

Алматы 2012 

Составитель: Ким Р.Е. Дискретная математика и математическая логика. Комбинаторика. Методические указания и задания к расчетно-графическим работам (для специальности 5В060200 – Информатика). -Алматы: АУЭС, 2012.- 28 стр.

 

Методические указания и задания к расчетно-графической работе №2 для студентов всех форм обучения специальности 5В060200 – Информатика составлены в соответствии с программой дисциплины «Дискретная математика и математическая логика» по разделу «Комбинаторика».

Приведены основные теоретические вопросы программы. Дано решение типового варианта.

Ил. 1, табл. 15, библиогр. – 7 назв.

Рецензент: канд. техн. наук,  доцент     Ни А.Г.

 

Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2012 г.

 

ã   НАО «Алматинский университет энергетики и связи», 2012 г.

                                                                       Сводный план  2012 г., поз. 181  

1 Расчетно-графическая работа № 2. Комбинаторика

 

1.1 Введение

 

Дисциплина «Дискретная математика и математическая логика» является неотъемлемой частью математического образования будущих инженеров. Аппарат  дискретной математики является основным инструментом исследования специалистов, занимающихся созданием  и эксплуатацией компьютеров, языков программирования, средств передачи и обработки информации, автоматизированных систем управления и проектирования, а язык дискретной математики – это язык, который используется в научной и технической литературе по данным проблемам.

Цель данной работы – вооружение будущих инженеров современным математическим аппаратом, который можно определить как взаимосвязанную совокупность языка, моделей и методов  математики, ориентированную на решение прикладных задач, возникающих в области информационных технологий, формирование у студентов знаний и умений, которые образуют теоретический фундамент, необходимый для корректной постановки и решения проблем в области информатики, для осознания целей и ограничений при создании структур, алгоритмов и программ обработки информации.

В представленной методической разработке даны задания расчетно-графической работы №2. Задания соответствуют программе раздела «Комбинаторика» курса «Дискретная математика и математическая логика» и предназначены для студентов всех форм обучения. В работе рассмотрены основные типы задач комбинаторики. Приводится подробное решение типового варианта.

Номер варианта для студента очного отделения определяется  его порядковым номером в списке группы.

Номер варианта для студента заочного отделения определяется как остаток от деления номера шифра студента (номера его зачетной книжки) на 30. Если остаток равен нулю, то студент выполняет вариант № 30. Например: номер зачетной книжки равен 115614. Это число предстсавляется в виде: 115614 = 3853×30 + 24. Следовательно, студент должен выполнить задания варианта № 24, т.е. решить задачи под номерами с 1.24 по 16.24 включительно.

 

1.2 Расчётные  задания

 

1 В автомашине п мест. Сколькими способами п человек могут усесться в эту машину, если занять место водителя могут только k из них?

 

Т а б л и ц а 1

№

п

k

№

п

k

№

п

k

№

п

k

№

п

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.1

5

2

1.2

6

3

1.3

7

4

1.4

8

3

1.5

5

3

1.6

6

4

1.7

7

3

1.8

8

4

1.9

5

4

1.10

6

2

1.11

7

2

1.12

8

2

1.13

5

5

1.14

6

5

1.15

7

5

1.16

8

5

1.17

5

4

1.18

6

2

1.19

7

6

1.20

8

6

1.21

5

1

1.22

6

1

1.23

7

1

1.24

8

1

1.25

5

3

1.26

6

5

1.27

7

2

1.28

8

7

1.29

5

2

1.30

6

3

 

2 Позывные радиостанции должны начинаться с буквы W.

1) Скольким радиостанциям можно присвоить различные позывные, если позывные состоят из  k  букв, причем эти буквы могут повторяться?

2) Если позывные состоят из  m букв, которые не повторяются?

 

Т а б л и ц а  2

№

k

m

№

k

m

№

k

m

№

k

m

№

k

m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.1

3

5

2.2

4

3

2.3

5

4

2.4

6

5

2.5

7

3

2.6

4

4

2.7

3

4

2.8

7

4

2.9

5

3

2.10

6

3

2.11

5

5

2.12

6

4

2.13

3

3

2.14

7

5

2.15

4

4

2.16

6

3

2.17

7

3

2.18

4

3

2.19

3

3

2.20

5

3

2.21

7

4

2.22

5

4

2.23

6

4

2.24

4

4

2.25

3

4

2.26

3

5

2.27

7

5

2.28

6

5

2.29

5

5

2.30

4

5

 

3 Из п различных цифр (из множества {1,2,3,4,5,6,7,8,9}) составляются всевозможные числа, каждое из которых содержит не менее  k  цифр. Сколько таких чисел можно составить, если повторения цифр в числах запрещены?

 

Т а б л и ц а  3

№

п

k

№

п

k

№

п

k

№

п

k

№

п

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3.1

5

2

3.2

6

3

3.3

7

4

3.4

8

2

3.5

9

4

3.6

6

4

3.7

7

2

3.8

8

3

3.9

9

5

3.10

5

3

3.11

8

5

3.12

5

4

3.13

6

2

3.14

7

3

3.15

9

2

3.16

9

6

3.17

8

4

3.18

5

5

3.19

6

5

3.20

7

5

3.21

7

6

3.22

9

3

3.23

8

6

3.24

5

2

3.25

6

2

3.26

5

3

3.27

7

2

3.28

9

4

3.29

6

3

3.30

8

7

 

4 Сколько «слов» можно образовать из букв данного слова, если «слова» должны состоять:

                                                 а) из n  букв,     б) из k букв?

Т а б л и ц а  4

№

слово

п

k

№

слово

п

k

 

 

 

 

 

 

 

 

4.1

экзамен

7

3

4.2

консультация

12

7

4.3

магистр

7

5

4.4

компьютер 

9

6

4.5

высота

6

4

4.6

интервал

8

5

4.7

консультация

12

5

4.8

экзамен

7

5

4.9

компьютер 

9

4

4.10

магистр

7

3

4.11

интервал

8

3

4.12

высота

6

4

4.13

экзамен

7

4

4.14

консультация

12

8

4.15

магистр

7

3

4.16

компьютер 

9

7

4.17

высота

6

5

4.18

интервал

8

6

4.19

консультация

12

6

4.20

экзамен

7

4

4.21

компьютер 

9

5

4.22

магистр

7

5

4.23

интервал

8

4

4.24

высота

6

3

4.25

экзамен

7

5

4.26

консультация

12

9

4.27

магистр

7

4

4.28

компьютер 

9

3

4.29

высота

6

3

4.30

интервал

8

7

           

5 Сколькими способами из n человек можно избрать комиссию, состоящую из k членов?

 

Та б л и ц а  5

№

п

k

№

п

k

№

п

k

№

п

k

№

п

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5.1

6

3

5.2

7

2

5.3

8

4

5.4

9

3

355

10

2

5.6

7

4

5.7

8

3

5.8

9

4

5.9

10

4

5.10

6

4

5.11

8

2

5.12

9

5

5.13

10

3

5.14

6

4

5.15

7

3

5.16

9

2

5.17

10

5

5.18

6

2

5.19

7

5

5.20

8

5

5.21

10

3

5.22

6

3

5.23

7

3

5.24

8

3

5.25

9

3

5.26

6

4

5.27

7

4

5.28

8

4

5.29

9

4

5.30

10

4

 

6 Сколькими способами можно распределить n выпускников по трем  фирмам, если в одной из них  имеется  m, в другой  — k и в третьей — p вакантных мест.

(Ответ записать в виде произведения сомножителей, не вычисляя его.)

 

Та б л и ц а  6

№

п

m

k

p

№

п

m

k

p

№

п

m

k

p

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6.1

30

10

8

12

6.2

20

5

7

8

6.3

40

13

16

11

6.4

30

11

9

10

6.5

20

6

4

10

6.6

40

12

15

13

6.7

30

7

12

11

6.8

20

4

7

9

6.9

40

11

17

12

6.10

30

12

9

9

6.11

20

3

8

9

6.12

40

10

17

13

6.13

30

13

8

9

6.14

20

9

5

6

6.15

40

9

15

16

6.16

30

7

5

18

6.17

20

10

5

5

6.18

40

17

14

9

6.19

30

8

11

11

6.20

20

8

4

8

6.21

40

14

16

10

6.22

30

6

9

15

6.23

20

6

8

6

6.24

40

18

15

7

6.25

30

8

15

7

6.26

20

7

3

10

6.27

40

10

11

9

6.28

30

7

9

14

6.29

20

5

4

11

6.30

40

6

17

7

 

7 Имеется N1 разных книг одного автора, N2 – второго и N3 – третьего.

Каким числом способов можно выбрать

а) две книги одного автора?

б) три книги одного автора?

в) одну книгу первого автора, две – второго и три – третьего?

 

Т а б л и ц а  7

№

N1

N2

N3

№

N1

N2

N3

№

N1

N2

N3

 

 

 

 

 

 

 

 

 

 

 

 

7.1

6

8

7

7.2

10

9

5

7.3

6

9

7

7.4

7

9

8

7.5

11

10

6

7.6

7

10

8

7.7

8

5

9

7.8

7

6

7

7.9

8

11

9

7.10

9

6

10

7.11

8

7

8

7.12

9

7

10

7.13

10

7

11

7.14

9

8

9

7.15

5

8

6

7.16

6

8

7

7.17

10

9

5

7.18

6

9

7

7.19

7

9

8

7.20

11

10

6

7.21

7

10

8

7.22

8

5

9

7.23

7

6

7

7.24

8

11

9

7.25

9

6

10

7.26

8

7

8

7.27

9

7

10

7.28

10

7

11

7.29

9

8

9

7.30

5

8

6

        

8 Сколькими способами можно составить букет из k цветов, если в наличии есть цветы  n сортов?

 

Т а б л и ц а  8

№

п

k

№

п

k

№

п

k

№

п

k

№

п

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

8.1

3

7

8.2

4

5

8.3

5

7

8.4

6

7

8.5

3

5

8.6

4

7

8.7

5

9

8.8

6

9

8.9

3

9

8.10

4

9

8.11

5

11

8.12

6

11

8.13

3

11

8.14

4

11

8.15

5

13

8.16

6

13

8.17

3

15

8.18

4

15

8.19

5

15

8.20

6

13

8.21

3

17

8.22

4

5

8.23

5

9

8.24

6

15

8.25

3

7

8.26

4

7

8.27

5

7

8.28

6

7

8.29

3

11

8.30

4

9

 

9 Сколько различных «слов» можно получить, переставляя буквы в данном слове?

Т а б л и ц а  9

№

слово

№

слово

№

слово

9.1

информатика

9.2

программа

9.3

математика

9.4

алгебра

9.5

уравнение

9.6

производная

9.7

комбинаторика

9.8

включение

9.9

исключение

9.10

перестановка

9.11

сочетание

9.12

размещение

9.13

множество

9.14

университет

9.15

институт

9.16

теорема

9.17

пример

9.18

сложение

9.19

вычитание

9.20

умножение

9.21

деление

9.22

доказательство

9.23

истина

9.24

вероятность

9.25

элемент

9.26

семестр

9.27

сессия

9.28

тестирование

9.29

результат

9.30

принтер

 

10 Сколько существует целых положительных чисел, меньших 1000, которые

а) делятся и на a, и на b;

б) делятся  на a, но не делятся на b;

в) делятся  на b, но не делятся на a;

г) делятся  на a или на b;

д) не делятся ни на a, ни на b.

 

Т а б л и ц а  10

№

a

b

№

a

b

№

a

b

№

a

b

№

a

b

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

10.1

3

7

10.2

5

11

10.3

7

2

10.4

11

3

10.5

13

3

10.6

3

5

10.7

5

2

10.8

7

11

10.9

11

2

10.10

13

2

10.11

3

17

10.12

5

7

10.13

7

13

10.14

11

17

10.15

13

5

10.16

3

19

10.17

5

17

10.18

7

17

10.19

11

13

10.20

13

17

10.21

3

23

10.22

5

19

10.23

7

19

10.24

11

19

10.25

13

23

10.26

3

29

10.27

5

23

10.28

7

23

10.29

11

23

10.30

13

29

 

11 Сколько существует целых положительных чисел, меньших 1000, которые не делятся ни на a, ни на b, ни на  c.

 

Т а б л и ц а 11

№

a

b

c

№

a

b

c

№

a

b

c

 

 

 

 

 

 

 

 

 

 

 

 

11.1

2

3

5

11.2

3

5

7

11.3

5

7

11

11.4

2

5

7

11.5

3

7

11

11.6

5

11

13

11.7

2

7

11

11.8

3

11

13

11.9

5

13

17

11.10

2

11

13

11.11

3

13

17

11.12

5

17

19

11.13

2

13

17

11.14

3

17

19

11.15

5

19

23

11.16

2

17

19

11.17

3

19

23

11.18

5

23

29

11.19

2

19

23

11.20

3

23

29

11.21

5

29

31

11.22

2

23

29

11.23

3

29

31

11.24

5

31

37

11.25

2

29

31

11.26

3

31

37

11.27

5

37

41

11.28

2

31

37

11.29

3

5

41

11.30

5

41

43

 

12 В группе N студентов, из них: N1 человек владеют языком программирования СИ, N2 − Паскалем, N3 − Бейсиком, N12 студентов программируют на СИ и Паскале, N13 − на СИ и Бейсике, N23 − на Паскале и Бейсике, N123 человек знают все три языка и N0 не знают ни одного из них. По данным значениям найти недостающую информацию (заполнить пустую клетку):

 

Т а б л и ц а  12

№

N

N1

N2

N3

N12

N13

N23

N123

N0

 

 

 

 

 

 

 

 

 

 

12.1

15

6

4

5

3

2

2

1

 

12.2

18

 

3

7

1

4

1

0

6

12.3

 

7

5

6

4

4

3

2

11

12.4

17

4

2

 

2

3

1

1

7

12.5

22

5

3

5

2

2

3

2

 

12.6

16

4

3

6

3

2

3

 

11

12.7

21

3

3

 

1

2

2

1

9

12.8

19

6

 

7

2

3

3

1

9

12.9

 

5

3

5

2

4

2

1

8

12.10

18

9

4

7

3

 

2

2

6

12.11

24

10

6

12

4

5

4

 

6

12.12

20

8

5

6

3

3

 

2

7

12.13

14

 

4

7

2

3

2

1

5

12.14

15

4

5

3

3

2

2

0

 

12.15

 

6

3

8

5

2

3

2

9

12.16

15

 

4

5

3

2

2

1

6

12.17

18

8

3

 

1

4

1

0

6

12.18

20

7

5

6

 

4

3

2

11

12.19

17

4

2

9

2

3

 

1

7

12.20

22

5

 

5

2

2

3

2

14

12.21

16

4

3

6

 

2

3

0

11

12.22

 

3

3

10

1

2

2

1

9

12.23

19

6

4

7

2

 

3

1

9

12.24

14

5

3

5

2

4

2

 

8

12.25

18

9

4

 

3

5

2

2

6

12.26

24

10

6

12

4

5

 

3

6

12.27

 

8

5

6

3

3

2

2

7

12.28

14

4

4

7

 

3

2

1

5

12.29

15

4

 

3

3

2

2

0

10

12.30

18

6

3

8

5

2

3

2

 

 

13 Чему равен коэффициент при   xk ym   в разложении (1 + x + y)n ?

 

Т а б л и ц а 13

№

n

k

m

№

n

k

m

№

n

k

m

 

 

 

 

 

 

 

 

 

 

 

 

13.1

15

2

7

13.2

16

3

8

13.3

17

5

4

13.4

18

7

6

13.5

19

5

3

13.6

20

6

8

13.7

15

3

9

13.8

16

4

2

13.9

17

7

5

13.10

18

8

3

13.11

19

8

9

13.12

20

8

10

13.13

15

4

8

13.14

16

9

4

13.15

17

9

6

13.16

18

9

5

13.17

19

6

10

13.18

20

10

3

13.19

15

5

6

13.20

16

10

5

13.21

17

11

5

13.22

18

11

4

13.23

19

13

2

13.24

20

12

1

13.25

15

6

3

13.26

16

7

8

13.27

17

13

2

13.28

18

5

10

13.29

19

5

12

13.30

20

14

4

        

14 Найти решение для рекуррентных отношений.

 

Т а б л и ц а 14

№

отношение

№

отношение

 

 

 

 

14.1

а0 = 2;

а 1= 5;

аn = 5аn-1 – 6аn-2    при   n > 2;

14.2

а0 = 2;

а 1= 4;

аn = 7аn-1 – 12аn-2    при   n > 2;

14.3

а0 = 0;

а 1= 5;

аn = 9аn-1 – 20аn-2    при   n > 2;

14.4

а0 = 2;

а 1= 5;

аn = 7аn-1 – 12аn-2    при   n > 2;

14.5

а0 = 2;

а 1= 1;

аn = 2аn-1 + 2аn-2    при   n > 2;

14.6

а0 = 2;

а 1= – 1;

аn = – аn-1 + 6аn-2    при   n > 2;

14.7

а0 =3;

а 1= 21;

аn = 6аn-1 – 9аn-2    при   n > 2;

14.8

а0 = 2;

а 1= 6;

аn = 4аn-1 – 4аn-2    при   n > 2;

14.9

а0 = 1;

а 1= –8;

аn = – 4аn-1 – 4аn-2    при   n > 2;

14.10

а0 = –3;

а 1= 1;

аn = 2аn-1 – аn-2    при   n > 2;

14.11

а0 = 2;

а 1= 6;

аn = –2аn-1 – аn-2    при   n > 2;

14.12

а0 = 3;

а 1= 4;

аn = – 4аn-2    при   n > 2;

14.13

а0 = 1;

а 1= 2;

аn = аn-1 – аn-2    при   n > 2;

14.14

а0 = 5;

а 1= 4;

аn = – 16аn-2    при   n > 2;

14.15

а0 = 1;

а 1= 0;

 при  n > 2;

14.16

а0 = 3;

а 1= 7;

аn = 5аn-1 – 6аn-2    при   n > 2;

14.17

а0 = 2;

а 1= 7;

аn = 7аn-1 – 12аn-2    при   n > 2;

14.18

а0 = 2;

а 1= 9;

аn = 9аn-1 – 20аn-2    при   n > 2;

14.19

а0 = 2;

а 1= 2;

аn = 2аn-1 + 2аn-2    при   n > 2;

14.20

а0 = 3;

а 1= 10;

аn = 7аn-1 – 12аn-2    при   n > 2;

14.21

а0 = 0;

а 1= 5;

аn = – аn-1 + 6аn-2    при   n > 2;

14.22

а0 =1;

а 1= 6;

аn = 6аn-1 – 9аn-2    при   n > 2;

14.23

а0 = 1;

а 1= 4;

аn = 4аn-1 – 4аn-2    при   n > 2;

14.24

а0 = 1;

а 1= –4;

аn = – 4аn-1 – 4аn-2    при   n > 2;

14.25

а0 = 2;

а 1= 3;

аn = 2аn-1 – аn-2    при   n > 2;

14.26

а0 = 1;

а 1= 4;

аn = –2аn-1 – аn-2    при   n > 2;

 14.27

а0 = 1;

а 1= 2;

аn = – 4аn-2    при   n > 2;

14.28

а0 = 3;

а 1= 1;

аn = – аn-1 +6аn-2    при   n > 2;

14.29

а0 = 2;

а 1= 3;

аn = 3аn-1 – 2аn-2    при   n > 2;

14.30

а0 = 3;

а 1= 8;

аn = 4аn-1 – 4аn-2    при   n > 2;

 

15 Найти производящую функцию, заданную рекуррентными отношениями.

 

Т а б л и ц а 15

№

отношение

№

отношение

 

 

 

 

15.1

а0 = 2;

аn = 5аn-1 + 6п

15.2

а0 = 3;

аn = 7аn-1 + 8п

15.3

а0 = 0;

аn = 9аn-1 + 10п

15.4

а0 = 7;

аn = 3аn-1 + 4п

15.5

а0 = 1;

аn = 2аn-1 + 3п

15.6

а0 = 5;

аn = аn-1 + 2п

15.7

а0 =3;

аn = 6аn-1 + 7п

15.8

а0 = 4;

аn = 5аn-1 + 6п

15.9

а0 = 1;

аn = 4аn-1 + 5п

15.10

а0 = 4;

аn = 7аn-1 + 8п

15.11

а0 = 2;

аn = 2аn-1 + 3п

15.12

а0 = 2;

аn = 6аn-1 + 7п

15.13

а0 = 4;

аn = аn-1 + 2п

15.14

а0 = 6;

аn = 3аn-1 + 4п

15.15

а0 = 5;

аn = 3аn-1 + 4п

15.16

а0 = 3;

аn = 5аn-1 + 6п

15.17

а0 = 2;

аn = 7аn-1 + 8п

15.18

а0 = 3;

аn = 3аn-1 + 4п

15.19

а0 = 2;

аn = 8аn-1 + 9п

15.20

а0 = 3;

аn = аn-1 + 2п

15.21

а0 = 0;

аn = аn-1 + 2п

15.22

а0 =5;

аn = 7аn-1 + 8п

15.23

а0 = 1;

аn = 5аn-1 + 6п

15.24

а0 = 2;

аn = 4аn-1 + 5п

15.25

а0 = 2;

аn = 3аn-1 + 4п

15.26

а0 = 1;

аn = 8аn-1 + 9п

 15.27

а0 = 5;

аn = 2аn-1+ 3п

15.28

а0 = 6;

аn = аn-1 + 2п

15.29

а0 = 1;

аn = 7аn-1 + 8п

15.30

а0 = 1;

аn = 3аn-1 + 4п

 

16 Используя производящую функцию, решить следующие задачи.

 

16.1 Найти количество способов размещения 30 человек в 3 комнатах гостиницы, если в каждой комнате находится хотя бы по одному человеку.

16.2 Определить количество чисел, состоящих из  10 цифр, все цифры в которых нечетные, а цифры 1 и 3 присутствуют в них не менее одного раза.

16.3 Найти количество способов размещения 19 роз по 3 вазам при  условии, что в каждой вазе будет нечетное количество цветов.

16.4 Найти количество способов размещения 25 объектов четырех типов по порядку, если количество объектов первого типа – четное, количество объектов второго типа – нечетное и хотя бы по одному объекту третьего и четвертого типа.

16.5 Сколько существует способов распределения 9 кусков торта между 4 детьми при  условии, что каждый ребенок из первых двух получает кусок торта.

16.6  Определить количество чисел, состоящих из  15 цифр, все цифры в которых нечетные, при условии, что все цифры присутствуют хотя бы один раз, а цифра 5 появляется четное число раз.

16.7 Сколько существует способов размещения 50 книг на 3 полках, при условии, что каждая полка не пуста.

16.8 Найти количество способов раскрашивания 8´8 – клеточной шахматной доски, используя красный, белый и синий цвета, при условии, что четное количество клеток – красные.

16.9 Найти количество способов размещения 40 человек в 4 комнатах гостиницы, если в каждой комнате находится нечетное количество человек.

16.10 Определить количество чисел, состоящих из  8 цифр, все цифры в которых нечетные, а цифры 3 и 5 присутствуют в них нечетное количество раз.

16.11 Найти количество способов размещения 30 роз по 4 вазам при  условии, что в каждой вазе будет нечетное количество цветов.

16.12 Найти количество способов размещения 20 объектов четырех типов по порядку, если количество объектов первого типа – нечетное, количество объектов второго типа – четное и хотя бы по одному объекту третьего и четвертого типа.

16.13 Сколько существует способов распределения 12 кусков торта между 5 детьми при  условии, что каждый ребенок из первых трех получает кусок торта.

16.14 Определить количество чисел, состоящих из  10 цифр, все цифры в которых нечетные, при условии, что все цифры присутствуют хотя бы один раз, а цифра 7 появляется нечетное число раз.

16.15 Сколько существует способов размещения 40 книг на 5 полках, при условии, что на первой полке находится нечетное число книг.

16.16 Найти количество способов раскрашивания 8´8 – клеточной шахматной доски, используя красный, белый и синий цвета, при условии, что нечетное количество клеток – синие.

16.17 Найти количество способов размещения 25 человек в 3 комнатах гостиницы, если все комнаты заселены.

16.18 Определить количество чисел, состоящих из  15 цифр, все цифры в которых нечетные, а цифры 1 и 3 присутствуют в них четное количество раз.

16.19 Найти количество способов размещения 16 роз по 2 вазам при  условии, что в каждой вазе будет нечетное количество цветов.

16.20 Найти количество способов размещения 30 объектов четырех типов по порядку, если количество объектов второго типа – четное, количество объектов третьего типа – нечетное и хотя бы по одному объекту первого и четвертого типа.

16.21 Сколько существует способов распределения 10 кусков торта между 3 детьми при  условии, что каждый ребенок получает кусок торта.

16.22 Определить количество чисел, состоящих из  8 цифр, все цифры в которых нечетные, при условии, что цифры 1 и 3 присутствуют хотя бы один раз, а цифра 5 появляется четное число раз.

16.23 Сколько существует способов размещения 50 книг на 6 полках, при условии, что на первой полке находится четное число книг.

16.24 Найти количество способов раскрашивания 8´8 – клеточной шахматной доски, используя красный, белый и синий цвета, при условии, что количество клеток каждого цвета – четное.

16.25 Найти количество способов размещения 20 человек в 3 комнатах гостиницы, если в каждой комнате находится четное количество человек.

16.26 Определить количество чисел, состоящих из  20 цифр, все цифры в которых нечетные, а цифры 7 и 9 присутствуют в них нечетное количество раз.

16.27 Найти количество способов размещения 15 роз по 3 вазам при  условии, что в каждой вазе будут цветы.

16.28 Найти количество способов размещения 30 объектов четырех типов по порядку, если количество объектов первого и второго типа – нечетное и хотя бы по одному объекту третьего и четвертого типа.

16.29 Сколько существует способов распределения 8 кусков торта между 3 детьми при  условии, что первый ребенок получает кусок торта.

16.30 Определить количество чисел, состоящих из  12 цифр, все цифры в которых нечетные, при условии, что цифры 5 и 7 присутствуют хотя бы один раз, а цифра 1 появляется нечетное число раз.

  

1.3 Решение типового варианта

 

1 В автомашине 7 мест. Сколькими способами семь человек могут усесться в эту машину, если занять место водителя могут только трое из них?

Решение: действие, которое должно быть выполнено особым способом, необходимо выполнять первым. Итак, на место водителя можно посадить только одного из трех человек (умеющего водить машину), т.е. существуют 3 способа занять первое место. Второе место может занять любой из 6 человек, оставшихся после того, как место водителя будет занято и т.д. Используя принцип умножения, получаем произведение:

                               = 36! = 3P6.

Ответ:    3P6 = 36!.

 

2 Позывные радиостанции должны начинаться с буквы W. 1) Скольким радиостанциям можно присвоить различные позывные, если позывные состоят из трех букв, причем эти буквы могут повторяться? 2) Если позывные состоят из четырех букв, которые не повторяются?

Решение: в современном латинском алфавите 26 букв. На первом месте всегда должна стоять одна буква, следовательно, существует только один способ занять первое место.

1) На оставшиеся два места может претендовать любая из 26-ти букв, т.к. буквы в позывных могут повторяться. Используя принцип умножения, получаем произведение:     = 262.

2) На второе место можно поставить любую из 25 букв, т.к. в позывных буквы не должны повторяться. На третье место — 24 буквы, на четвертое место — 23 буквы. Используя принцип умножения, получаем произведение:                     

                                     .

 

Ответ:  1) 262;   2) .

 

3 Из цифр 1, 2, 3, 4, 5 составляются всевозможные числа, каждое из которых содержит не менее трех цифр. Сколько таких чисел можно составить, если повторения цифр в числах запрещены?

Решение: необходимо посчитать, сколько существует трехзначных, четырехзначных и пятизначных чисел, составленных из этих пяти цифр. Трехзначных чисел — 543=, четырехзначных — 5432=, пятизначных  —  54321 = . Используем принцип сложения:

                               + +  = 60 + 120 + 120 = 300.

Ответ:  300.

 

4 Сколько слов можно образовать из букв слова фрагмент, если слова должны состоять:

                               а) из восьми букв,      б) из семи букв, в) из трех букв?

Решение: в слове фрагмент 8 различных, неповторяющихся букв алфавита.

а) Всевозможные перестановки 8 букв по восьми местам:

                                = =P8.

б) Размещения 8 букв по 7 местам: =.

в) Размещения 8 букв по 3 местам: =.

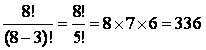Ответ:   а) 8!;     б) 8!;     в)336.

  

5 Сколькими способами из восьми человек можно избрать комиссию, состоящую из пяти членов?

Решение: для решения этой задачи необходимо использовать формулу для сочетания элементов, т.к. здесь не имеет значения порядок элементов в выборке. Запишем формулу для сочетаний и произведем вычисления:

= .

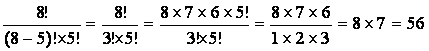Ответ: 56.

 

6 Сколькими способами можно распределить 20 выпускников по трем  фирмам, если в одной из них  имеется  3, в другой  — 5 и в третьей — 12 вакантных мест.

(Ответ записать в виде произведения сомножителей, не вычисляя его.)

Решение: из 20-ти элементов необходимо сделать три выборки, причем порядок внутри выборок значения не имеет. Поэтому используем формулу для сочетаний. Чтобы выбрать из 20-ти элементов 3, существует  способов. Остается 17 элементов, из которых выбирается 5 элементов —  способами. Остается 12 элементов, из которых выбирается 12 элементов. Это можно сделать = 1, т.е. одним способом. Используя принцип произведения, получаем:     .

Ответ:      .

        

7 .  Имеется 5 разных книг одного автора, 4 — второго и 6 — третьего.

Каким числом способов можно выбрать:

а) две книги одного автора?

б) три книги одного автора?

в) одну книгу первого автора, две — второго и три — третьего?

 

Решение: необходимо посчитать, сколько возможных способов существует персонально для  каждого автора.

а) Две книги первого автора можно выбрать  способами:                   

                            .

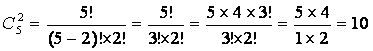Две книги второго автора  —   способами:           

                                      .

Две книги третьего автора  —   способами:           

                                      .

Используем принцип сложения:       .

б) Три книги первого автора можно выбрать  способами:                   

                            .

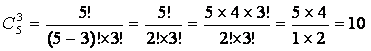Три книги второго автора  —   способами:           

                                      .

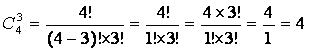Три книги третьего автора  —   способами:           

                                      .

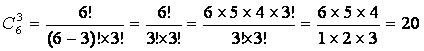Используем принцип сложения:       .

в) Одну книгу первого автора можно выбрать  способами:                   

                            .

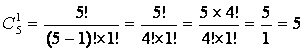Две книги второго автора  —   способами:           

                                      .

Три книги третьего автора  —   способами:           

                                      .

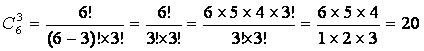Используя принцип умножения, получаем произведение:                     

                                     .

Ответ:   а) 31;    б) 34;    в) 600.

 

8 Сколькими способами можно составить букет из 5 цветов, если в наличии есть цветы 3 сортов?

Решение: поскольку в букете могут встречаться цветы одинакового сорта, то используем формулу для  сочетаний с повторениями:

.

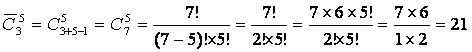Ответ: 21.

 

9 Сколько различных «слов» можно получить, переставляя буквы в слове  ИНСТИТУТ?

Решение: в данном слове, состоящем из 8 букв, есть повторяющиеся, поэтому выпишем все различные буквы с указанием частоты их повторения в слове:

                              И(2), Н(1), С(1), Т(3), У(1).

Используем формулу для  перестановок с повторениями:

.

 

Ответ: 3360.

         

10 Сколько существует целых положительных чисел, меньших 1000, которые

а) делятся и на 3, и на 7;

б) делятся на 3, но не делятся на 7;

в) делятся на 7, но не делятся на 3;

г) делятся на 3 или на 7;

д) не делятся ни на 3, ни на 7?

 

Решение: пусть А — множество целых положительных чисел, меньших 1000; А3 — множество целых положительных чисел, меньших 1000, которые делятся на 3; А7 — множество целых положительных чисел, меньших 1000, которые делятся на 7. Найдем мощности этих множеств:           

              ,     ,    ,

где  [х] — наибольшее целое число, не превосходящее  х.

а)  — множество целых положительных чисел, меньших 1000, которые делятся и на 3, и на 7, тогда 

                                    ;

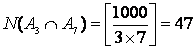б) для определения множества целых положительных чисел, меньших 1000, которые делятся на 3, но не делятся на 7 необходимо из множества А3 исключить элементы множества А3,7.

Найдем мощность множества :

            ;

в) аналогично пункту б) получаем:

            ;

г) используя формулу включения и исключения для двух множеств

                       ,

получаем:

       ;

д) в силу введенных обозначений получаем:

            .

Эту  же задачу можно решить с помощью диаграммы Эйлера – Венна

(см. рисунок 1.3.1)

Так как на 3 и на 7 делятся 47 чисел, то только на 3 делятся   

          (333 – 47) = 286 чисел;

только на 7 —

          (142 – 47) = 95 чисел;

делятся на 3 или на 7 — 

          (286 + 47 + 95) = 428 чисел;

не делятся ни на 3, ни на 7  —    

          999 – 428 = 571 число.

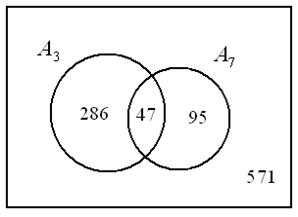
                     Рисунок 1.3.1

 

Ответ:   а) 47;     б) 286;     в) 95;    г) 428;    д) 571.

 

11 Сколько существует целых положительных чисел, меньших 1000, которые не делятся ни на 2, ни на 3, ни на 5?

Решение: пусть А — множество целых положительных чисел, меньших 1000, А2 — множество целых положительных чисел, меньших 1000, которые делятся на 2; А3 — множество целых положительных чисел, меньших 1000, которые делятся на 3; А5 — множество целых положительных чисел, меньших 1000, которые делятся на 5. Найдем мощности этих множеств:          

       ,

,     ,      .

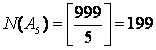Пусть — множество целых положительных чисел, меньших 1000, которые делятся и на 2, и на 3; — множество целых положительных чисел, меньших 1000, которые делятся и на 2, и на 5; — множество целых положительных чисел, меньших 1000, которые делятся и на 3, и на 5, — множество целых положительных чисел, меньших 1000, которые делятся и на 2, и на 3, и на 5, тогда 

,    ,   ,  .

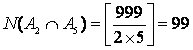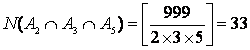Обозначим через    — количество целых положительных чисел, меньших 1000, которые не делятся ни на 2, ни на 3, ни на 5.

Воспользовавшись формулой включения и исключения для трех множеств

      

     , получаем:

499 + 333 + 199 – (166 + 99 + 66) + 33 = 1031–331 + 33 = 733.

Следовательно,

=  = 999 – 733 = 266.

Ответ: 266.

 

12 В группе N студентов, из них: N1 человек владеют языком программирования СИ, N2 − Паскалем, N3 − Бейсиком, N12 студентов программируют на СИ и Паскале, N13 − на СИ и Бейсике, N23 − на Паскале и Бейсике, N123 человек знают все три языка и N0 не знают ни одного из них. По данным значениям найти недостающую информацию.

 

Решение: пусть А — множество всех студентов группы,      

А1 — множество студентов, владеющих языком программирования СИ;

А2 — множество студентов, владеющих Паскалем;

А3 — множество студентов, владеющих Бейсиком.

Тогда в силу введенных обозначений  N — мощность множества  А, т.е.  

N = N(А),    N1 = N(А1),    N2 = N(А2),    N3 = N(А3),    N12 =,

N13 =,     N23 =,      N123 =,

N0 = .

Применяя  формулу включения и исключения для трех множеств, получаем:

                = N1 +  N2 +  N3 – (N12 +  N13 + N23) + N123.

Следовательно,  

                   N0 = N – (N1 +  N2 +  N3 – (N12 +  N13 + N23) + N123),

т.е.

         N0 = N – (N1 +  N2 +  N3) + (N12 +  N13 + N23) – N123.                  (*)

Недостающая информация по данным задачи находится по последней формуле (*). 

Например, если N = 25, N1 = 15, N2 = 12, N3 = 20,  N12 = 9, N13 = 10, N23 = 8, N0 = 2, то неизвестная величина N123 вычисляется следующим образом:

        N123 = 25 – (15 + 12 + 20) + (9 + 10 + 8) – 2 = 25 – 47 + 27 – 2 = 3.

Значит в данной группе 3 студента знают все три языка программирования.

Ответ: 3.

    

13 Чему равен коэффициент при   x4 y2    в разложении (1 +  x + y)20 ?

Решение: в силу полиномиальной теоремы   

        

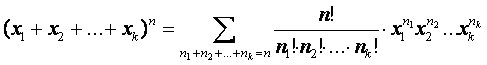
имеем

     .

Поэтому коэффициент при   x4 y2    в разложении (1 + x + y)20   находим следующим образом: т.к.   п = 20, п2 = 4, п3 = 2, то      п1 = 20 – 4 – 2 = 14.

Следовательно, коэффициент при   x4y2 равен   

                  .  

 

Ответ: 34200.

 

14 Найти решение для рекуррентного отношения.

(Поскольку структура общего решения линейного однородного рекуррентного отношения с постоянными коэффициентами зависит от вида корней  соответствующего характеристического уравнения, то в данном пункте рассмотрим три примера различных структур общего решения).

Линейное однородное рекуррентное отношение второго порядка с постоянными коэффициентами в общем случае имеет следующий вид:

 а0 = g;

 а1= h;

 аn = pаn-1 + qаn-2    при   n > 2, где  p, q, g, hÎR.

Решение поставленной задачи зависит от корней характеристического уравнения:         или     .

Корни характеристического уравнения:

;       .

Возможны случаи:

а) если характеристическое уравнение имеет два различных действительных   

    корня, т.е. k1 , k2 Î R  ( k1 ≠ k2 ), тогда общее решение имеет вид                        

                               ;

б) если характеристическое уравнение имеет два одинаковых действительных

    корня, т.е.  k1 , k2 Î R  ( k1 = k2 ), тогда общее решение имеет вид    

                                     ;                         

в) если характеристическое уравнение имеет два комплексных корня,

т.е.   k1 , k2 Î C:    ,    ,  где     ,

тогда общее решение имеет вид     ,

где    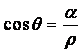    ,    и    .      

Зная первые два значения последовательности   ( а0 = g; а1= h ), можно полностью определить решение данного рекуррентного отношения, решая систему из двух уравнений  для определения коэффициентов С1 и С2.

                            

Пример 1. Найти решение для рекуррентного отношения:

 а0 = 1;

 а1= 8;

 аn = аn-1 + 6аn-2    при   n > 2.

Решение: составим характеристическое уравнение для данного рекуррентного отношения:    .

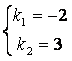        – разные действительные корни характеристического уравнения.

Следовательно, общее решение имеет вид   .

Зная первые два значения последовательности   ( а0 = 1; а1= 8 ), можно полностью определить решение данного рекуррентного отношения:

                    

Решая систему уравнений     

                                                

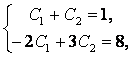
находим, что  С1 = –1  и  С2 = 2, поэтому решением  рекуррентного отношения

 а0 = 1;

 а1= 8;

                                аn = аn-1 + 6аn-2    при   n > 2

является    .

Ответ:   .

 

 

Пример 2. Найти решение для рекуррентного отношения:

 а0 = 2;

 а1= 6;

 аn = 4аn-1 – 4аn-2    при   n > 2.

Решение: составим характеристическое уравнение для данного рекуррентного отношения:    .

    – равные действительные корни характеристического уравнения.

Следовательно, общее решение имеет вид   .

Зная первые два значения последовательности   ( а0 = 2; а1= 6 ), можно полностью определить решение данного рекуррентного отношения:

  

Решая систему уравнений

                                              

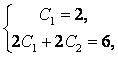
находим, что С1 = 2  и  С2 = 1, поэтому решением  рекуррентного отношения

 а0 = 2;

 а1= 6;

                                аn = 4аn-1 – 4аn-2    при   n > 2

является    .

Ответ: .

 

Пример 3. Найти решение для рекуррентного отношения:

 а0 = 1;

 а1= 4;

 аn = аn-1 – аn-2    при   n > 2.

Решение: составим характеристическое уравнение для данного рекуррентного отношения:    .

                – комплексные корни характеристического уравнения,           

для которых         ,     , 

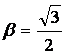                               и 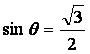   , т. е. .

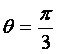Тогда общее решение имеет вид     .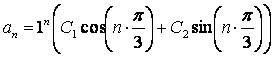      

Зная первые два значения последовательности   ( а0 = 1; а1= 4 ), можно полностью определить решение данного рекуррентного отношения:

,  .

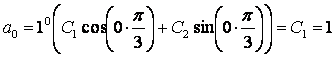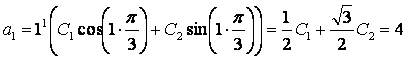Решая систему уравнений

                                              

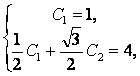
находим, что С1 = 1  и 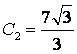 , поэтому решением  рекуррентного отношения

 а0 = 1;

 а1= 4;

                                аn = аn-1 – аn-2    при   n > 2

является    .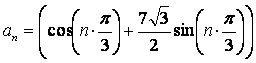

Ответ:     .

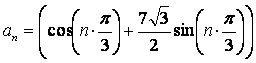15 Найти производящую функцию, заданную рекуррентными отношениями

                                                  а0 = 1;

                                       аn = 3аn-1 + 4п.

Решение: пусть производящая функция имеет вид  

                      f (x) = a0 + a1x + a2x2 + a3x3 + a4x4 + … + anxn + …

Поскольку в рекуррентном отношении коэффициент при   аn-1  равен 3, найдем

                 3х f (x) = 3a0 х + 3a1 x2 + 3a2 x3+ 3a3 x4 + 3a4 x5 + … + 3anxn+1 + …

Т.к.                     ,

это даст 4пхп. Поэтому

          a0 – 1 + (a1 – 3a0 + 4)х + (a2 – 3a1 + 42)х2 +

                                                  + (a3 – 3a2 + 43)х3 + … + (aп – 3aп-1 + 4п)хп + …

Поскольку    aп – 3aп-1 + 4п = 0    при всех   п ³ 1   и   а0 = 1  имеем

                               

                              a0 – 1 = 0.

 

Решая уравнение относительно   f (x), имеем

                                        .

Из математического анализа известно, что любая дробь вида

                                            ,

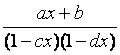где константы  с  и  d  различны, разлагается на простейшие дроби, т.е.

 

                                           ,

 

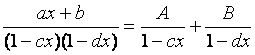где коэффициенты   А  и  В находятся следующим образом: приводим к общему знаменателю сумму дробей в правой части равенства и приравниваем числители. Если приравнять коэффициенты при одинаковых степенях  х  в левой и правой частях последнего тождества, то получим систему линейных уравнений относительно искомых коэффициентов. Можно определить коэффициенты и другим способом, придавая переменной  х  в этом тождестве произвольные числовые значения.

 

Итак, в нашем случае

                                    .

 

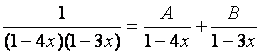Умножая обе части равенства на (1 – 4х)(1 – 3х), имеем

 

                                                1 = А(1 – 3х) + В(1 – 4х).

 

Полагая 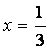  , получаем

                                 ,

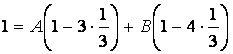так что  В = – 3.

Полагая 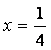  , получаем

                                 ,

поэтому  А = 4. Следовательно, имеем

 

 

                                  

 

                                        ,

поэтому          

                          аn = 4×4п – 3×3п = 4п+1 –3п+1.

 

Ответ:   аn = 4×4п – 3×3п = 4п+1 –3п+1.

 

16 Используя производящую функцию, найти количество способов размещения 20 объектов четырех типов по порядку, если количество объектов первого типа – нечетное, количество объектов второго типа – четное и имеется хотя бы один объект третьего типа.

Решение:

при решении подобных задач используем следующую теорему.

Теорема

а)  ;

б) ;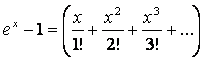

в) ;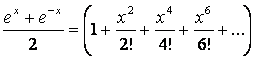

г) .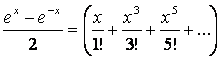

При составлении экспоненциальной производящей функции, соответствующей размещению произвольного числа объектов  различных типов учитывается особенность каждого типа в отдельности, а именно:

а) если на определенный тип нет никаких ограничений, то его вкладом в производящую функцию будет множитель  ;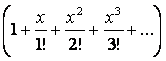

б) если есть условие, что имеется хотя бы один объект определенного типа, то его вкладом в производящую функцию будет множитель  

                                      ;

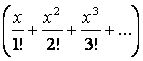в)  если есть условие, что количество объектов определенного типа – четное (при этом в данном случае под четным количеством будем понимать 0, 2, 4, …), то его вкладом в производящую функцию будет множитель               

                                   ;

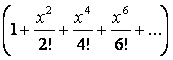г) если есть условие, что количество объектов определенного типа – нечетное, то его вкладом в производящую функцию будет множитель   

                                      .  

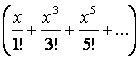Коэффициент при    в экспоненциальной производящей функции описывает количество способов размещения  п  объектов с заданными свойствами.

Найдем производящую функцию, описывающую данную ситуацию. Используя основное свойство обычных экспоненциальных функций, определяем, что искомая экспоненциальная производящая функция имеет вид

или в силу теоремы

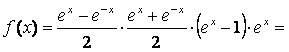
, поэтому коэффициент при   равен  .

Таким образом, количество способов размещения 20 объектов четырех типов с заданными свойствами равно   .

Ответ: .

1.4 Контрольные вопросы

 

         1 Элементы комбинаторики.

         2 Принцип сложения.

         3 Принцип умножения.

         4 Перестановки, размещения, сочетания без повторений.

         5 Перестановки, размещения, сочетания с повторениями.

6 Бином Ньютона. Биномиальные коэффициенты, их свойства.

7 Треугольник Паскаля.

8 Принцип включения и исключения.

9 Полиномиальная теорема. Полиномиальные коэффициенты.

         10 Рекуррентные соотношения.

11 Производящие функции.

Список литературы

 

1.     Андерсон А. Джеймс Дж. Дискретная математика и комбинаторика. – Москва, 2004.–960 с.

2.     Плотников А.Д. Дискретная математика: учебное пособие. – М.: Новое знание, 2006.–304 с.

3.     Новиков Ф.А. Дискретная математика для магистров и бакалавров: Учебник для вузов. Стандарт третьего поколения. – СПб.: Питер, 2011.– 384 с.

4.     Шапорев С.Д. Дискретная математика. Курс лекций и практических занятий. – СПб.: БХВ-Петербург, 2009. – 400 с.

5.     Виленкин Н.Я. Комбинаторика. – М.: Наука. Гл. ред. физ.-мат. лит., 1969.– 323 с. 

6.     Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной математике. – М.: Наука, 1977.–243 с.

7.     Судоплатов С.В., Овчинникова Е.В. Элементы дискретной математики. – М.: ИНФРА-М, Новосибирск: изд-во НГТУ, 2002.–280 с. 

 

Содержание

 

1 Расчетно-графическая работа № 2. Комбинаторика                                          3

1.1 Введение                                                                                                              3

1.2 Расчётные задания                                                                                              4

1.3 Решение типового варианта                                                                             13

1.4 Контрольные вопросы                                                                                      27                                                                            

Список литературы                                                                                                 28