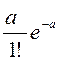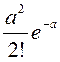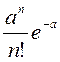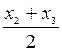Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ
ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра высшей математики
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Конспект лекций
для студентов специальностей
5В070400 – Вычислительная техника и программное
обеспечение,
5В070300 – Информационные системы
Алматы 2013
СОСТАВИТЕЛИ: Астраханцева Л.Н., Байсалова М.Ж. Теория вероятностей и математическая статистика. Конспект лекций для студентов специальности 5В070400 – Вычислительная техника и программное обеспечение, 5В070300 – Информационные системы всех форм обучения. - Алматы: АУЭС, 2013.- 49 стр.
Настоящий конспект содержит 8 лекций по основным разделам традиционно изучаемым в курсе теории вероятностей и математической статистики. Конспект лекций для студентов специальности 5В070400 – Вычислительная техника и программное обеспечение, 5В070300 – Информационные системы составлен в соответствии с программой дисциплины «Теория вероятностей и математическая статистика».
Ил. 10, табл. 10, библиогр. – 11 назв.
![]()
Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2013 г.
ã НАО «Алматинский университет энергетики и связи», 2013 г.
1 Элементы теории вероятностей
1.1 Лекция 1. Случайные события. Пространство элементарных
событий. Вероятность
Содержание лекции: предмет теории вероятностей. Пространство элементарных событий. Алгебра событий. Различные определения вероятности.
Цель лекции: познакомить с предметом и основными понятиями теории вероятностей.
События, происходящие в мире, можно разделить на те, исход которых можно предсказать, и те, предсказать исход которых невозможно. Деревянный кубик, брошенный в воду, обязательно всплывёт, а сколько очков выпадет на верхней грани брошенной игральной кости предсказать нельзя. Если подбрасывать монету один раз, то выпадет орёл или решка неизвестно, но если подбрасывать достаточно много раз, то примерно в половине случаев выпадает орёл, в половине – решка. Таким образом, появляется некоторая закономерность. Теория вероятностей – это математическая наука, изучающая закономерности массовых случайных явлений, причём она рассматривает не сами явления, а их математические модели. Понятие события является основным в теории вероятностей.
Определение. Случайным называется событие, которое при осуществлении совокупности условий может либо произойти, либо не произойти; эта совокупность условий называется испытанием или опытом.
В современной теории вероятностей используют аппарат
теории множеств, случайные события, как и множества, обозначают заглавными
буквами латинского алфавита ![]() и т.д.
и т.д.
Пример 1.1.1.
Рассмотрим испытание «бросание игральной кости». Случайными событиями могут
быть: A –
выпадение 2 очков; B –
выпадение нечётного числа очков; ![]() – выпадение 9 очков;
– выпадение 9 очков; ![]() – выпадение целого числа очков.
– выпадение целого числа очков.
Определение.
Непосредственные исходы опыта называются элементарными
событиями и обозначаются ![]() . Множество всех элементарных событий
называется пространством элементарных событий и обозначается
. Множество всех элементарных событий
называется пространством элементарных событий и обозначается ![]() .
.
Таким образом, произвольное случайное событие A
можно рассматривать как подмножество ![]() :
: ![]() . Заметим, что в разных задачах
. Заметим, что в разных задачах ![]() разные.
разные.
Пример 1.1.2.
В вышеприведённом примере при
бросании игральной кости возможны 6 элементарных событий: ![]() , где
, где ![]() - выпадение
- выпадение ![]() очков при бросании. Таким
образом, в этой задаче пространством элементарных событий будет множество
очков при бросании. Таким
образом, в этой задаче пространством элементарных событий будет множество ![]() или
или ![]() . Случайное событие A
– выпадение 2 очков – можно рассматривать как подмножество
. Случайное событие A
– выпадение 2 очков – можно рассматривать как подмножество ![]() : А=
: А=![]() ; аналогично
; аналогично ![]() .
.
Определения.
1.
Событие называется невозможным,
если оно заведомо не произойдёт в результате
опыта. Обозначается ![]() -
пустое множество.
-
пустое множество.
2.
Событие называется достоверным, если
в результате опыта оно обязательно наступит. Достоверное событие совпадает с ![]() .
.
3. События называются несовместными, если в результате опыта появ-ление одного исключает появление другого, совместными – в противном случае. Несколько событий попарно несовместны, если любые два из них несовместны.
4. События называются равновозможными, если все они имеют равные шансы для появления.
5. Несколько событий образуют полную группу, если:
а) они попарно несовместны;
б) в результате каждого опыта появляется только одно из них.
Итак, в первом примере событие ![]() - выпадение 9 очков,
невозможное:
- выпадение 9 очков,
невозможное: ![]() ;
событие
;
событие ![]() –
выпадение целого числа очков, достоверное:
–
выпадение целого числа очков, достоверное: ![]() ; события A и B
несовместные; A и D
совместные. События
; события A и B
несовместные; A и D
совместные. События ![]() равновозможные
и образуют полную группу.
равновозможные
и образуют полную группу.
Алгебра событий
Продолжая использовать аппарат теории множеств, можно
определить операции над случайными событиями, как операции над множествами. При
этом универсальным множеством будет пространство элементарных событий ![]() . Пустым
. Пустым ![]() – невозможное событие.
– невозможное событие.
1. Суммой (объединением) событий A
и B называется событие ![]() , состоящее в наступлении хотя бы одного из них (т.е.
или A, или B, или A
и B вместе):
, состоящее в наступлении хотя бы одного из них (т.е.
или A, или B, или A
и B вместе): ![]() .
.
2. Произведением (пересечением) событий A
и B называется событие ![]() , состоящее в совместном наступлении A
и B:
, состоящее в совместном наступлении A
и B: ![]() .
.
3. Разностью событий A и B
называется событие ![]() ,
которое происходит, когда происходит A и не
происходит B:
,
которое происходит, когда происходит A и не
происходит B: ![]() .
.
4. Противоположным событию A называется
событие ![]() ,
которое происходит тогда, когда событие A не
происходит:
,
которое происходит тогда, когда событие A не
происходит: ![]() .
.
5. Событие A влечет
событие ![]() , если
появление A означает и появление В, записывают
, если
появление A означает и появление В, записывают ![]() , т.е. A является
подмножеством B.
, т.е. A является
подмножеством B.
Эти определения операций, а также свойства операций и
их доказательства можно проиллюстрировать с помощью диаграмм Эйлера-Венна (см. [5],
стр. 4 - 6). Заметим, что некоторые понятия и выводы можно теперь коротко
записать с помощью определённых выше операций, например, если A
и B несовместны, то ![]() ; если
; если ![]() образуют полную группу, то 1)
образуют полную группу, то 1) ![]() ; 2)
; 2)  .
.
Относительная частота. Вероятность
Определение.
Пусть в n испытаниях событие A
наступило m раз.
Относительной частотой события A (обозначается ![]() ) называется отношение
числа появления события A к
общему числу проводимых испытаний, таким
образом,
) называется отношение
числа появления события A к
общему числу проводимых испытаний, таким
образом,  . Число m называют
частотой события A.
. Число m называют
частотой события A.
Ясно, что возможность появления события в каждом испытании различна. Ставится задача - определить степень этой возможности. Так возникает понятие вероятности события.
Определение.
Вероятностью события называется количественная мера объективной возможности появления этого события.
Существует несколько подходов к определению вероятности. Рассмотрим три из них.
Статистическое определение вероятности
Пусть некоторое испытание проводится сериями в
одинаковых условиях. Число испытаний в каждой серии различно: пусть в первой - ![]() испытаний, во второй -
испытаний, во второй - ![]() и т.д., в k – ой серии
-
и т.д., в k – ой серии
- ![]() испытаний.
Пусть событие A в i – ой серии появляется с частотой
испытаний.
Пусть событие A в i – ой серии появляется с частотой ![]() и, следовательно, с
относительной частотой
и, следовательно, с
относительной частотой
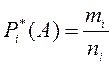 ( i =1,2,…,k).
( i =1,2,…,k).
Если неограниченно увеличивать число испытаний в каждой серии, то можно заметить, что относительные частоты в каждой серии колеблются около одного числа, обозначим его
![]() :
: 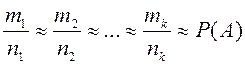 .
.
Это свойство относительной частоты с увеличением числа опытов группироваться около некоторого числа называется свойством статистической устойчивости, а это число – статистической вероятностью.
Определение.
Статистической вероятностью события A
называется число (обозначается ![]() ), около которого колеблется относительная
частота этого события, приближаясь к нему с увеличением числа испытаний:
), около которого колеблется относительная
частота этого события, приближаясь к нему с увеличением числа испытаний:![]()
 .
.
Вероятность, как и относительная частота, обладает следующими свойствами (аксиомы вероятности):
1) ![]() ,
, ![]() ,
, ![]() .
.
2) Если ![]() и
и ![]() несовместны (т.е.
несовместны (т.е. ![]() ), то
), то ![]() .
.
Статистическая вероятность опирается на реальный опыт и достаточно полно выявляет смысл этого понятия. Однако для надёжного определения вероятности этим способом нужно проделать достаточно много опытов, что не всегда просто. Но с появлением компьютеров эта задача упрощается (см., например, [1], стр. 22-23).
Классическое определение вероятности
Пусть проводится испытание с n равновозможными
элементарными исходами ![]() (i=1,2,…,n), которые
образуют полную группу. Таким образом, пространством элементарных событий будет
множество
(i=1,2,…,n), которые
образуют полную группу. Таким образом, пространством элементарных событий будет
множество ![]() ,
причём
,
причём ![]() ,
, 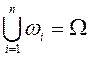 ,
, ![]() .
.
Такие элементарные события называют также случаями или
шансами, а испытание – классическим. Различные случайные события ![]() , связанные с этим
опытом, будут подмножествами
, связанные с этим
опытом, будут подмножествами ![]() (
(![]() ). Например,
). Например, ![]() . Элементарные события, входящие в
подмножество
. Элементарные события, входящие в
подмножество ![]() (т.е.
наступление которых влечёт за собой наступление
(т.е.
наступление которых влечёт за собой наступление ![]() ), называются благоприятствующими
событию A.
), называются благоприятствующими
событию A.
Пример 1.1.3.
Испытание – бросание игральной кости. ![]() =
= ![]() – пространство элементарных
событий. A –
появление чётного числа очков, т.е.
– пространство элементарных
событий. A –
появление чётного числа очков, т.е. ![]() . Таким образом, событию A
благоприятствуют три элементарных события:
. Таким образом, событию A
благоприятствуют три элементарных события:
![]() ,
, ![]() ,
, ![]() .
.
Определение.
Вероятностью события A
называется отношение числа m
элементарных событий, благоприятствующих событию A,
к общему числу n элементарных
событий, т.е. 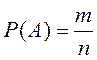 .
.
В простых случаях применение этой формулы не вызывает трудностей. В более сложных – при определении общего числа элементарных случаев и числа благоприятствующих случаев, применяют формулы комбинаторики (см. [1], стр. 25-27; [2], стр.20-24; [5], стр.68-73).
Пример 1.1.4. Электронное устройство состоит из 5 элементов и работает нормально, если все элементы исправны. Элементы выбираются из партии в 1000 элементов, в которой 950 исправных и 50 неисправных элементов. Найти вероятность того, что устройство, составленное из произвольно выбранных 5 элементов, работает нормально.
Событие A – устройство работает
нормально. Число всех возможных случаев выбора 5 элементов из 1000 (т.е. число
элементарных событий в ![]() ) равно числу сочетаний n=
) равно числу сочетаний n=![]() ; число
благоприятствующих случаев m=
; число
благоприятствующих случаев m=![]() ,
,
поэтому 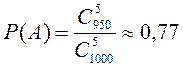 .
.
Геометрическое определение вероятности
Если пространство элементарных событий ![]() в задаче является
бесконечным несчётным множеством, а элементарные события
в задаче является
бесконечным несчётным множеством, а элементарные события ![]() равновозможные, то для
определения вероятности в этой задаче можно применить геометрическое
определение. При геометрическом подходе условия задачи можно свести к бросанию
наугад точки в определённую геометрическую область Q (отрезок,
часть плоскости или часть пространства). Так как точка бросается наугад, то
равновозможно её попадание в любую конечную часть q области Q
. Поэтому вероятность попадания точки в область q (q
равновозможные, то для
определения вероятности в этой задаче можно применить геометрическое
определение. При геометрическом подходе условия задачи можно свести к бросанию
наугад точки в определённую геометрическую область Q (отрезок,
часть плоскости или часть пространства). Так как точка бросается наугад, то
равновозможно её попадание в любую конечную часть q области Q
. Поэтому вероятность попадания точки в область q (q![]() Q)
будет пропорциональна мере q ( длине, площади или объёму) и не зависит от формы и
расположения q.
Q)
будет пропорциональна мере q ( длине, площади или объёму) и не зависит от формы и
расположения q.
Определение.
Пусть событие A – попадание
точки в область q (q![]() Q).
Тогда вероятность этого события равна
отношению меры области q к
мере всей области Q, в которой может появиться эта точка:
Q).
Тогда вероятность этого события равна
отношению меры области q к
мере всей области Q, в которой может появиться эта точка:
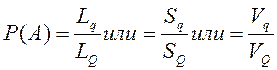 ,
,
где L, S, V – длины, площади и объёмы областей соответственно.
Пример 1.1.5. Круглый диск радиуса R разбит на два сектора. Длина дуги одного из них равна R. По быстро вращающемуся диску производят выстрел. Найти вероятность попадания в сектор с длиной дуги R.
Событие A – попадание в сектор с
длиной дуги R. 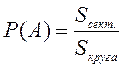 . По формуле
. По формуле 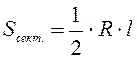 имеем
имеем 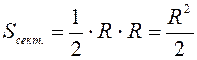 ,
, ![]() ,
поэтому
,
поэтому
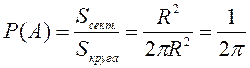 .
.
1.2 Лекция 2. Основные теоремы теории вероятностей
Содержание лекции: теоремы умножения и сложения. Формулы полной вероятности, Байеса, Бернулли. Локальная и интегральная теоремы Лапласа. Теорема Пуассона.
Цель лекции: познакомиться с основными теоремами и формулами
теории вероятностей.
Определения.
1. Два события А и В называются зависимыми, если вероятность
каждого
из
них меняется в связи с наступлением другого, независимыми – в противном случае;
события ![]() называются
независимыми в совокупности, если каждое из них и любые комбинации остальных в
произведении независимы.
называются
независимыми в совокупности, если каждое из них и любые комбинации остальных в
произведении независимы.
2. Условной вероятностью (обозначается ![]() или
или ![]() ) называется вероятность события А
при условии, что событие В уже произошло. Очевидно, что если А и В
независимые, то
) называется вероятность события А
при условии, что событие В уже произошло. Очевидно, что если А и В
независимые, то ![]() ,
если зависимые, то
,
если зависимые, то ![]() .
.
Пример
1.2.1. В урне 2 белых и 1 чёрный шар. Два лица извлекают из
урны по шару. Событие А – появление белого шара у первого, В - появление белого шара у
второго. Очевидно, что 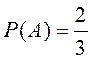 ;
; 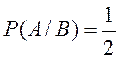 . Итак,
. Итак, ![]() , поэтому
, поэтому ![]() и В зависимые
события.
и В зависимые
события.
Теорема умножения
Вероятность
произведения (совместного появления) двух событий А и В равна
произведению вероятности одного из них на условную вероятность другого, при
условии, что первое событие произошло: ![]() .
.
Следствия.
1.
Если события А и
![]() независимые,
то
независимые,
то ![]() .
.
2.
Если события ![]() независимые в совокупности, то
для
независимые в совокупности, то
для
любых k из них выполняется ![]() .
.
3.
Теорема умножения обобщается на
случай n событий ![]() :
:
![]() .
.
Выше
была приведена аксиома, по которой определяется вероятность суммы двух
несовместных событий: ![]() ,
, ![]() . Общее правило сложения вероятностей,
справедливое как для совместных, так и для несовместных событий приводится в
теореме сложения.
. Общее правило сложения вероятностей,
справедливое как для совместных, так и для несовместных событий приводится в
теореме сложения.
Теорема сложения
Вероятность
суммы двух событий А и В
равна сумме вероятностей этих событий без вероятности их совместного появления:
![]() .
.
Если
события несовместные, то ![]() и, как выше,
и, как выше, ![]() .
.
Следствия.
1. Теорема сложения обобщается на случай n
событий ![]() :
:
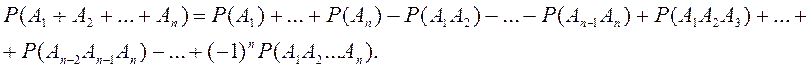 2. Если
событий
2. Если
событий ![]() образуют
полную группу, то
образуют
полную группу, то ![]() ,
,
![]() и, поскольку
и, поскольку
![]() , то
, то ![]() . В частности, противоположные
события
. В частности, противоположные
события ![]() и
и ![]() образуют полную группу,
поэтому
образуют полную группу,
поэтому ![]() или
или ![]() .
.
Заметим,
что первым следствием практически не пользуются. Если событие ![]() – появление хотя бы
одного из событий
– появление хотя бы
одного из событий ![]() ,
т.е.
,
т.е. ![]() , то
, то ![]() – не появление ни
одного из этих событий, поэтому
– не появление ни
одного из этих событий, поэтому ![]() =
= ![]() .
.
Формула полной вероятности
Помимо отдельного применения теорем сложения и умножения реальные задачи часто требуют их совместного применения.
Пусть событие А может появиться с одним из событий ![]() , образующих полную
группу событий (т.е.
, образующих полную
группу событий (т.е. ![]() ;
;
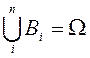 ). Заранее не
известно, какое из событий:
). Заранее не
известно, какое из событий: ![]() наступит, поэтому их называют гипотезами.
Вероятности гипотез, ввиду условия
наступит, поэтому их называют гипотезами.
Вероятности гипотез, ввиду условия 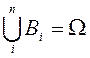 , удовлетворяют соотношению
, удовлетворяют соотношению ![]() и называются
априорными или доопытными. По условию событие А может произойти при выполнении
хотя бы одного из событий:
и называются
априорными или доопытными. По условию событие А может произойти при выполнении
хотя бы одного из событий: ![]() , т.е.
, т.е. ![]() . Но
. Но ![]() несовместны, значит,
несовместны, значит, ![]() также несовместны, поэтому
также несовместны, поэтому ![]()
![]() . По теореме умножения
. По теореме умножения ![]() . Подставляя эти
значения в
. Подставляя эти
значения в ![]() ,
получим формулу
,
получим формулу
![]()
![]() ,
,
называемую формулой полной вероятности.
Формула Байеса
Пусть условия относительно событий ![]() и
и ![]() , указанные выше,
сохраняются, т.е. событие
, указанные выше,
сохраняются, т.е. событие ![]() может появиться с одним из событий
может появиться с одним из событий ![]() , образующих полную
группу событий. Пусть испытание проведено и событие
, образующих полную
группу событий. Пусть испытание проведено и событие ![]() появилось. Это приведёт к
изменению вероятностей гипотез по сравнению с их априорными значениями.
Значения вероятностей гипотез при условии, что событие
появилось. Это приведёт к
изменению вероятностей гипотез по сравнению с их априорными значениями.
Значения вероятностей гипотез при условии, что событие ![]() уже произошло, обозначаются
уже произошло, обозначаются ![]() и называются
апостериорными или послеопытными. Они находятся по формуле Байеса:
и называются
апостериорными или послеопытными. Они находятся по формуле Байеса:
 .
.
Эту формулу легко получить, используя теорему умножения:
![]() .
.
Из последнего равенства имеем
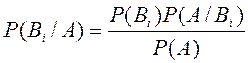 , подставляя в знаменатель
правую часть формулы полной вероятности, получим формулу Байеса.
, подставляя в знаменатель
правую часть формулы полной вероятности, получим формулу Байеса.
Повторение испытаний. Формула Бернулли
Пусть проводится n
испытаний, в каждом из которых два
исхода: появление и не появление события А. Эти
испытания независимы относительно события
А, т.е.
вероятность появления события А в каждом испытании не зависит от исходов в других
испытаниях. Вероятность появления события А в каждом
испытании может быть либо одна и та же, либо разная. Рассмотрим случай, когда
условия проведения испытаний одинаковы, а потому вероятность появления события А в каждом одна и та же. Пусть она равна ![]() , тогда
, тогда ![]() - вероятность не
появления А. Такая последовательность испытаний называется схемой
Бернулли.
- вероятность не
появления А. Такая последовательность испытаний называется схемой
Бернулли.
Поставим задачу найти вероятность того, что в серии из
n испытаний
событие А появилось ровно k
раз. Обозначим эту вероятность ![]() .
.
Будем рассуждать так: появление события А k раз в n
испытаниях может произойти в разных последовательностях. Рассмотрим один из
случаев сложного события В, когда А появилось в первых k испытаниях, и не появилось в остальных (n-k),
т.е. ![]() .
События
.
События ![]() и
и ![]() независимые, поэтому по
теореме умножения
независимые, поэтому по
теореме умножения
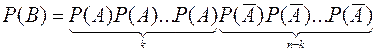 =
=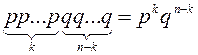 .
.
Таких событий, подобных событию ![]() , когда
, когда ![]() появилось k
раз, и не появилось (n-k) раз столько, сколько сочетаний из n
по k, т.е.
появилось k
раз, и не появилось (n-k) раз столько, сколько сочетаний из n
по k, т.е. ![]() . Все эти события несовместны, а искомое
событие равно их сумме. Поэтому по теореме сложения имеем
. Все эти события несовместны, а искомое
событие равно их сумме. Поэтому по теореме сложения имеем
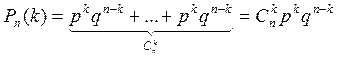 .
.
Формула ![]()
![]() называется формулой Бернулли.
называется формулой Бернулли.
Имея
формулу Бернулли, по которой находится вероятность наступления события ![]() ровно k
раз n в
испытаниях, легко получить формулы для определения вероятностей появления А в n
испытаниях не менее, чем k раз, (т.е. или k,
или k+1, …, или n раз,
обозначим
ровно k
раз n в
испытаниях, легко получить формулы для определения вероятностей появления А в n
испытаниях не менее, чем k раз, (т.е. или k,
или k+1, …, или n раз,
обозначим ![]() ) и
не более, чем k раз
(т.е. или 0, или 1,…, или k раз,
обозначим
) и
не более, чем k раз
(т.е. или 0, или 1,…, или k раз,
обозначим ![]() ):
):
![]() =
=![]() ;
; ![]() =
=![]() .
.
Практическое
использование формулы Бернулли при достаточно больших n
( уже при n>10) или, когда n
большое, а р малое, приводит к
увеличению объёмов вычислений и не всегда удобно. В этих случаях для вычисления
вероятности ![]() применяют
приближённые формулы.
применяют
приближённые формулы.
Теорема Пуассона
Если число испытаний n неограниченно возрастает, а вероятность р
появления события в каждом испытании мала, но произведение ![]() остаётся
постоянным, то вероятность
остаётся
постоянным, то вероятность![]() приближённо равна:
приближённо равна: 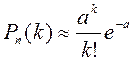 .
.
Последнюю формулу называют формулой Пуассона, обычно
её используют, когда ![]() ,
а
,
а ![]() . При вычислении по этой формуле можно пользоваться таблицами или
встроенными функциями в среде Mathcad (см. [1] или [6]).
. При вычислении по этой формуле можно пользоваться таблицами или
встроенными функциями в среде Mathcad (см. [1] или [6]).
Локальная теорема Муавра-Лапласа
Если вероятность р появления события в каждом испытании постоянна и не равна 0 и 1, а число испытаний n неограниченно возрастает, то вероятность появления события ровно k раз в n испытаниях приближённо равна
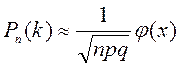 ,
,
где
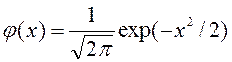 ,
, 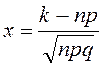 ,
, ![]() .
.
Функция
![]() вспомогательная.
Составлены таблицы её значений, при использовании которых следует учитывать
следующие свойства этой функции:
вспомогательная.
Составлены таблицы её значений, при использовании которых следует учитывать
следующие свойства этой функции:
1)
![]() чётная, т.е.
чётная, т.е. ![]() ;
;
2) можно
считать, что ![]() =0
при
=0
при ![]() .
.
Интегральная теорема Муавра-Лапласа
Если вероятность р появления события в каждом
испытании постоянна и не равна 0 и 1, а число испытаний n неограниченно
возрастает, то вероятность появления события не менее ![]() и не более
и не более ![]() раз (обозначается
раз (обозначается ![]() или
или ![]() ) приближённо равна
) приближённо равна ![]() , где
, где
 ,
, 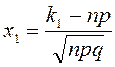 ,
, 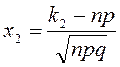 .
.
![]() - вспомогательная
функция, называемая функцией Лапласа или интегралом вероятностей. Значения этой
функции берут из специальных таблиц, при этом следует учитывать свойства функции
Лапласа:
- вспомогательная
функция, называемая функцией Лапласа или интегралом вероятностей. Значения этой
функции берут из специальных таблиц, при этом следует учитывать свойства функции
Лапласа:
1)
![]() нечётная, т.е.
нечётная, т.е. ![]() ;
;
2) можно
считать, что ![]() =0,5
при
=0,5
при ![]() .
.
При решении задач, относящихся к схеме Бернулли, следует учитывать условия и выбирать нужную формулу, а также весьма удобно использовать встроенные функции Mathcad (см. [1] или [6]).
1.3 Лекция 3. Случайные величины
Содержание лекции: дискретные и непрерывные случайные величины. Законы их распределения. Функция распределения.
Цель лекции: познакомиться со случайными величинами и законами их распределения.
Определение.
Случайной величиной называется переменная, которая может принимать то или иное значение из множества возможных значений, причём неизвестно заранее, какое именно.
Случайные величины будем обозначать прописными буквами
латинского алфавита X,Y,Z,..., а их
возможные значения строчными: x,y,z,… или ![]()
Случайные величины делятся на дискретные и непрерывные. Если множество возможных значений случайной величины конечное или бесконечное счетное, то она называется дискретной, если бесконечное несчетное, то – непрерывной.
Пример 1.3.1. Примеры дискретных случайных величин:
1) Х – число попаданий при трёх выстрелах. Возможные значения Х:
множество {0,1,2,3}.
2) X –число вызовов, поступивших на телефонную станцию за данный
промежуток времени. Возможные значения Х: множество {0,1,2,3,…}.
Примеры непрерывных случайных величин:
1) Х – расстояние от точки попадания до центра мишени.
2) Х – время безотказной работы радиолампы.
Возможные значения в этих случаях сплошь заполняют некоторые промежутки.
Для полного описания случайной величины надо знать не только множество их возможных значений, но и вероятности этих значений.
Определение.
Всякое правило (таблица, функция, график), устанавливающее связь между возможными значениями случайной величины и их вероятностями, называется её законом распределения.
Законы распределения дискретных случайных величин
Пусть дискретная случайная величина Х принимает
значения ![]() с
вероятностями
с
вероятностями ![]() (
(![]() или
или ![]() ).
).
Табличное задание закона распределения Х.
Т а б л ц а 1
|
Х |
|
|
… |
|
… |
|
Р |
|
|
… |
|
… |
Эта
таблица называется рядом распределения. Поскольку события ![]() ,
, ![]() несовместные и образуют полную группу, то
несовместные и образуют полную группу, то ![]() .
.
Графическое
задание закона распределения Х: в прямоугольной системе координат по
оси абсцисс откладывают значения ![]() , а по оси ординат – вероятности этих
значений
, а по оси ординат – вероятности этих
значений ![]() .
Точки с координатами (
.
Точки с координатами (![]() ,
,![]() ) последовательно
соединяют отрезками прямой. Полученную ломаную называют многоугольником
распределения.
) последовательно
соединяют отрезками прямой. Полученную ломаную называют многоугольником
распределения.
Аналитическое задание закона распределения требует определения формулы, связывающей возможные значения с их вероятностями. Такую формулу удаётся найти только для некоторых случайных величин.
Распределения, заданные формулами Бернулли и Пуассона, рассмотрим ниже в теме «Основные законы распределения случайных величин».
Непрерывные случайные величины. Функция распределения
Очевидно, что закон распределения непрерывной случайной величины нельзя задать рядом или многоугольником распределения. Существует универсальный способ задания закона распределения, пригодный как для дискретных, так и для непрерывных случайных величин.
Определение.
Функцией распределения (или интегральной функцией (законом) распределения) случайной величины Х называется функция F(x), определяющая для каждого значения х вероятность события X<x, т.е.
F(x) = P(X<x) (1).
Для
дискретной случайной величины Х, принимающей значения ![]() , формула (1) примет
вид
, формула (1) примет
вид ![]() , где
, где ![]() означает, что
суммирование распространяется на все те значения
означает, что
суммирование распространяется на все те значения ![]() , которые меньше х. Таким образом, для
дискретной случайной величины эта функция разрывная,
, которые меньше х. Таким образом, для
дискретной случайной величины эта функция разрывная, ![]() - её точки разрыва. Для
непрерывной - F(x)
непрерывная.
- её точки разрыва. Для
непрерывной - F(x)
непрерывная.
Свойства F(x)
1)
![]() для всех х.
для всех х.
Это свойство вытекает из определения F(x) как вероятности.
2) F(x) неубывающая,
т.е. если ![]() , то
, то
![]() .
.
Действительно, пусть ![]() . Событие
. Событие ![]() можно представить в виде суммы двух
событий:
можно представить в виде суммы двух
событий: ![]() . Поскольку
эти события несовместные, то по теореме сложения вероятностей имеем:
. Поскольку
эти события несовместные, то по теореме сложения вероятностей имеем: ![]() , откуда
, откуда ![]()
![]() . Так как любая вероятность
неотрицательна, то
. Так как любая вероятность
неотрицательна, то ![]() ,
т.е.
,
т.е. ![]() , ч.т.д.
, ч.т.д.
Следствие 1.
Вероятность попадания случайной величины в ![]() равна
равна ![]() , что следует из
равенства
, что следует из
равенства ![]() .
.
Следствие 2.
Вероятность того, что непрерывная случайная величина примет одно определённое значение равна нулю.
Если в формуле ![]() положить
положить ![]() и перейти к пределу при
и перейти к пределу при ![]() , то, ввиду
непрерывности
, то, ввиду
непрерывности ![]() ,
,
![]() и
и ![]() .
.
Следствие 3.
![]() .
.
3) Если возможные значения случайной величины
принадлежат интервалу ![]() ,
то
,
то ![]() и
и ![]() ; для непрерывной
случайной величины, возможные значения которой принадлежат всей числовой оси,
; для непрерывной
случайной величины, возможные значения которой принадлежат всей числовой оси, ![]() и
и ![]() .
.
Перечисленные свойства позволяют представить график непрерывной случайной величины в виде:
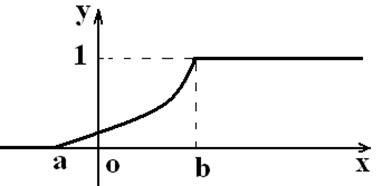
Рисунок 1
Заметим, что непрерывная случайная величина часто определяется как величина, имеющая всюду непрерывную функцию распределения.
Плотность распределения
Задание непрерывной случайной величины через функцию распределения не единственное. Другой важнейшей её характеристикой является плотность распределения вероятностей.
Определение.
Плотностью распределения вероятностей (или просто
плотностью распределения или дифференциальной функцией распределения,
обозначается ![]() )
непрерывной случайной величины называется производная её функции распределения,
т.е.
)
непрерывной случайной величины называется производная её функции распределения,
т.е.
![]() .
.
Определим вероятностный смысл плотности распределения. По определению производной
 = |свойство
= |свойство ![]() | =
| = 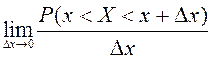 .
.
Так как отношение 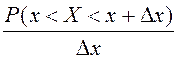 представляет собой среднюю вероятность,
которая приходится на интервал
представляет собой среднюю вероятность,
которая приходится на интервал ![]() , то
, то ![]() характеризует вероятность в точке
характеризует вероятность в точке ![]() и её окрестности. Здесь
просматривается аналогия с определением плотности распределения масс или
плотностью тока, откуда и название этой функции.
и её окрестности. Здесь
просматривается аналогия с определением плотности распределения масс или
плотностью тока, откуда и название этой функции.
Заметим, что дифференциальная функция распределения, как и интегральная, является одной из форм закона распределения, но в отличие от неё не является универсальной. Плотность распределения определяется только для непрерывных случайных величин.
Свойства f(x)
1.
Вероятность попадания Х в
интервал ![]() находится
по формуле:
находится
по формуле:
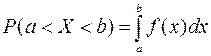 .
.
Действительно, 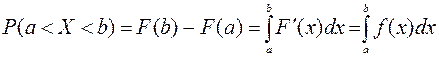 .
.
2.
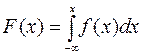 .
.
Действительно,  .
.
3. ![]() .
.
Действительно, ![]() , но
, но ![]() неубывающая, поэтому
неубывающая, поэтому ![]() , а значит, и
, а значит, и ![]() .
.
4. 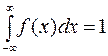 .
.
Положим, в первом свойстве ![]() , тогда
, тогда  , но
событие
, но
событие ![]() достоверное, и потому
достоверное, и потому ![]() , т.е.
, т.е. 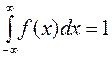 .
.
График плотности распределения ![]() называется кривой распределения
и, ввиду перечисленных выше свойств, имеет вид:
называется кривой распределения
и, ввиду перечисленных выше свойств, имеет вид:

Рисунок 2
Если вспомнить геометрический смысл определённого
интеграла, как площади криволинейной трапеции, то получим геометрическую
интерпретацию свойств![]() .
.
На рисунке 3 площади заштрихованных областей соответственно равны:
а) вероятности попадания Х в интервал ![]() ; б)
; б) 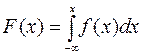 ; в)
; в) 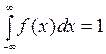 .
.

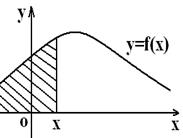

а) б) в)
Рисунок 3
1.4 Лекция 4. Числовые характеристики случайных величин
Содержание лекции: математическое ожидание, дисперсия, среднее квадратическое отклонение.
Цель лекции: познакомиться с основными числовыми характеристика-
ми случайных величин.
Закон распределения случайной величины полностью её характеризует с вероятностной точки зрения. Однако существует множество прикладных задач, в которых достаточно знать лишь отдельные свойства закона распределения, например, среднее значение, возле которого группируются возможные значения случайной величины, или их разброс относительно среднего.
Определение.
Числовыми характеристиками случайной величины называются неслучайные численные параметры, представляющие основные особенности её закона распределения.
Числовые характеристики можно условно подразделить на характеристики положения (математическое ожидание, мода, медиана, квантиль), характеристики рассеяния (дисперсия, среднее квадратическое отклонение), характеристики формы (асимметрия, эксцесс). Рассмотрим некоторые из них.
Математическое ожидание
Определение.
Математическим ожиданием дискретной случайной величины
Х называется сумма произведений всех её возможных
значений ![]() на
их вероятности
на
их вероятности ![]() (
(![]() или
или ![]() ), обозначается
), обозначается ![]() или
или ![]() :
:
![]() .
.
В случае бесконечного множества значений ![]() ряд в правой части
последнего равенства абсолютно сходится.
ряд в правой части
последнего равенства абсолютно сходится.
Вероятностный смысл математического ожидания дискретной случайной величины, возможные значения которой получены при большом числе опытов, состоит в том, что оно приближенно равно среднему арифметическому наблюдаемых значений (или среднее арифметическое наблюдаемых значений приближается к математическому ожиданию при неограниченном увеличении числа испытаний).
Действительно, пусть проводится n испытаний, в
которых значение ![]() появилось
появилось
![]() раз,
раз, ![]() -
- ![]() раз и т.д.,
раз и т.д., ![]() -
- ![]() раз, причём
раз, причём 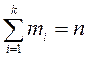 . Тогда среднее арифметическое всех
значений, принятых случайной величиной будет:
. Тогда среднее арифметическое всех
значений, принятых случайной величиной будет:
 .
.
Но ![]() - это относительная частота значения
- это относительная частота значения ![]() , и при увеличении числа
испытаний она стремится к вероятности
, и при увеличении числа
испытаний она стремится к вероятности ![]() этого значения, а поэтому среднее
арифметическое приближается к математическому ожиданию:
этого значения, а поэтому среднее
арифметическое приближается к математическому ожиданию:
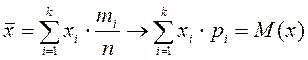 .
.
Для непрерывных случайных величин понятие математического ожидания вводится аналогично, только суммирование заменяется интегрированием.
Определение.
Математическое ожидание непрерывной случайной
величины, возможные значения которой принадлежат отрезку [a,b] (или![]() ), а плотность
распределения равна
), а плотность
распределения равна ![]() ,
находится по формуле:
,
находится по формуле:
 ( или
( или 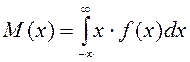 , предполагается,
что этот интеграл сходится абсолютно).
, предполагается,
что этот интеграл сходится абсолютно).
Свойства
![]() .
.
1.
![]() ;
;
2. ![]() ;
;
3. ![]() , где разность
, где разность ![]() называется отклонением случайной
величины от её математического ожидания;
называется отклонением случайной
величины от её математического ожидания;
4. ![]() для любых случайных величин
для любых случайных величин ![]() и
и ![]() ;
;
5. Если ![]() и
и ![]() независимые случайные величины, то
независимые случайные величины, то ![]() .
.
Свойства 2 и 4 обобщаются на случай любого конечного числа случайных величин:
![]()
![]() ,
,
где
![]() - константы.
- константы.
Доказательства этих свойств легко получить, подставляя соответствующие выражения в формулы, определяющие математическое ожидание для дискретных и непрерывных случайных величин (см., например, [3], стр.78-83).
Полезно знать формулы для определения математического ожидания числа появления события в независимых испытаниях.
Теорема. Математическое ожидание числа появления события в одном испытании равно вероятности этого события; математическое ожидание числа появления события в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании.
Действительно, если произведено одно испытание и
вероятность появления события в нём равна ![]() , то вероятность не появления равна
, то вероятность не появления равна ![]() . Ряд распределения этой
случайной величины имеет вид:
. Ряд распределения этой
случайной величины имеет вид:
Т а б л и ц а 2
|
|
0 |
1 |
|
|
|
|
Поэтому
математическое ожидание равно ![]() .
.
Если
Х – число появления события в n независимых испытаниях и ![]() - число появления в первом испытании,
- число появления в первом испытании, ![]() - во втором, и т.д.,
- во втором, и т.д., ![]() - в n-м,
то общее число появления события
- в n-м,
то общее число появления события ![]() . По четвёртому свойству
. По четвёртому свойству
![]() .
.
Каждое
из слагаемых правой части есть математическое ожидание числа появления события
в одном испытании, и по предыдущему равно ![]() . Поэтому
. Поэтому 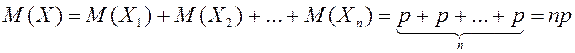 .
.
Дисперсия
Важнейшей характеристикой рассеяния случайных величин является дисперсия.
Определение.
Дисперсией случайной величины ![]() (обозначается
(обозначается ![]() ) называется
математическое ожидание квадрата её отклонения от математического ожидания:
) называется
математическое ожидание квадрата её отклонения от математического ожидания: ![]() .
.
Для
дискретной случайной величины, принимающей возможные значения ![]() с вероятностями
с вероятностями ![]() (
(![]() или
или ![]() ), дисперсия вычисляется по
формуле:
), дисперсия вычисляется по
формуле:
![]() .
.
Для
непрерывной случайной величины, возможные значения которой принадлежат отрезку [a,b] (или![]() ), а плотность распределения
равна
), а плотность распределения
равна ![]() ,
дисперсия находится по формуле:
,
дисперсия находится по формуле:
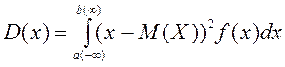 .
.
Эти формулы
непосредственно следуют из определения математического ожидания дискретной и
непрерывной случайных величин.![]()
Существуют другие формулы для вычисления дисперсии, часто практически удобнее вышеприведённых формул.
Теорема.
Дисперсия равна разности между математическим ожиданием квадрата случайной
величины и квадратом её математического ожидания, т.е. ![]() .
.
Действительно,
т.к. ![]() постоянное,
то
постоянное,
то ![]() и
и ![]() также постоянные,
поэтому по свойствам математического ожидания имеем:
также постоянные,
поэтому по свойствам математического ожидания имеем:
![]()
=
![]()
![]() .
.
Исходя из определения математического ожидания дискретных и непрерывных случайных величин, последняя формула перепишется:
для
дискретных – 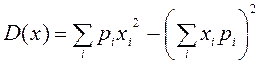 ;
;
для
непрерывных – 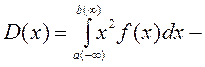
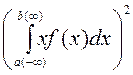 .
.
Свойства
![]() .
.
1. ![]() ;
;
2. ![]() ;
;
3. ![]() .
.
Обобщения и следствия свойств:
а) ![]() , где
, где ![]() - константы;
- константы;
б) ![]() ;
;
в) ![]() ,
, ![]() .
.
Дисперсию числа появления события в независимых
испытаниях так же, как и математическое ожидание, можно находить по
особым формулам: ![]() -
дисперсия числа появления события в одном испытании;
-
дисперсия числа появления события в одном испытании; ![]() - дисперсия числа появления
события в n испытаниях (
- дисперсия числа появления
события в n испытаниях (![]() - вероятность появления,
- вероятность появления, ![]() - вероятность не
появления события в каждом испытании;
- вероятность не
появления события в каждом испытании; ![]() – число испытаний).
– число испытаний).
Дисперсия имеет размерность квадрата случайной величины, часто для сравнения желательно иметь характеристику рассеяния той же размерности. Такой характеристикой является среднее квадратическое отклонение.
Определение.
Средним квадратическим отклонением или стандартным
отклонением случайной величины (обозначается ![]() ) называется квадратный корень из её
дисперсии, т.е.
) называется квадратный корень из её
дисперсии, т.е. ![]() .
.
Определения и свойства других числовых характеристик см. в приложении А, а также в [1], стр. 71-85; [2], стр. 80-83; [3], стр. 98-100.
1.5 Лекции 5-6. Основные законы распределения случайных величин
Содержание лекции: биноминальный закон распределения, распределение Пуассона, равномерное, показательное, нормальное распределения.
Цель лекции: познакомиться с основными законами распределения случайных величин.
Биноминальный закон распределения
Пусть ![]() – число появления события A в n
независимых испытаниях, p –
вероятность появления A в каждом испытании,
– число появления события A в n
независимых испытаниях, p –
вероятность появления A в каждом испытании, ![]() – вероятность не появления. Возможные
значения
– вероятность не появления. Возможные
значения ![]() :
0,1,2,…,
:
0,1,2,…, ![]() .
Вероятности этих возможных значений вычисляются по формуле
.
Вероятности этих возможных значений вычисляются по формуле
![]() =
=![]()
![]() ,
, ![]() (1).
(1).
Определение.
Распределение дискретной случайной величины ![]() , для которой закон
распределения задаётся формулой (1), называется биномиальным.
, для которой закон
распределения задаётся формулой (1), называется биномиальным.
Таким образом, ряд распределения этой случайной величины будет иметь вид:
Т а б л и ц а 3
|
Х |
0 |
1 |
2 |
… |
n |
|
Р(Х=k) |
|
|
|
… |
|
Функция распределения:
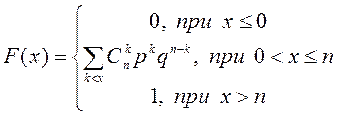 .
.
Для определения числовых характеристик можно
воспользоваться уже готовыми формулами, которые найдены при определении свойств
математического ожидания и дисперсии. Было показано, что математическое
ожидание и дисперсия числа появления события в ![]() независимых испытаниях равны:
независимых испытаниях равны: ![]() ,
, ![]() . Вероятность попадания
в интервал
. Вероятность попадания
в интервал ![]() можно
найти по формуле
можно
найти по формуле
![]() .
.
Исследование случайных величин, распределённых по биномиальному закону, удобно проводить в среде Mathcad с помощью специальных встроенных функций (см. [1], стр. 105).
Распределение Пуассона
Распределение
Пуассона является предельным для биномиального, когда число испытаний n неограниченно
возрастает, а вероятность появления события в каждом испытании p
уменьшается, но при этом произведение ![]() остаётся постоянным. В этом случае
вероятность появления события ровно k раз (k=0,1,2,…,
n,…) вычисляется по формуле Пуассона
остаётся постоянным. В этом случае
вероятность появления события ровно k раз (k=0,1,2,…,
n,…) вычисляется по формуле Пуассона
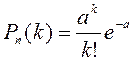 ,
,
а случайная величина, закон распределения которой задаётся этой форму-
лой, говорят, распределена по закону Пуассона.
Ряд распределения этой случайной величины будет иметь вид:
Т а б л и ц а 4
|
Х |
0 |
1 |
2 |
… |
n |
… |
|
Р(Х=k) |
|
|
|
… |
|
… |
Найдём числовые характеристики.
![]()
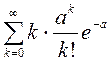 =
=![]()
 =
=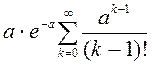 = =
= =![]() .
.
Итак, математическое ожидание равно ![]() . Аналогично рассуждая,
можно определить, что дисперсия равна
. Аналогично рассуждая,
можно определить, что дисперсия равна ![]() . Таким образом, для случайных величин,
распределённых по закону Пуассона, математическое ожидание и дисперсия равны
между собой. Это свойство закона Пуассона применяется на практике при проверке
гипотезы о том, что исследуемая случайная величина распределена по закону
Пуассона. О распределении Пуассона часто говорят как о «законе редких событий».
На практике это распределение встречается довольно часто. Примерами случайных
величин, распределённых по закону Пуассона, являются: число электронов,
вылетающих с катода за определённый промежуток времени; число вызовов,
поступающих на телефонную станцию за время t;
количество распадающегося за короткий промежуток времени радиоактивного
вещества; число обрывов пряжи определённого сорта за время t
и т.д.
. Таким образом, для случайных величин,
распределённых по закону Пуассона, математическое ожидание и дисперсия равны
между собой. Это свойство закона Пуассона применяется на практике при проверке
гипотезы о том, что исследуемая случайная величина распределена по закону
Пуассона. О распределении Пуассона часто говорят как о «законе редких событий».
На практике это распределение встречается довольно часто. Примерами случайных
величин, распределённых по закону Пуассона, являются: число электронов,
вылетающих с катода за определённый промежуток времени; число вызовов,
поступающих на телефонную станцию за время t;
количество распадающегося за короткий промежуток времени радиоактивного
вещества; число обрывов пряжи определённого сорта за время t
и т.д.
Равномерное распределение
В некоторых задачах практики встречаются непрерывные случайные величины, о которых известно, что их возможные значения лежат в определённом интервале и все они одинаково возможны. О таких величинах говорят, что они распределены равномерно.
Определение.
Непрерывная случайная величина ![]() имеет равномерное распределение
на отрезке [a,b], если на этом отрезке её плотность распределения
постоянна, а вне него равна нулю, т.е.
имеет равномерное распределение
на отрезке [a,b], если на этом отрезке её плотность распределения
постоянна, а вне него равна нулю, т.е.
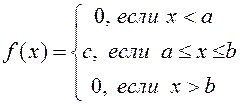 , где с – const.
, где с – const.
Таким образом, график плотности имеет вид:
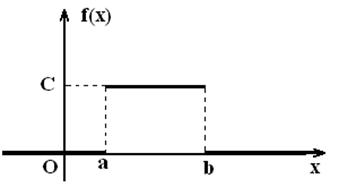
Рисунок 4
По свойствам плотности распределения f(x) площадь фигуры, ограниченной графиком ![]() и осью OX, равна 1, т.е.
и осью OX, равна 1, т.е. ![]() или
или 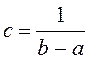 .
.
Поэтому окончательно,
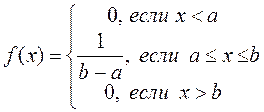 .
.
Найдём
функцию распределения ![]() .
Т.к. по формуле
.
Т.к. по формуле 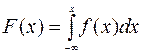 ,
то при
,
то при ![]()
 ;
;
при
![]()
 =
= ;
;
при
![]()
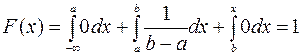 .
.
Таким
образом, 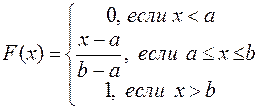 .
График
.
График ![]() имеет
вид:
имеет
вид:
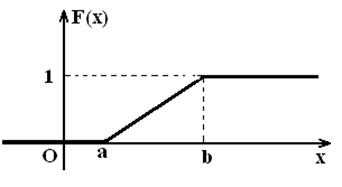
Рисунок 5
Числовые характеристики равномерного распределения: математическое ожидание
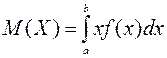 =
=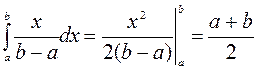 ;
;
дисперсия
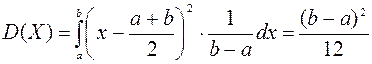 ;
;
среднее
квадратическое отклонение 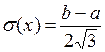 .
.
Вероятность
попадания в интервал ![]() :
:
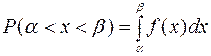 =
=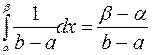 или
или ![]() . Эта вероятность
численно равна площади заштрихованного прямоугольника на рисунке 6.
. Эта вероятность
численно равна площади заштрихованного прямоугольника на рисунке 6.
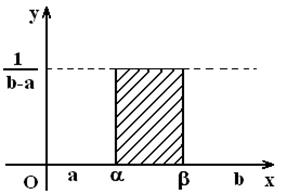
Рисунок 6
Показательное распределение
В практических приложениях теории вероятностей, например, в теории надёжности, теории массового обслуживания и др., используется показательный или экспоненциальный закон распределения.
Определение.
Непрерывная случайная величина ![]() распределена по показательному
закону, если её плотность распределения имеет вид
распределена по показательному
закону, если её плотность распределения имеет вид 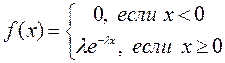 ,
,
где ![]() >0 – параметр распределения.
>0 – параметр распределения.
Найдём функцию
распределения 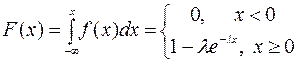 .
На рисунках 7 и 8 изображены графики
.
На рисунках 7 и 8 изображены графики ![]() и
и ![]() .
.
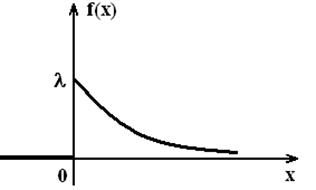
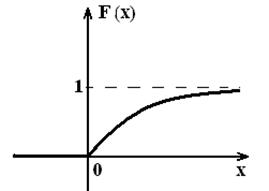
Рисунок 7 Рисунок 8
Числовые характеристики показательного распределения: математи- ческое ожидание
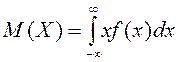 =
= 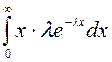 =
=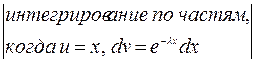 =
=![]() ;
;
дисперсия
![]() =
=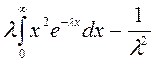 =
=![]() =
=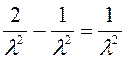 ;
;
среднее
квадратическое отклонение 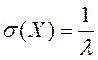 . Таким образом, у показательного
распределения
. Таким образом, у показательного
распределения 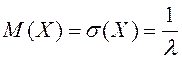 ,
что часто применяется на практике для проверки гипотезы о показательном
распределении исследуемой случайной величины. Вероятность попадания случайной
величины, распределённой по показательному закону в интервал
,
что часто применяется на практике для проверки гипотезы о показательном
распределении исследуемой случайной величины. Вероятность попадания случайной
величины, распределённой по показательному закону в интервал ![]() :
:
![]() = =
= =![]() .
.
Рассмотрим
применение показательного распределения в теории надёжности. Будем для простоты
некоторое устройство называть элементом, независимо от того простое оно или
сложное. Пусть элемент начинает работать в момент ![]() , а по истечении времени
, а по истечении времени ![]() происходит его отказ.
Обозначим
происходит его отказ.
Обозначим ![]() непрерывную
случайную величину – время безотказной работы элемента. Функция распределения
непрерывную
случайную величину – время безотказной работы элемента. Функция распределения ![]() определяет вероятность
отказа за время
определяет вероятность
отказа за время ![]() .
Следовательно, вероятность безотказной работы за то же время (т.е. вероятность
противоположного события
.
Следовательно, вероятность безотказной работы за то же время (т.е. вероятность
противоположного события ![]() ) равна
) равна ![]()
![]() . Функцию
. Функцию ![]() называют функцией надёжности, она
определяет вероятность безотказной работы элемента за время
называют функцией надёжности, она
определяет вероятность безотказной работы элемента за время ![]() . Часто
. Часто ![]() распределена по показательному
закону, тогда
распределена по показательному
закону, тогда ![]() ,
а
,
а ![]()
![]() . В этом случае
. В этом случае ![]() называют показательным
законом надёжности, а
называют показательным
законом надёжности, а ![]() определяет
интенсивность отказов.
определяет
интенсивность отказов.
Нормальное распределение
Нормальный закон распределения – важнейший в теории вероятностей. Он очень широко распространён на практике и появляется, например, в тех случаях, когда случайная величина является результатом действия большого числа факторов, каждый из которых на неё влияет незначительно. Примеры случайных величин, распределённых по нормальному закону: случайные ошибки измерений и наблюдений; случайные отклонения от цели при стрельбе; величина износа деталей во многих механизмах и т.д. Основная особенность, выделяющая нормальный закон среди других, состоит в том, что он является предельным законом, к которому приближаются при определённых условиях, другие законы распределения.
Определение.
Закон распределения вероятностей непрерывной случайной
величины, характеризуемый плотностью 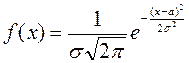 , называется нормальным законом.
, называется нормальным законом.
Таким
образом, нормальное распределение определяется двумя параметрами ![]() и
и ![]() . Раскроем вероятностный смысл
этих параметров. Покажем, что
. Раскроем вероятностный смысл
этих параметров. Покажем, что ![]() :
:
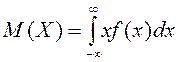 =
=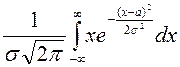 =
=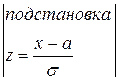 =…=
=…=![]() .
.
Подробно преобразования после указанной подстановки
см. в [1], стр. 96-97. Аналогично, определяя дисперсию, получим, что ![]() :
:
![]() =
=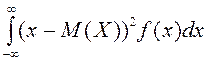 =
=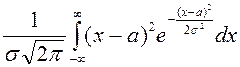 =
=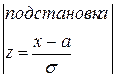 =
=
=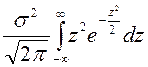 =
=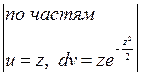 =…=
=…=![]() , откуда квадратическое отклонение
, откуда квадратическое отклонение ![]() .
.
Если a=0 и ![]() =1, то нормальное распределение называется
нормированным.
=1, то нормальное распределение называется
нормированным.
График
плотности вероятностей нормального распределения называется нормальной кривой
или кривой Гаусса. Исследуем функцию 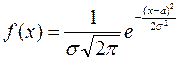 методами математического анализа и
построим её график кривую Гаусса:
методами математического анализа и
построим её график кривую Гаусса:
а)
область определения ![]() ;
;
б)
график расположен выше ![]() , т.к.
, т.к. ![]() ;
;
в)
![]() , т.е. ось
, т.е. ось ![]() – горизонтальная
асимптота;
– горизонтальная
асимптота;
г)
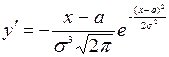 ,
, ![]() при
при ![]() - критическая точка; т.к.
- критическая точка; т.к. ![]() при
при ![]() и
и ![]() при
при ![]() , то
, то ![]() ,
, 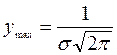 ;
;
д) по второй производной легко найти точки перегиба
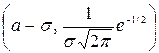 и
и  . Итак, кривая Гаусса имеет вид:
. Итак, кривая Гаусса имеет вид:
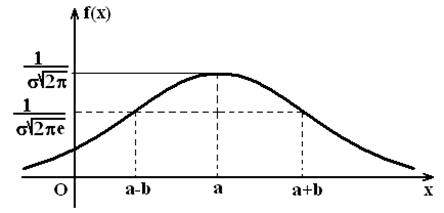
Рисунок 9
Влияние изменения параметров a и ![]() на нормальные кривые
следующее:
на нормальные кривые
следующее:
а)
изменение величины a при одном ![]() не меняет форму нормальной кривой,
происходит только её сдвиг вдоль оси ОХ влево при
не меняет форму нормальной кривой,
происходит только её сдвиг вдоль оси ОХ влево при ![]() , и вправо при
, и вправо при ![]() ;
;
б)
так как 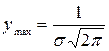 , то
с возрастанием
, то
с возрастанием ![]() максимальная
ордината убывает и наоборот; а поскольку площадь, ограниченная кривой
распределения всегда равна 1, то с изменением
максимальная
ордината убывает и наоборот; а поскольку площадь, ограниченная кривой
распределения всегда равна 1, то с изменением ![]() меняется только форма кривой: с
возрастанием
меняется только форма кривой: с
возрастанием ![]() она
становится более пологой и растягивается вдоль оси ОХ.
она
становится более пологой и растягивается вдоль оси ОХ.
Найдём вероятность
попадания нормально распределённой случайной величины в заданный интервал ![]() :
:
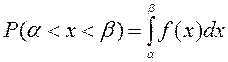 =
=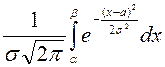 =
=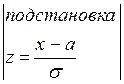 =
= =
=
=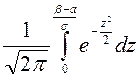 -
-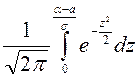 =
= 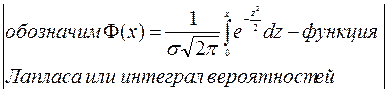 =
=
=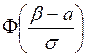 -
- 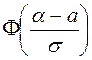 .
.
Значения функции Лапласа можно определить из специальных таблиц или в среде Mathcad. Полезно знать свойства этой функции:
1) ![]() определена для всех х;
определена для всех х;
2) ![]() ;
; 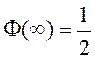 ;
;
3) ![]() , т.е. функция
нечётная;
, т.е. функция
нечётная;
4) ![]()
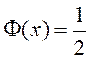 .
.
Таким образом, график функции Лапласа имеет вид:
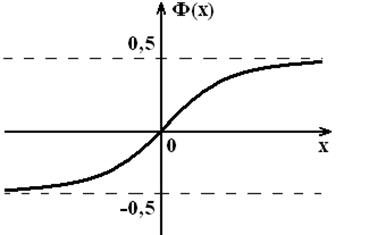
Рисунок 10
Через функцию Лапласа определяется и функция распределения F(x) нормально распределённой случайной величины:

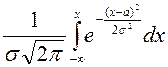 =
=![]()
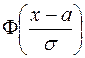 -
- ![]() =
=
=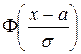 +
+ ![]() =
= 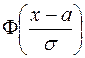 + 0,5.
+ 0,5.
На
практике часто приходится вычислять вероятность того, что отклонение нормально
распределённой случайной величины ![]() по абсолютной величине меньше заданного
числа
по абсолютной величине меньше заданного
числа ![]() , т.е.
, т.е. ![]() или, что то же самое,
вероятность попадания этой величины в интервал, симметричный относительно
центра рассеяния a, т.е.
или, что то же самое,
вероятность попадания этой величины в интервал, симметричный относительно
центра рассеяния a, т.е. ![]() .
.
Действительно,
т.к. ![]() , то
, то
![]()
![]()
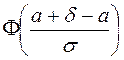 -
-  =
=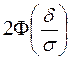 . Таким образом, чем
меньше
. Таким образом, чем
меньше ![]() (т.е.
рассеяние), тем больше вероятность нормально распределённой случайной величины
попасть в интервал
(т.е.
рассеяние), тем больше вероятность нормально распределённой случайной величины
попасть в интервал ![]() .
Определим, какой надо взять интервал с центром в точке
.
Определим, какой надо взять интервал с центром в точке ![]() , чтобы почти все значения
, чтобы почти все значения ![]() попали в него.
Используя таблицы значений
попали в него.
Используя таблицы значений ![]() , получим:
, получим:
![]() =
=![]() =0,6826;
=0,6826;
![]() =
=![]() =0,9594;
=0,9594;
![]() =
=![]() =0,9973;
=0,9973; ![]() =
=![]() =0,999936.
=0,999936.
Итак,
практически достоверно, что почти все значения нормально распределённой
случайной величины (~ 99,7%) попадают в интервал ![]() . Это утверждение называется «правилом трёх
сигм».
. Это утверждение называется «правилом трёх
сигм».
2 Элементы математической статистики
2.1 Лекция 7. Предмет и основные понятия математической
статистики
Содержание лекции: генеральная и выборочная совокупности, способы отбора. Статистическое распределение выборки. Полигон и гистограмма. Цель лекции: познакомить с предметом и основными понятиями математической статистики.
Математическая статистика – это раздел математики, изучающий методы сбора, обработки и анализа экспериментальных данных, полученных в результате наблюдений массовых случайных явлений. Теория вероятностей является теоретической основой прикладных задач, которые решает математическая статистика.
Введём некоторые общие понятия. Пусть требуется изучить совокупность объектов относительно некоторого качественного или количественного признака. Например, если изучается партия деталей, то качественный признак – стандартность деталей, количественный признак – некоторый размер деталей.
Определения.
1. Генеральной совокупностью называется множество всех возможных результатов экспериментов (измерений, наблюдений).
2. Выборочной совокупностью или просто выборкой называется совокупность случайно отобранных из генеральной совокупности объектов.
3. Объёмом генеральной совокупности или объёмом выборки называется число объектов этой совокупности, обозначаются N и n.
4.
Пусть для изучения некоторого признака ![]() из генеральной совокупности
извлечена выборка
из генеральной совокупности
извлечена выборка ![]() объёма
n. Наблюдаемые значения
объёма
n. Наблюдаемые значения ![]()
![]() называются вариантами.
называются вариантами.
5. Пусть ![]() наблюдалось
наблюдалось ![]() раз
раз ![]() , причём
, причём ![]() . Число
. Число ![]()
называется
частотой варианты ![]() ,
а отношение
,
а отношение 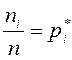 -
относительной частотой этой варианты.
-
относительной частотой этой варианты.
Определение неизвестного закона распределения
Пусть для изучения некоторого признака ![]() (случайной величины
(случайной величины ![]() ) проведены n независимых
испытаний (измерений, наблюдений), в каждом из которых величина
) проведены n независимых
испытаний (измерений, наблюдений), в каждом из которых величина ![]() принимает то или иное
значение. Получаем произвольную выборку (или простой статистический ряд):
принимает то или иное
значение. Получаем произвольную выборку (или простой статистический ряд):
Т а б л и ц а 5
|
№ наблюдения |
1 |
2 |
… |
|
варианты |
|
|
… |
Если расположить выборку в возрастающем порядке, то получим ряд называемый вариационным рядом:
Т а б л и ц а 6
|
№ |
1 |
2 |
… |
k |
|
|
|
|
… |
|
Здесь
![]() ,
, ![]() . Если частота и
относительная частота варианты
. Если частота и
относительная частота варианты ![]() соответственно равны
соответственно равны ![]() и
и 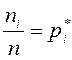
![]() , то можно построить статистический ряд
частот (таблица 7) и статистический ряд относительных частот (таблица 8), где
, то можно построить статистический ряд
частот (таблица 7) и статистический ряд относительных частот (таблица 8), где ![]() :
:
Т а б л и ц а 7
|
|
|
|
… |
|
|
|
|
|
… |
|
Т а б л и ц а 8
|
|
|
|
… |
|
|
|
|
|
… |
|
На практике встречаются выборки довольно большого
объёма, или изучаемый признак является непрерывным (т.е. ![]() может принимать любые значения
из некоторого промежутка). В таком случае составляют так называемый
интервальный статистический ряд. Для этого всё множество наблюдаемых значений
разбивают на промежутки
может принимать любые значения
из некоторого промежутка). В таком случае составляют так называемый
интервальный статистический ряд. Для этого всё множество наблюдаемых значений
разбивают на промежутки ![]() ,
, ![]() , и т.д., обычно равной длине
, и т.д., обычно равной длине ![]() Важным вопросом
является определение длины
Важным вопросом
является определение длины ![]() и их количества. Из различных рекомендаций
рассмотрим следующий способ:
и их количества. Из различных рекомендаций
рассмотрим следующий способ: 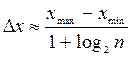 – формула Стерджеса. Здесь
– формула Стерджеса. Здесь ![]() - размах выборки;
- размах выборки; ![]() ;
;
![]() - число интервалов,
т.е.
- число интервалов,
т.е. 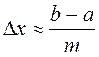 .
.
За начало первого интервала рекомендуется брать
величину 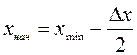 . Во
вторую и третью строки интервального ряда вписывают количество наблюдений,
попавших в соответствующий интервал (т.е. сумму частот вариант интервала), и
сумму относительных частот вариант интервала. Таким образом, интервальный ряд
имеет вид:
. Во
вторую и третью строки интервального ряда вписывают количество наблюдений,
попавших в соответствующий интервал (т.е. сумму частот вариант интервала), и
сумму относительных частот вариант интервала. Таким образом, интервальный ряд
имеет вид:
Т а б л и ц а 9
|
интервалы |
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
Из интервального ряда легко получить группированный или дискретный статистический ряд (см. таблицу 10), если в качестве вариант взять середины интервалов:
Т а б л и ц а 10
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
Статистические ряды (частот, относительных частот,
интервальный и дискретный ряды частот и относительных частот) являются оценкой
неизвестного закона распределения. В соответствии с теоремой Бернулли (см.
приложение Б), согласно которой относительная частота появления события по
вероятности стремится к вероятности этого события (![]() ), можно сделать вывод, что
статистические ряды относительных частот являются эмпирическими распределениями
изучаемой случайной величины, т.е. аналогом ряда распределения теоретической
случайной величины.
), можно сделать вывод, что
статистические ряды относительных частот являются эмпирическими распределениями
изучаемой случайной величины, т.е. аналогом ряда распределения теоретической
случайной величины.
Вариационный ряд можно обработать по-другому, получив аналог геометрического закона распределения – многоугольника распределения.
По
таблицам 7 или 8 на координатной плоскости строим точки ![]() или
или ![]() , соединяем их отрезками прямой.
Полученные фигуры называют полигоном частот или полигоном относительных частот
(см. рисунок11).
, соединяем их отрезками прямой.
Полученные фигуры называют полигоном частот или полигоном относительных частот
(см. рисунок11).
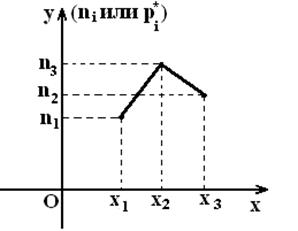
Рисунок 11
Более широко в статистике применяются другие
геометрические построения – гистограммы. Это объясняется тем, что гистограмма
относительных частот является статистическим аналогом дифференциальной функции
распределения (плотности) ![]() случайной величины. Например, в задачах
проверки статистических гипотез гистограмму сравнивают с графиком теоретических
плотностей распределения и выдвигают предварительное суждение о распределении
изучаемой случайной величины.
случайной величины. Например, в задачах
проверки статистических гипотез гистограмму сравнивают с графиком теоретических
плотностей распределения и выдвигают предварительное суждение о распределении
изучаемой случайной величины.
Для
построения гистограмм можно использовать интервальные ряды. Гистограмма – это
ступенчатая фигура, состоящая из прямоугольников, в основании которых интервалы
длины ![]() , а
высоты
, а
высоты 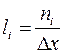 или
или 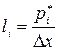 . В первом случае имеем
гистограмму частот, во втором – гистограмму относительных частот (см. рисунок 12).
. В первом случае имеем
гистограмму частот, во втором – гистограмму относительных частот (см. рисунок 12).
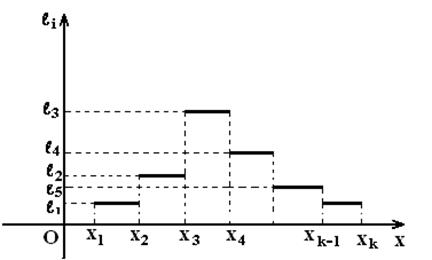
Рисунок 12
Очевидно,
площадь гистограммы частот равна объёму выборки ![]() , а площадь гистограммы относительных
частот равна единице
, а площадь гистограммы относительных
частот равна единице ![]() .
Если на каждой ступеньке гистограммы относительных частот взять произвольную
точку, например, середину, и соединить эти точки плавной линией, то получим
приблизительный график плотности
.
Если на каждой ступеньке гистограммы относительных частот взять произвольную
точку, например, середину, и соединить эти точки плавной линией, то получим
приблизительный график плотности ![]() .
.
Наиболее важным для описания экспериментального материала является построение статистической (эмпирической) функции распределения.
Определение.
Эмпирической функцией
распределения называется функция ![]() , определяющая для каждого значения x относительную
частоту события X<x, т.е.
, определяющая для каждого значения x относительную
частоту события X<x, т.е. 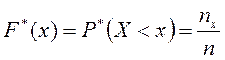 , где
, где ![]() - число вариант
- число вариант ![]() , меньших
, меньших ![]() ; n
– объём выборки.
; n
– объём выборки.
Из
определения функции ![]() ясно,
что она обладает теми же свойствами, что и функция
ясно,
что она обладает теми же свойствами, что и функция ![]() :
:
а) её значения принадлежат отрезку [0,1];
б) она неубывающая;
в) если ![]() - наименьшая варианта, а
- наименьшая варианта, а ![]() - наибольшая, то
- наибольшая, то
![]() ;
; ![]() .
.
По закону больших чисел Бернулли (см. приложение Б) относительная
частота появления события по вероятности стремится к вероятности этого события,
т.е. ![]() , а
значит
, а
значит ![]() .
Таким образом, эмпирическая функция распределения
.
Таким образом, эмпирическая функция распределения ![]() является оценкой теоретической (интегральной)
функции распределения
является оценкой теоретической (интегральной)
функции распределения ![]() .
.
Для построения воспользуемся статистическим рядом частот или
относительных частот: 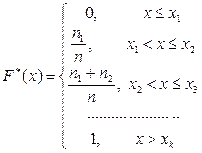 или
или 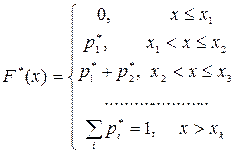 .
.
Графиком ![]() будет ступенчатая разрывная линия, скачки соответствуют
наблюдаемым значениями и равны относительным частотам этих значений (см. рисунок 13).
будет ступенчатая разрывная линия, скачки соответствуют
наблюдаемым значениями и равны относительным частотам этих значений (см. рисунок 13).
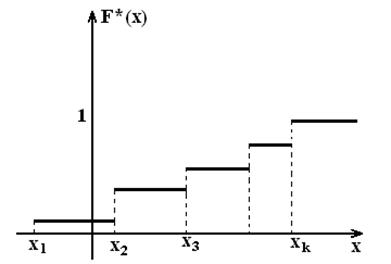
Рисунок 13
Если выборка большого объёма или изучаемый признак
являются непрерывными, то в качестве варианты ![]() можно взять границы интервалов из
интервального статистического ряда. Учитывая, что
можно взять границы интервалов из
интервального статистического ряда. Учитывая, что ![]() и
и ![]() , на координатной плоскости
строят точки
, на координатной плоскости
строят точки ![]() ,
,
![]() , …,
, …,  , … ,
, … , ![]() , соединяют их отрезками
прямой или плавной линией. Эта линия будет представлять приближённый график
теоретической функции распределения
, соединяют их отрезками
прямой или плавной линией. Эта линия будет представлять приближённый график
теоретической функции распределения ![]() (см. рисунок 14).
(см. рисунок 14).
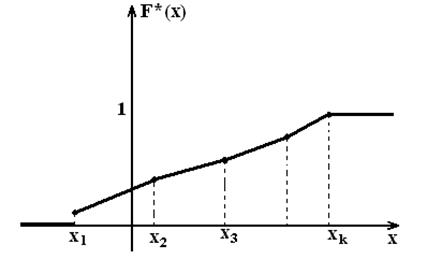
Рисунок 14
2.2 Лекция 8. Числовые характеристики статистических распределений. Статистические оценки параметров распределения
Содержание лекции: выборочная средняя и выборочная дисперсия. Несмещённые, состоятельные и эффективные оценки. Оценка генеральной и выборочной средней. Точечные и интервальные оценки.
Цель лекции: познакомить с оценками параметров распределения и их свойствами.
В статистических распределениях в математической статистике
вводятся характеристики аналогичные числовым характеристикам теоретических
распределений. Аналогом математического ожидания является выборочная средняя,
обозначается ![]() (или
(или
![]() ).
).
Определение.
Выборочной средней называется среднее арифметическое всех вариант выборки.
Таким образом, выборочную среднюю строят по статистическим рядам частот или относительных частот (см. таблицу 7 или 8):
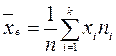 или
или  .
.
Если выборка большого объёма или изучаемая случайная
величина непрерывная, то для нахождения выборочной средней используют те же
формулы, где в качестве ![]() берут середины интервалов в интервальном
ряде, т.е. данные таблицы 10.
берут середины интервалов в интервальном
ряде, т.е. данные таблицы 10.
Определение.
Выборочной дисперсией ![]() называется среднее арифметическое
квадратов отклонений значений выборки от выборочной средней:
называется среднее арифметическое
квадратов отклонений значений выборки от выборочной средней:
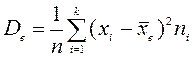 или
или 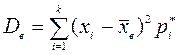 .
.
Аналогично как теоретическую дисперсию, выборочную дисперсию можно посчитать по другой формуле:
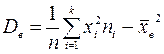 , т.е.
, т.е. ![]() ,
,
где ![]() .
.
Выборочное
среднее квадратическое отклонение находится по формуле ![]() , оно измеряется в тех же
единицах, что и изучаемый признак. При решении практических задач используют
также исправленную выборочную дисперсию и исправленное среднее квадратическое
отклонение.
, оно измеряется в тех же
единицах, что и изучаемый признак. При решении практических задач используют
также исправленную выборочную дисперсию и исправленное среднее квадратическое
отклонение.
 – исправленная
выборочная дисперсия. Таким образом,
– исправленная
выборочная дисперсия. Таким образом, 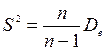 .
. ![]() – исправленное среднее квадратическое
отклонение. Все эти формулы можно использовать для непрерывных признаков,
полагая
– исправленное среднее квадратическое
отклонение. Все эти формулы можно использовать для непрерывных признаков,
полагая 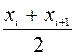 вместо
вместо
![]() .
.
Рассмотрим теперь подробнее вторую основную задачу
математической статистики – оценка неизвестных параметров распределения. На
практике часто бывает, что вид закона распределения изучаемой случайной
величины известен или не существенен. Известно, что он зависит от одного или
нескольких параметров. Например, закон Пуассона – от одного параметра ![]() , нормальный закон
распределения - от параметров
, нормальный закон
распределения - от параметров ![]() и
и ![]() , и т.д. Требуется по выборке, полученной в
результате n наблюдений, оценить эти параметры.
, и т.д. Требуется по выборке, полученной в
результате n наблюдений, оценить эти параметры.
Определение.
Оценкой параметра называется его приближённое значение, найденное на основе ограниченного числа опытов.
Пусть изучается случайная величина ![]() , закон распределения которой
зависит от параметра a. Проводим n опытов, в
результате которых имеем выборку
, закон распределения которой
зависит от параметра a. Проводим n опытов, в
результате которых имеем выборку ![]() . Каждое наблюдаемое значение
. Каждое наблюдаемое значение ![]() рассматриваем как
случайную величину
рассматриваем как
случайную величину ![]() (
т.е. получаем как бы n экземпляров случайной величины
(
т.е. получаем как бы n экземпляров случайной величины ![]() , которые распределены так же как
, которые распределены так же как
![]() ). Обозначим
). Обозначим ![]() оценку параметра a.
Очевидно, что оценка, вычисленная на основе n наблюдений,
должна являться некоторой функцией этих наблюдений, т.е.
оценку параметра a.
Очевидно, что оценка, вычисленная на основе n наблюдений,
должна являться некоторой функцией этих наблюдений, т.е. ![]() . Как было показано выше, оценкой
математического ожидания являлась выборочная средняя
. Как было показано выше, оценкой
математического ожидания являлась выборочная средняя  , оценкой функции распределения
, оценкой функции распределения ![]() – эмпирическая функция
распределения
– эмпирическая функция
распределения ![]() ,
оценкой плотности – гистограмма. Итак, оценка
,
оценкой плотности – гистограмма. Итак, оценка ![]() параметра
параметра ![]() является случайной величиной, так как
является функцией случайных величин
является случайной величиной, так как
является функцией случайных величин ![]() . Если возьмём другую выборку, то, вообще
говоря, получим другую оценку. Если же число наблюдений n мало, то замена
параметра
. Если возьмём другую выборку, то, вообще
говоря, получим другую оценку. Если же число наблюдений n мало, то замена
параметра ![]() его
оценкой может привести к ошибке. Поэтому, чтобы оценки давали «хорошие»
приближения к истинному значению параметра (т.е. были близкими к нему,
«доброкачественными») к ним предъявляют ряд требований.
его
оценкой может привести к ошибке. Поэтому, чтобы оценки давали «хорошие»
приближения к истинному значению параметра (т.е. были близкими к нему,
«доброкачественными») к ним предъявляют ряд требований.
Свойства статистических оценок
1. Несмещённость.
Определение.
Оценка ![]() параметра
параметра ![]() называется несмещённой, если её математичес-
кое ожидание равно оцениваемому параметру, т.е.
называется несмещённой, если её математичес-
кое ожидание равно оцениваемому параметру, т.е. ![]() ; если
; если ![]() , то оценка называется смещённой.
, то оценка называется смещённой.
Несмещённая оценка не даёт систематических ошибок, т.е. ошибок одного знака, либо в сторону завышения (оценка всегда больше оцениваемого параметра), либо в сторону занижения (меньше). Это особенно важно при малом объёме выборки.
2. Состоятельность.
Определение.
Оценка ![]() параметра a называется
состоятельной, если она сходится по вероятности к оцениваемому параметру, т.е.
параметра a называется
состоятельной, если она сходится по вероятности к оцениваемому параметру, т.е.
![]() или
или ![]() выполняется
выполняется ![]() .
.
Если оценка состоятельная, то с увеличением объёма выборки отличие оценки от истинного значения параметра будет уменьшаться.
3. Эффективность.
Определение.
Оценка ![]() параметра
параметра ![]() называется эффективной, если она имеет
называется эффективной, если она имеет
наименьшую дисперсию, среди всех возможных несмещённых оценок этого параметра.
Совмещение свойств несмещённости и эффективности оценки является с практической точки зрения очень важным. Оценку, обладающую этими двумя свойствами, обычно называют оптимальной.
Для проверки, обладает ли каким-либо из этих свойств данная оценка, применяют различные методы (см., например, [2], стр.227). Не всегда удаётся получить оценку, обладающую всеми тремя свойствами, и, если она ими обладает, то это сразу выделяет её среди других оценок.
Точечные оценки параметров распределения
Определение.
Точечной называется оценка, определяемая одним числом.
Все оценки числовых характеристик статистических
распределений, рассмотренные выше, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , являются точечными. Определим, какими
свойствами из перечисленных выше они обладают.
, являются точечными. Определим, какими
свойствами из перечисленных выше они обладают.
Пусть ![]() - выборка, полученная в результате n
независимых наблюдений случайной величины
- выборка, полученная в результате n
независимых наблюдений случайной величины ![]() . Так как
. Так как ![]() имеет случайный характер, то рассматриваем
её как случайную величину
имеет случайный характер, то рассматриваем
её как случайную величину ![]()
![]() ( т.е. получаем n
экземпляров случайной величины Х:
( т.е. получаем n
экземпляров случайной величины Х: ![]() . Поэтому
. Поэтому ![]() ,
, ![]() ,
, ![]() . Покажем, что выборочная средняя
. Покажем, что выборочная средняя  =
= 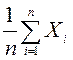 есть несмещённая и состоятельная
оценка математического ожидания.
есть несмещённая и состоятельная
оценка математического ожидания.
Действительно,
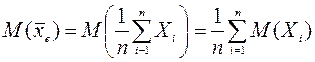 =
=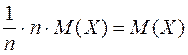 . Итак,
. Итак, ![]() , т.е.
, т.е. ![]() - несмещённая оценка
математического ожидания. Для доказательства состоятельности применяют теорему
Чебышева (см. приложение Б). В нашем случае указанное в этой теореме равенство перепишется
так:
- несмещённая оценка
математического ожидания. Для доказательства состоятельности применяют теорему
Чебышева (см. приложение Б). В нашем случае указанное в этой теореме равенство перепишется
так: ![]() , т.е.
, т.е. ![]() , и является
состоятельной оценкой математического ожидания.
, и является
состоятельной оценкой математического ожидания. ![]() является также и наиболее эффективной оценкой
математического ожидания, а для нормального распределения она будет
эффективной. На практике всегда в качестве оценки математического ожидания
берут выборочную среднюю
является также и наиболее эффективной оценкой
математического ожидания, а для нормального распределения она будет
эффективной. На практике всегда в качестве оценки математического ожидания
берут выборочную среднюю ![]() .
.
Рассмотрим
теперь оценку дисперсии D(X) – выборочную
дисперсию ![]() ,
которая запишется в нашем случае так
,
которая запишется в нашем случае так 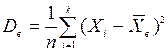 или
или 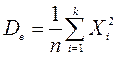 –
–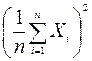 . Доказано, что
. Доказано, что 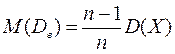 , т.е. эта оценка смещённая (см.
доказательство [2], стр.229). Поэтому выборочную дисперсию исправляют,
умножив её на
, т.е. эта оценка смещённая (см.
доказательство [2], стр.229). Поэтому выборочную дисперсию исправляют,
умножив её на ![]() .
Полученная оценка так и называется – исправленная выборочная дисперсия:
.
Полученная оценка так и называется – исправленная выборочная дисперсия: 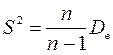 . Эта оценка дисперсии
будет уже несмещённой. При больших n разница между
. Эта оценка дисперсии
будет уже несмещённой. При больших n разница между ![]() и
и ![]() невелика, поэтому
невелика, поэтому ![]() используют для оценки
дисперсии обычно при
используют для оценки
дисперсии обычно при ![]() .
.
Интервальные оценки
Точечные оценки не всегда хорошо приближают оцениваемый параметр, особенно при малых объёмах выборки. Кроме того, они не дают возможности определить точность и надежность оценки.
Определение.
Интервальной называется оценка, которая определяется двумя числами – концами интервала.
Определим
смысл понятий точности и надежности оценки. Пусть по данным выборки построена
точечная оценка ![]() параметра а. Ясно, что
параметра а. Ясно, что ![]() тем точнее определяет
параметр а, чем меньше
тем точнее определяет
параметр а, чем меньше ![]() . Другими словами, если
. Другими словами, если ![]() и
и ![]() , то чем меньше
, то чем меньше ![]() , тем точнее оценка
, тем точнее оценка ![]() .
.
Определение.
Положительное число ![]() , такое, что
, такое, что ![]() , характеризует точность
оценки; чем меньше
, характеризует точность
оценки; чем меньше ![]() ,
тем точнее оценка.
,
тем точнее оценка.
В
статистических методах требуется оценить вероятность выполнения неравенства ![]() , поэтому возникает
понятие надёжности.
, поэтому возникает
понятие надёжности.
Определение.
Надёжностью
(доверительной вероятностью) оценки ![]() параметра
параметра ![]() называется вероятность
называется вероятность ![]() , с которой осуществляется
неравенство
, с которой осуществляется
неравенство ![]() ,
т.е.
,
т.е. ![]()
![]() .
.
Преобразуем
равенство ![]() :
:
![]() или
или ![]() .
.
Таким
образом, надёжность ![]() (доверительная
вероятность) есть вероятность того, что истинное значение параметра
(доверительная
вероятность) есть вероятность того, что истинное значение параметра ![]() лежит в интервале
лежит в интервале ![]() .
.
Определение.
Интервал ![]() , покрывающий с заданной
надёжностью
, покрывающий с заданной
надёжностью ![]() истинное
значение параметра
истинное
значение параметра ![]() ,
называется доверительным интервалом.
,
называется доверительным интервалом.
Обычно
величину ![]() выбирают
заранее, полагают
выбирают
заранее, полагают ![]() =
0,9 (0,95; 0,99…). Тогда практически достоверно, что точное значение
=
0,9 (0,95; 0,99…). Тогда практически достоверно, что точное значение ![]() находится в
доверительном интервале
находится в
доверительном интервале ![]() .
.
Доверительный интервал для оценки математического
ожидания нормального распределения при известном ![]()
Пусть изучаемая случайная величина ![]() распределена нормально с
параметрами a и
распределена нормально с
параметрами a и ![]() , причём среднее квадратическое отклонение
, причём среднее квадратическое отклонение ![]() известно. Требуется
оценить неизвестное математическое ожидание a. Поставим
задачу найти доверительный интервал, покрывающий параметр a с заданной
надёжностью
известно. Требуется
оценить неизвестное математическое ожидание a. Поставим
задачу найти доверительный интервал, покрывающий параметр a с заданной
надёжностью ![]() .
Проведём n испытаний случайной величины
.
Проведём n испытаний случайной величины ![]() , получим выборку
, получим выборку ![]() . Каждую варианту
рассматриваем как экземпляр случайной величины
. Каждую варианту
рассматриваем как экземпляр случайной величины ![]() , т.е. имеем n случайных
величин
, т.е. имеем n случайных
величин ![]() ,
распределённых так же, как
,
распределённых так же, как ![]() , т.е.
, т.е. ![]() ,
, ![]() . Найдём выборочные оценки на основе этих
наблюдений:
. Найдём выборочные оценки на основе этих
наблюдений: 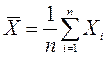 –выборочная
средняя;
–выборочная
средняя; 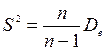 =
=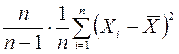 =
= – исправленная выборочная
дисперсия (здесь частоты
– исправленная выборочная
дисперсия (здесь частоты ![]() ). На основе центральной предельной теоремы
(см. приложение Б) делается вывод, что
). На основе центральной предельной теоремы
(см. приложение Б) делается вывод, что ![]() – случайная величина, распределённая, как
и
– случайная величина, распределённая, как
и ![]() , нормально.
По свойствам математического ожидания и дисперсии, найдём параметры
, нормально.
По свойствам математического ожидания и дисперсии, найдём параметры ![]() :
:
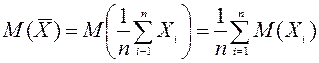 =
=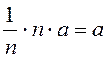 ;
;
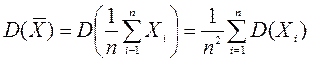 =
= ;
;
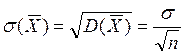 .
.
Теперь приступим к построению доверительного
интервала, покрывающего с надёжностью ![]() истинное значение математического ожидания
истинное значение математического ожидания
![]() случайной
величины
случайной
величины ![]() ,
т.е. требуется выполнение условия
,
т.е. требуется выполнение условия ![]() . Для нормального распределения известна
формула
. Для нормального распределения известна
формула
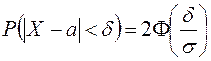 , поэтому, т.к. параметры
, поэтому, т.к. параметры
![]() –
– ![]() и
и ![]() , имеем
, имеем 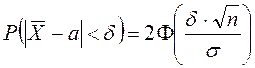 . Обозначим
. Обозначим 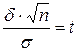 , тогда
, тогда 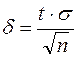 . Ввиду этого обозначения
последнее равенство запишется:
. Ввиду этого обозначения
последнее равенство запишется:

![]() или
или 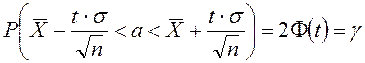 .
.
Итак,
доверительный интервал для оценки математического ожидания ![]() с известным
с известным ![]() будет:
будет: 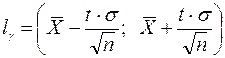 . Величина надёжности
. Величина надёжности ![]() выбирается заранее.
Выбор зависит от конкретной задачи, например, степень доверия авиапассажиров к
надёжности самолёта, очевидно, должна быть больше, чем степень доверия покупателя к
надёжности телевизора. Обычно принято надёжность
выбирается заранее.
Выбор зависит от конкретной задачи, например, степень доверия авиапассажиров к
надёжности самолёта, очевидно, должна быть больше, чем степень доверия покупателя к
надёжности телевизора. Обычно принято надёжность ![]() брать 0,9; 0,95; 0,99. Тогда практически
достоверно, что параметр
брать 0,9; 0,95; 0,99. Тогда практически
достоверно, что параметр ![]() попадёт в доверительный интервал. Значение
t определяют из условия
попадёт в доверительный интервал. Значение
t определяют из условия ![]() откуда
откуда 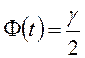 ; при данном
; при данном ![]() по таблице функции Лапласа
по таблице функции Лапласа ![]() находят аргумент t. Из равенства
находят аргумент t. Из равенства 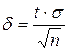 ясно, что чем больше n
(объём выборки), тем меньше
ясно, что чем больше n
(объём выборки), тем меньше ![]() (т.е. тем точнее оценка); из равенства
(т.е. тем точнее оценка); из равенства ![]() ясно, что с увеличением
надёжности
ясно, что с увеличением
надёжности ![]() увеличивается
t, т.к. функция
увеличивается
t, т.к. функция ![]() возрастающая, потому, ввиду равенства
возрастающая, потому, ввиду равенства  , увеличивается
, увеличивается ![]() , т.е. точность
уменьшается.
, т.е. точность
уменьшается.
Пример 2.8.1.
Найти доверительный интервал для
оценки с надёжностью 0,95 неизвестного математического ожидания a нормально
распределённой случайной величины ![]() , если среднее квадратическое отклонение
, если среднее квадратическое отклонение ![]() =5, выборочная средняя
=5, выборочная средняя ![]() =14, объём выборки n
=25.
=14, объём выборки n
=25.
Решение: по формуле 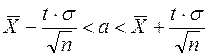 . Неизвестное t найдём из
равенства
. Неизвестное t найдём из
равенства 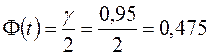 , по таблице t=1,96.
Таким образом,
, по таблице t=1,96.
Таким образом,
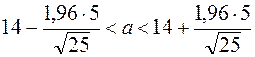 или
или ![]() . Итак, доверительный
интервал
. Итак, доверительный
интервал ![]() .
.
Приложение А
Понятие о моментах распределения. Мода, медиана, квантили
Некоторые основные числовые характеристики являются частным случаем понятия момента распределения. Термин «момент» из механики, где он описывает распределение масс. В теории вероятностей рассматриваются моменты двух видов: начальные и центральные.
Определение.
Начальным
моментом ![]() –го
порядка случайной величины
–го
порядка случайной величины ![]() называется математическое ожидание
случайной величины
называется математическое ожидание
случайной величины ![]() ,
т.е.
,
т.е. ![]() .
.
Следовательно,
для дискретных случайных величин начальный момент выражается формулой 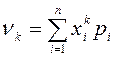 ; для непрерывных –
формулой
; для непрерывных –
формулой 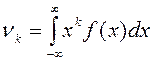 .
Особое значение имеет начальный момент первого порядка – это математическое
ожидание:
.
Особое значение имеет начальный момент первого порядка – это математическое
ожидание: ![]() .
Начальные моменты высших порядков используются в основном для вычисления
центральных моментов, также они позволяют лучше учесть влияние на
математическое ожидание тех возможных значений, которые велики и имеют малую
вероятность.
.
Начальные моменты высших порядков используются в основном для вычисления
центральных моментов, также они позволяют лучше учесть влияние на
математическое ожидание тех возможных значений, которые велики и имеют малую
вероятность.
Определение.
Центральным моментом ![]() –го порядка случайной величины
–го порядка случайной величины ![]() называется
математическое ожидание случайной величины
называется
математическое ожидание случайной величины ![]() , т.е.
, т.е. ![]() .
.
Для дискретных случайных величин центральный момент
выражается формулой 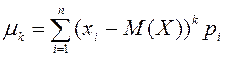 ;
для непрерывных – формулой
;
для непрерывных – формулой 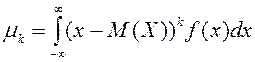 . Как было показано выше,
. Как было показано выше, ![]() ,
, ![]() . Для описания свойств случайных
величин широко применяются также центральные моменты третьего и четвёртого
порядков, они характеризуют форму – симметричность или несимметричность,
островершинность или плосковершинность.
. Для описания свойств случайных
величин широко применяются также центральные моменты третьего и четвёртого
порядков, они характеризуют форму – симметричность или несимметричность,
островершинность или плосковершинность.
Центральный момент третьего порядка ![]() служит характеристикой
симметрии. Доказано, что если случайная величина распределена симметрично
относительно своего математического ожидания, то
служит характеристикой
симметрии. Доказано, что если случайная величина распределена симметрично
относительно своего математического ожидания, то ![]() = 0 (как и все центральные моменты нечётных
порядков
= 0 (как и все центральные моменты нечётных
порядков ![]() ).
Так как
).
Так как ![]() имеет
размерность куба случайной величины, то обычно рассматривают безразмерную
характеристику:
имеет
размерность куба случайной величины, то обычно рассматривают безразмерную
характеристику: 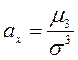 -
коэффициент асимметрии или просто асимметрию. От
-
коэффициент асимметрии или просто асимметрию. От ![]() зависит форма кривой распределения, если
зависит форма кривой распределения, если ![]() , то эта кривая более
полога справа от математического ожидания, если
, то эта кривая более
полога справа от математического ожидания, если ![]() , то слева (см. рисунок
А.1).
, то слева (см. рисунок
А.1).
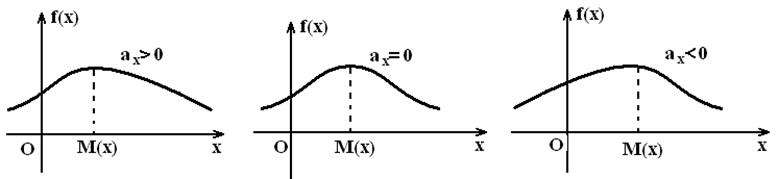
Рисунок А.1
Четвёртый центральный момент ![]() служит характеристикой
островершинности или плосковершинности распределения.
служит характеристикой
островершинности или плосковершинности распределения.
Определение.
Эксцессом случайной величины ![]() называется безразмерная величина
называется безразмерная величина
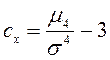 .
.
Для нормального распределения 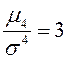 и
и ![]() . А, поскольку, среди законов распределения
нормальный закон считается «эталоном формы», то эксцесс, как и асимметрия,
позволяют оценить отличие формы распределения от нормального, для которого
. А, поскольку, среди законов распределения
нормальный закон считается «эталоном формы», то эксцесс, как и асимметрия,
позволяют оценить отличие формы распределения от нормального, для которого ![]() и
и ![]() . Кривые распределения более
островершинные, чем нормальная кривая, имеют эксцесс больше 0, менее – меньше 0
(см. рисунок А.2).
. Кривые распределения более
островершинные, чем нормальная кривая, имеют эксцесс больше 0, менее – меньше 0
(см. рисунок А.2).

Рисунок А.2
При вычислении центральных моментов полезно применять формулы, выражающие центральные моменты через начальные:
![]() ;
; ![]() ;
; ![]() .
.
Моменты более высоких порядков применяются на практике редко.
Кроме математического ожидания, на практике применяются и другие характеристики положения – мода, медиана, квантиль.
Модой дискретной случайной величины называется её
наиболее вероятное значение; модой непрерывной случайной величины называется
такое её значение, при котором плотность распределения имеет максимум.
Существуют распределения, не имеющие максимумов или имеющие один или несколько
максимумов. Мода обозначается ![]() или
или ![]() .
.
Медианой непрерывной случайной величины называется
такое её значение, относительно которого равновероятно, окажется ли случайная
величина больше или меньше этого значения, обозначается ![]() , т.е.
, т.е.
 . Так как функция
распределения
. Так как функция
распределения ![]() ,
то последнее равенство можно переписать
,
то последнее равенство можно переписать 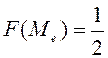 . Поэтому практически медиану находят как
корень уравнения
. Поэтому практически медиану находят как
корень уравнения  .
.
Квантилью
порядка ![]() называется
такое значение
называется
такое значение ![]() случайной
величины, для которого выполняется
случайной
величины, для которого выполняется ![]() . Таким образом, медиана есть одна из
квантилей, когда
. Таким образом, медиана есть одна из
квантилей, когда ![]() =1/2.
Квантили
=1/2.
Квантили ![]() иногда
называют соответственно нижней квантилью, медианой и верхней квантилью, они
делят область определения случайной величины на четыре части, вероятность
попадания в каждую одинакова и равна ¼.
иногда
называют соответственно нижней квантилью, медианой и верхней квантилью, они
делят область определения случайной величины на четыре части, вероятность
попадания в каждую одинакова и равна ¼.
Приложение Б
Предельные теоремы теории вероятностей
Математические законы теории вероятностей являются абстракцией реальных статистических закономерностей, свойственных массовым случайным явлениям. Если случайное явление носит массовый характер, то его характеристики становятся устойчивыми и перестают быть случайными. Например, частота появления случайного события в n испытаниях при увеличении n становится устойчивой и приближается к постоянному числу – вероятности; среднее арифметическое случайных величин приближается к математическому ожиданию и т.д. Группа теорем, устанавливающих факт приближения средних характеристик большого числа опытов к некоторым постоянным, а также другая группа теорем, касающихся предельных законов распределения, называется предельными теоремами теории вероятностей. Рассматривают два типа предельных теорем: 1) закон больших чисел;
2) центральная предельная теорема.
Закон больших чисел
Теоремы закона больших чисел рассматривают условия, при которых суммарное поведение достаточно большого числа случайных величин утрачивает случайный характер и становится закономерным. К таким теоремам относятся теоремы Чебышева и Бернулли (есть и другие теоремы, которые мы не рассматриваем). Сначала рассмотрим неравенство Чебышева, которое имеет большое теоретическое значение, на практике оно применяется реже.
Теорема.
Вероятность того, что отклонение случайной величины от её математического
ожидания будет по абсолютной величине не меньше любого положительного числа ![]() ограничена сверху
величиной
ограничена сверху
величиной 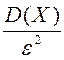 ,
т.е.
,
т.е. ![]()
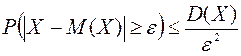 или, если перейти к
противоположному событию,
или, если перейти к
противоположному событию,
 . Эти две формы
неравенства Чебышева устанавливают соответственно верхнюю и нижнюю границы
вероятности события.
. Эти две формы
неравенства Чебышева устанавливают соответственно верхнюю и нижнюю границы
вероятности события.
Заметим, что
здесь, а также в других теоремах теории вероятностей, используется понятие
«сходимости по вероятности»: случайные величины ![]() сходятся по вероятности к величине A,
если для любого
сходятся по вероятности к величине A,
если для любого ![]() вероятность
события
вероятность
события ![]() при
при ![]() стремится к единице,
т.е.
стремится к единице,
т.е. ![]() схематически
это можно записать так
схематически
это можно записать так ![]() (как мы записывали выше). Отличие
сходимости по вероятности и сходимости, которую рассматривают в математическом
анализе, в том, что сходимость по вероятности требует, чтобы неравенство
(как мы записывали выше). Отличие
сходимости по вероятности и сходимости, которую рассматривают в математическом
анализе, в том, что сходимость по вероятности требует, чтобы неравенство
![]() выполнялось для
большинства членов последовательности
выполнялось для
большинства членов последовательности ![]() , в то время, как в математическом анализе
это неравенство должно выполняться для всех членов последовательности, начиная
с некоторого номера N (т.е.
, в то время, как в математическом анализе
это неравенство должно выполняться для всех членов последовательности, начиная
с некоторого номера N (т.е.![]() ).
).
Теорема
Чебышева. Если ![]() попарно
независимые случайные величины, причём дисперсии их ограничены (т.е. существует
число С, такое, что
попарно
независимые случайные величины, причём дисперсии их ограничены (т.е. существует
число С, такое, что ![]() ),
то при возрастании n среднее арифметическое этих величин сходится по
вероятности к среднему арифметическому их математических ожиданий, т.е. для
любого
),
то при возрастании n среднее арифметическое этих величин сходится по
вероятности к среднему арифметическому их математических ожиданий, т.е. для
любого![]()
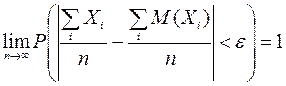 . Если
. Если ![]() , то имеем частный
случай теоремы Чебышева
, то имеем частный
случай теоремы Чебышева 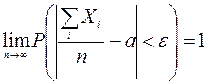 .
.
Сущность
теоремы Чебышева состоит в том, что если отдельные независимые случайные
величины могут принимать далёкие от своих математических ожиданий значения, то
среднее арифметическое достаточно большого числа случайных величин с большой
вероятностью принимают значения близкие к определённому числу (а именно к  ). Теорема Чебышева
имеет огромное значение для практики. На ней основан широко применяемый в
статистике выборочный метод, когда на основе небольшой случайной выборки судят
о всей совокупности объектов (о качестве зерна по небольшой его пробе). Или при
измерении физической величины за эту величину берут среднее арифметическое
результатов нескольких измерений.
). Теорема Чебышева
имеет огромное значение для практики. На ней основан широко применяемый в
статистике выборочный метод, когда на основе небольшой случайной выборки судят
о всей совокупности объектов (о качестве зерна по небольшой его пробе). Или при
измерении физической величины за эту величину берут среднее арифметическое
результатов нескольких измерений.
Естественно, этот способ может применяться при выполнении условий теоремы.
Теорема Бернулли
Теорема Бернулли является важнейшей и исторически первой формой закона больших чисел. Она устанавливает связь между частотой и вероятностью появления события в n независимых испытаниях.
Теорема.
Если в каждом из n испытаний вероятность p
появления события А постоянна, то
при увеличении числа испытаний как угодно близка к единице вероятность того,
что отклонение относительной частоты от вероятности р по абсолютной
величине будет меньше любого числа ![]() :
:
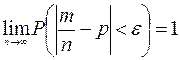 , т.е. относительная
частота события A сходится по вероятности к величине вероятности
события A.
, т.е. относительная
частота события A сходится по вероятности к величине вероятности
события A.
Доказательство Бернулли (1713 г.) было очень громоздким, простое доказательство было дано Чебышевым в 1846 году (см. доказательство в [1], стр.123 или в [2], стр. 168).
Центральная предельная теорема
Теоремы закона больших чисел определяют суммарное поведение достаточно большого числа случайных величин. Другая группа теорем, называемых центральной предельной теоремой, устанавливают закон распределения для суммы достаточно большого числа случайных величин. Все предельные теоремы из этой группы рассматривают условия, совокупность которых становится причиной появления нормально распределённых случайных величин. Центральная предельная теорема имеет разные формы в зависимости от этих условий. Мы приведём теорему Ляпунова и сформулируем её в самой простой форме:
Если
случайные величины ![]() взаимно
независимы и имеют один и тот же закон распределения с математическим ожиданием
a и дисперсией
взаимно
независимы и имеют один и тот же закон распределения с математическим ожиданием
a и дисперсией ![]() , причём существует абсолютный центральный
момент 3-го порядка
, причём существует абсолютный центральный
момент 3-го порядка ![]() ,
то при неограниченном увеличении n закон распределения суммы
,
то при неограниченном увеличении n закон распределения суммы 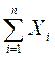 неограниченно
приближается к нормальному закону.
неограниченно
приближается к нормальному закону.
Многие случайные явления, встречающиеся в природе и общественной жизни, укладываются в рамки теоремы Ляпунова. Поэтому эта теорема имеет исключительное значение, а нормальный закон распределения является одним из основных в теории вероятностей. Вот несколько примеров:
1)
Пусть производятся измерения
некоторой величины а. Различные уклонения наблюдаемых значений ![]() от а получаются
в результате воздействия большого числа факторов, каждый из которых порождает
малую ошибку
от а получаются
в результате воздействия большого числа факторов, каждый из которых порождает
малую ошибку ![]() ,
причём
,
причём ![]() .
Тогда суммарная ошибка является случайной величиной, которая по теореме
Ляпунова должна быть распределена по нормальному закону.
.
Тогда суммарная ошибка является случайной величиной, которая по теореме
Ляпунова должна быть распределена по нормальному закону.
2) При стрельбе из орудия под влиянием большого числа причин случайного характера происходит рассеяние снарядов по большой площади. Случайные воздействия на траекторию снаряда можно считать независимыми. Каждая причина вызывает незначительные изменения траектории по сравнению с суммарным изменением под воздействием всех причин. Поэтому следует ожидать, что отклонение места разрыва снаряда от цели будет случайной величиной, распределённой по нормальному закону.
3) По теореме Ляпунова можно считать, что рост взрослого мужчины является случайной величиной, распределённой по нормальному закону и.т.д.
Заметим, что рассмотренная в начале курса интегральная теорема
Муавра-Лапласа
является частным простейшим случаем предельной теоремы, когда случайные
величины ![]() одинаково
распределены, дискретны и принимают только два значения 0 и 1 (см. [2],
стр. 172).
одинаково
распределены, дискретны и принимают только два значения 0 и 1 (см. [2],
стр. 172).
Список литературы
1. Ивановский Р.И. Теория вероятностей и математическая статистика.
Основы, прикладные аспекты с примерами и задачами в среде Mathcad.-СПб.: БХВ- Петербург, 2008.-528 с.
2. Письменный Д. Конспект лекций по теории вероятностей и
математической статистике, случайные процессы.- М.: Айрис- пресс, 2006.- 288 с.
3. Гмурман В.Е. Теория вероятностей и математическая статистика.
Учебное пособие для вузов.- М.: Высш. школа, 2003.- 279 с.
4. Гмурман В.Е. Руководство к решению задач по теории вероятностей
и математической статистике. –М.: Высш. школа, 1999.- 400 с.
5. Астраханцева Л.Н. Дискретная математика. Учебное пособие.- Алматы: АУЭС, 2011.- 78 с.
6. Астраханцева Л.Н., Байсалова М.Ж. Теория вероятностей и математическая статистика. Метод. указания и задания к выполнению РГР для студентов всех форм обучения специальности 5В070400- Вычислительная техника и программное обеспечение, 5В070300- Информационные системы. Ч.1. - Алматы: АУЭС, 2011.- 28 с.
7. Астраханцева Л.Н., Байсалова М.Ж. Теория вероятностей и математическая статистика. Метод. указания и задания к выполнению РГР для студентов всех форм обучения специальности 5В070400- Вычислительная техника и программное обеспечение, 5В070300- Информационные системы. Ч.2. Алматы: АУЭС, 2011.- 27 с.
Содержание
|
1 Элементы теории вероятностей |
|
|
1.1 Лекция 1. Случайные события. Пространство элементарных событий. Вероятность |
3 |
|
1.2 Лекция 2. Основные теоремы теории вероятностей |
7 |
|
1.3 Лекция 3. Случайные величины |
11 |
|
Лекция 4. Числовые характеристики случайных величин |
16 |
|
1.4 Лекция 5-6. Основные законы распределения случайных величин |
20 |
|
2 Элементы математической статистики |
|
|
2.1 Лекция 7. Предмет и основные понятия математической статистики |
28 |
|
2.2 Лекция 8. Числовые характеристики статистических распределений. Статистические оценки параметров распределения |
34 |
|
Приложение А. Понятие о моментах распределения. Мода, медиана, квантили |
40 |
|
Приложение Б. Предельные теоремы теории вероятностей |
43 |
|
Список литературы |
46
|
|
сводный план 2013 г., поз. 306
Астраханцева Людмила Николаевна Байсалова Маншук Жумамуратовна
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА Конспект лекций для студентов специальностей 5В070400 – Вычислительная техника и программное обеспечение, 5В070300 – Информационные системы
Редактор Л.Т.Сластихина Специалист по стандартизации Н.К.Молдабекова
Подписано в печать_______ Формат 6084 1/16 Тираж 150 экз. Бумага типографская №1 Объем 2,9 уч.-из.л. Заказ______ цена 290 тг.
Копировально-множительное бюро Некоммерческого акционерного общества «Алматинский университет энергетики и связи» 050013, Алматы, ул.Байтурсинова, 126 |
|