Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра высшей математики
Дифференциальные уравнения
Конспект лекций
для студентов специальности
5В060200 - Информатика
Алматы, 2013
Составители: Мустахишев К. М., Атабай Б.Ж. Дифференциальные уравнения. Конспект лекций для студентов специальности 5В060200 – Информатика. – Алматы, 2013 – 46 с.
Конспект лекций содержит конспекты к 12 лекциям по курсу «Дифференциальные уравнения», решение типовых задач и примеров, иллюстрирующих теоретический материал (всего 27 задач).
Ил. 5, библиогр.-7 назв.
Рецензент: канд. физ.-мат., наук, доцент Койлышов У.К.
Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2012 г.
© Некоммерческое акционерное общество АУЭС, 2013 г.
Сводный план 2012., поз.347
Модуль 1 Дифференциальные уравнения первого порядка
Лекция 1. Основные понятия дифференциальных уравнений. Геометрическая интерпретация
Цель лекции: рассмотрение задач, приводящих к понятию дифференциального уравнения (ДУ). Ознокомить студентов с основными понятиями ДУ.
Уравнение, в котором неизвестные находятся под знаком производной или дифференциала, называется дифференциальным уравнением (ДУ). Наивысший порядок производной от неизвестной функции в уравнении носит название порядка ДУ. Многие задачи науки и техники приводят к понятию ДУ. Рассмотрим некоторые из них.
I. 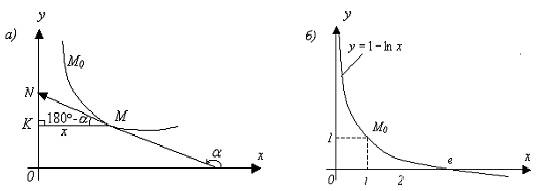 Найти линию, проходящую через точку
Найти линию, проходящую через точку ![]() и обладающую тем свойством, что в любой ее
точке
и обладающую тем свойством, что в любой ее
точке ![]() касательный
вектор
касательный
вектор ![]() (см. рисунок
1) с концом на оси
(см. рисунок
1) с концом на оси ![]() имеет
проекцию на ось
имеет
проекцию на ось ![]() ,
равную 1.
,
равную 1.
Рисунок 1 – Интегральная кривая, требуемая и найденная
Решение. Из
прямоугольного ![]() :
:
![]()
![]()
![]() .
.
Учитывая геометрический смысл производной, получим:
![]() . (1.1)
. (1.1)
Это есть ДУ первого порядка.
II. Найти закон движения груза
массы ![]() ,
подвешенного на пружине жесткости
,
подвешенного на пружине жесткости ![]() и предоставленного самому себе (см. рисунок
2).
и предоставленного самому себе (см. рисунок
2).
Решение. На груз
действуют его сила тяжести ![]() и упругая сила
и упругая сила ![]() пружины, пропорциональная
величине ее растяжения или сжатия. Эти силы имеют общую вертикальную линию
действия, которую примем за ось
пружины, пропорциональная
величине ее растяжения или сжатия. Эти силы имеют общую вертикальную линию
действия, которую примем за ось ![]() , поместив начало координат 0 в положении
так называемого статического равновесия центра тяжести груза. По второму закону
Ньютона
, поместив начало координат 0 в положении
так называемого статического равновесия центра тяжести груза. По второму закону
Ньютона
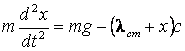 ,
,
где ![]() - статическое
растяжение пружины. Введя обозначение
- статическое
растяжение пружины. Введя обозначение ![]() , придем к ДУ второго порядка:
, придем к ДУ второго порядка:
![]() .
(1.2)
.
(1.2)
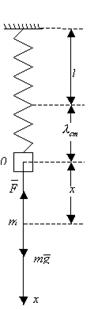
Рисунок 2 – Колебания груза, подвешенного на пружине
В
общем виде ДУ ![]() -порядка
записывается так:
-порядка
записывается так:
![]() .
(1.3)
.
(1.3)
Здесь ![]() - независимая
переменная,
- независимая
переменная, ![]() -
неизвестная функция,
-
неизвестная функция, ![]() -
ее производные. Присутствие в уравнении старшей производной
-
ее производные. Присутствие в уравнении старшей производной ![]() , определяющей порядок ДУ,
обязательно. Любые из остальных аргументов уравнение может не содержать в явном
виде. При выполнении требований, аналогичных условиям существования неявных
функций [1] (1.3) можно решить относительно
, определяющей порядок ДУ,
обязательно. Любые из остальных аргументов уравнение может не содержать в явном
виде. При выполнении требований, аналогичных условиям существования неявных
функций [1] (1.3) можно решить относительно ![]() и представить ДУ
и представить ДУ ![]() -порядка в виде,
разрешенном относительно старшей производной:
-порядка в виде,
разрешенном относительно старшей производной:
![]() .
(1.4)
.
(1.4)
Функция ![]() , имеющая в
рассматриваемой области
, имеющая в
рассматриваемой области ![]() производную
производную ![]() -го порядка и удовлетворяющая (1.3),
называется решением ДУ. График функции
-го порядка и удовлетворяющая (1.3),
называется решением ДУ. График функции ![]() называют интегральной кривой ДУ. Итак,
после подставления функции
называют интегральной кривой ДУ. Итак,
после подставления функции ![]() и ее производных в уравнение (1.3), оно
превращается в тождество (истинное равенство).
и ее производных в уравнение (1.3), оно
превращается в тождество (истинное равенство).
Задание 1. Является
ли функция ![]() решением
ДУ
решением
ДУ ![]() ?
?
Решение. Указанную
функцию и ее вторую производную ![]() подставим в заданное ДУ:
подставим в заданное ДУ:
![]() .
.
Ответ: да, является.
Решить ДУ означает
найти неизвестную функцию ![]() , освободив ее из-под знаков производных или
дифференциалов. Такая операция преполагает последовательное
, освободив ее из-под знаков производных или
дифференциалов. Такая операция преполагает последовательное ![]() -кратное (соответственно порядку
ДУ) нахождение неопределенных интегралов. Каждая квадратура вносит в решение
произвольную постоянную – постоянную интегрирования
-кратное (соответственно порядку
ДУ) нахождение неопределенных интегралов. Каждая квадратура вносит в решение
произвольную постоянную – постоянную интегрирования ![]() . Функция
. Функция ![]() , содержащая
, содержащая ![]() независимых постоянных и
охватывающая все возможные решения ДУ, называется его общим решением. Такое
решение, представленное в неявном виде
независимых постоянных и
охватывающая все возможные решения ДУ, называется его общим решением. Такое
решение, представленное в неявном виде ![]() , называют общим интегралом ДУ.
, называют общим интегралом ДУ.
Совокупность
значений неизвестной функции и ее производных до (![]() )-порядка включительно в некоторой точке
)-порядка включительно в некоторой точке ![]()
![]()
![]()
![]() (1.5)
(1.5)
называется начальными
условиями ДУ (задачи). Подставляя эти значения в общее решение и в его
производные до (![]() )-порядка,
получим систему
)-порядка,
получим систему ![]() алгебраических
уравнений с
алгебраических
уравнений с ![]() неизвестными
неизвестными
![]() . Решив эту
систему и подставив найденные конкретные значения постоянных интегрирования
обратно в общее решение, получим так называемое частное решение ДУ,
удовлетворяющее заданным начальным условиям. Впервые Коши поставил задачу о
нахождении частного решения ДУ, удовлетворяющего заданным начальным условиям, и
доказал теорему о существовании и единственности такого решения.
. Решив эту
систему и подставив найденные конкретные значения постоянных интегрирования
обратно в общее решение, получим так называемое частное решение ДУ,
удовлетворяющее заданным начальным условиям. Впервые Коши поставил задачу о
нахождении частного решения ДУ, удовлетворяющего заданным начальным условиям, и
доказал теорему о существовании и единственности такого решения.
Существует класс
задач, в условиях которых задаются значения неизвестной функции в ![]() точках
точках
![]()
![]() . (1.6)
. (1.6)
Их называют краевыми задачами, а (1.6) - краевыми условиями.
Лекция 2. Задача Коши (начальная задача). Уравнения с разделяющимися переменными
Цель лекции: пояснить постановку задачи Коши (начальной задачи) и теорему о существовании и единственности решения этой задачи. Показать студентам метод интегрирования ДУ с разделяющимися переменными.
ДУ первого порядка
(![]() ) в общем
виде и в виде, разрешенном относительно производной, записывают так:
) в общем
виде и в виде, разрешенном относительно производной, записывают так:
![]()
![]() . (1.7)
. (1.7)
Начальные условия – при
![]() . (1.8)
. (1.8)
Так как в (1.7) ![]() есть отношение
дифференциалов неизвестной функции и независимой переменной, то ДУ первого
порядка может быть представлено и в так называемой дифференциальной форме:
есть отношение
дифференциалов неизвестной функции и независимой переменной, то ДУ первого
порядка может быть представлено и в так называемой дифференциальной форме:
![]() .
(1.9)
.
(1.9)
Теорема существования и единственности решения.
Если функция ![]() непрерывна
в замкнутой области (прямоугольнике, см. рисунок 3)
непрерывна
в замкнутой области (прямоугольнике, см. рисунок 3)
![]()
![]() ,
,
имеет в ней
ограниченную частную производную по ![]() :
:
![]() ,
,
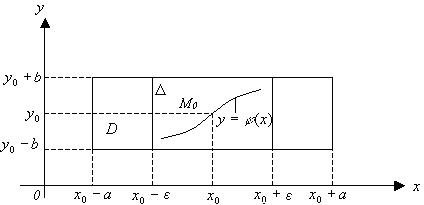
Рисунок 3 – Интегральная кривая, проходящая через
заданную точку ![]()
то на отрезке
![]() ,
,
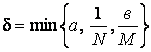 ,
, ![]()
существует, притом
единственное решение ![]() ДУ
ДУ
![]() ,
удовлетворяющее начальному условию (1.8):
,
удовлетворяющее начальному условию (1.8): ![]() . Функция
. Функция ![]() непрерывно дифференцируема на
непрерывно дифференцируема на ![]() и
и ![]()
![]() .
.
Итак, если условия
теоремы Коши выполняются, то через точку ![]() проходит единственная интегральная кривая
проходит единственная интегральная кривая ![]() , лежащая в
приямоугольнике
, лежащая в
приямоугольнике
![]()
![]() .
.
Уравнения с разделяющимися переменными.
Если функции двух переменных в уравнениях (1.7) и (1.9) распадаются на произведения двух функций одной переменной каждая, то они относятся к так называемым ДУ с разделяющимися переменными. Например,
![]()
![]()
есть ДУ с разделяющимися переменными. После простейших преобразований придем к уравнениям:
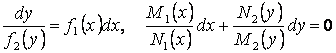
с разделенными переменными. Взяв неопределенные интегралы от обеих частей (почленно) последних равенств, найдем общие решения или общие интегралы заданных ДУ.
Решим задачу Коши для (1.1):
![]() .
.
![]() .
.
Это общее решение
(1.1). Использовав начальное условие: ![]() , найдем частное решение
, найдем частное решение ![]() . Теперь можем уточнить
вид (рис. 1) требуемой в задаче линии-единственной, проходящей через точку
. Теперь можем уточнить
вид (рис. 1) требуемой в задаче линии-единственной, проходящей через точку ![]() , интегральной кривой ДУ
(1.1).
, интегральной кривой ДУ
(1.1).
Задание 2. Найти общее решение (общий интеграл) ДУ
![]() .
.
Решение. Умножив обе части заданного ДУ на
выражение 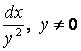 , получим уравнения с разделенными
переменными:
, получим уравнения с разделенными
переменными:
 .
.
Выполнение квадратуры приводит к общему интегралу или общему решению соответственно:
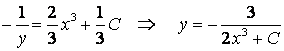 .
.
Задание 3. Найти решение задачи Коши и построить соответствующую интегральную кривую:
![]() .
.
Решение. Сперва найдем общее решение ДУ с разделенными переменными:
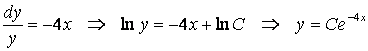 .
.
Пользуясь начальными условиями задачи, найдем значение постоянной интегрирования:
![]() .
.
Ось абсцисс
служит горизонтальной асимптотой интегральной кривой – графика функции ![]() , являющейся решением
задачи Коши (см. рисунок 4).
, являющейся решением
задачи Коши (см. рисунок 4).
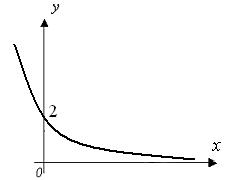
Рисунок 4 – График функции ![]()
Задание 4. Найти решение задачи Коши:
 .
.
Решение. Разделив переменные, уравнение представим в виде
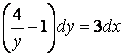 .
.
Его общий интеграл имеет вид
![]() .
.
Вставив сюда начальные данные, найдем ![]() . Частный интеграл,
удовлетворяющий заданным начальным условиям, выглядит:
. Частный интеграл,
удовлетворяющий заданным начальным условиям, выглядит:
![]() .
.
Лекция 3. Однородные, линейные и в полных дифференциалах уравнения
Цель лекции: ознокомить слушателей с интегрируемыми типами ДУ первого порядка: однородными, линейными, в полных дифференциалах уравнениями и приводящими к ним уравнениями.
1. Однородные уравнения.
Функция ![]() , удовлетворяющая
условию
, удовлетворяющая
условию ![]() при
любом параметре t, называется однородной функцией
при
любом параметре t, называется однородной функцией ![]() -степени. Если правая часть
разрешенного относительно производной ДУ (1.7) есть однородная функция нулевой
степени
-степени. Если правая часть
разрешенного относительно производной ДУ (1.7) есть однородная функция нулевой
степени ![]() , то
уравнение называют однородным. Если
, то
уравнение называют однородным. Если ![]() и
и ![]() есть однородные функции одинаковой
степени, то (1.9) тоже относится к однородным ДУ. Так как
эти уравнения легко преобразуются друг в друга, то рассмотрим (1.7) и произведем в нем замену неизвестной функции по схеме:
есть однородные функции одинаковой
степени, то (1.9) тоже относится к однородным ДУ. Так как
эти уравнения легко преобразуются друг в друга, то рассмотрим (1.7) и произведем в нем замену неизвестной функции по схеме:
![]() . (1.10)
. (1.10)![]()
Взяв в определении
однородной функции за параметр ![]() , правую часть (1.10) можем представить в
виде
, правую часть (1.10) можем представить в
виде
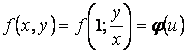 .
.
После замены неизвестной функции получим ДУ
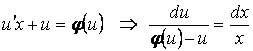 ,
,
решаемое в
квадратурах. В особенном случае: ![]() имеем
имеем
![]() ,
,
т.е. интегральные линии ДУ составляют семейство прямых, проходящих через начало координат.
Задание 5. Найти общее решение (общий интеграл) ДУ
![]() .
.
Решение. Заменив неизвестную функцию ![]() ,
, ![]() , получим уравнение с
разделяющимися переменными
, получим уравнение с
разделяющимися переменными
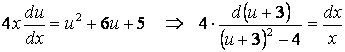 .
.
После интегрирования и освобождения от логарифмов получим общий интеграл:
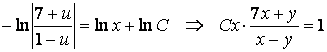 .
.
Общее решение выглядит так:
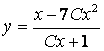 .
.
2. Линейные уравнения.
ДУ называется линейным, если оно содержит неизвестную функцию и ее производные только первой степени:
![]() . (1.11)
. (1.11)
Здесь ![]() ,
, ![]() - заданные, непрерывные в
рассматриваемой области функции.
Если в этой области
- заданные, непрерывные в
рассматриваемой области функции.
Если в этой области ![]() , то (1.11) называется неоднородным, а в
противном случае, т.е. при
, то (1.11) называется неоднородным, а в
противном случае, т.е. при ![]() - однородным линейным ДУ первого порядка.
Последнее (соответствующее (1.11)) выглядит так
- однородным линейным ДУ первого порядка.
Последнее (соответствующее (1.11)) выглядит так
![]()
и представляет собой ДУ с разделяющимися переменными. Его общее решение
![]() ,
, ![]() . (1.12)
. (1.12)
Заменив постоянную
интегрирования ![]() пока
неизвестной функцией
пока
неизвестной функцией ![]() ,
потребуем, чтобы функция
,
потребуем, чтобы функция
![]() (1.13)
(1.13)
была
решением (1.11). Функцию
(1.13) и ее производную подставим в (1.11), из полученного тождества
найдем неизвестную функцию ![]() и подставим ее на место в (1.13). В
результате получим общее решение (1.11)
и подставим ее на место в (1.13). В
результате получим общее решение (1.11)
![]() . (1.14)
. (1.14)
Примененный
способ называется методом вариации произвольной постоянной: ![]() . При решении задач, не повторяя
выкладки, равенством (1.14) можно пользоваться как готовой формулой.
. При решении задач, не повторяя
выкладки, равенством (1.14) можно пользоваться как готовой формулой.
Задание 6. Найти решение задачи Коши:
![]() .
.
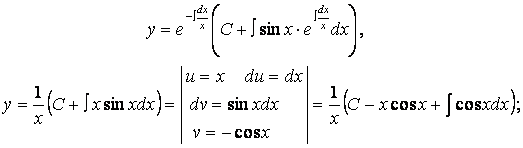
Решение. Сопоставление заданного уравнения с (1.11) дает:
![]() .
.
Вставив эти функции в (1.14), получим
Из общего решения
![]()
найдем:
![]() .
.
Решение задачи Коши:
![]() .
.
3. Уравнения, приводящиеся к интегрируемым типам.
ДУ, приводящиеся к однородным уравнениям.
ДУ вида
 (1.15)
(1.15)
с помощью линейной замены по схеме:
![]() (1.16)
(1.16)
приводятся к
однородным уравнениям. Неизвестные постоянные ![]() и
и ![]() выбирают так, чтобы в (1.15) дробно-линейное выражение в аргументе функции
выбирают так, чтобы в (1.15) дробно-линейное выражение в аргументе функции ![]() после замены переменных не
содержало свободных членов, т.е. чтобы
после замены переменных не
содержало свободных членов, т.е. чтобы
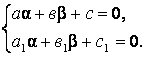 (1.17)
(1.17)
Так как в (1.16):
![]() ,
,
то в новых переменных заданное ДУ (1.15) будет иметь вид:
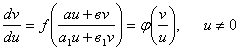 . (1.18)
. (1.18)
Это есть однородное ДУ первого порядка, которое заменой типа (1.10):
![]() (1.19)
(1.19)
приводится к уравнению с разделяющимися переменными.
Задание 7. Найти общий интеграл ДУ
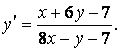
Решение. Составим и решим систему (3.8):
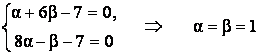 .
.
Последовательно
осуществим замены переменных: 1)![]() ,
, ![]() ,
2)
,
2) ![]() ,
,
![]() ,
преобразующие уравнение следующим образом:
,
преобразующие уравнение следующим образом:
![]() .
.
Разделив переменные в последнем уравнении, выполним квадратуры:
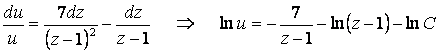 .
.
Освободимся от логарифмов и перейдем к старым переменным:
![]() .
.
Общий интеграл первоначального уравнения:
![]() .
.
Уравнение Бернулли.
Нелинейное ДУ первого порядка
![]() ,
(1.20)
,
(1.20)
где ![]() - заданные непрерывные
в рассматриваемой области функции, носит название уравнения Бернулли. При
- заданные непрерывные
в рассматриваемой области функции, носит название уравнения Бернулли. При ![]() и
и ![]() уравнение Бернулли превращается
в соответственно однородное и неоднородное линейные ДУ. Умоножим обе части (1.20) на
уравнение Бернулли превращается
в соответственно однородное и неоднородное линейные ДУ. Умоножим обе части (1.20) на ![]() и
осуществим замену неизвестной функции по схеме
и
осуществим замену неизвестной функции по схеме
![]() .
(1.21)
.
(1.21)
В преобразованное уравнение
![]()
введем обозначения: ![]() и придем к уравнению
типа (1.11):
и придем к уравнению
типа (1.11):
![]() .
(1.22)
.
(1.22)
Бернулли предложил искать решение (1.22) в виде
![]() (1.23)
(1.23)
и найти неизвестные
функции ![]() ,
, ![]() из требования, что (1.23) есть решение (1.22):
из требования, что (1.23) есть решение (1.22):
![]() . (1.24)
. (1.24)
Далее
ход решения совпадает с методом вариации произвольной постоянной: функцию ![]() находят так, чтобы в (1.24) сумма в
скобках была равна нулю. Подставив найденную таким образом функцию
находят так, чтобы в (1.24) сумма в
скобках была равна нулю. Подставив найденную таким образом функцию ![]() обратно в (1.24), получают уравнения с
разделяющимися переменными. Результат совпадает с (1.14), остается перейти к
старой переменной:
обратно в (1.24), получают уравнения с
разделяющимися переменными. Результат совпадает с (1.14), остается перейти к
старой переменной: ![]() .
.
Задание 8. Найти общее решение ДУ:
![]() .
.
Решение.
Так как ![]() , то
замена (1.21) осуществляется в виде:
, то
замена (1.21) осуществляется в виде:
![]() ,
,
и приводит к (1.11):
![]() ,
,
где ![]() . Применение
(1.14) приводит к общему решению:
. Применение
(1.14) приводит к общему решению:
 ;
;
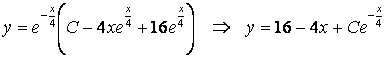 .
.
4. Уравнения в полных дифференциалах
Интегрирование полного дифференциала.
ДУ первого порядка в
дифференциальной форме (1.9) называется уравнением в полных дифференциалах,
если его левая часть представляет собой дифференциал некоторой дифференцируемой
в рассматриваемой области  функции
функции 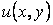 , т.е.
, т.е.
![]() . (1.25)
. (1.25)
Для выполнения (1.25) необходимо и достаточно чтобы
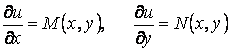 . (1.26)
. (1.26)
По теореме о смешанных частных производных [1]
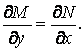 (1.27)
(1.27)
Условия (1.25-27) попарно равносильны, последним из них пользуются для проверки того, является ли (1.9) уравнением в полных дифференциалах. Если оно выполняется, то придем к выводу:
![]() (1.28)
(1.28)
Последнее представляет собой общий интеграл уравнения в полных дифференциалах. Для его нахождения поступают следующим образом.
Одно из уравнений (1.26) интегрируют по соответствующей переменной, считая вторую пока фиксированной. Например, из первого имеем
![]() . (1.29)
. (1.29)
Чтобы найти неизвестную функцию ![]() , пользуемся вторым из
условий (1.26):
, пользуемся вторым из
условий (1.26):
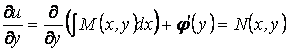 .
.
Пусть отсюда
![]() .
.
Подставив найденную функцию ![]() в (1.29), получим
функцию
в (1.29), получим
функцию ![]() ,
полный дифференциал которой равен левой части заданного ДУ (1.9).
,
полный дифференциал которой равен левой части заданного ДУ (1.9).
Для нахождения функции ![]() можно применять и следующий
прием:
можно применять и следующий
прием:
![]() , (1.30)
, (1.30)
где ![]() , а в качестве
, а в качестве ![]() из
из ![]() берут слагаемые, содержащие
берут слагаемые, содержащие ![]() и отсутствующие в
и отсутствующие в ![]() .
.
Задание 9. Найти общее решение ДУ
![]() .
.
Решение. Имеем ДУ в полных дифференциалах, так как
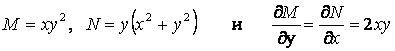 .
.
Поступая последовательно по излрженному методу, найдем:
![]() ,
,
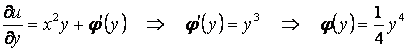 .
.
Общий интеграл заданного ДУ
![]() .
.
Интегрирующий множитель.
Если
условие (1.27) не выполняется, то (1.9) не является уравнением в полных
дифференциалах. Но при определенных условиях его можно привести к уравнению в
полных дифференциалах умножением на некоторую функцию ![]() , называемую интегрирующим множителем.
Нахождение интегрирующего
множителя в общем случае приводится к решению ДУ в частных производных. В самом
деле, если интегрирующий множитель существует, то
, называемую интегрирующим множителем.
Нахождение интегрирующего
множителя в общем случае приводится к решению ДУ в частных производных. В самом
деле, если интегрирующий множитель существует, то
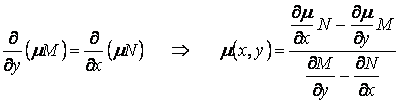 . (1.31)
. (1.31)
В
случаях, когда интегрирующий множитель является функцией одной из переменных ![]() или
или
![]() , по-очередно
полагая в (1.31)
, по-очередно
полагая в (1.31)
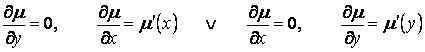 ,
,
найдем соответственно:
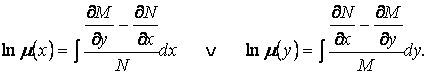 (3.23)
(3.23)
Пример 1. Найти интегрирующий множитель и решить уравнение
![]() (1)
(1)
Решение. Условие (1.27) не выполняется, так как
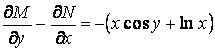 .
.
Первая из формул (1.32) дает:
![]()
После умножения на интегрирующий множитель (1) принимает вид
![]()
![]()
Теперь (1.27) выполняется и в (1.30):
![]() .
.
Общий интеграл (1.33)
![]()
Лекция 4. Графическая интерпретация теоремы существования и единственности решения ДУ первого порядка
Цель лекции: пояснить студентам геометрическую суть – дать графическую интерпретацию теоремы Коши. Изложить метод введения параметра в ДУ на основе уравнений Лагранжа и Клеро.
Пусть ДУ первого
порядка, разрешенное относительно производной, (1.7) удовлетворяет условиям
теоремы существования и единственности решения и ![]() (см. рисунок 5). По геометрическому смыслу
производной
(см. рисунок 5). По геометрическому смыслу
производной
![]()
есть угол наклона к
оси абсцисс касательной к интегральной кривой ![]() в точке
в точке ![]() . Геометрическое место точек
. Геометрическое место точек ![]() , где
, где ![]() , следовательно,
, следовательно, ![]() называется изоклиной (isos-равный,
klino-наклоняю, гр.) ДУ
называется изоклиной (isos-равный,
klino-наклоняю, гр.) ДУ ![]() . В точках изоклины интегральная кривая
всюду имеет одинаковый уклон к оси абсцисс, т.е. касательные к кривой
. В точках изоклины интегральная кривая
всюду имеет одинаковый уклон к оси абсцисс, т.е. касательные к кривой ![]() параллельны между
собой – одинаково направлены. Это направление указывают стрелками (векторами
параллельны между
собой – одинаково направлены. Это направление указывают стрелками (векторами ![]() ), проставленными вдоль
изкоклины. Если изоклины построены для различных значений
), проставленными вдоль
изкоклины. Если изоклины построены для различных значений ![]() в области
в области ![]() , то множество векторов
, то множество векторов ![]() ,
, ![]() носит название поля направлений
ДУ
носит название поля направлений
ДУ ![]() . Если оно
построено, то линия, проходящая через точку
. Если оно
построено, то линия, проходящая через точку ![]() и к которой в каждой ее точке направление
поля – вектор
и к которой в каждой ее точке направление
поля – вектор ![]() является
касательной (линия, идущая “вдоль поля”) представляет собой искомую интегральную
кривую.
является
касательной (линия, идущая “вдоль поля”) представляет собой искомую интегральную
кривую.
Если изоклины
посторены достаточно часто, то дуги интегральной кривой между ними можно
приближенно заменять отрезками касательных к ней. Поэтому за интегральную
кривую ![]() ,
проходящую через точку
,
проходящую через точку ![]() , приближенно принимают ломаную линию,
построенную, начиная из точки
, приближенно принимают ломаную линию,
построенную, начиная из точки ![]() в том и в другом направлениях и звенья
которой параллельны вектору
в том и в другом направлениях и звенья
которой параллельны вектору ![]() “предыдущей” изоклины.
“предыдущей” изоклины.
В качестве примера
построим интегральную кривую ДУ (1.1), проходящую через точку ![]() , т.е. графически решим
задачу Коши:
, т.е. графически решим
задачу Коши:
![]() . (1.34)
. (1.34)
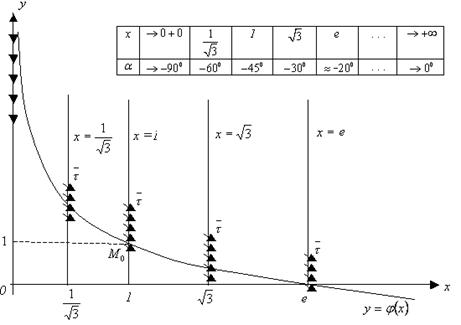
Рисунок 5 – К методу изоклин
В точке ![]() функция
функция ![]() не определена. Поэтому
интегральная кривая
не определена. Поэтому
интегральная кривая ![]() ,
,
![]() не может
пересечь ось ординат, т.е. область
не может
пересечь ось ординат, т.е. область ![]() , удовлетворяющая условиям теоремы
существования и единственности решения для (1.34),
расположена в правой полуплоскости. Изоклины
, удовлетворяющая условиям теоремы
существования и единственности решения для (1.34),
расположена в правой полуплоскости. Изоклины ![]() ,
, ![]() - прямые, параллельные оси ординат. При
- прямые, параллельные оси ординат. При ![]()
 , т.е. ось
, т.е. ось ![]() является вертикальной асимптотой
кривой
является вертикальной асимптотой
кривой ![]() . При
. При ![]() и
и ![]() т.е.
т.е.
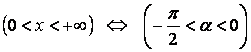 .
.
Для наглядности приняв разные масштабы по осям координат, построим поле направлений и требуемую интегральную кривую (см. рисунок 5).
Метод введения параметров в ДУ.
Известно [1], что функция трех переменных в левой части ДУ
(1.7), неразрешенного относительно производной ![]() , может быть представлена в параметрической
форме:
, может быть представлена в параметрической
форме:
![]() . (1.35)
. (1.35)
Считая первые две функции дифференцируемые по своим аргументам
в рассматриваемой области, подставим их дифференциалы в равенство ![]() :
:
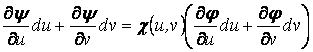 .
.
Это есть ДУ первого порядка, разрешенное относительно
производной, где, например, ![]() - независимая переменная, а
- независимая переменная, а ![]() - известная функция:
- известная функция:
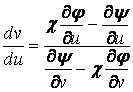 .
.
Полученное ДУ невсегда решается в квадратурах. В случаях,
когда удается найти его общее ![]() , первые два уравнения из (1.35) приводят к
общему решению первоначального ДУ в параметрической форме:
, первые два уравнения из (1.35) приводят к
общему решению первоначального ДУ в параметрической форме:
![]() .
.
Метод введения параметров – метод дифференцирования удобно
применять, когда уравнение ![]() легко разрешается относительно
легко разрешается относительно ![]() или
или ![]() . При этом за параметры принимают
соответственно
. При этом за параметры принимают
соответственно ![]() и
и
![]() или
или ![]() и
и ![]() .
.
Уравнение Лагранжа.
ДУ первого порядка, линейное относительно![]() и
и ![]() ,
,
![]() (1.36)
(1.36)
носит название уравнения Лагранжа.
Здесь все коэффициенты известные дифференцируемые в рассматриваемой области
функции параметра ![]() .
Пусть
.
Пусть ![]() . Тогда
(1.36) представимо в виде
. Тогда
(1.36) представимо в виде
![]() . (1.37)
. (1.37)
Продифференцируем равенство (1.37) по ![]() , считая
, считая ![]() функцией
функцией ![]() :
:
![]() .
.
Принимая ![]() за независимую переменную, а
за независимую переменную, а ![]() - за неизвестную
функцию, придем к линейному ДУ
- за неизвестную
функцию, придем к линейному ДУ
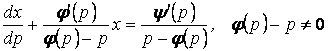 . (1.38)
. (1.38)
Найдя общее решение (1.38) по (1.14) и подставив его в (1.37), получим общее решение уравнения Лагранжа в параметрической форме:
![]() . (1.39)
. (1.39)
При определенных условиях, исключив параметр ![]() из (1.39), можно найти
общий интеграл уравнения Лагранжа в виде
из (1.39), можно найти
общий интеграл уравнения Лагранжа в виде ![]() .
.
Пример 2. Решить ДУ
![]() .
.
Решение. Имеем уравнение Лагранжа вида (4.4):
![]() .
.
Дифференцируем его по ![]() , считая
, считая ![]() функцией
функцией ![]() Ж
Ж
![]() .
.
Полученное равенство представим в виде линейного ДУ (1.38) и применим (1.14):
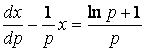 ,
, 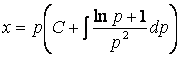 ;
;
 .
.
Подставив полученное выражение в заданное уравнение, найдем его общее решение в параметрической форме:
![]() .
.
Уравнение Клеро.
Частный случай уравнения Лагранжа, когда ![]() :
:
![]() (1.40)
(1.40)
носит название уравнения Клеро.
Характерной особенностью его является то, что после дифференцирования по ![]() , уравнение распадается
на два равенства:
, уравнение распадается
на два равенства:
![]() 1)
1) ![]() , 2)
, 2) ![]() .
.
Совместно рассматривая эти равенства с (1.40), получаем: 1) общее решение уравнения Клеро
![]()
и 2) так называемое особое решение его в параметрической форме
![]() .
.
Отсюда следует практическое правило [4] для решения
уравнения Клеро: заменив в (1.40) ![]() на
на ![]() , получим общее решение уравнения.
Дифференцируя его по
, получим общее решение уравнения.
Дифференцируя его по ![]() и
исключая
и
исключая ![]() из
системы двух уравнений (общего решения и результата дифференцирования),
получаем особое решение.
из
системы двух уравнений (общего решения и результата дифференцирования),
получаем особое решение.
Пример 3. Решить ДУ
![]() .
.
Решение. По практическому правилу общее решение уравнения имеет вид
![]() .
.
Дифференцирование по ![]() дает:
дает:
![]() .
.
Исключая произвольную постоянную, получаем особое решение
![]() .
.
Дифференциальные уравнения высших порядков
Уравнения, допускающие понижение порядка.
I. ДУ, не содержащие неизвестной функции и ее производных начальных порядков.
1. Пусть ДУ ![]() -порядка
-порядка ![]() , разрешенное
относительно старшей производной, (1.4) имеет простейший вид
, разрешенное
относительно старшей производной, (1.4) имеет простейший вид
![]() (1.41)
(1.41)
где ![]() - непрерывная в рассматриваемой области
функция. Порядок (4.7) можно понижать последовательным интегрированием. После
каждой квадратуры порядок уравнения понижается на единицу и прибавляется
постоянная интегрирования. Общее решение может быть представлено в виде:
- непрерывная в рассматриваемой области
функция. Порядок (4.7) можно понижать последовательным интегрированием. После
каждой квадратуры порядок уравнения понижается на единицу и прибавляется
постоянная интегрирования. Общее решение может быть представлено в виде:
![]() . (1.42)
. (1.42)
2.
Предположим, что ДУ ![]() -порядка
-порядка ![]() (1.3) не содержит явно неизвестной
функции
(1.3) не содержит явно неизвестной
функции ![]() и ее производных до
и ее производных до ![]() -порядка
включительно
-порядка
включительно ![]() , т.е. имеет вид
, т.е. имеет вид
![]() . (1.43)
. (1.43)
Введя новую неизвестную функцию
![]() ,
(1.44)
,
(1.44)
порядок уравнения (1.43)
можно понизить на ![]() единиц.
Если для полученного таким образом ДУ
единиц.
Если для полученного таким образом ДУ ![]() -порядка
-порядка
![]()
удается найти общее
решение ![]() , то
с помощью обратной замены придем к уравнению рассмотренного вида
, то
с помощью обратной замены придем к уравнению рассмотренного вида
![]() .
.
Итак, если в ДУ порядка ![]() отсутствует неизвестная
функция, то ее производную наименьшего порядка, содержащуюся в уравнении,
принимаем за новую неизвестную функцию.
отсутствует неизвестная
функция, то ее производную наименьшего порядка, содержащуюся в уравнении,
принимаем за новую неизвестную функцию.
Задание 10. Найти общее решение ДУ
![]() .
.
Решение. Два раза последовательно проинтегрируем уравнение, пользуясь приемом подведения под знак дифференциала:
![]() ,
,
![]() ,
,
![]() .
.
II. ДУ, не содержащие независимой переменной.
Рассмотрим
ДУ 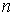 -порядка
-порядка
![]() , (1.45)
, (1.45)
не содержащее в явном
виде независимую переменную ![]() . Приняв вместо
. Приняв вместо ![]() “старую” неизвестную функцию
“старую” неизвестную функцию ![]() , введем новую
неизвестную функцию
, введем новую
неизвестную функцию ![]() .
Тогда:
.
Тогда:
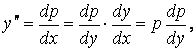
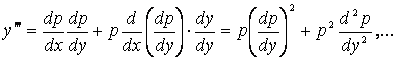 . (1.46)
. (1.46)
В каждом из равенств (1.46) справа порядок старшей производной на единицу ниже
порядка производной слева. Значит, подставив эти выражения в (1.45), получим ДУ
(![]() ) - порядка относительно
) - порядка относительно ![]() и
и ![]() :
:
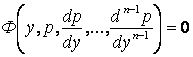 . (1.47)
. (1.47)
Если удается найти его общее решение, то в старых переменных будем иметь ДУ первого порядка
![]() .
(1.48)
.
(1.48)
Пример 4. Найти решение задачи Коши:
![]()
Решение. Для заданного уравнения равенство (1.47) выглядит так:
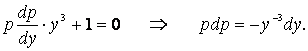
Так как ![]() , то после интегрирования:
, то после интегрирования:
![]() .
.
Вместо (1.48) имеем:
![]() .
.
Отсюда:
![]()
Интегральная кривая, проходящая через точку ![]() , есть
парабола
, есть
парабола ![]() .
.
Модуль 2 Общая теория линейных дифференциальных уравнений
высших порядков
Лекция 5. Линейные ДУ с непрерывными коффициентами
Цель лекции:
изложить основы общей теории линейных ДУ высших порядков с
непрерывными и постоянными коэффициентами. Ознокомить с основными понятиями:
фундаментальной системы решений (ФСР), определителя Вронского (вронскиан),
структуры общего решения однородного и неоднородного уравнений ![]() -го порядка. Привести
формулу Лиувилля.
-го порядка. Привести
формулу Лиувилля.
Линейное
неоднородное ДУ ![]() -порядка
в так называемом приведенном виде ((3.2),
-порядка
в так называемом приведенном виде ((3.2), ![]() ) записывается так:
) записывается так:
![]() , (2.1)
, (2.1)
где ![]() - заданные непрерывные
на
- заданные непрерывные
на ![]() функции.
Левую часть (2.1), представляющую собой линейную комбинацию неизвестной функции и ее производных до
функции.
Левую часть (2.1), представляющую собой линейную комбинацию неизвестной функции и ее производных до ![]() -порядка с
коэффициентами 1,
-порядка с
коэффициентами 1, ![]() ,
для краткости обозначают через
,
для краткости обозначают через ![]() . Символ
. Символ ![]() (linea - линия, лат.), обозначающий применение к
(linea - линия, лат.), обозначающий применение к ![]() совокупности операций
последовательного дифференцирования и
линейных действий, называется линейным дифференциальным оператором.
Итак, линейное неоднородное ДУ
совокупности операций
последовательного дифференцирования и
линейных действий, называется линейным дифференциальным оператором.
Итак, линейное неоднородное ДУ ![]() -порядка и соответствующее ему однородное
уравнение вкратце могут быть представлены в виде
-порядка и соответствующее ему однородное
уравнение вкратце могут быть представлены в виде
![]() .
(2.2)
.
(2.2)
Как и производная
функции оператор ![]() обладает
свойствами однородности и аддитивности:
обладает
свойствами однородности и аддитивности:
![]()
Оператор ![]() потому и называется линейным, что:
потому и называется линейным, что:
![]() .
(2.3)
.
(2.3)
Для уравнений (2.2)
на интервале ![]() выполняется
теорема существования и единственности решения, удовлетворяющего начальным
условиям (2.5). Из (2.3) следует, что если функции
выполняется
теорема существования и единственности решения, удовлетворяющего начальным
условиям (2.5). Из (2.3) следует, что если функции ![]() являются решениями однородного
уравнения (5.2), то их любая линейная комбинация также является решением этого
уравнения. Понятия линейной зависимости и независимости векторов [1] распространяются и на функции, определенные в некоторой области.
Линейное однородное ДУ
являются решениями однородного
уравнения (5.2), то их любая линейная комбинация также является решением этого
уравнения. Понятия линейной зависимости и независимости векторов [1] распространяются и на функции, определенные в некоторой области.
Линейное однородное ДУ ![]() -порядка имеет не более
-порядка имеет не более ![]() линейно независимых на
линейно независимых на ![]() решений.
решений.
Совокупность любых ![]() линейно независимых на
линейно независимых на ![]() частных решений
частных решений
![]() (2.4)
(2.4)
уравнения ![]() называется его
фундаментальной системой решений. Любое решение линейного однородного уравнения
может быть записано в виде линейной комбинации функций (2.4). Поэтому функция
называется его
фундаментальной системой решений. Любое решение линейного однородного уравнения
может быть записано в виде линейной комбинации функций (2.4). Поэтому функция
![]() , (2.5)
, (2.5)
где ![]() - независимые
(произвольные) постоянные является общим решением линейного однородного ДУ
- независимые
(произвольные) постоянные является общим решением линейного однородного ДУ ![]() -порядка. Итак, второе
из уравнений (2.2) считается решенным, если найдена его фундаментальная система
решений.
-порядка. Итак, второе
из уравнений (2.2) считается решенным, если найдена его фундаментальная система
решений.
Теорема. Для того,
чтобы функции ![]() ,
имеющие производные
,
имеющие производные ![]() -порядка
на
-порядка
на ![]() и
удовлетворяющие уравнению
и
удовлетворяющие уравнению ![]() , составили фундаментальную систему решений
этого уравнения необходимо и достаточно, чтобы их определитель Вронского [1] не был равен нулю на интервале:
, составили фундаментальную систему решений
этого уравнения необходимо и достаточно, чтобы их определитель Вронского [1] не был равен нулю на интервале: ![]() .
.
Сотношение
![]() , (2.6)
, (2.6)
Пусть функция ![]() есть любое частное
решение неоднородного уравнения (2.1) и найдено общее решение
есть любое частное
решение неоднородного уравнения (2.1) и найдено общее решение ![]() соответствующего ему
однородного уравнения (2.2), т.е.
соответствующего ему
однородного уравнения (2.2), т.е. ![]() , тогда функция
, тогда функция ![]() является общим решением
первоначального неоднородного уравнения (2.1).
является общим решением
первоначального неоднородного уравнения (2.1).
Лекция 6. Линейные ДУ с постоянными коэффициентами
Цель лекции: изложить методы решения линейного
ДУ ![]() -порядка с постоянными
коэффициентами: однородного в различных случаях корней характеристического
уравнения (построением ФСР) и неоднородного методами неопределенных
коэффициентов (в случае неоднородности типа квазимногочлена) и вариации
постоянных Лагранжа.
-порядка с постоянными
коэффициентами: однородного в различных случаях корней характеристического
уравнения (построением ФСР) и неоднородного методами неопределенных
коэффициентов (в случае неоднородности типа квазимногочлена) и вариации
постоянных Лагранжа.
Линейные однородные ДУ.
Пусть в линейном однородном ДУ ![]() -порядка
-порядка
![]() (2.7)
(2.7)
![]() . Линейная комбинация функции и
ее производных может быть тождественно равна нулю лишь когда эти функции
принадлежат одному и тому же классу. Таким свойством обладает экспонента,
поэтому частное решение (2.7) ищут в виде
. Линейная комбинация функции и
ее производных может быть тождественно равна нулю лишь когда эти функции
принадлежат одному и тому же классу. Таким свойством обладает экспонента,
поэтому частное решение (2.7) ищут в виде
![]() . (2.8)
. (2.8)
Подставив эти выражения в (2.7) и учитывая,
что ![]() , получим
алгебраическое уравнение
, получим
алгебраическое уравнение ![]() -степени
-степени
![]() .
(2.8)
.
(2.8)
Оно называется
характеристическим уравнением ДУ (2.7), имеет ![]() корней.
Структура общего решения (2.7) зависит от вида этих корней. Рассмотрим частные
случаи.
корней.
Структура общего решения (2.7) зависит от вида этих корней. Рассмотрим частные
случаи.
1. Допустим,
(2.9) имеет только вещественные простые (разные) корни: ![]() . Покажем, что функции
. Покажем, что функции
![]()
составляют фундаментальную систему решений (2.7). Их вронскиан

Присутствующий здесь определитель, состоящий
из степеней чисел ![]() ,
называется степенным определителем или определителем Вандермонда. Общее решение
(2.9) имеет вид
,
называется степенным определителем или определителем Вандермонда. Общее решение
(2.9) имеет вид
![]() .
(2.10)
.
(2.10)
Задание 11. Найти общее решение ДУ
![]() .
.
Решение. Характеристическое уравнение
![]()
имеет простые вещественные корни
![]() .
.
Общее решение ДУ
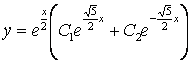 .
.
2. Все
корни (2.9) вещественные, но среди них имеются равные (кратные). Например, если
корень ![]() имеет
кратность
имеет
кратность ![]() , то
в общем решении (2.7) ему соответствуют слагаемые:
, то
в общем решении (2.7) ему соответствуют слагаемые:
![]() . (2.11)
. (2.11)
В частности, для однородного уравнения,
соответствующего (2.1), ![]() .
.
3. Пусть
теперь взаимно сопряженные комплексные числа ![]() являются простыми корнями (2.9). Общее
решение (2.7) будет содержать соответствующие им слагаемые:
являются простыми корнями (2.9). Общее
решение (2.7) будет содержать соответствующие им слагаемые:
![]() .
(2.12)
.
(2.12)
Например, для (1.2)
характеристическое уравнение и его корни: ![]() ,
, ![]() . Общее решение (1.2)
. Общее решение (1.2)
![]() . (2.13)
. (2.13)
После замены постоянных интегрирования:
![]()
найдем закон собственных гармонических колебаний груза
![]() . (2.14)
. (2.14)
Здесь ![]() - амплитуда (наибольшее отклонение точки
- амплитуда (наибольшее отклонение точки ![]() от центра колебаний
от центра колебаний ![]() ),
), ![]() - фаза,
- фаза, ![]() - начальная фаза,
- начальная фаза, ![]() - круговая частота
колебаний. Период колебаний
- круговая частота
колебаний. Период колебаний
![]() .
.
Теоретически
колебания должны продолжаться неограниченно долго (![]() ). Но они происходят в среде с
сопротивлением. Например, если сила сопротивления среды пропорциональна
скорости груза:
). Но они происходят в среде с
сопротивлением. Например, если сила сопротивления среды пропорциональна
скорости груза: ![]() (
(![]() - коэффициент
сопротивления среды), то дифференциальное уравнение движения будет иметь вид
- коэффициент
сопротивления среды), то дифференциальное уравнение движения будет иметь вид
![]() .
.
Его общее решение
![]()
или
![]()
выражает закон затухающих гармонических колебаний.
Неоднородное
линейное дифференциальное уравнение второго порядка с постоянными
коэффициентами, правая часть которого есть периодическая функция (возмущающая
сила) ![]() ,
описывает вынужденные колебания материальной точки в среде без сопротивления
или с сопротивлением.
,
описывает вынужденные колебания материальной точки в среде без сопротивления
или с сопротивлением.
Задание 12. Найти решение задачи Коши
![]() .
.
Решение. Характеристическое уравнение
![]()
имеет простые комплексные корни
![]() .
.
Общее решение ДУ и его производная:
![]() ,
,
![]() .
.
Использование начальных данных приводит к системе:
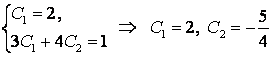 .
.
Решение задачи Коши
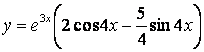 .
.
Линейные неоднородные (с квазимногочленом) ДУ с постоянными коэффициентами. Метод неопределенных коэффициентов.
Теперь для решения линейного
неоднородного ДУ ![]() -порядка
с постоянными коэффициентами
-порядка
с постоянными коэффициентами
![]() (2.15)
(2.15)
необходимо найти его любое частное
решение ![]() .
Для этого применяются известные методы неопределенных коэффициентов и вариации
произвольных постоянных.
.
Для этого применяются известные методы неопределенных коэффициентов и вариации
произвольных постоянных.
Если правая часть (2.15) представляет собой так нвзываемый квазимногочлен
![]() ,
(2.16)
,
(2.16)
то частное решение уравнения рекомендуется искать в аналогичном (2.16) виде
![]() . (2.17)
. (2.17)
Здесь ![]() - заданные многочлены
степени
- заданные многочлены
степени ![]() соответственно,
соответственно,
![]() - многочлены
степени
- многочлены
степени ![]() с
неизвестными пока коэффициентами. Эти коэффициенты определяются из требования,
что (2.16) есть решение уравнения (2.15).
с
неизвестными пока коэффициентами. Эти коэффициенты определяются из требования,
что (2.16) есть решение уравнения (2.15).
Если ![]() есть корень (2.9)
кратности
есть корень (2.9)
кратности ![]()
![]() , то говорят, что в
описываемом уравнением (2.15) процессе имеет место резонанс и в искомое частное
решение вводится множитель
, то говорят, что в
описываемом уравнением (2.15) процессе имеет место резонанс и в искомое частное
решение вводится множитель ![]() . Если явление резонанса отсутствует, то
. Если явление резонанса отсутствует, то ![]() .
.
Задание 13. Найти общее решение ДУ
![]() .
.
Решение. Характеристическое уравнение соответствующего однородного уравнения ![]()
![]()
имеет двукратный
вещественный корень ![]() .
Следовательно,
.
Следовательно,
![]() .
.
Итак как резонанс отсутствует ![]() , то частное решение
неоднородного уравнения ищем в виде функции
, то частное решение
неоднородного уравнения ищем в виде функции
![]()
с производными ![]() ,
, ![]() . После подставления их в
заданное ДУ получим систему
. После подставления их в
заданное ДУ получим систему
 .
.
Требуемое общее решение
![]() .
.
Задание 14. Найти общее решение ДУ
![]() .
.
Решение. Как и в задании 13 найдем корни характеристического уравнения соответствующего однородного уравнения:
![]() .
.
Общее решение однородного уравнения
![]() .
.
Имеет место «трехкратный» резонанс. Поэтому
![]() ,
,
![]() .
.
Подставление этих функций в заданное ДУ приводит к системе:
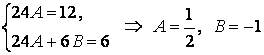 .
.
Искомое общее решение
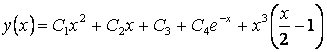 .
.
Теорема. Если
функции ![]() ,
,
![]() являются
решениями уравнений
являются
решениями уравнений ![]() , то их сумма
, то их сумма ![]() является решением уравнения
является решением уравнения ![]() .
.
Справедливость теоремы вытекает
из свойства аддитивности оператора ![]() .
.
Пример 5. Найти общее решение ДУ
![]()
Решение. Придерживаясь последовательности решения предыдущих заданий, имеем:
![]()
![]() ,
, ![]()
![]() .
.
Применяя теорему о “суммировании”
частных решений и учитывая наличие резонанса в уравнении ![]() , положим:
, положим:
![]() ,
,
![]() ,
,
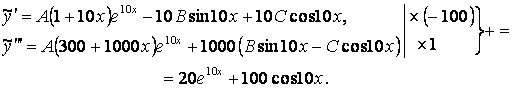
Приравнивая коэффициенты при линейно
независимых функциях ![]() ,
,
![]() и
и ![]() , найдем:
, найдем:
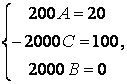
![]()
Искомое общее решение
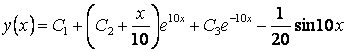 .
.
Метод вариации произвольных постоянных Лагранжа.
Если
правая часть линейного неоднородного ДУ не имеет “специального” вида (2.16), то
для нахождения его общего решения применяется метод вариации произвольных
постоянных. При этом находят фундаментальную систему решений (2.4)
соответствующего однородного уравнения и составляют общее решение последнего
(2.5). Далее, варируют произвольные постоянные ![]() , т.е., принимая их за пока неизвестные
функции
, т.е., принимая их за пока неизвестные
функции ![]() ,
требуют, чтобы функция
,
требуют, чтобы функция
![]() (2.18)
(2.18)
являлась решением неоднородного уравнения (2.1) или (2.15).
Систему
уравнений для нахождения неизвестных функций составляют следующим образом.
Находя производную (2.18), требуют, чтобы она имела вид как при постоянных
коэффициентах ![]() ,
т.е. кладут:
,
т.е. кладут:
![]() .
.
Этот процесс
продолжают до (![]() )-шага:
)-шага:
![]() ,
,
![]()
![]() Наконец,
Наконец,
![]() .
.
Подставив функцию (2.18) и все ее найденные производные в неоднородное уравнение и учитывая, что
![]() ,
,
получим систему ![]() линейных уравнений
линейных уравнений
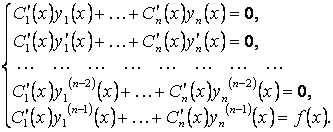 (2.19)
(2.19)
Определитель системы
![]() ,
,
так как функции (2.4)
линейно независимы на ![]() .
Значит, система (2.19) совместна и имеет единственное решение
.
Значит, система (2.19) совместна и имеет единственное решение
![]() .
.
Найденные
функции непрерывны, следовательно, интегрируемы на ![]() :
:
![]() .
.
Подставив последние в (2.18), получим общее решение заданного неоднородного уравнения
![]() . (2.20)
. (2.20)
И здесь заметна структура общего решения
линейного неоднородного уравнения как сумма функций ![]() и
и ![]() .
.
Задание 15. Найти решение задачи Коши:
![]()
Решение: ![]() .
.
![]()
Составим и решим систему (2.19):
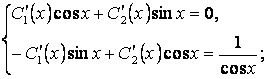
![]() .
.
Общее решение неоднородного уравнения и его производная:
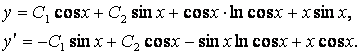
Удовлетворяя начальным условиям, найдем: ![]() . Решение задачи Коши
. Решение задачи Коши
![]() .
.
Лекция 7. Общая теория линейных систем ДУ
Цель лекции: ознокомить студентов с основами общей теории систем линейных ДУ в векторно-матричном изложении (определения, свойства решений, ФСР, фундаментальная матрица, вронскиан, формула Лиувилля и др. понятия).
Линейные однородные системы.
Нормальная система линейных однородных ДУ записывается в виде
![]() (2.21)
(2.21)
или в векторно-матричных обозначениях
![]() , (2.22)
, (2.22)
где ![]() -матрица системы, состоящая из коэффициентов
при неизвестных функциях;
-матрица системы, состоящая из коэффициентов
при неизвестных функциях; ![]() -заданные непрерывные на интервале
-заданные непрерывные на интервале ![]() функции (или числа);
функции (или числа); ![]() -столбец неизвестных
функций. На интервале
-столбец неизвестных
функций. На интервале ![]() система
(2.21) или (2.22) удовлетворяет условиям теоремы существования и единственности
решения задачи Коши.
система
(2.21) или (2.22) удовлетворяет условиям теоремы существования и единственности
решения задачи Коши.
Пусть векторы
![]() (2.23)
(2.23)
являются решениями системы (2.22). Определитель
![]() (2.24)
(2.24)
называют определителем Вронского,
вкратце, вронскианом системы векторов (2.23). При ![]() векторы (2.23) линейно
независимы и обратно. Заметим, что если
векторы (2.23) линейно
независимы и обратно. Заметим, что если ![]() хотя бы в одной точке интервала
хотя бы в одной точке интервала ![]() , то это условие
выполняется всюду в данном интервале.
, то это условие
выполняется всюду в данном интервале.
Любую совокупность ![]() линейно независимых на
линейно независимых на ![]() решений системы (2.22) называют
ее фундаментальной системой решений (ФСР). Матрица
решений системы (2.22) называют
ее фундаментальной системой решений (ФСР). Матрица ![]() , столбцы которой представляют
собой векторы из ФСР, носит название фундаментальной матрицы системы (2.21).
Для произвольного постоянного вектора
, столбцы которой представляют
собой векторы из ФСР, носит название фундаментальной матрицы системы (2.21).
Для произвольного постоянного вектора ![]() с независимыми координатами общее решение
системы (2.22) имеет вид
с независимыми координатами общее решение
системы (2.22) имеет вид
![]() . (2.25)
. (2.25)
Для решения задачи Коши при начальных условиях: ![]() в (2.25) положим
в (2.25) положим ![]() и найдем
соответствующее значение постоянного вектора:
и найдем
соответствующее значение постоянного вектора:
![]() .
.
Подставив последнее в (2.25), найдем решение задачи Коши
![]() .
.
Матрицу ![]() называют матрицей Коши. С ее
помощью решение задачи Коши можно представить в виде
называют матрицей Коши. С ее
помощью решение задачи Коши можно представить в виде
![]() . (2.26)
. (2.26)
Формула Лиувилля для системы (2.22) записывается в виде:
![]() . (2.27)
. (2.27)
Линейные неоднородные системы.
Нормальную систему линейных ДУ
![]() (2.28)
(2.28)
Называют неоднородной, если хотя бы одна из функций ![]() не равна тождественно
нулю на интервале
не равна тождественно
нулю на интервале ![]() .
Вводя в рассмотрение вектор-функцию
.
Вводя в рассмотрение вектор-функцию ![]() , систему (2.28) можно представить в
матричной форме
, систему (2.28) можно представить в
матричной форме
![]() . (2.29)
. (2.29)
В области непрерывности коэффициентов ![]() система (2.28) или (2.29) также
удовлетворяет условиям теоремы существования и единственности решения задачи
Коши. Систему (2.21) называют однородной системой, соответствующей
неоднородной системе (2.28).
система (2.28) или (2.29) также
удовлетворяет условиям теоремы существования и единственности решения задачи
Коши. Систему (2.21) называют однородной системой, соответствующей
неоднородной системе (2.28).
Путем непосредственного подставления можно убедиться, что вектор
![]() (2.30)
(2.30)
является общим решением неоднородной
системы (2.29). При этом следует иметь в виду, что производная матрицы есть
матрица, состоящая из производных элементов данной матрицы. В (2.29) первая
слагаемая есть общее решение (2.25)
однородной системы (2.22), соответствующей неоднородной системе (2.29), а ![]() -любое частное решение
рассматриваемой неоднородной системы. Поэтому если соответствующая
однородная система (2.21) решена, то задача сводится к нахождению какого-либо
частного решения заданной неоднородной системы (2.28). Для этого можно
применять предложенный Лагранжем
-любое частное решение
рассматриваемой неоднородной системы. Поэтому если соответствующая
однородная система (2.21) решена, то задача сводится к нахождению какого-либо
частного решения заданной неоднородной системы (2.28). Для этого можно
применять предложенный Лагранжем
Метод вариации произвольных постоянных.
Пусть общее решение однородной системы (2.22) найдена в виде (2.25). Введем в рассмотрение функцию
![]() , (2.31)
, (2.31)
где ![]() - пока неизвестная вектор-функция, которую
подберем так, чтобы (2.31) была решением неоднородной системы (2.29). Подставим
предполагаемое решение в систему:
- пока неизвестная вектор-функция, которую
подберем так, чтобы (2.31) была решением неоднородной системы (2.29). Подставим
предполагаемое решение в систему:
![]() .
.
Так как ![]() есть фундаментальная матрица
однородной системы (2.22), то
есть фундаментальная матрица
однородной системы (2.22), то
![]() . (2.32)
. (2.32)
Определитель линейной системы алгебраических уравнений (2.32),
как определитель фундаментальной матрицы, не равен нулю на ![]() . Система имеет единственное
решение
. Система имеет единственное
решение
![]() .
.
После интегрирования
![]()
или (условно)
![]() . (2.33)
. (2.33)
При ![]() (2.33) дает частное решение неоднородной
системы (2.29), а при произвольном постоянном векторе
(2.33) дает частное решение неоднородной
системы (2.29), а при произвольном постоянном векторе ![]() - ее общее решение, подтверждая
высказанное ранее предположение о структуре общего решения линейной
неоднородной системы.
- ее общее решение, подтверждая
высказанное ранее предположение о структуре общего решения линейной
неоднородной системы.
Заметим, что интегрирование
неоднородной системы (2.28) обычно проводится методом исключения неизвестных
функций, т.е. приведением системы к одному линейному неоднородному ДУ ![]() -порядка.
-порядка.
Лекция 8. Линейные системы с постоянными коэффициентами
Цель лекции: применение изложенных на предыдущей лекции основных положений и методов (характеристических уравнений, исключая неизвестных функций, вариации постоянных) к системам линейных ДУ с постоянными коэффициентами, выбор оптимальных методов.
Метод характеристических уравнений.
Линейные системы ДУ с постоянными коэффициентами
![]() (2.34)
(2.34)
представляют собой частный случай
системы (2.28), когда все коэффициенты ![]() заданные числа. Поэтому все сказанное
ранее относительно нормальной системы линейных уравнений справедливо и для
системы (2.34).
заданные числа. Поэтому все сказанное
ранее относительно нормальной системы линейных уравнений справедливо и для
системы (2.34).
Для отыскания фундаментальной матрицы однородной системы
![]() , (2.35)
, (2.35)
соответствующей системе (2.34) могут
быть использованы методы линейной алгебры. Характеристическое уравнение
числовой матрицы (оператора, [1]) ![]()
![]() (2.36)
(2.36)
есть характеристическое уравнение
системы (2.35). Оно совпадает с характеристическим уравнением ((2.9)) линейного
однородного ДУ ![]() -порядка,
эквивалентного системе (2.35).
-порядка,
эквивалентного системе (2.35).
Ограничимся рассмотрением случая ![]() простых (кратности 1)
вещественных корней
простых (кратности 1)
вещественных корней ![]() алгебраического
уравнения
алгебраического
уравнения ![]() -степени
(2.36). Каждому такому корню
-степени
(2.36). Каждому такому корню ![]() (собственному значению матрицы
(собственному значению матрицы ![]() системы) соответствует
так называемый собственный вектор
системы) соответствует
так называемый собственный вектор ![]() и решение
и решение ![]() системы (2.35). Собственные векторы,
следовательно, решения системы линейно независимы. Последние образуют
фундаментальную матрицу системы (2.35)
системы (2.35). Собственные векторы,
следовательно, решения системы линейно независимы. Последние образуют
фундаментальную матрицу системы (2.35)
![]() . (2.37)
. (2.37)
Общее решение однородной системы выглядит так:
![]() . (2.38)
. (2.38)
Частное или общее решение
неоднородной системы можно найти с помощью метода Лагранжа или сведением
системы к одному линейному неоднородному уравнению ![]() -порядка с постоянными
коэффициентами вида (2.15).
-порядка с постоянными
коэффициентами вида (2.15).
Задание 16. Решить систему ДУ
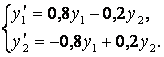
Решение. Характеристическое уравнение системы
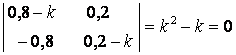
имеет корни: ![]() . Найдем соответствующие или
собственные векторы:
. Найдем соответствующие или
собственные векторы: ![]() ,
,
![]() ;
;
1) ![]() ,
, 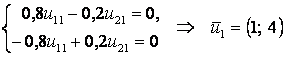 .
.
Здесь как свободная неизвестная взята ![]() .
.
2) ![]() ,
, 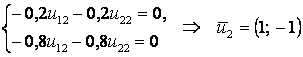 .
.
Фундаментальная система решений
 .
.
Общее решение системы
![]() . (1)
. (1)
Линейное ДУ второго порядка или нормальная система двух линейных ДУ с постоянными коэффициентами при чисто мнимых корнях характеристического уравнения описывает колебательное движения. Например, (1.2) как нормальную систему ДУ можно представить в виде
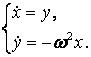
Ее характеристическое уравнение имеет чисто мнимые корни:
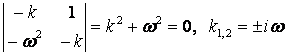 .
.
Закон колебаний груза (см. рисунок 2) имеет вид (2.13) или (2.14).
Пример 6. Найти общее решение системы ДУ

Решение. Корни характеристического уравнения
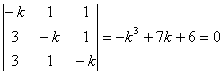
системы: ![]() . Найдем
соответствующие им собственные векторы:
. Найдем
соответствующие им собственные векторы:
1) 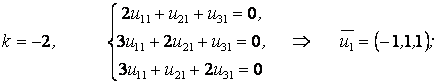
2) 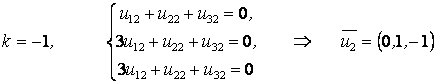 ;
; ![]()
3) 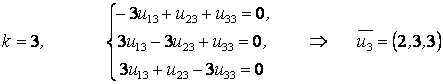 .
.
Фундаментальная система решений:

Общее решение системы:

Метод исключения неизвестных функций.
Нормальная система ![]() дифференциальных
уравнений эквивалентна одному ДУ
дифференциальных
уравнений эквивалентна одному ДУ ![]() - порядка и обратно. Систему (2.34) можно
привести к одному линейному неоднородному ДУ
- порядка и обратно. Систему (2.34) можно
привести к одному линейному неоднородному ДУ ![]() -порядка с постоянными коэффициентами. Для
этого достаточно почленно продифференцировать по
-порядка с постоянными коэффициентами. Для
этого достаточно почленно продифференцировать по ![]() одно из уравнений (2.34), например, первое
одно из уравнений (2.34), например, первое
![]() раз, а
остальные по
раз, а
остальные по ![]() раз.
Затем из заданных и полученных дифференцированием уравнений исключить
неизвестные функции
раз.
Затем из заданных и полученных дифференцированием уравнений исключить
неизвестные функции ![]() и
их производные. В результате придем к ДУ вида (2.2).
и
их производные. В результате придем к ДУ вида (2.2).
Задание 17. Решить систему ДУ из предыдущего задания методом исключения неизвестных функций.
Решение. Сложив уравнения системы, найдем
![]() . (2)
. (2)
Подставив это значение в
![]() ,
,
придем к линейному однородному ДУ второго порядка с постоянными коэффициентами
![]() , (3)
, (3)
характеристическое уравнение
которого имеет корни: ![]() .
.
Общее решение уравнения (3)
![]() .
.
Подставив это в (2), после интегрирования найдем
![]() .
.
Вставив функции ![]() в любое из уравнений первоначальной
системы найдем постоянную интегрирования
в любое из уравнений первоначальной
системы найдем постоянную интегрирования ![]() , тем самым общее решение системы
приводится к виду (1).
, тем самым общее решение системы
приводится к виду (1).
Пример 7. Найти решение задачи Коши методом вариации произвольных постоянных:
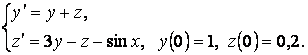 (1)
(1)
Решение. Составим и решим характеристическое уравнение соответствующей однородной системы
![]() ; (2)
; (2)
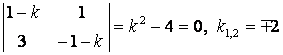 .
.
Найдем собственные
векторы ![]() ,
соответствующие собственным числам
,
соответствующие собственным числам ![]() :
:
1) ![]() ,
, 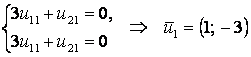 .
.
2) ![]() ,
, 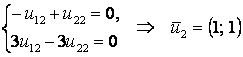 .
.
Фундаментальная система решений
 .
.
Общее решение системы
![]() .
.
Далее применяем метод Лагранжа; (2.31) и (2.32) примут вид:
![]() ; (3)
; (3)
-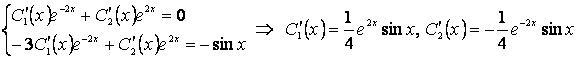 .
.
После интегрирования:
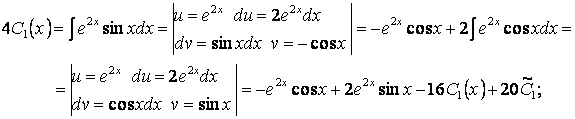
![]() .
.
Применяя замену ![]() , найдем
, найдем
![]() .
.
Подставив найденные функции в (3) , получим общее решение (1):
![]() .
.
Вставив эти функции в начальные условия, найдем:
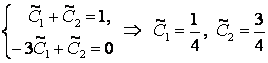 .
.
Решение задачи Коши:
![]() .
.
Заметим что, последовательное применение метода исключения
неизвестных функций и метода неопределенных коэффициентов в этом примере
быстрее приводит к цели. Действительно почленно сложим заданные уравнения, а
первое из них продифференцируем по ![]() :
:
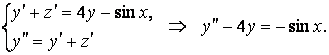
Полученное линейное неоднородное ДУ второго порядка с постоянными коэффициентами решим методом неопределенных коэффициентов:
![]()
![]()
![]() .
.
Так как по условию ![]() , то общее решение
системы примет вид (4).
, то общее решение
системы примет вид (4).
Модуль 3. Краевые задачи для линейных ДУ второго порядка
Лекция 9. Постановка краевых задач
Цель лекции: объяснить студентам постановку краевой задачи для линейного ДУ второго порядка при различных граничных условиях. Сравнение последних с условиями Коши. Изложить теорему существования и единственности решения краевой задачи.
При ![]() линейное неоднородное ДУ (2.1)
записывается так:
линейное неоднородное ДУ (2.1)
записывается так:
![]() , (3.1)
, (3.1)
а соответствующее ему однородное ДУ – в виде
![]() . (3.2)
. (3.2)
Функции ![]() предполагается непрерывными в
рассматриваемой области
предполагается непрерывными в
рассматриваемой области ![]() .
.
Для уравнений (3.1-2) справедливы все суждения относительно
решений уравнений (2.2) любого порядка ![]() . При решении задачи Коши начальные условия
задаются в виде
. При решении задачи Коши начальные условия
задаются в виде
![]() . (3.3)
. (3.3)
Решение начальной задачи при любом выборе чисел ![]() существует и является
единственным.
существует и является
единственным.
В ряде задач физики и техники приходится искать решение ДУ
не по заданным начальным условиям, а по его значениям на концах интервала. Их
называют краевыми (граничными) задачами. Краевые условия для интервала ![]() можно представить в
общем виде:
можно представить в
общем виде:
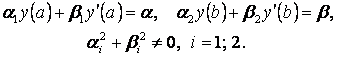 (3.4)
(3.4)
Условия (3.4) называются однородными, если ![]() и неоднородными – в
противном случае. Это означает, что если некоторые функции
и неоднородными – в
противном случае. Это означает, что если некоторые функции ![]() и
и ![]() удовлетворяют условиям (3.4) при
удовлетворяют условиям (3.4) при ![]() , то их линейная
комбинация
, то их линейная
комбинация ![]() ,
, ![]() также удовлетворяет
этим условиям. Если требуется решить однородное уравнение (3.2) при
неоднородных краевых условиях, то говорят, что имеем однородную краевую задачу.
А когда хотя бы одно из них (либо уравнение, либо условие) неоднородное, то и
краевая задача называется неоднородными. Встречаются также краевые условия типа
периодичности:
также удовлетворяет
этим условиям. Если требуется решить однородное уравнение (3.2) при
неоднородных краевых условиях, то говорят, что имеем однородную краевую задачу.
А когда хотя бы одно из них (либо уравнение, либо условие) неоднородное, то и
краевая задача называется неоднородными. Встречаются также краевые условия типа
периодичности:
![]() ,
(3.5)
,
(3.5)
относящиеся к однородным граничным условиям.
При решении краевой задачи соблюдается та же
последовательность, что и при решении задачи Коши. Сначала находят общее
решение данного ДУ вида (3.1) или (3.2). Подставив его в граничные условия
(3.4) получают систему алгебраических уравнений для определения соответствующих
значений постоянных интегрирования ![]() и
и ![]()
Пример 8. Решить заданную на интервале  краевую задачу:
краевую задачу:
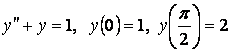 .
.
Решение. Так как заданное ДУ имеет частное решение ![]() , а соответствующее ему
однородное уравнение – общее решение
, а соответствующее ему
однородное уравнение – общее решение ![]() , то подставив их сумму в указанные
граничные условия, найдем:
, то подставив их сумму в указанные
граничные условия, найдем: ![]() . Искомое решение
представится функцией:
. Искомое решение
представится функцией: ![]() .
.
Рассмотрим линейное ДУ второго порядка с непрерывными на
отрезке ![]() коэффициентами
в общей форме
коэффициентами
в общей форме
![]() . (3.6)
. (3.6)
При ![]() (3.6) приводится к виду (3.1) делением
уравнения на
(3.6) приводится к виду (3.1) делением
уравнения на ![]() .
Но, при исследовании краевых задач допускается, что
.
Но, при исследовании краевых задач допускается, что ![]() в отдельных точках отрезка
в отдельных точках отрезка ![]() . Такие точки называются
особыми точками ДУ (3.6). Учитывая возможность разбиения отрезка на части,
достаточно предположить, что особая точка существует только на концах
. Такие точки называются
особыми точками ДУ (3.6). Учитывая возможность разбиения отрезка на части,
достаточно предположить, что особая точка существует только на концах ![]() , т.е.
, т.е. ![]() . В этих случаях
соответствующее граничное условие заменяется требованием ограниченности
значения
. В этих случаях
соответствующее граничное условие заменяется требованием ограниченности
значения ![]() или
или ![]() решения. Иногда эти
требования могут быть заменены условием роста модуля решения:
решения. Иногда эти
требования могут быть заменены условием роста модуля решения:
![]() (3.7)
(3.7)
Из теоремы Коши (см. рис.3) следует, что в постановке
начальной задачи не требуется, чтобы решение было определено на всех отрезке ![]() . Достаточно
существование его в некоторой окрестности начальной точки
. Достаточно
существование его в некоторой окрестности начальной точки ![]() . Существенное отличие краевой
задачи состоит в требовании, чтобы искомое решение было определено на всем
отрезке
. Существенное отличие краевой
задачи состоит в требовании, чтобы искомое решение было определено на всем
отрезке ![]() .
Утверждение об единственности решения может тоже не выполняться. Поэтому
краевая задача не всегда разрешима.
.
Утверждение об единственности решения может тоже не выполняться. Поэтому
краевая задача не всегда разрешима.
Считается, что однородная краевая задача разрешима, если она
имеет хотя бы одно ненулевое решение ![]() . В таком случае функция
. В таком случае функция ![]() при любом значении
постоянной
при любом значении
постоянной ![]() также
будет ее решением. Поэтому нетривиальное решение однородной краевой задачи
может быть определено только с точностью до постоянного множителя.
также
будет ее решением. Поэтому нетривиальное решение однородной краевой задачи
может быть определено только с точностью до постоянного множителя.
Теорема (существования и единственности решения краевой
задачи). Для того, чтобы ДУ (3.1) при произвольных краевых условиях (3.4)
обладало одним и только одним решением необходимо и достаточно, чтобы
соответствующая однородная задача, т.е. задача, для которой ![]() , обладала только тривиальным
решением
, обладала только тривиальным
решением ![]() .
.
Лекция 10. Задача Штурма-Лиувилля
Цель лекции: показать, что задача Штурма-Лиувилля является частным случаем общей краевой задачи для линейного ДУ второго порядка с неопределенными коэффициентами. Применять известные из линейной алгебры понятия собственных значений, собственных функций оператора и функций, ортогональных на отрезке. Дать понятие граничных функций краевой задачи, например, функции Грина и с ее помощью интегральную формулу решения краевой задачи.
Для краткости в (3.6) введем линейный дифференциальный оператор
![]() (3.8)
(3.8)
и рассмотрим однородное ДУ второго порядка
![]() . (3.9)
. (3.9)
Однородная краевая задача о нахождении ненулевого решения ДУ
(3.9), удовлетворяющего краевым условиям (3.4) при ![]() , носит название задачи Штурма-Лиувилля.
Значения параметра
, носит название задачи Штурма-Лиувилля.
Значения параметра ![]() ,
для которых задача Штурма-Лиувилля имеет решение
,
для которых задача Штурма-Лиувилля имеет решение ![]() , называют собственными значениями
оператора
, называют собственными значениями
оператора ![]() .
Соответствующие им решения
.
Соответствующие им решения ![]() называются собственными функциями
оператора или задач.
называются собственными функциями
оператора или задач.
В практических исследованиях считается оптимальным применять оператор (3.8) в виде
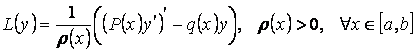 .
.
Здесь
![]() ,
,
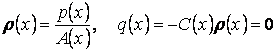 .
.
Функции ![]() непрерывны,
непрерывны, ![]() непрерывно дифференцируема на
непрерывно дифференцируема на ![]() ;
; ![]() - так называемая весовая функция
оператора
- так называемая весовая функция
оператора ![]() .
.
В задаче Штурма-Лиувилля собственные значения составляют возрастающую последовательность неотрицательных чисел:
![]()
и числовой ряд ![]() всегда сходящийся. Последовательности
собственных значений соответствует последовательность собственных функций
всегда сходящийся. Последовательности
собственных значений соответствует последовательность собственных функций
![]() . (3.10)
. (3.10)
С точностью до постоянного множителя для каждого
собственного значения ![]() найдется
единственная собственная функция
найдется
единственная собственная функция ![]() . В случае краевых условий типа
периодичности (3.5) одному собственному значению могут соответствовать две
линейно независимые собственные функции.
. В случае краевых условий типа
периодичности (3.5) одному собственному значению могут соответствовать две
линейно независимые собственные функции.
Собственные функции ![]() и
и ![]() , соответствующие различным собственным
значениям
, соответствующие различным собственным
значениям ![]() и
и ![]() , удовлетворяют
равенству
, удовлетворяют
равенству
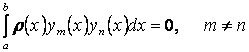 .
.
Они называют ортогональными [1] с весом ![]() функциями на отрезке
функциями на отрезке ![]() . В этом смысле выражение
. В этом смысле выражение
![]() можно считать
ортогонализирующим множителем для системы собственных функций (3.10).
можно считать
ортогонализирующим множителем для системы собственных функций (3.10).
Теорема. Непрерывно дифференцируемая, имеющая
кусочно-непрерывную вторую производную на отрезке ![]() функция
функция ![]() , удовлетворяющая однородным
, удовлетворяющая однородным ![]() граничным условиям
(3.4), по системе собственных функций (3.10) разлагается в абсолютно и
равномерно сходящийся ряд
граничным условиям
(3.4), по системе собственных функций (3.10) разлагается в абсолютно и
равномерно сходящийся ряд
![]()
с коэффициентами
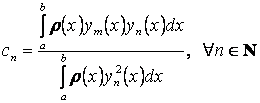 .
.
Граничные функции краевой задачи. Функция Грина.
На отрезке ![]() рассмотрим однородную краевую задачу
рассмотрим однородную краевую задачу
![]() (3.11)
(3.11)
![]() . (3.12)
. (3.12)
Пусть ![]() есть фундаментальная система решений
уравнения (3.11). Тогда любые два (различные) частные решения краевой задачи
(3.11-12) будут иметь вид:
есть фундаментальная система решений
уравнения (3.11). Тогда любые два (различные) частные решения краевой задачи
(3.11-12) будут иметь вид:
![]() ,
,
![]() .
.
Взяв ![]() и
и ![]() , составим функцию
, составим функцию

тождественно не равную нулю на
отрезке ![]() , но,
вообще говоря, разрывную в точке
, но,
вообще говоря, разрывную в точке ![]() . Функция
. Функция ![]() является решением краевой задачи (3.11-12)
всюду в рассматриваемой области кроме точки
является решением краевой задачи (3.11-12)
всюду в рассматриваемой области кроме точки ![]() . Определив произвольные постоянные из
уравнений
. Определив произвольные постоянные из
уравнений
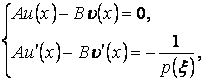
можно добиться, чтобы функция ![]() была непрерывной и в
точке
была непрерывной и в
точке ![]() , а ее
производная имела заданный скачок в этой точке:
, а ее
производная имела заданный скачок в этой точке:
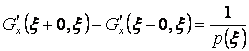 .
.
Функцию ![]() , удовлетворяющую всем приведенным
условиям, называют функцией Грина для системы (задачи) Штурма-Лиувилля при
, удовлетворяющую всем приведенным
условиям, называют функцией Грина для системы (задачи) Штурма-Лиувилля при ![]() . Доказано [7], что
каждое решение интегрального уравнения
. Доказано [7], что
каждое решение интегрального уравнения
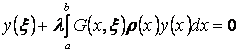
удовлетворяет уравнению
![]()
с граничными условиями (3.12) и обратно, т.е. эти уравнения являются эквивалентными (равносильными).
Лекция 11. Нормальная система ДУ
Цель лекции: ознокомить студентов с системами ДУ в общем, каноническом и нормальном видах. С интегралами и первыми интегралами нормальной системы ДУ, выделением интегрируемых комбинации из симметрической формы нормальной системы. С постановкой задачи Коши, теоремой существования и единственности решения для нормальной системы ДУ.
Система ДУ в общем виде записывается так:
![]() . (3.13)
. (3.13)
где ![]() - независимая переменная,
- независимая переменная, ![]() - неизвестные функции,
остальные аргументы их производные до
- неизвестные функции,
остальные аргументы их производные до ![]() -порядка. Решить систему (3.13) означает
найти все неизвестные функции
-порядка. Решить систему (3.13) означает
найти все неизвестные функции ![]() .
.
При определенных условиях систему (3.13) можно разрешить относительно старших производных неизвестных функций, т.е. представить систему в так называемой канонической форме:
![]() . (3.14)
. (3.14)
Систему (3.14) путем введения новых неизвестных функций
также можно привести в системе ![]() уравнений первого порядка разрешенных
относительно производных
уравнений первого порядка разрешенных
относительно производных
![]() . (3.15)
. (3.15)
Это есть система ДУ в так называемой нормальной форме.
Решением системы (3.15) на интервале ![]() называется совокупность функций
называется совокупность функций ![]() , непрерывно
дифференцируемых на
, непрерывно
дифференцируемых на ![]() и
обращающих уравнения системы в тождества относительно
и
обращающих уравнения системы в тождества относительно ![]() . Функцию
. Функцию ![]() , определенную и непрерывную
вместе со своими частными производными
, определенную и непрерывную
вместе со своими частными производными 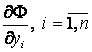 в некоторой области
в некоторой области ![]() изменения переменных и
принимающую для
изменения переменных и
принимающую для ![]() постоянное
значение при постановке в нее произвольного решения системы, называют
интегралом нормальной системы (3.15). Интеграл системы, приравненный
произвольной постоянной
постоянное
значение при постановке в нее произвольного решения системы, называют
интегралом нормальной системы (3.15). Интеграл системы, приравненный
произвольной постоянной
![]() , (3.16)
, (3.16)
называется первым интегралом системы (3.15).
Заметим, что если известен один первый интеграл системы, то
при выполнений определенных условий число уравнений в системе можно уменьшить
на единицу. Если известны ![]() независимых первых интегралов, то систему
можно считать решенной.
независимых первых интегралов, то систему
можно считать решенной.
В частности, для выделения интегрируемых комбинаций систему (3.15) удобнее записать в так называемой симметрической форме:
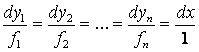 (3.17)
(3.17)
и использовать известное свойство равных дробей-пропорций:
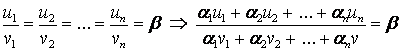 . (3.18)
. (3.18)
В (3.17) независимая переменная и искомые функции
«равноправны». Применяя (3.18), стараются числа ![]() подобрать так, чтобы числитель был полным
дифференциалом знаменателя или знаменатель был равен нулю.
подобрать так, чтобы числитель был полным
дифференциалом знаменателя или знаменатель был равен нулю.
Пример 9. Найти общее решение системы ДУ
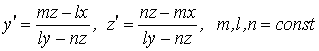 .
.
Решение. Запишем систему в симметрической форме:
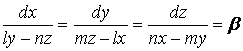 .
.
Теперь в (3.18) взяв первый раз ![]() и второй раз
и второй раз ![]()
![]() ,
, ![]() , найдем:
, найдем:
![]() и
и ![]() .
.
Приравнивая числители также нулю, после интегрирования найдем первые интегралы системы:
![]() ,
,
которые в неявной форме определяют требуемое общее решение системы.
Для системы (3.15) задача Коши ставится следующим образом:
найти решение ![]() системы,
удовлетворяющее начальным условиям
системы,
удовлетворяющее начальным условиям
![]() , (3.19)
, (3.19)
где ![]() - заданные числа.
- заданные числа.
Теорема Коши. Пусть правые части ![]() нормальной системы (3.15)
определены в
нормальной системы (3.15)
определены в ![]() -мерной
области
-мерной
области ![]() изменения
переменных
изменения
переменных ![]() .
Если в некоторой окрестности
.
Если в некоторой окрестности ![]() точки
точки ![]() функции
функции ![]() непрерывны и имеют непрерывные частные
производные
непрерывны и имеют непрерывные частные
производные 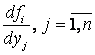 ,
то существует интервал
,
то существует интервал ![]() изменения переменной
изменения переменной ![]() , в котором существует и притом
единственное решение системы (3.15), удовлетворяющее начальным условиям (3.19).
, в котором существует и притом
единственное решение системы (3.15), удовлетворяющее начальным условиям (3.19).
Общим решением системы (3.15) называется совокупность функций
![]() , (3.20)
, (3.20)
зависящих от ![]() произвольных постоянных, которые
при любых допустимых значениях постоянных
произвольных постоянных, которые
при любых допустимых значениях постоянных ![]() обращают уравнения системы в тождества и в
области, в которой выполнены условия теоремы Коши, из совокупности функций (3.20)
можно получать решение любой задачи Коши.
обращают уравнения системы в тождества и в
области, в которой выполнены условия теоремы Коши, из совокупности функций (3.20)
можно получать решение любой задачи Коши.
Лекция 12. Линейные ДУ с частными производными
Цель лекции: изложить постановку задачи Коши для ДУ в частных производных первого порядка и раскрыть ее геометрический смысл в случае двух независимых переменных. Задачи о нахождении общего и частного решений линейного однородного уравнения с частными производными.
Постановка задачи Коши.
ДУ с частными производными первого порядка в общем виде записывается так:
![]()
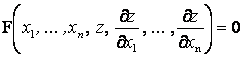 , (3.21)
, (3.21)
где ![]() - независимые переменные,
- независимые переменные, ![]() - неизвестная функция,
- неизвестная функция, ![]() - ее частные
производные.
- ее частные
производные.
При определенных условиях уравнение (3.21 имеет общее решение и решение его может содержать не только произвольные постоянные, но и некоторые произвольные функции. Поэтому обычно задача о нахождении общего решения уравнений типа (3.21) не ставится. Ищутся только частные решения, удовлетворяющие начальным данным Коши или другим условиям, однозначно определяющим требуемое решение. При этом задача интегрирования уравнений вида (3.21) сводится к интегрированию системы обыкновенных ДУ.
Для решения (3.21), разрешенного относительно одной из
частных производных, например, по переменной ![]()
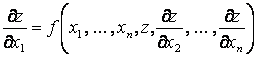 , (3.22)
, (3.22)
задача Коши ставится так: найти решение
![]() (3.23)
(3.23)
уравнения (3.22), которое при
заданном начальном значении ![]() обращается в заданную функцию остальных
независимых переменных
обращается в заданную функцию остальных
независимых переменных
![]() . (3.24)
. (3.24)
В случае двух независимых переменных задача интегрирования уравнения
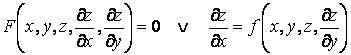 (3.25)
(3.25)
и условия Коши:
![]() (3.26)
(3.26)
допускают геометрическое истолкование. Решение
![]() (3.27)
(3.27)
уравнения (3.25) в пространстве ![]() изображает некоторую
поверхность, называемую интегральной поверхностью этого уравнения. Касательная
плоскость к интегральной поверхности в точке
изображает некоторую
поверхность, называемую интегральной поверхностью этого уравнения. Касательная
плоскость к интегральной поверхности в точке ![]() определяется уравнением
определяется уравнением
![]() . (3.28)
. (3.28)
Значит, уравнение в частных производных (4.5) выражает
соотношение между координатами точки ![]() его интегральной поверхности и угловыми
коэффициентами нормали
его интегральной поверхности и угловыми
коэффициентами нормали ![]() поверхности
поверхности ![]() в данной точке. Уравнения (3.26)
определяют кривую в пространстве.
в данной точке. Уравнения (3.26)
определяют кривую в пространстве.
Таким образом, задача Коши для уравнения (3.25) состоит в
нахождении интегральной поверхности, проходящей через плоскую кривую (3.26),
лежащую на плоскости ![]() .
.
Для уравнения (3.25), неразрешенного относительно одной из частных производных, задача Коши ставится в общем виде: найти интегральную поверхность, проходящую через заданную кривую
![]() . (3.29)
. (3.29)
Через некоторые из кривых (3.29), называемых характеристиками уравнения (3.25), в пространстве проходит бесконечное множество интегральных поверхностей.
Изложенное геометрическое истолкование распространяется и на
уравнение (3.21). При этом ![]() решение (3.23) уравнения определяет
интегральную поверхность в
решение (3.23) уравнения определяет
интегральную поверхность в ![]() - мерном пространстве. А начальные условия
(3.24) – поверхность в
- мерном пространстве. А начальные условия
(3.24) – поверхность в ![]() - мерном пространстве.
- мерном пространстве.
Линейные однородные уравнения.
Равенство
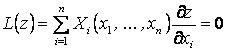 , (3.30)
, (3.30)
где ![]() - заданные непрерывно дифференцируемые в
рассматриваемой области функции, представляют собой линейное однородное ДУ в
частных производных первого порядка. Соотношения
- заданные непрерывно дифференцируемые в
рассматриваемой области функции, представляют собой линейное однородное ДУ в
частных производных первого порядка. Соотношения
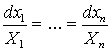 (3.31)
(3.31)
есть система ![]() обыкновенных ДУ, соответствующая
уравнению (3.30).
обыкновенных ДУ, соответствующая
уравнению (3.30).
Левая часть любого первого интеграла системы (3.31) вида (3.16) является решение уравнения (3.30). Обратно, любое решения уравнение (3.30). Обратно, любое решение уравнения (3.30), приравненное произвольной постоянной, служит первым интегралом системы (3.31).
В отличие от (3.21) для линейного однородного уравнения в
частных производных первого порядка (3.30) можно ставить задачу о нахождении
его общего решения. Если известна некоторая совокупность определенных в
рассматриваемой области ![]() независимых первых интегралов
независимых первых интегралов
![]() (3.32)
(3.32)
системы (3.31), то произвольная дифференцируемая в данной области сложная функция
![]() (3.33)
(3.33)
представляют собой общее решение уравнения (3.30). Это утверждение не противоречит предложению о том, что общее решение уравнения (3.21) содержит произвольные функции.
То что, функция (3.33) удовлетворяет уравнению (3.30)
следует из свойств линейного оператора. Действительно, так как ![]() и
и
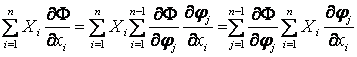 ,
,
то
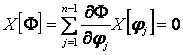 .
.
В качестве примера найдем общее решение уравнения
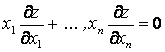 .
.
Соответствующая ему система (4.11) имеет вид
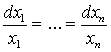 .
.
При ![]() систему ее независимых первых интегралов
можно представить в виде
систему ее независимых первых интегралов
можно представить в виде
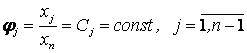 .
.
Тогда общее решение заданного ДУ в частных производных представляет собой произвольную однородную функцию нулевого измерения
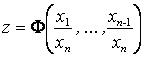 .
.
Задача Коши: для уравнения (3.30) найти решение ![]() такое, чтобы
такое, чтобы
![]() , (3.34)
, (3.34)
где ![]() - заданное число,
- заданное число, ![]() - заданная дифференцируемая
функция.
- заданная дифференцируемая
функция.
Чтобы найти решение задачи Коши для (3.31) составляют
систему ![]() независимых
первых интегралов (3.32) и решают ее относительно независимых переменных:
независимых
первых интегралов (3.32) и решают ее относительно независимых переменных:
![]() .
.
Тогда решение задачи Коши, удовлетворяющее начальному условию (3.34), запишется в виде [3]:
![]() .
.
Пример 10. Решить задачу Коши
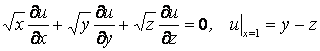 .
.
Решение. Система (3.30) и ее независимые первые интегралы имеют вид:
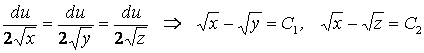 .
.
При ![]()
![]() .
.
Решение задачи Коши
![]() .
.
Список литературы
1. Мустахишев К.М., Ералиев С.Е., Атабай Б.Ж. Математика (полный курс). -Алматы: «TST-Company», 2009. -429 с.
2. Базарбаева С.Е., Дулэпо В.М. Высшая математика. Методические указания и задания к расчетно-графической работе. Ч.6. –Алматы: АИЭС, 2002. -34 с.
3. Степанов В.В. Курс дифференциальных уравнений. –М.: ГИФМЛ, 1959. -468 с.
4. Ефимов А.В., Демидович Б.П. (под ред.). Сборник задач по математике для ВТУЗов. Специальные разделы математического анализа. –М.: Наука, 1986. -366 с.
5. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. –М.: Наука, 1985. -464 с.
6. Камке Э. Справочник по дифференциальным уравнениям в частных производных первого порядка. –М.: Наука, 1966. -260 с.
7. Трикоми Ф. Дифференциальные уравнения. –М.: ИЛ, 1962.
Содержание
|
Модуль 1. Дифференциальные уравнения первого порядка |
3 |
|
Лекция 1. Общее понятия дифференциальных уравнений. Геометрическая интерпретация |
3 |
|
Лекция 2. Задача Коши (начальная задача). Уравнения с разделяющимися переменными |
5 |
|
Лекция 3. Однородные, линейные и в полных дифференциалах уравнения |
8 |
|
Лекция 4. Графическая интерпретация теоремы существования и единственности решения ДУ первого порядка |
15 |
|
Модуль 2. Общая теория линейных дифференциальных уравнений высших порядков |
21 |
|
Лекция 5. Линейные ДУ с непрерывными коэффициентами |
21 |
|
Лекция 6. Линейные ДУ с постоянными коэффициентами |
22 |
|
Лекция 7. Общая теория линейных систем ДУ. |
29 |
|
Лекция 8. Линейные системы с постоянными коэффициентами |
31 |
|
Модуль 3. Краевые задачи для линейных ДУ высших порядков |
36 |
|
Лекция 9. Постановка краевых задач |
36 |
|
Лекция 10. Задача Штурма-Лиувилля |
38 |
|
Лекция 11. Нормальная система ДУ |
41 |
|
Лекция 12. Линейные ДУ с частными производными |
43 |
|
Список литературы |
47 |