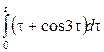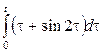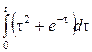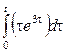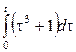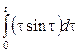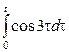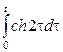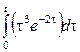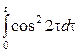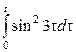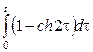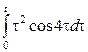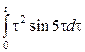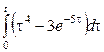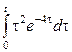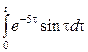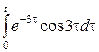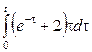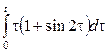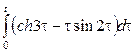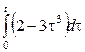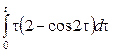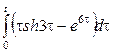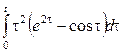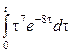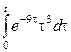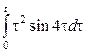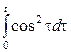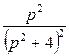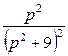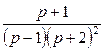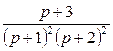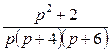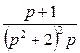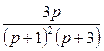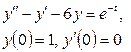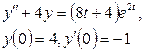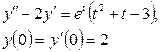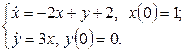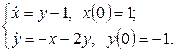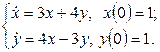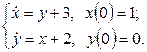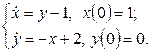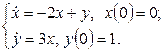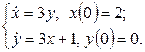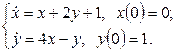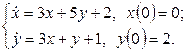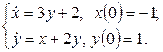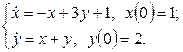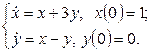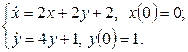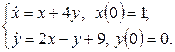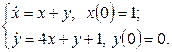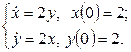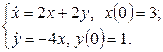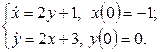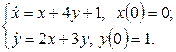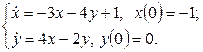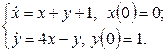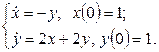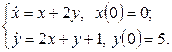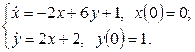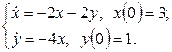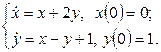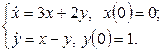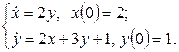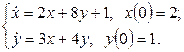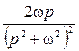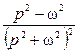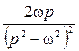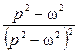Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра высшей математики

РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
с применением операционного исчисления
Методические указания и задания к расчетно-графическим работам
(для специальности 5В071800 Электроэнергетика).
Часть 1

Алматы 2014

СОСТАВИТЕЛИ: Мустахишев К.М., Атабай Б.Ж. Решение диференциальных уравнений с применением операционного исчисления. Методические указания и задания к расчетно-графическим работам (для специальности 5В071800 Электроэнергетика). Часть 1. – Алматы: АУЭиС, 2014. -19 с.

Методические указания и задания к выполнению  расчетно-графической работы составлены в соответствии с программой вновь введенного специального курса «Решение диференциальных уравнений». Они содержат по основам операционного исчисления, их применениям к решению линейных дифференциальных уравнений с постоянными коэффициентами и их систем теоретические вопросы и 11 заданий. Каждое задание состоит из 30 вариантов. Приведен справочный маериал, содержащий решение типового варианта с пояснениями, свойства (теоремы) преобразования Лапласа и таблицу изображений основных элементарных функций.

Ил. -31, библиогр. – 4 назв.

Рецензент: к.т.н., доцент К.А.Бакенов   

Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2014 г.

© НКАО “Алматинский университет энергетики и связи”,   2014 г.

Решение диференциальных уравнений (РДУ)

РГР №1. Операционное исчисление и РДУ

Теоретические вопросы:

1) Преобразование Лапласа. Оригиналы и изображения.

2) Теоремы линейности, подобия, смещения, запаздывания.

3) Теоремы дифференцирования и интегрирования оригиналов и изображений.

4) Свертка функций. Теорема умножения изображений.  Формулы Дюамеля.

5) Теорема обращения. Нахождение оригинала по известному изображению.

6) Применение преобразования Лапласа при решения дифференциальных уравнений и их систем.

Расчетные задания.

1. Является ли функция оригиналом или нет, и почему?

№	а)	б)	№	а)	б)
1.1			1.2
1.3			1.4
1.5			1.6
1.7			1.8
1.9			1.10
1.11			1.12
1.13			1.14
1.15			1.16
1.17			1.18
1.19			1.20
1.21			1.22
1.23			1.24
1.25			1.26
1.27			1.28
1.29			1.30

2. Найти изображение функции, пользуясь теоремами линейности, подобия, смещения, запаздывания.

№	а)	б)	в)	г)
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
2.10
2.11
2.12
2.13
2.14
2.15
2.16
2.17
2.18
2.19
2.20
2.21
2.22
2.23
2.24
2.25
2.26
2.27
2.28
2.29
2.30

3. Найти изображение функции, пользуясь теоремой о дифференцирования оригинала.

№		№		№		№
3.1		3.2		3.3		3.4
3.5		3.6		3.7		3.8
3.9		3.10		3.11		3.12
3.13		3.14		3.15		3.16
3.17		3.18		3.19		3.20
3.21		3.22		3.23		3.24
3.25		3.26		3.27		3.28
3.29		3.30		3.31		3.32

4. Найти изображение функции, пользуясь теоремами дифференцирования изображения, интегрирования оригинала и изображения.

5. По графику оригинала найти изображение.

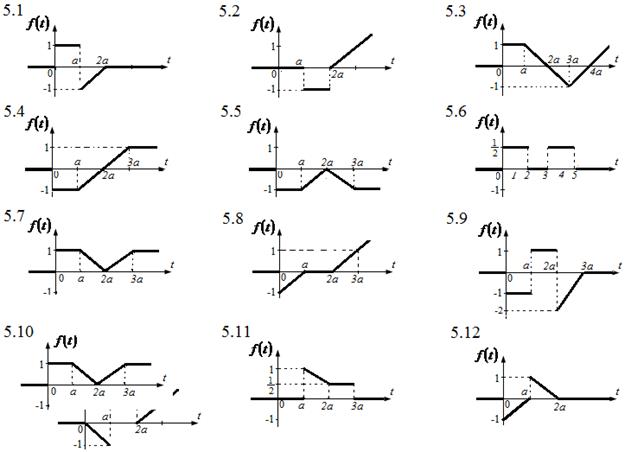
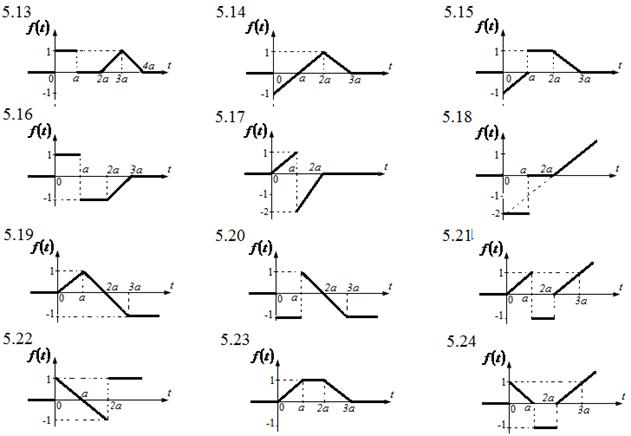
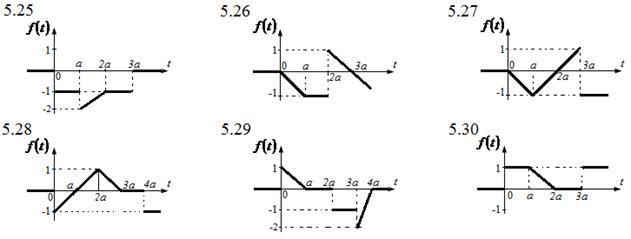
6. Найти свертку функций  и  и ее изображение.

№			№
6.1			6.2
6.3			6.4
6.5			6.6
6.7			6.8
6.9			6.10
6.11			6.12
6.13			6.14
6.15			6.16
6.17			6.18
6.19			6.20
6.21			6.22
6.23			6.24
6.25			6.26
6.27			6.28
6.29			6.30

7. Найти оригинал  функции , применяя  теорему умножения изображений.

№		№		№
7.1		7.2		7.3
7.4		7.5		7.6
7.7		7.8		7.9
7.10		7.11		7.12
7.13		7.14		7.15
7.16		7.17		7.18
7.19		7.20		7.21
7.22		7.23		7.24
7.25		7.26		7.27
7.28		7.29		7.30

8. Найти оригинал по заданному изображению.

№		№
8.1		8.2
8.3		8.4
8.5		8.6
8.7		8.8
8.9		8.10
8.11		8.12
8.13		8.14
8.15		8.16
8.17		8.18
8.19		8.20
8.21		8.22
8.23		8.24
8.25		8.26
8.27		8.28
8.29		8.30

9. Методом операционного исчисления решить задачу Коши.

9.1		9.2
9.3		9.4
9.5		9.6
9.7		9.8
9.9		9.10
9.11		9.12
9.13		9.14
9.15		9.16
9.17		9.18
9.19		9.20
9.21		9.22
9.23		9.24
9.25		9.26
9.27		9.28
9.29		9.30

10. Найти решение задачи Коши с помощью формулы Дюамеля.

10.1		10.2
10.3		10.4
10.5		10.6
10.7		10.8
10.9		10.10
10.11		10.12
10.13		10.14
10.15		10.16
10.17		10.18
10.19		10.20
10.21		10.22
10.23		10.24
10.25		10.26
10.27		10.28
10.29		10.30

11. Решить систему дифференциальных уравнений операционным методом.

11.1		11.2
11.3		11.4
11.5		11.6
11.7		11.8
11.9		11.10
11.11		11.12
11.13		11.14
11.15		11.16
11.17		11.18
11.19		11.20
11.21		11.22
11.23		11.24
11.25		11.26
11.27		11.28
11.29		11.30

Решение типового варианта.

1. Является ли функция оригиналом или нет, и почему?

а) ,   б) ,   в) .

Решение: функцией-оригиналом называется любая комплекснозначная или действительнозначная функция  действительного аргумента t, удовлетворяющая следующим трем условиям:

1)   - кусочно-непрерывная функция при ;

2)  при ;

3)  возрастает не быстрее показательной функции:  существуют такие постоянные , что   при .

Единичная функция:

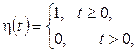
так называемая функция Хэвисайда, является функцией-оргиналом.

Если  удовлетворяет условиям 1 и 2, то  удовлетворяет всем трем условиям функции-оригинала:

а) Функция  является оригиналом, так как удовлетворяет условиям 1 и 3: .

б) Функция  не является оригиналом, так как в точке  имеем разрыв второго рода, т.е. не выполняется условие 1.

в) Функция  не является оригиналом,  так  как  растет  быстрее  показательной  функции для любых  и .

2-4. Найти изображение  функции , пользуясь свойствами преобразования Лапласа:

а) ,   б) ,   в) ,  г)  ,   д) ,   е) ,   ж) ,   и) .

Решение: 

а)  Используя таблицу 1 и теорему линейности, имеем:

.

б) По таблице соответствия: и по теореме смещения:

.

в) По таблице  по теореме запаздывания имеем:  .

г) Преобразуем данную функцию:  . Теперь, используя таблицу и теорему линейности, имеем:

.

д) По таблице  и по теореме о дифференцировании изображения 

.

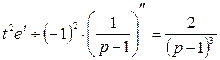е) Имеем .

По теореме об интегрировании оригинала:

 .

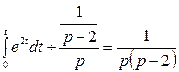ж) Так как ,   то по теореме об интегрировании изображения имеем: 

.

и) Так как , то . По теореме дифференцирования оригинала . Таким образом, , откуда .

5. По заданному графику оригинала найти изображение.

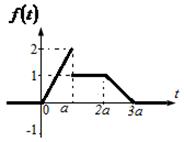
Решение: обозначим точки, в которых происходит разрыв или изменение функции через , скачок функции в точке разрыва через , угловой коэффициент -го участка - через  и . Изображение такого вида функций можно найти по формуле:

.

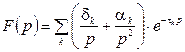На основе уравнений прямой, проходящей через две точки  и : ,  определим первую наклонную по точкам  и , а вторую наклонную по точкам  и . Тогда соответственно имеем:

 и . Следовательно, .

В нашем случае: ;   ;

;  .

Таким образом,

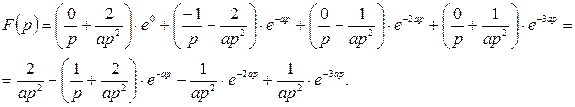
6. Найти свертку функций  и  и ее изображение.

Решение: свертка функций  и находится по формуле:

.

Поэтому   .

Изображение свертки найдем по таблице и теореме линейности:

.

7. Найти оригинал  функции , применяя  теорему умножения изображений.

Решение: по теореме умножения: если , , то . Таким образом,

.

8. Найти оригинал  по заданному изображению :

а) ,  б) .

Решение:

а) Разложим дробно-рациональную функцию на сумму простых дробей:

;

.

при  имеем ;

при   имеем: ;

при   имеем: .

Таким образом,

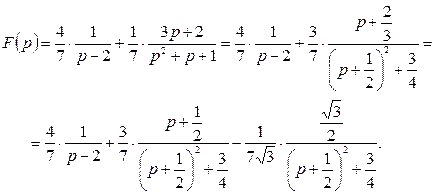
Итак, искомый оригинал .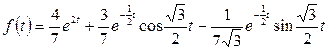

б) По таблице , теперь по теореме об интегрировании оригинала:  .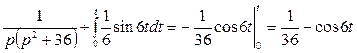

9. Операционным методом решить задачу Коши:

.

Решение: пусть , тогда по теореме дифференцировании оригинала:

, а .

Операторное уравнение имеет вид: .

Откуда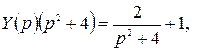

.

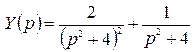Оригинал 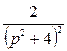  можно найти по теореме умножения изображений:

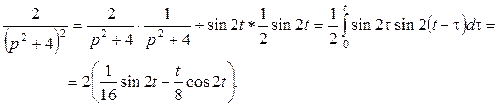
Таким образом, искомое решение

.

10. Найти решение задачи Коши с помощью формулы Дюамеля:

.

Решение: составим вспомогательное уравнение  и решим его операторным методом. Операторное уравнение: . Его решение  .

Известными методами найдем оригинал этого решения:

.

Для определения решения данного уравнения воспользуемся формулой:

.

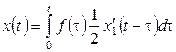Так как ,  а , 

то

.

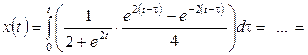
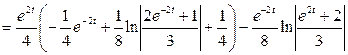11. Решить систему дифференциальных уравнений операционным методом:

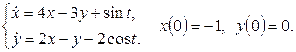
Решение: пусть . Составим систему операторных уравнений, используя свойства преобразования Лапласа, таблицу 1 и начальные условия:

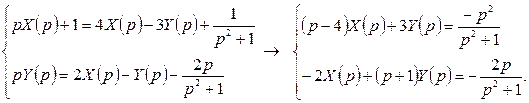
Решаем ее по правилу Крамера:

;

;

;

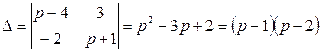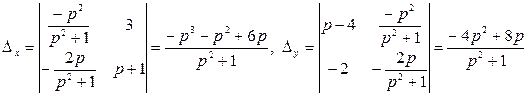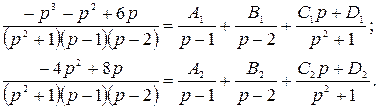
Известным способом найдем:

.

Таким образом,

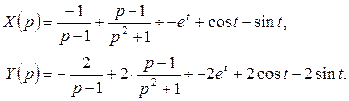
Ответ: .

Справочный материал.

Свойства преобразования Лапласа.   Пусть :

1)   (теорема линейности);

2)  (теорема подобия);

3)  (теорема смещения);

4)  ( теорема запаздывания);

5)  ,

 (теорема дифференциорования оригинала);

6)  (теорема интегрирования оригинала);

7)  (теорема дифференцирования изображения);

8) 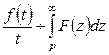 (теорема интегрирования изображения);

9) ,

(теорема умножения изображений);

10) ,

 (интегралы Дюамеля).

Таблица соответствия оригинал-изображение

Таблица 1

№			№
1	1		8
2			9
3			10
4			11
5			10
6			11
7			12

Список литературы

1. Мустахишев К.М., Ералиев С.Е., Атабай Б.Ж. Математика (полный курс). –Алматы: NSN-Company, 2009. -429 с.

2. Сборник индивидуальных заданий по высшей математике: В 3ч. /А.П. Рябушко, В.В. Бархатов и др. /Под ред.  А.П. Рябушко. –Минск: Вышэйшая школа, 2002. Ч.3 -351 с.

3. Чудесенко В.Ф. Сборник заданий по специальным курсам высшей математики. Учебники для вузов.  -Изд.: Лань., 2005, -128 с.

4. Лунгу К.Н. и др. Сборник задач по высшей математике (с контрольными работами). –М.: Айрис пресс, 2005, 1,2 – курсы.

Содержание

РГР №1 Операционное исчисление и РДУ	2
Теоретические вопросы	2
Расчетные задания	2
Решение типового варианта	12
Справочный материал	18
Таблица соответствия оригинал-изображение	18
Список литературы	19

Сводный план  2014, поз.219

Мустахишев Киров Мустахишевич,
Атабай Бегимбет Жумабайулы

РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
с применением операционного исчисления
Методические указания и задания к расчетно-графическим работам
(для специальности 5В071800 Электроэнергетика)
Часть 1

Редактор Д.Т. Сластихина
Специалист по стандартизации Н.К. Молдабекова

Подписано в печать _______        
Формат 60х84 1/16
Тираж 300 экз.
Бумага офсетная
Объем 1,3 уч. изд. лист        
Заказ_____ Цена 650 т

Копировольно-множительное бюро
Некомерческое акционерноео бщество
“Алматинский университет энергетики и связи”
050013, Алматы, Байтурсынова, 126