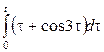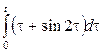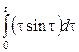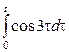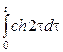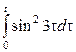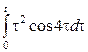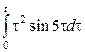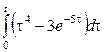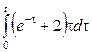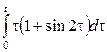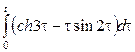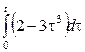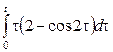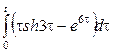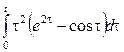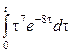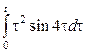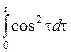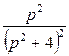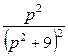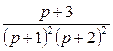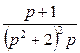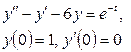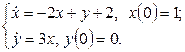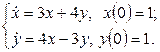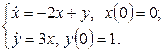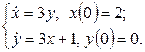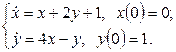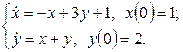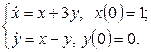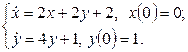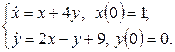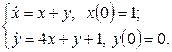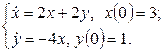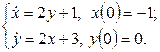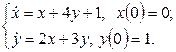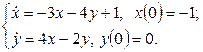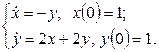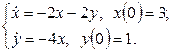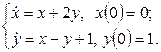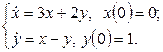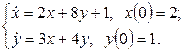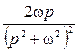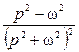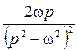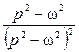Коммерциялық емес акционерлік қоғам
Алматы энергетика және байланыс Университеті
Жоғары математика кафедрасы

АМАЛДЫҚ ЕСЕПТЕУЛЕРДІ ҚОЛДАНЫП
ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕРДІ ШЕШУ
Есептеу-сызба жұмыстарға
әдістемелік нұсқаулар мен тапсырмалар
(5В071800 Электроэнергетика мамандығына арналған)
1 бөлім

Алматы 2014

Құрастырғандар: Мұстахишев К.М., Атабай Б.Ж. Амалдық есептеулерді қолданып дифференциалдық теңдеулерді шешу. Есептеу-сызба жұмыстарға әдістемелік нұсқаулар мен тапсырмалар (5В071800  Электроэнергетикасы мамандығына арналған). 1 бөлім. – Алматы: АЭжБУ, 2014. -20 б.

Есептеу-графиктік жұмысқа арналған әдістемелік нұсқаулар мен тапсырмалар жаңадан енгізілген. «Дифференциалдық теңдеулерді шешу (ДТШ)»  арнаулы курсының бағдарламасына сай құрылған. Мұнда операторлық есептеу негіздері, олардаң коэффициенттері тұрақты сызықтық дифференциалдақ теңдеулер мен олардың жүйелерін шешуге қолданылуы бойынша теориялық сұрақтар және 11 тапсырма бар. Әрбір тапсырма 30 нұсқадан тұрады. Типтік нұсқаның шешуі мен түсініктемелері, құрамында Лаплас түрлендіруінің қасиеттері (теоремалары) және негізгі элементар функциялардың бейнелерінің кестесі бар анықтамалық материал келтірілген.

Сурет-31, әдебиет көр. – 4 атау.

Пікір беруші: тех.ғылым.канд., доцент К.А. Бакенов

«Алматы энергетика және байланыс университеті» коммерциялық емес акционерлік қоғамының 2014 ж. жоспары бойынша басылды

© “Алматы энергетика және байланыс университеті”  КЕАҚ, 2014 ж.

Дифференциалдық теңдеулерді шешу (ДТШ)

№1 ЕГЖ  Операторлық есептеу және ДТШ

Теориялық сұрақтар:

1) Лаплас түрлендіруі. Түпнұсқа және бейне.

2) Сызықтық, ұқсастық, ығысу және кешігу теоремалары.

3) Түпнұсқа мен бейнені дифференциалдау және интегралдау теоремалары.

4) Функциялардың орамасы. Бейнелерді көбейту теоремасы. Дюамель формулалары.

5) Қайырылу теоремасы. Берілген бейне бойынша оның түпнұсқасын табу.

6) Лаплас түрлендіруінің көмегімен дифференциалдық теңдеулер мен олардың жүйесін шешу.

Есептеу тапсырмалары.

1. Берілген функциялар түпнұсқа бола алама, болмаса неге?

№	а)	б)	№	а)	б)
1.1			1.2
1.3			1.4
1.5			1.6
1.7			1.8
1.9			1.10
1.11			1.12
1.13			1.14
1.15			1.16
1.17			1.18
1.19			1.20
1.21			1.22
1.23			1.24
1.25			1.26
1.27			1.28
1.29			1.30

2. Сызықтық, ұқсастық, ығысу және кешігу теоремаларын пайдаланып, функциялардың бейнелерін табыңыз.

№	а)	б)	в)	г)
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
2.10
2.11
2.12
2.13
2.14
2.15
2.16
2.17
2.18
2.19
2.20
2.21
2.22
2.23
2.24
2.25
2.26
2.27
2.28
2.29
2.30

3. Түпнұсқаны дифференциалдау теоремасының көмегімен функцияның бейнесін табыңыз.

№		№		№		№
3.1		3.2		3.3		3.4
3.5		3.6		3.7		3.8
3.9		3.10		3.11		3.12
3.13		3.14		3.15		3.16
3.17		3.18		3.19		3.20
3.21		3.22		3.23		3.24
3.25		3.26		3.27		3.28
3.29		3.30		3.31		3.32

4. Түпнұсқа мен бейнені дифференциалдау және интегралдау теоремаларын пайдаланып, функциялардың бейнелерін табыңыз.

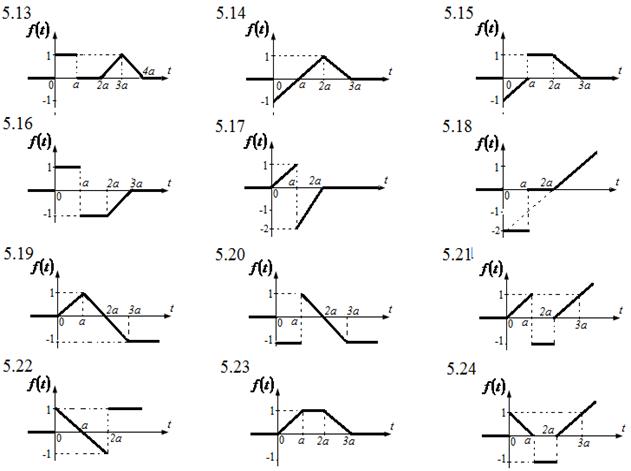
5. Түпнұсқаның графигі бойынша оның бейнесін табыңыз.

6. ,  функцияларының орамасын және оның бейнесін табыңыз.

№			№
6.1			6.2
6.3			6.4
6.5			6.6
6.7			6.8
6.9			6.10
6.11			6.12
6.13			6.14
6.15			6.16
6.17			6.18
6.19			6.20
6.21			6.22
6.23			6.24
6.25			6.26
6.27			6.28
6.29			6.30

7. Бейнелерді көбейту теоремасының көмегімен  функциясының түпнұсқасын  табыңыз.

№		№		№
7.1		7.2		7.3
7.4		7.5		7.6
7.7		7.8		7.9
7.10		7.11		7.12
7.13		7.14		7.15
7.16		7.17		7.18
7.19		7.20		7.21
7.22		7.23		7.24
7.25		7.26		7.27
7.28		7.29		7.30

8. Берілген бейненің түпнұсқасын табыңыз.

№		№
8.1		8.2
8.3		8.4
8.5		8.6
8.7		8.8
8.9		8.10
8.11		8.12
8.13		8.14
8.15		8.16
8.17		8.18
8.19		8.20
8.21		8.22
8.23		8.24
8.25		8.26
8.27		8.28
8.29		8.30

9. Операторлық есептеу әдісімен Коши есебін шешіңіз.

9.1		9.2
9.3		9.4
9.5		9.6
9.7		9.8
9.9		9.10
9.11		9.12
9.13		9.14
9.15		9.16
9.17		9.18
9.19		9.20
9.21		9.22
9.23		9.24
9.25		9.26
9.27		9.28
9.29		9.30

10. Дюамель интегралдарын пайдаланып, Коши есебінің шешуін табыңыз.

10.1		10.2
10.3		10.4
10.5		10.6
10.7		10.8
10.9		10.10
10.11		10.12
10.13		10.14
10.15		10.16
10.17		10.18
10.19		10.20
10.21		10.22
10.23		10.24
10.25		10.26
10.27		10.28
10.29		10.30

11. Операторлық әдіспен дифференциалдық теңдеулер жүйесін шешіңіз.

11.1		11.2
11.3		11.4
11.5		11.6
11.7		11.8
11.9		11.10
11.11		11.12
11.13		11.14
11.15		11.16
11.17		11.18
11.19		11.20
11.21		11.22
11.23		11.24
11.25		11.26
11.27		11.28
11.29		11.30

Типтік нұсқаның шешуі.

1. Берілген функциялар түпнұсқа бола алама, болмаса неге?

а) ,   б) ,   в) .

Шешу: төмендегі шарттар орындалғанда ғана заттық аргументтің комплекс мәнді функциясы  түпнұсқа бола алады:

1)   болғанда  - үзбе-үзіліссіз функция;

2)  үшін ;

3)  болатындай .

а)  функциясы түпнұсқа болады, өйткені ол жоғарыдағы талаптардың бәріне де қанағаттандырады:

1) функция сандық осьте үзіліссіз;

2) көбейткіш (Хэвисайд функциясы):

функцияны  болғанда нөлге айналдырады (өшіреді);

3) соңғы талап бойынша   десек жеткілікті.

б)  түпнұсқа болмайды, өйткені оның жоғарыдағы талаптардың алғашқы екеуіне қанағаттандырмайтыны анық:  - функцияның II текті үзіліс нүктесі;  көбейткіші болмағандықтан ;

в)  түпнұсқа болмайды, өйткені ол кез келген  және  үшін көрсеткіш фунциядан тез өседі.

2-4. Лаплас түрлендіруінің қасиеттерін пайдаланып,  функциясының бейнесін  табыңыз:

а) ,   б) ,   в) ,  г)  ,   д) ,   е) ,   ж) ,   и) .

Шешу:

а)  сызықтық теоремасын және 1-кестені пайдалансақ:

;

б) сәйкестік кестесінен:  болғандықтан ығысу теоремасы бойынша:

;

в) кестеден  десек, кешігу теоремасы бойынша  ;

г) белгілі тригонометриялық формуланы ескерсек:  

.

Енді кесте және сызықтық теоремасы бойынша:

;

д)  деп кестені тура пайдалансақ: . Бұл нәтижеге бейнені дифференциалдау теоремасын қолдану:  арқылы да келуге болады;

е) түпнұсқаны интегралдау теоремасы бойынша:

 ;

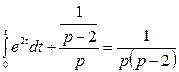ж)  болғандықтан бейнені интегралдау теоремасы бойынша: 

;

и) шарт бойынша ,  болғандықтан түпнұсқаны дифференциалдау теоремасын қолданалық:

.

Бұдан  демек,

.

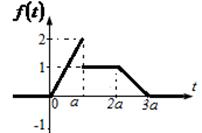5. Түпнұсқаның берілген графигі бойынша бейнені табыңыз:

Шешу: үзбе-сызықтық функцияның:

бейнесі

.

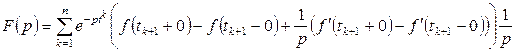Функцияның және оның туындысының үзіліс нүктелері . Бұл нүктелердегі біржақты шектер:

;

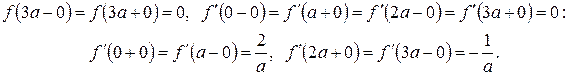
Ізделініп отырған бейне:

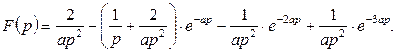
6. Функциялардың  және   орамасын және оның бейнесін табыңыз.

Шешу: анықтама материалдан орама:

.

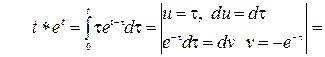
Ораманың бейнесі кестеден:  .

7. Бейнелерді көбейту теоремасының көмегімен

функциясының түпнұсқасын табыңыз.

Шешу:

, 

болғандықтан анықтама материалдан ізделініп отырған түпнұсқа

.

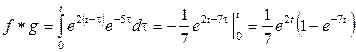8. Берілген  бейнесінің түпнұсқасын табыңыз.

а) ,  б) .

Шешу:

а) Анықталмаған коэффициенттер әдісімен бейнені қарапайым бөлшектердің қосындысына жіктейік:

.

Бұдан шығатын

 болуында  және теңдіктің екі жағынанда  ,   коэффициенттерін теңестіру арқылы белгісіз коэффициенттерді табамыз:

 ,   .

Бейнені түрлендірейік:

Кестеден түпнұсқа: .

б)  болғандықтан түпнұсқаны интегралдау теоремасы бойынша:

.

9. Операторлық әдіспен Коши есебін шешіңіз:

.

Шешу:  ізделініп отырған шешу  түпнұсқа болады және   десек, анықтама материал мен кестеден:

;   .

Бейнелерге көшкеннен кейін операторлық (алгебралық) теңдеуге келеміз:

,  .

Мұндағы бірінші қосылғыштың түпнұсқасын бейнелерді көбейту теоремасы бойынша табуға болады:

.

Тригонометриялық түрлендірулерден кейін

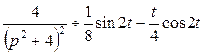
екенін көреміз. Ал,  болғандықтан есептің шешуі:

.

10. Коши есесбінің шешуін Дюамель формулаларының көмегімен табыңыз:

.

Шешу: қосымша теңдеу  құрып, оны операторлық әдіспен шешейік. Сәйкес операторлық теңдеу:

 .

Соңғыны жай бөлшектердің қосындысына жіктейік:

.

Параметрге кезек-кезек  мәндерін берсек:

.

Қосымша теңдеудің шешуі:

,

оның туындысы .

Бастапқы берілген теңдеудің шешуін табу үшін Дюамель формуласын:

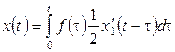
қолданайық. Шарт бойынша   болғандықтан:

.

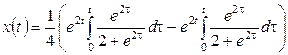Мұндағы екінші қосылғыш логарифмдік интеграл, ал біріншісінде айнымалыны алмастырсақ:

.

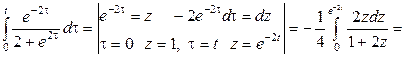
Ақырында,

.

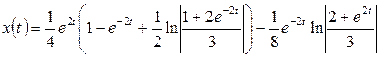11. Операторлық әдіспен дифференциалдық теңдеулер жүйесін шешіңіз:

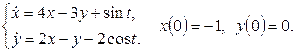
Шешу: жүйенің түпнұсқа болатын шешуі бар және    болсын делік. Лаплас түрлендіруінің қасиеттерін және 1-кестені пайдаланып, сәйкес операторлық (алгебралық) жүйені құралық:

Бұл сызықтық теңдеулер жүйесін Крамер ержесі бойынша немесе белгісіздерді жою әдісімен шешуге болады:

;

;

.

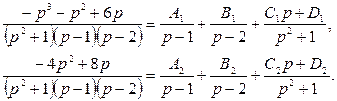
Бөлшектерді ортақ бөлімге келтіріп, алымдарын теңестіргеннен кейін параметрге  және  мәндерін берсек:  болатынын көреміз. Қалған белгісіз коэффициенттер сызықтық теңдеулер жүйелерін құру арқылы табылады: . Қорытындысында:

Бастапқы берілген жүйенің шешуі:

Анықтама материал.

Лаплас түрлендіруінің қасиеттері.  делік:

1)   (сызықтық теоремасы);

2)  (ұқсастық теоремасы);

3)  (ығысу теоремасы);

4)  ( кешігу теоремасы);

5)  

 (түпнұсқаны дифференциалдау теоремасы);

6) , (түпнұсқаны интегралдау теоремасы);

7) , (бейнені дифференциалдау теоремасы);

8) 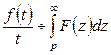, (бейнені интегралдау теоремасы);

9) , (бейнелерді көбейту теоремасы);

10) , (Дюамель интегралдары).

Түпнұсқа-бейне сәйкестігінің кестесі.

1 кесте

№			№
1	1		8
2			9
3			10
4			11
5			10
6			11
7			12

Әдебиеттер тізімі

1. Мустахишев К.М., Ералиев С.Е., Атабай Б.Ж. Математика (толық курс). –Алматы: NSN-Company, 2009. -429 б.

2. Сборник индивидуальных заданий по высшей математике: В 3ч. /А.П. Рябушко, В.В. Бархатов и др. /Под ред.  А.П. Рябушко. –Минск: Вышэйшая школа, 2002. Ч.3 -351 с.

3. Чудесенко В.Ф. Сборник заданий по специальным курсам высшей математики. Учебники для вузов.  -Изд.: Лань., 2005. -128 с.

4. Лунгу К.Н. и др. Сборник задач по высшей математике (с контрольными работами). –М.: Айрис пресс, 2005. 1,2 – курсы.

Мазмұны

1-ЕГЖ   Операторлық есептеу және ДТШ	3
Теориялық сұрақтар	3
Есептеу тапсырмалары	3
Типтік нұсқаның шешуі	12
Анықтама материал	19
Түпнұсқа-бейне сәйкестігінің кестесі	19
Әдебиеттер тізімі	20

Жиынтық жоспар 2014 ж., бап. 218

Керей Мұстахишевич Мұстахишев
Атабай Бегімбет Жұмабайұлы

АМАЛДЫҚ ЕСЕПТЕУЛЕРДІ ҚОЛДАНЫП
ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕРДІ ШЕШУ
Есептеу-сызба жұмыстарға әдістемелік нұсқаулар мен тапсырмалар
(5В071800 Электроэнергетикасы мамандығына арналған)
1 бөлім

Редакторы Б.С. Қасымжанова
Стандарттау бойынша маман  Н.К. Молдабекова

Басуға қол қойылды « ___» ____2014 ж.
Формат 60х84 1/16
Таралымы 500 дана.
№1 Баспаханалық қағаз
Көлемі 1,3 баспа табақ
Тапсырма №___ Бағасы 650 тг.

Көшірмелі-көбейткіш бюросы
Коммерциялық емес акционерлік қоғам
“Алматы энергетика және байланыс университеті”
050013, Алматы, Байтұрсынов, 126