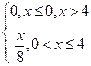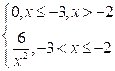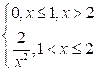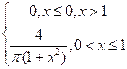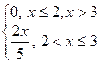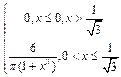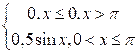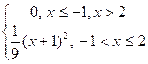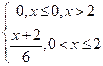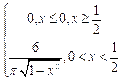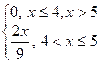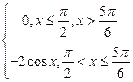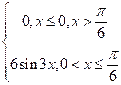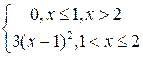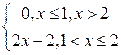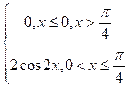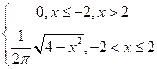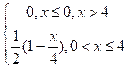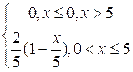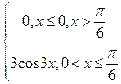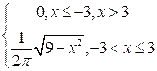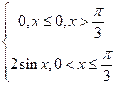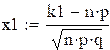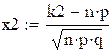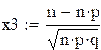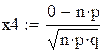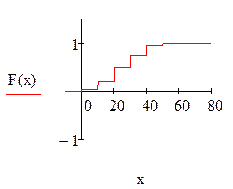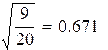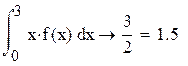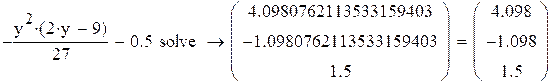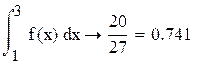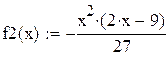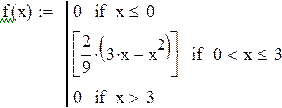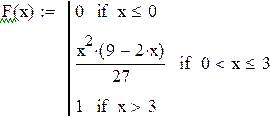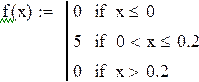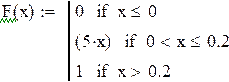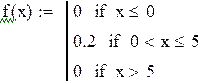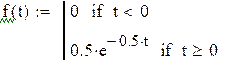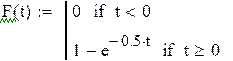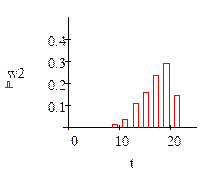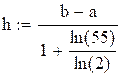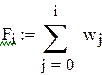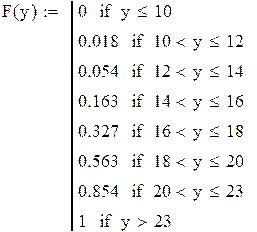Некоммерческое
акционерное общество
Кафедра Математическое моделирование и программное
обеспечение
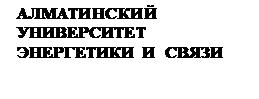


ПРИКЛАДНАЯ СТАТИСТИКА
Методические указания и задания по выполнению расчетно-графических работ для студентов специальности
5В070400- Вычислительная техника и программное обеспечение
Алматы 2017
СОСТАВИТЕЛИ: Астраханцева Л.Н., Байсалова М.Ж. Прикладная статистика. Методические указания и задания по выполнению расчетно -графических работ для студентов специальности 5В070400- Вычислительная техника и программное обеспечение. - Алматы: АУЭС, 2017.- 47 стр.
Методические указания и задания содержат расчетно-графические работы №1, №2 дисциплины «Прикладная статистика» для студентов специальности 5В070400 - Вычислительная техника и программное обеспечение. Приведены основные теоретические вопросы программы. Дано решение типового варианта.
Ил. 22 , табл. 24, библиогр. 6 назв.
![]()
Рецензент: к.х.н., старший преподаватель кафедры ТКСиС Данько Е.Т.
Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2017 г.
ã НАО «Алматинский университет энергетики и связи», 2017 г.
Введение
Математическая статистика тесно связана с теорией вероятностей. Обе эти дисциплины изучают массовые случайные явления. Теория вероятностей обеспечивает теоретическую базу для широкого круга практических задач, которыми занимается математическая статистика.
Поэтому методические указания содержат расчетно-графические работы по двум разделам. В первом рассматриваются основные вопросы теории вероятностей, во втором - математической статистики.
В каждой части приведены теоретические вопросы, задания и решение типового варианта.
Номер варианта студента определяется по списку группы. Расчетно- графическая работа должна выполняться четко и разборчиво в ученической тетради.
1 Расчетно-графическая работа №1. Случайные события и случайные величины
Цели: ознакомиться с понятиями случайного события и его вероятностью, основными теоремами теории вероятностей, изучить законы распределения и числовые характеристики дискретных и непрерывных случайных величин.
1.1 Теоретические вопросы
1. Предмет теории вероятностей. Случайные события. Пространство элементарных событий. Алгебра событий. Статистическое, геометрическое и классическое определения вероятности.
2. Теоремы сложения и умножения вероятностей. Условная вероятность.
3. Формула полной вероятности. Формула Байеса. Формула Бернулли.
4. Локальная и интегральная теоремы Лапласа. Формула Пуассона.
5. Дискретные и непрерывные случайные величины. Законы
распределения дискретной случайной величины.
6. Интегральная функция распределения. Плотность распределения.
7. Числовые характеристики случайных величин. Математическое ожидание, дисперсия и среднее квадратическое отклонение дискретных и непрерывных случайных величин.
8. Биномиальное распределение, распределение Пуассона. Равномерное и показательное распределения, функция надёжности.
9. Нормальное распределение.
10. Понятие о предельных теоремах. Закон больших чисел, центральная предельная теорема.
по интервальному статистическому ряду построить гистограмму частот и относительных частот;
1.2 Расчётные задания
1. В урне n шаров, среди них n![]() белых,
n
белых,
n![]() чёрных,
n
чёрных,
n![]() красных (
красных (![]() ). Найти:
). Найти:
а) относительную частоту белых шаров;
б) вероятность того, что все m выбранных шаров будут белыми;
в) вероятность того, что среди m выбранных шаров
будет m![]() белых;
белых;
г) вероятность того, что среди m
выбранных шаров будет m![]() белых шаров, m
белых шаров, m![]() -
чёрных, m
-
чёрных, m![]() -
красных (
-
красных (![]() );
);
д) вероятность того, что среди m выбранных шаров будет хотя бы один белый.
|
№ |
n |
n |
n |
n |
m |
m |
m |
m |
|
1.1 |
70 |
20 |
26 |
24 |
5 |
2 |
1 |
2 |
|
1.2 |
75 |
40 |
20 |
15 |
8 |
4 |
1 |
3 |
|
1.3 |
85 |
35 |
30 |
20 |
5 |
2 |
1 |
2 |
|
1.4 |
90 |
20 |
40 |
30 |
7 |
2 |
2 |
3 |
|
1.5 |
87 |
30 |
45 |
12 |
8 |
3 |
2 |
3 |
|
1.6 |
100 |
25 |
55 |
20 |
15 |
8 |
3 |
4 |
|
1.7 |
90 |
40 |
24 |
26 |
9 |
4 |
3 |
2 |
|
1.8 |
95 |
28 |
42 |
25 |
10 |
3 |
5 |
2 |
|
1.9 |
85 |
30 |
15 |
40 |
7 |
2 |
2 |
3 |
|
1.10 |
90 |
17 |
33 |
40 |
6 |
1 |
3 |
2 |
|
1.11 |
85 |
31 |
25 |
29 |
5 |
2 |
2 |
1 |
|
1.12 |
75 |
28 |
32 |
15 |
5 |
1 |
2 |
2 |
|
1.13 |
100 |
30 |
41 |
29 |
9 |
3 |
4 |
2 |
|
1.14 |
80 |
32 |
28 |
20 |
7 |
3 |
2 |
2 |
|
1.15 |
85 |
24 |
26 |
35 |
5 |
1 |
3 |
1 |
|
1.16 |
100 |
41 |
29 |
30 |
10 |
5 |
3 |
2 |
|
1.17 |
90 |
29 |
21 |
40 |
12 |
6 |
4 |
2 |
|
1.18 |
85 |
25 |
35 |
25 |
7 |
2 |
2 |
3 |
|
1.19 |
80 |
18 |
42 |
20 |
5 |
1 |
2 |
2 |
|
1.20 |
95 |
43 |
27 |
25 |
9 |
3 |
4 |
2 |
|
1.21 |
70 |
22 |
28 |
20 |
9 |
2 |
4 |
3 |
|
1.22 |
80 |
30 |
21 |
29 |
7 |
3 |
1 |
1 |
|
1.23 |
90 |
42 |
20 |
28 |
6 |
1 |
3 |
2 |
|
1.24 |
75 |
24 |
26 |
25 |
8 |
2 |
4 |
2 |
|
1.25 |
100 |
37 |
33 |
30 |
10 |
2 |
3 |
5 |
|
1.26 |
90 |
26 |
34 |
30 |
8 |
3 |
2 |
3 |
|
1.27 |
80 |
31 |
29 |
20 |
5 |
1 |
2 |
2 |
|
1.28 |
95 |
29 |
31 |
35 |
8 |
3 |
2 |
3 |
|
1.29 |
96 |
34 |
26 |
36 |
7 |
4 |
1 |
2 |
|
1.30 |
89 |
25 |
35 |
29 |
5 |
1 |
2 |
2 |
2. Три стрелка стреляют по цели. Вероятность попадания
в цель ![]() ,
, ![]() ,
, ![]() соответственно для первого,
второго и третьего стрелка. Найти вероятность того, что:
соответственно для первого,
второго и третьего стрелка. Найти вероятность того, что:
а) все трое попадут в цель;
б) попадёт только один;
в) попадут двое, один не попадёт;
г) попадёт хотя бы один.
|
№ |
|
|
|
№ |
|
|
|
№ |
|
|
|
|
2.1 |
0.9 |
0.6 |
0.5 |
2.11 |
0.5 |
0.9 |
0.4 |
2.21 |
0.5 |
0.7 |
0.9 |
|
2.2 |
0.8 |
0.7 |
0.6 |
2.12 |
0.7 |
0.8 |
0.5 |
2.22 |
0.6 |
0.5 |
0.8 |
|
2.3 |
0.7 |
0.5 |
0.8 |
2.13 |
0.5 |
0.7 |
0.6 |
2.23 |
0.7 |
0.9 |
0.7 |
|
2.4 |
0.6 |
0.9 |
0.8 |
2.14 |
0.4 |
0.6 |
0.7 |
2.24 |
0.8 |
0.4 |
0.6 |
|
2.5 |
0.5 |
0.7 |
0.9 |
2.15 |
0.5 |
0.5 |
0.8 |
2.25 |
0.9 |
0.5 |
0.5 |
|
2.6 |
0.9 |
0.6 |
0.8 |
2.16 |
0.6 |
0.9 |
0.5 |
2.26 |
0.4 |
0.6 |
0.8 |
|
2.7 |
0.8 |
0.5 |
0.7 |
2.17 |
0.7 |
0.8 |
0.6 |
2.27 |
0.5 |
0.7 |
0.9 |
|
2.8 |
0.5 |
0.8 |
0.6 |
2.18 |
0.8 |
0.5 |
0.7 |
2.28 |
0.6 |
0.8 |
0.7 |
|
2.9 |
0.6 |
0.9 |
0.5 |
2.19 |
0.9 |
0.6 |
0.8 |
2.29 |
0.7 |
0.9 |
0.5 |
|
2.10 |
0.7 |
0.9 |
0.4 |
2.20 |
0.9 |
0.4 |
0.9 |
2.30 |
0.8 |
0.9 |
0.4 |
3. На сборку поступают детали с трёх автоматов: n![]() с
первого автомата, n
с
первого автомата, n![]() со
второго, n
со
второго, n![]() с
третьего (
с
третьего (![]() ).
Первый автомат выпускает m
).
Первый автомат выпускает m![]() %
нестандартных деталей, второй - m
%
нестандартных деталей, второй - m![]() %, третий - m
%, третий - m![]() %.
%.
Требуется:
а) найти вероятность поступления на сборку нестандартной детали;
б) на сборку поступила нестандартная деталь. Найти вероятность того, что она поступила с i – го автомата ( i =1,2,3).
|
№ |
n |
n |
m |
m |
m |
i |
№ |
n |
n |
m |
m |
m |
i |
|
3.1 |
520 |
220 |
5 |
8 |
7 |
1 |
3.16 |
100 |
250 |
7 |
8 |
5 |
1 |
|
3.2 |
270 |
410 |
10 |
5 |
9 |
2 |
3.17 |
430 |
180 |
5 |
4 |
7 |
2 |
|
3.3 |
250 |
140 |
8 |
7 |
4 |
2 |
3.18 |
170 |
540 |
6 |
5 |
8 |
3 |
|
3.4 |
190 |
380 |
5 |
9 |
30 |
1 |
3.19 |
650 |
120 |
10 |
9 |
8 |
2 |
|
3.5 |
290 |
610 |
6 |
3 |
3 |
2 |
3.20 |
400 |
180 |
7 |
10 |
5 |
1 |
|
3.6 |
270 |
430 |
10 |
6 |
4 |
2 |
3.21 |
120 |
380 |
10 |
6 |
9 |
2 |
|
3.7 |
280 |
360 |
7 |
10 |
9 |
1 |
3.22 |
270 |
340 |
9 |
5 |
4 |
3 |
|
3.8 |
520 |
110 |
5 |
7 |
10 |
1 |
3.23 |
430 |
120 |
10 |
7 |
6 |
2 |
|
3.9 |
240 |
290 |
9 |
8 |
4 |
3 |
3.24 |
360 |
120 |
5 |
10 |
8 |
1 |
|
3.10 |
310 |
410 |
7 |
2 |
5 |
3 |
3.25 |
420 |
210 |
8 |
7 |
6 |
1 |
|
3.11 |
520 |
110 |
3 |
6 |
7 |
2 |
3.26 |
370 |
130 |
10 |
6 |
5 |
2 |
|
3.12 |
280 |
310 |
9 |
8 |
4 |
2 |
3.27 |
410 |
200 |
5 |
10 |
8 |
3 |
|
3.13 |
400 |
320 |
4 |
5 |
8 |
1 |
3.28 |
280 |
510 |
10 |
6 |
5 |
3 |
|
3.14 |
350 |
240 |
9 |
8 |
7 |
1 |
3.29 |
710 |
120 |
2 |
10 |
4 |
3 |
|
3.15 |
190 |
520 |
5 |
2 |
4 |
3 |
3.30 |
460 |
240 |
5 |
9 |
7 |
1 |
4. Вероятность появления события А в каждом испытании равна р. Найти вероятность того, что в n испытаниях событие А появится:
а) ровно k![]() раз;
раз;
б) не менее k![]() раз;
раз;
в) не более k![]() раз;
раз;
г) хотя бы один раз (для нечётных вариантов, где n=10);
д) от k![]() до k
до k![]() раз
(для чётных вариантов, где n=100).
раз
(для чётных вариантов, где n=100).
|
№ |
k |
k |
p |
№ |
k |
k |
p |
№ |
k |
k |
p |
|
4.1 |
3 |
5 |
0.6 |
4.11 |
2 |
5 |
0.4 |
4.21 |
6 |
8 |
0.7 |
|
4.2 |
62 |
82 |
0.6 |
4.12 |
80 |
95 |
0.4 |
4.22 |
70 |
80 |
0.7 |
|
4.3 |
5 |
7 |
0.8 |
4.13 |
5 |
8 |
0.8 |
4.23 |
4 |
7 |
0.6 |
|
4.4 |
55 |
75 |
0.8 |
4.14 |
60 |
90 |
0.6 |
4.24 |
65 |
80 |
0.75 |
|
4.5 |
4 |
8 |
0.8 |
4.15 |
2 |
8 |
0.7 |
4.25 |
7 |
9 |
0.75 |
|
4.6 |
40 |
60 |
0.8 |
4.16 |
80 |
90 |
0.8 |
4.26 |
78 |
92 |
0.75 |
|
4.7 |
3 |
7 |
0.3 |
4.17 |
5 |
9 |
0.8 |
4.27 |
2 |
6 |
0.7 |
|
4.8 |
50 |
80 |
0.3 |
4.18 |
70 |
95 |
0.8 |
4.28 |
30 |
85 |
0.7 |
|
4.9 |
4 |
6 |
0.3 |
4.19 |
3 |
6 |
0.7 |
4.29 |
4 |
9 |
0.7 |
|
4.10 |
45 |
75 |
0.4 |
4.20 |
50 |
60 |
0.7 |
4.30 |
80 |
95 |
0.6 |
5. Дискретная случайная величина Х задана рядом распределения. Найти:
а) её функцию распределения F(x), построить график F(x);
б) математическое ожидание, дисперсию, среднее квадратическое отклонение, моду;
в) вероятность попадания Х в интервал (a;b).
|
|
Х |
х |
х |
х |
х |
х |
х |
а |
b |
|
Р |
р |
р |
р |
р |
р |
р |
|||
|
5.1
|
Х |
0 |
1 |
2 |
4 |
6 |
9 |
-2 |
7 |
|
Р |
0.05 |
0.15 |
0.3 |
0.25 |
0.15 |
0.1 |
|||
|
5.2 |
Х |
-3 |
-2 |
-1 |
0 |
2 |
4 |
-1 |
3 |
|
Р |
0.15 |
0.3 |
0.02 |
0.14 |
0.18 |
0.21 |
|||
|
5.3
|
Х |
1 |
2 |
3 |
5 |
7 |
8 |
-3 |
6 |
|
Р |
0.3 |
0.14 |
0.16 |
0.1 |
0.2 |
0.1 |
|||
|
5.4
|
Х |
-4 |
-3 |
-2 |
0 |
1 |
2 |
0 |
1 |
|
Р |
0.2 |
0.08 |
0.23 |
0.27 |
0.12 |
0.1 |
|||
|
5.5
|
Х |
1 |
2 |
4 |
5 |
7 |
9 |
3 |
8 |
|
Р |
0.19 |
0.21 |
0.06 |
0.14 |
0.12 |
0.28 |
|||
|
6.6
|
Х |
-1 |
0 |
2 |
3 |
5 |
7 |
-4 |
4 |
|
Р |
0.26 |
0.14 |
0.07 |
0.2 |
0.03 |
0.3 |
|||
|
5.7
|
Х |
-2 |
-1 |
0 |
3 |
5 |
7 |
1 |
6 |
|
Р |
0.18 |
0.09 |
0.01 |
0.2 |
0.22 |
0.3 |
|||
|
5.8 |
Х |
1 |
2 |
4 |
5 |
6 |
8 |
0 |
6 |
|
Р |
0.3 |
0.17 |
0.13 |
0.1 |
0.2 |
0.1 |
|||
|
5.9 |
Х |
1 |
2 |
3 |
4 |
7 |
9 |
5 |
8 |
|
Р |
0.11 |
0.29 |
0.06 |
0.14 |
0.17 |
0.23 |
|||
|
5.10 |
Х |
0 |
1 |
2 |
3 |
7 |
9 |
4 |
8 |
|
Р |
0.06 |
0.14 |
0.3 |
0.25 |
0.15 |
0.1 |
|||
|
5.11 |
Х |
-3 |
-2 |
0 |
1 |
2 |
4 |
-1 |
3 |
|
Р |
0.15 |
0.3 |
0.01 |
0.14 |
0.19 |
0.21 |
|||
|
5.12 |
Х |
-1 |
0 |
3 |
5 |
7 |
8 |
1 |
6 |
|
Р |
0.25 |
0.14 |
0.16 |
0.1 |
0.2 |
0.15 |
|||
|
5.13 |
Х |
-4 |
-3 |
-2 |
0 |
2 |
4 |
-1 |
3 |
|
Р |
0.2 |
0.07 |
0.24 |
0.26 |
0.13 |
0.1 |
|||
|
5.14 |
Х |
-3 |
-1 |
0 |
3 |
4 |
7 |
-2 |
6 |
|
Р |
0.12 |
0.09 |
0.01 |
0.2 |
0.28 |
0.3 |
|||
|
5.15 |
Х |
-1 |
0 |
1 |
3 |
7 |
8 |
2 |
6 |
|
Р |
0.26 |
0.14 |
0.15 |
0.2 |
0.1 |
0.15 |
|||
|
5.16 |
Х |
-2 |
-1 |
0 |
1 |
2 |
7 |
-3 |
5 |
|
Р |
0.17 |
0.09 |
0.01 |
0.3 |
0.23 |
0.2 |
|||
|
5.17 |
Х |
1 |
2 |
3 |
5 |
6 |
7 |
0 |
4 |
|
Р |
0.1 |
0.14 |
0.16 |
0.1 |
0.2 |
0.3 |
|||
|
5.18 |
Х |
-3 |
-1 |
0 |
3 |
5 |
6 |
-2 |
4 |
|
Р |
0.16 |
0.09 |
0.01 |
0.3 |
0.24 |
0.2 |
|||
|
5.19 |
Х |
1 |
2 |
5 |
6 |
7 |
8 |
3 |
6 |
|
Р |
0.2 |
0.15 |
0.15 |
0.1 |
0.3 |
0.1 |
|||
|
5.20 |
Х |
-1 |
0 |
2 |
4 |
7 |
8 |
1 |
5 |
|
Р |
0.23 |
0.18 |
0.12 |
0.2 |
0.1 |
0.17 |
|||
|
5.21 |
Х |
1 |
2 |
4 |
5 |
6 |
8 |
0 |
7 |
|
Р |
0.3 |
0.14 |
0.16 |
0.03 |
0.2 |
0.17 |
|||
|
5.22 |
Х |
-4 |
-3 |
-1 |
0 |
1 |
3 |
-2 |
2 |
|
Р |
0.2 |
0.03 |
0.24 |
0.26 |
0.17 |
0.1 |
|||
|
5.23 |
Х |
1 |
2 |
3 |
4 |
7 |
9 |
0 |
8 |
|
Р |
0.17 |
0.23 |
0.09 |
0.11 |
0.12 |
0.28 |
|||
|
5.24 |
Х |
0 |
1 |
3 |
5 |
7 |
8 |
2 |
6 |
|
Р |
0.2 |
0.14 |
0.16 |
0.12 |
0.3 |
0.08 |
|||
|
5.25 |
Х |
-5 |
-3 |
-2 |
0 |
1 |
3 |
-4 |
2 |
|
Р |
0.2 |
0.06 |
0.21 |
0.29 |
0.14 |
0.1 |
|||
|
5.26 |
Х |
1 |
2 |
3 |
5 |
8 |
9 |
4 |
7 |
|
Р |
0.18 |
0.22 |
0.05 |
0.15 |
0.12 |
0.28 |
|||
|
5.27 |
Х |
1 |
3 |
4 |
5 |
7 |
8 |
2 |
6 |
|
Р |
0.3 |
0.16 |
0.14 |
0.01 |
0.2 |
0.19 |
|||
|
5.28 |
Х |
-5 |
-3 |
-1 |
0 |
1 |
3 |
-4 |
2 |
|
Р |
0.1 |
0.03 |
0.14 |
0.36 |
0.17 |
0.2 |
|||
|
5.29 |
Х |
0 |
2 |
3 |
4 |
6 |
8 |
1 |
7 |
|
Р |
0.26 |
0.14 |
0.05 |
0.15 |
0.12 |
0.28 |
|||
|
5.30 |
Х |
-1 |
0 |
2 |
3 |
7 |
8 |
1 |
6 |
|
Р |
0.21 |
0.16 |
0.14 |
0.1 |
0.2 |
0.19 |
6. Непрерывная случайная величина Х задана плотностью распределения f(x).
Найти:
а) её функцию распределения F(x);
б) математическое ожидание, дисперсию, среднее квадратическое отклонение, моду, медиану;
в) вероятность попадания Х в интервал (a;b).
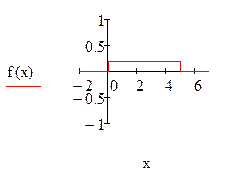
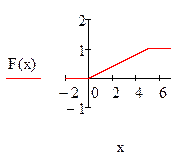
Построить графики F(x) и f(x).
|
№ |
f(x) |
а |
b |
№ |
f(x) |
а |
b |
|
6.1 |
|
1 |
3 |
6.16 |
|
-1 |
2 |
|
6.2 |
|
-2,5 |
0 |
6.17 |
|
0 |
|
|
6.3 |
|
0 |
|
6.18 |
|
0 |
1,5 |
|
6.4 |
|
0 |
|
6.19 |
|
1 |
2,5 |
|
6.5 |
|
0 |
|
6.20 |
|
0,1 |
1 |
|
6.6 |
|
0 |
|
6.21 |
|
0 |
1 |
|
6.7 |
|
1 |
2 |
6.22 |
|
|
1 |
|
6.8 |
|
3 |
4,5 |
6.23 |
|
2 |
4 |
|
6.9 |
|
0 |
|
6.24 |
|
0 |
|
|
6.10 |
|
1,5 |
2 |
6.25 |
|
0 |
1,5 |
|
6.11 |
|
|
|
6.26 |
|
0 |
1 |
|
6.12 |
|
1 |
3 |
6.27 |
|
1 |
4 |
|
6.13 |
|
-1 |
1 |
6.28 |
|
|
|
|
6.14 |
|
0,2 |
1,2 |
6.29 |
|
0 |
2 |
|
6.15 |
|
0 |
|
6.30 |
|
2 |
3 |
Биномиальное распределение.
7. Среди N отобранных деталей m% нестандартных. Составить закон распределения числа нестандартных деталей среди отобранных (случайная величина Х ). Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
|
№ |
N |
m |
№ |
N |
m |
№ |
N |
m |
|
7.1 |
3 |
10 |
7.11 |
4 |
15 |
7.21 |
3 |
11 |
|
7.2 |
2 |
12 |
7.12 |
5 |
13 |
7.22 |
2 |
16 |
|
7.3 |
4 |
20 |
7.13 |
3 |
14 |
7.23 |
4 |
29 |
|
7.4 |
5 |
25 |
7.14 |
2 |
20 |
7.24 |
5 |
10 |
|
7.5 |
3 |
30 |
7.15 |
4 |
27 |
7.25 |
3 |
17 |
|
7.6 |
2 |
10 |
7.16 |
5 |
20 |
7.26 |
2 |
21 |
|
7.7 |
4 |
15 |
7.17 |
3 |
19 |
7.27 |
4 |
22 |
|
7.8 |
5 |
17 |
7.18 |
2 |
23 |
7.28 |
5 |
24 |
|
7.9 |
3 |
12 |
7.19 |
4 |
11 |
7.29 |
3 |
18 |
|
7.10 |
2 |
15 |
7.20 |
5 |
28 |
7.30 |
2 |
22 |
Распределение Пуассона .
8. Радиоаппаратура состоит из N элементов. Вероятность отказа одного элемента в течение одного года работы равна р и не зависит от состояния других элементов. Требуется:
а) составить закон распределения числа отказавших элементов;
б) найти вероятность отказа не менее m элементов в год.
|
№ |
N |
m |
р |
№ |
N |
m |
р |
№ |
N |
m |
р |
|
8.1 |
2000 |
4 |
0,001 |
8.11 |
1500 |
6 |
0,005 |
8.21 |
1000 |
6 |
0,005 |
|
8.2 |
1000 |
5 |
0,007 |
8.12 |
4000 |
2 |
0,006 |
8.22 |
4500 |
2 |
0,003 |
|
8.3 |
3000 |
7 |
0,004 |
8.13 |
8000 |
2 |
0,001 |
8.23 |
2000 |
4 |
0,001 |
|
8.4 |
2000 |
5 |
0,002 |
8.14 |
6500 |
6 |
0,002 |
8.24 |
1000 |
5 |
0,007 |
|
8.5 |
1000 |
6 |
0,005 |
8.15 |
3000 |
2 |
0,005 |
8.25 |
3000 |
7 |
0,004 |
|
8.6 |
5000 |
2 |
0,001 |
8.16 |
1500 |
3 |
0,002 |
8.26 |
2000 |
5 |
0,002 |
|
8.7 |
2000 |
4 |
0,001 |
8.17 |
2000 |
4 |
0,001 |
8.27 |
1000 |
6 |
0,005 |
|
8.8 |
1500 |
5 |
0,008 |
8.18 |
1000 |
5 |
0,007 |
8.28 |
6500 |
8 |
0,007 |
|
8.9 |
3500 |
7 |
0,004 |
8.19 |
3500 |
1 |
0,002 |
8.29 |
7000 |
6 |
0,002 |
|
8.10 |
2000 |
2 |
0,003 |
8.20 |
2000 |
5 |
0,001 |
8.30 |
5500 |
9 |
0,004 |
Равномерное распределение.
9. а. Варианты 1-15.
Цена деления измерительного прибора равна a. Показания прибора округляются до ближайшего целого деления. Случайная величина Х – ошибка при округлении отсчёта. Найти:
а) её плотность распределения f(x);
б) функцию распределения F(x);
в) математическое ожидание, дисперсию;
г) вероятность того, что при отсчёте будет сделана ошибка, меньшая (большая) m.
Построить графики F(x) и f(x).
9. б. Варианты 16 - 30
Трамваи некоторого маршрута идут строго по расписанию. Интервал движения а минут. Случайная величина Х – время ожидания трамвая. Найти:
а) её плотность распределения f(x);
б) функцию распределения F(x);
в) математическое ожидание, дисперсию;
г) вероятность того, что пассажир, подошедший к остановке, будет ожидать трамвай менее (более) m минут.
Построить графики F(x) и f(x).
|
№ |
а |
m |
№ |
а |
m |
№ |
а |
m |
|
9.1 |
0,2 |
0,04 |
9.11 |
0,3 |
0,08 |
9.21 |
19 |
8 |
|
9.2 |
0,3 |
0,02 |
9.12 |
0,6 |
0,01 |
9.22 |
20 |
5 |
|
9.3 |
0,1 |
0,06 |
9.13 |
0,9 |
0,06 |
9.23 |
25 |
5 |
|
9.4 |
0,5 |
0,01 |
9.14 |
0,5 |
0,05 |
9.24 |
9 |
3 |
|
9.5 |
0,6 |
0,05 |
9.15 |
0,8 |
0,07 |
9.25 |
14 |
7 |
|
9.6 |
0,9 |
0,02 |
9.16 |
5 |
3 |
9.26 |
18 |
9 |
|
9.7 |
0,1 |
0,08 |
9.17 |
10 |
4 |
9.27 |
24 |
8 |
|
9.8 |
0,7 |
0,01 |
9.18 |
15 |
5 |
9.28 |
6 |
3 |
|
9.9 |
0,4 |
0,06 |
9.19 |
6 |
2 |
9.29 |
12 |
6 |
|
9.10 |
0,5 |
0,07 |
9.20 |
20 |
10 |
9.30 |
16 |
8 |
Показательное распределение.
10. Время безотказной работы элемента (случайная
величина Т) имеет показательное распределение с параметром ![]() , где
, где
![]() -
интенсивность отказов, т.е. среднее число отказов в единицу времени.
-
интенсивность отказов, т.е. среднее число отказов в единицу времени.
Найти:
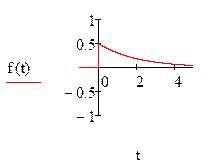
а) плотность распределения f(t);
б) функцию распределения F(t), указать её вероятностный смысл;
в) функцию надёжности R(t), указать её вероятностный смысл;
г) математическое ожидание, дисперсию;
д) вероятность того, что за время t элемент откажет и вероятность того, что за время t элемент не откажет.
Построить графики F(t), R(t) и f(t).
|
№ |
|
t |
№ |
|
t |
№ |
|
t |
|
10.1 |
1 |
5 |
10.11 |
2 |
5 |
10.21 |
3 |
8 |
|
10.2 |
2 |
10 |
10.12 |
3 |
10 |
10.22 |
4 |
4 |
|
10.3 |
3 |
6 |
10.13 |
4 |
6 |
10.23 |
6 |
3 |
|
10.4 |
4 |
8 |
10.14 |
6 |
8 |
10.24 |
7 |
2 |
|
10.5 |
6 |
4 |
10.15 |
7 |
4 |
10.25 |
8 |
1 |
|
10.6 |
7 |
3 |
10.16 |
8 |
3 |
10.26 |
9 |
10 |
|
10.7 |
8 |
2 |
10.17 |
9 |
2 |
10.27 |
10 |
6 |
|
10.8 |
9 |
1 |
10.18 |
10 |
1 |
10.28 |
1 |
7 |
|
10.9 |
10 |
7 |
10.19 |
1 |
10 |
10.29 |
2 |
8 |
|
10.10 |
1 |
9 |
10.20 |
2 |
6 |
10.30 |
3 |
2 |
Нормальный закон распределения.
11. Случайная ошибка измерения (случайная величина Х)
подчинена нормальному закону распределения с параметрами а и ![]() .
.
Найти:
а) плотность распределения f(х);
б) функцию распределения F(х);
в) математическое ожидание, дисперсию;
г) вероятность попадания в интервал ![]() ;
;
д) вероятность того, что измерение будет произведено с
ошибкой, не превосходящей по абсолютной величине ![]() .
.
Построить графики F(t) и f(t).
|
№ |
а |
|
|
|
|
№ |
а |
|
|
|
|
|
11.1 |
10 |
1 |
8 |
14 |
2 |
11.16 |
10 |
2 |
9 |
14 |
2 |
|
11.2 |
12 |
2 |
7 |
14 |
3 |
11.17 |
12 |
4 |
5 |
14 |
3 |
|
11.3 |
14 |
3 |
10 |
15 |
5 |
11.18 |
14 |
1 |
9 |
15 |
5 |
|
11.4 |
11 |
5 |
9 |
12 |
3 |
11.19 |
11 |
6 |
8 |
12 |
3 |
|
11.5 |
13 |
2 |
6 |
13 |
2 |
11.20 |
13 |
4 |
6 |
17 |
2 |
|
11.6 |
12 |
3 |
7 |
15 |
4 |
11.21 |
12 |
9 |
8 |
15 |
4 |
|
11.7 |
10 |
2 |
8 |
17 |
2 |
11.22 |
10 |
3 |
6 |
17 |
2 |
|
11.8 |
12 |
4 |
6 |
14 |
6 |
11.23 |
12 |
5 |
6 |
13 |
6 |
|
11.9 |
14 |
6 |
11 |
19 |
5 |
11.24 |
14 |
2 |
12 |
19 |
5 |
|
11.10 |
15 |
5 |
8 |
12 |
3 |
11.25 |
15 |
3 |
4 |
12 |
3 |
|
11.11 |
17 |
4 |
6 |
14 |
2 |
11.26 |
17 |
1 |
5 |
14 |
2 |
|
11.12 |
12 |
5 |
7 |
18 |
4 |
11.27 |
12 |
4 |
9 |
18 |
4 |
|
11.13 |
18 |
5 |
6 |
12 |
3 |
11.28 |
11 |
3 |
4 |
12 |
3 |
|
11.14 |
10 |
4 |
6 |
15 |
2 |
11.29 |
17 |
2 |
5 |
19 |
5 |
|
11.15 |
12 |
3 |
5 |
18 |
4 |
11.30 |
13 |
5 |
6 |
18 |
3 |
1.3 Решение типового варианта
1. В урне 120 шаров, среди них 40 белых, 50 чёрных, 30 красных. Найти:
а) относительную частоту белых шаров;
б) вероятность того, что все 20 выбранных шаров будут белыми;
в) вероятность того, что среди 20 выбранных шаров будет 9 белых;
г) вероятность того, что среди 20 выбранных шаров будет 9 белых шаров, 6 - чёрных, 5 – красных;
д) вероятность того, что среди 20 выбранных шаров будет хотя бы один белый.
Решение:
а) относительной частотой события А
(обозначается Р![]() (А)) называется отношение числа m испытаний,
в которых событие А появилось, к общему
(А)) называется отношение числа m испытаний,
в которых событие А появилось, к общему
числу
n произведённых испытаний: Р![]() (А)
= m/ n.
(А)
= m/ n.
Пусть событие А – выбор белого шара, тогда Р![]() (А)
= 40/120 = 1/3.
(А)
= 40/120 = 1/3.
В остальных пунктах используем классическое определение вероятности события А: Р(А) = m/ n, где m – число испытаний, благоприятствующих появлению события А, n – общее число испытаний;
б) пусть событие А - все 20 выбранных шаров будут белыми. Общее число элементарных событий равно числу различных
способов взять 20 шаров из 120 шаров, т.е. n = С![]() ; число
благоприятствующих событий равно числу различных способов взять из 40 белых шаров 20,
т.е. m = С
; число
благоприятствующих событий равно числу различных способов взять из 40 белых шаров 20,
т.е. m = С![]() . Таким образом, Р(А) = m/
n = С
. Таким образом, Р(А) = m/
n = С![]() / С
/ С![]() = 4,679
= 4,679![]() 10
10![]() ;
;
в) пусть событие А – среди 20 выбранных шаров будет 9 белых. Как выше сказано, n = С![]() . Число
m благоприятствующих событию А элементарных
событий находится по одному из правил комбинаторики: пусть во множестве из n
элементов имеются s подмножеств, состоящих соответственно из
. Число
m благоприятствующих событию А элементарных
событий находится по одному из правил комбинаторики: пусть во множестве из n
элементов имеются s подмножеств, состоящих соответственно из ![]() элементов (
элементов (![]() ). Тогда, если из этого множества
происходит отбор по схеме:
). Тогда, если из этого множества
происходит отбор по схеме: ![]() из
из ![]() элементов,
элементов, ![]() из
из ![]() элементов,…,
элементов,…, ![]() из
из ![]() элементов, то общее число N
способов образования s групп по
элементов, то общее число N
способов образования s групп по ![]() элементов без учёта порядка в каждой из
них равно N =
C
элементов без учёта порядка в каждой из
них равно N =
C![]() C
C![]() …C
…C![]() . Таким
образом, в этом пункте m = С
. Таким
образом, в этом пункте m = С![]() С
С![]() , где С
, где С![]() равно числу
различных способов выбрать 9 белых шаров из 40 белых, а С
равно числу
различных способов выбрать 9 белых шаров из 40 белых, а С![]() равно числу различных способов выбрать 11 не белых из 80 не белых шаров. Итак,
Р(А) = m/ n = С
равно числу различных способов выбрать 11 не белых из 80 не белых шаров. Итак,
Р(А) = m/ n = С![]() С
С![]() / С
/ С![]() =
0,097;
=
0,097;
г) пусть событие А - среди 20 выбранных наудачу
шаров 9 белых шаров, 6 - чёрных, 5 - красный. Для решения задачи также
используем классическое определение вероятности события А: Р(А)
= m/ n, где n
число всех возможных способов выбора 20 шаров из имеющихся 120, т.е. n
= С![]() . Число m,
благоприятствующих событию А элементарных событий, находится по выше
приведённому правилу комбинаторики, т.е. m = С
. Число m,
благоприятствующих событию А элементарных событий, находится по выше
приведённому правилу комбинаторики, т.е. m = С![]() С
С![]() С
С![]() .
Поэтому Р(А) = m/ n = 0,021.
.
Поэтому Р(А) = m/ n = 0,021.
д) пусть событие А – среди 20 выбранных шаров будет хотя бы один белый, тогда
противоположное событие ![]() - среди
20 выбранных шаров не будет ни одного
белого шара. Как в случае б) вероятность этого события найдём по формуле Р(
- среди
20 выбранных шаров не будет ни одного
белого шара. Как в случае б) вероятность этого события найдём по формуле Р(![]() ) = m/
n = С
) = m/
n = С![]() / С
/ С![]() = 1,2
= 1,2![]() 10
10![]() . Тогда вероятность события А равна
. Тогда вероятность события А равна ![]() , т.е. это событие
почти достоверное.
, т.е. это событие
почти достоверное.
При вычислении числа сочетаний была использована функция combin в Mathcad. Ниже приведена копия файла, в котором combin(Q,R) введена как функция пользователя C(Q,R), позволяющая получать значения сочетаний при произвольных Q и R.
![]()
|
|
![]()
|
|
|
|
|
|
![]()
![]()
2. Три стрелка стреляют по цели. Вероятность попадания в цель 0,75, 0,8, 0,9 соответственно для первого, второго и третьего стрелка. Найти вероятность того, что:
а) все трое попадут в цель;
б) попадёт только один;
в) попадут двое, один промахнётся;
г) попадёт хотя бы один.
Решение: пусть событие ![]() – попадание в цель первым стрелком,
– попадание в цель первым стрелком, ![]() – вторым,
– вторым, ![]() – третьим. По условию P(
– третьим. По условию P(![]() )=0,75, P(
)=0,75, P(![]() )=9,8, P(
)=9,8, P(![]() )=0,9.
)=0,9.
а) пусть событие А - все трое попадут в цель,
тогда ![]() и, т.к.
и, т.к.
![]() ,
, ![]() ,
,![]() события независимые, то P(А)
= P(
события независимые, то P(А)
= P(![]() ) = P(
) = P(![]() )P(
)P(![]() )P(
)P(![]() ) = =
) = =![]() = 0,54;
= 0,54;
б) пусть событие В - попадёт только один, тогда
![]() , где
, где ![]() события
противоположные
события
противоположные![]() ,
,
![]() ,
, ![]() , т.е. промах первого,
второго и третьего стрелка соответственно. Так как
, т.е. промах первого,
второго и третьего стрелка соответственно. Так как ![]() ,
, ![]() ,
, ![]()
![]() и т.к. слагаемые есть события
несовместные, то
и т.к. слагаемые есть события
несовместные, то ![]() =
=![]() = 0,08;
= 0,08;
в) событие С - попадут двое, один промахнётся
составляется аналогично, как в предыдущем пункте, т.е. ![]() . Его вероятность определяется
также аналогично:
. Его вероятность определяется
также аналогично: ![]() =
=![]() =0,3456;
=0,3456;
г) пусть событие D - попадёт
хотя бы один стрелок, рассмотрим противоположное событие ![]() - промахнутся все трое. Т.к.
- промахнутся все трое. Т.к. ![]() , то
, то ![]() =
=![]() =
=![]() =0,995.
=0,995.
3. На сборку поступают детали с трёх автоматов: n![]() =100
с первого автомата, n
=100
с первого автомата, n![]() =
300 - со второго, n
=
300 - со второго, n![]() = 1000
-
= 1000
- ![]() = 600 с третьего
(
= 600 с третьего
(![]() ). Первый
автомат выпускает 5% нестандартных деталей, второй - 4%, третий - 6%.
). Первый
автомат выпускает 5% нестандартных деталей, второй - 4%, третий - 6%.
Требуется:
а) найти вероятность поступления на сборку нестандартной детали;
б) на сборку поступила нестандартная деталь. Найти вероятность того, что она поступила со 2 – го автомата.
Решение:
пусть событие А – поступление на сборку нестандартной детали, а события В![]() ,
В
,
В![]() , В
, В![]() - деталь поступила
соответственно с первого, второго, третьего автоматов (эти события называются
гипотезами).
- деталь поступила
соответственно с первого, второго, третьего автоматов (эти события называются
гипотезами).
а)
вероятность события А находится по формуле полной вероятности: Р(А)
= Р(В![]() )Р(А/ В
)Р(А/ В![]() )+Р(В
)+Р(В![]() )Р(А/
В
)Р(А/
В![]() )+Р(В
)+Р(В![]() )Р(А/
В
)Р(А/
В![]() ), где Р(А/ В
), где Р(А/ В![]() ) –
условные вероятности того, что поступившая на сборку деталь с i–
го автомата (i=1,2,3). По условию задачи имеем: Р(В
) –
условные вероятности того, что поступившая на сборку деталь с i–
го автомата (i=1,2,3). По условию задачи имеем: Р(В![]() ) =
100/1000 = 0,1; Р(В
) =
100/1000 = 0,1; Р(В![]() ) = 300/1000 = 0,3; Р(В
) = 300/1000 = 0,3; Р(В![]() )
= 600/1000 = 0,6; Р(А/ В
)
= 600/1000 = 0,6; Р(А/ В![]() )=0,05; Р(А/ В
)=0,05; Р(А/ В![]() )=0,04;
Р(А/ В
)=0,04;
Р(А/ В![]() )=0,06. Поэтому Р(А) =
)=0,06. Поэтому Р(А) = ![]() =
0,053;
=
0,053;
б)
в этом пункте требуется найти условную вероятность Р(В![]() /А). Используем для этого формулу Байеса:
/А). Используем для этого формулу Байеса: 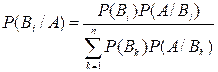 ,
,![]() .
.
В
нашем случае 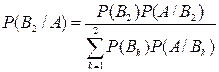 =
=
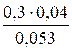 =
0,226.
=
0,226.
4. Вероятность появления события А в каждом испытании равна 0,8. Найти вероятность того, что в n испытаниях событие А появится:
а) ровно k![]() раз (событие А);
раз (событие А);
б) не менее k![]() раз (событие В);
раз (событие В);
в) не более k![]() раз (событие С);
раз (событие С);
г) хотя бы один раз (для нечётных вариантов, где n=10) (событие D);
д) от k![]() до k
до k![]() раз
(для чётных вариантов, где n=100) (событие E).
раз
(для чётных вариантов, где n=100) (событие E).
Решение: в этой задаче требуется найти вероятность
того, что в n испытаниях событие А появится k
раз, обозначается ![]() .
В зависимости от условий задачи, к её решению подходят по-разному:
.
В зависимости от условий задачи, к её решению подходят по-разному:
- пусть n =10, k![]() =9,
k
=9,
k![]() =2 (для
нечётных вариантов). Здесь n не велико, поэтому искомую вероятность
события А можно найти точно по формуле Бернулли:
=2 (для
нечётных вариантов). Здесь n не велико, поэтому искомую вероятность
события А можно найти точно по формуле Бернулли: ![]() , где
, где
![]() ,
, ![]() . Вероятности
событий В и С определяются как суммы вероятностей:
. Вероятности
событий В и С определяются как суммы вероятностей: ![]() -
вероятность того, что событие произойдёт не менее, чем
-
вероятность того, что событие произойдёт не менее, чем ![]() раз в
раз в
![]() независимых
испытаниях, т.е. или
независимых
испытаниях, т.е. или ![]() , или
, или ![]() +1,…, или
+1,…, или ![]() раз;
раз;
![]() -
вероятность того, что событие произойдёт не более
-
вероятность того, что событие произойдёт не более ![]() раз в
раз в
![]() независимых
испытаниях, т.е. или 0, или 1, или 2,…, или
независимых
испытаниях, т.е. или 0, или 1, или 2,…, или ![]() раз.
Эти вероятности называют комулятивными (накопленными). Таким образом,
раз.
Эти вероятности называют комулятивными (накопленными). Таким образом,
а) Р(А)=![]() =
=![]() ;
;
б)
![]()
![]()
![]() ;
;
в)
![]()
![]() 0,96;
0,96;
г) рассмотрим событие ![]() , противоположное D.
, противоположное D.
![]() - в серии из
10 независимых испытаний событие А не появилось ни разу. Тогда
- в серии из
10 независимых испытаний событие А не появилось ни разу. Тогда ![]() =
=![]()
![]() 0,566;
0,566;
Ниже приведена копия файла из Mathcad с вычислениями.
|
|
![]()
![]()
![]()
![]()
- пусть n =100, k![]() =70,
k
=70,
k![]() =80 (для
чётных вариантов). Поскольку число независимых испытаний
=80 (для
чётных вариантов). Поскольку число независимых испытаний ![]() велико, то вероятность
велико, то вероятность ![]() появления события А
появления события А ![]() раз в
раз в
![]() испытаниях
определяется по локальной теореме Муавра-Лапласа и приближённо равна:
испытаниях
определяется по локальной теореме Муавра-Лапласа и приближённо равна: 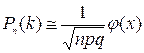 , где
, где
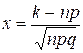 ,
, ![]() ,
, ![]() (значения
этой функции находят из таблиц или с помощью встроенной функции dnorm
в системе Mathcad).
(значения
этой функции находят из таблиц или с помощью встроенной функции dnorm
в системе Mathcad).
Для определения вероятностей событий В, С
и Е используют интегральную теорему Муавра-Лапласа: вероятность ![]() того,
что число
того,
что число ![]() появления некоторого события будет находится в промежутке от
появления некоторого события будет находится в промежутке от ![]() до
до ![]() приближённо
равна:
приближённо
равна: ![]() , где
, где  ,
, 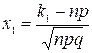 ,
, ![]() - функция Лапласа, значения которой находятся из
специальных таблиц или с помощью встроенной функции pnorm в системе Mathcad.
- функция Лапласа, значения которой находятся из
специальных таблиц или с помощью встроенной функции pnorm в системе Mathcad.
а) Р(А)=![]() ;
; ![]() =-2,5;
=-2,5;
б)
Р(В)=![]() ;
; ![]() ;
;
в)
Р(С)=![]() ;
; ![]() ;
;
д)
Р(Е)=![]() ,
, ![]() ,
, ![]() .
.
Ниже приведена копия файла, в котором сделаны вычисления в системе Mathcad.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]() ,
,
![]() ,
,
или другой вариант
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- известна ещё одна формула для определения
вероятности ![]() , которую применяют, если
, которую применяют, если ![]() велико,
велико, ![]() мало,
а произведение
мало,
а произведение ![]() - небольшое число. Это формула Пуассона
- небольшое число. Это формула Пуассона ![]() .
.
Пусть ![]() =1000,
=1000, ![]() =6,
=6, ![]() =0,003,
=0,003, ![]() , поэтому
, поэтому
Р(А)
= =![]() =0,05.
=0,05.
|
|
При вычислении можно использовать таблицу значений
функции ![]() , приводимую в некоторых учебниках, или функцию dpois в Mathcad. Ниже приведена копия файла, в котором проведены
вычисления в Mathcad.
, приводимую в некоторых учебниках, или функцию dpois в Mathcad. Ниже приведена копия файла, в котором проведены
вычисления в Mathcad.
|
|
5. Дискретная случайная величина Х задана рядом распределения.
|
Х |
0 |
10 |
20 |
30 |
40 |
50 |
|
Р |
0,05 |
0,15 |
0,3 |
0,25 |
0,2 |
0,05 |
Найти:
а) её функцию распределения F(x), построить график F(x);
б) математическое ожидание, дисперсию, среднее квадратическое отклонение, моду;
в) вероятность попадания Х в интервал (15;45).
Решение:
а) функция распределения F(x)
(интегральная функция распределения) случайной величины Х определяет
вероятность события Х<х. Для дискретной случайной величины она
находится по формуле ![]() = =
= =![]() , где суммирование распространяется на все те
, где суммирование распространяется на все те ![]() ,
которые меньше
,
которые меньше ![]() .
.
Итак:
- если ![]() , то
, то ![]() ;
;
-
если ![]() , то
, то ![]() ;
;
-
если ![]() , то
, то ![]() ;
;
-
если ![]() , то
, то
![]()
![]() ;
;
-
если ![]() , то
, то
![]()
![]() ;
;
-
если ![]() , то
, то
![]() +
+![]()
![]() ;
;
-
если ![]() , то
, то ![]() + +
+ +![]()
![]() .
.
Таким
образом, 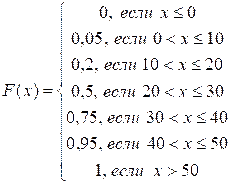 .
.
График F(x) построен в системе Mathcad (см. ниже).
б) найдём числовые характеристики. Для дискретной
случайной величины математическое ожидание равно сумме произведений всех её
возможных значений на вероятности этих значений: ![]() .
Поэтому
.
Поэтому
![]() 25,5.
25,5.
Дисперсия случайной величины Х находится либо
по формуле ![]() , либо по формуле
, либо по формуле ![]() . Для
дискретной случайной величины эти формулы перепишутся так:
. Для
дискретной случайной величины эти формулы перепишутся так: ![]() или
или ![]() .
Среднее квадратическое отклонение равно
.
Среднее квадратическое отклонение равно ![]() ;
мода дискретной случайной величины (обозначается
;
мода дискретной случайной величины (обозначается ![]() ) –
это её значение, принимаемое с наибольшей вероятностью; вероятность попадания Х
в интервал (а;b) находится по формуле
) –
это её значение, принимаемое с наибольшей вероятностью; вероятность попадания Х
в интервал (а;b) находится по формуле ![]() . В
нашей задаче эти величины равны:
. В
нашей задаче эти величины равны:
D(x)=154,75;
![]() ;
; ![]() =20;
=20;
![]() =0,75.
=0,75.
Ниже приведена копия файла, в котором сделаны вычисления в системе Mathcad, причём вычисление дисперсии проведено по обеим формулам.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. Непрерывная случайная величина Х задана плотностью распределения 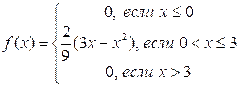 .
.
Найти:
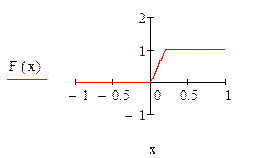
а) её функцию распределения F(x);
б) математическое ожидание, дисперсию, среднее квадратическое отклонение, моду, медиану;
в) вероятность попадания Х в интервал (1;4).
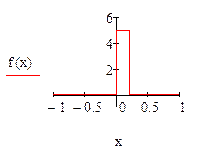
Построить графики F(x) и f(x).
Решение:
а) функцию распределения находим по формуле ![]() .
Итак: - если
.
Итак: - если ![]() , то
, то ![]() , поэтому
, поэтому ![]() ;
;
-
если ![]() , то
, то ![]() = -
= - ![]() ;
;
-
если ![]() , то
, то ![]() .
.
Таким образом, искомая функция распределения имеет вид
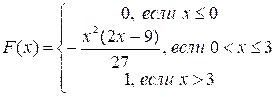 ;
;
б) числовые характеристики непрерывных случайных
величин находятся по формулам: математическое ожидание - 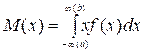 ;
дисперсия -
;
дисперсия -  или
или 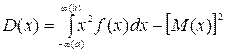 (пределы интегрирования зависят от того, принадлежат
ли возможные значения случайной величины всей оси Ох или интервалу (a;b));
среднее квадратическое отклонение -
(пределы интегрирования зависят от того, принадлежат
ли возможные значения случайной величины всей оси Ох или интервалу (a;b));
среднее квадратическое отклонение - ![]() ; модой непрерывной случайной величины
; модой непрерывной случайной величины ![]() называется
то её значение
называется
то её значение ![]() , при котором плотность распределения максимальна;
медианой непрерывной случайной величины
, при котором плотность распределения максимальна;
медианой непрерывной случайной величины ![]() называется
такое её значение
называется
такое её значение ![]() , для которого одинаково вероятно, окажется ли
случайная величина меньше или больше
, для которого одинаково вероятно, окажется ли
случайная величина меньше или больше ![]() , т.е.
, т.е. ![]() .
.
Таким образом, в нашей задаче ![]() =1,5;
=1,5;
![]() 0,45;
0,45;
![]() = 0,671.
= 0,671.
Для определения моды надо найти максимум функции ![]() на
отрезке [0; 3]. Для этого находим производную и приравниваем её к нулю:
на
отрезке [0; 3]. Для этого находим производную и приравниваем её к нулю: ![]() ,
, ![]() при х=3/2,
эта точка критическая. Проверяем её на экстремум:
при х=3/2,
эта точка критическая. Проверяем её на экстремум: ![]() . Итак,
при переходе через точку х=3/2 знак производной сменился с плюса на
минус, значит, х=3/2 точка максимума, поэтому
. Итак,
при переходе через точку х=3/2 знак производной сменился с плюса на
минус, значит, х=3/2 точка максимума, поэтому ![]() =3/2.
=3/2.
Медиану находим из условия ![]() , где
, где
![]() = =
= =![]()
![]() . Так как
. Так как ![]()
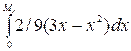 = = -
= = -![]() , то, решая
уравнение -
, то, решая
уравнение -![]() =0,5, получим три корня, из которых подходит один:
=0,5, получим три корня, из которых подходит один: ![]() = 1,5.
= 1,5.
Ниже приведёна копия файла с вычислениями в системе Mathcad.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) вероятность попадания Х в интервал (1;4)
равна ![]()
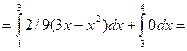 0,741
0,741
или
![]()
![]() =
= ![]()
![]() =
= ![]() = 0,74.
= 0,74.
|
|
Ниже приведёна копия файла из Mathcad с вычислениями.
|
|
|
|
|
|
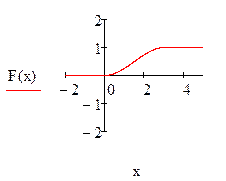
Графики функций F(x) и f(x) построим в системе Mathcad:
|
|
|
|
|
|
|
|
7. Среди 6 отобранных деталей 25% нестандартных. Составить закон
распределения числа нестандартных деталей среди отобранных (случайная величина Х ). Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
Решение: дискретная случайная величина Х –
число нестандартных деталей среди отобранных. Её возможные значения: ![]() (нет
нестандартных деталей среди отобранных),
(нет
нестандартных деталей среди отобранных), ![]() (одна нестандартная деталь среди
отобранных) и т.д.
(одна нестандартная деталь среди
отобранных) и т.д. ![]() (шесть
нестандартных деталей среди отобранных). Возможные значения независимы и
вероятность появления каждого из них одинакова и равна р=0,25, поэтому
случайная величина Х распределена по биномиальному закону:
(шесть
нестандартных деталей среди отобранных). Возможные значения независимы и
вероятность появления каждого из них одинакова и равна р=0,25, поэтому
случайная величина Х распределена по биномиальному закону: ![]() , где
, где
![]() ,
, ![]() ,
, ![]() .
.
Итак, ![]() =0,178;
=0,178;
![]() =0,356;
=0,356; ![]() =0,297;
=0,297;
![]() =0,132;
=0,132; ![]() =0,033;
=0,033;
![]() =0,004;
=0,004; ![]() =0,0002.
=0,0002.
Искомый закон распределения:
|
Х |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
р |
0,178 |
0,356 |
0,297 |
0,132 |
0,033 |
0,004 |
0,0002 |
Числовые характеристики биномиального распределения можно определить по известным формулам для дискретных случайных величин:
![]() ,
, ![]() или
или ![]() . Однако
проще воспользоваться свойствами математического ожидания и дисперсии, когда Х
– число появления события в n испытаниях:
. Однако
проще воспользоваться свойствами математического ожидания и дисперсии, когда Х
– число появления события в n испытаниях: ![]() ,
, ![]() . Итак, в нашем случае
. Итак, в нашем случае ![]() ,
, ![]() .
. ![]()
![]() 1,06.
1,06.
Ниже приведена копия файла из Mathcad с вычислениями.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Анализ биномиального распределения удобно проводить в среде Mathcad с использованием специальных функций с корневым словом binom (dbinom, pbinom, qbinom, rbinom). Например, функция dbinom(k,n,p) выводит значения вероятностей и т.д.
8. Радиоаппаратура состоит из 1000 элементов. Вероятность отказа одного элемента в течение одного года работы равна 0,001 и не зависит от состояния других элементов.
Требуется:
а) составить закон распределения числа отказавших элементов;
б) найти вероятность отказа не менее 2 элементов в год.
Решение:
а) дискретная случайная величина Х – число
отказавших элементов распределена по закону Пуассона (предельный для
биномиального закон распределения, когда вероятность р появления события
в каждом испытании мала, а число n проводимых испытаний
велико): ![]() , где
, где ![]() =
=![]() =1,
=1, ![]() ,
, ![]() .
.
Таким
образом, ![]() =0,368;
=0,368; ![]() = 0,368;
= 0,368; ![]() =0,184;
=0,184;
![]() 0,061, и т.д.
0,061, и т.д. ![]() =0,0000001
и т.д. Искомый закон распределения:
=0,0000001
и т.д. Искомый закон распределения:
|
Х |
0 |
1 |
2 |
3 |
… |
10 |
… |
|
р |
0,368 |
0,368 |
0,184 |
0,061 |
… |
0,0000001 |
… |
Ниже приведена копия файла из Mathcad с вычислениями.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) вероятность отказа не менее двух элементов вычисляется по формуле:
![]() или
или ![]() = 1
- 0,368 - 0,368 = 0,264.
= 1
- 0,368 - 0,368 = 0,264.
В среде Mathcad закону распределения Пуассона соответствуют специальные функции с корневым словом pois (dpois, ppois, qpois, rpois). Например, функция dpois(k,n,p) выводит значения вероятностей и т.д.
9. а. Цена деления измерительного прибора равна 0,2. Показания прибора округляются до ближайшего целого деления. Случайная величина Х – ошибка при округлении отсчёта.
Найти:
а) плотность распределения f(x);
б) функцию распределения F(x);
в) математическое ожидание, дисперсию;
г) вероятность того, что при отсчёте будет сделана ошибка, меньшая (большая) 0,04.
Построить графики F(x) и f(x).
Решение: случайная
величина Х – ошибка при округлении отсчёта распределена равномерно между
двумя целыми делениями; ![]() – длина интервала, в котором заключены возможные
значения Х. Для равномерного распределения имеют место формулы:
– длина интервала, в котором заключены возможные
значения Х. Для равномерного распределения имеют место формулы:
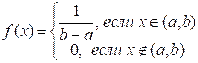 - плотность распределения;
- плотность распределения; 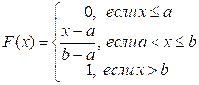 - функция
распределения;
- функция
распределения; ![]() - математическое ожидание;
- математическое ожидание; ![]() - дисперсия;
- дисперсия;
![]() - вероятность
попадания в интервал
- вероятность
попадания в интервал ![]() .
.
Поэтому в нашей задаче:
а) 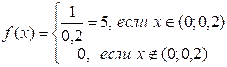 ;
;
б) 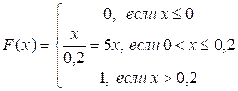 ;
;
в) ![]() ;
; ![]() ;
;
г) ясно, что при отсчёте будет сделана ошибка, меньшая
0,04,
если она попадёт в интервал (0; 0,04) или в интервал (0,16; 0,2) (событие А),
т.е. вероятность этого события равна ![]() =
=![]() +
+ ![]() =
=
=![]() =0,4;
при отсчёте будет сделана ошибка, большая 0,04, если она попадёт в интервал (0,04; 0,16) (событие В),
т.е. вероятность этого события равна
=0,4;
при отсчёте будет сделана ошибка, большая 0,04, если она попадёт в интервал (0,04; 0,16) (событие В),
т.е. вероятность этого события равна ![]() =
=![]() =
=![]() =0,6
или
=0,6
или ![]() .
.
|
|
Построим графики F(x) и f(x) в системе Mathcad.
|
|
|
|
|
|
9. б. Трамваи некоторого маршрута идут строго по расписанию. Интервал движения 5 минут. Случайная величина Х – время ожидания трамвая.
Найти:
а) плотность распределения f(x);
б) функцию распределения F(x);
в) математическое ожидание, дисперсию;
г) вероятность того, что пассажир, подошедший к остановке, будет ожидать трамвай менее (более) 3 минут.
Построить графики F(x) и f(x).
Решение: случайная
величина Х – время ожидания трамвая распределена равномерно между двумя последовательными прибытиями
автобуса; ![]() – длина интервала, в котором заключены возможные значения Х.
Все формулы для равномерного распределения смотри в предыдущей задаче 9. а.
– длина интервала, в котором заключены возможные значения Х.
Все формулы для равномерного распределения смотри в предыдущей задаче 9. а.
В нашей задаче:
а)  ;
;
б) 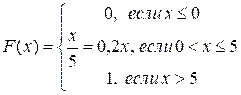 ;
;
в) ![]() ;
; ![]() ;
;
г) ясно, что пассажир будет ждать трамвай менее 3
минут, если он подойдёт к остановке в интервал времени (0; 3) или, что всё
равно, в интервал (2; 5) (событие А), т.е. вероятность этого события равна ![]() =
=![]() =
=
=![]() =0,6;
пассажир будет ждать трамвай более 3 минут, если он подойдёт к остановке в
интервал времени (0; 2) или, что всё равно, в интервал (3; 5) (событие В),
т.е. вероятность этого события равна
=0,6;
пассажир будет ждать трамвай более 3 минут, если он подойдёт к остановке в
интервал времени (0; 2) или, что всё равно, в интервал (3; 5) (событие В),
т.е. вероятность этого события равна ![]() =
= ![]() = =
= =![]() =0,4
или
=0,4
или ![]() .
.
Построим графики F(x) и f(x) в системе Mathcad.
|
|
|
|
|
|
|
|
В среде Mathcad равномерному закону распределения соответствуют специальные функции с корневым словом unif: dunif(x,a,b)– выводит значения плотности распределения; punif(x,a,b) – выводит значения функции распределения; runif(n,a,b) – выводит массив из n значений независимых случайных чисел, распределённых равномерно в интервале (a,b).
10. Время безотказной работы элемента (случайная
величина Т) имеет показательное распределение с параметром ![]() , где
, где
![]() – интенсивность отказов, т.е. среднее число отказов в единицу времени.
– интенсивность отказов, т.е. среднее число отказов в единицу времени.
Найти:
а) плотность распределения f(t);
б) функцию распределения F(t), указать её вероятностный смысл;
в) функцию надёжности R(t), указать её вероятностный смысл;
г) математическое ожидание, дисперсию;
д) вероятность того, что за время t=5 ч. элемент откажет и вероятность того, что за время t=5ч. элемент не откажет.
Построить графики F(t), R(t) и f(t).
Решение: показательным называют закон распределения
непрерывной случайной величины Х с плотностью 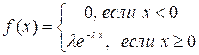 .
Другие понятия и формулы для показательного распределения:
.
Другие понятия и формулы для показательного распределения:  -
функция распределения; если случайная
величина Х=Т – время безотказной работы элемента, то
-
функция распределения; если случайная
величина Х=Т – время безотказной работы элемента, то ![]() определяет
вероятность отказа элемента за время t;
определяет
вероятность отказа элемента за время t; ![]() – функция надёжности, определяет вероятность
безотказной работы элемента за время t;
– функция надёжности, определяет вероятность
безотказной работы элемента за время t;
![]() ,
, ![]() ,
, ![]() ;
; ![]() .
.
В
нашей задаче, учитывая то, что ![]() , имеем:
, имеем:
а) ![]() ;
;
б)
![]() ,
определяет вероятность отказа элемента за время t;
,
определяет вероятность отказа элемента за время t;
в)
![]() , определяет
вероятность безотказной работы элемента за время t;
, определяет
вероятность безотказной работы элемента за время t;
г) 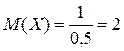 ;
; 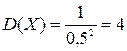 ;
;
д) поскольку функция распределения определяет
вероятность отказа за время t, то, подставив в неё t=5, получим
вероятность отказа за время t=5ч: ![]() =0,918; события «элемент откажет» и «элемент не
откажет» - противоположные, поэтому вероятность безотказной работы элемента за
время t=5 равна 1-0,918=0,082. Этот же результат можно
получить непосредственно, пользуясь функцией надёжности:
=0,918; события «элемент откажет» и «элемент не
откажет» - противоположные, поэтому вероятность безотказной работы элемента за
время t=5 равна 1-0,918=0,082. Этот же результат можно
получить непосредственно, пользуясь функцией надёжности: ![]() =0,082.
=0,082.
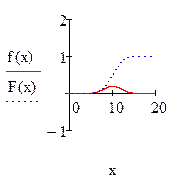
Построим графики F(t), R(t) и f(t) и сделаем некоторые вычисления в системе Mathcad:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В среде Mathcad показательному закону
распределения соответствуют специальные функции с корневым словом exp: dexp(x,![]() ) –
выводит значения плотности распределения; pexp(x,
) –
выводит значения плотности распределения; pexp(x,![]() ) –
выводит значения функции распределения; rexp(n,
) –
выводит значения функции распределения; rexp(n,
![]() ) –
выводит массив из n значений независимых случайных чисел, распределённых
по показательному закону с параметром
) –
выводит массив из n значений независимых случайных чисел, распределённых
по показательному закону с параметром ![]() .
.
11. Случайная ошибка измерения (случайная величина Х)
подчинена нормальному закону распределения с параметрами а=10 и ![]() =2.
=2.
Найти:
а) плотность распределения f(х);
б) функцию распределения F(х);
в) математическое ожидание, дисперсию;
г) вероятность попадания в интервал ![]() ;
;
д) вероятность того, что измерение будет произведено с
ошибкой, не превосходящей по абсолютной величине ![]() =3.
=3.
Построить графики F(х) и f(х).
Решение: нормальным называют закон распределения
непрерывной случайной величины Х с плотностью 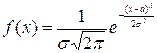 , где
а =M(Х) – математическое ожидание,
, где
а =M(Х) – математическое ожидание, ![]()
![]() – среднее квадратическое отклонение Х. Другие понятия и формулы для нормального
распределения: функция распределения –
– среднее квадратическое отклонение Х. Другие понятия и формулы для нормального
распределения: функция распределения – ![]()
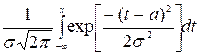 или
или  , где
, где
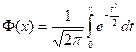 –
функция Лапласа, её значения табулированы или их можно найти в системе Mathcad
;
–
функция Лапласа, её значения табулированы или их можно найти в системе Mathcad
;
![]()
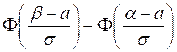 ;
;
вероятность
того, что случайная величина отклонится от своего математического ожидания не
более чем на ![]() , находится по формуле:
, находится по формуле: 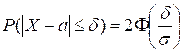 .
.
В нашей задаче:
а)
 ;
;
б)
 ;
;
в)
![]() ,
, ![]() ,
, ![]() ;
;
г)
![]()
 =
=![]() =0,4772-0,3413=0,1359;
=0,4772-0,3413=0,1359;
д) вероятность того, что измерение произведено с
ошибкой, не превосходящей по абсолютной величине ![]() =3,
будет равна
=3,
будет равна 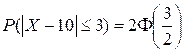 =
= ![]() =0,4332.
=0,4332.
Здесь значения функции Лапласа взяты из таблицы, хотя их можно было бы найти в системе Mathcad,
где нормальному закону распределения
соответствуют функции, в названии имеющие корневое слово norm
и начинающиеся с букв d, p, q, r. Например, dnorm (x,a,![]() ) –
выводит значения плотности распределения f(x);
pnorm (x,a,
) –
выводит значения плотности распределения f(x);
pnorm (x,a,![]() ) – выводит значения функции распределения F(x).
Воспользуемся этими функциями для построения соответствующих графиков. Копия файла из Mathcad
приведена ниже.
) – выводит значения функции распределения F(x).
Воспользуемся этими функциями для построения соответствующих графиков. Копия файла из Mathcad
приведена ниже.
|
|
|
|
|
|
2 Расчётно-графическая работа №2. Элементы математической статистики
Цели: изучить основные задачи математической статистики: задачи обработки и анализа результатов наблюдений случайных массовых явлений.
2.1 Теоретические вопросы
1. Предмет математической статистики и её основные задачи. Основные понятия (выборка, объём выборки, варианты, статистический ряд, интервальный ряд).
2. Эмпирическая функция распределения, полигон, гистограмма.
3. Определение неизвестных параметров распределения (выборочная средняя, выборочная и исправленная выборочная дисперсии).
4. Точечные и интервальные оценки параметров распределения.
5. Точность и надёжность оценки. Доверительный интервал.
6. Доверительный интервал для оценки математического
ожидания нормально распределённой случайной величины с известным ![]() .
.
7. Доверительный интервал для оценки среднего квадратического отклонения нормально распределённой случайной величины.
8. Понятие корреляционной зависимости. Функции и линии регрессии.
2.2 Расчётные задания
1. Для данной выборки выполнить задачу обработки и систематизации, определить:
а) вариационный ряд (выборку в порядке возрастания);
б) статистические ряды частот и относительных частот;
в) интервальные статистические ряды частот и относительных частот (минимальную и максимальную варианты, размах выборки, число интервалов, длину интервалов);
г) дискретные (группированные) статистические ряды частот и относительных частот.
2. Для данной выборки выполнить задачу анализа и оценки, определить:
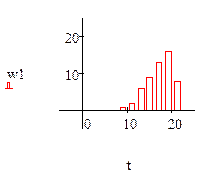
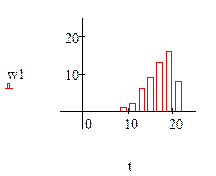
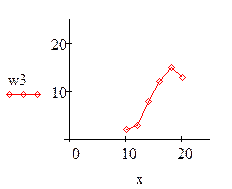
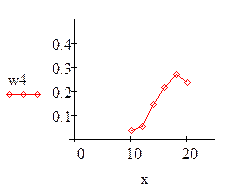
а) по интервальному статистическому ряду построить гистограмму частот и относительных частот;
б) по дискретному статистическому ряду найти:
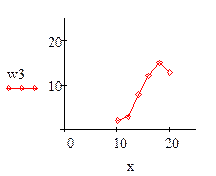
- полигон частот и относительных частот;
- эмпирическую функцию распределения;
- выборочную среднюю;
- выборочную и исправленную выборочную дисперсии;
- исправленное выборочное среднеквадратическое отклонение;
- выборочные моду и медиану,
в) по статистическим рядам частот и относительных частот найти:
- выборочные начальные моменты третьего и четвёртого порядков;
- выборочный эксцесс;
- выборочный коэффициент асимметрии.
|
1 |
112 125 106 120 132 128 112 |
101 125 109 118 132 118 121 |
155 142 138 133 138 126 105 |
137 140 145 118 128 132 117 |
109 125 118 129 122 134 112 |
129 118 128 149 115 123 129 |
152 125 125 124 143 122 129 |
128 135 105 153 140 159 118 |
132 149 122 132 122 112 112 |
116 145 138 118 152 110 116 |
|
2
|
87 120 115 88 95 94 100 |
85 122 100 90 105 106 101 |
91 101 97 101 112 112 123 |
94 88 91 95 116 122 97 |
102 80 87 93 118 100 90 |
80 97 116 92 108 92 104 |
75 92 121 88 95 93 108 |
102 91 101 94 99 82 101 |
99 94 123 98 92 111 96 |
101 82 97 99 100 102 111 |
|
3 |
547 565 543 552 558 577 599 |
565 555 568 545 563 554 561 |
587 563 574 554 563 552 552 |
553 568 564 571 547 566 551 |
548 586 547 569 552 557 561 |
554 549 549 539 562 551 538 |
561 575 553 549 554 552 533 |
562 537 572 553 563 571 541 |
551 581 535 562 558 551 588 |
572 553 555 561 572 552 558 |
|
4 |
90 118 106 102 112 95 103 |
123 105 92 130 115 124 122 |
132 115 118 112 88 103 94 |
85 92 105 98 118 102 112 |
122 115 118 115 103 118 97 |
105 142 86 120 102 112 128 |
125 98 125 118 95 115 102 |
142 123 105 103 124 92 116 |
99 103 122 118 106 115 125 |
125 144 138 129 135 119 132 |
|
5 |
139 116 106 102 112 95 125 134 |
112 105 92 130 115 124 118 112 |
132 92 118 112 88 103 96 101 |
85 115 86 98 118 102 126 105 |
122 98 125 115 103 118 98 117 |
105 123 105 120 102 112 106 92 |
125 103 122 118 95 115 128 129 |
142 144 138 103 124 103 118 99 |
99 115 105 118 106 95 126 118 |
125 142 118 129 135 122 103 112 |
|
6 |
154 145 146 157 155 163 168 |
143 168 152 178 152 169 157 |
155 122 142 149 145 165 143 |
113 163 132 195 198 148 179 |
155 117 152 146 192 151 165 |
171 165 161 166 143 153 159 |
168 132 148 182 159 139 149 |
153 139 136 135 116 166 141 |
135 107 138 136 126 138 102 |
168 125 149 170 155 128 169 |
|
7 |
470 699 797 950 532 584 950 |
801 840 797 741 885 967 458 |
790 869 789 473 590 950 511 |
764 551 875 988 590 531 857 |
764 707 698 737 975 775 536 |
950 635 580 787 910 485 699 |
533 703 821 667 731 756 474 |
402 801 737 649 869 656 789 |
520 859 910 797 435 680 889 |
780 475 856 939 889 741 533 |
|
8 |
450 442 438 496 466 481 444 |
434 452 442 468 488 468 498 |
424 444 482 424 452 404 466 |
432 425 432 438 489 498 442 |
440 403 416 452 451 467 483 |
443 458 477 446 422 398 462 |
415 455 431 418 442 440 492 |
446 431 432 474 492 449 435 |
423 446 412 432 473 417 449 |
472 424 462 452 402 425 422 |
|
9 |
250 248 242 296 276 244 271 |
244 216 212 242 254 276 212 |
224 230 231 254 282 224 234 |
232 254 251 218 242 240 262 |
240 258 204 226 270 272 204 |
224 202 246 252 254 268 261 |
244 225 232 238 260 281 254 |
226 224 282 224 232 234 266 |
253 252 242 298 268 268 278 |
232 234 252 260 242 251 248 |
|
10 |
165 147 175 187 153 148 154 161 |
143 155 153 158 186 161 175 164 |
152 158 174 154 147 189 163 178 |
167 145 154 171 169 199 149 138 |
164 158 163 163 147 162 162 164 |
199 177 174 172 166 167 161 172 |
171 161 152 152 161 198 161 187 |
171 181 188 178 171 168 193 178 |
156 153 162 151 161 135 172 143 |
149 171 197 172 186 152 175 161 |
|
11 |
153 188 155 149 156 162 165 |
174 158 186 161 175 164 163 |
154 154 147 189 163 178 177 |
163 171 169 199 149 138 161 |
174 163 147 162 162 164 149 |
152 172 166 167 161 172 146 |
188 152 161 198 161 187 152 |
162 178 171 168 193 178 139 |
197 151 161 135 172 143 156 |
234 172 186 152 175 161 152 |
|
12 |
212 297 277 345 272 253 237 238 |
231 242 254 276 212 262 264 242 |
251 254 282 224 234 256 252 254 |
204 218 242 240 292 264 248 263 |
246 226 270 272 204 272 247 261 |
232 252 254 268 261 242 268 266 |
282 238 260 281 254 244 229 254 |
242 224 232 234 266 246 235 264 |
252 298 268 268 278 253 262 248 |
276 260 242 232 248 234 212 251 |
|
13 |
165 148 176 189 157 150 158 |
143 155 153 158 186 161 175 |
52 158 174 154 147 189 163 |
166 145 154 171 169 199 149 |
164 158 163 163 147 162 162 |
199 177 174 172 166 167 161 |
171 161 152 152 161 198 161 |
171 181 188 178 171 168 193 |
156 153 162 151 161 135 172 |
171 197 172 186 152 175 |
|
14 |
216 243 298 278 246 273 254 239 |
230 212 242 254 276 212 262 264 |
254 231 254 282 224 234 256 252 |
258 251 218 242 240 262 264 248 |
202 204 226 270 272 201 272 247 |
225 246 252 254 268 261 242 268 |
224 232 238 260 281 254 244 229 |
252 282 224 232 234 266 246 235 |
234 242 298 268 268 278 253 262 |
250 252 260 242 232 248 234 212 |
|
15 |
165 149 153 190 159 151 160 165 |
143 155 174 158 186 161 175 164 |
152 158 154 154 147 189 163 178 |
167 145 163 171 169 199 149 137 |
165 158 174 163 147 162 162 164 |
199 177 152 172 166 167 161 172 |
171 161 188 152 161 198 161 187 |
171 181 162 178 171 168 193 178 |
156 153 197 151 161 135 172 143 |
152 171 178 172 186 152 175 161 |
|
16 |
147 169 150 157 156 164 169 180 |
153 154 152 178 152 169 169 177 |
179 143 142 149 145 165 155 162 |
165 155 132 195 198 148 152 149 |
159 113 152 146 192 151 175 146 |
149 155 161 166 143 153 177 113 |
141 171 148 182 159 139 131 151 |
102 168 136 135 116 166 154 152 |
169 153 138 136 126 138 174 134 |
157 135 149 170 155 128 187 125 |
|
17 |
558 561 547 566 567 544 553 577 |
563 552 565 555 556 568 545 552 |
569 551 587 563 546 574 554 566 |
547 561 553 568 552 564 571 557 |
552 538 548 586 543 547 569 551 |
562 533 554 549 554 549 539 552 |
554 547 561 575 556 553 549 546 |
549 552 564 564 566 578 538 584 |
575 557 562 553 592 557 575 572 |
578 543 558 555 562 561 554 535 |
|
18 |
577 554 558 547 555 577 601 555 |
568 5455 563 595 563 554 561 541 |
557 554 563 587 568 552 552 588 |
564 571 547 553 586 566 551 558 |
547 569 552 548 549 557 561 563 |
549 539 562 554 575 551 538 558 |
553 549 554 561 564 552 533 572 |
578 538 549 564 553 546 547 578 |
557 575 575 562 585 584 552 539 |
575 566 558 544 592 556 557 556 |
|
19 |
77 48 38 63 68 12 55 74 |
45 25 53 55 55 39 69 51 |
49 59 48 16 49 57 31 82 |
92 57 68 78 65 51 62 52 |
13 65 52 52 79 65 48 46 |
69 69 73 95 48 66 46 75 |
52 55 42 77 59 43 51 49 |
26 68 62 66 53 52 43 55 |
22 49 71 35 41 63 16 57 |
36 63 45 54 38 43 34 54 |
|
20 |
347 365 343 352 366 377 399 |
365 355 368 345 358 354 363 |
387 363 374 354 363 352 361 |
348 368 364 352 347 366 352 |
354 359 347 371 352 357 351 |
361 375 349 369 362 351 361 |
364 364 353 349 354 352 338 |
362 353 378 338 349 346 353 |
346 385 357 375 375 384 333 |
358 363 358 388 341 351 357 |
|
21 |
9 6 6 7 5 6 3 |
9 10 6 7 5 13 6 |
6 6 7 5 12 11 9 |
9 7 12 11 9 11 8 |
9 6 5 9 8 5 12 |
7 8 7 7 7 8 11 |
6 6 8 6 9 10 9 |
11 5 5 5 8 9 10 |
6 5 10 7 5 4 4 |
7 4 9 6 5 7 14 |
|
22 |
39 41 34 47 41 43 57 39 |
40 40 36 48 42 42 52 37 |
38 42 37 52 39 43 41 42 |
43 39 42 56 33 41 42 43 |
41 41 42 68 34 42 46 54 |
42 41 42 70 37 47 48 58 |
40 36 40 68 43 48 49 59 |
38 43 41 64 45 49 39 64 |
41 41 41 56 47 52 32 66 |
42 42 46 58 71 53 40 68 |
|
23 |
10 17 20 27 26 42 58 |
15 12 20 24 32 24 54 |
16 13 21 25 26 23 49 |
17 14 23 25 27 35 47 |
18 15 26 26 28 23 32 |
19 11 28 32 29 25 36 |
20 18 23 33 30 36 43 |
15 16 28 31 21 37 23 |
16 15 27 34 22 24 24 |
11 18 24 43 23 21 28 |
|
24 |
150 116 142 152 144 144 162 |
144 130 121 196 176 112 164 |
124 154 112 142 124 134 164 |
132 158 131 154 140 162 172 |
140 102 151 158 172 104 142 |
124 125 104 118 168 161 144 |
144 124 146 126 181 154 146 |
153 152 132 152 134 166 112 |
151 134 182 138 168 178 171 |
148 148 142 124 132 148 |
|
25 |
128 112 95 92 106 102 103 |
105 115 124 112 92 130 122 |
115 88 103 132 118 112 94 |
92 118 102 85 105 98 112 |
115 103 118 122 118 115 97 |
142 102 112 105 86 120 128 |
98 95 115 125 125 118 102 |
123 124 92 142 105 103 116 |
103 106 115 99 122 118 125 |
144 135 119 125 138 129 132 |
|
26 |
102 157 157 151 152 153 157 165 |
112 178 143 168 152 154 152 169 |
118 149 179 122 142 143 145 165 |
85 195 165 163 132 155 198 148 |
112 146 159 117 152 113 192 151 |
115 166 149 165 161 155 143 153 |
103 182 141 132 148 171 159 139 |
95 135 102 139 136 168 116 166 |
122 136 169 107 138 153 126 138 |
125 170 168 125 149 135 155 128 |
|
27 |
242 250 244 299 276 274 255 240 |
254 216 212 254 224 212 262 264 |
218 230 231 282 240 234 256 252 |
226 254 251 242 272 262 264 248 |
252 258 204 270 268 204 272 247 |
238 202 246 254 281 261 242 268 |
224 225 232 260 234 254 244 229 |
298 224 282 232 268 266 246 235 |
260 252 242 268 232 278 253 262 |
287 234 252 242 300 248 234 212 |
|
28 |
262 259 253 253 249 267 254 249 |
267 248 286 268 288 232 244 252 |
275 266 275 277 213 258 265 294 |
266 259 235 249 264 246 274 232 |
246 252 202 248 247 278 252 269 |
252 248 239 263 242 279 265 263 |
261 252 225 243 228 257 222 269 |
269 232 236 266 277 255 269 271 |
262 269 237 212 256 243 254 245 |
268 287 224 255 251 258 278 235 |
|
29 |
558 563 563 546 557 558 602 556 |
565 568 564 577 577 554 561 541 |
587 586 547 568 568 552 552 588 |
553 549 552 574 574 566 551 558 |
548 575 562 564 564 557 561 563 |
554 564 554 547 547 551 538 558 |
561 553 549 549 549 552 533 572 |
564 585 575 553 538 546 547 578 |
562 577 558 578 575 584 552 539 |
544 553 592 557 566 532 557 556 |
|
30 |
165 155 177 191 161 161 162 153 |
143 155 153 158 186 189 175 164 |
152 158 174 154 147 199 163 178 |
167 145 154 171 169 162 149 138 |
164 158 163 163 147 167 162 164 |
199 177 174 172 166 198 161 172 |
171 161 152 152 161 168 161 187 |
171 181 188 178 171 135 193 178 |
156 153 162 151 161 152 172 1433 |
151 171 197 172 186 146 175 161 |
3. Найти доверительный интервал для оценки
математического ожидания а нормального распределения с надёжностью ![]() , зная выборочную
, зная выборочную
среднюю
![]() , объём
выборки n и среднее квадратическое отклонение
, объём
выборки n и среднее квадратическое отклонение ![]() .
.
|
№ |
|
|
n |
|
№ |
|
|
n |
|
№ |
|
|
n |
|
|
3.1 |
0.95 |
75.17 |
36 |
6 |
3.11 |
0.97 |
5.21 |
46 |
6 |
3.21 |
0.92 |
11.48 |
36 |
6 |
|
3.2 |
0.97 |
7.27 |
56 |
7 |
3.12 |
0.96 |
55.23 |
38 |
5 |
3.22 |
0.94 |
23.38 |
39 |
8 |
|
3.3 |
0.93 |
75.17 |
35 |
5 |
3.13 |
0.92 |
5.21 |
36 |
7 |
3.23 |
0.93 |
30.44 |
56 |
7 |
|
3.4 |
0.94 |
8.27 |
58 |
9 |
3.14 |
0.95 |
55.23 |
68 |
7 |
3.24 |
0.99 |
15.32 |
38 |
5 |
|
3.5 |
0.98 |
76.17 |
46 |
6 |
3.15 |
0.98 |
7.21 |
56 |
6 |
3.25 |
0.95 |
10.48 |
46 |
6 |
|
3.6 |
0.99 |
7.37 |
58 |
7 |
3.16 |
0.93 |
65.23 |
78 |
5 |
3.26 |
0.98 |
13.38 |
39 |
8 |
|
3.7 |
0.93 |
65.13 |
34 |
6 |
3.17 |
0.92 |
8.21 |
49 |
7 |
3.27 |
0.93 |
20.44 |
66 |
7 |
|
3.8 |
0.94 |
9.27 |
53 |
8 |
3.18 |
0.95 |
51.23 |
58 |
9 |
3.28 |
0.97 |
14.32 |
58 |
6 |
|
3.9 |
0.93 |
85.17 |
35 |
6 |
3.19 |
0.94 |
5.21 |
39 |
6 |
3.29 |
0.94 |
30.44 |
86 |
7 |
|
3.10 |
0.95 |
8.27 |
57 |
9 |
3.20 |
0.95 |
85.23 |
58 |
7 |
3.30 |
0.99 |
16.32 |
38 |
9 |
4. Для данных задач 1-2 и результатов этих задач, предполагая, что задано нормальное распределение.
Найти:
а) точность оценки математического ожидания а
по выборочной средней ![]() с
надёжностью
с
надёжностью ![]() ;
;
б) доверительный интервал для оценки математического
ожидания а с надёжностью ![]() .
.
Выборочную
среднюю ![]() , объём
выборки n, среднее квадратическое отклонение
, объём
выборки n, среднее квадратическое отклонение ![]() взять из задач 1-2,
взять из задач 1-2, ![]() - из задачи 3.
- из задачи 3.
5.
Глубина моря измеряется прибором, систематическая ошибка которого равна нулю, а
случайные ошибки измерения распределены нормально со средним квадратическим
отклонением ![]() .
Сколько надо сделать независимых измерений, чтобы определить глубину моря с
ошибкой не более
.
Сколько надо сделать независимых измерений, чтобы определить глубину моря с
ошибкой не более ![]() при
надёжности
при
надёжности ![]() ?
?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.1 |
0.95 |
23 |
6 |
5.11 |
0.97 |
15 |
5 |
5.21 |
0.92 |
11 |
4 |
|
5.2 |
0.97 |
14 |
8 |
5.12 |
0.96 |
14 |
6 |
5.22 |
0.94 |
23 |
8 |
|
5.3 |
0.93 |
21 |
9 |
5.13 |
0.92 |
23 |
4 |
5.23 |
0.93 |
25 |
7 |
|
5.4 |
0.94 |
15 |
5 |
5.14 |
0.95 |
12 |
3 |
5.24 |
0.99 |
17 |
5 |
|
5.5 |
0.98 |
13 |
6 |
5.15 |
0.98 |
14 |
8 |
5.25 |
0.95 |
10 |
3 |
|
5.6 |
0.99 |
20 |
4 |
5.16 |
0.93 |
20 |
6 |
5.26 |
0.98 |
13 |
4 |
|
5.7 |
0.93 |
24 |
7 |
5.17 |
0.92 |
22 |
7 |
5.27 |
0.93 |
21 |
7 |
|
5.8 |
0.94 |
18 |
4 |
5.18 |
0.95 |
19 |
5 |
5.28 |
0.97 |
14 |
5 |
|
5.9 |
0.93 |
16 |
7 |
5.19 |
0.94 |
16 |
3 |
5.29 |
0.94 |
24 |
8 |
|
5.10 |
0.95 |
19 |
6 |
5.20 |
0.95 |
18 |
4 |
5.30 |
0.99 |
12 |
4 |
2.3 Решение типового варианта
1. Для данной выборки выполнить задачу обработки и систематизации. Определить:
а) вариационный ряд (выборку в порядке возрастания);
б) статистические ряды частот и относительных частот;
в) интервальные статистические ряды частот и относительных частот (минимальную и максимальную варианты, размах выборки, число интервалов, длину интервалов);
г) дискретные (группированные) статистические ряды частот и относительных частот.
2. Для данной выборки выполнить задачу анализа, определить:
а) по интервальному статистическому ряду построить гистограмму частот и относительных частот;
б) по дискретному статистическому ряду найти:
- полигон частот и относительных частот;
- эмпирическую функцию распределения;
- выборочную среднюю;
- выборочную и исправленную выборочную дисперсии;
- выборочное и исправленное выборочное среднеквадратические отклонения;
- выборочные моду и медиану;
в) по статистическим рядам частот и относительных частот найти:
- выборочные начальные и центральные моменты третьего и четвёртого порядков;
- выборочный эксцесс;
- выборочный коэффициент асимметрии.
|
20 20 15 18 16 13 |
15 16 19 14 20 17 |
17 19 17 14 19 11 |
19 20 16 18 17 18 |
23 14 15 18 19 19 |
18 20 22 13 17 |
21 16 21 19 21 |
15 14 12 18 17 |
16 20 10 20 19 |
13 19 21 23 17 |
Решение: заметим, что вычисления и построение графиков производится в среде Mathcad. Копия файла из Mathcad приведена ниже. То, что получено в Mathcad, следует оформить и пояснить.
1. а) объём выборки n = 55. Вариационный ряд (выборка в порядке возрастания):
|
|
![]()
(в среде Mathcad эта таблица просматривается вся нажатием на указатель направления движения);
б)
по вариационному ряду посчитаем, сколько раз имеет место каждая варианта, т.е.
частоту (![]() )
каждой варианты. Полученные данные занесём в таблицу – статистический ряд
частот:
)
каждой варианты. Полученные данные занесём в таблицу – статистический ряд
частот:
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
|
1 |
1 |
1 |
2 |
4 |
4 |
5 |
7 |
6 |
8 |
7 |
5 |
1 |
2 |
Относительные
частоты вариант найдём по формуле ![]() , где n
объём выборки, полученные результаты
занесём в таблицу - статистический ряд относительных частот:
, где n
объём выборки, полученные результаты
занесём в таблицу - статистический ряд относительных частот:
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
|
0,018 |
0,018 |
0,018 |
0,036 |
0,073 |
0,073 |
0,091 |
0.127 |
0,109 |
|
|
19 |
20 |
21 |
22 |
23 |
|
|
|
|
|
|
0,145 |
0,127 |
0,091 |
0,018 |
0,036 |
|
|
|
|
в) для
построения интервального статистического ряда определим сначала следующее: наибольшая и наименьшая варианты: ![]() ,
, ![]() ;
размах выборки:
;
размах выборки: ![]() ; величину интервалов найдём по формуле Стерджеса
; величину интервалов найдём по формуле Стерджеса 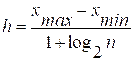 ,
, ![]() =
1,917 и округляем до целого
=
1,917 и округляем до целого ![]() ; число интервалов – знаменатель этой формулы
; число интервалов – знаменатель этой формулы ![]() или
или ![]() =6,781,
округляем до целого
=6,781,
округляем до целого ![]() ; за начало первого интервала рекомендуется брать
величину
; за начало первого интервала рекомендуется брать
величину ![]() ,
, ![]() ; число вариант, попавших в каждый интервал ( т.е. частоты
; число вариант, попавших в каждый интервал ( т.е. частоты ![]() ), и
относительные частоты ( т.е.
), и
относительные частоты ( т.е. ![]() ) найдены в среде
Mathcad (см.
) найдены в среде
Mathcad (см. ![]() и
и ![]() ).
).
Таким образом, искомый интервальный ряд имеет вид:
|
интервалы |
[9,11) |
[11,13) |
[13,15) |
[15,17) |
[17,19) |
[19,21) |
[21,23] |
|
|
1 |
2 |
6 |
9 |
13 |
16 |
8 |
|
|
0,018 |
0,036 |
0,109 |
0,164 |
0,236 |
0,291 |
0,145 |
в) для построения дискретного статистического ряда
(или в некоторых учебниках его называют группированным статистическим рядом)
найдём середины интервалов ![]() (см.
(см. ![]() в Mathcad), им будут отвечать соответствующие частоты и
относительные частоты из интервального ряда.
в Mathcad), им будут отвечать соответствующие частоты и
относительные частоты из интервального ряда.
Искомый дискретный статистический ряд:
|
|
10 |
12 |
14 |
16 |
18 |
20 |
22 |
|
|
1 |
2 |
6 |
9 |
13 |
16 |
8 |
|
|
0,018 |
0,036 |
0,109 |
0,164 |
0,236 |
0,291 |
0,145 |
2. а) по интервальному статистическому ряду построим гистограмму частот и относительных частот (в среде Mathcad):
|
|
|
|
б) по дискретному статистическому ряду найдём:
- полигон частот и относительных частот:
|
|
|
|
- эмпирическую функцию распределения (см.![]() и
и ![]() в Mathcad):
в Mathcad):
|
|
|
|

-
выборочную среднюю (см. mean(X) в Mathcad): 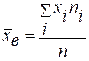 или
или ![]() =17,564;
=17,564;
- выборочную и исправленную выборочную дисперсии (см. var(X)
и s2 в Mathcad): 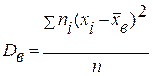 или
или  = 8,428 – выборочная дисперсия;
= 8,428 – выборочная дисперсия; ![]() =
8,584 – исправленная выборочная дисперсия;
=
8,584 – исправленная выборочная дисперсия;
-
выборочное среднеквадратическое отклонение (см. stdev(X) или
![]() в Mathcad) и исправленное
выборочное среднеквадратическое отклонение (см. s в Mathcad):
в Mathcad) и исправленное
выборочное среднеквадратическое отклонение (см. s в Mathcad): ![]() ;
; ![]() ;
;
- выборочные моду и медиану (см. mode(X) и median(X) в Mathcad): мо-
да
![]() = 19
определяет варианту, имеющую наибольшую частоту (мода может быть не одна, её
просто найти по статистическому ряду частот); медиана
= 19
определяет варианту, имеющую наибольшую частоту (мода может быть не одна, её
просто найти по статистическому ряду частот); медиана ![]() =18
определяет середину вариационного ряда и зависит от чётности объёма выборки:
=18
определяет середину вариационного ряда и зависит от чётности объёма выборки: 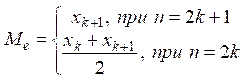 ;
;
в) по статистическим рядам частот и относительных частот (см. у и р в Mathcad) найдём:
- сначала выборочные начальные и центральные моменты k-го порядка (М(k) и m(k) в Mathcad),
затем, полагая k равно 3 и 4, выборочные начальные М(3)=![]() , М(4)=
, М(4)=![]() и выборочные
центральные
и выборочные
центральные ![]() ,
,
![]() моменты
третьего и четвёртого порядков;
моменты
третьего и четвёртого порядков;
- выборочный эксцесс ![]() ;
;
- выборочный коэффициент асимметрии ![]() .
.
Заметим,
что здесь найдены также выборочная средняя ![]() , выборочная дисперсия
, выборочная дисперсия ![]() , выборочное среднеквадратическое
отклонение
, выборочное среднеквадратическое
отклонение ![]() .
Они отличаются от найденых выше, т.к. определены по другим статистическим рядам.
.
Они отличаются от найденых выше, т.к. определены по другим статистическим рядам.
Копия файла из Mathcad :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
|
|
![]()
![]()
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
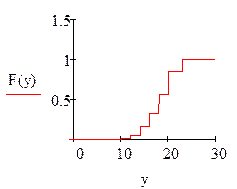
![]()
![]()
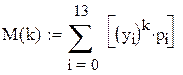
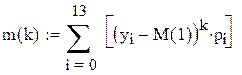
![]()
![]()
![]()
![]()
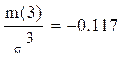
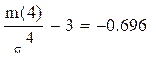
![]()
![]()
![]()
![]()
3. Найти доверительный интервал для оценки математического ожидания а нормального распределения с надёжностью 0,95, зная выборочную среднюю 18, объём выборки 25 и среднее квадратическое отклонение 3.
Решение:
доверительный интервал для оценки математического ожидания а имеет вид ![]() . Все величины, кроме t,
известны. Найдём t из соотношения
. Все величины, кроме t,
известны. Найдём t из соотношения ![]() , где
, где ![]() функция Лапласа, её значения табулированы.
По таблице
функция Лапласа, её значения табулированы.
По таблице ![]() .
Таким образом,
.
Таким образом, ![]() .
.
Ответ: (16,824; 19,176).
4. Для данных задач 1-2 и результатов этих задач, предполагая, что задано нормальное распределение, найти:
а) точность оценки математического ожидания а
по выборочной средней ![]() с
надёжностью
с
надёжностью ![]() ;
;
б) доверительный интервал для оценки математического
ожидания а с надёжностью ![]() .
.
Выборочную
среднюю ![]() ,
объём выборки n, среднее квадратическое отклонение
,
объём выборки n, среднее квадратическое отклонение ![]() взять из задач 1-2;
взять из задач 1-2; ![]() - из задачи 3.
- из задачи 3.
Решение:
из задач 1-2 выборочная средняя ![]() =17,564, объём выборки n=55, среднее
квадратическое отклонение
=17,564, объём выборки n=55, среднее
квадратическое отклонение ![]() =2,903, из задачи 3
=2,903, из задачи 3![]() = 0,95;
= 0,95;
а)
точность оценки математического ожидания а определяется формулой ![]() . t найдено в
задаче 3:
. t найдено в
задаче 3: ![]() . Поэтому
точность будет равна
. Поэтому
точность будет равна ![]() 0,77;
0,77;
б)
по формуле, указанной в задаче 3, найдём доверительный интервал: ![]() или
или ![]() .
.
5.
Глубина моря измеряется прибором, систематическая ошибка которого равна нулю, а
случайные ошибки измерения распределены нормально со средним квадратическим
отклонением ![]() =15.
Сколько надо сделать независимых измерений, чтобы определить глубину моря с
ошибкой не более
=15.
Сколько надо сделать независимых измерений, чтобы определить глубину моря с
ошибкой не более ![]() =5
при надёжности
=5
при надёжности ![]() =0,9?
=0,9?
Решение:
из формулы, определяющей точность оценки математического ожидания ![]() найдём
найдём ![]() . Определим t из
соотношения
. Определим t из
соотношения ![]() .
По таблице
.
По таблице ![]() .
Поэтому
.
Поэтому ![]() .
Таким образом, надо сделать не менее 25 измерений.
.
Таким образом, надо сделать не менее 25 измерений.
Список литературы
1 Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие для вузов. – М.: Высш. школа, 2013.- 279 с.
2 Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высш. школа, 2003.- 400 с.
3 Ивановский Р.И. Теория вероятностей и математическая статистика. Основы, прикладные аспекты с примерами изадачами в среде Mathcad. - СПб.: БХВ- Петербург, 2008. – 528 с.
4 Письменный Д. Конспект лекций по теории вероятностей и математической статистики, случайные процессы. – М.: Айрис -пресс, 2006. – 288 с.
5 Лунгу К.Н. и др. Сборник задач по высшей математике. 2 курс – М.: Айрис-пресс, 2011. – 576 с.
Содержание
|
1 Расчётно-графическая работа №1. Случайные события и случайные величины………………………………………………………………………... |
3 |
|
1.2 Расчётные задания…………………………………………………………. |
4 |
|
1.3 Решение типового варианта………………………………………………. |
12 |
|
2 Расчётно-графическая работа №2. Элементы математической статистики. …………..………………………………………………………… |
30 |
|
2.2 Расчётные задания…………………………………………………………. |
30 |
|
2.3 Решение типового варианта………………………………………………. |
38 |
|
Список литературы…………………………………………………………….. |
46 |
Сводный план 2017 г., поз. 127
Астраханцева Людмила Николаевна
Байсалова Маншук Жумамуратовна
ПРИКЛАДНАЯ СТАТИСТИКА
Методические указания и задания по выполнению расчетно-графических работ для студентов специальности
5В070400- Вычислительная техника и программное обеспечение
Редактор Л.Т.Сластихина
Специалист по стандартизации Н.К.Молдабекова
Подписано в печать_______ Формат 60х84 1/16
Тираж 25 экз. Бумага типографская №1
Объем 2,88 уч.-из.л. Заказ______ цена 1440 тг.
Копировально-множительное бюро
некоммерческого акционерного общества
«Алматинский университет энергетики и связи»
050013 Алматы, ул.Байтурсынова, 126