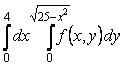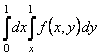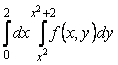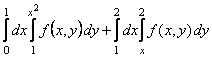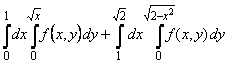ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ
БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
«Алматы энергетика және байланыс институтының»
Коммерциялық емес акционерлік қоғамы
С.Е.Ералиев, М.Ш.Тілепиев
КӨП АЙНЫМАЛЫ ФУНКЦИЯЛАРДЫҢ
ИНТЕГРАЛДЫҚ ЕСЕПТЕУЛЕРІ
Оқу құралы
Алматы 2007
ӘОК: 378(075.8):51
ББК 22.161.6 я 73
Ералиев С.Е., Тілепиев М.Ш.
Е64 Көп айнымалы функциялардың интегралдық есептеулері. Оқу құралы. Алматы: АЭжБИ, 2007. - 64 бет.
JSBN 9965-708-46-0
Бұл оқулық техникалық жоғары оқу орындарының бағдарламасына сәйкес жазылған. Мұнда көп айнымалы функциялардың интегралдық есептеу теориясының негізгі анықтамалары мен қасиеттерін терең түсіну үшін, таңдалып алынған мысалдар қарастырылған және әрбір параграфтың соңында есептер берілген. Сондықтан бұл оқулықты есептер жинағы ретінде пайдалануға болады.
Бұл оқулық кредиттік жүйе бойынша оқылатын оқу орындарының студенттеріне арналған.
ББК 22.161.6 я 73
Пікір берушілер: ҚазҰУ, физ. – мат. ғыл. д-р, проф., акад. Н.Т.Данаев.
АЭжБИ, физ. – мат. ғыл. канд., проф. С.Е.Базарбаева
Қазақстан Республикасының Білім және Ғылым министірлігінің 2007 жылғы баспа жоспары бойынша басылды.
JSBN 9965-708-46-0
© «Алматы энергетика және байланыс институтының» КЕАҚ, 2007ж.
Мазмұны
|
1 |
Көп айнымалы функциялар (Бейнелер)........................................... |
3 |
|
1.1 |
Көп айнымалы функцияның анықтау облысы (аймағы)………… |
3 |
|
1.2 |
Көп айнымалы функцияның дербес, толық |
|
|
өсімшелері және дербес жуындылары………………………………….. |
4 |
|
|
1.3 |
Көп айнымалы функцияның толық дифференциалы……………. |
6 |
|
1.4 |
Көп айнымалы функциялардың жоғары ретті дербес |
|
|
туындылары мен дифференциалдары………………………………….. |
8 |
|
|
1.5 |
Күрделі функцияны дифференциалдау…………………………... |
11 |
|
1.6 |
Айқындалмаған функциялардың туындысы……………………... |
13 |
|
1.7 |
Бетке жүргізілген жанама жазықтық |
|
|
және нормаль (тіктеме) түзу…………………………………………….. |
14 |
|
|
1.8 |
Екі айнымалы функцияның экстремумы…………………………. |
16 |
|
1.9 |
Шартты экстремум. Функцияның ең үлкен |
|
|
және ең кіші мәндері……………………………………………………... |
18 |
|
|
2 |
Екі еселі интегралдар………………………………………………. |
21 |
|
2.1 |
Тік бұрышты координаталар (мекендіктер) жүйесінде |
|
|
анықталған екі еселі интегралдар……………………………………….. |
21 |
|
|
2.2 |
Екі еселі интегралдағы айнымалыларды ауыстыру……………... |
29 |
|
2.3 |
Полярлық координаталар жүйесінде анықталған |
|
|
екі еселі инегралдар……………………………………………………… |
29 |
|
|
2.4 |
Жазық фигуралардың (пішіндердің) аудандарын |
|
|
есептеу.......................................................................................................... |
32 |
|
|
2.5 |
Денелердің көлемдерін есептеу…………………………………… |
35 |
|
2.6 |
Беттің ауданын есептеу …………………………………………… |
37 |
|
2.7 |
Екі еселі интегралдардың механикада және |
|
|
физикада қолданылуы …………………………………………………… |
39 |
|
|
3 |
Үш еселі интегралдар……………………………………………… |
43 |
|
3.1 |
Тік бұрышты координаталар жүйесіндегі үш еселі |
|
|
интегралдар……………………………………………………………….. |
43 |
|
|
3.2 |
Үш еселі интегралдағы айнымалыларды алмастыру……………. |
47 |
|
3.3 |
Үш еселі интегралдың механикада және физикада |
|
|
қолданылуы……………………………………………………………….. |
49 |
|
|
Жауаптары………………………………………………………………… |
54 |
|
|
Әдебиеттер тізімі…………………………………………………………. |
60 |
|
1 Көп айнымалы функциялар (бейнелер)
1.1 Көп айнымалы функцияның анықталу облысы (аймағы)
Егер D облысында бір-бірінен тәуелсіз қос (x,y) айнымалыларының әрбір мәніне z айнымалысының анықталған бір мәні сәйкес келсе, онда z айнымалысы x және y айнымалыларына байланысты екі айнымалы функция деп аталады және оны
![]() ,
,
және тағы да басқа символдардың (ишараттардың) бірімен белгілейді.
![]() функциясы
анықталатын x және y мәндерінің қос
функциясы
анықталатын x және y мәндерінің қос
![]() жиынын осы
функцияның анықталу облысы деп атайды.
жиынын осы
функцияның анықталу облысы деп атайды.
Қарапайым жағдайда, ![]() функциясының
анықталу облысы
функциясының
анықталу облысы ![]() жазықтығы,
жазықтығы,
![]() жазықтығының
тұйық сызықтармен шектелген бөлігі немесе осы
жазықтықтың бірнеше бөліктерінің жиынтығы
болады.
жазықтығының
тұйық сызықтармен шектелген бөлігі немесе осы
жазықтықтың бірнеше бөліктерінің жиынтығы
болады. ![]() функциясының
функциясының
![]() тік
бұрышты координаталар жүйесіндегі геометриялық бейнесі
(графигі) осы теңдеумен анықталатын бет болып табылады.
тік
бұрышты координаталар жүйесіндегі геометриялық бейнесі
(графигі) осы теңдеумен анықталатын бет болып табылады.
Егер бір-бірінен тәуелсіз ![]() айнымалыларының
әрбір мәніне u айнымалысының
анықталған бір мәні сәйкес келсе, онда u
айнымалысы
айнымалыларының
әрбір мәніне u айнымалысының
анықталған бір мәні сәйкес келсе, онда u
айнымалысы ![]() айнымалыларына
байланысты көп айнымалы функция деп аталады да
айнымалыларына
байланысты көп айнымалы функция деп аталады да
![]()
және тағыда басқа символдардың бірімен белгіленеді.
1-мысал. ![]() функциясының анықталу облысын
табу керек.
функциясының анықталу облысын
табу керек.
Шешуі. Берілген функция x пен y-тің
кезкелген мәнінде анықталған, яғни анықталу
облысы бүкіл ![]() жазықтығы
болып табылады.
жазықтығы
болып табылады.
2-мысал. ![]() функциясының анықталу облысын
табу керек.
функциясының анықталу облысын
табу керек.
Шешуі. Логарифмдік функция ![]() , яғни
, яғни ![]() болғанда ғана
анықталады. Осыдан, функцияның анықталу облысы
болғанда ғана
анықталады. Осыдан, функцияның анықталу облысы ![]() түзуінен
төмен орналасқан
түзуінен
төмен орналасқан ![]() жазықтығының
бөлігі болып табылады.
жазықтығының
бөлігі болып табылады.
3-мысал. ![]() функциясының анықталу облысын
табу керек.
функциясының анықталу облысын
табу керек.
Шешуі. Фунция нақты мәндерін ![]() немесе
немесе ![]() болғанда
ғана қабылдайды,
яғни функцияның анықталу облысы центрі координаталар
жүйесінің бас нүктесі, ал радиусы
болғанда
ғана қабылдайды,
яғни функцияның анықталу облысы центрі координаталар
жүйесінің бас нүктесі, ал радиусы ![]() -ға тең болатын
дөңгелектен тыс орналасқан
-ға тең болатын
дөңгелектен тыс орналасқан ![]() жазықтығының бөлігі.
жазықтығының бөлігі.
4-мысал. ![]() функциясының
анықталу облысын табу керек.
функциясының
анықталу облысын табу керек.
Шешуі. Берілген функция ![]() теңсіздігі
орындалғанда ғана анықталады. Осыдан функцияның
анықталу облысы
теңсіздігі
орындалғанда ғана анықталады. Осыдан функцияның
анықталу облысы ![]() және
және ![]() түзулерінің арасында
орналасқан
түзулерінің арасында
орналасқан ![]() жазықтығының бөлігі болады.
жазықтығының бөлігі болады.
Берілген функцияларының анықталу облысын табу керек:
1. ![]() 2.
2.
![]()
3. ![]() 4.
4.
![]()
5. ![]() 6.
6.
![]()
7. ![]() 8.
8.
![]()
9. 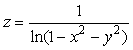 10.
10.
![]()
1.2 Көп айнымалы функцияның дербес, толық өсімшелері және дербес туындылары
![]() жазықтығының D облысында анықталған
жазықтығының D облысында анықталған
![]() функциясын
қарастырайық. Мұндағы x пен y-ті бекітіп
алып,
функциясын
қарастырайық. Мұндағы x пен y-ті бекітіп
алып, ![]() айнымалысына
айнымалысына
![]() өсімшесін
берейік. Сонда
өсімшесін
берейік. Сонда ![]() айнымалысы
бойынша z функциясының
айнымалысы
бойынша z функциясының ![]() дербес өсімшесі
дербес өсімшесі
![]() (1)
(1)
формуласымен (кейіптемесімен) анықталады.
![]() функциясындағы x пен y
айнымалыларын бекітіп алып, y айнымалысына
функциясындағы x пен y
айнымалыларын бекітіп алып, y айнымалысына ![]() өсімшесін берсек, онда y
айнымалысы бойынша дербес өсімшесі
өсімшесін берсек, онда y
айнымалысы бойынша дербес өсімшесі
![]() (2)
(2)
формуласымен анықталады.
Егер x пен y айнымалылары бекітіліп
алынып, олар сәйкесінше ![]() және
және ![]() өсімшелерін қабылдаса, онда
өсімшелерін қабылдаса, онда ![]() функциясының
толық өсімшесі
функциясының
толық өсімшесі
![]() (3)
(3)
формуласымен анықталады.
5-мысал. ![]() функциясының x және y
айнымалылары бойынша дердес өсімшелерін және толық
өсімшесін табу керек.
функциясының x және y
айнымалылары бойынша дердес өсімшелерін және толық
өсімшесін табу керек.
Шешуі. ![]()
![]()
![]()
![]()
![]()
![]()

![]() функциясының x айнымалысы
бойынша дербес туындысы деп
функциясының x айнымалысы
бойынша дербес туындысы деп
![]() (4)
(4)
шегін айтады. Бұл жағдайда ![]() -ті тұрақты деп алу керек.
-ті тұрақты деп алу керек.
![]() функциясының
функциясының ![]() айнымалысы бойынша дербес
туындысы деп
айнымалысы бойынша дербес
туындысы деп
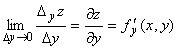 (5)
(5)
шегін айтады. Бұл жағдайда ![]() -ті тұрақты деп алу керек.
-ті тұрақты деп алу керек.
6-мысал. ![]() функциясының
дербес туындысын табу керек.
функциясының
дербес туындысын табу керек.
Шешуі. ![]() -ті тұрақты деп алып,
-ті тұрақты деп алып,
![]() табамыз.
табамыз.
Осы сияқты, ![]() -ті тұрақты деп алып,
-ті тұрақты деп алып,
![]() табамыз.
табамыз.
7-мысал. 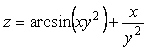 функциясының дербес туындыларын
табу керек.
функциясының дербес туындыларын
табу керек.
Шешуі. 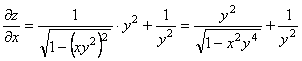
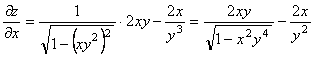 .
.
8-мысал. Үш айнымалы ![]() функциясының дербес
туындыларын табу керек.
функциясының дербес
туындыларын табу керек.
Шешуі. ![]()
![]() ;
; ![]()
Берілген функциялардың дербес өсімшелерін табу керек:
11. ![]() 12.
12.
![]()
13. ![]() 14.
14.
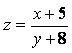
15. ![]() 16.
16.
![]()
Берілген функциялардың дербес туындыларын табу керек:
17. ![]() 18.
18.
![]()
19. ![]() 20.
20.
![]()
21. ![]() 22.
22.
![]()
23. ![]() 24.
24.
![]()
25. ![]() 26.
26.
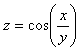
27. ![]() 28.
28.
![]()
29. ![]() 30.
30.
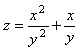
31. ![]() 32.
32.
![]()
33. ![]() 34.
34.
![]()
35. ![]() 36.
36.
![]() .
.
1.3 Көп айнымалы функцияның толық дифференциалы.
![]() функциясының толық
өсімшесі
функциясының толық
өсімшесі ![]() -ті
дербес
-ті
дербес ![]() туындылары
арқылы
туындылары
арқылы
![]() (6)
(6)
түрінде жазуға болады, мұндағы
алдыңғы екі қосынды өсімшенің негізгі
бөлігі, ал кейінгі екі қосынды қосалқы бөлігі деп
аталады. ![]() және
және
![]() шамаларымен
салыстырғанда қосалқы жоғары ретті ақырсыз аз
шама болғандықтан
шамаларымен
салыстырғанда қосалқы жоғары ретті ақырсыз аз
шама болғандықтан ![]() ұмтылғанда
ұмтылғанда ![]() .
.
Толық өсімшенің негізгі бөлігі функцияның толық дифференциалы деп аталып
![]() (7)
(7)
арқылы белгіленеді. Мұндағы ![]() ал
ал ![]()
![]() сәйкес
сәйкес ![]() және
және ![]() айнымалылары бойынша дербес
диффееренциалдары деп аталады.
айнымалылары бойынша дербес
диффееренциалдары деп аталады.
Егер ![]() көп айнымалы функциясы берілсе,
онда оның толық дифференциалы
көп айнымалы функциясы берілсе,
онда оның толық дифференциалы
![]() (8)
(8)
формуласымен анықталады.
![]() -ң аз мәнінде
дифференциалданатын
-ң аз мәнінде
дифференциалданатын ![]() функциясы
үшін төмендегі жуықтап есептеу формуласы қолданылады.
функциясы
үшін төмендегі жуықтап есептеу формуласы қолданылады.
![]() осыдан
осыдан
![]() (9)
(9)
9-мысал.
![]() функциясының
толық дифференциалын табу керек.
функциясының
толық дифференциалын табу керек.
Шешуі. Дербес туындыларын табайық.
![]()
Осыдан
![]() .
.
10-мысал. ![]() функциясының толық
дифференциалын табу керек.
функциясының толық
дифференциалын табу керек.
Шешуі.
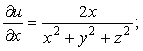
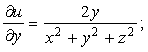
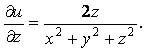
Осыдан
![]() .
.
11-мысал. ![]() санының жуық мәнін табу
керек.
санының жуық мәнін табу
керек.
Шешуі. ![]() функциясын қарастырайық.
функциясын қарастырайық.
![]() осыдан
осыдан ![]()
![]() осыдан
осыдан ![]()
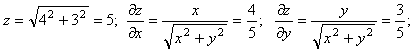
![]()
Берілген функциялардың толық дифференциалдарын табу керек:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() санын
жуықтап есептеу керек.
санын
жуықтап есептеу керек.
![]() санын
жуықтап есептеу керек.
санын
жуықтап есептеу керек.
![]() санын
есептеу керек.
санын
есептеу керек.
![]() санын
есептеу керек.
санын
есептеу керек.
1.4 Көп айнымалы функциялардың жоғары ретті дербес туындылары мен дифференциалдары
![]() функциясының екінші ретті дербес
туындысы деп осы функцияның дербес туындысының дербес туындысын
айтады және оны былай белгілейді:
функциясының екінші ретті дербес
туындысы деп осы функцияның дербес туындысының дербес туындысын
айтады және оны былай белгілейді:
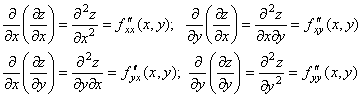 (10)
(10)
Осылай үшінші және жоғары ретті дербес туындылары табылады:
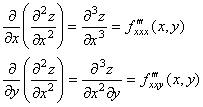 (11)
(11)
және т.с.с.
![]() функциясы және оның
функциясы және оның ![]() дербес туындылары
дербес туындылары ![]() облысында
анықталған және үзіліссіз болса, онда осы облыста
“аралас” туындылары тең болады:
облысында
анықталған және үзіліссіз болса, онда осы облыста
“аралас” туындылары тең болады:
![]() (12)
(12)
![]() функциясының екінші ретті
дифференциалы деп осы функцияның дифференциалының дифференциалын
айтады:
функциясының екінші ретті
дифференциалы деп осы функцияның дифференциалының дифференциалын
айтады:
![]() (13)
(13)
Осы сияқты үшінші және жоғары ретті дифференциалдары анықталады:
![]() (14)
(14)
Егер ![]() және
және ![]() бір – бірінен тәуелсіз айнымалылар,
ал
бір – бірінен тәуелсіз айнымалылар,
ал ![]() функциясының
үзіліссіз дербес туындылары бар болса, онда жоғары ретті
дифференциалдар
функциясының
үзіліссіз дербес туындылары бар болса, онда жоғары ретті
дифференциалдар
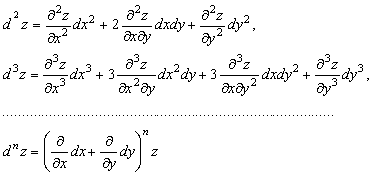 (15)
(15)
формулаларымен анықталады.
12-мысал. ![]() функциясының екінші ретті дербес
туындыларын және екінші ретті дифференциалын табу керек.
функциясының екінші ретті дербес
туындыларын және екінші ретті дифференциалын табу керек.
Шешуі. Алдымен дербес туындыларын табайық:
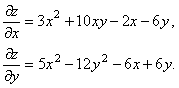
Енді
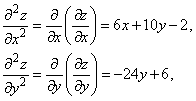
![]()
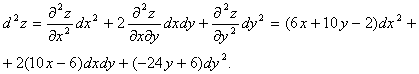
Берілген функциялардың екінші ретті дербес туындыларын табу керек:
![]()
![]()
![]()
![]()
![]()
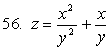
![]()
![]()
![]()
![]()
Берілген функциялардың екінші ретті дифференциалдарын табу керек:
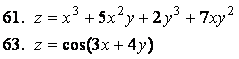
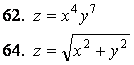
![]() функциясының
функциясының
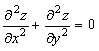 теңдеуін
қанағаттандыратындығын дәлелдеу керек.
теңдеуін
қанағаттандыратындығын дәлелдеу керек.
66. Екі рет дифференциалданатын кез келген ![]() функциясының
функциясының 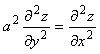 теңдеуін
қанағаттандыратындығын дәлелдеу керек.
теңдеуін
қанағаттандыратындығын дәлелдеу керек.
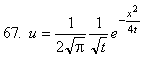 функциясының
функциясының
![]() теңдеуін
қанағаттандыратындығын дәлелдеу керек.
теңдеуін
қанағаттандыратындығын дәлелдеу керек.
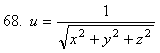 функциясының
функциясының
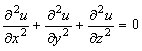 теңдеуін
қанағаттандыратындығын дәлелдеу керек.
теңдеуін
қанағаттандыратындығын дәлелдеу керек.
1.5 Күрделі функцияны дифференциалдау
Дифференциалданатын ![]() функциясы берілсін, мұнда
функциясы берілсін, мұнда ![]() . Бұл
күрделі
. Бұл
күрделі ![]() функциясының
дербес туындылары
функциясының
дербес туындылары
![]() (16)
(16)
формулаларымен есептеледі.
Дифференциалданатын ![]() функциясы берілсін, мұнда
функциясы берілсін, мұнда ![]() Бұл
күрделі
Бұл
күрделі ![]() функциясының
функциясының
![]() бойынша
туындысы
бойынша
туындысы
![]() (17)
(17)
формуласымен есептеледі.
Дифференциалданатын ![]() функциясы берілсін, мұнда
функциясы берілсін, мұнда ![]() . Бұл
. Бұл ![]() функциясының
функциясының ![]() бойынша туындысы
бойынша туындысы
![]() (18)
(18)
формуласымен есептеледі.
13-мысал. ![]() функциясының, мұндағы
функциясының, мұндағы ![]() дербес туындыларын
табу керек.
дербес туындыларын
табу керек.
Шешуі.
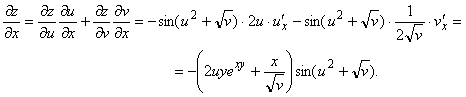
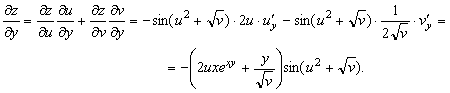
14-мысал. ![]() функциясы берілген, мұндағы
функциясы берілген, мұндағы ![]() ,
, ![]() туындысын табу керек.
туындысын табу керек.
Шешуі.
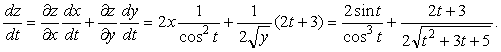
15-мысал. ![]() функциясы берілген, мұндағы
функциясы берілген, мұндағы ![]() туындысын табу
керек.
туындысын табу
керек.
Шешуі. ![]()
Осыдан
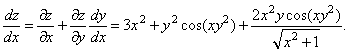
![]() функциясы
берілген, мұндағы
функциясы
берілген, мұндағы ![]() ,
, ![]() дербес туындыларын табу керек.
дербес туындыларын табу керек.
![]() функциясы
берілген, мұндағы
функциясы
берілген, мұндағы ![]() ,
, ![]() дербес туындыларын табу керек.
дербес туындыларын табу керек.
![]() функциясы
берілген, мұндағы
функциясы
берілген, мұндағы ![]() ,
, ![]() дербес туындыларын табу керек.
дербес туындыларын табу керек.
72. ![]() функциясы берілген, мұндағы
функциясы берілген, мұндағы ![]() ,
, ![]() дербес туындыларын табу керек.
дербес туындыларын табу керек.
73. ![]() функциясы
берілген, мұндағы
функциясы
берілген, мұндағы ![]() туындысын табу керек.
туындысын табу керек.
74. ![]() функциясы
берілген, мұндағы
функциясы
берілген, мұндағы ![]() туындысын табу керек.
туындысын табу керек.
75. ![]() функциясы
берілген, мұндағы
функциясы
берілген, мұндағы ![]() туындысын табу керек.
туындысын табу керек.
76. ![]() функциясы
берілген, мұндағы
функциясы
берілген, мұндағы ![]() туындысын табу керек.
туындысын табу керек.
77. ![]() функциясы
берілген, мұндағы
функциясы
берілген, мұндағы ![]() туындысын табу керек.
туындысын табу керек.
78. ![]() функциясы
берілген, мұндағы
функциясы
берілген, мұндағы ![]() туындысын табу керек.
туындысын табу керек.
79. ![]() функциясы
берілген, мұндағы
функциясы
берілген, мұндағы ![]() туындысын табу керек.
туындысын табу керек.
80. ![]() функциясы
берілген, мұндағы
функциясы
берілген, мұндағы ![]() туындысын табу керек.
туындысын табу керек.
1.6 Айқындалмаған функциялардың туындысы
![]() теңдеуі түрінде берілген
айқындалмаған
теңдеуі түрінде берілген
айқындалмаған ![]() функциясының туындысы
функциясының туындысы
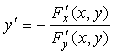
формуласымен анықталады, мұндағы ![]() функциясы x және y айнымалылары бойынша дифференциалданатын
әрі
функциясы x және y айнымалылары бойынша дифференциалданатын
әрі ![]() функция.
функция.
![]() теңдеуі түрінде берілген
айқындалмаған
теңдеуі түрінде берілген
айқындалмаған ![]() функциясының x және y
айнымалылары бойынша дербес туындылары
функциясының x және y
айнымалылары бойынша дербес туындылары
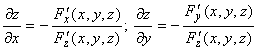 (19)
(19)
формулаларымен анықталады, мұндағы ![]() функциясы
функциясы ![]() және
және ![]() айнымалылары
бойынша дифференциалданатын әрі
айнымалылары
бойынша дифференциалданатын әрі ![]() функция.
функция.
17-мысал. ![]() функциясы берілген.
функциясы берілген. ![]() туындысын табу керек.
туындысын табу керек.
Шешуі. ![]() ,
,
![]() ,
, ![]()
Осыдан
![]() .
.
18-мысал. ![]() функциясы берілген.
функциясы берілген. ![]() туындыларын табу керек.
туындыларын табу керек.
Шешуі. ![]() ,
,
![]() ,
, ![]() ,
, ![]()
Осыдан
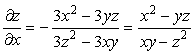 ,
, 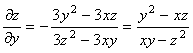
Айқындалмаған ![]() функциясының туындысын
табу керек:
функциясының туындысын
табу керек:
81. ![]() 82.
82.
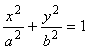
83. ![]() 84.
84.
![]()
85. ![]() 86.
86.
![]() .
.
Айқындалмаған ![]() функциясының x
және y айнымалылары бойынша дербес туындыларын табу керек:
функциясының x
және y айнымалылары бойынша дербес туындыларын табу керек:
87. ![]() 88.
88.
![]()
89. ![]() 90.
90.
![]()
91. ![]() 92.
92.
![]() .
.
1.7 Бетке жүргізілген жанама жазықтық және нормаль(тіктеме) түзу
Қарастырылатын ![]() беті
беті ![]() теңдеуімен берілсін. Беттің
бойынан
теңдеуімен берілсін. Беттің
бойынан ![]() нүктесін
алайық. Осы нүктеде
нүктесін
алайық. Осы нүктеде ![]() функциясы дифференциалданатын болсын.
функциясы дифференциалданатын болсын.
Беттің ![]() нүктесі арқылы өтетін
барлық қисықтарға жүргізілген жанамалардан
тұратын жазықтықты жанама жазықтық дейді.
Оның теңдеуі
нүктесі арқылы өтетін
барлық қисықтарға жүргізілген жанамалардан
тұратын жазықтықты жанама жазықтық дейді.
Оның теңдеуі
![]() (20)
(20)
![]() нүктесі
арқылы өтетін және жанама жазықтыққа
перпендикуляр болатын түзуді беттің нормалі дейді. Оның
теңдеуі
нүктесі
арқылы өтетін және жанама жазықтыққа
перпендикуляр болатын түзуді беттің нормалі дейді. Оның
теңдеуі
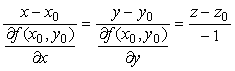 (21)
(21)
Егер ![]() беті
беті ![]() теңдеуімен берілсе, онда
теңдеуімен берілсе, онда ![]() нүктесіндегі жанама
жазықтықтың теңдеуі
нүктесіндегі жанама
жазықтықтың теңдеуі
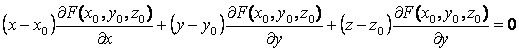 , (22)
, (22)
ал нормальдің теңдеуі
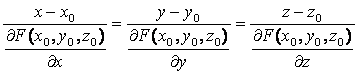 (23)
(23)
19-мысал. ![]() функциясының
функциясының ![]() нүктесіндегі жанама
жазықтығының және нормалінің теңдеулерін
жазу керек.
нүктесіндегі жанама
жазықтығының және нормалінің теңдеулерін
жазу керек.
Шешуі. ![]()
![]() нүктесінде
нүктесінде
![]()
Осыдан жанама жазықтығының теңдеуі
![]() немесе
немесе ![]()
ал нормалінің теңдеуі
![]() .
.
20-мысал. ![]() функциясының
функциясының ![]() нүктесіндегі жанама
жазықтығының және нормаль түзуінің
теңдеулерін жазу керек.
нүктесіндегі жанама
жазықтығының және нормаль түзуінің
теңдеулерін жазу керек.
Шешуі. 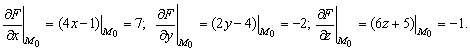
Осыдан жанама жазықтығының теңдеуі
![]()
немесе ![]() , ал
нормаль түзуінің теңдеуі
, ал
нормаль түзуінің теңдеуі
![]() .
.
Берілген ![]() беттерінің
беттерінің ![]() нүктелеріндегі жанама
жазықтықтарының және тіктемелерінің
теңдеулерін жазу керек:
нүктелеріндегі жанама
жазықтықтарының және тіктемелерінің
теңдеулерін жазу керек:
93. ![]()
94. ![]()
95. ![]()
96. 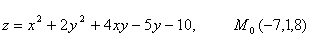
97. ![]()
98. ![]()
99. 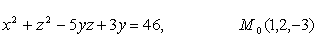
100.![]()
1.8 Екі айнымалы функцияның экстремумы
![]() аймағында анықталған
аймағында анықталған ![]() функциясы берілсін.
Осы аймақта жататын
функциясы берілсін.
Осы аймақта жататын ![]() нүктесінің маңайында
жататын барлық
нүктесінің маңайында
жататын барлық ![]() нүктелерінде
нүктелерінде
![]()
![]() теңсіздігі орындалса,
онда
теңсіздігі орындалса,
онда ![]() функциясы
функциясы
![]() нүктесінде
максимум (минимум) мәнін қабылдайды. “Максимум” және
“минимум” мәндері экстремум мәндері деп аталады. Үш
және одан көп айнымалылардың функцияларының
экстремумдарыда осылайша анықталады. Кез келген дифференциалданатын екі
айнымалы функция экстремум мәндерін тек оның барлық дербес
туындылары нөлге тең болатын нүктелерде ғана
қабылдайды. Мұндай нүктелер стационарлық
(тұрақты) нүктелер деп аталады. Мысалы, дифференциалданатын
нүктесінде
максимум (минимум) мәнін қабылдайды. “Максимум” және
“минимум” мәндері экстремум мәндері деп аталады. Үш
және одан көп айнымалылардың функцияларының
экстремумдарыда осылайша анықталады. Кез келген дифференциалданатын екі
айнымалы функция экстремум мәндерін тек оның барлық дербес
туындылары нөлге тең болатын нүктелерде ғана
қабылдайды. Мұндай нүктелер стационарлық
(тұрақты) нүктелер деп аталады. Мысалы, дифференциалданатын ![]() функциясының
стационарлық нүктесі
функциясының
стационарлық нүктесі ![]()
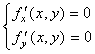 (24)
(24)
жүйесін шешу арқылы анықталады. (24) – шарт ![]() функциясының
экстремум мәндерін қабылдауының қажеттілік шарты болып
табылады. Яғни стационарлық нүктелердің барлығы
бірдей экстремум нүктелері бола бермейді. Сондықтан олардың
әрқайсы төмендегі функцияның экстремум мәндерін
қабылдауының жеткілікті шартын қанағантандыру керек.
функциясының
экстремум мәндерін қабылдауының қажеттілік шарты болып
табылады. Яғни стационарлық нүктелердің барлығы
бірдей экстремум нүктелері бола бермейді. Сондықтан олардың
әрқайсы төмендегі функцияның экстремум мәндерін
қабылдауының жеткілікті шартын қанағантандыру керек. ![]() нүктесі
нүктесі ![]() функциясының
стационар нүктесі болсын.
функциясының
стационар нүктесі болсын.
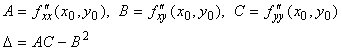 (25)
(25)
деп белгілейік. Егер стационарлық ![]() нүктесінде:
нүктесінде:
а) ![]() және
және ![]() болса, онда
болса, онда ![]() минимум нүктесі болады,
минимум нүктесі болады,
![]() және
және ![]() болса, онда
болса, онда ![]() максимум нүктесі болады;
максимум нүктесі болады;
б) ![]() болса, онда
болса, онда ![]() нүктесінде экстремум болмайды;
нүктесінде экстремум болмайды;
в) ![]() болса, онда бұл нүктеде
экстремум болуы да болмауы да мүмкін.
болса, онда бұл нүктеде
экстремум болуы да болмауы да мүмкін.
21-мысал. ![]() функциясын экстремумге зерттеу керек.
функциясын экстремумге зерттеу керек.
Шешуі. Бірінші ретті дербес туындылары
![]()
болады, осыдан
![]()
теңдеулер жүйесінің шешімі ![]() .
. ![]() нүктесіндегі екінші ретті дербес
туындылары
нүктесіндегі екінші ретті дербес
туындылары
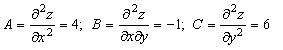
болады. Сонымен
![]() .
.
Яғни ![]() нүктесінде
берілген функция минимум мәнін қабылдайды және ол
нүктесінде
берілген функция минимум мәнін қабылдайды және ол
![]()
болады.
22-мысал. ![]() функциясын экстремумге зерттеу керек (
функциясын экстремумге зерттеу керек (![]() ).
).
Шешуі.
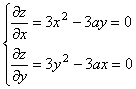
теңдеулер жүйесінің шешімі
![]() және
және ![]() .
.
Екінші ретті дербес туындысын табайық.
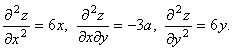
![]() нүктесінде
нүктесінде
![]()
![]()
Яғни ![]() нүктесінде
берілген функция минимум мәнін қабылдайды және ол
нүктесінде
берілген функция минимум мәнін қабылдайды және ол ![]() тең болады.
тең болады. ![]() нүктесінде
нүктесінде
![]()
![]()
Яғни ![]() нүктесінде
экстремум жоқ.
нүктесінде
экстремум жоқ.
Берілген функцияларды экстремумге зерттеу керек:
101. ![]() 102.
102.
![]()
103. ![]() 104.
104.
![]()
105. ![]() 106.
106.
![]() .
.
1.9 Шартты эктремум. Функцияның ең үлкен және ең кіші мәндері
![]() функциясының шартты экстремумы деп
осы функцияның, x және y айнымалыларының
функциясының шартты экстремумы деп
осы функцияның, x және y айнымалыларының ![]() теңдеуімен
байланысты болған жағдайдағы экстремум мәнін айтады.
Мұндағы
теңдеуімен
байланысты болған жағдайдағы экстремум мәнін айтады.
Мұндағы ![]() теңдеуі
байланыс теңдеуі деп аталады.
теңдеуі
байланыс теңдеуі деп аталады.
Шартты экстремумды табу үшін Лагранж функциясы
деп аталатын ![]() функциясының
экстремумын табу жеткілікті, мұндағы
функциясының
экстремумын табу жеткілікті, мұндағы ![]() - анықталмаған
тұрақты көбейткіш.
- анықталмаған
тұрақты көбейткіш.
Лагранж функциясының экстремумының бар болуының қажетті шарты:
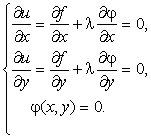 (26)
(26)
Осы үш теңдеуден тұратын жүйеден ![]() және
және ![]() мәндерін
табуға болады.
мәндерін
табуға болады.
![]() тұйық облысында
тұйық облысында ![]() функциясының
ең үлкен
функциясының
ең үлкен ![]() және
ең кіші
және
ең кіші ![]() мәндерін
табу үшін:
мәндерін
табу үшін:
а) ![]() облысының ішінде жатқан
барлық стационарлық нүктелерді тауып, осы нүктелердегі
функцияның мәндерін есептеу керек (бұл нүктелерде
экстремум мәндерінің болуын не болмауын тексерудің
қажеті жоқ).
облысының ішінде жатқан
барлық стационарлық нүктелерді тауып, осы нүктелердегі
функцияның мәндерін есептеу керек (бұл нүктелерде
экстремум мәндерінің болуын не болмауын тексерудің
қажеті жоқ).
б) ![]() облысының шекарасында
функцияның ең үлкен және ең кіші мәндерін
табу керек.
облысының шекарасында
функцияның ең үлкен және ең кіші мәндерін
табу керек.
в) Барлық табылған мәндердің ең кішісін (бұл ең кіші мән) және ең үлкенін (бұл ең үлкен мән) таңдап аламыз.
23-мысал. ![]() функциясының байланыс теңдеуі
функциясының байланыс теңдеуі
![]() берілген
жағдайдағы шартты экстремумын табу керек.
берілген
жағдайдағы шартты экстремумын табу керек.
Шешуі. Лагранж функциясын қарастырайық:
![]()
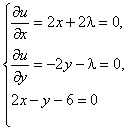
жүйесінен ![]() мәндері табылады. Осыдан
мәндері табылады. Осыдан ![]() нүктесінде
нүктесінде ![]() функциясы шартты
максимум мәнін қабылдайды және ол
функциясы шартты
максимум мәнін қабылдайды және ол ![]() болады.
болады.
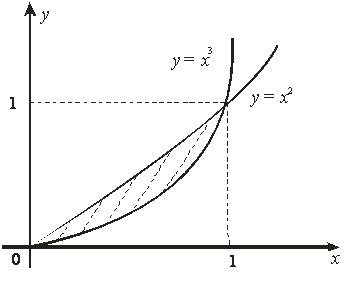
24-мысал. ![]() функциясының
функциясының ![]() ,
, ![]() ,
, ![]() сызықтарымен шектелген тұйық
сызықтарымен шектелген тұйық
![]() облысындағы
(аймағындағы) ең үлкен және ең кіші
мәндерін табу керек.
облысындағы
(аймағындағы) ең үлкен және ең кіші
мәндерін табу керек.
Шешуі. Стационар (тұрақты) ![]() нүктесін
табайық.
нүктесін
табайық.
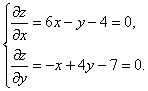
Осы жүйеден ![]() нүктесі
нүктесі ![]() облысының ішінде жатыр.
облысының ішінде жатыр. ![]()
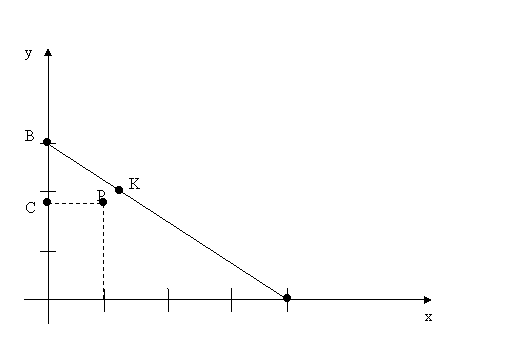
A N 0
1 – сурет
Енді берілген функцияны ![]() облысының шекарасында зерттейік.
Облыс шекарасы ОА, АВ және ОВ кесінділерінен тұрады:
облысының шекарасында зерттейік.
Облыс шекарасы ОА, АВ және ОВ кесінділерінен тұрады:
1) ОА
бөлігінде ![]() осыдан
осыдан
![]()
![]()
![]()
ОА
кесіндісінің шеткі нүктелерінде ![]() ,
, ![]()
2) ОВ бөлігінде ![]() , осыдан
, осыдан ![]()
![]()
![]()
ОВ кесіндісінің шеткі нүктелерінде ![]()
АВ бөлігінде ![]()
![]()
немесе ![]()
![]()
![]() ,
, ![]() ,
, ![]()
![]()
АВ кесіндісінің шеткі нүктелеріндегі мәндері белгілі.
Табылған ![]() мәндерін салыстыра отырып,
мәндерін салыстыра отырып, ![]() функциясының
функциясының ![]() облысындағы ең
үлкен мәні
облысындағы ең
үлкен мәні ![]() ал ең кіші мәні
ал ең кіші мәні ![]() болатындығын
анықтаймыз.
болатындығын
анықтаймыз.
![]() функциясының
байланыс теңдеуі
функциясының
байланыс теңдеуі ![]() берілген жағдайдағы шартты
экстремумын табу керек.
берілген жағдайдағы шартты
экстремумын табу керек.
![]() функциясының
байланыс теңдеуі
функциясының
байланыс теңдеуі ![]() берілген жағдайдағы шартты
экстремумын табу керек.
берілген жағдайдағы шартты
экстремумын табу керек.
Берілген ![]() функциясының берілген
сызықтармен шектелген
функциясының берілген
сызықтармен шектелген ![]() облысында ең үлкен және
ең кіші мәндерін табу керек:
облысында ең үлкен және
ең кіші мәндерін табу керек:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
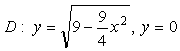
2 ЕКІ ЕСЕЛІ ИНТЕГРАЛДАР
2.1 Тік бұрышты координаталар (мекендіктер) жүйесінде анықталған екі еселі интегралдар.
![]() жазықтығының
жабық
жазықтығының
жабық ![]() аймағында
анықталған
аймағында
анықталған ![]() функциясы берілсін.
функциясы берілсін.
![]() аймағын кез
келген жолмен
аймағын кез
келген жолмен ![]() жай
аймақтарға бөлейік. Осы жай (қарапайым) аймақтардың аудандарын
жай
аймақтарға бөлейік. Осы жай (қарапайым) аймақтардың аудандарын ![]() деп, ал сәйкес
диаметрлерін
деп, ал сәйкес
диаметрлерін ![]() арқылы
белгілейік, мұндағы аймақ диаметрі деп осы аймақта
жататын кезкелеген екі нүктенің ара
қашықтықтарының ең үлкенін айтады.
Әрбір жай аймақтан кез келген бір
арқылы
белгілейік, мұндағы аймақ диаметрі деп осы аймақта
жататын кезкелеген екі нүктенің ара
қашықтықтарының ең үлкенін айтады.
Әрбір жай аймақтан кез келген бір ![]() ,
, ![]() нүктеден таңдап алып, осы
нүктелердегі анықталатын функциялардың мәндерін
сәйкес
нүктеден таңдап алып, осы
нүктелердегі анықталатын функциялардың мәндерін
сәйкес ![]() аудандарына
көбейтіп қолдансақ:
аудандарына
көбейтіп қолдансақ:
![]() .
.
Осы қосынды ![]() функциясының
функциясының ![]() аймағындағы
интегралдық қосындысы деп аталады.
аймағындағы
интегралдық қосындысы деп аталады.
Егер интегралдық қосындының ![]() шегі бар және ол
шек
шегі бар және ол
шек ![]() аймағын
аймағын
![]() жай
аймақтарға қалай бөлгенімізге де, әрбір жай
аймақтан
жай
аймақтарға қалай бөлгенімізге де, әрбір жай
аймақтан ![]() нүктелерін
қалай алғанымызға да байланысты болмаса, онда осы шек
нүктелерін
қалай алғанымызға да байланысты болмаса, онда осы шек ![]() функциясының
функциясының ![]() аймағындағы
екі еселі интегралы деп аталады да былай белгіленеді:
аймағындағы
екі еселі интегралы деп аталады да былай белгіленеді:
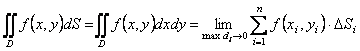 (1)
(1)
Егер ![]() аймағында
аймағында ![]() болса, онда
болса, онда ![]() екі еселі интегралы
жоғарыдан
екі еселі интегралы
жоғарыдан ![]() бетімен,
бүйір жағынан
бетімен,
бүйір жағынан ![]() аймағының шекарасы
арқылы өтетін
аймағының шекарасы
арқылы өтетін ![]() осіне параллель болатын цилиндр бетімен,
төменнен
осіне параллель болатын цилиндр бетімен,
төменнен ![]() жазықтығымен
шектелген цилиндрлік дененің көлеміне тең болады.
жазықтығымен
шектелген цилиндрлік дененің көлеміне тең болады.
Екі еселі интегралдың негізгі қасиеттері:
1.
![]() .
.
2.
![]() , мұндағы
, мұндағы ![]() – тұрақты
сан.
– тұрақты
сан.
3.
Егер ![]() аймағын
аймағын ![]() және
және ![]() аймақтарына
бөлсек, онда
аймақтарына
бөлсек, онда
![]() .
.
4.
Егер ![]() аймағында
аймағында ![]() болса, онда
болса, онда ![]() .
.
5. Екі еселі интегралды бағалау.
Егер ![]() болма, онда
болма, онда ![]() ,
,
мұндағы ![]() –
– ![]() аймағының ауданы, ал
аймағының ауданы, ал ![]() мен
мен ![]() сәйкесінше
сәйкесінше ![]() функциясының осы
аймақтағы ең кіші және ең үлкен
мәндері.
функциясының осы
аймақтағы ең кіші және ең үлкен
мәндері.
6.
![]() функциясының
функциясының ![]() аймағындағы
орта мәні туралы теорема.
аймағындағы
орта мәні туралы теорема.
Егер ![]() аймағында
аймағында ![]() функциясы үзіліссіз
болса, онда
функциясы үзіліссіз
болса, онда ![]() теңдігі
орындалатындай осы аймақта жататын
теңдігі
орындалатындай осы аймақта жататын ![]() нүктесі табылады.
нүктесі табылады.
Екі еселі интегралды есептеу
Интегралдау аймағы берілу пішіні (тұрпаты) бойынша екі түрге бөлінеді.
а) ![]() аймағы
аймағы ![]() мен
мен ![]()
![]() түзулерімен
түзулерімен ![]() пен
пен ![]() (
(![]() жатқанда
жатқанда ![]() ) үзіліссіз
қисық сызықтарымен шектелсін әрі
) үзіліссіз
қисық сызықтарымен шектелсін әрі ![]() осіне (беліне) параллель
(қатарлас) жүргізілген түзулер осы
қисықтардың әрқайсысын тек бір нүктеде
қисын (2 - сурет).
осіне (беліне) параллель
(қатарлас) жүргізілген түзулер осы
қисықтардың әрқайсысын тек бір нүктеде
қисын (2 - сурет).
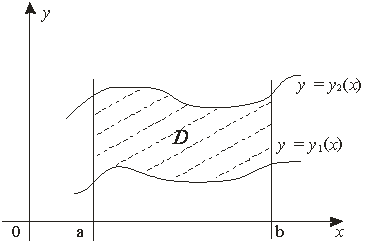
2 – сурет
Осындай аймақ үшін екі еселі интеграл формуласымен
(кейіптемесімен) есептелінеді. Есептеу кезінде алдымен ішкі 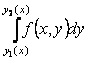 интегралы есептелінеді
әрі бұл жағдайда
интегралы есептелінеді
әрі бұл жағдайда ![]() айнымалысы тұрақты деп
саналады.
айнымалысы тұрақты деп
саналады.
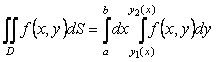 (2)
(2)
б) ![]() аймағы
аймағы ![]() мен
мен ![]()
![]() түзулерімен
түзулерімен ![]() пен
пен ![]() (
(![]() жатқанда
жатқанда ![]() ) үзіліссіз
қисық сызықтарымен шектелсін әрі
) үзіліссіз
қисық сызықтарымен шектелсін әрі ![]() осіне (беліне) параллель
(қатарлас) жүргізілген түзулер осы
қисықтардың әрқайсысын тек бір нүктеде
қисын (3 – сурет).
осіне (беліне) параллель
(қатарлас) жүргізілген түзулер осы
қисықтардың әрқайсысын тек бір нүктеде
қисын (3 – сурет).
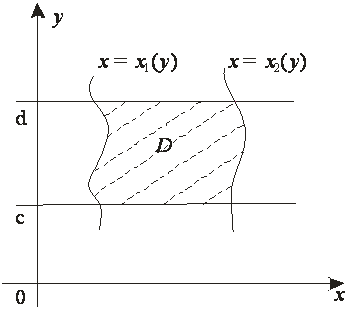
3-сурет
Осындай аймақ үшін екі еселі интеграл
формуласымен (кейіптемесімен) есептелінеді. Есептеу кезінде алдымен ішкі 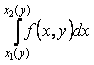 интегралы есептелінеді
әрі бұл жағдайда
интегралы есептелінеді
әрі бұл жағдайда ![]() айнымалысы тұрақты деп
саналады.
айнымалысы тұрақты деп
саналады.
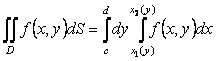 (3)
(3)
Берілген формулалардың оң жақтары қайталама интегралдар деп аталады.
1-мысал. 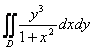 интегралын
есептеу керек, мұндағы
интегралын
есептеу керек, мұндағы ![]() аймағы тіктөртбұрыш:
аймағы тіктөртбұрыш: ![]() .
.
Шешуі. 
2-мысал. ![]() интегралын
есептеу керек, мұндағы
интегралын
есептеу керек, мұндағы ![]() аймағы квадрат:
аймағы квадрат: ![]() .
.
Шешуі. 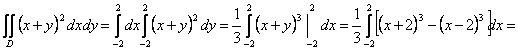
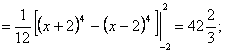
3-мысал. 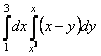 интегралын есептеу керек.
интегралын есептеу керек.
Шешуі.  .
.
4-мысал. ![]() интегалын есептеу керек,
мұндағы
интегалын есептеу керек,
мұндағы ![]() аймағы
аймағы
![]() параболаларымен
шектелген.
параболаларымен
шектелген.
Шешуі. ![]() аймағын сызайық.
аймағын сызайық. ![]() және
және ![]() параболаларының
қиылысу нүктелері
параболаларының
қиылысу нүктелері ![]() және
және ![]() болады (4 - сурет).
болады (4 - сурет).
![]() болғандықтан
болғандықтан
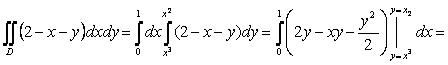
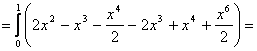
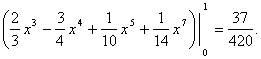
4-сурет
Енді осы интегралдың интегралдау ретін
өзгертейік. Алдымен ![]() бойынша одан кейін
бойынша одан кейін ![]() бойынша интегралдайық.
бойынша интегралдайық.
![]() болғандықтан
болғандықтан ![]()

5-мысал. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() аймағы
аймағы
![]() параболасымен
параболасымен
![]() түзулерімен
шектелген.
түзулерімен
шектелген.
Шешуі. ![]() аймағын құрайық (5-сурет).
аймағын құрайық (5-сурет).
Қиылысу нүктелері ![]() ,
, ![]() болады. Алдымен
болады. Алдымен ![]() бойынша, одан кейін
бойынша, одан кейін ![]() бойынша
интегралдайық.
бойынша
интегралдайық. ![]() болғандықтан
болғандықтан

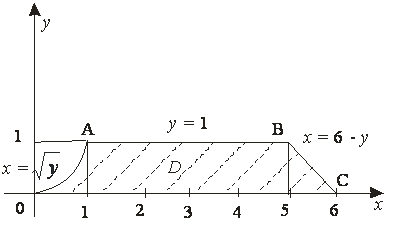
5-сурет
Енді интегралдау ретін өгертейік. Алдымен ![]() бойынша, содан кейін
бойынша, содан кейін ![]() бойынша
интегралдайық (6-сурет).
бойынша
интегралдайық (6-сурет).
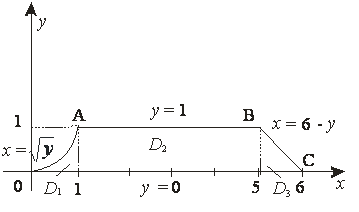
6-сурет
Бұл жағдайда ![]() облысы үш
облысы үш ![]() облыстарына бөлінеді:
облыстарына бөлінеді:
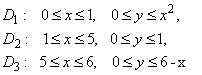
![]() ,
,
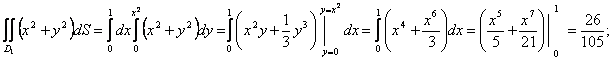
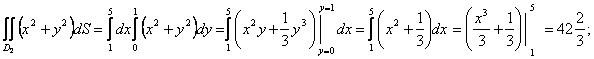
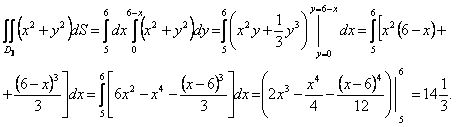
Сонымен 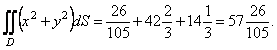
6-мысал. ![]() функциясының
функциясының ![]() аймағындағы орта
мәнін табу керек, мұндағы
аймағындағы орта
мәнін табу керек, мұндағы ![]() аймағы:
аймағы: ![]()
Шешуі. ![]() ,
,
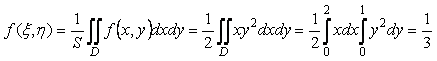 .
.
7-мысал. 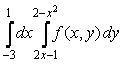 интегралының интегралдау ретін
өзгерту керек.
интегралының интегралдау ретін
өзгерту керек.
Шешуі. ![]() аймағы
аймағы ![]() сызықтарымен шектелеген.
Интегралдау ретін өзгерту үшін
сызықтарымен шектелеген.
Интегралдау ретін өзгерту үшін ![]() аймағын
аймағын ![]() түзуімен
түзуімен ![]() және
және ![]() аймақтарына
бөлеміз (7-сурет):
аймақтарына
бөлеміз (7-сурет):
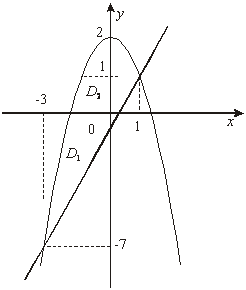
6-сурет
![]() аймағы сол жағынан
аймағы сол жағынан ![]() параболасымен, ал
оң жағынан
параболасымен, ал
оң жағынан ![]() түзуімен шектелген, яғни
түзуімен шектелген, яғни ![]() ,
, ![]() .
.
![]() аймағы оң және сол
жағынан
аймағы оң және сол
жағынан ![]() параболасымен
шектелген, яғни
параболасымен
шектелген, яғни ![]() .
.
Сонымен 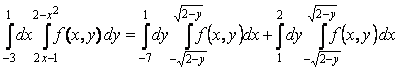
1. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() тіктөртбұрыш:
тіктөртбұрыш:
![]() .
.
2. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() тіктөртбұрыш:
тіктөртбұрыш:
![]() .
.
3. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() тіктөртбұрыш:
тіктөртбұрыш:
![]() .
.
4. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() квадрат:
квадрат:
![]() .
.
5. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() тіктөртбұрыш:
тіктөртбұрыш:
![]() .
.
6. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() квадрат:
квадрат:
![]() .
.
7. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() квадрат:
квадрат:
![]() .
.
8. 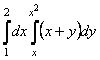 интегралын есептеу керек.
интегралын есептеу керек.
9. 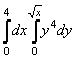 интегралын есептеу керек.
интегралын есептеу керек.
10. 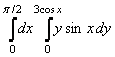 интегралын есептеу керек.
интегралын есептеу керек.
11. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() аймағы
аймағы
![]() сызықтарымен
шектелген.
сызықтарымен
шектелген.
12. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() аймағы
аймағы
![]() және
және ![]() параболаларымен
шектелген.
параболаларымен
шектелген.
13. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() аймағы
аймағы
![]() түзулерімен
шектелген.
түзулерімен
шектелген.
14. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() аймағы
аймағы
![]() сызықтарымен
шектелген.
сызықтарымен
шектелген.
15. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() аймағы
аймағы
![]() сызықтарымен
шектелген.
сызықтарымен
шектелген.
16. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() аймағы
аймағы
![]() сызықтарымен
шектелген.
сызықтарымен
шектелген.
17. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() аймағы
аймағы
![]() сызықтарымен
шектелген.
сызықтарымен
шектелген.
Екі еселі интегралдардың интегралдау реттерін өзгерту керек:
|
18. |
19. |
|
20. |
21. |
|
22. |
23. |
|
24. |
25. |
2.2 Екі еселі интегралдағы айнымалыларды алмастыру
Екі еселі интегралда ![]() координатасынан,
координатасынан, ![]() формуласының
көмегімен,
формуласының
көмегімен, ![]() координатасына
көшу
координатасына
көшу
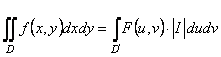 (4)
(4)
формуласымен жүзеге асады, мұндағы ![]() ;
;
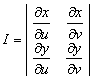 – якобиян,
– якобиян,
ал ![]() өзара
бірмәнді,
өзара
бірмәнді, ![]() аймағында
үзіліссіз әрі осы аймақта үзіліссіз бірінші ретті
дербес туындылары бар функциялар.
аймағында
үзіліссіз әрі осы аймақта үзіліссіз бірінші ретті
дербес туындылары бар функциялар.
2.3 Полярлық координаталар жүйесінде анықталған екі еселі интегралдар
Екі еселі интегралдарда тік бұрышты ![]() координаталарынан,
координаталарынан, ![]() ,
, ![]() формулаларының
көмегімен,
формулаларының
көмегімен, ![]() полярлық
координаталарына көшу
полярлық
координаталарына көшу
![]() (5)
(5)
формуласымен жүзеге асады. Мұндағы
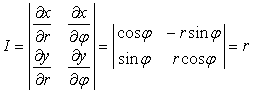
болады.
Егер интегралдау ![]() аймағы
аймағы ![]() және
және ![]()
![]() сәулелерімен,
сәулелерімен, ![]() және
және ![]() (
(![]() жатқанда
жатқанда ![]() болса) қисық
сызықтарымен шектелсе, онда екі еселі интеграл
болса) қисық
сызықтарымен шектелсе, онда екі еселі интеграл
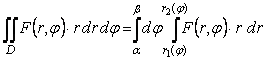
формуласымен есептелінеді (8-сурет).
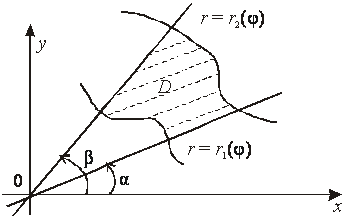
8-сурет
Егер екі еселі интегралдағы айнымалыларды
алмастыру ![]()
![]()
формулаларының көмегімен жасалса, онда мұндағы ![]() мен
мен ![]() жалпы
полярлық координаталар деп аталады да якобиян
жалпы
полярлық координаталар деп аталады да якобиян ![]() .
.
8-мысал. Полярлық координаталар жүйесіне
көшу арқылы ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() аймағы
аймағы
![]() шеңберімен
шектелген
шеңберімен
шектелген ![]() .
.
Шешуі. ![]() аймағы радиусы
аймағы радиусы ![]() тең, центрі
тең, центрі ![]() болатын
дөңгелек болғандықтан полярлық
координаталарға көшеміз.
болатын
дөңгелек болғандықтан полярлық
координаталарға көшеміз. ![]() шеңбері полярлық
координаталар жүйесінде
шеңбері полярлық
координаталар жүйесінде ![]() формуласы арқылы анықталады.
формуласы арқылы анықталады. ![]() болғандықтан
(5) – формуланы қолдансақ
болғандықтан
(5) – формуланы қолдансақ

9-мысал. 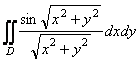 интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() аймағы
аймағы
![]() ,
, ![]() шеңберлерімен
шектелген.
шеңберлерімен
шектелген.
Шешуі. ![]() аймағы радиустары
аймағы радиустары ![]() -ке және
-ке және ![]() -ге тең, ал
центрлері координаталар жүйесінің бас нүктесі болатын екі
шеңбердің арасындағы сақина болғандықтан
полярлық координаталарға көшеміз. Бұл шеңберлер
полярлық координаталар жүйесінде
-ге тең, ал
центрлері координаталар жүйесінің бас нүктесі болатын екі
шеңбердің арасындағы сақина болғандықтан
полярлық координаталарға көшеміз. Бұл шеңберлер
полярлық координаталар жүйесінде ![]() және
және ![]() формулалры арқылы анықталады.
Сондықтан
формулалры арқылы анықталады.
Сондықтан ![]() болғандықтан,
(5)-формуланы қолдансақ
болғандықтан,
(5)-формуланы қолдансақ
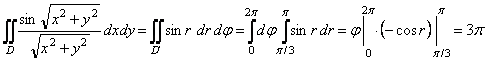 .
.
10-мысал.  интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() аймағы
аймағы
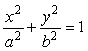 эллипсімен
шектелген.
эллипсімен
шектелген.
Шешуі. ![]()
![]() деп алсақ, онда
деп алсақ, онда ![]() эллипсінің полярлық
координаталар жүйесіндегі теңдеуі
эллипсінің полярлық
координаталар жүйесіндегі теңдеуі ![]() . Якобиян
. Якобиян 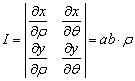 , ал
, ал ![]() болғандықтан
болғандықтан

11-мысал. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() аймағы
аймағы
![]()
![]()
![]() түзулерімен шектелген.
түзулерімен шектелген.
Шешуі. ![]() немесе
немесе ![]() деп алсақ, онда
деп алсақ, онда ![]() , ал якобиян
, ал якобиян
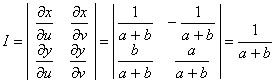 болады.
Сонымен
болады.
Сонымен
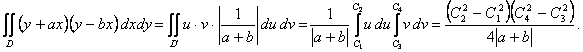
Полярлық координаталарға көшу арқылы келесі екі еселі интегралдарды есептеу керек:
26. ![]() , мұндағы
, мұндағы ![]() аймағы
аймағы ![]() шеңберімен
шектелген.
шеңберімен
шектелген.
27. ![]() , мұндағы
, мұндағы ![]() аймағы
аймағы ![]() дөңгелегінің
бірінші ширегі.
дөңгелегінің
бірінші ширегі.
28.  , мұндағы
, мұндағы ![]() аймағы
аймағы ![]() және
және ![]() шеңберлерімен
шектелген.
шеңберлерімен
шектелген.
29. ![]() , мұндағы
, мұндағы ![]() аймағы
аймағы ![]() жарты
шеңберімен,
жарты
шеңберімен, ![]() осімен
шектелген
осімен
шектелген ![]() .
.
30. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() аймағы
аймағы
![]() пен
пен ![]()
![]() және
және ![]() мен
мен ![]() гиперболасымен шектелген.
гиперболасымен шектелген.
Ескерту. ![]() .
.
2.4 Жазық фигуралардың (пішіндердің) аудандарын есептеу
![]() аймағымен шектелген жазық
фигураның ауданы
аймағымен шектелген жазық
фигураның ауданы
![]() (6)
(6)
формуласымен анықталады.
Егер ![]() аймағы
аймағы ![]() теңсіздіктерімен
шектелсе, онда
теңсіздіктерімен
шектелсе, онда
 .
.
Егер ![]() аймағы полярлық координаталар
жүйесінде
аймағы полярлық координаталар
жүйесінде ![]() ,
,
![]() теңсіздіктерімен
шектелсе, онда
теңсіздіктерімен
шектелсе, онда
 .
.
12-мысал. ![]() және
және ![]() сызықтарымен шектелген жазық
фигураның ауданын табу керек.
сызықтарымен шектелген жазық
фигураның ауданын табу керек.
Шешуі. Берілген сызықтардың қиылысу нүктелерін табамыз:
![]()
олар ![]() және
және
![]() нүктелері
(9-сурет). Сонымен
нүктелері
(9-сурет). Сонымен ![]() ,
,
![]() болғандықтан
болғандықтан
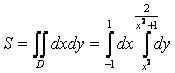
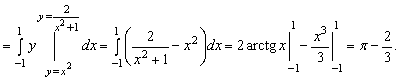
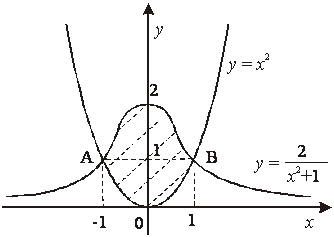
9-сурет
13-мысал. Полярлық координаталар жүйесіне
көшу арқылы ![]() қисық сызығымен
шектелген жазық фигураның ауданын табу керек
қисық сызығымен
шектелген жазық фигураның ауданын табу керек ![]() .
.
Шешуі. ![]() формулалары арқылы полярлық
координаталар жүйесіне көшсек
формулалары арқылы полярлық
координаталар жүйесіне көшсек ![]() немесе
немесе
![]() , мұндағы
, мұндағы ![]() болғандықтан
болғандықтан ![]() . Яғни
. Яғни ![]() 0-ден
0-ден ![]() -ке дейін
өзгергендегі фигураның ауданы берілген фигураның
ауданының жартысына тең болады (10-сурет).
-ке дейін
өзгергендегі фигураның ауданы берілген фигураның
ауданының жартысына тең болады (10-сурет).
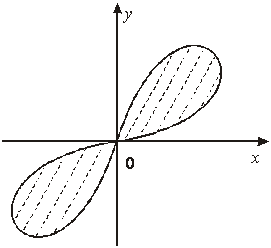
10- сурет
Сонымен

Берілген сызықтармен шектелген жазық фигуралардың аудандарын табу керек:
31. ![]() .
32.
.
32. ![]() .
.
33. ![]() .
34.
.
34. ![]()
35. ![]() (эллипс).
36.
(эллипс).
36. ![]() .
.
37. ![]() .
38.
.
38. ![]() .
.
39. ![]() .
40.
.
40. ![]() .
.
2.5 Денелердің көлемдерін есептеу
Жоғарыдан ![]() бетімен, төменнен
бетімен, төменнен ![]() жазықтығымен,
бүйір жағынан
жазықтығымен,
бүйір жағынан ![]() облысының шекарасы арқылы
өтетін
облысының шекарасы арқылы
өтетін ![]() осіне
параллель болатын цилиндр бетімен шектелеген дененің көлемі
осіне
параллель болатын цилиндр бетімен шектелеген дененің көлемі
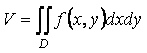 (7)
(7)
формуласымен есептеледі.
14-мысал. ![]() бетімен,
бетімен, ![]() ,
, ![]() жазықтықтарымен шектелген
дененің көлемін табу керек.
жазықтықтарымен шектелген
дененің көлемін табу керек.
Шешуі. Берілген дене жоғарыдан ![]() бетімен,
төменнен
бетімен,
төменнен ![]() жазықтығымен,
ал бүйір жағынан
жазықтығымен,
ал бүйір жағынан ![]() және
және ![]() жазықтықтармен шектелген (11-сурет).
жазықтықтармен шектелген (11-сурет).
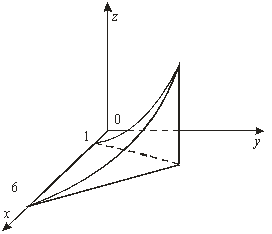
11-сурет
Сондықтан ![]() , ал интегралдау
, ал интегралдау ![]() аймағы
аймағы ![]() теңсіздіктерімен
шектелген (12-сурет). Сонымен
теңсіздіктерімен
шектелген (12-сурет). Сонымен

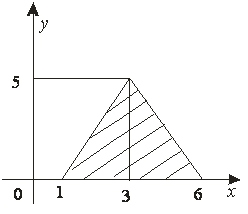
12-сурет
15-мысал. ![]() параболоидымен және
параболоидымен және ![]() жазықтығы-мен
шектелген дененің көлемін табу керек (13-сурет).
жазықтығы-мен
шектелген дененің көлемін табу керек (13-сурет).
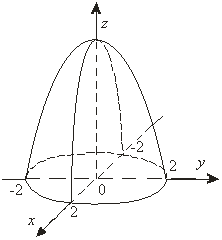
13-сурет
Шешуі. Жоғарыдан ![]() параболоидымен, төменнен
параболоидымен, төменнен ![]() жазықтығымен
шектелген дененің көлемі
жазықтығымен
шектелген дененің көлемі
![]() .
.
Интегралымен анықталады, мұндағы ![]() аймағы
аймағы ![]() шеңберімен
шектелген. Бұл жағдайда
шеңберімен
шектелген. Бұл жағдайда ![]() формулаларының көмегімен
полярлық координаталар жүйесіне көшеміз.
формулаларының көмегімен
полярлық координаталар жүйесіне көшеміз. ![]() ,
, ![]() болғандықтан
болғандықтан
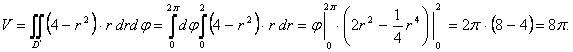
Берілген беттермен шектелген денелердің көлемдерін табу керек:
41. ![]() (бірінші октантта орналасқан).
(бірінші октантта орналасқан).
42. ![]() .
.
43. ![]() .
.
44. ![]()
![]() (бірінші октантта орналасқан).
(бірінші октантта орналасқан).
45. ![]() .
.
2.6 Беттің ауданын есептеу
Егер бет ![]() теңдеуімен берілсе, онда оның
ауданы
теңдеуімен берілсе, онда оның
ауданы
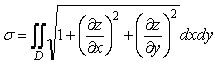 (8)
(8)
формуласымен анықталады, мұндағы ![]() аймағы берілген
беттің
аймағы берілген
беттің ![]() жазықтығындағы
проекциясы.
жазықтығындағы
проекциясы.
Егер бет ![]() теңдеуімен берілсе, онда оның
ауданы
теңдеуімен берілсе, онда оның
ауданы
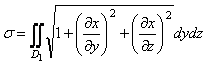
формуласымен анықталады, мұндағы ![]() аймағы берілген
беттің
аймағы берілген
беттің ![]() жазықтығындағы
проекциясы.
жазықтығындағы
проекциясы.
Егер бет ![]() теңдеуімен берілсе, онда оның
ауданы
теңдеуімен берілсе, онда оның
ауданы
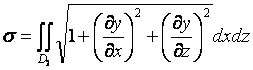
формуласымен анықталады, мұндағы ![]() аймағы берілген
беттің
аймағы берілген
беттің ![]() жазықтығындағы
проекциясы.
жазықтығындағы
проекциясы.
16-мысал. ![]() сферасының
сферасының ![]() цилиндрінің ішіндегі
бөлігінің бетінің ауданын табу керек
цилиндрінің ішіндегі
бөлігінің бетінің ауданын табу керек ![]() , (14-сурет).
, (14-сурет).
Шешуі. Сфера теңдеуінен
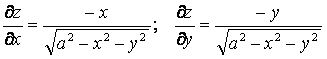
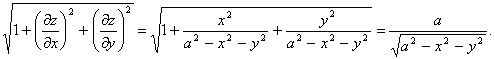
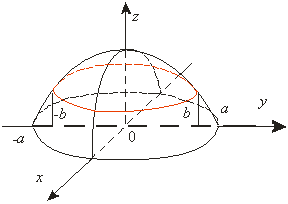
14-сурет
Интегралдау аймағы ![]() дөңгелегі болады. Осыдан
дөңгелегі болады. Осыдан
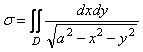 .
.
Полярлық координаталар жүйесіне көшсек, онда
дөңгелектің теңдеуі ![]() болғандықтан
болғандықтан
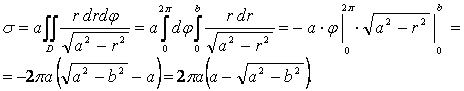
46. ![]() конусының
конусының ![]() цилиндрінің ішіндегі
бөлігінің бетінің ауданын табу керек.
цилиндрінің ішіндегі
бөлігінің бетінің ауданын табу керек.
47. ![]() параболоидының
параболоидының ![]() цилиндрімен
қиғандағы бөлігінің бетінің ауданын табу
керек.
цилиндрімен
қиғандағы бөлігінің бетінің ауданын табу
керек.
48. ![]() жазықтығының координата
жазықтықтарымен шектелген бөлігінің ауданын табу керек.
жазықтығының координата
жазықтықтарымен шектелген бөлігінің ауданын табу керек.
49. ![]() цилиндрін
цилиндрін ![]() жазықтықтарымен қиғандағы
бөлігінің ауданын табу керек
жазықтықтарымен қиғандағы
бөлігінің ауданын табу керек ![]() .
.
50. ![]() бетін
бетін ![]() жазықтықтарымен
қиғандағы бөлігінің ауданын табу керек.
жазықтықтарымен
қиғандағы бөлігінің ауданын табу керек.
2.7 Екі еселі интегралдардың механикада және физикада қолданылуы
![]() жазықтығында аумағы
жазықтығында аумағы ![]() аймағы, ал
тығыздығы
аймағы, ал
тығыздығы ![]() болатын пластинканың массасы
болатын пластинканың массасы
![]() ,
,
![]() және
және ![]() остеріне қарағандағы
статикалық моменттері
остеріне қарағандағы
статикалық моменттері
![]()
формулаларымен анықталады.
Біртекті пластинка үшін ![]() .
.
Пластинканың аурылық орталығы (кіндігі)
![]()
формулаларымен анықталады. Егер ![]() (яғни пластинка біртекті) болса,
онда
(яғни пластинка біртекті) болса,
онда
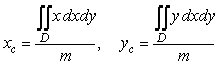 .
.
![]() және
және ![]() остеріне қарағандағы
инерция моменттері
остеріне қарағандағы
инерция моменттері
![]() ,
,
ал координата бас нүктесіне қарағандағы инерция моменті
![]()
формулаларымен анықталады.
17-мысал. ![]() эллипсін
эллипсін ![]() түзуімен қиғанда пайда
болатын сегменттің ауырлық орталығын табу керек
түзуімен қиғанда пайда
болатын сегменттің ауырлық орталығын табу керек ![]() , (15-сурет).
, (15-сурет).
Шешуі.
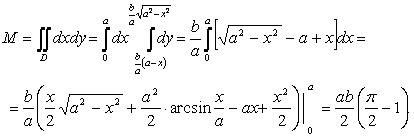


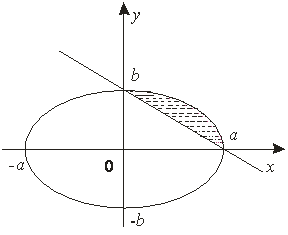
15-сурет
18-мысал. ![]() сызықтарымен шектелген
пластинканың
сызықтарымен шектелген
пластинканың ![]() остеріне,
координаталар жүйесінің бас нүктесіне
қарағандағы инерция моменттерін табу керек
остеріне,
координаталар жүйесінің бас нүктесіне
қарағандағы инерция моменттерін табу керек ![]() , (16-сурет).
, (16-сурет).
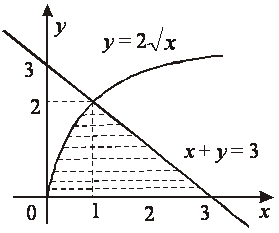
16-сурет
Шешуі.
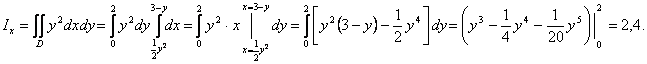

![]() .
.
51.
Тығыздығы ![]() тең
тең ![]() түзулерімен шектелген
үшбұрышты түрде берілген пластинканың массасын,
статикалық моменттерін, ауырлық орталығын (кіндігін) табу
керек.
түзулерімен шектелген
үшбұрышты түрде берілген пластинканың массасын,
статикалық моменттерін, ауырлық орталығын (кіндігін) табу
керек.
52. ![]() параболаларымен
шектелген біртекті пішіннің ауырлық орталығын табу керек.
параболаларымен
шектелген біртекті пішіннің ауырлық орталығын табу керек.
53. ![]() сызықтарымен
шектелген біртекті пішіннің ауырлық орталығын табу керек.
сызықтарымен
шектелген біртекті пішіннің ауырлық орталығын табу керек.
54. ![]() параболасымен
және
параболасымен
және ![]() түзуінің
қиылысынан пайда болған біртекті пішіннің ауырлық
орталығын табу керек.
түзуінің
қиылысынан пайда болған біртекті пішіннің ауырлық
орталығын табу керек.
55. ![]() шеңберімен
және
шеңберімен
және ![]() түзуімен
шектелген біртекті пішіннің ауырлық орталығын табу керек.
түзуімен
шектелген біртекті пішіннің ауырлық орталығын табу керек.
56. ![]() кардиоидасымен
шектелген біртекті пішіннің ауырлық орталығын табу керек.
кардиоидасымен
шектелген біртекті пішіннің ауырлық орталығын табу керек.
57. ![]() түзулерімен
шектелген біртекті пішіннің
түзулерімен
шектелген біртекті пішіннің ![]() өстеріне (белдеріне) және
координаталар жүйесінің бас нүктесіне
қарағандағы инерция моменттерін есептеу керек.
өстеріне (белдеріне) және
координаталар жүйесінің бас нүктесіне
қарағандағы инерция моменттерін есептеу керек.
58. ![]() шеңберлерімен
шектелген біртекті сақинаның
шеңберлерімен
шектелген біртекті сақинаның ![]() остеріне және координаталар
жүйесінің бас нүктесіне қарағандағы инерция
моменттерін есептеу керек.
остеріне және координаталар
жүйесінің бас нүктесіне қарағандағы инерция
моменттерін есептеу керек.
59. ![]() параболасымен,
параболасымен,
![]() түзуімен
шектелген біртекті пішіннің
түзуімен
шектелген біртекті пішіннің ![]() өстеріне және координаталар
жүйесінің бас нүктесіне қарағандағы инерция
моменттерін есептеу керек.
өстеріне және координаталар
жүйесінің бас нүктесіне қарағандағы инерция
моменттерін есептеу керек.
60. ![]() кардиоидасының
кардиоидасының
![]() өстеріне
(белдеріне) және координаталар жүйесінің бас нүктесіне
қарағандағы инерция моменттерін есептеу керек.
өстеріне
(белдеріне) және координаталар жүйесінің бас нүктесіне
қарағандағы инерция моменттерін есептеу керек.
3 ҮШ ЕСЕЛІ ИНТЕГРАЛДАР
3.1 Тік бұрышты координаталар жүйесіндегі үш еселі интегралдар.
![]() кеңістігіндегі тұйық
кеңістігіндегі тұйық ![]() аймақта
анықталған
аймақта
анықталған ![]() функциясы берілсін. Үш
өлшемді
функциясы берілсін. Үш
өлшемді ![]() аймағын
кез келген жолмен
аймағын
кез келген жолмен ![]() қарапайым
аймақтарға бөлейік. Осы қарапайым
аймақтардың көлемдерін
қарапайым
аймақтарға бөлейік. Осы қарапайым
аймақтардың көлемдерін ![]() , ал оларға сәйкес диаметрлерін
, ал оларға сәйкес диаметрлерін ![]() арқылы белгілейік,
мұндағы аймақтардың диаметрі деп осы
аймақтың шекарасындағы (бетіндегі) екі нүктенің
ара қашықтықтарының ең үлкенін айтады.
арқылы белгілейік,
мұндағы аймақтардың диаметрі деп осы
аймақтың шекарасындағы (бетіндегі) екі нүктенің
ара қашықтықтарының ең үлкенін айтады.
Әрбір қарапайым аймақтардан кез
келген бір ![]() нүктеден
таңдап алып, осы нүктелердегі берілген функциялардың
мәндерін сәйкес
нүктеден
таңдап алып, осы нүктелердегі берілген функциялардың
мәндерін сәйкес ![]() көлемдеріне көбейтіп
қоссақ
көлемдеріне көбейтіп
қоссақ ![]() өрнегіне
шығады. Осы қосынды
өрнегіне
шығады. Осы қосынды ![]() функциясының
функциясының ![]() аймағындағы
интегралдық қосындысы деп аталады.
аймағындағы
интегралдық қосындысы деп аталады.
Егер осы интегралдық қосындының ![]() шегі бар және ол
шек үш өлшемдіге аймағының
шегі бар және ол
шек үш өлшемдіге аймағының ![]() қарапайым
аймақтарға қалай бөлгенінен де, әрбір
қарапайым аймақтардан
қарапайым
аймақтарға қалай бөлгенінен де, әрбір
қарапайым аймақтардан ![]() нүктесінің қалай
алғанынанда тәуелсіз болса, онда осы шек
нүктесінің қалай
алғанынанда тәуелсіз болса, онда осы шек ![]() функциясының
функциясының ![]() аймағындағы
үш еселі интегралы деп аталады да былай белгіленеді:
аймағындағы
үш еселі интегралы деп аталады да былай белгіленеді:
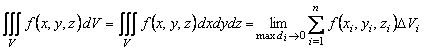 . (3.1)
. (3.1)
Егер үш өлшемді ![]() аймағында
аймағында ![]() болса, онда
болса, онда ![]() үш еселі интегралы
тығыздығы
үш еселі интегралы
тығыздығы ![]() болатын
болатын ![]() денесінің массасына тең
болады.
денесінің массасына тең
болады.
Үш еселі интегралдың негізгі қасиеттері екі еселі интегралдың негізгі қасиеттері сияқты болады.
Интегралдау ![]() аймағы
аймағы ![]() ,
, ![]() ,
, ![]() теңсіздіктерінен анықталсын,
мұндағы
теңсіздіктерінен анықталсын,
мұндағы ![]() –
үзіліссіз функциялар. Осы
–
үзіліссіз функциялар. Осы ![]() аймағында
аймағында ![]() функциясының үш
еселі интегралы
функциясының үш
еселі интегралы
 (3.2)
(3.2)
формуласымен анықталады.
19-мысал. 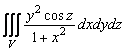 интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() денесі
денесі
![]() теңсіздіктерімен
анықталады.
теңсіздіктерімен
анықталады.
Шешуі.
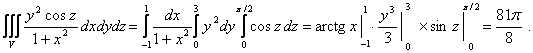
20-мысал. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() денесі
денесі
![]() теңсіздіктерімен
анықталады.
теңсіздіктерімен
анықталады.
Шешуі.

21-мысал. 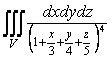 интегралын есептеу керек,
мұндағы үш өлшемді
интегралын есептеу керек,
мұндағы үш өлшемді ![]() денесі координаталар
жазықтықтары мен
денесі координаталар
жазықтықтары мен ![]() жазықтығымен шектелген.
жазықтығымен шектелген.
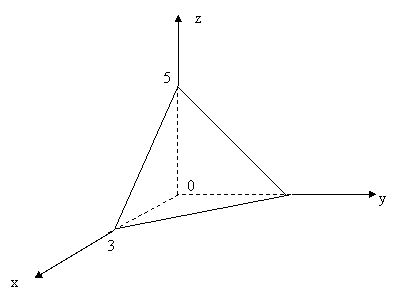 |

17-сурет
![]()
Шешуі. ![]() денесі жоғарыдан
денесі жоғарыдан
![]() , ал төменнен
, ал төменнен ![]() жазықтығымен
шектелген.
жазықтығымен
шектелген. ![]() денесінің
денесінің
![]() жазықтығындағы
проекциясы
жазықтығындағы
проекциясы 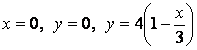 түзулермен
шектелген үшбұрыш. Сонымен
түзулермен
шектелген үшбұрыш. Сонымен

 |
18-сурет
22-мысал. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() денесі
денесі
![]()
![]() жазықтықтарымен шектелген.
жазықтықтарымен шектелген.
Шешуі. ![]() денесі жоғарыдан
денесі жоғарыдан ![]() , төменнен
, төменнен ![]() жазықтығымен
шектелген.
жазықтығымен
шектелген. ![]() денесінің
денесінің
![]() жазықтығындағы
проекциясы
жазықтығындағы
проекциясы ![]()
![]()
![]() жузулерімен шектелген,
яғни
жузулерімен шектелген,
яғни ![]() ,
,
![]() .
.
Сонымен
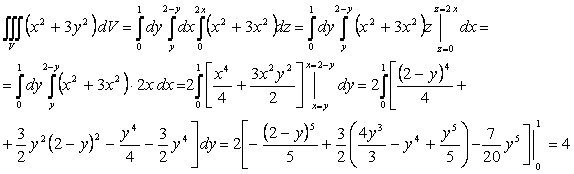
19-сурет
61. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() денесі
денесі
![]() теңсіздіктерімен
анықталған.
теңсіздіктерімен
анықталған.
62. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() денесі
денесі
![]() теңсіздіктерімен
анықталған.
теңсіздіктерімен
анықталған.
63. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() денесі
денесі
![]() теңсіздіктерімен
анықталған.
теңсіздіктерімен
анықталған.
64. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() денесі
денесі
![]() ,
, ![]() ,
, ![]() ,
, ![]() жазықтықтарымен шектелген.
жазықтықтарымен шектелген.
65. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() денесі
денесі
![]() конустық
бетімен және
конустық
бетімен және ![]() жазықтығымен
шектелген.
жазықтығымен
шектелген.
3.2 Үш еселі интегралдағы айнымалыларды алмастыру
Үш еселі интегралда ![]() координаталарынан
координаталарынан ![]()
![]()
![]() формулаларының көмегімен
формулаларының көмегімен ![]() координатасына
көшу
координатасына
көшу
![]() (3.3)
(3.3)
формуласымен жүзеге асады, мұндағы
![]() ,
,
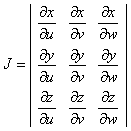 – якобиян, ал
– якобиян, ал
![]()
![]()
![]() өзара бір мәнді
функциялар. Бұл функнциялар үш өлшемді
өзара бір мәнді
функциялар. Бұл функнциялар үш өлшемді ![]() аймағында үзіліссіз
әрі олардың үзіліссіз бірінші ретті дербес туындылары бар.
аймағында үзіліссіз
әрі олардың үзіліссіз бірінші ретті дербес туындылары бар.
Дербес жағдайда ![]() тікбұрышты координаталардан
тікбұрышты координаталардан
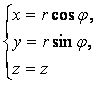 (3.4)
(3.4)
![]()
формулаларының көмегімен ![]() цилиндрлік координатларға
көшкенде якобиан
цилиндрлік координатларға
көшкенде якобиан ![]() болады. Сондықтан
болады. Сондықтан
![]() . (3.5)
. (3.5)
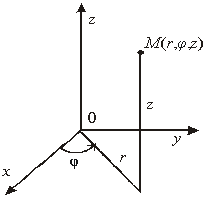
20-сурет
Ал ![]() тікбұрышты координаталардан
тікбұрышты координаталардан
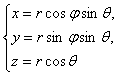 (3.6)
(3.6)
![]()
формулаларының көмегімен ![]() сфералық координаталарға
көшкенде якобиан
сфералық координаталарға
көшкенде якобиан ![]() болады. Сондықтан
болады. Сондықтан
![]() . (3.7)
. (3.7)
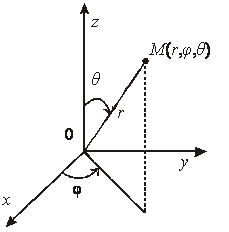
21-сурет
23-мысал. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() аймағы
аймағы
![]() цилиндрімен
және
цилиндрімен
және ![]() жазықтық-тарымен
шектелген.
жазықтық-тарымен
шектелген.
Шешуі. Цилиндрлік координаталарға көшейік.
Бұл жағдайда ![]() немесе
немесе ![]() ;
; ![]()
![]() . Сондықтан
. Сондықтан

24-мысал. ![]() интегралын есептеу керек,
мұндағы үш өлшемді
интегралын есептеу керек,
мұндағы үш өлшемді ![]() аймағы
аймағы ![]() шарымен шектелген.
шарымен шектелген.
Шешуі. Сфералық координаталар жүйесіне
көшейік. Бұл жағдайда ![]() ,
, ![]() ,
, ![]() . Сондықтан
. Сондықтан

66. 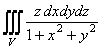 интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() денесі
денесі
![]() цилиндрімен
және
цилиндрімен
және ![]() жазықтықтарымен
шектелген.
жазықтықтарымен
шектелген.
67. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() денесі
денесі
![]() цилиндрімен,
цилиндрімен,
![]() конусымен
және
конусымен
және ![]() жазықтығымен
шектелген.
жазықтығымен
шектелген.
68. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() денесі
денесі
![]() цилиндрімен
және
цилиндрімен
және ![]() жазықтықтарымен
шектелген.
жазықтықтарымен
шектелген.
69. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() –
шар:
–
шар: ![]() .
.
70. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() –
шар:
–
шар: ![]() .
.
71. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() денесі
денесі
![]() сферасымен
және
сферасымен
және ![]() жазықтықтарымен
шектелген.
жазықтықтарымен
шектелген.
3.3 Үш еселі интегралдың механикада және физикада қолданылуы.
![]() денесінің көлемі
денесінің көлемі
![]() (3.8)
(3.8)
формуласымен есептеледі.
Тығыздығы ![]() болатын
болатын ![]() денесінің массасы
денесінің массасы
![]() ,
(3.9)
,
(3.9)
ал ![]() жазықтықтарына
қарағандағы статикалық моменттері сәйкесінше
жазықтықтарына
қарағандағы статикалық моменттері сәйкесінше
 (3.10)
(3.10)
формуласымен есептелінеді. Біртекті дене үшін ![]()
Дененің ауырлық орталығының (кіндігінің) координаталары
![]() (3.11)
(3.11)
формулаларымен анықталады. Егер дене біртекті болса, онда
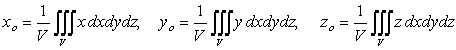 (3.12)
(3.12)
![]() өстеріне (белдеріне) және
өстеріне (белдеріне) және ![]() нүктесіне
қарағандағы инерция моменттері (екпіндік қарымдары)
сәйкес
нүктесіне
қарағандағы инерция моменттері (екпіндік қарымдары)
сәйкес
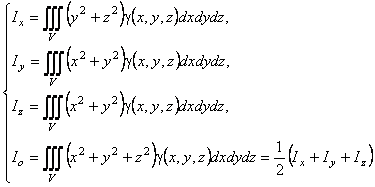 (3.13)
(3.13)
формулаларымен есептелінеді.
25-мысал. ![]() параболоидымен және
параболоидымен және ![]() жазықтығымен
шектелген дененің көлемін табу керек.
жазықтығымен
шектелген дененің көлемін табу керек.
Шешуі. Берілген дене жоғарыдан ![]() жазықтығымен,
ал төменнен
жазықтығымен,
ал төменнен ![]() параболоидымен
шектелген. Оның
параболоидымен
шектелген. Оның ![]() жазықтығындағы
проекциясы
жазықтығындағы
проекциясы ![]() теңсіздігімен
анықталатын дөңгелек. Бұл жағдайда цилиндрлік
координаталарға көшсек параболоидтың теңдеуі
теңсіздігімен
анықталатын дөңгелек. Бұл жағдайда цилиндрлік
координаталарға көшсек параболоидтың теңдеуі ![]() болады. Осыдан
болады. Осыдан

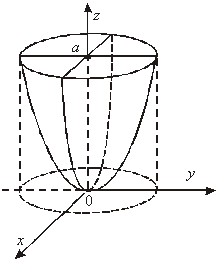
22-сурет
26-мысал. Тығыздығы тұрақты ![]() жарты шарының
ауырлық орталығының координаталарын табу керек.
жарты шарының
ауырлық орталығының координаталарын табу керек.
Шешуі. Жарты шар симметриялы дене
болғандықтан ![]() . Дене жоғарыдан
. Дене жоғарыдан ![]() бетімен,
төменнен
бетімен,
төменнен ![]() жазықтығымен
шектелген, ал оның
жазықтығымен
шектелген, ал оның ![]() жазықтығындағы
проекциясы
жазықтығындағы
проекциясы ![]() дөңгелегі
болады.
дөңгелегі
болады.
Сфералық координаталарға көшсек, онда
![]()
![]() болады. Осыдан
болады. Осыдан
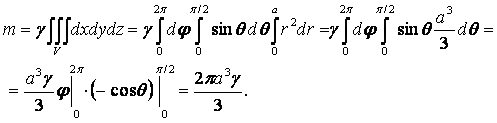
 .
.
![]()
27-мысал. ![]() конустық бетімен
конустық бетімен ![]() жазықтығымен
шектелген, дененің координаттық өстеріне (белдеріне) және
бас нүктеге қарағандағы инерция моменттерін табу керек
жазықтығымен
шектелген, дененің координаттық өстеріне (белдеріне) және
бас нүктеге қарағандағы инерция моменттерін табу керек ![]() .
.
Шешуі. Дене жоғарыдан ![]() жазықтығымен,
төменнен
жазықтығымен,
төменнен ![]() конустық
бетімен шектелген. Оның
конустық
бетімен шектелген. Оның ![]() жазықтығындағы
проекциясы
жазықтығындағы
проекциясы ![]() дөңгелегі
болады.
дөңгелегі
болады.
Инерция моменттерін цилиндрлік координаталарға көшу арқылы есептейміз.
![]()

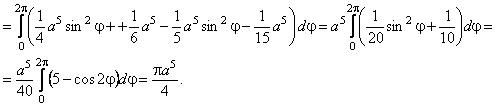


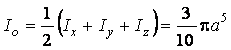 .
.
72. ![]() беттерімен шектелген дененің
көлемін табу керек.
беттерімен шектелген дененің
көлемін табу керек.
73. ![]() беттерімен шектелген дененің
көлемін табу керек.
беттерімен шектелген дененің
көлемін табу керек.
74. ![]() жазықтықтарымен шектелген
дененің көлемін табу керек.
жазықтықтарымен шектелген
дененің көлемін табу керек.
75. ![]() беттерімен шектелген дененің
көлемін табу керек.
беттерімен шектелген дененің
көлемін табу керек.
76. ![]() беттерімен шектелген дененің
көлемін табу керек.
беттерімен шектелген дененің
көлемін табу керек.
77. Тығыздығы ![]() функциясымен
анықталған
функциясымен
анықталған ![]() параллелипипедінің массасын табу
керек.
параллелипипедінің массасын табу
керек.
78. ![]() жазықтықтарымен шектелген,
тығыздығы
жазықтықтарымен шектелген,
тығыздығы ![]() болатын пирамиданың массасын табу
керек.
болатын пирамиданың массасын табу
керек.
79. ![]() параболоидымен және
параболоидымен және ![]() жазықтығымен
шектелген біртекті дененің ауырлық орталығын табу керек.
жазықтығымен
шектелген біртекті дененің ауырлық орталығын табу керек.
80. ![]() жазықтықтарымен шектелген
біртекті дененің ауырлық орталығын табу керек.
жазықтықтарымен шектелген
біртекті дененің ауырлық орталығын табу керек.
81. ![]() жазықтықтарымен шектелген
дененің ауырлық отралығын табу керек
жазықтықтарымен шектелген
дененің ауырлық отралығын табу керек ![]() .
.
82. Біртекті ![]() шарының координаттық өстеріне
(белдеріне) және оның бас нүктесіне
қарағандағы инерция моменттерін (екпіндік қарымдарын)
есептеу керек
шарының координаттық өстеріне
(белдеріне) және оның бас нүктесіне
қарағандағы инерция моменттерін (екпіндік қарымдарын)
есептеу керек ![]() .
.
83. ![]() жазықтықтарымен шектелген
дене-нің координаттық өстеріне және оның бас
нүктесіне қарағандағы инерция моменттерін есептеу керек
жазықтықтарымен шектелген
дене-нің координаттық өстеріне және оның бас
нүктесіне қарағандағы инерция моменттерін есептеу керек
![]() .
.
84. ![]() цилиндрімен
цилиндрімен ![]() және
және ![]() жазықтықтарымен шектелген
дененің координаттық өстеріне (белдеріне) және
оның бас нүктесіне қарағандағы инерция
моменттерін (екпіндік қарымдарын) есептеу керек
жазықтықтарымен шектелген
дененің координаттық өстеріне (белдеріне) және
оның бас нүктесіне қарағандағы инерция
моменттерін (екпіндік қарымдарын) есептеу керек ![]() .
.
ЖАУАПТАРЫ
1. ![]() -
центрі
-
центрі ![]() , ал
радиусы
, ал
радиусы ![]() болатын
шеңберімен шектелген
болатын
шеңберімен шектелген ![]() жазықтығының бөлігі.
жазықтығының бөлігі.
2. ![]() және
және ![]() параболаларының арасында орналасқан және
параболаларының арасында орналасқан және ![]() нүктесі тиісті емес
нүктесі тиісті емес ![]() жазықтығының бөлігі.
жазықтығының бөлігі.
3. Бүкіл ![]() жазықтығы.
жазықтығы.
4. ![]() түзуінен жоғары орналасқан
түзуінен жоғары орналасқан ![]() жазықтығының бөлігі.
жазықтығының бөлігі.
5. ![]() параболасынан
жоғары орналасқан
параболасынан
жоғары орналасқан ![]() жазықтығының бөлігі.
жазықтығының бөлігі.
6. ![]() 1
және 3 ширектерінде орналасқан
1
және 3 ширектерінде орналасқан ![]() жазықтығының бөлігі.
жазықтығының бөлігі.
7. ![]() түзуі тиісті емес
түзуі тиісті емес ![]() жазықтығының бөлігі.
жазықтығының бөлігі.
8. ![]() параболасы
және
параболасы
және ![]() түзуімен шектелген
түзуімен шектелген ![]() жазықтығының бөлігі.
жазықтығының бөлігі.
9. ![]() шеңберімен шектелген және
шеңберімен шектелген және ![]() нүктесі тиісті емес
нүктесі тиісті емес ![]() жазықтығының бөлігі.
жазықтығының бөлігі.
11. ![]()
![]()
12. ![]()
![]()
13. ![]()
![]()
14. ![]()
![]()
15. ![]()
![]()
16. ![]()
![]()
17. ![]()
![]()
18. ![]()
![]()
19. ![]()
![]() 20.
20.
![]()
![]()
21. ![]()
![]() 22.
22.
![]()
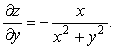
23. ![]()
![]() 24.
24. ![]()
![]()
25. ![]()
![]()
26.![]()
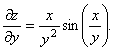
27. ![]()
![]()
28. ![]()
![]() 29.
29.
![]()
![]()
30. ![]()
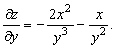 31.
31. 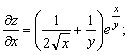
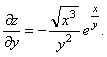
32. ![]()
![]()
![]()
33. ![]()
![]()
![]()
34. ![]()
![]()
![]()
35. 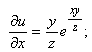
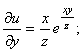
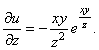
36. ![]()
![]()
![]()
37. ![]() 38.
38.
![]()
39. ![]() 40.
40. ![]()
41. ![]() 42.
42. ![]()
43. 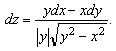 44.
44.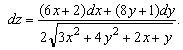
45. 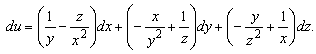
46. ![]()
47. ![]() 48.
48. ![]() 49.
49. ![]() Ескерту
Ескерту ![]() деп алу керек.
деп алу керек.
50. 0,82. 51. ![]()
![]()
![]()
52. ![]()
![]()
![]()
53. ![]()
![]()
![]()
54. ![]()
![]()
![]() .
.
55. ![]()
![]()
![]()
56. ![]()
![]()
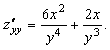
57. ![]()
![]()
![]()
58. ![]()
![]()
![]()
59. ![]()
![]()
![]()
60. ![]()
![]()
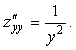
61. ![]()
62. ![]()
63. ![]()
64. 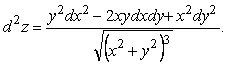
69. ![]()
![]()
70. 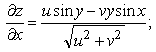
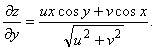
71. ![]()
![]()
72. ![]()
![]()
73. ![]() 74.
74.
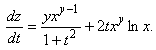
75.  76.
76. 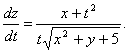
77. ![]() 78.
78. 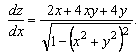
79. 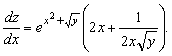 80.
80.
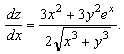
81. ![]() 82.
82. 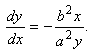
83. 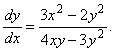 84.
84. 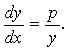
85. ![]() 86.
86. ![]()
87. ![]()
![]() 88.
88. ![]()
![]()
89. ![]()
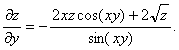
90.![]()
![]()
91. ![]()
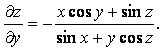
92. 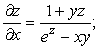
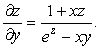
93. ![]()
![]()
94.
![]()
![]()
95.
![]()
![]()
96.
![]()
![]()
97.
![]()
![]()
98.
![]()
![]()
99.
![]()
![]()
100.
![]()
![]() 101.
101. ![]()
102.
![]() 103.
103.
![]()
104.
![]() 105.
Экстремум жоқ.
105.
Экстремум жоқ.
106.
![]()
107.
![]() болғанда
болғанда ![]()
108.
![]() болғанда
болғанда ![]()
![]() болғанда
болғанда ![]()
109.
![]()
![]()
110.
![]()
![]()
111.
![]()
![]()
112.
![]()
![]()
113.
![]()
![]()
114.
![]()
![]()
115. 8. 116. 39. 117. 24. 118. 45. 119.
304. 120. ![]() .
.
121. 168. 122. 3,35. 123.
![]() . 124.
1,5. 125.
. 124.
1,5. 125. ![]() .
126.
.
126. ![]() .
.
127. 0,5. 128. ![]() . 129. 214,65. 130.
. 129. 214,65. 130.
![]() . 131.
16,65.
. 131.
16,65.
132. 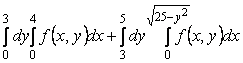 .
.
133. 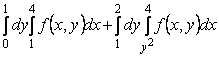 . 134.
. 134. 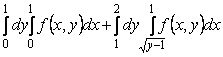 .
.
135. 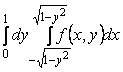 . 136.
. 136. 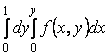 .
.
137. 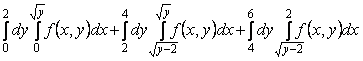 .
.
138. 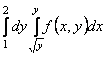 . 139.
. 139.
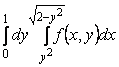 .
.
140. 1,5![]() . 141. 0,5
. 141. 0,5![]() . 142.
. 142. ![]() . 143.
. 143. ![]() .
.
144. ![]() . 145.
. 145. ![]() .
.
146. ![]() . 147.
. 147.
![]() . 148.
. 148.
![]() .
.
149. ![]() . 150.
1,25
. 150.
1,25![]() . 151.
. 151.
![]() .
.
152. ![]() . 153.
. 153.
![]() . 154.
. 154.
![]() .
.
155. 12. 156.
![]() . 157.
24.
. 157.
24.
158. ![]() . 159.
. 159.
![]() . 160.
. 160.
![]() .
.
161. ![]() . 162.
. 162.
![]() . 163.
. 163.
![]() .
.
164. 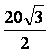 . 165.
. 165.
![]()
![]() .
.
166. 0,4. 167.
![]() . 168.
. 168.
![]() .
.
169. ![]() . 170.
. 170.
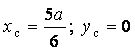 .
.
171. ![]() . 172.
. 172. ![]() ;
; ![]() .
.
173. ![]() . 174.
. 174. ![]()
![]() .
.
175. ![]() . 176. -2,25. 177.
. 176. -2,25. 177.
![]() .
.
178. ![]() . 179.
. 179.
![]() . 180.
. 180.
![]() .
.
181. ![]() . 182.
. 182.
![]() . 183.
. 183.
![]() .
.
184. ![]() . 185.
. 185.
![]() . 186.
. 186.
![]() .
.
187. ![]() . 188.
4,5. 189.
. 188.
4,5. 189. ![]() .
.
190. ![]() . 191.
. 191. ![]() . 192.
. 192. ![]() .
.
193. ![]() . 194.
. 194. ![]() . 195.
. 195. ![]() .
.
196. ![]() ;
; ![]() . 197.
. 197. ![]()
198. ![]() ;
; ![]() ;
; 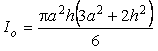 .
.
Әдебиеттер тізімі
1. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа. – Москва: Наука, 1966.-736 с.
2. Пискунов Н.С. Дифференциальное и интегральное исчисления. – Москва: Наука, 1995.
3. Берман Г.И. Сборник задач по курсу математического анализа. – Москва: Наука, 1985.-384 с.
4. Кручкович Г.И., Гутарина Н.И., Дюбюк П.Е. и другие. – Москва: Высшая школа, 1973.-576 с.
5. Хасеинов К.А. Каноны математики. – Алматы: Атамұра, 2003.
Сайлаубек Ералы ұлы Ералы
Мұрат Шәпен ұлы Тілепі
Көп айнымалы функциялардың
интегралдық есептеулері
Оқу құралы
Редакторы Ж.А. Байбураева
2007ж. қосымша жоспары, ______ реті л
_____________ терілуге берілді
Пішіні 60х84 1/16
№2 типографиялық қағаз
Оқу-баспа таб.- 3,9. Таралымы 100 дана.
Тапсырыс . Бағасы тг.
Басуға қол қойылды.
«Алматы энергетика және байланыс институтының»
Коммерциялық емес акционерлік қоғамының көшірмелі-көбейткіш бюросы
050013, Алматы, А.Байтұрсынұлы көшесі, 126