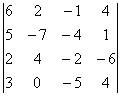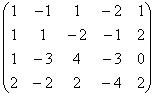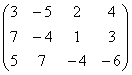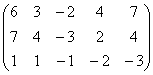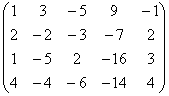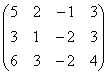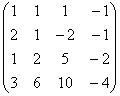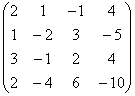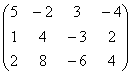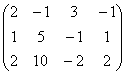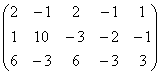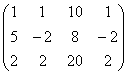АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ
Алгебра и геометрия.
Методические указания и задания
к выполнению расчетно-графических работ
(для студентов очной формы обучения специальности
050704 – Вычислительная техника и программное обеспечение)
Часть 1
Алматы 2007
СОСТАВИТЕЛИ: Л.Н. Астраханцева, Л.Н.Ким, М.Ж.Байсалова. Алгебра и геометрия. Методические указания и задания к выполнению расчетно-графической работы для студентов очной формы обучения специальности 050704 – Вычислительная техника и программное обеспечение. -Алматы: АИЭС, 2007.- 26 с.
Методические указания и задания к расчетно-графической работе содержат типовой расчет №1 дисциплины «Алгебра и геометрия» для студентов очной формы обучения специальности 050704 – Вычислительная техника и программное обеспечение. Приведены основные теоретические вопросы программы. Дано решение типового варианта.
Ил. 1, табл. 9, библиогр. – 4 назв.
![]()
Рецензент: канд.физ.-мат.наук, проф. С.Е.Базарбаева.
Печатается по плану издания некоммерческого акционерного общества «Алматинский институт энергетики и связи» на 2007 г.
ã НАО «Алматинский институт энергетики и связи», 2007 г.
1 Типовой расчёт 1. Векторная и линейная алгебры
1.1 Теоретические вопросы
1 Определители, их свойства, вычисление.
2 Матрицы, действия над ними, обратная матрица.
3 Ранг матрицы и его вычисление.
4 Векторы, их длина, линейные операции над векторами. Коллинеарность, компланарность, ортогональность векторов, угол между векторами.
5 Скалярное, векторное, смешанное произведения векторов, их приложения.
1.2 Расчётные задания
1 Вычислить определитель второго порядка
Т а б л и ц а 1
|
1.1 |
1.2 |
1.3 |
1.4 |
1.5 |
|
|
1.6 |
1.7 |
1.8 |
1.9 |
1.10 |
|
|
1.11 |
1.12 |
1.13 |
1.14 |
1.15 |
|
|
1.16 |
1.17 |
1.18 |
1.19 |
1.20 |
|
|
1.21 |
1.22 |
1.23 |
1.24 |
1.25 |
|
|
1.26 |
1.27 |
1.28 |
1.29 |
1.30 |
|
2 Дан определитель третьего порядка:
а) найти минор M![]() и алгебраическое
дополнение A
и алгебраическое
дополнение A![]() элемента
a
элемента
a![]() ;
;
б) разложить определитель по i-ой строке;
в) вычислить определитель, разложив его по j-му столбцу;
г) вычислить по правилу треугольника (правилу Саррюса).
Т а б л и ц а 2
|
2.1 |
2.2 |
2.3 |
|
2.4 |
2.5 |
2.6 |
|
2.7 |
2.8 |
2.9 |
|
2.10 |
2.11 |
2.12 |
|
2.13 |
2.14 |
2.15 |
|
2.16 |
2.17 |
2.18 |
|
2.19 |
2.20 |
2.21 |
|
2.22 |
2.23 |
2.24 |
|
2.25 |
2.26 |
2.27 |
|
2.28 |
2.29 |
2.30 |
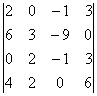
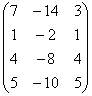
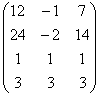
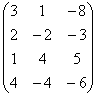
3 Даны матрицы А, В, С, Д:
а) найти матрицы 3С+2Д, С-4Д;![]()
б) найти матрицу В![]() , транспонированную
матрице В.
, транспонированную
матрице В.
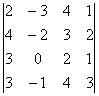
Т а б л и ц а 3
|
3.1 А= |
|
3.2 А= |
|
3.3 А= |
|
3.4 А= |
|
3.5 А= |
|
3.6 А= |
|
3.7 А= |
|
3.8 А= |
|
3.9 А= |
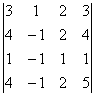
продолжение таблицы 3
|
3.10 А= |
|
3.11 А= |
|
3.12 А= |
|
3.13 А= |
|
3.14 А= |
|
3.15 А= |
|
3.16 А= |
|
3.17 А= |
|
3.18 А= |
|
3.19 А= |
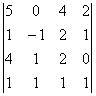
продолжение таблицы 3
|
3.20 А= |
|
3.21 А= |
|
3.22 А= |
|
3.23 А= |
|
3.24 А= |
|
3.25 А= |
|
3.26 А= |
|
3.27 А= |
|
3.28 А= |
продолжение таблицы 3
|
3.29 А= |
|
3.30 А= |
4 Даны матрицы А, В, С (в задании 3):
а) возможно ли произведение матриц АВ, ВС ? Объяснить почему, если невозможно; найти произведение, если возможно;
б) найти матрицу
![]() , обратную матрице А.
, обратную матрице А.
5 Даны точки А и В:
а) найти координаты
векторов ![]() и
и ![]() ;
;
б) найти длину вектора ![]() (или расстояние между
точками А и В);
(или расстояние между
точками А и В);
в) найти середину отрезка АВ.
Т а б л и ц а 4
|
5.1 А(5, -4, 3), В(1, 2, -8) |
5.2 А(-3, 1, 0), В(7, 1, -5) |
5.3 А(0, 4, 5), В(3, -2, 1) |
|
5.4 А(3, -2, 5), В(4, 5, 7) |
5.5 А(2, -3, 7), В(3, 2, 8) |
5.6 А(2, -1, 7), В(6, 3, 4) |
|
5.7 А(3, 1, 7), В(2, -3, 9) |
5.8 А(2, 1, -6), В(1, 4, 9) |
5.9 А(2, -4, 8), В(5, 4, 7) |
|
5.10 А(3, 2, 5), В(4, 0, -3) |
5.11А(2, 3, -1),В(-6, 4, 2) |
5.12А(-4, 2, 3),В(8, 7, -2) |
|
5.13 А(5, 3, 6), В(-2, 3, 5) |
5.14 А(0, 6, 0), В(5, 3, -4) |
5.15 А(4, 2, 0), В(1, -7, 8) |
|
5.16 А(4, 2, 5), В(-1, 0, 6) |
5.17 А(3,-5, 8), В(6, 3, 9) |
5.18А(7, 2, 2),В(-5, 7, -7) |
|
5.19 А(5, -3, 1), В(2, 3, 7) |
5.20А(8, -6, 4),В(10, 5, 1) |
5.21 А(5, 6,-8), В(8, 10,7) |
|
5.22 А(1, -1, 3), В(6, 5, 8) |
5.23 А(3, 5,-7), В(8, 4, 1) |
5.24 А(6, -6, 5), В(4, 9, 5) |
|
5.25А(4, 6, 11),В(9, 3, -4) |
5.26 А(5, 7, 4),В(4,-10, 9) |
5.27 А(-9, 8, 9),В(7, 1,-2) |
|
5.28 А(5, 2, 6), В(1, 8, -2) |
5.29 А(2, 8, -9),В(7, 5,-5) |
5.30 А(-2, 7, 0), В(6, 3, 5) |
6 Даны векторы ![]() ,
, ![]() ,
, ![]() :
:
а) найти модуль (длину)
вектора ![]() ;
;
б) найти скалярное
произведение векторов ![]() и
и
![]() . Будут ли эти
векторы ортогональны?
. Будут ли эти
векторы ортогональны?
в) найти векторное
произведение векторов ![]() и
и
![]() ;
;
г) найти смешанное
произведение векторов ![]() ,
,
![]() ,
, ![]() . Будут ли эти векторы
компланарны?
. Будут ли эти векторы
компланарны?
д) проверить, будут ли
векторы ![]() и
и ![]() коллинеарны?
коллинеарны?
е) найти косинус угла
между векторами ![]() и
и
![]() ;
;
ж) найти проекцию
вектора ![]() на
вектор
на
вектор ![]() .
.
Т а б л и ц а 5
|
6.1 |
6.2 |
|
|
6.3 |
6.4 |
|
|
6.5 |
6.6 |
|
|
6.7 |
6.8 |
|
|
6.9 |
6.10 |
|
|
6.11 |
6.12 |
|
|
6.13 |
6.14 |
|
|
6.15 |
6.16 |
|
|
6.17 |
6.18 |
|
|
6.19 |
6.20 |
|
|
6.21 |
6.22 |
|
|
6.23 |
6.24 |
|
|
6.25 |
6.26 |
|
|
6.27 |
6.28 |
|
|
6.29 |
6.30 |
|
7 Вычислить определитель четвёртого порядка
Т а б л и ц а 6
|
7.1 |
7.2 |
7.3
|
7.4 |
|||||
|
7.5
|
7.6
|
7.7 |
7.8 |
|||||
|
7.9
|
7.10 |
7.11
|
7.12 |
|||||
|
7.13
|
7.14
|
7.15
|
7.16 |
|||||
|
7.17 |
7.18
|
7.19 |
7.20
|
|
||||
|
7.21 |
7.22
|
7.23 |
7.24 |
|
||||
продолжение таблицы 6
|
7.25
|
7.26 |
7.27
|
7.28 |
|
7.29 |
7.30
|
7.31
|
7.32 |
8 Вычислить площадь
параллелограмма, построенного на векторах
![]() и
и
![]() , если даны разложения этих векторов
по базису
, если даны разложения этих векторов
по базису ![]() , длины векторов
, длины векторов
![]() , угол
, угол
![]() между векторами
между векторами
![]()
Т а б л и ц а 7
|
|
|
|
|
|
|
|
|
|
|
|
|
8.1
|
|
1 |
2 |
|
8.16
|
|
4 |
1 |
|
|
|
8.2
|
|
5 |
1 |
|
8.17
|
|
4 |
2 |
|
|
|
8.3
|
|
2 |
3 |
|
8.18
|
|
2 |
3 |
|
|
|
8.4 |
|
3 |
2 |
|
8.19
|
|
7 |
2 |
|
|
|
8.5 |
|
1 |
2 |
|
8.20
|
|
6 |
2 |
|
|
|
8.6 |
|
5 |
4 |
|
8.21
|
|
9 |
1 |
|
|
|
8.7
|
|
3 |
4 |
|
8.22
|
|
6 |
7 |
|
|
|
8.8 |
|
1 |
2 |
|
8.23
|
|
2 |
3 |
|
|
|
8.9
|
|
3 |
4 |
|
8.24
|
|
4 |
1 |
|
|
|
8.10 |
|
3 |
1 |
|
8.25
|
|
1 |
2 |
|
|
продолжение таблицы 7
|
8.11
|
|
8 |
1 |
|
8.26
|
|
4 |
1 |
|
|
8.12
|
|
3 |
5 |
|
8.27
|
|
3 |
2 |
|
|
8.13
|
|
7 |
2 |
|
8.28
|
|
2 |
3 |
|
|
8.14
|
|
5 |
3 |
|
8.29
|
|
2 |
1 |
|
|
8.15
|
|
2 |
4 |
|
8.30
|
|
4 |
2 |
|
9 Даны вершины А, В, С, D пирамиды:
а) найти площадь указанной грани;
б) найти площадь сечения, проходящего через середину указанного ребра и две вершины пирамиды;
в) найти объём пирамиды.
Т а б л и ц а 8
|
9.1 A(2, 1, 7), B(3, 3, 6),C(2, -3, 9), D(1, 2, 5); АСD; l=BC, A, D |
9.2 A(2, -1, 7), B(6, 4, 1),C(3, 2, 8), D(2, -3, 7); ABD; l=AD, B, C |
|
9.3 A(4, 3, 5), B(1, 9, 7), C(0, 2, 0), D(5, 3, 10); ACD; l=BD, A, C |
9.4 A(3, 2, 5), B(4, 0, 6), C(2, 6, 5), D(6, 4, -1); BCD; l=CD, A, B |
|
9.5 A(4, 2, 10), B(1, 2, 0),C(3, 5,7), D(2, -3, 5); ACD; l=AB, C, D |
9.6 A(2, 3, 5), B(5, 3, -7),C(1, 2, 7), D(4, 2, 0); ACD; l=AD, B, C |
|
9.7 A(8, -6, 4), B(1, 5, 5),C(5, 6, 8), D(8, 10, 7); ABD; l=BD, A, C |
9.8 A(1, -1, 3), B(6, 5, 8), C(3, 5,8), D(8, 4, 1); ACD; l=BC, A, D |
|
9.9A(0, 4, 5), B(3, -2, 1),C(4, 5, 6), D(3, 3, 2); BCD; l=BC, A, D |
9.10A(2, 1, 6), B(1, 4, 9),C(2, -5,8), D(5, 4, 2); ABD; l=AB, C, D |
|
9.11 A(3, 1, 4), B(-1, 6, 1),C(1,1,6), D(0, 4, -1); ACD; l=BD, A, C |
9.12 A(3,-1,2), B(-1,0, 1),C(1,1,3), D(8, 5, 8); BCD; l=AD, B, C |
|
9.13 A(2, 4, 3), B(1,1,5), C(4,9, 3), D(3, 6, 7); ABD; l=BD, A, C |
9.14 A(9, 5,5), B(-3, 7,1),C(5, 7, 8), D(6, 9, 2); BCD; l=BC, A, D |
|
9.15 A(5,-5, 4), B(1,-1,4),C(3, 5,1), D(5, 8, -1); ACD; l=AD, B, C |
9.16 A(6,1, 1), B(4, 6,6), C(4,2,0), D(1, 2, 6); ABD; l=BD, A, C |
|
9.17 A(6, 8, 2), B(5, 4,7),C(2, 4, 7), D(7, 3, 7); ACD; l=BC, A, D |
9.18 A(4, 2, 5), B(0, 7,1),C(0, 3, 7), D(1, 5, 0); BCD; l=BC, A, D |
|
9.19 A(4,6,5), B(6,9,4), C(2,10,10), D(7, 5, 9); ABD; l=AB, C, D |
9.20 A(3, 5,4), B(8, 7,4),C(5,10,4), D(4, 7, 8); ACD; l=BD, A, C |
продолжение таблицы 8
|
9.21 A(1, 8, 2), B(5,2, 6), C(5,7,4), D(4, 10, 9); BCD; l=AD, B, C |
9.22 A(6, 6,5), B(4, 9,5), C(4,6,11), D(6, 9, 3); ABD; l=BD, A, C |
|
9.23 A(0, 7,1), B(2,-1,5), C(1, 6,3), D(3, -9, 8); BCD; l=BC, A, D |
9.24 A(7, 5,3), B(9,4,4), C(4, 5,7), D(7, 9, 6); ACD; l=AD, B, C |
|
9.25 A(4,4,10), B(7, 9,2), C(2,8, 4), D(9, 6, 9); ABD; l=BD, A, C |
9.26 A(5, 3,7), B(-2,3,5), C(4,2,10), D(1, 2, 7); ACD; l=BC, A, D |
|
9.27 A(1,-2,7). B(4, 2, 1), C(2, 3,5), D(5, 3, 7); ABD; l=AC, B, D |
9.28 A(7, 2,2), B(-5,7,7), C(5,-3,1), D(2, 3, 7); ACD; l=BC, A, D |
|
9.29 A(10,9, 6), B(2, 8,2), C(9,8,9), D(7, 10, 3); BCD; l=CD, A, B |
9.30 A(3, 5,4), B(5, 8,3), C(1, 2,-1), D(-1, 0, 2); ACD; l=AB, C, D |
10 Вычислить ранг матрицы двумя способами:
а) методом окаймляющих миноров;
б) методом элементарных преобразований.
Указать базисный минор.
Т а б л и ц а 9
|
10.1
|
10.2
|
10.3
|
|
10.4
|
10.5
|
10.6
|
|
10.7
|
10.8
|
10.9 |
продолжение таблицы 9
|
10.10
|
10.11
|
10.12
|
|
10.13
|
10.14
|
10.15
|
|
10.16
|
10.17
|
10.18 |
|
10.19
|
10.20
|
10.21
|
|
10.22
|
10.23
|
10.24
|
|
10.25
|
10.26
|
10.27 |
|
10.28 |
10.29 |
10.30 |
1.3 Решение типового варианта
1
Вычислить
определитель второго порядка ![]() .
.
Решение:
по формуле 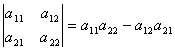 имеем
имеем ![]() =(-2) 7-4 5= -14-20 = -34.
=(-2) 7-4 5= -14-20 = -34.
2 Дан определитель
третьего порядка  ,
i=2, j=3:
,
i=2, j=3:
а) найти минор M![]() и алгебраическое
дополнение A
и алгебраическое
дополнение A![]() элемента
a
элемента
a![]() ;
;
б) разложить определитель по i-ой строке;
в) вычислить определитель, разложив его по j-му столбцу;
г) вычислить по правилу треугольника (правилу Саррюса).
Решение:
a) минор M![]() элемента
a
элемента
a![]() равен определителю, полученному из данного после
вычёркивания i-ой строки и
j-го столбца. Таким образом, вычёркиваем в нашем определителе
вторую строку и третий столбец, получаем М
равен определителю, полученному из данного после
вычёркивания i-ой строки и
j-го столбца. Таким образом, вычёркиваем в нашем определителе
вторую строку и третий столбец, получаем М![]() =
=![]() = 15 – 4 = 11. Алгебраическое дополнение
элемента a
= 15 – 4 = 11. Алгебраическое дополнение
элемента a![]() вычисляем по формуле
вычисляем по формуле
A![]() =(-1)
=(-1)![]() M
M![]() . Значит А
. Значит А![]() =(-1)
=(-1)![]() 11= -11;
11= -11;
б) формула разложения
определителя по i-ой строке для
определителя n - го порядка имеет вид 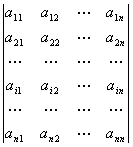 =
= ![]() ,где
A
,где
A![]() алгебраическое дополнение элемента
a
алгебраическое дополнение элемента
a![]() . Так как
i = 2,
j = 3, то формула перепишется так
. Так как
i = 2,
j = 3, то формула перепишется так
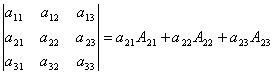 . Искомое разложение имеет вид
. Искомое разложение имеет вид
 ;
;
в)
j = 3. Формула разложения по третьему
столбцу имеет вид  . Таким образом,
. Таким образом,
 = 2 – 88 – 12 = - 98;
= 2 – 88 – 12 = - 98;
г) правило треугольника:
определитель третьего порядка равен сумме шести членов; члены со знаком плюс
получают при перемножении по три элемента определителя, взятых по схеме 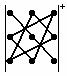 , члены со знаком минус – по
схеме
, члены со знаком минус – по
схеме . Поэтому
. Поэтому
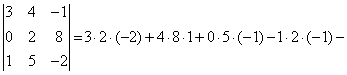
![]()
3-4. Даны матрицы А=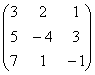 , В=
, В=![]() , С=
, С=![]() , Д=
, Д=![]() :
:
а) найти матрицы 3С+2Д,
С-4Д;![]()
б) найти матрицу В![]() , транспонированную
матрице В;
, транспонированную
матрице В;
в) возможно ли произведение матриц АВ, ВС ? Объяснить почему, если невозможно; найти произведение, если возможно;
г) найти матрицу А![]() , обратную для матрицы А.
, обратную для матрицы А.
Решение:
а) 3С+2Д = 3![]() +2
+2![]() =
=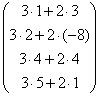
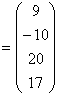 .
.
С - 4Д =
![]() -4
-4![]() =
= =
=![]() ;
;
б) матрица,
транспонированная матрице В, получается заменой строк матрицы В её столбцами с
теми же номерами: В![]() =
=
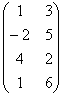 ;
;
в) произведение матриц
АВ возможно, если число столбцов матрицы А равно числу строк матрицы В. Размеры
матриц: А![]() , В
, В![]() , С
, С![]() , Д
, Д![]() . Таким образом, А
. Таким образом, А![]() В
В![]() =
= ![]() – произведение невозможно. В
– произведение невозможно. В![]() С
С![]() =
= ![]() – произведение возможно.
– произведение возможно.
Произведением матриц АВ является
матрица С, число строк которой равно числу строк матрицы А, число столбцов
равно числу столбцов матрицы В:
![]() . Элемент
. Элемент ![]() матрицы С равен сумме
произведений i–ой строки матрицы А на
j–ый столбец матрицы В. Таким образом,
В С =
матрицы С равен сумме
произведений i–ой строки матрицы А на
j–ый столбец матрицы В. Таким образом,
В С = ![]()
![]() =
= ![]() .
.![]()
![]() .
.
Итак, ![]()
![]() ;
;
г) обратная матрица для
квадратной матрицы существует, если определитель матрицы не равен нулю; не
существует, если – равен нулю. Обратная матрица А![]() для матрицы
для матрицы
А =  находится по формуле
находится по формуле  где
где ![]() – определитель матрицы А;
– определитель матрицы А; ![]() – алгебраические
дополнения элементов
– алгебраические
дополнения элементов ![]() .
Найдём определитель матрицы А:
.
Найдём определитель матрицы А: ![]() =
= 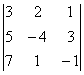 = 88
= 88![]() 0, следовательно А
0, следовательно А![]() существует. Определим
алгебраические дополнения всех элементов матрицы А
существует. Определим
алгебраические дополнения всех элементов матрицы А
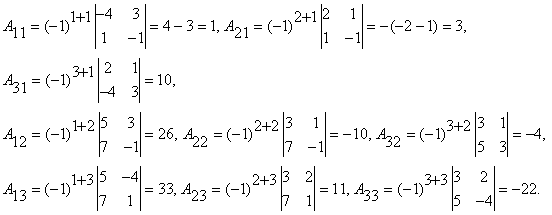
Составим А![]() по вышеуказанной формуле
по вышеуказанной формуле
А![]() = =
= =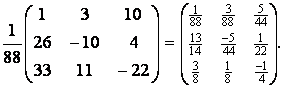
5 Даны точки А(7, -9, 3) и В(1, 0, -5):
а) найти координаты
векторов ![]() и
и ![]() ;
;
б) найти длину вектора ![]() (или расстояние между
точками А и В);
(или расстояние между
точками А и В);
в) найти середину отрезка АВ.
Решение:
а) координаты вектора ![]() по координатам начала
А(
по координатам начала
А(![]() ) и конца
) и конца
В(![]() ) находят по формуле
) находят по формуле ![]() = (
= (![]() ). Таким образом,
). Таким образом, ![]() = (1-7, 0-(-9), -5-3) = (-6, 9,
-8);
= (1-7, 0-(-9), -5-3) = (-6, 9,
-8); ![]() = (7-1,
-9-0, 3-(-5)) = (6, -9, 8) или
= (7-1,
-9-0, 3-(-5)) = (6, -9, 8) или
![]() = -
= - ![]() = - (-6, 9, -8) = (6, -9, 8);
= - (-6, 9, -8) = (6, -9, 8);
б) длина (модуль) вектора
![]() или
расстояние между точками А и В обозначается
или
расстояние между точками А и В обозначается ![]() и находится по формуле
и находится по формуле ![]() =
= ![]() . Значит в нашем случае
. Значит в нашем случае ![]() =
=![]() =
= ![]() ;
;
в) середина С отрезка АВ
имеет координаты С![]() .
.
У нас С![]() = С( 4, -9/2, -1 ).
= С( 4, -9/2, -1 ).
6 Даны векторы ![]() :
:
а) найти модуль (длину)
вектора ![]() ;
;
б) найти скалярное
произведение векторов ![]() и
и
![]() . Будут ли эти
векторы ортогональны?
. Будут ли эти
векторы ортогональны?
в) найти векторное
произведение векторов ![]() и
и
![]() ;
;
г) найти смешанное
произведение векторов ![]() ,
,
![]() ,
, ![]() . Будут ли эти векторы
компланарны?
. Будут ли эти векторы
компланарны?
д) проверить, будут ли
векторы ![]() и
и ![]() коллинеарны?
коллинеарны?
е) найти косинус угла
между векторами ![]() и
и
![]() ;
;
ж) найти проекцию
вектора ![]() на
вектор
на
вектор ![]() .
.
Решение:
для векторов ![]() имеют место формулы:
имеют место формулы:
а) модуль (длина) вектора
![]() :
: ![]() ;
;
б) скалярное произведение
векторов ![]() и
и ![]() :
:
![]() . Если векторы ортогональны, то
. Если векторы ортогональны, то ![]() ;
;
в) векторное произведение
векторов ![]() и
и ![]()
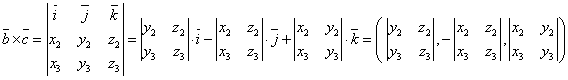 ;
;
г) смешанное
произведение векторов ![]() ,
,
![]() ,
, ![]() :
:
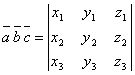 , если эти векторы компланарны, то
, если эти векторы компланарны, то
![]() ;
;
д) если векторы
![]() и
и
![]() коллинеарны, то
коллинеарны, то
![]() или
или
![]() ;
;
е) косинус угла
![]() между векторами
между векторами ![]() и
и ![]()
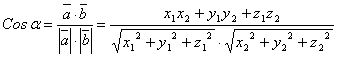 ;
;
ж) проекция вектора ![]() на вектор
на вектор ![]()
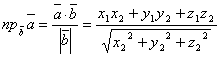 .
.
По этим формулам в нашем варианте мы получим:
а) ![]() ;
;
б)
![]() , так как
, так как
![]() , то векторы
, то векторы ![]() и
и ![]() не ортогональны;
не ортогональны;
в)
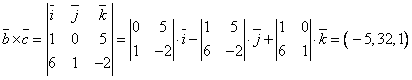 ;
;
г)
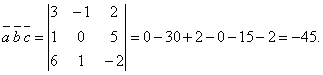 Так как
Так как ![]() , то векторы не компланарны;
, то векторы не компланарны;
д) для векторов
![]() и
и
![]() :
: ![]() и
и
![]() , следовательно векторы
, следовательно векторы
![]() и
и
![]() не коллинеарны;
не коллинеарны;
е)
![]() ;
;
ж)
![]() .
.
7 Вычислить определитель
четвёртого порядка 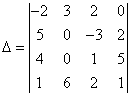
Решение:
используя свойства
определителей получим в одной из его строк или столбцов нули. Выберем второй
столбец, где уже есть два нуля: умножим первую строку на (-2) и прибавим к
последней, получим 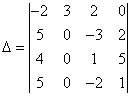 . Теперь разложим
определитель по второму столбцу
. Теперь разложим
определитель по второму столбцу
 .
.
8 Вычислить площадь
параллелограмма, построенного на векторах
![]() =
=
![]() и
и
![]() =
=![]() , если длины векторов равны
, если длины векторов равны
![]() =3,
=3,
![]() =2, угол
=2, угол
![]() между векторами
между векторами
![]() равен
равен
![]() .
.
Решение:
по свойствам векторного
произведения имеем: ![]() . Площадь параллелограмма,
построенного на векторах
. Площадь параллелограмма,
построенного на векторах ![]() и
и ![]() равна
равна
![]() .
.
9 Даны вершины пирамиды А(-1,0,4), В(2,1,-1), С(-3,4,5), D(0,1,-2):
а) найти площадь указанной грани АВD;
б) найти площадь сечения, проходящего через середину указанного ребра ВD и вершины А и С;
в) найти объём пирамиды.
Решение:
сделаем схематический чертеж
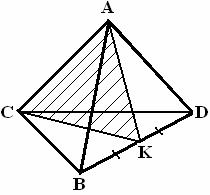
Рисунок 1
а) так как площадь
треугольника, построенного на векторах ![]() и
и ![]() , равна
, равна ![]() , то
, то ![]() . Найдем координаты векторов
. Найдем координаты векторов
![]() ,
, ![]() =(1,1,-6).
=(1,1,-6). 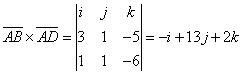 .
.
![]() ;
;
б) К(1;1;-1,5) – середина ВD. ![]() ,
,
![]() .
. 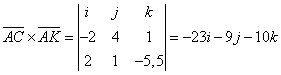 .
. ![]() ;
;
в) объем пирамиды, построенной
на векторах ![]() ,
, ![]() ,
, ![]() равен
равен ![]() . Поэтому
. Поэтому ![]() .
.
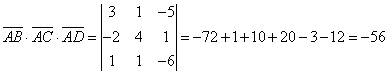 .
.
Таким образом ![]() .
.
10 Вычислить ранг матрицы
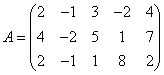 двумя
способами:
двумя
способами:
а) методом окаймляющих миноров;
б) элементарных преобразований.
Указать базисный минор.
Решение:
а) начнем с левого
верхнего угла. Минор второго порядка ![]() , поэтому возьмем другой
, поэтому возьмем другой ![]() . Рассмотрим миноры, окаймляющие
. Рассмотрим миноры, окаймляющие
![]() , (т.е.
содержащие в себе
, (т.е.
содержащие в себе ![]() ):
):
 .
.
Так как все окаймляющие миноры
третьего порядка равны нулю, то ранг матрицы равен 2 (![]() , ранг – наибольший порядок не
равного нулю минора). Базисный минор
, ранг – наибольший порядок не
равного нулю минора). Базисный минор ![]() ;
;
б) с помощью элементарных преобразований будем приводить матрицу к ступенчатому виду
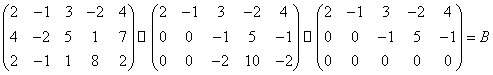 .
.
На первом шаге первая строка была
умножена на (-2) и прибавлена ко второй, затем умножена на (-1) и прибавлена к
третьей, получены нули в первом столбце ниже первой строки. На втором шаге
вторую строку умножили на (-2) и прибавили к третьей. Получена ступенчатая
матрица ![]() . В
ней две ненулевые строки или существует минор второго порядка, например,
. В
ней две ненулевые строки или существует минор второго порядка, например, ![]() . Поэтому
. Поэтому ![]() . Так как матрицы
. Так как матрицы ![]() и
и ![]() эквивалентны
эквивалентны ![]() , то их ранги равны
, то их ранги равны ![]() . За базисный минор
можно взять
. За базисный минор
можно взять ![]() .
.
Список литературы
1. Апатенок Р.Ф., Маркина А.М. Сборник задач по линейной алгебре. - Мн.: Выш. Школа, 1980. – 192 с.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: в 2 ч. – М.: Высшая школа, 2003. – ч. 1,2.-352 с.
3. Сборник индивидуальных заданий по высшей математике: в 3 ч. (Рябушко А.П., Бархатов В.В. и др.). Под ред. Рябушко А.П. – Минск: Высш. школа, 2000.-ч.1.-396 с.
4. Хасеинов К.А. Каноны математики: Учебник. – Алматы, 2003.-686 с.
Содержание
1 Теоретические вопросы………………………………….....…………….….3
2 Расчётные задания……………………………………..………………….….3
3 Решение типового варианта……………………………..………………….15
Список литературы ……………………………………………………………24
Сводный план 2007 г., поз. 139
Астраханцева Людмила Николаевна
Ким Людмила Николаевна
Байсалова Маншук Жумамуратовна
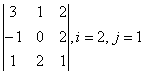
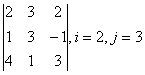

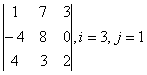
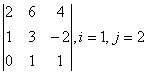
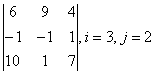
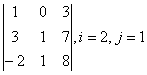

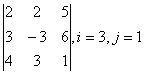
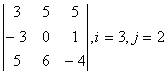
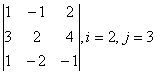
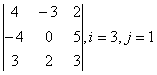
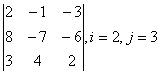
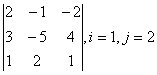
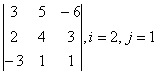
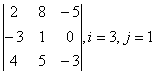
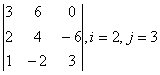

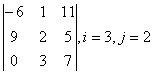
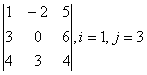
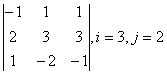
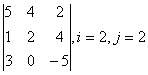
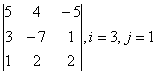
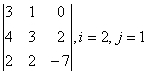
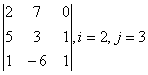
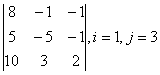
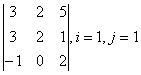
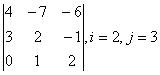
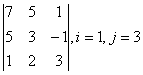

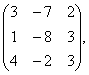 В=
В=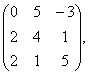 В=
В= В=
В= Д=
Д= .
.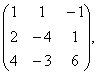 В=
В=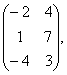 С=
С= В=
В= В=
В=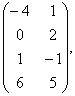 С=
С= В=
В=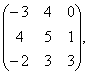 В=
В= В=
В=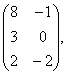 Д=
Д=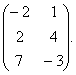
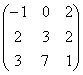 , В=
, В=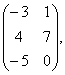 С=
С=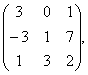 В=
В=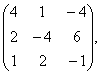 В=
В= С=
С= В=
В=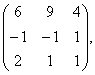 В=
В=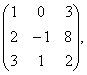 В=
В=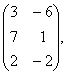 Д=
Д=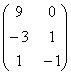
 В=
В= , С=
, С= В=
В= В=
В=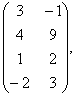 С=
С=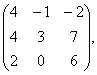 В=
В=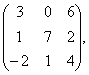 В=
В=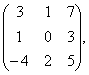 В=
В=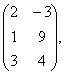 Д=
Д=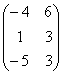
 В=
В=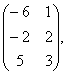 С=
С=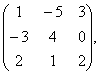 В=
В=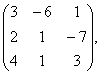 В=
В=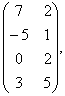 С=
С=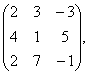 В=
В= В=
В=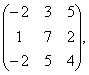 В=
В=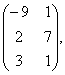 Д=
Д=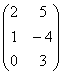
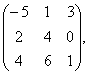 В=
В=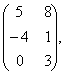 С=
С=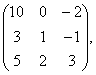 В=
В=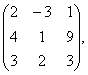 В=
В=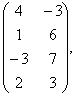 С=
С=