ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ
МИНИСТІРЛІГІ
"Алматы энергетика және байланыс институтының "
Коммерциялық емес акционерлік қоғамы
С.Е. Ералиев
Сызықтық алгебраның элементтері
Оқу құралы
Бұл оқулық техникалық жоғары оқу орындарының бағдарламасына сай жазылған. Оқулықта анықтауыштар, векторлар, матрицалар және сызықты теңдеулер жүйесін шешу тәсілдері қарастырылған. Тақырыптарды терең түсіну үшін таңдалынып алынған мысалдар қарастырылған және әрбір параграфтың соңында есептер берілген. Сондықтан бұл оқулықты есептер жинағы ретінде пайдалануға болады.
Оқулық техникалық жоғары оқу орындары мен колледждердің студенттеріне арналған.
1 Анықтауыштар
1.1 Екінші және үшінші ретті анықтауыштар. Қасиеттері
1- анықтама. Екінші және үшінші ретті анықтауыштар келесі теңдіктермен анықталады:
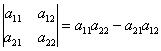 ,
(1)
,
(1) 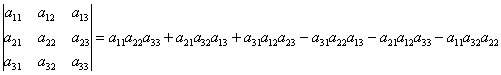 .
(2)
.
(2)
![]() сандары
анықтауыштың элементтері деп аталады. Элементтің бірінші
сандары
анықтауыштың элементтері деп аталады. Элементтің бірінші ![]() индексі жатық
жолының нөмірін, ал екінші
индексі жатық
жолының нөмірін, ал екінші ![]() индексі тік жолының нөмірін
анықтайды.(1)- дегі
индексі тік жолының нөмірін
анықтайды.(1)- дегі ![]() сандары және (2)- дегі
сандары және (2)- дегі ![]() сандары
орналасқан диогональ негізгі, ал (1)- дегі
сандары
орналасқан диогональ негізгі, ал (1)- дегі ![]() және (2)- дегі
және (2)- дегі ![]()
![]() сандары орналасқан
диогональ қосалқы деп аталады.
сандары орналасқан
диогональ қосалқы деп аталады.
Екінші ретті анықтауышты есептеу үшін
оның негізгі диогональ элементтерінің көбейтіндісінен ![]() қосалқы
диогональ элементтерінің көбейтіндісін
қосалқы
диогональ элементтерінің көбейтіндісін ![]() шегеру қажет.
шегеру қажет.
Үшінші ретті анықтауыштың мәні үшбұрыштар немесе Сайрюс ережесі деп аталатын сұлба бойынша алғашқы үш қосылғыш « + » таңбасымен, ал қалған үш қосылғыш «-» таңбасымен алынып, былай есептелінеді:
 |
Төртінші және одан да жоғары ретті анықтауыштарды есептеу үшін анықтауыштың қасиеттерін білу қажет.
Екінші ретті анықтауыштың қасиеттері кез келген анықтауыштарға да орындалады, сондықтан оның қасиеттерін тек екінші ретті анықтауыш үшін дәлелдейік.
1-қасиет. Анықтауыштың жатық жолдарын оның сәйкес тік жолдарымен орын алмастырсақ ( транспонирлесек), онда оның мәні өзгермейді:
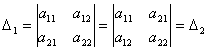
Дәлелдеуі. ![]() яғни олар тең.
яғни олар тең.
2-қасиет. Анықтауыштың екі жатық (тік) жолының сәйкес элементтерінің орнын алмастырсақ, онда оның тек таңбасы өзгереді:
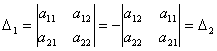
Дәлелдеуі. Шынында
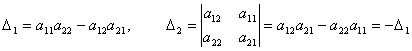
3-қасиет. Анықтауыштың бір жатық (тік)
жолының барлық элементтерін ![]() санына көбейтсек, онда
анықтауыштың мәні
санына көбейтсек, онда
анықтауыштың мәні ![]() есе артады:
есе артады:
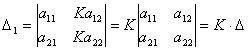
Дәлелдеуі.
![]()
Салдар. Анықтауыштың жатық (тік) жолының әр элементіндегі ортақ көбейткішті анықтауыш таңбасының алдына шығаруға болады.
2-салдар. Анықтауыштың екі жатық (тік) жолының сәйкес элементтері пропорционал болса, онда ол нөлге тең болады.
4-қасиет. Анықтауыштың ![]() - жатық (тік) жолының
элементтері екі қосылғыштан тұрса, онда ол
анықтауыштың мәні төмендегідей екі
анықтауыштың мәндерінің қосындысына тең
болады:
- жатық (тік) жолының
элементтері екі қосылғыштан тұрса, онда ол
анықтауыштың мәні төмендегідей екі
анықтауыштың мәндерінің қосындысына тең
болады:
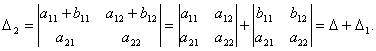
Дәлелдеуі. Шынында
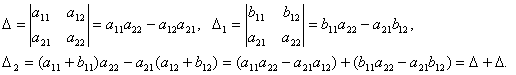
Яғни ![]()
5-қасиет. Анықтауыштың кез келген жатық (тік) жолының барлық элементтерін К санына көбейтіп, басқа кез келген жатық (тік) жолының сәйкес элементтеріне қоссақ, онда оның мәні өзгермейді:
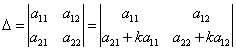
Дәлелдеуі: ![]()
![]()
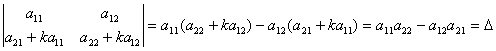
Анықтауыштың келесі екі қасиеті минор және алгебралық толықтауыш түсініктемелеріне байланысты.
2-анықтама. Анықтауыштың ![]() элементтерінің
элементтерінің ![]() миноры деп сол элемент
тұрған жатық
миноры деп сол элемент
тұрған жатық ![]() жолымен тік
жолымен тік ![]() жолын сызып тастағанда пайда болатын
анықтауышты айтады. Мысалы,
жолын сызып тастағанда пайда болатын
анықтауышты айтады. Мысалы,  анықтауышының
анықтауышының ![]() элементінің
миноры деп
элементінің
миноры деп 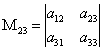 анықтауышын
айтады.
анықтауышын
айтады.
3-анықтама. Анықтауыштың ![]() элементінің
элементінің ![]() алгебралық
толықтауышы деп
алгебралық
толықтауышы деп ![]() таңбасымен
алынған осы элементтің минорын айтады, яғни
таңбасымен
алынған осы элементтің минорын айтады, яғни
![]()
![]()
Мысалы, жоғарыдағы үшінші ретті
анықтауыштың ![]() элементінің алгебралық
толықтауышы деп
элементінің алгебралық
толықтауышы деп ![]() ,
, ![]() , элементінің алгебралық
толықтауышы деп
, элементінің алгебралық
толықтауышы деп ![]() анықтауышын айтады.
анықтауышын айтады.
6-қасиет. Анықтауыштың кез келген жатық (тік) жолының элементтері мен олардың сәйкес алгебралық толықтауыштарының көбейтінділерінің қосындысы осы анықтауыштың мәніне тең болады:
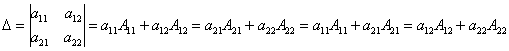
Дәлелдеуі.
![]()
Салдар. Егер анықтауыштың ![]() - жатық жолының (тік
жолының) бір элементінен өзге барлық элементтері нөлге
тең болса, онда анықтауыштың мәні осы элементпен
оның алгебралық толықтауышының көбейтіндісіне
тең болады.
- жатық жолының (тік
жолының) бір элементінен өзге барлық элементтері нөлге
тең болса, онда анықтауыштың мәні осы элементпен
оның алгебралық толықтауышының көбейтіндісіне
тең болады.

1-мысал. Есептеу керек.
![]()
Шешуі: 1- формуланы қолданамыз
![]()
2-мысал. Анықтауышты есептеу керек
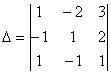
Шешуі: 2-формуланы қолдансақ
![]()
3-мысал. ![]() -ң қандай мәнінде
-ң қандай мәнінде ![]() анықтауышы нөлге тең
болады? Мұндағы
анықтауышы нөлге тең
болады? Мұндағы
![]()
Шешуі: ![]() ;
; ![]() болады, егер
болады, егер ![]()
4-мысал. ![]() анықтауышын бірінші жатық жолдың элементтерінің
көмегімен жіктеу арқылы есептеу керек.
анықтауышын бірінші жатық жолдың элементтерінің
көмегімен жіктеу арқылы есептеу керек.
Мұндағы
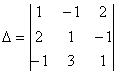
Шешуі: Мұндағы ![]() . Олардың алгебралық
толықтауыштары:
. Олардың алгебралық
толықтауыштары:

6-қасиет бойынша
![]()
5-мысал. 4-мысалдағы ![]() анықтауышын 6-қасиеттің
салдарын пайдалана отырып есептеу керек.
анықтауышын 6-қасиеттің
салдарын пайдалана отырып есептеу керек.
Шешуі: 
Төмендегі анықтауыштарды есептеу керек:
1.![]() 2.
2.![]() 3.
3.![]()
4.![]() 5.
5.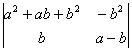 6.
6.![]()
7. 8.
8. 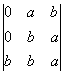 9.
9.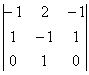
Төмендегі анықтауыштарды 6-қасиетті немесе оның салдарын пайдалана отырып есептеу керек:
10.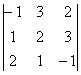 11.
11.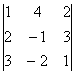 12.
12.
13.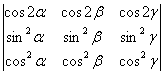 14.
14.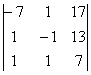
1.2 n ретті анықтауыш және оның қасиеттері
Жоғарыда қарастырылған анықтауыштың қасиеттері кез келген ретті анықтауыш үшін де орындалады. Оларды есептеу үшін анықтауыштың 5 және 6 - қасиеттерін пайдаланып ретін төмендетуге болады. Осы тәсілді қайталай отырып жоғары ретті анықтауыштың ретін 3 немесе 2-ретті анықтауыштарға алып келуге болады.
6- мысал. Төмендегі 4- ретті анықтауышты есептеу керек.
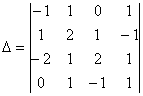
Шешуі: Бұл жағдайда екінші тік жолдан төртінші тік жолды шегерсек
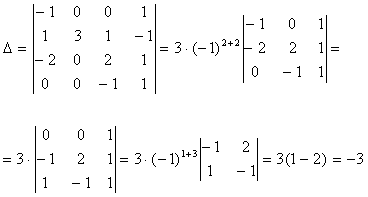
7-мысал. 5- ретті анықтауышты есептеу керек

Шешуі: Бірінші жатық жолдағы 1 санын пайдалана отырып, 3-жатық жолдағы 4 пен 4-жолдағы 5-ті нөлге айналдырамыз.Ол үшін бірінші жатық жолды 4-ке көбейтіп, үшінші жатық жолға , 5-ке көбейтіп төртінші жатық жолға қосамыз. Одан кейін бірінші тік жол арқылы жіктеп, төртінші ретті анықтауыш аламыз:
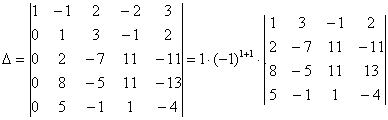
Алынған анықтауыштың жатық жолындағы 1санын пайдалана отырып,жоғарыдағыдай осы жолдың қалған элементтерін нөлге айналдырамыз:
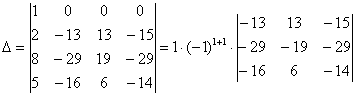
Соңғы анықтауыштағы 1-жатық жолды 3-жатық жолға қосып, шыққан интегралдың нөлге тең екендігін көруге болады.
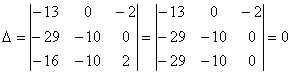
Келесі интегралды есептеу керек:
15. 16.
16.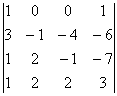
17.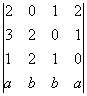 18
18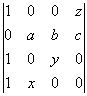
2 Векторлар. Оларға қолданылатын сызықтық амалдар
Таңдалынып алынған жүйелер бірлігінде бір санмен сипатталатын физикалық шама скалярлық шама деп аталады. Мысалы, тығыздық, дененің массасы, оның тампературасы электрлік заряд т.с.-скалярлық шамалар.
Тек санмен ғана емес әрі кеңістікте
бағыты бар шамалар векторлық шамалар немесе векторлар деп
аталады. Мұндай шамаларға жылдамдық, үдеу, күш,
электрлік немесе магниттік өрістердің кернеулері т.с. жатады.
Векторлар бағытталған кесінділермен бейнеленеді. Олар бір семіз ![]() әрпімен
немесе сызығы бар екі әріппен яғни
әрпімен
немесе сызығы бар екі әріппен яғни ![]() арқылы белгіленеді.
арқылы белгіленеді.
Мұндағы ![]() вектордың басы, ал
вектордың басы, ал ![]() оның соңы. Вектордың
ұзындығы оның модулі деп аталады.
оның соңы. Вектордың
ұзындығы оның модулі деп аталады.![]() немесе
немесе ![]() арқылы белгіленеді. Ұзындығы
нөлге тең, вектор нөл- вектор деп аталып
арқылы белгіленеді. Ұзындығы
нөлге тең, вектор нөл- вектор деп аталып ![]() арқылы белгіленеді.
арқылы белгіленеді.
Екі вектор тең болады, егер 1) олардың ұзындығы тең, 2) олар параллель және 3) бір жаққа бағытталған болса.
Бұл анықтамадан векторды кез келген нүктеге параллель көшіруге болатындығы шығады.
Бір түзудің немесе параллель түзулердің бойында жататын векторлар коллинеарлы, ал бір жазықтықтың немесе параллель жазықтықтардың бойында жататын векторлар компланарлы векторлар деп аталады.
Ұзындығы бірге тең ![]() векторы бірлік вектор
немесе орта деп аталып,
векторы бірлік вектор
немесе орта деп аталып, ![]() арқылы белгіленеді.
арқылы белгіленеді.
2.2 Векторларға қолданылатын сызықтық амалдар
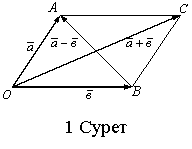 Векторларды
қосу параллелограмм ережесі бойынша орындалады:
Векторларды
қосу параллелограмм ережесі бойынша орындалады: ![]() және
және ![]() векторлары ортақ О
нүктесіне орналастырылып, оларға ОАВС параллелограмы
құрылады. Мұндағы оның диогоналының бойында
орналасқан
векторлары ортақ О
нүктесіне орналастырылып, оларға ОАВС параллелограмы
құрылады. Мұндағы оның диогоналының бойында
орналасқан ![]() векторы
векторы
![]() және
және
![]() векторларының
қосындысы деп аталады.
векторларының
қосындысы деп аталады.
![]() векторы
векторы ![]() векторына тең
болғандықтан,
векторына тең
болғандықтан, ![]() және
және ![]() векторларының қосындысы деп
векторларының қосындысы деп ![]() векторының бас
нүктесін оның соңғы нүктесіне
жалғастырылған
векторының бас
нүктесін оның соңғы нүктесіне
жалғастырылған ![]() векторының соңғы
нүктесімен қосатын векторды айтады. (үшбұрыштар
ережесі). Яғни
векторының соңғы
нүктесімен қосатын векторды айтады. (үшбұрыштар
ережесі). Яғни
![]() +
+![]() =
=![]() (1)
(1)
Ортақ О нүктесіне келтірілген ![]() және
және ![]() векторларының
айырымы деп алынатын
векторларының
айырымы деп алынатын ![]() векторының
соңғы нүктесінен
векторының
соңғы нүктесінен ![]() векторының соңғы
нүктесіне бағытталған векторды, яғни
векторының соңғы
нүктесіне бағытталған векторды, яғни ![]() -
-![]() =
=![]()
![]() айтады.
айтады.
(1)-формула бойынша ![]() +
+![]() =
=![]() , бұдан
, бұдан
![]() =
=![]() -
-![]() (2)
(2)
![]() векторының
векторының
![]() санына
көбейтіндісі деп төмендегі шарттарды қанағаттандыратын
санына
көбейтіндісі деп төмендегі шарттарды қанағаттандыратын ![]() векторын айтады:1)
векторын айтады:1) ![]() векторы
векторы ![]() -ға коллинеарлы,
-ға коллинеарлы,
2) ![]()
![]()
![]() ,
, ![]() болғанда
болғанда ![]() және
және ![]() векторлары бір
жаққа бағытталған,
векторлары бір
жаққа бағытталған, ![]() болғанда қарама-қарсы
бағытталған.
болғанда қарама-қарсы
бағытталған.
Қасиеттері:
1) ![]() =
=![]() ;
;
2) ![]() =0,
=0,
![]()
![]() ;
;
3) ![]() =
=![]() ;
;
4) ![]() ;
;
5) ![]() .
.
![]() өсімен
өсімен
![]() =
=![]() векторы берілсін.
Вектордың басы мен соңын
векторы берілсін.
Вектордың басы мен соңын ![]() өсіне проекциялап ,
өсіне проекциялап ,![]() векторын аламыз.
векторын аламыз.
 |
![]() векторының
өсіне проекциясы пр
векторының
өсіне проекциясы пр![]()
![]() арқылы белгіленіп,
арқылы белгіленіп, ![]() векторының
ұзындығына тең болады, егер
векторының
ұзындығына тең болады, егер ![]() мен
мен ![]() бағыттас болса; қарама-қарсы
болған жағдайда теріс таңбамен алынады.
бағыттас болса; қарама-қарсы
болған жағдайда теріс таңбамен алынады.
Қасиеттері:
1) пр![]()
![]() =
=![]() , мұндағы
, мұндағы ![]()
2) пр![]()
![]()
![]()
![]()
![]() ;
;
3) ![]() .
.
1-мысал. ![]() болу үшін
болу үшін ![]() және
және ![]() векторлары қандай шартты
қанағаттандыру керек?
векторлары қандай шартты
қанағаттандыру керек?
Шешуі: ![]() және
және ![]() векторларын ортақ бір О
нүктесінен шығатындай етіп орналастырып, оларға
параллелограмм құрастырамыз. (1- сурет). Бұл жағдайда
векторларын ортақ бір О
нүктесінен шығатындай етіп орналастырып, оларға
параллелограмм құрастырамыз. (1- сурет). Бұл жағдайда ![]() деп
отырғанымыз осы параллелограммның ОС диогоналының
ұзындығы, ал
деп
отырғанымыз осы параллелограммның ОС диогоналының
ұзындығы, ал ![]() -ВА диогоналының ұзындығы
болады. Геометриядан параллелограммның диогоналдары тек олар
тікбұрышты болғанда ғана тең болатындығы бізге
мәлім. Сондықтан
-ВА диогоналының ұзындығы
болады. Геометриядан параллелограммның диогоналдары тек олар
тікбұрышты болғанда ғана тең болатындығы бізге
мәлім. Сондықтан ![]() болу үшін
болу үшін ![]() және
және ![]() векторлары
перпендикуляр болуы қажет.
векторлары
перпендикуляр болуы қажет.
2-мысал Берілген ![]() және
және ![]() векторлары арқылы
векторлары арқылы ![]() және
және ![]() векторларын
салыңыз.
векторларын
салыңыз.
 |
Шешуі:
19. Берілген![]() және
және ![]() векторлары
арқылы
векторлары
арқылы ![]()
![]() ;
; ![]() ;
; ![]() векторларын салыңыз.
векторларын салыңыз.
20. ![]() ,
,
![]() және
және ![]() векторларының
қосындысының
векторларының
қосындысының ![]()
![]() өсіне проекциясын табу керек, егер
өсіне проекциясын табу керек, егер ![]() ,
, ![]() ,
, ![]() ал осы векторлардың
ал осы векторлардың ![]() өсімен
бұрыштары сәйкесінше
өсімен
бұрыштары сәйкесінше ![]() ,
,![]() ,
,![]() -ге тең.
-ге тең.
21. Егер: 1) ![]() , 2)
, 2) ![]() болса, онда
болса, онда ![]() және
және ![]() векторлары қандай
шарттарды қанағаттандыруы қажет?
векторлары қандай
шарттарды қанағаттандыруы қажет?
3. Кеңістіктегі тікбұрышты декарттық координаталар
3.1 Нүктенің координаталары
Кеңістікте тікбұрышты декарттық координаталар
жүйесі ұзындықты өлшеу үшін масштаб
бірлігінің және О нүктесінде қиылысатын бір-бірімен
перпендикуляр үш өстің берілуімен анықталады.Біріншісі
(![]() абсцисс
өсі, екіншісі
абсцисс
өсі, екіншісі ![]() ордината
өсі, үшіншісі
ордината
өсі, үшіншісі ![]() аппликата өсі , ал О нүктесі
деп аталады. Координаттық өстердің орны сәйкесінше осы
(
аппликата өсі , ал О нүктесі
деп аталады. Координаттық өстердің орны сәйкесінше осы
(![]() ,
,![]() ,
,![]() өстерімен бағыттас
өстерімен бағыттас ![]() ,
,![]() ,
,![]() бірлік векторлары арқылы
анықталады. Бұл векторлар базистік векторлар деп аталады.
бірлік векторлары арқылы
анықталады. Бұл векторлар базистік векторлар деп аталады.
Кеңістікте А нүктесі берілсін (4 Сурет)
 |
Оның
Сонымен кеңістіктегі әрбір ![]() нүктесіне тек бір
ғана
нүктесіне тек бір
ғана ![]() сандары
сәйкестендіріледі.
сандары
сәйкестендіріледі.
Координаталар жүйесі оң деп аталады, егер ![]() өсінің
ұшынан қарағанда
өсінің
ұшынан қарағанда ![]() өсінен
өсінен ![]() өсіне айналдырғандағы кіші
бұрыш сағат бағытына қарсы болса; теріс деп аталады,
егер бағыттас болса, 4- суретте оң координаталар жүйесі
бейнеленген.
өсіне айналдырғандағы кіші
бұрыш сағат бағытына қарсы болса; теріс деп аталады,
егер бағыттас болса, 4- суретте оң координаталар жүйесі
бейнеленген.
![]() координата жазықтықтары кеңістікті
октанталар деп аталатын сегіз бөлікке бөледі.
координата жазықтықтары кеңістікті
октанталар деп аталатын сегіз бөлікке бөледі.
1-мысал. Барлық координаттың
жазықтықтармен жанасатын әрі 3- октантада
орналасқан, радиусы ![]() болатын шардың центрін анықтау
керек.
болатын шардың центрін анықтау
керек.
Шешуі: Егер шардың центрін ![]() деп белгілеп
алсақ, онда бұл нүктенің
деп белгілеп
алсақ, онда бұл нүктенің ![]() координаттық жазықтығына
дейінгі қашықтығы
координаттық жазықтығына
дейінгі қашықтығы ![]() векторының ұзындығына (4
Cурет), яғни оның абсциссаның модуліне тең болады. Осылайша,
векторының ұзындығына (4
Cурет), яғни оның абсциссаның модуліне тең болады. Осылайша,
![]() нүктесінің
нүктесінің
![]() жазықтығына
дейінгі қашықтығы
жазықтығына
дейінгі қашықтығы ![]() ал
ал ![]() нүктесінің
нүктесінің ![]() жазықтығына дейінгі
қашықтығы
жазықтығына дейінгі
қашықтығы ![]() тең болады.
тең болады.
Есептің шарты бойынша бұл
қашықтықтар шардың радиусына тең
болғандықтан ![]() 3-октантада
3-октантада ![]() болғандықтан
болғандықтан ![]() (-5,-5,5).
(-5,-5,5).
22.![]() (3,0,0),
(3,0,0),![]() нүктелері координат жүйесінде
қалай орналасқан?
нүктелері координат жүйесінде
қалай орналасқан?
23. ![]() нүктесіне симметриялы болатын
нүктелердің координаталарын табу керек: 1)
нүктесіне симметриялы болатын
нүктелердің координаталарын табу керек: 1) ![]() жазықтығына
қарағанда, 2)
жазықтығына
қарағанда, 2) ![]() жазықтығына
қарағанда, 3)
жазықтығына
қарағанда, 3) ![]() өсіне қарағанда, 4)
координат жүйесінің бас нүктесіне қарағанда.
өсіне қарағанда, 4)
координат жүйесінің бас нүктесіне қарағанда.
24. Қабырғалары координат өстерінің бойында жататын ұзындығы 5-ке тең 5-октантада орналасқан кубтың төбелерінің координаталарын табу керек.
3.2 Вектордың координаталары
![]() векторының
векторының ![]() координат өстеріндегі
проекциялары
координат өстеріндегі
проекциялары ![]() оның
координаталары деп аталып,
оның
координаталары деп аталып, ![]() деп жазылады.
деп жазылады. ![]() векторының координаталары
оның орталарға жіктелгендегі коэффициенттері болады:
векторының координаталары
оның орталарға жіктелгендегі коэффициенттері болады:
![]() (1)
(1)
Координаттың басында ![]() нүктесіне
бағытталған
нүктесіне
бағытталған ![]() векторы
векторы ![]() нүктесінің радиус-векторы деп
аталады. Оның координат өстеріндегі проекциялары
нүктесінің радиус-векторы деп
аталады. Оның координат өстеріндегі проекциялары ![]() нүктесінің
координаталарына тең, яғни
нүктесінің
координаталарына тең, яғни
![]() (2)
(2)
Егер ![]() және
және ![]() нүктелері координаталары
арқылы берілсе, онда
нүктелері координаталары
арқылы берілсе, онда ![]() векторының координаталары
төмендегі формуламен табылады:
векторының координаталары
төмендегі формуламен табылады:
![]() (3)
(3)
Векторларды қосқанда (алғанда)
олардың координаталары қосылады (алынады), векторды санға
көбейткенде оның барлық координаталары осы санға
көбейтіледі, яғни егер ![]() және
және ![]() болса,онда
болса,онда
![]() (4)
(4)
![]() (5)
(5)
Егер ![]() және
және ![]() векторлары коллинеарлы болcа, онда
векторлары коллинеарлы болcа, онда ![]() . Коллинеарлы
векторлардың сәйкес координаталары пропорционал болады:
. Коллинеарлы
векторлардың сәйкес координаталары пропорционал болады:
![]() (6)
(6)
![]() векторының ұзындығы
векторының ұзындығы ![]() (7)
(7)
формуласымен анықталады.
![]() және
және ![]() нүктелерінің
қашықтығы
нүктелерінің
қашықтығы
![]() (8)
(8)
формуласымен анықталады.
2-мысал. ![]() және
және ![]() нүктелерінің
бір түзудің бойында жататындығын дәлелдеу керек.
нүктелерінің
бір түзудің бойында жататындығын дәлелдеу керек.
Шешуі: Ол үшін ![]() және
және ![]()
![]() векторларының коллинеарлы
болатындығын дәлелдесек болады.
векторларының коллинеарлы
болатындығын дәлелдесек болады.
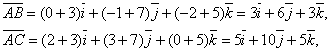
Бұдан ![]() болатындығын көреміз. Яғни
болатындығын көреміз. Яғни
![]() ,
,![]() және
және ![]() нүктелері бір
түзудің бойында жатады.
нүктелері бір
түзудің бойында жатады.
3-мысал. ![]() және
және ![]() -ң қандай мәндерінде
-ң қандай мәндерінде ![]() және
және![]() векторлары коллинеарлы
болады?
векторлары коллинеарлы
болады?
Шешуі:
![]() және
және ![]()
![]() векторларының координаталары
пропорционал болуы керек:
векторларының координаталары
пропорционал болуы керек: ![]() . Осыдан
. Осыдан ![]() =2,
=2,
![]() =-1,5.
=-1,5. ![]() және
және ![]() -ң осы мәндерінде
-ң осы мәндерінде ![]() және
және ![]() векторлары коллинеарлы
болады.
векторлары коллинеарлы
болады.
4-мысал. ![]() және
және ![]() нүктелерінен
бірдей қашықтықта орналасқан , әрі
нүктелерінен
бірдей қашықтықта орналасқан , әрі ![]() өсінде жататын
нүктені табу керек.
өсінде жататын
нүктені табу керек.
Шешуі: Іздеп отырған ![]() нүктесінің
координатасы
нүктесінің
координатасы ![]() .
.
Оның ![]() және
және ![]() нүктелеріне дейінгі
қашықтықтары:
нүктелеріне дейінгі
қашықтықтары:
![]()
![]() .
.
Есептің шарты бойынша ![]() яғни
яғни ![]() немесе
немесе ![]()
![]()
25. ![]() және
және ![]() нүктелері берілген.
нүктелері берілген. ![]() -ң қандай
мәндерінде С нүктесі
-ң қандай
мәндерінде С нүктесі ![]() түзуінің бойында жатады.
түзуінің бойында жатады.
26. ![]() және
және ![]() нүктелері трапецияның
төбелері болатындығын тексеру керек.
нүктелері трапецияның
төбелері болатындығын тексеру керек.
27.![]() және
және ![]() нүктелерінен бірдей
қашықтықта орналасқан әрі
нүктелерінен бірдей
қашықтықта орналасқан әрі ![]() өсінде жататын
нүктені табу керек.
өсінде жататын
нүктені табу керек.
3.3 Кесіндіні берілген қатынасқа бөлу
![]() нүктесі
нүктесі
![]() және
және ![]() нүктелерінің
арасындағы кесіндіні
нүктелерінің
арасындағы кесіндіні ![]() етіп бөлсін. Бұл
жағдайда
етіп бөлсін. Бұл
жағдайда ![]() нүктесінің
нүктесінің
![]() радиус
векторы
радиус
векторы ![]() нүктелерінің
нүктелерінің
![]() радиус
векторлары арқылы төмендегі формуламен өрнектеледі:
радиус
векторлары арқылы төмендегі формуламен өрнектеледі:
![]() (9)
(9)
Осы теңдеуден
![]() (10)
(10)
Дербес жағдайда, егер ![]() нүктесі
нүктесі ![]() кесіндісінің ортасында жатса, онда
кесіндісінің ортасында жатса, онда ![]() әрі
әрі ![]() (9')
(9')
![]() (10')
(10')
5-мысал. ![]() координат
жазықтығы
координат
жазықтығы ![]() және
және ![]() нүктелерінің
арасындағы кесіндіні қандай қатынаста бөліп
тұрғанын анықтау керек.
нүктелерінің
арасындағы кесіндіні қандай қатынаста бөліп
тұрғанын анықтау керек.
Шешуі: ![]() кесіндісі
кесіндісі
![]() жазықтығын
жазықтығын
![]() нүктесінде
бөлсін. 10-формула бойынша
нүктесінде
бөлсін. 10-формула бойынша ![]() және
және![]() нүктелерінің аппликаталарын
қойсақ
нүктелерінің аппликаталарын
қойсақ
![]() яғни
яғни
![]()
28. ![]() кесіндісі
кесіндісі ![]() нүктелерінің
көмегімен теңдей бес бөлікке бөлінген.
нүктелерінің
көмегімен теңдей бес бөлікке бөлінген.![]() және
және![]() нүктелерінің координаталары белгілі. Қалған
нүктелерінің координаталары белгілі. Қалған ![]() нүктелерін табу
керек.
нүктелерін табу
керек.
29. ![]()
![]() және
және ![]() нүктелері берілген.
нүктелері берілген. ![]() үшбұрышының
медианаларының қиылысу нүктесін анықтау керек.
үшбұрышының
медианаларының қиылысу нүктесін анықтау керек.
3.4 Бағыттаушы косинустар
![]() векторы
берілсін.
векторы
берілсін. ![]() векторының
орты деп осы вектормен бағыттас ұзындығы бірге
тең
векторының
орты деп осы вектормен бағыттас ұзындығы бірге
тең ![]() векторын
айтамыз. Ол
векторын
айтамыз. Ол
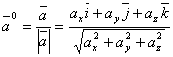 (11)
(11)
формуласымен анықталады.
![]() түзуі координат өстерімен
сәйкесінше
түзуі координат өстерімен
сәйкесінше ![]() бұрыштарын
жасасын. Осы түзудің бағыттаушы косинустары деп
жоғарыдағы бұрыштардың косинустарын айтады:
бұрыштарын
жасасын. Осы түзудің бағыттаушы косинустары деп
жоғарыдағы бұрыштардың косинустарын айтады: ![]() Егер
Егер ![]() түзуінің
бағыты
түзуінің
бағыты ![]() бірлік
векторымен берілсе, онда :
бірлік
векторымен берілсе, онда :
![]()
![]() (12)
(12)
Бағыттаушы косинустар бір-бірімен төмендегі формуламен байланысты.
![]() (13)
(13)
Егер ![]() түзуінің бағыты
түзуінің бағыты ![]() векторымен берілсе,
онда оның орты табылып, 12-формуламен салыстыру арқылы
векторымен берілсе,
онда оның орты табылып, 12-формуламен салыстыру арқылы
![]()
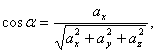
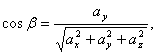
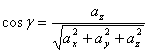 (14)
(14)
формулалары алынады.
6-мысал. ![]() векторының ортын және
оның бағыттаушы косинустарын табу керек.
векторының ортын және
оның бағыттаушы косинустарын табу керек.
Шешуі: ![]() векторының ұзындығын табамыз:
векторының ұзындығын табамыз:
![]()
яғни, (11) -формула бойынша
![]() .
.
![]() бірлік векторының координаталары
берілген
бірлік векторының координаталары
берілген ![]() векторының
бағыттаушы косинустары болатындықтан:
векторының
бағыттаушы косинустары болатындықтан:
![]()
![]()
![]()
7-мысал. ![]() векторы координата өстерімен
векторы координата өстерімен ![]() сүйір
бұрыш жасайды.
сүйір
бұрыш жасайды. ![]() болғандағы
болғандағы
![]() векторының
координаталарын табу керек.
векторының
координаталарын табу керек.
Шешуі: Алғаш (13)-теңдеуден ![]() бұрышын табамыз:
бұрышын табамыз:
![]()
![]() .
.
Есептің шарты бойынша ![]() сүйір бұрыш
болғандықтан,
сүйір бұрыш
болғандықтан, ![]() Сондықтан
Сондықтан ![]() Яғни
Яғни ![]() сондықтан
сондықтан ![]() немесе
немесе ![]()
30. ![]() векторымен берілген
векторымен берілген ![]() түзуінің
бағыттаушы векторларын табу керек, мұндағы
түзуінің
бағыттаушы векторларын табу керек, мұндағы ![]() және
және ![]() .
.
31. ![]() түзуі координат өстерімен
төмендегідей бұрыштар құрай алама? а)
түзуі координат өстерімен
төмендегідей бұрыштар құрай алама? а) ![]() ; б)
; б) ![]() ?
?
32. ![]() векторының ортын табу керек.
векторының ортын табу керек.
33. ![]() түзуі координат өстерімен
теңдей сүйір бұрыш құрайды. Осы түзудің
бойында жатқан вектордың ортын табу керек.
түзуі координат өстерімен
теңдей сүйір бұрыш құрайды. Осы түзудің
бойында жатқан вектордың ортын табу керек.
4. Векторлардың көбейтіндісі
4.1 Скалярлық көбейтінді
![]() және
және ![]() векторларының скалярлық
көбейтіндісі
векторларының скалярлық
көбейтіндісі ![]() деп
осы векторлардың ұзындықтарын олардың арасындағы
деп
осы векторлардың ұзындықтарын олардың арасындағы ![]() бұрышына
көбейткенде шығатын санды айтады:
бұрышына
көбейткенде шығатын санды айтады:
![]() (1)
(1)
Қасиеттері
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() және
және ![]() векторлары нөлдік векторлар
болмағанда,
векторлары нөлдік векторлар
болмағанда, ![]() болса,
онда бұл векторлар перпендикуляр болады. Егер
болса,
онда бұл векторлар перпендикуляр болады. Егер ![]() болса, онда олардың
арасындағы бұрыш сүйір, егер
болса, онда олардың
арасындағы бұрыш сүйір, егер ![]() болса, онда
болса, онда ![]() доғал болады;
доғал болады;
5) ![]() векторының скалярлық квадраты
оның ұзындығының квадратына тең, яғни
векторының скалярлық квадраты
оның ұзындығының квадратына тең, яғни ![]() . Соңғы
қасиеттен
. Соңғы
қасиеттен
![]() . (2)
. (2)
(1)-формуладан
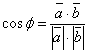 .
(3)
.
(3) ![]()
![]()
![]()
Геометриялық мағынасы:
![]() векторының
векторының ![]() векторының бағытына
түсірілген проекциясы
векторының бағытына
түсірілген проекциясы
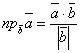 (4)
(4)
формуласымен анықталады.
Механикалық мағынасы:
![]() күшінің
күшінің ![]() векторына скалярлық
көбейтіндісі осы күштің әсерінен материалдық
нүктенің
векторына скалярлық
көбейтіндісі осы күштің әсерінен материалдық
нүктенің ![]() векторының
бойында орын ауыстырғандағы
векторының
бойында орын ауыстырғандағы ![]() жұмысына тең болады, яғни
жұмысына тең болады, яғни
![]() (5)
(5)
Скалярлық көбейтіндінің
анықтамасын пайдаланып, ![]() орттарының
көбейтіндісінің кестесін алуға болады:
орттарының
көбейтіндісінің кестесін алуға болады:
![]() (6)
(6)
Егер векторлар өздерінің координаталарымен
берілсе ![]() ,
, ![]() , онда бұл
векторлардың скалярлық көбейтіндісі
, онда бұл
векторлардың скалярлық көбейтіндісі
![]()
![]() . (7)
. (7)
1-мысал. ![]() және
және ![]() векторларының арасындағы
бұрыш
векторларының арасындағы
бұрыш ![]() тең.
тең.
![]() болғандағы
болғандағы
![]() векторының
ұзындығын табу керек.
векторының
ұзындығын табу керек.
Шешуі: ![]() векторының
ұзындығын (2)-формуласымен табуға болады:
векторының
ұзындығын (2)-формуласымен табуға болады:
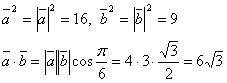
Яғни ![]() Осыдан
Осыдан ![]() .
.
2-мысал. Материалдық нүктеге ![]() күштері әсер етсін.
Осы күштерге сай әсер ететін
күштері әсер етсін.
Осы күштерге сай әсер ететін ![]() күшін анықтап, осы
күштің әсерінен материалдық нүктенің
күшін анықтап, осы
күштің әсерінен материалдық нүктенің ![]() -дан
-дан ![]() -ға
жылжығандағы істелінетін жұмысты анықтау керек.
-ға
жылжығандағы істелінетін жұмысты анықтау керек.
Шешуі: ![]() мен
мен ![]() күштеріне тең болатын
күштеріне тең болатын ![]() күшін тауып
аламыз:
күшін тауып
аламыз:
![]() , орын ауыстыру векторы
, орын ауыстыру векторы ![]()
![]()
(5)-формула бойынша істелінген жұмыс ![]() .
.
3-мысал. ![]() және
және ![]() векторлары
берілген.
векторлары
берілген. ![]() векторының
векторының
![]() векторының
бағытына түсірілген проекциясын табу керек.
векторының
бағытына түсірілген проекциясын табу керек.
Шешуі: Алғаш ![]() векторының
координаталарын анықтаймыз:
векторының
координаталарын анықтаймыз:
![]()
(4)-формула бойынша 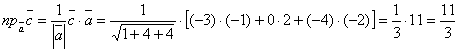 .
.
34. Бір-бірімен перпендикуляр болатын ![]() және
және ![]() векторлары
векторлары ![]() векторымен
векторымен ![]() бұрыш жасасын әрі
бұрыш жасасын әрі
![]() болсын. Табу
керек:
болсын. Табу
керек:
1) ![]() 2)
2)![]() .
.
35. Төбелері ![]() және
және ![]() нүктелері болатын
төртбұрыш берілген. Оның диогоналдары перпендикуляр болатынын
дәлелдеу керек.
нүктелері болатын
төртбұрыш берілген. Оның диогоналдары перпендикуляр болатынын
дәлелдеу керек.
36. Төбелері ![]()
![]() және
және ![]() нүктелері болатын
ұшбұрыш берілген. Оның
нүктелері болатын
ұшбұрыш берілген. Оның ![]() төбесіндегі ішкі бұрышы
төбесіндегі ішкі бұрышы ![]() -ді табу керек.
-ді табу керек.
37. ![]() және
және ![]() векторлары берілген.
векторлары берілген. ![]() векторының
векторының ![]() векторының
бағытына түсірілген проекциясын табу керек.
векторының
бағытына түсірілген проекциясын табу керек.
4.1 Векторлық көбейтінді
![]() және
және ![]() векторларының
векторлық көбейтіндісі деп төмендегі шарттарды
қанағаттандыратын үшінші
векторларының
векторлық көбейтіндісі деп төмендегі шарттарды
қанағаттандыратын үшінші ![]() векторын айтамыз:
векторын айтамыз:
1) ![]() , мұндағы
, мұндағы ![]() бұрышы
бұрышы ![]() және
және ![]() -ның
арасындағы бұрыш;
-ның
арасындағы бұрыш;
2) ![]() векторы,
векторы, ![]() және
және ![]() векторларының
әрқайсысымен тікбұрыш жасайды;
векторларының
әрқайсысымен тікбұрыш жасайды;
3) ![]() векторының бағыты, оның
ұшынан қарағанда
векторының бағыты, оның
ұшынан қарағанда ![]() векторын
векторын ![]() векторына кіші бұрыш бойынша
бұру сағат бағытына қарсы бағытталады
векторына кіші бұрыш бойынша
бұру сағат бағытына қарсы бағытталады
(5-сурет).
 |
Касиеттері:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) нөлге тең емес ![]() және
және ![]() векторларының
векторлық көбейтіндісі нөлге тең болса, онда
векторларының
векторлық көбейтіндісі нөлге тең болса, онда ![]() және
және ![]() векторлары коллинеарлы
векторлар деп аталады. Дербес жағдайда кез келген
векторлары коллинеарлы
векторлар деп аталады. Дербес жағдайда кез келген ![]() векторы үшін
векторы үшін ![]() болады.
болады.
5) Егер ![]() мен
мен ![]() коллинеарлы емес болса, онда олардың
векторлық көбейтіндісінің модулі сол векторларға
салынған параллелограмның ауданына тең болады (5-сурет).
коллинеарлы емес болса, онда олардың
векторлық көбейтіндісінің модулі сол векторларға
салынған параллелограмның ауданына тең болады (5-сурет).
Механикалық мағынасы:
Егер ![]() күші
күші ![]() нүктесіне әсер ететін болса,
онда бұл күштің
нүктесіне әсер ететін болса,
онда бұл күштің ![]() нүктесіне
қарағандағы моменті
нүктесіне
қарағандағы моменті ![]() -деп
-деп ![]() мен
мен ![]() -тің векторлық
көбейтіндісін айтамыз:
-тің векторлық
көбейтіндісін айтамыз:
![]() (8)
(8)
Дербес жағдайда координаттың бас
нүктесіне қарағандағы моменті ![]() мұндағы
мұндағы ![]() - күш әсер
ететін нүктенің радиус векторы.
- күш әсер
ететін нүктенің радиус векторы.
Егер ![]() және
және ![]() болса, онда
болса, онда
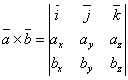 .
(9)
.
(9)
4-мысал. ![]() ,
,![]() ,
,![]() векторлары
векторлары ![]() шартын
қанағаттандырады.
шартын
қанағаттандырады. ![]() болатындығын дәлелдеу керек.
болатындығын дәлелдеу керек.
Шешуі. ![]() теңдігінің
теңдігінің
![]() -ға
векторлық көбейтіндісін анықтаймыз:
-ға
векторлық көбейтіндісін анықтаймыз:
![]()
Бұдан ![]()
![]()
![]()
Дәл осылайша ![]() болатындығын дәлелдеуге
болады.
болатындығын дәлелдеуге
болады.
5-мысал. ![]() күші
күші ![]() нүктесіне
әсер етсін. Осы күштің
нүктесіне
әсер етсін. Осы күштің ![]() нүктесімен салыстырғандағы
моментін табу керек.
нүктесімен салыстырғандағы
моментін табу керек.
Шешуі: ![]() векторын анықтаймыз:
векторын анықтаймыз:
![]()
(8) және (9)- формулалар арқылы
![]()
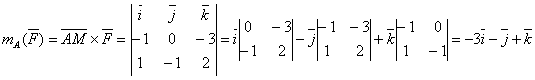 .
.
6-мысал. Төбелері ![]()
![]() және
және ![]() нүктелері болатын
үшбұрыштың ауданын табу керек.
нүктелері болатын
үшбұрыштың ауданын табу керек.
Шешуі: ![]() үшбұрышының ауданы,
қабырғалары
үшбұрышының ауданы,
қабырғалары ![]() және
және ![]() векторы болатын параллелограмның
ауданының жарымына тең болатындықтан
векторы болатын параллелограмның
ауданының жарымына тең болатындықтан
![]() .
.
![]() және
және
![]() векторларын
табамыз:
векторларын
табамыз:
![]()
![]()
Олардың векторлық көбейтіндісі
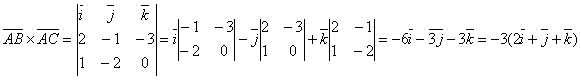
Сондықтан ![]()
![]() квадрат бірлік.
квадрат бірлік.
7-мысал. ![]() векторлары берілген. Табу керек
векторлары берілген. Табу керек ![]() және
және ![]() .
.
Шешуі:
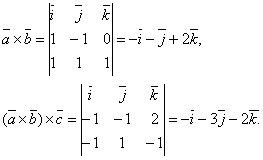
Осылайша 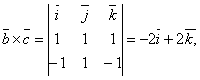
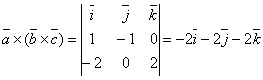
Бұдан ![]() болатындығын көреміз.
болатындығын көреміз.
38. ![]() өрнегін ықшамдау керек.
өрнегін ықшамдау керек.
39. ![]() және
және ![]() векторлары берілген. Табу
керек
векторлары берілген. Табу
керек ![]()
40. Төбелері ![]() нүктелері болатын
үшбұрыш берілген. Оның ауданын табу керек.
нүктелері болатын
үшбұрыш берілген. Оның ауданын табу керек.
41.![]() күші
күші ![]() нүктесіне әсер етсін.Осы
күштің координаттың бас нүктесіне
қарағандағы моментін табу керек.
нүктесіне әсер етсін.Осы
күштің координаттың бас нүктесіне
қарағандағы моментін табу керек.
42.![]() нүктесіне әсер ететін үш күш берілген:
нүктесіне әсер ететін үш күш берілген:![]() . Осы күштерге
сай әсер ететін күштің
. Осы күштерге
сай әсер ететін күштің ![]() нүктесіне
қарағандағы моментін анықтау керек.
нүктесіне
қарағандағы моментін анықтау керек.
4.3 Үш вектордың аралас көбейтіндісі
Үш вектордың аралас көбейтіндісі ![]() деп олардың
векторлы – скалярлық көбейтіндісін айтады:
деп олардың
векторлы – скалярлық көбейтіндісін айтады:
![]() (10)
(10)
 |
Егер
Егер компланарлы емес ![]() векторларын бір нүктеден
шығатындай етіп орналастырсақ, онда олардың аралас
көбейтіндісінің модулі, негізгі үш өлшемі осы
векторлардың ұзындығы болатын параллелепипедтің
көлемін береді ( 6 Cурет) .
векторларын бір нүктеден
шығатындай етіп орналастырсақ, онда олардың аралас
көбейтіндісінің модулі, негізгі үш өлшемі осы
векторлардың ұзындығы болатын параллелепипедтің
көлемін береді ( 6 Cурет) .
Егер ![]() векторлары
өздерінің координаталарымен берілсе, онда
векторлары
өздерінің координаталарымен берілсе, онда
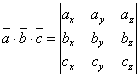 (11)
(11)
8-мысал. ![]() ,
, ![]() ,
, ![]() векторларының компланарлы болатындығын дәлелдеу
керек.
векторларының компланарлы болатындығын дәлелдеу
керек.
Шешуі:
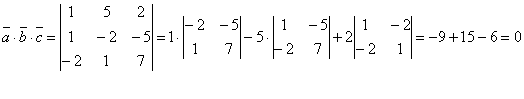
![]() болғандықтан
болғандықтан
![]() ,
,![]() және
және ![]() векторлары
компланарлы.
векторлары
компланарлы.
9-мысал. Төбелері ![]() нүктелері болатын тетраэдрдің
көлемін табу керек.
нүктелері болатын тетраэдрдің
көлемін табу керек.
Шешуі: Алғаш ![]() векторларын тауып аламыз.
векторларын тауып аламыз. ![]() тетраэдрадасының
көлемі
тетраэдрадасының
көлемі ![]() болатындығы
белгілі.
болатындығы
белгілі. ![]() ,
,![]() ,
,![]() векторлары арқылы
құралатын параллелепипедтің биіктігімен тетраэдрдің
биіктіктері тең, ал табанының ауданы екі есе үлкен
болатындығын ескерсек
векторлары арқылы
құралатын параллелепипедтің биіктігімен тетраэдрдің
биіктіктері тең, ал табанының ауданы екі есе үлкен
болатындығын ескерсек
![]()
яғни ![]() болғандықтан,
болғандықтан,
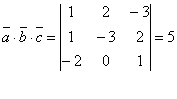
Сонымен ![]() .
.
43. Төмендегі векторлар компланар бола ма, әлде болмай ма?
1) ![]() ,
, ![]() ,
, ![]()
2) ![]()
44. ![]() және
және
![]() нүктелерінің
бір жазықтықтың бойында жататындығын дәлелдеу
керек.
нүктелерінің
бір жазықтықтың бойында жататындығын дәлелдеу
керек.
45. Негізгі өлшемдері ![]() ,
, ![]() ,
, ![]() векторларының ұзындығы
болатын параллелепипедтің көлемін табу керек.
векторларының ұзындығы
болатын параллелепипедтің көлемін табу керек.
46. Тетраэдрдің төбелері ![]() берілген.
берілген. ![]() төбесінен
төбесінен ![]() жағына жүргізілген
жағына жүргізілген ![]() биіктігін табу керек.
биіктігін табу керек.
5 Матрицалар
5.1 Матрицаларға сызықтық амалдар қолдану. Транспонирлеу.
![]() өлшемді квадраттық матрица деп
өлшемді квадраттық матрица деп
![]() жатық
және
жатық
және ![]() тік
жолда орналаласқан
тік
жолда орналаласқан ![]() саннан тұратын
саннан тұратын ![]() кестесін айтамыз:
кестесін айтамыз:
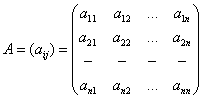 (1)
(1)
![]() элементінің
бірінші
элементінің
бірінші ![]() индексі
жатық жолдың нөмірін, екінші
индексі
жатық жолдың нөмірін, екінші ![]() индексі тік жолдың
(бағананың) нөмірін көрсетеді.
индексі тік жолдың
(бағананың) нөмірін көрсетеді.
![]() диагоналы
диагоналы
![]() матрицасының
негізгі, ал
матрицасының
негізгі, ал![]() диагоналы қосалқы диагоналдары деп аталады.
диагоналы қосалқы диагоналдары деп аталады.
Егер олардың барлық сәйкес элементтері тең
болса, реттері бірдей ![]() мен
мен
![]() матрицалары тең
болады, яғни
матрицалары тең
болады, яғни ![]()
![]() .
.
Матрицаларға сызықтық амалдар қолдануды оларды алгебралық қосу, санға көбейту деп түсінеміз
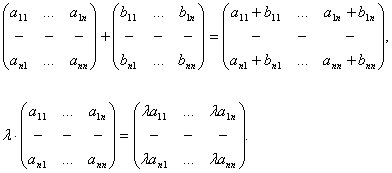
Матрицаларды қосу мен оларды санға көбейтудің қасиеттері:
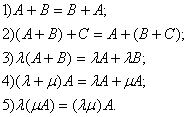 (2)
(2)
Тек нөлдерден тұратын О матрицасын
нөлдік матрица деп айтамыз. Ол үшін ![]() .
.
![]() матрицасының жатық жолдарын
сәйкес сол нөмірлі тік жолдарға айналдыру немесе керісінше
тік жолдарды сәйкес жатық жолдарға айналдыру амалын транспонирлеу
деп атап,
матрицасының жатық жолдарын
сәйкес сол нөмірлі тік жолдарға айналдыру немесе керісінше
тік жолдарды сәйкес жатық жолдарға айналдыру амалын транспонирлеу
деп атап, ![]() арқылы
белгілейміз. Мысалы, егер
арқылы
белгілейміз. Мысалы, егер
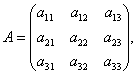 онда
онда 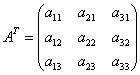 .
.
Транспонирлеу амалының қасиеттері:
![]() (3)
(3)
Негізгі диоганалының бойында жатпайтын элементтердің барлығы нөлге тең болатын матрицаны диоганалдық матрица деп айтамыз.
![]() матрицасы симметриялы деп аталады, егер
матрицасы симметриялы деп аталады, егер ![]()
![]() -ретті
-ретті ![]() матрицасының элементтерінен
құралған анықтауыш
матрицасының элементтерінен
құралған анықтауыш ![]() арқылы белгіленеді.
арқылы белгіленеді.
1-мысал. ![]() матрицалары берілген. Табу керек
матрицалары берілген. Табу керек ![]() .
.
Шешуі: ![]() сондықтан
сондықтан
![]() ,
, ![]()
![]()
және ![]() .
.
Табылған С матрицасы 2-ретті диагоналдық матрица болып табылады.
2-мысал. 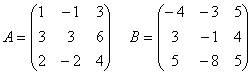 болғанда,
болғанда, ![]() матрицасы симметриялы болатындығын
көрсету керек.
матрицасы симметриялы болатындығын
көрсету керек.
Шешуі:

Алынған ![]() матрицасы симметриялы, өйткені
матрицасы симметриялы, өйткені ![]() .
.
3-мысал. Кез келген ![]() матрицасы үшін
матрицасы үшін ![]() матрицасы симметриялы болатындығын
дәлелдеу керек.
матрицасы симметриялы болатындығын
дәлелдеу керек.
Шешуі: ![]() яғни
яғни ![]() симметриялы матрица.
симметриялы матрица.
47. ![]()
![]() болғандағы
болғандағы ![]() матрицасын табу керек.
матрицасын табу керек.
48. 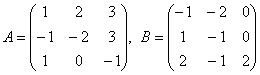 болғандағы
болғандағы ![]() матрицасын табу керек.
матрицасын табу керек.
5.2 Матрицалардың көбейтіндісі
Реттері бірдей ![]() матрицасының
матрицасының ![]() матрицасына көбейтіндісі
матрицасына көбейтіндісі ![]() төмендегіше
анықталады: оның элементтері
төмендегіше
анықталады: оның элементтері ![]() -табу үшін
-табу үшін ![]() матрицасының
матрицасының
![]() -жатық
жолының элементтерін
-жатық
жолының элементтерін ![]() матрицасының
матрицасының ![]() тік жолының сәйкес
элементтеріне көбейтіп қосу қажет, яғни
тік жолының сәйкес
элементтеріне көбейтіп қосу қажет, яғни
![]() (4)
(4)
Қасиеттері
 (5)
(5)
мұндағы  - бірлік матрица.
- бірлік матрица.
6) ![]() . (6)
. (6)
Жалпы жағдайда ![]() .
.
Ескерту. а) ![]() жатық жолдан
жатық жолдан ![]() бағанадан тұратын матрицалар
бағанадан тұратын матрицалар
![]() ретті
матрицалар деп аталады.
ретті
матрицалар деп аталады.
б) Кез келген ![]() және
және ![]() матрицаларын көбейтуге болмайды.
матрицаларын көбейтуге болмайды.
Оларды көбейту үшін алғашқы көбейткіштің бағаналарының саны екінші көбейткіштің жатық жолдарының санына тең болу керек.
4-мысал.
 Табу керек
Табу керек ![]() мен
мен
![]()
Шешуі:
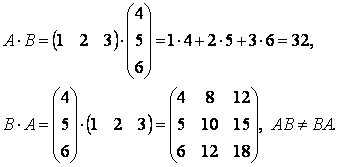
5-мысал.
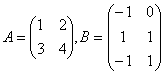 берілген. Мүмкін болса
берілген. Мүмкін болса ![]() мен
мен ![]() табу керек.
табу керек.
Шешуі: ![]() матрицасы 2 тік жолдан, ал
матрицасы 2 тік жолдан, ал ![]() матрицасы 3 жатық
жолдан тұратындықтан,
матрицасы 3 жатық
жолдан тұратындықтан, ![]() -ны
-ны ![]() -ға көбейтуге болмайды.
-ға көбейтуге болмайды. ![]() матрицасы екі тік
жолдан, ал
матрицасы екі тік
жолдан, ал ![]() екі
жатық жолдан тұратындықтан, олардың көбейтіндісі
екі
жатық жолдан тұратындықтан, олардың көбейтіндісі
 .
.
49. берілген. Табу керек
берілген. Табу керек ![]() .
.![]()
50. Төмендегі матрицаларды көбейту керек:
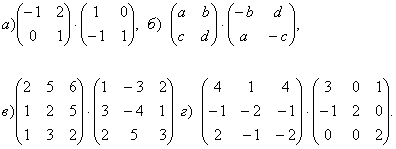
![]()
51. Табу керек ![]() , егер
, егер
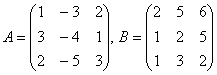 .
.
5.3 Матрицалардың дәрежесі. Матрицалардың көпмүшелері.
Матрицаның бүтін оң дәрежесі төмендегі теңдеумен анықталады
![]() және
және![]() .
.
Мұнда, ![]() формуласымен есептелінеді.
формуласымен есептелінеді.
Егер көпмүшелік
![]() берілсе, онда
берілсе, онда ![]() матрицасының
көпмүшелігі деп
матрицасының
көпмүшелігі деп
![]()
матрицасын аламыз.
Кез келген ![]() матрицасының
көпмүшеліктері үшін
матрицасының
көпмүшеліктері үшін
![]()
теңдігі орындалады.
Егер ![]() болса, онда
болса, онда ![]() матрицасы көпмүшеліктің
түбірі деп аталады.
матрицасы көпмүшеліктің
түбірі деп аталады.
6-мысал.
![]() берілген. Табу керек
берілген. Табу керек ![]()
Шешуі:
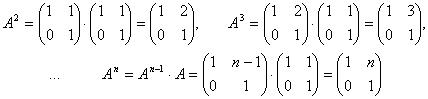
7-мысал.
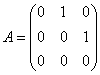 берілген. Табу керек
берілген. Табу керек ![]()
Шешуі:
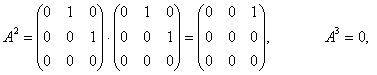 яғни
яғни ![]()
8-мысал. ![]() көпмүшелігі
берілген.
көпмүшелігі
берілген.
 матрицасының
көпмүшелігін табу керек.
матрицасының
көпмүшелігін табу керек.
Шешуі: ![]() матрицасы төмендегіше
анықталады.
матрицасы төмендегіше
анықталады.
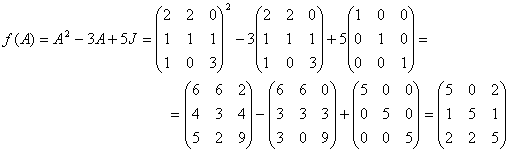
9-мысал. ![]() матрицасының
матрицасының ![]() көпмүшелігінің
түбірі болатындығын дәлелдеу керек.
көпмүшелігінің
түбірі болатындығын дәлелдеу керек.
Шешуі:
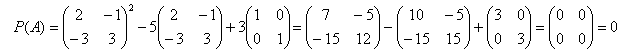
Яғни ![]() матрицасы
матрицасы
![]() көпмүшелігінің
түбірі.
көпмүшелігінің
түбірі.
52. Төмендегі матрицалар үшін ![]() табу керек:
табу керек:
![]() б)
б)![]() в)
в) 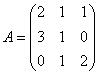 .
.
53. Табу керек![]() егер:
егер:
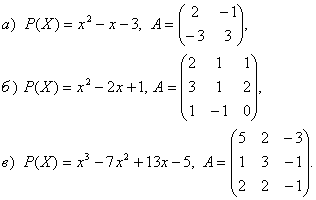
5.3 Кері матрица
![]() матрицасы
матрицасы ![]() матрицасына кері матрица деп аталады, егер
матрицасына кері матрица деп аталады, егер
![]() .
. ![]() матрицасының кері
матрицасы болу үшін
матрицасының кері
матрицасы болу үшін ![]() болуы керек. Кері матрица
төмендегі формуламен анықталады
болуы керек. Кері матрица
төмендегі формуламен анықталады
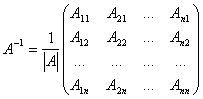 , (7)
, (7)
мұндағы ![]() - алгебралық толықтауыштар.
- алгебралық толықтауыштар.
Кері матрицаның көмегімен
![]() (8)
(8)
түріндегі матрицалық теңдеулерді шешуге болады.
Теңдеуді сол жағынан ![]() -ге көбейту арқылы оның
түбірін төмендегі түрде алуға болады:
-ге көбейту арқылы оның
түбірін төмендегі түрде алуға болады:
![]() (9)
(9)
Қасиеттері
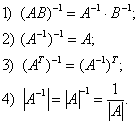
10-мысал. ![]() матрицасына кері
матрицасына кері ![]() матрицасын табу керек.
матрицасын табу керек.
Шешуі: ![]()
![]() .
.
Сондықтан 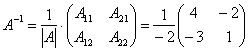
11-мысал. ![]() немесе
немесе ![]() матрицалық
теңдеуін шешу керек.
матрицалық
теңдеуін шешу керек.
Шешуі: 10-мысалдан ![]() . Сондықтан
. Сондықтан
![]()
54. ![]() матрицалық
теңдеуін шешу керек.
матрицалық
теңдеуін шешу керек.
55. Төмендегі матрицалардың кері матрицаларын табу керек:
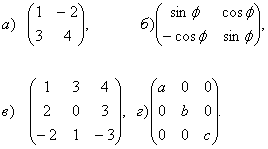
56. Төмендегі матрицалық теңдеулерді шешу керек:
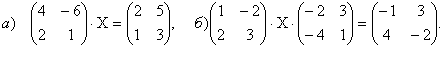
![]() және
және
![]() егер
егер 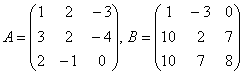
57. Егер ![]() болса,
онда
болса,
онда ![]() болатындығын
көрсету керек.
болатындығын
көрсету керек.
5.4 Тікбұрышты матрицалар және оларды түрлендіру
![]() жатық және
жатық және ![]() тік жолдан тұратын тікбұрышты
сандар кестесі
тік жолдан тұратын тікбұрышты
сандар кестесі ![]() өлшемді
тікбұрышты матрица деп аталады:
өлшемді
тікбұрышты матрица деп аталады:
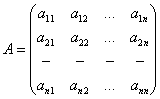 (11)
(11)
![]() матрицасының
элементарлық түрлендірулері деп келесі шараларды айтады:
матрицасының
элементарлық түрлендірулері деп келесі шараларды айтады:
1) кезкелген қатарды ![]() санына көбейту;
санына көбейту;
2) параллель екі қатарды ауыстыру;
3) қатардың элементтерін соған параллель болатын
қатардың сәйкес элементтерін ![]() санына көбейтіп қосу.
санына көбейтіп қосу.
Элементарлық түрлендірулердің көмегімен кез келген
![]() матрицасын
арнайы түрге келтіруге болады:
матрицасын
арнайы түрге келтіруге болады:
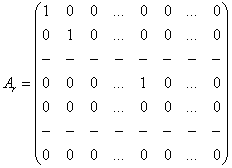
Бас диогоналдың бойында тұрған ![]() бір сандары
бір сандары ![]() матрицасын
матрицасын ![]() матрицасына алып келу
тәсіліне байланысты болмайды және
матрицасына алып келу
тәсіліне байланысты болмайды және![]() матрицасының рангы деп
аталады.
матрицасының рангы деп
аталады.
Бір-бірінен элементарлық түрлендірулер
арқылы алынатын матрицалар эквивалентті деп аталып, ![]() белгісімен жалғанады. Эквивалентті
матрицалардың рангы тең болады.
белгісімен жалғанады. Эквивалентті
матрицалардың рангы тең болады.
13-мысал. Келесі матрицаның рангын табу керек
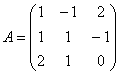
Шешуі: Бірінші жатық жолды (-1)-ге көбейтіп, екінші жатық жолға, содан кейін бірінші жатық жолды (-2)-ге көбейтіп, үшінші жатық жолға қоссақ
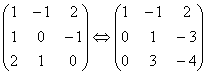 .
.
Енді екінші жатық жолды (-3)-ке көбейтіп үшінші жатық жолға қосамыз. Сонда
 ,
,
яғни берілген матрицаның рангы ![]() .
.
58. Төмендегі матрицалардың рангын табу керек:
6 Сызықтық теңдеулер жүйесі
6.1 Крамердің формулалары
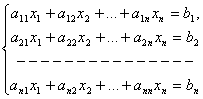 (1)
(1)
сызықтық теңдеулер жүйесі берілсін.
Белгісіздердің алдында тұрған
коэффициенттерден құралған ![]() - ретті анықтауыш
- ретті анықтауыш ![]() , жүйенің
анықтауышы деп аталады. Жүйенің анықтауышына байланысты
төмендегі жағдайлардың бірі орын алады:
, жүйенің
анықтауышы деп аталады. Жүйенің анықтауышына байланысты
төмендегі жағдайлардың бірі орын алады:
а) Егер (1)-жүйенің анықтауышы нөлге тең болмаса, онда жүйенің жалғыз түбірі бар болып, оны Крамер формулалары арқылы анықтауға болады:
![]() (2)
(2)
Мұндағы ![]() - ретті
- ретті ![]() анықтауыштары
анықтауыштары ![]() анықтауышының
анықтауышының ![]() -тік жолын
-тік жолын ![]() бос мүшелерімен
ауыстыру арқылы алынады.
бос мүшелерімен
ауыстыру арқылы алынады.
б) егер ![]() болып, болмағанда бір
болып, болмағанда бір ![]() болса, онда
болса, онда
(1)-жүйе үйлесімсіз болады;
в) егер ![]() және
және ![]()
![]() болса, онда (1)-жүйенің
түбірі болмайды немесе ақырсыз көп түбірі бар болады.
болса, онда (1)-жүйенің
түбірі болмайды немесе ақырсыз көп түбірі бар болады.
1-мысал. ![]() жүйесін шешу керек.
жүйесін шешу керек.
Шешуі: Жүйенің анықтауышы
![]() сондықтан оның
түбірі Крамер формулалары арқылы анықталады:
сондықтан оның
түбірі Крамер формулалары арқылы анықталады:
![]() және
және ![]()
мұндағы ![]() сондықтан
сондықтан ![]() .
.
Берілген жүйедегі теңдеулер ![]() жазықтығындағы
түзулер болғандықтан,
жазықтығындағы
түзулер болғандықтан, ![]() олардың қиылысу
нүктесін береді.
олардың қиылысу
нүктесін береді.
2-мысал. ![]() ; жүйесін шешу керек.
; жүйесін шешу керек.
Шешуі: Жүйенің анықтауышы ![]()
![]() ал
ал ![]() болғандықтан, жүйе
үйлесімсіз, яғни геометриялық мағынасы бойынша берілген
түзулер параллель болады.
болғандықтан, жүйе
үйлесімсіз, яғни геометриялық мағынасы бойынша берілген
түзулер параллель болады.
3-мысал. ![]() жүйесін шешу керек.
жүйесін шешу керек.
Шешуі. ![]() Мұндағы
жүйенің екі теңдеуі де бір түзуді анықтайды,
сондықтан жүйенің шешімі осы түзудің бойында
жатқан кез келген нүктенің координаталары болады, яғни
жүйенің шексіз көп шешімі бар:
Мұндағы
жүйенің екі теңдеуі де бір түзуді анықтайды,
сондықтан жүйенің шешімі осы түзудің бойында
жатқан кез келген нүктенің координаталары болады, яғни
жүйенің шексіз көп шешімі бар:
![]() болғанда
болғанда
![]()
4-мысал. 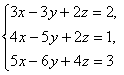 жүйесін шешу керек.
жүйесін шешу керек.
Шешуі:
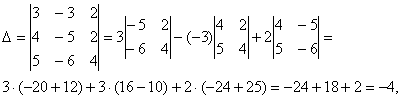
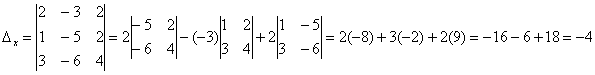 ,
,
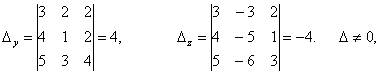 болғандықтан,
жүйенің жалғыз түбірі бар. Оны Крамер формуласымен
жазамыз:
болғандықтан,
жүйенің жалғыз түбірі бар. Оны Крамер формуласымен
жазамыз:
![]()
Жүйелерді шешу керек:
59.![]() 60.
60.![]()
![]()
![]()
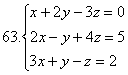
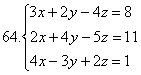
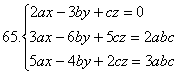
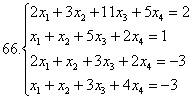
6.2 Жүйені кері матрицаның көмегімен шешу
(1)- жүйені матрицалық теңдеу түрінде жазуға болады:
![]()
мұндағы ![]() - белгісіздердің жанындағы
коэффициенттердің матрицасы, ал
- белгісіздердің жанындағы
коэффициенттердің матрицасы, ал ![]() және
және ![]() - сәйкесінше бос мүшелерден
және белгісіздерден құралған бағаналар. Егер
- сәйкесінше бос мүшелерден
және белгісіздерден құралған бағаналар. Егер ![]() болса, онда
(3)-теңдеудің екі жағын да сол жағынан
болса, онда
(3)-теңдеудің екі жағын да сол жағынан ![]() матрицасына
көбейту арқылы оның шешуін матрицалық пішінде алуға
болады:
матрицасына
көбейту арқылы оның шешуін матрицалық пішінде алуға
болады:
![]() (4)
(4)
5-мысал. ![]()
Шешуі: ![]() болғандықтан
болғандықтан
![]()
яғни ![]()
6-мысал. 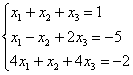
Шешуі:
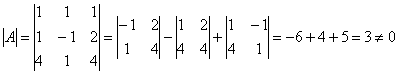
Сондықтан
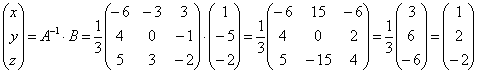 ,
,
яғни ![]()
Келесі жүйелерді кері матрицаның көмегімен шешу керек:
![]()
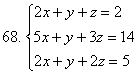

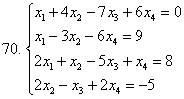
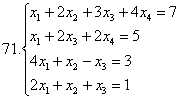
6.3 Біртекті сызықтық теңдеулердің жүйелері
Егер (1)- жүйенің барлық бос
мүшелері ![]() болса,
онда ол біртекті жүйе деп аталады. Оның матрицалық
теңдеуінің түрі
болса,
онда ол біртекті жүйе деп аталады. Оның матрицалық
теңдеуінің түрі
![]() мұндағы 0 –
нөлдік бағана (5)
мұндағы 0 –
нөлдік бағана (5)
. Біртекті жүйенің әр уақытта нөлдік түбірі болатындықтан ол үйлесімді жүйе.
Егер жүйенің анықтауышы ![]() болса, онда нөлдік
түбір оның жалғыз түбірі болады. (5)-
жүйенің нөлге тең емес түбірлері болу үшін
оның анықтауышы
болса, онда нөлдік
түбір оның жалғыз түбірі болады. (5)-
жүйенің нөлге тең емес түбірлері болу үшін
оның анықтауышы ![]() болу керек.
болу керек.
Егер (5)- жүйенің нөлге тең
емес бір түбірі бар болса, онда оның ақырсыз көп
түбірі бар болады. Егер ![]() және
және ![]() болса, онда кез келген
болса, онда кез келген ![]() үшін
үшін ![]() .
.
Бізге үш белгісізі бар үш теңдеуден тұратын біртекті жүйе берілсе, онда төмендегі жағдайлардың бірі орындалады:
а) егер ![]() , онда оның жалғыз нөлдік
, онда оның жалғыз нөлдік
![]() түбірі
бар;
түбірі
бар;
б) егер ![]() , бірақ оның екінші ретті
минорларының бірі нөлге тең емес болса, онда
жүйенің бір теңдеуі қалған екі
теңдеудің салдары болғандықтан, ол жүйе
ақырсыз көп түбірі бар үш белгісізі бар екі
теңдеуге келеді;
, бірақ оның екінші ретті
минорларының бірі нөлге тең емес болса, онда
жүйенің бір теңдеуі қалған екі
теңдеудің салдары болғандықтан, ол жүйе
ақырсыз көп түбірі бар үш белгісізі бар екі
теңдеуге келеді;
в) егер ![]() және оның барлық екінші
ретті минорлары да нөлге тең болса, онда жүйені үш
белгісізі бар бір теңдеу түрінде жазуға болады. Сондықтан
берілген жүйенің нөлге тең емес ақырсыз көп
түбірлері болады.
және оның барлық екінші
ретті минорлары да нөлге тең болса, онда жүйені үш
белгісізі бар бір теңдеу түрінде жазуға болады. Сондықтан
берілген жүйенің нөлге тең емес ақырсыз көп
түбірлері болады.
7-мысал.
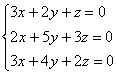 біртекті жүйені шешу керек.
біртекті жүйені шешу керек.
Шешуі: Жүйенің анықтауышын есептейміз:
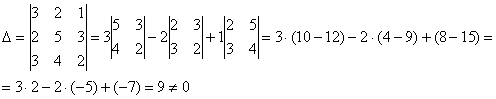
Сондықтан жүйенің жалғыз
нөлдік түбірі бар: ![]()
8-мысал.
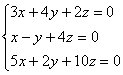 жүйесінің шешімін табу
керек.
жүйесінің шешімін табу
керек.
Шешуі: Бұл жүйенің анықтауышы
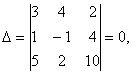 сондықтан жүйенің нөлге тең емес
түбірлері бар. Алғашқы екі жатық жолда жататын
сондықтан жүйенің нөлге тең емес
түбірлері бар. Алғашқы екі жатық жолда жататын ![]() миноры нөлге
тең емес болғандықтан, жүйені үш белгісізі бар
екі теңдеу түрінде жазуға болады:
миноры нөлге
тең емес болғандықтан, жүйені үш белгісізі бар
екі теңдеу түрінде жазуға болады:
![]()
![]() деп алып, жүйені
деп алып, жүйені ![]() түрінде жазуға болады,
бұдан
түрінде жазуға болады,
бұдан
![]() яғни жүйенің шешімі
яғни жүйенің шешімі ![]()
![]() . Мұндағы
. Мұндағы ![]() .
.
9-мысал.  жүйесінің шешімін табу
керек.
жүйесінің шешімін табу
керек.
Шешуі: Бұл жерде жүйенің
анықтауышы және оның барлық 2-ретті минорлары
нөлге тең, яғни бұл жүйде бір теңдеу
ғана тәуелсіз қалған екеуі оған пропорционал
болады. Мысалы, бірінші теңдеуден ![]() -ті
-ті ![]() және
және ![]() арқылы өрнектеп, берілген
жүйенің шешімін аламыз. Шешімнің жалпы түрі
төмендегіше жазылады:
арқылы өрнектеп, берілген
жүйенің шешімін аламыз. Шешімнің жалпы түрі
төмендегіше жазылады:
![]() мұндағы
мұндағы ![]() және
және ![]() - кез келген нақты сан.
- кез келген нақты сан.
Төмендегі біртекті жүйелердің барлық түбірлерін табу керек:

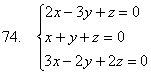
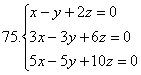
6.4 Жалпы жағдай. Үйлесімділіктің шарты
![]() белгісізі бар
белгісізі бар ![]() теңдеуден тұратын
жүйе берілсін
теңдеуден тұратын
жүйе берілсін
![]() , (6)
, (6)
мұндағы 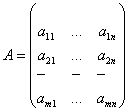 - жүйенің матрицасы,
- жүйенің матрицасы,
ал 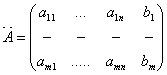 - жүйенің кеңейтілген
матрицасы.
- жүйенің кеңейтілген
матрицасы.
Жүйені шешу барысында екі жағдайболуы мүмкін:
1) ![]() матрицасының рангы
матрицасының рангы ![]() кеңейтілген
кеңейтілген ![]() матрицаның рангы
матрицаның рангы ![]() -дан кем болады, яғни
-дан кем болады, яғни
![]() болғанда,
жүйе үйлесімсіз және түбірі болмайды.
болғанда,
жүйе үйлесімсіз және түбірі болмайды.
2) ![]() болғанда жүйенің
түбірі бар болады, әрі
болғанда жүйенің
түбірі бар болады, әрі ![]() болғанда, жүйенің
жалғыз түбірі
болғанда, жүйенің
жалғыз түбірі ![]() болғанда, жүйенің
ақырсыз көп түбірі бар болып, келесі сұлба бойынша
анықталады:
болғанда, жүйенің
ақырсыз көп түбірі бар болып, келесі сұлба бойынша
анықталады:
а) ![]() матрицасынан реті
матрицасынан реті ![]() -ге тең
-ге тең ![]() миноры бөлініп алынады;
миноры бөлініп алынады;
б) белгісіздердің алдындағы
коэффициенттері ![]() минорының
құрамына кіретін теңдеулерден тұратын жүйе
негізгі жүйеден бөлініп алынады;
минорының
құрамына кіретін теңдеулерден тұратын жүйе
негізгі жүйеден бөлініп алынады;
в) коэффициенттері ![]() минорының құрамына
кірмейтін
минорының құрамына
кірмейтін ![]() айнымалыларын
кез келген нақты мән қабылдайды деп алып, алынған
жүйені Крамер ережесімен шешеміз.
айнымалыларын
кез келген нақты мән қабылдайды деп алып, алынған
жүйені Крамер ережесімен шешеміз.
![]()
10-мысал.
![]() жүйесінің үйлесімді
болатындығын анықтау керек.
жүйесінің үйлесімді
болатындығын анықтау керек.
Шешуі: ![]() және
және ![]()
![]()
Бұдан ![]() , яғни жүйе үйлесімді
, яғни жүйе үйлесімді
11-мысал.
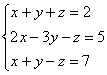 жүйесінің үйлесімді
болатындығын анықтап, үйлесімді
жүйесінің үйлесімді
болатындығын анықтап, үйлесімді
болса түбірін табу керек.
Шешуі:
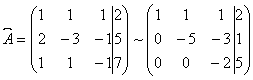 , бұдан
, бұдан ![]() екендігін көреміз,
екендігін көреміз,
яғни жүйе үйлесімді әрі жалғыз
түбірі бар. Оны төмендегіше Гаусс тәсілімен
шығаруға болады: соңғы матрицаның 1-
бағанасын ![]() -қа,
2-бағанасын
-қа,
2-бағанасын ![]() -ке
, 3- бағанасын
-ке
, 3- бағанасын ![]() -ке
көбейтіп бос мүшелерімен теңестірсек
-ке
көбейтіп бос мүшелерімен теңестірсек
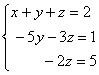 - жүйесі шығады.
- жүйесі шығады.
Үшінші теңдеуден ![]() екінші теңдеуге
екінші теңдеуге ![]() -тің мәнін
қойсақ,
-тің мәнін
қойсақ, ![]() ,
,
![]() ; ендігі
жерде
; ендігі
жерде ![]() пен
пен ![]() -тің
мәндерін бірінші теңдеуге қойсақ
-тің
мәндерін бірінші теңдеуге қойсақ
![]()
Яғни жүйенің жалғыз
түбірі бар: ![]()
12-мысал.
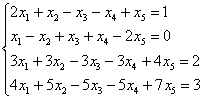 жүйесін шешу керек.
жүйесін шешу керек.
Шешуі: Берілген жүйенің кеңейтілген матрицасын құрамыз:
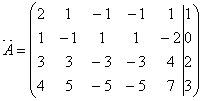
Жүйенің матрицасының рангымен
кеңейтілген матрицаның рангы оның қатарларының
санынан аспайтыны анық, яғни ![]() Екінші жағынан матрицаның
жоғары сол бұрышында орналасқан екінші ретті минор
Екінші жағынан матрицаның
жоғары сол бұрышында орналасқан екінші ретті минор
![]()
яғни жүйенің рангы ![]() . Кеңейтілген матрицаны
төмендегіше түрлендіреміз: үшінші қатарға екінші
қатарды қосамыз, одан бірінші қатарды екіге көбейтіп алып
тастаймыз; осылайша төртінші қатарға екі еселенген екінші
қатарды қосып, одан бірінші қатарды үшке көбейтіп
алып тастаймыз. Сонда матрицамыз
. Кеңейтілген матрицаны
төмендегіше түрлендіреміз: үшінші қатарға екінші
қатарды қосамыз, одан бірінші қатарды екіге көбейтіп алып
тастаймыз; осылайша төртінші қатарға екі еселенген екінші
қатарды қосып, одан бірінші қатарды үшке көбейтіп
алып тастаймыз. Сонда матрицамыз
 түріне келеді,
бұдан соңғы екі теңдеудің алғашқы
екеуінің сызықтық комбинациясы болатындығын
көреміз әрі
түріне келеді,
бұдан соңғы екі теңдеудің алғашқы
екеуінің сызықтық комбинациясы болатындығын
көреміз әрі ![]() сондықтан жүйенің
ақырсыз көп шешімі болады.
сондықтан жүйенің
ақырсыз көп шешімі болады.
Жүйенің алғашқы екі теңдеуінен тұратын жаңа жүйе құрып
![]() минорының
құрамына кірмейтіндіктен,
минорының
құрамына кірмейтіндіктен, ![]() белгісіздерін теңдіктің
оң жағына көшіреміз:
белгісіздерін теңдіктің
оң жағына көшіреміз: 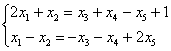
Алынған жүйені Крамер ережесімен шешеміз:
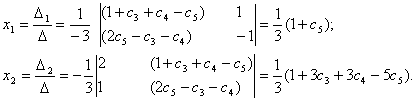
Алынған шешім жүйенің жалпы шешімі деп аталады.
Төмендегі жүйелердің үйлесімдігін тексеру керек:
76. ![]()
![]()
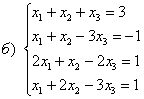
в) 
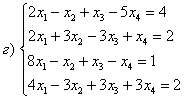
77. Жүйелерді шешу керек:
а) 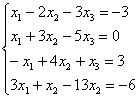

7 Сызықтық турлендіру
7.1 Сызықтық түрлендіру және оның матрицасы
 немесе
немесе ![]() (1)
теңдеуімен анықталатын,
(1)
теңдеуімен анықталатын, 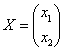 векторын
векторын 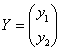 векторына түрлендіру жазықтықты
сызықты түрлендіру деп, ал
векторына түрлендіру жазықтықты
сызықты түрлендіру деп, ал 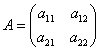 түрлендіру матрицасы деп аталады.
түрлендіру матрицасы деп аталады.
Егер ![]() болса, онда бұл түрлендіру
болса, онда бұл түрлендіру ![]() және
және ![]() орталарын
сәйкесінше
орталарын
сәйкесінше 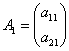 және
және
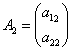 векторларына
аударады. (1)- түрлендіру координаттық пішінде төмендегі
формуламен анықталады:
векторларына
аударады. (1)- түрлендіру координаттық пішінде төмендегі
формуламен анықталады:
![]() . (2)
. (2)
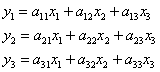 (3)
(3)
формулаларымен анықталатын түрлендіру, кеңістікті
сызықты түрлендіру деп аталады. Бұл түрлендірудің
матрицалық пішіні ![]() , мұндағы
, мұндағы

Кез келген сызықты түрлендірудің негізгі қасиеттері төмендегіше анықталады:
![]()
Егер ![]() болса,
онда
болса,
онда ![]() сызықты
түрлендіруі нұқсансыз түрлендіру деп аталады. Кез келген
нұқсансыз
сызықты
түрлендіруі нұқсансыз түрлендіру деп аталады. Кез келген
нұқсансыз ![]() түрлендіруіне кері жалғыз
түрлендіруіне кері жалғыз
![]() түрлендіруі
бар болады. Бұл түрлендіру
түрлендіруі
бар болады. Бұл түрлендіру ![]() векторын
векторын ![]() векторына аударады әрі кері
түрлендірудің
векторына аударады әрі кері
түрлендірудің ![]() матрицасы
матрицасы ![]() матрицасына кері болады.
матрицасына кері болады.
Егер ![]() векторы
векторы
![]() векторына
векторына ![]() сызықты
түрлендіруі арқылы аударылса, онда осы екі
сызықты
түрлендіруі арқылы аударылса, онда осы екі ![]() және
және ![]() сызықты
түрлендірулерінің нәтижесі жалғыз
сызықты
түрлендірулерінің нәтижесі жалғыз ![]() түрлендіруінің
нәтижесімен бірдей болады:
түрлендіруінің
нәтижесімен бірдей болады:
![]()
Сызықтық түрлендірудің қарапайым мысалдары:
1) Кеңістіктің (немесе
жазықтықтың) ![]() векторына нөлдік векторды
векторына нөлдік векторды
сәйкестендіретін түрлендіру нөлдік түрлендіру деп аталады:
![]() , мұндағы
нөлдік түрлендірудің матрицасы 0 – нөлдік матрица.
, мұндағы
нөлдік түрлендірудің матрицасы 0 – нөлдік матрица.
2) Кеңістіктің (немесе
жазықтықтың) ![]() векторына осы
векторына осы ![]() векторын
векторын
сәйкестендіретін түрлендіру тепе-тең түрлендіру деп аталады:
![]() , мұндағы
тепе-тең түрлендірудің матрицасы
, мұндағы
тепе-тең түрлендірудің матрицасы ![]() - бірлік матрица.
- бірлік матрица.
1- мысал.
![]() және
және ![]()
сызықтық түрлендірулерінің қосындысының түрлендіру матрицасын табу керек.
Шешуі: Берілген ![]() және
және ![]() түрлендірулерінің сәйкес
матрицалары
түрлендірулерінің сәйкес
матрицалары
![]() және
және ![]() .
.
Сызықтық түрлендірулердің
қосындысының анықтамасы бойынша ![]() , сондықтан
қосындының түрлендіруінің матрицасы берілген
түрлендірулердің қос матрицаларының қосындысына
тең болады:
, сондықтан
қосындының түрлендіруінің матрицасы берілген
түрлендірулердің қос матрицаларының қосындысына
тең болады:
![]()
2-мысал. ![]() және
және ![]() түрлендірулері
берілген, мұндағы
түрлендірулері
берілген, мұндағы ![]() және
және ![]() .
. ![]() векторын
векторын ![]() векторына аударатын
векторына аударатын ![]() түрлендіру матрицасын табу
керек.
түрлендіру матрицасын табу
керек.
Шешуі: ![]() векторының мәнін бірінші теңдеуге
қою арқылы
векторының мәнін бірінші теңдеуге
қою арқылы ![]() аламыз, яғни
аламыз, яғни
![]() .
.
Сонымен, ![]() және
және ![]() сызықтық түрлендірулерінің
нәтижесі бір
сызықтық түрлендірулерінің
нәтижесі бір
![]()
түрлендіруінің матрицасына тең болады.
3-мысал.
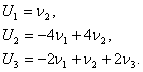
сызық түрлендіруінің нұқсансыз болатындығын көрсетіп, оның кері түрлендіруін табу керек.
Шешуі: Берілген ![]() түрлендіруінің матрицасы
түрлендіруінің матрицасы ![]() нұқсансыз
болады, өйткені оның анықтауышы
нұқсансыз
болады, өйткені оның анықтауышы
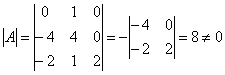 .
.
Сондықтан оның кері түрлендіруі ![]() .
. ![]() кері матрицасын есептейміз:
кері матрицасын есептейміз:
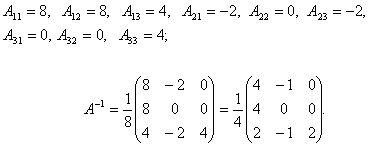
Яғни іздеп отырған кері түрлендіруіміз
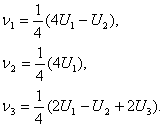
78. ![]() және
және ![]() сызықтық түрлендірулері
берілсін.
сызықтық түрлендірулері
берілсін.
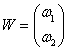 векторын
векторын 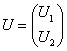 векторына ауыстыратын
түрлендірудің матрицасын табу керек.
векторына ауыстыратын
түрлендірудің матрицасын табу керек.
79. ![]() түрлендіруінің нұқсансыз
болатындығын көрсетіп, оның кері түрлендіруін табу
керек. Мұндағы
түрлендіруінің нұқсансыз
болатындығын көрсетіп, оның кері түрлендіруін табу
керек. Мұндағы
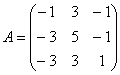
7.2 Матрицаның меншікті векторлары және сипаттамалық сандары
![]()
![]() (4)
(4)
шартын қанағаттандыратын нөлге тең болмайтын ![]() векторы
векторы ![]() түрлендіруінің
меншікті векторы, ал
түрлендіруінің
меншікті векторы, ал ![]() саны
осы
саны
осы ![]() векторына
сай сипаттамалық сан деп аталады.
векторына
сай сипаттамалық сан деп аталады. ![]() матрицасының сипаттамалық
сандары
матрицасының сипаттамалық
сандары ![]() ,
оның төмендегі сипаттамалық теңдеуінің
түбірлері болады:
,
оның төмендегі сипаттамалық теңдеуінің
түбірлері болады:
![]() (5)
(5)
немесе ашып жазсақ
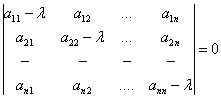 (5')
(5')
Жалпы жағдайда (5) – теңдеудің ![]() сипаттамалық
мәндері (түбірі)
сипаттамалық
мәндері (түбірі)
болады, бірақ түбірлері еселі болғанда сипаттамалық сандар кемиді.
Сипаттамалық ![]() санына сай болатын меншікті
санына сай болатын меншікті ![]() векторы
төмендегі жүйеден анықталады
векторы
төмендегі жүйеден анықталады
 (6)
(6)
(4) – теңдеумен анықталатын меншікті
векторлар, сандық көбейтінді дәлдігімен
анықталатындықтан, (6) – жүйені шешкенде ![]() векторының бір координатын
тұрақты бір мәнге тең етіп алуымызға болады. Егер
векторының бір координатын
тұрақты бір мәнге тең етіп алуымызға болады. Егер
![]() еселі
түбір болса, онда (6) – жүйе біреуден артық (көп)
өзіндік бағыттар анықтайды.
еселі
түбір болса, онда (6) – жүйе біреуден артық (көп)
өзіндік бағыттар анықтайды.
4- мысал. ![]() матрицасымен берілген сызықтық
түрлендірудің сипаттамалық сандарымен меншікті векторларын
табу керек.
матрицасымен берілген сызықтық
түрлендірудің сипаттамалық сандарымен меншікті векторларын
табу керек.
Шешуі: Берілген түрлендірудің сипаттамалық теңдеуін құрамыз:
![]() оның түбірі
оның түбірі ![]() түрлендірудің
сипаттамалық сандары болады.
түрлендірудің
сипаттамалық сандары болады.
![]() сипаттамалық
санына сай келетін меншікті
сипаттамалық
санына сай келетін меншікті ![]() векторы төмендегі жүйемен
анықталады:
векторы төмендегі жүйемен
анықталады:
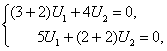 яғни
яғни ![]() .
.
![]() деп алып,
деп алып, ![]() болатындығын көреміз. Сондықтан
болатындығын көреміз. Сондықтан
![]() .
.
![]() сипаттамалық санына сай келетін
меншікті
сипаттамалық санына сай келетін
меншікті ![]() векторы
төмендегі жүйемен анықталады:
векторы
төмендегі жүйемен анықталады:
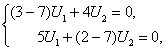 яғни
яғни ![]()
![]() деп алып,
деп алып, ![]() болатындығын көреміз. Сондықтан
болатындығын көреміз. Сондықтан
![]()
5-мысал. ![]() матрицасымен берілген
сызықтық түрлендіруге кері түрлендіру
матрицасымен берілген
сызықтық түрлендіруге кері түрлендіру ![]() -дің
сипаттамалық сандары бастапқы
-дің
сипаттамалық сандары бастапқы ![]() түрлендіруінің
сипаттамалық сандарына кері болатындығын көрсету керек.
түрлендіруінің
сипаттамалық сандарына кері болатындығын көрсету керек.
Шешуі: ![]() матрицасын табамыз:
матрицасын табамыз:
![]()
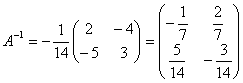
Оның сипаттамалық теңдеуін құрастырамыз:
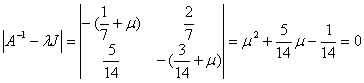 .
.
Оның түбірі ![]() . Дәлелдеу керегіде осы еді.
. Дәлелдеу керегіде осы еді.
6-мысал.
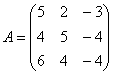 матрицасымен берілген
түрлендірудің сипаттамалық сандарымен меншікті векторларын
табу керек.
матрицасымен берілген
түрлендірудің сипаттамалық сандарымен меншікті векторларын
табу керек.
Шешуі: Берілген түрлендірудің сипаттамалық теңдеуін құрамыз:
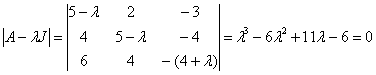
Оның түбірі ![]() түрлендірудің
сипаттамалық сандары болады.
түрлендірудің
сипаттамалық сандары болады.
![]() сипаттамалық санына сай келетін
меншікті
сипаттамалық санына сай келетін
меншікті ![]() векторы
төмендегі жүйемен анықталады:
векторы
төмендегі жүйемен анықталады:
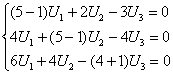 немесе
немесе 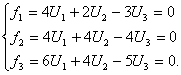
Соңғы жүйедегі үшінші теңдеу
алғашқы екеуінің сызықтық комбинациясы болады. ![]() сондықтан оны
төмендегі екі теңдеудің жүйесіне келтіреміз:
сондықтан оны
төмендегі екі теңдеудің жүйесіне келтіреміз:
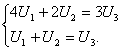
![]() деп
алып жүйені шешсек,
деп
алып жүйені шешсек,

![]() Сонымен
Сонымен
![]() .
.
![]() сипаттамалық санына сай келетін
сипаттамалық санына сай келетін ![]() векторы
төмендегі жүйемен анықталады:
векторы
төмендегі жүйемен анықталады:![]()
![]()
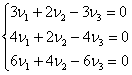
Жүйені шешу арқылы ![]() табамыз.
табамыз.
![]() сипаттамалық санына сай келетін
сипаттамалық санына сай келетін ![]() векторы
жоғарыдағыдай анықталады.
векторы
жоғарыдағыдай анықталады.
80.![]() және
және ![]() матрицалары берілген,
матрицалары берілген, ![]() , бірақ
, бірақ ![]() және
және ![]() түрлендірулерінің
сипаттамалық сандары тең болатындығын көрсету керек.
түрлендірулерінің
сипаттамалық сандары тең болатындығын көрсету керек.
81. Симметриялық
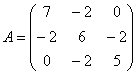 матрицасының
сипаттамалық сандарымен меншікті векторларын табу керек.
матрицасының
сипаттамалық сандарымен меншікті векторларын табу керек.
Жауаптар
1.1
2. 1 3. ![]() 4.
4.
![]() 5.
5.![]() 6.
6.![]() 7.
7.![]() 8.
8.![]() 9.
9. ![]() 10.
10. ![]() 11.
11.![]() 12.
12. ![]() 13.
13. ![]() 14.
14. ![]() 15.
15. ![]() 16.
16. ![]() 17.
17.![]() 18.
18.![]() 20. 21.
20. 21. ![]() және
және ![]() векторларының
арасындағы бұрыштар: 1) сүйір, 2) доғал. 22.
векторларының
арасындағы бұрыштар: 1) сүйір, 2) доғал. 22.![]() нүктесі
нүктесі ![]() өсінің
бойында,
өсінің
бойында, ![]() өсінің
бойында,
өсінің
бойында,![]() өсінің
бойында жатыр.
өсінің
бойында жатыр. ![]() нүктесі
нүктесі
![]() жазықтығында,
жазықтығында,
![]() жазықтығында,
жазықтығында,
![]() нүктесі 4-октантада
орналасқан.
нүктесі 4-октантада
орналасқан.
23. ![]()
24. ![]() 25.
25. ![]()
27. ![]() 28.
28.![]() 29.
29.![]() 30.
30.![]() 31.
31.![]() құрай алмайды; б) құрай алмайды.
құрай алмайды; б) құрай алмайды.
32. ![]() 33.
33. ![]() 34.
34. ![]()
36. ![]() 37.
37. ![]() 38.
38. ![]() 39.
39.![]() 40.
40. ![]() 41.
41.![]() 42.
42. ![]() 43. 1) жоқ, 2) болады. 45.
43. 1) жоқ, 2) болады. 45.![]() 46.
46. ![]()
47. ![]() 48.
48.  49.
49.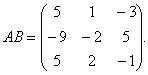 50. а)
50. а) ![]() б)
б)![]() в)
в) 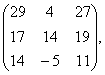 г)
г) 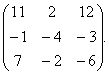 51.
51.  52. а)
52. а)![]() б)
б) ![]() в)
в) 53. а)
53. а) ![]() б)
б) 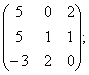 в)
в) 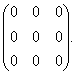 54.
54. ![]() 55.
55. ![]() б)
б) ![]() в)
в) 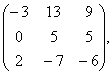 г)
г) 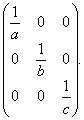 56. а)
56. а) ![]() б)
б) ![]()
в) 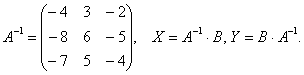 58.
а) 2, б) 1, в) 2, г) 2, д) 2, е) 4.
58.
а) 2, б) 1, в) 2, г) 2, д) 2, е) 4.
59. ![]() 60.
60.![]() 61.
61. ![]() 62. Үйлесімсіз.
62. Үйлесімсіз.
63. ![]() 64.
64. ![]() 65.
65. ![]()
66. ![]() 67.
67. ![]() 68.
68. ![]()
69. ![]() 70.
70. ![]() 71.
71. ![]()
72. ![]() 73.
73. ![]() 74.
74. ![]() 75.
75. ![]() кез келген сандар. 76. а) үйлесімді,
б) үйлесімді емес, в) үйлесімді емес, г) үйлесімді емес.
кез келген сандар. 76. а) үйлесімді,
б) үйлесімді емес, в) үйлесімді емес, г) үйлесімді емес.
77. а)![]() б)
б)![]() кез келген нақты сан. 78.
кез келген нақты сан. 78. ![]() 79.
79. 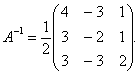 81.
81. ![]()
Әдебиеттер тізімі
1. Айдос Е.Ж. Жоғары математика (қысқаша курс). -Алматы: «Иль-Тех –Кітап».ЖШС, 2000.-744б.
2. Әубәкір С.Б. Жоғары математика.-Алматы: ҚазТУ, 2000, -254 б.
3. Дүйсек А.К., Қасымбеков С.К. Жоғары математика. – Алматы:КБГ, 2004.- 409б.
4. Ш.И.Оспанова, С.Е.Ералиев, С.Қ. Қасымбеков. Жоғары математикаға кіріспе.- Алматы: Кітап, 1989.- 88 б.
5. Хасеинов К.А. Каноны математики.- Алматы: Атамұра, - 2003.
6. А.Ф.Бермант, И.Г. Араманович. Краткий курс математического анализа.- Москва: Наука, 1966.-736с.
7. Г.И.Кручкович, Н.И.Гутарина,П.Б. Дюбюк и другие.- Москва: Высшая школа, 1973.- 576с.
8. Пискинов Н.С. Дифференциальное и интегральное исчисления.-Москва: Наука, 1998.
Мазмұны
1 Анықтауыштар....................................................................................................3
1.1 Екінші және үшінші ретті анықтауыштар. Қасиеттері..................................3
1.2 ![]() ретті
анықтауыш және оның
қасиеттері....................................................7
ретті
анықтауыш және оның
қасиеттері....................................................7
2 Векторлар. Оларға қолданылатын сызықтық амалдар.....................................8
2.1 Негізгі түсініктер...............................................................................................8
2.2 Векторларға қолданылатын сызықтық амалдар.............................................9
3 Кеңістіктегі тікбұрышты декарттық координаталар...................................... 11
3.1 Нүктенің координаталары............................................................................. 11
3.2 Векторлардың координаталары................................................................... 12
3.3 Кесіндіні берілген қатынасқа бөлу............................................................. 14
3.4 Бағыттаушы косинустар.............................................................................. 15
4 Векторлардың көбейтіндісі......................................................................... 16
4.1 Скалярлық көбейтінді.............................................................................. 16
4.2 Векторлық көбейтінді............................................................................. 18
4.3 Үш вектордың аралас көбейтіндісі........................................................ 21
5 Матрицалар( тікшемдер)........................................................................... 22
5.1 Матрицаларға сызықтық амалдар қолдану.......................................... 22
5.2 Матрицалардың көбейтіндісі............................................................... 24
5.3 Матрицалардың дәрежесі, матрицалардың көпмүшелері................... 26
5.4 Кері матрица................................................................................................ 27
5.5 Тікбұрышты матрицалар және оларды түрлендіру................................ 29
6 Сызықтық теңдеулер жүйесі.......................................................................... 30
6.1 Крамердің формулалары............................................................................ 30
6.2 Жүйені кері матрицаның көмегімен шешу............................................. 32
6.3 Біртекті сызықты теңдеулердің жүйелері................................................ 33
6.4 Жалпы жағдай. Үйлесілімділіктің шарты............................................... 35
7 Сызықтық түрлендіру................................................................................ 38
7.1 Сызықтық түрлендіру және оның матрицасы........................................ 38
7.2 Матрицаның меншікті векторлары және сипаттамалық сандары......... 41
Жауаптары........................................................................................................ 44
Әдебиеттер тізімі.............................................................................................. 46