ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТІРЛІГІ
"Алматы энергетика және байланыс институтының "
Коммерциялық емес акционерлік қоғамы
С.Е. Ералиев
Аналитикалық геометрияның негіздері
Оқу құралы
Алматы 2009
Бұл оқулық техникалық жоғары оқу орындарының бағдарламасына сай жазылған. Оқулықтың 1-тарауында жазықтықтағы аналитикалық геометрияның, ал екінші тарауында кеңістіктегі аналитикалық геометрияның
негізгі түсініктемелері берілген. Тақырыптарды терең түсіну үшін таңдалынып алынған мысалдар қарастырылған. Тақырыптардың соңында есептер беріліп оқулықтың аяғында жауаптары берілген.
Бұл оқулық кредиттік жүйе бойынша оқылатын жоғары оқу орындары мен колледждердің студенттеріне арналған.
Ι – тарау
Жазықтықтағы аналитикалық геометрия
1. Жазықтықтағы декартттық координаталар
1.1 Нүктенің координаталары (мекендігі). Қарапайым есептер
Жазықтықтағы декарттық
тікбұрышты координаталар жүйесі ұзындықты өлшеу
үшін масштаб бірлігінің берілуімен және бір – бірімен
перпендикуляр екі өстің берілуімен анықталады. Олардың
біреуі абсцисса ![]() екіншісі
ордината
екіншісі
ордината ![]() өстері
деп аталады. Бұл өстер жазықтықты квадранттар деп
аталатын төрт ширекке бөледі. Нөмірленуі 1 Суретте көрсетілген.
өстері
деп аталады. Бұл өстер жазықтықты квадранттар деп
аталатын төрт ширекке бөледі. Нөмірленуі 1 Суретте көрсетілген.
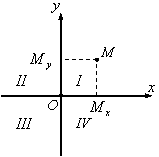 |
1 Сурет
![]() жазықтықтың кезкелген
нүктесі болсын. Оны координат өстеріне проекциялау арқылы
жазықтықтың кезкелген
нүктесі болсын. Оны координат өстеріне проекциялау арқылы ![]() және
және ![]() нүктелерін
аламыз.
нүктелерін
аламыз. ![]() нүктесінің
абсциссасы
нүктесінің
абсциссасы ![]() деп
оң немесе теріс таңбамен алынған
деп
оң немесе теріс таңбамен алынған ![]() кесіндісінің
ұзындығын айтамыз: егер
кесіндісінің
ұзындығын айтамыз: егер ![]() кесіндісі
кесіндісі ![]() өсімен бағыттас болса,
оң таңба, қарсы болса, теріс таңба алынады. Осылайша
өсімен бағыттас болса,
оң таңба, қарсы болса, теріс таңба алынады. Осылайша ![]() нүктесінің
ординатасы
нүктесінің
ординатасы ![]() анықталады.
анықталады.
![]() қос
саны жазықтықтың
қос
саны жазықтықтың ![]() нүктесін толық
анықтайды. Бұл геометриялық есептерді шешуде
аналитикалық тәсілдерді қолдануға мүмкіндік
береді.
нүктесін толық
анықтайды. Бұл геометриялық есептерді шешуде
аналитикалық тәсілдерді қолдануға мүмкіндік
береді.
Егер жазақтақта жататын ![]() және
және ![]() нүктелері берілсе,
онда осы нүктелердің арасындағы қашақтық
нүктелері берілсе,
онда осы нүктелердің арасындағы қашақтық ![]() төмендегі
формуламен анықталады:
төмендегі
формуламен анықталады:
![]() (1)
(1)
Дербес жағдайда, кезкелген ![]() нүктесінің координаттың
бас нүктесі
нүктесінің координаттың
бас нүктесі ![]() -
дан қашақтығы
-
дан қашақтығы
![]() (2)
(2)
формуласымен анықталады.
Төбелерінің координаталары ![]() ,
,![]() ,
,![]() болатын үшбұрыштың
ауданы келесі формуламен анықталады:
болатын үшбұрыштың
ауданы келесі формуламен анықталады:
![]() (3)
(3)
1. Мысал - ![]() нүктесінен
нүктесінен ![]() қашықтықта
орналасқан,
қашықтықта
орналасқан, ![]() өсінде
жататын нүктені табу керек.
өсінде
жататын нүктені табу керек.
Шешуі: ![]() іздеп отырған нүктеміз
болсын. Ол
іздеп отырған нүктеміз
болсын. Ол ![]() өсінде
жататын
өсінде
жататын
болғандықтан, ол үшін ![]() .
. ![]() -ті табу үшін (1)-формуланы
пайдаланамыз:
-ті табу үшін (1)-формуланы
пайдаланамыз: ![]() орнына
орнына
![]()
![]() -ң, ал
-ң, ал ![]() орнына
орнына ![]() -ң координаталарын
алсақ
-ң координаталарын
алсақ
![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
Осыдан ![]() ,
, ![]() . Сондықтан, есептің шартын
. Сондықтан, есептің шартын ![]() және
және ![]() нүктелері
қанағаттандырады.
нүктелері
қанағаттандырады.
2. Мысал -Төбелері ![]() нүктелері болатын
нүктелері болатын
үшбұрыштың ауданын табу керек.
Шешуі: Нүктелердің координаталарын (3) формулаға қойсақ
![]()
1. ![]() нүктесінен
нүктесінен ![]() қашықтықта
орналасқан,
қашықтықта
орналасқан, ![]() өсінде
жататын нүктені табу керек.
өсінде
жататын нүктені табу керек.
2. Төбелері ![]() нүктелері болатын
үшбұрыштың ауданын табу керек.
нүктелері болатын
үшбұрыштың ауданын табу керек.
1.2 Кесіндіні берілген қатынасқа бөлу
Бағытталған ![]() кесіндісін берілген
кесіндісін берілген ![]() қатынасындай етіп бөлетін
қатынасындай етіп бөлетін
![]() нүктесінің
координаталары
нүктесінің
координаталары
![]() ,
, ![]() .
(4)
.
(4)
формулаларымен анықталады. Мұндағы ![]() координаталары
координаталары ![]() нүктесінің,
ал
нүктесінің,
ал ![]() координаталары
координаталары
![]() нүктесінің
координаталары болады. Дербес жағдайда, егер
нүктесінің
координаталары болады. Дербес жағдайда, егер ![]() нүктесі
нүктесі ![]() кесіндісін
қақ ортасынан бөлсе, онда
кесіндісін
қақ ортасынан бөлсе, онда ![]() болады да
болады да
![]() ,
, ![]() . (5)
. (5)
3. Мысал -![]() кесіндісі
кесіндісі ![]() нүктелері
арқылы теңдей бөліктерге бөлінген (2 Сурет).
нүктелері
арқылы теңдей бөліктерге бөлінген (2 Сурет).
![]()
2 Сурет
![]() және
және ![]() нүктелері берілген.
нүктелері берілген. ![]() және
және ![]() нүктелерінің
координаталарын табу керек.
нүктелерінің
координаталарын табу керек.
Шешуі: ![]() нүктесі
нүктесі ![]() кесіндісінің ортасы
болғандықтан
кесіндісінің ортасы
болғандықтан ![]() . Сондықтан,
. Сондықтан, ![]() -ті
-ті ![]() -ң координатасы деп алып,
(5)-формуланы қолданамыз:
-ң координатасы деп алып,
(5)-формуланы қолданамыз:
![]()
Осылайша, ![]() нүктесі
нүктесі ![]() кесіндісінің ортасы
болғандықтан
кесіндісінің ортасы
болғандықтан
![]()
![]() .
.
4. Мысал - Төбелері ![]() нүктелері болатын
ұшбұрыш берілген.
нүктелері болатын
ұшбұрыш берілген. ![]() нүктесінен түсірілген
медиананың ұзындығын табу керек.
нүктесінен түсірілген
медиананың ұзындығын табу керек.
Шешуі: ![]() кесіндісін тең бөліп тұрған
кесіндісін тең бөліп тұрған ![]() нүктесінің
координаталарын табамыз:
нүктесінің
координаталарын табамыз:
![]() яғни
яғни ![]() .
. ![]() іздеп отырған медиана болғандықтан
іздеп отырған медиана болғандықтан
![]()
3.
Төбелері ![]() нүктелері
болатын ұшбұрыштың
нүктелері
болатын ұшбұрыштың ![]()
бұрышының биссектрисасының ұзындығын табу керек.
4.![]() үшбұрышының қабырғаларының орта
нүктелері
үшбұрышының қабырғаларының орта
нүктелері ![]() берілген.
Осы үшбұрыштың төбелерін анықтау керек.
берілген.
Осы үшбұрыштың төбелерін анықтау керек.
5. Параллелограмның ![]() төбелері берілген. Оның
төбелері берілген. Оның ![]() төбесіне
қарсы жатқан төртінші
төбесіне
қарсы жатқан төртінші ![]() төбесін анықтау керек.
төбесін анықтау керек.
1.3 Сызықтың теңдеуі
Жазықтықтағы сызық ![]() теңдеуімен беріледі.
Сызықтың бойында жататын кез келген
теңдеуімен беріледі.
Сызықтың бойында жататын кез келген ![]() нүктесінің координаталары
теңдеуді қанағаттандырады, ал оның бойында жатпайтын
бірде-бір нүкте теңдеуді қанағаттандырмайды.
Сызықты қозғалыстағы (жылжымалы)
нүктесінің координаталары
теңдеуді қанағаттандырады, ал оның бойында жатпайтын
бірде-бір нүкте теңдеуді қанағаттандырмайды.
Сызықты қозғалыстағы (жылжымалы) ![]() нүктесінің
траекториясы ретінде қарастыруға болады. Сондықтан
нүктесінің
траекториясы ретінде қарастыруға болады. Сондықтан ![]() нүктесінің
нүктесінің ![]() координаталары
ағымдағы координаталар деп аталады. Ағымдағы
координаталарды байланыстырып тұрған сызықтың
теңдеуі осы сызықтың бойында жататын барлық
нүктелерге тән жалпы қасиетін анықтайды.
координаталары
ағымдағы координаталар деп аталады. Ағымдағы
координаталарды байланыстырып тұрған сызықтың
теңдеуі осы сызықтың бойында жататын барлық
нүктелерге тән жалпы қасиетін анықтайды.
Жазықтықтағы сызық параметрлік
деп аталатын басқа тәсілмен берілуіде мүмкін. Бұл
жағдайда ағымдағы ![]() координаталары бір
координаталары бір ![]() параметрінің функциясы
түрінде анықталады:
параметрінің функциясы
түрінде анықталады:
![]() .
(6)
.
(6)
Мұндағы ![]() параметрін уақыт, бекітіліп
алынған нүктенің айналасындағы бұрыштық
бұрылу немесе сызықтың бойында жататын бір
алғашқы нүктеден қисықтың бойымен
алынған қашықтық тағы да сол сияқтылар деп
қарастыруға болады. (6)-формула бойынша параметр
параметрін уақыт, бекітіліп
алынған нүктенің айналасындағы бұрыштық
бұрылу немесе сызықтың бойында жататын бір
алғашқы нүктеден қисықтың бойымен
алынған қашықтық тағы да сол сияқтылар деп
қарастыруға болады. (6)-формула бойынша параметр ![]() -ң әрбір мәніне
сызықтың тек бір анықталған
-ң әрбір мәніне
сызықтың тек бір анықталған ![]() нүктесі сай келеді.
нүктесі сай келеді.
Түрлендіру арқылы (6)-ң екі теңдеуіндегі ![]() параметрінен
құтылсақ, онда сызықтың теңдеуі
параметрінен
құтылсақ, онда сызықтың теңдеуі ![]() түріне келеді.
түріне келеді.
Сызықтармен танысу барысында екі түрлі есептер кездеседі:
1) Берілген теңдеу бойынша түзуді салып оның қасиеттерін тексеру.
2) Берілген түзу бойынша оның теңдеуін табу.
5. Мысал - Радиусы ![]() , центрі (кіндігі)
, центрі (кіндігі) ![]() нүктесі болатын
шеңбердің теңдеуін табу керек. Кіндіктің айналасында
бұрылу бұрышын параметр
нүктесі болатын
шеңбердің теңдеуін табу керек. Кіндіктің айналасында
бұрылу бұрышын параметр ![]() деп алып осы шеңбердің
параметрлік теңдеуін жазу керек.
деп алып осы шеңбердің
параметрлік теңдеуін жазу керек.
Шешуі: Шеңбер берілген ![]() нүктесінен
нүктесінен ![]() қашықтықта
орналасқан жазықтықтың
қашықтықта
орналасқан жазықтықтың ![]() нүктелерінің
геометриялық орны болғандықтан
нүктелерінің
геометриялық орны болғандықтан
(1)-формуланы қолдансақ
![]() немесе
немесе ![]() . (7)
. (7)
 |
3 Сурет
3-Суреттен ![]() екендігін көреміз.
екендігін көреміз. ![]() болатындығын ескерсек
шеңбердің параметрлік теңдеуін
болатындығын ескерсек
шеңбердің параметрлік теңдеуін
![]() (8)
(8)
түрінде жазуға болады. Мұндағы ![]() бұрышы 0-ден
бұрышы 0-ден ![]() -ге дейін
өзгергенде,
-ге дейін
өзгергенде, ![]() нүктесі
шеңберді сағат бағытына қарсы толық айналып
өтеді.
нүктесі
шеңберді сағат бағытына қарсы толық айналып
өтеді.
6. Төмендегі теңдеулермен қандай сызықтар
берілген: а) ![]() б)
б)
![]()
в) ![]() ; г)
; г) ![]() д)
д) ![]() е)
е) ![]() ж)
ж) ![]() ?
?
7. Келесі теңдеулермен қандай сызықтар берілген: а) ![]() ; б)
; б) ![]()
в) ![]() г)
г) ![]() д)
д) ![]() е)
е) ![]() ж)
ж) ![]()
з) ![]() и)
и) ![]() ?
?
2. Түзу сызық
2.1 Түзу сызықтың жалпы теңдеуі. Бұрыштық коэффициенттері арқылы берілген теңдеуі
Декарттық координаталар жүйесінде жазақтықтағы түзулердің жалпы теңдеуі
![]() (1)
(1)
теңдеуімен анықталады.
![]() (2)
(2)
түрінде берілген сызықтың теңдеуі
бұрыштық коэффициенті арқылы берілген теңдеу болады. Бұл
жерде бұрыштық коэффициент ![]() , мұндағы
, мұндағы
![]() -түзуімен
-түзуімен
![]() өсінің
(оқтығының) арасындағы бұрыш, ал
өсінің
(оқтығының) арасындағы бұрыш, ал ![]()
![]() (4 Сурет)
(4 Сурет)
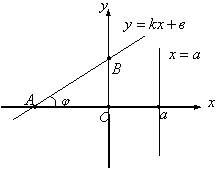 |
4 Сурет
Дербес жағдайда, ![]() болғанда (2)-формуладан
болғанда (2)-формуладан ![]() өсіне параллель
өсіне параллель ![]() түзуін;
түзуін; ![]() болғанда
координаттың бас нүктесі
болғанда
координаттың бас нүктесі ![]() арқылы өтетін
арқылы өтетін ![]() түзуін аламыз.
түзуін аламыз.![]() оқтығына
параллель (қатарлас) түзу (2)-формуламен берілмейді, өйткені
ол түзудің бұрыштық коэффициенті
оқтығына
параллель (қатарлас) түзу (2)-формуламен берілмейді, өйткені
ол түзудің бұрыштық коэффициенті ![]() анықталмаған.
Бұндай түзудің теңдеуі
анықталмаған.
Бұндай түзудің теңдеуі ![]() (4 Сурет).
(4 Сурет).
![]() нүктесі арқылы өтетін
әрі бұрыштық коэффициентті
нүктесі арқылы өтетін
әрі бұрыштық коэффициентті ![]() -ға тең болатын
түзудің теңдеуі
-ға тең болатын
түзудің теңдеуі
![]() (3)
(3)
формуласымен анықталады. Егер түзу ![]() оқтығына параллель
болып
оқтығына параллель
болып ![]() нүктесі
арқылы өтсе, онда оның теңдеуі
нүктесі
арқылы өтсе, онда оның теңдеуі ![]() .
.
![]() (I) және
(I) және ![]() (II) түзулері
берілсін. Олардың арасындағы сүйір
(II) түзулері
берілсін. Олардың арасындағы сүйір ![]() бұрышы келесі формуламен
анықталады:
бұрышы келесі формуламен
анықталады:
![]() (4)
(4)
Түзулердің параллельдігінің шарты:
![]() (5)
(5)
ал перпендикулярлығының шарты:
![]() (6)
(6)
1. Мысал - ![]() түзуімен координат өстерінің қиылысу
нүктелерін табу керек.
түзуімен координат өстерінің қиылысу
нүктелерін табу керек.
Шешуі: Түзумен ![]() оқтығының қиылысу
нүктесі
оқтығының қиылысу
нүктесі ![]() -ны
табу үшін түзудің теңдеуіндегі
-ны
табу үшін түзудің теңдеуіндегі ![]() -ті 0-ге тең деп алып
-ті 0-ге тең деп алып ![]() -ті табамыз:
-ті табамыз: ![]() Сондықтан
Сондықтан ![]() . Осылайша, түзүмен
. Осылайша, түзүмен
![]() оқтығының
қиылысу нүктесі
оқтығының
қиылысу нүктесі ![]() -ны табу үшін түзудің
теңдеуіндегі
-ны табу үшін түзудің
теңдеуіндегі ![]() -ті
0-ге тең деп алып
-ті
0-ге тең деп алып ![]() -ті табамыз:
-ті табамыз: ![]() Яғни
Яғни ![]() Егер түзуді салу керек болса, онда
осы
Егер түзуді салу керек болса, онда
осы ![]() және
және
![]() нүктелері
арқылы түзу жүргіземіз.
нүктелері
арқылы түзу жүргіземіз.
2. Мысал - ![]() түзуі және
түзуі және ![]() нүктесі берілсін.
нүктесі берілсін. ![]() нүктесі
арқылы өтетін әрі берілген түзуге перпендикуляр және
параллель болатын түзулердің теңдеулерін табу керек.
нүктесі
арқылы өтетін әрі берілген түзуге перпендикуляр және
параллель болатын түзулердің теңдеулерін табу керек.
Шешуі: Алғаш берілген теңдеудің бұрыштық коэффициентін анықтаймыз:
![]()
Параллель түзулердің бұрыштық коэффициенттері тең болатындығын ескере отырып (3)-формуланы қолдансақ
![]()
Перпендикуляр болатын түзудің бұрыштық
коэффициентін ![]() деп
алып
деп
алып
(6)-формуладан
![]()
![]()
болатындығын көреміз. Сондықтан оның теңдеуі
![]()
3. Мысал - Теңбүйірлі тікбұрышты
үшбұрыштың тікбұрышының төбесі ![]() және оның
гипотенузасы
және оның
гипотенузасы ![]() берілген.
Оның катеттерінің теңдеулерін табу керек.
берілген.
Оның катеттерінің теңдеулерін табу керек.
Шешуі: Гипотенузаның бұрыштық коэффициентін
табамыз: ![]() Теңбүйірлі
тікбұрышты үшбұрыштың катеттерімен гипотенузаның
арасындағы бұрыштар
Теңбүйірлі
тікбұрышты үшбұрыштың катеттерімен гипотенузаның
арасындағы бұрыштар ![]() болғандықтан (4)-формуланы
пайдалана отырып катеттердің бұрыштық коэффициенттерін
анықтаймыз:
болғандықтан (4)-формуланы
пайдалана отырып катеттердің бұрыштық коэффициенттерін
анықтаймыз:
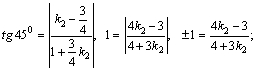
![]()
![]()
![]() нүктесі
катеттердің бойында жататындықтан (3)-формуланы пайдалана отырып
олардың теңдеулерін аламыз:
нүктесі
катеттердің бойында жататындықтан (3)-формуланы пайдалана отырып
олардың теңдеулерін аламыз:
![]()
8. ![]() теңдеулерімен
берілген түзулердің бұрыштық коэффициентерін
анықтап графиктерін салу керек.
теңдеулерімен
берілген түзулердің бұрыштық коэффициентерін
анықтап графиктерін салу керек.
9. ![]() түзуі
және
түзуі
және ![]() нүктесі
берілген.
нүктесі
берілген. ![]() нүктесі
арқылы өтетін әрі берілген түзуге параллель және
перпендикуляр болатын түзулердің теңдеулерін табу керек.
нүктесі
арқылы өтетін әрі берілген түзуге параллель және
перпендикуляр болатын түзулердің теңдеулерін табу керек.
10. ![]() нүктесі
арқылы өтетін әрі координат оқтықтарына параллель
(қатарлас) өтетін түзулердің теңдеулерін табу
керек.
нүктесі
арқылы өтетін әрі координат оқтықтарына параллель
(қатарлас) өтетін түзулердің теңдеулерін табу
керек.
11. Тік төртбұрыштың бір
қабырғасы ![]() теңдеуімен және оның екі
төбесі
теңдеуімен және оның екі
төбесі ![]() және
және
![]() берілген.
Оның қалған қабырғаларының
теңдеулерін анықтау керек?
берілген.
Оның қалған қабырғаларының
теңдеулерін анықтау керек?
12. ![]() нүктесі
арқылы өтетін әрі
нүктесі
арқылы өтетін әрі ![]() түзуімен
түзуімен ![]() құрайтын
түзудің теңдеуін табу керек.
құрайтын
түзудің теңдеуін табу керек.
2.2 Екі нүктесі арқылы берілген теңдеулер
Берілген ![]() және
және
![]() нүктелері
арқылы өтетін түзудің теңдеуі
нүктелері
арқылы өтетін түзудің теңдеуі
![]() (7)
(7)
түрінде жазылады.
(7)-формуладағы бөлімдердің біреуі нөлге тең
болса, онда координат оқтықтарына параллель түзулерді
шығарып тастамау үшін оған сәйкес алымды нөлге тең
деп аламыз. Мысалы, егер түзу ![]() және
және ![]() нүктелері арқылы өтсе,
онда оның теңдеуі
нүктелері арқылы өтсе,
онда оның теңдеуі
![]() яғни
яғни ![]() немесе
немесе ![]()
Бұл түзу ![]() оқтығына
параллель.
оқтығына
параллель.
Егер түзу ![]() нүктелері
арқылы анықталса, онда (7)-формуладан
нүктелері
арқылы анықталса, онда (7)-формуладан
![]() (8)
(8)
кесінділік теңдеуін аламыз.
4. Мысал - Төбелері ![]() нүктелері болатын
үшбұрыш берілген. Оның қабырғаларымен ішкі
нүктелері болатын
үшбұрыш берілген. Оның қабырғаларымен ішкі ![]() бұрышын табу
керек.
бұрышын табу
керек.
Шешуі: Оның қабырғаларының теңдеулерін табу үшін (7)-формуланы пайдаланамыз:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 Ішкі
Ішкі
![]() бұрышын
анықтау үшін
бұрышын
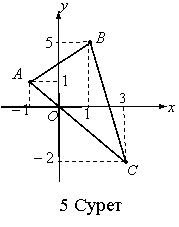
анықтау үшін ![]() -ны бірінші түзу деп, ал
-ны бірінші түзу деп, ал ![]() -ны екінші түзу
деп алып (5 Сурет)
-ны екінші түзу
деп алып (5 Сурет) ![]() формуласын
қолданамыз:
формуласын
қолданамыз:
![]() сондықтан
сондықтан
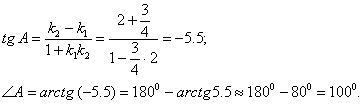
Бұл жағдайда ![]() қабырғасын сағат
бағытына қарсы бұрып
қабырғасын сағат
бағытына қарсы бұрып ![]() қабырғасымен беттестіргенде
ішкі
қабырғасымен беттестіргенде
ішкі ![]() бұрышы
анықталады.
бұрышы
анықталады.
13.Төбелері ![]() нүктелері болатын
үшбұрыш берілген. Оның қабырғаларының
теңдеулерімен ішкі бұрыштарын табу керек.
нүктелері болатын
үшбұрыш берілген. Оның қабырғаларының
теңдеулерімен ішкі бұрыштарын табу керек.
14. Төбелері ![]() нүктелері болатын үщбұрыш
берілген.
нүктелері болатын үщбұрыш
берілген. ![]() төбесі
арқылы өтетін медиананың теңдеуін табу керек.
төбесі
арқылы өтетін медиананың теңдеуін табу керек.
15. ![]() түзулері
берілген. Олардың кесінділік теңдеулерін құру керек.
түзулері
берілген. Олардың кесінділік теңдеулерін құру керек.
2.3 Түзудің қалыпты теңдеуі. Нүктеден түзуге дейінгі қашықтық
![]() (9)
(9)
түзудің қалыпты теңдеуі деп аталады.
Мұндағы ![]() -координаттың
бас нүктесінен түзуге түсірілген тіктеменің
ұзындығы, ал
-координаттың
бас нүктесінен түзуге түсірілген тіктеменің
ұзындығы, ал ![]() - тіктемемен оң бағытпен
алынған
- тіктемемен оң бағытпен
алынған ![]() оқтығының
арасындағы бұрыш (6 Сурет)
оқтығының
арасындағы бұрыш (6 Сурет)
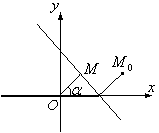
6 Сурет
Қалыпты теңдеудегі ![]() пен
пен ![]() -тің алдындағы
коэффициенттердің квадраттарының қосындысы әр
уақытта бірге тең болады.
-тің алдындағы
коэффициенттердің квадраттарының қосындысы әр
уақытта бірге тең болады.
Түзудің (1) жалпы теңдеуін қалыпты түрге келтіру үшін оны мөлшерлеуші көбейткіш деп аталатын
![]() (10)
(10)
көбейткішіне көбейту керек. Мұндағы таңба
түзудің жалпы теңдеуіндегі бос мүшенің
алдындағы таңбаға қарсы етіп алынады. (Егер ![]() болса, онда кез келген
таңба алынады).
болса, онда кез келген
таңба алынады).
![]() нүктесімен
нүктесімен ![]() түзуінің
арасындағы қашықтық
түзуінің
арасындағы қашықтық
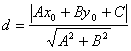 (11)
(11)
формуласымен есептеледі. Егер түзу (9)- қалыпты теңдеумен берілсе, онда
![]() (12)
(12)
5. Мысал - Координаттың бас нүктесінен ![]() түзуіне дейінгі
арақашықтық
түзуіне дейінгі
арақашықтық ![]() -ны табу керек.
-ны табу керек.
Шешуі: ![]() -ны
анықтау үшін түзудің жалпы теңдеуін қалыпты
түрге келтіреміз.
-ны
анықтау үшін түзудің жалпы теңдеуін қалыпты
түрге келтіреміз. ![]() болғандықтан
болғандықтан
![]()
енді берілген
теңдеуді ![]() -ға
көбейтсек
-ға
көбейтсек ![]() Осыдан
Осыдан
![]()
6. Мысал - Бір-біріне параллель ![]() және
және ![]() түзулерінің
арақашықтығын анықтау керек.
түзулерінің
арақашықтығын анықтау керек.
Шешуі: Түзулердің біреуінің бойында жатқан кез келген нүктені тауып алып, сол нүктеден екінші түзуге дейінгі арақашықтықты анықтаймыз:
Бірінші теңдеудегі ![]() алып,
алып, ![]() болатындығын көреміз.
Яғни
болатындығын көреміз.
Яғни ![]() нүктесі
бірінші түзудің бойында жататын нүкте. Сондықтан
нүктесі
бірінші түзудің бойында жататын нүкте. Сондықтан ![]() нүктесімен екінші
нүктесімен екінші
![]() түзуінің
арасындағы қашықтық (11)-формуламен анықталады:
түзуінің
арасындағы қашықтық (11)-формуламен анықталады:
![]()
7. Мысал - ![]() түзуінен
түзуінен ![]() қашықтықта
орналасқан әрі берілген түзуге параллель болатын
түзулердің теңдеулерін табу керек.
қашықтықта
орналасқан әрі берілген түзуге параллель болатын
түзулердің теңдеулерін табу керек.
Шешуі: Іздеп отырған түзулердің бойында
жататын кез келген ![]() нүктесі
үшін (12)-формула орындалатындықтан
нүктесі
үшін (12)-формула орындалатындықтан
![]() немесе
немесе ![]()
Бұдан ![]() болады. Нәтижесінде есептің
шарттарын қанағаттандыратын
болады. Нәтижесінде есептің
шарттарын қанағаттандыратын
![]()
түзулерін аламыз.
8. Мысал - ![]() және
және ![]() түзулерінің
қиылысуынан пайда болған бұрыштың
биссектрисасаның теңдеуін табу керек.
түзулерінің
қиылысуынан пайда болған бұрыштың
биссектрисасаның теңдеуін табу керек.
Шешуі: Бұрыштың биссектрисаның кез келген ![]() нүктесі
оның қабырғаларынан бірдей қашықтықта
жататындықтан, оларды (11)-формуламен тауып одан кейін
теңестіреміз:
нүктесі
оның қабырғаларынан бірдей қашықтықта
жататындықтан, оларды (11)-формуламен тауып одан кейін
теңестіреміз:
![]()
![]()
![]() .
.
Бұдан биссектрисалардың екі теңдеуін аламыз:
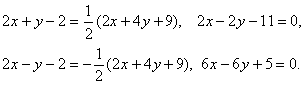
16. Координаттың бас нүктесінен ![]() түзуіне дейінгі
арақашықтық
түзуіне дейінгі
арақашықтық ![]() -ны табу керек.
-ны табу керек.
17. Бір-біріне параллель ![]() және
және ![]() түзулерінің
арақашықтығын анықтау керек.
түзулерінің
арақашықтығын анықтау керек.
18. ![]() түзуінен
түзуінен
![]() қашықтықта
орналасқан әрі берілген түзуге параллель болатын
түзулердің теңдеулерін табу керек.
қашықтықта
орналасқан әрі берілген түзуге параллель болатын
түзулердің теңдеулерін табу керек.
19. Төбелері ![]() нүктелері болатын
үшбұрыштын
нүктелері болатын
үшбұрыштын ![]() бұрышының
биссектрисасының теңдеуін табу керек.
бұрышының
биссектрисасының теңдеуін табу керек.
2.4 Екі түзудің қиылысуы
Егер ![]() және
және ![]() түзулері берілсе, онда
түзулері берілсе, онда
олардың қиылысу нүктелері берілген екі теңдеуді бірге шешу арқылы табылады. Егер жүйе үйлесімсіз болса, онда түзулер параллель болады.
9. Мысал - ![]() нүктесінің
нүктесінің ![]() түзуіне
қарағандағы симметриялы (беттеспе)
түзуіне
қарағандағы симметриялы (беттеспе) ![]() нүктесін табу керек.
нүктесін табу керек.
Шешуі: Беттеспе ![]() және
және ![]() нүктелері берілген түзуге
тіктеме түзудің бойында әрі одан бірдей
қашықтықта жататындықтан алғаш тіктеменің
теңдеуін тауып аламыз: Берілген түзудің бұрыштық
коэффициенті (еселеуші)
нүктелері берілген түзуге
тіктеме түзудің бойында әрі одан бірдей
қашықтықта жататындықтан алғаш тіктеменің
теңдеуін тауып аламыз: Берілген түзудің бұрыштық
коэффициенті (еселеуші) ![]() болғандықтан тіктеменің
бұрыштық еселеуіші
болғандықтан тіктеменің
бұрыштық еселеуіші ![]() Сондықтан тіктеменің
теңдеуі
Сондықтан тіктеменің
теңдеуі
![]()
Енді берілген түзумен тіктеменің қиылысу нүктесін табамыз
![]()
![]() нүктесі
нүктесі
![]() кесіндісінің
қақ ортасы болғандықтан 1.2-дегі (5)-формуладан
кесіндісінің
қақ ортасы болғандықтан 1.2-дегі (5)-формуладан ![]() нүктесінің
координаталарын анықтаймыз:
нүктесінің
координаталарын анықтаймыз:
![]()
20. Үшбұрыштың
қабырғалары ![]() теңдеулерімен берілген. Оның
төбелерін табу керек.
теңдеулерімен берілген. Оның
төбелерін табу керек.
21. Үшбұрыштың төбелері ![]() берілген. Оның
биіктіктерінің қиылысу нүктесін табу керек.
берілген. Оның
биіктіктерінің қиылысу нүктесін табу керек.
22. Параллелограмның екі қабырғасы ![]() ,
, ![]() және оның
диогональдарының қиылысу нүктесі
және оның
диогональдарының қиылысу нүктесі ![]() берілген. Оның
қалған екі қабырғасының теңдеулерін табу
керек.
берілген. Оның
қалған екі қабырғасының теңдеулерін табу
керек.
3. Екінші ретті сызықтар
3.1 Шеңбер
Центрі (кіндігі) ![]() нүктесі. Радиусы (өресі)
нүктесі. Радиусы (өресі)![]() ге тең болатын шеңбердің
теңдеуі
ге тең болатын шеңбердің
теңдеуі
![]() (1)
(1)
формуласымен анықталады. Дербес жағдайда, егер
шеңбердің центрі координаттың бас нүктесінде жатса,
яғни ![]() онда
оның теңдеуі
онда
оның теңдеуі
![]()
Екінші дәрежелі сызықтардың жалпы теңдеуі
![]() (2)
(2)
формуласымен анықталады. Егер ![]() болса, онда шеңбердің жалпы
теңдеуі шығады:
болса, онда шеңбердің жалпы
теңдеуі шығады:
![]() (3)
(3)
Бұл теңдеуді ![]() -ға бөліп, одан соң одан
-ға бөліп, одан соң одан ![]() және
және ![]() бойынша толық
квадратын ерекшелеп, (1)-түрге келтіреміз:
бойынша толық
квадратын ерекшелеп, (1)-түрге келтіреміз:
![]()
1. Мысал - ![]() шеңберін (1) – түрге келтіру керек.
шеңберін (1) – түрге келтіру керек.
Шешуі: Теңдеуді 3-ке бөліп, одан кейін ![]() және
және ![]() бойынша толық
квадратын ерекшелейміз:
бойынша толық
квадратын ерекшелейміз:
![]() .
.
Яғни шеңбердің центрі ![]() нүктесі, ал радиусы
нүктесі, ал радиусы ![]()
2. Мысал - ![]() түзуімен
түзуімен ![]() шеңберінің қиылысу
нүктелерін табу керек.
шеңберінің қиылысу
нүктелерін табу керек.
Шешуі: Олардың қиылысу нүктелерін табу үшін төмендегі жүйені шешеміз:
![]()
![]()
![]()
![]() .
.
Яғни (2,4) және (-2,0) нүктелерінде қиылысады.
23. ![]() шеңберін
қарапайым түрге келтіру керек.
шеңберін
қарапайым түрге келтіру керек.
24. ![]() түзуімен
түзуімен
![]() шеңберінің
қиылысу нүктелерін табу керек.
шеңберінің
қиылысу нүктелерін табу керек.
3.2 Эллипс
Эллипс деп ( фокустар (тоғыстар) деп аталатын)
жазықтықтың екі ![]() және
және ![]() нүктесінен
қашықтықтарының қосындысы тұрақты
болатын, осы жазықтықты нүктелерінің геометриялық
орнын айтады. Бұл тұрақты
нүктесінен
қашықтықтарының қосындысы тұрақты
болатын, осы жазықтықты нүктелерінің геометриялық
орнын айтады. Бұл тұрақты ![]() , ал фокустардың арасы
, ал фокустардың арасы ![]() арқылы
белгіленеді әрі
арқылы
белгіленеді әрі ![]() .
Егер координаттар жүйесінің
.
Егер координаттар жүйесінің ![]() өсі фокустар арқылы
өтіп, ал оның төбесі фокустардың ортасында жатса, онда
эллипстің қарапайым теңдеуі
өсі фокустар арқылы
өтіп, ал оның төбесі фокустардың ортасында жатса, онда
эллипстің қарапайым теңдеуі
![]()
![]() (4)
(4)
түрінде беріледі. Бұл жағдайда эллипстің
фокустарының координаталары ![]() болады (7 Сурет).
болады (7 Сурет).
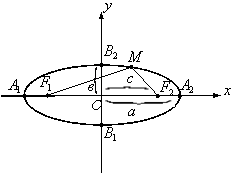
7 Сурет
Координаттың бас нүктесі ![]() - эллипстің
симметриялық (беттеспе) нүктесі.
- эллипстің
симметриялық (беттеспе) нүктесі. ![]() эллипстің төбелері, ал
эллипстің төбелері, ал ![]() және
және ![]() сәйкесінше
оның үлкен және кіші жарты өстері деп аталады.
сәйкесінше
оның үлкен және кіші жарты өстері деп аталады.
![]() (5)
(5)
эллипстің эксцентриситеті деп аталады, оның созылмалы болатындығын анықтайды.
![]() болғанда эллипс шеңберге
айналады да,
болғанда эллипс шеңберге
айналады да, ![]()
Егер эллипстің фокустары ![]() өстерінде жатса, онда
оның теңдеуі
өстерінде жатса, онда
оның теңдеуі
![]() (6)
(6)
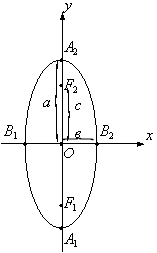 |
түрінде беріледі. Бұл жағдайда оның төбелерінің координаталары
8 Сурет
3. Мысал - ![]() эллипсінің фокустарының координаталарымен
эксцентриситетін табу керек.
эллипсінің фокустарының координаталарымен
эксцентриситетін табу керек.
Шешуі: Бұл эллипс үшін ![]() сондықтан
сондықтан ![]()
Яғни, ![]() және
және ![]() , эксцентриситет
, эксцентриситет ![]()
4. Мысал - Егер эллипстің үлкен жарты өсі ![]() , ал эксцентриситеті
, ал эксцентриситеті
![]() болса, онда
оның қарапайым теңдеуін құру керек.
болса, онда
оның қарапайым теңдеуін құру керек.
Шешуі: ![]() болғандықтан орнына
қойсақ
болғандықтан орнына
қойсақ ![]() бұдан
бұдан
![]() Яғни
элиппстің қарапайым теңдеуі
Яғни
элиппстің қарапайым теңдеуі ![]() .
.
25. ![]() эллипсінің
фокустарының координаталарымен эксцентриситетін табу керек.
эллипсінің
фокустарының координаталарымен эксцентриситетін табу керек.
26.
Егер эллипстің үлкен жарты өсі ![]() ал эксцентриситеті
ал эксцентриситеті ![]() болса, онда оның
қарапайым теңдеуін құру керек.
болса, онда оның
қарапайым теңдеуін құру керек.
27.
Егер эллипстің кіші жарты өсі ![]() , ал фокустарының
арақашықтығы
, ал фокустарының
арақашықтығы ![]() болса, онда оның қарапайым
теңдеуін құру керек.
болса, онда оның қарапайым
теңдеуін құру керек.
3.3 Гипербола
Берілген фокустар деп аталатын екі ![]() және
және![]() нүктелерінен
қашықтықтарының айырымының абсолют шамасы
нүктелерінен
қашықтықтарының айырымының абсолют шамасы ![]() деп белгіленетін
тұрақты шамаға тең болатын
жазықтықтағы нүктелер жиынтығын гипербола деп
атайды.
деп белгіленетін
тұрақты шамаға тең болатын
жазықтықтағы нүктелер жиынтығын гипербола деп
атайды. ![]() қашықтығы
қашықтығы
![]() арқылы
белгіленеді, әрі
арқылы
белгіленеді, әрі ![]() . Егер
. Егер ![]() оқтығы гиперболаның
фокустары арқылы өтетін, ал координаттың бас нүктесі
оқтығы гиперболаның
фокустары арқылы өтетін, ал координаттың бас нүктесі ![]() кесіндісінің
ортасында жатса, онда гиперболаның қарапайым теңдеуі
кесіндісінің
ортасында жатса, онда гиперболаның қарапайым теңдеуі
![]() (7)
(7)
формуласымен анықталады. Бұл жағдайда
фокустардың координаталары ![]() және
және ![]() .
.
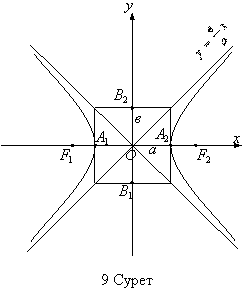 Мұнда координат оқтықтары
гиперболаның симметриялық өстері, ал О нүктесі
оның симметриялық орталығы болады. Гипербола абсцисс
оқтығын
Мұнда координат оқтықтары
гиперболаның симметриялық өстері, ал О нүктесі
оның симметриялық орталығы болады. Гипербола абсцисс
оқтығын ![]() және
және
![]() нүктелерінде
қиып өтеді де оның нақты төбелері деп, ал
нүктелерінде
қиып өтеді де оның нақты төбелері деп, ал ![]() нақты жарты өсі
деп аталады.
нақты жарты өсі
деп аталады. ![]() және
және
![]() гиперболаның
жорамал төбелері деп, ал
гиперболаның
жорамал төбелері деп, ал ![]() жорамал жарты өсі деп аталады (9
Сурет).
жорамал жарты өсі деп аталады (9
Сурет).
Центрі (орталығы) координаттың бас нүктесі, ал қабырғалары координат оқтықтарына параллель және гиперболаның төбелері арқылы өтетін тікбұрыш гиперболаның негізгі тікбұрышы деп аталады. Оның диогоналдары
![]() (8)
(8)
гиперболаның асимптоталары, яғни оның тармақтары шексіз жақындайтын түзулер болады.
Гиперболаның эксцентриситеті
![]() .
(9)
.
(9)
Эксцентриситет гиперболаның негізгі тікбұрышының созыңқылығын көрсетеді.
Егер ![]() болса, онда гипербола теңқабырғалы
деп аталады да тікбұрыш квадратқа айналады, ал
болса, онда гипербола теңқабырғалы
деп аталады да тікбұрыш квадратқа айналады, ал ![]() .
.
Егер гиперболаның фокустары ![]() оқтығына орналасса
(10 сурет), онда оның қарапайым теңдеуі
оқтығына орналасса
(10 сурет), онда оның қарапайым теңдеуі
![]() (10)
(10)
формуласымен анықталады.
 |
10 Сурет
Бұл жағдайда гиперболаның асимптотасы
![]() ,
(11)
,
(11)
мұндағы ![]() нақты, ал
нақты, ал ![]() жорамал жарты өстер.
Гиперболаның төбелері:
жорамал жарты өстер.
Гиперболаның төбелері: ![]()
![]() фокустары
фокустары ![]() мұндағы
мұндағы ![]() .
.
5. Мысал - ![]() гиперболасын қарапайым түрге келтіріп, оның
төбелерінің және фокустарының координаталарын,
эксцентриситетін және асипмтоталарының теңдеулерін табу
керек.
гиперболасын қарапайым түрге келтіріп, оның
төбелерінің және фокустарының координаталарын,
эксцентриситетін және асипмтоталарының теңдеулерін табу
керек.
Шешуі: Берілген теңдеуді 144 бөлсек
![]()
түріне келеді.
Бұдан ![]() ,
, ![]() екендігін
көреміз.
екендігін
көреміз. ![]() Яғни
Яғни
![]()
![]() және
және ![]() , ал
, ал ![]() және
және ![]() . Эксцентриситеті
. Эксцентриситеті ![]() ал асимптоталары
ал асимптоталары ![]() .
.
6. Мысал - Гиперболаның нақты жарты өсі 5, эксцентриситеті ![]()
Оның қарапайым теңдеуін жазу керек.
Шешуі: ![]() болғандықтан,
болғандықтан, ![]() екендігін ескерсек,
екендігін ескерсек, ![]() Гиперболаның
жорамал жарты өсі
Гиперболаның
жорамал жарты өсі ![]() Яғни оның қарапайым
теңдеуі
Яғни оның қарапайым
теңдеуі
![]()
28. ![]() гиперболасы
берілген. Оның фокустарын, төбелерін, эксцентриситетін,
асимптоталарын анықтау керек.
гиперболасы
берілген. Оның фокустарын, төбелерін, эксцентриситетін,
асимптоталарын анықтау керек.
29. Гиперболаның асимптоталарының теңдеуі ![]() берілген. Оның
фокустарының арақашықтығы 20, қарапайым
теңдеуін табу керек.
берілген. Оның
фокустарының арақашықтығы 20, қарапайым
теңдеуін табу керек.
30. ![]() гиперболасы
берілген. Оның фокустарын, төбелерін, эксцентриситетін,
асимптоталарын табу керек.
гиперболасы
берілген. Оның фокустарын, төбелерін, эксцентриситетін,
асимптоталарын табу керек.
3.4 Парабола
Жазықтықтың фокус деп аталатын нүктесімен бұл нүктеден өтпейтін директриса деп аталатын түзуден бірдей (теңдей) қашықта орналасқан нүктелердің геометриялық орнын парабола дейміз (11 Сурет).
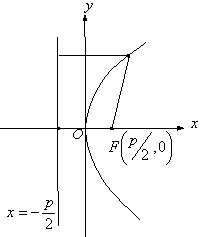 |
11 Сурет
Параболаның қарапайым теңдеуінің түрі
![]()
![]() ,
(12)
,
(12)
мұндағы ![]() параметрі фокуспен директрисаның
арақашықтығы. Координат жүйесі 11 Суретте
көрсетілгендей етіп алынады. Бұл жағдайда директрисаның
теңдеуі
параметрі фокуспен директрисаның
арақашықтығы. Координат жүйесі 11 Суретте
көрсетілгендей етіп алынады. Бұл жағдайда директрисаның
теңдеуі
![]() ,
(13)
,
(13)
ал фокустың координаталары ![]() . Координаттың бас нүктесі
параболаның төбесі, ал абсцисса өсі – оның симметриалық
өсі болады. Параболаның эксцентриситеті
. Координаттың бас нүктесі
параболаның төбесі, ал абсцисса өсі – оның симметриалық
өсі болады. Параболаның эксцентриситеті ![]() .
.
Кейбір жағдайларда төмендегі
теңдеулермен берілген параболалар қарастырылады: ![]() бұл
жағдайда парабола
бұл
жағдайда парабола ![]() өсіне қарағанда
симметриялы әрі тармақтары оған қарсы бағытталады
(12 Сурет)
өсіне қарағанда
симметриялы әрі тармақтары оған қарсы бағытталады
(12 Сурет)
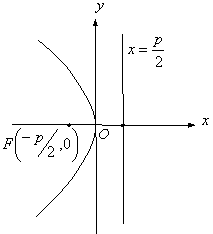 |
12 сурет
Фокусының координатасы ![]() , ал директрисасының теңдеуі
, ал директрисасының теңдеуі ![]()
б) ![]() бұл жағдайда парабола
бұл жағдайда парабола ![]() өсіне симметриялы
әрі тармақтары оған бағыттас болады (13 сурет).
өсіне симметриялы
әрі тармақтары оған бағыттас болады (13 сурет).
 |
13 Сурет
Фокусының координатасы ![]() ал директрисасы
ал директрисасы ![]() .
.
в) ![]() бұл жағдайда парабола
бұл жағдайда парабола ![]() өсіне симметриялы
әрі тармақтары оған қарсы бағытталады. (14 Сурет)
өсіне симметриялы
әрі тармақтары оған қарсы бағытталады. (14 Сурет)
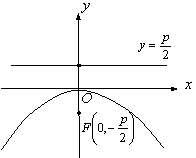 |
14 сурет
Фокусының координатасы ![]() ал директрисасы
ал директрисасы ![]()
7. Мысал - Төбесі координаттың
бас нүктесі болатын әрі ![]() өсіне симметриялы парабола
өсіне симметриялы парабола ![]() нүктесі
арқылы өтсін. Оның теңдеуін жазу керек.
нүктесі
арқылы өтсін. Оның теңдеуін жазу керек.
Шешуі: Парабола ![]() өсіне симметриялы әрі
абсциссасы теріс
өсіне симметриялы әрі
абсциссасы теріс ![]() нүктесі
арқылы өтетіндіктен оның теңдеуі
нүктесі
арқылы өтетіндіктен оның теңдеуі ![]() формуласы арқылы
анықталады.
формуласы арқылы
анықталады. ![]() нүктесінің
координаталарын теңдеуге қою арқылы
нүктесінің
координаталарын теңдеуге қою арқылы ![]()
![]() болатындығын көреміз.
Яғни оның теңдеуі
болатындығын көреміз.
Яғни оның теңдеуі ![]() Олай болса оның фокусы
Олай болса оның фокусы ![]() , ал директрисасы
, ал директрисасы ![]() .
.
8. Мысал - Төбесі координаттың
бас нүктесі болатын әрі ![]() өсіне симметриялы парабола
өсіне симметриялы парабола ![]()
![]() нүктесі арқылы
өтсін. Параболаның теңдеуін жазу керек.
нүктесі арқылы
өтсін. Параболаның теңдеуін жазу керек.
Шешуі: Парабола ![]() өсіне симметриялы әрі
ординатасы теріс
өсіне симметриялы әрі
ординатасы теріс ![]() нүктесі
арқылы өтетіндіктен оның теңдеуі
нүктесі
арқылы өтетіндіктен оның теңдеуі ![]() формуласы арқылы
анықталады.
формуласы арқылы
анықталады.
![]() нүктесінің
координаталарын теңдеуге қою арқылы
нүктесінің
координаталарын теңдеуге қою арқылы ![]() болатындығын
көреміз. Яғни оның теңдеуі
болатындығын
көреміз. Яғни оның теңдеуі
![]() .
.
Олай болса оның фокусы ![]() ал директрисасы
ал директрисасы ![]()
31. ![]() параболасының
фокусымен директрисасын табу керек.
параболасының
фокусымен директрисасын табу керек.
32. Төбесі координаттың бас нүктесі болатын әрі
![]() өсіне
симметриялы парабола
өсіне
симметриялы парабола ![]() нүктесі
арқылы өтсін. Оның теңдеуін жазу керек.
нүктесі
арқылы өтсін. Оның теңдеуін жазу керек.
33. Директрисасы және фокусы белгілі параболаның теңдеуін табу керек:
![]()
4. Екінші ретті сызықтардың теңдеулерін қарапайым түрге келтіру
4.1 Координат өстерін параллель жылжытуды пайдалану
Екінші ретті сызықтардың жалпы теңдеуі
![]() (1)
(1)
формуласымен анықталады. Мұндағы ![]() және
және ![]() коэффициенттерінің
бәрі бірдей нөлге тең емес. Координат жүйесін
түрлендіру арқылы екінші ретті сызықтардың
теңдеуін қарапайым түрге келтіруге болады. Егер (1)-теңдеудегі
коэффициенттерінің
бәрі бірдей нөлге тең емес. Координат жүйесін
түрлендіру арқылы екінші ретті сызықтардың
теңдеуін қарапайым түрге келтіруге болады. Егер (1)-теңдеудегі
![]() болса, онда
оны
болса, онда
оны
![]() (2)
(2)
түрінде жазуға болады.
Бұл теңдеу қарапайым түрге координаттар жүйесін
![]() (3)
(3)
формулаларының көмегімен түрлендіру арқылы келтіріледі. Мұндағы
![]() -
жаңа жүйенің бас
-
жаңа жүйенің бас ![]() нүктесінің координаталары.
Жаңа
нүктесінің координаталары.
Жаңа ![]() және
және
![]() өстері
ескі
өстері
ескі ![]() және
және
![]() өстеріне
параллель болады. (2)-теңдеуді қарапайым түрге келтіру
үшін одан толық квадратын бөліп алу тәсілін
қолданған ыңғайлы.
өстеріне
параллель болады. (2)-теңдеуді қарапайым түрге келтіру
үшін одан толық квадратын бөліп алу тәсілін
қолданған ыңғайлы.
1. Мысал - ![]() теңдеуін қарапайым түрге
келтіріп, оның түрін және фокустарының координаталарын
анықтап, графигін салу керек.
теңдеуін қарапайым түрге
келтіріп, оның түрін және фокустарының координаталарын
анықтап, графигін салу керек.
Шешуі: Тек ![]() және тек
және тек ![]() бар мүшелерді топтастырып,
бар мүшелерді топтастырып,
![]() және
және ![]() алдындағы
коэффициенттерді жақшаның алдына шығарып, одан соң
толық квадратын бөліп аламыз:
алдындағы
коэффициенттерді жақшаның алдына шығарып, одан соң
толық квадратын бөліп аламыз:
![]()
Бұдан ![]() Сонымен берілген теңдеу
төмендегі түрге келтіріледі.
Сонымен берілген теңдеу
төмендегі түрге келтіріледі.
![]()
. ![]() белгілеуін енгізсек
белгілеуін енгізсек ![]() (3)-теңдеулермен
салыстыра отырып, соңғы формулалар координат жүйесін
(3)-теңдеулермен
салыстыра отырып, соңғы формулалар координат жүйесін ![]() нүктесіне
параллель жылжытатындығын көреміз. Жаңа координаттар
жүйесінде соңғы теңдеуді
нүктесіне
параллель жылжытатындығын көреміз. Жаңа координаттар
жүйесінде соңғы теңдеуді
![]()
түрінде жазуға болады.
Сонымен, екінші ретті сызығымыздың жарты
өстері ![]()
![]() болатын эллипс
екендігін көріп отырмыз. Эллипстің центрі жаңа
координаттың бас нүктесі болады. Фокустардың центрден
қашықтығы
болатын эллипс
екендігін көріп отырмыз. Эллипстің центрі жаңа
координаттың бас нүктесі болады. Фокустардың центрден
қашықтығы ![]() болғандықтан оның
жаңа фокустарының координаталары
болғандықтан оның
жаңа фокустарының координаталары ![]() . Бұл фокустардың ескі
координаталары параллель жылжыту формулалары арқылы анықталады:
. Бұл фокустардың ескі
координаталары параллель жылжыту формулалары арқылы анықталады:
![]()
 |
15 Сурет
2. Мысал - ![]() теңдеуін қарапайым түрге
келтіріп, оның түрін және фокусының координаталарын
анықтап, графигін салу керек.
теңдеуін қарапайым түрге
келтіріп, оның түрін және фокусының координаталарын
анықтап, графигін салу керек.
Шешуі: ![]() бар мүше жоқ
болғандықтан тек
бар мүше жоқ
болғандықтан тек ![]() бар мүшелерді топтастырып одан
толық квадратын бөліп аламыз:
бар мүшелерді топтастырып одан
толық квадратын бөліп аламыз:
![]()
 белгілеуін енгізсек,
белгілеуін енгізсек, ![]() (3)-теңдеумен салыстыра отырып,
соңғы формулалар координат жүйесін
(3)-теңдеумен салыстыра отырып,
соңғы формулалар координат жүйесін ![]() нүктесіне параллель
жылжытатындығын көреміз.
нүктесіне параллель
жылжытатындығын көреміз.
 |
16 Сурет
Жаңа координаттар жүйесінде соңғы теңдеуді
![]()
түрінде жазуға болады.
Сонымен, екінші ретті сызығымыздың
жаңа координаталар жүйесінде, төбесі ![]() нүктесі болатын,
нүктесі болатын, ![]() өсіне симметриялы,
парабола болатынын көреміз. Ол үшін
өсіне симметриялы,
парабола болатынын көреміз. Ол үшін ![]() сондықтан оның фокусының
жаңа координаталары
сондықтан оның фокусының
жаңа координаталары ![]()
![]()
Оның ескі координаталары
![]() .
.
Келесі теңдеулерді қарапайым түрге келтіру керек. Олардың түрлерін және фокустарының координаталарын анықтап графиктерін салу керек.
34. ![]() 35.
35. ![]()
36. ![]() 37.
37. ![]()
4.2 Координат өстерін (мекендік оқтығын) бұруды пайдалану
Екінші ретті сызықтың жалпы
теңдеуі (2) теңдеу арқылы берілген түрге координат
өстерін ![]() бұрышына
бұру
бұрышына
бұру
![]() (4)
(4)
формулалары арқылы беріледі. Мұндағы ![]() - жаңа
координаттар.
- жаңа
координаттар. ![]() бұрышы
бұрышы
![]() (5)
(5)
теңдеуінен табылады. Координат өстері бұл
жағдайда оның жаңа өстері ![]() және
және ![]() , екінші ретті сызықтың
симметриялық өстерімен параллель болатындай болып бұрылады.
, екінші ретті сызықтың
симметриялық өстерімен параллель болатындай болып бұрылады.
![]() белгілі
болғандықтан
белгілі
болғандықтан ![]() және
және ![]() төмендегі формулалар арқылы
анықталады:
төмендегі формулалар арқылы
анықталады:
![]()
Егер ![]() бұру бұрышын сүйір
болады деп шарт қойсақ, онда бұл формулаларда оң
таңба алынады әрі (5)-формуладан табылатын
бұру бұрышын сүйір
болады деп шарт қойсақ, онда бұл формулаларда оң
таңба алынады әрі (5)-формуладан табылатын ![]() да оң таңбамен
алынады. Дербес жағдайда, егер (1)-теңдеудегі
да оң таңбамен
алынады. Дербес жағдайда, егер (1)-теңдеудегі ![]() болса, онда координат
өстерін
болса, онда координат
өстерін ![]() бұрышына
бұру қажет.
бұрышына
бұру қажет.
Бұл жағдайда
![]() (6)
(6)
3. Мысал - Екінші ретті ![]() сызығының теңдеуін
қарапайым түрге келтіріп, оның түрін анықтап,
графигін сызу керек.
сызығының теңдеуін
қарапайым түрге келтіріп, оның түрін анықтап,
графигін сызу керек.
Шешуі: Бұл жағдайда ![]() Сондықтан
бұру бұрышы
Сондықтан
бұру бұрышы ![]()
![]() теңдеуі
арқылы анықталады. Бұл теңдеудің түбірі
теңдеуі
арқылы анықталады. Бұл теңдеудің түбірі ![]() және
және ![]() Бұру
бұрышының сүйір бұрышымен шектелейік. Сонда
Бұру
бұрышының сүйір бұрышымен шектелейік. Сонда
![]() және
және ![]()
![]() және
және ![]() -тің мәндерін берілген
теңдеуге қойсақ
-тің мәндерін берілген
теңдеуге қойсақ
![]() немесе
немесе ![]()
Соңғы теңдеудегі жақшаларды ашып түрлендіру арқылы
![]()
гиперболасын аламыз. Мұнда ![]() әрі оның үлкен өсі
әрі оның үлкен өсі
![]() -ң
бойында, ал кіші өсі
-ң
бойында, ал кіші өсі ![]() -ң бойында жатады.
-ң бойында жатады.
Бұл гиперболаны салу үшін алғаш ![]() және
және ![]() өстерін салып аламыз. Ол
үшін
өстерін салып аламыз. Ол
үшін ![]() өсінің
бойынан 1, ал
өсінің
бойынан 1, ал ![]() өсінің
бойынан 2 алып
өсінің
бойынан 2 алып ![]() нүктесін
саламыз. Пайда болған
нүктесін
саламыз. Пайда болған ![]() радиусы
радиусы ![]() өсімен
өсімен ![]() бұрышын жасайды, әрі
бұрышын жасайды, әрі ![]()
Сондықтан бұл ![]() нүктесі арқылы жаңа
абсциса өсі өтеді.
нүктесі арқылы жаңа
абсциса өсі өтеді.
Осы жаңа координаттар жүйесінде гиперболаның графигін саламыз
(17 Сурет).
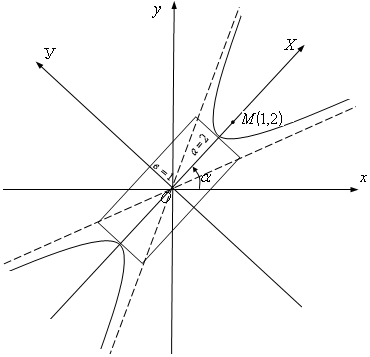 |
17 Сурет
Төмендегі екінші ретті сызықтарды қарапайым түрге келтіріп, түрлерін анықтап, графиктерін салу керек.
38. ![]() 39.
39.
![]()
40. ![]() 41.
41.
![]()
4.3 Екінші ретті сызықтың бөлінуі және жұпталуы
Егер (1)-теңдеудің сол бөлігі екі сызықтық көбейткіштерге жіктелсе
![]()
![]() онда екінші ретті
сызығымыз екі түзуге бөлінеді.
онда екінші ретті
сызығымыз екі түзуге бөлінеді.
Кейбір жағдайларда, (1)-теңдеуді
жалғыз нақты ![]() нүктесінің координаталары
ғана қанағаттандыруы немесе бірде бір нүктенің
координаталары қанағаттандырмауы мүмкін. Бірінші
жағдайда сызық нүктеге айналады, ал екінші жағдайда
сызықты жорамалды деп есептейді.
нүктесінің координаталары
ғана қанағаттандыруы немесе бірде бір нүктенің
координаталары қанағаттандырмауы мүмкін. Бірінші
жағдайда сызық нүктеге айналады, ал екінші жағдайда
сызықты жорамалды деп есептейді.
Мысалы, ![]() теңдеуі
жалғыз
теңдеуі
жалғыз ![]() нүктесін
анықтайды, ал
нүктесін
анықтайды, ал ![]() теңдеуінің
бірде-бір нақты түбірі болмайды. Сондықтан жорамал екінші
ретті сызықты анықтайды.
теңдеуінің
бірде-бір нақты түбірі болмайды. Сондықтан жорамал екінші
ретті сызықты анықтайды.
4. Мысал - Екінші ретті ![]() сызығының екі түзуге
жіктелетіндігін көрсету керек.
сызығының екі түзуге
жіктелетіндігін көрсету керек.
Шешуі: Теңдеудің сол жағы толық квадрат құратындықтан
![]() немесе
немесе ![]()
Квадраттардың айырымы қосындымен айырымының
көбейтіндісіне тең болғандықтан, соңғы
теңдеуді ![]() түрінде
жазуға болады. Яғни екінші ретті сызық екі түзуге
жіктеледі:
түрінде
жазуға болады. Яғни екінші ретті сызық екі түзуге
жіктеледі:
![]()
![]() және
және ![]()
Бұл түзулер параллель болады, өйткені олардың бұрыштық коэффициенттері тең.
5. Мысал - Екінші ретті ![]() сызығының екі түзуге
жіктелетіндігін көрсету керек.
сызығының екі түзуге
жіктелетіндігін көрсету керек.
Шешуі: Теңдеуді ![]() түрінде жазып
түрінде жазып ![]() айнымалысына қатысты
шешеміз:
айнымалысына қатысты
шешеміз:
![]() бұдан
бұдан ![]() және
және ![]() Яғни, берілген екінші ретті
сызық
Яғни, берілген екінші ретті
сызық ![]() және
және
![]() түзулеріне
жіктеледі.
түзулеріне
жіктеледі.
Келесі екінші ретті сызықтар нені береді?
42. ![]() 43.
43.![]()
44. ![]() 45.
45.
![]()
5. Полярлық координаталар (мекендіктер)
5.1 Полярлық координаттар жүйесі
Жазықтықта полярлық координаттар
жүйесі ![]() нүктесінің
осы нүктеден шығатын
нүктесінің
осы нүктеден шығатын ![]() сәулесінің және
сәулесінің және ![]() масштаб бірлігінің
берілуімен анықталады
масштаб бірлігінің
берілуімен анықталады
(18 Сурет). ![]() нүктесі
полюс, ал
нүктесі
полюс, ал ![]() сәулесі
полярлық өс (оқтық) деп аталады.
сәулесі
полярлық өс (оқтық) деп аталады.
 |
18 Сурет
![]() нүктесі жазықтықтың
кез келген нүктесі болсын.
нүктесі жазықтықтың
кез келген нүктесі болсын. ![]() арқылы оның полюстан
қашықтығын, ал
арқылы оның полюстан
қашықтығын, ал![]() арқылы полярлық өспен
арқылы полярлық өспен ![]() кесіндісінің
сағат бағытына қарсы бағытталған бұрышын
белгілейміз. Бұл сандар
кесіндісінің
сағат бағытына қарсы бағытталған бұрышын
белгілейміз. Бұл сандар ![]() нүктесінің полярлық координаталары
болады, әрі
нүктесінің полярлық координаталары
болады, әрі ![]() шамасы
полярлық радиусы, ал
шамасы
полярлық радиусы, ал ![]() полярлық бұрышы деп аталады.
Мұндағы
полярлық бұрышы деп аталады.
Мұндағы ![]()
![]() екі санының
берілуі жазықтықтағы тек бір
екі санының
берілуі жазықтықтағы тек бір ![]() нүктесін анықтайды. Егер
нүктесін анықтайды. Егер ![]() немесе
немесе![]() деп алсақ, онда
жазықтықтың әрбір нүктесіне тек бір
деп алсақ, онда
жазықтықтың әрбір нүктесіне тек бір ![]() сандары
сәйкестендіріледі. Тек
сандары
сәйкестендіріледі. Тек ![]() полюсы
полюсы ![]() болғанда анықталып, ал
болғанда анықталып, ал ![]() бұрышы
анықталмайды.
бұрышы
анықталмайды.
Егер декарттық координаталар
жүйесінің бас нүктесі ![]() , полярлық координаталар
жүйесінің полюсымен беттессе, ал
, полярлық координаталар
жүйесінің полюсымен беттессе, ал ![]() өсі
өсі ![]() полярлық өсінің бойында
жатса, онда кез келген
полярлық өсінің бойында
жатса, онда кез келген ![]() нүктесінің полярлық
координаталарының арасында төмендегідей байланыс орнайды (19
Сурет):
нүктесінің полярлық
координаталарының арасында төмендегідей байланыс орнайды (19
Сурет):
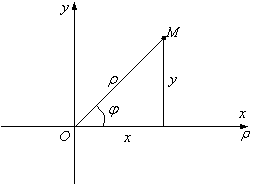 |
19 Сурет
![]() (1)
(1)
![]() (2)
(2)
Бұл теңдеуден
![]() (3)
(3)
болатындығын көреміз.
Ескерту. (2)-теңдеудің соңғысынан
бұрыштың ![]() мен
мен
![]() -дің
арасында жататын екі
-дің
арасында жататын екі ![]() және
және
![]() мәндері
бар болатындығын көруге болады. Сондықтан (3) формулалар
арқылы сол мәндердің қайсысын алуға
болатындығы анықталады.
мәндері
бар болатындығын көруге болады. Сондықтан (3) формулалар
арқылы сол мәндердің қайсысын алуға
болатындығы анықталады.
1. Мысал - Полярлық координаталары арқылы берілген ![]()
![]()
нүктелерін салу керек.
Нүктелердің салынуы 20 Суретте берілген.
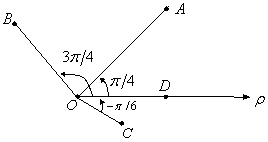 |
20 сурет
2. Мысал - ![]() нүктелері полярлық
координаталар жүйесінде берілген. Декарттық координаталар
жүйесін 19 Суретте көрсетілгендей етіп алып олардың декарттық
координаталарын табу керек.
нүктелері полярлық
координаталар жүйесінде берілген. Декарттық координаталар
жүйесін 19 Суретте көрсетілгендей етіп алып олардың декарттық
координаталарын табу керек.
Шешуі: Полярлық координаталарды (1) формулаға қою арқылы олардың декарттық координаталарын табамыз:
![]()
46. ![]() нүктелері
полярлық координаталар жүйесінде берілген. Декарттық
координаталар жүйесін 19 Суретте көрсетілгендей етіп алып,
олардың декарттық координаталарын табу керек.
нүктелері
полярлық координаталар жүйесінде берілген. Декарттық
координаталар жүйесін 19 Суретте көрсетілгендей етіп алып,
олардың декарттық координаталарын табу керек.
47. ![]() нүктелері
полярлық координаталар жүйесінде берілген. Осы нүктелерге
полярлық өсіне қарағанда симметриялы болатын
нүктелердің полярлық координаталарын табу керек.
нүктелері
полярлық координаталар жүйесінде берілген. Осы нүктелерге
полярлық өсіне қарағанда симметриялы болатын
нүктелердің полярлық координаталарын табу керек.
5.2 Сызықтардың полярлық теңдеулері
Сызық полярлық координаталар
жүйесінде оның нүктелерінің координаталарын ![]() теңдеуімен берілді.
Егер мүмкін болса, оны
теңдеуімен берілді.
Егер мүмкін болса, оны ![]() түрінде жазуға болады.
Бұл функция периодты болмаса, онда
түрінде жазуға болады.
Бұл функция периодты болмаса, онда ![]() -ге мүмкін болатын мәндерін
беру арқылы сәйкес
-ге мүмкін болатын мәндерін
беру арқылы сәйкес ![]() -ң мәндерін тауып алып
сызықтың графигін салуға болады.
-ң мәндерін тауып алып
сызықтың графигін салуға болады.
Декарттық координаталары арқылы берілген
сызықтың ![]() теңдеуінен
оның полярлық теңдеуіне көшу үшін декарттық
теңдеудегі
теңдеуінен
оның полярлық теңдеуіне көшу үшін декарттық
теңдеудегі ![]() пен
пен
![]() -ң
орнына (1)-формуладағы өрнектерді қоямыз: керісінше,
-ң
орнына (1)-формуладағы өрнектерді қоямыз: керісінше, ![]() полярлық
теңдеуінен декарттық теңдеуіне көшу үшін (2), (3)
формулаларды пайдаланамыз.
полярлық
теңдеуінен декарттық теңдеуіне көшу үшін (2), (3)
формулаларды пайдаланамыз.
3. Мысал - ![]() түзуінің полярлық теңдеуін табу керек.
түзуінің полярлық теңдеуін табу керек.
Шешуі: (1) формуланың біріншісін қолдансақ ![]() немесе
немесе ![]() полярлық
теңдеуін аламыз.
полярлық
теңдеуін аламыз. ![]() оң болатындықтан,
оң болатындықтан, ![]() бұрышы
бұрышы ![]() тек оң
мәндер қабылдайтындай болып өзгеру керек. Осыдан
тек оң
мәндер қабылдайтындай болып өзгеру керек. Осыдан ![]() -ң I және IV
ширектен мәндер қабылдайтындығын көреміз. (21 Сурет)
-ң I және IV
ширектен мәндер қабылдайтындығын көреміз. (21 Сурет)

21 Сурет
4. Мысал - Координат жүйесінің бас нүктесінен өтпейтін түзудің полярлық теңдеуін табу керек.
Шешуі: Түзудің теңдеуін қалыпты
түрге келтіреміз: ![]() Бұл теңдеудегі
Бұл теңдеудегі ![]() пен
пен ![]() -ті (1) формуладағы
өрнекпен алмастырамыз:
-ті (1) формуладағы
өрнекпен алмастырамыз:
![]() яғни
яғни ![]()
Түзу координаттың бас нүктесінен
өтпейтіндіктен оның координаттың бас нүктесінен
қашықтығы ![]() нөлге тең болмайды. Соңғы
теңдіктен,
нөлге тең болмайды. Соңғы
теңдіктен, ![]() -ң
кез келген мәнінде және
-ң
кез келген мәнінде және ![]() болғанда, түзудің
полярлық теңдеуі
болғанда, түзудің
полярлық теңдеуі
![]()
5. Мысал - Полярлық координаталар жүйесінде берілген ![]() (тұрақты)
және
(тұрақты)
және ![]() (тұрақты)
теңдеулері қандай сызықтарды береді?
(тұрақты)
теңдеулері қандай сызықтарды береді?
Шешуі: Жазықтықта полюске дейінгі
қашықтығы ![]() тұрақты болатын
нүктелердің жиыны шеңбер болады. Сондықтан
тұрақты болатын
нүктелердің жиыны шеңбер болады. Сондықтан ![]() теңдеуі радиусы
теңдеуі радиусы ![]() , центрі О полюсі
болатын шеңберді береді.
, центрі О полюсі
болатын шеңберді береді. ![]() теңдеуін полярлық өспен
теңдеуін полярлық өспен ![]() бұрышын жасайтын,
полюстан басталатын жарты түзудің барлық нүктелері қанағаттандырады.
Полярлық координаталар жүйесінде полюс арқылы өтетін
түзу
бұрышын жасайтын,
полюстан басталатын жарты түзудің барлық нүктелері қанағаттандырады.
Полярлық координаталар жүйесінде полюс арқылы өтетін
түзу ![]() және
және
![]() теңдеулері
арқылы анықталады.
теңдеулері
арқылы анықталады.
6. Мысал - ![]() полярлық теңдеуі берілген. Осы сызықты,
полярлық теңдеуі берілген. Осы сызықты, ![]() адымымен мәндер
беру арқылы нүктелерін анықтап құру керек.
Декарттық өстерді 19 суретте көрсетілгендей орналастырып,
оның декарттық теңдеуің табу керек.
адымымен мәндер
беру арқылы нүктелерін анықтап құру керек.
Декарттық өстерді 19 суретте көрсетілгендей орналастырып,
оның декарттық теңдеуің табу керек.
Шешуі: Берілген теңдеудің сол жағы тек
оң мәндер қабылдайтындықтан, ![]() бұрышы
бұрышы ![]() болатын аралықтарда
ғана мәндер қабылдайды, яғни
болатын аралықтарда
ғана мәндер қабылдайды, яғни ![]() және
және ![]() ;
; ![]() -ң мәндерін мәндерін
анықтау үшін (0,01 дәлдікпен) төмендегі кестені
құрастырамыз:
-ң мәндерін мәндерін
анықтау үшін (0,01 дәлдікпен) төмендегі кестені
құрастырамыз:
Кесте
|
Нүктелердің реті |
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
|
2 |
|
|
0,50 |
2,12 |
|
3 |
|
|
0,87 |
2,79 |
|
4 |
|
|
1 |
3 |
|
5 |
|
|
0,87 |
2,79 |
|
6 |
|
|
0,50 |
2,12 |
|
7 |
|
|
0 |
0 |
![]() бұрышы
үшінші ширекте мәндер қабылдағанда
бұрышы
үшінші ширекте мәндер қабылдағанда ![]() бірінші ширекте
қабылданған мәндерін қабылдайтындықтан, іздеп
отырған сызығымыз координаттың бас нүктесіне қарағанда
симметриялы болады. Оны құру үшін полюстан
бірінші ширекте
қабылданған мәндерін қабылдайтындықтан, іздеп
отырған сызығымыз координаттың бас нүктесіне қарағанда
симметриялы болады. Оны құру үшін полюстан ![]() -ң мәндеріне
сай сәулелер салып, әр сәуленің бойына полярлық
радиустардың мәндерін саламыз. Алынған нүктелерді
бірсарынды қосамыз (22 сурет). Алынған сызық
Бернуллидің лимнискатасы деп аталады.
-ң мәндеріне
сай сәулелер салып, әр сәуленің бойына полярлық
радиустардың мәндерін саламыз. Алынған нүктелерді
бірсарынды қосамыз (22 сурет). Алынған сызық
Бернуллидің лимнискатасы деп аталады.
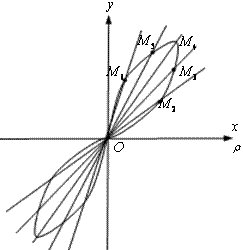
22 Сурет
Оның декарттық координаталар
жүйесіндегі теңдеуін анықтау үшін ![]() түріне келтіріп
түріне келтіріп ![]() және
және ![]() -дің (2)
және (3) теңдеулердегі мәндерін қойсақ:
-дің (2)
және (3) теңдеулердегі мәндерін қойсақ:
![]()
48. ![]() түзудің
полярлық теңдеуін табу керек.
түзудің
полярлық теңдеуін табу керек.
49. ![]() шеңберінің
полярлық теңдеуін табу керек.
шеңберінің
полярлық теңдеуін табу керек.
50. ![]() полярлық
теңдеуі берілген. Осы сызықты
полярлық
теңдеуі берілген. Осы сызықты ![]() -ге
-ге ![]() адымымен мәндер беру арқылы
нүктелерін анықтап құру керек. Декарттық
өстерді
адымымен мәндер беру арқылы
нүктелерін анықтап құру керек. Декарттық
өстерді
19 Суретте көрсетілгендей орналастырып оның декарттық теңдеуін табу керек.
II-тарау. Кеңістіктегі аналитикалық геометрия
1. Жазықтық. Оның теңдеуі
1.1 Жазықтықтың жалпы кесінділік және қалыпты теңдеулері
Кеңістікте декарттық координаталар жүйесінде кез келген бет
![]() (1)
(1)
теңдеуімен беріледі. Егер ![]() функциясы
функциясы ![]() дәрежелі көпмүшелік
болса, онда оған сәйкес бет
дәрежелі көпмүшелік
болса, онда оған сәйкес бет ![]() дәрежелі алгебралық бет деп
аталады.
дәрежелі алгебралық бет деп
аталады.
Кез келген бірінші ретті бет жазықтық болады да,
![]() (2)
(2)
теңдеуімен анықталады. Бұл теңдеу
жазықтықтың жалпы теңдеуі деп аталады. Координаталары ![]() -ң коэффициенттері
болатын
-ң коэффициенттері
болатын ![]() векторы
(2) жазықтығына перпендикуляр (тіктеме) болады да
жазықтықтың нормаль векторы (тіктеме мегземе) деп аталады.
векторы
(2) жазықтығына перпендикуляр (тіктеме) болады да
жазықтықтың нормаль векторы (тіктеме мегземе) деп аталады. ![]() векторына перпендикуляр
болатын әрі
векторына перпендикуляр
болатын әрі ![]() нүктесі
арқылы өтетін жазықтықтың теңдеуі
нүктесі
арқылы өтетін жазықтықтың теңдеуі
![]() (3)
(3)
Егер (1) жазықтықтың
теңдеудегі D=0 болса, онда мұндай жазықтық
координаттың бас нүктесі арқылы өтеді. Егер А=0 болса,
онда жазықтық ![]() өсіне паралелль, В=0 болса
-
өсіне паралелль, В=0 болса
- ![]() өсіне
параллель, С=0 болса -
өсіне
параллель, С=0 болса - ![]() өсіне параллель болады. Егер
өсіне параллель болады. Егер ![]() болса, онда
жазықтық
болса, онда
жазықтық ![]() өсі
арқылы;
өсі
арқылы; ![]() болса,
онда
болса,
онда ![]() өсі
арқылы; егер
өсі
арқылы; егер ![]() болса,
онда онда
болса,
онда онда ![]() өсі
арқылы өтеді. Егер
өсі
арқылы өтеді. Егер ![]() болса, онда жазықтық
болса, онда жазықтық ![]() жазықтығына
параллель; егер
жазықтығына
параллель; егер ![]() болса,
онда жазықтық
болса,
онда жазықтық ![]() жазықтығына параллель; егер
жазықтығына параллель; егер ![]() болса, онда
жазықтық
болса, онда
жазықтық ![]() жазықтығына
параллель болады. Ал
жазықтығына
параллель болады. Ал ![]() ,
,![]() ,
,![]() координат
жазықтықтарының теңдеулері сәйкесінше
координат
жазықтықтарының теңдеулері сәйкесінше ![]() .
.
Егер (2)-теңдеудегі барлық ![]() коэффициенттері
нөлге тең болмаса, онда теңдеуді кесінділік деп аталатын
коэффициенттері
нөлге тең болмаса, онда теңдеуді кесінділік деп аталатын
![]() (4)
(4)
түрінде жазуға болады. Мұндағы ![]() -координаттың бас
нүктесінен жазықтықтың координат өстерімен
қиылысу нүктелеріне дейінгі аралық.
-координаттың бас
нүктесінен жазықтықтың координат өстерімен
қиылысу нүктелеріне дейінгі аралық.
Жазықтықтың теңдеуі қалыпты деп аталады, егер координаттың бас нүктесінен жазықтыққа бағытталған тіктеме вектордың ұзындығы бірге тең болса, қалыпты теңдеу
![]() (5)
(5)
формуласымен анықталады. Мұндағы ![]() координаттың бас
нүктесімен ізделінеді жазықтықтың арасындағы
қашықтық.
координаттың бас
нүктесімен ізделінеді жазықтықтың арасындағы
қашықтық.
Жазықтықтың жалпы теңдеуінен қалыпты түріне көшу үшін теңдеуді қалыптаушы деп аталатын
![]() (6)
(6)
көбейткішіне көбейтсе болғаны. Мұндағы
таңба жазықтықтың жалпы теңдеуіндегі бос
мүше ![]() -ның
таңбасына қарама-қарсы алынады.
-ның
таңбасына қарама-қарсы алынады.
1. Мысал - ![]() нүктесі әрі
нүктесі әрі ![]() өсі арқылы
өтетін жазықтықтың теңдеуін жазу керек.
өсі арқылы
өтетін жазықтықтың теңдеуін жазу керек.
Шешуі: Жазықтықтың жалпы теңдеуіндегі
![]() болғанда,
ол
болғанда,
ол ![]() өсі арқылы
өтетіндіктен
өсі арқылы
өтетіндіктен ![]() теңдеуін
қарастырамыз.
теңдеуін
қарастырамыз. ![]() нүктесі
есептің шарты бойынша жазықтықтың бойында
жататындықтан оның координаталары теңдеуді
қанағаттандырады.
нүктесі
есептің шарты бойынша жазықтықтың бойында
жататындықтан оның координаталары теңдеуді
қанағаттандырады.
![]() бұдан
бұдан ![]()
Мәнін жазықтықтың
теңдеуіне қойып ![]() -ға қысқартсақ,
іздеп отырған теңдеуіміз шығады.
-ға қысқартсақ,
іздеп отырған теңдеуіміз шығады.
![]()
2. Мысал - ![]() жазықтығына параллель әрі
жазықтығына параллель әрі
![]() нүктесі
арқылы өтетін жазықтықтың теңдеуін
құру керек.
нүктесі
арқылы өтетін жазықтықтың теңдеуін
құру керек.
Шешуі:![]() жазықтығына паралелль болатын
жазықтықтын теңдеуі
жазықтығына паралелль болатын
жазықтықтын теңдеуі
![]()
Оған М нүктесінің координаталарын қойсақ
![]() немесе
немесе ![]()
Олай болса, іздеп отырған теңдеуіміз
![]() немесе
немесе ![]()
3. Мысал - Жазықтық ![]() нүктесі арқылы өтіп абсцисса
өсінен
нүктесі арқылы өтіп абсцисса
өсінен ![]() аппликата
өснен
аппликата
өснен ![]() кесінділерін
қияды. Жазықтықтың теңдеуін құру
керек.
кесінділерін
қияды. Жазықтықтың теңдеуін құру
керек.
Шешуі: Жазықтықтың кесінділік (4)-теңдеуін
пайдаланамыз. Шарт бойынша ![]() болғандықтан
болғандықтан
![]()
P нүктесі жазықтықтың бойында жататындықтан оның координаталары жазықтықтың теңдеуін қанағаттандырады:
![]() .
.
Яғни іздеп отырған теңдеуіміз
![]() немесе
немесе ![]()
51. Жазықтықтың ![]() өсі және
өсі және ![]() нүктесі арқылы
өтетін теңдеуін құру керек.
нүктесі арқылы
өтетін теңдеуін құру керек.
52. Жазықтықтың ![]() нүктесі арқылы өтетін
нүктесі арқылы өтетін ![]() жазықтығына
параллель болатын, теңдеуін құру керек.
жазықтығына
параллель болатын, теңдеуін құру керек.
53. ![]() теңдеуі
берілген. Оның кесінділік теңдеуін жазу керек.
теңдеуі
берілген. Оның кесінділік теңдеуін жазу керек.
54. ![]() нүктесі
арқылы өтіп,
нүктесі
арқылы өтіп, ![]() және
және ![]() өстерінен сәйкесінше
өстерінен сәйкесінше ![]() кесінділерін
қиятын жазықтықтың теңдеуін құру
керек.
кесінділерін
қиятын жазықтықтың теңдеуін құру
керек.
55. ![]() нүктесінен
жазықтыққа тіктеме түсірілген, оның табаны
нүктесінен
жазықтыққа тіктеме түсірілген, оның табаны ![]() .
Жазықтықтың теңдеуін табу керек.
.
Жазықтықтың теңдеуін табу керек.
56. Төмендегі жазықтық теңдеулерінің қалыпты теңдеулер болар болмастығын анықтау керек:
а) ![]() б)
б) ![]()
57. ![]() теңдеуін
қалыпты түрге келтіріп, жазықтықпен координаттың
бас нүктесінің ара қашықтығын табу керек.
теңдеуін
қалыпты түрге келтіріп, жазықтықпен координаттың
бас нүктесінің ара қашықтығын табу керек.
1.2 Жазықтықтардың өзара орналасуы
![]() және
және ![]() жазықтықтары берілсін.
Бұл жазықтықтардың арасындағы бұрыш
олардың тіктеме
жазықтықтары берілсін.
Бұл жазықтықтардың арасындағы бұрыш
олардың тіктеме ![]() және
және
![]() векторларының
арасындағы бұрышқа тең болады. Сондықтан
олардың арасындағы бұрыш
векторларының
арасындағы бұрышқа тең болады. Сондықтан
олардың арасындағы бұрыш
 (7)
(7)
формуласымен анықталады.
Жазықтықтар параллель болады, егер ![]() және
және ![]() векторлары коллинеарлы болса,
яғни
векторлары коллинеарлы болса,
яғни
![]() (8)
(8)
Жазықтықтрдың перпендикулярлық шарты
![]() , яғни
, яғни ![]() (9)
(9)
Егер үш жазықтық өздерінің теңдеулерімен берілсе
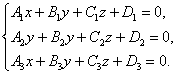 (10)
(10)
онда олардың ортақ нүктелері (10)-теңдеулер
жүйесімен анықталады. Олардың тіктеме векторлары ![]() компланарлы болмаса,
онда жазықтықтар бір нүктеде қиылысады.
Шындығында
компланарлы болмаса,
онда жазықтықтар бір нүктеде қиылысады.
Шындығында
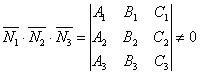
болғандықтан әрі бұл анықтауыш (10)-жүйенің анықтауышы екендігін ескерсек, онда жүйенің жалғыз түбірі болады.
4. Мысал - ![]() және
және ![]() жазықтықтарының
арасындағы бұрышты табу керек.
жазықтықтарының
арасындағы бұрышты табу керек.
Шешуі:
Берілген жазықтықтарға перпендикуляр болатын ![]() және
және ![]() векторларының
координаталарын жазамыз:
векторларының
координаталарын жазамыз: ![]() (7)-формула бойынша
(7)-формула бойынша
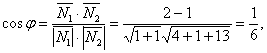
яғни ![]()
5. Мысал - ![]() және
және ![]() жазықтықтырының
жалғыз ортақ нүктесі болатындығын анықтап оны
табу керек.
жазықтықтырының
жалғыз ортақ нүктесі болатындығын анықтап оны
табу керек.
Шешуі: Жазықтықтардың нормаль (тіктеме)
векторларын жазамыз: ![]()
Олардың аралас көбейтінділерін анықтаймыз:
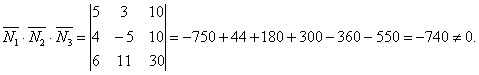
![]() болғандықтан,
берілген жазықтықтар тек бір нүктеде қиылысады. Оны
табу үшін төмендегі жүйені шешеміз:
болғандықтан,
берілген жазықтықтар тек бір нүктеде қиылысады. Оны
табу үшін төмендегі жүйені шешеміз:
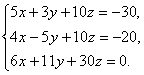
Крамер ережесін қолдансақ
![]() сондықтан
сондықтан
![]() о
о
Яғни, берілген үш жазықтықтың ортақ
нүктесі ![]() болады.
болады.
Төмендегі жазықтықтардың арасындағы бұрышты есептеу керек:
58. ![]() және
және ![]()
59. ![]() және
және ![]()
60. ![]() және
және ![]() жазықтықтарының
жалғыз ортақ нүктесі болатындығын анықтап, оны
табу керек.
жазықтықтарының
жалғыз ортақ нүктесі болатындығын анықтап, оны
табу керек.
1.3 Нүктемен жазықтықтың арасындағы қашықтық
![]() нүктесімен (2)-теңдеу
арқылы берілген жазықтықтың арасындағы
қашықтық келесі формуламен анықталады
нүктесімен (2)-теңдеу
арқылы берілген жазықтықтың арасындағы
қашықтық келесі формуламен анықталады
![]() (11)
(11)
6. Мысал - Параллель ![]()
жазықтықтарының ара қашықтығын табу керек.
Шешуі: Екі жазықтықтың біреуінде жататын
кез келген бір нүкте алып, (11)-формула арқылы екінші
жазықтыққа дейінгі қашықтықты
анықтаймыз. Бірінші теңдеуде ![]() ,
, ![]() алсақ.
алсақ. ![]() болады, яғни
болады, яғни ![]() нүктесі бірінші
жазықтықтың бойында жатады. Осыдан
нүктесі бірінші
жазықтықтың бойында жатады. Осыдан
![]() .
.
7. Мысал - ![]() жазықтығына параллель болатын,
одан
жазықтығына параллель болатын,
одан ![]()
![]() қашықтықта
орналасқан жазықтықтардың теңдеулерін
құру керек.
қашықтықта
орналасқан жазықтықтардың теңдеулерін
құру керек.
Шешуі:![]()
![]() ізделінді жазықтықтың кез
келген нүктесі болсын. Шарт бойынша оның
қашықтығы берілген жазықтықтан
ізделінді жазықтықтың кез
келген нүктесі болсын. Шарт бойынша оның
қашықтығы берілген жазықтықтан ![]() болғандықтан,
болғандықтан,
(11)-формула бойынша ![]() Бұдан
Бұдан ![]() немесе
немесе ![]()
Бұл екі жазықтық ізделінді жазықтықтар.
61. ![]() нүктесімен
нүктесімен
![]() жазықтығының
арасындағы қашықтықты табу керек.
жазықтығының
арасындағы қашықтықты табу керек.
62. ![]() жазықтығына
параллель болатын, одан
жазықтығына
параллель болатын, одан ![]() қашықтықта орналасқан
жазықтықтардың теңдеуін табу керек.
қашықтықта орналасқан
жазықтықтардың теңдеуін табу керек.
63. ![]() өсінің
(оқтығының) бойында жататын
өсінің
(оқтығының) бойында жататын ![]() жазықтығынан
жазықтығынан ![]() қашықтықта
орналасқан нүктелерді табу керек.
қашықтықта
орналасқан нүктелерді табу керек.
2. Түзу сызықтар
2.1 Түзудің теңдеулері
Кеңістіктегі сызықты екі беттің қиылысуы арқылы анықтауға болады:
![]()
 (1)
(1)
![]() сызығының
параметрілі теңдеуін
сызығының
параметрілі теңдеуін
![]()
![]() (2)
(2)
алу үшін оның ағымдағы ![]() нүктесінің
функциялары болып өрнектелуі керек.
нүктесінің
функциялары болып өрнектелуі керек. ![]() параметрін таңдау арқылы
(2)-теңдеулерді сызықты теңдеулер
параметрін таңдау арқылы
(2)-теңдеулерді сызықты теңдеулер
![]() (3)
(3)
түрінде жазуға болатын болса, онда ![]() сызығы түзуге
айналады да түзудің параметрлік теңдеуі деп аталады.
Мұндағы:
сызығы түзуге
айналады да түзудің параметрлік теңдеуі деп аталады.
Мұндағы: ![]() -осы
түзудің бойындағы бір
-осы
түзудің бойындағы бір ![]() нүктесінің координаталары;
нүктесінің координаталары; ![]() -осы түзуге
параллель болатын бір
-осы түзуге
параллель болатын бір ![]() векторының
координаталары.
векторының
координаталары. ![]()
![]() векторы
түзудің бағыттаушы векторы деп аталады.
векторы
түзудің бағыттаушы векторы деп аталады.
(3)-теңдеулердегі ![]() параметрінен құтылсақ,
түзудің канондық (қарапайым) түріне келеміз:
параметрінен құтылсақ,
түзудің канондық (қарапайым) түріне келеміз:
![]() (4)
(4)
Кеңістіктегі түзудің жалпы теңдеуі екі жазықтықтың қиылысуы арқылы
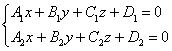 (5)
(5)
теңдеуімен беріледі. Бұл теңдеуден канондық
теңдеуге көшу үшін осы түзудің бойында жататын
кез келган ![]() нүктесін
анықтап, оның бағыттаушы
нүктесін
анықтап, оның бағыттаушы ![]() векторын табу қажет.
векторын табу қажет.
![]() және
және ![]() нүктелері арқылы өтетін
түзудің канондық теңдеуі
нүктелері арқылы өтетін
түзудің канондық теңдеуі
![]() (6)
(6)
формуласымен анықталады. Мұнда бағыттаушы ![]() векторы деп
векторы деп ![]() векторы алынған.
векторы алынған.
1. Мысал - Координат өстерімен ![]() бұрыштарын
құрайтын және
бұрыштарын
құрайтын және ![]() нүктесінен өтетін түзудің
канондық және параметрлік теңдеулерін жазу керек.
нүктесінен өтетін түзудің
канондық және параметрлік теңдеулерін жазу керек.
Шешуі: Бағыттаушы ![]() векторы деп түзудің
бірлік векторын алуға болады. Оның координаталары бағыттаушы
косинустар болып табылады
векторы деп түзудің
бірлік векторын алуға болады. Оның координаталары бағыттаушы
косинустар болып табылады
![]()
(4)-формула бойынша түзудің канондық теңдеуін табамыз
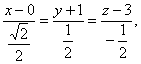 немесе, бөлімдерін 2-ге
көбейтіп
немесе, бөлімдерін 2-ге
көбейтіп ![]() теңдеулерін
аламыз.
теңдеулерін
аламыз.
Соңғы қатынастардың
әрқайсысын ![]() -ға
теңестіру арқылы түзудің параметрлік теңдеулерін
аламыз:
-ға
теңестіру арқылы түзудің параметрлік теңдеулерін
аламыз:
![]()
2. Мысал - ![]() нүктесі арқылы өтетін
әрі
нүктесі арқылы өтетін
әрі ![]() өсіне
параллель болатын түзудің канондық және параметрлік
теңдеулерін жазу керек.
өсіне
параллель болатын түзудің канондық және параметрлік
теңдеулерін жазу керек.
Шешуі: ![]() векторы
векторы ![]() өсінің бойында
жататындықтан, есептің шарты бойынша ол ізделінді түзуге
параллель (қатарлас) болады. Яғни ол ізделінді түзудің
бағыттаушы векторы болады. Сондықтан (4)-формула бойынша
өсінің бойында
жататындықтан, есептің шарты бойынша ол ізделінді түзуге
параллель (қатарлас) болады. Яғни ол ізделінді түзудің
бағыттаушы векторы болады. Сондықтан (4)-формула бойынша
![]()
Түзудің параметрлік теңдеуін алу
үшін бірінші және екінші қатынастардағы бөлімдегі
нөлдер ![]() болатындығын
көрсетеді. Үшінші қатынасты
болатындығын
көрсетеді. Үшінші қатынасты ![]() параметріне теңестірсек
параметріне теңестірсек ![]()
Яғни ізделінді түзудің параметрлік теңдеуі
![]()
3. Мысал
![]()
түзуін канондық түрге келтіру керек.
Шешуі: Түзудің бойында жататын кез келген бір
нүктенің координаталарын анықтаймыз. Ол үшін екі
теңдеудегі ![]() деп
аламыз:
деп
аламыз:
![]()
Бұдан ![]() Сонымен
Сонымен
![]() нүктесі
түзудің бойында жатады. Оның бағыттаушы векторы
нүктесі
түзудің бойында жатады. Оның бағыттаушы векторы ![]() -ті анықтау
үшін берілген екі жазықтықтың нормаль (тіктеме)
-ті анықтау
үшін берілген екі жазықтықтың нормаль (тіктеме) ![]() векторларын алып,
векторлық көбейтіндісін анықтау қажет.
векторларын алып,
векторлық көбейтіндісін анықтау қажет.

(4)-формула бойынша түзудің канондық теңдеуі
![]() .
.
64. ![]() нүктесі
арқылы өтетін әрі
нүктесі
арқылы өтетін әрі ![]() векторына параллель болатын
түзудің канондық және параметрлік теңдеулерін
жазу керек.
векторына параллель болатын
түзудің канондық және параметрлік теңдеулерін
жазу керек.
65. ![]() және
және
![]() нүктелері
арқылы өтетін түзудің канондық және
параметрлік теңдеулерін жазу керек.
нүктелері
арқылы өтетін түзудің канондық және
параметрлік теңдеулерін жазу керек.
66. ![]() нүктесі
арқылы өтетін әрі
нүктесі
арқылы өтетін әрі ![]() өсіне параллель болатын
түзудің канондық және параметрлік теңдеулерін
жазу керек.
өсіне параллель болатын
түзудің канондық және параметрлік теңдеулерін
жазу керек.
67. Координат өстерімен ![]() бұрыштарын құрайтын
және
бұрыштарын құрайтын
және ![]() нүктесінен
өтетін түзудің канондық және параметрлік
теңдеулерін жазу керек.
нүктесінен
өтетін түзудің канондық және параметрлік
теңдеулерін жазу керек.
Келесі түзулердің теңдеулерін канондық түрге келтіру керек:
68. ![]() 69.
69.
![]()
70. ![]() нүктесі
арқылы өтетін әрі
нүктесі
арқылы өтетін әрі ![]() жазықтығына перпендикуляр
болатын түзудің канондық теңдеуін табу керек.
жазықтығына перпендикуляр
болатын түзудің канондық теңдеуін табу керек.
2.2 Екі түзудің орналасуы
Екі түзу өздерінің канондық теңдеулері арқылы берілсін:
![]() (7)
(7)
Бұл түзулер өздерінің ![]()
![]() ,
, ![]() нүктелері және
нүктелері және ![]()
![]() ,
, ![]()
![]() бағыттаушы векторлары арқылы
берілген. Бұл түзулердің арасындағы
бағыттаушы векторлары арқылы
берілген. Бұл түзулердің арасындағы ![]() бұрышы ретінде олардың
бағыттаушы векторларының арасындағы бұрыш алынады да
бұрышы ретінде олардың
бағыттаушы векторларының арасындағы бұрыш алынады да
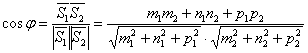 (8)
(8)
формуласымен анықталады.
(7)-түзулердің перпендикулярлық белгісі
![]() немесе
немесе ![]() (9)
(9)
Түзулердің параллельдік белгісі
![]() (10)
(10)
Екі түзудің орналасуының жағдайлары.
1). Түзулер беттесіп жатыр:
![]() яғни
яғни ![]()
2). Түзулер параллель (қатарлас):
![]()
![]() ╫
╫![]() , бірақ
, бірақ ![]() , яғни
, яғни ![]() .
.
3). Түзулер қиылысады:
![]() ╫
╫![]() , бірақ
, бірақ ![]() ,
, ![]() ,
,![]() компланарлы, яғни
компланарлы, яғни
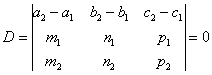
4) Түзулер айқасады:
![]() ,
, ![]() ,
,![]() компланарлы емес, яғни
компланарлы емес, яғни ![]()
4. Мысал
![]() және
және ![]()
түзулерінің арасындағы бұрышты анықтау керек.
Шешуі: Бұл түзулердің бағыттаушы векторларын анықтап аламыз:
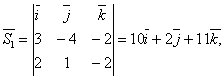
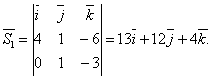
Яғни, түзулердің арасындағы бұрыштың косинусы
 бұдан
бұдан ![]()
5. Мысал - ![]() жазықтығында жататын
координаттың бас нүктесінен өтетін және
жазықтығында жататын
координаттың бас нүктесінен өтетін және
![]()
![]()
түзуіне перпендикуляр болатын түзудің канондық теңдеуін құру керек.
Шешуі: ![]() векторы ізделінді түзудің
бағыттаушы векторы болсын. Түзу
векторы ізделінді түзудің
бағыттаушы векторы болсын. Түзу ![]() жазықтығында
жататындықтан,
жазықтығында
жататындықтан, ![]() векторының
векторының
![]() өсіне
проекциясы
өсіне
проекциясы
нөлге тең болады, яғни ![]() Берілген түзудің
бағыттаушы векторы
Берілген түзудің
бағыттаушы векторы ![]() ізделінді түзудің
бағыттаушы векторы
ізделінді түзудің
бағыттаушы векторы ![]() -ке перпендикуляр болғандықтан
-ке перпендикуляр болғандықтан ![]()
Бағыттаушы вектор ![]() көбейткіш тік дәлдікпен
берілетіндіктен, оның бір
көбейткіш тік дәлдікпен
берілетіндіктен, оның бір
координатын еркін алуға болады. Мысалы, ![]() деп алсақ,
деп алсақ, ![]() Сондықтан
Сондықтан
![]() .
Ізделінді түзу
.
Ізделінді түзу ![]() нүктесі
арқылы өтетіндіктен оның канондық теңдеуі
нүктесі
арқылы өтетіндіктен оның канондық теңдеуі
![]() .
.
![]() 6. Мысал -
6. Мысал - ![]() және
және ![]() түзулерінің қиылысатындығын
дәлелдеп, қиылысу нүктесін табу керек.
түзулерінің қиылысатындығын
дәлелдеп, қиылысу нүктесін табу керек.
Шешуі: ![]() нүктесі бірінші, ал
нүктесі бірінші, ал ![]() нүктесі екінші түзудің
бойында жатыр.
нүктесі екінші түзудің
бойында жатыр. ![]() векторларының
аралас
векторларының
аралас
көбейтіндісін табамыз:
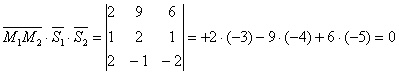
яғни, бұл векторлар компланарлы әрі берілген
түзулер бір жазықтың бойында жатыр. ![]() және
және ![]() векторларының
координаталары пропорционал емес, сондықтан қиылысады. Берілген
түзулердің қиылысу нүктесін табу үшін
олардың біреуін параметрлік түрге келтіріп, оны екінші
теңдеуге қойып қиылысу нүктесіне сай келетін
векторларының
координаталары пропорционал емес, сондықтан қиылысады. Берілген
түзулердің қиылысу нүктесін табу үшін
олардың біреуін параметрлік түрге келтіріп, оны екінші
теңдеуге қойып қиылысу нүктесіне сай келетін ![]() параметрінің
мәнін анықтау қажет.
параметрінің
мәнін анықтау қажет.
Екінші теңдеудің параметрлік теңдеуі
![]()
Бұл өрнектерді бірінші теңдеудегі ![]() -ң орындарына қойсақ
-ң орындарына қойсақ
![]() бұдан
бұдан
![]() болатындығын
көреміз.
болатындығын
көреміз.
Сонымен ![]()
71. ![]() және
және
![]() түзулерінің
арасындағы бұрышты табу керек.
түзулерінің
арасындағы бұрышты табу керек.
Төмендегі түзулердің перпендикуляр болатындығын дәлелдеу керек:
72. ![]() және
және
![]()
73. 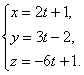 және
және
![]()
74. ![]() және
және
![]()
түзулерінің параллель болатындығын дәлелдеу керек.
75. ![]() және
және
![]()
түзулерінің айқас болатындығын дәлелдеу керек.
76. ![]() және
және
![]()
түзулерінің қиылысатындығын дәлелдеп, оның қиылысу нүктесін табу керек.
3.Түзумен жазықтықтың орналасуы
![]() (1)
(1)
жазықтығымен
![]() (2)
(2)
түзуі берілсін.
Түзумен жазықтықтың арасындағы
бұрыш ![]() деп,
түзумен осы түзудің жазықтықтағы
проекциясының (көлеңінің) арасындағы сүйір
бұрышты айтады. Ол
деп,
түзумен осы түзудің жазықтықтағы
проекциясының (көлеңінің) арасындағы сүйір
бұрышты айтады. Ол
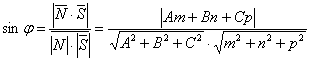 (3)
(3)
формуласымен анықталады.
Түзумен жазықтықтың паралельдігі:
![]() яғни
яғни ![]() (4)
(4)
Түзумен жазықтықтың перпендикулярлығы:
![]() яғни
яғни ![]() (5)
(5)
Түзумен жазықтықтың
қиылысу нүктесі ![]() төмендегідей анықталады:
түзудің теңдеуі параметрлік түрге келтіріледі
төмендегідей анықталады:
түзудің теңдеуі параметрлік түрге келтіріледі
![]() ,
,
одан кейін (1) теңдеуге қою арқылы ![]() қиылысу
нүктесіне сай келетін
қиылысу
нүктесіне сай келетін ![]() параметрінің (демеуіштің)
мәні анықталады.
параметрінің (демеуіштің)
мәні анықталады.
1. Мысал - ![]() жазықтығымен
жазықтығымен ![]() түзуінің
қиылысу нүктесін табу керек.
түзуінің
қиылысу нүктесін табу керек.
Шешуі: Түзудің теңдеуін параметрлік
түрге
келтіреміз:
![]()
![]() -ң мәндерін
жазықтықтың теңдеуіне қоямыз
-ң мәндерін
жазықтықтың теңдеуіне қоямыз
![]() бұдан
бұдан ![]()
Сонымен жазықтықпен нүктенің қиылысу нүктесінің координаталары
![]()
2. Мысал - ![]() және
және ![]() нүктесі арқылы өтетін
түзумен
нүктесі арқылы өтетін
түзумен ![]() жазықтығының
арасындағы бұрышты табу керек.
жазықтығының
арасындағы бұрышты табу керек.
Шешуі: Түзудің бағыттаушы векторы деп ![]() векторын алуға
болады. Жазықтықтың тіктеме векторы
векторын алуға
болады. Жазықтықтың тіктеме векторы ![]() болғандықтан
(3)-формула бойынша
болғандықтан
(3)-формула бойынша

77. ![]() жазықтығымен
жазықтығымен
![]() түзуінің
арасындағы бұрышты табу керек.
түзуінің
арасындағы бұрышты табу керек.
78. ![]() жазықтығымен
жазықтығымен
![]() түзуінің
арасындағы бұрышты табу керек.
түзуінің
арасындағы бұрышты табу керек.
79. ![]() жазықтығымен
жазықтығымен
![]() түзуінің
қиылысу нүктесін табу керек.
түзуінің
қиылысу нүктесін табу керек.
4. Беттер
4.1 Цилиндрлік беттер
Берілген ![]() түзуіне параллель
қозғалатын және берілген
түзуіне параллель
қозғалатын және берілген ![]() сызығымен қиылысатын
түзулер бет құрайды да цилиндрлік бет деп аталады.
сызығымен қиылысатын
түзулер бет құрайды да цилиндрлік бет деп аталады. ![]() сызығы
беттің бағыттаушысы, ал қозғалатын түзудің
әрбір орны жасаушы деп аталады.
сызығы
беттің бағыттаушысы, ал қозғалатын түзудің
әрбір орны жасаушы деп аталады.
 |
23 Сурет
Координат жүйесінің өстерінің біреуін әр
уақытта ![]() түзуіне
параллель етіп алуға болады: жасаушысы
түзуіне
параллель етіп алуға болады: жасаушысы ![]() өсіне параллель болатын цилиндрлік
беттің (23 Сурет) теңдеуі
өсіне параллель болатын цилиндрлік
беттің (23 Сурет) теңдеуі
![]() ,
(1)
,
(1)
жасаушысы ![]() өсіне
параллель болатын цилиндрлік беттің теңдеуі
өсіне
параллель болатын цилиндрлік беттің теңдеуі
![]() ,
(2)
,
(2)
жасаушысы ![]() өсіне
параллель болатын цилиндрлік беттің теңдеуі
өсіне
параллель болатын цилиндрлік беттің теңдеуі
![]() .
(3)
.
(3)
(1)- беттің ![]() бағыттаушысы етіп оның
бағыттаушысы етіп оның ![]() жазықтығымен
қиылысуынан пайда болатын сызықты алуға болады:
жазықтығымен
қиылысуынан пайда болатын сызықты алуға болады:
![]()
(2) және (3) цилиндрлік беттердің бағыттаушылары сәйкесінше
![]() және
және ![]()
1. Мысал - ![]() теңдеуі қандай бетті
анықтайды?
теңдеуі қандай бетті
анықтайды?
Шешуі: Берілген теңдеудің құрамында ![]() айнымалысы
болмағандықтан, бет жасаушылары
айнымалысы
болмағандықтан, бет жасаушылары ![]() өсіне параллель цилиндр болады.
Бұл цилиндрдің бағыттаушысы
өсіне параллель цилиндр болады.
Бұл цилиндрдің бағыттаушысы

центрі (кіндігі) ![]() өсінің бойында жататын
өсінің бойында жататын ![]() нүкте, радиусы
нүкте, радиусы ![]() шеңбер болады.
шеңбер болады.
Сонымен берілген теңдеу өсі ![]() нүктесі
арқылы өтетін, жасаушылары
нүктесі
арқылы өтетін, жасаушылары ![]() өсіне параллель болатын,
дөңгелек цилиндр болады.
өсіне параллель болатын,
дөңгелек цилиндр болады.
2. Мысал - ![]() теңдеуі қандай бетті
анықтайды?
теңдеуі қандай бетті
анықтайды?
Шешуі: Берілген теңдеудің құрамында ![]() айнымалысы болмағандықтан,
бет жасаушылары
айнымалысы болмағандықтан,
бет жасаушылары ![]() өсіне
(оқтығына) параллель цилиндр болады. Бұл цилиндрдің
бағыттаушысы
өсіне
(оқтығына) параллель цилиндр болады. Бұл цилиндрдің
бағыттаушысы

![]() жазықтыында
жататын, төбесі
жазықтыында
жататын, төбесі ![]() нүктесі
болатын, әрі
нүктесі
болатын, әрі ![]() оқтығының
оң бағытына сай бағытталған парабола болады.
оқтығының
оң бағытына сай бағытталған парабола болады.
Сонымен, жоғарыда берілген теңдеу параболалық цилиндр болады.
Төмендегі теңдеулер қандай беттерді анықтайды (сызбасын салу керек):
80. ![]() 81.
81.
![]()
82. ![]() 83.
83.
![]()
84. ![]()
4.2 Екінші ретті беттердің канондық теңдеулері
![]() Екінші ретті беттер, декарттық координаталар арқылы, екінші
дәрежелі
Екінші ретті беттер, декарттық координаталар арқылы, екінші
дәрежелі
![]() (4)
(4)
теңдеуімен беріледі. Бұл теңдеуді, арнайы координаттар жүйесін тандап алу арқылы, қарапайым түрге айналдыруға болады:
сфера ![]()
эллипсоид (24 сурет) ![]()
екіқуысты гиперболоид (25 сурет) ![]()
бірқуысты гиперболоид (26 сурет) ![]()
конус (27 сурет) ![]()
эллипстік параболоид (28 сурет) ![]()
гиперболалық параболоид (29 сурет) ![]()
(4)-теңдеудің сол жағы екі сызықтық көбейткішке жіктелгенде, екі жазықтық береді.
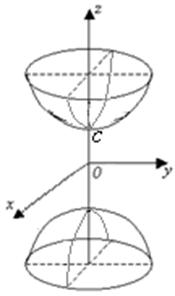
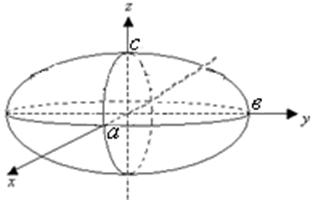
24 Сурет
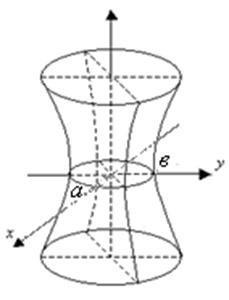 25
Сурет
25
Сурет

26 Сурет 27 Сурет


28 Сурет 29 Сурет
3. Мысал - Сфера ![]() нүктесі арқылы өтеді, ал
оның центрі (кіндігі) координаттың бас нүктесі.
Сфераның теңдеуін құру керек.
нүктесі арқылы өтеді, ал
оның центрі (кіндігі) координаттың бас нүктесі.
Сфераның теңдеуін құру керек.
Шешуі: Сфераның радиусы ![]() векторының ұзындығына
тең болғандықтан
векторының ұзындығына
тең болғандықтан
![]() .
.
Сондықтан ![]() сфераның теңдеуі болады.
сфераның теңдеуі болады.
4. Мысал - ![]() теңдеуімен қандай бет анықталады?
теңдеуімен қандай бет анықталады?
Шешуі: Берілген теңдеуден толық квадраттарын бөліп аламыз:

Бұл центрі ![]() нүктесі болатын эллипсоид.
нүктесі болатын эллипсоид.
4.3 Праллель қию тәсілі
Бет өзінің жалпы теңдеуімен берілгенде оның пішімін әрі координаттық өстерге қарағанда орналасуын зерттеу қажет болады. Бұл жағдайда параллель қию тәсілі қолданылады. Ол үшін бет координат жазықтықтарына параллель жазықтықтармен қиылыстырылады. Қималардың пішімі және өлшемдеріне қарап, беттің пішімін анықтауға болады.
85. Сфера ![]() нүктесі
арқылы өтеді, ал оның центрі
нүктесі
арқылы өтеді, ал оның центрі ![]() нүктесі. Сфераның
теңдеуін құру керек.
нүктесі. Сфераның
теңдеуін құру керек.
86. Центрі ![]() нүктесі
болатын сфера
нүктесі
болатын сфера ![]() жазықтығымен
жанасады. Сфераның теңдеуін құру керек.
жазықтығымен
жанасады. Сфераның теңдеуін құру керек.
Қима тәсілін қолданып, төмендегі беттердің пішімін зерттеңіз. (Сызбасын салу керек):
87. ![]() 88.
88.
![]()
Төмендегі теңдеулермен қандай беттер анықталады:
89. ![]()
90. ![]()
Жауаптары
1. ![]() 2.
2.![]() 3.
3. ![]() 4.
4. ![]() 5.
5. ![]() 6. а)
6. а)![]() оқтығы; б)
оқтығы; б) ![]() оқтығына
параллель түзу; в) координаттық бұрыштардың
биссектрисалары. г) кіндігі координат жүйесінің бас нүктесі
болатын радиусы
оқтығына
параллель түзу; в) координаттық бұрыштардың
биссектрисалары. г) кіндігі координат жүйесінің бас нүктесі
болатын радиусы ![]() -ге
тең шеңбер, д) I және III-ширекте орналасқан гипербола;
е)
-ге
тең шеңбер, д) I және III-ширекте орналасқан гипербола;
е) ![]() нүктесі,
ж) бос жиын. 7.
нүктесі,
ж) бос жиын. 7. ![]() оқтығына параллель түзу;
б)
оқтығына параллель түзу;
б) ![]() оқтығы;
в) координат өстері; г) парабола; д) I-ші және II-ширекте жататын
сызық; е) кіндігі координат жүйесінің бас нүктесі,
радиусы
оқтығы;
в) координат өстері; г) парабола; д) I-ші және II-ширекте жататын
сызық; е) кіндігі координат жүйесінің бас нүктесі,
радиусы ![]() болатын
шеңбер; ж)
болатын
шеңбер; ж) ![]() оқтығы
және кіндігі
оқтығы
және кіндігі ![]() радиусы
радиусы
![]() болатын
шеңбер; з)
болатын
шеңбер; з) ![]() нүктесі,
и) бос жиын. 8.
нүктесі,
и) бос жиын. 8. ![]() 9.
9. ![]()
10. ![]() 11.
11.![]() 12.
12. ![]()
![]() .
.
13. ![]()
![]() .
.
14. ![]() 15.
15.
![]()
16. ![]() 17.
17. ![]() 18.
18.
![]() және
және ![]()
19. ![]() 20.
20.
![]() 21.
21.
![]() .
.
22. ![]()
![]() 23.
23. ![]()
24. ![]() 25.
25.
![]()
![]() .
.
26. ![]() 27.
27.
![]()
28. ![]()
![]()
![]() .
.
29. ![]() 30.
30.
![]() ,
, ![]() ,
, ![]() .
.
31. ![]() 32.
32. ![]() . 33. а)
. 33. а)
![]() б)
б) ![]()
34.
Гипербола ![]()
35.
Эллипс ![]() .
36. Гипербола
.
36. Гипербола ![]() .
.
37. Парабола ![]()
![]() (ескі координат жүйесінде). 38. Эллипс
(ескі координат жүйесінде). 38. Эллипс ![]()
![]() 39.
39. ![]() Эллипс
Эллипс ![]()
40.
Парабола ![]()
![]()
![]()
41.
Гипербола ![]()
42. ![]() және
және
![]() түзулері
түзулері
43.
Параллель ![]() және
және
![]() түзулері.
түзулері.
44. ![]() және
және ![]() түзулері.
түзулері.
45. ![]() нүктесі. 46.
нүктесі. 46.
![]()
47. ![]() . 48.
. 48. 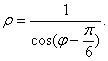 49.
49.
![]()
50. ![]() 51.
51.
![]() 52.
52.
![]()
53. ![]() 54.
54.
![]() 55.
55.
![]()
56.
а) болады, б) болмайды 57. ![]()
58.
жазықтықтар параллель 59. ![]() 60.
60.![]()
61.
3. 62.![]()
63. ![]() және
және ![]() 64.
64.![]()
65.![]() 66.
66.![]() 67.
67.![]() 68.
68. ![]() .
.
69. ![]() 70.
70. ![]() 71.
71. ![]()
76. ![]() 77.
77.
![]() .
78.
.
78. ![]()
79. ![]()
![]() 80.
80. ![]() өсі
өсі ![]() болатын дөңгелек
цилиндр. 81. Жасаушылары
болатын дөңгелек
цилиндр. 81. Жасаушылары ![]() өсіне параллель болатын
гиперболалық цилиндр. 82. Жасаушылары
өсіне параллель болатын
гиперболалық цилиндр. 82. Жасаушылары ![]() өсіне параллель
болатын қатары
өсіне параллель
болатын қатары ![]() өсіне
қарсы бағытталған параболалық цилиндр. 83.
Жасаушылары
өсіне
қарсы бағытталған параболалық цилиндр. 83.
Жасаушылары ![]() өсіне
параллель болатын гиперболалық цилиндр. 84. Жасаушылары
өсіне
параллель болатын гиперболалық цилиндр. 84. Жасаушылары ![]() өсіне параллель
болатын, бағыттаушы
өсіне параллель
болатын, бағыттаушы ![]() теңдеуімен анықталған
эллипстік цилиндр. 85.
теңдеуімен анықталған
эллипстік цилиндр. 85. ![]() 86.
86. ![]() 87.
87. ![]() және
және ![]() болғанда қима нақты
өсі
болғанда қима нақты
өсі ![]() болатын
гипербола,
болатын
гипербола, ![]() болғанда
қима эллипс. 88.
болғанда
қима эллипс. 88. ![]() және
және ![]() болғанда,тармақтары
болғанда,тармақтары ![]() өсімен
бағыттас парабола,
өсімен
бағыттас парабола, ![]() болғанда эллипстер,
болғанда эллипстер, ![]() болғанда
нүкте. 90. Төбесі
болғанда
нүкте. 90. Төбесі ![]() нүктесі болатын параболоид.
нүктесі болатын параболоид.
Әдебиеттер тізімі
1. Мустахишев К.М., Ералиев С.Е., Атабай Б.Ж., Математика толық курс. -Алматы.: «TST-company», 2009.
2. Аяпбергенов С.А. Аналитикалық геометрия. -Алматы: Мектеп, 1971.
3. Касымов Қ.Ә., Касымов Е.Ә. Жоғары математика курсы Сызықты алгебра. -Алматы: «Санат», 1997.
4. Г.И. Кручкович, и др., Сборник задач по курсу высшей математики. –М.: Высшая школа, 1973.
5. Клетеник Д.В. Сборник задач по аналитической геометрии. - М.: Наука, 1967.
6. Минорский В.П. Сборник задач по высшей математике. -М.: Наука, 1987.
7. Пискунов Н.С. Дифференциальное и интегральное исчисления. –М.: Наука, 1978.
8. Задачи и упражнения по математическому анализу для ВТУЗов (под.ред. Б.П. Демидовича). -М.: Наука, 1977.
9. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. -М.: Высшая школа, 1980.
10. Берман. Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1977.
Мазмұны
Ι – тарау. Жазықтықтағы аналитикалық геометрия....................................3
1.Жазықтықтағы декартттық координаталар...............................................3
1.1 Нүктенің координаталары (мекендігі). Қарапайым есептер................3
1.2 Кесіндіні берілген қатынасқа бөлу .........................................................4
1.3 Сызықтың теңдеуі.....................................................................................5
2. Түзу сызық...................................................................................................7
2.1 Түзу сызықтың жалпы теңдеуі. Бұрыштық коэффициенттері арқылы берілген теңдеуі........7
2.2 Екі нүктесі арқылы берілген түзулер......................................................9
2.3 Түзудің қалыпты теңдеуі. Нүктеден түзуге дейінгі қашықтық..........10
2.4 Екі түзудің қиылысуы ............................................................................12
3. Екінші ретті сызықтар...............................................................................13
3.1Шеңбер......................................................................................................14
3.2 Эллипс......................................................................................................14
3.3 Гипербола.................................................................................................16
3.4 Парабола...................................................................................................18
4. Екінші ретті сызықтардың теңдеулерін қарапайым түрге келтіру ......21
4.1Координат өстерін (мекенді оқтығын) параллель жылжытуды пайдалану..................21
4.2 Координат өстерін бұруды пайдалану..................................................23
4.3 Екінші ретті сызықтың бөлінуі және жұпыналуы................................25
5. Полярлық координаталар (мекендіктер).................................................25
5.1 Полярлық координаттар жүйесі.............................................................25
5.2 Сызықтардың полярлық теңдеулері......................................................27
II-тарау. Кеңістіктегі аналитикалық геометрия.........................................30
1. Жазықтық. Оның теңдеуі..........................................................................30
1.1 Жазықтықтың жалпы, кесінділік және қалыпты теңдеулері..............30
1.2 Жазықтықтардың өзара орналасуы.......................................................32
1.3 Нүктемен жазықтықтың арасындағы қашықтық.................................34
2. Түзу сызықтар............................................................................................35
2.1 Түзудің теңдеулері..................................................................................35
2.2 Екі түзудің орналасуы.............................................................................37
3. Түзумен жазықтықтың орналасуы...........................................................40
4.Беттер...........................................................................................................41
4.1 Цилиндрлік беттер...................................................................................41
4.2 Екінші ретті беттердің канондық теңдеулері ......................................42
4.3 Параллель қию тәсілі..............................................................................44
Жауаптары..................................................................................................46
Әдебиеттер тізімі.......................................................................................48