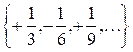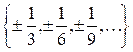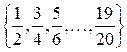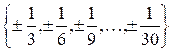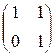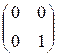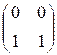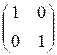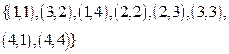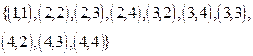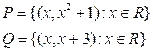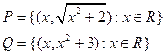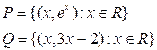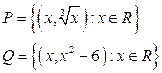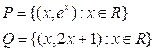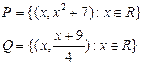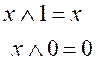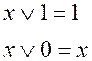Некоммерческое
акционерное общество
Кафедра Математическое моделирование и программное
обеспечение



ДИСКРЕТНАЯ МАТЕМАТИКА
Методические указания и задания по выполнению расчетно-графических
работ для студентов специальности 5В070300 – Информационные системы
Алматы 2017
СОСТАВИТЕЛИ: Астраханцева Л.Н., Байсалова М.Ж. Дискретная математика. Методические указания и задания по выполнению расчетно-графических работ для студентов специальности 5В070300– Информационные системы. – Алматы: АУЭС, 2017. - 43 стр.
Настоящие методические указания содержат расчетно-графические работы №1 и №2 дисциплины «Дискретная математика» для студентов специальности 5В070300 – Информационные системы. Они составлены в соответствии с программой дисциплины «Дискретная математика» по разделам «Множества, отношения» и «Элементы математической логики». Приведены варианты заданий, необходимые теоретические сведения и подробные решения типовых задач.
Ил. 10, табл. 14, библиогр. – 11 назв.
![]()
Рецензент: доцент кафедры ТКСиС Ю.М.Гармашова
Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2017 г.
ã НАО «Алматинский университет энергетики и связи», 2017 г.
050013 Алматы, ул.Байтурсынова, 126
Введение
Дисциплина «Дискретная математика» посвящена той области математики, которая изучает конечные множества и различные структуры на них. Она имеет широкий спектр приложений, прежде всего в областях, связанных с информационными технологиями и компьютерами. В результате изучения дисциплины студенты должны овладеть основными методами формализации рассуждений, получить навыки моделирования для использования их в программировании, при решении задач в области искусственного интеллекта, при доказательстве правильности программ, при построении математических моделей.
1 Расчетно-графическая работа №1. Множества, отношения
Цели: изучить понятия множеств и отношений. Познакомиться с их свойствами и классификацией.
1.1 Теоретические вопросы
1. Множества, их способы задания. Подмножества, булеан. Операции над множествами.
2. Свойства операции над множествами. Разбиения и покрытия множеств.
3. Прямое произведение множеств. Отношения. Способы задания бинарных отношений. Обратное отношение, дополнение отношения, тождественное отношение. Композиция бинарных отношений.
4. Основные свойства матриц бинарных отношений. Свойства бинарных отношений.
5. Отношение эквивалентности. Классы эквивалентности, фактор-множество.
6. Отношение порядка. Лексикографический порядок.
7. Функциональные отношения. Инъекция, сюръекция, биекция. Понятие о мощности множеств.
1.2 Расчётные задания
1. Данное множество задать:
а) перечислением элементов;
б) общим свойством.
|
№ |
а) |
б) |
|
|
1.1 |
|
|
|
|
1.2 |
|
|
|
|
1.3 |
|
|
|
|
1.4 |
|
|
|
|
1.5 |
|
|
|
|
1.6 |
|
|
|
|
1.7 |
|
|
|
|
1.8 |
|
|
|
|
1.9 |
|
|
|
|
1.10 |
|
|
|
|
1.11 |
|
|
|
|
1.12 |
|
|
|
|
1.13 |
|
|
|
|
1.14 |
|
|
|
|
1.15 |
|
|
|
|
1.16 |
|
|
|
|
1.17 |
|
|
|
|
1.18 |
|
|
|
|
1.19 |
|
|
|
|
1.20 |
|
|
|
|
1.21 |
|
|
|
|
1.22 |
|
|
|
|
1.23 |
|
|
|
|
1.24 |
|
|
|
|
1.25 |
|
|
|
|
1.26 |
|
|
|
|
1.27 |
|
|
|
|
1.28 |
|
|
|
|
1.29 |
|
|
|
|
1.30 |
|
|
|
2. Пусть U = {1,2,3,4,5,6,7,8,9,10} - универсальное множество. Для данных множеств А, В, С найти:
а)![]() ;
;
б)![]() ;
;
в)![]() ;
;
г)![]() ;
;
д)![]() ;
;
е) ![]() ;
;
ж) ![]() ;
;
и) ![]() .
.
|
№ |
A |
B |
C |
|
2.1 |
{1,2,3,4,5,6,7} |
{4,5,6,7,8,9,10} |
{2,4,6,8,10} |
|
2.2 |
{2,3,4,5,6,7,8} |
{5,6,7,8,9,10} |
{1,3,5,7,9} |
|
2.3 |
{3,4,5,6,7,8,9} |
{6,7,8,9,10} |
{1,2,4,6,8,9} |
|
2.4 |
{6,7,8,9,10} |
{1,2,4,6,8,9} |
{3,4,5,6,7,8,9} |
|
2.5 |
{4,5,6,7,8,9,10} |
{2,4,6,8,10} |
{1,2,3,4,5,6,7} |
|
2.6 |
{1,3,5,7,9} |
{2,3,4,5,6,7,8} |
{5,6,7,8,9,10} |
|
2.7 |
{1,2,3,5,7,9,10} |
{3,4,5,6,7,8} |
{2,4,6,7,8,9} |
|
2.8 |
{6,7,8,9,10} |
{1,2,3,4,5,6,7} |
{3,4,5,6,7,8} |
|
2.9 |
{1,3,5,7,8,9} |
{2,4,6,8,10} |
{7,8,9,1,2,3} |
|
2.10 |
{2,4,6,7,8,9} |
{1,3,5,6,7,8} |
{8,9,10,1,2,3} |
|
2.11 |
{2,4,6,8,10} |
{1,2,3,4,5,6,7} |
{4,5,6,7,8,9,10} |
|
2.12 |
{1,3,5,7,9} |
{2,3,4,5,6,7,8} |
{5,6,7,8,9,10} |
|
2.13 |
{1,2,4,6,8,9} |
{3,4,5,6,7,8,9} |
{6,7,8,9,10} |
|
2.14 |
{3,4,5,6,7,8,9} |
{6,7,8,9,10} |
{1,2,4,6,8,9} |
|
2.15 |
{1,2,3,4,5,6,7} |
{4,5,6,7,8,9,10} |
{2,4,6,8,10} |
|
2.16 |
{5,6,7,8,9,10} |
{1,3,5,7,9} |
{2,3,4,5,6,7,8} |
|
2.17 |
{2,4,6,7,8,9} |
{1,2,3,5,7,9,10} |
{3,4,5,6,7,8} |
|
2.18 |
{3,4,5,6,7,8} |
{6,7,8,9,10} |
{1,2,3,4,5,6,7} |
|
2.19 |
{7,8,9,1,2,3} |
{1,3,5,7,8,9} |
{2,4,6,8,10} |
|
2.20 |
{8,9,10,1,2,3} |
{2,4,6,7,8,9} |
{1,3,5,6,7,8} |
|
2.21 |
{4,5,6,7,8,9,10} |
{2,4,6,8,10} |
{1,2,3,4,5,6,7} |
|
2.22 |
{5,6,7,8,9,10} |
{1,3,5,7,9} |
{2,3,4,5,6,7,8} |
|
2.23 |
{6,7,8,9,10} |
{1,2,4,6,8,9} |
{3,4,5,6,7,8,9} |
|
2.24 |
{1,2,4,6,8,9} |
{3,4,5,6,7,8,9} |
{6,7,8,9,10} |
|
2,25 |
{2,4,6,8,10} |
{1,2,3,4,5,6,7} |
{4,5,6,7,8,9,10} |
|
2.26 |
{2,3,4,5,6,7,8} |
{5,6,7,8,9,10} |
{1,3,5,7,9} |
|
2.27 |
{3,4,5,6,7,8} |
{2,4,6,7,8,9} |
{1,2,3,5,7,9,10} |
|
2.28 |
{1,2,3,4,5,6,7} |
{3,4,5,6,7,8} |
{6,7,8,9,10} |
|
2.29 |
{2,4,6,8,10} |
{7,8,9,1,2,3} |
{1,3,5,7,8,9} |
|
2.30 |
{1,3,5,6,7,8} |
{8,9,10,1,2,3} |
{2,4,6,7,8,9} |
3. Для данных множеств А и В найти:
а)![]() ;
;
б)![]() ;
;
в)![]() ;
;
г) булеан множества А (т.е. множество всех подмножеств);
д) какое-нибудь покрытие множества A;
е) какое-нибудь разбиение множества A;
ж) произвольное множество подмножеств А (ни булеан, ни покрытие, ни разбиение).
|
№ |
A |
B |
№ |
A |
B |
|
3.1 |
{1,2,3} |
{4,5} |
3.2 |
{3,4,5} |
{7,8} |
|
3.3 |
{7,8,9} |
{1,2,3} |
3.4 |
{7,8,9} |
{3,4,5} |
|
3.5 |
{4,5,8} |
{2,3,5} |
3.6 |
{4,7,8} |
{9,0} |
|
3.7 |
{3,4,9} |
{6,7,8} |
3.8 |
{2,6,8} |
{1,2,3} |
|
3.9 |
{3,5,7} |
{1,4,6} |
3.10 |
{8,9,0} |
{1,2,4} |
|
3.11 |
{1,3,5} |
{6,7,8} |
3.12 |
{0,1,2} |
{8,9} |
|
3.13 |
{6,7,8} |
{4,5} |
3.14 |
{4,5,6} |
{1,2} |
|
3.15 |
{3,4,8} |
{1,9} |
3.16 |
{2,9,5} |
{3,4} |
|
3.17 |
{4,6,8} |
{1,2,3} |
3.18 |
{1,2,3} |
{4,7,9} |
|
3.19 |
{1,5,6} |
{2,3} |
3.20 |
{1,3,5} |
{2,7,8} |
|
3.21 |
{6,7,9} |
{5,8} |
3.22 |
{6,7,8} |
{5,9} |
|
3.23 |
{2,4,6} |
{3,5} |
3.24 |
{3,4,7} |
{8,9} |
|
3.25 |
{5,6,0} |
{1,2} |
3.26 |
{5,6,8} |
{2,3,7} |
|
3.27 |
{1,3,4} |
{7,8} |
3.28 |
{1,3,5} |
{6,7} |
|
3.29 |
{2,7,8} |
{4,6,9} |
3.30 |
{3,4,6} |
{1,9} |
4. Доказать тождество с помощью диаграмм Эйлера-Венна.
|
4.1 |
A \
(B |
4.2 |
(A |
|
4.3 |
A \ (B∩C)=(A \ B)
|
4.4 |
|
|
4.5 |
(A \ B)∩C=(A∩C) \ (B∩C) |
4.6 |
|
|
4.7 |
(A \ B) |
4.8 |
|
|
4.9 |
A∩(B \ C)=(A∩B) \ (A∩C) |
4.10 |
|
|
4.11 |
(A \ B) \ C=(A \ C) \ (B \ C) |
4.12 |
|
|
4.13 |
(A \ C) |
4.14 |
B \ (A∩C)=(B \ A) |
|
4.15 |
(A∩B) \ C =A∩(B\ C ) |
4.16 |
|
|
4.17 |
(A |
4.18 |
|
|
4.19 |
(A∩B) \ (A∩C)= (A∩B) \ C |
4.20 |
|
|
4.21 |
(A |
4.22 |
|
|
4.23 |
A \
(B \ C)=(A \ B) |
4.24 |
|
|
4.25 |
A \ (B |
4.26 |
(B \ A) |
|
4.27 |
(A \ B) |
4.28 |
(B \ C) |
|
4.29 |
(A \ B) |
4.30 |
(В \ А) \ С = (В \ С) \ (А \ С) |
5. Пусть [P] и [Q]
матрицы некоторых бинарных отношений. Найти: [P![]() Q],
[P
Q],
[P![]() Q], [P
Q], [P![]() Q], [P
Q], [P![]() ], [
], [![]() ] .
Проверить выполнение включений P
] .
Проверить выполнение включений P![]() Q и Q
Q и Q![]() P.
P.
|
№ |
[P] |
[Q] |
№ |
[P] |
[Q] |
|
5.1 |
|
|
5.2 |
|
|
|
5.3 |
|
|
5.4 |
|
|
|
5.5 |
|
|
5.6 |
|
|
|
5.7 |
|
|
5.8 |
|
|
|
5.9 |
|
|
5.10 |
|
|
|
5.11 |
|
|
5.12 |
|
|
|
5.13 |
|
|
5.14 |
|
|
|
5.15 |
|
|
5.16 |
|
|
|
5.17 |
|
|
5.18 |
|
|
|
5.19 |
|
|
5.20 |
|
|
|
5.21 |
|
|
5.22 |
|
|
|
5.23 |
|
|
5.24 |
|
|
|
5.25 |
|
|
5.26 |
|
|
|
5.27 |
|
|
5.28 |
|
|
|
5.29 |
|
|
5.30 |
|
|
6. Для данных множеств А={a,b,c}
и В={1,2,3,4} и отношений ![]()
![]() найти:
найти:
a) построить матрицы отношений ![]() и
и ![]() ;
;
б) изобразить отношения графически;
в) найти ![]() ;
; ![]() ;
; ![]() ;
;
г) проверить для отношения ![]() выполнение свойств
рефлексивности, симметричности, антисимметричности, транзитивности.
выполнение свойств
рефлексивности, симметричности, антисимметричности, транзитивности.
|
№ |
|
|
|
6.1 |
|
|
|
6.2 |
|
|
|
6.3 |
|
|
|
6.4 |
|
|
|
6.5 |
|
|
|
6.6 |
|
|
|
6.7 |
|
|
|
6.8 |
|
|
|
6.9 |
|
|
|
6.10 |
|
|
|
6.11 |
|
|
|
6.12 |
|
|
|
6.13 |
|
|
|
6.14 |
|
|
|
6.15 |
|
|
|
6.16 |
|
|
|
6.17 |
|
|
|
6.18 |
|
|
|
6.19 |
|
|
|
6.20 |
|
|
|
6.21 |
|
|
|
6.22 |
|
|
|
6.23 |
|
|
|
6.24 |
|
|
|
6.25 |
|
|
|
6.26 |
|
|
|
6.27 |
|
|
|
6.28 |
|
|
|
6.29 |
|
|
|
6.30 |
|
|
7. Доказать, что отношение ![]() является отношением порядка
является отношением порядка ![]() на множестве A={a,b,c,d,e}
или A={a,b,c,d}. Какой это порядок (частичный нестрогий, строгий,
линейный)? Построить диаграмму Хассе для упорядоченного множества
на множестве A={a,b,c,d,e}
или A={a,b,c,d}. Какой это порядок (частичный нестрогий, строгий,
линейный)? Построить диаграмму Хассе для упорядоченного множества ![]() .
.
|
№ |
Р |
№ |
Р |
|
7.1 |
{(a,a),(b,b),(c,c),(d,d),(a,c),(b,c)} |
7.2 |
{(a,c),(b,c),(b,d),(c,d),(a,d)} |
|
7.3 |
{(a,a),(b,b),(c,c),(d,d),(a,c),(b,c),(c,d), (a,d),(b,d)} |
7.4 |
{(a,a),(b,b),(c,c),(d,d),(e,e),(a,b),(a,c), (a,e), (d,b),(e,b)} |
|
7.5 |
{(a,a),(b,b),(c,c),(d,d),(a,b),(a,c),(b,c), (b,d),(c,d),(a,d)} |
7.6 |
{(a,a),(b,b),(c,c),(d,d),(e,e),(c,a),(c,b), (c,e),(d,a),(d,b),(d,e),(e,a),(e,b)} |
|
7.7 |
{(a,a),(b,b),(c,c),(d,d),(e,e),(d,a),(d,b), (d,c),(e,a),(e,b),(e,c),(e,d)} |
7.8 |
{(a,a),(b,b),(c,c),(d,d),(e,e),(a,b),(a,c), (e,d), (e,c)} |
|
7.9 |
{(a,b),(c,a),(c,b,),(d,a),(d,b),(e,a),(e,b)} |
7.10 |
{(a,b),(a,c),(b,c),(b,d),(c,d),(a,d)} |
|
7.11 |
{(a,b),(c,b),(d,a),(d,b),(d,c),(d,e)} |
7.12 |
{(c,a),(c,b),(c,e),(d,a),(d,b),(d,e),(e,a), (e,b)} |
|
7.13 |
{(a,a),(b,b),(c,c),(d,d),(e,e),(a,b),(c,b), (d,a),(d,b),(d,c),(d,e)} |
7.14 |
{(a,a),(b,b),(c,c),(d,d),(e,e),(a,b),(c,a), (c,b), (d,a),(d,b),(e,a),(e,b)} |
|
7.15 |
{(a,b),(a,c),(a,e),(d,b),(e,b)} |
7.16 |
{(a,b),(c,b),(a,c),(e,d),(e,c),(e,b)} |
|
7.17 |
{(a,a),(b,b),(c,c),(d,d),(a,c),(b,c)} |
7.18 |
{(a,c),(b,c),(b,d),(c,d),(a,d)} |
|
7.19 |
{(a,a),(b,b),(c,c),(d,d),(a,c),(b,c),(c,d), (a,d),(b,d)} |
7.20 |
{(a,a),(b,b),(c,c),(d,d),(e,e),(a,b),(a,c), (a,e), (d,b),(e,b)} |
|
7.21 |
{(a,a),(b,b),(c,c),(d,d),(a,b),(a,c),(b,c), (b,d),(c,d),(a,d)} |
7.22 |
{(a,a),(b,b),(c,c),(d,d),(e,e),(c,a),(c,b), (c,e),(d,a),(d,b),(d,e),(e,a),(e,b)} |
|
7.23 |
{(a,a),(b,b),(c,c),(d,d),(e,e),(d,a),(d,b), (d,c),(e,a),(e,b),(e,c),(e,d)} |
7.24 |
{(a,a),(b,b),(c,c),(d,d),(e,e),(a,b),(a,c), (e,d), (e,c)} |
|
7.25 |
{(a,b),(c,a),(c,b,),(d,a),(d,b),(e,a),(e,b)} |
7.26 |
{(a,b),(a,c),(b,c),(b,d),(c,d),(a,d)} |
|
7.27 |
{(a,b),(c,b),(d,a),(d,b),(d,c),(d,e)} |
7.28 |
{(c,a),(c,b),(c,e),(d,a),(d,b),(d,e),(e,a), (e,b)} |
|
7.29 |
{(a,a),(b,b),(c,c),(d,d),(e,e),(a,b),(c,b), (d,a),(d,b),(d,c),(d,e)} |
7.30 |
{(a,a),(b,b),(c,c),(d,d),(e,e),(a,b),(c,a), (c,b),(d,a),(d,b),(e,a),(e,b)} |
8. Доказать, что отношение ![]() является отношением
эквивалентности на множестве
является отношением
эквивалентности на множестве ![]() . Построить классы эквивалентности и
фактор-множество.
. Построить классы эквивалентности и
фактор-множество.
|
№ |
Р |
№ |
Р |
|
8.1 |
|
8.2 |
|
|
8.3 |
|
8.4 |
|
|
8.5 |
|
8.6 |
|
|
8.7 |
|
8.8 |
|
|
8.9 |
|
8.10 |
|
|
8.11 |
|
8.12 |
|
|
8.13 |
|
8.14 |
|
|
8.15 |
|
8.16 |
|
|
8.17 |
|
8.18 |
|
|
8.19 |
|
8.20 |
|
|
8.21 |
|
8.22 |
|
|
8.23 |
|
8.24 |
|
|
8.25 |
|
8.26 |
|
|
8.27 |
|
8.28 |
|
|
8.29 |
|
8.30 |
|
9. Для данного разбиения A множества А={1,2,3,4,5,6} построить соответствующее отношение эквивалентности. Почему оно является отношением эквивалентности? Записать классы эквивалентности и фактор – множество.
|
№ |
A |
№ |
A |
|
9.1 |
{{1,2},{3,4},{5,6}} |
9.2 |
{{1},{2},{3},{4,5},{6}} |
|
9.3 |
{{1},{2,3},{4,5,6}} |
9.4 |
{{1},{2,3,4},{5,6}} |
|
9.5 |
{{1,2,3},{4},{5,6}} |
9.6 |
{{1},{2,3},{4},{5,6}} |
|
9.7 |
{{1},{2},{3,4},{5,6}} |
9.8 |
{{1,2},{3},{4,5},{6}} |
|
9.9 |
{{1,2,3,4},{5},{6}} |
9.10 |
{{1,2,3,4},{5,6}} |
|
9.11 |
{{1,2},{3},{4},{5,6}} |
9.12 |
{{1},{2,3,4,5},{6}} |
|
9.13 |
{{1},{2,3,4},{5},{6}} |
9.14 |
{{1},{2},{3},{4},{5,6}} |
|
9.15 |
{{1,2},{3,4}{5},{6}} |
9.16 |
{{1},{2},{3,4},{5},{6}} |
|
9.17 |
{{1},{2},{3},{4,5,6}} |
9.18 |
{{1},{2},{3},{4},{5},{6}} |
|
9.19 |
{{1},{2},{3,4,5},{6}} |
9.20 |
{{1},{2},{3,4,5,6}} |
|
9.21 |
{{1,2,3,4,5},{6}} |
9.22 |
{{1,2,3},{4},{5},{6}} |
|
9.23 |
{{1,2,3},{4,5,6}} |
9.24 |
{{1},{2,3},{4,5},{6}} |
|
9.25 |
{{1,2},{3,4,5,6}} |
9.26 |
{{1},{2,3,4,5,6}} |
|
9.27 |
{{1,2},{3},{4},{5},{6}} |
9.28 |
{{2},{1,3,4,5},{6}} |
|
9.29 |
{{1,2,3},{4,5},{6}} |
9.30 |
{{3},{1,2,4,5},{6}} |
10. Даны два отношения ![]() и
и ![]() . Доказать, что эти отношения являются
функциями. Найти композиции
. Доказать, что эти отношения являются
функциями. Найти композиции ![]() . Какими свойствами обладают эти отношения
(инъективность, сюръективность, биективность)?
. Какими свойствами обладают эти отношения
(инъективность, сюръективность, биективность)?
|
10.1 |
|
10.2 |
|
|
10.3 |
|
10.4 |
|
|
10.5 |
|
10.6 |
|
|
10.7 |
|
10.8 |
|
|
10.9 |
|
10.10 |
|
|
10.11 |
|
10.12 |
|
|
10.13 |
|
10.14 |
|
|
10.15 |
|
10.16 |
|
|
10.17 |
|
10.18 |
|
|
10.19 |
|
10.20 |
|
|
10.21 |
|
10.22 |
|
|
10.23 |
|
10.24 |
|
|
10.25 |
|
10.26 |
|
|
10.27 |
|
10.28 |
|
|
10.29 |
|
10.30 |
|
1.3 Решение типового варианта
1.
а) Множество![]() задать перечислением элементов.
задать перечислением элементов.
Решение: так как N = {1,2,3,4,…}, то А = {1,2,3}.
1.
б) Множество 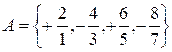 задать общим свойством.
задать общим свойством.
Решение: 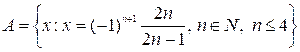 .
.
2 Пусть U = {1,2,3,4,5,6,7,8,9,10} - универсальное множество. Для данных множеств А = {1,2,3,8,9,10}, В = {1,3,5,6,7,8}, С = {2,4,6,7,8,9} найти:
а)![]() ;
;
б)![]() ;
;
в)![]() ;
;
г)![]() ;
;
д)![]() ;
;
е) ![]() ;
;
ж) ![]() ;
;
и) ![]() .
.
Решение:
а) ![]() ;
;
б)![]() ;
;
в)![]() ;
;
г)![]() ;
;
д)![]() ;
;
е)![]() ;
;
ж) ![]() ;
;
и) ![]() .
.
3. Для данных множеств А = {3,4,5} и В = {6,7,9} найти:
а)![]() ;
;
б)![]() ;
;
в) ![]() ;
;
г) булеан множества А (т.е. множество всех подмножеств);
д) какое-нибудь покрытие множества A;
е) какое-нибудь разбиение множества A;
ж) произвольное множество подмножеств А ( ни булеан, ни покрытие, ни разбиение).
Решение:
a)![]() =
=
![]() ;
;
б)![]() ; в)
; в)![]()
![]() ;
;
г) так как ![]() состоит из трёх элементов, то булеан
состоит из трёх элементов, то булеан ![]() P
P ![]() имеет
имеет ![]() элементов: P
элементов: P ![]()
![]() ;
;
д) например, A![]() =
=![]() - покрытие
- покрытие ![]() ;
;
е) например, A![]() =
= ![]() - разбиение
- разбиение ![]() ;
;
ж) например, A![]() =
= ![]() - ни булеан, ни разбиение, ни покрытие.
- ни булеан, ни разбиение, ни покрытие.
4. Доказать тождество ![]() с помощью диаграмм Эйлера-Венна.
с помощью диаграмм Эйлера-Венна.
Решение: изобразим диаграммами Эйлера-Венна левую и правую части отдельно.
Левая часть:
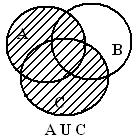

Рисунок 1- Диаграммы Эйлера-Венна для левой части
Правая часть:

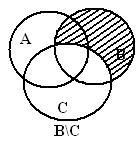
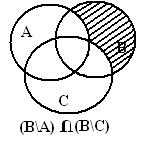
Рисунок 2- Диаграммы Эйлера-Венна для правой части
На последних рисунках левой и правой частей отмечена одна и та же область, что доказывает тождество.
5. Пусть [P] =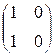 и [Q] =
и [Q] = 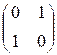 матрицы некоторых
бинарных отношений. Найти [P
матрицы некоторых
бинарных отношений. Найти [P![]() Q], [P
Q], [P![]() Q],
[P
Q],
[P![]() Q], [P
Q], [P![]() ], [
], [![]() ] .
Проверить выполнение включений P
] .
Проверить выполнение включений P![]() Q и Q
Q и Q![]() P.
P.
Решение: если [P] = ![]() , [Q]
=
, [Q]
= ![]() , то [P
, то [P![]() Q]
=
Q]
=![]() = [P]+[Q],
где элементы матриц складываются по правилам: 0+0=0, 1+0 = 0+1 = 1+1 =1; [P
= [P]+[Q],
где элементы матриц складываются по правилам: 0+0=0, 1+0 = 0+1 = 1+1 =1; [P![]() Q]
= =
Q]
= =![]() = [P]*[Q],
т.е. соответствующие элементы перемножаются по обычным правилам:
= [P]*[Q],
т.е. соответствующие элементы перемножаются по обычным правилам: ![]() =
= ![]() =
= ![]() = 0,
= 0, ![]() = 1; [P
= 1; [P![]() Q]=
Q]=![]() - обычное умножение матриц,
но элементы матриц [P] и [Q] складываются и умножаются по выше приведённым
правилам; [P-1]=[P]T,
где P-1
отношение, обратное к P;
- обычное умножение матриц,
но элементы матриц [P] и [Q] складываются и умножаются по выше приведённым
правилам; [P-1]=[P]T,
где P-1
отношение, обратное к P; ![]() - дополнение Р и её матрица [
- дополнение Р и её матрица [![]() ]
равна матрице отношения Р, в которой нули заменены единицами и единицы
нулями; если P
]
равна матрице отношения Р, в которой нули заменены единицами и единицы
нулями; если P![]() Q, то
Q, то ![]()
![]() .
.
В нашем случае:
[P![]() Q]=
Q]=
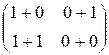 =
=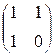 ;
;
[P![]() Q]
=
Q]
=  = =
= = ;
;
[P![]() Q]=
Q]=
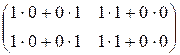 =
= 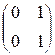 ;
;
[P![]() ]=
]= =
= 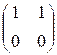 ;
;
[![]() ]=
]=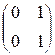 ;
; 
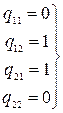
![]() т.к.,
например,
т.к.,
например, ![]() не
не ![]() , то P не
, то P не ![]() Q; т.к., например,
Q; т.к., например, ![]() не
не ![]() , то Q не
, то Q не ![]() P .
P .
6. Для данных множеств А = {a,b,c,d} и В = {1,2,3,4} и отношений
![]() и
и ![]() ,
, ![]() ,
, ![]() найти:
найти:
a) построить матрицы отношений ![]() и
и ![]() ;
;
б) изобразить отношения графически;
в) найти ![]() ;
; ![]() ;
; ![]() ;
;
г) проверить для отношения ![]() выполнение свойств
рефлексивности, симметричности, антисимметричности, транзитивности.
выполнение свойств
рефлексивности, симметричности, антисимметричности, транзитивности.
Решение:
а) по определению ![]() - матрица отношения
- матрица отношения ![]() , если
, если 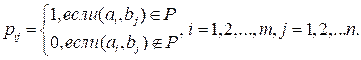
Таким образом, 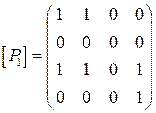 ,
,  .
.
б) Графическое изображение ![]() и
и ![]() приведено на рисунках 3 и 4.
приведено на рисунках 3 и 4.

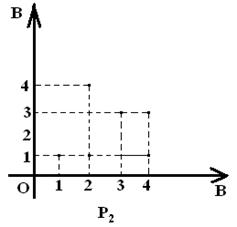
Рисунок 3- График ![]() Рисунок
4- График
Рисунок
4- График ![]()
Заметим, что существуют другие способы графического
изображения отношений. Например, отношение ![]() можно изобразить как на рисунке 5, а
отношение
можно изобразить как на рисунке 5, а
отношение ![]() –
как на рисунке 6 (т.е. ориентированным графом).
–
как на рисунке 6 (т.е. ориентированным графом).

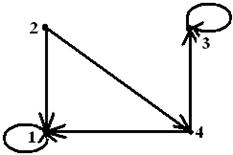
Рисунок 5 - График ![]() Рисунок
6 - График
Рисунок
6 - График ![]()
в) Так как ![]() , то
, то ![]()
![]() ,
, ![]() . Поскольку
. Поскольку ![]() ,
, ![]() и
и ![]()
![]() , то дополнением к
, то дополнением к ![]() будет отношение
будет отношение
![]() .
.
Поскольку по определению P1![]() P2 = {(a,c)|
a
P2 = {(a,c)|
a![]() A, c
A, c![]() C и
C и ![]() b
b![]() B,
что (a,b)
B,
что (a,b)![]() P1 и (b,c)
P1 и (b,c)![]() P2}, где
P2}, где ![]() ,
, ![]() , то
, то
![]() .
.
г) Свойства отношения ![]() проще определить по его матрице
проще определить по его матрице 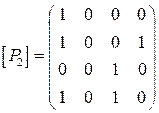 . Так как на главной
диагонали этой матрицы не все единицы, то отношение
. Так как на главной
диагонали этой матрицы не все единицы, то отношение ![]() не рефлексивное; так как
не рефлексивное; так как ![]() , то оно не
симметричное. Поскольку все элементы вне главной диагонали матрицы
, то оно не
симметричное. Поскольку все элементы вне главной диагонали матрицы ![]() являются нулями, то
являются нулями, то ![]() антисимметричное; так
как, например,
антисимметричное; так
как, например, ![]() ,
но
,
но ![]() , то
, то ![]() не транзитивное.
не транзитивное.
7. Доказать, что отношение ![]() является отношением порядка
является отношением порядка ![]() на множестве A={a,b,c,d,e}.
Какой это порядок (частичный нестрогий, строгий, линейный)? Построить диаграмму
Хассе для упорядоченного множества
на множестве A={a,b,c,d,e}.
Какой это порядок (частичный нестрогий, строгий, линейный)? Построить диаграмму
Хассе для упорядоченного множества ![]() .
.
Решение: заметим, что терминология и классификация
отношений порядка различны почти в каждом учебнике. Мы придерживаемся тех,
которые указаны в ниже приведенной схеме (рисунок 7). На рисунке 7
отношение ![]() . Сокращения
ч.у.м., л.у.м., в.у.м. приняты для обозначений частично, линейно и вполне
упорядоченных множеств. Кроме того, если А конечно, то л.у.м. будет и в.у.м.
. Сокращения
ч.у.м., л.у.м., в.у.м. приняты для обозначений частично, линейно и вполне
упорядоченных множеств. Кроме того, если А конечно, то л.у.м. будет и в.у.м.
Проверим для нашего отношения выполнение свойств рефлексивнос- ти, симметричности, антисимметричности и транзитивности. Это, как выяснилось выше, легче всего определить по матрице отношения.
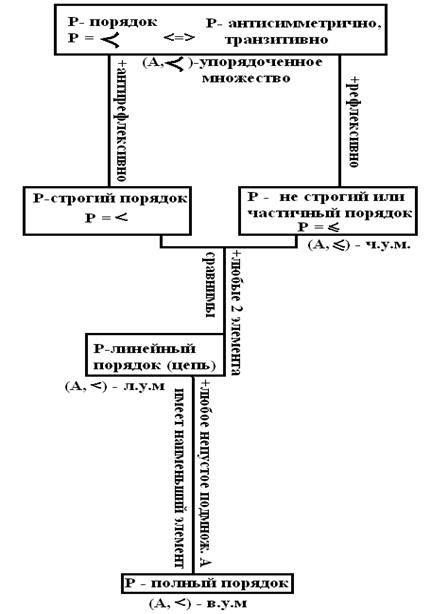
Рисунок 7- Классификация отношений порядка
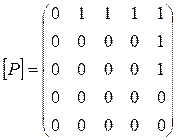 - матрица данного отношения. Так как на
главной диагонали этой матрицы не единицы, то
- матрица данного отношения. Так как на
главной диагонали этой матрицы не единицы, то ![]() не рефлексивно;
не рефлексивно; 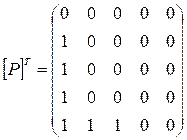
![]() , значит,
, значит, ![]() не симметрично;
не симметрично;
![]()
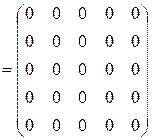 , вне главной диагонали этой
матрицы все нули, поэтому
, вне главной диагонали этой
матрицы все нули, поэтому ![]() антисимметрично; для транзитивности
отношения
антисимметрично; для транзитивности
отношения ![]() надо,
чтобы
надо,
чтобы ![]() или,
если
или,
если ![]() ,
, ![]() , то
, то ![]() .
.
Найдём
![]()
![]()
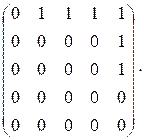
 =
= . Видим, что
. Видим, что ![]()
![]() , что доказывает транзитивность
, что доказывает транзитивность ![]() .
.
Итак,![]() не рефлексивно, антисимметрично и
транзитивно, поэтому оно является отношением строгого порядка. Так как элементы
не рефлексивно, антисимметрично и
транзитивно, поэтому оно является отношением строгого порядка. Так как элементы
![]() и
и ![]() ,
, ![]() и
и ![]() ,
, ![]() и
и ![]() не сравнимы, то
не сравнимы, то ![]() - не линейный порядок. Если
порядок, определённый на конечном множестве, не линейный, то он и не полный.
- не линейный порядок. Если
порядок, определённый на конечном множестве, не линейный, то он и не полный.
Пусть ![]() - упорядоченное множество. Если А
конечно, то
- упорядоченное множество. Если А
конечно, то ![]() можно
изобразить в виде схемы (диаграммы Хассе), на которой, если
можно
изобразить в виде схемы (диаграммы Хассе), на которой, если ![]() , то
, то ![]() и
и ![]() изображаются точками, соединёнными
линией,
изображаются точками, соединёнными
линией, ![]() ниже
ниже
![]() .
.
Построим диаграмму Хассе, причём, в силу
транзитивности отношения порядка не нужно, например, соединять линией элементы ![]() и
и ![]() , так как если
, так как если ![]() и
и ![]() , то
, то ![]() .
.
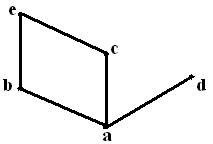
Рисунок 8- Диаграмма Хассе
Заметим, что в случае рефлексивности ![]() , т.е. когда
, т.е. когда ![]() является частичным или
нестрогим порядком, на диаграмме Хассе в каждой вершине появятся петли.
является частичным или
нестрогим порядком, на диаграмме Хассе в каждой вершине появятся петли.
8. Доказать, что отношение ![]()
![]()
![]() является отношением эквивалентности на
множестве
является отношением эквивалентности на
множестве ![]() . Построить
классы эквивалентности и фактор-множество.
. Построить
классы эквивалентности и фактор-множество.
Решение:
отношение ![]() является
отношением эквивалентности, если оно рефлексивно, симметрично, транзитивно.
Построим матрицу отношения
является
отношением эквивалентности, если оно рефлексивно, симметрично, транзитивно.
Построим матрицу отношения ![]() и по ней определим его свойства.
и по ней определим его свойства.
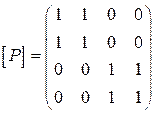 . Так как эта матрица
содержит единицы на главной диагонали, то
. Так как эта матрица
содержит единицы на главной диагонали, то ![]() - рефлексивно; так как
- рефлексивно; так как ![]() , то оно симметрично.
, то оно симметрично.
Найдём ![]()
![]()
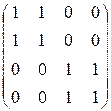 . Итак,
. Итак, ![]() , что доказывает транзитивность
, что доказывает транзитивность ![]() .
.
![]() -
рефлексивно, симметрично, транзитивно, поэтому оно является отношением
эквивалентности.
-
рефлексивно, симметрично, транзитивно, поэтому оно является отношением
эквивалентности.
Классом
эквивалентности элемента ![]() называется множество
называется множество ![]() . Множество всех классов
эквивалентности
. Множество всех классов
эквивалентности ![]() называется
фактор-множеством множества
называется
фактор-множеством множества ![]() по отношению
по отношению ![]() . Множество
. Множество ![]() является разбиением множества
является разбиением множества ![]() .
.
Построим классы эквивалентности для каждого элемента
множества ![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Таким образом, ![]() . Фактор-множеством множества
. Фактор-множеством множества ![]() по отношению
по отношению ![]() будет:
будет: ![]() .
.
9. Для данного разбиения A = {{1,3},{2,4,5},{6}} множества А={1,2,3,4,5,6} построить соответствующее отношение эквивалентности. Почему оно является отношением эквивалентности? Записать классы эквивалентности и фактор – множество.
Решение: пусть A =![]() - разбиение
множества А, где
- разбиение
множества А, где ![]() (
(![]() ) - подмножества А. Тогда
) - подмножества А. Тогда ![]() - отношение
эквивалентности, соответствующее этому разбиению.
- отношение
эквивалентности, соответствующее этому разбиению.
Таким образом, в нашем случае
![]() ={(1,1),(1,3),(3,1),(3,3),(2,2)(2,4),(2,5),(4,2),(4,4)(4,5),(5,2),(5,4),(5,5),(6,6)}
- отношение эквивалентности, соответствующее данному разбиению. Чтобы убедиться
в том, что это отношение эквивалентности, найдём его матрицу:
={(1,1),(1,3),(3,1),(3,3),(2,2)(2,4),(2,5),(4,2),(4,4)(4,5),(5,2),(5,4),(5,5),(6,6)}
- отношение эквивалентности, соответствующее данному разбиению. Чтобы убедиться
в том, что это отношение эквивалентности, найдём его матрицу:
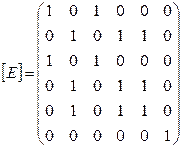 .
.
По матрице определяем, что ![]() рефлексивно (на главной
диагонали все единицы), симметрично (
рефлексивно (на главной
диагонали все единицы), симметрично (![]() ), транзитивно (
), транзитивно (![]() ). Поэтому
). Поэтому ![]() - отношение эквивалентности.
Классы эквивалентности: [1]=[3]={1,3}, [2]=[4]=[5]={2,4,5}, [6]={6}. Фактор-множеством
- отношение эквивалентности.
Классы эквивалентности: [1]=[3]={1,3}, [2]=[4]=[5]={2,4,5}, [6]={6}. Фактор-множеством
![]() по отношению
по отношению
![]() будет данное
разбиение A =
будет данное
разбиение A =![]() = ={{1,3},{2,4,5},{6}}.
= ={{1,3},{2,4,5},{6}}.
10. Даны два отношения ![]() и
и ![]() :
:
а) доказать, что эти отношения являются функциями;
б) найти композиции ![]() ;
;
в) какими свойствами обладают отношения (инъективность, сюръек-тивность, биективность)?
Решение:
а) отношение ![]() является функцией, если
является функцией, если ![]() или
или ![]() для любого
для любого ![]() существует
единственный
существует
единственный ![]() ,
что
,
что ![]() .
.
В нашем случае ![]() и
и ![]() являются функциями, так как для любого
действительного числа
являются функциями, так как для любого
действительного числа ![]() , числа
, числа ![]() и
и ![]() существуют и будут единственными;
существуют и будут единственными;
б) ![]() ,
, ![]() ;
;
в) проверим данные функции на инъективность.
Функция ![]()
называется
инъективной, если ![]() или
или
![]() .
.
Для функции ![]() условие инъективности не
условие инъективности не
выполняется,
т.к. существуют пары значений ![]() (
(![]() ), которым соответствует одно
), которым соответствует одно ![]() , например,
, например, ![]() , но
, но ![]() и
и ![]() , т.е.
, т.е. ![]() .
.
Функция ![]() инъективна, так как для любых
действительных
инъективна, так как для любых
действительных ![]()
![]() выполняется
выполняется ![]() .
.
Проверим функции на сюръективность. Функция ![]() называется сюръективной,
если для любого
называется сюръективной,
если для любого ![]() существует
существует
![]() , что
, что ![]() или область значений отношения
или область значений отношения
![]() совпадает с
совпадает с ![]() .
.
Функция ![]() ,
, ![]() не сюръективна, так как область значений
не сюръективна, так как область значений ![]() .
.
Функция ![]() ,
, ![]() сюръективна, так как
сюръективна, так как ![]() .
.
Функция называется биективной, если она и инъективна
и сюръективна, поэтому ![]() не биективная функция,
не биективная функция, ![]() - биективная.
- биективная.
Заметим, что свойства инъективности, сюръективности и
биективности легко определить по графикам функций. Запишем данные
функциональные отношения как обычно записывают функции: ![]() ;
; ![]() . Графики этих функций изображены на
рисунках 9 и 10.
. Графики этих функций изображены на
рисунках 9 и 10.
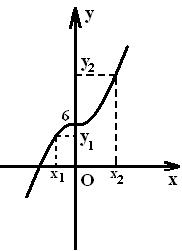
Рисунок 9 - График ![]() Рисунок
10 - График
Рисунок
10 - График ![]()
2 Расчетно-графическая работа №2. Элементы математической логики
Цели: познакомиться с основными понятиями математической логики, рассмотреть их свойства и некоторые приложения.
2.1 Теоретические вопросы
1. Основные понятия логики высказываний. Высказывание, основные логические операции.
2. Логические переменные и формулы. Таблицы истинности логических операций и формул.
3. Функции алгебры логики. Способы задания логических функций.
4. Эквивалентность формул. Основные эквивалентные соотношения алгебры логики.
5. Полные системы логических функций. Приведение логических формул к ДНФ, КНФ.
6. Совершенные ДНФ и КНФ (СДНФ и СКНФ).
7. Минимизация в классе ДНФ. Карты Карно.
8. Коммутационные схемы.
9. Двойственность. Булева алгебра и теория множеств.
2.2 Расчётные задания
1. Данную функцию f(x,y) заданную формулой, задать:
а) таблицей истинности;
б) единичными и нулевыми наборами;
в) вектором значений.
|
№ |
f(x,y) |
№ |
f(x,y) |
|
1.1 |
|
1.2 |
|
|
1.3 |
|
1.4 |
|
|
1.5 |
|
1.6 |
|
|
1.7 |
|
1.8 |
|
|
1.9 |
|
1.10 |
|
|
1.11 |
|
1.12 |
|
|
1.13 |
|
1.14 |
|
|
1.15 |
|
1.16 |
|
|
1.17 |
|
1.18 |
|
|
1.19 |
|
1.20 |
|
|
1.21 |
|
1.22 |
|
|
1.23 |
|
1.24 |
|
|
1.25 |
|
1.26 |
|
|
1.27 |
|
1.28 |
|
|
1.29 |
|
1.30 |
|
2. Используя соглашение о приоритетах логических операций,
расставить скобки в формуле f(x,y). Записать полученную формулу в виде, содержащем только операции отрицание, конъюнкцию и дизъюнкцию; упростить эту формулу.
|
№ |
f(x,y) |
№ |
f(x,y) |
|
2.1 |
|
2.2 |
|
|
2.3 |
|
2.4 |
|
|
2.5 |
|
2.6 |
|
|
2.7 |
|
2.8 |
|
|
2.9 |
|
2.10 |
|
|
2.11 |
|
2.12 |
|
|
2.13 |
|
2.14 |
|
|
2.15 |
|
2.16 |
|
|
2.17 |
|
2.18 |
|
|
2.19 |
|
2.20 |
|
|
2.21 |
|
2.22 |
|
|
2.23 |
|
2.24 |
|
|
2.25 |
|
2.26 |
|
|
2.27 |
|
2.28 |
|
|
2.29 |
|
2.30 |
|
3. Проверить эквивалентность формул ![]() и
и ![]() :
:
а) с помощью таблиц истинности;
б) приведением формул к СДНФ или СКНФ с помощью эквива-
лентных преобразований.
|
№ |
|
|
|
3.1 |
|
|
|
3.2 |
|
|
|
3.3 |
|
|
|
3.4 |
|
|
|
3.5 |
|
|
|
3.6 |
|
|
|
3.7 |
|
|
|
3.8 |
|
|
|
3.9 |
|
|
|
3.10 |
|
|
|
3.11 |
|
|
|
3.12 |
|
|
|
3.13 |
|
|
|
3.14 |
|
|
|
3.15 |
|
|
|
3.16 |
|
|
|
3.17 |
|
|
|
3.18 |
|
|
|
3.19 |
|
|
|
3.20 |
|
|
|
3.21 |
|
|
|
3.22 |
|
|
|
3.23 |
|
|
|
3.24 |
|
|
|
3.25 |
|
|
|
3.26 |
|
|
|
3.27 |
|
|
|
3.28 |
|
|
|
3.29 |
|
|
|
3.30 |
|
|
Дана функция f(A,B,C).
4. Составить таблицу истинности.
5. Привести к ДНФ.
6. Составить СДНФ.
7. Построить карту Карно и найти минимальную ДНФ (МДНФ).
8. От МДНФ перейти к КНФ.
9. Найти СКНФ.
10. По карте Карно двумя способами найти МКНФ.
|
№ |
f(A,B,C) |
№ |
f(A,B,C) |
|
1 |
|
2 |
|
|
3 |
|
4 |
|
|
5 |
|
6 |
|
|
7 |
|
8 |
|
|
9 |
|
10 |
|
|
11 |
|
12 |
|
|
13 |
|
14 |
|
|
15 |
|
16 |
|
|
17 |
|
18 |
|
|
19 |
|
20 |
|
|
21 |
|
22 |
|
|
23 |
|
24 |
|
|
25 |
|
26 |
|
|
27 |
|
28 |
|
|
29 |
|
30 |
|
11. По данной схеме составить и упростить переключательную функцию, построить упрощённую схему.
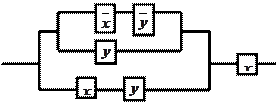 |
11.1
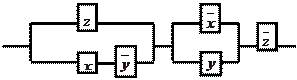
11.2
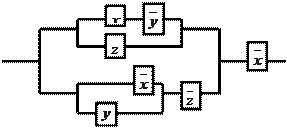 |
11.3
 |
11.4
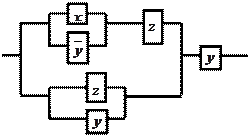 |
11.5
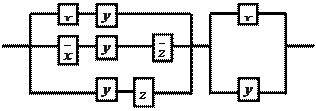 |
11.6
 |
11.7
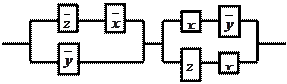 |
11.8
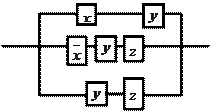 |
11.9
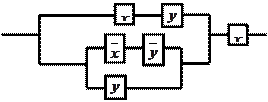 |
11.10
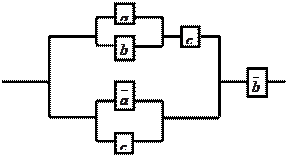 |
11.11
 11.12
11.12
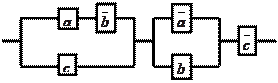 |
11.13
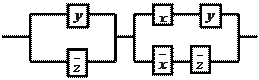 |
11.14

11.15
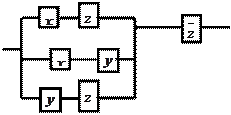 |
11.16
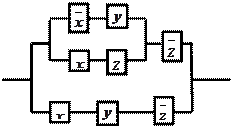 |
11.17
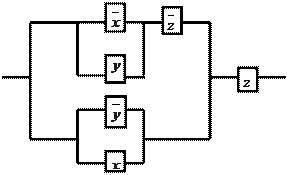 |
11.18
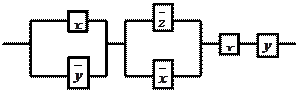 |
11.19
 |
11.20
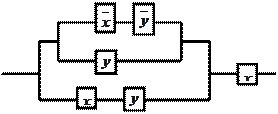 |
11.21
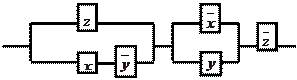
11.22
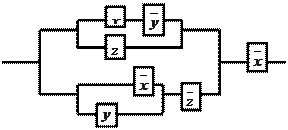 |
11.23
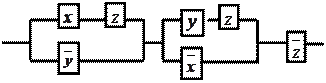 |
11.24
 |
11.25
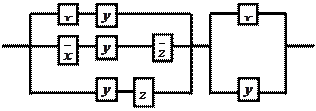 |
11.26
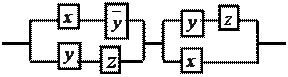 11.27
11.27
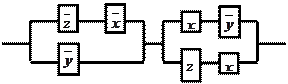 |
11.28

11.29
 |
11.30
2.3 Решение типового варианта
1. Функцию f(x,y) = 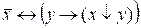 , заданную формулой, задать:
, заданную формулой, задать:
а) таблицей истинности;
б) единичными и нулевыми наборами;
в) вектором значений.
Решение:
а) таблица истинности:
|
|
|
|
|
|
f(x,y) |
|
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
б) единичные наборы: 1=f(0,0)=f(1,1); нулевые наборы: 0=f(0,1)=f(1,0);
в) вектор значений: (1001).
2. Используя соглашение о приоритетах логических операций,
расставить
скобки в формуле f(x,y)= ![]() . Записать полученную формулу в виде, содержащем
только операции отрицание, конъюнкцию и дизъюнкцию; упростить эту формулу.
. Записать полученную формулу в виде, содержащем
только операции отрицание, конъюнкцию и дизъюнкцию; упростить эту формулу.
Решение: согласно схеме приоритетов логических
операций ![]() , в
нашей формуле скобки должны быть расставлены так:
, в
нашей формуле скобки должны быть расставлены так: ![]() =
= ![]() .
.
Упростим полученную формулу: ![]() = | 14, 15 | =
= | 14, 15 | = ![]() = | 6 | =
= | 6 | = ![]() = | 1 | =
= | 1 | = ![]() = | 5 | =
= | 5 | = ![]() . В
преобразовании указаны номера формул из справочного материала на странице 38.
Под упрощением будем понимать получение формулы в виде, содержащем наименьшее
число переменных.
. В
преобразовании указаны номера формул из справочного материала на странице 38.
Под упрощением будем понимать получение формулы в виде, содержащем наименьшее
число переменных.
3. Проверить эквивалентность формул ![]() =
=![]() и
и
![]() =
= ![]() :
:
а) с помощью таблиц истинности;
б) приведением формул к СДНФ или СКНФ с помощью эквивалент-
ных преобразований.
Решение:
а) таблица истинности ![]() и
и ![]() :
:
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Так как столбцы значений формул ![]() и
и ![]() совпадают, то эти формулы эквивалентны;
совпадают, то эти формулы эквивалентны;
б) используя известные свойства логических операций,
номера которых будем указывать, преобразуем формулы сначала к ДНФ - дизъюнктивной
нормальной форме, затем, пользуясь законом расщепления, к совершенной
дизъюнктивной нормальной форме (СДНФ): ![]() =
=![]() = | 14 | =
= | 14 | = ![]() = |
ДНФ,10а | =
= |
ДНФ,10а | = ![]() =
=
![]() =| 4 |=
=| 4 |=![]() - СДНФ;
- СДНФ;
![]() =
= ![]() = | 14 | =
= | 14 | = ![]() = | 3
| =
= | 3
| =
= ![]() = |
4,10a | =
= |
4,10a | = ![]() =
=
=
|1,10a | = ![]() = | 1,4 | =
= | 1,4 | =
= ![]() - СДНФ. Если закон
дистрибутивности использовать по - другому – не «раскрыть скобки», а «вынести
за скобки», то преобразования будут короче:
- СДНФ. Если закон
дистрибутивности использовать по - другому – не «раскрыть скобки», а «вынести
за скобки», то преобразования будут короче: ![]() =
= ![]() = | 14 | =
= | 14 | =
= ![]() = | 3
| =
= | 3
| =![]() = | 10a | =…=
= | 10a | =…=![]() .
.
Так как СДНФ обеих формул совпадают, то эти формулы эквивалентны.
4-10. Дана функция ![]() .
.
4. Составить таблицу истинности.
5. Привести к ДНФ.
6. Составить СДНФ.
7. Построить карту Карно и найти минимальную ДНФ (МДНФ).
8. От МДНФ перейти к КНФ.
9. Найти СКНФ.
10. По карте Карно двумя способами найти МКНФ.
4. Для функции ![]() составить таблицу истинности.
составить таблицу истинности.
Решение: таблица истинности формулы:
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
0 |
0 |
1 |
5. Привести формулу ![]() к ДНФ.
к ДНФ.
Решение:
![]() = | 14, 15,16 | =
= | 14, 15,16 | = ![]() = |
6, 7 | =
= |
6, 7 | = ![]() =
= ![]() =
=
=![]() = |
3 | =
= |
3 | =![]() =
=
=
| 9,3 | = ![]() = | 4,9 | =
= | 4,9 | = ![]() - ДНФ (а также СДНФ).
- ДНФ (а также СДНФ).
6. Для функции ![]() составить СДНФ.
составить СДНФ.
Решение:
по таблице истинности формулы выпишем её единичные наборы: ![]() . Теперь применяем правило, по
которому СДНФ функции
. Теперь применяем правило, по
которому СДНФ функции ![]() содержит столько конъюнкт, сколько единиц
в столбце значений
содержит столько конъюнкт, сколько единиц
в столбце значений ![]() ;
каждому единичному набору нулей и единиц
;
каждому единичному набору нулей и единиц ![]() соответствует конъюнкта всех переменных,
в которых
соответствует конъюнкта всех переменных,
в которых ![]() взято
с отрицанием, если
взято
с отрицанием, если ![]() ;
и без отрицания, если
;
и без отрицания, если ![]() . Итак, СДНФ нашей формулы содержит
дизъюнкцию двух конъюнкт:
. Итак, СДНФ нашей формулы содержит
дизъюнкцию двух конъюнкт: ![]()
![]() (знак
(знак
![]() опущен).
Заметим, что СДНФ можно было получить методом эквивалентных преобразований. В
нашем случае это сделано в предыдущем пункте.
опущен).
Заметим, что СДНФ можно было получить методом эквивалентных преобразований. В
нашем случае это сделано в предыдущем пункте.
7. Для функции ![]() построить карту Карно и найти
минимальную ДНФ (МДНФ).
построить карту Карно и найти
минимальную ДНФ (МДНФ).
Решение: карта Карно функции трёх переменных представляет
собой таблицу, содержащую ![]() ячеек (столько, сколько всех возможных
наборов 0 и 1 функции трёх переменных), строки и столбцы соответствуют
значениям переменных или их отрицаниям так, чтобы соседние ячейки отличались
только значением одной переменной. Для получения МДНФ каждая конъюнкта СДНФ
функции отмечается единицей в соответствующей ячейке карты Карно:
ячеек (столько, сколько всех возможных
наборов 0 и 1 функции трёх переменных), строки и столбцы соответствуют
значениям переменных или их отрицаниям так, чтобы соседние ячейки отличались
только значением одной переменной. Для получения МДНФ каждая конъюнкта СДНФ
функции отмечается единицей в соответствующей ячейке карты Карно:
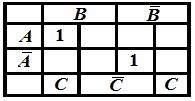
Чтобы получить МДНФ, надо объединить рядом стоящие по
вертикали и горизонтали единицы в так называемые блоки, состоящие из 2 и 4 ячеек
(блоком из 2 ячеек считаются также единицы, стоящие в углах при одной стороне
таблицы или из 4 – единицы, стоящие во всех углах, т.к., например, в последнем
случае карту можно «свернуть» как тор столбцы к столбцам и строки к строкам). В
нашей карте Карно только две единицы, и они не объединяются в блок, поэтому
МДНФ = СДНФ: ![]()
![]() .
.
8. Для функции ![]() от МДНФ перейти к КНФ.
от МДНФ перейти к КНФ.
Решение: с помощью эквивалентных преобразований, используя свойства логических операций, номера которых будем указывать, преобразуем формулу к КНФ:
![]()
![]() = |
7 | =
= |
7 | =![]() = | 6 | =
= | 6 | = ![]() =
=
=![]() = |
3 | =
= |
3 | =
=
![]() = |
9, 8, 6 | =
= |
9, 8, 6 | =
= ![]() = |
6 | =
= |
6 | =
=![]() - КНФ.
- КНФ.
9.
Для функции ![]() найти
СКНФ.
найти
СКНФ.
Решение: пользуясь законом расщепления, КНФ, полученную в предыдущем пункте, приведём к СКНФ:
![]()
![]() = | 10a | =
= | 10a | =
![]()
![]()
![]() =|1,4
| =
=|1,4
| =![]()
![]()
![]() -
СКНФ.
-
СКНФ.
Совершенную конъюнктивную нормальную форму (СКНФ) можно
получить, используя нулевые наборы значений переменных, которые выпишем из
таблицы истинности формулы: ![]() =
=
=![]() . Теперь, следуя
правилу, что СКНФ содержит столько дизъюнкт, сколько нулей в столбце значений
. Теперь, следуя
правилу, что СКНФ содержит столько дизъюнкт, сколько нулей в столбце значений
![]() , и каждому
нулевому набору нулей и единиц
, и каждому
нулевому набору нулей и единиц ![]() соответствует дизъюнкта всех переменных,
в которой i-ая переменная взята с отрицанием, если
соответствует дизъюнкта всех переменных,
в которой i-ая переменная взята с отрицанием, если ![]() , и без отрицания, если
, и без отрицания, если
![]() , получим
СКНФ:
, получим
СКНФ:
![]()
![]()
![]()
![]() .
.
10. Для функции ![]() по карте Карно двумя способами
найти МКНФ.
по карте Карно двумя способами
найти МКНФ.
Решение: первый способ: для получения МКНФ можно использовать карту Карно, по которой находили МДНФ. В этой карте следует заменить переменные на их отрицания и наоборот; на пустые места поставить 0 и убрать 1. Затем отметить на карте максимальные блоки, содержащие 2 или 4 нулевые соседние ячейки. В нашем случае имеется 3 блока по 2 ячейки, которым соответствуют упрощённые дизъюнкты двух переменных. Заметим, что блоки по две ячейки в этом случае можно отметить по-разному. Мы выбрали один из вариантов.
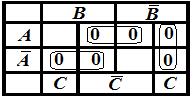
По
этой карте МКНФ формулы имеет вид: ![]() .
.
Второй способ: в обычной карте Карно заполнить нулями
ячейки, соответствующие дизъюнктам СКНФ, и отметить максимальные блоки,
содержащие 2 или 4 нулевые соседние ячейки. Так как СКНФ функции ![]()
![]()
![]()
![]() , то карта Карно и отмеченные блоки имеют вид:
, то карта Карно и отмеченные блоки имеют вид:
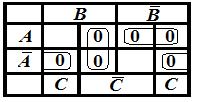
Итак, МКНФ функции: ![]() . Мы выбрали эти блоки, чтобы получить
МКНФ в том же виде, что и в первом случае. Можно было бы отметить другие блоки,
тогда была бы получена другая МКНФ.
. Мы выбрали эти блоки, чтобы получить
МКНФ в том же виде, что и в первом случае. Можно было бы отметить другие блоки,
тогда была бы получена другая МКНФ.
11. По данной схеме составить и упростить переключательную функ-
цию, построить упрощённую схему.
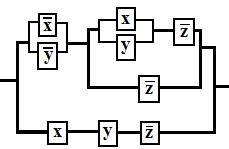
Решение:
составим функцию проводимости для
данной схемы ![]() .
Для упрощения этой функции используем два метода. По методу элементарных
преобразований имеем:
.
Для упрощения этой функции используем два метода. По методу элементарных
преобразований имеем:![]() =
| 3 | =
=
| 3 | = ![]() = |
5 | =
= |
5 | =![]() = =
= =![]()
![]() . Для наглядности знак
. Для наглядности знак ![]() в некоторых местах опущен.
в некоторых местах опущен.
Для минимизации с помощью карт Карно сначала получим СДНФ:
![]() = | 5 | =
= | 5 | = ![]() = |
3 | =
= |
3 | = ![]() =
=
=
| 10a | = ![]() = | 1,
4 | =
= | 1,
4 | = ![]() - СДНФ.
- СДНФ.
В карте Карно отметим единицами конъюнкты, рядом стоящие единицы объединим в блоки и составим МДНФ.
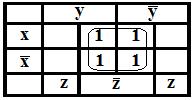
Таким
образом МДНФ: ![]() .
.
Полученной формуле соответствует упрощённая схема:
![]()
2.4 Справочный материал
Логические операции и их таблицы истинности
1. Конъюнкция – (![]() ), читается «x и y».
), читается «x и y».
2. Дизъюнкция – ( ![]() ), читается «x или y».
), читается «x или y».
3. Отрицание
(инверсия) – (![]() ),
читается «не x».
),
читается «не x».
4. Импликация - (![]() ), читается «если х, то
у».
), читается «если х, то
у».
5. Эквиваленция – (![]() ), читается «х если и
только, если у».
), читается «х если и
только, если у».
6. Штрих Шеффера – (![]() ), определяется как
отрицание конъюнкции, т.е. читается «не x и y».
), определяется как
отрицание конъюнкции, т.е. читается «не x и y».
7. Стрелка Пирса – (![]() ), определяется как
отрицание дизъюнкции, т.е. читается «не x или y».
), определяется как
отрицание дизъюнкции, т.е. читается «не x или y».
8. Кольцевая сумма –
(![]() ),
определяется как отрицание эквиваленции (исключающее «или»), т.е. читается «или
х, или у».
),
определяется как отрицание эквиваленции (исключающее «или»), т.е. читается «или
х, или у».
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
|
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
1 |
|
1 |
1 |
1 |
1 |
0 |
0 |
0 |
Основные эквивалентные соотношения (законы)
|
1 |
Коммутативность |
|
|
||
|
2 |
Ассоциативность |
|
|
||
|
3 |
Дистрибутив— ность |
|
|
||
|
4 |
Идемпотентность |
|
|
||
|
5 |
Законы поглощения |
|
|
||
|
6 |
Законы Де-Моргана |
|
|
||
|
7 |
Двойное отрицание
|
||||
|
8 |
Свойства констант |
|
|
||
|
9 |
|
|
|||
Некоторые другие полезные эквивалентные соотношения:
|
10 |
Закон склеивания |
|
|
10а |
Закон расщепления |
|
|
11 |
Обобщённое склеивание |
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
Схема приоритетов логически операций: ![]() . В этой схеме
знаки операций расположены в порядке убывания старшинства, в круглых скобках указаны
равносильные операции. Схему приоритетов можно построить и так:
. В этой схеме
знаки операций расположены в порядке убывания старшинства, в круглых скобках указаны
равносильные операции. Схему приоритетов можно построить и так:
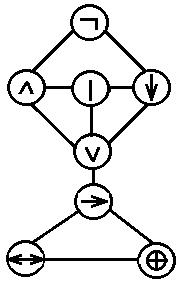
В этой схеме, чем выше знак, тем он сильнее, а знаки, расположенные на одном уровне, равносильны.
Список литературы
1 Судоплатов С.В., Овчинникова Е.В. Элементы дискретной математики. – М.: ИНФРА-М, Новосибирск: изд-во НГТУ, 2002.
2 Новиков Ф.А. Дискретная математика для программистов.Учебник для вузов. 2-е изд. – СПб.: Питер, 2004. – 364 с.: ил. (Серия «Учебник для вузов»).
3 Андерсон Д. Дискретная математика и комбинаторика.: Пер. с англ. – М.: Издатель- ский дом «Вильямс», 2004. – 960 с.: ил.–Парал. тит. англ.
4 Шапорев С.Д. Дискретная математика. Курс лекций и практических занятий. – СПб.: БХВ-Петербург, 2006.
5 Палий И.А. Дискретная математика. Курс лекций. – М.: Эксмо, 2008. – 352 с. (Техническое образование).
6 Плотников А.Д. Дискретная математика. Учебное пособие. – 2-е изд. - М.: Новое знание, 2006. – 304 с.
7 Галушкина Ю.И., Марьямов А.Н. Конспект лекций по дискретной математике. – М.: Айрис – пресс, 2007. – 176 с. (Высшее образование).
8 Данилов В.Г. и др. Дискретная математика. Учебное пособие для вузов. – М.: Горячая линия - Телеком, 2008. – 136 с.
9 Астраханцева Л.Н. Дискретная математика. Учебное пособие. – Алматы: АУЭС, 2011. – 78 с.
10 Астраханцева Л.Н., Байсалова М.Ж. Дискретная математика. Методические указания к расчетно- графической работе для студентов специальностей 5В070400 – Вычислительная техника и программное обеспечение, 5В070300 – Информационные системы всех форм обучения - Алматы: АУЭС, 2012. - Ч.1 - 23 с.
11 Астраханцева Л.Н., Байсалова М.Ж. Дискретная математика. Методические указания и задания к выполнению расчетно- графич. Работам (для спец. 5В070400 – «Вычислительная техника и программное обеспечение»). Часть 2. -Алматы: АУЭС, 2014. - 23 с.
Содержание
|
1 |
Расчетно-графическая работа №1. Множества, отношения…………… |
3 |
|
1.1 |
Теоретические вопросы……………………………………………… |
3 |
|
1.2 |
Расчётные задания……………………………………………………… |
3 |
|
1.3 |
Решение типового варианта…………………………………………… |
12 |
|
2 |
Расчетно-графическая работа №2. Элементы математической логики |
22 |
|
2.1 |
Теоретические вопросы……………………………………………… |
22 |
|
2.2 |
Расчётные задания…………………………………………………… |
22 |
|
2.3 |
Решение типового варианта…………………………………………… |
30 |
|
2.4 |
Справочный материал…………………………………………………… |
36 |
|
|
Список литературы…………………………………………………… |
38 |
Сводный план 2017 г., поз. 129
Астраханцева Людмила Николаевна
Байсалова Маншук Жумамуратовна
ДИСКРЕТНАЯ МАТЕМАТИКА
Методические указания и задания по выполнению расчетно-графических
работ для студентов специальности 5В070300 – Информационные системы
Редактор Л.Т. Сластихина
Специалист по стандартизации Н.К.Молдабекова
Подписано в печать_______ Формат 6084 1/16
Тираж 25 экз. Бумага типографская №1
Объем 2,56 уч.-из.л. Заказ______ цена 1280 тг.
Копировально-множительное бюро
некоммерческого акционерного общества
«Алматинский университет энергетики и связи»