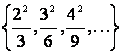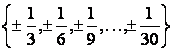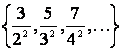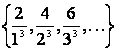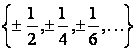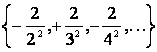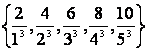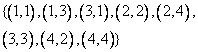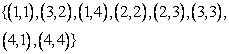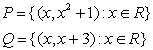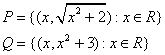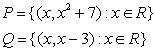Коммерциялық емес акционерлік қоғам

АЛМАТЫ ЭНЕРГЕТИКА  ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ

Жоғары математика кафедрасы

 

 

ДИСКРЕТ МАТЕМАТИКА 

5В070400 – Есептеу техникасы мен бағдарламалық қамтамасыз ету,

 5В070300 – Ақпараттық жүйелер мамандықтарының барлық оқу түрінің

студенттері үшін есептеу-графикалық жұмыстарды орындауға арналған әдістемелік нұсқаулар мен тапсырмалар

1-бөлім

 

Алматы 2012 

ҚҰРАСТЫРУШЫЛАР: Астраханцева Л.Н., Байсалова М.Ж. Дискрет математика. 5В070400 – Есептеу техникасы мен бағдарламалық қамтамасыз ету және 5В070300 – Ақпараттық жүйелер мамандықтарының барлық оқу түрінің студенттері үшін есептеу-графикалық жұмыстарды орындауға арналған әдістемелік нұсқаулар мен тапсырмалар. 1-бөлім  - Алматы: АЭжБУ, 2012.- 24 б.

Бұл әдістемелік нұсқаулар мен тапсырмалар 5В070400 – Есептеу техникасы мен бағдарламалық қамтамасыз ету және 5В070300 – Ақпараттық жүйелер мамандықтарының барлық оқу түрінің студенттеріне «Дискрет математика» пәнінің №1 есептеу-графикалық жұмыстарын орындауға арналған.

Бұл материал көрсетілген мамандықтың «Дискрет матемтика» пәнінің «Жиындар. Қатынастар» тарауының бағдарламасына сәйкес құрылған.

Тапсырмалар берілген және қажет теориялық мәліметтер келтірілген. Типтік нұсқаның шешуі толық көрсетілген.

Кестелер 10, без. 10, әдеб.көрсеткіші – 12 атау. 

 

Пікір беруші: ӨКЭЖ  кафедрасының доценті  Башкиров М.В.

  

«Алматы энергетика және байланыс университеті» коммерциялық емес акционерлік қоғамының  2012 ж. жоспары бойынша басылды 

 

ã «Алматы энергетика және байланыс университеті» КЕАҚ, 2012 ж.

 

Кіріспе 

   «Дискрет математика» пәні аппарат құралдарының терминдерінде және  бағдарламалық қамтамасыз етуде  компьютерде символдар мен берілімдерді қолданып есеп шығаратын математика бөліміне  арналған.

  «Дискрет математика» пәні жасанды интеллект саласында есеп шығару үшін, программаның дұрыстығын дәлелдеу үшін, математикалық модель құра білуге дағдылану үшін, тұжырымдарды формализациялаудың негізгі әдістерін меңгеру үшін оқытылады.

 

1       Есептік-графикалық жұмыс 1. Жиындар, катынастар

 

  «Жиындар, катынастар» бөлімдерін оқудың мақсаты «Алгоритмдер және берілімдердің структурасы», «Автоматтар және тілдер теориясы» тағы басқа пәндерді оқып меңгеру қажеттілігінен туындаған.

 

1.1 Есептік тапсырмалар

 

1 Берілген жиынды

а) элементтерін тізу арқылы

б) жалпы қасиеті бойынша жазу керек

 

1 к е с т е

№

а)

б)

1.1

                                            

1.2

                                    

1.3

                                             

1.4

                                

1.5

                                              

1.6

                                                 

1.7

                                    

1.8

                                      

1.9

                                               

1.10

                       

1.11

                                     

1.12

                                        

  

1 кестенің жалғасы

1.13

 

                                       

1.14

 

                                     

1.15

 

                          

1.16

 

 

1.17

 

 

1.18

 

1.19

 

 

1.20

 

 

1.21

 

 

1.22

 

 

1.23

 

        

1.24

 

 

1.25

 

 

1.26

 

 

1.27

 

   

1.28

 

 

1.29

 

 

1.30

 

 

 

2 U={1,2,3,4,5,6,7,8,9,10} – универсалды жиын болсын. Берілген А, В, С жиындары үшін табу керек

а);

б);

в);

г);

д);

е) ;

ж) ;

з) .

  

2  к е с т е

№

A

B

C

2.1

{1,2,3,4,5,6,7}

{4,5,6,7,8,9,10}

{2,4,6,8,10}

2.2

{2,3,4,5,6,7,8}

{5,6,7,8,9,10}

{1,3,5,7,9}

2.3

{3,4,5,6,7,8,9}

{6,7,8,9,10}

{1,2,4,6,8,9}

2.4

{6,7,8,9,10}

{1,2,4,6,8,9}

{3,4,5,6,7,8,9}

2.5

{4,5,6,7,8,9,10}

{2,4,6,8,10}

{1,2,3,4,5,6,7}

2.6

{1,3,5,7,9}

{2,3,4,5,6,7,8}

{5,6,7,8,9,10}

2.7

{1,2,3,5,7,9,10}

{3,4,5,6,7,8}

{2,4,6,7,8,9}

2.8

{6,7,8,9,10}

{1,2,3,4,5,6,7}

{3,4,5,6,7,8}

2.9

{1,3,5,7,8,9}

{2,4,6,8,10}

{7,8,9,1,2,3}

2.10

{2,4,6,7,8,9}

{1,3,5,6,7,8}

{8,9,10,1,2,3}

2.11

{2,4,6,8,10}

{1,2,3,4,5,6,7}

{4,5,6,7,8,9,10}

2.12

{1,3,5,7,9}

{2,3,4,5,6,7,8}

{5,6,7,8,9,10}

2.13

{1,2,4,6,8,9}

{3,4,5,6,7,8,9}

{6,7,8,9,10}

2.14

{3,4,5,6,7,8,9}

{6,7,8,9,10}

{1,2,4,6,8,9}

2.15

{1,2,3,4,5,6,7}

{4,5,6,7,8,9,10}

{2,4,6,8,10}

2.16

{5,6,7,8,9,10}

{1,3,5,7,9}

{2,3,4,5,6,7,8}

2.17

{2,4,6,7,8,9}

{1,2,3,5,7,9,10}

{3,4,5,6,7,8}

2.18

{3,4,5,6,7,8}

{6,7,8,9,10}

{1,2,3,4,5,6,7}

2.19

{7,8,9,1,2,3}

{1,3,5,7,8,9}

{2,4,6,8,10}

2.20

{8,9,10,1,2,3}

{2,4,6,7,8,9}

{1,3,5,6,7,8}

2.21

{4,5,6,7,8,9,10}

{2,4,6,8,10}

{1,2,3,4,5,6,7}

2.22

{5,6,7,8,9,10}

{1,3,5,7,9}

{2,3,4,5,6,7,8}

2.23

{6,7,8,9,10}

{1,2,4,6,8,9}

{3,4,5,6,7,8,9}

2.24

{1,2,4,6,8,9}

{3,4,5,6,7,8,9}

{6,7,8,9,10}

2,25

{2,4,6,8,10}

{1,2,3,4,5,6,7}

{4,5,6,7,8,9,10}

2.26

{2,3,4,5,6,7,8}

{5,6,7,8,9,10}

{1,3,5,7,9}

2.27

{3,4,5,6,7,8}

{2,4,6,7,8,9}

{1,2,3,5,7,9,10}

2.28

{1,2,3,4,5,6,7}

{3,4,5,6,7,8}

{6,7,8,9,10}

2.29

{2,4,6,8,10}

{7,8,9,1,2,3}

{1,3,5,7,8,9}

2.30

{1,3,5,6,7,8}

{8,9,10,1,2,3}

{2,4,6,7,8,9}

          

3 Берілген А  және  В жиындары үшін табу керек

а);

б);

в);

г) А жиынының булеанын (яғни ішкі жиындар жиынын);

д) A жиынының қандай да бір бүркеуін;

е) A жиынының қандай да бір бөліктеуін;

ж) ішкі жиындардың кез келген А  жиынын (булеан да емес, бүркеу де емес, бөліктеу де емес).

 

3 к е с т е

№

A

B

№

A

B

3.1 

{1,2,3}

{4,5}

3.2

{3,4,5}

{7,8}

3.3

{7,8,9}

{1,2,3}

3.4

{7,8,9}

{3,4,5}

3.5

{4,5,8}

{2,3,5}

3.6

{4,7,8}

{9,0}

3.7

{3,4,9}

{6,7,8}

3.8

{2,6,8}

{1,2,3}

3.9

{3,5,7}

{1,4,6}

3.10 

{8,9,0}

{1,2,4}

3.11

{1,3,5}

{6,7,8}

3.12

{0,1,2}

{8,9}

3.13

{6,7,8}

{4,5}

3.14

{4,5,6}

{1,2}

3.15

{3,4,8}

{1,9}

3.16

{2,9,5}

{3,4}

3.17

{4,6,8}

{1,2,3}

3.18

{1,2,3}

{4,7,9}

3.19 

{1,5,6}

{2,3}

3.20

{1,3,5}

{2,7,8}

3.21

{6,7,9}

{5,8}

3.22

{6,7,8}

{5,9}

3.23

{2,4,6}

{3,5}

3.24

{3,4,7}

{8,9}

3.25

{5,6,0}

{1,2}

3.26

{5,6,8}

{2,3,7}

3.27

{1,3,4}

{7,8}

3.28

{1,3,5}

{6,7}

3.29

{2,7,8}

{4,6,9}

3.30

{3,4,6}

{1,9}

 

4 Теңдікті Эйлер-Венн диаграммасы көмегімен дәлелдеу керек.

 

4 к е с т е

4.1

A \ (BC)=(A \ B)∩(A \ C)

4.2

(AB) \ (C∩A)=(A \ C) (B \ A)

4.3

A \ (B∩C)=(A \ B) (A \ C)

4.4

4.5

(A \ B)∩C=(A∩C) \ (B∩C)

4.6

4.7

(A \ B)C=(AC) \ (B\C)

4.8

4.9

A∩(B \ C)=(A∩B) \ (A∩C)

4.10

4.11

(A \ B) \ C=(A \ C) \ (B \ C)

4.12

4.13

(A \ C)(A∩B)=A \ (C \ B)

4.14

B \ (A∩C)=(B \ A) (B \ C)

4.15

(A∩B) \ C =A∩(B\ C )

4.16

4.17

(AC) \ (B\A)=A(C \ B )

4.18

4.19

(A∩B) \ (A∩C)= (A∩B) \ C

4.20

4.21

(AB )\ C=(A \ C) (B \ C)

4.22

4.23

A \ (B \ C)=(A \ B)(A∩C)

4.24

4.25

A \ (BC)=(A \ B) \ C

4.26

(B \ A) (B \ C) = B \ (A∩C)

4.27

(A \ B)C=(AC) \ B

4.28

(B \ C)(A∩B)=B \ (C \ A)

4.29

(A \ B)(C \ B)=(AC) \ В                          

4.30

(В \ А) \ С = (В \ С) \ (А \ С)

 

5 [P] және [Q] матрицалары қандай да бір бинарлық қатынастың матрицалары болсын. Табу керек  [PQ], [PQ], [PQ], [P], [] .

 PQ және Q P ену қатынастарының орындалуын тексеру керек

 

5 к е с т е

№

[P]

[Q]

№

[P]

[Q]

5.1 

5.2

5.3

5.4

5.5

5.6

5.7

5.8

5.9

5.10 

5.11

5.12

5.13

5.14

5.15

5.16

5.17

5.18

5.19 

5.20

5.21

5.22

5.23

5.24

5.25

5.26

5.27

5.28

5 кестенің жалғасы

5.29

5.30

 

6 А={a,b,c} және В={1,2,3,4} жиындары мен   қатынастары үшін

a)  және  қатынастарының матрицасын құру керек;

б) қатынастарды графиктік түрде кескіндеу керек;

в) табу керек ;

г)  қатынасы үшін рефлексивтік, симметриялық, антисимметриялық, транзитивтілік қасиеттері орындалатынын тексеру керек.

 

6 к е с т е

№

6.1

6.2

6.3

6.4

6.5

6.6

6.7

6.8

6.9

6.10

6.11

6.12

6.13

6.14

6.15

6.16

6.17

6.18

6.19

 

 

6  кестенің жалғасы

6.20

6.21

6.22

6.23

6.24

6.25

6.26

6.27

6.28

6.29

6.30

 

7 A={a,d,c,d,е} немесе A={a,d,c,d} жиынында  қатынасының реттік қатынас  болатындығын дәлелдеу керек. Бұл қандай реттілік (бөліктеп қатаң емес, қатаң, сызықты)? Реттелген  жиыны үшін Хассе диаграммасын құру керек.

 

7 к е с т е

№

Р

№

Р

7.1

 {(a,a),(b,b),(c,c),(d,d),(a,c),(b,c)}

7.2

{(a,c),(b,c),(b,d),(c,d),(a,d)}

7.3

{(a,a),(b,b),(c,c),(d,d),(a,c),(b,c),(c,d),

(a,d),(b,d)}

7.4

{(a,a),(b,b),(c,c),(d,d),(e,e),(a,b),(a,c),

(a,e), (d,b),(e,b)}

7.5

 {(a,a),(b,b),(c,c),(d,d),(a,b),(a,c),(b,c),

 (b,d),(c,d),(a,d)}

7.6

{(a,a),(b,b),(c,c),(d,d),(e,e),(c,a),(c,b),

(c,e),(d,a),(d,b),(d,e),(e,a),(e,b)}

7.7

{(a,a),(b,b),(c,c),(d,d),(e,e),(d,a),(d,b),

(d,c),(e,a),(e,b),(e,c),(e,d)}

7.8

{(a,a),(b,b),(c,c),(d,d),(e,e),(a,b),(a,c),

(e,d), (e,c)}

7.9

{(a,b),(c,a),(c,b,),(d,a),(d,b),(e,a),(e,b)}

7.10

{(a,b),(a,c),(b,c),(b,d),(c,d),(a,d)}

7.11

{(a,b),(c,b),(d,a),(d,b),(d,c),(d,e)}

7.12

{(c,a),(c,b),(c,e),(d,a),(d,b),(d,e),(e,a),

(e,b)}

7.13

{(a,a),(b,b),(c,c),(d,d),(e,e),(a,b),(c,b),

 (d,a),(d,b),(d,c),(d,e)}

7.14

{(a,a),(b,b),(c,c),(d,d),(e,e),(a,b),(c,a),(c,b), (d,a),(d,b),(e,a),(e,b)}

 

7  кестенің жалғасы

7.15

{(a,b),(a,c),(a,e),(d,b),(e,b)}

7.16

{(a,b),(c,b),(a,c),(e,d,),(e,c),(e,b)}

7.17

 {(a,a),(b,b),(c,c),(d,d),(a,c),(b,c)}

7.18

{(a,c),(b,c),(b,d),(c,d),(a,d)}

7.19

{(a,a),(b,b),(c,c),(d,d),(a,c),(b,c),(c,d),

(a,d),(b,d)}

7.20

{(a,a),(b,b),(c,c),(d,d),(e,e),(a,b),(a,c),

(a,e), (d,b),(e,b)}

7.21

 {(a,a),(b,b),(c,c),(d,d),(a,b),(a,c),(b,c),

 (b,d),(c,d),(a,d)}

7.22

{(a,a),(b,b),(c,c),(d,d),(e,e),(c,a),(c,b),

(c,e),(d,a),(d,b),(d,e),(e,a),(e,b)}

7.23

{(a,a),(b,b),(c,c),(d,d),(e,e),(d,a),(d,b),

(d,c),(e,a),(e,b),(e,c),(e,d)}

7.24

{(a,a),(b,b),(c,c),(d,d),(e,e),(a,b),(a,c),

(e,d), (e,c)}

7.25

{(a,b),(c,a),(c,b,),(d,a),(d,b),(e,a),(e,b)}

7.26

{(a,b),(a,c),(b,c),(b,d),(c,d),(a,d)}

7.27

{(a,b),(c,b),(d,a),(d,b),(d,c),(d,e)}

7.28

{(c,a),(c,b),(c,e),(d,a),(d,b),(d,e),(e,a),

(e,b)}

7.29

{(a,a),(b,b),(c,c),(d,d),(e,e),(a,b),(c,b),

 (d,a),(d,b),(d,c),(d,e)}

7.30

{(a,a),(b,b),(c,c),(d,d),(e,e),(a,b),(c,a),(c,b),(d,a),(d,b),(e,a),(e,b)}

 

8  жиынында  қатынасының эквиваленттік қатынас  болатындығын дәлелдеу керек. Эквиваленттік класстарын және фактор-жиынды құру керек. 

 

8 к е с т е 

№

Р

№

Р

8.1

8.2

8.3

8.4

8.5

8.6

8.7

8.8

8.9

8.10

8.11

8.12

8.13

8.14

8.15

8.16

8.17

8.18

 

 

8 кестенің жалғасы

8.19

8.20

8.21

8.22

8.23

8.24

8.25

8.26

8.27

8.28

8.29

8.30

 

 

9 А={1,2,3,4,5,6} жиынының бөліктеуі үшін сәйкес эквиваленттілік қатынасын құру керек. Ол неге эквиваленттілік қатынасы болады? Эквиваленттілік класстар мен фактор – жиынды жазу керек.

 

9 к е с т е

№

 А бөліктеуі

№

А бөліктеуі

9.1

{{1,2},{3,4},{5,6}}

9.2

{{1},{2},{3},{4,5},{6}}

9.3

{{1},{2,3},{4,5,6}}

9.4

{{1},{2,3,4},{5,6}}

9.5

{{1,2,3},{4},{5,6}}

9.6

{{1},{2,3},{4},{5,6}}

9.7

{{1},{2},{3,4},{5,6}}

9.8

{{1,2},{3},{4,5},{6}}

9.9

{{1,2,3,4},{5},{6}}

9.10

{{1,2,3,4},{5,6}}

9.11

{{1,2},{3},{4},{5,6}}

9.12

{{1},{2,3,4,5},{6}}

9.13

{{1},{2,3,4},{5},{6}}

9.14

{{1},{2},{3},{4},{5,6}}

9.15

{{1,2},{3,4}{5},{6}}

9.16

{{1},{2},{3,4},{5},{6}}

9.17

{{1},{2},{3},{4,5,6}}

9.18

{{1},{2},{3},{4},{5},{6}}

9.19

{{1},{2},{3,4,5},{6}}

9.20

{{1},{2},{3,4,5,6}}

9.21

{{1,2,3,4,5},{6}}

9.22

{{1,2,3},{4},{5},{6}}

9.23

{{1,2,3},{4,5,6}}

9.24

{{1},{2,3},{4,5},{6}}

9.25

{{1,2},{3,4,5,6}}

9.26

{{1},{2,3,4,5,6}}

9 кестенің жалғасы

9.27

{{1,2},{3},{4},{5},{6}}

9.28

{{2},{1,3,4,5},{6}}

9.29

{{1,2,3},{4,5},{6}}

9.30

{{3},{1,2,4,5},{6}}

 

10  және  қатынастары берілген. Бұл қатынастардың функция болатындығын дәлелдеу керек.  композицияларын табу керек. Бұл қатынастарға инъективтілік, сюръективтілік, биективтілік қасиеттерінің орындалуын тексеру керек.

 

10 к е с т е

10.1

10.2

10.3

 

10.4

10.5

10.6

10.7

10.8

10.9

10.10

10.11

10.12

10.13

10.14

10.15

10.16

10.17

10.18

10.19

10.20

10.21

10.22

10.23

10.24

10.25

10.26

 

10 кестенің жалғасы

10.27

10.28

10.29

10.30

 

1.2 Типтік варианттың шешуі

 

1а)  жиынын элементтерін тізу арқылы жазу керек.

Шешуі:

N={1,2,3,4,…} болғандықтан  А={1,2,3}.

 

1б) 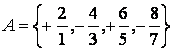  жиынын жалпы қасиеті бойынша арқылы

жазу керек.

 

Шешуі:

.

 

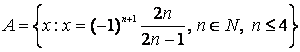2 U={1,2,3,4,5,6,7,8,9,10} – универсал жиыны берілген болсын. Берілген А={1,2,3,8,9,10}, В={1,3,5,6,7,8}, С={2,4,6,7,8,9} жиындары үшін табу керек

а);

б);

в);

г);

д);

е) ;

ж) ;

и) .

Шешуі:

а) ;

б);

в); г); д); е);

ж) ;

и) .

3 Берілген А={3,4,5}  және В={6,7,9} жиындары үшін:

a) ;

б) ;

в) ;

г) А жиынының булеанын құру керек (яғни ішкі жиындардың жиынын);

д) А жиынының қандай да бір бүркеуін;

е) А жиынының қандай да бір бөліктеуін;

ж) А жиынының қандай да бір ішкі жиындардың жиынын (бүркеу де, бөліктеу де емес) табу керек.

Шешуі:

a) =

;

б); в);

г)  жиыны үш элементтен тұрғандықтан, оның P  булеаны  элементтен тұрады:   P  ;

д) мысалы,  - -ның бүркеуі;

е) мысалы,, - -ның бөліктеуі;

ж) мысалы,  -  булеан да емес, бөліктеу де емес, бүркеу де емес.

 

4  теңдігін Эйлер-Венн диаграммасы көмегімен дәлелдеу керек.

Шешуі: теңдіктің сол және оң жақтарын Эйлер-Венн диаграммасында бейнелейміз.

         Сол жағы:

                      

 

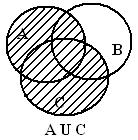
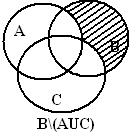
1 сурет - Эйлер –Венн диаграммасы

          

Оң жағы:

 

                                

 

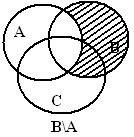
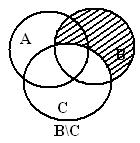
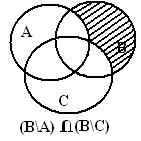
2 сурет - Эйлер –Венн диаграммасы

 

Сол және оң жақтарды бейнелейтін суреттерде жиындардың бірдей бөліктері белгіленген, бұл теңдікті дәлелдейді.

5 [P] = және [Q] =  матрицалары қандай да бір бинарлық қатынастың матрицалары болсын. Табу керек  [PQ], [PQ], [PQ], [P], [].     PQ және Q P енулерінің орындалуын тексеру керек.

Шешуі:

егер [P] = , [Q] = , онда [PQ] == [P]+[Q], мұндағы матрицалардың  элементтері келесі ережелермен қосылады: 0+0=0, 1+0 = 0+1 = 1+1 =1; [PQ] = == [P]*[Q], яғни сәйкес элементтер кәдімгі ереже бойынша көбейтіледі: = = = 0, = 1; [PQ]= - матрицалар кәдімгідей көбейтіледі, бірақ [P] және [Q] матрицаларының элементтері жоғарыда келтірілген ереже бойынша қосылып, көбейтіледі; [P-1]=[P]T, мұндағы P-1 қатынасы  P қатынасына кері қатынас; - Р қатынасының толықтауышы және оның [] матрицасы  Р қатынасының матрицасына тең, тек нөлдер бірмен, ал бірлер нөлдермен алмастырылған; егер PQ, онда  .

          Біздің жағдайда ;

; 

;

;

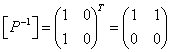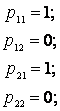
;     мысалы, элементінің мәні  элементінің мәнінен кіші не тең емес болғандықтан,  P Q енуі орынды емес;  

 элементінің мәні   элементінің мәнінен кіші не тең емес болғандықтан,    енуі де орынды емес.

                  

6 А={a,b,c,d} эәне В={1,2,3,4} жиындары мен , ,  қатынастары үшін

a)  және  қатынастарының матрицасын құру керек;

б) қатынастарды графиктік түрде кескіндеу керек;

в) табу керек ;

г)  қатынасы үшін рефлексивтілік, симметриялық, антисимметриялық

транзитивтілік қасиеттері орындалатынын тексеру керек.

 

         Шешуі:

а) егер 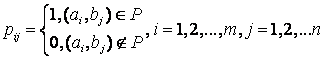 болса, онда анықтама бойынша -  қатынасының матрицасы

Сонымен,  , .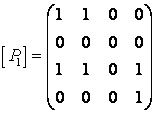

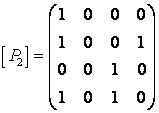б)  және  қатынастарының графиктік түрде кескінделуі 3 және 4 суреттерінде көрсетілген.

     

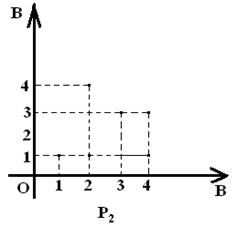
           3 сурет --дің графигі                 4 сурет - -нің графигі

 

Қатынастардың графиктік түрде кескінделуінің басқа да тәсілдері бар. Мысалы,  графиктік түрде кескінделуі 5 суретте, ал   қатынасыныкі – 6 суретте көрсетілген (яғни бағытталған граф ретінде).

 

                                

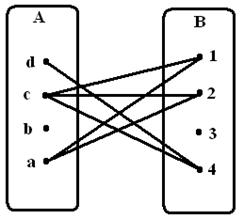
                    5  сурет -  графы                                  6 сурет -  графы

 

в)  болғандықтан, онда

 , .

, және

 ескерсек, онда  -дің толықтауышы

 болады.

Анықтама бойынша P1P2 = {(a,c)| aA, cC және bB: (a,b) P1 және (b,c)P2}, мұндағы ,  онда             

.

г)  қатынасының қасиеттерін оның матрицасы  арқылы анықтаған қолайлы. Бұл матрицаның бас диагоналінде бәрі бірлер емес болғандықтан,  қатынасы рефлексивті емес;  болғандықтан,  ол симметриялы емес.  матрицасының бас диагоналден басқа элементтердің бәрі нөлдер   болғандықтан,  қатынасы антисимметриялы; мысалы, , бірақ , онда  транзитивті емес.

 

7 A={a,d,c,d,е} жиынында  қатынасының реттік қатынас  болатындығын дәлелдеу керек. Бұл қандай реттілік (бөліктеп қатаң емес, қатаң, сызықты)? Реттелген  жиыны үшін Хассе диаграммасын құру керек.

 

 

7 сурет - Реттік қатынастың классификациясы

 

Шешуі:

Қатынас ретінің  терминологиясы мен классификациясы әр оқулықта әртүрлі екенін айта кетелік. Біз төменде келтірілген сұлбаны ұстанамыз (7 суретті қара). Суреттегі қатынас

Келесі қысқартып жазулар енгізілген: д.р.ж., с.р.ж., т.р.ж. – сәйкес дербес, сызықты, толық реттелген жиындар. Сонымен қатар, егер А ақырлы жиын болса, онда с.р.ж.  т.р.ж. болады.

Біздің қатынас үшін рефлексивтілік, симметриялық, антисимметриялық және транзитивтік қасиеттерінің орындалуын тексереміз. Оны қатынастың матрицасы арқылы тексерген қолайлы.

 – берілген қатынастың матрицасы.

Бұл матрицаның бас диагоналінде тек бірлер емес болғандықтан,  қатынасы рефлексивті емес; ,

яғни  симметриялы емес;  ,

матрицасының бас диагоналден басқа элементтердің бәрі нөлдер   болғандықтан,  қатынасы антисимметриялы;  қатынастың транзитивті болуы үшін,  енуі немесе егер , , онда  

орындалуы керек. Ол үшін

=.

Бұдан  , бұл -ның транзитивтілігіне көз жеткізеді.

Сонымен,  рефлексивті емес, антисимметриялы және транзитивті, сондықтан бұл қатынас қатаң ретті болады.  және , және ,  және  элементтері салыстырылмайтын болғандықтан,  сызықты ретті емес. Егер ақырлы жиында анықталған реттілік сызықты болмаса, онда ол толық емес.

- реттелген жиын болсын. Егер А ақырлы болса, онда  жиынын сұлба ретінде (Хассе диаграммасы) бейнелеуге болады. Егер  болса, онда  және  нүктелермен бейнеленеді, егер  элементі -тен төмен болса, сызықпен қосылады.

Хассе диаграммасын құрайық. Реттік қатынастың транзитивтілігін ескерсек, мысалы,  және элементтерін сызықпен қосудың қажеті жоқ, себебі егер  және , онда .

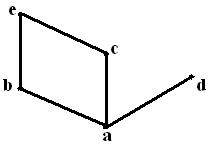
8 сурет - Хассе диаграммасы

 

 рефлексивті болған жағдайда, яғни  дербес ретті немесе қатаң емес ретті болса,  Хассе диаграммасында әрбір төбеде тұзақ пайда болар еді.

 

8  жиынында   қатынасының эквиваленттік қатынас  болатындығын дәлелдеу керек. Эквиваленттік класстарын және фактор-жиынды құру керек. 

         Шешуі:

егер  қатынасы  рефлексивті, симметриялы, транзитивті болса, онда ол эквивалентті болады.  қатынасының матрицасын құрып, ол бойынша қасиеттерін анықтаймыз.

.

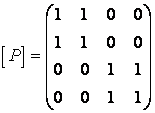Бұл матрицаның бас диагоналінде тек бірлер  болғандықтан,  қатынасы рефлексивті;  болғандықтан, ол симметриялы.

.

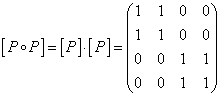Сонымен, , бұл -ның транзитивтілігін дәлелдейді.

          – рефлексивті, симметриялы, транзитивті, сондықтан ол эквивалентті қатынас болады.

          элементінің эквивалентті классы деп  жиыны айтылады. Барлық эквиваленттік класстар жиыны   жиынының -ге қатысты фактор-жиыны деп аталады.

 жиыны  жиынының бөліктеуі болып табылады.

 жиынының әрбір элементі үшін эквивалентті класстары:

,

,

,

.

Сонымен, .

 жиынының -ге қатысты фактор-жиыны: .

 

9 А={1,2,3,4,5,6} жиынының {{1,3},{2,4,5},{6}} бөліктеуі үшін сәйкес эквиваленттілік қатынасын құру керек. Ол неге эквиваленттілік қатынасы болады? Эквиваленттілік кластар мен фактор – жиындарды жазу керек.

Шешуі:

A= – А жиынының бөліктеуі болсын, мұндағы () – А жиынының ішкі жиындары. Сонда

 – осы бөліктеуге сәйкес эквиваленттік қатынасы.

Сонымен, біздің жағдайда  ={(1,1),(1,3),(3,1),(3,3),(2,2)(2,4),(2,5),

(4,2),(4,4)(4,5),(5,2),(5,4),(5,5),(6,6)} – берілген бөліктеуге сәйкес эквиваленттік қатынасы. Бұл эквиваленттік қатынас екендігіне көз жеткізу үшін, оның матрицасын табамыз:

 .

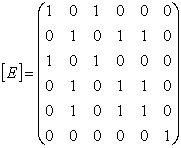Матрица бойынша  рефлексивті екендігін анықтаймыз (бас диагоналда бәрі нөлдер), симметриялы (), транзитивті (). Сондықтан,  – эквиваленттік қатынас. Эквиваленттік класстары: [1]=[3]={1,3}, [2]=[4]=[5]={2,4,5}, [6]={6}.  жиынының -ге қатысты фактор-жиыны берілген бөліктеу  = ={{1,3},{2,4,5},{6}} болып табылады.

 

10  және  қатынастары берілген.

а) бұл қатынастардың функция болатындығын дәлелдеу керек;

б)  композицияларын табу керек;

в) бұл қатынастарға инъективті, сюръективті, биективті қасиеттерінің орындалуын тексеру керек

Шешуі:

а) Егер  немесе кез келген  үшін  орындалатындай  жалғыз табылатын болса,  қатынасы функция болады,

Біздің жағдайда  және  функциялар болады, себебі кез келген нақты  саны үшін,  және   сандары табылып, олар жалғыз болады.

б) , ;

в) берілген функцияларды инъективтілікке тексереміз. Егер  немесе  болса, онда

 функциясы инъективті деп аталады.

 функциясы үшін инъективтілік шарттары орындалмайды себебі -тің екі мәніне () -тің жалғыз мәні сәйкес келеді. Мысалы, , бірақ  және  , яғни  .

 инъективті, себебі кез келген нақты   саны үшін  орындалады.

Функцияны сюръективтілікке тексереміз. Егер кез келген  үшін  орындалатындай  табылса, онда  функциясы сюръективті деп аталады немесе  қатынасының мәндерінің жиыны  жиынымен беттеседі.

,  функциясы сюръективті емес,  себебі мәндерінің жиыны .

,  функциясы сюръективті, себебі

Егер функция әрі инъективті, әрі  сюръективті болса, онда ол биективті деп аталады.  Сондықтан –  биективті емес функция,  – биективті.

Инъективті, сюръективті және  биективті қасиеттерді функцияның графигі бойынша анықтауға болады. Берілген функционалдық қатынастарды кәдімгі функция етіп жазамыз: ; . Бұл функциялардың графиктері  9 және 10 суреттерде кескінделген.

                            

 

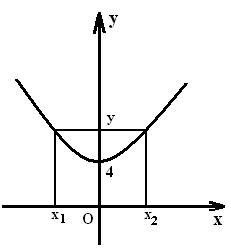
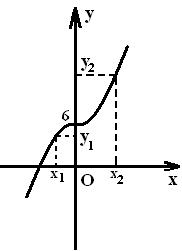
        9  сурет -   графигі                         10 сурет-  графигі

 

1.3 Бақылау сұрақтары

 

1 Жиындар, олардың берілу жолдары. Ішкі жиындар, булеан. Жиындарға қолданылатын қисаптар.

          2 Жиындарға қолданылатын қисаптардың қасиеттері. Жиынның бөліктеуі мен бүркеуі.

          3 Жиындардың тура көбейтіндісі. Қатынастар (унарлы, бинарлы, n-арлы). Бинарлы қатынастардың берілу жолдары. Кері қатынас, қатынастың толықтауышы, тепе-тең қатынас. Бинарлы қатынастардың композициясы.

         4 Бинарлы қатынастың матрицаларының негізгі қасиеттері (рефлексивтік, симметриялық, антисимметриялық, транзитивтік).

          5 Эквивалентті қатынас. Эквиваленттілік кластары, фактор-жиын.

          6 Реттік қатынас. Лексигографиктік реттілік.

          7 Функционалдық қатынас. Инъекция, сюръекция, биекция. Жиынның қуаты.

 

Әдебиеттер тізімі

  1. Судоплатов С.В., Овчинникова Е.В. Элементы дискретной математики. – М.: ИНФРА-М, Новосибирск: изд-во НГТУ, 2002.
  2. Москинова Г.И. Дискретная математика. Математика для менеджера в примерах и упражнениях: Учебное пособие. – М.: Логос, 2004. – 240 с.
  3. Новиков Ф.А. Дискретная математика для программистов.Учебник для вузов. 2-е изд.  – СПб.: Питер, 2004. – 364 с.: ил. – (Серия «Учебник для вузов»).
  4. Андерсон Д. Дискретная математика и комбинаторика.: Пер. с англ. – М.: Издатель- ский дом «Вильямс», 2004. – 960 с.: ил. – Парал. тит. англ.
  5. Шапорев С.Д. Дискретная математика. Курс лекций и практических занятий. – СПб.: БХВ-Петербург, 2006.
  6. Яблонский С.В. Введение в дискретную математику. – М.: «Высшая школа», 2001.
  7. Палий И.А. Дискретная математика. Курс лекций. – М.: Эксмо, 2008. – 352с. – (Техническое образование).
  8. Плотников А.Д. Дискретная математика. Учебное пособие. – 2-е изд., - М.: Новое знание, 2006. – 304 с.
  9. Галушкина Ю.И., Марьямов А.Н. Конспект лекций по дискретной математике. – М.: Айрис – пресс, 2007. – 176 с. – (Высшее образование).
  10.  Данилов В.Г. и др. Дискретная математика. Учебное пособие для вузов. – М.: Горячая линия - Телеком, 2008. – 136 с.
  11.  Астраханцева Л.Н. Дискретная математика. Учебное пособие. – Алматы: АУЭС, 2011. – 78 с.  

     12. Байсалова М.Ж. Дискрет  математика. ОУчебное пособие. – Алматы: АУЭС, 2011. – 78 с.  

 

Мазмұны

 

Кіріспе                                                                                                                      3

1.1 Есептік-графикалық жұмыс 1. Жиындар, қатынастар                                   3

1.2 Есептік тапсырмалар                                                                                         3

1.2 Типтік варианттың шешуі                                                                               13

1.3 Бақылау сұрақтары                                                                                          24

Әдебиеттер тізімі                                                                                                   24

 

                                                                     2012 ж. жиынтық жоспары, реті 180