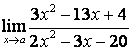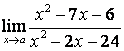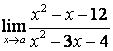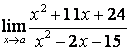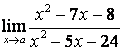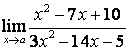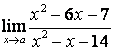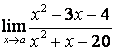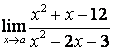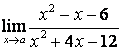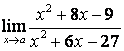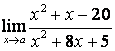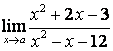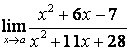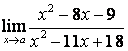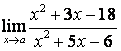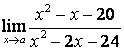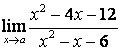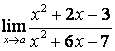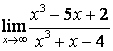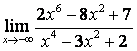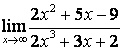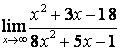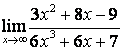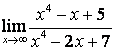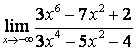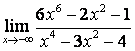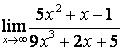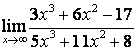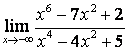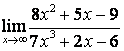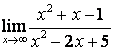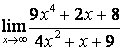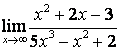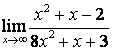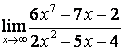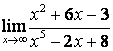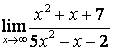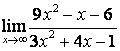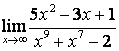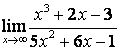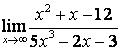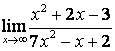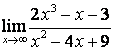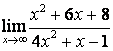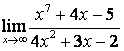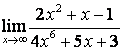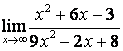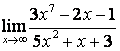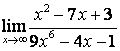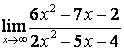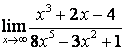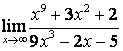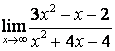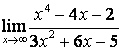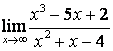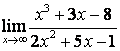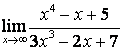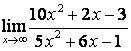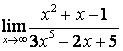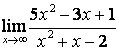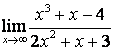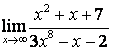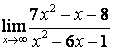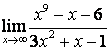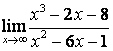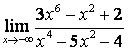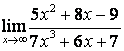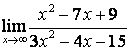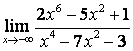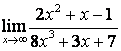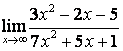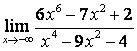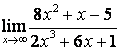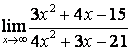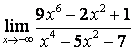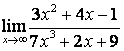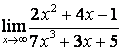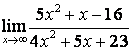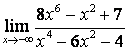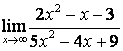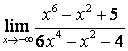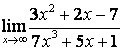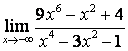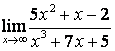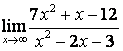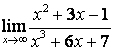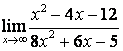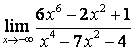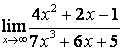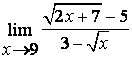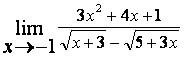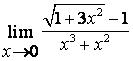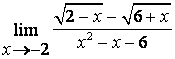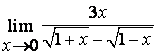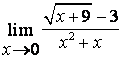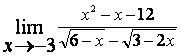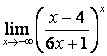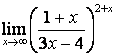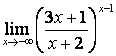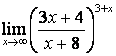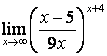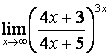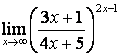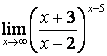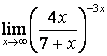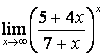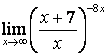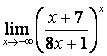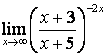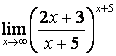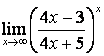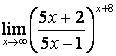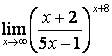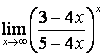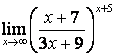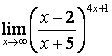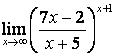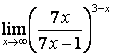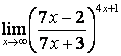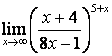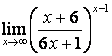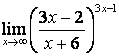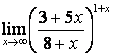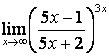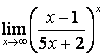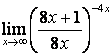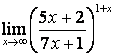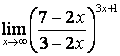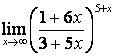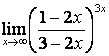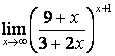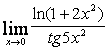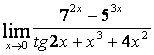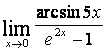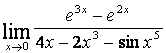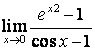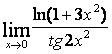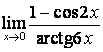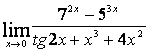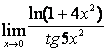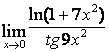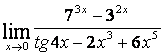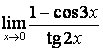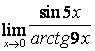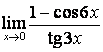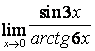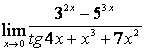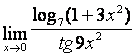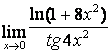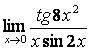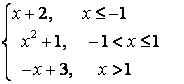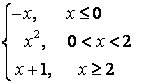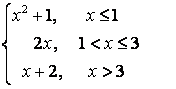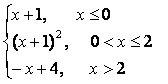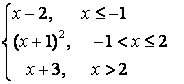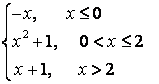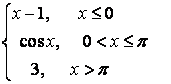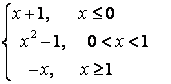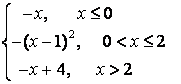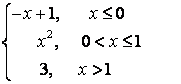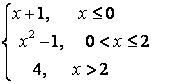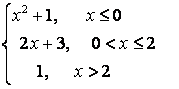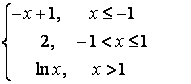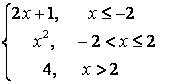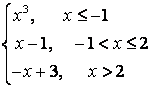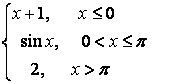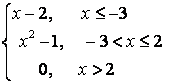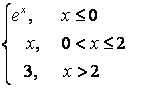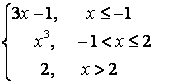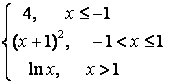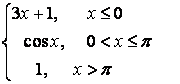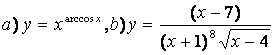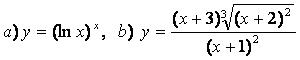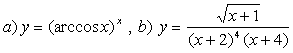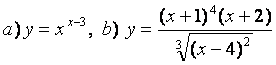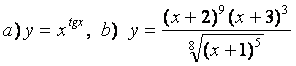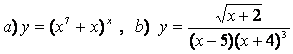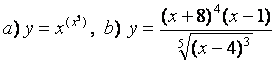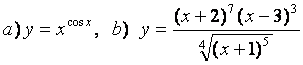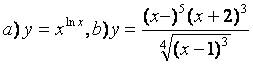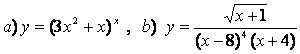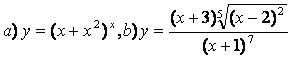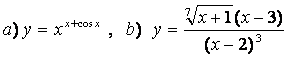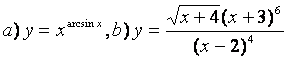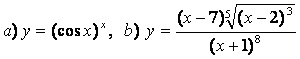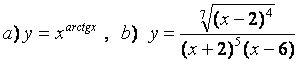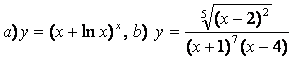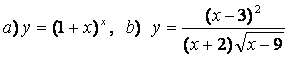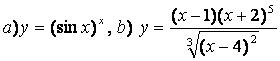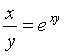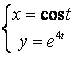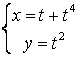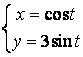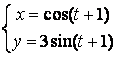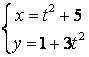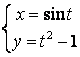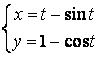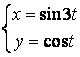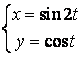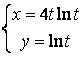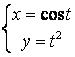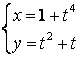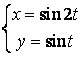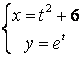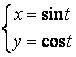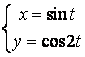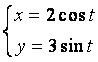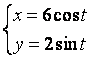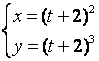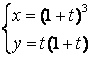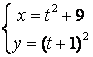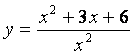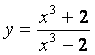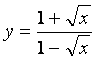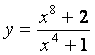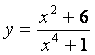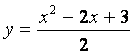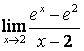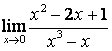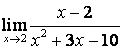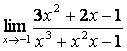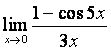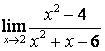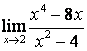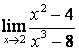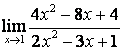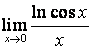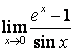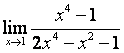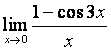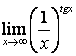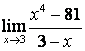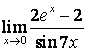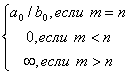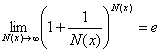1 Типовой расчёт 2

Некоммерческое акционерное общество

АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра высшей математики

Математический анализ

Введение в анализ

Методические указания и задания

к выполнению расчетно-графической работы

для студентов всех форм обучения специальности

5В060200 – Информатика

Часть 2

Алматы 2011

СОСТАВИТЕЛЬ: Р.Е.Ким.

Математический анализ. Введение в анализ. Методические указания и задания к выполнению расчетно-графической работы для студентов всех форм обучения специальности 5В060200 – Информатика. Часть 2. -Алматы: АУЭС, 2011.- 34 с.

Методические указания и задания к расчетно-графической работе содержат типовой расчет №2 дисциплины «Математический анализ. Введение в анализ» для студентов всех форм обучения специальности 5В060200 – Информатика. Приведены основные теоретические вопросы программы. Дано решение типового варианта.

Ил. 1, табл. 18, библиогр. – 4 назв.

Рецензент: канд. физ.-мат. наук, доц. Л.Н.Астраханцева

Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2011 г.

ã НАО «Алматинский университет энергетики и связи», 2011 г.

Сводный план 2011 г., поз. 228

Ким Регина Евгеньевна

Математический анализ

Введение в анализ

Методические указания и задания

к выполнению расчетно-графической работы

для студентов всех форм обучения специальности

5В060200 – Информатика

Часть 2

Специалист по стандартизации Н.К.Молдабекова

Редактор Л.Т.Сластихина

Подписано в печать Формат 6084 1/16

Тираж 50 экз Бумага типографская №1

Объем 2,2 уч.-изд.л. Заказ______ Цена 220 тг.

Копировально-множительное бюро

некоммерческого акционерного общества

«Алматинский университет энергетики и связи»

050013, Алматы, Байтурсынова, 126

АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра высшей математики

УТВЕРЖДАЮ

Проректор по учебно-методической работе

_____________ Э.А. Сериков

«____» ____________ 2011

Математический анализ

Введение в анализ

Методические указания и задания к расчетно-графической работе

(для студентов всех форм обучения специальности

5В060200 – Информатика)

Часть 2

СОГЛАСОВАНО Рассмотрено и одобрено на

Начальник УМО заседании кафедры _________________

М.А.Мустафин _______________ Протокол №___ от «____» ______ 2011 г

«____» ___________ 2011г. Зав. кафедрой

C.Е.Базарбаева _______________

Редактор

Л.Т.Сластихина _____________ Составитель

Р.Е. Ким ______________

«___» __________2011г.

Специалист по стандартизации

Н.К.Молдабекова____________

«___» ___________ 2011г.

Алматы 2011

1 Типовой расчёт 2. Предел функции. Непрерывность функции.
Дифференцирование функции одной переменной

1.1 Теоретические вопросы

1 Предел функции.

2 Теоремы о пределах. Односторонние пределы. Первый и второй замечательные пределы.

3 Бесконечно малые и бесконечно большие величины. Теоремы о бесконечно малых.

4 Сравнение бесконечно малых. Теоремы об эквивалентных бесконечно малых.

5 Непрерывные функции. Точки разрыва, их классификация. Равномерная непрерывность функции.

6 Определение производной, её физический и геометрический смысл. Связь дифференцируемости и непрерывности.

7 Основные правила дифференцирования.

8 Производные основных элементарных функций.

9 Логарифмическое дифференцирование.

10 Производные функций, заданных неявно и параметрически.

11 Уравнения касательной и нормали к графику функции.

12 Дифференциал, его геометрический смысл и применение.

1.2 Расчётные задания

1 Найти пределы функции, если предельная точка а принимает два

значения а) и б).

Т а б л и ц а 1

№	а) а =	б) а =	№	а) а =	б) а =

1.1	2	-3	1.2	8	0
1.3	-1	2	1.4	-1	2
1.5	-5	3	1.6	-2	3
1.7	-1	4	1.8	8	1
1.9	4	-1	1.10	-6	2
1.11	2	1	1.12	4	3

продолжение таблицы 1

1.13	-2	3	1.14	-3	1
1.15	8	-1	1.16	5	-1
1.17	7	0	1.18	-3	2
1.19	4	1	1.20	3	-1
1.21	3	2	1.22	-9	2
1.23	-5	1	1.24	-3	4
1.25	-7	3	1.26	9	-1
1.27	-6	1	1.28	-4	1
1.29	-2	4	1.30	1	5

2 Найти пределы.

Т а б л и ц а 2

№	а)	б)	в)

2.1
2.2
2.3
2.4
2.5
2.6
2.7

продолжение таблицы 2

2.8
2.9
2.10
2.11
2.12
2.13
2.14
2.15
2.16
2.17
2.18
2.19
2.20
2.21
2.22
2.23
2.24
2.25

продолжение таблицы 2

2.26
2.27
2.28
2.29
2.30

3 Найти пределы.

Т а б л и ц а 3

№	№	№

3.1	3.2	3.3
3.4	3.5	3.6
3.7	3.8	3.9
3.10	3.11	3.12
3.13	3.14	3.15
3.16	3.17	3.18
3.19	3.20	3.21

продолжение таблицы 3

3.22	3.23	3.24
3.25	3.26	3.27
3.28	3.29	3.30

4 Найти пределы.

Т а б л и ц а 4

№	а)	б)	№	а)	б)

4.1			4.2
4.3			4.4
4.5			4.6
4.7			4.8
4.9			4.10
4.11			4.12
4.13			4.14
4.15			4.16
4.17			4.18
4.19			4.20

продолжение таблицы 4

4.21			4.22
4.23			4.24
4.25			4.26
4.27			4.28
4.29			4.30

5 Доказать, что функции f (x) и φ(x) при х → 0 являются бесконечно малыми одного порядка малости.

Та б л и ц а 5

№	f (x)	φ(x)	№	f (x)	φ(x)

5.1			5.2
5.3			5.4
5.5			5.6
5.7			5.8
5.9			5.10
5.11			5.12
5.13			5.14
5.15			5.16
5.17			5.18
5.19			5.20
5.21			5.22
5.23			5.24
5.25			5.26
5.27			5.28
5.29			5.30

6 Найти пределы, используя эквивалентные бесконечно малые.

Та б л и ц а 6

№	а)	б)	№	а)	б)

6.1			6.2

продолжение таблицы 6

6.3			6.4
6.5			6.6
6.7			6.8
6.9			6.10
6.11			6.12
6.13			6.14
6.15			6.16
6.17			6.18
6.19			6.20
6.21			6.22
6.23			6.24
6.25			6.26
6.27			6.28
6.29			6.30

7 Для данных функций f (x) и g(x) найти: а) точку разрыва; б) левый и правый пределы в точке разрыва; в) определить характер точки разрыва.

Т а б л и ц а 7

№	f (x)	g(x)	№	f (x)	g(x)

7.1			7.2
7.3			7.4
7.5			7.6
7.7			7.8
7.9			7.10
7.11			7.12
7.13			7.14
7.15			7.16
7.17			7.18
7.19			7.20
7.21			7.22
7.23			7.24
7.25			7.26
7.27			7.28
7.29			7.30

8 Исследовать функцию на непрерывность и построить график.

Т а б л и ц а 8

№	f(x)	№	f(x)

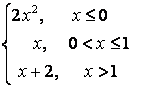
8.1		8.2

продолжение таблицы 8

8.3		8.4
8.5		8.6
8.7		8.8
8.9		8.10
8.11		8.12
8.13		8.14
8.15		8.16
8.17		8.18
8.19		8.20
8.21		8.22

продолжение таблицы 8

8.23		8.24
8.25		8.26
8.27		8.28
8.29		8.30

9 Найти:

1) производные функций;

2) дифференциал функции из пункта б).

Т а б л и ц а 9

9.1

а)

б)

в)

г)

д)

9.2

а)

б)

в)

г)

д)

9.3

а)

б)

в)

г)

д)

9.4

а)

б)

в)

г)

д)

9.5

а)

б)

в)

г)

д)

9.6

а)

б)

в)

г)

д)

продолжение таблицы 9

9.7

а)

б)

в)

г)

д)

9.8

а)

б)

в)

г)

д)

9.9

б)

в)

г)

д)

9.10

а)

б)

в)

г)

д)

9.11

а)

б)

в)

г)

д)

9.12

а)

б)

в)

г)

д)

9.13

а)

б)

в)

г)

д)

9.14

а)

б)

в)

г)

д)

9.15

а)

б)

в)

г)

д)

9.16

а)

б)

в)

г)

д)

9.17

а)

б)

в)

г)

д)

9.18

а)

б)

в)

г)

д)

9.19

а)

б)

в)

г)

д)

9.20

а)

б)

в)

г)

д)

9.21

б)

в)

г)

д)

продолжение таблицы 9

9.22

а)

б)

в)

г)

д)

9.23

а)

б)

в)

г)

д)

9.24

а)

б)

в)

г)

д)

9.25

а)

б)

в)

г)

д)

9.26

а)

б)

в)

г)

д)

9.27

а)

б)

в)

г)

д)

9.28

а)

б)

в)

г)

д)

9.29

а)

б)

в)

г)

д)

9.30

а)

б)

в)

г)

д)

10 Найти производные методом логарифмического дифференцирования

Т а б л и ц а 10

10.1

10.2

10.3

10.4

10.5

10.6

продолжение таблицы 10

10.7	10.8
10.9	10.10
10.11	10.12
10.13	10.14
10.15	10.16
10.17	10.18
10.19	10.20
10.21	10.22
10.23	10.24
10.25	10.26

продолжение таблицы 10

10.27	10.28
10.29	10.30

11 Найти производные неявных функций.

Т а б л и ц а 11

11.1 xy – 6 = cos y	11.2 xy + cos(x + y) = 0	11.3 + sin(x + y) = 0
11.4 xy = ln xy	11.5 x + y =	11.6 x = ln(x + y)
11.7 x – y + arctg y = 0	11.8	11.9 x – y +3sin y = 0
11.10	11.11	11.12 xy =
11.13 y = cos xy	11.14	11.15 x – y + 4sin y = 0
11.16	11.17	11.18
11.19 xy + sin(x + y) = 0	11.20 xy = ctg y	11.21 tg y = 4y – 5x
11.22 y – = 0	11.23 y = sin xy	11.24 y=
11.25 – ln xy = 0	11.26 x + y= tg(x + y)	11.27 + cos(x + y) = 0
11.28 y + = 0	11.29 + x = cos xy	11.30 xy = ln(1 + y)

12 Найти производную 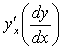функции, заданной параметрически.

Т а б л и ц а 12

12.1	12.2	12.3
12.4	12.5	12.6

продолжение таблицы 12

12.7	12.8	12.9
12.10	12.11	12.12
12.13	12.14	12.15
12.16	12.17	12.18
12.19	12.20	12.21
12.22	12.23	12.24
12.25	12.26	12.27
12.28	12.29	12.30

13 Составить уравнение касательной и нормали к графику функции в точке с абсциссой х₀.

Т а б л и ц а 13

№	y = f (x)		№	y = f (x)

13.1		-2	13.2		-1
13.3		4	13.4		1
13.5		-8	13.6		1
13.7		16	13.8		-1
13.9		3	13.10		2

продолжение таблицы 13

13.11	2	13.12	4
13.13	64	13.14	2
13.15	1	13.16	1
13.17	1	13.18	-2
13.19	2	13.20	1
13.21	3	13.22	1
13.23	1	13.24	-1
13.25	1	13.26	1
13.27	1	13.28	2
13.29	3	12.30	-2

14 Вычислить приближённое значение функции в точке х₁ с помощью дифференциала.

Т а б л и ц а 14

№	y = f (x)	х₁	№	y = f (x)	х₁

14.1		1,03	14.2		1,97
14.3		0,98	14.4		7,64
14.5		2,002	14.6		1,03
14.7		8,36	14.8		17
14.9		2,56	14.10		3,998
14.11		1,996	14.12		2,997
14.13		2,01	14.14		1,98
14.15		0,998	14.16		31,85

продолжение таблицы 14

14.17	1,021	14.18	16,62
14.19	26,46	14.20	1,012
14.21	0,08	14.22	27,54
14.23	7,76	14.24	0,97
14.25	16,6	14.26	0,01
14.27	1,02	14.28	1,05
14.29	0,98	14.30	1,97

15 Найти пределы по правилу Лопиталя.

Т а б л и ц а 15

№	а)	б)	№	а)	б)

15.1			15.2
15.3			15.4
15.5			15.6
15.7			15.8
15.9			15.10
15.11			15.12
15.13			15.14
15.15			15.16
15.17			15.18
15.19			15.20

продолжение таблицы 15

15.21			15.22
15.23			15.24
15.25			15.26
15.27			15.28
15.29			15.30

1.3 Решение типового варианта

При вычислении пределов, прежде всего, следует подставить предельную точку в функцию вместо переменной.

Если получено вполне определённое значение (константа или бесконечность), то это значение является ответом.

Возможные виды определённостей:

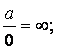
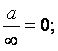
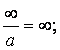
Если в результате подстановки получена одна из неопределённостей (возможны семь видов неопределённостей: ), то, говорят, следует раскрыть неопределённость, т.е. вычислить предел,

используя различные методы, приведенные в таблице 16.

Рассмотрим эти методы на примерах.

1 Найти предел 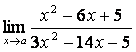при

а) а=2;

б) а=5.

Решение:

а) подставим предельную точку а=2 в данную функцию вместо х, получим сразу ответ: ;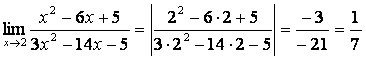

б) при подстановке а = 5 получим неопределённость вида 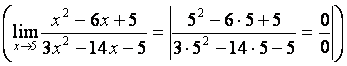, которую можно раскрыть, применяя один из двух методов:

1) разложить числитель и знаменатель дроби на множители, а затем

сократить дробь на общий множитель:

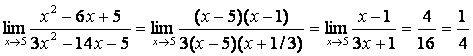2) применяя правило Лопиталя: .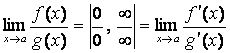

По этому правилу имеем: .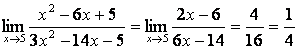

2 Найти пределы:

а) ;

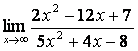б) ;

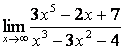в) .

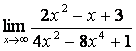Решение:

при вычислении данных пределов после подстановки получается неопределённость вида , для её раскрытия применяем правило 1 таблицы 16.

а) числитель и знаменатель имеют одинаковые степени (), поэтому предел равен отношению коэффициентов старших степеней:

;

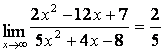б) степень числителя больше степени знаменателя (), поэтому ;

в) степень знаменателя больше степени числителя (), поэтому .

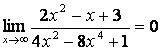3 Найти предел .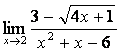

Решение:

при подстановке предельного значения получается неопределённость вида , которую в данном случае лучше раскрыть, умножая числитель и знаменатель на выражение, сопряжённое числителю. Одновременно знаменатель следует разложить на множители и затем сократить дробь на общий множитель:

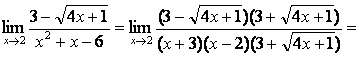
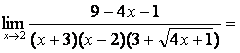
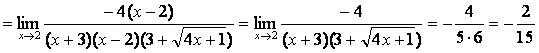Если применить правило Лопиталя, то получится тот же результат:

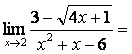
4 Найти пределы:

а) ;

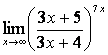б) .

Решение:

а) при подстановке получим неопределённость вида , которую можно раскрыть, применяя, например, следующие методы:

1) первый метод – это приведение данного предела к форме второго замечательного предела

или его обобщенной форме :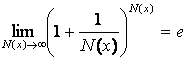

===.

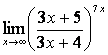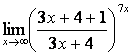2) второй метод – это использование формулы, которую часто применяют для раскрытия неопределённостей вида:

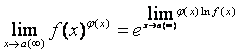По этой формуле == =

(используем теорему о замене бесконечно малой функции эквивалентной ей бесконечно малой: при )

= = .

Приведённую выше формулу можно не помнить, но использовать приём, который привёл к этой формуле:

положим , прологарифмируем это равенство по основанию е:

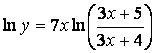, и найдём

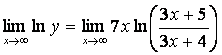= (см. вычисление этого предела выше) = .

Итак, , откуда ;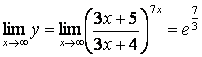

б) ==.

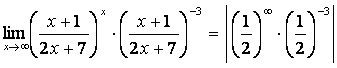5 Доказать, что функции f (x) = cos 2x – cos³ 2x и φ(x) = 3x² – 5x³ при х → 0 являются бесконечно малыми одного порядка малости.

Решение:

для доказательства того, что две функции f (x) и φ(x) при х → 0 являются бесконечно малыми одного порядка малости, необходимо показать, что :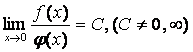

(применяя таблицу 17, имеем: при )

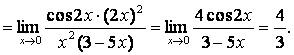
6 Найти пределы:

а) ;

б) 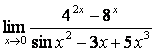, используя эквивалентные бесконечно малые.

Решение:

а) применяя таблицу 17, имеем:

, при .

Поэтому

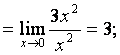
б) с учётом таблицы 17 преобразуем

– т.о., эта б.м. второго порядка по сравнению с х;

5х³– б.м. третьего порядка относительно х;

() – б.м. первого порядка или одного порядка с х, поэтому по теореме 2 (см. справочный материал 1.4.2): .

Следовательно, .

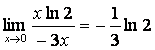7 Для функций и найти:

а) точку разрыва;

б) левый и правый пределы в точке разрыва;

в) определить характер точки разрыва.

Решение:

1) Рассмотрим :

а) точка х = –2 не входит в область определения этой функции, но функция определена в её окрестности, значит, х = –2 точка разрыва;

б) 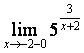== 0,

= =;

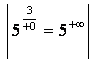в) так как один из односторонних пределов , то х = –2 точка разрыва второго рода.

2) Рассмотрим :

а) точка х = 6 не входит в область определения этой функции, но функция определена в её окрестности, значит, х = 6 точка разрыва;

б) == –, == +;

в) так как оба односторонних предела «равны» , то х = 6 точка разрыва второго рода.

8 Исследовать функцию на непрерывность и построить график.

Решение:

данная функция определена на промежутке (–;) и три составляющие её функции определены для всех x из соответствующих интервалов, таким образом, точками разрыва могут быть только точки, в которых меняется аналитическое выражение функции, т.е. х = 0 и х = 2.

Исследуем эти точки.

Найдём односторонние пределы в х = 0:

; ;

значение функции в этой точке .

Итак, , поэтому х = 0 точка непрерывности.

Аналогично для х = 2:

; ;

значение функции в этой точке .

Так как , то х = 2 точка разрыва первого рода, – скачок функции в этой точке.

График имеет вид:

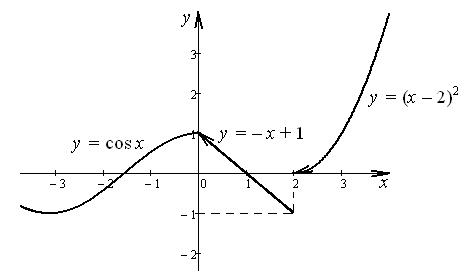
Рисунок 1

9 Найти:

1) производные функций

а) ,

б) ,

в) ,

г) ,

д) ;

2) дифференциал функции из пункта б).

Решение:

1) по определению производной функции называется предел . На практике при дифференцировании функций используют таблицу производных (см. таблицу 18) и основные правила дифференцирования:

1) ; 2) ; 3);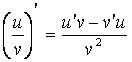

4) если или 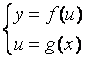(где и промежуточный аргумент), то

или ;

5) если и взаимно обратные функции, то :

а) запишем функцию в виде , затем по правилу 1) и формулам таблицы 18 имеем:

;

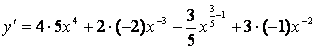
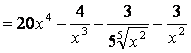б) данную сложную функцию можно представить в виде

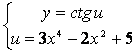. По правилу 4) нахождения производной сложной функции и, учитывая формулу 9) таблицы 18, имеем:

;

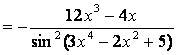в) используя таблицу 18 и правило 2), получим ;

г) используя таблицу производных 18 и правило 3), получим ;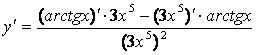

д) представим данную функцию в виде цепочки элементарных функций, вводя промежуточные аргументы . Теперь находим производную, используя таблицу производных 18 и правило 4) нахождения производной сложной функции ;

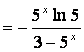2) дифференциалом функции называется выражение , поэтому для функции дифференциал равен .

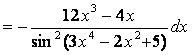10 Найти производные методом логарифмического дифференцирования

а);

б) .

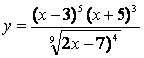Решение:

– метод логарифмического дифференцирования применяется для определения производных функций вида или громоздких, но удобных для логарифмирования функций (т.е. содержащих только операции умножения, деления, возведения в степень и извлечения корня). Он состоит в последовательном выполнении следующих действий: логарифмированию функции по основанию е, дифференцированию полученного выражения (при этом производная находится как производная сложной функции) и нахождению производной из последнего равенства, как находят неизвестные из алгебраического уравнения.

а) после логарифмирования данной функции по основанию е получим , продифференцируем результат: .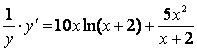

Из последнего равенства найдём

;

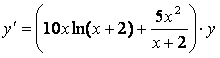
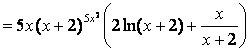б) применяя метод логарифмического дифференцирования,

последовательно находим:

;

; ;

; .

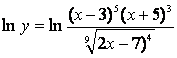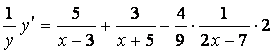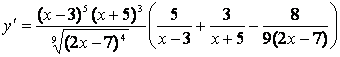11 Найти производную неявной функции .

Решение:

дифференцируем данное равенство, имея в виду, что у есть функция от х (т.е. сложная функция): .

Из последнего равенства как из уравнения находим

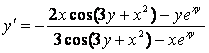12 Найти производную от функции, заданной параметрически

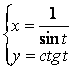Решение:

первая производная или просто производная параметрически заданной функции 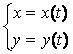находится по формуле .

Так как , , то ;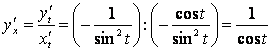

13 Составить уравнение касательной и нормали к графику функции в точке с абсциссой х₀= 1.

Решение:

уравнение касательной к графику функции в точке х₀ имеет вид: ,

уравнение нормали – .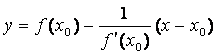

Найдём , , .

Таким образом, уравнение касательной: или ;

уравнение нормали: или .

14 Вычислить приближённое значение функции в точке

x₁= 26,9 с помощью дифференциала.

Решение:

при достаточно малых значениях приращение функции может быть заменено её дифференциалом . Развернув это приближённое равенство, получим формулу , (*)

которую применяют для приближённых вычислений, если требуется вычислить и если проще вычислить и , где достаточно близкая к x точка.

В нашем примере x= 26,9 , пусть x₀= 27, тогда

, , .

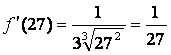Подставляя эти значения в формулу (*), получим

15 Найти пределы по правилу Лопиталя:

а);

б) .

Решение:

а) применяя правило Лопиталя (см. в примере 1б)), имеем

;

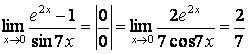б) при вычислении пределов вида подстановка предельной точки в функции может привести к следующим неопределенностям: , которые можно раскрыть по формуле 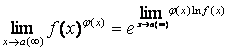, приведённой в примере 4а), или с помощью приёма, указанного в этом же примере.

В нашем случае после подстановки предельной точки в функцию получим неопределённость вида , Положим и прологарифмируем это равенство по основанию е: .

Применим правило Лопиталя при нахождении предела

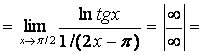
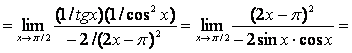
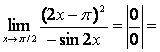
(применим повторно правило Лопиталя)

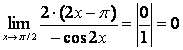Таким образом, , откуда .

1.4 Справочный материал

1.4.1 Виды пределов и методы их вычисления

Т а б л и ц а 16

Виды пределов	Результат подстановки предельной точки	Результат или метод вычисления предела

1	неопределённость
2	, неопределённости	а) разложение на множители; б) правило Лопиталя; в) умножение на сопряжённое выражение; г) применение эквивалентных бесконечно малых; д) правило 1 этой таблицы
3	, ,	0
4	, ,
5	неопределённость	привести к неопределённостям вида или , затем как в 1 или 2 этой таблицы
6	,
7	,	0
8	неопределённость	привести к неопределённостям вида или , затем как в 1 или 2 этой таблицы
9
10	неопределённости	а) привести ко 2-му замеч. пределу ; б) использовать формулу
11
12

1.4.2 Сравнение бесконечно малых функций

Если , то называется бесконечно малой функцией или просто бесконечно малой (б. м.) при . Для сравнения бесконечно малых вычисляют предел их отношения.

Пусть и бесконечно малые при , тогда если

1) , то б.м. более высокого порядка малости, чем , в этом случае пишут ;

2) , то б.м. более низкого порядка малости, чем ;

3) 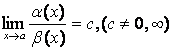, то б.м. и одного порядка;

4) 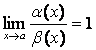, то б.м. и эквивалентны, записывают ;

5) 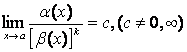, то есть б.м. - го порядка по сравнению с.

При вычислении пределов с б.м. в ряде случаев используют теоремы об эквивалентных б.м.:

Теорема 1. Если , при , то

1) ;

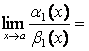
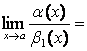
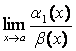2) .

Теорема 2. Алгебраическая сумма конечного числа б.м. эквивалентна слагаемому низшего порядка.

Итак, следуя этим теоремам, в пределах одну б.м. можно заменить другой эквивалентной ей, при этом используют таблицу эквивалентных б.м.

Т а б л и ц а 17

, т.е. – бесконечно малая при , а £ ¥.
1	5	9
2	6	10
3	7	11
4	8

1.4.3 Непрерывные функции. Точки разрыва, их классификация

Точками разрыва элементарной функции являются точки, в которых она не определена, но определена в их окрестности; если функция задана несколькими различными аналитическими выражениями, то точками разрыва могут быть точки, в которых меняется аналитическое выражение функции.

Односторонние пределы функции в точке а определяются как предел , вычисленный в предположении, что всегда или . Итак, левый предел: =;

правый предел: =.

Если функция непрерывна в точке а, то выполняются равенства

Если а точка разрыва, то последние равенства нарушаются, и характер этого нарушения лежит в основе классификации точек разрыва:

1) если и существуют, но ,

то а точка разрыва первого рода с конечным скачком,

разность – – скачок функции в точке а;

2) если =, то а – устранимая точка разрыва первого рода.

3) если хотя бы один из пределов или не существует или «равен» , то а – точка разрыва второго рода.

1.4.4 Производные основных элементарных функций

Т а б л и ц а 18

1	7	13
2	8	14
3	9	15
4	10	16
5	11	17
6	12

Список литературы

1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: В 2 ч.–М.: Высшая школа, 1986.–Ч.1–352 с.

2. Сборник индивидуальных заданий по высшей математике: В 3 ч. /А.П. Рябушко, В.В. Бархатов и др./Под редакцией А.П. Рябушко.–Минск: Вышэйшая школа, 2000.–Ч.1.–303 с.

3. Кузнецов Л.А. Сборник заданий по высшей математике: Типовые расчеты.–М.: Высшая школа, 1983.–175 с.

4. Пискунов Н.С. Дифференциальное и интегральное исчисления. Учебник для втузов: В 2 т.–М.: Наука, 1976.–Т.1–456 с.

Содержание

1 Типовой расчёт 2. Предел функции. Непрерывность функции.
Дифференцирование функции одной переменной 3

1.1 Теоретические вопросы 3

1.2 Расчётные задания 3

1.3 Решение типового варианта 20

1.4 Справочный материал 31

Список литературы 34