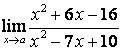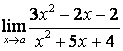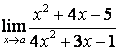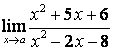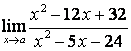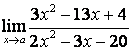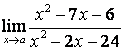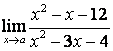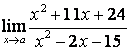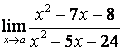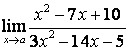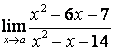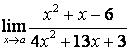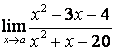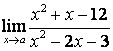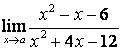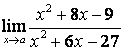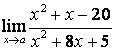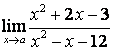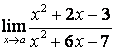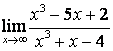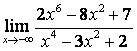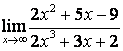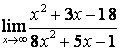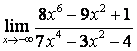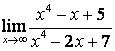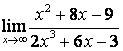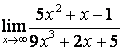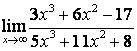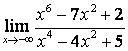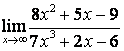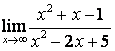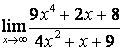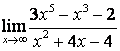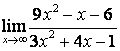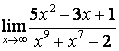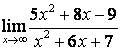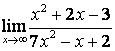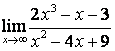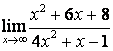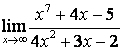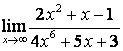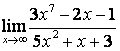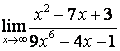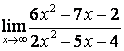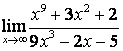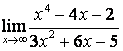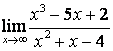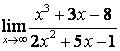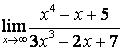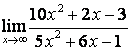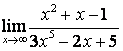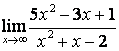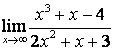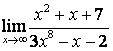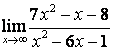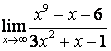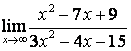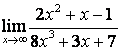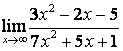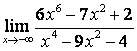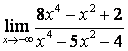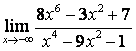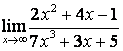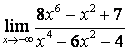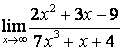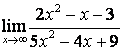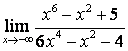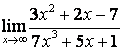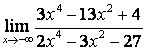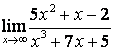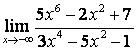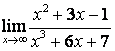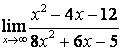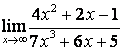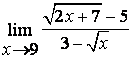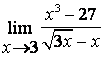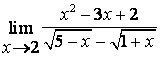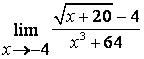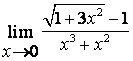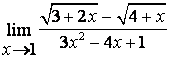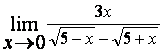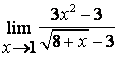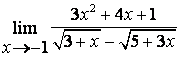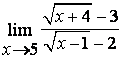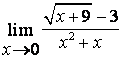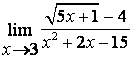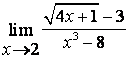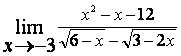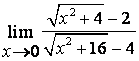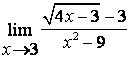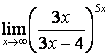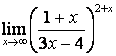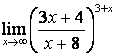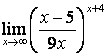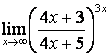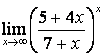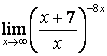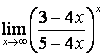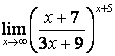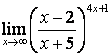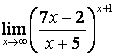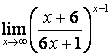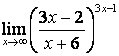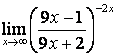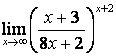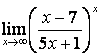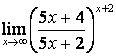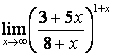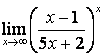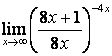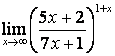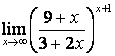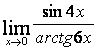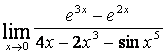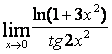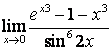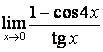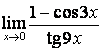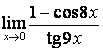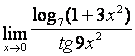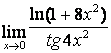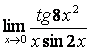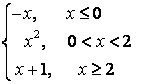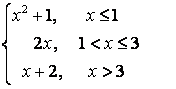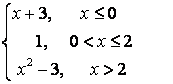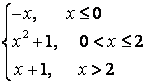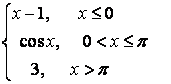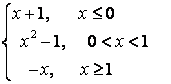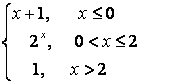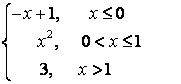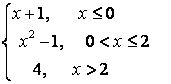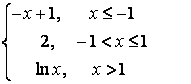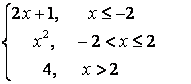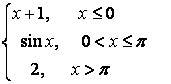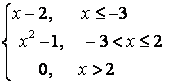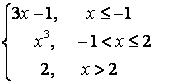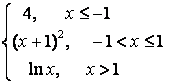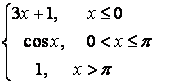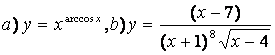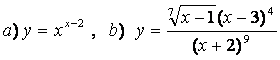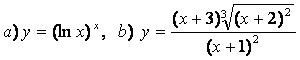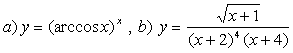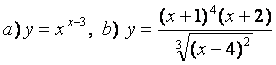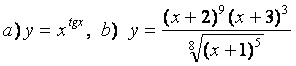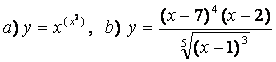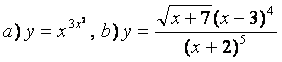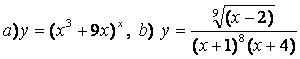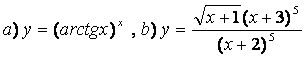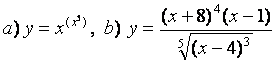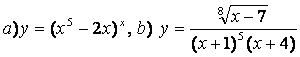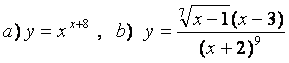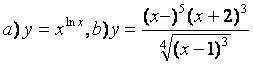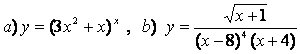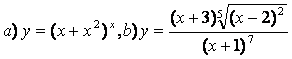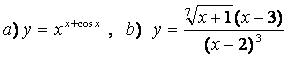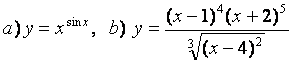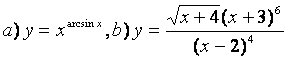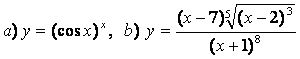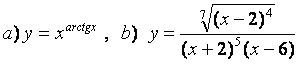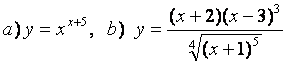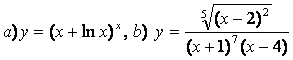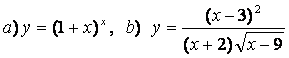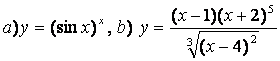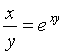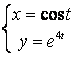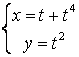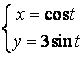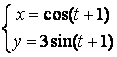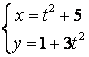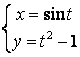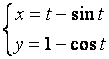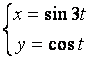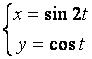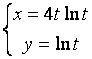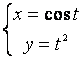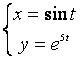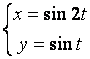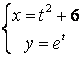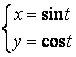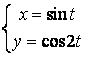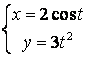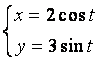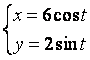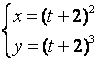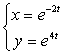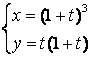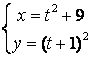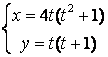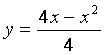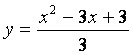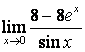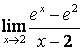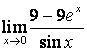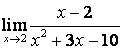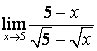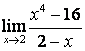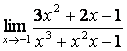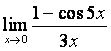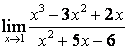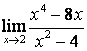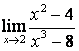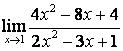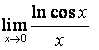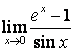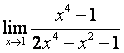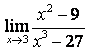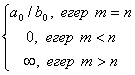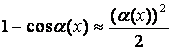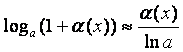Коммерциялық емес акционерлік қоғам

Алматы энергетика және байланыс Университеті

Жоғары математика кафедрасы

 

 

 

МАТЕМАТИКАЛЫҚ ТАЛДАУ

 5В060200 – «Информатика» мамандығы бойынша оқитын барлық бөлімдер студенттері  үшін есептеу-графикалық жұмыстарын орындауға арналған әдістемелік нұсқаулар мен тапсырмалар

 1-бөлім

 

Алматы 2011

    Құрастырушылар: К.М. Мұстахишев, Р.Е. Ким. Математикалық талдау. 5В060200 – «Информатика» мамандығы бойынша оқитын барлық бөлімдер студенттері  үшін есептеу-графикалық жұмыстарды орындауға арналған әдістемелік нұсқаулар мен тапсырмалар. 1-бөлім. –Алматы: АЭжБУ, 2011. -34б.

  

5В060200 – «Информатика» мамандығы бойынша оқитын барлық бөлім студенттері  үшін «Математикалық талдау» пәнінен №1 есептеу-графикалық жұмысын орындауға арналған әдістемелік нұсқаулар мен тапсырмалар келтірілген.

Кесте саны 18, сурет 1, әдебиет көрсеткіші – 4 атау.

Пікір жазған: мат.-физ. ғыл., канд. доцент М.Ж. Байсалова

 

«Алматы энергетика және байланыс университеті» коммерциялық емес акционерлік қоғамының 2011 жылғы баспа жоспары бойынша басылды

 

ã «Алматы энергетика және байланыс университеті» КЕАҚ, 2011 ж.

 

Типтік есептеу №1.Функцияның шегі мен үзіліссіздігі. Бір айнымалы функциясын дифференциалдау

 

1.1   Теориялық сұрақтар

 

         1. Функцияның шегі.

         2. Шектер туралы теоремалар. Біржақты шектер. Бірінші және екінші тамаша шектер.

         3. Шексіз аз және шексіз үлкен шамалар. Шексіз аздар туралы теоремалар.

         4. Шексіз аздарды салыстыру. Балама (эквивалентті) шексіз аздар туралы теоремалар.

         5. Үзіліссіз функциялар. Үзіліс нүктелері, оларды сұрыптау. Функцияның бірқалыпты үзіліссіздігі.

6. Туындының анықтамасы. Оның геометриялық және механикалық мағынасы. Дифференциалдану мен үзіліссіздіктің байланысы.

7. Дифференциалдаудың негізгі ережелері.

8. Негізгі элементар функциялардың туындылары.

     9. Логарифмдік дифференциалдау.

10. Айқын емес және параметрлік түрде берілген функциялардың туындылары.

11. Функция графигіне жанама мен нормалдің теңдеулер.

12. Функция диффференциалы, оның геометриялық мағынасы және қолданылуы.

 

1.2   Есептеу тапсырмалары

 

1. Функцияның берілген нүктелердегі  шектерін табыңыз.

1 кесте

№

а) а =

б) а =

№

а) а =

б) а =

1.1

             

2

-3

1.2

8

0

1.3

-1

2

1.4

-1

2

1.5

-5

3

1.6

-2

3

1.7

-1

4

1.8

8

1

1.9

4

-1

1.10

-6

2

1.11

        

2

1

1.12

4

3

 

1 кестенің соңы

1.13

                                                                             

-2

3

1.14

-3

1

1.15

                                                            

8

-1

1.16

5

-1

1.17

                                                  

7

0

1.18

-3

2

1.19

                                          

4

1

1.20

3

-1

1.21

                                        

3

2

1.22

-9

2

1.23

                                                      

-5

1

1.24

-3

4

1.25

                                          

-7

3

1.26

9

-1

1.27

-6

1

1.28

-4

1

1.29

                        

-2

4

1.30

1

5

 

2. Шектерді табыңыз.

2  кесте

№

а)

б)

в)

 

 

 

 

2.1

2.2

2.3

2.4

2.5

2.6

 

 

2 кестенің жалғасы

2.7

2.8

2.9

2.10

2.11

2.12

2.13

2.14

2.15

2.16

2.17

2.18

2.19

2.20

2.21

2.22

2.23

 

2 кестенің соңы

2.24

2.25

2.26

2.27

2.28

2.29

2.30

 

3. Шекті табыңыз.

3 кесте

№

№

№

3.1

3.2

3.3

3.4

3.5

3.6

3.7

3.8

3.9

3.10

3.11

3.12

3.13

3.14

3.15

3.16

3.17

3.18

3 кестенің соңы

3.19

3.20

3.21

3.22

3.23

3.24

3.25

3.26

3.27

3.28

3.29

3.30

 

4. Шектерді табыңыз.

4 кесте

№

а)

б)

№

а)

б)

4.1

4.2

4.3

4.4

4.5

4.6

4.7

4.8

4.9

4.10

4.11

4.12

                                   

4.13

4.14

4.15

4.16

4.17

4.18

 

4 кестенің соңы

4.19

4.20

4.21

4.22

4.23

4.24

4.25

4.26

4.27

4.28

4.29

4.30

        

5. -да  мен -ның бірдей ретті шексіз аз функциялар екенін дәлелдеңіз.

5 кесте

№

f (x)

φ(x)

№

f (x)

φ(x)

5.1

5.2

5.3

5.4

5.5

5.6

5.7

5.8

5.9

5.10

5.11

5.12

5.13

5.14

5.15

5.16

5.17

5.18

5.19

5.20

5.21

5.22

5.23

5.24

5.25

5.26

5.27

5.28

5.29

5.30

 

6. Балама шексіз аздарды пайдаланып, шектерді табыңыз.

6 кесте

№

а)

б)

№

а)

б)

6.1

                              

                          

6.2

           

6.3

6.4

6.5

6.6

6.7

6.8

6.9

6.10

6.11

6.12

6.13

6.14

6.15

6.16

6.17

6.18

6.19

6.20

6.21

6.22

6.23

6.24

6.25

6.26

6.27

6.28

6.29

6.30

 

 

7. Берілген  және  функцияларының:: а) үзіліс нүктелерін,                ә) біржақты (оң және сол) шектерін табыңыз, б) үзіліс нүктелерін сұрыптаңыз.

7 кесте

№

f (x)

g(x)

№

f (x)

g(x)

7.1

7.2

7.3

7.4

7.5

7.6

7.7

7.8

7.9

7.10

7.11

7.12

7.13

7.14

7.15

7.16

7.17

7.18

7.19

7.20

7.21

7.22

7.23

7.24

7.25

7.26

7.27

7.28

7.29

7.30

               

 

8. Функцияны үзіліссіздікке зерттеп, графигін тұрғызыңыз.

8 кесте

№

f(x)

№

f(x)

8.1

 

8.2

 

8.3

 

8.4

 

8.5

 

8.6

 

8.7

 

8.8

 

8.9

 

8.10

 

8.11

 

8.12

 

8.13

 

8.14

 

8.15

 

8.16

 

8.17

 

8.18

 

8.19

 

8.20

 

 

8 кестенің соңы

8.21

 

8.22

 

8.23

 

8.24

 

8.25

 

8.26

 

8.27

 

8.28

 

8.29

 

8.30

 

 

9. Функциялардың: 1) туындыларын; 2) б) тармағында дифференциалын табыңыз.

9 кесте

9.1

а)

б)

в)

г)

д)

9.2

а)

б)  

в)

г)

д)

9.3

а)

б)

в)

г)

д)

9.4

а)

б)

в)

г)

д)

9.5

а)

б)

в)

г)

д)

9.6

а)

б)

в)  

г)

д)

 

9 кестенің жалғасы

9.7

а)

б)

в)

г)

д)

9.8

а)

б)

в)

г)

д)

9.9

a)

б)

в)

г)

д)

9.10

а)

б)

в)

г)

д)

9.11

а)

б)

в)

г)

д)

9.12

а)  

б)

в)

г)

д)

9.13

а)

б)

в)

г)

д)

9.14

а)

б)

в)

г)

д)

9.15

а)

б)

в)

г)

д)

9.16

а)

б)

в)

г)

д)

9.17

а)

б)

в)

г)

д)

9.18

а)

б)

в)

г)

д)

9.19

а)

б)

в)

г)

д)

9.20

а)

б)

в)

г)

д)

9.21

a)

б)

в)

г)

д)

9 кестенің соңы

9.22

а)

б)

в)

г)

д)   

9.23

а)

б)

в)

г)

д)

9.24

а)

б)

в)

г)

д)

9.25

а)

б)

в)

г)

д)

9.26

а)

б)

в)

г)

д)

9.27

а)

б)

в)

г)

д)

9.28

а)

б)

в)

г)

д)

9.29

а)

б)

в)

г)

д)

9.30

а)

б)

в)

г)

д)

 

10. Функциялардың туындыларын алдын ала логарифмдеу әдісімен табыңыз.

10 кесте

10.1

10.2  

10.3 

10.4

10.5

10.6

10 кестенің жалғасы

10.7

10.8

10.9  

10.10

10.11

10.12

10.13  

10.14

10.15 

10.16 

10.17

10.18

 

10.19

10.20  

10.21

10.22  

10.23

10.24

10.25

10.26  

  

10 кестенің соңы

10.27

10.28 

10.29

10.30 

 

11.Айқын емес функцияның туындысын табыңыз.

11 кесте

11.1     xy – 6 = cos y

11.2    xy + cos(x + y) = 0

11.3   + sin(x + y) = 0

11.4     xy = ln xy

11.5     x + y =

11.6     x = ln(x + y)

11.7    x – y + arctg y = 0 

11.8      

11.9     x – y +3sin y = 0

11.10   

11.11    

11.12      xy =

11.13     y = cos xy

11.14   

11.15    x – y + 4sin y = 0

11.16       

11.17  

11.18      

11.19   xy + sin(x + y) = 0

11.20       xy = ctg y

11.21    tg y = 4y – 5x

11.22      y – = 0

11.23      y = sin xy

11.24        y=

11.25    – ln xy = 0

11.26    x + y= tg(x + y)

11.27  + cos(x + y) = 0

11.28       y + = 0

11.29   + x = cos xy

11.30      xy = ln(1 + y)

 

12. Параметрлік түрде берілген функцияның туындысын   табыңыз.

12 кесте

12.1     

12.2     

12.3     

12.4     

12.5     

12.6     

 

12 кестенің соңы

12.7

12.8     

12.9     

12.10   

12.11

12.12   

12.13  

12.14   

12.15  

12.16   

12.17   

12.18   

12.19   

12.20   

12.21   

12.22

12.23

12.24

12.25

12.26

12.27

12.28

12.29

12.30

 

13. Функция графигіне абсциссасы  болатын нүктеде тұрғызылған жанама мен нормалдің теңдеулерін құрыңыз.

13 кесте

№

y = f (x)

№

y = f (x)

13.1            

-2

13.2     

-1

13.3   

4

13.4    

1

13.5   

-8

13.6         

1

13.7   

16

13.8    

-1

13.9   

3

13.10  

2

 

 

13 кестенің соңы

13.11 

2

13.12

4

13.13 

64

13.14  

2

13.15 

1

13.16  

1

13.17 

1

13.18  

-2

13.19       

2

13.20        

1

13.21 

3

13.22  

1

13.23        

1

13.24  

-1

13.25    

1

13.26     

1

13.27     

1

13.28      

2

13.29    

3

12.30         

-2

        

14. Дифференциалдың көмегімен функцияның  нүктесіндегі жуық мәнін есептеңіз.

14 кесте

№

y = f (x)

х1

№

y = f (x)

х1

14.1            

 1,03

14.2     

 1,97

14.3   

0,98

14.4    

7,64

14.5   

2,002

14.6         

1,03

14.7   

8,36

14.8    

17

14.9   

2,56

14.10  

3,998

14.11 

1,996

14.12

2,997

14.13 

2,01

14.14  

1,98

14.15 

0,998

14.16  

31,85

14.17 

1,021

14.18  

16,62

14 кестенің соңы

14.19       

26,46

14.20         

1,012

14.21 

0,08

14.22  

27,54

14.23        

7,76

14.24  

0,97

14.25 

16,6

14.26  

0,01

14.27 

1,02

14.28  

1,05

14.29 

0,98

14.30         

1,97

 

 

15. Лопиталь ережесі бойынша шектерді табыңыз.

15 кесте

№

а)

б)

№

а)

б)

15.1

15.2

15.3

15.4

 

15.5

15.6

15.7

15.8

15.9

15.10

15.11

15.12

15.13

15.14

15.15

15.16

15.17

15.18

15.19

15.20

15.21

15.22

15 кестенің соңы

15.23

15.24

15.25

15.26

15.27

15.28

15.29

15.30  

 

 

1.3   Типтік нұсқаның шешуі

 

Шектерді есептегенде алдымен шекке тура көшу арқылы функцияның берілген нүктедегі мәнін табамыз. Егер ол нақты санға немесе -ке тең болса, онда функцияның шегі табылғаны.

Мұнда ескеретін жағдайлар :

          

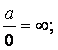
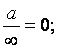
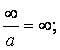
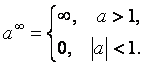
Ал, тура шекке көшу нәтижесінде анықталмағандықтардың:

,

бірі пайда болса, онда оны ашу, яғни 16-кестеде келтірілген әдістерді қолданып, шекті табу қажет.

Мысалдар қарастыралық:

1). Шекті табыңыз 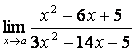  ,   а) а=2;    б) а=5.

Шешу: а) Берілген функцияда  десек, табылған нақты сан оның шегі болады:   

 ;

б)  болғанда анықталмағандыққа келеміз:

.

Оны ашу үшін бөлшектің алымында да, бөлімін де жәй көбейткіштерге жіктеп, ықшамдаймыз:

                 .

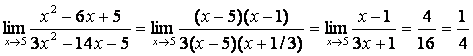2). Шектерді табыңыз:

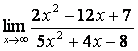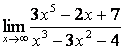а) ;   б) ;    в) .

Шешу: берілген функцияларда шекке тура көшу  түріндегі анықталмағандыққа келтіреді. Оны ашу үшін 16-кестедегі бірінші ережені қолданамыз.

а) Бөлшектің алымын да, бөлімінде де -тің ең жоғарғы дәрежесі бірдей () болғандықтан функцияның шегі сол бас мүшелердің коэффициентерінің қатынасына тең:  

;

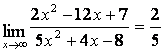б) Алымындағы көпмүшеліктің дәрежесі бөліміндегінікінен үлкен () болғандықтан:

;

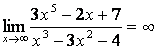в) Алымындағы квадрат үшмүшелікке қарағанда бөлімінің дәрежесі үлкен () болғандықтан:

.

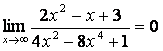3). Шекті табыңыз .

Шешу:  болғанда функция  түріндегі анықталмағандыққа айналады. Иррационалдықтан құтылу үшін бөлшекті алымының түйіндесіне көбейтіп, бөлеміз де, бөлімін жәй көбейткіштерге жіктеп, ықшамдаймыз:

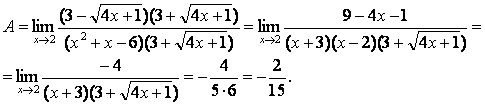
         4). Шектерді табыңыз:  

а) 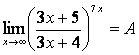;      б) .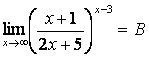

         Шешу: берілген функцияларда шекке тура көшсек,  түріндегі дәрежелі анықталмағандыққа келеміз. Оны екінші тамаша шектің

 

көмегімен немесе функцияны алдын ала логарифмдеу арқылы ашуға болады.

а)

1).  =.

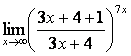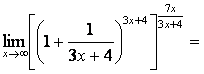
2) Үзіліссіз функцияларда логарифм белгісінің астында шекке көшуге болатынын ескеріп, балама шексіз аздар үшін:

теңдігін (17 кестені қара) пайдаланайық:

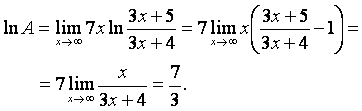                               (1)

Логарифмнен құтылғаннан кейін (1) нәтижеге келеміз.

         б) Мұнда шекке тура көшсек болғаны:

        

5).   және   функциялары -да реттері бірдей шексіз аздар болатынын дәлелдеңіз:

Шешу: функцияларды салыстыру олардың қатынасынан шек табу арқылы орындалады. Егер

 

болса, онда берілген функциялар -да реттері бірдей шексіз аз не шексіз үлкен шамалар болады.

         Тригонометриялық түрлендіруден кейін ,  (17 кестені қара) екенін ескерсек:

.

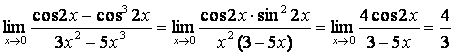6). Балама шексіз аздарды пайдаланып, шектерді табыңыз:

а) 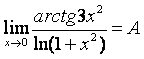,      б) .

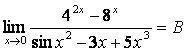         Шешу: Шек табу барысында балама шексіз аздарды өзара алмастыруға болады. Ал, -да  қосындысының бас бөлігі  болады. Онымен салыстырғанда қалған қосылғыштар сәйкес 2- және 3- ретті шексіз аздар екені айқын, яғни

.

Сондықтан 17-кестеге сүйеніп:

,

.

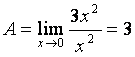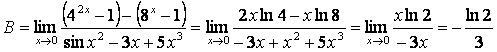7).  және  функциялары үшін:

а) үзіліс нүктелерін;

ә) үзіліс нүктесіндегі біржақты (сол және оң) шектерді;

б) үзіліс нүктелерінің сипатын анықтаңыз.

Шешу: 1). а)  нүктесі функцияның анықталу аймағына кірмейді, бірақ, функция ол нүктенің кезкелген аймағында анықталған: . Демек,   функцияның үзіліс нүктесі.

ә)  нүктесіндегі біржақты шектер:

; 

 .

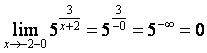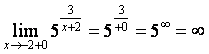б) Біржақты шектердің бірі -ке тең болғандықтан  функцияның екінші текті үзіліс нүктесі болады.

2) а)  болғандықтан  функцияның үзіліс нүктесі.

ә)  нүктесіндегі біржақты шектер:

 == –,   == +.

б) Біржақты шектер -ке айналғандықтан  функцияның екінші текті үзіліс нүктесі болады.

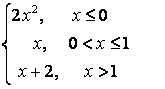
8).     

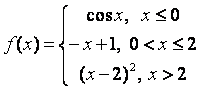
функциясын үзіліссіздікке зерттеп, графигін тұрғызыңыз.

Шешу: құраушы функциялар көрсетілген аралықтарда анықталған, демек,  функциясы барлық сандық осьте анықталған. Сондықтан үзіліс тек құраушы аралықтардың түйіскен нүктелерінде:  х = 0, х = 2 ғана болуы мүмкін. Бұл нүктелердегі біржақты шектерді табайық:

           1)  ,          .

Шарт бойынша . Демек, функция  нүктесінде үзіліссіз.

2) ,   .

Функцияның мәні  . Функция х = 2 нүктесінде сол жағынан ғана үзіліссіз, -ге тең шекті секіріс жасайды. Оның графигі:

         

 

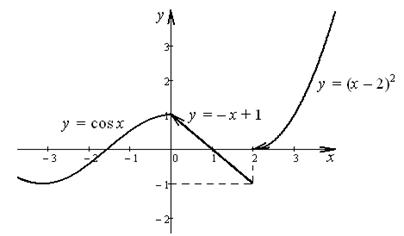
            9). Функциялардың:

а) ;

б) ;

в) ;

г) ;

д) ;

1) туындыларын,

2) б) тармағында дифференциалын табыңыз.

          Шешу:

          1) Функцияны дифференциалдаудың негізгі ережесі туындының анықтамасына:

           

негізделеді. Бірақ, іс жүзінде туындылардың кестесін (18-кесте) және дифференциалдаудың негізгі ережелерін құрайтын төмендегі формуларды қолдану ыңғайлы:

1).  ,  2). ,

3). ,        4). .

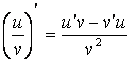5). Күрделі функцияның:  туындысы

.                                                                           (2)

6). Кері функцияның туындысыи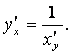  

          а) Функцияны дифференциалдауға ыңғайлы түрге

           

келтіріп, туындылар кестесіндегі 1-формуланы қолданайық:

          ,

                  .

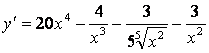б) Берілген күрделі функция:  болғандықтан (2) формула мен кестеден

           .

Әрі қарай да дифференциалдау ережелері мен туындылар кестесін сәйкестіре пайдаланамыз.

в)  ;

г) .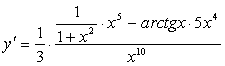

д) Күрделі функцияның:  туындысын ә) тармағындағыша табамыз

 .

          2)  функциясының дифференциалы деп  өрнегін айтамыз. Сондықтан ә) тармағында берілген функцияның дифференциалы 

          .

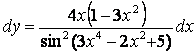10).  а),       ә)

функцияларының туындыларын логарифмдік дифференциалдау әдісімен табыңыз.

Шешу. құрамында көбейту, бөлу, дәрежелеу және түбір табу амалдары бар (логарифмдеуге ыңғайлы) күрделі өрнектің туындысын табу үшін одан алдын ала логарифм (көбіне  негізі бойынша) тауып,  екенін ескерсек болғаны. Пайда болған теңдікті алгебралық теңдеу ретінде қарап, ізделініп отырған туындыны  табамыз.

а) Берілген теңдіктің екі жағынан да натурал логарифм тауып, туынды алсақ:

 ;

 .

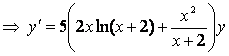ә) Алдыңғы тармақтың ізімен:    

;

;  .

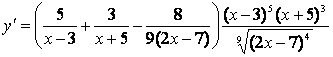11). Айқын емес функцияның

туындысын табыңыз.

Шешу. -ті -тің функциясы деп есептеп, берілген теңдіктің екі жағынан да күрделі функция ретінде туынды алайық:

.

Бұдан

                                        .

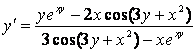12). Параметрлік түрде берілген функцияның:  

    

туындысын  табыңыз.

Шешу: параметрлік түрде  берілген функцияның туындысы 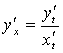  формуласының көмегімен табылады.

Бізде

         ,   

болғандықтан

         .

13). Абсциссасы  болатын нүктеде  функциясының графигіне тұрғызылған жанама мен нормальдің теңдеулерін құрыңыз.

Шешу:  функциясының графигіне  нүктесінде тұрғызылған жанама мен нормаль жазықтықта өзара перпендикуляр түзулер болғандықтан теңдеулері сәйкес

   ,       

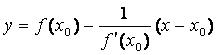
түрінде жазылады. Бізде

, ,   

болғандықтан ізделініп отырған теңдеулер сәйкес

 ,        

немесе

  ,   

түрінде жазылады.

14). Дифференциалдың көмегімен  функциясының  x1 = 26,9  нүктесіндегі жуық мәнін есептеңіз.

Шешу. Аргументтің жеткілікті аз өсімшесіне  сай  функциясының өсімшесін оның дифференциалымен жуықтап алмастыруға болады: . Бұдан әртүрлі жуықтап есептеулерде қолданылатын

                                                                            (3)

формуласына келеміз.

         Есептеуді жеңілдету үшін x0 = 27 деп алсақ,

           ,     ,

.

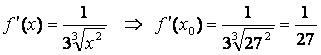Табылған мәндерді (3)-ке қойсақ: 

                        .

15). Шектерді:

а) ;

б) .

Лопиталь ережесі бойынша ашыңыз.     

Шешу: дифференциалданатын функциялар қатынасының шегін табуда кездесетін  түріндегі анықталмағандықтарды ашу үшін Лопиталь ережесін құрайтын

формуласын қолдануға болады.

         а)  .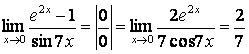

         б) Дәрежелі анықталмағандықтарға:  келтіретін  түріндегі шектерді ашу үшін өрнекті алдын ала логарифмдеу әдісіне негізделген

                                                           (4)

формуласын қолдануға болады.

         Берілген функцияда шекке тура көшу () анықталмағандығына келтіреді; (4) бойынша

 

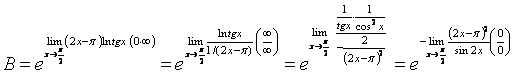
Лопиталь ережесін қайталап қолдансақ:

 .

 

          Салыстыру мақсатында Лопиталь ережесін бұрын элементарлық түрлендірудің көмегімен шығарылған есептерге қолданып көрелік.

1). .

2). .

 

1.4   Анықтама  материалдар

 

1.4.1 Шектердің түрлері мен есептеулері 

16 кесте

Шектердің түрлері

Шекке тура көшудің нәтижесі

Шекті есептеу әдісі,

нәтижесі

1.

 

анықталмағандық

2.

   

,  анықталмағандық

а) жәй көбейткіштерге жіктеу;

б) Лопиталь ережесі;

в) түйіндес өрнекке көбейту;

г) балама шексіз аздарды қолдану;

д) осы кестенің 1-ережесін қолдану

3.  

, ,

0

4.  

, ,

5.  

 

анықталмағандық

,  түріндегі анықталмағандыққа келтіріп, осы кестенің 1-немесе 2-ережесін қолдану

6.  

,

7.  

,

0

8.  

 анықталмағандық

немесе  түріндегі анықталмағандыққа келтіріп, осы кестенің 1- немесе 2- ережесін қолдану

9.  

10. 

 анықталмағандық

а) екінші тамаша шекке  келтіру;

б)  формуласын қолдану

11. 

12.

 

 

1.4.2 Шексіз аз функцияларды салыстыру

Егер  болса, онда -да  шексіз аз функция, қысқаша, шексіз аз (ш.а) делінеді. Шексіз аздарды салыстыру үшін олардың қатынасының шегін табу қажет.

Айталық, -да  және  шексіз аздар болсын. Онда егер:

1)  болса,  -да -ды -ға қарағанда жоғары ретті ш.а. деп, жазуда «-кіші» рәмізін қолдануға болады: ;

2)  болса, онда  болғаны;

3) 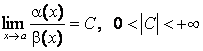 болса, онда  -да   мен  бірдей ретті шексіз аздар болғаны;

4)  болса,  мен -ды -да балама шексіз аздар:  дейміз;

5) 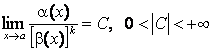 болса, онда  -да  -ды -мен салыстырғанда -ретті ш.а. дейміз.

Шек табу барысында төмендегі теоремаларды және шексіз аздар кестесін пайдаланып, балама шексіз аздарды бір-бірімен алмастыруға болады.

1-Теорема. Егер  -да ,  болса, онда

 1)  ,

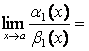
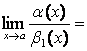
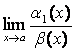 2) .

2-Теорема. Саны шекті шексіз аздардың алгебралық қосындысы шексіз аздық реті ең кіші қосылғышқа балама болады.

 

17 кесте

, яғни -да,  а £ ¥    шексіз аз

1.

5.

9.

2.

6.

10.

3.

7.

11.

4.

8.

 

 

 1.4.3      Үзіліссіз функциялар. Үзіліс нүктелері, оларды сұрыптау

Функция нүктенің өзінде анықталмаған, бірақ оның маңында анықталған болса, онда мұндай нүкте функцияның үзіліс нүктесі болады. Егер функция бірнеше аналитикалық (үзіліссіз) өрнектерден тұрса, онда сол өрнектердің ауысу нүктелері функцияның үзіліс нүктелері болуы мүмкін.

Функцияның  нүктесіндегі біржақты: сол жақ () және оң жақ () шектері сәйкес талаптарды (теңсздіктерді) сақтай отырып, әдеттегі шектерше есептелінеді және сәйкес ,  арқылы белгіленеді:

=,

 =.

Егер = болса, онда функция  нүктесінде үзіліссіз және керісінше. Бұл шарт орындалмаса,  функцияның үзіліс нүктесі болғаны. Үзіліс нүктесінің сипаты (классификациясы) қос теңдіктің қайсысының орындалуына байланысты.

1) Біржақты шектердің екеуі де бар, бірақ,  болса, онда а  функцияның I-текті үзіліс нүктесі делінеді. Бұл нүктеде функция шекті секіріс: – жасайды. Ал, функцияның мәні біржақты шектердің қайсысына тең:   немесе    болса, онда функция сәйкес сол жағынан не оң жағынан үзіліссіз болады.

2) Егер = болса, онда а-ны функцияның  құтылуға болатын үзіліс нүктесі дейміз.

3) Егер біржақты шектердің кем дегенде біреуі -ке айналса, не жоқ болса, онда а  функцияның II-текті үзіліс нүктесі деп аталады.

 

1.4.4 Негізгі элементар функциялардың туындылары

18 кесте

1.

7.

13.

2. 

8.

14.

3.

9.

15.

4.

10.

16.

5.

11.

17.

6.

12.

18.

 

Әдебиеттер тізімі

 

1.     Данко П.Е., Попов А.Г., Кожевникова Т.Я. Жоғарғы математика жаттығулар мен есептерде (2 бөлімнен). –М.: Жоғарғы мектеп, 1986,             –1б., –352 б.

2.     Жоғарғы математикадан жеке тапсырмалар жинағы (3 бөлімнен, А.П. Рябушко, В.В. Бархатов  т.б. А.П. Рябушко редакциясымен). –Минск: Жоғарғы мектеп, 2000, 1б., –303 б.

3.     Кузнецов Л.А. Жоғарғы математикадан есептер жинағы (типтік есептеулер). –М.: Жоғарғы мектеп, 1983, –175 б.

4.     Пискунов Н.С. Дифференциалдық және интегралдық есептеулер. ЖТОО үшін оқулық (2 бөлімнен). –М.: Ғылым, 1976, 1т., –456 б.

 

Мазмұны 

1 Типтік есептеу. Функцияның шегі мен үзіліссіздігі. Бір айнымалы функциясын дифференциалдау

 

3

1.1 Теориялық сұрақтар

3

1.2 Есептеу тапсырмалары

3

1.3 Типтік нұсқаның шешуі

20

1.4 Анықтама материалдар

29

Әдебиеттер тізімі

32