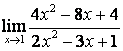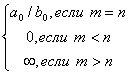АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Методические указания и задания к расчетно-графической работе
(для студентов всех форм обучения специальности 050704 –
Вычислительная техника и программное обеспечение)
Часть 1
Алматы 2009
СОСТАВИТЕЛИ: Л.Н. Астраханцева, М.Ж.Байсалова.
Математический анализ. Методические указания и задания к выполнению расчетно-графической работы для студентов всех форм обучения специальности 050704 – Вычислительная техника и программное обеспечение. Часть 1. -Алматы: АИЭС, 2009.- 34 с.
Методические указания и задания к расчетно-графической работе содержат типовой расчет №1 дисциплины «Математический анализ» для студентов всех форм обучения специальности 050704 – Вычислительная техника и программное обеспечение. Приведены основные теоретические вопросы программы. Дано решение типового варианта.
1 Типовой расчёт 1. Введение в анализ. Дифференциальное исчисление функции одной переменной
1.1 Теоретические вопросы
1. Понятие функции. Способы задания, свойства, классификация функций.
2. Числовые последовательности. Предел числовой последовательности. Предел функции.
3. Бесконечно малые и бесконечно большие величины. Теоремы о бесконечно малых.
4. Теоремы о пределах. Односторонние пределы. Первый и второй замечательные пределы.
5. Сравнение бесконечно малых. Теоремы об эквивалентных бесконечно малых.
6. Непрерывные функции. Точки разрыва, их классификация.
7. Определение производной, её физический и геометрический смысл. Связь дифференцируемости и непрерывности.
8. Основные правила дифференцирования.
9. Производные основных элементарных функций.
10. Логарифмическое дифференцирование. Производные высших порядков.
11. Производные функций, заданных неявно и параметрически.
Уравнения касательной и нормали к графику функции.
12. Дифференциал, его геометрический смысл и применение.
13. Дифференциалы высших порядков. Дифференциал сложной
функции. Инвариантность формы первого дифференциала.
14. Правило Лопиталя. Теоремы о возрастании и убывании функции.
15. Экстремумы функции одной переменной. Необходимое и
достаточные условия экстремума.
16. Выпуклость и вогнутость графика функции, точки перегиба.
17. Асимптоты графика функции. Полное исследование функции.
1.2 Расчётные задания
1. Найти пределы функции, если предельная точка а принимает два
значения а) и б).
Т а б л и ц а 1
|
|
а) а= |
б) а= |
|
а) а= |
б) а= |
|
1.1
|
2 |
1 |
1.2
|
-9 |
2 |
|
1.3
|
-2 |
3 |
1.4
|
-3 |
4 |
|
1.5
|
8 |
-1 |
1.6
|
9 |
-1 |
продолжение таблицы 1
|
1.7
|
7 |
0 |
1.8
|
-4 |
1 |
|
1.9
|
4 |
1 |
1.10
|
1 |
5 |
|
1.11
|
3 |
2 |
1.12
|
8 |
0 |
|
1.13
|
-5 |
1 |
1.14
|
-1 |
2 |
|
1.15
|
-7 |
3 |
1.16
|
-2 |
3 |
|
1.17
|
-6 |
1 |
1.18
|
8 |
1 |
|
1.19
|
-2 |
4 |
1.20
|
6 |
2 |
|
1.21
|
2 |
-3 |
1.22
|
4 |
3 |
|
1.23 |
-1 |
2 |
1.24 |
-3 |
1 |
|
1.25 |
-5 |
3 |
1.26 |
5 |
-1 |
|
1.27 |
-1 |
4 |
1.28 |
-3 |
2 |
|
1.29 |
4 |
-1 |
1.30 |
3 |
-1 |
2. Найти пределы
Т а б л и ц а 2
|
2.1
а) |
|
2.2
а) |
|
2.3
а)
|
|
2.4 а) |
|
2.5
а)
|
продолжение таблицы 2
|
2.6
а) |
|
2.7
а) |
|
2.8
а) |
|
2.9
а) |
|
2.10 а) |
|
2.11
а)
|
|
2.12
а)
|
|
2.13 а) |
|
2.14
а) |
|
2.15 а) |
|
2.16 а) |
|
2.17 а) |
|
2.18 а) |
|
2.19
а)
|
|
2.20
а)
|
|
2.21 а)
|
|
2.22
а)
|
|
2.23
а)
|
продолжение таблицы 2
|
2.24
а) |
|
2.25
а) |
|
2.26
а) |
|
2.27
а) |
|
2.28
а) |
|
2.29
а) |
|
2.30
а) |
3. Найти пределы
Т а б л и ц а 3
|
3.1 |
3.2 |
3.3 |
|
3.4 |
3.5 |
3.6 |
|
3.7 |
3.8 |
3.9 |
|
3.10 |
3.11 |
3.12 |
|
3.13 |
3.14 |
3.15 |
|
3.16 |
3.17 |
3.18 |
|
3.19 |
3.20 |
3.21 |
продолжение таблицы 3
|
3.22 |
3.23 |
3.24 |
|
3.25 |
3.26 |
3.27 |
|
3.28 |
3.29 |
3.30 |
4. Найти пределы
Т а б л и ц а 4
|
|
а) |
б) |
|
а) |
б) |
|
4.1 |
|
|
4.2 |
|
|
|
4.3 |
|
|
4.4 |
|
|
|
4.5 |
|
|
4.6 |
|
|
|
4.7 |
|
|
4.8 |
|
|
|
4.9 |
|
|
4.10 |
|
|
|
4.11 |
|
|
4.12 |
|
|
|
4.13 |
|
|
4.14 |
|
|
|
4.15 |
|
|
4.16 |
|
|
|
4.17 |
|
|
4.18 |
|
|
|
4.19 |
|
|
4.20 |
|
|
|
4.21 |
|
|
4.22 |
|
|
продолжение таблицы 4
|
4.23 |
|
|
4.24 |
|
|
|
4.25 |
|
|
4.26 |
|
|
|
4.27 |
|
|
4.28 |
|
|
|
4.29 |
|
|
4.30 |
|
|
5. Найти пределы, используя эквивалентные бесконечно малые
Та б л и ц а 5
|
|
а) |
б) |
|
а) |
б) |
|
5.1 |
|
|
5.2 |
|
|
|
5.3 |
|
|
5.4 |
|
|
|
5.5 |
|
|
5.6 |
|
|
|
5.7 |
|
|
5.8 |
|
|
|
5.9 |
|
|
5.10 |
|
|
|
5.11 |
|
|
5.12 |
|
|
|
5.13 |
|
|
5.14 |
|
|
|
5.15 |
|
|
5.16 |
|
|
продолжение таблицы 5
|
5.17 |
|
|
5.18 |
|
|
|
5.19 |
|
|
5.20 |
|
|
|
5.21 |
|
|
5.22 |
|
|
|
5.23 |
|
|
5.24 |
|
|
|
5.25 |
|
|
5.26 |
|
|
|
5.27 |
|
|
5.28 |
|
|
|
5.29 |
|
|
5.30 |
|
|
6. Для данных функций f(x) и g(x) найти
а) точку разрыва;
б) левый и правый пределы в точке разрыва;
в) определить характер точки разрыва.
Т а б л и ц а 6
|
|
f(x) |
g(x) |
|
f(x) |
g(x) |
|
6.1 |
|
|
6.2 |
|
|
|
6.3 |
|
|
6.4 |
|
|
|
6.5 |
|
|
6.6 |
|
|
|
6.7 |
|
|
6.8 |
|
|
|
6.9 |
|
|
6.10 |
|
|
|
6.11 |
|
|
6.12 |
|
|
|
6.13. |
|
|
6.14 |
|
|
|
6.15 |
|
|
6.16 |
|
|
продолжение таблицы 6
|
6.17 |
|
|
6.18. |
|
|
|
6.19 |
|
|
6.20 |
|
|
|
6.21 |
|
|
6.22 |
|
|
|
6.23 |
|
|
6.24. |
|
|
|
6.25 |
|
|
6.26 |
|
|
|
6.27 |
|
|
6.28 |
|
|
|
6.29 |
|
|
6.30 |
|
|
7. Исследовать функцию на непрерывность и построить график.
Т а б л и ц а 7
|
f(x) |
f(x) |
|
7.1 |
7.2 |
|
7.3 |
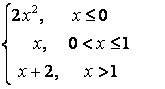
7.4 |
|
7.5 |
7.6 |
|
7.7 |
7.8 |
|
7.9 |
7.10 |
продолжение таблицы 7
|
7.11 |
7.12 |
|
7.13 |
7.14 |
|
7.15 |
7.16 |
|
7.17 |
7.18 |
|
7.19 |
7.20 |
|
7.21 |
7.22 |
|
7.23 |
7.24 |
|
7.25 |
7.26 |
|
7.27 |
7.28 |
|
7.29 |
7.30 |
8. Найти
1) производные функций;
2) дифференциал функции из пункта б).
Т а б л и ц а 8
|
8.1 а) б) в) г) д) |
8.2 а) б) в) г) д) |
8.3 а) б) в) г) д) |
|
8.4 а) б) в) г) д) |
8.5 а) б) в) г) д) |
8.6 а) б) в) г) д) |
|
8.7 а) б) в) г) д) |
8.8 а) б) в) г) д) |
8.9 a) б) в) г) д)
|
продолжение таблицы 8
|
8.10 а) б) в) г) д) |
8.11 а) б) в) г) д) |
8.12 а) б) в) г) д) |
|
8.13 а) б) в) г) д) |
8.14 а) б) в) г) д) |
8.15 а) б) в) г) д) |
|
8.16 а) б) в) г) д) |
8.17 а) б) в) г) д) |
8.18 а) б) в) г) д) |
продолжение таблицы 8
|
8.19 а) б) в) г) д) |
8.20 а) б) в) г) д) |
8.21 a) б) в) г) д) |
|
8.22 а) б) в) г) д) |
8.23 а) б) в) г) д) |
8.24 а) б) в) г) д) |
|
8.25 а) б) в) г) д) |
8.26 а) б) в) г) д) |
8.27 а) б) в) г) д) |
продолжение таблицы 8
|
8.28 а) б) в) г) д) |
8.29 а) б) в) г) д) |
8.30 а) б) в) г) д) |
9. Найти производные методом логарифмического дифференцирования.
Т а б л и ц а 9
|
9.1 |
9.2 |
|
9.3 |
9.4 |
|
9.5 |
9.6 |
|
9.7 |
9.8 |
|
9.9 |
9.10 |
|
9.1 |
9.12 |
|
9.13 |
9.14 |
|
9.15 |
9.16 |
|
9.17 |
9.18 |
продолжение таблицы 9
|
9.19 |
9.20 |
|
9.21 |
9.22 |
|
9.23 |
9.24 |
|
9.2 |
9.26 |
|
9.27 |
9.28 |
|
9.29 |
9.30 |
10. Найти производные неявных функций.
Т а б л и ц а 10
|
10.1 x – y + arctg y = 0 |
10.2 xy = |
10.3 |
|
10.4 y = cos xy |
10.5 xy = ln(1 + y) |
10.6 x – y +3sin y = 0 |
|
10.7 |
10.8 x – y + 4sin y = 0 |
10.9 |
|
10.10 |
10.11 |
10.12 |
|
10.13 |
10.14 y + |
10.15 x = ln(x + y) |
|
10.16 y - |
10.17 |
10.18 x + y = |
|
10.19 y = sin xy |
10.20 |
10.21 xy = ln xy |
|
10.22 x + y |
10.23 y |
10.24 |
|
10.25 |
10.26 xy + sin(x + y) = 0 |
10.27 xy + cos(x + y) = 0 |
|
10.28 tg y = 4y – 5x |
10.29 xy = ctg y |
10.30 xy – 6 = cos y |
11. Найти производные 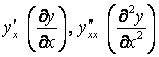 функций, заданных параметрически.
функций, заданных параметрически.
Т а б л и ц а 11
|
11.1 |
11.2 |
11.3 |
|
11.4 |
11.5 |
11.6 |
|
11.7 |
11.8 |
11.9 |
|
11.10 |
11.11 |
11.12 |
|
11.13 |
11.14 |
11.15 |
|
11.16 |
11.17 |
11.18 |
|
11.19 |
11.20 |
11.21 |
|
11.22 |
11.23 |
11.24 |
|
11.25 |
11.26 |
11.27 |
|
11.28 |
11.29 |
11.30 |
12.
а) Составить уравнение касательной и нормали к графику функции в точке с
абсциссой ![]() ;
;
б)
вычислить приближённое значение функции в точке ![]() с помощью дифференциала.
с помощью дифференциала.
Т а б л и ц а 12
|
f(x) |
|
|
f(x) |
|
|
|
12.1 |
27 |
7,96 |
12.2 |
1 |
1,02 |
|
12.3 |
1 |
31,8 |
12.4 |
1 |
16,04 |
|
12.5 |
3 |
2,9 |
12.6 |
-1 |
27,05 |
|
12.7 |
9 |
24,95 |
12.8 |
1 |
25,05 |
|
12.9 |
1 |
1,03 |
12.10 |
-128 |
128,5 |
|
12.11 |
1 |
15,98 |
11.12 |
-1 |
31,85 |
|
12.13 |
1 |
1,04 |
12.14 |
16 |
1,05 |
|
12.15 |
-1 |
32,05 |
12.16 |
-1 |
31,5 |
|
12.17 |
1 |
16,07 |
12.18 |
1 |
15,95 |
|
12.19
|
4 |
15,92 |
12.20 |
-1 |
1,01 |
|
12.21 |
1 |
31,95 |
12.22 |
1 |
16,05 |
|
12.23 |
1 |
0.95 |
12.24 |
-1 |
1,03 |
|
12.25 |
1 |
16,06 |
12.26 |
1 |
64,05 |
|
12.27 |
8 |
1,02 |
12.28 |
-8 |
1,05 |
|
12.29 |
1 |
15,91 |
12.30 |
1 |
0,98 |
13. Найти наибольшее и наименьшее значения функции на отрезке.
Т а б л и ц а 13
|
f(x) |
|
f(x) |
|
|
13.1 |
|
13.2 |
|
|
13.3 |
|
13.4 |
|
|
13.5 |
|
13.6 |
|
|
13.7 |
|
13.8 |
|
|
13.9 |
|
13.10 |
|
|
13.11 |
|
13.12 |
|
|
13.13 |
|
13.14 |
|
|
13.15 |
|
13.16 |
|
|
13.17 |
|
13.18 |
|
|
13.19 |
|
13.20 |
|
|
13.21 |
|
13.22 |
|
|
13.23 |
|
13.24 |
|
|
13.25 |
|
13.26 |
|
продолжение таблицы 13
|
13.27 |
|
13.28 |
|
|
13.29 |
|
13.30 |
|
14. Для данной функции найти:
а) область определения и точки разрыва;
б) асимптоты графика функции;
в) точки пересечения графика с осями координат;
г) чётность и нечётность;
д) интервалы монотонности, точки экстремума;
е) интервалы выпуклости, вогнутости, точки перегиба;
ж) построить график.
Т а б л и ц а 14 9(3)
|
f(x) |
f(x) |
f(x) |
|
14.1 |
14.2 |
14.3 |
|
14.4 |
14.5 |
14.6 |
|
14.7 |
14.8 |
14.9 |
|
14.10 |
14.11 |
14.12 |
|
14.13 |
14.14 |
14.15 |
|
14.16 |
14.17 |
14.18 |
|
14.19 |
14.20 |
14.21 |
|
14.22 |
14.23 |
14.24 |
|
14.25 |
14.26 |
14.27 |
|
14.28 |
14.29 |
14.30 |
15 Найти пределы по правилу Лопиталя
Т а б л и ц а 15
|
15.1 а)
|
15.2 а) |
|
15.3 а) |
15.4 а)
|
|
15.5 а) |
15.6 а) |
|
15.7 а) |
15.8 а) |
|
15.9 а) |
15.10 а) |
|
15.11 а) |
15.12 а) |
|
15.13 а) |
15.14 а) |
|
15.15 а) |
15.16 а) |
|
15.17 а) |
15.18 а) |
|
15.19 а) |
15.20 а) |
|
15.21 а) |
15.22 а) |
|
15.23 а) |
15.24 а) |
|
15.25 а) |
15.26 а) |
|
15.27 а) |
15.28 а) б) |
|
15.29 а) |
15.30 а) |
1.3 Решение типового варианта
При вычислении пределов, прежде всего, следует
подставить предельную точку в функцию вместо переменной. Если получено вполне
определённое значение (константа или бесконечность), то это значение является
ответом. Если в результате подстановки получена одна из неопределённостей
(возможны семь видов неопределённостей: 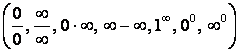 , то, говорят, следует раскрыть
неопределённость, т.е. вычислить предел, используя различные методы. Рассмотрим
эти методы на примерах.
, то, говорят, следует раскрыть
неопределённость, т.е. вычислить предел, используя различные методы. Рассмотрим
эти методы на примерах.
1. Найти предел ![]() при
при
а) а=1;
б) а=5.
Решение:
а) подставим предельную точку а=1 в функцию вместо ![]() , получим сразу ответ:
, получим сразу ответ: 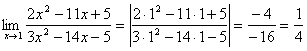 ;
;
б) при подстановке а=5 получим неопределённость вида ![]()
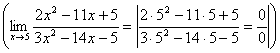 , которую можно раскрыть,
применяя один из двух методов. Первый состоит в разложении числителя и
знаменателя дроби на множители и сокращении на общий множитель:
, которую можно раскрыть,
применяя один из двух методов. Первый состоит в разложении числителя и
знаменателя дроби на множители и сокращении на общий множитель: ![]() . Во втором методе
применяют правило Лопиталя:
. Во втором методе
применяют правило Лопиталя: ![]() . По этому правилу имеем
. По этому правилу имеем ![]() .
.
2. Найти пределы:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
Решение:
в каждом из этих пределов после подстановки ![]() получается
неопределённость вида
получается
неопределённость вида ![]() ,
для её раскрытия применяют правило 1.7 таблицы 18. В случае а) числитель и
знаменатель имеют одинаковые степени
,
для её раскрытия применяют правило 1.7 таблицы 18. В случае а) числитель и
знаменатель имеют одинаковые степени ![]() , поэтому предел равен отношению
коэффициентов старших степеней:
, поэтому предел равен отношению
коэффициентов старших степеней: ![]() ; в случае б) степень числителя больше
степени знаменателя
; в случае б) степень числителя больше
степени знаменателя ![]() ,
поэтому
,
поэтому ![]() ; в
случае в) степень знаменателя больше степени числителя
; в
случае в) степень знаменателя больше степени числителя ![]() , поэтому
, поэтому ![]() .
.
3. Найти предел ![]() .
.
Решение:
при подстановке предельного значения получается
неопределённость вида ![]() ,
которую в данном случае лучше раскрыть, умножая числитель и знаменатель на
выражение, сопряжённое числителю. Одновременно знаменатель следует разложить на
множители и затем сократить дробь на общий множитель:
,
которую в данном случае лучше раскрыть, умножая числитель и знаменатель на
выражение, сопряжённое числителю. Одновременно знаменатель следует разложить на
множители и затем сократить дробь на общий множитель: 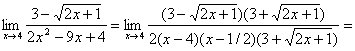
![]() . Если применить
правило Лопиталя, то получится тот же результат:
. Если применить
правило Лопиталя, то получится тот же результат: ![]()
![]() =
=![]() .
.
4. Найти пределы:
а) ![]() ;
;
б) ![]() .
.
Решение:
а)
при подстановке ![]() получим
неопределённость вида
получим
неопределённость вида ![]() ,
которую можно раскрыть, применяя, например, следующие методы. Первый – это
приведение данного предела к форме второго замечательного предела
,
которую можно раскрыть, применяя, например, следующие методы. Первый – это
приведение данного предела к форме второго замечательного предела ![]() :
:![]() =
=![]() =
=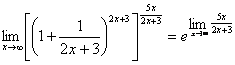 =
=![]() .
.
Здесь
мы использовали обобщённую форму второго замечательного предела 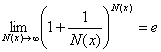 . Второй метод – это
использование формулы, которую часто применяют для раскрытия неопределённостей
вида
. Второй метод – это
использование формулы, которую часто применяют для раскрытия неопределённостей
вида![]() :
:
![]() . По этой формуле
. По этой формуле ![]() =
=![]() =
= ![]() =(используем теорему о замене бесконечно
малой функции эквивалентной ей бесконечно малой:
=(используем теорему о замене бесконечно
малой функции эквивалентной ей бесконечно малой: ![]() при
при ![]() ) =
) =
![]() =
= ![]() . Формулу, приведённую выше можно
не помнить, но использовать приём, который привёл к этой формуле: положим
. Формулу, приведённую выше можно
не помнить, но использовать приём, который привёл к этой формуле: положим ![]()
![]() , прологарифмируем это равенство
по основанию е:
, прологарифмируем это равенство
по основанию е: ![]() , и найдём
, и найдём ![]() =(см. вычисление этого
предела выше)=5/2. Итак,
=(см. вычисление этого
предела выше)=5/2. Итак, ![]() , откуда
, откуда ![]() ;
;
б)
![]() =
=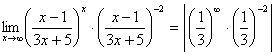 =
=![]() .
.
5. Найти пределы:
а) ![]() ;
;
б) ![]() , используя эквивалентные бесконечно малые.
, используя эквивалентные бесконечно малые.
Решение:
если ![]() , то
, то ![]() называется бесконечно малой функцией или
просто бесконечно малой (б. м.) при
называется бесконечно малой функцией или
просто бесконечно малой (б. м.) при ![]() . Для сравнения бесконечно малых вычисляют
предел их отношения. Пусть
. Для сравнения бесконечно малых вычисляют
предел их отношения. Пусть ![]() и
и ![]() бесконечно малые при
бесконечно малые при ![]() , тогда если
, тогда если
1) ![]() , то б.м.
, то б.м. ![]() более высокого порядка малости, чем
более высокого порядка малости, чем ![]() , в этом случае пишут
, в этом случае пишут ![]() ;
;
2) ![]() , то б.м.
, то б.м. ![]() более низкого порядка малости, чем
более низкого порядка малости, чем ![]() ;
;
3) ![]() , то б.м.
, то б.м. ![]() и
и ![]() одного порядка;
одного порядка;
4) ![]() , то б.м.
, то б.м. ![]() и
и ![]() эквивалентны, записывают
эквивалентны, записывают ![]() ;
;
5) ![]() , то
, то ![]() есть б.м.
есть б.м. ![]() - го порядка по сравнению с
- го порядка по сравнению с![]() .
.
При вычислении пределов с б.м. в ряде случаев используют теоремы об эквивалентных б.м.:
Теорема 1. Если ![]() ,
, ![]() при
при ![]() , то
, то
1) ![]()
![]()
![]()
![]() ;
;
2) ![]() .
.
Теорема 2. Алгебраическая сумма конечного числа б.м. эквивалентна слагаемому низшего порядка.
Итак, следуя этим теоремам, в пределах одну б.м. можно заменить другой эквивалентной ей, при этом используют таблицу эквивалентных б.м. (см. таблицу 19).
а) ![]() =(по таблице 19
=(по таблице 19 ![]() ,
, ![]() при
при ![]() )=
)=
![]() =-8;
=-8;
б)
![]() =(с учётом
таблицы 19 преобразуем
=(с учётом
таблицы 19 преобразуем ![]()
![]() =
=![]() ;
; ![]() - т.о. эта б.м. третьего порядка по
сравнению с
- т.о. эта б.м. третьего порядка по
сравнению с ![]() ,
, ![]() - б.м. второго порядка
относительно
- б.м. второго порядка
относительно ![]() ,
(
,
(![]() ) – б.м.
первого порядка или одного порядка с
) – б.м.
первого порядка или одного порядка с ![]() , поэтому по теореме 2 сумма
, поэтому по теореме 2 сумма ![]() эквивалентна (
эквивалентна (![]() ))=
))=![]() .
.
6. Для функций ![]() и
и ![]() найти:
найти:
а) точку разрыва;
б) левый и правый пределы в точке разрыва;
в) определить характер точки разрыва.
Решение:
точками разрыва элементарной функции являются точки, в которых она не определена, но определена в их окрестности; если функция задана несколькими различными аналитическими выражениями, то точками разрыва могут быть точки, в которых меняется аналитическое выражение функции.
Односторонние пределы функции ![]() в точке
в точке ![]() определяются как предел
определяются как предел ![]() , вычисленный в
предположении, что всегда
, вычисленный в
предположении, что всегда ![]() или
или ![]() . Итак, левый предел:
. Итак, левый предел: ![]()
![]() =
=![]() ; правый предел:
; правый предел: ![]()
![]() =
=![]() .
.
Если функция ![]() непрерывна в точке
непрерывна в точке ![]() , то выполняются равенства
, то выполняются равенства ![]()
![]() =
=![]() ; если
; если ![]() точка разрыва, то последние равенства
нарушаются, и характер этого нарушения лежит в основе классификации точек
разрыва. Если
точка разрыва, то последние равенства
нарушаются, и характер этого нарушения лежит в основе классификации точек
разрыва. Если ![]() и
и
![]() существуют,
но
существуют,
но ![]()
![]()
![]() , то
, то ![]() точка разрыва первого рода с
конечным скачком, разность
точка разрыва первого рода с
конечным скачком, разность ![]() -
-![]() - скачок функции
- скачок функции ![]() в точке
в точке ![]() ; если
; если ![]()
![]()
![]()
![]() , то
, то ![]() устранимая точка разрыва первого рода.
Если хотя бы один из пределов
устранимая точка разрыва первого рода.
Если хотя бы один из пределов ![]() или
или ![]() не существует или «равен»
не существует или «равен» ![]() , то
, то ![]() точка разрыва второго рода.
точка разрыва второго рода.
1) Рассмотрим ![]() . а) Точка х=-6 не входит в область
определения этой функции, но функция определена в её окрестности, значит х=-6
точка разрыва; б)
. а) Точка х=-6 не входит в область
определения этой функции, но функция определена в её окрестности, значит х=-6
точка разрыва; б) ![]()
![]() =
=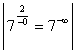 = 0,
= 0, ![]()
![]() =
= 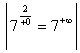 =
=![]() ; в) так как один из односторонних пределов
; в) так как один из односторонних пределов
![]()
![]() , то х=-6 точка разрыва
второго рода.
, то х=-6 точка разрыва
второго рода.
2) Рассмотрим ![]() . а) Точка х=3 не входит в область
определения этой функции, но функция определена в её окрестности, значит х=3
точка разрыва; б)
. а) Точка х=3 не входит в область
определения этой функции, но функция определена в её окрестности, значит х=3
точка разрыва; б) ![]()
![]() =
=![]() = -
= -![]() ,
, ![]()
![]() =
=![]() =+
=+![]() ; в) так как оба односторонних предела
«равны»
; в) так как оба односторонних предела
«равны» ![]() , то
х=3 точка разрыва второго рода.
, то
х=3 точка разрыва второго рода.
7. Исследовать функцию 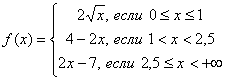 на непрерывность и построить график.
на непрерывность и построить график.
Решение:
данная функция определена на промежутке [0; ![]() ) и три составляющие её функции определены
для всех
) и три составляющие её функции определены
для всех ![]() из
соответствующих интервалов, таким образом, точками разрыва могут быть только
точки, в которых меняется аналитическое выражение функции, т.е. х=1 и х=2,5.
Исследуем эти точки. Найдём односторонние пределы в х=1:
из
соответствующих интервалов, таким образом, точками разрыва могут быть только
точки, в которых меняется аналитическое выражение функции, т.е. х=1 и х=2,5.
Исследуем эти точки. Найдём односторонние пределы в х=1: ![]()
![]() =2;
=2; ![]()
![]() =2; значение функции в этой точке
=2; значение функции в этой точке ![]() . Итак,
. Итак, ![]()
![]()
![]() , поэтому х=1 точка непрерывности.
, поэтому х=1 точка непрерывности.
Аналогично для х=2,5: ![]()
![]() =-1;
=-1;![]()
![]() = - 2;
= - 2; ![]() . Так как
. Так как ![]()
![]()
![]() , то х=2,5 точка разрыва первого рода,
, то х=2,5 точка разрыва первого рода, ![]() -
-![]() =-1 – скачок функции в этой
точке. График имеет вид:
=-1 – скачок функции в этой
точке. График имеет вид:

Рисунок 1
8. Найти:
1) производные функций
а) ![]() ;
;
б) ![]() ;
;
в) ![]() ;
;
г) ![]() ;
;
д) ![]() ;
;
2) дифференциал функции из пункта б).
Решение:
1)
по определению производной функции ![]() называется предел
называется предел ![]() . На практике при
дифференцировании функций используют таблицу производных (см. таблицу 20) и
основные правила дифференцирования: 1)
. На практике при
дифференцировании функций используют таблицу производных (см. таблицу 20) и
основные правила дифференцирования: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3)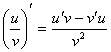 ;
;
4)
если ![]() или
или ![]() (где
(где ![]() промежуточный
аргумент), то
промежуточный
аргумент), то ![]() или
или
![]() ; 5) если
; 5) если ![]() и
и ![]() взаимно обратные функции, то
взаимно обратные функции, то ![]()
а)
Запишем функцию в виде ![]() , затем по правилу 1) и формулам 1), 2),
3), таблицы 20 имеем
, затем по правилу 1) и формулам 1), 2),
3), таблицы 20 имеем
![]() =
=![]() ;
;
б)
данную сложную функцию можно представить в виде ![]() . По правилу 4) нахождения производной
сложной функции и, учитывая формулу 11) таблицы 20, имеем
. По правилу 4) нахождения производной
сложной функции и, учитывая формулу 11) таблицы 20, имеем
![]()
![]()
![]() ;
;
в)
используя таблицу производных 20 и правило 2), получим ![]()
![]() ; г) используя таблицу производных 20 и
правило 3), получим
; г) используя таблицу производных 20 и
правило 3), получим
![]()

![]() ;
;
г)
представим данную функцию в виде цепочки элементарных функций, вводя
промежуточные аргументы 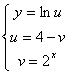 . Теперь находим производную, используя
таблицу производных 20 и правило 4) нахождения производной сложной функции
. Теперь находим производную, используя
таблицу производных 20 и правило 4) нахождения производной сложной функции ![]()
![]() ;
;
2)
дифференциалом функции ![]() называется выражение
называется выражение ![]() , поэтому для функции
, поэтому для функции ![]() дифференциал равен
дифференциал равен ![]()
![]()
![]() .
.
9. Найти производные методом логарифмического
дифференцирования а)![]() ;
б)
;
б) 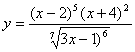 .
.
Решение:
метод логарифмического дифференцирования применяется
для определения производных функций вида ![]() или громоздких, но удобных для
логарифмирования функций (т.е. содержащих только операции умножения, деления,
возведения в степень и извлечения корня). Он состоит в последовательном
выполнении следующих действий: логарифмированию функции по основанию е,
дифференцированию полученного выражения (при этом производная
или громоздких, но удобных для
логарифмирования функций (т.е. содержащих только операции умножения, деления,
возведения в степень и извлечения корня). Он состоит в последовательном
выполнении следующих действий: логарифмированию функции по основанию е,
дифференцированию полученного выражения (при этом производная ![]() находится как
производная сложной функции) и нахождению производной
находится как
производная сложной функции) и нахождению производной ![]() из последнего равенства, как
находят неизвестные из алгебраического уравнения.
из последнего равенства, как
находят неизвестные из алгебраического уравнения.
а) после логарифмирования данной функции по основанию
е получим ![]() ,
продифференцируем результат
,
продифференцируем результат ![]() . Из последнего равенства найдём
. Из последнего равенства найдём ![]()
![]()
![]() ;
;
б) применяя метод логарифмического дифференцирования,
последовательно находим:
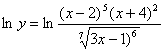 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
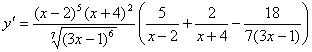 .
.
10. Найти производную неявной функции ![]() .
.
Решение:
дифференцируем данное равенство, имея в виду, что ![]() есть функция от
есть функция от ![]() (т.е. сложная функция):
(т.е. сложная функция): ![]() . Из последнего
равенства как из уравнения находим
. Из последнего
равенства как из уравнения находим ![]()
![]() .
.
11. Найти производные ![]() и
и 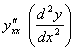 от функции, заданной параметрически
от функции, заданной параметрически 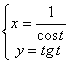 .
.
Решение:
первая производная или просто производная
параметрически заданной функции ![]() находится по формуле
находится по формуле ![]() . Вторая производная – по формуле
. Вторая производная – по формуле
![]() ; третья -
; третья - ![]() и т.д. Для нашей функции,
так как
и т.д. Для нашей функции,
так как
![]() ,
, ![]() , то
, то ![]()
![]() ;
; 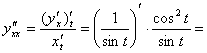
![]()
![]() .
.
12. а) Составить уравнение касательной и нормали к
графику функции ![]() в
точке с абсциссой
в
точке с абсциссой ![]() ;
;
б) вычислить приближённое значение функции в точке ![]() с помощью дифференциала.
с помощью дифференциала.
Решение:
а) уравнение касательной к графику функции ![]() в точке
в точке ![]() имеет
вид
имеет
вид ![]() , уравнение нормали -
, уравнение нормали - ![]() . Найдём
. Найдём ![]() ,
, ![]() ,
, ![]() . Таким образом, уравнение касательной
. Таким образом, уравнение касательной ![]() или
или ![]() ; уравнение нормали
; уравнение нормали ![]() или
или ![]() ;
;
б) при достаточно малых значениях ![]() приращение функции может быть
заменено её дифференциалом
приращение функции может быть
заменено её дифференциалом ![]() . Развернув это приближённое равенство,
получим формулу
. Развернув это приближённое равенство,
получим формулу ![]() (*),
которую применяют для приближённых вычислений, если требуется вычислить
(*),
которую применяют для приближённых вычислений, если требуется вычислить ![]() и если проще вычислить
и если проще вычислить ![]() и
и ![]() , где
, где ![]() достаточно близкая к
достаточно близкая к ![]() точка. В нашем примере
точка. В нашем примере ![]() , пусть
, пусть ![]() , тогда
, тогда ![]() ,
, ![]() ,
, ![]() . Подставляя эти значения в формулу (*) получим
. Подставляя эти значения в формулу (*) получим
![]() .
.
13. Найти наибольшее и наименьшее значения функции ![]() на отрезке [1;e].
на отрезке [1;e].
Решение:
если функция непрерывна на отрезке, то она обязательно имеет на этом отрезке наибольшее и наименьшее значения, которые достигаются ей или в точках экстремума, лежащих внутри отрезка, или на границах этого отрезка.
Отсюда вытекает практическое правило для нахождения наибольшего
и наименьшего значений функции ![]() на отрезке [a;b]: 1) найти критические точки, лежащие внутри отрезка
(т.е. точки, в которых производная функции равна 0 или не существует); 2)
вычислить значения функции в этих критических точках и на концах отрезка, т.е.
на отрезке [a;b]: 1) найти критические точки, лежащие внутри отрезка
(т.е. точки, в которых производная функции равна 0 или не существует); 2)
вычислить значения функции в этих критических точках и на концах отрезка, т.е. ![]() и
и ![]() ; 3) сравнить полученные значения: самое большое
будет наибольшим значением, самое маленькое – наименьшим.
; 3) сравнить полученные значения: самое большое
будет наибольшим значением, самое маленькое – наименьшим.
1) найдём критические точки функции ![]() , лежащие внутри отрезка
[1;e]:
, лежащие внутри отрезка
[1;e]: ![]() ;
; ![]() при
при ![]() ,
, ![]() не существует при
не существует при ![]() . Но
. Но ![]() не входит в данный отрезок (и
даже не входит в область определения функции),
не входит в данный отрезок (и
даже не входит в область определения функции), ![]() ; 2) вычислим значения функции на концах
отрезка и в точке
; 2) вычислим значения функции на концах
отрезка и в точке ![]() :
:
![]() ,
, ![]() ,
, ![]()
![]() ; 3) сравнивая полученные значения, делаем
вывод: наибольшее значение функции равно
; 3) сравнивая полученные значения, делаем
вывод: наибольшее значение функции равно ![]() при
при ![]() , наименьшее -
, наименьшее - ![]() при
при ![]() .
.
14. Для функции ![]() найти:
найти:
а) область определения и точки разрыва;
б) асимптоты графика функции;
в) точки пересечения графика с осями координат;
г) чётность и нечётность;
д) интервалы монотонности, точки экстремума;
е) интервалы выпуклости, вогнутости, точки перегиба;
ж) построить график.
Решение:
а) областью определения функции является множество
таких ![]() , при
которых формула, задающая функцию, имеет смысл. Итак, для нашей функции
, при
которых формула, задающая функцию, имеет смысл. Итак, для нашей функции ![]() - область определения,
в неё не входят точки, при которых знаменатель равен 0, т.е. -2 и 2, эти точки
являются точками разрыва функции;
- область определения,
в неё не входят точки, при которых знаменатель равен 0, т.е. -2 и 2, эти точки
являются точками разрыва функции;
б) вычислим односторонние пределы в точках разрыва ![]()
![]() =-
=-![]() ,
, ![]()
![]() =+
=+![]() . Итак,
точки -2 и 2 являются точками разрыва второго рода, поэтому прямые
. Итак,
точки -2 и 2 являются точками разрыва второго рода, поэтому прямые ![]() и
и ![]() будут вертикальными асимптотами.
Найдём наклонную асимптоту
будут вертикальными асимптотами.
Найдём наклонную асимптоту ![]() , где
, где ![]()
![]() ,
, ![]()
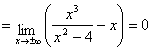 . Таким образом,
. Таким образом, ![]() - наклонная асимптота;
- наклонная асимптота;
в) точки пересечения графика функции с осями
координат: с ОХ: ![]()
![]()
![]()
![]()
![]() ; с ОУ:
; с ОУ: ![]()
![]()
![]() . Таким образом, график пересекает оси
координат в начале координат, точке (0;0);
. Таким образом, график пересекает оси
координат в начале координат, точке (0;0);
г) т.к. ![]() , то функция нечётная, её график симметричен
относительно начала координат;
, то функция нечётная, её график симметричен
относительно начала координат;
д) исследуем функцию на монотонность и найдём точки экстремума.
![]() .
. ![]()
![]()
![]()
![]()
![]() ,
, ![]() -
-
критические
точки; ![]() не
существует при
не
существует при ![]() ,
эти точки не являются критическими, т.к. не принадлежат области определения
функции. Результаты исследования сведём в таблицу.
,
эти точки не являются критическими, т.к. не принадлежат области определения
функции. Результаты исследования сведём в таблицу.
Т а б л и ц а 16
|
|
|
|
|
|
0 |
|
|
|
|
|
|
+ |
0 |
- |
- |
0 |
- |
- |
0 |
+ |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
возраст. |
max |
убыв. |
убыв. |
нет экстр |
убыв. |
убыв. |
min |
возраст. |
е) найдём интервалы выпуклости и вогнутости, точки перегиба.
![]() .
. ![]()
![]()
![]()
![]()
![]() ,
,![]() не существует при
не существует при ![]() , эти точки не могут быть
абсциссами точек перегиба, т.к. не принадлежат области определения функции. Результаты
исследования сведём в таблицу.
, эти точки не могут быть
абсциссами точек перегиба, т.к. не принадлежат области определения функции. Результаты
исследования сведём в таблицу.
Т а б л и ц а 17
|
|
|
|
0 |
|
|
|
|
- |
+ |
0 |
- |
+ |
|
|
|
|
0 |
|
|
|
|
выпукла |
вогнута |
перегиб |
выпукла |
вогнута |
(0;0) - точка перегиба;
ж) построим график функции:

Рисунок 2
15. Найти пределы по правилу Лопиталя:
а)![]() ;
;
б) ![]() .
.
Решение:
а)
правило Лопиталя см. в примере 1б). По этому правилу имеем ![]()
![]()
![]() ;
;
б)![]() . После подстановки
предельной точки в функцию получим неопределённость вида
. После подстановки
предельной точки в функцию получим неопределённость вида ![]() , которую можно раскрыть по
формуле
, которую можно раскрыть по
формуле![]() ,
приведённой в примере 4а), или с помощью
приёма, указанного в этом же примере. Положим
,
приведённой в примере 4а), или с помощью
приёма, указанного в этом же примере. Положим ![]() и
прологарифмируем это равенство по основанию е:
и
прологарифмируем это равенство по основанию е: ![]()
![]() . Применим правило Лопиталя при нахождении
предела
. Применим правило Лопиталя при нахождении
предела ![]()
![]()
![]()
![]()
![]() . Таким образом,
. Таким образом, ![]() , откуда
, откуда ![]() .
.
Т а б л и ц а 18
|
Виды пределов |
Результат подстановки предельной точки |
Результат или метод вычисления предела |
|
1. |
неопределённость |
|
|
2. |
неопределённость |
а) разложение на множители; б) правило Лопиталя; в) умножение на сопряжённое выражение; г) применение эквивалентных бесконечно малых; д) правило 1 этой таблицы |
|
3. |
|
0 |
|
4. |
|
|
|
5. |
неопределённость |
привести к неопределённостям
вида |
|
6. |
|
|
|
7. |
|
0 |
|
8. |
|
привести к неопределённостям
вида |
|
9. |
|
|
|
10. |
|
а) привести ко второму
замечательному пределу б) использовать формулу |
|
11. |
|
|
|
12. |
|
|
Т а б л и ц а 19
|
|
||
|
1. |
2. |
3. |
|
4. |
5. |
6. |
|
7. |
8. |
9. |
|
10. |
11. |
|
Т а б л и ц а 20
|
1. |
2. |
3. |
|
4. |
5. |
6. |
|
7. |
8. |
9. |
|
10. |
11. |
12. |
|
13. |
14. |
15. |
|
16. |
17. |
18. |
|
19. |
|
|
![]()
Список литературы
1. Хасеинов К.А. Каноны математики: Учебник. – Алматы: 2003.-686 с.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: в 2 ч. – М.: Высшая школа, 2003. – ч. 1,2.-352 с.
3. Сборник индивидуальных заданий по высшей математике: в 3 ч. (Рябушко А.П., Бархатов В.В. и др.). Под ред. Рябушко А.П. – Минск: Высш. школа, 2000.-ч.2,3 .-396 с.
Содержание
1 Теоретические вопросы………………………………….....…………….….3
2 Расчётные задания……………………………………..………………….….3
3 Решение типового варианта……………………………..………………….21
Список литературы ……………………………………………………………34

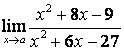





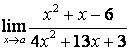
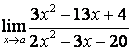
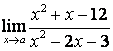
 б)
б)
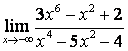 в)
в)
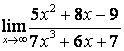
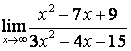 б)
б)
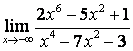
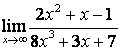
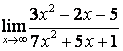

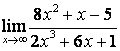
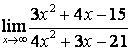
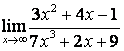
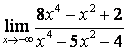
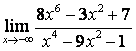
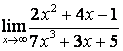
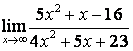
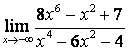
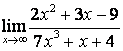
 б)
б) 


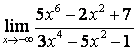
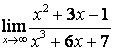
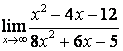
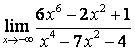

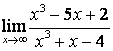
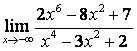

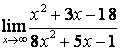


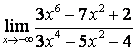
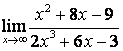
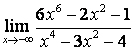
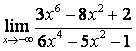
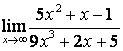
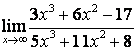
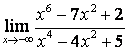
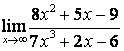
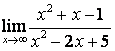
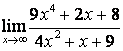
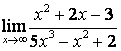
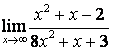
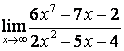
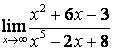
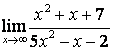



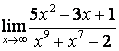
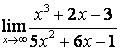
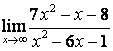
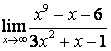
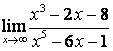
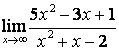
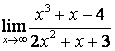
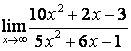
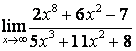
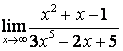

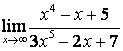
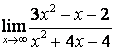
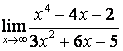
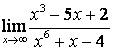
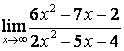
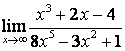

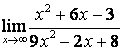
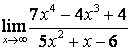
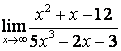
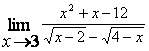



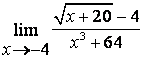










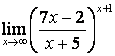
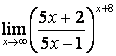
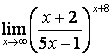

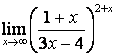














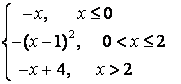
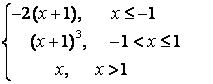

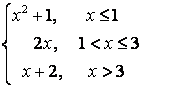



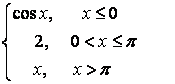
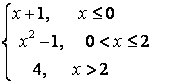
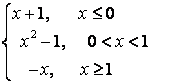

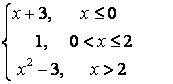

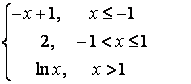
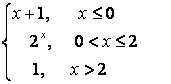
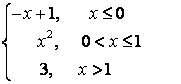
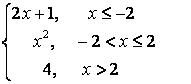
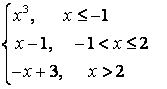
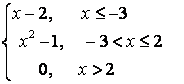
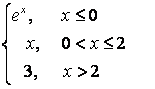
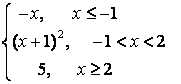
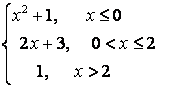
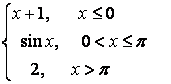

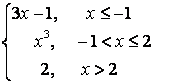
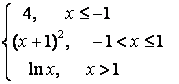
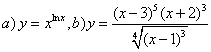

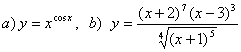
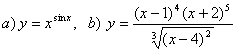

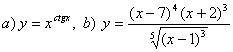

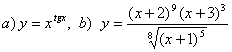

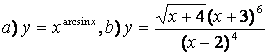
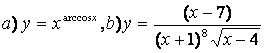

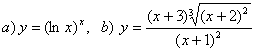


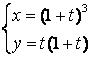
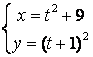
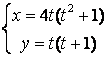

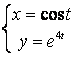
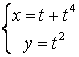
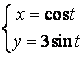
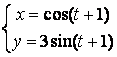
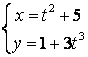
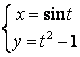
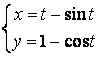
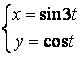
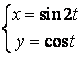


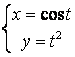
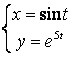
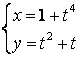



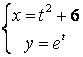
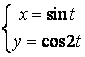






 б)
б)  б)
б)  б)
б)  б)
б)  б)
б)  б)
б)  б)
б) 
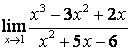 б)
б) 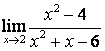
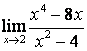 б)
б)