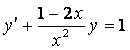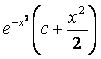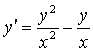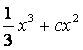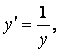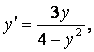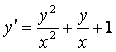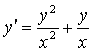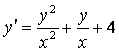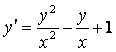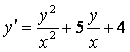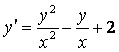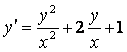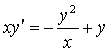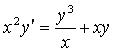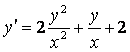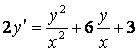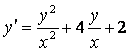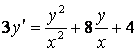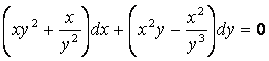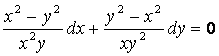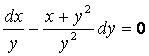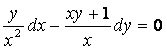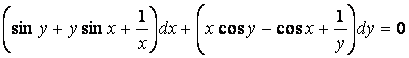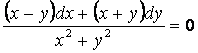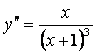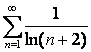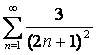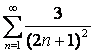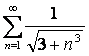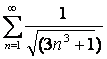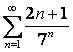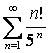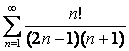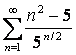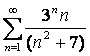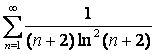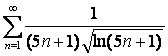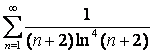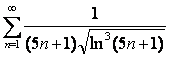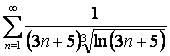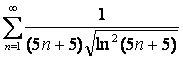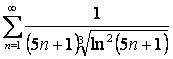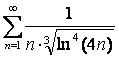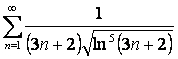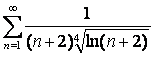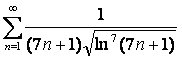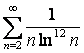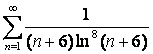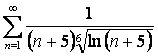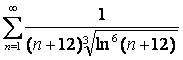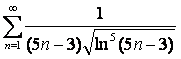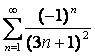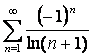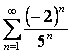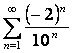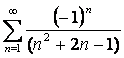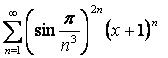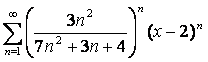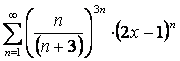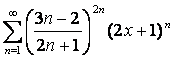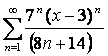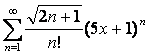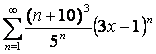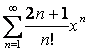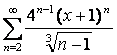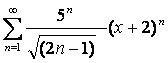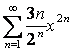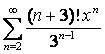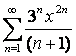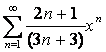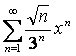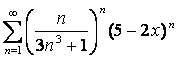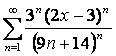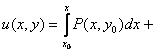АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ
Математический анализ
Методические указания и задания
к выполнению расчетно-графической работы
для студентов всех форм обучения специальностей
050704 – Вычислительная техника и программное обеспечение и
050703 – Информационные системы
Часть 3
Алматы 2009
СОСТАВИТЕЛИ: Р.Е. Ким, А.Ж. Масанова. Математический анализ. Методические указания и задания к выполнению расчетно-графической работы для студентов всех форм обучения специальностей 050704 – Вычислительная техника и программное обеспечение и 050703 – Информационные системы. Часть 3. -Алматы: АИЭС, 2009.- 38 с.
Методические указания и задания к расчетно-графической работе содержат типовой расчет №3 дисциплины «Математический анализ» для студентов всех форм обучения специальностей 050704 – Вычислительная техника и программное обеспечение и 050703 – Информационные системы. Приведены основные теоретические вопросы программы. Дано решение типового варианта.
1 Типовой расчёт 3. Дифференциальные уравнения. Ряды.
1.1 Теоретические вопросы
1. Основные понятия дифференциальных уравнений (определение, порядок, общее и частное решение, общий интеграл, задача Коши, теорема существования и единственности).
2. Дифференциальные уравнения первого порядка. Уравнения с разделяющимися переменными, однородные уравнения.
3. Линейные уравнения первого порядка, уравнения Бернулли, уравнения в полных дифференциалах.
4. Дифференциальные уравнения высших порядков (основные понятия), уравнения, допускающие понижения порядка.
5. Линейные уравнения высших порядков. Линейный дифференциальный оператор, его свойства. Линейные однородные уравнения (ЛОУ), структура их общего решения.
6. ЛОУ с постоянными коэффициентами.
7. Линейные неоднородные уравнения (ЛНУ), структура их общего решения. Метод вариации произвольных постоянных.
8. ЛНУ с постоянными коэффициентами, метод подбора частного решения.
9. Числовые ряды. Сходимость и сумма ряда. Необходимое условие сходимости ряда.
10. Признаки сравнения.
11. Признаки Даламбера и Коши. Интегральный признак Коши.
12. Знакочередующиеся ряды. Теорема Лейбница. Оценка остатка ряда.
13. Знакопеременные ряды. Абсолютно и условно сходящиеся ряды.
14. Функциональные ряды. Область сходимости.
15. Правильно сходящиеся ряды и их свойства.
16. Степенные ряды. Теорема Абеля. Интервал и радиус сходимости степенных рядов.
17. Ряды Тейлора. Разложение по степеням х функций ех , sin x, cos x, ln(1+ x), (1+ x)m.
1.2 Расчётные задания
1 Проверить, является ли функция ![]() решением данного
дифференциального уравнения (ДУ) (с – произвольная постоянная).
решением данного
дифференциального уравнения (ДУ) (с – произвольная постоянная).
Т а б л и ц а 1
|
№ |
|
ДУ |
|
1.1 |
|
|
|
1.2 |
|
|
продолжение таблицы 1
|
1.3 |
|
|
|
1.4 |
|
|
|
1.5 |
|
|
|
1.6 |
|
|
|
1.7 |
|
|
|
1.8 |
|
|
|
1.9 |
|
|
|
1.10 |
|
|
|
1.11 |
|
|
|
1.12 |
|
|
|
1.13 |
|
|
|
1.14 |
|
|
|
1.15 |
|
|
|
1.16 |
|
|
|
1.17 |
|
|
|
1.18 |
|
|
|
1.19 |
|
|
|
1.20 |
|
|
|
1.21 |
|
|
|
1.22 |
|
|
|
1.23 |
|
|
|
1.24 |
|
|
|
1.25 |
|
|
продолжение таблицы 1
|
1.26 |
|
|
|
1.27 |
|
|
|
1.28 |
|
|
|
1.29 |
|
|
|
1.30 |
|
|
2 Найти общее решение (общий интеграл) дифференциального уравнения.
Т а б л и ц а 2
|
2.1 |
|
2.2 |
|
2.3 |
|
|
2.4 |
|
2.5 |
|
2.6 |
|
|
2.7 |
|
2.8 |
|
2.9 |
|
|
2.10 |
|
2.11 |
|
2.12 |
|
|
2.13 |
|
2.14 |
|
2.15 |
|
|
2.16 |
|
2.17 |
|
2.18 |
|
|
2.19 |
|
2.20 |
|
2.21 |
|
|
2.22 |
|
2.23 |
|
2.24 |
|
|
2.25 |
|
2.26 |
|
2.27 |
|
|
2.28 |
|
2.29 |
|
2.30 |
|
3 Найти решение задачи Коши.
Т а б л и ц а 3
|
3.1 |
|
3.2 |
|
|
3.3 |
|
3.4 |
|
|
3.5 |
|
3.6 |
|
|
3.7 |
|
3.8 |
|
|
3.9 |
|
3.10 |
|
продолжение таблицы 3
|
3.11 |
|
3.12 |
|
|
3.13 |
|
3.14 |
|
|
3.15 |
|
3.16 |
|
|
3.17 |
|
3.18 |
|
|
3.19 |
|
3.20 |
|
|
3.21 |
|
3.22 |
|
|
3.23 |
|
3.24 |
|
|
3.25 |
|
3.26 |
|
|
3.27 |
|
3.28 |
|
|
3.29 |
|
3.30 |
|
4 Найти общее решение (общий интеграл) дифференциального уравнения.
Т а б л и ц а 4
|
4.1 |
|
4.2 |
|
|
4.3 |
|
4.4 |
|
|
4.5 |
|
4.6 |
|
|
4.7 |
|
4.8 |
|
|
4.9 |
|
4.10 |
|
|
4.11 |
|
4.12 |
|
|
4.13 |
|
4.14 |
|
|
4.15 |
|
4.16 |
|
|
4.17 |
|
4.18 |
|
продолжение таблицы 4
|
4.19 |
|
4.20 |
|
|
4.21 |
|
4.22 |
|
|
4.23 |
|
4.24 |
|
|
4.25 |
|
4.26 |
|
|
4.27 |
|
4.28 |
|
|
4.29 |
|
4.30 |
|
5 Найти решение задачи Коши.
Т а б л и ц а 5
|
5.1 |
|
5.2 |
|
|
5.3 |
|
5.4 |
|
|
5.5 |
|
5.6 |
|
|
5.7 |
|
5.8 |
|
|
5.9 |
|
5.10 |
|
|
5.11 |
|
5.12 |
|
|
5.13 |
|
5.14 |
|
|
5.15 |
|
5.16 |
|
|
5.17 |
|
5.18 |
|
|
5.19 |
|
5.20 |
|
|
5.21 |
|
5.22 |
|
|
5.23 |
|
5.24 |
|
продолжение таблицы 5
|
5.25 |
|
5.26 |
|
|
5.27 |
|
5.28 |
|
|
5.29 |
|
5.30 |
|
6 Найти общий интеграл дифференциального уравнения.
Т а б л и ц а 6
|
6.1 |
|
|
6.2 |
|
|
6.3 |
|
|
6.4 |
|
|
6.5 |
|
|
6.6 |
|
|
6.7 |
|
|
6.8 |
|
|
6.9 |
|
|
6.10 |
|
|
6.11 |
|
|
6.12 |
|
|
6.13 |
|
|
6.14 |
|
продолжение таблицы 6
|
6.15 |
|
|
6.16 |
|
|
6.17 |
|
|
6.18 |
|
|
6.19 |
|
|
6.20 |
|
|
6.21 |
|
|
6.22 |
|
|
6.23 |
|
|
6.24 |
|
|
6.25 |
|
|
6.26 |
|
|
6.27 |
|
|
6.28 |
|
|
6.29 |
|
|
6.30 |
|
7 Найти общее решение дифференциального уравнения.
Т а б л и ц а 7
|
7.1 |
|
7.2 |
|
|
7.3 |
|
7.4 |
|
|
7.5 |
|
7.6 |
|
|
7.7 |
|
7.8 |
|
|
7.9 |
|
7.10 |
|
|
7.11 |
|
7.12 |
|
|
7.13 |
|
7.14 |
|
продолжение таблицы 7
|
7.15 |
|
7.16 |
|
|
7.17 |
|
7.18 |
|
|
7.19 |
|
7.20 |
|
|
7.21 |
|
7.22 |
|
|
7.23 |
|
7.24 |
|
|
7.25 |
|
7.26 |
|
|
7.27 |
|
7.28 |
|
|
7.29 |
|
7.30 |
|
8 Найти общее решение дифференциального уравнения.
Т а б л и ц а 8
|
8.1 |
|
8.2 |
|
|
8.3 |
|
8.4 |
|
|
8.5 |
|
8.6 |
|
|
8.7 |
|
8.8 |
|
|
8.9 |
|
8.10 |
|
|
8.11 |
|
8.12 |
|
|
8.13 |
|
8.14 |
|
|
8.15 |
|
8.16 |
|
|
8.17 |
|
8.18 |
|
|
8.19 |
|
8.20 |
|
|
8.21 |
|
8.22 |
|
продолжение таблицы 8
|
8.23 |
|
8.24 |
|
|
8.25 |
|
8.26 |
|
|
8.27 |
|
8.28 |
|
|
8.29 |
|
8.30 |
|
9 Найти общее решение однородного линейного дифференциального уравнения с постоянными коэффициентами.
Т а б л и ц а 9
|
9.1 |
|
9.2 |
|
|
9.3 |
|
9.4 |
|
|
9.5 |
|
9.6 |
|
|
9.7 |
|
9.8 |
|
|
9.9 |
|
9.10 |
|
|
9.11 |
|
9.12 |
|
|
9.13 |
|
9.14 |
|
|
9.15 |
|
9.16 |
|
|
9.17 |
|
9.18 |
|
|
9.19 |
|
9.20 |
|
|
9.21 |
|
9.22 |
|
|
9.23 |
|
9.24 |
|
|
9.25 |
|
9.26 |
|
|
9.27 |
|
9.28 |
|
|
9.29 |
|
9.30 |
|
10 Найти общее решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами.
Т а б л и ц а 10
|
10.1 |
|
10.2 |
|
|
10.3 |
|
10.4 |
|
|
10.5 |
|
10.6 |
|
|
10.7 |
|
10.8 |
|
|
10.9 |
|
10.10 |
|
|
10.11 |
|
10.12 |
|
|
10.13 |
|
10.14 |
|
продолжение таблицы 10
|
10.15 |
|
10.16 |
|
|
10.17 |
|
10.18 |
|
|
10.19 |
|
10.20 |
|
|
10.21 |
|
10.22 |
|
|
10.23 |
|
10.24 |
|
|
10.25 |
|
10.26 |
|
|
10.27 |
|
10.28 |
|
|
10.29 |
|
10.30 |
|
11 Дан ряд 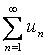 :
:
а) составить формулу общего члена ряда ![]() и написать первые пять членов;
и написать первые пять членов;
б) записать n-ую
частичную сумму ряда ![]() ;
;
в) записать остаток ряда ![]() ;
;
г) проверить необходимое условие сходимости ряда.
Т а б л и ц а 11
|
11.1 |
|
11.2 |
|
11.3 |
|
|
11.4 |
|
11.5 |
|
11.6 |
|
|
11.7 |
|
11.8 |
|
11.9 |
|
|
11.10 |
|
11.11 |
|
11.12 |
|
|
11.13 |
|
11.14 |
|
11.15 |
|
|
11.16 |
|
11.17 |
|
11.18 |
|
|
11.19 |
|
11.20 |
|
11.21 |
|
|
11.22 |
|
11.23 |
|
11.24 |
|
продолжение таблицы 11
|
11.25 |
|
11.26 |
|
11.27 |
|
|
11.28 |
|
11.29 |
|
11.30 |
|
12 Сравнить с рядом Дирихле 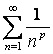 , т.е. найти параметр p,
и исследовать на сходимость ряд.
, т.е. найти параметр p,
и исследовать на сходимость ряд.
Т а б л и ц а 12
|
12.1 |
|
12.2 |
|
12.3 |
|
|
12.4 |
|
12.5 |
|
12.6 |
|
|
12.7 |
|
12.8 |
|
12.9 |
|
|
12.10 |
|
12.11 |
|
12.12 |
|
|
12.13 |
|
12.14 |
|
12.15 |
|
|
12.16 |
|
12.17 |
|
12.18 |
|
|
12.19 |
|
12.20 |
|
12.21 |
|
|
12.22 |
|
12.23 |
|
12.24 |
|
|
12.25 |
|
12.26 |
|
12.27 |
|
|
12.28 |
|
12.29 |
|
12.30 |
|
13 Исследовать на сходимость с помощью признака Даламбера.
Т а б л и ц а 13
|
13.1 |
|
13.2 |
|
13.3 |
|
|
13.4 |
|
13.5 |
|
13.6 |
|
|
13.7 |
|
13.8 |
|
13.9 |
|
|
13.10 |
|
13.11 |
|
13.12 |
|
|
13.13 |
|
13.14 |
|
13.15 |
|
|
13.16 |
|
13.17 |
|
13.18 |
|
|
13.19 |
|
13.20 |
|
13.21 |
|
|
13.22 |
|
13.23 |
|
13.24 |
|
|
13.25 |
|
13.26 |
|
13.27 |
|
|
13.28 |
|
13.29 |
|
13.30 |
|
14 Исследовать на сходимость с помощью радикального признака Коши.
Т а б л и ц а 14
|
14.1 |
|
14.2 |
|
14.3 |
|
|
14.4 |
|
14.5 |
|
14.6 |
|
|
14.7 |
|
14.8 |
|
14.9 |
|
|
14.10 |
|
14.11 |
|
14.12 |
|
продолжение таблицы 14
|
14.13 |
|
14.14 |
|
14.15 |
|
|
14.16 |
|
14.17 |
|
14.18 |
|
|
14.19 |
|
14.20 |
|
14.21 |
|
|
14.22 |
|
14.23 |
|
14.24 |
|
|
14.25 |
|
14.26 |
|
14.27 |
|
|
14.28 |
|
14.29 |
|
14.30 |
|
15 Исследовать на сходимость с помощью интегрального признака Коши.
Т а б л и ц а 15
|
15.1 |
|
15.2 |
|
|
15.3 |
|
15.4 |
|
|
15.5 |
|
15.6 |
|
|
15.7 |
|
15.8 |
|
|
15.9 |
|
15.10 |
|
|
15.11 |
|
15.12 |
|
|
15.13 |
|
15.14 |
|
|
15.15 |
|
15.16 |
|
продолжение таблицы 15
|
15.17 |
|
15.18 |
|
|
15.19 |
|
15.20 |
|
|
15.21 |
|
15.22 |
|
|
15.23 |
|
15.24 |
|
|
15.25 |
|
15.26 |
|
|
15.27 |
|
15.28 |
|
|
15.29 |
|
15.30 |
|
16 Исследовать на условную или абсолютную сходимость знакочередующиеся ряды.
Т а б л и ц а 16
|
16.1 |
|
16.2 |
|
16.3 |
|
||||
|
16.4 |
|
16.5 |
|
16.6 |
|
||||
|
16.7 |
|
16.8 |
|
16.9 |
|
||||
|
16.10 |
|
16.11 |
|
16.12 |
|
||||
|
16.13 |
|
16.14 |
|
16.15 |
|
||||
|
16.16 |
|
16.17 |
|
16.18 |
|
||||
|
16.19 |
|
16.20 |
|
16.21 |
|
||||
продолжение таблицы 16
|
16.22 |
|
16.23 |
|
16.24 |
|
|
16.25 |
|
16.26 |
|
16.27 |
|
|
16.28 |
|
16.29 |
|
16.30 |
|
17
Дан степенной ряд 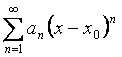 . Найти радиус и
интервал сходимости ряда.
. Найти радиус и
интервал сходимости ряда.
Т а б л и ц а 17
|
17.1 |
|
17.2 |
|
|
17.3 |
|
17.4 |
|
|
17.5 |
|
17.6 |
|
|
17.7 |
|
17.8 |
|
|
17.9 |
|
17.10 |
|
|
17.11 |
|
17.12 |
|
|
17.13 |
|
17.14 |
|
|
17.15 |
|
17.16 |
|
|
17.17 |
|
17.18 |
|
|
17.19 |
|
17.20 |
|
продолжение таблицы 17
|
17.21 |
|
17.22 |
|
|
17.23 |
|
17.24 |
|
|
17.25 |
|
17.26 |
|
|
17.27 |
|
17.28 |
|
|
17.29 |
|
17.30 |
|
1.3 Решение типового варианта
1. Проверить, является ли функция ![]() решением дифференциального
уравнения
решением дифференциального
уравнения ![]() .
.
Решение:
Для выполнения задания необходимо:
а) найти производную данной функции:
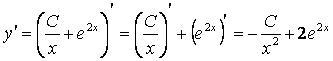 ;
;
б) подставить ![]() и
и ![]() в уравнение и поверить, преобразуется ли
данное уравнение в тождество:
в уравнение и поверить, преобразуется ли
данное уравнение в тождество:
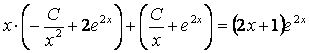 ;
;
![]() ;
;
![]() – тождество.
– тождество.
Значит, указанная функция является решением данного уравнения.
Замечание. Если после подстановки ![]() и
и ![]() в исходное уравнение оно не преобразуется
в тождество, то указанная функция не является решением данного уравнения.
в исходное уравнение оно не преобразуется
в тождество, то указанная функция не является решением данного уравнения.
2. Найти общее решение (общий интеграл)
дифференциального уравнения ![]() .
.
Решение:
![]()
![]()
![]() – уравнение с разделяющимися переменными
(см. справочный материал 1.4.1).
– уравнение с разделяющимися переменными
(см. справочный материал 1.4.1).
![]()
![]()
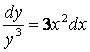 – уравнение с разделенными переменными.
– уравнение с разделенными переменными.
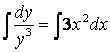
![]()
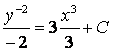
![]()

Ответ:
 – общий
интеграл уравнения.
– общий
интеграл уравнения.
3. Найти решение задачи Коши: ![]() ,
, ![]() .
.
Решение:
![]()
![]()
![]()
![]()
![]() – уравнение с разделяющимися
– уравнение с разделяющимися
переменными.
![]()
![]()
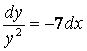 –
уравнение с разделенными переменными.
–
уравнение с разделенными переменными.
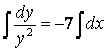
![]()

![]()
![]() – общее решение.
– общее решение.
Найдем частное решение, удовлетворяющее начальному условию:
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
т.е.
частное решение имеет вид: 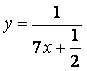
![]()
![]() .
.
Примечание.
При делении на ![]() могло быть потеряно решение
могло быть потеряно решение ![]() , или
, или ![]() . Непосредственной
подстановкой в исходное уравнение убеждаемся, что
. Непосредственной
подстановкой в исходное уравнение убеждаемся, что ![]() является особым решением, т.к.
оно не включено в общее решение. Однако данное особое решение не удовлетворяет начальному
условию, поэтому оно не может быть решением задачи Коши.
является особым решением, т.к.
оно не включено в общее решение. Однако данное особое решение не удовлетворяет начальному
условию, поэтому оно не может быть решением задачи Коши.
Ответ:
![]() .
.
4. Найти общее решение (общий интеграл)
дифференциального уравнения ![]() .
.
Решение:
![]() – однородное относительно переменных дифференциальное
уравнение первого порядка (см. справочный материал 1.4.1).
– однородное относительно переменных дифференциальное
уравнение первого порядка (см. справочный материал 1.4.1).
Замена
![]()
![]()
![]()
![]()
![]() .
.
Подставим в исходное уравнение: ![]()
![]()
![]() – уравнение с разделяющимися переменными.
– уравнение с разделяющимися переменными.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
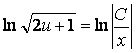
![]()
![]()
![]()
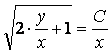 – общий интеграл.
– общий интеграл.
Ответ:
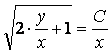 .
.
5. Найти решение задачи Коши: ![]() ,
, ![]() .
.
Решение:
Данное уравнение является линейным неоднородным уравнением (см. справочный материал 1.4.1).
Выполним это задание двумя способами:
1) методом Бернулли (подстановка ![]() );
);
2) методом вариации произвольных постоянных;
(Способ решения студент выбирает самостоятельно).
1 способ (метод Бернулли).
Подстановка
![]() (где u
= u(x), v = v(x) – новые неизвестные функции)
(где u
= u(x), v = v(x) – новые неизвестные функции) ![]()
![]() .
.
Подставим в исходное уравнение:
![]()
![]()
![]() .
.
Выберем функцию v такую,
чтобы ![]() . Это уравнение с разделяющимися
переменными.
. Это уравнение с разделяющимися
переменными.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
С учетом выбранной функции v, из исходного уравнения получим:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Функции u = u(x) и v = v(x) найдены.
Следовательно,
 –
общее решение.
–
общее решение.
Используя
начальное условие ![]() , получим:
, получим: ![]()
![]()
![]() .
.
Ответ: ![]() .
.
2 способ (метод вариации произвольных постоянных).
![]() – линейное неоднородное уравнение первого порядка.
– линейное неоднородное уравнение первого порядка.
Соответствующее
однородное уравнение: ![]() . Оно является уравнением с разделяющимися переменными.
. Оно является уравнением с разделяющимися переменными.
![]()
![]()
![]()
![]()
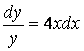
![]()

![]()
![]()
![]()
![]() –
общее решение линейного однородного уравнения.
–
общее решение линейного однородного уравнения.
Ищем
решение неоднородного уравнения в виде: ![]() ,
где
,
где ![]() – неизвестная функция.
– неизвестная функция.
Подставим
![]() и
и ![]() в исходное уравнение:
в исходное уравнение:
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Итак,  – общее решение исходного уравнения. Используя
начальное условие
– общее решение исходного уравнения. Используя
начальное условие ![]() , получим:
, получим: ![]()
![]()
![]() .
.
Ответ: ![]() .
.
6. Найти общий интеграл дифференциального уравнения
![]() .
.
Решение:
Уравнение
имеет структуру ![]() .
.
Найдем
![]() и
и ![]() :
:  ,
,
следовательно,
выполнено условие полного дифференциала и: ![]() ,
т.е. исходное уравнение является уравнением в полных дифференциалах (см. справочный материал 1.4.1).
,
т.е. исходное уравнение является уравнением в полных дифференциалах (см. справочный материал 1.4.1).
Неизвестную функцию ![]() найдем
с помощью формулы:
найдем
с помощью формулы: 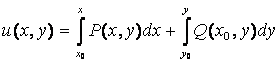 .
.
Возьмем х0 = 0, у0 = 0 (т.к. в точке (0,0) определены обе функции Р(х, у) и
Q(x, y)):
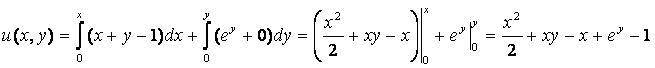 Т.к.
Т.к.
![]() , то
и = С – общий интеграл
дифференциального уравнения.
, то
и = С – общий интеграл
дифференциального уравнения.
Ответ:
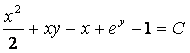 .
.
7. Найти общее решение дифференциального уравнения ![]() .
.
Решение:
![]() – уравнение Бернулли (см. справочный материал 1.4.1).
– уравнение Бернулли (см. справочный материал 1.4.1).
Выполним замену ![]()
![]()

![]()
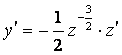 . Подставим
. Подставим ![]() и
и ![]() в исходное уравнение:
в исходное уравнение:
 .
Умножим полученное уравнение на
.
Умножим полученное уравнение на ![]() :
:
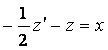
![]()
![]() – линейное
неоднородное уравнение первого порядка. Решаем данное уравнение методом
Бернулли (см. 1-ый способ решения задания 5).
– линейное
неоднородное уравнение первого порядка. Решаем данное уравнение методом
Бернулли (см. 1-ый способ решения задания 5).
Замена ![]()
![]()
![]() .
Подставляя в уравнение, получим:
.
Подставляя в уравнение, получим:
![]()
![]()
![]() (*)
(*)
Выберем функцию v такую,
чтобы ![]() . Это уравнение с разделяющимися
переменными.
. Это уравнение с разделяющимися
переменными.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
С учетом выбранной функции v, из уравнения (*) получим:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
Т.о. 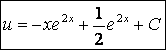
Функции u = u(x) и v = v(x) найдены.
Следовательно,
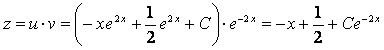
 – общее решение.
– общее решение.
Ответ:
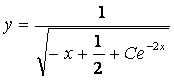 .
.
8. Найти общее решение дифференциального уравнения ![]() .
.
Решение:
![]() – уравнение второго порядка вида
– уравнение второго порядка вида ![]() .
Понижаем порядок двукратным интегрированием.
.
Понижаем порядок двукратным интегрированием.
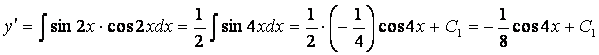
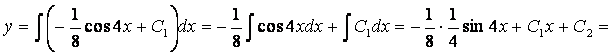

Ответ:
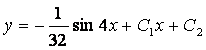 .
.
9. Найти общее решение однородного линейного дифференциального уравнения с постоянными коэффициентами.
(Поскольку структура общего решения линейного однородного дифференциального уравнения с постоянными коэффициентами зависит от вида корней соответствующего характеристического уравнения (см. 1.4.2), то в данном пункте рассмотрим три примера различных структур общего решения.)
Пример 1. ![]() .
.
Решение:
Составим
характеристическое уравнение для данного дифференциального уравнения: ![]() .
.
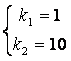 – разные действительные корни характеристического
уравнения.
– разные действительные корни характеристического
уравнения.
Следовательно, общее решение
имеет вид ![]() .
.
Ответ: ![]() .
.
Пример 2. ![]() .
.
Решение:
Составим
характеристическое уравнение для данного дифференциального уравнения: ![]() .
.
![]() – равные действительные корни
характеристического уравнения.
– равные действительные корни
характеристического уравнения.
Следовательно, общее решение
имеет вид ![]() .
.
Ответ: ![]() .
.
Пример 3. ![]() .
.
Решение:
Составим
характеристическое уравнение для данного дифференциального уравнения: ![]() .
.
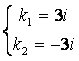 –
комплексные корни характеристического уравнения,
–
комплексные корни характеристического уравнения,
(![]() ,
,
![]() (см. 1.4.2)).
(см. 1.4.2)).
Следовательно, общее решение
имеет вид ![]()
Ответ: ![]() .
.
10. Найти общее решение линейного неоднородного дифференциального
уравнения с постоянными коэффициентами ![]() .
.
Решение:
![]() – линейное
неоднородное дифференциальное уравнение с постоянными коэффициентами. Его общее
решение имеет вид
– линейное
неоднородное дифференциальное уравнение с постоянными коэффициентами. Его общее
решение имеет вид ![]() (см. справочный материал 1.4.3),
(см. справочный материал 1.4.3),
где ![]() – общее решение соответствующего однородного уравнения
– общее решение соответствующего однородного уравнения
![]() ,
,
а ![]() – частное решение исходного неоднородного уравнения.
Поэтому нахождение общего решения проведем в два этапа:
– частное решение исходного неоднородного уравнения.
Поэтому нахождение общего решения проведем в два этапа:
1)
Найдем ![]() .
.
![]() – характеристическое уравнение.
– характеристическое уравнение.
 –
комплексные корни характеристического
уравнения,
–
комплексные корни характеристического
уравнения,
(![]() ,
, ![]() (см. 1.4.2)).
(см. 1.4.2)).
Следовательно,
![]() .
.
2) Найдем ![]() методом неопределенных коэффициентов по
виду правой части f (x) неоднородного уравнения.
методом неопределенных коэффициентов по
виду правой части f (x) неоднородного уравнения.
Так как ![]() (P0(x) – многочлен
нулевой степени, т.е. в данном случае просто константа С = 6;
(P0(x) – многочлен
нулевой степени, т.е. в данном случае просто константа С = 6; ![]() ) и
) и ![]() не является корнем
характеристического уравнения, то, в соответствии с теорией (см. 1.4.3),
частное решение будем искать в виде
не является корнем
характеристического уравнения, то, в соответствии с теорией (см. 1.4.3),
частное решение будем искать в виде ![]() .
.
Для нахождения неизвестного коэффициента А подставим
![]() ,
, ![]() ,
, ![]() в исходное уравнение.
в исходное уравнение.
Так как ![]() ,
то
,
то ![]() ;
; ![]() и исходное уравнение
принимает следующий вид:
и исходное уравнение
принимает следующий вид: ![]() .
.
Откуда
получаем: ![]()
![]()
![]()
![]()
![]() .
.
Следовательно, ![]() , а
общее решение исходного уравнения имеет вид:
, а
общее решение исходного уравнения имеет вид: ![]() .
.
Ответ: ![]() .
.
11. Дан ряд 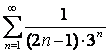 :
:
а) составить формулу общего члена ряда ![]() и написать первые пять членов;
и написать первые пять членов;
б) записать n-ую
частичную сумму ряда ![]() ;
;
в) записать остаток ряда ![]() ;
;
г) проверить необходимое условие сходимости ряда.
Решение:
а) 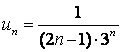 ;
;
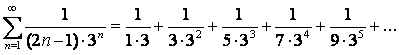 ;
;
б) по определению: ![]() – n-ая
частичная сумма ряда – равна сумме первых n
слагаемых ряда, т.е.
– n-ая
частичная сумма ряда – равна сумме первых n
слагаемых ряда, т.е.  , поэтому
, поэтому
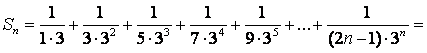
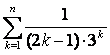 ;
;
в)
по определению: ![]() –
остаток ряда – является рядом, полученным из исходного, без первых n слагаемых,
т.е.
–
остаток ряда – является рядом, полученным из исходного, без первых n слагаемых,
т.е. 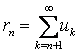 , поэтому
, поэтому
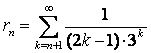 ;
;
г) проверим необходимое условие сходимости ряда (см. 1.4.4):
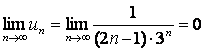 , следовательно,
необходимое условие сходимости ряда выполнено.
, следовательно,
необходимое условие сходимости ряда выполнено.
12. Сравнить с рядом Дирихле 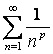 , т.е. найти параметр p,
и исследовать на сходимость ряд
, т.е. найти параметр p,
и исследовать на сходимость ряд  .
.
Решение:
Сходимость
ряда Дирихле 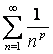 зависит
от параметра
зависит
от параметра ![]() :
:
если
![]() , то ряд
сходится, если
, то ряд
сходится, если ![]() ,
то ряд расходится.
,
то ряд расходится.
Для сравнения ряда ![]() с
рядом Дирихле
с
рядом Дирихле 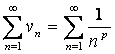 необходимо
найти параметр p по правилу: p = (степень знаменателя
необходимо
найти параметр p по правилу: p = (степень знаменателя ![]() – степень числителя
– степень числителя ![]() ) и сделать соответствующий
вывод.
) и сделать соответствующий
вывод.
Т.к. в нашем случае 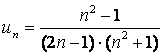 , то степень числителя
, то степень числителя ![]() равна 2, степень знаменателя
равна 2, степень знаменателя ![]() равна 3.
равна 3.
Следовательно, p = 3 – 2 = 1,
т.е. исходный ряд сравним по 2-му признаку сравнения (см.1.4.4) с рядом ![]() (гармонический ряд,
расходится).
(гармонический ряд,
расходится).
Так как 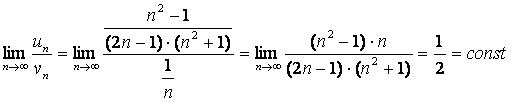 , то оба ряда одновременно расходятся.
, то оба ряда одновременно расходятся.
13.
Исследовать на сходимость ряд 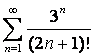 с помощью признака Даламбера.
с помощью признака Даламбера.
Решение:
Для данного ряда 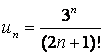 ,
, 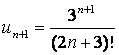 .
.
По признаку Даламбера (см.1.4.4) имеем:
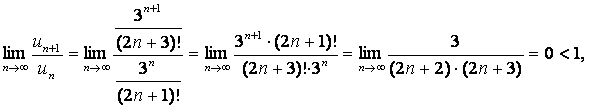 следовательно, ряд сходится.
следовательно, ряд сходится.
14. Исследовать на сходимость ряд 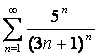 с помощью радикального
признака Коши.
с помощью радикального
признака Коши.
Решение:
Для данного ряда 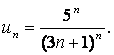
По радикальному признаку Коши (см.1.4.4) имеем:
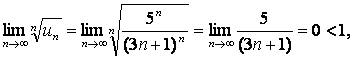
следовательно, ряд сходится.
15. Исследовать на сходимость ряд 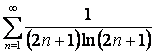 с помощью интегрального признака Коши.
с помощью интегрального признака Коши.
Решение:
Для данного ряда 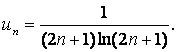
Очевидно, что все ![]() положительны
и не возрастают, т.е. u1 ³ u2 ³ u3 ³ …
положительны
и не возрастают, т.е. u1 ³ u2 ³ u3 ³ …
и
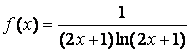 –
такая непрерывная, не возрастающая функция, что
–
такая непрерывная, не возрастающая функция, что
f (1) = u1, f (2) = u2 , …, f (п) = uп .
Тогда
исходный ряд и несобственный интеграл 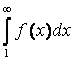 одновременно сходятся или расходятся
(по интегральному признаку Коши (см.1.4.4)).
одновременно сходятся или расходятся
(по интегральному признаку Коши (см.1.4.4)).
Поэтому исследуем несобственный интеграл 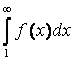 :
: 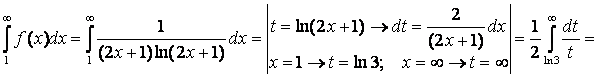
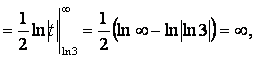
т.е. несобственный интеграл 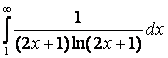 расходится.
расходится.
Следовательно, и исходный ряд расходится.
16. Исследовать на условную или абсолютную сходимость знакочередующиеся ряды.
(Поскольку при исследовании на условную или абсолютную сходимость возможны три варианта: 1) ряд сходится абсолютно; или 2) ряд сходится условно; или 3) ряд расходится (см. 1.4.4), то в данном пункте рассмотрим три примера.)
Пример 1. 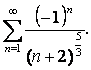
Решение:
Рассмотрим ряд  Этот
ряд сходится по второму признаку сравнения: сравниваем его с рядом
Этот
ряд сходится по второму признаку сравнения: сравниваем его с рядом ![]() (это ряд Дирихле
(это ряд Дирихле 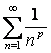 , где
, где 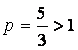 –
сходится);
–
сходится); 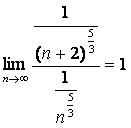 ,
поэтому оба ряда сходятся одновременно. Так как ряд
,
поэтому оба ряда сходятся одновременно. Так как ряд 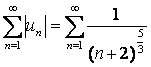 – сходится, то исходный ряд
– сходится, то исходный ряд 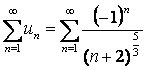 – сходится
абсолютно.
– сходится
абсолютно.
Пример
2. 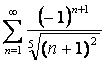 .
.
Решение:
Рассмотрим ряд 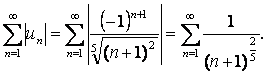 Сравним
его с рядом
Сравним
его с рядом 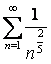 (это ряд
Дирихле
(это ряд
Дирихле 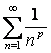 , где
, где 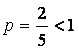 – расходится);
– расходится);  , поэтому оба ряда расходятся
одновременно. Т.е. ряд
, поэтому оба ряда расходятся
одновременно. Т.е. ряд ![]() расходится
(по второму признаку сравнения). Следовательно, исходный ряд не может сходиться
абсолютно.
расходится
(по второму признаку сравнения). Следовательно, исходный ряд не может сходиться
абсолютно.
Проверим выполнение условий Лейбница (см.1.4.4):
1)  ; 2)
; 2) 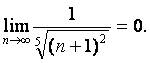
Они выполняются, следовательно, исходный ряд сходится условно.
Пример
3.  .
.
Решение:
Рассмотрим ряд  Сравнивая
его с рядом Дирихле
Сравнивая
его с рядом Дирихле 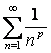 , получаем:
, получаем: ![]() ,
т.е. ряд
,
т.е. ряд ![]() расходится (по второму признаку сравнения).
Следовательно, исходный ряд не может сходиться абсолютно.
расходится (по второму признаку сравнения).
Следовательно, исходный ряд не может сходиться абсолютно.
Проверим выполнение условий Лейбница (см.1.4.4):
1) 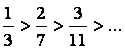 ; 2)
; 2) 
Т.е.
для исходного ряда не выполняется второе условие Лейбница (![]() ). Следовательно, исходный ряд расходится.
). Следовательно, исходный ряд расходится.
17. Дан степенной ряд 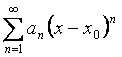 . Найти радиус и
интервал сходимости ряда.
. Найти радиус и
интервал сходимости ряда.
(Поскольку радиус сходимости степенного ряда (см.1.4.5) находится по одной из двух формул
 или
или 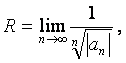
то в данном пункте рассмотрим два примера).
Пример 1.
Найти радиус и интервал сходимости ряда 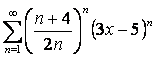 .
.
Решение:
Приведем данный ряд к стандартному виду:
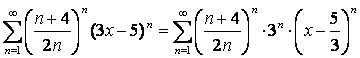 .
.
Для
полученного ряда 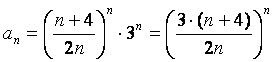 ,
,
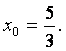
Поэтому радиус сходимости ряда находим по
формуле 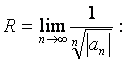
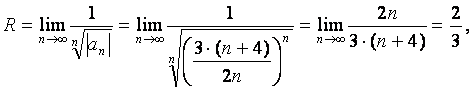
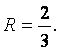
Находим
интервал сходимости ряда, решая неравенство ![]() :
:
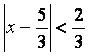
![]()
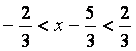
![]()
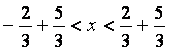
![]()
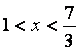 .
.
Пример 2.
Найти радиус и интервал сходимости ряда 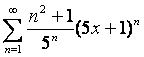 .
.
Решение:
Приведем данный ряд к стандартному виду:
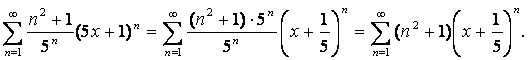
Для
полученного ряда ![]() ,
,
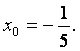
Поэтому
радиус сходимости ряда находим по формуле 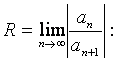

![]()
Находим
интервал сходимости ряда, решая неравенство ![]() :
:
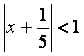
![]()
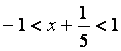
![]()
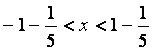
![]()
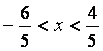 .
.
1.4 Справочный материал
1.4.1 Таблица основных видов дифференциальных уравнений 1-го порядка
|
№ |
Тип уравнения |
Вид уравнения |
Метод решения |
Примечания |
|
1 |
С разделя- ющимися перемен- ными |
а) б) |
а) умножить на б) |
|
|
2 |
Однород-ные |
а) где функция нулевого порядка, т.е. б) где однородные функции одного
порядка, т.е. |
Подстановка где |
Приводится к уравнению (1), причем в одной из сторон полу-ченного
уравнения всегда должно быть выражение |
|
3 |
Линейные |
|
а) Метод Бернулли. Подстановка Решают уравнения: б) Метод вариации. Решают уравнение |
а) При решении уравнения |
|
4 |
Уравне-ние Бернулли |
|
а) Метод Бернулли. Подстановка для линейных уравнений (*) б) Подстановка сводит к линейному уравнению (*) относительно новой функции z . |
При |
|
5 |
Уравне-ние в полных диф- ференци-алах |
|
Решение |
Проверка
|
1.4.2 Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами имеет вид
у¢¢ + pу¢ + qу = 0, p, q ÎR.
Его общее решение зависит от корней характеристического уравнения:
k 2 + pk + q = 0.
Корни характеристического уравнения:
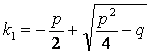 ;
; 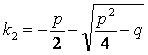 .
.
Возможны случаи:
а) Если характеристическое уравнение имеет два различных действительных
корня, т.е. k1 , k2 Î R ( k1 ≠ k2 ), тогда общее решение имеет вид
![]() .
.
б) Если характеристическое уравнение имеет два одинаковых действительных
корня, т.е. k1 , k2 Î R ( k1 = k2 ), тогда общее решение имеет вид
![]()
в) Если характеристическое уравнение имеет два комплексных корня,
т.е. k1 , k2 Î C: ![]() ,
, ![]() , где
, где ![]()
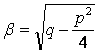 ,
,
тогда общее решение имеет вид ![]() .
.
1.4.3 Неоднородное линейное уравнение 2-го порядка с постоянными коэффициентами имеет вид
у¢¢ + ру¢ + qу = f (x), p, q Î R.
Его
общее решение имеет вид ![]() ,
,
где ![]() – общее решение соответствующего однородного уравнения
– общее решение соответствующего однородного уравнения
у¢¢ + ру¢ + qу = 0,
а ![]() – частное решение исходного неоднородного уравнения.
– частное решение исходного неоднородного уравнения.
Метод подбора частного решения по специальной правой части f (x).
1. Если правая часть
имеет вид ![]() ,
где Pn(x) – многочлен п-ой степени, то структура частного
решения
,
где Pn(x) – многочлен п-ой степени, то структура частного
решения ![]() зависит от того, является ли a корнем
характеристического уравнения k 2 + pk + q = 0 или
нет. Поэтому возможны варианты:
зависит от того, является ли a корнем
характеристического уравнения k 2 + pk + q = 0 или
нет. Поэтому возможны варианты:
а) если число a не является корнем характеристического уравнения, то частное решение ищется в следующем виде:
![]() ,
,
где Qn(x) – многочлен п-ой степени (такой же степени, что и Pn(x)) с
неопределенными
коэффициентами, которые находятся после подстановки ![]() ,
, ![]() ,
, ![]() в исходное уравнение.
в исходное уравнение.
б) если число a есть простой (однократный) корень характеристического уравнения,
то ![]() .
.
в) если число a есть двукратный корень характеристического уравнения, то
![]() .
.
2. Если правая часть имеет вид ![]() , где Pп(x),
Qт(x)
– многочлены
п-ой и т-ой степени соответственно, то структура
частного решения
, где Pп(x),
Qт(x)
– многочлены
п-ой и т-ой степени соответственно, то структура
частного решения ![]() зависит от того, являются
ли a ± ib корнями характеристического уравнения k 2 + pk +
q =
0 или нет. Поэтому возможны варианты:
зависит от того, являются
ли a ± ib корнями характеристического уравнения k 2 + pk +
q =
0 или нет. Поэтому возможны варианты:
а) если числа a ± ib не являются корнями характеристического уравнения, то
![]() ,
,
где
Up(x), Vp(x)
– многочлены
(с неопределенными коэффициентами), степень которых равна наивысшей степени
многочленов Pn(x), Qm(x),
т.е. ![]() ;
;
б) если числа a ± ib являются корнями характеристического уравнения, то
![]() ,
,
где Up(x), Vp(x) – многочлены как в пункте а).
Частный случай:
если f (x) = М cos bx + N sin bx, где М, N – постоянные числа, то
а) если числа ±ib не являются корнями характеристического уравнения, то
![]()
(где А и В – числа, подлежащие определению).
б) если числа ± ib являются корнями характеристического уравнения, то
![]()
(где А и В – числа, подлежащие определению).
1.4.4 Числовые ряды
Выражение вида  (1)
(1)
где ип Î R ( n = 1, 2, …), называется числовым рядом.
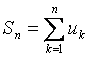 – частичная
сумма ряда,
– частичная
сумма ряда, 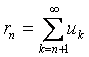 –
остаток ряда.
–
остаток ряда.
Ряд сходится, если
существует предел 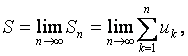
и число S называется суммой ряда.
Если
ряд сходится, то ![]() .
.
Это условие называется необходимым признаком сходимости ряда.
Если все члены ряда ип > 0, то данный ряд называется положительным рядом.
Признаки сходимости положительных рядов
1. Признак Даламбера.
Если
существует 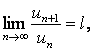 то
при l
< 1 ряд сходится;
то
при l
< 1 ряд сходится;
при l > 1 ряд расходится;
при l = 1 признак не применим.
Признак Даламбера можно применять, если ип содержит показательную функцию или факториалы.
2. Признак Коши (радикальный признак Коши).
Если
существует ![]() то
при l
< 1 ряд сходится;
то
при l
< 1 ряд сходится;
при l > 1 ряд расходится;
при l = 1 признак не применим.
3. Признаки сравнения.
Наряду с рядом (1) рассмотрим
ряд  (2)
(2)
1-ый признак сравнения:
а) если un £ vn ( п = 1, 2, …) и ряд (2) сходится, то и ряд (1) сходится;
б) если un ³ vn ( п = 1, 2, …) и ряд (2) расходится, то и ряд (1) расходится.
2-ый признак сравнения:
если существует  ( А ≠ 0, А ≠
∞ ),
( А ≠ 0, А ≠
∞ ),
то ряды (1) и (2) одновременно сходятся или одновременно расходятся.
4. Интегральный признак (интегральный признак Коши).
Пусть члены ряда (1) положительны и не возрастают, т.е. u1 ³ u2 ³ u3 ³ …
и f (x) – такая непрерывная не возрастающая функция, что
f (1) = u1, f (2) = u2 , …, f (п) = uп .
Тогда
ряд (1) и несобственный интеграл 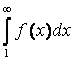 одновременно сходятся или расходятся.
одновременно сходятся или расходятся.
Знакочередующиеся ряды
Ряд 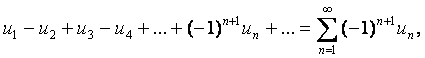 (3)
(3)
где uп ³ 0 ( п = 1, 2, …) – называется знакочередующимся.
Теорема Лейбница.
Если члены ряда (3) таковы, что: 1) u1 > u2 > u3 > … (монотонно убывают);
2) ![]()
то ряд (3) сходится и его сумма положительна и меньше u1 , т.е. 0 < S < u1 .
Если сходится ряд 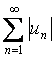 , то ряд (3) называется абсолютно
сходящимся; если же ряд (3) сходится, а ряд
, то ряд (3) называется абсолютно
сходящимся; если же ряд (3) сходится, а ряд 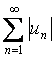 расходится, то ряд (3) называется условно
сходящимся.
расходится, то ряд (3) называется условно
сходящимся.
1.4.5 Функциональные ряды
Ряд
 называется
функциональным.
называется
функциональным.
Частным случаем функционального ряда является степенной ряд (по степеням х):
 ,
,
где ап ( п = 1, 2, …) – коэффициенты степенного ряда (постоянные числа).
Степенной ряд (по степеням х) сходится в интервале (–R; R) и расходится вне этого интервала. Число R называется радиусом сходимости ряда и вычисляется по формулам:
 или
или 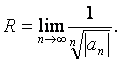
В общем случае степенной ряд (по степеням (х – х0)) имеет вид:
 ,
,
где постоянные ап ( п = 1, 2, …) также называются коэффициентами ряда.
Интервалом сходимости такого ряда является интервал ( х0 – R; х0 + R ) с центром в точке х0 . Число R – радиус сходимости ряда – вычисляется как и прежде.
Если R = ∞, то интервалом сходимости степенного ряда является вся числовая прямая, если R = 0, то интервал сходимости вырождается в точку
х = х0.
Список литературы
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: В 2 ч.–М.: Высшая школа, 1986.–Ч.1–352 с.
2. Сборник индивидуальных заданий по высшей математике: В 3 ч. /А.П. Рябушко, В.В. Бархатов и др./Под редакцией А.П. Рябушко.–Минск: Вышэйшая школа, 1991.–Ч.3.–351с.
3. Кузнецов А.А. Сборник заданий по высшей математике: Типовые расчеты.–М.: Высшая школа, 1983.–176 с.
4. Пискунов Н.С. Дифференциальное и интегральное исчисления. Учебник для втузов: В 2 т.–М.: Наука, 1976.–Т.2–576 с.
Содержание
1 Типовой расчёт 3. Дифференциальные уравнения. Ряды.…………………...3
1.1 Теоретические вопросы.………………………………….....……………......3
1.2 Расчётные задания……………………………………..………………...…....3
1.3 Решение типового варианта……….……………………..………………....18
1.4 Справочный материал…………………………………………………….....32
Список литературы ………………………………………..…………………....38