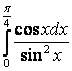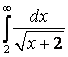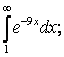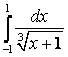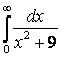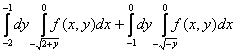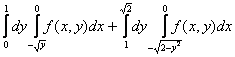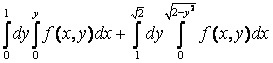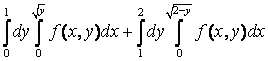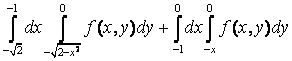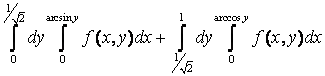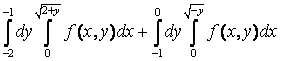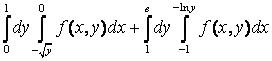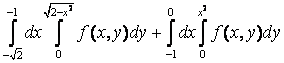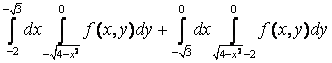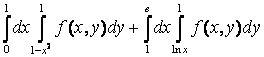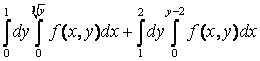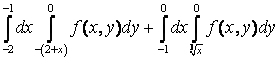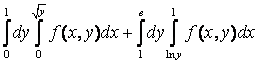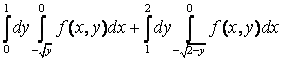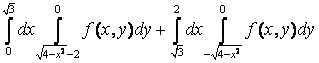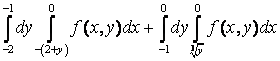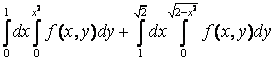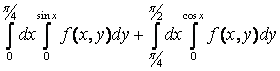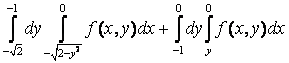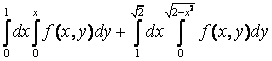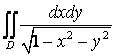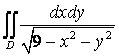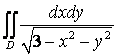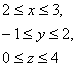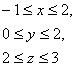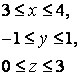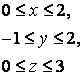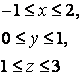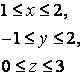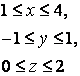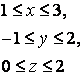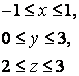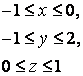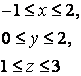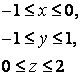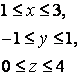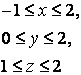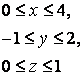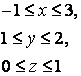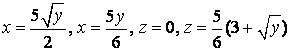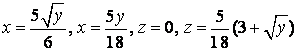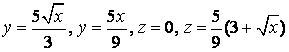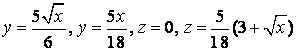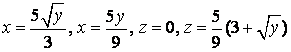АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ
Математический анализ
Методические указания и задания
к выполнению расчетно-графических работ
(для студентов всех форм обучения специальности
050704 – Вычислительная техника и программное обеспечение,
050703 – Информационные системы)
Часть 2
Алматы 2009
СОСТАВИТЕЛИ: Л.Н. Астраханцева, М.Ж.Байсалова. Математический анализ. Методические указания и задания к выполнению расчетно-графической работы для студентов всех форм обучения специальности 050704 – Вычислительная техника и программное обеспечение, 050703 – Информационные системы.
Методические указания и задания к расчетно-графической работе содержат типовой расчет №2 дисциплины «Математический анализ» для студентов всех форм обучения специальности 050704 – Вычислительная техника и программное обеспечение, 050703 – Информационные системы, 050703 – Информационные системы. Приведены основные теоретические вопросы программы. Дано решение типового варианта.
1 Типовой расчёт 2. Функции нескольких переменных. Интегральное исчисление функций одной и нескольких переменных
1.1 Теоретические вопросы
1. Первообразная, неопределённый интеграл, его свойства, таблица интегралов.
2. Методы интегрирования: метод разложения, метод замены переменной (группы интегралов, берущихся с помощью одной подстановки).
3. Интегралы от квадратного трёхчлена, тригонометрические
подстановки. Интегрирование по частям.
4. Интегрирование рациональных дробей, некоторых иррациональных
функций.
5. Интегрирование некоторых тригонометрических функций,
тригонометрические подстановки.
6. Определённый интеграл и его свойства.
7. Определённый интеграл как функция верхнего предела. Формула Ньютона-Лейбница. Замена переменных и интегрирование по частям для определённого интеграла.
8. Несобственные интегралы с бесконечными пределами (1-го рода) и несобственные интегралы от неограниченных функций (2-го рода).
9. Функции нескольких переменных. Предел и непрерывность.
10. Частные приращения и частные производные. Частные производные высших порядков.
11.Частные дифференциалы. Полное приращение и полный
дифференциал.
12. Дифференциалы высших порядков. Инвариантность формы полного
дифференциала.
13. Дифференцирование сложных и неявных функций нескольких
переменных.
14. Экстремум функции двух переменных. Необходимые и достаточные
условия экстремума.
15. Условный экстремум. Наибольшее и наименьшее значения функции
двух переменных в замкнутой области.
16. Задачи, приводящие к понятию кратного интеграла. Двойные и тройные интегралы, их свойства.
17. Вычисление двойных и тройных интегралов в прямоугольных координатах.
18. Замена переменных в кратных интегралах, переход к полярным, цилиндрическим и сферическим координатам.
1.2 Расчётные задания
1. Найти интегралы.
Т а б л и ц а 1
|
1.1
а) |
|
1.2 а) |
|
1.3
а) |
|
1.4 а) |
|
1.5 а) |
|
1.6 а) |
|
1.7 а) |
|
1.8 а) |
|
1.9 а) |
|
1.10
а) |
|
1.11
а) |
|
1.12
а) |
|
1.13
а) |
|
1.14
а) |
|
1.15
а) |
продолжение таблицы 1
|
1.16
а) |
|
1.17 а) |
|
1.18 а) |
|
1.19 а) |
|
1.20 а) |
|
1.21 а) |
|
1.22 а) |
|
1.23 а) |
|
1.24 а) |
|
1.25 а) |
|
1.26 а) |
|
1.27 а) |
|
1.28
а)
|
|
1.29
а) |
|
1.30
а) |
2. Найти интегралы, применяя формулу интегрирования по частям.
Т а б л и ц а 2
|
2.1 |
2.2 |
|
2.3 |
2.4 |
|
2.5 |
2.6 |
|
2.7 |
2.8 |
|
2.9 |
2.10 |
|
2.11 |
2.12 |
|
2.13 |
2.14 |
|
2.15 |
2.16 |
|
2.17 |
2.18 |
|
2.19 |
2.20 |
|
2.21 |
2.22 |
|
2.23 |
2.24 |
|
2.25 |
2.26 |
|
2.27 |
2.28 |
|
2.29 |
2.30 |
3. Найти интегралы.
Та б л и ц а 3
|
3.1 |
3.2 |
3.3 |
|
3.4 |
3.5 |
3.6 |
|
3.7 |
3.8 |
3.9 |
|
3.10 |
3.11 |
3.12 |
|
3.13 |
3.14 |
3.15 |
|
3.16 |
3.17 |
3.18 |
|
3.19 |
3.20 |
3.21 |
|
3.22 |
3.23 |
3.24 |
продолжение таблицы 3
|
3.25 |
3.26 |
3.27 |
|
3.28 |
3.29 |
3.30 |
4. Найти интегралы.
Т а б л и ц а 4
|
4.1 а) б) |
4.2 а) б) |
4.3 а) б) |
|
4.4 а) б) |
4.5 а) б) |
4.6 а) б) |
|
4.7 а) б) |
4.8 а) б) |
4.9 а) б) |
|
4.10 а) б) |
4.11 а) б) |
4.12 а) б) |
|
4.13 а) б) |
4.14 а) б) |
4.15 а) б) |
|
4.16 а) б) |
4.17 а) б) |
4.18 а) б) |
|
4.19 а) б) |
4.20 а) б) |
4.21 а) б) |
|
4.22 а) б) |
4.23 а) б) |
4.24 а) б) |
продолжение таблицы 4
|
4.25 а) б) |
4.26 а) б) |
4.27 а) б) |
|
4.28 а) б) |
4.29 а) б) |
4.30 а) б) |
5. Найти интегралы:
а) используя универсальную подстановку;
б) понижая степень.
Т а б л и ц а 5
|
5.1 а) б) |
5.2 а) б) |
5.3 а) б) |
|
5.4 а) б) |
5.5 а) б) |
5.6 а) б) |
|
5.7 а) б) |
5.8 а) б) |
5.9 а) б) |
|
5.10 а) б) |
5.11 а) б) |
5.12 а) б) |
|
5.13 а) б) |
5.14 а) б) |
5.15 а) б) |
|
5.16 а) б) |
5.17 а) б) |
5.18 а) б) |
|
5.19 а) б) |
5.20 а) б) |
5.21 а) б) |
продолжение таблицы 5
|
5.22 а) б) |
5.23 а) б) |
5.24 а) б) |
|
5.25 а) б) |
5.26 а) б) |
5.27 а) б) |
|
5.28 а) б) |
5.29 а) б) |
5.30 а) б) |
6. Вычислить определённые интегралы.
Т а б л и ц а 6
|
6.1 а) б) |
6.2 а) б) |
6.3 а) б) |
|
6.4 а) б) |
6.5 а) б) |
6.6 а)
б) |
|
6.7 а) б) |
6.8 а) |
6.9 а) б) |
|
6.10 а) б) |
6.11 а) б) |
6.12 а) б) |
|
6.13 а) б) |
6.14 а) б) |
6.15 а) б) |
продолжение таблицы 6
|
6.16 а) б) |
6.17 а) б) |
6.18 а) б) |
|
6.19 а) б) |
6.20 а) б) |
6.21 а) б) |
|
6.22 а) б) |
6.23 а) б) |
6.24 а) б) |
|
6.25 а) б) |
6.26 а) б) |
6.27 а) б) |
|
6.28 а) б) |
6.29 а) б) |
6.30 а) б) |
7. Вычислить несобственные интегралы или доказать их расcходимость.
Т а б л и ц а 7
|
7.1 а) |
7.2 а) |
7.3а) |
|
7.4а) |
7.5 а) |
7.6а) |
|
7.7а) |
7.8а) |
7.9а) |
продолжение таблицы 7
|
7.10а) |
7.11а) |
7.12а) |
|
7.13 а) б) |
7.14 а) б) |
7.15 а) б) |
|
7.16 а) б) |
7.17 а) б) |
7.18 а) б) |
|
7.19 а) б) |
7.20 а) б) |
7.21а) б) |
|
7.22 а)
б) |
7.23 а) б) |
7.24 а) б) |
|
7.25 а) б) |
7.26 а) б) |
7.27 а) б) |
|
7.28 а) б) |
7.29 а) б) |
7.30 а) б) |
8. Для функции z=f(x,y) найти:
а)![]() ; б)
; б) ![]() ;
;
в)
![]() .
.
Т а б л и ц а 8
|
8.1 |
8.2 |
8.3 |
|
8.4 |
8.5 |
8.6 |
|
8.7 |
8.8 |
8.9 |
|
8.10 |
8.11 |
8.12 |
|
8.13 |
8.14 |
8.15 |
|
8.16 |
8.17 |
8.18 |
|
8.19 |
8.20 |
8.21 |
|
8.22 |
8.23 |
8.24 |
|
8.25 |
8.26 |
8.27 |
|
8.28 |
8.29 |
8.30 |
9. Найти:
а)
уравнение касательной плоскости и нормали к поверхности F(x,y,z)=0 в
точке ![]() ;
;
б)
производные ![]() функции
z, заданной неявно уравнением F(x,y,z)=0.
функции
z, заданной неявно уравнением F(x,y,z)=0.
Т а б л и ц а 9
|
F(x,y,z) |
|
F(x,y,z) |
|
|
9.1 |
(2,1,-1) |
9.2 |
(-2,1,2) |
|
9.3 |
(1,2,1) |
9.4 |
(-1,1,2) |
|
9.5 |
(2,1,-1) |
9.6 |
(-2,1,2) |
|
9.7 |
(1,2,1) |
9.8 |
(-1,1,2) |
|
9.9 |
(2,1,-1) |
9.10 |
(-2,1,2) |
|
9.11 |
(1,2,1) |
9.12 |
(-1,1,2) |
|
9.13 |
(2,1,-1) |
9.14 |
(-2,1,2) |
|
9.15 |
(1,2,1) |
9.16 |
(-1,1,2) |
|
9.17 |
(2,1,-1) |
9.18 |
(-2,1,2) |
|
9.19 |
(1,2,1) |
9.20 |
(-1,1,2) |
|
9.21 |
(2,1,-1) |
9.22 |
(-2,1,2) |
|
9.23 |
(1,2,1) |
9.24 |
(-1,1,2) |
|
9.25 |
(2,1,-1) |
9.26 |
(-2,1,2) |
|
9.27 |
(-1,2,1) |
9.28 |
(-1,1,2) |
|
9.29 |
(1,2,1) |
9.30 |
(-1,1,2) |
10. Исследовать на экстремум функцию z=f(x,y).
Т а б л и ц а 10
|
f(x,y) |
f(x,y) |
f(x,y) |
||
|
10.1 |
10.2
|
10.3
|
||
|
10.4 |
10.5
|
10.6 |
||
|
10.7
|
10.8 |
10.9
|
||
|
10.10 |
10.11 |
10.12
|
||
|
10.13
|
10.14
|
10.15 |
||
|
10.16 |
10.17 |
10.18 |
||
|
10.19 |
10.20 |
10.21 |
||
|
10.22 |
10.23 |
10.24
|
||
|
10.25
|
10.26 |
10.27
|
||
|
10.28
|
10.29 |
10.30 |
||
11. Вычислить двойной интеграл по области D, ограниченной данными линиями.
Т а б л и ц а 11
|
|
D |
|
D |
|
11.1 |
x=-1, x=2, y=1, y=3 |
11.2 |
x=2, x=5, y=-1,y=2 |
|
11.3 |
x=0, x=2, y=1, y=2 |
11.4 |
x=1, x=5, y=-1, y=1 |
|
11.5 |
x=-1, x=1, y=1, y=2 |
11.6 |
x=2, x=3, y=-1, y=2 |
|
11.7 |
x=0, x=1, y=1, y=4 |
11.8 |
x=-1, x=3, y=-1, y=2 |
|
11.9 |
x=-1, x=1, y=1, y=3 |
11.10 |
x=4, x=5, y=-1, y=1 |
продолжение таблицы 11
|
11.11 |
x=-1, x=2, y=1, y=3 |
11.12 |
x=2, x=4,y=-1, y=1 |
|
11.13 |
x=-1, x=1,y=1, y=3 |
11.14 |
x=2, x=3,y=-1, y=2 |
|
11.15 |
x=-1, x=1 y=1, y=2 |
11.16 |
x=3 x=6,y=-1, y=2 |
|
11.17 |
x=-1, x=2, y=2 y=4 |
11.18 |
x=2, x=3,y=-1, y=1 |
|
11.19 |
x=-1, x=3,y=1, y=4 |
11.20 |
x=2, x=4,y=-1, y=5 |
|
11.21 |
x=-1, x=2, y=1, y=4 |
11.22 |
x=2, x=5, y=2,y=4 |
|
11.23 |
x=0 x=1 y=1, y=2 |
11.24 |
x=2, x=5, y=-1, y=3 |
|
11.25 |
x=-1, x=1y=1, y=4 |
11.26 |
x=-1,=3,y=-1, y=2 |
|
11.27 |
x=-1, x=2, y=1, y=3 |
11.288 |
x=2, x=3,y=0,y=2 |
|
11.29 |
x=1,x=3,y=-1, y=2 |
11.30 |
x=0,x=3 ,=-1, y=2 |
12. Изменить порядок интегрирования.
Т а б л и ц а 12
|
12.1 |
12.2 |
|
12.3 |
12.4 |
|
12.5 |
12.6 |
|
12.7 |
12.8 |
|
12.9 |
12.10 |
продолжение таблицы 12
|
12.11 |
12.12
|
|
12.13 |
12.14
|
|
12.15
|
12.16
|
|
12.17
|
12.18
|
|
12.19
|
12.20
|
|
12.21
|
12.22
|
|
12.23
|
12.24
|
|
12.25
|
12.26
|
|
12.27
|
12.28
|
|
12.29
|
12.30
|
13. Вычислить двойной интеграл, используя полярные координаты.
Т а б л и ц а 13
|
|
D |
|
D |
|
13.1 |
|
13.2 |
|
|
13.3 |
|
13.4
|
|
|
13.5 |
|
13.6 |
|
|
13.7 |
|
13.8
|
|
|
13.9
|
|
13.10 |
|
|
13.11
|
|
13.12
|
|
|
13.13
|
|
13.14
|
|
|
13.15
|
|
13.16 |
|
|
13.17 |
|
13.18
|
|
|
13.19 |
|
13.20 |
|
|
13.21 |
|
13.22 |
|
|
13.23 |
|
13.24 |
|
|
13.25 |
|
13.26 |
|
|
13.27 |
|
13.28 |
|
|
13.29 |
|
13.30 |
|
14. Вычислить тройной интеграл.
Т а б л и ц а 14
|
|
T |
|
Т |
|
14.1 |
|
14.2
|
|
|
14.3 |
|
14.4 |
|
|
14.5 |
|
14.6 |
|
|
14.7 |
|
14.8 |
|
|
14.9 |
|
14.10 |
|
|
14.11 |
|
14.12 |
|
|
14.13 |
|
14.14
|
|
|
14.15
|
|
14.16
|
|
|
14.17 |
|
14.18 |
|
продолжение таблицы 14
|
14.19
|
|
14.20 |
|
|
14.21 |
|
14.22 |
|
|
14.23 |
|
14.24 |
|
|
14.25 |
|
14.26 |
|
|
14.27 |
|
14.28 |
|
|
14.29 |
|
14.30 |
|
15. Найти объём тела, ограниченного данными поверхностями.
Т а б л и ц а 15
|
15.1 |
15.2 |
|
15.3 |
15.4
|
|
15.5 |
15.6
|
продолжение таблицы 15
|
15.7 |
15.8
|
|
15.9
|
15.10
|
|
15.11
|
15.12 |
|
15.13
|
15.14
|
|
15.15
|
15.16
|
|
15.17
|
15.18
|
|
15.19
|
15.20
|
|
15.21
|
15.22
|
|
15.23
|
15.24
|
|
15.25
|
15.26
|
|
15.27
|
15.28
|
|
15.29
|
15.30 |
1.3 Решение типового варианта
Неопределённый
интеграл от функции ![]() обозначается
обозначается
![]() , где
, где ![]() - совокупность
первообразных (т.е.
- совокупность
первообразных (т.е. ![]()
![]() или
или ![]() ).
).
Свойства неопределённого интеграла
1)
![]() ; 2)
; 2)
![]() ;
;
3)![]() ; 4)
; 4)![]() .
.
Правила интегрирования
1)
![]() ;
;
2)
![]() ,
, ![]() - постоянная;
- постоянная;
3)
Если ![]() и
и ![]() , то
, то ![]() .
.
Т а б л и ц а 16 – Основные интегралы
|
1 |
1а 1б |
2 |
|
3 |
3а |
4 |
|
5 |
6 |
7 |
|
8 |
8а |
9
|
|
9а |
10 |
11 |
|
12 |
13 |
|
1. Найти интегралы:
а)![]() ;
;
б)
![]() ;
;
в)![]() .
.
Решение:
а) подынтегральная функция представляет собой алгебраическую сумму табличных интегралов, поэтому по правилам 1) и 2) и формулам 1, 5, 9а таблицы 16 имеем:
![]() =
=![]() =
=
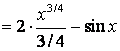
![]() =
=![]() .
.
В примерах б) и в) можно применить один из трёх способов:
1)
метод замены переменной по формуле ![]() или по формуле
или по формуле ![]() ;
;
2)
по формуле ![]() внести
под знак дифференциала часть подынтегральной функции и затем интегрировать по
правилу 3);
внести
под знак дифференциала часть подынтегральной функции и затем интегрировать по
правилу 3);
3)
применить формулу![]() ,
если
,
если ![]() .
.
б)
![]() =( формула 4
таблицы 16 и третий способ, когда
=( формула 4
таблицы 16 и третий способ, когда ![]() =2) =
=2) =
= ![]() ;
;
в)
решим этот интеграл первым и вторым способами: 1) ![]() = =
= =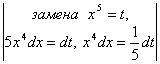 =
=![]() ; 2)
; 2) ![]() = (внесём под знак дифференциала
= (внесём под знак дифференциала ![]() ) =
) =![]() = (вынесем 1/5 за знак интеграла
и применим правило 3), когда
= (вынесем 1/5 за знак интеграла
и применим правило 3), когда ![]() ) =
) = ![]() .
.
2.
Найти интеграл ![]() .
.
Решение:
по
формуле интегрирования по частям ![]() имеем:
имеем: ![]() =
= 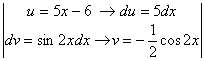 =
= ![]()
-![]() =
= ![]()
![]() .
.
3
Найти интеграл ![]() .
.
Решение:
выделим полный квадрат из квадратного трёхчлена, затем сделаем замену:
![]() =
= 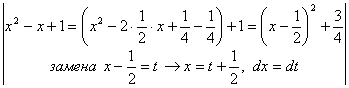 =
=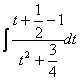 =
=
=![]() =
= ![]() =
= ![]()
![]() =
= ![]() .
.
4. Найти интегралы:
а)
![]() ;
;
б)
![]() .
.
Решение:
это
интегралы от рациональных функций. Функция вида ![]() называется рациональной функцией (или
рациональной дробью), где
называется рациональной функцией (или
рациональной дробью), где ![]() и
и ![]() многочлены степеней
многочлены степеней ![]() и
и ![]() . Если
. Если ![]() , то рациональная дробь правильная, если
, то рациональная дробь правильная, если ![]() , то – неправильная.
Среди правильных дробей различают четыре типа простейших дробей: 1)
, то – неправильная.
Среди правильных дробей различают четыре типа простейших дробей: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() где
где ![]() - действительные числа,
- действительные числа, ![]() - натуральные числа,
квадратный трёхчлен
- натуральные числа,
квадратный трёхчлен ![]() не
имеет действительных корней. Интегралы от дробей первого, второго и третьего
типов берутся просто (см. примеры выше), интеграл от дроби четвёртого типа
берут по рекуррентной формуле (см. например, [1], стр.257). Правило
интегрирования рациональных функций:
не
имеет действительных корней. Интегралы от дробей первого, второго и третьего
типов берутся просто (см. примеры выше), интеграл от дроби четвёртого типа
берут по рекуррентной формуле (см. например, [1], стр.257). Правило
интегрирования рациональных функций:
1)
если под интегралом неправильная дробь, то путём деления числителя на
знаменатель выделяем целую часть, т.е. представляем дробь в виде ![]() =
= ![]() , где
, где ![]() - многочлен,
- многочлен, ![]() - правильная дробь;
- правильная дробь;
2)
разлагаем знаменатель дроби на множители ![]() ;
;
3)
правильную дробь ![]() разлагаем
на простейшие дроби:
разлагаем
на простейшие дроби:
![]() =
=![]()
![]() +…+
+…+![]() +…+
+…+![]() +
+![]() +…+
+…+![]() …;
…;
4)
находим неопределённые коэффициенты ![]() , для чего приводим к общему знаменателю
сумму дробей в правой части равенства и приравниваем числители. Если приравнять
коэффициенты при одинаковых степенях
, для чего приводим к общему знаменателю
сумму дробей в правой части равенства и приравниваем числители. Если приравнять
коэффициенты при одинаковых степенях ![]() в левой и правой частях последнего
тождества, то получим систему линейных уравнений относительно искомых
коэффициентов. Можно определить коэффициенты и другим способом, придавая переменной
в левой и правой частях последнего
тождества, то получим систему линейных уравнений относительно искомых
коэффициентов. Можно определить коэффициенты и другим способом, придавая переменной
![]() в этом
тождестве произвольные числовые значения.
в этом
тождестве произвольные числовые значения.
Итак, интеграл от рациональной функции всегда берётся, т.к. его можно свести к интегралам от многочлена и от простейших дробей.
а)
Под интегралом неправильная дробь, т.к. степени числителя и знаменателя равны (![]() ). Делим числитель на
знаменатель предварительно раскрыв скобки в знаменателе:
). Делим числитель на
знаменатель предварительно раскрыв скобки в знаменателе:
|
|
|
|
|
2 |
|
|
Итак,![]() =
=![]() =
= 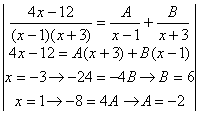 =
= ![]() -
-
-![]() =
= ![]() =
= ![]() ;
;
б)
![]() =
= =
=
= =
=![]() =…=
=…=![]()
![]()
![]() .
.
5. Найти интегралы:
а)
![]() ;
;
б)
![]() ;
;
в)![]() .
.
Решение:
интегралы
вида ![]() , где
, где ![]() - рациональная функция
приводятся к интегралам от рациональных функций с помощью универсальной
подстановки
- рациональная функция
приводятся к интегралам от рациональных функций с помощью универсальной
подстановки ![]() ,
при этом
,
при этом
![]() ;
;
![]()
![]() ;
;
![]() ;
; ![]() .
.
а)
![]() =
= ![]() =
= 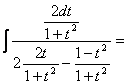
![]()
![]() =
=
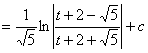 =
=  .
.
Универсальная подстановка часто ведёт к громоздким выкладкам, поэтому её надо применять в случаях, если нельзя найти более лёгкий способ определения интеграла. Так, если встречаются интегралы вида
(1)![]() ;
; ![]() ;
;
(2)![]() ;
;
(3)![]() ,
, ![]() ;
;
(4)![]() ,
, ![]() ,
, ![]() ,
,
то применяют одно из следующих правил:
1)
интегралы вида (1) при ![]() чётном можно найти путём понижения степени
по формулам:
чётном можно найти путём понижения степени
по формулам:
![]() ;
; ![]() ;
; ![]() ;
;
2)
при ![]() нечётном
интегралы вида (1) находят путём отделения от этой степени множителя и замены
кофункции новой переменной;
нечётном
интегралы вида (1) находят путём отделения от этой степени множителя и замены
кофункции новой переменной;
3)
интегралы вида (2) можно найти по правилу 1), если ![]() и
и ![]() оба чётные, или по правилу 2), если
оба чётные, или по правилу 2), если ![]() или
или ![]() (или и
(или и ![]() и
и ![]() ) нечётно;
) нечётно;
4)
интегралы вида (3) можно найти путём замены ![]() или
или ![]() новой переменной;
новой переменной;
5) интегралы вида (4) можно найти путём разложения на слагаемые по формулам:
![]() ;
;
![]()
![]() ;
;
![]() .
.
б)![]() = (по правилу 1)
понижаем степень) = =
= (по правилу 1)
понижаем степень) = =![]() =
= 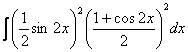 =
=![]()
![]() =
= ![]() =
=![]()
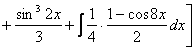 =
=![]() ;
;
в)![]() = (по правилу 2)
отделяем множитель
= (по правилу 2)
отделяем множитель ![]() и
заменяем кофункцию
и
заменяем кофункцию ![]() через
через
![]() ) =
) =![]() =
=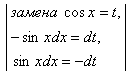 =
=
= ![]() =
= ![]() =
=![]() .
.
6. Вычислить определённые интегралы:
а)
 ;
;
б)![]() .
.
Формула Ньютона-Лейбница для вычисления определённого интеграла:
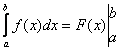 =
=![]() , где
, где ![]() первообразная для
первообразная для ![]() .
.
Основные свойства определённых интегралов
1)
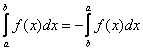 ;
2)
;
2) 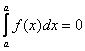 ;
;
3) 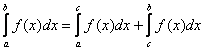 ; 4)
; 4)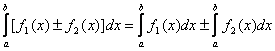 ;
;
5)
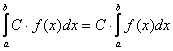 , С – постоянная;
, С – постоянная;
6)
если ![]() на
на ![]() , то
, то  ;
;
7)
 , если
, если ![]() - нечётная функция;
- нечётная функция;
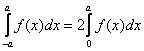 , если
, если ![]() - чётная функция.
- чётная функция.
Методы интегрирования:
1)
интегрирование по частям: 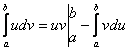 ;
;
2)
замена переменных: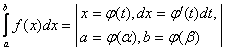 =
= 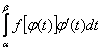 .
.
а) Для нахождения первообразной данного интеграла применяют одну
из
тригонометрических подстановок. Эти подстановки приводят к интегралам от
функций, рациональных относительно ![]() и
и ![]() , следующие интегралы:
, следующие интегралы:
![]() - подстановкой
- подстановкой ![]() ;
;
![]() -
подстановкой
-
подстановкой ![]() ;
;
![]() - подстановкой
- подстановкой ![]() .
.
 =
=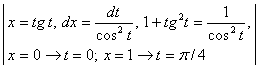 =
=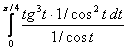 =
= =
=
=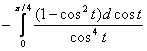 =
=![]() =
= ;
;
б)
по методу интегрирования по частям имеем: ![]() = =
= =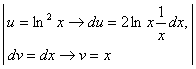 =
=![]()
![]() =
=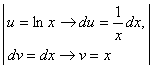 =
=
=![]() =
=![]() .
.
7. Вычислить несобственные интегралы или доказать их расcходимость:
а)
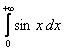 ;
;
б)
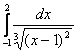 .
.
Решение:
Существуют несобственные интегралы двух видов:
1) интегралы с бесконечными пределами;
2) интегралы от неограниченных функций.
Несобственные
интегралы с бесконечными пределами находятся либо по определению: 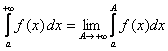 ;
; ![]() ;
; ![]() =
=![]()
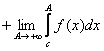 , либо по формуле
, либо по формуле 
![]() (остальные интегралы аналогично).
(остальные интегралы аналогично).
Несобственные
интегралы от функций с бесконечными разрывами находятся по определению: 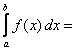 =
=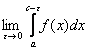
 , где
, где ![]() - точка бесконечного разрыва, в частности
разрыв может быть на концах промежутка интегрирования в точках
- точка бесконечного разрыва, в частности
разрыв может быть на концах промежутка интегрирования в точках ![]() или
или ![]() . Несобственные интегралы называются
сходящимися, если указанные выше пределы существуют; расходящимися, - если не
существуют.
. Несобственные интегралы называются
сходящимися, если указанные выше пределы существуют; расходящимися, - если не
существуют.
а)
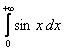 =
=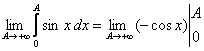 =
=![]() +
+![]() = 1-
= 1-![]() - предел не существует, поэтому
несобственный интеграл расходится.
- предел не существует, поэтому
несобственный интеграл расходится.
б)
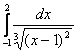 =
= ![]() =
= + +
+ +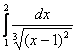 =
=![]()
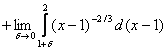 =
=![]() +
+ ![]() =
=![]() +
+![]() =
=![]() .
.
8.
Для функции ![]() найти
найти
а)![]() ;
;
б) ![]() ;
;
в) ![]()
Решение:
функцию
нескольких аргументов ![]() можно дифференцировать по каждому
аргументу, считая все остальные аргументы постоянными. Полученные при этом
частные производные
можно дифференцировать по каждому
аргументу, считая все остальные аргументы постоянными. Полученные при этом
частные производные ![]() находятся
по известным правилам дифференцирования функции одной переменной. Частные
производные высших порядков
находятся
по известным правилам дифференцирования функции одной переменной. Частные
производные высших порядков ![]() находят по тем же правилам: частные
производные второго порядка это производные от частных производных первого
порядка, третьего – от второго и т.д. Полный дифференциал функции
находят по тем же правилам: частные
производные второго порядка это производные от частных производных первого
порядка, третьего – от второго и т.д. Полный дифференциал функции ![]() определяется по
формуле
определяется по
формуле ![]() .
.
а)
Для функции ![]() частные
производные имеют вид
частные
производные имеют вид ![]() ,
, ![]() ;
;
б)
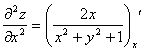 =
=![]() ,
, ![]() =
=![]() ,
, ![]()
![]() ;
;
в)
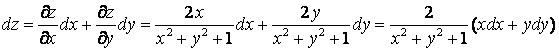
9. Найти
а) уравнение касательной плоскости и нормали к поверхности
![]() в точке
в точке ![]() ;
;
б)
производные ![]() функции
z, заданной неявно уравнением
функции
z, заданной неявно уравнением
![]() .
.
Решение:
а) если поверхность задана уравнением ![]() и точка
и точка ![]() лежит на ней, то
касательная плоскость к поверхности в этой точке определяется уравнением
лежит на ней, то
касательная плоскость к поверхности в этой точке определяется уравнением ![]() ; нормаль к поверхности
в этой точке – уравнением
; нормаль к поверхности
в этой точке – уравнением ![]()
![]() .
.
Итак, поскольку ![]() , то
, то
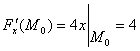 ;
; 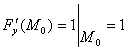 ;
; 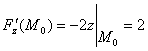 .
.
Уравнение касательной плоскости имеет вид ![]() или
или ![]() ; уравнение нормали
; уравнение нормали
![]()
![]() ;
;
б) производные ![]() неявной функции
неявной функции ![]() , заданной уравнением
, заданной уравнением ![]() , определяются по
формулам
, определяются по
формулам ![]() ;
; ![]() ,….
,….
В
частности, если ![]() есть
неявная функция одной переменной
есть
неявная функция одной переменной ![]() , заданной уравнением
, заданной уравнением ![]() , то
, то ![]() .
.
В
нашем примере уравнение ![]() задаёт неявную функцию z,
задаёт неявную функцию z, ![]() , поэтому
, поэтому ![]() ;
; ![]() .
.
10. Исследовать на экстремум функцию ![]() .
.
Решение:
функция ![]() имеет максимум (минимум) в точке
имеет максимум (минимум) в точке ![]() , если её значение в
этой точке больше (меньше) её значений во всех достаточно близких точках.
Максимумы или минимумы (экстремумы) могут быть только в точках, лежащих внутри
области определения функции, в которых все её частные производные первого
порядка равны нулю или не существуют. Такие точки называются критическими. Не
всякая критическая точка является точкой экстремума. Для проверки критической
точки на экстремум применяют достаточные условия: пусть
, если её значение в
этой точке больше (меньше) её значений во всех достаточно близких точках.
Максимумы или минимумы (экстремумы) могут быть только в точках, лежащих внутри
области определения функции, в которых все её частные производные первого
порядка равны нулю или не существуют. Такие точки называются критическими. Не
всякая критическая точка является точкой экстремума. Для проверки критической
точки на экстремум применяют достаточные условия: пусть ![]() и
и ![]() - критическая точка, обозначим
- критическая точка, обозначим 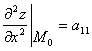 ,
, ,
, 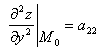 ;
; 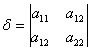 =
=
![]() . Если
. Если ![]() , то
, то ![]() - точка минимума; если
- точка минимума; если ![]() , то
, то ![]() - точка максимума; если
- точка максимума; если ![]() , то в точке
, то в точке ![]()
нет
экстремума; если ![]() ,
то нужны дополнительные исследования.
,
то нужны дополнительные исследования.
Находим частные производные функции ![]() и критические точки, в
которых они равны нулю или не существуют и которые лежат внутри области
определения функции:
и критические точки, в
которых они равны нулю или не существуют и которые лежат внутри области
определения функции: ![]() ;
;
![]() . Решаем
систему
. Решаем
систему  ,
находим две точки
,
находим две точки ![]() и
и
![]() . Обе точки
являются критическими, так как функция определена на всей плоскости хОу.
Проверим эти точки на экстремум по достаточному признаку:
. Обе точки
являются критическими, так как функция определена на всей плоскости хОу.
Проверим эти точки на экстремум по достаточному признаку: ![]() ,
, ![]() ,
, ![]() . Для точки
. Для точки ![]() получим
получим 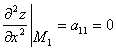 ,
, 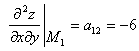 ,
, 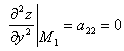 ,
, ![]() , поэтому в точке
, поэтому в точке ![]() нет экстремума. Для точки
нет экстремума. Для точки ![]() имеем
имеем ![]() ,
, ![]() ,
, ![]() ,
, ![]() , поэтому точка
, поэтому точка ![]() есть точка минимума.
есть точка минимума. ![]() .
.
11. Вычислить двойной интеграл ![]() по области D,
ограниченной указанными линиями: x=0, x=3, y=-1, y=2.
по области D,
ограниченной указанными линиями: x=0, x=3, y=-1, y=2.
Решение:
область интегрирования D ограничена прямыми линиями параллельными координатным осям, т.е. является прямоугольником. Это простейший случай, когда все четыре предела интегрирования в двукратном интеграле, к которому сводится данный интеграл, будут числа и, когда безразличен порядок интегрирования (по переменной х затем по у или наоборот). Поэтому
![]() =
=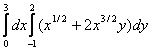 =
=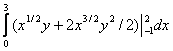
=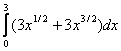 =
=![]() .
.
12. Изменить порядок интегрирования 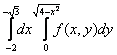 +
+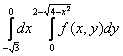 .
.
Решение:
построим область интегрирования, которая состоит из
двух областей ![]() и
и
![]() , ограниченных
линиями:
, ограниченных
линиями: ![]() :
: ![]() ;
;
![]() :
: ![]() . Чтобы построить кривые
. Чтобы построить кривые ![]() и
и ![]() , приведём их уравнения к
каноническому виду.
, приведём их уравнения к
каноническому виду. ![]()
![]()
![]()
![]() . Таким образом,
. Таким образом, ![]() есть уравнение верхней половины
окружности с центром в начале координат, радиус равен 2.
есть уравнение верхней половины
окружности с центром в начале координат, радиус равен 2. ![]()
![]()
![]() . Итак,
. Итак, ![]() есть уравнение нижней половины окружности
с центром в точке (0,2) и радиусом, равным 2.
есть уравнение нижней половины окружности
с центром в точке (0,2) и радиусом, равным 2.
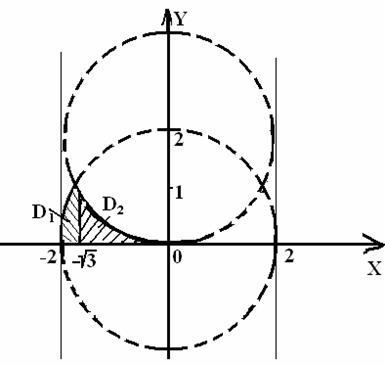
Рисунок 1
На рисунке области ![]() и
и ![]() складываются в одну область
складываются в одну область ![]() , ограниченную слева
полуокружностью
, ограниченную слева
полуокружностью ![]() ,
справа – полуокружностью
,
справа – полуокружностью ![]() . Поэтому, меняя порядок интегрирования по
области
. Поэтому, меняя порядок интегрирования по
области ![]() ,
получим один двукратный интеграл:
,
получим один двукратный интеграл: 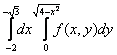 +
+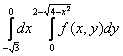 =
= .
.
13. Переходя к полярным координатам, вычислить двойной интеграл
![]() ,
, ![]() .
.
Решение:
формула перехода к полярным координатам имеет вид:
![]() =
=![]() .
.
Так
как область интегрирования круг с центром в начале координат, т.е. полюс лежит
внутри области, то ![]() =
=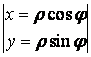 =
=
=![]() =
=![]() =
=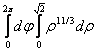 =
=![]() .
.
14. Вычислить тройной интеграл
![]() ,
, ![]() .
.
Решение:
областью
интегрирования ![]() является
прямоугольный параллелепипед с гранями, параллельными координатным плоскостям,
поэтому данный тройной интеграл сводится к трехкратному, у которого все пределы
интегрирования будут константами и порядок интегрирования не имеет значения:
является
прямоугольный параллелепипед с гранями, параллельными координатным плоскостям,
поэтому данный тройной интеграл сводится к трехкратному, у которого все пределы
интегрирования будут константами и порядок интегрирования не имеет значения: ![]() =
= =
=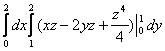 =
=
=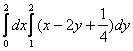 =
=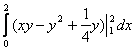 =
=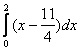 =
=![]() .
.
15.
Найти объём тела, ограниченного поверхностями ![]() ,
, ![]() ,
, ![]() .
.
Решение:
объём
v трёхмерной
области V вычисляется по формуле ![]() . По заданным уравнениям поверхностей
строим область V.
. По заданным уравнениям поверхностей
строим область V. ![]()
![]() ,
, ![]()
![]() есть уравнения параболических цилиндров с
образующими параллельными оси Oz;
есть уравнения параболических цилиндров с
образующими параллельными оси Oz; ![]() - уравнение координатной плоскости xOy;
- уравнение координатной плоскости xOy;
![]() - уравнение
плоскости , параллельной оси Oy и пересекающей Ox в точке
(2,0,0), Oz – в точке (0,0,4).
- уравнение
плоскости , параллельной оси Oy и пересекающей Ox в точке
(2,0,0), Oz – в точке (0,0,4).
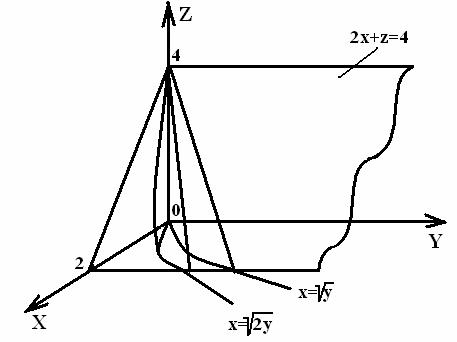
Рисунок 2
По виду области выбираем следующий порядок
интегрирования при переходе от тройного интеграла к трёхкратному: ![]() =
= =
=
=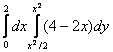 =
=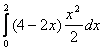 =
=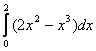 =
=![]() .
.
Список литературы
1. Хасеинов К.А. Каноны математики: Учебник. – Алматы: 2003.-686 с.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: в 2 ч. – М.: Высшая школа, 2003. – ч. 1,2.-352 с.
3. Сборник индивидуальных заданий по высшей математике: в 3 ч. (Рябушко А.П., Бархатов В.В. и др.). Под ред. Рябушко А.П. – Минск: Высш. школа, 2000.-ч.2,3 .-396 с.
Содержание
1 Теоретические вопросы………………………………….....…………….….3
2 Расчётные задания……………………………………..………………….….3
3 Решение типового варианта……………………………..………………….20
Список литературы ……………………………………………………………33
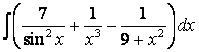
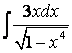
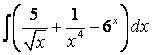
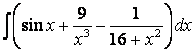
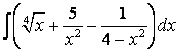
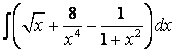
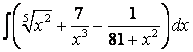 , б)
, б)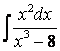
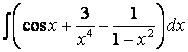
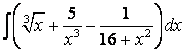
 , б)
, б) , б)
, б) , б)
, б)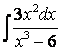
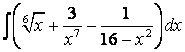 , б)
, б)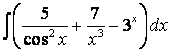 , б)
, б)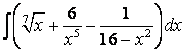
 ,
, 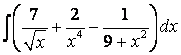 , б)
, б)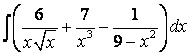 , б)
, б)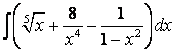 , б)
, б) 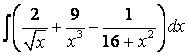 , б)
, б) 
 ,
,  ,
,  , б)
, б)
 , б)
, б)  , б)
, б)  ,
,  ,
,

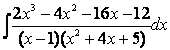




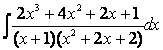



 б)
б)










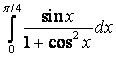
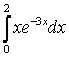
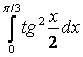

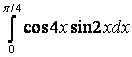

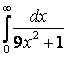 ; б)
; б)  ; б)
; б)
 ; б)
; б) 
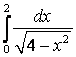

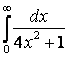
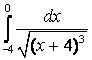
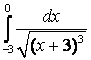
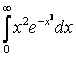
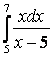
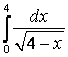
 ;
;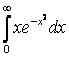
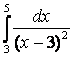
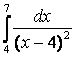
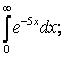


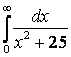
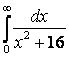
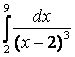
 ;
;