ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТІРЛІГІ
"Алматы энергетика және байланыс институтының "
Коммерциялық емес акционерлік қоғамы
С.Е. Ералиев
Математикалық талдауға кіріспе
Оқу құралы
Алматы 2010
Бұл оқулық техникалық жоғары оқу орындарының бағдарламасына сәйкес жазылған. Мұнда функцияның анықтамасы, шегі, үзіліссіздігі, туындылары, дифференциалдары қарастырылған. 3-тарауда дифференциалдауды шектерді есептеуде, функцияларды зерттеуде және сызбасын салуда әрі геометрияда қалай қолданалатындығы көрсетілген. Әрбір бөлімде мысалдар қарастырылып, соңында есептер берілген. Сондықтан бұл оқулықты есептер жинағы ретінде күндізгі әрі сырттан оқитын жоғары оқу орындарының студенттері пайдалана алады.
I-тарау. Талдамға кіріспе
1. Функциялар (Бернелер)
1.1 Анықтамасы
![]() айнымалысының әрбір
мәніне
айнымалысының әрбір
мәніне ![]() айнымалысының
белгілі бір мәні сәйкес келсе, онда у-ті х-тің функциясы деп
атап, оны
айнымалысының
белгілі бір мәні сәйкес келсе, онда у-ті х-тің функциясы деп
атап, оны ![]() немесе
немесе
![]()
![]() , т.с.с деп белгілейді.
Мұндағы х- тәуелсіз айнымалы немесе аргумент
айғағы деп аталады. Х аргументінің
(айғағының) қабылдайтын мәндер жиыны D
анықталу облысы деп, ал у функциясының
, т.с.с деп белгілейді.
Мұндағы х- тәуелсіз айнымалы немесе аргумент
айғағы деп аталады. Х аргументінің
(айғағының) қабылдайтын мәндер жиыны D
анықталу облысы деп, ал у функциясының ![]() cәйкестігі бойынша
қабылдайтын мәндер жиыны Е өзгеру облысы деп аталады.
cәйкестігі бойынша
қабылдайтын мәндер жиыны Е өзгеру облысы деп аталады.
Егер ![]() функциясы үшін аргументтің
үлкен мәніне функцияның үлкен мәні сәйкес
келсе, онда функция өспелі; керісінше аргументтің үлкен
мәніне функцияның кіші мәні сәйкес келсе, онда функция
кемімелі функция деп аталады.
функциясы үшін аргументтің
үлкен мәніне функцияның үлкен мәні сәйкес
келсе, онда функция өспелі; керісінше аргументтің үлкен
мәніне функцияның кіші мәні сәйкес келсе, онда функция
кемімелі функция деп аталады.
![]() функциясы үшін
функциясы үшін ![]() теңдігі орындалса, онда ол
тақ функция деп; ал
теңдігі орындалса, онда ол
тақ функция деп; ал ![]() теңдігі орындалса жұп функция
деп аталады.
теңдігі орындалса жұп функция
деп аталады.
Функцияның берілу тәсілдері:
а) Кестелік берілуі. Бұл жағдайда белгілі бір ретпен х-тің мәндері әрі оған сәйкес у мәндері жазылады.
|
|
|
|
... |
|
|
|
|
|
... |
|
б) Графиктік берілуі сан жиындарының
арасындағы қатынастарды оның графигін пайдалана отырып
көрсетуге болады. Ол үшін жазықтықта барлық ![]() нүктелерін салу
жеткілікті. Осы нүктелер графикпен анықталған
нүктелерді береді.
нүктелерін салу
жеткілікті. Осы нүктелер графикпен анықталған
нүктелерді береді.
в) Аналитикалық тәсілмен берілуі. Математикада екі айнымалының қатынасы (тәуелділігі) формула арқылы беріледі. Бұл тәсіл функцияның аналитикалық тәсілмен берілуі деп аталады.
Егер қандайда бір ![]() саны табылып
саны табылып ![]() теңдігі орындалса, онда
теңдігі орындалса, онда ![]() функциясы периодты
функция болады. Ал теңдік орындалатын ең кіші Т оның негізгі
периоды деп аталады.
функциясы периодты
функция болады. Ал теңдік орындалатын ең кіші Т оның негізгі
периоды деп аталады.
Мысалы, ![]()
![]() үшін
үшін ![]() ал
ал ![]()
![]() үшін
үшін ![]() .
.
Қандайда бір оң М саны табылып,
анықталу облысында жататын кезкелген ![]() үшін
үшін ![]() теңсіздігі орындалса, онда
теңсіздігі орындалса, онда ![]() шектелген функция деп
аталады.
шектелген функция деп
аталады.
1.2 Негізгі элементар функциялар (қарапайым бернеулер)
Негізгі элементар функциялар деп келесі аналитикалық түрде берілген функцияларды айтады:
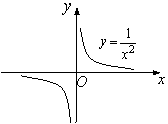
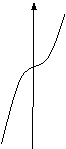
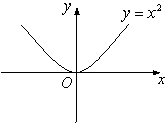
1. Дәрежелік функция ![]()
![]() - нақты сан.
- нақты сан.
![]()
 |
|||||
 |
|||||
 |
|||||
1 Сурет 2 Сурет 3 Сурет
2. Көрсеткіштік функция ![]()
![]() ,
, ![]() Анықталу облысы- барлық сандар
өсі
Анықталу облысы- барлық сандар
өсі ![]()
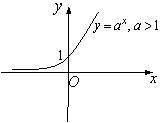 |
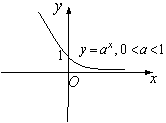 |
4 Сурет 5 Сурет
3. Логарифмдік функция ![]()
![]()
![]()
![]()
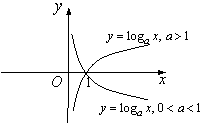 |
6 Сурет
4. Тригонометриялық функциялар
![]()
![]()
![]()
![]()
![]()
Мұндағы ![]()
![]() функцияларының анықталу
облысы
функцияларының анықталу
облысы ![]()
![]() функциясының
анықталу облысына
функциясының
анықталу облысына ![]()
![]()
![]()
нүкелерінен басқа нүктелердің барлығы, ал
![]() функциясының
анықталу облысына
функциясының
анықталу облысына ![]() нүктелерінен басқа
нүктелердің барлығы кіреді.
нүктелерінен басқа
нүктелердің барлығы кіреді.
5. Кері тригонометриялық функциялар.
![]()
![]()
![]() функцияларының анықталу облысы
функцияларының анықталу облысы
![]() ал
ал ![]()
![]() - (-
- (-![]() .
.
Анықтама. Негізгі элементар функцияларға амалдар қолдану арқылы алынатын функция элементар функция деп аталады.
1. Мысал - ![]() .
.
Табу керек: ![]()
![]()
![]()
![]() .
.
Шешуі: ![]()
![]()
![]() ;
;
![]()
2. Мысал - ![]() функциясының анықталу
облысын табу керек.
функциясының анықталу
облысын табу керек.
Шешуі: Мұндағы ![]() болу керек. Яғни
болу керек. Яғни
![]()
![]() ,
,
![]()
Сондықтан
функцияның анықталу облысы (-![]()
![]() болады.
болады.
3. Мысал - ![]()
![]() функциясының анықталу
облысын табу керек.
функциясының анықталу
облысын табу керек.
Шешуі: Берілген функция анықталады, егер ![]() Бұдан
Бұдан ![]()
4. Мысал - ![]()
![]() +
+![]() функциясының анықталу облысын
табу керек.
функциясының анықталу облысын
табу керек.
Шешуі: Әрбір қосылғыштың
анықталу облысын табамыз. Бұл облыстардың ортақ
бөлігі функцияның анықталу облысы болады. Бірінші
қосылғыш ![]() интервалында
анықталған. Екінші қосылғыш (
интервалында
анықталған. Екінші қосылғыш (![]()
![]() (
(![]() интервалында, ал үшінші қосылғыш
интервалында, ал үшінші қосылғыш ![]()
![]() интервалында анықталған.
Бұл үш интервалдың ортақ бөлігі
интервалында анықталған.
Бұл үш интервалдың ортақ бөлігі ![]() облысы берілген
функцияның анықталу облысы болады.
облысы берілген
функцияның анықталу облысы болады.
5. Мысал - Тақ функциямен жұп функцияның көбейтіндісі, тақ функция болатындығын дәлелдеу керек.
Шешуі: ![]() -тақ,
-тақ, ![]() -жұп функция болсын.
-жұп функция болсын. ![]()
![]() функциясының тақ
болатындығын дәлелдеу керек:
функциясының тақ
болатындығын дәлелдеу керек: ![]()
1. ![]() берілген. Табу керек
берілген. Табу керек ![]()
![]() .
.
2. Берілген ![]() .
Табу керек
.
Табу керек ![]()
![]()
![]()
3. ![]() берілген.
Табу керек
берілген.
Табу керек ![]()
![]()
![]()
![]()
![]()
4. ![]()
![]() берілген. Табу керек
берілген. Табу керек ![]()
Келесі функциялардың анықталу облыстарын табу керек:
5. ![]() 6.
6.
![]()
7. ![]() 8.
8.
![]()
9. ![]() 10.
10.
![]()
11. Екі тақ функцияның көбейтіндісі жұп функция болатындығын дәлелдеу керек.
12. Екі жұп функцияның көбейтіндісі жұп функция болатындығын дәлелдеу керек.
13. Келесі функциялардың қайсысы тақ, қайсысы жұп болатындығын анықтау керек:
а) ![]() б)
б) ![]()
в) ![]()
![]()
![]() г)
г)
![]()
д) ![]()
![]()
![]()
14. Келесі функциялардың қайсысы периодты болатындығын анықтап, олардың периодын табу керек:
а) ![]()
![]() б)
б) ![]()
в) ![]() д)
д) ![]()
2. Сандық тізбектер және оның шектері
2.1. Анықтамасы
Реттері өсуіне қарай бүтін сандармен нөмірленген
![]()
сандар жиыны тізбек деп аталады. Тізбекті бүтін сандардың
функциясы түрінде жазуға болады: ![]()
Егер тізбектің әрбір мүшесі алдыңғы мүшесінен үлкен болса, онда сандық тізбек бірсарынды өспелі деп аталады. Мысалы,
![]()
Егер тізбектің әрбір мүшесі алдыңғы мүшесінен кіші болса, онда сандық тізбек бірсарынды кемімелі деп аталады. Мысалы:
![]()
Сандық тізбек жоғарыдан шенелген
деп аталады, егер М саны табылып, кез келген n үшін ![]() .
.
Сандық тізбек төменнен шенелген
деп аталады, егер N саны табылып, кез келген n үшін ![]()
Егер сандық тізбек төменнен
және жоғарыдан шенелген болса, онда ол шенелген деп аталады,
Бұл жағдайда М > 0 саны табылып, кез келген n үшін ![]() яғни
яғни ![]()
![]()
![]() Мысалы:
Мысалы: ![]() шенелген сандық қатар болады,
себебі
шенелген сандық қатар болады,
себебі ![]()
![]()
2.2 Шектер
Кез келген ![]() > 0 саны үшін
> 0 саны үшін ![]() саны табылып,
саны табылып, ![]() саны табылып,
саны табылып, ![]() болғанда
болғанда ![]()
![]() орындалса, онда А саны
сандық тізбектің шегі деп аталады да
орындалса, онда А саны
сандық тізбектің шегі деп аталады да
![]()
деп жазылады.
Сандық тізбектің тек бір ғана шегі болады.
Шегі бар болатын тізбек жинақты тізбек деп, ал шегі болмайтын тізбек жинақсыз тізбек деп аталады. Жинақты болатын тізбектер үшін келесі теңдіктер орындалады:
![]() (1)
(1)
![]() ;
(2)
;
(2)
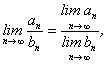 егер
егер ![]() . (3)
. (3)
1. Мысал - Тізбектің шегі туралы анықтаманы
пайдалана отырып, жалпы мүшесі ![]() болатын тізбектің шегі нөлге
тең болатындығын дәлелдеу керек.
болатын тізбектің шегі нөлге
тең болатындығын дәлелдеу керек.
Шешуі: ![]() -ға байланысты болатын
-ға байланысты болатын ![]() санын анықтаймыз.
Кез келген
санын анықтаймыз.
Кез келген ![]() үшін
үшін
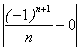
![]() немесе
немесе ![]() орындалады.
Бұл теңсіздіктен
орындалады.
Бұл теңсіздіктен ![]() яғни
яғни ![]() деп алуға болады.
деп алуға болады.
Сонымен, кезкелген ![]() үшін
үшін ![]() саны табылып,
саны табылып, ![]() болғанда
болғанда 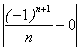
![]() теңсіздігі орындалады.
Бұл берілген тізбектің шегі нөлге тең
болатындығын көрсетеді.
теңсіздігі орындалады.
Бұл берілген тізбектің шегі нөлге тең
болатындығын көрсетеді.
2. Мысал - ![]() тізбегінің жалпы мүшесін
анықтау керек.
тізбегінің жалпы мүшесін
анықтау керек.
Шешуі: ![]()
![]()
![]() ,
, ![]()
![]() ,
, ![]()
3. Мысал - Жалпы мүшесі ![]() болатын тізбектің шегін табу керек.
болатын тізбектің шегін табу керек.
Шешуі: Ол үшін бөлшектің алымы мен
бөлімін ![]() қа
бөліп, одан кейін шекке көшеміз:
қа
бөліп, одан кейін шекке көшеміз:
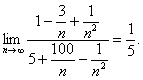
Келесі тізбектердің жалпы мүшелерін анықтау керек:
15. ![]()
![]()
![]()
![]()
16. ![]()
![]()
![]() .
.
Тізбектің шегі туралы теореманы пайдалана отырып, келесі теңдіктерді дәлелдеу керек:
17. ![]() 18.
18.
![]()
19. ![]() 20.
20.
![]()
Келесі тізбектердің шектерін табу керек:
21. ![]() 22.
22.
![]()
23. ![]() 24.
24.
![]()
25. ![]() 26.
26. ![]()
3. Функцияның шегі
3.1 Функцияның шегінің анықтамасы
Егер кез келген ![]() санына сәйкес
санына сәйкес ![]() саны табылып,
саны табылып, ![]()
![]() шартын
қанағаттандыратын барлық
шартын
қанағаттандыратын барлық ![]() үшін
үшін ![]()
![]() теңсіздігі орындалса, онда
теңсіздігі орындалса, онда ![]() санын
санын ![]() функциясының
функциясының ![]() -тің
-тің ![]() -ға ұмтылғандағы
шегі деп атайды да
-ға ұмтылғандағы
шегі деп атайды да
![]()
![]()
деп жазады.
1. Мысал - Функция шегінің анықтамасын пайдалана
отырып, ![]() болатындығын
дәлелдеу керек.
болатындығын
дәлелдеу керек.
Шешуі: ![]() саны берілсін.
саны берілсін. ![]()
![]() теңсіздігін
қанағаттандыратын, барлық
теңсіздігін
қанағаттандыратын, барлық ![]() -тер үшін,
-тер үшін, ![]()
![]() теңсіздігі орындалатын
теңсіздігі орындалатын ![]() санын табу қажет.
санын табу қажет.
Егер ![]()
![]() болса, онда
болса, онда ![]()
![]()
![]()
![]() Сондықтан
Сондықтан ![]()
![]()
![]()
![]()
![]()
![]() теңсіздігі орындалу үшін,
теңсіздігі орындалу үшін, ![]() деп алсақ
жеткілікті. Бұдан
деп алсақ
жеткілікті. Бұдан ![]()
![]()
![]()
Сонымен кез-келген ![]() үшін
үшін ![]() саны табылып,
саны табылып, ![]()
![]() теңсіздігінен
теңсіздігінен ![]()
![]() орындалады, яғни
орындалады, яғни
![]()
Келесі есептерде функцияның шегінің анықтамасын пайдаланып дәлелдеу керек:
27. ![]() 28.
28.
![]()
29. ![]() 30.
30.
![]()
3.2 Ақырсыз кішкене және ақырсыз үлкен функциялар
Егер ![]() болса, онда
болса, онда ![]() функциясы ақырсыз кішкене функция
деп аталады. Символмен былай анықталады:
функциясы ақырсыз кішкене функция
деп аталады. Символмен былай анықталады: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Егер ![]() болса, онда
болса, онда ![]() функциясы ақырсыз үлкен
функция деп аталады. Символмен былай анықталады:
функциясы ақырсыз үлкен
функция деп аталады. Символмен былай анықталады: ![]()
![]() ,
, ![]()
![]()
![]()
![]() ,
, ![]()
![]() ақырсыз кішкене
және ақырсыз үлкен функциялар жоғарыдағыдай анықталады.
Ақырсыз үлкен функциялармен ақырсыз кішкене функциялар
тығыз байланыста болады. Егер:
ақырсыз кішкене
және ақырсыз үлкен функциялар жоғарыдағыдай анықталады.
Ақырсыз үлкен функциялармен ақырсыз кішкене функциялар
тығыз байланыста болады. Егер: ![]() болса, онда
болса, онда ![]() яғни
яғни ![]()
Ақырысыз кішкене функциялардың қасиеттері:
а) Шектеулі ақырсыз кішкене функциялардың алгебралық қосындысы ақырсыз кішкене функция болады.
б) Шектеулі ақырсыз кішкене функциялардың көбейтіндісі ақырсыз кішкене функция болады.
в) Ақырсыз кішкене функцияның шенелген функцияға көбейтіндісі ақырсыз кішкене функция болады.
4. Шектерді есептеу
4.1 Негізгі теоремаларды (түйіндерді) қолдану
Функциялардың шектерін есептеу үшін келесі теоремаларды білу керек:
![]() мұндағы
мұндағы ![]() тұрақты;
(1)
тұрақты;
(1)
![]() мұндағы
мұндағы ![]() тұрақты;
(2)
тұрақты;
(2)
Егер ![]() және
және ![]() бар болса, онда:
бар болса, онда:
![]() (3)
(3)
![]() (4)
(4)
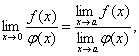 егер
егер ![]() (5)
(5)
![]()
![]()
![]() (6)
(6)
Барлық негізгі элементар функциялар үшін олардың анықталу облысында жататын нүктелерде:
![]() (7)
(7)
теңдігі орындалады.
Егер ![]() болса,
онда
болса,
онда ![]() (8)
(8)
Егер ![]() болса,
онда
болса,
онда![]() (9)
(9)
Егер ![]() және
және
![]() болса, онда
болса, онда
![]() (10)
(10)
1.
Мысал - Табу керек ![]()
Шешуі: ![]()
2. Мысал - ![]() табу керек.
табу керек.
Шешуі: ![]() және
және ![]() сондықтан
сондықтан ![]()
3. Мысал - ![]() табу керек.
табу керек.
Шешуі: ![]() сондықтан
сондықтан ![]()
4. Мысал - ![]() табу керек.
табу керек.
Шешуі: ![]()
![]() сондықтан
сондықтан ![]()
![]()
Келесі шектерді анықтау керек:
31. ![]() 32.
32.
![]()
33. ![]() 34.
34.
![]()
35. ![]() 36.
36.
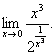
4.2 Анықталмағандықтарды ашу
Көп жағдайда аргументтің (айғақтың) мәнін қою нәтижесінде
төмендегі анықталмағандықтарға келеміз: ![]()
![]()
![]() Осындай жағдайлардағы
функциялардың шегін табуды анықталмағандықтарды ашу деп
атайды. Анықталмағандықтарды ашу үшін, шекке
көшпестен бұрын, берілген өрнек түрлендіріледі:
Осындай жағдайлардағы
функциялардың шегін табуды анықталмағандықтарды ашу деп
атайды. Анықталмағандықтарды ашу үшін, шекке
көшпестен бұрын, берілген өрнек түрлендіріледі:
5. Мысал - ![]() табу керек.
табу керек.
Шешуі: Берілген өрнекте аргументтің шектік
мәнін қойсақ ![]() түріндегі
анықталмағандыққа келеміз. Сондықтан берілген
өрнекті түрлендіреміз. Бөлшектің алымы мен
бөлімі
түріндегі
анықталмағандыққа келеміз. Сондықтан берілген
өрнекті түрлендіреміз. Бөлшектің алымы мен
бөлімі ![]() болғанда
нөлге айналатындықтан
болғанда
нөлге айналатындықтан ![]() және
және ![]() көпмүшеліктері
көпмүшеліктері ![]() ге қалдықсыз
бөлінеді.
ге қалдықсыз
бөлінеді.
Сондықтан ![]()
6. Мысал - ![]() табу керек.
табу керек.
Шешуі:
 =
= 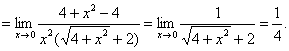
7. Мысал - ![]() табу керек.
табу керек.
Шешуі: 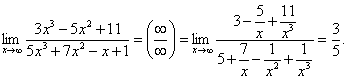
8. Мысал - ![]() табу керек.
табу керек.
Шешуі: ![]()
![]()
Келесі шектерді табу керек:
37. ![]() 38.
38.
![]()
39. ![]() 40.
40. ![]()
41. ![]() 42.
42.
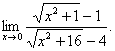
43. ![]() 44.
44.
![]()
4.3 Бірінші және екінші тамаша шек
Берілген ![]() функциясы
функциясы ![]() нүктесінде
нүктесінде ![]() түріндегі
анықталмағандық болғандықтан, оны шешу үшін
бірінші тамаша шек қолданылады:
түріндегі
анықталмағандық болғандықтан, оны шешу үшін
бірінші тамаша шек қолданылады:
![]() (11)
(11)
Берілген ![]() функциясы
функциясы ![]() ұмтылғанда
ұмтылғанда ![]() түріндегі
анықталмағандықты береді. Бұндай шектерді анықтау
үшін екінші тамаша шек қолданылады:
түріндегі
анықталмағандықты береді. Бұндай шектерді анықтау
үшін екінші тамаша шек қолданылады:
![]() (12)
(12)
9. Мысал - Табу керек: ![]()
![]()
![]()
![]()
Шешуі: ![]() ұмтылғанда
ұмтылғанда ![]() нөлге
ұмтылады, сондықтан өрнектің алымы мен бөлімін
3-ке көбейтіп (11)-формуланы (кейіптемені) пайдаланамыз:
нөлге
ұмтылады, сондықтан өрнектің алымы мен бөлімін
3-ке көбейтіп (11)-формуланы (кейіптемені) пайдаланамыз:
![]() =
=![]()
![]()
10. Мысал - Табу керек. ![]()
Шешуі: ![]() болғандықтан
болғандықтан ![]()
11. Мысал - Табу керек. ![]()
Шешуі:
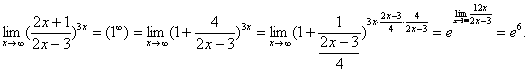
Келесі шекткерді табу керек:
45. ![]() 46.
46.
![]()
47. ![]() 48.
48.
![]()
49. ![]() 50.
50.
![]()
51. ![]() 52.
52.
![]()
53. ![]() 54.
54.
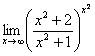
5. Ақырсыз аз функцияларды салыстыру. Эквиваленттік (баламалық)
5.1 Ақырсыз кішкене шамаларды салыстыру
![]() және
және
![]() ақырсыз
кішкене функциялары реттері бірдей ақырсыз шамалар деп аталады, егер
ақырсыз
кішкене функциялары реттері бірдей ақырсыз шамалар деп аталады, егер ![]()
![]()
![]() Егер
Егер ![]() болса, онда
болса, онда ![]() ақырсыз кішкене шамасы
ақырсыз кішкене шамасы ![]() -қа
қарағанда жоғары ретті ақырсыз кішкене шама деп
аталады.
-қа
қарағанда жоғары ретті ақырсыз кішкене шама деп
аталады.
Кейбір жағдайда ақырсыз кішкене
шаманың біреуін негізгі етіп алып, қалған кіші
шамалардың реттерін негізгі кішкене шамамен салыстыра отырып
анықтауға болады. Егер ![]() және
және ![]() кішкене шамаларының екіншісі негізгі
болса, онда
кішкене шамаларының екіншісі негізгі
болса, онда ![]() орындалғанда
орындалғанда
![]() шамасы
шамасы ![]() -пен
салыстырғанда
-пен
салыстырғанда ![]() -ретті
ақырсыз кішкене шама деп аталады.
-ретті
ақырсыз кішкене шама деп аталады.
Егер ![]() болса, онда
болса, онда ![]() және
және ![]() эквивалентті (баламалы) ақырсыз
кішкене шамалар деп аталады да ²~² символымен белгілінеді. Яғни
эквивалентті (баламалы) ақырсыз
кішкене шамалар деп аталады да ²~² символымен белгілінеді. Яғни ![]() ~b(x).
~b(x).
Екі ақырсыз кішкене шаманың қатынасының шегі, ақырсыз кішкене шамаларды эквивалентті ақырсыз кішкене шамалармен ауыстырғаннан өзгермейді.
Егер ![]() және b(x) ақырсыз кішкене шамалар болса, онда
олардың айырымы
және b(x) ақырсыз кішкене шамалар болса, онда
олардың айырымы ![]() b
b![]() берілген
берілген ![]() пен b
пен b![]() қарағанда жоғары ретті
ақырсыз кішкене шамалар болады.
қарағанда жоғары ретті
ақырсыз кішкене шамалар болады.
Керісінше, егер ![]() b
b![]() айырымы
айырымы ![]() пен b
пен b![]() -ға қарағанда
жоғары ретті ақырсыз кішкене шама болса,онда
-ға қарағанда
жоғары ретті ақырсыз кішкене шама болса,онда ![]() және
және ![]() эквивалентті ақырсыз
кішкене шамалар болады.
эквивалентті ақырсыз
кішкене шамалар болады.
Негізгі эквиваленттіктер (баламалар):
![]() ~
~ ![]() (1)
(1)
![]() ~
~ ![]() (2)
(2)
![]() ~
~ ![]() (3)
(3)
![]()
![]() ~
~ ![]() (4)
(4)
1-![]() ~
~ ![]() (5)
(5)
![]() ~
~ ![]() (6)
(6)
![]() ~
~ ![]() (7)
(7)
a![]() ~
~ ![]() (8)
(8)
![]() ~
~ ![]() (9)
(9)
![]() ~
~ ![]() (10)
(10)
![]()
![]() ~
~ ![]() (11)
(11)
![]() ~
~ ![]() (12)
(12)
9-баламаны дәлелдеп көрсетейік.

![]()
Олай болса, ![]() ~
~![]() егер
егер ![]() ұмтылғанда
ұмтылғанда ![]()
1. Мысал - ![]() ұмтылғанда
ұмтылғанда ![]() және
және ![]() функцияларының реттері
функцияларының реттері
бірдей ақырсыз аз шамалар болатындығын дәлелдеу керек.
Шешуі: Берілген екі функцияның қатынастарының шегін анықтаймыз:
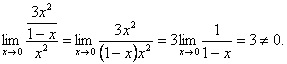
Яғни берілген ақырсыз аз функциялардың реттері бірдей.
2. Мысал - ![]() ұмтылғанда
ұмтылғанда ![]() функциясының реті
функциясының реті ![]() функциясының
ретінен жоғары болатындығын дәлелдеу керек.
функциясының
ретінен жоғары болатындығын дәлелдеу керек.
Шешуі: 
![]()
яғни ![]() функциясы
функциясы ![]() функциясына қарағанда жоғары
ретті ақырсыз кішкене шама.
функциясына қарағанда жоғары
ретті ақырсыз кішкене шама.
3. Мысал - ![]() ұмтылғанда,
ұмтылғанда, ![]() мен
мен ![]() -ң қандай
мәндерінде,
-ң қандай
мәндерінде, ![]()
функциясы ![]() функциясымен эквивалентті болады.
функциясымен эквивалентті болады.
Шешуі: Бұл екі функция эквивалентті болу үшін ![]() болу керек.
болу керек.
Бұдан ![]()
![]() Яғни, берілген екі функция
эквивалентті болу үшін
Яғни, берілген екі функция
эквивалентті болу үшін ![]() және
және ![]()
![]() ұмтылғанда келесі
ақырсыз кішкене функциялардың эквивалентті болатынын дәлелдеу
керек:
ұмтылғанда келесі
ақырсыз кішкене функциялардың эквивалентті болатынын дәлелдеу
керек:
55. ![]() және
және
![]()
![]() 56.
56.
![]() және
және ![]()
57. ![]() және
және
![]() 58.
58.
![]()
![]() және
және ![]()
Келесі есептерде, ![]() ұмтылғанда
ұмтылғанда ![]() мен
мен ![]() -ң қандай
мәндерінде
-ң қандай
мәндерінде ![]() функциясы
функциясы
![]()
![]() функциясымен
эквивалентті болады:
функциясымен
эквивалентті болады:
59. ![]() 60.
60.
![]()
61. ![]()
5.2 Эквивалентті ақырсыз аз шамаларды шектерді есептеуге қолдану.
Бізге екі ақырсыз кішкене шаманың қатынасының шегі, ақырсыз кішкене шамаларды эквивалентті ақырсыз кішкене шамалармен ауыстырғаннан өзгермейтіндігі белгілі.
4. Мысал - ![]() табу керек.
табу керек.
Шешуі: ![]()
5. Мысал - Табу керек ![]() .
.
Шешуі:
![]()
![]()
6. Мысал - Табу керек ![]()
![]()
Шешуі.
![]()
![]()
![]()
7. Мысал - Табу керек ![]()
![]() .
.
Шешуі:
![]()
![]()
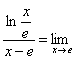
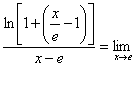
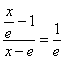
![]()
![]()
8. Мысал - Табу керек ![]()
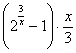 .
.
Шешуі:
![]()
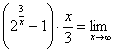
![]()
9. Мысал - Табу керек ![]()
![]() .
.
Шешуі: Бұл өрнекте ![]() және
және ![]() ақырсыз кішкене шамалар. Бірақ
ақырсыз кішкене шамалар. Бірақ
![]() ақырсыз
кішкене шама емес, сондықтан
ақырсыз
кішкене шама емес, сондықтан ![]() функциясы
функциясы ![]() -қа эквивалентті болмайды.
-қа эквивалентті болмайды.
Сол себепті ![]() ақырсыз кішкене шамасын енгіземіз.
Бұдан
ақырсыз кішкене шамасын енгіземіз.
Бұдан ![]() және
және
![]()
![]()
![]()
![]()
![]()
![]() .
.
10. Мысал - Табу керек ![]()
![]()
Шешуі:

11. Мысал - Табу керек ![]()
![]() .
.
Шешуі: ![]()
![]()
![]() .
.
Келесі шектерді табу керек:
62. ![]()
![]() .
.![]()
![]() 63.
63.
![]() .
.
64. ![]() .
65.
.
65. ![]() .
.
66. ![]() .
67.
.
67. ![]() .
.
68. ![]() .
69.
.
69. ![]() .
.
70. ![]() .
71.
.
71. ![]() .
.
72. ![]() .
73.
.
73. ![]() .
.
74. ![]()
![]() .
75.
.
75. 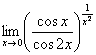
![]()
76. ![]() .
77.
.
77. ![]() .
.
6. Функцияның үзіліссіздігі. Үзіліс нүктелері және оларды
классификациялау.
6.1 Анықтамасы.
![]() функциясы
функциясы ![]() нүктесінде үзіліссіз функция деп
аталады, егер:
нүктесінде үзіліссіз функция деп
аталады, егер:
1) ол осы нүктеде анықталса; 2) ![]() бар болса; 3) осы шек
функцияның
бар болса; 3) осы шек
функцияның ![]() нүктесіндегі
мәніне тең болса, яғни
нүктесіндегі
мәніне тең болса, яғни ![]() .
.
Егер осы үш шарттың болмағанда
біреуі орындалмаса, онда функция ![]() нүктесінде үзілісті болады, ал
нүктесінде үзілісті болады, ал
![]() нүктесі
үзіліс нүктесі деп аталады.
нүктесі
үзіліс нүктесі деп аталады.
Үзіліс нүктелері келесі түрлерге
бөлінеді: а) егер ![]() бар болып, бірақ
бар болып, бірақ ![]() функциясы
функциясы ![]() нүктесінде
анықталмаса немесе анықталғанмен
нүктесінде
анықталмаса немесе анықталғанмен ![]() болса, онда
болса, онда ![]() нүктесі жөнделетін
үзік нүкте деп аталады. Бұл жағдайда үзікті
жөндеу үшін функцияның
нүктесі жөнделетін
үзік нүкте деп аталады. Бұл жағдайда үзікті
жөндеу үшін функцияның ![]() нүктесіндегі мәнін
қосымша анықтау қажет немесе оның
нүктесіндегі мәнін
қосымша анықтау қажет немесе оның ![]() нүктесіндегі мәнін
нүктесіндегі мәнін ![]()
![]() теңдігі орындалатындай
етіп өзгерту керек.
теңдігі орындалатындай
етіп өзгерту керек.
б) Егер ![]() болмаса, бірақ
болмаса, бірақ ![]() нүктесіндегі
функцияның сол жақты және оң жақты шектері бар
болып, олар бір-біріне тең болмаса, онда
нүктесіндегі
функцияның сол жақты және оң жақты шектері бар
болып, олар бір-біріне тең болмаса, онда ![]() нүктесі
нүктесі ![]() функциясының бірінші текті
үзік нүктесі деп аталады.
функциясының бірінші текті
үзік нүктесі деп аталады.
в) Егер ![]() нүктесінде
нүктесінде ![]() функциясының бір жақты шектерінің
болмағанда біреуі болмаса немесе шексіздікке тең болса, онда
функциясының бір жақты шектерінің
болмағанда біреуі болмаса немесе шексіздікке тең болса, онда ![]() нүктесі
нүктесі ![]() функциясының
екінші текті үзіліс нүктесі деп аталады.
функциясының
екінші текті үзіліс нүктесі деп аталады.
6.2 Үзіліссіз функциялардың қасиеттері
Келесі теоремалардың маңызы зор
1)Негізгі элементар функциялар
![]() өздерінің анықталу
облыстарының барлық нүктелерінде үзіліссіз болады.
өздерінің анықталу
облыстарының барлық нүктелерінде үзіліссіз болады.
2) Егер ![]() және
және ![]() функциялары
функциялары ![]() нүктесінде үзіліссіз болса,
онда осы нүктеде
нүктесінде үзіліссіз болса,
онда осы нүктеде ![]() ;
; ![]() ;
; ![]() ; мұнда
; мұнда ![]() функциялары да үзіліссіз болады.
функциялары да үзіліссіз болады.
3) Егер ![]() функциясы
функциясы ![]() нүктесінде үзіліссіз болып, ал
нүктесінде үзіліссіз болып, ал
![]() функциясы
функциясы ![]() нүктесінде
үзіліссіз болса, онда
нүктесінде
үзіліссіз болса, онда ![]() күрделі функциясы
күрделі функциясы ![]() нүктесінде
үзіліссіз болады.
нүктесінде
үзіліссіз болады.
4) Кез келген элементар функция анықталу облысының әрбір нүктесінде үзіліссіз болады.
1. Мысал - Келесі функцияны үзіліссіздікке тексеріп, үзік нүктелерін табу керек:
![]() .
.
Шешуі: Бұл функцияны күрделі функция түріне келтіреміз:
![]() , мұнда
, мұнда ![]() .
.
Бірінші бөлшекте бөлімі ешбір
нүктеде нөлге айналмайды. ![]() функциясы
функциясы ![]() нүктесінен басқа барлық
нүктелерде үзіліссіз болады.
нүктесінен басқа барлық
нүктелерде үзіліссіз болады.
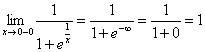 ,
,
![]() .
.
Сонымен, сол және оң шектері бар,
бірақ олар тең емес, сондықтан ![]() нүктесі 1-текті үзік
нүкте болады.
нүктесі 1-текті үзік
нүкте болады.
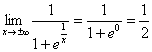 .
.
Функцияның сызбасы:
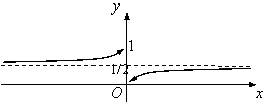
7 Сурет
2. Мысал - Функцияны үзіліссіздікке тексеріп үзік нүктелерін табу керек:
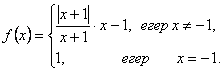
Шешуі.
![]() болғанда функция үзіліссіз
болады.
болғанда функция үзіліссіз
болады. ![]() болғандықтан
болғандықтан
![]() болады да
болады да ![]() . Бұл
жағдайда
. Бұл
жағдайда ![]()
![]() болғанда,
болғанда, ![]() болады.
Сондықтан
болады.
Сондықтан ![]()
Енді ![]() нүктесін
зерттейміз:
нүктесін
зерттейміз:
![]()
![]()
Бұл нүкте бірінші текті үзік нүктесі.
Функцияны келесі түрде жазуға болады: 
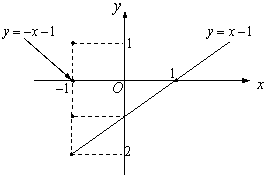 |
8 Сурет.
Келесі функцияларды үзіліссіздікке тексеріп үзік нүктелерін табу керек.
78. ![]() . 79.
. 79.
![]() .
.
80. ![]() 81.
81.
![]()
![]()
II-тарау. Туынды және дифференциал
1.Функциялардың туындылары
1.1 Анықтамасы
![]() функциясының
функциясының ![]() нүктесіндегі туындысы деп
нүктесіндегі туындысы деп ![]() нөлге
ұмтылғандағы функция өсімшесінің аргумент
өсімшесіне қатынасының шегін айтады.
нөлге
ұмтылғандағы функция өсімшесінің аргумент
өсімшесіне қатынасының шегін айтады. ![]() функциясының
функциясының ![]() нүктесіндегі
туындысын
нүктесіндегі
туындысын ![]() немесе
немесе
![]() деп
белгілейді.
деп
белгілейді.
![]() (1)
(1)
Егер ![]() функциясының анықталу
облысында жататын әрбір
функциясының анықталу
облысында жататын әрбір ![]() нүктесінде туындысы бар болса, онда
ол туынды
нүктесінде туындысы бар болса, онда
ол туынды ![]() аргументінің
функциясы болады, әрі
аргументінің
функциясы болады, әрі
![]()
деп белгіленеді.
Функцияның туындысын табу амалын осы функцияны дифференциалдау деп атайды.
1.2 Туындының геометриялық және механикалық мағынасы
а) Туындының геометриялық мағынасы
![]() бір
қисықтың теңдеуі болсын, ал
бір
қисықтың теңдеуі болсын, ал ![]() - осы қисықтың
бойында жататын нүкте болғандықтан
- осы қисықтың
бойында жататын нүкте болғандықтан ![]() (9 сурет).
(9 сурет). ![]() функциясының
функциясының ![]() нүктесіндегі
туындысының мәні қисықтың осы нүктесі
арқылы өтетін жанаманың бұрыштық коэффициентіне
тең болады:
нүктесіндегі
туындысының мәні қисықтың осы нүктесі
арқылы өтетін жанаманың бұрыштық коэффициентіне
тең болады: ![]() мұндағы
мұндағы
![]() жанама мен
абсцисса өсінің арасындағы бұрыш.
жанама мен
абсцисса өсінің арасындағы бұрыш.
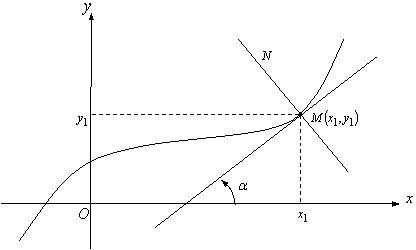 |
9 Сурет
![]() қисығының
қисығының ![]() нүктесі
арқылы өтетеін жанаманың теңдеуі
нүктесі
арқылы өтетеін жанаманың теңдеуі
![]()
![]() . (1)
. (1)
Қисықтың ![]() нүктесі
арқылы өтіп, осы нүктеден өтетін жанамаға
перпендикуляр болатын
нүктесі
арқылы өтіп, осы нүктеден өтетін жанамаға
перпендикуляр болатын ![]() түзуін
нормаль (тіктеме) түзу деп аталып, оның теңдеуі
түзуін
нормаль (тіктеме) түзу деп аталып, оның теңдеуі
![]()
![]() (2)
(2)
болады.
б) Туындының механикалық мағынасы
Қарапайым мысал есебінде ![]() материалдық
нүктесінің түзу бойымен қозғалысын
қарастырайық.
материалдық
нүктесінің түзу бойымен қозғалысын
қарастырайық. ![]() арқылы бастапқы
арқылы бастапқы ![]() нүктесінен
қозғалыстағы нүктеге дейінгі
қашықтықты белгілейік. Уақыт
нүктесінен
қозғалыстағы нүктеге дейінгі
қашықтықты белгілейік. Уақыт ![]() -ң әрбір сәтіне
-ң әрбір сәтіне
![]() -ң
белгілі мәні сәйкестендіріледі.
-ң
белгілі мәні сәйкестендіріледі.
Сондықтан
![]() .
.
![]() нүктесінің
нүктесінің ![]() аралығында жүрген
жолы
аралығында жүрген
жолы ![]() болса,
онда осы аралықтағы орташа жылдамдығы
болса,
онда осы аралықтағы орташа жылдамдығы ![]() , ал
, ал ![]() уақытындағы лездік
жылдамдығы
уақытындағы лездік
жылдамдығы
![]() (3)
(3)
1. Мысал - ![]() қисығының
қисығының ![]() нүктесі
арқылы өтетін жанамамен тіктеменің теңдеулерін табу
керек.
нүктесі
арқылы өтетін жанамамен тіктеменің теңдеулерін табу
керек.
Шешуі: Жанаманың бұрыштық коэффициентін
табу үшін берілген функцияның туындысын табамыз: ![]() . Туындының
. Туындының ![]() нүктесіндегі
мәні ізделінді бұрыштық коэффициентті береді.
нүктесіндегі
мәні ізделінді бұрыштық коэффициентті береді. ![]() .
.
Сонымен жанаманың теңдеуі ![]() , немесе
, немесе ![]() ал тіктеменің
теңдеуі
ал тіктеменің
теңдеуі ![]() немесе
немесе
![]()
2. Мысал - ![]() параболасының абсцисса өсімен
қандай бұрышпен қиылысатындығын анықтау керек.
параболасының абсцисса өсімен
қандай бұрышпен қиылысатындығын анықтау керек.
Шешуі: Ол үшін алғаш ![]() қисығымен абсцисса
өсінің қиылысу нүктесінің абсциссасын
анықтаймыз:
қисығымен абсцисса
өсінің қиылысу нүктесінің абсциссасын
анықтаймыз: 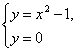
![]()
![]()
![]()
Ендігі жерде, нүктелердегі параболаға
жүргізілген жанамалардың бұрыштық коэффициенттерін
табамыз: ![]()
![]()
![]()
Сондықтан
![]()
![]()
3. Мысал - ![]() қисығының бойында
жататын, ординатасы абсциссасынан 3 есе жылдам өсетін нүктені табу
керек.
қисығының бойында
жататын, ординатасы абсциссасынан 3 есе жылдам өсетін нүктені табу
керек.
Шешуі: Функцияның туындысын табамыз: ![]()
Туынды функцияның өсу
жылдамдығының оның аргументінің өсу
жылдамдығымен салыстырғандағы өзгерісті
көрсететіндіктен ![]() шарты абсциссасы
шарты абсциссасы ![]() болатын ізделінді нүктені
анықтайды. Ал бұл нүктенің ординатасы
болатын ізделінді нүктені
анықтайды. Ал бұл нүктенің ординатасы ![]()
82. ![]() қисығының
қисығының
![]() нүктесі
арқылы өтетін жанаманың теңдеуін жазу керек.
нүктесі
арқылы өтетін жанаманың теңдеуін жазу керек.
83. ![]() қисығының
қисығының
![]() нүктесі
арқылы өтетін жанаманың теңдеуін табу керек.
нүктесі
арқылы өтетін жанаманың теңдеуін табу керек.
84. ![]() қисығының
қисығының
![]() нүктесі
арқылы өтетін жанаманың және тіктеменің
теңдеулерін табу керек.
нүктесі
арқылы өтетін жанаманың және тіктеменің
теңдеулерін табу керек.
85. ![]() қисығының
абсцисса өсін қандай бұрышпен қиятындығын
анықтау керек.
қисығының
абсцисса өсін қандай бұрышпен қиятындығын
анықтау керек.
86. ![]() синусойдасы
абсцисса өсін координаттың бас нүктесінде қандай
бұрышпен қиятындығын анықтау керек.
синусойдасы
абсцисса өсін координаттың бас нүктесінде қандай
бұрышпен қиятындығын анықтау керек.
87. ![]() параболасының
қай нүктесінен өтетін жанама,
параболасының
қай нүктесінен өтетін жанама, ![]() түзуіне параллель болатындығын
анықтау керек.
түзуіне параллель болатындығын
анықтау керек.
1.3 Дифференциалдаудың негізгі ережелері
Егер ![]() ,
, ![]() функцияларының
функцияларының ![]() нүктесінде шенелген
туындылары бар болса, онда
нүктесінде шенелген
туындылары бар болса, онда
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
мұндағы С-тұрақты.
1.4 Негізгі элементар функциялардың туындылары
![]() (1)
(1)
![]() (10)
(10)
![]() (2)
(2) ![]() (11)
(11)
![]() (3)
(3)
![]() (12)
(12)
![]() (4)
(4)
![]() (13)
(13)
![]() (5)
(5)
![]() (14)
(14)
![]() (6)
(6)
![]() (15)
(15)
![]() (7)
(7) ![]() (16)
(16)
![]() (8)
(8)
![]() (17)
(17)
![]() (9)
(9) ![]() (18)
(18)
1.
Мысал - ![]() функциясының туындысын табу керек
функциясының туындысын табу керек
Шешуі: ![]()
2. Мысал - ![]() . Табу керек
. Табу керек ![]() .
.
Шешуі: ![]()
3. Мысал - ![]() функциясының туындысын табу керек.
функциясының туындысын табу керек.
Шешуі: ![]()
4. Мысал - ![]() функциясының туындысын табу керек.
функциясының туындысын табу керек.
Шешуі: 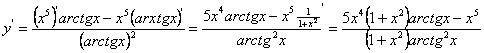
5. Мысал - ![]() функциясының туындысын табу керек.
функциясының туындысын табу керек.
Шешуі: ![]()
6-мысал. ![]() функциясының туындысын табу керек.
функциясының туындысын табу керек.
Шешуі: ![]()
![]()
7-мысал. - ![]() функциясының туындысын табу керек.
функциясының туындысын табу керек.
Шешуі:

Келесі функциялардың туындысын табу керек:
88. ![]() 89.
89. ![]()
90. ![]() 91.
91. ![]()
92. ![]() 93.
93. ![]()
94. ![]() 95.
95. ![]()
96. ![]() 97.
97.
![]()
98. ![]() 99.
99.
![]()
100.![]() 101.
101. ![]()
102. ![]() 103.
103. ![]()
104. ![]() 105.
105.![]()
106. ![]() 107.
107.
![]()
108. ![]() 109.
109. ![]()
110. ![]() 111.
111.![]()
112. ![]() 113.
113.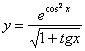
114. ![]() 115.
115.
![]()
116. ![]() 117.
117.
![]()
1.5 Логарифимдік дифференциалдау
Кейде берілген өрнектен туынды таппастан бұрын, туындысы оңай табылатындай етіп, түрлендіріп алу қажет. Дербес жағдайда, егер көбейтінділердің, бөлінділердің, дәрежелік және түбір астындағы өрнектердің логарифимдерінің туындыларын табу керек болғанда, алдын ала логаримфдерін тауып алу қажет. Көптеген жағдайда функцияны логарифмдеп алып туындысын тауып, одан берілген функцияның туындысын анықтап есептеуді жеңілдетеді. Бұндай әдіс логорифмдік дифференциалдау тәсілі деп аталады.
![]() функциясы берілсін. Бұл
функцияның екі жағында логорифмдеп, соңынан туындысын
табамыз:
функциясы берілсін. Бұл
функцияның екі жағында логорифмдеп, соңынан туындысын
табамыз:
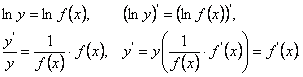
8. Мысал - ![]()
![]() функциясының туындысын табу керек.
функциясының туындысын табу керек.
Шешуі:
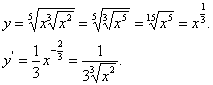
9. Мысал - ![]()
![]() функциясының туындысын табу керек.
функциясының туындысын табу керек.
Шешуі:
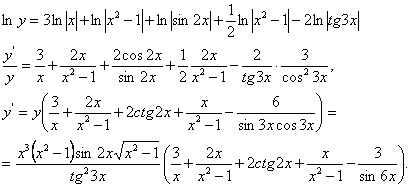
10. Мысал - ![]() функциясының туындысын табу керек
функциясының туындысын табу керек
Шешуі: 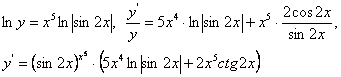
Келесі функциялардың туындысын табу керек:
118. ![]() 119.
119.
![]()
120. 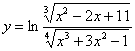 121.
121. ![]()
122. ![]() 123.
123.
![]()
124. ![]() 125.
125.
![]()
126. ![]() 127.
127.
![]()
2. Дифференциал және оның қолданылуы
2.1 Анықтамасы
Егер ![]() функциясының
функциясының ![]() нүктесіндегі
нүктесіндегі ![]() өсімшесін
өсімшесін
![]() (1)
(1)
түрінде өрнектеуге болатын болса, онда оны осы ![]() нүктесінде
дифференциалданатын функция деп атайды.
нүктесінде
дифференциалданатын функция деп атайды.
Мұндағы:
![]()
![]() теңдіктегі
бірінші қосылғыш
теңдіктегі
бірінші қосылғыш ![]() ке пропорционал және оған
сызықты тәуелді, ал екінші қосылғыш
ке пропорционал және оған
сызықты тәуелді, ал екінші қосылғыш ![]() н салыстырғанда
жоғары ретті ақырсыз кішкене шама. Осыған байланысты
н салыстырғанда
жоғары ретті ақырсыз кішкене шама. Осыған байланысты ![]() қосылғышы
қосылғышы ![]() ұмтылғанда
функция өсімшесінің бас мүшесі дейді де, ол функцияның
ұмтылғанда
функция өсімшесінің бас мүшесі дейді де, ол функцияның ![]() нүктесіндегі
дифференциалы деп аталады да
нүктесіндегі
дифференциалы деп аталады да ![]() символдарының бірімен белгіленеді:
символдарының бірімен белгіленеді:
![]() (2)
(2)
![]() функциясының
функциясының ![]() нүктесіне
нүктесіне ![]() өсімше берген
кездегі дифференциалдың геометриялық мағынасы функция
графигінің
өсімше берген
кездегі дифференциалдың геометриялық мағынасы функция
графигінің ![]() нүктесі
арқылы жүргізілген жанаманың ординатасы болып табылады.
нүктесі
арқылы жүргізілген жанаманың ординатасы болып табылады.
Дифференциалдарды табудың негізгі ережелері:
![]() (3)
(3) ![]() (6)
(6)
![]() (4)
(4) ![]() (7)
(7)
![]() (5)
(5)
Мұндағы ![]() және
және ![]() туындылары бар
туындылары бар ![]() ң функциялары, ал
ң функциялары, ал ![]() тұрақты.
тұрақты.
1. Мысал - ![]() функциясының дифференциалын табу
керек.
функциясының дифференциалын табу
керек.
Шешуі:
1-тәсіл. Функцияның туындысын
табамыз: 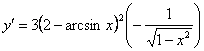 ,
,
бұдан дифференциалдың анықтамасы бойынша
![]() .
. ![]()
2-тәсіл. 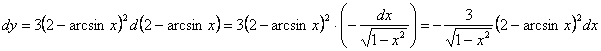 .
.
2. Мысал - ![]()
![]() функциясының дифференциалын табу
керек.
функциясының дифференциалын табу
керек.
Шешуі: 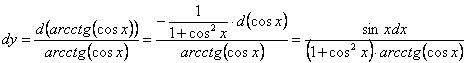 .
.
Келесі функциялардың дифференциалдарын табу керек:
128. ![]() 134.
134.
![]()
129. ![]() 135.
135.
![]()
130. ![]() 136.
136.
![]()
131. ![]() 137.
137.
![]()
132. ![]() 138.
138.
![]()
133. ![]()
2.2. Дифференциалды жуықтап есептеуге қолдану
Функция дифференциалы функция мәнін
жуықтап есептеуде жиі қолданылады. Ол үшін ![]() теңдеуден
теңдеуден
![]() (8)
(8)
теңдігін алып, туындылары табылатын функциялардың ![]() нүктесіндегі
мәнін жуықтап есептеуге болады.
нүктесіндегі
мәнін жуықтап есептеуге болады.
3. Мысал - ![]() өрнегінің жуық
мәнін табу керек.
өрнегінің жуық
мәнін табу керек.
Шешуі. Бұл жағдайда: ![]()
![]()
![]() .
.
![]()
![]() деп алып,
деп алып, ![]() -формуланы қолданамыз:
-формуланы қолданамыз: ![]()
139. ![]() өрнегінің
жуық мәнін табу керек.
өрнегінің
жуық мәнін табу керек.
140. ![]() өрнегінің
жуық мәнін табу керек.
өрнегінің
жуық мәнін табу керек.
141. ![]()
![]() өрнегінің
жуық мәнін табу керек.
өрнегінің
жуық мәнін табу керек.
142. ![]() өрнегінің
жуық мәнін табу керек.
өрнегінің
жуық мәнін табу керек.
3. Жоғары ретті туындылар мен дифференциалдар
3. 1 Жоғары ретті туындылар
Берілген ![]() функциясының туындысы
функциясының туындысы ![]() тәуелсіз айнымалы
тәуелсіз айнымалы
![]() ң
функциясы болады. Бұл
ң
функциясы болады. Бұл ![]() бірінші ретті туынды деп аталады.
бірінші ретті туынды деп аталады.
Бірінші ретті туындыдан алынған туынды екінші
ретті туынды, сол сияқты ![]() ші ретті туындыдан алынған туынды
ші ретті туындыдан алынған туынды ![]() ші ретті туынды деп
аталады да,төмендегіше белгіленеді:
ші ретті туынды деп
аталады да,төмендегіше белгіленеді:
![]()
![]()
![]() және
және
![]() функцияларының
көбейтіндісінің
функцияларының
көбейтіндісінің ![]() ретті туындыларын табу үшін Лейбниц
формуласын қолданған дұрыс:
ретті туындыларын табу үшін Лейбниц
формуласын қолданған дұрыс: ![]() (9)
(9)
3.2 Жоғары ретті дифференциалдар
Берілген ![]() функциясының дифференциалы
функциясының дифференциалы ![]() тәуелсіз айнымалы
тәуелсіз айнымалы
![]() -ң
функциясы болады. Функцияның бірінші ретті дифференциалынан алынған
дифференциал-екінші, ал екінші ретті дифференциалдан алынған
дифференциал-үшінші, сол сияқты
-ң
функциясы болады. Функцияның бірінші ретті дифференциалынан алынған
дифференциал-екінші, ал екінші ретті дифференциалдан алынған
дифференциал-үшінші, сол сияқты ![]() ші ретті дифференциалдан алынған
дифференциал
ші ретті дифференциалдан алынған
дифференциал ![]() ші
ретті дифференциал деп аталады.
ші
ретті дифференциал деп аталады.
Егер ![]() функциясының
функциясының ![]() ретті туындысы болса, онда
ретті туындысы болса, онда
![]()
![]()
![]()
....................................
![]()
теңдіктерін аламыз.
![]()
![]() күрделі функция
болсын.
күрделі функция
болсын. ![]() ал
ал ![]() болады, яғни 1-ші
дифференциал үшін инвариантық қасиет орындалады. Жоғары
ретті дифференциалдар үшін бұл қасиет орындалмайды:
болады, яғни 1-ші
дифференциал үшін инвариантық қасиет орындалады. Жоғары
ретті дифференциалдар үшін бұл қасиет орындалмайды:
![]()
1. Мысал - ![]() Табу керек
Табу керек ![]()
Шешуі: ![]()
![]()
![]()
2. Мысал - ![]()
![]() ші ретті туындысын табу керек.
ші ретті туындысын табу керек.
Шешуі: ![]()
![]()
![]()
3. Мысал - ![]()
![]() ші ретті туындысын табу керек.
ші ретті туындысын табу керек.
Шешуі: ![]() ,
,
![]() ,
,
![]() ,
,
......................................
![]()
4. Мысал - ![]()
![]() табу керек.
табу керек.
![]()
![]()
![]() ;
; ![]()
![]()
![]()
![]() болғандағы Лейбниц формуласын
жазамыз:
болғандағы Лейбниц формуласын
жазамыз:
![]()
![]()
![]()
деп алып осы формуланы қолданамыз:
![]()
143. ![]() табу
керек
табу
керек ![]()
![]()
144. ![]() табу
керек
табу
керек ![]()
![]()
145. ![]() табу
керек
табу
керек ![]()
146. ![]() табу
керек
табу
керек ![]()
147. ![]() табу
керек
табу
керек ![]()
4. Айқын емес және параметрлік түрде берілген функциялардың туындылары
4.1 Айқын емес функциялар.
Егер ![]() айнымалысының функциясы
айнымалысының функциясы
![]()
![]() (1)
(1)
қатынасы арқылы берілсе, онда ![]() функциясы
функциясы ![]() ң айқындалмаған функциясы
деп аталады. Айқындалмаған түрде берілген
ң айқындалмаған функциясы
деп аталады. Айқындалмаған түрде берілген ![]() функциясының туындысы
төмендегіше анықталады:
функциясының туындысы
төмендегіше анықталады:
1. ![]() ші
теңдеудің сол жағынан
ші
теңдеудің сол жағынан ![]() ті
ті ![]() ң функциясы деп қарастыра
отырып туынды алып, одан соң нөлге теңестіреміз.
ң функциясы деп қарастыра
отырып туынды алып, одан соң нөлге теңестіреміз.
2. Алынған теңдеуден ![]() ті табамыз:
ті табамыз:
![]() (2)
(2)
түрінде анықталады.
Айқын емес функцияның екінші ретті
туындысын анықтау үшін ![]() теңдікті тағы да
дифференциалдаймыз
теңдікті тағы да
дифференциалдаймыз ![]() ті
ті
![]() ң
функциясы деп қарастыра отырып
ң
функциясы деп қарастыра отырып![]() , одан кейін теңдіктің оң
жағында пайда болған
, одан кейін теңдіктің оң
жағында пайда болған ![]() ті
ті ![]() -теңдіктің оң
жағындағы өрнекпен ауыстырамыз. Осы тәсілмен
жоғары ретті туындыларды анықтауға болады.
-теңдіктің оң
жағындағы өрнекпен ауыстырамыз. Осы тәсілмен
жоғары ретті туындыларды анықтауға болады.
1. Мысал - ![]() табу керек
табу керек ![]()
![]()
![]()
![]() .
.
2. Мысал - ![]()
![]() табу керек
табу керек ![]()
Шешуі. ![]()
![]()
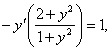
![]() .
.
Бұл теңдеуден ![]() ті табамыз:
ті табамыз:
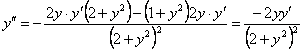 .
.
Соңғы өрнектегі ![]() ң орнына жоғарыда
анықталған оның мәнін қоямыз:
ң орнына жоғарыда
анықталған оның мәнін қоямыз:
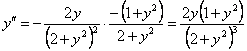 .
.
3. Мысал - ![]() эллипсі берілген.
эллипсі берілген.
Эллипстің бойында жататын 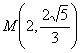 нүктесі арқылы
өтетін жанаманың теңдеуін жазу керек.
нүктесі арқылы
өтетін жанаманың теңдеуін жазу керек.
Шешуі: Эллипстің теңдеуін ![]() түрінде жазуға
болады.
түрінде жазуға
болады.
Бұл теңдеудің екі жағында
дифференциалдасақ: ![]()
бұдан ![]() .
.
Туындының 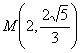 нүктесіндегі мәні,
эллипстің осы нүктесінен өтетін жанаманың
бұрыштық коэффициенті болады:
нүктесіндегі мәні,
эллипстің осы нүктесінен өтетін жанаманың
бұрыштық коэффициенті болады: ![]() . Сондықтан
. Сондықтан ![]() нүктесінен өтетін
жанаманың теңдеуі
нүктесінен өтетін
жанаманың теңдеуі ![]() бұдан
бұдан ![]()
148. ![]() табу
керек
табу
керек ![]()
149. ![]() н
табу керек.
н
табу керек.
150. ![]()
![]() н табу керек.
н табу керек.
151. ![]() түрінде
берілген
түрінде
берілген ![]() функциясының
функциясының
![]() нүктесіндегі
екінші ретті туындысының мәнін табу керек.
нүктесіндегі
екінші ретті туындысының мәнін табу керек.
152. ![]() параболасының
параболасының
![]() нүктесі
арқылы өтетін жанаманың теңдеуін жазу керек.
нүктесі
арқылы өтетін жанаманың теңдеуін жазу керек.
4.2 Параметрлік түрде берілген функциялар
Аргументі ![]() болатын
болатын ![]() функциясы
функциясы
![]()
![]() (3)
(3)
түрінде параметрлік қатынастар арқылы берілсін.
Мұндағы ![]() және
және
![]() функциялары
дифференциалданатын әрі
функциялары
дифференциалданатын әрі ![]() болсын. Бұл шарттар
орындалғанда
болсын. Бұл шарттар
орындалғанда
![]() .
(4)
.
(4)
![]() функциясынан
функциясынан ![]() айнымалысы бойынша екінші ретті туындыны
алу үшін,
айнымалысы бойынша екінші ретті туындыны
алу үшін, ![]() -қатынасты
-қатынасты
![]() бойынша
дифференциалдаймыз:
бойынша
дифференциалдаймыз:
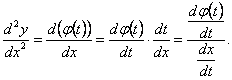 (5)
(5)
4. Мысал - ![]()
![]() берілсін. Табу керек
берілсін. Табу керек ![]() .
.
Шешуі: ![]()
![]() бұдан
бұдан ![]() .
.
Екінші ретті туындысын табамыз:
 .
.
![]()
Келесі есептерде ![]() табу керек:
табу керек:
153. ![]()
154. ![]()
155. ![]() .
.
Келесі есептерде ![]() табу керек:
табу керек:
156. ![]() 157.
157.
![]()
158. Жанамасы ![]() түзуіне
паралелль болатын
түзуіне
паралелль болатын ![]()
![]() сызығының
бойында жататын
сызығының
бойында жататын ![]() нүктесін
табу керек.
нүктесін
табу керек.
III-тарау. Дифференциалдық есептеуді қолдану
1 Орта мән туралы теоремалар
Бұл теоремалар кесіндінің шеткі нүктелеріндегі функцияның мәндерін оның ішкі “ортаңғы” нүктесіндегі функцияның туындысының мәнімен байланыстырады.
Ролль теоремасы. Егер ![]() функциясы:
функциясы:
1) ![]() кесіндісінде
үзіліссіз болса,
кесіндісінде
үзіліссіз болса,
2) ![]() аралығында
дифференциалданса,
аралығында
дифференциалданса,
3) ![]() болса,
онда
болса,
онда ![]() аралығында
жататын болмағанда бір
аралығында
жататын болмағанда бір ![]() нүктесі табылып, ол нүктеде
нүктесі табылып, ол нүктеде ![]()
Бұл теореманың геометриялық мағынасы: егер
функцияның графигі үзіліссіз қисық болып, оның
ішкі нүктелерінде жанама жүргізуге болса және
доғаның ұшын қосатын хорда ![]() өсіне параллель болса,
онда қисықтын бойында жататын болмағанда бір нүкте
табылып, сол нүкте арқылы жүргізілген жанама
өсіне параллель болса,
онда қисықтын бойында жататын болмағанда бір нүкте
табылып, сол нүкте арқылы жүргізілген жанама ![]() өсіне параллель
болады. (10 Сурет).
өсіне параллель
болады. (10 Сурет).
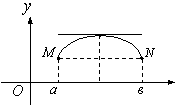 |
10 Сурет
Лагранж теоремасы. Егер ![]() функциясы:
функциясы:
1) ![]() кесіндісінде
үзіліссіз болса,
кесіндісінде
үзіліссіз болса,
2) ![]() аралығында дифференциалданса, онда
аралығында дифференциалданса, онда ![]() аралығында
жататын болмағанда бір
аралығында
жататын болмағанда бір ![]() нүктесі табылып, ол нүктеде
нүктесі табылып, ол нүктеде
![]()
![]() (1)
(1)
Бұл теореманың геометриялық мағынасы:
(1)-теңдеудің сол жағында ![]() хордасының
хордасының ![]() өсімен
жасайтын бұрыштың тангенсі, ал оң жағында бір
өсімен
жасайтын бұрыштың тангенсі, ал оң жағында бір ![]() нүктесінде
функцияның графигіне жүргізілген жанамамен
нүктесінде
функцияның графигіне жүргізілген жанамамен ![]() өсінің
арасындағы бұрыштың тангенсі тұр. Теорема
қисықтын тегіс доғасының бойында жататын нүкте
табылып, сол нүкте арқылы өтетін жанама, доғаны керіп
тұрған хордаға параллель болатындығын көрсетеді (11
Сурет)
өсінің
арасындағы бұрыштың тангенсі тұр. Теорема
қисықтын тегіс доғасының бойында жататын нүкте
табылып, сол нүкте арқылы өтетін жанама, доғаны керіп
тұрған хордаға параллель болатындығын көрсетеді (11
Сурет)
 |
11 Сурет
Жоғарыдағы Ролль теоремасы Лагранж теоремасының дербес жағдайы болады.
Коши теоремасы. Егер ![]() және
және ![]() функциялары:
функциялары:
1) ![]() кесіндісінде
үзіліссіз болса,
кесіндісінде
үзіліссіз болса,
2) ![]() аралығында дифференциалданса,
аралығында дифференциалданса,
3) ![]() аралығында
аралығында ![]() онда
онда ![]() аралығында жататын болмағанда бір
аралығында жататын болмағанда бір ![]() нүктесі
табылып, ол нүктеде
нүктесі
табылып, ол нүктеде
![]() (2)
(2)
1. Мысал - Ролль теоремасын пайдаланып, ![]() көпмүшелігі
үшін
көпмүшелігі
үшін ![]() интервалында
интервалында
![]() теңдеуінің
түбірі болатындығын дәлелдеу керек.
теңдеуінің
түбірі болатындығын дәлелдеу керек.
Шешуі: ![]() көпмүшелігі
көпмүшелігі ![]() нүктелерінде нөлге тең
болады. әрі
нүктелерінде нөлге тең
болады. әрі ![]() аралығында
дифференциалданатын функция. Сондықтан
аралығында
дифференциалданатын функция. Сондықтан ![]() және
және ![]() аралығында
аралығында ![]() функциясына Ролль теоремасын
қолдануға болады,
функциясына Ролль теоремасын
қолдануға болады,
![]() аралығында
жататын
аралығында
жататын ![]() ,
, ![]() аралығында
жататын
аралығында
жататын ![]() табылып,
табылып,
![]()
![]() кесіндісінде
кесіндісінде
![]() функциясына
Ролль теоремасын тағыда қолдануға болады. Сондықтан
функциясына
Ролль теоремасын тағыда қолдануға болады. Сондықтан ![]() аралығында
жататын
аралығында
жататын ![]() нүктесі
табылып
нүктесі
табылып ![]() .
.
2 Лопиталь ережесі
2.1 ![]()
![]() және
және ![]() түріндегі
анықталмағандықтар
түріндегі
анықталмағандықтар
Көп жағдайларда функцияның шектерін іздеу кезінде
аргументтердің шектік мәндерін қою нәтижесінде ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() түріндегі өрнектер аламыз.
Мұндай жағдайларда функцияның шегін анықтау анықталмағандықтарды
ашу деп аталады.
түріндегі өрнектер аламыз.
Мұндай жағдайларда функцияның шегін анықтау анықталмағандықтарды
ашу деп аталады.
Лопиталь ережесі деп аталатын келесі теорема анықталмағандықтарды ашудың негізгі жолы болып табылады.
Теорема. Егер ![]() және
және ![]() функциялары:
функциялары:
1) ![]() ұмтылғанда
ақырсыз кішкене немесе ақырсыз үлкен шамалар болса,
ұмтылғанда
ақырсыз кішкене немесе ақырсыз үлкен шамалар болса,
2) ![]() нүктесінің
төңірегінде дифференциалданса,
нүктесінің
төңірегінде дифференциалданса,
3) ![]() нүктесінің
төңірегінде,
нүктесінің
төңірегінде, ![]() нүктесін есептемегенде,
нүктесін есептемегенде, ![]() болса, және
болса, және
4) ![]()
шегі арқылы немесе ақырсыз болса, онда бұл функциялардың бөлінділерінің шектері олардың туындыларының бөлінділерінің шектеріне тең болады, яғни
![]() (1)
(1)
Бұл теорема біржақты шектерді анықтауда және ![]() ұмтылғанда
да қолданылады.
ұмтылғанда
да қолданылады.
Лопиталь ережесін пайдалана отырып келесі шектерді есептеу керек:
1. Мысал - 
2. Мысал - ![]()
3. Мысал - 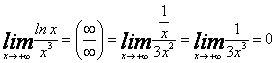
4. Мысал - ![]()
159. ![]() 160.
160. ![]()
161. ![]() 162.
162. ![]()
163.  164.
164. 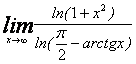
2.2 ![]() және
және ![]() түріндегі анықталмағандықтар
түріндегі анықталмағандықтар
Егер 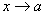 ұмтылғанда
ұмтылғанда 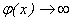 және
және 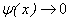 ұмтылса, онда
ұмтылса, онда 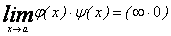 шегін тепе-тең
түрлендіру арқылы жоғарыдағы
шегін тепе-тең
түрлендіру арқылы жоғарыдағы 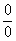 немесе
немесе 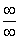 анықталмағандығына
алып келуге болады:
анықталмағандығына
алып келуге болады:
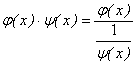 немесе
немесе 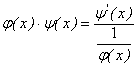
Егер ![]() ұмтылғанда
ұмтылғанда ![]() және
және
![]() ұмтылса,
онда
ұмтылса,
онда ![]() шегін
тепе-тең түрлендіру арқылы
шегін
тепе-тең түрлендіру арқылы ![]() анықталмағандығына алып
келуге болады:
анықталмағандығына алып
келуге болады:
![]() .
.
Кейбір жағдайларда басқа да түрлендірулерді қолдану ыңғайлы болады:
![]() немесе
немесе ![]()
Келесі есептердегі функциялардың шектерін есептеу керек:
1. Мысал - ![]()
2. Мысал - ![]()
165.  166.
166.
![]()
2.3 ![]() ,
, ![]() ,
, ![]() түріндегі анықталмағандықтар
түріндегі анықталмағандықтар
![]() түріндегі функциялардың
түріндегі функциялардың ![]() ұмтылғандағы
шегін табу кезінде:
ұмтылғандағы
шегін табу кезінде:
1) ![]()
![]() ;
;
2) ![]() ;
;
3) ![]() .
.
түріндегі анықталмағандықтарға тап боламыз.
Бұл анықталмағандықтарды ашу
үшін функцияларды түрлендіру арқылы ![]() түріндегі
анықталмағандыққа алып келеміз:
түріндегі
анықталмағандыққа алып келеміз:
![]()
Көрсеткіштік функцияның үзіліссіз болатындығын ескерсек
![]() (2)
(2)
Келесі есептердегі функциялардың шектерін табу керек:
1. Мысал - 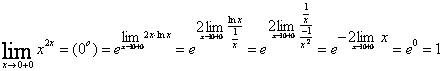
2. Мысал -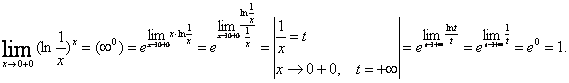
3. Мысал -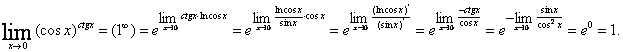
167. ![]() 168.
168. ![]()
169. ![]() 170.
170. ![]()
2.4 Шектерді есептеудің басқа тәсілдері
Лопиталь ережесі шектерді есептеудің күшті құралы болғанмен, ол шектерді есептеу тәсілдерін толық қамти алмайды.
1. Мысал - ![]()
Соңғы өрнектің ![]() ұмтылғанда
шегі болмайды. Яғни Лопиталь ережесінің 4-шарты орындалмайды.
ұмтылғанда
шегі болмайды. Яғни Лопиталь ережесінің 4-шарты орындалмайды.
Дегенмен берілген функцияның шегін анықтауға болады:
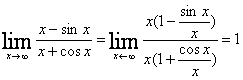
2. Мысал -
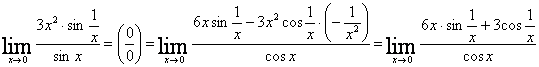
Соңғы өрнектің ![]() ұмтылғанда шегі болмайды.
ұмтылғанда шегі болмайды.
Дегенмен
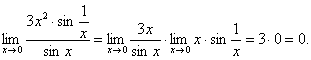
3. Туындыны функцияларды зерртеуде және графиктерін (сызбасын) салуда қолдану
3.1 Асимптоталар (шектемдер)
Функциялардың графиктерін салуда
қисықтардың асимптоталарының алатын орны
айырықша. ![]() түзуі
қисықтың тік асимптотасы деп аталады, егер
түзуі
қисықтың тік асимптотасы деп аталады, егер ![]() теңдіктерінің
біреуі орындалса,
теңдіктерінің
біреуі орындалса,
![]() түзуі
түзуі ![]() қисығының көлбеу
асимптотасы деп аталады, егер келесі шарттар орындалса:
қисығының көлбеу
асимптотасы деп аталады, егер келесі шарттар орындалса:
![]() (1)
(1)
![]() (2)
(2)
сәйкесінше
![]()
Көлбеу асимптотаның ![]() болғандағы дербес
жағдайы көлденең асимптота болады.
болғандағы дербес
жағдайы көлденең асимптота болады.
![]() түзуі
түзуі ![]() қисығының көлденең
асимптотасы деп аталады, егер келесі шарт орындалса:
қисығының көлденең
асимптотасы деп аталады, егер келесі шарт орындалса:
![]() ,
(3)
,
(3)
сәйкесінше
![]() .
.
Келесі есептерде қисықтардың асимптоталарының теңдеулерін табу керек:
1. Мысал - ![]()
Шешуі: ![]() түзуі берілген қисықтың тік асимптотасы болады,
себебі
түзуі берілген қисықтың тік асимптотасы болады,
себебі
![]()
Бұл қисықтың
көлденең асимптотасы ![]() , себебі
, себебі
![]()
2. Мысал - ![]()
Шешуі: ![]() функциясы
функциясы ![]() аралығында
анықталған және үзіліссіз болдады.
аралығында
анықталған және үзіліссіз болдады.
![]() болатындықтан
болатындықтан ![]() түзуі
қисықтың тік асимптотасы болады.
түзуі
қисықтың тік асимптотасы болады.
Енді қисықтың көлбеу ![]() асимптотасы болар-болмастығын
білу үшін
асимптотасы болар-болмастығын
білу үшін ![]() мен
мен
![]() -ны
анықтаймыз:
-ны
анықтаймыз:
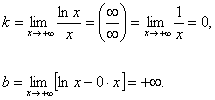
яғни ![]() қисығының
көлбеуде көлденеңде асимптотасы болмайды.
қисығының
көлбеуде көлденеңде асимптотасы болмайды.
3. Мысал - ![]()
Шешуі: Функция ![]() аралығында үзіліссіз
болатындықтан оның тік асимптотасы болмайды.
аралығында үзіліссіз
болатындықтан оның тік асимптотасы болмайды.
Қисықтын көлбеу асимптотасын табу
үшін ![]() мен
мен
![]() -ны
анықтаймыз:
-ны
анықтаймыз:
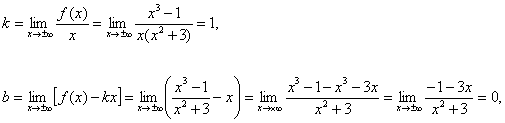
яғни ![]() көлбеу
асимптота болады.
көлбеу
асимптота болады.
171. ![]() 172.
172.
![]()
173. ![]() 174.
174.
![]()
175. ![]() 176.
176.
![]()
3.2 Функцияның бірсарындылық шарттары
![]() функциясы
функциясы ![]() аралығында бірсарынды өспелі
функция деп аталады, егер осы аралықта жататын кезкелген
аралығында бірсарынды өспелі
функция деп аталады, егер осы аралықта жататын кезкелген ![]() үшін
үшін
![]() (4)
(4)
![]() функциясы
функциясы ![]() аралығында бірсарынды кемімелі
функция деп аталады, егер осы аралықта жататын кезкелген
аралығында бірсарынды кемімелі
функция деп аталады, егер осы аралықта жататын кезкелген ![]() үшін
үшін
![]() (5)
(5)
![]() функциясы қатаң бірсарынды
өспелі (кемімелі) болады, егер (4), (5) шарттарында теңдік белгісі
болмаса.
функциясы қатаң бірсарынды
өспелі (кемімелі) болады, егер (4), (5) шарттарында теңдік белгісі
болмаса.
Дифференциалданатын ![]() функциясы
функциясы ![]() аралығында бірсарынды өспелі
болады, егер
аралығында бірсарынды өспелі
болады, егер ![]() үшін
үшін
![]() (6)
(6)
және бірсарынды кемімелі болады, егер ![]() үшін
үшін
![]() (7)
(7)
![]() болады,
тек барлық
болады,
тек барлық ![]() үшін
үшін
![]()
(6)-формуланың геометриялық мағынасы:
а) бірсарынды өспелі функцияның графигіне
жүргізілген жанама ![]()
![]()
![]() өсінің
оң бағытымен сүйір бұрыш жасайды немесе оған
параллель болады.
өсінің
оң бағытымен сүйір бұрыш жасайды немесе оған
параллель болады.
б) бірсарынды кемімелі функцияның графигіне
жүргізілген жанама ![]() өсінің оң бағытымен
доғал бұрыш жасайды немесе оған параллель болады.
өсінің оң бағытымен
доғал бұрыш жасайды немесе оған параллель болады.
![]() нүктесі
функцияның 1-текті күдікті нүктесі деп аталады, егер келесі
шарттардың біреуі орындалса:
нүктесі
функцияның 1-текті күдікті нүктесі деп аталады, егер келесі
шарттардың біреуі орындалса:
1) ![]()
2) ![]()
3) ![]() функциясы
функциясы ![]() нүктесінде анықталған
бірақ осы нүктеде оның туындысы болмаса.
нүктесінде анықталған
бірақ осы нүктеде оның туындысы болмаса.
Бұл шарттардың геометриялық мағынасы:
1-шарт орындалғанда күдікті нүктедегі жанама ![]() өсіне параллель
болады.
өсіне параллель
болады.
2-шарт орындалғанда күдікті нүктедегі жанама ![]() өсіне параллель
болады.
өсіне параллель
болады.
3-шарт орындалғанда күдікті нүктеде жанама болмайды (12 Сурет)
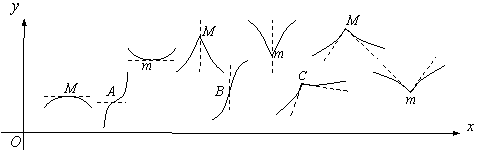 |
12 Сурет
Барлық нүктелерде (6) және (7)
теңсіздіктері орындалатын ![]() аралығы
аралығы ![]() функциясының бірсарынды
аралығы деп аталады. Бұл аралықтарды табу үшін сандар
өсіне функцияның анықталу облысының шекарасын
және күдікті нүктелерін саламыз. Бұл жағдайда
сандар өсі бірқатар сандық аралықтарға
бөлінеді. Бұл аралықтарда туындылардың таңбалары
өзгермейді, сондықтан олар бірсарынды аралықтар болады.
Бұл аралықтарда функциялардың өсетіндігін немесе
кемитіндігін білу үшін функцияның туындысының осы аралықта
жататын кезкелген нүктедегі мәнін білсек болғаны:егер
функциясының бірсарынды
аралығы деп аталады. Бұл аралықтарды табу үшін сандар
өсіне функцияның анықталу облысының шекарасын
және күдікті нүктелерін саламыз. Бұл жағдайда
сандар өсі бірқатар сандық аралықтарға
бөлінеді. Бұл аралықтарда туындылардың таңбалары
өзгермейді, сондықтан олар бірсарынды аралықтар болады.
Бұл аралықтарда функциялардың өсетіндігін немесе
кемитіндігін білу үшін функцияның туындысының осы аралықта
жататын кезкелген нүктедегі мәнін білсек болғаны:егер ![]() онда функция
өспелі; егер
онда функция
өспелі; егер ![]() ,
онда функция кемімелі болады.
,
онда функция кемімелі болады.
1. Мысал - ![]() функциясының бірсарынды
аралығын табу керек.
функциясының бірсарынды
аралығын табу керек.
Шешуі:
![]()
күдікті
нүктелер. Сондықтан сандар өсі ![]() аралықтарына бөлінеді. Бірінші
аралықта жататын кезкелген нүктені аламыз. Мысалы
аралықтарына бөлінеді. Бірінші
аралықта жататын кезкелген нүктені аламыз. Мысалы ![]() нүктесінде
нүктесінде ![]() , сондықтан
, сондықтан ![]() аралығында
функция кемімелі болады. Екінші аралықта жататын
аралығында
функция кемімелі болады. Екінші аралықта жататын ![]() нүктесінде
нүктесінде ![]() сондықтан
сондықтан ![]() аралығында
функция өспелі болады.
аралығында
функция өспелі болады.
Үшінші аралықта
жататын ![]() нүктесінде
нүктесінде![]() , сондықтан (0,1)
аралығында функция кемімелі болады. Төртінші аралықта жататын
, сондықтан (0,1)
аралығында функция кемімелі болады. Төртінші аралықта жататын
![]() нүктесінде
нүктесінде
![]() ,
сондықтан
,
сондықтан ![]() аралығында
функция өспелі болады.
аралығында
функция өспелі болады.
Келесі функциялардың бірсарынды аралықтарын табу керек:
177. ![]() 178.
178.
![]()
179. ![]() 180.
180.
![]()
3.3 Төңіректік (жергілікті) экстремум (шеттеме)
![]() функциясының
функциясының ![]() нүктесінде максимумы
(минимумы) бар болады, егер
нүктесінде максимумы
(минимумы) бар болады, егер ![]() маңайы табылып, оның
барлық нүктелерінде
маңайы табылып, оның
барлық нүктелерінде ![]()
![]() . Максимум (төбелік) немесе минимум
(табандық) нүктелері экстремум нүктесі деп аталады.
Функцияның максимумын
. Максимум (төбелік) немесе минимум
(табандық) нүктелері экстремум нүктесі деп аталады.
Функцияның максимумын ![]() арқылы, ал минимумын
арқылы, ал минимумын ![]() арқылы белгілеу
қабылданған. Үзіліссіз функциялар үшін экстремум
нүктелері тек күдікті нүктелерде ғана болады. 12
суреттен бұл шарттың жеткіліксіз екендігін көру қиын
емес.
арқылы белгілеу
қабылданған. Үзіліссіз функциялар үшін экстремум
нүктелері тек күдікті нүктелерде ғана болады. 12
суреттен бұл шарттың жеткіліксіз екендігін көру қиын
емес. ![]() нүктелерінде
сәйкесінше 1,2,3 шарттары орындалады, бірақ бұл
нүктелер максимумда, минимумда нүктелері емес.
нүктелерінде
сәйкесінше 1,2,3 шарттары орындалады, бірақ бұл
нүктелер максимумда, минимумда нүктелері емес.
Экстремумның бірінші жеткілікті шарты.
Егер функцияның туындысы күдікті нүктеден өткенде таңбасын өзгертсе, онда бұл нүкте функцияның экстремум нүктесі деп аталады.
Күдікті ![]() нүктесі максимум нүктесі
болады, егер
нүктесі максимум нүктесі
болады, егер ![]() үшін
үшін
![]() және
және ![]() .
.
Күдікті ![]() нүктесі минимум нүктесі
болады, егер
нүктесі минимум нүктесі
болады, егер ![]() үшін
үшін
![]() және
және ![]() .(13 сурет).
.(13 сурет).
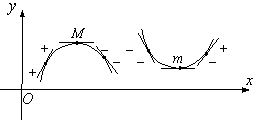 |
13 Сурет
Егер функцияның бірінші ретті туындысы күдікті нүктеден өткенде таңбасын өзгертпесе, онда бұл нүктеде функцияның экстремумы болмайды.
Егер ![]() күдікті нүктесінде
күдікті нүктесінде ![]() болса және осы
нүктеде функцияның жоғары ретті туындылары бар болса, онда
экстремум нүктесінің бар болуының басқа жеткілікті
шартын пайдалануға болады.
болса және осы
нүктеде функцияның жоғары ретті туындылары бар болса, онда
экстремум нүктесінің бар болуының басқа жеткілікті
шартын пайдалануға болады.
Экстремумның екінші жеткілікті шарты.
![]() күдікті нүктесі экстремум
нүктесі болады, егер осы нүктеде алғашқы ретті
жұп болатын туынды нөлге тең емес болса: егер бұл
туынды теріс болса, онда
күдікті нүктесі экстремум
нүктесі болады, егер осы нүктеде алғашқы ретті
жұп болатын туынды нөлге тең емес болса: егер бұл
туынды теріс болса, онда ![]() нүктесі максимум; егер туынды
оң болса, онда
нүктесі максимум; егер туынды
оң болса, онда ![]() нүктесі
минимум нүктесі болады. Мысалы,
нүктесі
минимум нүктесі болады. Мысалы, ![]() және
және ![]() болсын, бұл жағдайда
болсын, бұл жағдайда
егер ![]() болса, онда
болса, онда ![]() ;
;
егер ![]() болса, онда
болса, онда ![]()
1. Мысал - ![]() функциясының бірсарынды аралықтарын
және экстремальды мәндерін анықтау керек.
функциясының бірсарынды аралықтарын
және экстремальды мәндерін анықтау керек.
Шешуі: ![]() нүктелері күдікті нүктелер.
нүктелері күдікті нүктелер.
Бұл нүктелерге мінездеме беру үшін бірінші жеткілікті шартты пайдаланайық:
1 Кесте
|
|
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
|
|
-9 |
|
Сонымен, ![]() және
және ![]() аралықтарында функция өседі,
аралықтарында функция өседі, ![]() аралығында
кемиді.
аралығында
кемиді. ![]() нүктесі
максимум,
нүктесі
максимум, ![]() нүктесі
минимум нүктесі болады. Функцияның экстремальды мәндері: максимум
нүктесі
минимум нүктесі болады. Функцияның экстремальды мәндері: максимум
![]() минимум
минимум ![]()
2. Мысал - ![]() функциясының экстремум нүктелерін табу керек.
функциясының экстремум нүктелерін табу керек.
Шешуі: Функцияның анықталу аймағы ![]() болады. Күдікті
нүктелерін анықтаймыз:
болады. Күдікті
нүктелерін анықтаймыз:
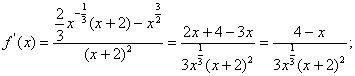
![]() егер
егер ![]() ;
; ![]() егер
егер ![]() және
және ![]() .
.
Сонымен ![]() және
және ![]() берілген функцияның күдікті
нүктелері болады, ал
берілген функцияның күдікті
нүктелері болады, ал ![]() нүктесі функцияның
анықталу аймағына кірмейтіндіктен күдікті нүкте
болмайды.
нүктесі функцияның
анықталу аймағына кірмейтіндіктен күдікті нүкте
болмайды. ![]() -ң
таңбаларының ауысуы туралы кесте құрамыз:
-ң
таңбаларының ауысуы туралы кесте құрамыз:
2 Кесте
|
|
|
|
|
|
|
|
|
|
|
- |
|
- |
|
+ |
0 |
- |
|
|
|
айм. жатп. |
|
|
|
|
|
Бұл мысалда, ![]() күдікті нүктесіне мінездеме
беру үшін, екінші жеткілікті шартты пайдалануға болмайды,
өйткені бұл нүктеде функция дифференциалданбайды.
күдікті нүктесіне мінездеме
беру үшін, екінші жеткілікті шартты пайдалануға болмайды,
өйткені бұл нүктеде функция дифференциалданбайды.
Келесі есептерде функцияның экстремум нүктелерін табу керек:
181. ![]() 182.
182.
![]()
183. ![]() 184.
184.
![]()
3.4 Кесіндідегі және аралықтағы функцияның экстремумы
Функцияның ![]() кесіндісіндегі ең үлкен
мәні
кесіндісіндегі ең үлкен
мәні ![]()
![]() , ең кіші
мәні
, ең кіші
мәні ![]()
![]() арқылы
белгілінеді.
арқылы
белгілінеді.
![]() кесіндісінде үзіліссіз болатын
функция әр уақытта өзінің ең үлкен
мәнін және ең кіші мәнін қабылдайды.
кесіндісінде үзіліссіз болатын
функция әр уақытта өзінің ең үлкен
мәнін және ең кіші мәнін қабылдайды.![]()
![]() анықтау үшін
функцияның
анықтау үшін
функцияның ![]() кесіндісіндегі
барлық максимумдарының мәндерін әрі кесіндісінің
шеткі
кесіндісіндегі
барлық максимумдарының мәндерін әрі кесіндісінің
шеткі ![]() және
және
![]() нүктелеріндегі
функцияның
нүктелеріндегі
функцияның ![]() мәндерін
есептеп, алынған мәндердің ең үлкенін алу керек
(14 сурет)
мәндерін
есептеп, алынған мәндердің ең үлкенін алу керек
(14 сурет)
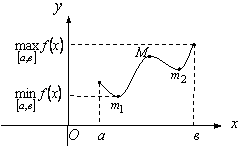 |
14 Сурет
![]()
![]() табу үшін
табу үшін ![]() кесіндісіндегі функцияның
барлық минимум мәндерін және
кесіндісіндегі функцияның
барлық минимум мәндерін және ![]() тауып олардың ең кішісін алу
керек (14 Сурет).
тауып олардың ең кішісін алу
керек (14 Сурет).
1. Мысал - ![]() функциясының
функциясының ![]() кесіндісіндегі ең
үлкен және ең кіші мәндерін табу керек.
кесіндісіндегі ең
үлкен және ең кіші мәндерін табу керек.
Шешуі:
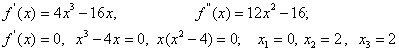
күдікті нүктелер. Бұл нүктелерде
![]()
сондықтан
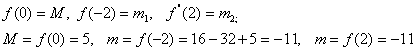
Кесіндінің шеткі нүктелеріндегі
мәндері ![]()
Сондықтан
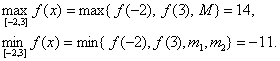
2. Мысал - Цилиндрлік тұрпатты ашық бакқа ![]() л сию керек.
Оған жұмсалатын материалдың мөлшері ең аз болу
үшін оның табанының радиусы мен биіктігі қандай болу керек?
л сию керек.
Оған жұмсалатын материалдың мөлшері ең аз болу
үшін оның табанының радиусы мен биіктігі қандай болу керек?
Шешуі: Ашық бакқа жұмсалатын
материалдың мөлшері ![]()
Оның көлемі ![]() болғандықтан
болғандықтан
![]()
Сондықтан
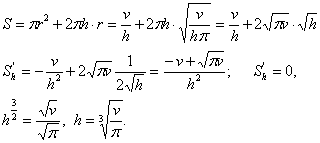
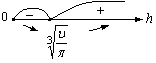
15 сурет
Ал 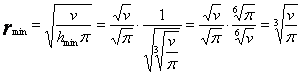 .
.
Сонымен ![]() .
.
3.
Мысал - ![]()
![]() болатын квадраттың картон парағының
болатын квадраттың картон парағының
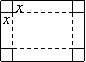 бұрыштарынан бірдей квадраттарды кесіп тастап,
парақты пунктирленген сызықтардың бойымен майыстыру
қажет. Нәтижесінде пайда болатын қораптың көлемі
ең үлкен болу үшін кесіп тасталатын квадраттың
қабырғасы неге тең болу керек (16 сурет)
бұрыштарынан бірдей квадраттарды кесіп тастап,
парақты пунктирленген сызықтардың бойымен майыстыру
қажет. Нәтижесінде пайда болатын қораптың көлемі
ең үлкен болу үшін кесіп тасталатын квадраттың
қабырғасы неге тең болу керек (16 сурет)
16 сурет
Шешуі: Кесіп тасталатын квадраттың
қабырғасын ![]() -деп белгілеп аламыз. Бұл
қораптың көлемі:
-деп белгілеп аламыз. Бұл
қораптың көлемі:
![]()
Сондықтан 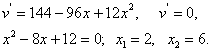
![]()
![]() болуы мүмкін
емес. Яғни
болуы мүмкін
емес. Яғни ![]() болғанда
болғанда ![]() өзінің
ең үлкен мәнін
өзінің
ең үлкен мәнін
қабылдайды.
17 сурет
Келесі есептерде функциялардың ең үлкен және ең кіші мәндерін табу керек.
185. ![]() кесіндісінде
кесіндісінде
![]()
186. ![]() кесіндісінде
кесіндісінде
![]()
187. ![]() аралығында
аралығында
![]()
188. 44 санын көбейтінділері ең үлкен санға тең болатындай екі оң саның қосындысы түрінде жазу керек.
189. Бүйір қабырғалары ![]() -ға тең,
ауданы ең үлкен болатын тең бүйірлі
үшбұрышты табу керек.
-ға тең,
ауданы ең үлкен болатын тең бүйірлі
үшбұрышты табу керек.
3.5 Иілу нүктелері
Тегіс қисық ![]() нүктесінде ойыс болады, егер осы
нүктенің
нүктесінде ойыс болады, егер осы
нүктенің ![]() маңайында
қисық осы нүкте арқылы жүргізілген жанамадан
жоғары жатса (18, а) Сурет); және
маңайында
қисық осы нүкте арқылы жүргізілген жанамадан
жоғары жатса (18, а) Сурет); және ![]() нүктесінде дөңес болады,
егер жанамадан төмен жатса (18, б) Сурет).
нүктесінде дөңес болады,
егер жанамадан төмен жатса (18, б) Сурет).
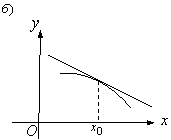 |
|||||
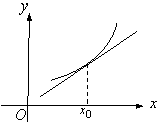 |
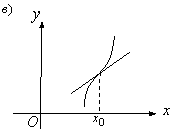 |
||||
18 Сурет
![]() нүктесі иілу нүктесі деп
аталады, егер осы нүкте арқылы жүргізілген жанама
нүктенің маңайында қисықты екі бөлікке
бөлсе (18, в) Сурет)
нүктесі иілу нүктесі деп
аталады, егер осы нүкте арқылы жүргізілген жанама
нүктенің маңайында қисықты екі бөлікке
бөлсе (18, в) Сурет)
Қисық ![]() аралығында ойыс (
аралығында ойыс (![]() белгіленеді) болады, егер осы
аралықтың әрбір нүктесінде
белгіленеді) болады, егер осы
аралықтың әрбір нүктесінде
![]() (8)
(8)
және ![]() аралығында
дөңес (
аралығында
дөңес (![]() белгіленеді) болады, егер осы аралықтың әрбір
нүктесінде
белгіленеді) болады, егер осы аралықтың әрбір
нүктесінде
![]() (9)
(9)
![]() нүктесі 2-текті күдікті
нүкте деп аталады, егер осы нүктеде келесі шарттардың біреуі
орындалса:
нүктесі 2-текті күдікті
нүкте деп аталады, егер осы нүктеде келесі шарттардың біреуі
орындалса:
1) ![]() 2)
2) ![]() 3)
3) ![]() нүктесінде функция
анықталғанмен
нүктесінде функция
анықталғанмен ![]() табылмаса.
табылмаса.
Функцияның иілу нүктесі бар болса ол тек 2-текті күдікті нүктелердің арасында болады. 2-текті күдікті нүктені басып өткенде функцияның екінші ретті туындысы таңбасын өзгертсе, онда ол нүкте қисықтың иілу нүктесі болады.
Сонымен ойыс және дөңес аралықтарды
анықтау үшін сандар өсіне функцияның анықталу
аймағының шекарасын және 2-текті күдікті
нүктелерін саламыз. Бұл жағдайларда сандар өсі
бірқатар сандық аралықтарға бөлінеді. Бұл
аралықтарда ![]() таңбалары
өзгермейді.
таңбалары
өзгермейді.
1. Мысал - ![]() функциясының иілу нүктелерін табу керек.
функциясының иілу нүктелерін табу керек.
Шешуі: Функция сандар өсінде анықталған әрі оның екінші ретті туындысы бар.
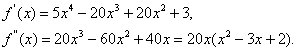
![]() функциясын
сызықтық көбейткіштерге жіктейміз:
функциясын
сызықтық көбейткіштерге жіктейміз:
![]()
Яғни ![]() нүктелері 2-текті күдікті
нүктелер болады.
нүктелері 2-текті күдікті
нүктелер болады. ![]() функциясының
таңбаларының өзгеру кестесін қарастырамыз:
функциясының
таңбаларының өзгеру кестесін қарастырамыз:
3 Кесте
|
х |
|
|
|
|
|
|
|
|
|
- |
0 |
+ |
0 |
- |
0 |
+ |
|
|
|
иілу нүктесі |
|
иілу нүктесі |
|
иілу нүктесі |
|
Бұл кестеден ![]() нүктелерінің иілу
нүктелері болатындығын көреміз.
нүктелерінің иілу
нүктелері болатындығын көреміз.
Келесі есептердегі функциялардың иілу нүктелерін табу керек:
190. ![]() 191.
191.
![]()
192. ![]() 193.
193.
![]()
4. Функцияның сызбасын салудың жалпы сүлбесі
Функцияның сызбасын салудың жалпы сүлбесін негізгі үш этапқа (кезеңге) бөлуге болады:
1)Функция сызбасына жалпы мінездемелік анықтама. Бұған функцияның анықталу аймағын анықтау; осы аймақтардағы шектік шекаралық мәндерді есептеу; егер бар болса, тік, көлбеу және көлденең асимптоталардың теңдеулерін табу; сызбаның координата өстерімен қилысу нүктелерін табу; функцияның тақтығын, жұптығын және периодтылығын анықтау жатады. Ендігі жерде өткізілген зерттеулерге сай функцияның жуық сызбасын салу.
2) бірінші ретті туындыны пайдалана отырып функция сызбасына нақты анықталған өзгерістер енгізу (функцияның экстремумдарын тауып, өспелі және кемімелі болатын аралықтарын анықтаймыз).
3) екінші ретті туындыны пайдалана отырып функция сызбасына өзгерістер енгізу (функцияның ойыс, дөңес болатын аралықтарын, иілу нүктелерін табу).
1. Мысал - ![]() функциясының сызбасын салу креек.
функциясының сызбасын салу креек.
Шешуі: 1. Функцияның анықталу аймағы ![]() . Шектік
шекаралық мәндерін табамыз:
. Шектік
шекаралық мәндерін табамыз:
![]()
Соңғы шек, ![]() ұмтылғанда функцияның
көлденең асимптотасы
ұмтылғанда функцияның
көлденең асимптотасы ![]() болатындығын көрсетеді.
болатындығын көрсетеді.
Көлбеу асимптота ![]() формуласымен (кейіптемесімен)
анықталады:
формуласымен (кейіптемесімен)
анықталады:
![]()
яғни көлбеу асимптота болмайды.
Сызбаның координат өстерімен қиылысу нүктесін табамыз:
![]()
яғни сызба координаттың бас нүктесі арқылы өтеді.
Функциямыз тақта, жұпта, периодты да болмайды.
Жүргізілген зерттеудің нәтижесінде функцияның толық сызбасын құру мүмкін емес. Дегенмен оның жуық сызбасын салуға болады (19 сурет).
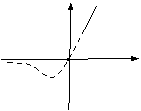 |
19 Сурет
2. Берілген функцияның туындысын табамыз:
![]()
![]() деп алып,
деп алып, ![]() нүктесінің 1-ретті
күдікті болатындығын анықтаймыз. Бұл нүкте
анықталу аймағын
нүктесінің 1-ретті
күдікті болатындығын анықтаймыз. Бұл нүкте
анықталу аймағын ![]() аралықтарына бөледі.
аралықтарына бөледі.
![]() , ал
, ал ![]() болғандықтан
болғандықтан ![]() нүктесі минимум
нүктесі болады. Сондықтан
нүктесі минимум
нүктесі болады. Сондықтан ![]()
Бұл зерттеудің нәтижесінде 20 суреттегі сызбаға қосымша анықтаулар енгізілді.
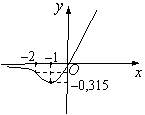 |
20 сурет
3. ![]() функциясын анықтаймыз:
функциясын анықтаймыз:
![]() .
.
![]() деп алып,
деп алып, ![]() нүктесінің 2-текті
күдікті нүкте болатындығын көреміз.
нүктесінің 2-текті
күдікті нүкте болатындығын көреміз.
Бұл нүкте анықталу аймағын ![]() аралықтарына
бөледі.
аралықтарына
бөледі.
![]() ал
ал ![]() болғандықтан,
болғандықтан, ![]() аралығында сызба
дөңес, ал
аралығында сызба
дөңес, ал ![]() аралығында сызба ойыс, яғни
аралығында сызба ойыс, яғни ![]() нүктесі иілу
нүктесі болады.
нүктесі иілу
нүктесі болады.
Бұл зерттеудің нәтижесінде 20 суреттегі сызбаға қосымша анықтаулар енгізіп, берілген функцияның сызбасын анықтадық.
2. Мысал - ![]() функциясының сызбасын салу
керек.
функциясының сызбасын салу
керек.
Шешуі: 1. функцияның анықталу аймағы ![]() болады, себебі
болады, себебі
![]()
яғни ![]() тік асимптота. Көлбеу асимптота
тік асимптота. Көлбеу асимптота ![]() формуласымен
анықталады:
формуласымен
анықталады:

сондықтан ![]() көлденең асимптота болады.
көлденең асимптота болады.
Функцияның шектік шекаралық мәндерін табамыз:
![]()
Сызбаның координат өстерімен қиылысу нүктесін анықтаймыз:
![]()
яғни сызба ![]() өсін 1 нүктесі арқылы,
ал
өсін 1 нүктесі арқылы,
ал ![]() өсін
-2 нүктесі арқылы қиып өтеді.
өсін
-2 нүктесі арқылы қиып өтеді.
Функциямыз тақта, жұпта әрі периодты да емес.
 Жүргізілген
зерттеулердің нәтижесінде функцияның жуық сызбасын
салуға болады (21 Сурет).
Жүргізілген
зерттеулердің нәтижесінде функцияның жуық сызбасын
салуға болады (21 Сурет).
21 Сурет
2. Берілген функцияның туындысын табамыз:
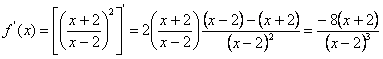
![]() деп алып,
деп алып, ![]() нүктесінің 1-ретті
күдікті нүкте болатындығын көреміз.
нүктесінің 1-ретті
күдікті нүкте болатындығын көреміз.
4 Кесте
|
|
|
|
|
|
|
|
|
- |
0 |
+ |
|
- |
|
|
|
|
|
анықталмаған |
|
3. ![]() функциясын анықтаймыз:
функциясын анықтаймыз:

![]() деп
алып,
деп
алып, ![]() нүктесінің
2-текті күдікті нүкте болатындығын көреміз. Яғни
нүктесінің
2-текті күдікті нүкте болатындығын көреміз. Яғни
5 Кесте
|
|
|
|
|
|
|
|
|
- |
0 |
+ |
|
+ |
|
|
|
иілу нүктесі |
|
анықталмаған |
|
2-ші және 3- кезеңдегі зерттеудің нәтижесінде 21 Суреттегі сызбаға қосымша анықтаулар енгізіп, берілген функцияның сызбасын анықтадық.
Келесі функциялардың сызбасын құру керек:
194. ![]() 195.
195.
![]()
196. ![]() 197.
197.
![]()
5. Геометриялық қолданылуы
5.1 Жазық қисықтың имектігі
Қисықтың имектігі деп оның
түзу сызықтан ауытқуын айтады. Қисықтың ![]() нүктесіндегі
имектігі
нүктесіндегі
имектігі ![]() «сыбайлас
бұрыштың», яғни
«сыбайлас
бұрыштың», яғни ![]() және
және ![]() нүктелеріне жүргізілген
жанамалардың арасындағы бұрыштың
нүктелеріне жүргізілген
жанамалардың арасындағы бұрыштың ![]() доғасының
ұзындығына қатынасының,
доғасының
ұзындығына қатынасының, ![]() -ғы шегін айтады (22 Сурет),
-ғы шегін айтады (22 Сурет), ![]()
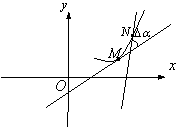 |
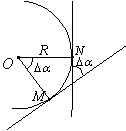 |
||
22 Сурет 23 Сурет
яғни
![]() (1)
(1)
![]() теңдеуімен берілген
қисықтың имектілігі
теңдеуімен берілген
қисықтың имектілігі
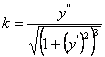 (2)
(2)
формуласымен (кейіптемесімен) анықталады.
Параметрлік ![]() теңдеуімен берілген
қисықтың имектілігі
теңдеуімен берілген
қисықтың имектілігі
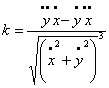 (3)
(3)
кейіптемесімен анықталады.
1. Мысал - Радиусы (өрісі) ![]() -ге тең шеңбердің
имектігін анықтау керек.
-ге тең шеңбердің
имектігін анықтау керек.
Шешу: (1)-формуланы қолданамыз. 23 Суреттен
көрініп тұрғандай, сыбайлас ![]() бұрышы шеңбердің
орталық
бұрышы шеңбердің
орталық ![]() бұрышына
тең. Осы бұрышқа сәйкес келетін
бұрышына
тең. Осы бұрышқа сәйкес келетін ![]() доғасының
ұзындығы
доғасының
ұзындығы
![]()
Сондықтан
![]()
Бұдан шеңбердің имектілігі оның радиусына кері пропорционал болатын, тұрақты шамаға тең болатындығын көруге болады.
2. Мысал - ![]() қисығының
қисығының ![]() нүктесіндегі
имектігін табу керек.
нүктесіндегі
имектігін табу керек.
Шешуі: (2)-формуланы қолданамыз.![]() және
және ![]() табамыз:
табамыз:

198. ![]() қисығының
қисығының ![]() нүктесіндегі
имектігін табу керек.
нүктесіндегі
имектігін табу керек.
199. ![]() эллипсінің ең үлкен және
ең кіші имекті нүктелерін табу керек.
эллипсінің ең үлкен және
ең кіші имекті нүктелерін табу керек.
5.2 Қисықтың өресі
Жоғарыдағы 1-мысалда,
шеңбердің өресі оның имектілігіне кері пропорционал
болатындығы көрсетілді. Осыған ұқсас кез келген
қисық үшін қисықтың өресі ![]() туралы
түсініктеме енгізілді:
туралы
түсініктеме енгізілді:
![]() (4)
(4)
мұндағы ![]() қисықтың имектілігі.
қисықтың имектілігі.
1. Мысал - ![]() қисығының
қисығының ![]() нүктесіндегі
өресін табу керек.
нүктесіндегі
өресін табу керек.
Шешуі: Берілген қисықтың имектілігі
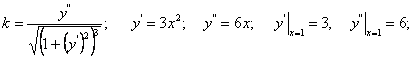
Яғни ![]()
Бұдан қисықтын өресі
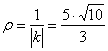
200. ![]() қисығының
қисығының
![]() нүктесіндегі
өресін табу керек.
нүктесіндегі
өресін табу керек.
201. ![]() параболасының
параболасының
![]() нүктесіндегі
өресін табу керек.
нүктесіндегі
өресін табу керек.
5.3 Қисықтың кіндігі және дөңгелегі.
Эволюта және эвольвента (жайылма және жайылғыш)
Қисықтың ![]() нүктесіндегі
дөңгелегі деп қисықтың
нүктесіндегі
дөңгелегі деп қисықтың ![]() нүктесі және
оған жақын орналасқан
нүктесі және
оған жақын орналасқан ![]() және
және ![]() нүктелері арқылы өтетін
дөңгелектің
нүктелері арқылы өтетін
дөңгелектің ![]() және
және ![]() ұмтылғандағы
шектік орнын айтады (24 Сурет)
ұмтылғандағы
шектік орнын айтады (24 Сурет)
Дөңгелектің
қисықтық өресі нүктенің
қисықтық өресіне тең.
Дөңгелектің қисықтық кіндігі С
қисықтың ![]() нүктесінің
қисықтық
кіндігі деп аталады
нүктесінің
қисықтық
кіндігі деп аталады
.
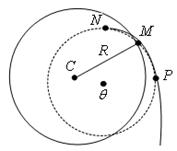
24 Сурет
![]() теңдеуімен берілген
қисықтың имектілігінің кіндігінің координаталары
теңдеуімен берілген
қисықтың имектілігінің кіндігінің координаталары
![]() (5)
(5)
формулаларыменмен анықталады.
![]() параметрлік теңдеуімен берілген
қисықтың имектілігінің кіндігінің координаталары
параметрлік теңдеуімен берілген
қисықтың имектілігінің кіндігінің координаталары
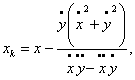
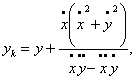 (6)
(6)
формулаларымен анықталады.
Қисықтың имектілігінің кіндіктерінің геометриялық орны оның эволютасы (жайылымы) деп аталады. Берілген қисық эволютасы болатын қисық оның эвольвентасы (жайылғышы) деп аталады.
1. Мысал - ![]() қисығының
қисығының ![]() нүктесіндегі
имектілік кіндігін табу керек.
нүктесіндегі
имектілік кіндігін табу керек.
Шешуі: (6)-формулаларды пайдаланамыз.
![]()
Бұл туындылардың ![]() нүктесіндегі
мәндері керек, яғни
нүктесіндегі
мәндері керек, яғни ![]() болғанда:
болғанда:
![]()
Табылған мәндерді (6)-формулаға қойсақ
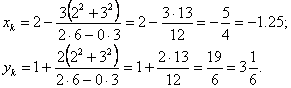
202. ![]() қисығының
қисығының
![]() нүктесіндегі
имектілік кіндігін табу керек.
нүктесіндегі
имектілік кіндігін табу керек.
203. ![]() қисығының
қисығының ![]() нүктесіндегі имектілік
кіндігінің координаталарын табу керек.
нүктесіндегі имектілік
кіндігінің координаталарын табу керек.
Жауаптары
1.![]() 2.
2.![]()
3. ![]()
4. ![]() . 5.
. 5. ![]() . 6.
. 6.![]() . 7.
. 7. ![]() 8.
8. ![]()
мүндағы ![]() 9.
9. ![]() 10.
10. ![]()
13. а) жұп, б) тақ, тақ емес в) жұп, г) тақта , , жұпта емес, д) тақ .
14)
а) Периодты, ![]() б)
Периодты,
б)
Периодты, ![]() в)
Периодты,
в)
Периодты, ![]() г)
Периодты емес
г)
Периодты емес
15. ![]() 16.
16. ![]() 21.
21. ![]() 22.
22. ![]() 23.
23. ![]() 24. 0 25.
0. 26. 1 31.
24. 0 25.
0. 26. 1 31. ![]() 32.
32. ![]() 33. 1. 34.
33. 1. 34.![]() 35. 0.
36. 0. 37. 8. 38. -1. 39. 2,5. 40.
-0,5. 41. 1. 42. 4. 43. 0. 44. 3. 45.
1,5. 46. 0,5. 47. 0. 48. 0,25 49. 2. 50.
0. 51.
35. 0.
36. 0. 37. 8. 38. -1. 39. 2,5. 40.
-0,5. 41. 1. 42. 4. 43. 0. 44. 3. 45.
1,5. 46. 0,5. 47. 0. 48. 0,25 49. 2. 50.
0. 51. ![]() 52.
52.
![]() . 53.
1. 54.
. 53.
1. 54. ![]() 55.
55.
![]() 60.
60.
![]() 61.
61. ![]()
![]() 62. 0,5. 63.
0,6 64. 2. 65.0 66. 3. 67.
62. 0,5. 63.
0,6 64. 2. 65.0 66. 3. 67. ![]() 68. 2. 69.
-2. 70. -1,5. 71. 0. 72. 9. 73. 1.
74. -0,5. 75.
68. 2. 69.
-2. 70. -1,5. 71. 0. 72. 9. 73. 1.
74. -0,5. 75. ![]() 76. 1. 77. 1.
78.
76. 1. 77. 1.
78. ![]() екінші
текті үзіліс нүктесі. 79.
екінші
текті үзіліс нүктесі. 79. ![]() нүктесі бірінші текті үздік
нүкте:
нүктесі бірінші текті үздік
нүкте: ![]() 80.
80.
![]() нүктесі
бірінші текті үзік нүкте:
нүктесі
бірінші текті үзік нүкте: ![]() 81.
81. ![]() нүктесі жөнделетін
үзік:
нүктесі жөнделетін
үзік: ![]() 82.
82.
![]() 83.
83.
![]() 84.
Жанама
84.
Жанама ![]() тектеме
тектеме
![]() 85.
85.
![]() 86.
86.
![]() 87.
87. ![]() 88.
88. ![]() 89.
89. ![]() . 90.
. 90. ![]() 91.
91. ![]() 92.
92. ![]() . 93.
. 93. ![]() 94.
94. ![]() . 95.
. 95. ![]() .
.
96. ![]() 97.
97. ![]() 98.
98. ![]() 99.
-
99.
-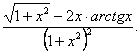 100.
100.
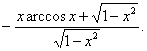 101.
101.
![]() 102.
102.
![]() 103.
103.
![]() 104.
104.
![]() 105.
105.
![]() 106.
106.
 107.
107.
![]() 108.
108.
![]() 109.
109.
![]() 110.
110. ![]() 111.
111. ![]() 112.
112.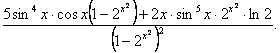 113
113![]() 114.
114.
![]()
115.
![]() 116.
116.
![]() 117.
117.
![]() 118.
118.![]() .
.
119.
![]() 120.
120.
![]()
121.
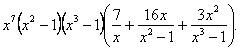 122.
122.
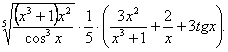
123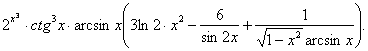 124
124![]() 125.
125.![]() 126.
126.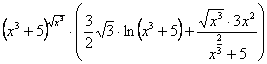
127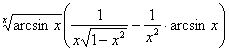 . 128.
. 128.
![]()
129.
![]() . 130.
. 130.
![]() 131.
131.
![]() 132.
132.
![]() 133.
133.
![]() 134.
134.
![]() 135.
135.
![]() 136.
136.
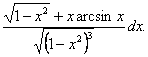 137.
137.
![]()
138. ![]() 139.
139. ![]() 140.
140. ![]() 141.
141. ![]()
142.
![]() 143.
143.
![]() 144.
144.
![]() 145.
145.
![]() .
.
146.
![]() 147.
147.
![]() 148.
148.
![]() 149.
149.
![]() 150.
150.
![]() 151.
151.
![]() 152.
152.
![]() 153.
153.
![]() 154.
154.
![]() 155.
155.
![]() . 156.
. 156.
![]() 157.
157.
![]() 158.
158.
![]() болғанда,
болғанда,
![]() . 159.
. 159.
![]() 160.
160.
![]() 161.
161.
![]()
162.
![]() 163.
163.
![]() 164.
-2. 165. -1. 166.
164.
-2. 165. -1. 166. ![]() 167. 1. 168. 1. 169.
167. 1. 168. 1. 169.
![]()
170.
![]() . 171.
. 171.
![]()
![]() тік асимптота,
тік асимптота, ![]() көлбеу
асимптота.
көлбеу
асимптота.
172.
![]() 173.
173.
![]() тік
асимптота,
тік
асимптота, ![]() көлбеу
асимптота. 174.
көлбеу
асимптота. 174. ![]() ,
, ![]() көлбеу асимптота,
көлбеу асимптота, ![]() тік асимптота. 175.
тік асимптота. 175.
![]() көлденең
асимптота. 176.
көлденең
асимптота. 176. ![]() тік асимптота. 177.
тік асимптота. 177. ![]() аралығында
өспелі. 178.
аралығында
өспелі. 178. ![]()
![]() аралығында өспелі. 179.
аралығында өспелі. 179.
![]() аралығында
кемімелі,
аралығында
кемімелі, ![]() аралығында
өспелі.
аралығында
өспелі.
180.
![]() аралығында
кемімелі,
аралығында
кемімелі, ![]() аралығында
өспелі. 181. жоқ.
аралығында
өспелі. 181. жоқ.
182.
![]() 183.
183.
![]() 184.
184.
![]()
185.
![]()
![]() 186.
186. ![]() 187.
187. ![]() 188. 22+22.
189.
188. 22+22.
189. ![]() 190.
190. ![]() .
.
191.
![]() 192.
192.
![]() 193.
193.
![]()
194.
![]() иілу
нүктелері.
иілу
нүктелері.
195.
Асимптоталары: ![]() иілу
нүктелері жоқ.
иілу
нүктелері жоқ.
196.![]() ;
;![]() және
және ![]()
иілу нүктелері: ![]() 197.
197. ![]() жұп функция;
асимптоталары:
жұп функция;
асимптоталары: ![]() және
және
![]() иілу
нүктелері жоқ. 198.
иілу
нүктелері жоқ. 198. ![]()
199.
![]() -эллипстің
төбелері. 200.
-эллипстің
төбелері. 200. ![]() 201.
201. ![]()
202.
![]()
![]() 203.
203. ![]()
Јдебиеттер тізімі
1. Мустахишев К.М., Ералиев С.Е., Атабай Б.Ж., Математика (толық курс). -Алматы.: «TST-company», 2009.
2. Аяпбергенов С.А. Аналитикалық геометрия. -Алматы: Мектеп, 1971.
3. Касымов Қ.Ә., Касымов Е.Ә. Жоғары математика курсы Сызықты алгебра. -Алматы: «Санат», 1997.
4. Г.И. Кручкович, и др., Сборник задач по курсу высшей математики. -М: Высшая школа, 1973.
5. Клетеник Д.В. Сборник задач по аналитической геометрии.- М: Наука, 1967.
6. Минорский В.П. Сборник задач по высшей математике. -М.: Наука, 1987.
7. Пискунов Н.С. Дифференциальное и интегральное исчисления. –М.: Наука, 1978.
8. Задачи и упражнения по математическому анализу для ВТУЗов под.ред. Б.П. Демидовича. -М.: Наука, 1977.
9. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. -М.: Высшая школа, 1980.
10. Берман. Г.Н. Сборник задач по курсу математического анализа. -М.: Наука, 1977.
11. Мустахишев К. М., Ералиев С. Е., Атабай Б. Ж., Математика (полный курс). – Алматы.: «TST-company», 2009.
Мазмұны
Iтарау.Талдауға кіріспе..................................................................................3
1 Функциялар. (Бернелер).............................................................................3
1.1Анықтамасы................................................................................................3
1.2 Негізгі элементар функциялар (Қарапайым бернелер).........................4
2. Сандық тізбектер және оның шектері ......................................................6
2.1 Анықтамасы...............................................................................................6
2.2 Шектері......................................................................................................7
3. Функцияның шегі........................................................................................9
3.1 Функцияның шегінің анықтамасы...........................................................9
3.2 Ақырсыз аз және ақырсызүлкен функциялар.......................................10
4 Шектерді есептеу.......................................................................................10
4.1 Негізгі теоремаларды (түйіндерді) қолдану..........................................10
4.2 Анықталмағандықтарды ашу.................................................................12
4.3 Бірінші және екінші тамаша шек...........................................................13
5 Ақырсыз аз функцияларды салыстыру. Эквиваленттілік (баламалық) .........14
5.1 Ақырсыз кішкене шамаларды салыстыру.............................................14
5.2 Эквивалентті ақырсыз аз шамаларды шектерді есептеуде қолдану ..17
6 Функцияның үзіліссіздігі. Үзіліс нүктелері және оларды
классификациялау.........................................................................................19
6.1 Анықтамасы.............................................................................................19
6.2 Үзіліссіз функциялардың қасиеттері.....................................................20
II-тарау. Туынды және дифференциал.......................................................22
1 Функциялардың туындылары..................................................................22
1.1 Анықтамасы.............................................................................................22
1.2 Туындының геометриялық және механикалық мағынасы..................23
1.3 Дифференциалдаудың негізгі ережелері...............................................25
1.4 Негізгі элементар функциялардың туындылары..................................25
1.5 Логарифимдік дифференциалдау..........................................................27
2 Дифференциал және оның қолданылуы.................................................28
2.1Анықтамасы..............................................................................................28
2.2 Дифференциалды жуықтап есептеуде қолдану....................................30
3 Жоғары ретті туындылар мен дифференциалдар...................................30
3.1 Жоғары ретті туындылар........................................................................30
3.2 Жоғары ретті дифференциалдар............................................................30
4 Айқын емес және параметрлік түрде берілген функциялардың
туындлары......................................................................................................32
4.1 Айқын емес функциялар.........................................................................32
4.2 Параметрлік түрде берілген функциялар..............................................33
III-тарау. Дифференциалдық есептеуді қолдану........................................34
1 Орта мән туралы теоремалар....................................................................34
2 Лопиталь ережесі......................................................................................36
2.1 ![]() және
және ![]() түріндегі
анықталмағандықтар...........................................36
түріндегі
анықталмағандықтар...........................................36
2.2 ![]() және
және ![]() түріндегі анықталмағандықтар..................................37
түріндегі анықталмағандықтар..................................37
2.3 ![]() ,
, ![]() ,
, ![]() түріндегі
анықталмағандықтар............................................38
түріндегі
анықталмағандықтар............................................38
2.4 Шектерді есептеудің басқа тәсілдері....................................................39
3 Туындыны функцияларды зерттеуде және графиктерін (сызбасын)
салуда қолдану..............................................................................................40
3.1 Асимптоталар...........................................................................................40
3.2 Функцияның бірсарындылық шарттары...............................................42
3.3 Төңіректік (жергілікті) экстремум (шеттеме).......................................44
3.4 Кесіндідегі және аралықтағы функцияның экстремумы.....................46
3.5 Иілу нүктелері..........................................................................................48
4 Функцияның сызбасын салудың жалпы сүлбесі....................................50
5 Геометриялық қолданылуы......................................................................53
5.1 Жазық қисықтың имектігі................................................................... ..53
5.2 Қисықтың өресі........................................................................................55
5.3 Қисықтың кіндігі және дөңгелегі. Эволюта және эвалвента
(жайылма және жайылғыш).........................................................................56
Жауаптары......................................................................................................58
Әдебиеттер тізімі...........................................................................................61