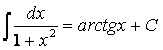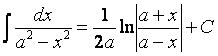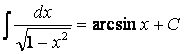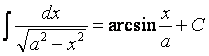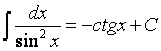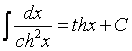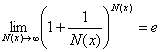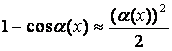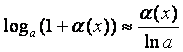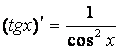АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ
Математический анализ
Конспект лекций
для студентов всех форм обучения специальностей
5В0704 – Вычислительная техника и программное обеспечение и
5В0703 – Информационные системы
Алматы 2010
СОСТАВИТЕЛЬ: Р.Е. Ким. Математический анализ. Конспект лекций для студентов всех форм обучения специальностей 5В0704 – Вычислительная техника и программное обеспечение и 5В0703 – Информационные системы. -Алматы: АИЭС, 2010.- 60 с.
Настоящий конспект содержит 12 лекций по основным разделам, традиционно изучаемым в курсе математического анализа: «Введение в анализ. Дифференциальное исчисление функции одной переменной», «Функции нескольких переменных. Интегральное исчисление функции одной и нескольких переменных», «Дифференциальные уравнения. Ряды».
Конспект лекций предназначен для студентов всех форм обучения специальностей 5В0704 – вычислительная техника и программное обеспечение и 5В0703 – информационные системы.
Предисловие
Настоящий конспект содержит 12 лекций по основным разделам, традиционно изучаемым в курсе математического анализа: «Введение в анализ. Дифференциальное исчисление функции одной переменной», «Функции нескольких переменных. Интегральное исчисление функции одной и нескольких переменных», «Дифференциальные уравнения. Ряды» и соответствует учебному плану второго семестра бакалавриата всех форм обучения специальностей 5В0704 – вычислительная техника и программное обеспечение и 5В0703 – информационные системы. Содержание разделов взаимосвязано друг с другом. В доступной форме изложены основные теоретические сведения, приведены примеры, помогающие усвоить и закрепить изучаемый материал.
Конспект лекций будет полезен преподавателям и студентам и предназначен для проведения самостоятельных работ во время аудиторных занятий по курсу математического анализа.
Значком ◙ отмечены определения математических понятий.
1 Введение в анализ. Дифференциальное исчисление функции одной переменной
1.1 Лекция 1. Функция. Числовая последовательность. Пределы
Содержание лекции: Понятие функции. Способы задания, свойства, классификация функций. Числовые последовательности. Предел числовой последовательности. Предел функции. Теоремы о пределах. Односторонние пределы. Первый и второй замечательные пределы.
Цели лекции: знакомство с основными понятиями математического анализа.
◙ Переменной величиной называется всякая величина х, способная принимать различные числовые значения.
Величина, численные значения которой не меняются, называется постоянной величиной.
◙ Переменная величина у называется функцией независимой переменной х, если любому определенному значению х (из множества возможных значений) соответствует единственное определенное значение у.
Обозначение: у = f (х).
Переменная х называется при этом аргументом или независимой переменной, у называют зависимой переменной.
◙ Совокупность значений х, для которых определяются значения функции у в силу правила f (х), называют областью определения функции (обозначают D(y)), а совокупность всевозможных значений функции у в силу правила f (х), называют областью изменения функции (обозначают E(y)).
Способы задания функции:
1) аналитический (формулой);
2) табличный;
3) графический;
◙ Графиком называется совокупность точек (х, f (х)) плоскости (хОу), абсциссы которых являются значениями независимой переменной, а ординаты – соответствующими значениями функции.
4) словесный.
Основные свойства функций:
1) четность;
◙ Функция у = f (х) называется четной, если f (– х) = f (х) " хÎD(у)
(график функции симметричен относительно оси ординат).
2) нечетность;
◙ Функция у = f (х) называется нечетной, если f (– х) = – f (х) " хÎD(у)
(график функции симметричен относительно начала координат).
3) монотонность;
◙ Если функция у = f (х) такова, что большему значению аргумента х соответствует большее (меньшее) значение функции, то функция у = f (х) называется возрастающей (убывающей).
◙ Функция у = f (х) называется монотонной, если она является либо возрастающей, либо убывающей.
4) ограниченность;
◙ Функция у = f (х) называется ограниченной в данной области D (в области изменения аргумента х), если $ М > 0: | f (х)| ≤ М " хÎD.
Если же такого М не существует, то функция у = f (х) называется неограниченной в данной области.
5) периодичность;
◙ Функция у = f (х) называется периодической, если
$ С > 0: f (х + С) = f (х) " хÎD(у).
Наименьшее такое число называется периодом функции.
Основные виды функций:
1) Явная и неявная функции.
◙ Функция задана явно, если она определена уравнением у = f (х); функция задана неявно, если она определена уравнением F(x, y) = 0.
2) Обратная функция.
Если между значениями x и соответствующими им значениями y = f (х) устанавливается взаимно однозначное соответствие, то, рассматривая эти значения y как значения аргумента, а значения х как значения функции, получаем х как функцию у: х = φ(y). Эта функция называется обратной для функции у = f (х). Очевидно, что и функция у = f (х) является обратной для функции х = φ(y).
3) Сложная функция (суперпозиция, композиция, функция от функции).
Если у является функцией от и, а и в свою очередь зависит от переменной х, то у также зависит от х, т.е. если у = F(и), и = φ(х),
то у = F [φ(х)]. Последняя функция называется функцией от функции или сложной функцией или суперпозицией или композицией.
Числовая последовательность
Если функция у = f (х) определена на множестве натуральных чисел (т.е. D(y)= N, где N = {1, 2, 3, …}), то мы имеем дело с упорядоченной переменной величиной, значения которой образуют числовую последовательность
у1, у2, у3, …, уп, … (где уп = f (n), пÎN ).
Предел числовой последовательности
◙ 1. Постоянное число а называется пределом переменной величины уп при п → ∞, если "e > 0 $ N > 0 : ½уп – а½< e при п > N. (Последняя запись читается следующим образом: «если для любого наперед заданного произвольного малого положительного числа ε существует такой номер N > 0, что будет выполняться неравенство ½уп – а½< e для всех п > N »)
Обозначения:
![]() или
или
![]() .
.
2. Последовательность уп стремится к бесконечности, если
" М > 0 $ N > 0: ½уп ½ > М при п > N.
Обозначения:
![]() или
или
![]() .
.
Примеры:
1) уп =
п, ![]() ;
2) уп = (–1)п
п,
;
2) уп = (–1)п
п,
![]() .
.
Предел функции
Пусть функция y = f (x) определена в некоторой окрестности точки а или в некоторых точках этой окрестности.
◙ (предел функции в точке)
Функция y = f (x) стремится к пределу b ( y ® b ) при x, стремящемся к a (x ® a), если "e > 0 $ d (e) > 0: ½уп – а½< e при всех х, удовлетворяющих неравенству | х – а | < d (e).
Обозначение:
f
(x)
® b при
x
® a
или ![]()
Односторонние пределы:
◙ а) (предел функции f (x) в точке а слева)
Функция y = f (x) стремится к пределу b1 ( y ® b1 ) при x, стремящемся к a слева ( x ® a – 0), если "e > 0 $ d (e) > 0: ½ f (x) – b1½< e при всех х, удовлетворяющих неравенству 0 < а – х < d (e).
Обозначение:
![]() .
.
◙ б) (предел функции f (x) в точке а справа)
Функция y = f (x) стремится к пределу b2 ( y ® b2 ) при x, стремящемся к a справа ( x ® a + 0), если "e > 0 $ d (e) > 0: ½f (x) – b2½< e при всех х, удовлетворяющих неравенству 0 < х – а < d (e).
Обозначение:
![]() .
.
◙ (бесконечные пределы функции)
Функция y = f (x) стремится к бесконечности ( y ® ¥) при x, стремящемся к a ( x ® a), если " М > 0 $ d (М) > 0: ½f (x)½> М при всех х, удовлетворяющих неравенству | х – а | < d (М).
Обозначение:
![]() .
.
Если
f (x)
стремится к бесконечности при
x
® a и при этом принимает только положительные или только
отрицательные значения, то соответственно пишут
![]() или
или
![]() .
.
◙ (предел функции на бесконечности)
Функция y = f (x) стремится к пределу b при x ® ¥, если
"e > 0 $ N > 0: ½ f (x) – b½< e , при всех значений х, удовлетворяющих неравенству | х | > N.
Обозначения: 1)
f
(x)
® b при
x
®
¥ или
![]()
2)
f
(x)
® b при
x
®
–
¥ или
![]()
3) f (x)
® b при
x
® +
¥
или ![]()
Пример. 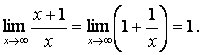
Если
f
(x)
®
¥
при
x
®
¥ , то пишут
![]()
В частности, может быть: ![]()
![]()
![]() и т.д.
и т.д.
Примеры: ![]()
![]()
! З а м е ч а н и е. Функция y = f (x) при x ® a или при х ® ¥ может не стремиться к конечному пределу или к бесконечности. (Пример. y = sin x.)
Основные теоремы о пределах
Пусть а £ ¥ (константа или бесконечность).
Теорема 1. ![]()
![]() .
.
Теорема 2. ![]()
![]() .
.
Следствие. ![]() , С – константа.
, С – константа.
Теорема 3. 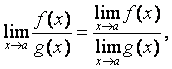 если
если ![]()
Теорема 4. Если между соответствующими
значениями трёх функций
u(x),
y(x),
v(x) выполняется неравенство
u(x)
£
y(x)
£
v(x) и ![]() , то
, то ![]() .
.
Теорема 5. Если между соответствующими
значениями двух функций
u(x),
v(x) выполняется неравенство
u(x)
£
v(x) и существуют пределы ![]()
![]() то
то ![]() .
.
Теорема 6. Если при х ® а функция у ³ 0 и при этом у ® b, то b ³ 0.
Теорема 7. Если у
– возрастающая и ограниченная функция,
т.е. у
<
M, то существует предел ![]() где
В
£
M.
где
В
£
M.
Первый и второй замечательные пределы
Первый
замечательный предел: ![]() .
.
Следствия: 1)![]() ;
2)
;
2) ![]() ; 3)
; 3)
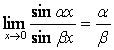 .
.
Второй
замечательный предел:  , е = 2,7182818284…,
, е = 2,7182818284…,
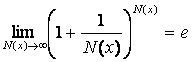 –
обобщённая форма.
–
обобщённая форма.
1.2 Лекция 2. Непрерывность функций
Содержание лекции: Техника вычисления пределов. Бесконечно малые и бесконечно большие величины. Теоремы о бесконечно малых. Сравнение бесконечно малых. Теоремы об эквивалентных бесконечно малых. Непрерывность функций в точке и на интервале. Точки разрыва и их классификация. Непрерывность на отрезке.
Цели лекции: знакомство с техникой вычисления пределов, понятиями непрерывных и разрывных функций и классификацией точек разрыва.
Техника вычисления пределов. Виды определенностей и неопределенностей и способы их раскрытия
При вычислении пределов, прежде всего, следует подставить предельную точку в функцию вместо переменной.
Если получено вполне определённое значение (константа или бесконечность), то это значение является ответом.
Возможные виды определённостей:
![]()
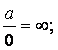
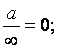
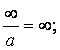
![]()
![]()
![]()
![]()
![]() .
.
Если в результате подстановки
получена одна из неопределённостей (возможны семь видов неопределённостей: ![]() ), то, говорят, следует
раскрыть неопределённость, т.е. вычислить предел,
), то, говорят, следует
раскрыть неопределённость, т.е. вычислить предел,
используя различные методы, приведенные в таблице 4.1 (см. Приложения).
Бесконечно малые и бесконечно большие функции
◙ Функция a(х) называется бесконечно малой (б.м.) при х ® а
(а
– вещественное число или символ
¥), если ![]() .
.
Аналогично определяется бесконечно малая функция при х ® а – 0 и
х ® а + 0, а также при х ® –¥ или х ® +¥.
З а м е ч а н и е. Если ![]() то f (x) – A есть
бесконечно малая.
то f (x) – A есть
бесконечно малая.
◙ Функция f (х) называется бесконечно большой (б.б.) при х ® а
(а
– вещественное число или символ
¥), если ![]() .
.
Лемма. 1)
если f
(х)
® ∞ при
х ® а, то 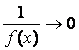 при х
® а;
при х
® а;
2) если a(х)
® 0 при
х ® а, то 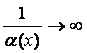 при х
® а.
при х
® а.
Основные теоремы о бесконечно малых
Теорема 1. Алгебраическая сумма конечного числа бесконечно малых при х ® а функций есть функция бесконечно малая при х ® а.
Теорема 2. Произведение ограниченной при х ® а функции на б.м. при х ® а функцию есть функция бесконечно малая при х ® а.
Теорема 3. Произведение конечного числа б.м. при х ® а функций есть функция бесконечно малая при х ® а.
З а м е ч а н и е. Целая положительная степень [a(х)]п б.м. функции a(х) ® 0 при х ® а есть бесконечно малая функция при х ® а.
З а м е ч а н и е. Отношение двух б.м. функций a(х) ® 0 и b(х) ® 0 при х ® а может быть функцией произвольного поведения при х ® а.
Сравнение бесконечно малых
Для сравнения бесконечно малых вычисляют предел их
отношения. Пусть ![]() и
и
![]() бесконечно малые при
х
® а, тогда если
бесконечно малые при
х
® а, тогда если
1)
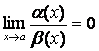 , то б.м.
, то б.м.
![]() более высокого порядка малости, чем
более высокого порядка малости, чем
![]() , в
этом случае пишут
, в
этом случае пишут ![]() ;
;
2)
 , то б.м.
, то б.м.![]() более низкого порядка малости, чем
более низкого порядка малости, чем
![]() ;
;
3)
 , то б.м.
, то б.м.![]() и
и
![]() одного порядка;
одного порядка;
4)
 , то б.м.
, то б.м.
![]() и
и
![]() эквивалентны, записывают
эквивалентны, записывают
![]() ;
;
5)
 , то
, то
![]() есть б.м.
есть б.м.
![]() - го порядка по сравнению с
- го порядка по сравнению с
![]() .
.
Эквивалентные б.м. Их применение при вычислении пределов
При вычислении пределов с б.м. в ряде случаев используют теоремы об эквивалентных б.м.:
Теорема 4.
Если ![]() ,
,
![]() при х
®
а, то
при х
®
а, то
1)
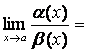
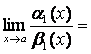

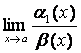 ;
;
2)
![]() .
.
Теорема 5. Алгебраическая сумма конечного числа б.м. эквивалентна слагаемому низшего порядка.
Итак, следуя этим теоремам, в пределах одну б.м. можно заменить другой эквивалентной ей, при этом используют таблицу эквивалентных б.м. (см. Приложения, таблица 4.2).
Непрерывность функций
◙ Функция у = f (x), определенная при x = х0 и всех значениях х, достаточно близких к х0 , называется непрерывной при x = х0 (в точке х0), если
f (х0 + 0) = f (х0 – 0) = f (х0).
Это по определению предела означает, что для каждого положительного числа ε, как бы мало оно не было, можно указать такое d (e) > 0, что для всех х, отличных от х0 и удовлетворяющих неравенству | х – х0 | < d (e), имеет место неравенство ½f (x) – f (х0) ½< e.
Введем понятия приращений:
приращение аргумента: ∆x = x – х0 ,
приращение функции: ∆у = f (x) – f (х0).
Тогда описательно геометрически непрерывность функции в точке x = х0 означает, что бесконечно малому приращению аргумента (от начального значения x = х0) соответствует бесконечно малое приращение функции.
Опираясь на свойства пределов, можно получить
Основные свойства непрерывных в точке функций:
1) Если функции f1(x) и f2(x) непрерывны в точке x = х0 , то сумма
(f1(x) + f2(x)) также есть непрерывная функция в точке x = х0.
(Это свойство справедливо для любого конечного числа слагаемых.)
2) Если функции f1(x) и f2(x) непрерывны в точке x = х0 , то
произведение (f1(x)∙f2(x)) также есть непрерывная функция в точке x = х0.
(Это свойство справедливо для любого конечного числа множителей.)
3) Если функции f1(x) и f2(x) непрерывны в точке x = х0 , то
частное 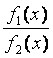 также есть непрерывная функция в точке
x = х0
,
также есть непрерывная функция в точке
x = х0
,
за исключением тех значений независимой переменной, при которых знаменатель обращается в нуль.
4) Если функция u = φ(x) непрерывна в точке x = х0 и f (u) непрерывна в точке u0 = φ(х0), то сложная функция f [φ(x)] непрерывна в точке x = х0 .
5) Всякая элементарная функция непрерывна в каждой точке, в которой она определена.
непрерывные на отрезке функции
Пусть a £ x £ b.
◙ Функция непрерывна на отрезке [a, b], если функция непрерывна при любом значении х из этого промежутка.
При этом
![]() ,
,
![]() .
.
Основные свойства непрерывных на отрезке функций:
1) Если f (x) непрерывна на отрезке [a, b], то существует в этом промежутке, по крайней мере, одно такое значение х, при котором f (x) принимает свое
наибольшее значение и, по крайней мере, одно такое значение х, при котором f (x) принимает свое наименьшее значение.
2) Если f (x) непрерывна на отрезке [a, b], причем f (а) = т, f (b) = п,
то для любого k, заключенного между числами m и n, найдется такая точка x = с, что f (с) = k.
В частности, если f (a) и f (b) разных знаков, то найдется такая точка x = с, что f (с) = 0.
Односторонняя непрерывность.
Точки разрыва и их классификация
◙ Если в какой-то точке x = х0 для функции у = f (x) не выполняется, по крайней мере, одно из условий непрерывности, то при x = х0 функция у = f (x) разрывна. Точка x = х0 в этом случае называется точкой разрыва функции.
Если пределы f (х0 – 0) и f (х0 + 0) существуют, то разность
f (х0 + 0) – f (х0 – 0) называется разрывом, или скачком, функции f (x) при
x = х0 (в точке х0).
При этом функция f (x) имеет в точке х0 разрыв первого рода, если пределы справа и слева конечны, но не равны друг другу, т.е.
f (х0 + 0) ¹ f (х0 – 0).
Если f (х0 + 0) = f (х0 – 0) ¹ f (х0), то х0 – устранимая точка разрыва первого рода.
Функция f (x) имеет в точке х0 разрыв второго рода, если хотя бы один из пределов f (х0 – 0) (или f (х0 + 0)) бесконечен или не существует.
Пример. Исследовать функции на непрерывность.
Определить характер точек разрыва: 1)  ; 2)
; 2)![]() .
.
Решение.
1) ![]() ,
, ![]() .
.
Так как ![]()
![]()
![]() , то х0
= 2 точка разрыва первого рода,
, то х0
= 2 точка разрыва первого рода,
![]() –
–![]() = 1 – скачок функции в этой точке.
= 1 – скачок функции в этой точке.
2) 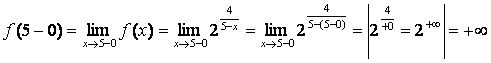 ,
,
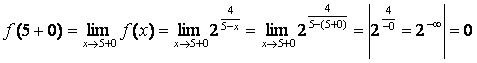 .
.
Так как один из односторонних пределов
![]() ,
то х0 = 5 точка разрыва второго рода.
,
то х0 = 5 точка разрыва второго рода.
1.3 Лекция 3. Дифференциальное исчисление функции одной переменной
Содержание лекции: Производная функции одной переменной. Основные правила дифференцирования. Производные основных элементарных функций. Логарифмическое дифференцирование. Производные неявных и параметрически заданных функций. Дифференциал.
Цели лекции: знакомство с основными понятиями дифференциального исчисления функции одной переменной.
Производная функции одной переменной
а) механический смысл производной
Пусть s
=
f (t) –
путь, пройденный за время t,
D t
– приращение времени,
D s – приращение расстояния. Тогда
![]() – средняя скорость движения за промежуток времени от
D t до (t
+D t),
– средняя скорость движения за промежуток времени от
D t до (t
+D t),
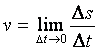 – скорость в
данный момент t
или v(t)
– производная от пути по времени.
– скорость в
данный момент t
или v(t)
– производная от пути по времени.
б) общее определение производной
Пусть функция y = f (x) определена при х и (х + h) для любого достаточно малого h: ½h½<< 1.
Тогда при условии, что D x = h, D y = f (x + h) – f (x), получим
![]() .
.
Т.к
х фиксировано, то ![]() – функция, зависящая от
h, определенная
в промежутке –
e
£ h
£
e
, кроме h = 0.
– функция, зависящая от
h, определенная
в промежутке –
e
£ h
£
e
, кроме h = 0.
◙ Если существует предел
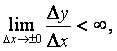 то
этот предел называется производной функции
f (x) при
заданном х, а сама функция
f (x) при этом
называется дифференцируемой в точке х.
то
этот предел называется производной функции
f (x) при
заданном х, а сама функция
f (x) при этом
называется дифференцируемой в точке х.
Обозначение:

 .
.
◙ Операция нахождения производной называется дифференцированием функции.
! З а м е ч а н и е. Если при некотором значении х производная f¢ (x) существует, то при этом значении х функция f (x) непрерывна. Обратное утверждение неверно.
в) геометрический смысл производной: производная f¢ (x) равна тангенсу угла a, образованного касательной к кривой в точке М(х, у) с положительным направлением оси Ох, т.е. равна угловому коэффициенту этой касательной.
Уравнение касательной к графику функции одной переменной
y – y0 = f¢ (x0)(x – x0) , где y0 = f (x0),
f¢ (x0) – угловой коэффициент касательной к графику функции y = f (x)
в точке (x0 , y0).
Уравнение нормали к графику функции одной переменной
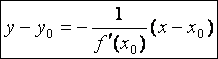 , где
, где  – угловой коэффициент нормали
к графику функции y =
f (x) в точке (x0
, y0),
– угловой коэффициент нормали
к графику функции y =
f (x) в точке (x0
, y0), ![]() – вектор нормали.
– вектор нормали.
Основные правила дифференцирования
Пусть u = u(x), v = v(x), u1 = u1(х) , u2 = u2(х) , ... , un = uп(х) – дифференцируемые функции. Тогда имеют место равенства:
1. Производная постоянной:
(С)¢ = 0, С – const,
2. Производная суммы и разности:
(u1 ± u2 ± ... ± un)¢ = u1¢ ± u2¢ ± ... ± un¢
3. Производная произведения:
(uv)¢ = u¢v + uv¢ 3´. (Сu)¢ = Сu¢ (следствие п.3)
4. Производная частного:
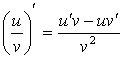 4´.
4´.  (следствие п.4)
(следствие п.4)
5. Производная сложной функции:
Пусть y = f (u), u = j (x). Тогда [ f (j (x)) ]¢ = f¢u(и)× j¢ (x) или y¢x = y¢u× u¢x .
6. Производная обратной функции:
Если для дифференцируемой функции y =
f (x)
существует обратная функция x
=
j
(y),
то 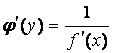 .
.
Производные основных элементарных функций приведены в таблице 4.3 (см. Приложения).
Теоремы о дифференцируемых функциях
1. Теорема
(Правило
Лопиталя) Пусть функции f
(х),
g(х) – непрерывны и дифференцируемы в
окрестности точки х = а и обращаются в нуль в этой точке, т.е.
f (а)
= g(а) = 0. Тогда, если существует 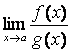 , то существует и
, то существует и  , причем
, причем 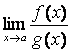 =
= .
.
З а м е ч а н и е. Правило Лопиталя
применимо и для раскрытия неопределенности вида ![]() . Некоторые виды неопределенностей также можно
свести к использованию правила Лопиталя:
. Некоторые виды неопределенностей также можно
свести к использованию правила Лопиталя:
1) Рассмотрим ![]() , где
, где ![]() ,
, ![]() . Неопределенность вида 0·∞ можно
свести к неопределенности вида
. Неопределенность вида 0·∞ можно
свести к неопределенности вида ![]() или
или![]() , представив произведение
f (х)·g(х)
в одном из следующих видов:
, представив произведение
f (х)·g(х)
в одном из следующих видов:
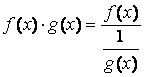 или
или 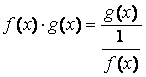 .
.
2) Рассмотрим ![]() , где
, где ![]() ,
, ![]() .
.
Неопределенность
вида 1¥ (после
проведения преобразований
![]() ) сводится к неопределенности вида 0×¥ .
) сводится к неопределенности вида 0×¥ .
Аналогично, неопределенности вида ¥0 , 00 сводятся к неопределенности вида 0×¥.
2. Теорема Ферма.
Если функция f (x) непрерывна в промежутке (a, b), в каждой точке внутри этого промежутка имеет производную и в некоторой точке x = c внутри промежутка достигает наибольшего (наименьшего) значения, то f¢ (c) = 0.
3. Теорема Лагранжа. (Формула конечных приращений)
Если функция f (x) непрерывна на [a, b] и дифференцируема во всех внутренних точках этого отрезка, то внутри [a, b] найдется, по крайней мере, одна такая точка c, a < c < b, что выполняется равенство
f (b) – f (a) = f¢ (c)(b – a).
Если формулу Лагранжа записать в виде:
![]() , где
левая часть – тангенс угла наклона секущей, а правая часть – тангенс угла
наклона касательной, то получаем геометрический смысл теоремы Лагранжа: найдется такая точка с, в которой касательная будет параллельна секущей.
, где
левая часть – тангенс угла наклона секущей, а правая часть – тангенс угла
наклона касательной, то получаем геометрический смысл теоремы Лагранжа: найдется такая точка с, в которой касательная будет параллельна секущей.

Рисунок 1.3.1
Логарифмическое дифференцирование
Пусть u = u(x) и v = v(x) – дифференцируемые функции.
Составим из них степенно-показательную функцию y = uv.
Найдем производную у¢ (х) методом логарифмического дифференцирования: 1) прологарифмируем равенство y = uv: ln y = ln uv = v× ln u;
2) продифференцируем: 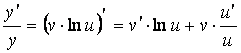 ;
;
3) выразим y¢ : y¢ = uv ( v¢× ln u + v× u¢ / u ) = v¢× uv ln u + v uv-1× u¢.
Производная функции, заданной неявно
Пусть функция y = j (x) задана неявно, т.е. уравнением: F(x, y) = 0,
тогда F¢x (x,
y) +
F¢y
(x,
y)
y¢ =
0 ![]()
 .
.
Производная функции, заданной параметрически
Пусть функция
y от
x задана
параметрическими уравнениями:
тогда производная параметрически заданной функции находится по формуле
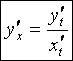 .
.
Дифференциал и его применение в приближенных вычислениях
Пусть функция y = f (x) дифференцируема на отрезке [а, b]. Производная этой функции в некоторой точке х отрезка [а, b] определяется равенством
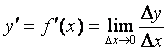 .
.
Следовательно,
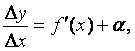 где
a
®
0
при
Dх
®
0.
Умножая
все члены последнего равенства на
Dх, получим:
где
a
®
0
при
Dх
®
0.
Умножая
все члены последнего равенства на
Dх, получим:
![]()
где
aDх – б.м. высшего порядка
относительно
Dх, т.к.

Таким образом, приращение Dу функции состоит из двух слагаемых, из которых первое слагаемое есть так называемая главная часть приращения, линейная относительно Dх.
◙ Произведение f¢ (x)Dх называют дифференциалом функции y = f (x) и обозначают через dy или df (x): dy = f¢ (x)Dх
Найдем дифференциал для функции у = х: dy = dх = Dх.
Таким
образом, dy =
f¢ (x)
dх, откуда
следует, что
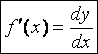 .
.
Следовательно, производная f¢ (x) есть отношение дифференциала функции к дифференциалу независимого переменного.
Геометрический смысл дифференциала: дифференциал функции
y = f (x) в данной точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получает приращение Dх.
Поскольку![]() где
aDх – б.м. высшего порядка
относительно
Dх, то
Dу
» dy, или в
развернутом виде f
(x+Dx)
– f (x)
» f¢
(x)Dx,
откуда получаем формулу для приближенного вычисления: f (x+Dx)
» f (x) +
f¢ (x)Dx
где
aDх – б.м. высшего порядка
относительно
Dх, то
Dу
» dy, или в
развернутом виде f
(x+Dx)
– f (x)
» f¢
(x)Dx,
откуда получаем формулу для приближенного вычисления: f (x+Dx)
» f (x) +
f¢ (x)Dx
Свойства дифференциалов
1)
d(u+v) = du +
dv; 2) d(uv)
= udv +vdu; 3) 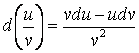 .
.
1.4 Лекция 4. Исследование функций с помощью производных
Содержание лекции: Теоремы о возрастании и убывании функции. Экстремумы функции одной переменной. Необходимое и достаточное условия экстремума. Наибольшее и наименьшее значения функции на отрезке. Выпуклость и вогнутость графика функции, точки перегиба. Асимптоты графика функции. Полное исследование функции.
Цели лекции: исследование отдельных свойств функции с помощью производных.
Условия монотонности функции
Теорема 1. (для возрастающей функции)
Если f (x), имеющая производную на отрезке [a, b], возрастает на этом отрезке, то f¢ (x) ³ 0 на [a, b].
Если f (x) непрерывна на отрезке [a, b] и дифференцируема в промежутке (a, b), причем f¢ (x) > 0 на (a, b), то эта функция возрастает на отрезке [a, b] .
Теорема 2. (для убывающей функции)
Если f (x), имеющая производную на отрезке [a, b], убывает на этом отрезке, то f¢ (x) £ 0 на [a, b].
Если f (x) непрерывна на отрезке [a, b] и дифференцируема в промежутке (a, b), причем f¢ (x)< 0 на (a, b), то эта функция убывает на отрезке [a, b].
Геометрический смысл теорем:
на участке возрастания функции касательная образует с осью абсцисс острый угол, тангенс (производная) которого положителен;
на участке убывания функции касательная образует с осью абсцисс тупой угол, тангенс (производная) которого отрицателен.
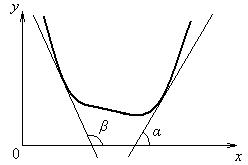
Рисунок 1.4.1
Экстремумы функции одной переменной
◙ Функция f (x) имеет максимум при х = х1, если f (x1 + Dх) < f (x1) при любых Dх (положительных и отрицательных), достаточно малых по абсолютной величине (т.е. ½Dх½<< 1).
◙ Функция f (x) имеет минимум при х = х2, если f (x2 + Dх) > f (x2) при любых Dх (положительных и отрицательных), достаточно малых по абсолютной величине.
З а м е ч а н и е. Функция, определенная на отрезке, может достигать максимума и минимума при значениях х, заключенных внутри рассматриваемого отрезка.
! Не следует думать, что максимум и минимум функции являются, соответственно, наибольшим и наименьшим значениями на рассматриваемом отрезке.
◙ Максимумы и минимумы функции называют экстремумами (экстремальными значениями) функции.
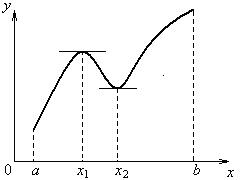
Рисунок 1.4.2
Теорема 3. (необходимое условие существования экстремума)
Если дифференцируемая функция y = f (x) имеет в точке х = х1 максимум или минимум, то f¢ (x1) = 0.
З а м е ч а н и е.
1. Условие теоремы не является достаточным. (Пример: y = x3).
2. Экстремум может существовать в точках, где производная не существует (терпит разрыв). (Пример: у = ½х½, х = 0).
◙ Значения аргумента, при которых производная обращается в нуль или терпит разрыв, называются критическими точками (критическими значениями).
Теорема 4. (первое достаточное условие существования экстремума)
Пусть f (x) непрерывна в некотором интервале, содержащем критическую точку х1, и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки х1). Тогда
А) если f¢ (x) > 0 при х < х1 и f¢ (x) < 0 при х > х1,
то в точке х1 функция имеет максимум.
Б) если f¢ (x) < 0 при х < х1 и f¢ (x) > 0 при х > х1,
то в точке х1 функция имеет минимум.
Теорема 5. (второе достаточное условие существования экстремума)
Пусть f¢ (x1) = 0; f¢¢ (x) существует и непрерывна в некоторой окрестности точки х1. Тогда при х = х1 функция имеет максимум, если f¢¢ (x1) < 0 ,
и минимум, если f¢¢ (x1) > 0.
Наибольшее и наименьшее значения функции на отрезке
Пусть y = f (x) непрерывна на отрезке [a, b] .
Тогда на этом отрезке функция достигает своего наибольшего (наименьшего) значения либо на одном из концов этого отрезка, либо в такой внутренней точке этого отрезка, которая является максимумом (минимумом).
Из предыдущего вытекает следующее
правило нахождения наибольшего (наименьшего) значения функции на отрезке [a, b]:
1) найти все максимумы (минимумы) на отрезке;
2) вычислить f (a) и f (b);
3) из всех полученных выше значений выбрать наибольшее (наименьшее); оно и будет представлять собой наибольшее (наименьшее) значение функции на отрезке.
Выпуклость, вогнутость и асимптоты функции
Пусть y = f (x) – однозначная дифференцируемая функция.
◙ Кривая y = f (x) обращена выпуклостью вверх (кривая выпуклая) на интервале (a, b) , если все точки кривой лежат ниже любой касательной на этом интервале.
◙ Кривая y = f (x) обращена выпуклостью вниз (кривая вогнутая) на интервале (b, с), если все точки кривой лежат выше любой касательной на этом интервале.
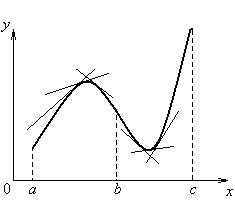
Рисунок 1.4.3
Теорема 6.
Если " х Î (a, b) f ¢¢(x) < 0, то кривая y = f (x) выпукла на этом интервале.
Теорема 6¢.
Если " х Î (a, b) f ¢¢(x) > 0, то кривая y = f (x) вогнута на этом интервале.
◙ Точка, отделяющая выпуклую часть от вогнутой, называется точкой перегиба кривой.
З а м е ч а н и е. В точке перегиба касательная, если она существует, пересекает кривую.
Теорема 7. (необходимое условие существования точки перегиба)
Если дифференцируемая функция y = f (x) имеет точку перегиба с абсциссой x = a, то f¢¢ (a) = 0.
Теорема 8. (достаточное условие существования точки перегиба)
Пусть кривая определяется уравнением y = f (x).
Если f¢¢ (a) = 0 или f¢¢ (a) не существует и при переходе через значение
x = a f¢¢ (x) меняет знак, то точка кривой с абсциссой x = a есть точка перегиба.
Асимптоты
◙ Прямая А называется асимптотой кривой, если расстояние d от переменной точки М кривой до этой прямой при удалении точки М на бесконечность стремится к нулю.
Различают три вида асимптот: вертикальные, наклонные и горизонтальные.
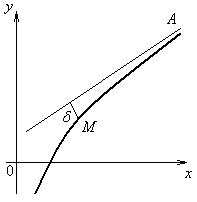
Рисунок 1.4.4
1) Вертикальные асимптоты.
Если ![]() , или
, или ![]() , или
, или ![]() , то
, то
прямая х = а есть асимптота кривой y = f (x); верно и обратное утверждение.
2) Наклонные асимптоты.
Если существуют пределы  и
и ![]() , то
, то
прямая y = kx + b есть асимптота. Если хотя бы один из пределов не существует, то кривая y = f (x) асимптоты не имеет.
З а м е ч а н и е. Рассуждения справедливы и для x ® – ¥.
3) Горизонтальные асимптоты.
Данный вид является частным случаем наклонных
асимптот, а именно, если 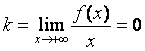 , то прямая y
= b есть
горизонтальная асимптота.
, то прямая y
= b есть
горизонтальная асимптота.
Пример. Найти
асимптоты кривой 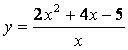 .
.
Решение.
1) вертикальные асимптоты:
т.к. у ® + ¥ при х ® – 0 и у ® – ¥ при х ® + 0, то х = 0 – вертикальная асимптота.
2) наклонные асимптоты:
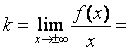
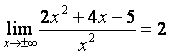 , т.е.
k = 2.
, т.е.
k = 2.
![]()
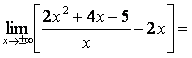
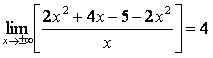 , т.е.
b
= 4.
, т.е.
b
= 4.
Следовательно, у = 2х + 4 есть наклонная асимптота данной кривой.
Общий план исследования функций и построения графиков
Для проведения полного исследования функции необходимо найти:
1) область определения функции и точки разрыва;
2) точки пересечения графика с осями координат;
3) четность, нечетность, периодичность функции;
4) интервалы монотонности, точки экстремума;
5) интервалы выпуклости, вогнутости, точки перегиба;
6) асимптоты графика функции;
7) построить график.
2 Функции нескольких переменных. Интегральное исчисление функции одной и нескольких переменных
2.1 Лекция 5. Первообразная и неопределенный интеграл
Содержание лекции: Первообразная, неопределённый интеграл, таблица интегралов. Правила и методы интегрирования. Метод подстановки. Интегрирование по частям.
Цели лекции: ввести понятие неопределенного интеграла, изучить его свойства и некоторые правила и методы интегрирования.
◙ Функция F(x) – называется первообразной от функции f (x) на [a, b], если F ¢(x) = f (x) " xÎ[a, b]
Пример.
f (x) = х2
![]()
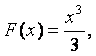
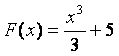 – частные случаи общего вида
первообразной:
– частные случаи общего вида
первообразной: 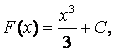 (C
– const).
(C
– const).
Теорема. Если F1(x), F2(x) – первообразные от f (x) на [a, b], то
F1(x) – F2(x) = С, (C – const ).
◙ Если F(x)
– первообразная для f (x),
то выражение F(x) + С называется
неопределенным интегралом от функции
f (x) и обозначается
![]() .
.
Таким образом, по определению,
![]() если
F
¢(x) =
f (x).
если
F
¢(x) =
f (x).
При
этом f
(x) – подынтегральная функция,
f (x)dx
– подынтегральное выражение, ![]() – знак интеграла.
– знак интеграла.
Таким образом, неопределенный интеграл – семейство функций y = F(x) + C.
? Для всякой ли функции f (x) существуют первообразные?
З а м е ч а н и е. Если функция f (x) непрерывна на [a, b], то для этой функции существует первообразная (а значит, и неопределенный интеграл).
◙ Нахождение первообразной для данной функции f (x) называется интегрированием функции f (x).
Свойства неопределенного интеграла
1.
![]()
2.
![]()
3.
![]()
4.
![]()
![]()
5.
![]() ,
a –
const .
,
a –
const .
Если ![]() то
то
6. 
7. ![]()
8. 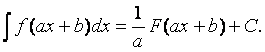
Таблица интегралов
Т а б л и ц а 2.1.1
|
1. |
11. |
|
2. |
11¢.
|
|
3. |
12. |
|
4 |
13. |
|
5. |
13¢.
|
|
6. |
14. |
|
7. |
15. |
|
8. |
16. |
|
9. |
17. |
|
10. |
18. |
Методы интегрирования
1) Непосредственное интегрирование
Интегрирование с применением таблицы интегралов.
2) Внесение функции под знак дифференциала
Для функции у = f (x) справедлива формула dy = y' dx. Использование этой формулы слева направо позволяет вынести функцию из-под знака дифференциала, справа налево – внести функцию под знак дифференциала:
→ – вынесение (дифференцирование)
dy = y' dx
← – внесение (интегрирование)
Пример. ![]()
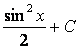 .
.
3) Замена переменной или способ подстановки
Интеграл![]() можно
упростить, введя новую переменную t в виде замены
x =
j (t)
или t =
ψ(x).
можно
упростить, введя новую переменную t в виде замены
x =
j (t)
или t =
ψ(x).
Тогда 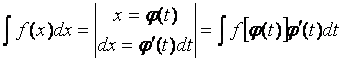
или  .
.
Пример.
![]() =
=  =
=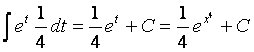 .
.
4) Интегрирование по частям
Пусть u = и(х), v = v (х) – две дифференцируемые функции от х.
Тогда т.к. d (uv) = u dv + v du , то u dv = d (uv) - v du.
Интегрируя, получаем: ![]() .
.
Данный способ применяется при вычислении интегралов типа:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Пример. 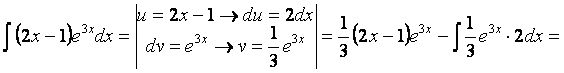

2.2 Лекция 6. Интегрирование рациональных, иррациональных, тригонометрических функций
Содержание лекции: Интегрирование функций, содержащих квадратный трехчлен. Интегрирование дробно-рациональных функций. Интегрирование функций, содержащих иррациональные выражения. Интегрирование тригонометрических функций.
Цели лекции: изучить основные методы и освоить технику интегрирования указанных видов функций.
Интегрирование функций, содержащих квадратный трехчлен
Рассмотрим интегралы 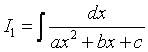 ,
,
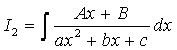 ,
,
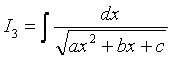 ,
,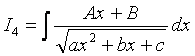 .
.
1)
С помощью выделения полного квадрата 
получаем 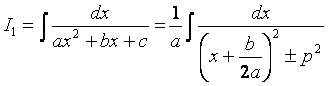 , где
, где 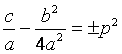 .
.
( Знак «+» берется, если 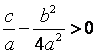 ; знак «–» – если
; знак «–» – если 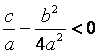 )
)
Таким образом, (после замены переменной: 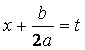 ,
, ![]() )
)
 .
.
Это табличные интегралы (см. формулы 11´, 12)
2) Проведем тождественное преобразование подынтегральной функции:
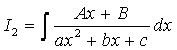

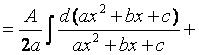
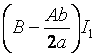 =
=
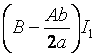 .
.
3) Аналогично п.1), после выделения полного квадрата получим
 .
.
Далее проводим преобразования в зависимости от числа а.
а < 0: 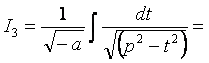
 .
(см. формулу 13´)
.
(см. формулу 13´)
а > 0: 
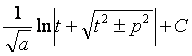 .
(см. формулу 14)
.
(см. формулу 14)
4) Проведем преобразование, аналогично п.2):
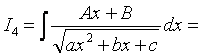

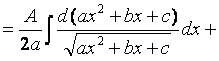
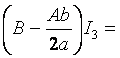
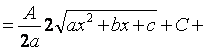
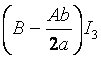 .
.
Разложение правильной дробно-рациональной функции на простейшие дроби
◙ Функция вида
 называется
дробно-рациональной функцией (или
рациональной дробью).
называется
дробно-рациональной функцией (или
рациональной дробью).
При этом если
m
< n, то рациональная
дробь правильная; если
m
> n – рациональная
дробь неправильная. Неправильную дробь всегда можно представить в виде:  ,
,
где M(x) – многочлен,
 –
правильная дробь.
–
правильная дробь.
Среди правильных дробей различают четыре типа простейших дробей:
![]() ,
,
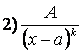 ,
, 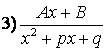 ,
, 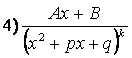 ,
,
где
![]() – действительные
числа,
– действительные
числа, ![]() – натуральное число, квадратный трёхчлен
– натуральное число, квадратный трёхчлен
![]() не
имеет действительных корней.
не
имеет действительных корней.
З а м е ч а н и е. Любую
правильную дробь ![]() можно разложить
в сумму простейших дробей. При этом вид разложения определяется корнями
знаменателя f
(x).
можно разложить
в сумму простейших дробей. При этом вид разложения определяется корнями
знаменателя f
(x).
1 случай. Корни знаменателя действительны и различны, т.е.
![]() ,
,
тогда
 ,
,
где A, B, …, D – неопределенные коэффициенты.
2 случай. Корни знаменателя действительны, причем некоторые из
них кратные: ![]() ,
,
тогда
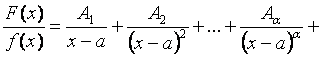

 , (*)
, (*)
где Ai, Bi, …, Di – неопределенные коэффициенты.
3 случай. Среди корней знаменателя есть комплексные различные:
![]() ,
,
тогда
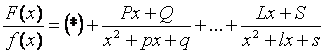 ,
,
где Р, Q, …, S – неопределенные коэффициенты.
4 случай. Среди корней знаменателя есть комплексные кратные:
![]() ,
,
тогда


 ,
,
где Pi, Qi, …, Si – неопределенные коэффициенты.
З а м е ч а н и е. Неопределённые коэффициенты
![]() вычисляются следующим образом: приводим к общему
знаменателю сумму дробей в правой части равенства и приравниваем числители.
Далее составляем систему линейных уравнений относительно искомых коэффициентов одним
из двух способов:
вычисляются следующим образом: приводим к общему
знаменателю сумму дробей в правой части равенства и приравниваем числители.
Далее составляем систему линейных уравнений относительно искомых коэффициентов одним
из двух способов:
1 способ: приравнивая коэффициенты при одинаковых степенях х в левой и правой частях последнего тождества;
2 способ: придавая переменной х в этом тождестве произвольные числовые значения.
Интегрирование правильной дробно-рациональной функции
Т.к. любая правильная дробь
![]() раскладывается в сумму простейших
дробей, то ее интегрирование сводится к интегрированию простейших дробей:
раскладывается в сумму простейших
дробей, то ее интегрирование сводится к интегрированию простейших дробей:
 ;
;
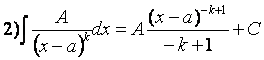 ;
;
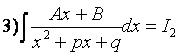 ;
;
(см. Интегрирование функций, содержащих квадратный трехчлен)
 с
помощью тождественных преобразований, используемых при вычислении
I2, сводится к табличным интегралам типа 1 и 11′ (см.[4],
с.353).
с
помощью тождественных преобразований, используемых при вычислении
I2, сводится к табличным интегралам типа 1 и 11′ (см.[4],
с.353).
Интегрирование неправильной дробно-рациональной функции
сводится к интегрированию многочлена и нескольких простейших дробей.
Интегрирование функций, содержащих иррациональные выражения
Интеграл вида
 приводится
к табличному с помощью подстановки:
приводится
к табличному с помощью подстановки: 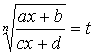 .
.
Интегралы вида
![]() ,
,
![]() ,
,
![]() приводятся
к табличным с помощью соответствующих тригонометрических подстановок: 1)
x =
a sin t, 2)
x =
a tg t, 3)
приводятся
к табличным с помощью соответствующих тригонометрических подстановок: 1)
x =
a sin t, 2)
x =
a tg t, 3)
 .
.
Интегрирование тригонометрических функций
1.Универсальная подстановка
Интегралы вида
![]() , где
R – рациональная функция, приводятся к интегралам от
рациональных функций с помощью универсальной
, где
R – рациональная функция, приводятся к интегралам от
рациональных функций с помощью универсальной
подстановки
![]() , при этом:
, при этом:
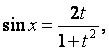
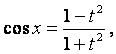
![]()
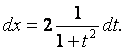
Универсальная подстановка часто приводит к громоздким выкладкам, поэтому её надо применять в случаях, если нельзя найти более лёгкий способ определения интеграла.
2. Интегралы вида:
![]() .
.
Возможны два случая:
1) если хотя бы одно из (m, n) нечетное, например, п = 2р +1, тогда
![]()
![]()
![]() ,
,
т.е. после замены
![]() получаем
интеграл от многочлена.
получаем
интеграл от многочлена.
2)
если оба значения т и
п –
четные, т.е. т = 2р, п = 2q, тогда путём понижения степени по формулам: ![]()
![]() получим
получим
интеграл
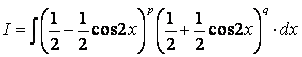 , содержащий в себе
, содержащий в себе
![]() в четных и нечетных степенях. Члены с нечетными
степенями интегрируются, как указано в случае 1). Четные показатели степеней
снова понижаем по указанным формулам. Продолжая так, дойдем до членов вида
в четных и нечетных степенях. Члены с нечетными
степенями интегрируются, как указано в случае 1). Четные показатели степеней
снова понижаем по указанным формулам. Продолжая так, дойдем до членов вида
![]() , которые
легко интегрируются.
, которые
легко интегрируются.
3. Интегралы вида:
![]() ,
,
![]() ,
,
![]() .
.
Интегралы
данного вида можно вычислить путём разложения на слагаемые по формулам: ![]()
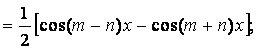
![]()
 .
.
2.3 Лекция 7. Определённый интеграл, основные свойства. Формула Ньютона-Лейбница. Методы подстановки. Интегрирование по частям
Содержание лекции: Определенный интеграл, его свойства.
Формула Ньютона-Лейбница. Замена переменных и интегрирование по частям для определенного интеграла.
Цели лекции: знакомство с определенным интегралом, его свойствами и техникой вычисления.
Интегральные суммы
Пусть y = f (x) – непрерывная функция на [a, b];
т, М – наименьшее и наибольшее значения функции на [a, b].
Разобьем [a, b] на п частей: a = х0 < х1 < х2 < …< хп = b.
Положим х1 – х0 = D х1, х2 – х1 = D х2, …, хп – хп-1 = D хп .
Обозначим наибольшее и наименьшее значения f (x) на [х0, х1] через т1 и М1 , на [х1, х2] через т2 и М2 ,…, на [хп-1, хп] через тп и Мп .
Составим интегральные суммы:
1)
нижняя интегральная сумма ![]()
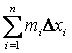 ; 2) верхняя интегральная
сумма
; 2) верхняя интегральная
сумма ![]()
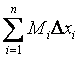 ;
;
Свойства верхней и нижней интегральных сумм:
а)
![]() ;
;
б) ![]() ;
;
в) ![]() ;
;
г) ![]() .
.
Определенный интеграл
Возьмем точки x1 , x2 , …, xп : х0 < x1 < х1 , х1 < x2 < х2 , …, хп-1 < xп < хп .
Каждой точке xi
сопоставим значение f
(xi), ![]() .
.
Составим интегральную сумму для f (x) на [a, b]:
![]()
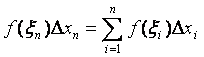 .
.
Т.к. mi
£ f (xi )
£ Mi "xi
Î
[xi-1,
xi] (![]() ),
),
то
mi
Dxi
£ f
(xi
)Dxi
£ Mi
Dxi
, следовательно, ![]() .
.
Пусть max Dxi – наибольшая из длин отрезков [x0 , x1], [x1 , x2], …, [xп-1 , xп].
Заметим, что если max Dxi ® 0, то п ® ¥.
◙ Если при любых разбиениях отрезка [a, b] таких, что max Dxi ® 0 , и при любом выборе точек xi на отрезках [xi-1, xi] интегральная сумма
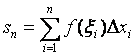 стремится к одному и тому же
пределу s, то этот предел называют
определен-
стремится к одному и тому же
пределу s, то этот предел называют
определен-
ным
интегралом от функции f
(x) на отрезке
[a,
b]
и обозначают
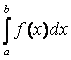 .
.
Таким образом, по определению, 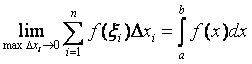 ,
где
,
где
a – нижний предел интеграла, b – верхний предел интеграла,
[a, b] – отрезок интегрирования, х – переменная интегрирования.
◙ Если для функции f (x) выше указанный предел существует, то функцию называют интегрируемой на отрезке [a, b].
З а м е ч а н и е. Т.к. ![]() ,
,![]() – частные случаи интегральной суммы sп,
то
– частные случаи интегральной суммы sп,
то ![]() ,
, ![]() ®
s, поэтому
®
s, поэтому
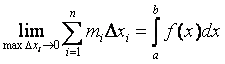 и
и  .
.
Геометрический смысл определенного интеграла (в случае f (x) ³ 0):
определенный интеграл  численно равен площади криволинейной
трапеции, ограниченной кривой
y
=
f
(x), прямыми
x
= a,
x
=
b
и осью
Ох.
численно равен площади криволинейной
трапеции, ограниченной кривой
y
=
f
(x), прямыми
x
= a,
x
=
b
и осью
Ох.
Основные свойства определенного интеграла:
1)
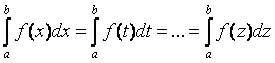 ;
;
2)
 ;
;
3)
 ;
;
4)
 , А
= const;
, А
= const;
5)
 ;
;
6)
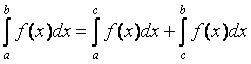 "
a, b, c
Î
R,
"
a, b, c
Î
R,
если только все эти три интеграла существуют;
7) если
f
(x)
£
j
(x) на отрезке
[a,
b] (a
<
b), то 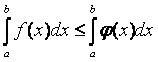 ;
;
8) если т и М – наименьшее и наибольшее значения функции f (x) на [a, b]
и
a
£
b , то 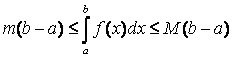 ; (Рисунок 2.3.1)
; (Рисунок 2.3.1)

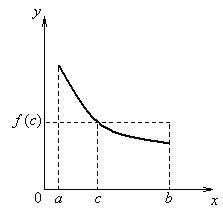
Рисунок 2.3.1 Рисунок 2.3.2
9) (Теорема о среднем) Если f (x) непрерывная функция на [a, b], то $сÎ[a, b]:
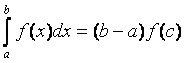 .
.
При этом f (с) называется средним значением функции на отрезке [a, b]. (Рисунок 2.3.2)
10)
 ,
если
,
если ![]() – нечётная функция;
– нечётная функция;
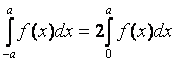 , если
, если
![]() – чётная функция.
– чётная функция.
Вычисление определенного интеграла
1. Формула Ньютона-Лейбница
Пусть
f (x) – непрерывная
функция на [a,
b]. Рассмотрим интеграл
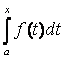 , где
нижний предел а закреплен, верхний предел х меняется, т.е. интеграл
, где
нижний предел а закреплен, верхний предел х меняется, т.е. интеграл
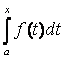 является
функцией от верхнего предела.
является
функцией от верхнего предела.
Поэтому 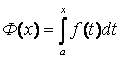 называют интегралом с
переменным верхним
называют интегралом с
переменным верхним
пределом. (Геометрически Ф(х) представляет площадь криволинейной трапеции с изменяющейся правой границей.)
Теорема 1.
Если f (x) – непрерывная функция и
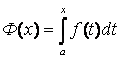 ,
,
то имеет место равенство Ф¢(х) = f (x), т.е. производная от определенного интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела.
З а м е ч а н и е. Из Теоремы 1 следует, что всякая непрерывная функция имеет первообразную.
Теорема 2.
Если F(x)
есть какая-либо первообразная от
непрерывной функции f (x), то справедлива формула
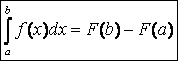 .
.
Эта формула называется формулой Ньютона-Лейбница.
Сокращенная
запись: 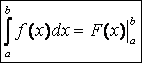 , где
, где
![]() .
.
Пример.
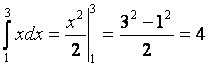 .
.
2. Замена переменной в определенном интеграле
Теорема 3.
Пусть дан интеграл  ,
где f
(x) – непрерывная функция на
[a,
b]. Введем новую переменную
t, связанную со старой переменной
соотношением x =
j (t).
Если выполняются условия:
,
где f
(x) – непрерывная функция на
[a,
b]. Введем новую переменную
t, связанную со старой переменной
соотношением x =
j (t).
Если выполняются условия:
1) j (a) = а , j (b) = b,
2) j (t) и j¢ (t) непрерывны на [a, b],
3) f [j (t)] определена и непрерывна на [a, b],
то
 .
.
3. Интегрирование по частям в определенном интеграле
Пусть u и v – дифференцируемые функции от x. Тогда
(uv)¢ = u¢v + uv¢
Интегрируя обе части тождества, получим:
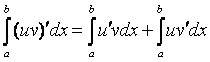 .
.
Т.к.
![]() , то
, то
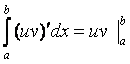 ;
;
следовательно,
 , или окончательно
, или окончательно
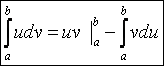 .
.
2.4 Лекция 8. Двойные интегралы
Содержание лекции: Двойной интеграл и его свойства. Вычисление двойных интегралов в прямоугольных координатах. Замена переменных в двойном интеграле.
Цели лекции: знакомство с двойным интегралом, его свойствами и техникой вычисления.
Рассмотрим в плоскости Oxy замкнутую область D , ограниченную линией L.
Пусть в области D задана непрерывная функция z = f (x, y).
Разобьем область D произвольным образом на п частей:
D s1 , D s2 , D s3 , …, D sп .
Каждую часть (площадку) отождествим с ее площадью.
Выберем
в каждой площадке произвольную точку
Рi
Î
D
si
(![]() ), и
сопоставим ей значение
f (Pi).
Составим сумму:
), и
сопоставим ей значение
f (Pi).
Составим сумму: 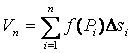 .
.
Эта сумма называется интегральной суммой для функции f (x, y) в области D.
Если f ³ 0 в области D , то геометрически каждое слагаемое f (Pi) D si можно представить как объем малого цилиндра, высота которого есть f (Pi), а основание D si.
Таким образом, Vn – объем «ступенчатого» тела. Предположим, что diam Dsi ® 0 при n ® ¥. Тогда справедлива следующая теорема.
Теорема 1.
Если функция
f (x,
y) непрерывна в
замкнутой области D
,
то  .
.
Этот предел не зависит ни от способа разбиения области D на Dsi , ни от выбора точки Рi Î D si.
Этот предел называется двойным интегралом от
функции f
(x,
y) в области
D
и обозначается: ![]() или
или
![]() .
.
Таким образом,  ,
,
где D – область интегрирования.
Геометрический смысл двойного интеграла (в случае
f (x,
y)
³
0):
двойной
интеграл ![]() равен
объему тела V, ограниченного
поверхностью z =
f (x,
y), плоскостью
z
= 0 и цилиндрической
поверхностью с образующей, параллельной оси
Оz и направляющей
L .
равен
объему тела V, ограниченного
поверхностью z =
f (x,
y), плоскостью
z
= 0 и цилиндрической
поверхностью с образующей, параллельной оси
Оz и направляющей
L .
Свойства двойного интеграла:
1)
![]()
![]() ;
;
2)
![]() , С
= const;
, С
= const;
3) Если D разбита на D1 и D2 без общих внутренних точек, то
![]()

 .
.
Вычисление двойных интегралов
Пусть D - замкнутая область в плоскости Oxy.
◙ Область D называется правильной в направлении оси Oy (Ox),
если всякая прямая
l,
параллельная оси
Oy
(Ox) и проходящая через внутреннюю точку
D,
пересекает границу области в двух точках, т.е.
![]() .
.
Таким образом,
◙ D – правильная область в направлении оси Оу, если
D ограничена линиями: y = j 1(x), y = j 2(x), x = a, x =b, причем
j 1(x) £ j 2(x), a < b,
j 1(x), j 2(x) – непрерывны на [a, b] (Рисунок 2.4.1.);
◙ D – правильная область в направлении оси Ох, если
D ограничена линиями: х = y 1(у), х = y 2(у), y = с, у = d, причем
y 1(у) £ y 2(у), с < d,
y 1(у),y 2(у) – непрерывны на [с, d] (Рисунок 2.4.2.).
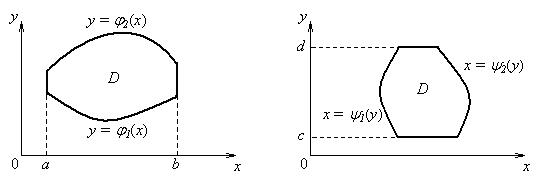
Рисунок 2.4.1 Рисунок 2.4.2
◙ Правильная область – область, правильная как в направлении оси Ох, так и в направлении оси Оу.
Пусть f (x, y) непрерывна в D.
◙ Выражение
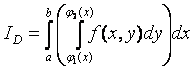 назовем
двукратным интегралом от f
(x,
y)
по области D. Т.е.
назовем
двукратным интегралом от f
(x,
y)
по области D. Т.е.
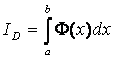 , где
, где
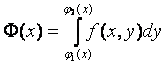 .
.
Свойства двукратного интеграла:
1) Если правильную в
направлении оси Оу область D
разбить на две области
D1
и D2 прямой, параллельной
оси Оу или Ох, то
![]() .
.
Следствие.
![]() .
.
2) (оценка двукратного интеграла) Если m – наименьшее, M – наибольшее значения функции f (x, y) в D, S – площадь области D, то
![]() .
.
3) (теорема о среднем) Существует точка Р ÎD такая, что
![]() .
.
Теорема 2. (Вычисление двойных интегралов)
Если
f
(x,
y)
– непрерывная функция, D
– правильная область в направлении Оу, то 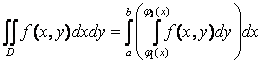 ;
;
если D – правильная область в направлении Ох, то
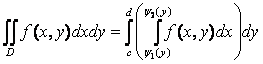 .
.
З а м е ч а н и е. а) Правые части представленных формул являются двукратными или повторными интегралами. Переход от одной формулы к другой называется изменением порядка интегрирования.
б) Если область D не является правильной, то необходимо для начала разбить ее на конечное множество правильных областей.
Замена переменных в двойных интегралах
Пусть в плоскости Оху дана область D, ограниченная линией L.
Предположим, что координаты х и у являются функциями новых переменных u и v: x = х (u, v), y = у (u, v),
причем х(u, v), у(u, v) – однозначны, непрерывны и имеют непрерывные производные в некоторой области D¢ , т.е. установлено взаимно однозначное соответствие между областями D и D¢ : Р(x, y) « Р¢ (u, v),
где u, v – криволинейные координаты точки Р.
Введем обозначение:
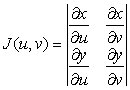
– функциональный определитель (якобиан) функций х(u, v), у(u, v).
Тогда формула замены переменных в двойном интеграле имеет вид:
 .
.
З а м е ч а н и е. Частным случаем замены переменных в двойном интеграле является переход к полярным координатам.
Полярные координаты
Положение точки на плоскости определяется двумя полярными координатами r и j , которые связаны с прямоугольными координатами х и у следующими формулами:
x = r cosj ,
y = r sinj, где 0 £ j < 2p .
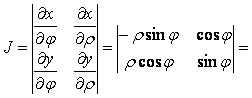
![]() .
.

Рисунок 2.4.4
Следовательно, формула замены переменных принимает вид:
![]()
При этом если область D соответствует рисунку 2.4.5, то
 ;
;
если область D соответствует рисунку 2.4.6, то
 .
.
![]()
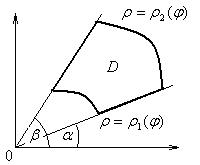

Рисунок 2.4.5 Рисунок 2.4.6
2.5 Лекция 9. Тройные интегралы
Содержание лекции: Тройной интеграл и его свойства. Вычисление тройных интегралов в прямоугольных координатах. Замена переменных в тройном интеграле.
Цели лекции: знакомство с тройным интегралом, его свойствами и техникой вычисления.
Пусть f (x, y, z) – непрерывная функция, определенная в трехмерной области V, ограниченной замкнутой поверхностью S.
Разобьем область V произвольным образом на п элементарных областей:
Dv1 , Dv2 , Dv3 , …, Dvп .
Каждую область отождествим с ее объемом.
Выберем
в каждой области произвольную точку РiÎ
D
v i
(![]() ), и
сопоставим ей значение
f (Pi).
Составим сумму:
), и
сопоставим ей значение
f (Pi).
Составим сумму: 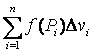 .
.
Эта сумма называется интегральной суммой для функции f (x, y, z) в области V.
Предположим, что diam D vi ® 0 при n ® ¥. Тогда справедлива следующая теорема.
Теорема 1. Если функция f (x, y, z) непрерывна в замкнутой области V,
то
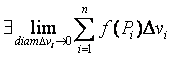 .
.
Этот предел не зависит ни от способа разбиения области V на D vi , ни от выбора Рi Î D vi.
Этот предел называется тройным интегралом от
функции f
(x,
y,
z) в области
V и
обозначается: ![]() или
или
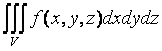 .
.
Физический смысл тройного интеграла:
если f ³ 0 в области V, то можно считать, что f (x, y, z) – плотность распределения некоторого вещества в области V. Тогда тройной интеграл численно равен массе вещества, заключенного в области V.
Вычисление тройных интегралов
Пусть V - область в пространстве, ограниченная замкнутой поверхностью S.
◙ Область V называется правильной (трехмерной) областью, если:
1) всякая
прямая l,
параллельная
оси Oz и проходящая
через внутреннюю точку V, пересекает границу области в двух точках, т.е.
![]() ;
;
2) вся V проектируется на Oxy в правильную (двумерную) область D;
3) всякая часть области V, отсеченная плоскостью, параллельной любой из координатных плоскостей (Оху, Оxz, Oyz), также обладает свойствами 1) и 2).
Таким образом,
V – правильная область, если V ограничена снизу и сверху двумя поверхностями, заданными соответственно уравнениями z = y1(x, y) z = y2(x, y).
Введем понятие трехкратного интеграла.
Пусть D – проекция области V на плоскость Oxy, ограниченная линиями: y = j 1(x), y = j 2(x),
x = a, x =b,
j 1(x) £ j 2(x), a < b.
Тогда трехкратный интеграл от функции f (x, y, z) по области V определяется так:

Рисунок 2.5.1
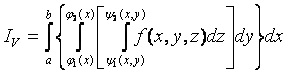 .
.
Свойства трехкратного интеграла:
1) Если область V разбить
на области V1 ,V2 плоскостью, параллельной
какой-либо из координатных плоскостей, то ![]() .
.
Следствие.
![]() .
.
2) (оценка трехкратного интеграла)
Если m –
наименьшее, M
–
наибольшее значения функции
f (x,
y,
z)
в области
V, V –
объем области V, то
![]() .
.
3) (теорема о среднем) Существует точка Р Î V такая, что
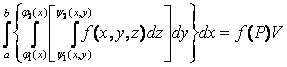 .
.
Теорема 2. Если
f
(x,
y,
z)
–
непрерывная функция, V – правильная область, то 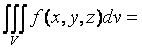
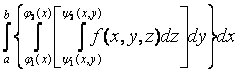 .
.
Замена переменных в тройных интегралах
Пусть V – замкнутая область в пространстве.
Предположим, что координаты х, у и z являются функциями новых переменных u, t, w: x = х(u, t, w), y = у(u, t, w), z = z(u, t, w),
причем х(u, t, w), у(u, t, w), z(u, t, w) – однозначны, непрерывны и имеют непрерывные производные в некоторой области V¢, т.е. установлено взаимно однозначное соответствие между областями V¢и V¢ : Р(x, y, z) « Р¢ (u, t, w),
где u, t, w – криволинейные координаты точки Р.
Введем обозначение:
– функциональный определитель
(якобиан) функций
x = х(u, t, w), y = у(u, t, w), z = z(u, t, w).
Тогда формула замены переменных в тройном интеграле имеет вид:
![]()
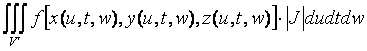
З а м е ч а н и е. Частным случаем замены переменных в тройном интеграле является переход к сферическим или цилиндрическим координатам.
Сферические координаты
Положение точки в пространстве определяется тремя сферическими координатами r, j , q , которые связаны с прямоугольными координатами х, у, z следующими формулами:
x = r sin j cos q ,
y = r sin j sin q ,
z = r cos j ,
где 0 £ r < ¥ , 0 £ j £ p , 0 £ q < 2p .
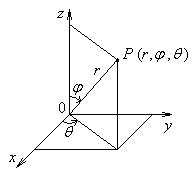
Рисунок 2.5.3
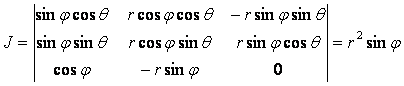 .
.
Следовательно, формула замены переменных принимает вид:
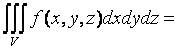
![]()
Цилиндрические координаты
Положение точки в пространстве определяется тремя цилиндрическими координатами r,q, z которые связаны с прямоугольными координатами х, у, z следующими формулами:
x = r cosq,
y = r sinq,
z = z, где 0 £ r < ¥ , 0 £ q < 2p.
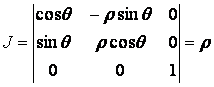 .
.

Рисунок 2.5.4
Следовательно, формула замены переменных принимает вид:
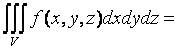
Пример. Вычислить
![]() , где
V – полушар радиуса
R с центром
в начале координат О.
, где
V – полушар радиуса
R с центром
в начале координат О.
Решение.
Данная область V ограничена
снизу поверхностью z = 0,
а сверху – поверхностью
![]()
(в цилиндрических координатах
![]() ).
).
Следовательно,
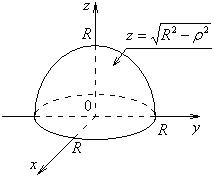
Рисунок 2.5.5
![]()

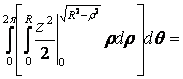
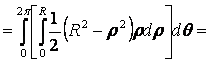
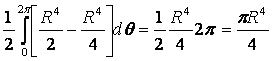 .
.
3 Дифференциальные уравнения. Ряды
3.1 Лекция 10. Дифференциальные уравнения, основные понятия
Содержание лекции: Дифференциальные уравнения, основные понятия. Дифференциальные уравнения 1-го порядка. Дифференциальные уравнения высших порядков. Уравнения, допускающие понижение порядка.
Цели лекции: знакомство с основными понятиями теории дифференциальных уравнений.
1. Основные определения
◙ Дифференциальным уравнением (Д.У.) называется уравнение, связывающее независимую переменную х, искомую функцию y = f (x) и ее производные y¢, y¢¢, …, y(n): F (x, y, y¢, y¢¢, …, y(n)) = 0. (1)
Если это уравнение можно разрешить относительно п-ой производной, то его можно записать в виде y(n) = f (x, y, y¢, y¢¢, …, y(n-1)). (1¢)
◙ Порядком Д.У. называется порядок наивысшей производной, входящей в уравнение.
◙ Д.У. (1) называется линейным, если левая часть его есть многочлен первой степени относительно y, y¢, y¢¢, …, y(n) (и не содержит их произведний), т.е. a0(x)y(n)+ a1(x)y(n-1)+…+ an(x)y = f (x) , (2)
где a0(x), a1(x), …, an(x) – коэффициенты уравнения (определены и непрерывны в некотором интервале); f (x) – правая часть уравнения.
◙ Уравнение (2) называется однородным (без правой части), если f (x) = 0.
◙ Уравнение (2) называется неоднородным (с правой частью), если f (x) ¹ 0.
◙ Решением или интегралом Д.У. называется всякая функция y = j (x), которая, будучи подставлена в уравнение (1), превращает его в тождество.
Решить, или проинтегрировать, данное Д.У. означает найти все его решения в заданной области.
График решения называется интегральной кривой.
◙ Общим решением Д.У. (1) называется такое его решение:
у = j ( х, С1, С2, …, Сп ),
которое содержит столько независимых произвольных постоянных С1, С2, …, Сп , каков порядок этого уравнения.
Если общее решение задано в неявном виде Ф(х, у, С1, С2, …, Сп ) = 0, то оно называется общим интегралом.
◙ Всякое решение Д.У., которое получается из общего решения, если приписать определенные значения произвольным постоянным, в него входящим, называется частным решением этого Д.У. , у = j ( х, С1, С2, …, Сп ), и, соответственно, Ф(х, у, С1, С2, …, Сп ) = 0, называется частным интегралом.
При заданных
начальных
условиях при х
= х0:
 (н.у.)
(н.у.)
постоянные С1, С2, …, Сп можно подобрать так, что функция
у = j ( х, С1, С2, …, Сп ), являющаяся решением уравнения (1), будет удовлетворять этим условиям. Таким образом, введем новое понятие:
Задача Коши (начальная задача)
Найти решение y = j (x) Д.У. (1), удовлетворяющее начальному условию (н.у.).
Теорема 1. Если в уравнении y(n) = f (x, y, y¢, y¢¢, …, y(n-1))
функция f (x, y, y¢, y¢¢, …, y(n-1)) и ее частные производные по аргументам y, y¢, y¢¢, …, y(n-1) непрерывны в некоторой области, содержащей значения
х = х0,
y = у0,
y¢ =
у¢0, ![]() ,
,
то существует и при том единственное решение y = j (x) задачи Коши.
2. Дифференциальные уравнения 1-го порядка
Д.У. 1-го порядка имеет вид: F(x, y, y¢ ) = 0, (3)
или если уравнение разрешено относительно производной, то
y¢ = f (x, y). (3¢)
Общее решение y = j (x, C) зависит от одного произвольного постоянного С.
Теорема 2. (о существовании и единственности решения Д.У.)
Если в уравнении y¢ = f (x, y) функция f (x, y) и ее частная производная f ′y (x, y) – непрерывны в некоторой области D, содержащей некоторую точку (x0, y0), то существует единственное решение этого уравнения
у =j (х), удовлетворяющее начальному условию: j (x0) = у0.
Геометрический смысл теоремы: Существует единственная функция
у =j (х), график которой проходит через точку (x0, y0).
Рассмотрим основные виды Д.У. 1-го порядка.
1) Уравнения с разделяющимися и разделенными переменными
◙ Д.У. вида M (x) dx + N (y)dy = 0 (4)
называют уравнением с разделенными переменными.
Общий интеграл его есть
![]() .
.
а) Д.У. вида y¢ = f (x)g(y) (5)
можно привести к уравнению с разделенными переменными:
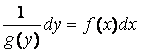 , (предполагая, что
g(y)
¹
0).
, (предполагая, что
g(y)
¹
0).
Интегрируя, находим обший
интеграл уравнения (5):
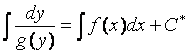 .
.
◙ б) Д.У. вида M1(x)N1(y)dx + M2(x)N2(y)dy = 0 (6)
называется уравнением с разделяющимися переменными.
Его можно привести к уравнению с разделенными переменными.
Умножим
(6) на
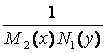 :
:
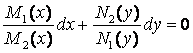 .
.
Интегрируя, получим общий интеграл уравнения (6):
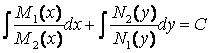 .
.
2) Однородные уравнения
◙ Функция f (x, y) – однородная функция п-го порядка относительно х и у Û "l Î R f (lx, ly) = ln f (x, y).
◙ Уравнение y¢ = f (x, y) (7)
называется однородным уравнением 1-го порядка, если f (x, y) – однородная функция нулевого порядка относительно х и у.
Метод решения однородного уравнения
По условию "l Î R f (lx, ly) = f (x, y).
Рассмотрим
это тождество при ![]()
![]() .
.
Тогда уравнение (7) примет
вид: ![]() (7′)
(7′)
Сделаем подстановку:  Û у
= их
Þ
Û у
= их
Þ
Þ
 Þ
(7′)
Û
Þ
(7′)
Û
![]() Û
Û
Û
 – уравнение с разделенными переменными.
– уравнение с разделенными переменными.
Интегрируя, найдем: 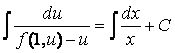 .
.
Подставляя
после интегрирования вместо и отношение
![]() ,
получим общий интеграл уравнения (7′).
,
получим общий интеграл уравнения (7′).
З а м е ч а н и е. М(х,у)dx + N(x,y)dy = 0 однородное уравнение 1-го порядка Û М(х,у) и N(x,y)однородные функции одного порядка.
3) Линейные уравнения
◙ Линейным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и ее производной. Оно имеет вид:
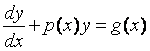 ,
(8)
,
(8)
где p(x) и g(x) – заданные непрерывные функции от х (или постоянные).
Meтоды решения линейного уравнения
а) метод Бернулли
Будем искать решение уравнения (8) в виде y(x) = u(x)v(x)
Дифференцируя
обе части равенства (9), находим:
![]() .
.
Подставим полученное
выражение в уравнение (8):
 или
или
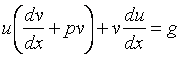 . (10)
. (10)
Выберем
функцию v
такой,
чтобы  . (11)
. (11)
Разделяя переменные в этом Д.У. относительно функции v, находим
![]() .
.
Так
как достаточно одного отличного от нуля решения уравнения (11), то положим
C1
= 1, тогда ![]() (12)
(12)
Очевидно, что v(x) ≠ 0.
Подставляя найденное значение v(x) в уравнение (10), получим
![]() Þ
Þ
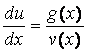 Þ
Þ
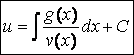 .
.
Таким образом,
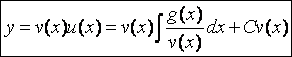 .
.
б) Метод вариации
Для решения уравнения (8)
первоначально решают уравнение:
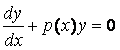
и заменяют в общем решении
![]() константу
С1 на функцию С(х), такую, чтобы она
удовлетворяла уравнению (8).
константу
С1 на функцию С(х), такую, чтобы она
удовлетворяла уравнению (8).
4) Уравнение Бернулли
◙ Уравнение вида
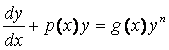 , (п ≠ 0, п ≠ 1)
(13)
, (п ≠ 0, п ≠ 1)
(13)
называется уравнением Бернулли.
Методы решения уравнения Бернулли:
а) метод Бернулли
(поиск решения в виде y(x) = u(x)v(x) как для линейных уравнений);
б) подстановка z = y -n+1 сводит уравнение (13) к линейному уравнению относительно новой функции z.
Так как 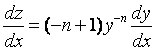 ,
то, умножив уравнение (13) на (–п +1)у –п, получим:
,
то, умножив уравнение (13) на (–п +1)у –п, получим:
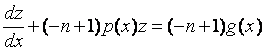 . (14)
. (14)
Решив это линейное уравнение относительно z, и подставив вместо z выражение y -n+1, найдем у(х) – решение уравнения (13).
5) Уравнение в полных дифференциалах
◙ Уравнение вида P(x, y)dx + Q(x, y)dy = 0, (15)
где P(x, y), Q(x, y) – некоторые функции, непрерывные вместе со своими частными производными в некоторой области и
![]() , (16)
, (16)
называется уравнением в полных дифференциалах.
Выполнение условия (16) равносильно тому, что левая часть уравнения (15) есть полный дифференциал некоторой функции u(x, y), т.е.
P(x, y)dx + Q(x, y)dy = du(x, y) Þ (15) Û du(x, y) = 0 Þ u(x, y) = C,
где 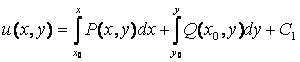
(здесь (х0, у0) – точка, в окрестности которой существует решение Д.У.(15))
Таким образом, получаем общий интеграл уравнения (15):
 .
.
3. Дифференциальные уравнения высших порядков
Т.к. основные общие понятия дифференциальных уравнений высших порядков были уже введены в п.1 данной лекции, то остановимся только на отдельных их видах и методах их решения.
1)
Уравнения вида ![]() .
.
Найдем общий интеграл этого уравнения.
Т.к.
у(п) = (у(п-1))¢ , то
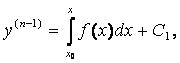
где х0 – любое фиксированное значение х, а С1 – постоянная интегрирования.
Интегрируя еще раз, получим:
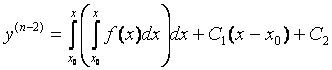 .
.
Продолжая далее, получим, наконец, выражение общего интеграла:
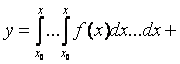
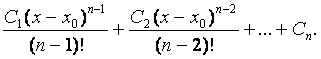
2) Д.У. высших порядков, допускающие понижения порядка
А) Уравнения вида у¢¢ = f (x, y¢ ) (17)
Введем замену: y¢ = р(х). Тогда у¢¢ = р¢.
Следовательно, уравнение (17) приводится к уравнению р¢ = f (x, р), которое является уравнением 1-го порядка.
Если
р = р(х,С1) – общее решение
полученного уравнения, то общий интеграл уравнения (17) имеет вид:
![]()
З а м е ч а н и е. Аналогичным способом можно решить уравнение
у(п) = f ( x, y(п-1)), полагая y(п-1) = р.
Б) Уравнения вида у¢¢ = f ( у, y¢ ) (18)
Введем
замену: y¢ =
z(у). Тогда

Следовательно,
уравнение (18) приводится к уравнению
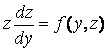 , которое
является уравнением 1-го порядка.
, которое
является уравнением 1-го порядка.
Если z = z( у, С1) – общее решение полученного уравнения, то поскольку
 ,
то
,
то 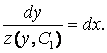
Интегрируя это уравнение, получим общий интеграл исходного уравнения (18): Ф ( х, у, С1, С2) = 0.
3.2 Лекция 11. Линейные дифференциальные уравнения высших порядков. Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами
Содержание лекции: Линейные дифференциальные уравнения высших порядков (ЛДУ). Линейные однородные дифференциальные уравнения (ЛОДУ), структура их общего решения. ЛОДУ с постоянными коэффициентами. Линейные неоднородные дифференциальные уравнения (ЛНДУ), структура их общего решения. Метод вариации произвольных постоянных.
ЛНДУ с постоянными коэффициентами, метод подбора частного решения.
Цели лекции: знакомство с основными методами решения ЛОДУ и ЛНДУ.
Линейные дифференциальные уравнения высших порядков
◙ Д.У. п-го порядка называется линейным, если оно является многочленом первой степени относительно искомой функции y и ее производных y¢, y¢¢, …, y(n), т.е. имеет вид:
a0(x)y(n) + a1(x)y(n-1) +…+ an(x)y = f (x), (1)
где a0(x), a1(x), …, an(x) и f (x) – заданные функции от х или постоянные, причем a0(x) ¹ 0 для всех значений х из той области, в которой рассматривается уравнение (1).
Функция f (x) называется правой частью уравнения.
В дальнейшем будем предполагать, что a0(x), a1(x), …, an(x) и f (x) – непрерывны при всех значениях х, причем a0(x)= 1.
Если f (x) º 0, то уравнение имеет вид
a0(x)y(n) + a1(x)y(n-1) +…+ an(x)y = 0 (2)
и называется линейным однородным (без правой части).
Если f (x) ¹ 0, то уравнение называется линейным неоднородным (с правой частью).
Рассмотрим некоторые свойства ЛОДУ, ограничиваясь уравнениями 2-го порядка.
Теорема 1. Если у1 и у2 – два частных решения ЛОДУ 2-го порядка
у¢¢ + а1у¢ + а2у = 0, (3)
то у1 + у2 – есть также решение этого уравнения.
Теорема 2. Если у1 есть решение ЛОДУ 2-го порядка (3) и С – постоянная, то Су1 есть также решение уравнения (3).
◙ Два решения уравнения (3) у1
и
у2 называются
линейно независимыми на отрезке
[a,
b], если

В противном случае решения называются линейно зависимыми,
т.е. $ l ÎR: у1 = l у2 .
◙ Если у1 и у2 – функции от х, то определитель
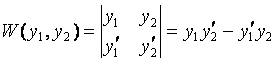
называется определителем Вронского (вронскианом) данных функций.
Теорема 3.
Если функции у1 и
у2 линейно
зависимы на отрезке [a,
b], то
![]()
Теорема 4. Если определитель Вронского W(y1 , y2), составленный для решений y1 и y2 ЛОДУ(3), не равен нулю при каком-нибудь значении х = х0 на отрезке [a, b], где коэффициенты уравнения непрерывны, то он не обращается в нуль ни при каком значении х на этом отрезке.
Теорема 5. Если
решения у1
и у2 уравнения
(3)
линейно независимы на отрезке
[a,
b], то
![]() ни в
одной точке указанного отрезка.
ни в
одной точке указанного отрезка.
Теорема 6. Если у1 и у2 – два линейно независимых решения уравнения (3), то у = С1у1 + С2у2 , где С1 и С2 – произвольные постоянные, есть его общее решение.
Теорема 7. Каковы
бы ни были н.у. ![]()
![]()
можно так подобрать значения С1, С2 , чтобы соответствующее частное решение С1у1 + С2у2 удовлетворяло заданным н.у.
З а м е ч а н и е. Не существует общих методов для нахождения в конечном виде общего решения ЛДУ с переменными коэффициентами. Однако для уравнений с постоянными коэффициентами такой метод существует.
ЛОДУ с постоянными коэффициентами
1. ЛОДУ 2-го порядка с постоянными коэффициентами имеет вид:
у¢¢ + pу¢ + qу = 0, p, q ÎR (4)
Достаточно найти два линейно независимых частных решения.
Будем искать частные решения в виде:
y = ekx , где k – const , (5)
тогда y¢ = kekx, y¢¢ = k2ekx.
Подставляя эти выражения в (1), получим: ekx( k2 + pk + q) = 0.
Т.к. ekx ≠ 0 , то
k2 + pk + q = 0. (6)
Следовательно, если k будет удовлетворять уравнению (6), то ekx будет решением уравнения (4).
◙ Уравнение (6) называется характеристическим уравнением по отношению к уравнению (4).
Корни характеристического уравнения имеют вид:
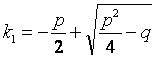 ,
,
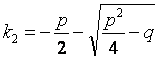 .
.
Возможны случаи:
а) Если характеристическое уравнение имеет два различных действительных
корня, т.е. k1 , k2 Î R ( k1 ≠ k2 ), тогда общее решение имеет вид
![]() .
.
б) Если характеристическое уравнение имеет два одинаковых действительных
корня, т.е. k1 , k2 Î R ( k1 = k2 ), тогда общее решение имеет вид
![]() .
.
в) Если характеристическое уравнение имеет два комплексных корня,
т.е.
k1 ,
k2
Î C:
![]() ,
,
![]() , где
, где
![]()
 ,
,
тогда общее решение имеет вид
![]() .
.
2. ЛОДУ п-го порядка с постоянными коэффициентами имеет вид:
y(n) + a1y(n-1) + … + any = 0, (7)
где a1, …, an – постоянные.
Общее решение находится по следующему алгоритму:
1) составляем характеристическое уравнение;
2) находим его корни: k1, k2, …, kп;
3) по характеру корней находим п линейно независимых частных решений;
4) строим общее решение.
З а м е ч а н и е. Трудность решения ЛОДУ с постоянными коэффициентами заключается в решении характеристического уравнения.
ЛНДУ 2-го порядка имеет вид:
у¢¢ + а1у¢ + а2у = f (x), (8)
где a1, a2 – заданные функции.
Теорема 8. Общее
решение неоднородного уравнения
(8) представляется
как сумма какого-нибудь частного решения этого уравнения
![]() и
общего решения у0
соответствующего однородного
уравнения
и
общего решения у0
соответствующего однородного
уравнения
у¢¢ + а1у¢ + а2у = 0, (9)
т.е.
общее решение неоднородного уравнения (8) имеет вид
![]() .
.
П р и м е ч а н и е. Общий метод нахождения частных решений неоднородного уравнения (метод вариации произвольных постоянных) рассмотреть самостоятельно. (См.[5],стр.88)
Рассмотрим лишь метод подбора частного решения для ЛНДУ с постоянными коэффициентами.
Сначала рассмотрим
Метод подбора частного решения по специальной правой части f (x) для линейного неоднородного уравнения 2-го порядка с постоянными коэффициентами:
у¢¢ + ру¢ + qу = f (x), p, q Î R.
1. Если правая часть имеет вид
![]() , где
Pn(x) – многочлен
п-ой степени, то структура частного
решения
, где
Pn(x) – многочлен
п-ой степени, то структура частного
решения
![]() зависит от того,
является ли
a
корнем
характеристического уравнения
k
2 +
pk
+
q
= 0 или нет. Поэтому возможны варианты:
зависит от того,
является ли
a
корнем
характеристического уравнения
k
2 +
pk
+
q
= 0 или нет. Поэтому возможны варианты:
а) если число a не является корнем характеристического уравнения, то частное решение ищется в следующем виде:
![]() ,
,
где Qn(x) – многочлен п-ой степени (такой же степени, что и Pn(x)) с
неопределенными
коэффициентами, которые находятся после подстановки
![]() ,
, ![]() ,
, ![]() в исходное уравнение;
в исходное уравнение;
б) если число
a
есть простой (однократный) корень характеристического уравнения, то ![]() ;
;
в)
если
число a есть
двукратный корень характеристического
уравнения, то
![]() .
.
2.
Если
правая часть имеет вид ![]() , где
Pп(x),
Qт(x) – многочлены
п-ой и
т-ой степени соответственно, то
структура частного решения
, где
Pп(x),
Qт(x) – многочлены
п-ой и
т-ой степени соответственно, то
структура частного решения
![]() зависит от того, являются ли
a
±
ib
корнями характеристического
уравнения
k 2 +
pk
+
q
=
0 или нет. Поэтому возможны варианты:
зависит от того, являются ли
a
±
ib
корнями характеристического
уравнения
k 2 +
pk
+
q
=
0 или нет. Поэтому возможны варианты:
а) если числа
a
±
ib не являются корнями характеристического уравнения, то ![]() ,
,
где
Up(x),
Vp(x)
– многочлены (с неопределенными коэффициентами), степень которых равна наивысшей
степени многочленов
Pn(x),
Qm(x), т.е.
![]() ;
;
б)
если
числа a
±
ib являются корнями характеристического уравнения, то
![]() ,
,
где Up(x), Vp(x) – многочлены как в пункте а).
Частный случай: если f (x) = М cos bx + N sin bx,
где М, N – постоянные числа, то
а)
если
числа ±ib не являются корнями характеристического уравнения, то ![]()
(где А и В – числа, подлежащие определению);
б)
если
числа ±
ib являются корнями характеристического уравнения, то
![]()
(где А и В – числа, подлежащие определению).
Метод подбора частного решения по специальной правой части f (x) для неоднородного линейного уравнения высшего порядка с постоянными коэффициентами
1. Если правая часть имеет вид f (x) = Pn(x) eax, где Pn(x) – многочлен п-ой степени, то различают два случая:
а) если число a не является корнем характеристического уравнения, то
![]() =
Qn(x)eax
;
=
Qn(x)eax
;
б)
если число
a есть корень кратности m характеристического уравнения, то
![]() = хm
Qn(x)eax.
= хm
Qn(x)eax.
2. Если правая часть имеет вид f (x) = М cos bx + N sin bx, где М, N – постоянные числа, то различают два случая:
а) если число ib не является корнем характеристического уравнения, то
![]() = А
cos
bx
+ В
sin
bx;
= А
cos
bx
+ В
sin
bx;
б)
если
число
ib
есть корень характеристического уравнения
кратности
m,
то ![]() = хm
[ А
cos
bx + В
sin
bx
].
= хm
[ А
cos
bx + В
sin
bx
].
3. Если правая часть имеет вид f (x) = P(x) eax cos bx + Q(x) eax sin bx,
где P(x), Q(x) – многочлены, то различают два случая:
а) если число
a
+
ib не является корнем характеристического уравнения, то ![]() =
U(x)
eax
cos
bx
+
V
(x)
eax
sin
bx,
=
U(x)
eax
cos
bx
+
V
(x)
eax
sin
bx,
U(x), V(x) – многочлены, степень которых равна наивысшей степени многочленов P(x), Q(x);
б) если число a + ib есть корень кратности m характеристического
уравнения, то ![]() =
хm
[U(x)eax
cos
bx
+ V
(x)
eax
sin
bx
].
=
хm
[U(x)eax
cos
bx
+ V
(x)
eax
sin
bx
].
3.3 Лекция 12. Числовые ряды. Функциональные ряды. Степенные ряды, ряды Тейлора.
Содержание лекции: Числовые ряды. Положительные ряды, признаки сходимости положительных рядов. Знакопеременные и знакочередующиеся ряды. Функциональные ряды, степенные ряды. Ряды Тейлора.
Цели лекции: знакомство с основными понятиями числовых и функциональных рядов, методами исследования рядов на сходимость, примерами разложения в степенные ряды некоторых элементарных функций.
1. Числовые ряды
◙ Выражение
вида  (1)
(1)
где ип Î R (n = 1, 2, …) называется числовым рядом. Числа и1, и2, …, ип, … называются членами ряда, число ип – общим членом ряда.
◙ Сумма
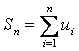 называется
частичной суммой ряда, а сумма
называется
частичной суммой ряда, а сумма
 называется п-ым
остатком ряда.
называется п-ым
остатком ряда.
◙ Если существует конечный предел
![]() ,
то его называют суммой ряда (1),
а ряд (1) называется сходящимся. Если
,
то его называют суммой ряда (1),
а ряд (1) называется сходящимся. Если ![]() не
существует (в частности бесконечен), то ряд (1) называется расходящимся.
не
существует (в частности бесконечен), то ряд (1) называется расходящимся.
Теорема 1. (необходимый признак сходимости ряда).
Если ряд (1) сходится, то ![]() .
.
Обратное утверждение не верно.
Пример. Гармонический ряд 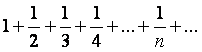 расходится,
хотя
расходится,
хотя 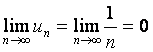 .
.
Теорема 2. (достаточный признак расходимости ряда).
Если ![]() , то ряд (1) расходится.
, то ряд (1) расходится.
З а м е ч а н и е. Сходимость или расходимость числового ряда не нарушается, если в нем отбросить любое конечное число членов. Но его сумма, если она существует, при этом изменяется.
◙ Если все члены ряда ип > 0, то данный ряд называется положительным рядом.
Признаки сходимости положительных рядов
Теорема 3. (признак
Даламбера) Если в ряде с положительными членами (1) существует
конечный предел 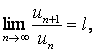 то
то
при l < 1 ряд сходится;
при l > 1 ряд расходится;
при l = 1 признак не применим.
З а м е ч а н и е. Если
 но отношение
но отношение
 для всех номеров, начиная с
некоторого N, то ряд расходится.
для всех номеров, начиная с
некоторого N, то ряд расходится.
Теорема 4. (радикальный
признак Коши) Если для ряда с положительными членами (1) существует
конечный предел ![]() то:
то:
при l < 1 ряд сходится;
при l > 1 ряд расходится;
при l = 1 признак не применим.
Теорема 5. (интегральный признак Коши) Пусть члены ряда (1) положительны и не возрастают, т.е. u1 ³ u2 ³ u3 ³ …
и f (x) – такая непрерывная не возрастающая функция, что
f (1) = u1, f (2) = u2 , …, f (п) = uп .
Тогда ряд (1) и несобственный интеграл
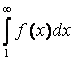 одновременно сходятся или расходятся.
одновременно сходятся или расходятся.
Теорема 6.(1-ый признак сравнения) Пусть даны два ряда
 (1)
(1)
 где
ui > 0,
vi > 0. (2)
где
ui > 0,
vi > 0. (2)
Если un £ vn ( п = 1, 2, …), (3)
то: а) если ряд (2) сходится, то сходится и ряд (1);
б) если ряд (1) расходится, то расходится и ряд (2).
З а м е ч а н и е 1. Данные признаки справедливы только для рядов с положительными членами. Они остаются в силе и для того случая, если некоторые члены 1-го или 2-го ряда – нули. Однако эти признаки перестают быть верными, если среди членов ряда имеются отрицательные числа.
З а м е ч а н и е 2. Теорема 6 справедлива и в случае, если условие (3) начинает выполняться лишь для n ³ N, а не для всех п = 1, 2, 3, …
Теорема 7.(2-ой признак сравнения) Если существует предел
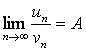 ( А ≠ 0, А ≠
∞),
( А ≠ 0, А ≠
∞),
то ряды (1) и (2) одновременно сходятся или одновременно расходятся.
З а м е ч а н и е 3. Сходимость многих
рядов можно исследовать путем сравнения их с рядом Дирихле
 ,
сходимость которого зависит от параметра р: если
,
сходимость которого зависит от параметра р: если
![]() , то
ряд сходится, если
, то
ряд сходится, если ![]() , то ряд расходится.
, то ряд расходится.
Знакочередующиеся ряды
◙
Ряд  (4)
(4)
где uп ³ 0 ( п = 1, 2, …) – называется знакочередующимся.
Теорема Лейбница. Если члены ряда (4) таковы, что:
1) u1 > u2 > u3 > … (монотонно убывают); (5)
2)![]() (6)
(6)
то ряд (4) сходится и его сумма положительна и меньше u1 , т.е. 0 < S < u1 .
З а м е ч а н и е 1. Теорема Лейбница справедлива, если неравенство (5) выполняется, начиная с некоторого N.
З а м е ч а н и е 2. Теорема Лейбница иллюстрируется геометрически.
Если на числовой прямой откладывать частичные суммы (Рисунок 3.3.1):
s1 = u1, s2 = u1 – u2 = s1 – u2, s3 = s2 + u3, s4 = s3 – u4, … ,
то точки, соответствующие частичным суммам, будут приближаться к некоторой точке s, которая изображает сумму ряда. При этом
s2 < s4 < s6 < …< s < …< s5 < s3 < s1.
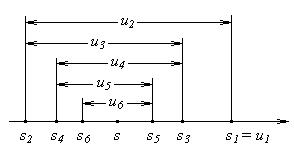
Рисунок 3.3.1
З а м е ч а н и е 3. (Оценка остатка ряда)
Если знакочередующийся ряд удовлетворяет условию Лейбница, то
 –
знакочередующийся ряд с первым членом (–1)п+2 ип+1, следовательно, |
rn | <
ип+1 .
–
знакочередующийся ряд с первым членом (–1)п+2 ип+1, следовательно, |
rn | <
ип+1 .
Таким образом, (т.к. , s = sп+ rn) оценка ошибки: | s – sп | < ип+1 ,
т.е. ошибка, совершаемая при замене s на sп, не превосходит по абсолютной величине первого из отброшенных членов.
Знакопеременные ряды
◙ Знакопеременный ряд – ряд, среди членов которого имеются как положительные, так и отрицательные.
Знакочередующийся ряд – частный случай знакопеременного ряда.
Пусть дан знакопеременный ряд
 (7)
(7)
Рассмотрим ряд, составленный из абсолютных величин
 (8)
(8)
Теорема 8. (Достаточный признак сходимости знакопеременного ряда) Если сходится ряд (8), составленный из абсолютных величин, то сходится и знакопеременный ряд (7).
З а м е ч а н и е. Теорема дает только достаточный признак сходимости знакопеременного ряда, который не является необходимым.
◙ Знакопеременный ряд (7) называется абсолютно сходящимся, если сходится ряд (8), составленный из абсолютных величин его членов.
◙ Если же знакопеременный ряд (7) сходится, а ряд (8) расходится, то данный знакопеременный ряд (7)называется условно (или не абсолютно) сходящимся рядом.
Свойства абсолютно и условно сходящихся рядов
С помощью понятия абсолютной сходимости Теорему 8 формулируют следующим образом: всякий абсолютно сходящийся ряд есть ряд сходящийся.
Теорема 9. Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов. При этом сумма ряда не зависит от порядка его членов.
Теорема 10. Если ряд сходится условно, то, какое бы мы ни задали число А, можно так переставить члены этого ряда, чтобы его сумма оказалась равной А. Более того, можно так переставить члены условно сходящегося ряда, что полученный ряд окажется расходящимся.
2. Функциональные ряды
◙ Выражение вида
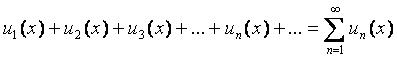 ,
(9)
,
(9)
где ип (х) (n = 1, 2, …) – функции от х, называется функциональным рядом.
При определенных числовых значениях х ряд (9) становится числовым рядом, который может оказаться сходящимся или расходящимся.
◙ Совокупность тех значений х, при которых функциональный ряд сходится, называется областью сходимости этого ряда.
В области сходимости ряда его сумма является некоторой функцией от х. Поэтому сумму функционального ряда обозначают через s(x).
◙ Сумма
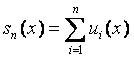 называется
частичной суммой ряда, а сумма
называется
частичной суммой ряда, а сумма
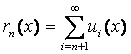 называется п-ым
остатком ряда.
называется п-ым
остатком ряда.
Если функциональный ряд сходится и сумма его равна s(x), то
s(x) = sn(x) + rn(x).
Тогда для любого х из области сходимости имеет место соотношение:
![]() ,
,
т.е. остаток rn(x) сходящегося ряда стремится к нулю при п ® ¥.
◙ Ряд (9) называется мажорируемым в некоторой области (D) изменения х, если существует такой сходящийся числовой ряд
a1 + a2 + …+ an+…, (ai > 0) (10)
что "xÎD справедливы неравенства:½ui(х)½≤ ai (i = 1, 2, …).
При этом ряд (10) называется мажорирующим (мажорантным) рядом.
◙ Степенным рядом (по степеням х) называется функциональный ряд вида а0 + а1х + а2х2 + … + ап хп + … (11)
где аi (i = 0, 1, 2, …) – коэффициенты степенного ряда (постоянные числа).
Областью сходимости степенного ряда всегда является некоторый интервал, который, в частности, может вырождаться в точку.
Теорема 11. (теорема Абеля)
1) Если степенной ряд сходится при некотором х0 ¹ 0, то он абсолютно сходится при "х: ½х½< х0;
2) Если степенной ряд расходится при некотором х0, то он расходится при "х: ½х½> х0.
Теорема 12. Областью сходимости степенного ряда является интервал с центром в 0.
◙ Интервалом сходимости степенного ряда называется такой интервал (–R, R), что при всех хÎ(–R, R) ряд (11) сходится и притом абсолютно, а при всех çхç> R ряд (11) расходится. Число R называют радиусом сходимости степенного ряда.
На концах интервала (т.е. при х = ± R) вопрос о сходимости или расходимости решается индивидуально.
Если R = ∞, то интервалом сходимости степенного ряда является вся числовая прямая, если R = 0, то интервал сходимости вырождается в точку.
Число
R вычисляется по формулам:
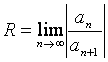 или
или
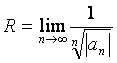 ,
,
которые легко получить, воспользовавшись соответственно признаком Даламбера или радикальным признаком Коши.
Степенные ряды можно почленно дифференцировать и интегрировать в их интервалах сходимости. Радиус сходимости при этом не изменяется.
В общем случае степенной ряд (по степеням (х – х0)) имеет вид:
 ,
,
где постоянные ап ( п = 1, 2, …) также называются коэффициентами ряда.
Интервалом сходимости такого ряда является интервал ( х0 – R; х0 + R ) с центром в точке х0 . Число R – радиус сходимости ряда – вычисляется, как и прежде.
Ряды Тейлора и Маклорена
Если функция f (x) имеет производные в окрестности точки x = a до (n+1)-го порядка включительно, то справедлива формула Тейлора:
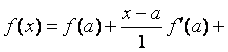

 (12)
(12)
где остаточный
член ![]() вычисляется по формуле
вычисляется по формуле
 ,
0 < θ <
1.
,
0 < θ <
1.
Допустим,
что в окрестности точки x
= a
![]()
Тогда, переходя в формуле (12) к пределу при п ® ¥, получим
ряд Тейлора:
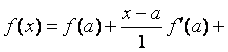

 (13)
(13)
Равенство (13) справедливо лишь в случае, если Rn(x) → 0 при п → ∞.
В этом случае написанный справа ряд сходится и его сумма равна данной функции f (x).
З а м е ч а н и е. Ряд
Тейлора представляет данную функцию f
(x) только тогда, когда
![]()
Если
![]() то ряд не
представляет данной функции, хотя может и сходиться (к другой функции).
то ряд не
представляет данной функции, хотя может и сходиться (к другой функции).
Если в ряде Тейлора a = 0, то получаем частный случай ряда Тейлора – Ряд Маклорена:
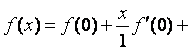

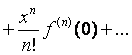 (14)
(14)
Примеры разложения функций в степенные ряды
1. 
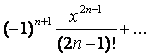 (–¥ <
x <
¥);
(–¥ <
x <
¥);
2. 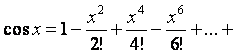
 (–¥ <
x <
¥);
(–¥ <
x <
¥);
3. 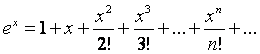 (–¥ <
x <
¥);
(–¥ <
x <
¥);
4.
 (
(![]() );
);
5. Биномиальный ряд
![]()
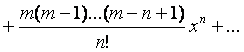 ,
,
где т –
произвольное постоянное число, (![]() );
);
В частности,
при т = –1:
 (
(![]() );
);
при
 :
:
![]() (
(![]() );
);
при
![]() :
:
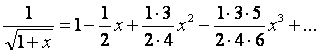 (
(![]() ).
).
Для каждого случая в скобках указана область, в
которой степенной ряд сходится к соответствующей функции. Биномиальный ряд на
концах интервала сходимости ведет себя по-разному в зависимости от
тÎR:
при ![]() абсолютно
сходится в точках
абсолютно
сходится в точках![]() ;
при
;
при ![]() расходится
в точке х = –1 и условно сходится в точке х = 1; при
расходится
в точке х = –1 и условно сходится в точке х = 1; при ![]() расходится в точках
расходится в точках![]() .
.
4 Приложения
Приложение 1. Виды пределов и методы их вычисления
Т а б л и ц а 4.1
|
Виды пределов |
Результат подстановки предельной точки |
Результат или метод вычисления предела |
|
|
|
|
|
1.
|
неопределённость |
|
|
2.
|
|
а) разложение на множители; б) правило Лопиталя; в) умножение на сопряжённое выражение; г) применение эквивалентных бесконечно малых; д) правило 1 этой таблицы |
|
3.
|
|
0 |
|
4. |
|
|
|
5.
|
неопределённость |
привести к неопределённостям
вида |
|
6.
|
|
|
|
7.
|
|
0 |
|
8.
|
|
привести к неопределённостям
вида |
|
9.
|
|
|
|
10.
|
|
а) привести ко второму замечательному
пределу б)
использовать формулу |
|
11.
|
|
|
|
12.
|
|
|
Приложение 2. Таблица эквивалентных бесконечно малых
Т а б л и ц а 4.2
|
|
||
|
1.
|
5.
|
9. |
|
2.
|
6.
|
10. |
|
3.
|
7.
|
11.
|
|
4.
|
8.
|
|
Приложение 3. Производные основных элементарных функций.
Т а б л и ц а 4.3
|
1.
|
7.
|
13.
|
|
2.
|
8.
|
14. |
|
3.
|
9.
|
15. |
|
4.
|
10. |
16. |
|
5.
|
11.
|
17. |
|
6.
|
12. |
|
Список литературы
1. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов. – М.: Наука, 1973. – 720 с.
2. Бугров Я.С., Никольский С.М. Вывшая математика. Дифференциальное и интегральное исчисления. – М.: Наука, 1980. – 432 с.
3. Натансон И.П. Краткий курс высшей математики. – СПб.: Издательство Лань, 1997. – 736 с.
4. Пискунов Н.С. Дифференциальное и интегральное исчисления. Учебник для втузов: В 2 т.–М.: Наука, 1976.–Т.1–456 с.
5. Пискунов Н.С. Дифференциальное и интегральное исчисления. Учебник для втузов: В 2 т.–М.: Наука, 1976.–Т.2–576 с.
6. Хасеинов К.А. Каноны математики. Учебник. – Алматы: 2003. – 686 с.
Содержание
Предисловие 3
1 Введение в анализ
Дифференциальное исчисление функции одной переменной
1.1 Лекция 1. Функция. Числовая последовательность. Пределы 4
1.2 Лекция 2. Непрерывность функций 8
1.3 Лекция 3. Дифференциальное исчисление функции одной переменной 12
1.4 Лекция 4. Исследование функций с помощью производных 16
2 Функции нескольких переменных
Интегральное исчисление функции одной и нескольких переменных 20
2.1 Лекция 5. Первообразная и неопределенный интеграл 20
2.2 Лекция 6. Интегрирование рациональных, иррациональных,
тригонометрических функций 23
2.3 Лекция 7. Определённый интеграл, основные свойства.
Формула Ньютона-Лейбница. Методы подстановки.
Интегрирование по частям 28
2.4 Лекция 8. Двойные интегралы 32
2.5 Лекция 9. Тройные интегралы 36
3 Дифференциальные уравнения. Ряды 40
3.1 Лекция 10. Дифференциальные уравнения, основные понятия 40
3.2 Лекция 11. Линейные дифференциальные уравнения высших
порядков. Линейные однородные и неоднородные
дифференциальные уравнения высших порядков
с постоянными коэффициентами 45
3.3 Лекция 12. Числовые ряды. Функциональные ряды.
Степенные ряды, ряды Тейлора 50
4 Приложения 57
Список литературы 59