Некоммерческое акционерное общество

АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

 

Кафедра высшей математики

 

 

 

МАТЕМАТИЧЕСКИЙ  АНАЛИЗ

Методические указания и тестовые задания

для подготовки к экзамену

для студентов очной формы обучения специальностей

5В070400 - Вычислительная техника и программное обеспечение 

5В070300 - информационные системы

 

 

 

Алматы 2010

Составители: Т.Каирбеков, О.А.Кноль. Математический анализ.   Методические указания и тестовые задания для подготовки к экзамену для студентов очной формы обучения специальностей 5В070400 - Вычислительная техника и программное обеспечение , 5В070300 - Информационные системы. –Алматы: АУЭиС, 2010. – 24 с. 

        Методические указания содержат рекомендации для самостоятельной работы студентов при изучении дисциплины «Математический анализ». Они содержат образцы тестовых заданий  рубежного контроля к первым двум модулям с ответами и образец экзаменационного теста на бумажном носителе и теста компьютерной части экзамена. Приведены теоретические вопросы , база тестовых заданий для компьютерного тестирования .      

 

  1 Модуль .  Введение в математический анализ. Дифференциальное

исчисление функции одной переменной

 

1.1   Теоретические вопросы

 

1.1.1 Понятие функции. Способы задания функции. Приращение функции.           

1.1.2 Числовые последовательности. Предел последовательности. Предел функции.

1.1.3 Бесконечно малые и бесконечно большие величины. Свойства бесконечно малых.

1.1.4 Теоремы о пределах. Односторонние пределы. Замечательные пределы.

1.1.5 Непрерывные функции. Точки разрыва. Классификация точек разрыва.

1.1.6 Определение производной функции. Физический и геометрический смысл производной функции. Связь между дифференцируемостью и непрерывностью функций.

1.1.7 Правило дифференцирования функций. Производные элементарных функций.

1.1.8 Производные сложных функций.

1.1.9 Логарифмические дифференцирования. Производные высших порядков.

1.1.10  Производные параметрически и неявно заданных функций. Уравнение нормали и касательной к кривой.

1.1.11  Дифференциал функции, его геометрический смысл и применение.

1.1.12  Дифференциал высших порядков. Дифференциал сложной функции.

1.1.13  Правило Лопиталя. Теоремы о возрастании и убывании функции.

1.1.14  Экстремум функции. Необходимые и достаточные условия экстремума.

1.1.15  Выпуклость и вогнутость графика кривой. Точки перегиба.

1.1.16 Асимптоты графика кривой. Полное исследование функции.

  

1.2 Образцы билетов рубежного контроля для модуля 1

 

Билет 1

 

Задание	Ответы
1 Вычислить  предел: .	0
2 Вычислить предел: .
3 Вычислить предел: .
4 Вычислить предел: .	0
5 Вычислить предел: .	2
Дана функция
6  Вычислить предел слева в точке  .	0
7  Вычислить предел справа в точке  .	1
8  Определить разрыв функции в точке  .	Разрыв первого рода
9
10
11
12 Найти дифференциал функции .
Дана функция
13 Найти абсциссу точки максимума (минимума) .	абсцисса точки максимума
14  Найти интервал возрастания функции.
15  Найти интервал убывания функции.
16  Найти абсциссу точки перегиба функции.

       

 

 

Билет 2

 

Задание	Ответы
1  Вычислить предел: .
2  Вычислить предел: .
3  Вычислить предел: .
4  Вычислить предел: .
5  Вычислить предел: .
Дана функция
6  Вычислить предел слева .	0
7  Вычислить предел справа .
8 Определить разрыв функции в точке  .	Разрыв первого рода
9
10
11
12  Найти производную функции  .
13 Найти абсциссу точки максимума .	абсцисса точки максимума
14  Найти асимптоту функции .	горизонтальная асимптота,  вертикальная асимптота
15 Найти уравнение касательной  к кривой ,проведённой в т.  .
16 Вычислить предел по правилу Лопиталя                 .

              

Билет 3

 

Задание	Ответы
1 Вычислить предел: .	0
2  Вычислить предел: .
3  Вычислить предел: .
4  Вычислить предел: .
5  Вычислить предел: .	2
Дана функция
6  Вычислить предел справа при .	0
7  Вычислить предел слева при  .	1
8  Определить,какого рода разрыв функции в т. .	Разрыв второго рода
9-12. Вычислить производную первого порядка:
9
10
11
12   Найти производную функции  .
Дана функция
13  Найти абсциссу точки  максимума (минимума).	абсцисса точки максимума
14 Найти интервалы возрастания (убывания) функции.	интервал возрастания
15 Найти интервал убывания функции.
16  Найти точку перегиба функции.

 

2 Модуль. Интегральные исчисления функции одной переменной. Кратные интегралы    

 

2.1 Теоретические вопросы

 

2.1.1 Первообразные функций. Неопределённый интеграл. Табличные интегралы элементарных функций.

2.1.2 Правила интегрирования функции. Метод подстановки и интегрирования по частям.

2.1.3 Интегрирование рациональных, иррациональных и тригонометрических функций.

2.1.4 Определённый интеграл, основные свойства. Формула Ньютона-Лейбница.

2.1.5 Замена переменной и интегрирование по частям.

2.1.6 Кратные интегралы. Двойные и тройные интегралы и их свойства.

2.1.7   Интегрирование кратных интегралов.

2.1.8 Применение кратных интегралов.

2.1.9.Замена переменных в кратных интегралах. Якобиан.

 

 

2.2 Образцы  билетов рубежного контроля для  модуля 2

 

Билет 1

	Задание	Ответы
	1-3 Вычислить интегралы
1	.
2	.
3	.
4	.
5	Записать вид разложения дроби на простейшие   дроби.
6	Каким методом интегрировать? Вычислить: .	Выделение полного квадрата.
	7-8.  Дан интеграл  :                  .
7	После   замены  интеграл имеет   вид...
8	Вычислить интеграл,полученный в п.7.
9	Вычислить несобственный интеграл и исследовать на сходимость.	, сходится
10	Вычислить интеграл в области  .
11	Вычислить повторный интеграл: .
12	Вычислить повторный интеграл  .
	13-14 Вычислить интеграл  по области ,    - замена переменных .
13	Чему равен якобиан преобразования?
14	Вычислить двойной интеграл по указанной замене переменных .
	15-16  Дан интеграл:
15	В тройном интеграле расставить пределы интегрирования .
16	Вычислить тройной интеграл по области .

 

 

Билет 2

 

	Задание	Ответы
	1-4 Вычислить интегралы
1
2
3
4
5	Записать вид разложения дроби  на простейшие дроби .
6	Каким методом интегрировать ? Вычислить .	интегрирование по частям
	7-8 Дан интеграл :
7	После   замены  интеграл имеет   вид...
8	Вычислить интеграл,полученный в п.7 .
9	Вычислить несобственный интеграл   и исследовать на сходимость .	1, сходится
10	Вычислить интеграл  в области
11	Вычислить повторный интеграл   .
12	Вычислить повторный интеграл .
	13-14 Вычислить интеграл по области ,      - замена переменных .

 

13	Чему равен якобиан преобразования?
14	Вычислить двойной интеграл по указанной замене переменных .
	15-16. Дан интеграл:
15	В тройном интеграле расставить пределы интегрирования .
16	Вычислить тройной интеграл по области  .

 

 

 

 

 

 

 

 

 

 

 

 

2.3 Образцы тестовых билетов для модуля 2

 

Билет 1

1-3       Вычислить интегралы:

1) ;                    2) ;                     3)  .

4  Интегрируя по частям ,какую часть надо принять за  ?

5 Разложить функцию  на простые множители (метод неопределённых коэффициентов).

6  Указать метод решения интеграла :

а) интегрирование по частям ;                         

б) выделение полного квадрата ;

в) универсальная подстановка  ;         

г) разложение на простые множители ;

д) другой способ.

7 Привести интеграл 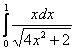 к новому виду путём замены переменной:   .

8  Вычислить интеграл из задания 7.

9  Исследовать на сходимость несобственный интеграл .

 

 

10 Двойной интеграл , где  , сводится к повторному.

11  Вычислить повторный интеграл: .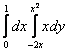

12  Вычислить повторный интеграл .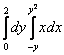

13-14. ,      - замена переменных .

13  Чему равен якобиан преобразования?

14  Сделать замену в двойном интеграле (не вычисляя).

15-16  Дано:  .

15  Расставить пределы интегрирования в тройном интеграле по области  .

16  Вычислить интеграл по области .

                                        

 

Билет 2

 

1-3  Вычислить интегралы:

1) ;                    2)  ;                    3)  .

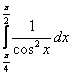4 В интеграле  , какое выражение нужно принять за , если интегрировать по частям?

5  Запишите вид разложения дроби  на простейшие множители.

6 Какой метод интегрирования применяется для вычисления интеграла?  .

а) интегрирование по частям ;                       

б) выделение полного квадрата ;

в) универсальная подстановка ;          

г) разложение на простые множители ;

д) другой метод .

7  Какой вид примет интеграл 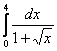после замены переменной    ?

8  Вычислить интеграл из задания 7.

9  Вычислить интеграл:  .

10  Вычислить двойной интеграл :

 

 по области   .

11  Вычислить повторный интеграл  .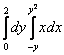

12  Вычислить повторный интеграл: .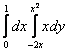

          13-14 ,      -замена переменных .

13  Чему равен якобиан преобразования?

14  Сделать замену в двойном интеграле.

15-16  Дан интеграл .

15  Расставить пределы интегрирования в тройном интеграле по области   .

16  Вычислить этот тройной интеграл по области .

 

 

Билет 3

 

          1-3  Вычислить интегралы:

1) ;                  2) ;                    3) .

4 В интеграле   какое выражение нужно принять за  ,если интегрировать по частям?

5  Запишите вид разложения дроби  на простейшие дроби.

6 Какой метод интегрирования применяется для вычисления интеграла  ?

а) интегрирование по частям ;                       

б) выделение полного квадрата ;

в) универсальная подстановка ;         

г) разложение на простые множители ;

д) другой метод .

7  Какой вид примет интеграл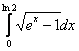 после замены переменной  ?

8  Вычислить интеграл из задания 7.

9  Несобственный интеграл 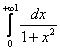 исследовать на сходимость.

10 Вычислить двойной интеграл  по области   .

11  Вычислить повторный интеграл  .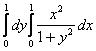

12  Вычислить повторный интеграл  .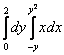

13-14  Дан интеграл ,    -замена переменных .

13  Чему равен якобиан преобразования?

14  Сделать замену в повторном интеграле.

15-16  Дано:   .

15  Расставить пределы интегрирования в тройном интеграле по области .

16  Вычислить этот тройной интеграл по области  .

 

 

3 База тестовых заданий компьютерной части к экзамену по предмету

«Математический анализ»

 

1           Найти область определения функции . (Ответ: ).

2               Исследовать функцию  на чётность, нечётность .(Ответ: чётная).

3               График функции симметричен относительно оси или оси ? ( Ответ: ).

4               Найти точку разрыва функции . Какого рода точка разрыва? (Ответ: , первого рода).

5               В точке разрыва функции вычислить предел справа.                                                                             (Ответ: 1).

 

6               В точке разрыва функции вычислить предел слева.                                                                              (Ответ: -1).

7               Найти точку разрыва функции   . Какого рода точка разрыва? (Ответ: , второго рода).

8               В точке  разрыва функции найти преденл справа.                                                                                (Ответ: ).

9               В точке разрыва функции  найти предел слева. (Ответ: 0).

10          Найти предел:    .        (Ответ: 1).

11          Найти предел:    .       (Ответ: 0).

12          Найти предел:     .      (Ответ: 0).

13          Найти предел,используя эквивалентные бесконечно малые:                                                    .        (Ответ:  ).

14          Найти предел, используя эквивалентные бесконечно малые:                                                   .         (Ответ:  ).

15          Найти предел, используя эквивалентные бесконечно малые:                                                   .         (Ответ:  ).

16          Функция в точке  не определена. Для функции при      найти такое , чтобы функция была непрерывна, если: .      (Ответ: 1).

17          Функция в точке  не определена. Для функции при  найти такое, чтобы функция была непрерывна,если :   .                                      (Ответ: ).

18          Найти:  .       (Ответ: ).

19          Найти: .        (Ответ: ).

20          Найти :  .      (Ответ : -2).

21          Найти :  .       (Ответ : ).

22          Найти первую производную функции .

(Ответ: ).

23          Найти вторую производную функции. 

(Ответ: ).

24          Найти дифференциал функции.

(Ответ: ).

25          Найти приращение функции,если  .

(Ответ: ).

26          Найти первую производную функции .

(Ответ: ).

27          Дано:. Найти: .   (Ответ:  ).

28          Найти производную функции: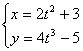   (Ответ: ).

29          Найти производную функции, заданной неявно:.  ( Ответ:   ).

30          Найти касательную, проведённую к кривой  в точке с абсциссой   .            (Ответ:   ).

31          Найти уравнение нормали, проведённой к кривой  в точке с абсциссой    .            (Ответ:   ).

32          Найти дифференциал второго порядка функции  .

(Ответ: ) .

33  Найти вторую производную функции  .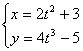   

(Ответ: ) .

 

 34  Найти вторую производную функции, заданной неявно:.       (Ответ:   ).

35  Найти предел по правилу Лопиталя:  .      

(Ответ: ).

36  Найти предел по правилу Лопиталя :  .      

( Ответ: ).

37   Найти промежутки убывания функции .  

( Ответ: ).

38  Исследовать функцию   на экстремум.

( Ответ:   ).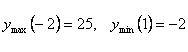

39  Исследовать функцию  на экстремум.    

(Ответ:   ).

40  Найти наибольшее и наименьшее значения функции    на интервале:   .

(Ответ:    наибольшее значение    ,   наименьшее значение ).

41  Найти наибольшее и наименьшее значения функции на интервале:     .

(Ответ:наибольшее значение ,  наименьшее значение ).

42  Максимальное значение функции  в точке х =...                   (Ответ:   х = -2) .

43  Минимальное значение функци   в точке х =...                   (Ответ:  х =1).

44  Найти вертикальную (горизонтальную) асимптоту функции  .        (Ответ:   ).

45  Разложить функцию  в ряд Маклорена.

(Ответ: ).

46  Вычислить интеграл:  .

(Ответ : ).

47  Вычислить интеграл :    .

(Ответ : ).

48  В интеграле какую часть надо взять за   ,чтобы интегрировать по частям ?

(Ответ : ).

49  В интеграле  какую часть надо взять за  ,чтобы интегрировать по частям ?

(Ответ: ).

50  В интегралекакую часть надо взять за   ,чтобы интегрировать по частям?

( Ответ: ).

51  Разложить  дробь   на простейшие дроби.

(Ответ: ).

52 Какой метод применяется для решения интеграла ?

( Ответ:универсальная подстановка  ).

53 В интеграле  можно ли сделать замену переменной :     .      (Ответ: нельзя).

54  Вычислить неопределённый интеграл  .

( Ответ: ).

55  Вычислить двойной интеграл  по области  .

(Ответ:  ).

56  Вычислить повторный интеграл .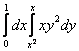

( Ответ: ).

57  Расставить пределы интегрирования в тройном интеграле     , где  - область интегрирования.

( Ответ: ).

58  Найти объём тела, заданного ограничивающими его поверхностями      .

(Ответ: ).

 

4 Образец теста на бумажном носителе закрытого типа

 

Выберите один правильный ответ из вариантов ответа.

 

Задания	Варианты ответов
Дана функция	1.
1  Найти область определения функции .	2.     а))     б)      с)    д)
2  Исследовать функцию на чётность, нечётность .	а) чётная   б)  нечётная 3.     с) ни чётная,ни нечётн. д)  периодическая
4.       3  График функции симметричен относительно оси     5.     оси , начала координат или не симметричен?	6.     а)     б) 7.     с) не симметричен д)симметричен относительно начала координат
8.      4   Найти точки разрыва функции. Какого рода эти     точки разрыва?	а) нет точек разрыва б) ,  первого рода 9.       с) ,  второго рода д) ,  второго рода
Дана функция
5     Найти точки разрыва функции. Какого рода эти точки разрыва?	а)  нет точек разрыва б)  , первого рода  10. с)   , второго р. д) , второго рода
6  Найти предел справа в точке разрыва .	а)  не существует      б)  с)                    д)
7  Найти предел слева в точке разрыва .	а) не существует       б)  с)                    д)
8  Найти предел функции:   .	а)                     б)  с)                    д)   1
9  Найти предел функции :   .	а)                   б)   с)                    д)   1
10  Найти предел функции :   .	а)                   б)   с)                    д)
11.   11  Функция  в точке   не определена. 12. Чтобы функция в точке  была 13. непрерывной,      найти, если:  .	а)                   б)   с)                    д)
12  Функция   в точке    не определена.    Чтобы функция   в точке    была непрерывной,        найти, если :  .	а)                   б)   с)                    д)
13  Вычислить:  .	а)                   б)  с)                    д)
14  Вычислить : .	а)                   б)  с)                    д)
15  Вычислить :  .	а)                   б)  с)                    д)
16  Вычислить : .	а)                     б) с)                    д)
14.   17  Найти первую производную функции 15.  . 16.	а)б) с)д)
17.  18  Найти дифференциал функции .	а)           б)  с)           д)
18.  19  Дано:  Найти:  .	а)                     б) с)                 д)
19.  20  Найти производную неявной функции 20.  . 21.	а)            б)   с)            д)
21 Для функции  укажите уравнение касательной, проходящей через точку  .	а)        б) с)         д)
22.  22  Для функции   найти дифференциал 23.     второго порядка .	а)                  б) ( с)   д)
24.  23  Найти производную третьего порядка     функции     .	а)         б) с)       д)
25.  24  Найти производную второго порядка функции 26. .	а)         б) с)       д)
25 Найти уравнение касательной, проведённой к кривой  .	а)    в) с)       д)
26  Вычислите по правилу Лопиталя:   .	а)         б) с)       д)
27  Вычислите по правилу Лопиталя: .	а)         б) с)       д)
28  Вычислите по правилу Лопиталя: .	а)         б) с)       д)
29 Найти промежутки убывания функции .	а)     б)  с)      д)
30  Исследовать на экстремум функцию  .	а) б) с) д)  нет экстремума
31  Найти абсциссу точки перегиба функции .	а)   б) с)       д)
32  Найти промежуток вогнутости функции .	А)(-1;1)      б)(-6;1) В)(1;5)       г)(-1;3)
33  Горизонтальная (вертикальная) асимптота  графика функции  имеет вид :	а)   б) с)       д)
34  Разложить функцию  в ряд Маклорена . 27.	а) б) с)  д)
35  Найти интеграл: .	а)        б) с)   д)
36  Найти интеграл :   .	а)   б) с)       д)
37  В интеграле  какую часть надо взять за      , чтобы интегрировать по частям? 28.	а)    б) с)           д)
38  В интеграле какую часть надо взять за 29.   , чтобы интегрировать по частям? 30.	а)      б) с)           д)
39  Указать вид разложения дроби  на    31.  простейшие дроби .	а)    б) с)      д)
40  Для интеграла   указать метод 32. вычисления .	а) интегрирование по частям                          б)выделение полного квадрата    с)универсальная подстановка               д)  другой метод
41  Вычислить несобственный интеграл.	а)   б) с)       д)
42  Вычислить двойной интеграл 33.   по области  .	а)   б) с)       д)
43   Поменять порядок интегрирования : 34. .	а)    б) с)        д)
35.44  Вычислить тройной интеграл по области, 36.перейдя к цилиндрическим координатам: 37.   .	а)       б) с)       д)
38.45  Найти объём тела, ограниченного поверхностью 39. .	а)     б) с)       д)

 

Список литературы 

1.     Мустахишев К.М., Ералиев С.Е., Атабай Б.Ж. Математика (краткий курс высшей математики).-Алматы, 2009.

2.     Хасеинов К.А.  Каноны математики.-Алматы, 2004.

3.     Задачи и упражнения по математическому анализу для втузов /под редакцией Б.П.Демидовича. –Москва,1966 или более позднее издание.

4.     П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова Высшая математика в упражнениях и задачах. - Москва, 1986. ч.1,2.

5.     Индивидуальные задания по высшей математике:  Учеб.пособие. ч.1 /под ред. А.П.Рябушко.-Мн.: Высш.школа, 2000.                                                

6.     Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов.-М.: Наука,1985. т.1,2

 

         

Содержание

Введение

1. Модуль 1.          

          1.1   Теоретические вопросы                                                             4 

1.2  Образцы билетов рубежного контроля для модуля 1                            4

2. Модуль 2.

2.1   Теоретические вопросы                                                             8

2.2   Образцы билетов рубежного контроля для модуля 2                   8

2.3  Образцы тестовых билетов для модуля 2                                               12

3. База тестовых заданий компьютерной части  к экзамену по

предмету «Математический анализ»                                                                       16

4. Образец теста на бумажном носителе закрытого типа                                       21

5. Рекомендуемая литература                                                                                  23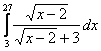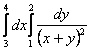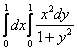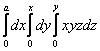
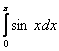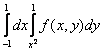