ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

 «Алматы энергетика және байланыс университеті»

коммерциялық емес акционерлік қоғам

 

 

 

 

Т. Дәуменов 

ЭЛЕКТРОДИНАМИКА

 Оқу құралы

 

 

 

Алматы 2011

 

УДК 53:519.6 (075.8)

ББК 31.26Я73

Д 21. Дәуменов Т. Оқу құралы;

Электродинамика.

АУЭС. Алматы, 2010 - 79 б. 

 

ISBN  9965-850-30-5

  

Оқулықта электродинамиканың тәжірибелік заңдары мен Максвелл теңдеулерінің арасындағы байланыс көрсетілген. Квазистационарлы және айнымалы электромагниттік өрістердің қасиеттері суреттелген. Гармоникалық осциллятор және тогы бар раманың толқын шығаруы, сонымен қатар электромагниттік толқындардың әртурлі ортада таралуы қарастырылған. Оқулықта статикалық өрістер қарастырылмаған.

Барлық мамандықтар бойынша оқитын студенттерге арналған оқу құралы.

Сур. 19.

 

ББК 31.26Я73

 

ПІКІР БЕРУШІЛЕР: КБТУ,  физ.-мат. ғыл.д-р., проф. Ф.Ф. Умаров.

                                   АУЭС, техн. ғыл.канд., Т.С. Байпақбаев.  

 

         Қазақстан Республикасының Білім және Ғылым Министрлігінің 2010 ж. баспа жоспары бойынша басылады.

 

ISBN  9965-850-30-5

  

 

© «Алматы энергетика және байланыс университеті» КеАҚ, 2011.

 

Кіріспе 

         Электромагниттік құбылыстар табиғатта кездесетін құбылыстардың ішінде ерекше орын алады. Электродинамика – электромагниттік құбылыстарды зерттейтін ғылым, ондағы барлық заңдылықтар Максвелл теориясына негізделген. Максвелл теңдеулері тәжірибе арқылы алынған заңдардың математикалық модельдері. Сондықтан, классикалық механикадағы Ньютон заңдары сыяқты Максвелл теориясының электродинамикада алатын орны ерекше зор.

«Электродинамика» деген сөзді тікелей аударсақ, ол электр зарядтарының қозғалуын және өзара әсерлесуін зерттейтін ілім деуге болады. Мұндай анықтама электродинамиканың негізгі мазмұнын аша алмайды, оның басты мақсаты және негізгі мазмұны – электромагниттік өріс туралы, электромагниттік өрістің зарядтар және токтармен байланысы туралы ілім.

Өріс туралы ұғым классикалық механикада да қолданылады, бірақ ол математикалық жеңілдік үшін формальды түрде енгізілген.

Электродинамикадағы өріс табиғатта кездесетін материяның ерекше бір түрі. Электромагнит өрісінің энергиясы да, импульсы да бар, оларды алып жүретін өрістің өзі. Электромагниттік өріс алғаш зарядтардың қозғалуымен пайда болғанымен, олар өзін тудырған өріс көздерінен ажырап, кеңістікте электромагниттік толқын ретінде таралады. Мұндай тұжырымға келу үшін көптеген ғалымдардың (Кулон, Эрстед, Ампер, Био-Савара, Фарадей) еңбегі сіңді. Ағылшын ғалымы Дж. Максвеллдің электродинамика ғылымына қосқан үлесі өте зор десек артық болмас. Ол өз атымен аталған теңдеулер жүйесінің негізін қалаған ғалым.

Қазір электромагниттік өрістің материялық қасиеттері мен көріністерінің қалтқысыз дәлелденгеніне ешқандай күман жоқ. Г. Герц 1887 ж. тәжірибе жүзінде электромагниттік толқынның бар екенін байқады, П.Н. Лебедев 1901 ж. жарық қысымын өлшеу, 1960 ж. Р. Паунда мен Г. Ребки «жарықты өлшеу» тәжірибесін жасады. Ал, электротехникалық, радиотехникалық және электрондық құралдар мен тетіктер электродинамика заңдылықтарына негізделгенін айтпаса да түсінікті.

Классикалық электродинамика пәні әртүрлі деңгейде мазмұндалады. Көбінесе, электромагниттік құбылыстарды сыйпаттаған кезде денелердің материалдық құрылысын және электр зерядтарының дискреттілігін еске алудың қажеті жоқ. Заттардың электрлік және магниттік қасиеттерін диэлектриктік , магниттік , өтімділіктермен, ал өткізгіштерді меншікті электрөткізгіштікпен  сыйпаттап, зарядтар мен токтар кеңістікте үздіксіз көлемдік заряд  және ток  тығыздықтарымен орналасқан десек, осыған негізделген электромагниттік өріс теориясын макроэлектродинамикалық (феноменологикалық) теория деп атайды. Бұл теорияның негізгі теңдеулері – жоғарыда аталған Максвелл теңдеулері. Микроэлетродинамикада (электрондық теория) электромагниттік өріс теориясы электрлік зарядтардың дискреттілігімен қатар қарастырылады. Мұндай көзқарасты алғаш Г. Лоренц енгізгендіктен, классикалық электрондық теорияның негізгі теңдеулерін Максвелл – Лоренц теңдеулері деп атайды.

Өзінің шектілігіне қарамастан Лоренцтің электрондық теориясы макротеория тұрғысынан қарағандағы түсініксіз мәселелерді қанағаттандырарлық түрде тәжірибе нәтижелеріне сай келетін түсініктер бере алды. Ал, бүгінгі электрондық теория электродинамика мен классикалық механикаға ғана емес, сонымен қатар кванттық механика және статистикалық физикаға да негізделген.

Оқушыға ұсынылып отырған кітапта макро – және микроэлектродинамика теориялары мүмкіндігінше қатар мазмұндалады, электромагниттік құбылыстарды қарастырғанда осы екі теория бірін-бірі толықтырады деген ойдамыз. Оқулықта электростатика және магнитостатика бөлімдері қарастырылмаған.

 

I  ТАРАУ

Максвелл теңдеулері – тәжірибе арқылы алынған заңдардың математикалық модельдері

 

1. Электрлік заряд және ток. Электромагниттік өріс

 

1.1 Заряд және ток тығыздықтары

 

«Электрлік заряд», «электромагниттік өріс» - электродинамиканың негізгі ұғымдарына жатады. «Электрлік заряд» ұғымы зарядталған денелердің және бөлшектердің фундаменталды қасиеттерімен тығыз байланысты. Ол қасиеттер, біріншіден, әрбір заряд өз айналасында электромагнитік өріс туғызуында, екіншіден, өрістің зарядтарға тигізетін күш әсерінде. Осы аталған екі қасиетті элетрлік зарядтың шамасы  сыйпаттай алады. Оның өлшем бірлігі – 1 кулон (Кл). Анытама бойынша ток күші  зарядың уақытқа қатынасымен өрнектеледі:

 

                                                       

Бұл жерде  -  уақыт ішінде өткізгіштің көлденең қимасы арқылы өткен заряд шамасы. Си өлшем бірлігі жүйесінде ток күшін ампермен (А) өлшегендіктен, зарядтың өлшем бірлігі токтың өлшем бірлігінің туындысы ретінде қарастырылады: 1 Кл = 1 А с.

         Заряд – скалярлық шама, ол – оң және теріс, я болмаса нөлге тең болуы мүмкін.

         Толық заряд  - Лоренц түрлендіруінің инварианты (бір инерциалды есеп жүйесінен екінші инерциалды жүйеге көшкенде өзгермейтін шама).

         Заряд – аддитивтік шама: кез келген зарядталған денелердің жалпы заряды сол денелердің зарядтарының алгебралық қосындысына тең.

         Аталған заряд қасиеттері тәжірибе арқылы анықталған. Зарядтардың дискретті, немесе үздіксіз орналасуы да тәжірибе арқылы анықталады. Зарядтардың ең кіші бөлінбейтін мөлшері – элементарлық заряд электронға, протонға және басқа да элементарлық бөлшектерге тән, оның мөлшерінің модулі  (субэлементарлы бөлшектер – кварктерді еске алмасақ).

Сонымен, зарядтардың табиғи қасиеті – дискреттілік болғанымен, классикалық макроэлектродинамикада ззарядтарды үздіксіз, белгілі бір тығыздықпен  кеңістікте орналаса алады деп айтуға болады:

 

                                                                                                         (1.1)

 

 - кеңістіктегі  - көлем элементіндегі шексіз аз заряд мөлшері. (физикалық шексіз аз шама математикалық шексіз аз шама емес,  заряды  зарядына қарағанда әлдеқайда аз, бірақ элементарлы зарядтарға қарағанда көп, сондықтан зарядтардың дискреттілігін еске алмауға болады. Сол сыяқты  элементі  көлемінен әлдеқайда аз болғанымен, әрбір атомның көлемінен әлдеқайда көп).

         Кеңістіктің шекті көлемінде жатқан зарядтар зарядтың көлемдік тығыздығы  арқылы былай табылады:

 

                                                  .                                               (1.2)

 

Қозғалыстағы зарятар ток туғызатыны белгілі, сондықтан, оны сыйпаттау үшін ток тығыздығы  ұғымын келесі түрде енгізуге болады:

 

                                                                                             (1.3)

 

 - белгілі нүктедегі  зарядының жылдамдығы.

Ток тығыздығынан ток күшіне көшу қиын емес, егер ток күшін ,  - векторының  беті арқылы өтетін заряд ағыны ретінде қарастырсақ (1.1 сурет):

 

                                                                                         (1.4)

 

 векторының  бетінің нормалына  түсірілген проекциясы.

 

 

1.1 сурет

 

Егер зарядтардың қозғалыуына байланысты олардың тығыздығы кеңістікте уақытқа байланысты өзгеріп отырса, онда зарядтың тығыздығы кеңістіктегі нүкте координаттарының және уақыт кезеңінің функциясы ретінде қарастырылуы керек:

                                                   

 

Онда токтың тығыздығы да жалпы түрде нүкте координаттары мен уақытқа тәуелді функция болады:

                                                    .

 

         1.2 Зарядтың сақталу заңы

 

Зарядтың сақталу заңы табиғаттың негізгі абсолюттік заңдарының қатарына жатады. Элементарлық бөлшектердің өзара әсерлесу кезіндегі зарядтардың алгебралық қосындысы ешуақытта өзгермейді (элементарлық бөлшектердің бір-біріне түрленуі классикалық электродинамикада қаралмайды).

Егер  тұйық бетімен қошалған  көлеміндегі  зарядының азаюы, кейбір зарядтардың  тұйық беті арқылы өткен ағынына байланыстылығы математикалық түрде былай жазылады:

 

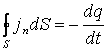                                                 .                                              (1.5)

 

(1.5) өрнегі зарядтың сақталу заңының интегралдық түрі деп аталады. Егер осы формулаға векторлық анализдегі Гаусс теоремасын қолдансақ және (1.2) өрнекті ескерсек, онда зарядтың сақталу заңының дифференциалдық түрін былай жазуға болады:

 

                                                 .                                              (1.6)

 

Бұл алынған теңдеу токтың үздіксіздік теңдеуі деп те аталады. Тұрақты ток үшін , сондықтан:

 

                                                      .                                                  (1.7)

 

Соңғы теңдеудің физикалық мағынасы: тізбекте тұрақты ток болу үшін, ток тығыздығының сызықтары тұйық болуы қажет. Бұл - өрістің стационарлы болу шарты.

 

         1.3 Электромагниттік өріс

 

         Электромагниттік өріс – электрлік және магниттік әсерлер байқалатын кеңістіктің белгілі бір бөлігі. Өрісті электр өрісінің кернеулігі , электрлік ығысу , магнит өрісінің кернеулігі , магнит өрісінің индукциясы  веторларымен сыйпаттауға болады. Бұл векторлар өзара байланысты:

 

                                                     ,                                                  (1.8)

 

                                                     ,                                                 (1.9)

 

Халықаралық СИ өлшемдер жүйесінде диэлектрлік , магниттік  тұрақтылар - өлшемді шамалар, сондықтан тіпті вакуум үшін де  және ,  және  векторларының өлшем бірліктері бірдей емес.

 

                                              ,                                          (1.10)

 

                                              .                                          (1.11)

Осы тұрақтылардың мәндерінің өзара байланысы электродинамикалық тұрақты – с арқылы ( - жарықтың вакуумдегі жылдамдығы) анықталады.

 

                                               .                                                    (1.12)

 

         Өріс векторлары  жалпы түрде координаттар мен уақыттың функциялары, ал диэлектриктік  және магниттік  өтімділіктер тек координаттарға ғана байланысты шамалар, бұлар уақытқа тікелей байланысты емес.

 

2. Кулон заңының өріс тұрғысынан қарағандағы мазмұны

 

Кулон заңы  арақашықтықта жатқан екі нүктелік  және  зардтарының өзара әсерлесу күшін анықтайды:

 

                                                .                                             (2.1)

 

Егер екі зарядтың біреуі нөлге тең болса, онда күш те нөлге тең. Бір ғана  (немесе ) заряды арқылы Кулон заңы (2.1) бойынша ешнәрсе айтуға болмайды. Айталық,  заряды ғана бар екен делік. Екінші  - «байқаушы» зарядын индикатор ретінде қолданып, оны «шексіздіктен» бірте-бірте  зарядының қай жағыныа болмасын оған жақындатсақ, «байқаушы» зарядқа әсер ететін күш барын байқауға болады (механикалық жанасу жоқ!). Ол күштің бар екенін біз  - заряды арқылы анықтай аламыз. Сондықтан, 1-де айтылған көзқарасқа байланысты зарядтардың өзара әсерлесуін мына түрде сыйпаттауға болады: а) кезкелген нүктелік заряд, мысалы  өзінің төңірегінде электр өрісін туғызады, ол өрістің әсер ету күші сол электр өрісінің кернеулігі  арқылы анықталады:

 

                                                .                                             (2.2)

 

 заряды орналасқан нүктеден кернеулік анықталатын нүктеге тартылған радиус-вектор. б)  нүктелік заряды  кернеулігі бар өрісіне қойылған болса, онда ол өрістің әсер ететін күшін «сезеді»:

                                                     .                                                  (2.3)

 

(2.2) формуласын (2.3)-ке қойсақ, онда  және  зарядтарының күшін былайша жазуға болады:

 

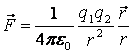                                               .                                           (2.4)

 

Сондықтан (2.3) формула - өріс тұрғысынан қарағандағы Кулон заңы деп қарауға болады. Ол формуладағы  зарядынан басқа бүкіл кеңістіктегі барлық зарядтардың  - орналасқан нүктедегі қорытынды өріс кернеулігі деп түсіну керек.  Егер  болса

 

                                                       .                                                    (2.5)

 

Соңғы формула кернеуліктің физикалық мағынасын ашуға көмектеседі: электр өрісінің кернеулігі – бірлік оң зарядқа әсер ететін күш, басқаша айтсақ, электр өрісінің кернеулігі - өрістің күштік сыйпаттамасы болып табылады.

 

         3. Электростатикалық Гаусс теоремасы

 

 тұйық бетінің ішінде орналасқан  нүктелік зарядының кернеулігінің  осы бет арқылы өтетін  ағынын  есептеп көрейік (3.1 сурет):

 

                                                                                                     (3.1)

 

 

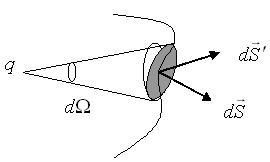
3.1 сурет

 

3.1 суретінен  және  арасындағы байланысты табуға болады

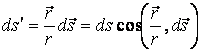                                                                             (3.2)

элементі  элементінің радиусқа перпендикуляр жазықтығына проекциясы, демек,

 

                                                                                                       (3.3)

 

 заряды жатқан нүктеден көрінетін денелік бұрыш элементі. Олай болса, (3.1) интегралы (2.2), (3.2), (3.3) формулалары арқылы, келесі түрде жазуға болады:

 

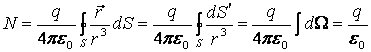                       .                    (3.4)

Мұнда  тұйық бетінің ішкі нүктеден қарағандағы толық денелік бұрыштың  болатыны ескерілген, яғни:

 

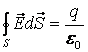                                                   .                                                (3.5)

 

Егер  тұйық бетінің ішінде көптеген  нүктелік зарядтар болған болса, толық кернеулік барлық зарядтардың кернеуліктерінің векторлық қосындысына тең:

 

                                                                                                       (3.6)

Бұл жағдайда (3.5) теңдеуінің оң жағы зарядтардың алгебралық қосындысына тең болу керек:

 

                                                                                                        (3.7)

Онда электростатикалық Гаусс теоремасы дискретті зарядтар жүйесі үшін келесі түрде жазылады:

 

                                                                                               (3.8)

 

         4. Өріс кернеулігінің дивергенциясы. Максвелл теңдеуі

 

Зарядтар көлем бойынша үздіксіз орналасса, толық заряд келесі интегралмен анықталады:

                                                                                                        (4.1)

 

(3.8) теңдеуінің сол жағын векторлық анализдегі Гаусс теоремасымен (Қ 8) түрлендірейік:

 

                                                                                             (4.2)

 

Онда (3.8) және (4.2) өрнектерін қолданып, электростатикалық Гаусс теоремасын былай өрнектеуге болады:

 

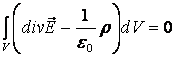                                          .                                       (4.3)

 

 көлемі нөлге тең емес, демек

 

                                                    .                                                 (4.4)

 

Бұл бірінші ретті дербес туындылы дифференциалдық теңдеу – вакуумдегі электростатика үшін Максвелл теңдеулерінің бірі болып табылады. Декарт координаттар жүйесінде ол мына түрде жазылады:

 

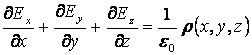                                   .                               (4.5)

 

Сонымен, Максвелл теңдеуі (4.4) электростатикалық Гаусс теоремасының (3.8) дифференциалдық түрі екеніне көз жеткіздік. Керісінше, электростатикалық Гаусс теоремасы – Максвелл теңдеуінің интегралдық түрі. (4.4) Максвелл теңдеуінің  физикалық мағынасын келесі түрде ашуға болады: электр өрісінің күш сызықтары зарядтан басталып, зарядта аяқталады, немесе, бір шеті шексіздікке кетеді. Егер заряд оң болса, , сол нүктеде өрістің көзі (бастауы) бар, ал зарядтеріс таңбалы болса , ол нүтедекернеуліктің күш сызықтары аяқталады да, заряд жоқ нүктклерде кернеулік күш сызықтарының басталуы да, аяқталуы да мүмкін емес. Былайша айтқанда, заряд электр өрісінің көзі болып табылады (4.1 сурет).

 

 

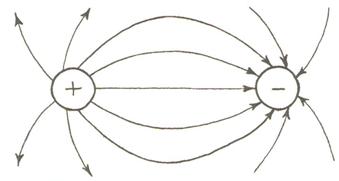
                                                     4.1 сурет

 

         5. Ығысу тогы

 

         Айнымалы токтарды қарастырған кезде зарядтың сақталу заңын сыйпаттайтын үздіксіздік теңдеуі (1.6) және тұрақты ток тізбегінің тұйық болу шартының (1.7) арасында қайшылық бар екені көрініп тұр. Сонымен, біріншіден

 

                                                 ,                                              (1.6)

 

екіншіден

 

                                                      .                                                  (1.7)

 

Айнымалы ток үшін

 

                                                  .                                              (5.1)

 

өткізгіштік ток тығыздығының векторы  заряд тығыздығы өзгерген нүктелерден басталып, сондай нүктелерде аяқталады. Сонымен, айнымалы ток үшін өткізгіштік тогының сызықтары тұйық бола алмайды. Мысал үшін, конденсаторы  бар электр тізбегін қарастырайық (5.1 сурет):

 

 

5.1 сурет

 

         Бұл тізбек бойымен тұрақты ток жүрмейтініне ешқандай күман жоқ, себебі конденсатодың екі жақтауының арасыснда вакуум, ол арқылы заряд өте алмайды, яғни (1.7) теңдеуі қанағаттандырылмайды. Керісінше, (5.1 суретте) көрсетілген тізбек бойымен айнымалы ток жүруіне конденсатор кедергі бола алмайды. Бірақ, бұл жағдайда да конденсатордың ішінде зарядтар жүрмейді. Демек, конденсатор жақтауларының арасында өткізгіштік тогын жалғастыратын табиғаты басқа ток түрі болуы керек. Ол ток ығысу  тогы деп аталды, ол өткізгіштік тогын тұйықтайды. Сонда тізбек бойымен токтың жүру шарты (1.7) жалпы түрде толық ток  сызығына жазылу керек:

 

                                           .                                       (5.2)

 

Енді Максвелл теңдеуінің

 

                                                   

Екі жағынан да уақыт бойынша дербес туынды алайық

 

                                      .                                   (5.3)

 

Бұл жерде координаттар мен уақыт бойынша алынған дербес туындылардың орнын ауыстыруға болатыны ескетілген. (5.3) – ті (1.6) – ға қойып,алынған нәтижені (5.2) мен салыстырып, ығысу тогы  үшін жалпы түрде келесі байланысты табамыз:

                                                    .                                                 (5.4)

 

Расында, ығысу ток тығыздығының табиғаты тіпті басқа екені көрініп тұр. Оның өлшем бірлігі өткізгіштік ток тығыздығының өлшем бірлігімен бірдей. Бұл токтың шамасы электр өрісінің берілген нүктедегі өзгеру жылдамдығына тура пропорционал. Тізбекте өткізгіштік ток жүргенде Джоуль жылуы бөлінетіні белгілі, ал ығысу тогы жүргенде жылу бөлінбейді. Кезінде Максвелл енгізген физикалық шама -  ток деп бекер аталмайтыны түсінікті, өйткені өткізгіштік тогы қандай магнит өрісін тудырса, ығысу тогы да дәл сондай магнит өрісін тудырады.

 

         6. Толық ток заңын қорытындылау

 

         Тұрақты ток үшін толық ток заңы былай оқылады: магнит өрісінің индукция векторының тұйық контур  бойымен алынған циркуляциясы  - ге көбейтілген осы контур орап жатқан токтардың алгебралық қосындысына тең:

 

                                                                                     (6.1)

 

 - тұйық контур  орап жатқан барлық токтардың алгебралық қосындысы, яғни, толық өткізгіштік ток. Интегралдау кезінде  контурын айналу бағыты толық ток бағытымен оң винттік жүйе құрайды. Толық ток заңын шексіз түзу сызықты токқа арналған Био-Савара заңынан алуға болады. Егер  контуры ешқандай ток орамаған болса, интеграл нөлге тең. Егер сызықтық ток саны көп болса, жалпы магнит өрісін табу үшін, әрбір токтың тудырған өрісін өзара алгебра ережесімен қосу керек:

                                     .                                 (6.2)

 

Соңғы формуладағы  тогының таңбасы оның бағытына және интегралдаған кезде  контурын айналу бағытына байланысты. Егер  контурын айналу бағыты токтың бағытымен оң винтті жүйе құрса  оң таңбамен жазылады, керісінше болса – теріс таңбаға ие болады. Осы заңның дифференциалдық түрін алайық. Ол үшін (1.4) өрнегі арқылы (6.2) формуланы төмендегідей өрнектеуге болады:

 

                                               .                                            (6.3)

 

Осы өрнектің сол жағын Стокс теоремасы (Қ 10)бойынша түрлендіріп,

 

                                                                                            (6.4)

келесі түрде жазайық:

 

                                            .                                         (6.5)

 

 беті ерікті түрде алынғандықтан

 

                                                   .                                                (6.6)

 

(6.6) тұрақты токтың магнит өрісі үшін вакуумдегі Максвелл теңдеулерінің бірі болып табылады. Магнит өрісі потенциалды өріс емес, ол  - құйынды өріс.Өріс құйынын ток туғызады, құйынның қуаты ток күшіне тура пропорционал. Максвелл теңдеуінің интегралдық түрі – толық ток заңы. Жоғарыда магнит өрісі тек өткізгіштік ток емес, сонымен қатар ығысу тогымен де тудырылатыны сөз болған. Ендеше, табиғатта ығысу тогы болатынын, оның өткізгіштік токтың үзілген жеріндегі сызықтарын одан әрі қарай жалғастыратынын қорытындай келе, вакуумдегі толық ток заңын келесі түрде жазуға болады:

 

                                         .                                      (6.7)

 

Одан

 

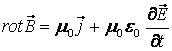                                           .                                       (6.8)

 

Соңғы теңдеу вакуумдегі айнымалы өріс үшін Максвеллдің дифференциалдық теңдеулерінің бірі болып шықты. Бұл теңдеу айнымалы электромагнитік өріс үшін қосымша деректер бере алады. Мысалы, магнит өрісі мен электр өрісінің векторлары кеңістіктің әр нүктесінде бір-бірімен байланысты екендігін, өткізгіштік ток пен ығысу тогының магнит өрісін тудыру заңдылығы бірдей екендігін, сонымен қатар (6.8) теңдеу табиғаты екі түрлі токтардың әрқайсысы магнит өрісінің қуаты бірдей құйындарын тудыруға себепкер болатынын сыйпаттайды.

 

         7. Электромагнитік индукция заңының дифференциалдық түрі

 

          контурымен шектелген  беті арқылы өткен магнит индукциясының ағыны  өзгеретін болса,  индукция электр қозғаушы күшінің әсерімен контурда индукциялық ток пайда болады. Фарадейдің тәжірибе арқылы алынған электромагниттік индукция заңы келесі түрде жазылады:

 

                                                  .                                               (7.1)

 

Минус белгісі (Ленц ережесі) индукциялық токтың бағыты өзін тудырған магнит өрісі ағынының өзгеруіне әрқашан қарсы әсер ететіндігін сыйпаттайды (7.1, 7.2 суреттер). Мұндағы назар аударатын нәрсе, электр қозғаушы күшінің әсерімен пайда болған электр тогының бағыты сыртқы магнит өрісінің  бағытына байланысты емес.  контурындағы индукциялық токэлектр өрісінің  әсерінің салдары деп түсіну керек. Шама жағынан элетр қозғаушы күш осы контурдың бойымен бірлік оң зарядты қозғауға жұмсалған электр өрісінің жұмысына тең:

 

                                                  .                                               (7.2)

 

 

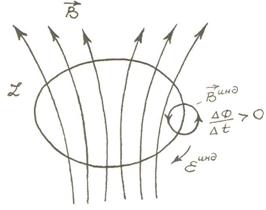
7.1 сурет

 

Ол вольтпен өлшенеді . Анықтама бойынша манит индукциясының ағыны  келесі формуламен өрнектеледі:

                                                    .                                                 (7.3)

 

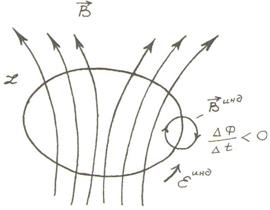
7.2 сурет

 

Ағынның өлшем бірлігі . (7.2), (7.3) арқылы (7.1) теңдігі келесі түрге келтіруге болады:

 

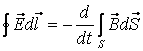                                              .                                          (7.4)

 

Жалпы айтқанда, электромагниттік индукция құбылысы кеңістікте тұйық өткізгіштің бар-жоғына байланысты емес, магниттік индукция өзгерген болса, кеңістікте әрқашан электр өрісі пайда болады. Ал, сол кеңістікте тұйық өткізгіштің болуы, электр өрісінің әсерімен өткізгіште индукциялық ток жүруін қамтамасыз етеді.

         (7.4) теңдігінің сол жағын Стокс теоремасымен түрлендіріп, интеграл алынып отырған  бетінің ауданы уақытқа байланысты емес деп есептеп уақыт алвнған туындыны интеграл астына кіргізгеннен кейін Фарадей заңын мына түрге келтіруге болады:

 

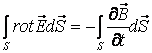                                             .                                         (7.5)

 беті ерікті түрде алынғандықтан

 

                                                  .                                               (7.6)

 

Декарт координаттар жүйесінде осы векторлық теңдеу төмендегідей өрнектеледі:

 

                                                                                    (7.6а)

 

(7.6) – Максвелл теңдеуі Фарадейдің элетромагниттік индукция заңының дифференциалдық түрі. Бұл теңдеу айнымалы өрістерде электр өрісі құйынды өріс екенін сыйпаттайды. Электр өрісінің құйыны кеңістіктегі әр нүктеде магнит өрісінің өзгеруіне байланысты пайда болады және оның қуаты магнитөрісінің өзгеру жылдамдығына тура пропорционал. Құйынды электр өрісінің бағыты магниттік индукция бағытымен сол винтті жүйе құрайды (минус таңбасының мағынасы, 7.3 сурет):

 

 

7.3 сурет

 

 

         8. Магнит өрісі сызықтарының тұйықтылығы

 

Максвелл теңдеуінің (7.6) екіжағынан да дивергенция операциясын алайық

 

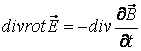                                              .                                           (8.1)

Ротордың дивергенциясы әрқашан нөлге тең.

 

                                              .                                           (8.2)

 

 уақытқа байланысты емес. Берілген  үшін  қандай болса,  векторының басқа мәндері үшін де оның дивергенциясы өзгермеу керек, мысалы,  нөлге тең болған мәні үшін де. Олай болса, оның дивергенциясы да нөлге тең:

 

                                                     .                                                  (8.3)

 

Магнит өрісі сызықтарының не басталу, не аяқталу нүктелері жоқ, басқа сөзбен айтқанда, магниттік индукция векторының сызықтар – тұйық сызықтар. Соңғы Максвелл теңдеуін электр өрісі векторының дивергенциясымен салыстырсақ, онда табиғатта магниттік зарядтар болмайды деген тұжырым жасауға болады. Максвелл теңдеуін (8.3) Гаусс теоремасымен (Қ 8) интегралдық түрін жазу қиын емес:

 

                                                    .                                                 (8.4)

 

Индукцияның  сызықтары тұйық болғандықтан, кез келген  тұйық бетінің ішіне қанша ветор сыззықтары кірсе, сонша сызықтар сыртқа шығады (8.1 сурет):

 

 

8.1 сурет

 

        

         9. Вакуумдегі Максвелл теңдеулері. Электромагниттік өріс энергиясының сақталу заңы. Пойнтинг теоремасы

 

         9.1 Максвелл теңдеулерінің жүйесі

 

         Алдыңғы параграфтарда электродинамика ғылымының негздері болып саналатын, тәжірибе арқылы табылған заңдарды жаңа ұғымдар енгізу және математикалық түрлендірумен бірінші ретті дербес туындылы дифференциалдық теңдеулер – Максвелл теңдеулерін алдық. Оларды (4.4), (6.14), (7.6), (8.3) вакуумдегі теңдеулер жүйесі ретінде қарастырайық:

 

                                                               (9.1)

 

Бұл жүйені скалярлық түрде жазсақ, оған он айнымалы шамалары  бар сегіз скалярлық теңдеулер кіреді. Соңғы төрт шама берілді деп есептесек, анықталатын алты шама сегіз теңдеу арқылы ізделінеді. Жүйенің толықтық шарты орындалмайтын сыяқты. Бірақ I және III, II және IV теңдеулер өзара байланысты, дәлірек айтсақ, I, II – теңдеулерді негізгі теңдеулер, ал, соңғыларын алдыңғы теңдеулердің салдары ретінде қарастыруға болады. Оны дәлелдеу үшін I – теңдеудің екі жағынан да дивергенция операциясын алайық:

 

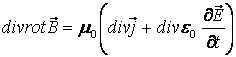                                    .                                 (9.2)

 

(9.2) теңдігінің сол жағы нөлге тең.Ал, оң жағы мына түрге келтіріледі:

 

                                            .                                        (9.3)

 

Зарядтың сақталу заңын ескерсек:

 

                                                    .                                                 (9.4)

 

III – теңдеуді аламыз. Яғни, III – теңдеу I – теңдеудің салдары болып шықты. Сол сыяқты II – теңдеудің екі жағынан дивергенция операциясын, ал IV – теңдеуден уақыт бойынша туынды алсақ, екеуі де бір теңдеуді қанағаттандырады:

 

                                                    

 

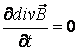
Сонымен,сегіз теңдеулер арасында екі дифференциалдық байланыс барлығының арқасында анықталатын алты шама үшін (9.1) теңдеулер жүйесі толық жүйе болады. Сондықтан бастапқы және шекаралық шарттар белгілі болса,  және  векторлары толық анықталады.

 

         9.2 Электромагниттік энергияның сақталуы

 

         (9.1) теңдеулері электромагниттік өрістің уақыт бойынша өзгерісін көрсеткенмен, олардың әрқайсысын жеке-жеке тәжірибе арқылы тексеруге болмайды. Олардың негізгі физикалық мағынасы энергиясының түрленуін тәжірибе жүзінде тексерумен толық анықталады. Сондықтан электромагниттік өріс векторлары арқылы өрнектелген энергияны анықтауымыз керек. Ол үшін  тұйық бетімен қошалған  көлемінде электромагнит өрісі және қозғалыстағы зарядтар ьар деп есептейік. Электр өрісі зарядтардың қозғалыс күйінің өзгеруіндегі істелінген жұмыстың себепкері, ал магнит өрісінің ол жұмысқа қатысы жоқ, өйткені магнитөрісінің зарядқа әсер ететін күш бағыты жылдамдыққа перпендикуляр. Кернеулігі  электр өрісінің  зарядын  жылдамдықпен қозғағандағы қуаты  келесі түрде өрнекткледі:

 

                            

 

Онда  көлеміндегі толық қуат

 

                                                                                                   (9.5)

 

түгел дерлік жылуға айналады. Интеграл астындағы өткізгіштік ток тығыздығының  орнына (9.1-I) –өрнегі арқылы оның мәнін қояйық:

 

                                  .                               (9.6)

 

(9.6) теңдігінің оң жағындағы бірінші интеграл астындағы өрнекті былай түрлендіруге болады (Қ 25):

 

                                         .                                      (9.7)

 

Енді (9.1-II) теңдеуді пайдаланып, төменгі қатынастарды

 

                                                                                              (9.8)

 

 

ескерсек, (9.6) теңдігі келесі түрге келтіріледі:

 

                            .                        (9.9)

 

Мұнда векторлық анализдегі Гаусс теоремасы қолданылған

 

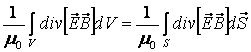                                                                  (9.10)

 

және

 

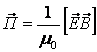                                                                                                 (9.11)

 

Пойнтинг векторы деп аталатын шама енгізілген.

         (9.9) теңдігінің сол жағында уақыт бойынша туындының астында электромагниттік энергия мәні тұр. Өйткені теңдіктің оң жағында бір өлшем уақытта  көлемінен бөлініп шыққан жылу мөлшері бар, ал кері таңбалы  тұйық бетінен алынған интеграл

 

                                                      

 

Осы бет  арқылы өткен электромагниттік өріс энергиясының ағыны болып табылады. Олай болса, (9.9) теңдіктің физикалық мағынасын мына түрде ашуға болады:  бетімен қошалған  көлеміндегі электромагнит өрісінің энергиясы осы  көлемінің ішіндегі жылу бөлінуінің және  беті арқылы  көлемінен шыққан энергия ағынының болу салдарынын азаяды. Басқа сөзбен айтсақ, (9.9) өрнек электромагниттік өріс энергиясының сақталу заңын сыйпаттайды. Осы айтылған тұжырым – Пойнтинг теоремасы деп аталады. Ал, Пойнтинг векторы

 

                                                  

                                                           

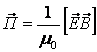
секундына  бетінің бір өлшемі арқылы өткен электромагниттік энергия ағынын сыйпаттайды. Электромагниттік энергия  (9.9) өрнек бойынша клесі формуламен анықталады:

 

                                     .                                (9.12)

 

Электромагниттік энергия әрқашан оң шама, бір өлшем көлемдегі энергия шамасын

 

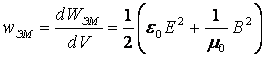                                 .                             (9.13)

 

вакуумдегі электромагниттік өріс энергиясының тығыздығы деп атайды.

 

ІI - тарау

 

Квазистационарлы электромагнит өрісі

 

         10. Квазистационарлық шарттар. Максвелл теңдеулері

 

         Көптеген электродинамикалық есептерді шешкен кезде айнымалы өрісті квазистационарлы жуықтаумен қарастырудың пайдасы көп. Ол жуықтауды айнымалы токтың сызықты тізбегін және ұзын тізбекті линияларды қарастырғанда және т.б. жағдайларда қолданады. Квазистационарлы өріс – айнымалы өрістің дербес түрі, уақыт бойынша мейлінше бәсеңдеу өзгеретін өрістер. Өріс квазистационарлы болу ұшін келесі шарттарды қанағаттандыру керек:

a)                     Электромагнит өрісі уақыт бойынша бәсеңдеу өзгеретіні соншалық, өткізгіш ортада ығыстыру тогын өткізгіштік токқа қарағанда елемеуге болады:

 

                                               .                                           (10.1)

 

Айталық, электромагниттік өріс, мысалы, электр өрісі - жиілігімен өзгерсін

 

                                                    .                                                (10.2)

 

Электростатикалық индукция арқылы кез-келген ортада ығысу тогының келесідей    анықталуын түсіну қиын емес:

 

                                                     .                                                 (10.3)

 

Ал, өткізгіштік ток Ом заңы бойынша бөтен  э. қ. к. жоқ осы есептесек

 

                                                      .                                                  (10.4)

Онда

 

                                           (10.5)

 

болатыны көрініп төр. Ендеше, (10.1) шарт орындалу ұшін

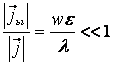                                                 .                                            (10.6)

Егер қарастырып отырған орта (ток жұретін) металл болса, онда                          болғандықтан, (10.6) шарт келесі тұрде бағаланады

 

                                              .                                          (10.7)

Яғни, өткізгіш ортада қарастырып отырған жағдайда спектрдің ультрофиолет облысына дейінгі жиілікте ығыстыру тогын елемеуге болады (әрине, бұл мейлінше жуық баға).

б) өрістің баяу өзгеруі сонша, қарастырып отырған облыста кешігу эффектісін елемеуге болады. Ол эффект электромагниттік толқындардың таралу жылдамдығының шектілігіне байланысты.

Бұл шартты математикалық тұрде өрнектеу ұшін  өсі оң бағытымен  жылдамдықпен таралған жазық электромагнит өрісін қарастырайық. Мысалы, электрлік вектор

 

                                   .                               (10.8)

 

Қарастырып отырған облыстың сызықтық өлшемі мейлінше аз болғандықтан    көбейтіндісін қатарға жіктейік:

 

                                      .                                  (10.9)

 

Соңғы теңдік бойынша, егер оның оң жағы  координатына тәуелді болмаса ғана кешігу эффектісін елемеуге болатыны көрініп тұр, яғни:

 

                                                      .                                                (10.10)

Енді

 

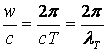                                                                                               (10.11)

 

болатынын ескерсек (- толқын ұзындығы), ақырында өрістің квазистационарлы болу шарты мына тұрде жазылады:

 

                                                      .                                                 (10.12)

Сонымен, егер облыстың сызықтық өлшемі толқын ұзындығынан мейлінше аз болса, онда кешігу эффектісін елемеуге болады. Басқаша айтқанда, (10.12) шарты орындалған облыстарда толқынның таралу жылдамдығы шексіз деп есептелінеді. Мысалы, кәдімгі 50 Гц жиілікті техникалық токтың толқын ұзындығы 6000 км., демек бұл токтың квазистационарлы болу облысының өлшемі мыңдаған км болып шықты.

2.                     Квазистационарлы электромагнит өрісіне арналған Максвелл теңдеулері ерікті орта ұшін келесі тұрде жазылады:

 

                                                                                               (10.13)

 

Бұл жерде

 

Электромагнит өрісінің квазистационарлы облысында электр және магнит өрістерін жеке-жеке қарастыруға болмайды. Өйткені, олар Фарадейдің электромагниттік индукция заңы арқылы бір-біріне тәуелді. Ал, (10.6), (10.12) шарттар бойынша ығысу тогы арқылы болған байланысты елемеуге болады.

 

         11. Өріс векторлары  және потенциалдар  арасындағы байланыс. Потенциалдарға арналған теңдеулер

 

1.                     Магниттік индукция   теңдеуін қанағаттандырады, егер

                                    

                                                                                                       (11.1)

болса және векторлы потенциал  ұшін қосымша шарт

 

                                                                                                       (11.2)

 

орындалуы қажет. Себебі, ығысу тоғын елемесек, токты квазитұйық деп есептеуге болады. Ал, электр өрісінің кернеулігі Фарадейдің дифференциалды түрдегі заңы бойынша потенциалды өріс бола алмайды. Сондықтан, ол тек қана скалярлы потенциал емес, сонымен бірге векторлық потенциалмен де анықталуы керек. (11.1) теңдігі арқылы Фарадей заңын сыйпаттайтын Максвелл теңдеуін түрлендірейік:

 

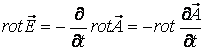                                       .                                   (11.3)

 

Мұнда уақыт бойынша туынды, координаттар бойынша туындының орны ауыстырылған. Соңғы теңдеуді былай жазайық:

 

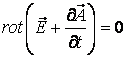                                               .                                           (11.4)

 

Жақша ішіндегі вектор потенциалды вектор болғандықтан, оны скалярлы функцияның градиенті ретінде көрсетуге болады

 

                                              .                                          (11.5)

немесе

 

                                              .                                          (11.6)

 

Расында, электр өрісінің кернеулігі квазистационарлы облысты әрі скалярлы, әрі векторлы потенциалдармен анықталады және екінші қосынды  кернеуліктің тұйық контур бойынша істеген жұмысы нөл болмайтынын көрсетеді.

 

2.                     Скалярлы потенциалға   дифференциалды теңдеу алу үшін  Максвелл теңдеуіне (11.6) кернеуліктің мәнін қояйық:

 

                       

немесе

 

                                                   .                                               (11.7)

 

Бұл Пуассон теңдеуі, электростатикалық өрістегі теңдеумен бірдей болғанымен скалярлық потенциал  және заряд тығыздығы , жалпы тұрде тек қана координаттар емес, сонымен бірге уақыттың функциясы. Бірақ, кешігу эффектісін елемеу себепті скалярлы функция кеңістіктегі белгілі бір нұктеде  уақыт кезеңінде, зарядтардың сол  уақытындағы орналасу жағдайымен анықталады.

Тура сол сияқты векторлы потенциалға да Пуассон теңдеуін жазуға болады

 

                                                    .                                               (11.8)

 

         12. Айнымалы ток тізбегі ұшін Ом заңы

 

Ом заңының дифференциалдық тұрін

 

                                                  ,                                              (12.1)

- нөмірлі өткізгішке қолданып, екі жағын да -ға бөліп тұйық контур бойынша сызықтық интеграл алайық:

 

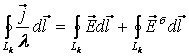                                                                               (12.2)

 

 -нөмірлі өткізгіштің контуры. Сол жақтағы интегралдың астындағы өрнекті тұрлендірейік

 

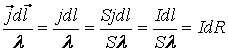                                     .                                 (12.3)

 

  және  векторларының бағыттары бірдей екені ескерілді,    қималы өткізгіштің  бөлімінің кедергісі,  - өткізгіштегі сызықтық ток. Онда

 

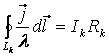                                                                                               (12.4)

Өйткені, тұйық өткізгіштің кез-келген қимасынан өтетін ток күші осы контур бойынша өзгермейді. (12.2) өрнегінің оң жағын қарастырайық. Бірінші интегралды (11.6) формуласы арқылы тұрлендірейік:

 

                                     .                                (12.5)

 

Бірінші интеграл контур тұйық болғандықтан, нөлге тең:

 

                                           .                                          

 

Екінші интегралды түрлендірейік:

 

                     .                (12.6)

 

 - нөмірлі өткізгіштің    контурына тартылған  беті арқылы өткен магнит индукциясының  ағыны. Ал, интеграл

 

                                                  .                                              (12.7)

 

 - контурындағы сырт Э. Қ. К.

 

Ақырында (12.2) теңдік (12.4), (12.6), (12.7) қатынастарын ескергенде келесі түрге келеді

 

                                              .                                          (12.8)

 

Бұл айнымалы ток ұшін - өткізгішіне жазылған Ом заңы. Онда Фарадейдің электромагниттік индукция заңы ескерілген. Магнит индукциясының - өткізгіш контурына тартылған беті арқылы өтетін ағын  индуктивтілік арқылы келесі түрде жазылады:

 

                                                 .                                             (12.9)

Өткізгіштер саны  болғанда Ом заңы индуктивтілік арқылы былай өрнектеледі

 

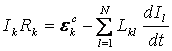                                           .                                      (12.10)

Мұнда - индукитивтіліктер коэффициенті тұрақты деп есептелінген. (12.10) өрнек  белгісізі бар  теңдеулер системасы болып табылады. Бастапқы шарттар белгілі болса бұл система бірмәнді болып шешіледі.

 

13. Электрлік кернеудің айнымалы ток тізбегіндегі жол түріне тәуелділігі. Айнымалы ток кернеуі

 

1.                     Стационарлы өрісте кернеу электр өрісінің кернеулігінен алынған сызықтық интеграл арқылы анықталған болатын

 

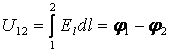                                                                                   (13.1)

 

және бұл интеграл жол формасына байланысты емес екендігі дәлелденген.

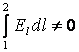Ал айнымалы өрісте потенциал ұғымының мағынасы жоқ, ал интегралдың  мәні ілгеріде ескертілгендей жол түріне байланысты болады, басқаша айтқанда, тұйық тізбек бойынша алынған интеграл  нөлге тең емес. Дегенмен, айнымалы ток үшін де кернеу ұғымы қолданылады. Бірақ, бұл ұғымның мағынасы сол уақытта болады, егер екі нүктенің арасындағы дәл көрсетілген жолмен алынған интеграл болса. Мысал қарастырайық. Айталық, 1 және 2 сандары тұйық тізбектің      ерікті алынған екі нүктесі болсын (13.1 cурет). Осы тізбекке параллель етіп гальванометр  қосылсын.

 

13.1- сурет

 

Егер гальванометр бар тізбектің кедергісі  болса, онда Ом заңы бойынша

 

                                         .                                     (13.2)

Тізбектерде бөтен Э. Қ. К.  жоқ деп есептейік.  және  токтары жүретін тізбек бөлімдерінің кедергілері болсын.  контуры арқылы өткен магнит индукциясының ағыны болсын, ал  бөлім қосылған гальванометр тізбегінің контуры арқылы өткен ағын дейік. Енді суретте көрсетілгендей контурды бойлау бағытын қалап алайық. - контурына (12.8) ескере Кирхгофтың екінші заңын қолданайық:

 

                                    .                                (13.3)

 

Сол сияқты  контуры үшін:

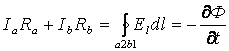                                     .                                 (13.4)

 

Тізбектің тармақталатын 1 және 2 нүктелері үшін Кирхгофтың бірінші заңы бойынша

 

                                                   .                                              (13.5)

(13.3)- (13.5) теңдіктерін  арқылы біріктіріп шешсек:

 

                 .             (13.6)

         (13.6) бойынша гальванометрдің көрсетуі  контуры арқылы өтетін ағынның  өзгеру жылдамдығына байланысты, ал  ағынның өзі гальванометр тізбегінің орналасу жағдайына байланысты. Яғни,  сызықтық интегралының мәні интегралдау жолының түріне байланысты болғаны.

2. Айнымалы ток үшін кернеу ұғымын қолдану қажеттігін көрсету үшін қарапайым электростанция тізбегін қарастырайық. (13.2 cурет). Ол тізбек екі тұйық тәріздес І  және ІІ контурлар бір-бірімен өте жақын орналасқан  және  екі өткізгішпен жалғанған екен дейік.

 

13.2- сурет

         Тізбектің І-бөлімі генераторды, ІІ-бөлімі ток тұтынушы тетік болсын.  бөлімі арқылы ағын мейлінше аз болғандықтан, барлық контурдың магнит индукциясының ағыны  І және ІІ- ілмектерден өткен  ағындарының қосындысына тең болады деп есептейік. ,  қашықтықтары мейлінше аз болғандықтан І-ІІ-ілмектерді тұйық контур тәріздес деп ұйғарсақ, онда

 

                                                               (13.7)

 

болатынына көз жеткізу қиын емес. Мұнда  және  нүктелеріне дейінгі І-бөлімнің жалпы кедергісі, - ІІ бөлімнің кедергісі, ал  осы бөлімдерде болуы ықтимал делінген сырт э.қ.к.

(13.7) теңдігін басқаша жазайық

                                                    (13.8)

         – соңғы теңдіктің кез-келген жағы. Егер І және ІІ ілмектер бір-бірінен алыс жатса, онда олардың арасындағы өзара индукциясын елемеуге болады. Ал  ағындарын өздік индуктивтіліктер  арқылы былай өрнектеуге болады

                                                                              (13.9)

Ендеше,  – мәнін табу үшін тек қана генератордың бөліміне ғана қатысы бар  шамаларды білсек болғаны. Және егер,  белгілі болса тізбектегі ток  тек тұтынушы ІІ-бөлімге ғана тиісті  шамалары арқылы есептелінеді. Онда - ІІ-тұйық тәріздес контурға түсірілген қосымша Э.Қ.К. ретінде қарастыруға болады. Басқаша айтқанда, осы екі нүктенің арасына қосылған гальванометр көрсеткен ток арқылы өлшеуге болатын интегралды

 

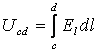                                                                                                (13.10)

айнымалы токтың кернеуі деп есептеуге болады.

 

14. Айнымалы ток тізбегіне арналған теорияның қолданылуы

 

         1. Алдымен -сырт Э.Қ.К.,  - индуктивтілік және  - сыйымдылық, -кедергісі бар тізбектегі токтың уақыт бойынша өзгеру заңдылығын сыйпаттайтын дифференциалдық теңдеу алайық (14.1 cурет).

 

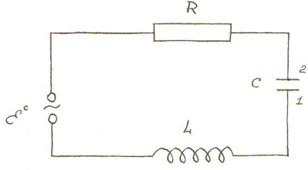
14.1 сурет

 

Ом заңының

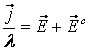                                                                                                   (14.1)

екі жағын  элементіне көбейтіп суретте кқрсетілген тізбек ұшін І нұктеден ІІ нұктеге дейін интеграл алсақ, онда

                                                                                      (14.2)

Мұнда  болатыны ескерілді. Ал,

 

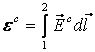                                                                                                  (14.3)

тізбектегі Э.Қ.К.

                                                                                                  (14.4)

конденсаторға түсетін кернеу.

Ары қарай

                                                                                                        (14.5)

және

                                                                                                        (14.6)

екенін ескерсек (-кондесатор жақтауының заряды), (14.2) теңдеу мына тұрде жазылады

                                                                                       (14.7)

         Соңғы теңдеудің екі жағынан да уақыт бойынша туынды алсақ, қарастырылып отырған айнымалы тогы бар тізбек үшін екінші ретті, сызықты, тұрақты коэффициенттері бар дифференциалды теңдеу аламыз:

                                                                           (14.8)

Мұнда  теңдеуі қолданылды.

2. Айталық, тізбекте сыйымдылық жоқ екен делік,  моментінде сырт Э.Қ.К.      тізбекке қосылған болсын. Токтың өсу заңын  табу керек делік. Бұл жағдайда (14.7) теңдеуін қолданған ыңғайлы,  моменті ұшін, ол мына тұрде жазылады

 

                                                                                                (14.9)

         Бастапқы шарт келесі түрде қойылуын түсіну қиын емес:

 

                                                                                                       (14.10)

(14.9) дифференциалдық теңдеудің жалпы шешімі мына түрде беріледі:

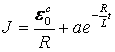                                                                                             (14.11)

- ерікті тұрақты (14.10) шартымен анықталады

                                                                                                                    (14.12)

Онда токтың  моментінен бастап өсу заңдылығы келесі функциямен анықталады:

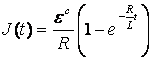                                        ,                                     (14.12)

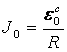Сол сияқты  моменті кезінде  ток жүріп тұрған тізбектен сырт Э.Қ.К.  ағытқанда

                                            ,                                         (14.13)

    токтың азаю заңдылығын табамыз. Сонымен, (14.12), (14.13) – функцияларды зерттеу арқылы өзіндік функция құбылысының арқасында тізбектегі ток өзінің максималды мәніне лезде жетпейді. Сол сияқты сырт Э.Қ.К. ағытылғанда ток лезде нөлге тең болмайды. Мысалы, (14.13) функциясы бойынша ток өзінің максималды мәнінен

                                                                                                         (14.14)

уақыт арасында  рет азаяды, бұл уақытты релаксация уақыты деп атайды.

3. Тізбектегі активті  кедергісін мейлінше аз деп есептесек  және сырт Э.Қ.К. жоқ болса , (14.8) теңдеу мына тұрге келеді:

                                                                                           (14.15)

Оның жалпы шешімі жиілігі  гармоникалық функциялар арқылы өрнектеледі

                                                                                 (14.16)

және

                                                                                             (14.17)

одан

                                                                                                 (14.18)

болатынын көрініп тұр.

Тізбектің осындай түрі тербелмелі контур деп аталады, ал (14.17) осы идеалды   контурдың жиілігі (Томпсон формуласы) және (14.18) – тербеліс периоды  болады. Активті кедергі  тербелістің бірте-бірте өшуіне әкеп соғады.

4. Енді (14.8) дифференциалды теңдеуінің жалпы түрін қарастырайық, сырт Э.Қ.К. - жиілігі  периодты функция болсын дейік

                                                                                                     (14.19)

Ендеше, тізбектегі ток та осы жиілікпен өзгереді, сондықтан (14.8) теңдеуінің шешімін келесі түрде іздеу керек:

                                                                                                      (14.20)

(14.20) өрнегін (14.8) –ге қойып, оны Ом заңы түріне келтіруге болады:

                                                                                                        (14.21)

      Мұндағы

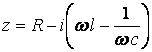                                                                                     (14.22)

тізбектің импедансы деп аталады. Тізбектегі ток Э.Қ.К. заттық бөлігін ғана қарастырғанда былай анықталады:

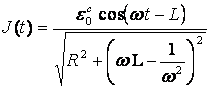                                                                         (14.23)

                                                                                   (14.24)

Бұл ток тізбекке түсірілген кернеуге байланысты:

                                                                                             (14.25)

Ток күші мен кернеу бірдей фазада өзгермейтіні көрініп тұр. Екеуінің арасында фазалық ығысу бар, оның шамасы (14.24) теңдігімен анықталады. Егер сырт Э.Қ.К. ағытылса , тізбектегі ток тербелмелі қозғалысты болуы мұмкін. Онда комплексті тербеліс жиілігі (14.22) қатынасымен  шарты арқылы табылады, яғни

                                                                           (14.26)

Егер түбір астындағы шама теріс болса

                                                   

онда комплексті жиілік таза жорамал сан болады да  көбейтіндісі периодты функция бола алмайды. Сондықтан, бұл жағдайда тізбекте тербеліс болмайды, ондағы процесс апериодты болады. Егер түбір астындағы шама оң болса

                                                   

онда бірте-бірте өшетін тербелістер қоздырылады, оның жиілігі

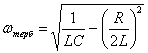                                                                                       (14.27)

ал тербеліс амплитудасы уақыт бойынша

                                                  

заңдылығымен азаяды,  - тербелістің  - өшу декременті деп аталынады. Егер активті кедергі мейлінше аз болған жағдайда (R=0) тербеліс жиілігі  (14.18) - Томпсон формуласына дәл келеді.

 

15. Қозғалыстағы өткізгіштегі ток индукциясы

 

         Сыртқы магнит өрісінде  ерікті қозғалыстағы тұйық сызықты  өткізгішін қарастырайық және өткізгіштің деформациялану мұмкіндігі бар делік. Егер өтікізгіш элементі сыртқы өрісте  жылдамдықымен қозғалса,  элементіндегі әрбір электронға Лоренц кұші әсер етеді де

 

                                                                                                    (15.1)

 

электрондардың ретті қозғалуының себебі болады, яғни электр тоғы пайда болады. Онда (15.1) теңдігіндегі векторлық көбейтінді  эффективті электр өрісінің кернеулігі  пайда болуымен бірдей деуге болады және ол  тұйық контурда индукциялық Э.Қ.К.  қоздырады:

 

                                                                                      (15.2)

 

Ендігі ойларды 15.1- суреті арқылы түсіндірейік. Егер өткізгіш элементі    уақыт ішінде  кесіндісіне қозғалса, онда

                                                                                                          (15.3)

 

(15.2) –формуласының орнына

 

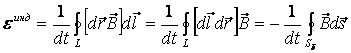                                               (15.4)

 

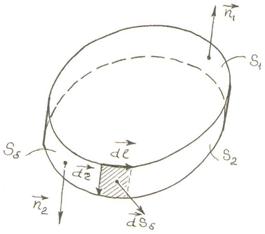
15.1 сурет

                                                           

 уақыт ішіндегі  контуры қозғалғанда  бетінің  орнынан  –орнына ауысқандағы  контуры жасаған бүйір беті. Алдындағы минус таңбасы бүйір бетке салынған сыртқы нормаль  векторымен бағыттары қарама-қарсы болғандықтан қойылды. Сонымен  уақыт моментінен бастап  моментіне дейін  контуры қозғалғанда ,  және  беттерімен шектелген тұйық бет  пайда болды. Максвелл теңдеуінің  интегралдық тұрі бойынша осы тұйық бет арқылы алынған магнит индукциясының  ағыны нөлге тең:

 

                                                                 (15.5)

 

Суретте көрсетілгендей  контурын бойлау бағыты  нормаль бағытымен оң винтті система құратынын ескерсек

 

                                                              (15.6)

 

онда,

 

                                                                  (15.7)

 

болғандықтан (15.4) формуласы келесі түрде жазылады:

 

                                                                                                  (15.8)

 

Бұл  Фарадейдің электромагниттік индукция заңы (7) қаралған түрімен сәйкес болғанымен олардың физикалық мағынасы әртүрлі. Онда біз өткізгіш контуры жылжымайды және ешқандай контур деформациясы жоқ деп есептедік те, магнит ағынының өзгеруі тек қана сыртқы магнит өрісінің өзгеруімен түсіндірілген. Ал, бүл параграфта біз магнит өрісінде  контуры кеңістікте қозғалу мүмкіндігін де және контурдың деформациялану мүмкіндігін де ескердік.

Сондықтан, (15.8), (7.1) формулаларын магнит ағынының кез-келген өзгеру жағдайларында қолдануға болады.

 

         16. Скин - эффект

 

         Тұрақты ток өткізгіштің көлденең қимасы  бойынша бірқалыпты таратылған болса, ал айнымалы токта олай емес. Электромагниттік индукция арқасында ток өткізгіштің бетіне қарай ығысады, айнымалы ток жиілігі өскен сайын ток жүретін өткізгіш қабаты мейлінше жұқара береді де, мейлінше үлкен жиіліктерде ток өте жұқа қабықшамен жүретін болады. Бұл құбылысты скин-эффект дейді (ағылшынша  - тері, ток өткізгіштің “терісіне“ ығысады.).

1. Осы құбылыстың элементарлы теориясын қарастырайық. Ол ұшін  шамалары тұрақты біртекті өткізгіш қарастырайық. Максвелл теңдеулерін

                                                                                                      (16.1)

 

                                                                                                  (16.2)

 

пайдаланып, сырт Э.Қ.К. жоқ деп үйғарайық, онда Ом заңы бойынша

 

                                                                                                         (16.3)

 

Соңғы теңдікті (16.1) теңдеуінің оң жағына қойып, оның екі жағынан ротор алайық та, оң жағына (16.2) теңдеуді пайдалансақ, онда  векторы ұшін дербес туындылы дифференциалдық теңдеу аламыз:

 

                                                                                               (16.4)

 

 Бұл теңдеуді алғанда (Қ 21)  және координаттар мен уақыт бойынша алынған туындылардың орнын ауыстыруға болатыны ескерілді.

Сол сияқты электр өрісінің кернеулігі үшін де осындай теңдеу алуға болатынын тексеру қиын емес

 

                                                                                                (16.3)

 

2. Электрлік өріс пен магниттік өріс векторларының  екеуі де бірдей дифференциалды теңдеуді қанағаттандыратындықтан (16.3) теңдеуінің ғана шешімін көрсетейік. Қарапайымдылық үшін  кеңістікті алып жатқан жартылай шексіз біртекті өткізгіштің беті  жазықтығымен дәл келсін (16.2 cурет).

 

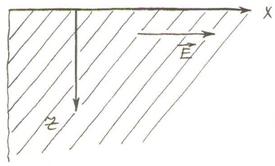
16.2 сурет

 

Айнымалы ток  өсі бойынша жүреді деп есептейік:

 

                                                                                (16.4)

 

оның жиілігі  болсын. Онда Ом заңы бойынша электр өрісінің кернеулігі үшін келесі қатынастар дұрыс болады:

 

                                                                          (16.5)

 

Сонда (16.3) дифференциалды теңдеу қарапайымдалынады:

 

                                                                                        (16.6)

 

Айнымалы ток  жиілігімен ағу үшін ток тудыратын электр өрісі де уақыт бойынша сондай жиілікпен өзгеруі керек. Сондықтан (16.6) теңдеудің шешімі мына тұрде ізделуі керек:

 

                                                                                      (16.7)

 

Соңғы шешімді (16.6) дифференциалды теңдеуге қойып,         көбейтіндісіне қысқартқаннан кейін ол мына тұрге келеді:

 

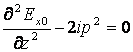                                                                                          (16.8)

 

мұнда ыңғайлылық ұшін

                                                                                                 (16.9)

 

белгілеу енгізілді, - заттық сан. (16.8) теңдеуінің шешімі

 

                                                                                         (16.10)

 

осы түрде ізделінетіні белгілі,  және  ерікті тұрақтылар, ал

 

                                                                                                     (16.11)

 

немесе

 

                                                                   (16.12)

 

Соңғы қатынастар арқылы (42.10) өрнек келесі түрде жазылады:

 

                                                                             (16.13)

 

Ерікті тұрақты  нолге тең болуы керек. Расында,  өткізгіштің бетімен сәйкес, ол өскен сайын өткізгіштің бетінен ішіне қарай алыстағанда  шексіз өсуі керек, ол мүмкін емес, оның физикалық мағынасы жоқ. (16.13), (16.7.) арқылы ізделінген шешімді ақырында былай жазуға болады:

 

                                                                                 (16.14)

 

Немесе жорамал бөлімін елемесек

 

                                                                       (16.15)

 

Осыған сәйкес ток тығыздығы келесі түрде өрнектеледі:

 

                                                                   (16.16)

 

Мұндағы  ток тығыздығының өткізгіштің бетіндегі амплитудасы белгіленеді. Соңғы теңдіктер бойынша өткізгіштің бетінен алыстаған сайын электрлік вектор мен ток тығыздығының векторының фазалары сызықтық заңдылықпен өзгереді, ал олардың амплитудасы экспоненциалды түрде   азаяды. Іс жүзінде айнымалы ток тығыздығы өткізгіштің бетінен

 

                                                                                           (16.17)

 

қашықтығында  рет өшеді (шамамен 2,7 рет). Осы беттік қабат қалыңдығы токтың кіру тереңдігі деп аталынады, осы қалыңдықта токтың және оған сәйкес өрістің негізгі бөлігі шоғырланды.  – шамасын бағалау үшін мысал қарастырайық, металлдар үшін  ,

онда

 

                                   

 

Ал,  болса,  болады.

Келтірілген бағаламалар жоғарғы жиіліктерде скин-эффект айнымалы токтың өткізгіш қимасы бойынша таралуына мейлінше зор әсер ететінін көрсетеді. Тұрақты ток үшін . Сондықтан ток тығыздығы және өріс кернеулігі өткізгіштің қалыңдығы бойынша өзінің тұрақты мәнін сақтайды. Келтірілген элементарлы теория цилиндрлі өткізгіштерде де қолдануға болады. Бұл жағдайда да айнымалы ток жиілігі өскен сайын өткізгіштің жұқа қабықшасына шоғырланатынын көрсетуге болады. Яғни, өткізгіштегі ток жүретін облыс формасы қуыс цилиндрге ұқсайды.

Скин-эффект іс жұзінде маңызы зор, экономикалық және техникалық жағынан тиімді шешімдер жасауға мұмкіндік береді. Өткізгіштің тек сыртқы ток жүретін қабықшасын ғана қымбат металдардан, ал ток жүрмейтін өзекшесін арзан металдардан жасауға болады.

Өткізгіштің кедергісі оның көлденең қимасының ауданына кері пропорционал екені белгілі. Ендеше тұрақты токқа қарағанда жиілігі жоғары айнымалы токқа өткізгіштің кедергісі ұлғаяды.

Сондай-ақ, өткізгіштің ток жүрмейтін өзегінде магнит өрісі нөлге тең. Олай болса, магниттік энергия азайғандықтан ток күші өзгермейді деп есептегенде өткізгіштің өзіндік индуктивтілігі де азаяды.

 

 

III - тарау

 

Айнымалы электромагнит өрісі. Электромагниттік толқын шығару

 

17. Максвелл теңдеулерінің жүйесі. Теңдеулер жүйесінің шешімінің бірден-бірлігі

 

1. Алдымен (9) алынған Максвелл теңдеулерін материалдық орта бар жағдайға сәйкес қорытайық. Ол үшін келесі шарттар орындалады деп ұйғарайық:

a) Өрістегі барлық материалдық денелер қозғалмайды; б) орта қасиеттерін сыйпаттайтын материалдық тұрақтылар  және  уақыт бойынша өзгермейді, өріс кернеуліктеріне тәуелсіз және берілген шамалар, в) өрісте тұрақты магнит және ферромагнетиктер жоқ.

Зарядтардың сақталу заңы (1.6), (7.8) теңдеулері арқылы келесі тұрде жазылады.

 

                                              .                                          (17.1)

 

Сондықтан ығысу тогы  электрлік индукция  векторымен өрнектеледі:

 

                                                     .                                                 (17.2)

 

Ал Максвелл теңдеулері бұл жағдайда электромагнит өрісінің төрт  векторлары арқылы жазылуы керек:

 

                                                                          (17.3)

 

Бұл жүйеге материалдық теңдеулер

                        ,                    (17.4)

электромагнит өрісінің энергиясы

                                          (17.5)

және бастапқы және шекаралық шарттар енгізіледі.

2. (17.4) материалдық теңдеулер арқылы (9) айтылған теңдеулер жүйесінің толықтығы туралы пікірлерді бұл жерде де қолдануға болатынын түсіну қиын емес. Сонда да бастапқы және шекаралық шарттар белгілі болса және заряд және ток тығыздықтары  берілген деп есептесек, Максвелл теңдеулерінің бірден-бірлік шешімдері болатынын келесі мысал арқылы көз жеткізуге болады.

Жүйенің екі шешімі бар екен делік  және . Теңдеулер сызықты болғандықтан бұл шешімдердің айырымдары  да жүйенің шешімі бола алады, бірақ бастапқы және шекаралық шарттар және  шамалары да нөлдік шарттарды қанағаттандырулары керек.

Мысалы

                                                                    (17.6)

болғандықтан

                                               .                                           (17.7)

Біріншіден,  векторлары сыйпаттайтын өріс нөлдік шекаралық шарт орындалуы керек болғандықтан облысты шектеп тұрған  тұйық беті арқылы энергия ағыны болмайды. Екіншіден  болғандықтан осыған сәйкес энергия  өзгеруі мұмкін емес. Бастапқы уақыт моментінде  болғандықтан энергия кейінгі уақыттың кез-келген моментінде де нөл болады.

Ендеше

                                    

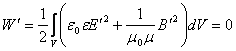
Энергияның нөл болуы тек  болғанда ғана орындалады. Ал онда  яғни жүйенің бірден-бір ғана шешімі бар.

3.Сөйтіп, Максвелл теңдеулерінің бірден-бір шешімі болатынына көз жеткіздік. (17.3) теңдеулерінің әрқайсысының физикалық мағынасы алдыңғы тараулардағы әдіс бойынша ашылады. Ал, олардың кең түрдегі физикалық мағынасы тек қана ол теңдеулерді тәжірибе жүзінде тексергенде ғана болатынын естен шығармау керек. Максвелл теңдеулерін жеке тәжірибе арқылы тексерудің ешқандай маңызы да, мағынасы да жоқ. Оларды (17.4) теңдеулерін еске алып, электромагнит өрісінің энергиясының (17.5) өзгеруі арқылы біртұтас жүйе ретінде тексеруге болады. Сонда ғана Максвелл теңдеулерінің физикалық мәні кең түрде ашылатынын айта кету керек. Сондықтан, айнымалы электромагнит өрісінің толық теңдеулер системасына Максвелл теңдеулерінен (І-ІV) басқа материалдық теңдеулер (V) энергияға арналған өрнек (ІV) және бастапқы, шекаралық шарттар кіреді.

Материалды орта бар кезде Пойнтинг векторы  келесі түрге келтіріледі:

                                                    .                                                (17.9)

         18. Электромагнит өрісінің потенциалдарына арналған теңдеулер

         1. Электродинамикадағы негізгі мәселе - Максвелл теңдеулерін шешіп, өріс векторларының мәнін табу. Ол теңдеулерді тікелей интегралдау көптеген математикалық қиыншылықтарға әкеп соғады. Сондықтан, Максвелл теңдеулерін шешудің ең бір тиімді және іс жүзінде көп қолданылатын тәсілі - өрістің потенциалдары үшін алынған жақсы зерттелген екінші ретті дербес туындылы дифференциалды теңдеулерді қолдану. Ол теңдеулерді алу үшін алдымен кернеуліктер мен потенциалдардың арасындағы байланыстарды табайық. Айнымалы электромагнит өрісі үшін де (11) алынған қатынастарды қолдануға болады.

                                                     ,                                                 (18.1)

                                              .                                          (18.2)

2.  Бұл теңдіктер электромагнит өріс векторларын  бірмәнді етіп анықтай алмайды. Сондықтан  - векторлық және скалярлық потенциалдар белгілі ерікпен алынады. Максвелл теңдеулерінің шешімдерінің бірден-бірлігі бұзылмау үшін екі түрлі алынған потенциалдар бір өрісті анықтау керек. Мінеки, потенциалдардың түрін қалағандағы еркіндік осындай талаптармен шектеледі. Айталық,  – скалярлық ерікті үздіксіз функция болсын, ал  және  (18.1), (18.2) формулалары бойынша  электромагнит өрісін анықтасын. Онда

                                                                  (18.3)

түрлендірулер арқылы жазылған потенциалдар  тура сол  және  векторларын анықтайды:

                              ,                          (18.4)

   

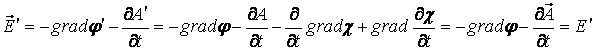
                                                                                                                     (18.5)

(18.4), (18.5) теңдіктерінде уақыт  және координаттар бойынша дифференциалдау ретін өзгертуге болатыны ескерілді.

Сонымен  және  ерікті  функциясымен (18.3) түрлендіру арқылы байланысқан потенциалдар  векторларымен сыйпатталатын өрісті анықтап тұр. Потенциалдардың инвариантты түрде анықтауға арналған (18.3) түрлендіруін калибровкалық түрлендіру деп аталынады. Потенциалдардың  көп мәнділігін қолданып, оларға қосымша шарт қоюға болады.

3. (18.1) теңдеуінің екі жағынан да ротор операциясын алсақ, сол жағы (17.1, І) және (44.2) материалдық теңдеу арқылы келесі түрге келтіріледі де  

                                 .                             (18.6)

оң жағы (Қ 21) формуласы бойынша

                                         .                                     (18.7)

(18.6), (18.7) өрнектерін теңестірейік, онда

                        .                    (18.8)

Енді (18.2) теңдеуінің екі жағынан да дивергенция алып, (17.1,  І І І) және сәйкес материалды теңдеуді ескерсек,

                                                                                    (18.9)

болатынына көз жеткізуге болады.

3. (18.8), (18.9) теңдеулерін едәуір қарапайым түрде жазуға болады. Ол үшін потенциалдарға жоғарыда айтылған қосымша шарт қоюға болады:

                                               .                                          (18.10)

Бұл шарт – Лоренц шарты, ол оның дербес түрі стационарлық өрісте қолданылған, ол

                                                                                                       (18.11)

Кулон шарты деп аталады.

Лоренц қосымша шартын қолдансақ және (17.9) теңдігін ескергенде (18.8), (18.9) теңдеулер мына түрге келтіріледі:

                                             ,                                        (18.11)             

                                            .                                       (18.12)

Соңғы теңдеулер біздің іздеп отырған айнымалы  электромагнит өрісінің потенциалдары үшін жазылған теңдеулер.

Стационарлық өрістерде олар Пуассон теңдеулеріне айналатыны көрініп тұр.

                                                    ,                                               (18.13)

                                                   .                                              (18.14)

 

  19. Толқындық теңдеу және Даламбер теңдеуі. Олардың жалпы шешімдері туралы ұғым

         1. (18.11), (18.12) теңдеулер (18.1), (18.2) қатынастармен бірге Максвелл теңдеулеріне (17.3) эквивалентті. Дегенмен потенциалдар үшін алынған теңдеулердің ерекше артықшылығы  - олардың жалпы шешімін алуға болады. Заряд тығыздығы , ток тығыздығы  берілген екен дейік, олар қоздыратын өріс-  және  векторларын табу үшін алдымен потенциалдар  шамаларын тауып, сонан кейін (18.1), (18.2) өрнектері арқылы іздеп отырған өріс векторларын табамыз.

         2. Скалярлы потенциал да  және векторлық потенциалдың, мысалы, декарт координат жүйесіндегі әрбір құраушысы да  (18.11), (18.12) бойынша олардың әрқайсысы келесі дифференциалдық теңдеуді қанағаттандырады:

                                                                                (19.1)

 ұйғаруымыз бойынша берілген координат пен уақыт функциясы,   және  шамаларының кез-келген біреуін сипаттайтын скалярлы шама. (19.1) тәрізді теңдеулер Даламбер теңдеуі деп аталады.

Егер  функциясы нөлге тең болса, Даламбер теңдеуі толқындық теңдеуге айналады:

                                                                                           (19.2)

(19.1), (19.2) теңдеулері стационарлық жағдайда, яғни  уақытқа тәуелді болмаса Пуассон және Лаплас теңдеулеріне айналады:

 

                                                                                               (19.3)

                                                                                                          (19.4)

3. Даламбер теңдеуінің шешімін іздеуден бұрын бір өлшемді толқындық теңдеудің шешімін қарастырайыұ:

                                                    .                                                (19.5)

Бұл жағдайда  функциясы ішек тербелісін сипаттайтын теңдеуді қанағаттандырады:

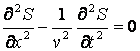                                              .                                          (19.6)

Бұл теңдеудің жалпы шешімі қума толқындар арқылы келесі тұрде өрнектеледі:

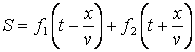                                        ,                                    (19.7)

-  аргументтері  болып келген ерікті функциялар.  – дербес шешім тура толқындарды ( осінің оң бағыты бойынша таралған толқын) сипаттайды, расында тұрақты фаза нүктесін қарастырайық:

                                                                                                   (19.8)

уақыт  өзгерген сайын айырым тұрақты болу үшін  мәні де соған сәйкес  өсінің бағытына қарай өсуі керек, сол сияқты - функциясы кері толқындарды сипаттайды. Бұл дербес шешімдердің әрқайсысы (19.6) теңдеуін қанағаттандыратынын тікелей қою арқылы көз жеткізуге болады.

4. Айталық, - функциясы кеңістіктегі бір  нұктесінің мейлінше аз төңірегінде ғана белгілі уақыт функциясы             ретінде берілсін де, ал басқа нүктелердің барлығында нөлге айналсын. Бұл жағдайда  нүктесін өріс көзі ретінде қарастыруға болады. Ендеше  нүктесінен басқа нүктелерде  функциясы үш өлшемді толқындық теңдеуді (45.2) қанағаттандырады және ол теңдеудің шешімінің сфералық симметриясы болатынын түсіну қиын емес. Сондықтан  функциясы  радиус-векторына ғана тәуелді болады, ал ,   бұрыштарына тәуелді емес.

Осыны ескеріп, сфералық координаттар системасында толқындық теңдеу келесі түрге келтіріледі:

 

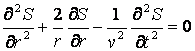                                        .                                    (19.9)

 

Соңғы теңдеудің екі жағын да - ге көбейтіп,          функциясын енгізсек, толқындық теңдеу едәуір қарапайымдалынып, ішек тербелісінің теңдеуіне сәйкес болады:

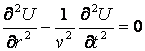                                             .                                        (19.10)

Оның шешімі

                                     ,                                (19.11)

болады да,  функциясы келесі түрде өрнектеледі:

                                  .                             (19.12)

Бұл шешімнің бірінші қосындысы  нүктесінен таралған сфералық толқын болса, ал екінші қосынды шексіздіктен  нүктесіне түйісетін толқын болатынына көз жеткізуге болады. Толқындық теңдеудің сфералық шешімдері (19.12)  нүктесінен басқа нүктелер ұшін дұрыс шешім болатынын тағы қайталаймыз. Өйткені  нүктесінде  нөлге ұмтылып, () теңдеу шешімі  шексіздікке ұмытылады().  нөль болмаған нүктелерде  функциясы толқындық теңдеу емес, Даламбер теңдеуін қанағаттандыру керек. Жоғарыда айтылғандай,  функциясы  функцияларының кез-келген біреуі болғандықтан       функциясы зарядтың  немесе токтың  нүктедегі тығыздығын  сипаттайды. Сондықтан, Даламбер теңдеуінің шешімін бір жағынан Лаплас теңдеуі мен (19.4) толқындық теңдеуді (19.2), екінші жағынан Пуассон (19.3) және Даламбер (19.1) теңдеулерін салыстыру арқылы жазуға болатынын айта кетейік. Лаплас теңдеуінің  сфералық - симметриялы шешімі                болатыны белгілі, ал Пуассон теңдеуінің  шешімін осы Лаплас теңдеуінің сфералық-симметриялы шешімдерін қосу арқылы табылған:

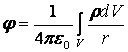                                               .                                          (19.13)

Бұл интеграл кеңістіктің кез-келген нүктесінде (заряд жатқан нүктені де қосқанда) өзінің шекті мәнін сақтайды. Сол сияқты толқындық теңдеудің сфералық-симметриялы шешімдерін бүкіл кеңістік бойынша қоссақ, онда Даламбер теңдеуінің шешімін алуымыз керек.

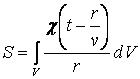                                              .                                         (19.14)

 

Бұл жерде (19.12) теңдігінің бірінші қосындысымен ғана шектелдік (19.14) теңдігінің Даламбер теңдеуінің шешімі болатынын тікелей қою арқылы дәлелдеуге болады.

 

20. Кешігуші және озушы потенциалдар

 

1. (20.14) теңдігіндегі  және  функцияларының нақ түрлері арқылы скалярлық  және векторлық потенциалдың құраушылары  үшін Даламбер теңдеулерінің шешімін келесі түрде жазуға болады (20.1 cурет):

                                                                      (20.1)

(20.1) түрінде жазылған потенциалдар кешігуші потенциалдар деп аталады. Расында, бақылау нүктесіндегі  потенциалдардың  уақытындағы мәні зарядтар мен токтардың  нүктесінде орналасу жағдайларының сол  уақыт моментіндегі мәні емес, оның алдындағы  уақыт моментіндегі токтар мәнімен анықталады. Бұл толқынның таралу жылдамдығының шекті болуының салдары деп түсіну керек.  құраушылары векторлы түрде былай өрнектеледі.

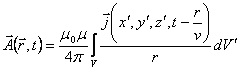                                    .                                (20.2)

(19.14) теңдігінде біз (19.12) – толқынды теңдеуінің алдыңғы  дербес шешімін ғана алдық. Ал, екінші дербес шешімін де 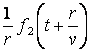 қолдана отырып электромагнит өрісінің потенциалдарын келесі түрде өрнектеуге болады.  

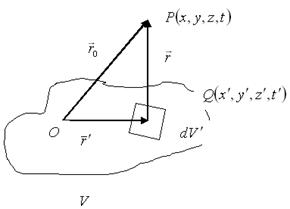
20.1- сурет

 

                                    .                                (20.3)

                                   .                              (20.4)

Бұл потенциалдар озушы потенциалдар деп аталынады. Мысалы, теориялық зерттеулерде шағылған толқындарды қарастырғанда потенциалдардың осы түрін қолданады.

2. (20.1)- (20.4) теңдіктерімен анықталған Даламбер теңдеулерінің (18.11), (18.12) шешімдері дәл математикалық әдіспен табылмағанын айта кету керек. Ол шешімдер, былайша айтқанда, бір жағынан Лаплас теңдеуі мен толқындық теңдеудің, екінші жағынан Пуассон мен Даламбер теңдеулерінің сәйкестігін пайдалану арқылы тұжырымдағанымызды ескерейік. Сондықтан олардың дұрыстығын тек тікелей теңдеуге қою арқылы тексеріп көрген жөн. (20.1) скалярлы потенциалды мына теңдеуге қояйық:

                                            .

20.1 – суретіндегі белгімелерді қолданып, дифференциалдау бақылау нүктесінің координаттары  бойынша, ал интегралдау зарядтар орналасқан облыстың координаттары  бойынша алынатынын ескерсек, онда

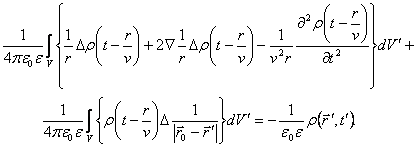                                 (20.5)

 

Бірінші интегралдың астындағы екінші мүше лапласианның сфералық координаттар системасында пайда болатыны ескерілді. Екінші интеграл (20.5) теңдігінің оң жағына тең. Сондықтан бірінші интеграл нөлге тең болуы керек.

Бірінші интегралдың астындағы операцияларды жеке-жеке көрсетейік:

1)

            

 

2)

                     

3)

                                                

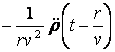
Бірінші пукттегі өрнекті  – ге көбейтіп, осы үш операцияның нәтижесін қоссақ, (20.5) теңдігіндегі бірінші интеграл нөл болатынын дәлелдеген боламыз.

Сонымен (20.5) тепе-теңдік болып шықты, яғни кешігуші скалярлы потенциал Даламбер теңдеуінің шешімі болатынына көз жеткіздік.

 

         21. Электромагниттік толқындар шығару. Дипольдық толқын шығарудағы өріс потенциалдары

         Қарапайым толқын шығарушы тетік ретінде Герц вибраторын және тогы бар раманы қарастыруға болады. Герц вибраторы- өткізгішпен қосылған әртүрлі зарядтармен зарядталған екі металл шариктер жиынтығы.

Егер осы шариктерді шамасы бірдей, бірақ таңбасы әртүрлі зарядтармен зарядтап, оларды өз еркіне қойсақ, шариктердің қайта зарядталуы салдарынан өткізгіш арқылы белгілі периодпен бірте-бірте сөнетін айнымалы ток жұреді.

Егер өткізгіш кедергісі мейлінше аз болса, көптеген периодтар ішінде тербелістердің сөнуін ескермеуге болады. Ендеше, кез-келген айнымалы ток  (төңірегінде айнымалы магнит өрісін  туғызады, ал ол Максвелл теңдеуі (17.3) бойынша айнымалы электр өрісін  туғызады және т. б.). Сонымен, электромагнит өрісі өзін тудырған тoк көзінен айырылып кете алады (21.1 сурет).

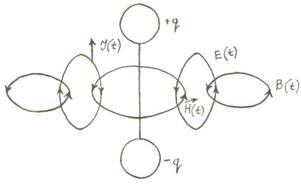
21.1  сурет

Осындай өрісті электромагниттік толқындар деп атайды. Сондықтан осы вибратордан оның сызықтық өлшемімен салыстырғанда, мейлінше көп қашықтықтағы электромагнит өрісін электрлік дипольдің  моментінің уақыт бойынша өзгеруінен пайда болған дипольдық электромагниттік толқындар ретінде қарастыруымыз керек. Осы тәрізді толқын шығарушы жүйелерді сызықтық осциллятор деп те атайды.

         2. Ілгеріде айтылған ойларды жалпы электр нейтралды зарядтар системасына пайдаланайық. Айталық, зарядтар системасы белгілі бір шекті көлемнің  ішінде ғана орналасқан екен делік.  нүктесін зарядтар системасының центрі болсын деп шарттасайық.  нүтесінен бақылау нүктесіне  тартылған радиус-вектор болсын.  - ерікті  нүктесінен бақылау нүктесіне тартылған радиус - вектор,  нүктесінің системаның  центрінен қашықтығы – ол көлемнің сызықтық өлшемін сипаттасын делік (20.1 cурет).

         Осындай белгімелерден кейін  нүктесінің алыста жатқанын мына теңсіздікпен көрсетуге болады. 

                                                   .                                              (21.1)

 облысындағы ерікті зарядтардың потенциалдары  және  (20.1) теңдіктерімен анықталады. Осы формулаларды тікелей пайдаланудың қиындықтары бар. Олардың негізгісі – кешігу эффектісін есептеу керектігі:  шамаларының әрбір  нүктесіндегі мәні әртұрлі  уақыт моментінде  есептелуі керек. Егер (21.1) шарт орындалса, онда жүйе электрлік  және магнит  моменттерімен сыйпатталатынын көрсетуге болады.

3. (20.1) – теңдеулерінен скалярлық потенциалға жазылған формуланы қарастырайық:

 

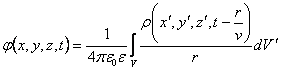                                .                            (21.2)

 

Осы интеграл астындағы өрнекті түрлендірейік. 20.1 сурет бойынша:

                                                                                                    (21.3)

(21.1) теңсіздігін ескерсек:

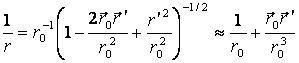                              ,                          (21.4)

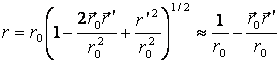                                ,                            (21.5)

(21.4), (21.5) өрнектерін қатарға жіктегенде бірінші жуықтаумен шектелдік. Соңғы формуланы ескеріп потенциалдардың формуласындағы аргументі  бірінші жуықтауда келесі түрге келтіруге болады:

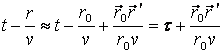                                      .                                 (21.6)

МөндаҚы  - системадан жалпы  қашықтығындағы кешігу уақытын есепке алады да, ал 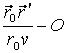 нүктесіне қарағандағы меншікті кешігу уақытын ескереді. Бақылау нүкте бағытында бірлік вектор 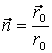 енгізсек:

                                                 .                                            (21.7)

Меншікті кешігу уақыты системаның барлық нүктелері үшін системаның жалпы кешігу уақытынан мейлінше аз деп ұйғарсақ, онда 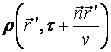 функциясын аз шама  бойынша жіктеп, екі мүшемен шектелейік:

                                      .                                  (21.8)

Мұнда және ары қарай нүкте -  немесе  бойынша алынған туындыны көрсетеді. (21.4), (21.8) формулаларын пайдаланып (21.2) өрнекті бірінші жуықтауда мына түрде жазамыз:

           

                                                                                                                     (21.9)

Бұл алынған формула меншікті кешігу уақыты  жалпы кешігу уақытынан  мейлінше аз деп есептегенде дұрыс екенін айта кетелік. Екінші естен шығармайтын нәрсе меншікті кешігу уақыты кезінде заряд тығыздығы  көп өзгермеу керек: егер  - осы уақыт ішінде көп өзгерген болса, жоғарыдағы жіктеуді пайдалануға болмай қалады. Егер системадағы зарядтар меншікті кешігу уақыты ішінде  - қашықтыққа қозғала алса, онда бұл қашықтық жүйенің сызықтық өлшемінен әлдеқайда аз болу керек:

                                                    .                                               (21.10)

Соңғы шарт бойынша зарядтардың қозғалу жылдамдығы толқынның таралу жылдамдығын мейлінше аз болу керек, яғни қарастырып отырған жағдай релятивті бөлшектерге қолдануға болмайды.

(21.9) формуласындағы  - мағынасы бойынша нүктелік зарядтың потенциалына тең, бірақ система электр нейтралды болған соң, ол нөлге тең.  –жүйенің кешігу эффектісін ескергендегі дипольды момент арқылы анықталатын потенциал:

                               .                          (21.11)

Ал,  - осы дипольды моменттің  уақыт бойынша туындысы арқылы сипатталады:

                              .                         (21.12)

Сонымен

                                       .                                  (21.13)

Электр нейтралды зарядтар системасы бірінші жуықтауда осы системаның дипольдық моментімен  толық сипатталады. Системадан тым алыс жатқан нүктелерде (21.13) өрнектің бірінші қосындысы соңғы қосындыға қарағанда тезірек азаятыны көрініп тұр.

4. Векторлық потенциал  (20.2) теңдігімен анықталады. (21.7) – жіктеуді пайдаланып  – ток тығыздығын мына түрде жазуға болады:

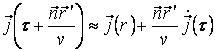                                      .                                 (21.14)

Онда

           

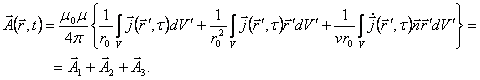
                                                                                                                    (21.15)

Бұл жерде  өрнектерін келесі түрге келтіруге болатынын айта кетейік:

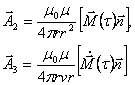                                                                                       (21.15 a)

Скалярлы потенциалдай емес, векторлы потенциалдың бірінші мүшесінің өзі нөлге тең емес. Өйткені айнымалы ток үшін стационарлы өрістегі сияқты  интегралы нөл болмайды. Сондықтан векторлы потенциал  негізгі мүшемен анықталады:

                                          .                                     (21.16)

Соңғы теңдікті скалярлы потенциалдың негізгі мүшесімен салыстырайық:

                                        .                                   (21.17)

Зарядтың сақталу заңын қолданып

                                                                                            (21.18)

интеграл астындағы өрнекті түрлендірейік:

 

                   .              (21.19)

Бұл жерде бақылау нүктесінің бірлік векторы  іс жүзінде тұрақты деп есептеуге болатыны ескерілді.

Енді (21.19) пайдаланып (21.17) формуласына қойсақ, бірінші интегралды Гаусс теоремасынан  векторының  көлемін шектеп тұрған  тұйық бетінен өткен ағын арқылы жазуға болады. Бірақ, біздің ұйғаруымыз бойынша зарядтар  көлемінен ешқайда шықпайды. Сондықтан  тұйық беті арқылы алынған интеграл  нөлге тең. Сонда

                                      .                                 (21.20)

яғни

                                              ,                                        (21.21)

немесе

                                      .                                 (21.22)

Сонымен скалярлы  және векторлы  потенциалдар (21.21), (21.22) өрнектері бойынша электр нейтралды зарядтар системасының дипольды моментінің  уақыт бойынша өзгеру жылдамдығымен анықталатынын көрдік. Дипольдық моменттің уақытқа тәуелділік заңдылығын  ескерсек (21.21), (21.22) формулаларымен анықталған өрістің системадан радиалдық бағытта таралатын электромагниттік толқындар екенін көруге болады. Ол толқындарды қозғалыстағы зарядтар шығарады.  – потенциалдарымен анықталатын өріс – электрлік дипольдық толқын шығару болып табылады.

Скалярлық (21.13) және векторлық (21.15) потенциалдарды қатарға жіктегендегі келесі мүшелерді дипольдық толқын шығару нөл болғанда ғана зерттеледі. Мысалы, (21.15) формуладағы соңғы мүше магниттік дипольдық толқын шығаруын анықтайды.

 

22. Дипольдық толқын шығарудағы өріс векторлары. Интенсивтілік

         1. потенциалдары арқылы дипольды толқын шығарудағы өріс  векторларын  табайық. (18.1) теңдігі бойынша

 

                                      (22.1)

Екінші қосынды қашықтықтың квадратына кері пропорционал, сондықтан оны бірінші қосындымен салыстырғанда елемеуге болады. (Бұл жерде және ары қарай  қашықтығының “0” индексі түсірілді: өйткені  – ерікті түрде алынды және дербес туындылар бақылау нүктесінің координаттары бойынша алынады).

                                (22.2)

(44.2) бойынша электр өрісінің векторын  табамыз.

 екенін ескеріп, (18.2) пайдалансақ:

                                    .                                (22.3)

Соңғы теңдікті (21.22) арқылы келесі түрге келтіруге болады:

                                                .                                           (22.4)

Енді (22.2), (22.4) өрнектерін салыстырсақ,

                                                    .                                                (22.5)

(22.2), (22.4) формулалары бойынша  функциялары уақыт бойынша сфералық толқындарға сай аргументке - тәуелді. Ол векторлардың әрқайсысы жүйеден ұзаған сайын, қашықтыққа кері пропорционал заңдылығымен  азаяды. Толқын бағыты радиус – вектордың бағытындағы  бірлік вектормен бағыттас. Электрлік вектор , магниттік вектор  және бірлік вектор өзара перпендикулярлы оң винтті система құрайды. Осы векторлардың модульдері келесі формуламен байланысқан:

                                                       .                                                   (22.6)

Жоғарыда айтылған электр нейтралды системаның толқын шығару шарты  болатынын айта кету керек. Егер электрлік момент  уақыт бойынша периодты функция болса, онда толқын өрісі де периодты болатынын түсіну қиын емес. Дипольдық толқын шығару кеңістіктегі барлық бағытта бірдей емес. Соны көрсету үшін момент  бағыты сфералық координаттар системасында  бағытымен сәйкес деп ұйғарайық. Онда,

                                 .                            (22.7)

Яғни,  векторының сызығы  және  нормаль жатқан меридиандық жазықтықта жатыр. (22.1 сурет)

                

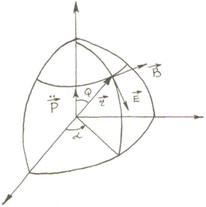
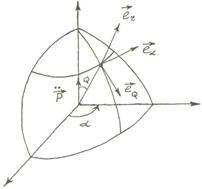
                   22.1 сурет                                        22.2 сурет

 

Ал  векторының сызықтары сфералық системаның параллелдерімен сәйкес келеді. Егер  бірлік векторларын енгізсек (22.2 cурет), онда  векторларын жазу оңайға түседі. (22.2) бойынша:

 

                                               .                                           (22.8)

 

Ал, осы теңдікті (22.5)- ке қолдансақ,

 

                                                .                                           (22.9)

 

болатыны көрініп төр.

 бағыттарында толқын шықпайды, ал  бағытында – векторына перпендикуляр бағытта максималды толқын шығарылады.

 

2. Энергия ағынының тығыздығын Пойнтинг векторымен анықтауға болады:

 

                                       .                                  (22.10)

 

Уақыттың бір өлшемі ішінде барлық бағыттағы энергия ағынын табу үшін  тұйық бет арқылы интеграл алу керек, бұны толқын шығару қуаты деп есептеуге болады:

 

                           .                      (22.11)

 

Сәуле шығаратын жүйелер үшін соңғы алынған толқын шығару қуатын оның интенсивтілігі деп атауға болады.

 

         23. Гармоникалық осциллятордың толқын шығаруы. Жақын және толқындық зоналар

 

1. Дипольдық моменті  белгілі жиілікпен  өзгеретін системаны гармоникалық осциллятор деп дейді.

                                                   .                                               (23.1)

 

Гармоникалық осциллятордың дипольдық толқын шығаруындағы өріс векторларын (22.8), (22.9) теңдіктері арқылы анықтауға болады:

 

                                        .                                   (23.2)

                                         .                                    (23.3)

 

Мұнда  - толқындық сан, ол толқын таралу бағытымен келесі формуламен байланысады:

 

                                                      .                                                 (23.4)

 

 векторларының әрқайсысы қашықтыққа кері пропорционал .

Толқын шығару қуатын период бойынша орташаласақ, онда осциллятордың период бойынша орташа қуаты:

 

                                                 .                                             (23.5)

 

Ол жиілік өсуімен () тез өседі және тербеліс амплитудасының квадратына () тура пропорционал. Толқын шығару қуатын күшейту тұрғысынан қарағанда (мысалы радиостанция қуатын көбейту үшін) тасушы тербелістер әруақытта төменгі жиілікті (сөз, ән, музыка) тербелістерден мейлінше жоғары () болуы керек. Интенсивтіліктің  заңдылықпен өсуі аспанның күлгін түсін түсіндіре алады. Расында, күн сәулесі ауа молекулаларымен шашыратылатыны белгілі. Осы молекулаларды элементарлық осцилляторға ұқсатуға болады. Күн сәулесінің шашыратылуы – жарық толқындарының әсерімен осциллятордың “еріксіз тербеліс” жасауға мәжбұр болатындығымен түсіндіріледі. Осциллятордың меншікті тербелістерінің периоды жарық толқындарының периодынан әлдеқайда бөлек болғандықтан (резонанс жоқ), еріксіз тербелістердің амплитудасы  жарық толқынының периодына онша тәуелді емес. Сондықтан шашыраған жарық интенсивтілігі, яғни осцилляторлардың еріксіз сәуле шығару интенсивтілігі  заңдылығына байланысты өседі. Сонымен, қысқа толқынды жарық (көгілдір түсті) қызыл түсті толқындардан гөрі күштірек шашырап, аспанның көгілдір болуын қамтамасыз етеді.

2. Гармоникалық осциллятор ұшін өзіне сай параметр ретінде толқын ұзындығын  алуға болады. Толқын шығарушы системаларды қарастырғанда скалярлық, векторлық потенциалдар үшін жуық өрнектер алынған. (21.13), (21.15) формулалары бақылау нүктесінің нейтралдық жүйеден тым қашықтықта жату шарты орындалғанда ғана дұрыс екендігі туралы айтылған. Енді дәлдік дәрежесін жоғарылату мақсатымен  қашықтықтарын толқын ұзындығымен салыстырайық.

Айталық, жүйенің сызықтық өлшемі толқынның ұзындығынан әлдеқайда аз екен делік:

 

                                                      .                                                  (23.6)

 

Онда бүкіл кеңістікті екі зонаға бөлуге болады: бірі – жақын зона , екіншісі -   алыс, немесе толқындық зона. Осы екі зонаның екеуіне де потенциалдарды жіктеген формулаларды (21.13), (21.15) қолдануға болады.

Жүйеге жақын зонаны ққарастырайық. Онда (21.13) өрнегіндегі бірінші мүшені елемеуге ешқандай негіз жоқ:

 

                                                ,                                            (23.7)

 

(23.1) – ескерсек,

 

                                              ,                                          (23.8)

 

Соңғы потенциалды (22.13) – формуласындағы соңғы мүшемен салыстырайық. Біздің жағдайда:

 

                                      ,                                  (23.9)

 

 

жақын зона үшін

 

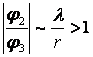                                                   .                                              (23.10)

 

Қалған нүктелердің барлығы (скалярлық және векторлық потенциалдар үшін) - ден  – рет аз. Сондықтан жақын зоналарда өріс электростатикадағы дипольдық жуықтауға ұқсас  потенциалымен анықталатыны айқын болды. Жақын зоналарда  кешігу эффектісін елемеуге болады. Жоғарыда келтірілген салыстыру векторлық потенциал  (21.15) үшін де орындалатынын айта кеткен жөн. Оны оқушының өзі тексере алады.

Сондықтан жақын зонадағы өріс кейде квазистатикалық зона деп те аталынады. Толқындық зоналар туралы (22)-де жеткілікті түрде айтылды. Сондықтан оған оралмаймыз.

 

         24. Магниттік дипольдық толқын шығару. Тогы бар раманың толқын шығаруы

 

1. Егер  болса, онда өріс потенциалдарына кіретін қосындылардың шамалық реті бойынша  қаралуы керек, ол магниттік дипольды толқын шығаруды сипаттайды:

 

                                               .                                           (24.1)

 

 және  векторларын (18.1), (18.2) арқылы табамыз. (Бұл жуықтауда  нөлге тең деп алуымыз керек, өйткені (21.13) формуласында жазылмаған келесі мүше квадрупольдық момент арқылы анықталады):

 

                                                                                (24.2)

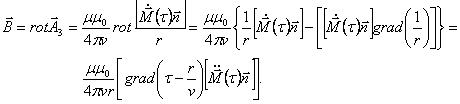                                                                                                                     (24.3)

Соңғы теңдіктегі шамалық реті  көбейтіндісі бар екінші қосындыны бірінші қосыныдымен және (24.2) – мен салыстырғанда елемеуге болады.

Сондықтан        

 

                                             

 

екенін еске алып  векторын мына тұрде жазамыз:

 

                                               .                                           (24.4)

 

Енді (24.2) және (24.4) салыстырсақ, магниттік толқын шығарудағы  векторларының арасындағы байланысты табамыз.

 

                                                    .                                                (24.5)

 

Айталық,  векторы  осінің бойымен бағытталсын делік, онда қарастырылып отырған жуықтауда  векторының сызықтары сфералық координаттар системасының параллельдеріне, ал - сызықтары меридиандарға сәйкес келеді (24.1 сурет).

 

 

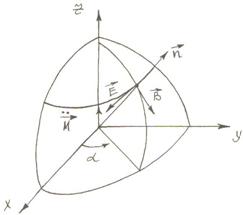
24.1 сурет

Сонымен бұл жуықтауда электромагнит өрісінің векторлары магнит дипольдық моментінің  екінші туындысы арқылы бірмәнді анықталады. Бұл жағдайда сфералық толқындар шығарылатынын атап айту керек (толқын векторының амплитудасы қашықтық өскен сайын  заңдылығымен азаяды.)

Толқын шығарудың бұл түрі де жоқ болса (мысалы, ), онда келесі жуықтау – электрлік квадрупольдық толқын шығаруын қарастыру керек.

2. Мысал ретінде тогы бар шеңберлі раманың толқын шығаруын қарастырайық. Айталық, рама  жазықтығында орналассын делік, оның центрі координаттың бас нүктесінде болсын. Ток күші  заңдылығымен өзгерсін. Тогы бар бұл раманың магниттік моменті былай анықталады:

 

                                        .                                    (24.6)

 

Мұнда - раманың ауданы,  – оның радиусы,  өсінің бірлік векторы.

(24.2), (24.5) пайдаланып өріс векторын мына түрге келтіруге болады:

 

                                              .                                         (24.7)

 

                                              .                                          (24.8)

 

Магнит моментінің векторы  осімен бағытталған.

                                          .                                      (24.9)

 

Сондықтан толқын шығару бағыты негізінде рама жатқан жазықтық бойында шоғырланған десе болады. Өйткені  ( осінің бағыты) және  бағыттарда толқын шығарылмайды. Толқын шығару интенсивтілігі Пойнтинг векторымен анықталады:

 

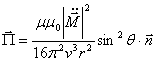                                            .                                       (24.10)

 

Онда токты раманың толқын шығару қуаты радиусы  сфера беті арқылы былай табылады:

 

                                       .                                  (24.11)

 

Гармоникалық осциллятордың толқын шығару қуатын (23.7) соңғы теңдікпен салыстырсақ, жалпы заңдылықтарының ұқсас екендігін аңғарамыз, ал екеуін шама жағынан салыстырайық:

 

                                                 .                                            (24.12)

 

  Егер  екенін еске алсақ, онда электрлік дипольды толқын шығару қуатының магниттік дипольды толқын шығару қуатынан едәуір басым екені байқалады.

 

  25. Толқын шығарудағы тежелу

 

         1.  Жоғарыда қарастырылған толқын шығарудың классикалық теориясы бойынша келесі мазмұнды тұжырымға келдік: әрбір үдемелі қозғалған заряд өз төңірегінде өзінің шығу көзінен ажырап кете алатын электромагниттік өріс қоздыра алады, ол өрісті электромагниттік толқындар деп атадық. Негізінен біз дипольдық толқын шығару теориясын қарастырдық. Ол теорияның қолдануының негізгі бір шарты зарядтар қозғалған облыстың сызықтық өлшемінің өріс анықталатын нүктелерге дейінгі қашықтықтан мейлінше аз болуы.

Толқын шығарушы тетіктердің ең қарапайым моделі ретінде Герц вибраторын, сызықтық осцилляторды қарастырдық. Олар үшін ілгеріде айтылған шарт әруақытта орындалатынын айтпаса да түсінікті. Сондықтан мысалы, дипольдық толқын шығару үшін дипольдық моменттің уақыт бойынша екінші туындысы, , яғни үдеу  нолге тең болмау керектігін ескертеміз. Егер заряд өзінің орнықты жағдайынан ауытқыған болса, оған квазисерпімді күш әсерінің арқасында еркін тербелісте болады да, осы құбылыс келесі дифференциалдық теңдеумен сипатталатыны бізге мәлім:

 

                                                   .                                               (25.1)

 

         Бұл жерде  – серпімділік коэффициенті, - зарядтың массасы. Ал, (25.1) теңдеуінің шешімі де белгілі:

                                         ,                                     (25.2)

 

– ерікті тұрақтылар, олар бастапқы шарттар бойынша анықталады. Ал  - бұрыштық жиілік. (25.2) өрнегі бойынша еркін тербелістегі энергия келесі түрде анықталады:

 

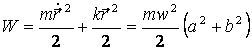                                   .                              (25.3)

 

Сонымен, ерікті тербелістегі заряд өз төңірегіне белгілі жиілікпен сөнбейтін толқындар шығарады деген тұжырымға келуге болады. Бірақ, (23.7) формула бойынша бір өлшем уақыт ішінде толқын шығарғыштан шамасы  энергия бөлініп шығады, яғни уақыт бойынша тербеліс энергиясы азаюға тиіс:

 

                                     .                                 (25.4)

 

Бұл теңдеудің шешімі

  

                                                    .                                                (25.5)

 

болатынын тексеру қиын емес. Бұл жерде

 

                                                                                                  (25.6)

 

тербелістің сөну коэффициенті,

ал  – бастапқы () уақыттағы тербеліс энергиясы.

 Расында, энергияның сақталу заңы бойынша толқын шығару кезінде тербеліс энергиясы бірте-бірте азайып, (25.3) теңдігі бойынша энергияның азаю заңдылығы тек тербеліс амплитудалары келесі заңдылықпен өзгергенде ғана орындалады:

 

                                                                     (25.7)

 

Ендеше, (25.1) теңдеу толқын шығару құбылысын толық сипаттай алмайды. Шешімі (25.7) өрнегіне сәйкес теңдеу алу ұшін (22.11) теңдігі бойынша:

 

                                                   .                                               (25.8)

 

Зарядқа серпімділік күшімен () қатар, оның үдемелі қозғалысын тежейтін күш әсер етуі керектігін ескерту қажет және ол күш   жылдамдыққа  қарсы бағытта болуы керек.

 

                                                 .                                            (25.9)

 

Мұндай  күшті радиациялық күш, немесе толқын шығарудағы тежеу күші деп атайды.  болғандықтан соңғы теңдікті түрлендіруге болады:

 

                                                                                          (25.10)

 - уақыт бойынша толық туынды. Егер зарядтың мейлінше тар облыста қозғалатынын ескеріп, тежеу күшін системаның толқын шығару уақыт аралығы бойынша орташаласақ, онда  көбейтіндісінің өзгеру уақыт аралығы шекті болғандықтан, жоғарыдағы аталған толық туында мейлінше аз болып нөлге ұмтылады:

                                .                           (25.11)

 

Онда тежеу күші  келесі өрнекпен анықталуы керек:

 

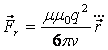                                                 .                                            (25.12)

 

Ендеше, осы тежеу күшін  серпімділік күшімен  қатар ескергенде (25.1) теңдігі былай түрленеді:

 

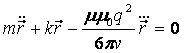                                          .                                    (25.13)

(25.12) формуланы қолдану шартын тағы да ескертуді жөн көрдік: біріншіден, қозғалыс релятивті емес (), әйтпесе, дипольдық жуықтаудың өзі дұрыс болмас еді. Екіншіден, толқын шығарудағы тежеу күші зарядқа әсер ететін Лоренц күшінен әлдеқайда аз болу керектігін – оған төмендегі тұжырымдар дәлел. Лоренц күші  және тежеу күші  әсер еткенде қозғалыс теңдеуі келесі түрде өрнектеледі:

 

                                               .                                          (25.14)

Егер  болған жағдайда,

 

                                                  .                                             (25.15)

 

немесе

 

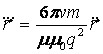                                                  .                                             (25.16)

Соңғы теңдеудің шешімі келесі тұрде

 

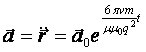                                                                                       (25.17)

 

жазуға болатынын тексеру қиын емес.  – заряд таситын материалдық нүкте үдеуі, яғни толқын шығару кезінде, қозғалыс үдеуі шексіз өседі. Сондықтан, толқын шығару интенсивтілігі уақыт бойынша үлкейе береді. Ал, бұл энергияның сақталу заңына қайшылық келтіреді, өйткені өзін-өзі шексіз үдету мүмкін емес. Сонымен, (25.14.) теңдеуін  болған жағдайда ғана қолдануға болады. Бұл жағдайда зарядқа үдеу беретін күш негізінен Лоренц күші, ал тежелу күші қозғалыс жылдамдығына елеусіз ғана әсер етеді.

 

2. Енді (25.13) теңдеуіне оралайық. Оны (25.6) арқылы түрлендірейік те:

 

                                                                                       (25.18)

 

шешімін комплексті түрде іздейік:

 

                                                    .                                              (25.19)

 

Осы шешімді (25.18) – ге қойсақ,  үшін келесі теңдеу аламыз:

 

                                         .                                    (25.20)

 

Жоғарыда тежеу күшінің мейлінше аз екенін ескерткеміз, ендеше бір период    уақыт аралығындағы тербелістің сөнуі де соншалықты аз шама болу керек (). Егер,  болса, (25.20) теңдеуінің шешімі келесі түрде анықталады:

 

                                                     .                                                (25.21)

Ал,  шамасының аздығын ескеріп, ол нөл болмаған жағдайда шешімді төмендегідей іздейміз:

 

                                                  .                                             (25.22)

- мейлінше аз шама (). Соңғы теңдікті (25.20)-ге қойып,  және одан жоғарғы ретті аз шамаларды елемесек,  екенін табамыз.

 

                                                 .                                            (25.23)

 

Сонымен (25.18) –дифференциалды теңдеудің жалпы шешімі былай өрнектеледі:

 

                                       .                                  (25.24)

 

(25.7)- формуласымен салыстырсақ, заттық және жорамал бөлімдері сәйкес екені көрініп тұр.

(25.12)- тежеу күші тек периодты қозғалысқа жақын, тербеліс сөнуі мейлінше аз қозғалыстар үшін қолданылады, сондықтан оны келесі түрге келтіруге болады:

 

                                          .                                     (25.25)

 

 

Онда (25.13) қозғалыс теңдеуі үйкеліс күші бар тербеліс теңдеуі ретінде былай жазылады:

 

                                             .                                        (25.26)

 

         26. Спектрлік сызық ені

 

  Толқын шығарудағы тежелу сол толқынның қасиеттеріне айтарлықтай әсер етеді. Толқын шығарған тетіктер тежеу күші жоқ болған кезде (), () бойынша монохраматты (жиілігі ) электромагниттік толқындарын шығарады. Ал, тежеу күшінің әсерімен монохраматты толқын тербелістің бірте-бірте сөнуіне байланысты осы  жиілігінің төңірегінде белгілі интервалдағы жиіліктер жиынтығына айналады. Басқаша айтқанда, тербелістің сөнуі үздіксіз спектрлі толқындар шығуына әкеп соғады.

Соны көрсету үшін толқын шығарғыш тетіктің қарапайым түрі – сызықтық гармоникалық осцилляторды қарастырайық. Айталық, зарядталған бөлшек квазисерпімді күш арқасында  осі бойымен тербелмелі қозғалыста болсын делік. Онда (25.26) теңдеуі келесі түрде өрнектеледі:

 

                                             .                                         (26.1)

 

Бұл теңдеу радиациялы үйкеліс күші квазисерпімді күштен мейлінше аз () жағдайда дұрыс болатынын ескерте кетейік. Онда (26.1) теңдеуінің бастапқы шарт  болғанда келесі түрде жазуға болады:

 

                                               .                                           (26.2)

 

Сөнетін осциллятордың толқын шығаруын сипаттау үшін оның үдеуін былайша жазайық:

 

                                            .                                           

 

- тұрақты (мысалы,   болғанда, ). Радиациялы үйкеліс күші әсер еткендегі осциллятор үдеуі уақыт бойынша периодты функция болмайды. Сондықтан шығарылған толқындардың құрамында барлық  жиіліктер бар. Біздің ендігі мақсатымыз – осы үздіксіз жиілік спектрінің әр интервалына () сәйкес келетін толық энергия  үлесін табу. Басқа сөзбен айтқанда, бізге спектральды таратылу функциясын  табу керек. Ол функция осциллятор шығаратын толқынның толық энергисымен  келесі формуламен байланысқан:

 

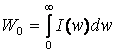                                                .                                            (26.3)

 

Ал, осциллятор шығарған толқынның толық энергиясы (22.11) формула бойынша былай өрнектеледі:

 

                                .                           (26.4)

 

Мұнда  кезінде осциллятор толқын шығармайтындығы ескерілді. Үдеуді Фурье интегралына жіктейік:

 

                                          ,                                      (26.5)

 – Фурье құраушысы:

 

                           ,       (26.6)

 

Фурье интегралының қасиеті бойынша:

 

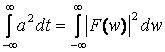                                                                                    (26.7)

Сондықтан,

 

                                                      (26.8)

(52.8) формуланы (52.4) –ке қойсақ:

 

 

                                                                                                (26.9)

болатынын көреміз.

Соңғы өрнектен

                                                                                                (26.10)

Екінші жағынан (26.8), (26.9), (26.3) формулаларын салыстырайық. Тек жиіліктердің оң шамасы үшін спектральды таратылу функциясын табамыз:

 

                                      .                                 (26.11)

 

 - функциясының жиілікке () тәуелділігі 26.1 суретте берілген.

 

 

26.1 сурет

 

 болғанда, яғни тербеліс сөнуі жоқ кезде:

 

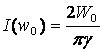                                                  .                                             (26.12)

 

 функциясының - максимумы бар, ал  болғанда толқын шығару интенсивтілігі:

 

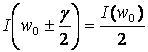                                             .                                       (26.13)

 

Максимум кезіндегі интенсивтіліктен екі есе кемиді, осы себепті  шамасы толқын шығарудағы спектрлік сызықтың жартылай ені деп аталады.

 

         27. Еркін зарядтың электромагниттік толқынды шашыратуы

 

Зарядқа монохраматты электромагниттік толқын түскенде, ол үдемелі қозғалысқа ұшырайды. Яғни, өзі де екінші ретті толқын шығарады. Бұл процесс электромагниттік толқынның шашырауы деп аталады. Зарядқа әсер ететін күш Лоренц күшімен анықталады.

 болғандықтан магнит өрісінің әсері электр өрісінің әсерінен мейлінше аз, сондықтан Лоренц күшінің тек электрлік құраушысына ғана қарастыруға болады:

 

                                                  .                                              (27.1)

 

Онда (25.14) өрнегі бойынша зарядтың үдемелі қозғалысы келесі теңдеумен өрнектеледі:

 

                                            .                                        (27.2)

 

Радиациялық үйкеліс күші мейлінше аз болғандықтан, оны Лоренц күшімен  салыстырғанда елемеуге болады:

 

                                                   .                                              (27.3)

 

Оның шешімі

 

                                                 .                                            (27.4)

 

Соңғы теңдік бойынша заряд түскен толқынға ілесіп  жиілігімен тербеледі. Келесі есептеулерді электрон үшін істейік.

Электронның екінші ретті толқын шығару өрісі дипольдық жуықтауда (22.2), (22.4) формулаларымен анықталады. Ол формулаларға келесі өрнекті қойсақ:

 

                                               .                                           (27.5)

 

Электр өрісінің керенулігі мен магнит индукция мына тұрде өрнектеледі:

 

                                              ,                                          (27.6)

                                                .                                           (27.7)

 

Мұнда

 

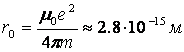                                          .                                     (27.8)

-         электронның классикалық радиусы.

(22.10) формуласы бойынша шыққан толқынның энергия ағынының тығыздығын есептейік:

 

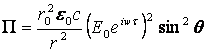                                       .                                   (27.9)

 

Соңғы теңдікті заттық бөлімін бөліп, период бойынша орташа тығыздығын мына түрде жазуға болады:

 

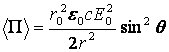                                           .                                      (27.10)

 

Онда  элементі арқылы  денелік бұрышына сәйкес келетін толқын шығару интенсивтілігі  келесі түрде өрнектеледі:

 

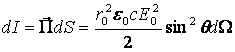                                    .                               (27.11)

 

Электронға түскен электромагнит толқынының орташа ағын тығыздығы былай есептеледі:

 

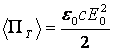                                                 .                                            (27.12)

 

Енді шашыраған толқынның интенсивтілігінің толқынның интенсивтілігіне қатынасын табайық:

 

                                        .                                   (27.13)

 

Бұл шаманың өлшемділігі аудан өлшемділігіне сәйкес және электрон радиусының квадратына пропорционал. Ол шашыраудың дифференциалдық қимасы деп аталады.

Шашыраудың толық қимасы шашыраған толқын қуатының түскен толқынның энергиясының ағын тығыздығына қатынасы ретінде табылады:

 

                                              .                                         (27.14)

 

Толық қиманың геометриялық мәнісін түсіну қиын емес; электронға түскен толқынның осы  ауданына сәйкес бөлімі ғана шашырайды, ол ауданның шамасы   – радиусты электронның қима ауданына шамалас. (27.14) формула оптикада Томсон формуласы деген атпен белгілі.

 

         28. Электромагнит өрісінің импульсы. Жарық қысымы

 

1. Кеңістіктің  көлемінде электромагнит өрісі сол көлемдегі зарядтармен өзара әсерлеседі деп ұйғарайық. Әрбір зарядқа Лоренц күші әсер етеді, ол зарядтар  тығыздығымен орналасса, онда Лоренц күшінің тығыздығын  мына түрде жазуға болады:

 

                                               .                                           (28.1)

 

Онда  облысындағы зарядталған бөлшектердің импульсының өзгеруі қозғалыс теңдеуімен анықталады:

 

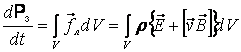                                    .                                (28.2)

 

Соңғы теңдеудің оң жағын Максвелл теңдеулерін

 

                                                                      (28.3)

 

қолданып түрлендірейік:

 

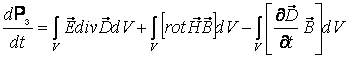                         .                     (28.4)

 (54.4) – теңдеуінің оң жағына нөлге тең шаманы қосайық та:

 

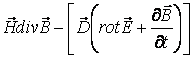                                         .                                    (28.5)

 

Оны симметриялы түрде өрнектейік:

                                                           

           .       (28.6)

 

Енді  материалды теңдеулерді қолданайық және  болатынын ескерейік:

 

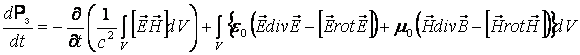  . (28.7)

 

Соңғы өрнектің оң жағындағы екінші интегралды беттік интегралға айналдыруға болады. Ол интеграл  мен  үшін симметриялы түрде жазылғандықтан, тек мына интегралды ғана қарастырайық:

 

                                           .                                       (28.8)

 

Векторлық анализдегі (Қ 25), (Қ 26) формулалары арқылы бірінші қосындыны келесі түрге келтіруге болады:

 

                               .                           (28.9)

 

  тұйық беті  – көлемін шектеп тұр. Екінші қосындыны түрлендіргенде:

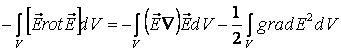                          .                     (28.10)

 

Ал, (28.10) – теңдігіндегі соңғы интегралға (Қ 27) формуланы қолданып, (28.9), (28.10) өрнектерді мүшелеп қосайық:

 

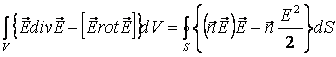                          .                     (28.11)

 

Соңғы өрнекті “толық өріске” таратқанада, өріс векторларының әрқайсысы шексіздікте  заңдылығынан гөрі жылдамырақ азаяды деп есептесек  тұйық беті арқылы алынған интеграл нөлге айналады. Онда

 

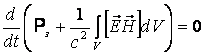                                                                           (28.12)

болатынын көреміз.  – зарядталған бөлшектер импульсы болғандықтан, интеграл:

 

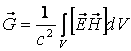                                               .                                          (28.13)

осы  – көлеміндегі электромагниттік өріс импульсы болуы керек. (28.12) теңдігі система үшін импульстың сақталу заңын сипаттайды. (28.13) бойынша электромагниттік импульс тығыздығы  электромагниттік энергияның ағын тығыздығымен  келесі формуламен байланысқан:

 

                                            .                                       (28.14)

 

2. Сонымен, электромагниттік өрістің энергиясымен қатар оның импульсы бар. Егер электромагниттік толқын материалды денеге түскен кезде жұтылған болса, онда электромагниттік импульс өзгеруінің арқасында дене электромагнит толқынынан қысым сезінуі керек (Егер жарық толқыны түссе, жарық қысымы). Материалды дене бетіне нормаль бойымен түскен толқын толық жұтылса, бір өлшем ауданға түсетін қысым бір өлшем уақытта осы ауданға берілген импульс ретінде анықталады, яғни:

 

                    ,               (28.15)

 

– электромагниттік энергия тығыздығы. Сонымен, электромагниттік толқын түсірген қысым сан жағынан электромагниттік энергия тығыздығына тең.

Егер дене беті абсолютті шағылыстырушы болса, түскен электромагниттік импульс бағытын кері өзгертеді. Сондықтан, денеге толық жұтылуға қарағанда екі есе көп қысым түседі.

Теорияның электромагниттік импульс болуы туралы болжаманы бірінші рет тәжірибе жүзінде орыс ғалымы П. Н. Лебедев 1901 жылы дәлелдеді.

 

 

ЌОСЫМША

 

ВЕКТОРЛЫҚ АНАЛИЗДІҢ НЕГІЗГІ ФОРМУЛАЛАРЫ

 

                    (бағыты бойынша  скалярының туындысы)   (1)

                                                                                                       (2)

                                                                             (3)

                                                                                                        (4)

                                                                                           (5)

                                                                                            (6)

                    ()                                                                   (7)

                    ( Гаусс теоремасы)                                            (8)

                                                                                 (9)

                    (Стокс теоремасы)                                                        (10)

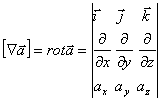                                                                                          (11)

                                                                                                       (12)

                    (вектордың бағыты бойынша туындысы)           (13)

 

Екінші ретті туындылар:

 

                                                                                 (14)

                                                                          (15)

                                                                                             (16)

                                                                                                            (17)

                                                                                          (18)

                                                                                                         (19)

                                                                                                           (20)

                                                                                        (21)

 

Көбейтінділердің туындылары:

 

                                                                                 (22)

                                                                                        (23)

                                                                                       (24)

                                                                                            (25)

                                                               (26)

                                                                                          (27)

                                                                     (28)

 

Грин теоремасы:

 

                                                                       (29)

                                                               (30)

                                                                                             (31)

                                                                                             (32)

  

МАЗМҰНЫ

Кіріспе                                                                                                               3

I ТАРАУ Максвелл теңдеулері – тәжірибе арқылы алынған заңдардың математикалық модельдері.

1. Электрлік заряд және ток. Электромагниттік өріс                                       5

2. Кулон заңының өріс тұрғысынан қарағандағы мазмұны                                     8

3. Электростатикалық Гаусс теоремасы                                                          9

4. Өріс кернеулігінің дивергенциясы. Максвелл теңдеуі                                  11

5. Ығысу тогы                                                                                                  12

6. Толық ток заңын қорытындылау                                                                           14

7. Электромагнитік индукция заңының дифференциалдық түрі                     15

8. Магнит өрісі сызықтарының тұйықтылығы                                                18

9. Вакуумдегі Максвелл теңдеулері. Электромагниттік өріс энергиясының

 сақталу заңы. Пойнтинг теоремасы                                                                19

II ТАРАУ Квазистационарлы электромагнит өрісі.

10. Квазистационарлық шарттар. Максвелл теңдеулері                                   23

11. Өріс векторлары  және потенциалдар  арасындағы

 байланыс. Потенциалдарға арналған теңдеулер                                              25

12. Айнымалы ток тізбегі ұшін Ом заңы                                                          27

13. Электрлік кернеудің айнымалы ток тізбегіндегі жол түріне тәуелділігі. Айнымалы ток кернеуі                                                                                            29

14. Айнымалы ток тізбегіне арналған теорияның қолданылуы                       32

15. Қозғалыстағы өткізгіштегі ток индукциясы                                                        36

16. Скин - эффект                                                                                              38

III ТАРАУ Айнымалы электромагнит өрісі.Электромагниттік толқын шығару

17. Максвелл теңдеулерінің жүйесі. Теңдеулер жүйесінің шешімінің бірден-бірлігі                                                                                                         42

18. Электромагнит өрісінің потенциалдарына арналған теңдеулер                 44

19. Толқындық теңдеу және Даламбер теңдеуі. Олардың жалпы шешімдері

 туралы ұғым                                                                                                    46

20. Кешігуші және озушы потенциалдар                                                          49

21. Электромагниттік толқындар шығару                                                                 52

22. Дипольдық толқын шығарудағы өріс векторлары. Интенсивтілік            57

23. Гармоникалық осциллятордың толқын шығаруы.

Жақын және толқындық зоналар                                                                     59

24. Магниттік дипольдық толқын шығару. Тогы бар раманың

толқын шығаруы                                                                                              62

25. Толқын шығарудағы тежелу                                                                       64

26. Спектрлік сызық ені                                                                                    69

27. Еркін зарядтың электромагниттік толқынды шашыратуы                         72

28. Электромагнит өрісінің импульсы. Жарық қысымы                                 74

Қосымша                                                                                                          77

Мазмұны                                                                                                           79