Алматинский институт энергетики и связи

 

Кафедра физики

 

 

 

 

 

ФИЗИКА 1

Конспект лекций

 

(для студентов очной формы обучения специальностей  

050718-Электро­энергетика, 050717-Теплоэнергетика)

 

 

 

 

 

Алматы 2006

СОСТАВИТЕЛИ: Л.В.Завадская, Л.Х.Мажитова, Л.А.Тонконогая. Физика 1. Конспект лекций (для студентов очной формы обучения спе­ци­альностей 050718 – Электроэнергетика, 050717 – Теплоэнергетика) – Ал­маты: АИЭС, 2006. –  60с.

 

Излагается краткое содержание лекций по дисциплине  «Физика1» для энергетических специальностей бакалавриата. Приве­дены цели учения, определяющие уровень усвоения определенного учебного ма­териала.

«Конспект лекций Физика 1» представляет собой ещё один элемент системы методического обеспечения учебного процесса по дисциплине и может быть использован в качестве раздаточного материала на лекционных занятиях, а также  в СРС над теоретическим материалам при подготовке к практическим, лабораторным занятиям и экзамену. Рекомендуется студентам и молодым преподавателям.

 

 

 

         Ил. 17.

 

 

 

 

 

 

 

 

Рецензент: канд. физ.-мат. наук, доцент Кулымбаева М.Ш.

 

 

 

 

 

 

 

 

 

 

         Печатается по плану издания Алматинского института энергетики и связи на 2006 год

 

 

 

 

 

Ó Алматинский институт энергетики и связи, 2006 г.

                                   Содержание

 

Введение ……………………………………………………………………………..   5

1 Лекция 1. Введение. Динамика твердого тела         …………………………………..   6

1.1   Механическое движение. Пространство и время. Система отсчета……   7

1.2   Основная задача механики. Уравнение движения твердого тела……….  7

1.3   Основные понятия динамики вращательного движения: момент  им­пульса, момент силы, момент инерции……………………………………………    8

2          Лекция 2. Энергия, работа, мощность…………………………………………  10

2.1        Энергия как общая мера различных форм движения материи…………10

2.2        Кинетическая энергия и работа силы…………………………………….11

2.3        Консервативные и неконсервативные силы. Потенциальное поле сил. 13

3 Лекция 3. Законы сохранения в механике……………………………………….  15

3.1 Закон сохранения импульса   ………………………………………………15

3.2 Закон сохранения момента импульса     …………………………………...15

3.3 Закон сохранения энергии в механике …………………………………….16

4 Лекция 4. Принцип относительности. Элементы релятивистской механики ….17

4.1 Принцип относительности Галилея     ……………………………………. 17

        4.2 Постулаты Эйнштейна. Специальная теория относительности ………... 19

        4.3 Преобразования Лоренца …………………………………………………..20

        4.4 Инварианты специальной теории относительности …………………….. 21

 4.5 Элементы релятивистской динамики ……………………………………. 21

5 Лекция 5. Статистические распределения ………………………………………. 22

         5.1 Статистический и термодинамический методы исследования ……….. 22

         5.2 Закон равномерного распределения энергии по степеням свободы … . 23

         5.3 Закон Максвелла для распределения молекул по скоростям …………. 24

         5.4 Закон Больцмана для распределения частиц во внешнем потенциальном поле …………………………………………………………………………………..  25

6 Лекция 6.Основы термодинамики ……………………………………………….. 26

         6.1 Теплота и работа как формы обмена энергией в термодинамике. Первое начало термодинамики ……………………………………………………………    26

         6.2 Второе начало термодинамики ………………………………………..    27

7 Лекция 7. Явления переноса …………………………………………………….   31

         7.1 Общая характеристика явлений переноса ……………………………… 31

         7.2 Элементы молекулярно-кинетической теории явлений переноса ……  33

8 Лекция 8. Электростатическое поле в вакууме …………………………………. 35

         8.1 Электрический заряд …………………………………………………….. 35

         8.2 Электростатическое поле. Характеристики электростатического поля  35

         8.3 Основная задача электростатики …………………………………………38

         8.4 Основные теоремы электростатики в вакууме …………………………. 38

9 Лекция 9. Электростатическое поле в веществе ………………………………… 39

9.1 Диэлектрики. Поляризация диэлектриков ……………………………… 39

9.2 Поляризованность. Объемные и поверхностные связанные заряды ….  40

9.3 Вектор электрического смещения. Теорема Гаусса для электростатиче­ского поля в диэлектрике ………………………………………………………..     42

9.4 Условия на границе двух диэлектриков ……………………………….  43

10 Лекция 10. Энергия электрического поля …………………………………….. 44

10.1 Энергия взаимодействия системы зарядов ……………………………44

10.2 Энергия уединенного проводника и конденсатора ………………….  45

10.3 Энергия электрического поля …………………………………………. 45

11 Лекция 11. Постоянный электрический ток ………………………………….. 46

         11.1 Общие характеристики и условия существования тока ………………46

         11.2 Уравнение непрерывности. Условие стационарности электрического тока ………………………………………………………………………………….. 47

         11.3 Классическая электронная теория электропроводности металлов …  48

12 Лекция 12. Магнитное поле в вакууме …………………………………………50

         12.1 Магнитное поле. Вектор магнитной индукции ……………………… 50

         12.2 Принцип суперпозиции. Закон Био-Савара-Лапласа …………………51

         12.3 Магнитный поток. Основные законы магнитного поля …………….. 52

         12.4 Работа перемещения проводника с током в магнитном поле ………  53

12.5 Эффект Холла ………………………………………………………….. 53

13 Лекция 13. Магнитное поле в веществе ………………………………………. 54

         13.1 Намагничивание вещества. Намагниченность ………………………. 54

         13.2 Основные теоремы магнитостатики для поля в веществе   …………. 55

         13.3 Граничные условия для магнитного поля. Расчет магнитных полей в неоднородных средах………………..……………………………………………    57

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение

 

Конспект лекций «Физика 1» представляет собой очень краткое изложение содержания лекций по этой дисциплине для энергетических специальностей бакалавриата.

В каждой лекции отражены основные вопросы темы в их логиче­ской связи и структурной целостности, но без детальной проработки математиче­ских выкладок или примеров. Поэтому данная учебно–методическая разработка может и должна служить лишь ориентировочной основой для учебной деятельности студента, как на лекционном занятии, так и в самостоятельной работе вне аудито­рии.

Задание конкретных целей учения в каждой лекции, форма изложения учеб­ного материала, адекватная, на наш взгляд, его содержанию, делает этот материал хорошо воспринимаемым, организованным внешне, что, в конечном счете, будет способствовать лучшему его усвоению, систематизации СРС по освоению курса «Физика 1».

Настоящий конспект лекций предназначен студентам электро– и теплоэнер­гетических специальностей. Программы «Физика 1» для этих специальностей имеют общее содержание, отличающееся лишь глубиной проработки некоторых разделов, что достигается всей системой учебно–методического обеспечения учебного процесса по каждой специальности, и в краткой учебно–методической разработке не может быть отражено.

1 Лекция 1. Введение. Динамика твердого тела

 

Цели лекции:

- осмыслить назначение курса физики и предмет физической науки;

- уяснить смысл основной задачи механики и сущность методов её решения.

 

Введение

 

Одного лоцмана спросили: «Как вам уда­ется запомнить все подводные камни и мели?» Ответ был таков: «Мне нет дела до всех этих ме­лочей. Я плыву по фарватеру»

 

Физика в техническом вузе выполняет общеобразовательную функцию, дает будущему специалисту фундаментальные базовые знания, формирует его инже­нерно – техническое мышление и создает целостное представление о современной естественно – научной картине мира.

Современная физика изучает наиболее общие законы неживой при­роды и их частные проявления на любых структурных уровнях организации материи. Объ­ект исследований физики – все многообразие неживой природы (поля, элементар­ные частицы, молекулы, макротела, космические среды, вакуум и т.д.). Мир изученных (и изучаемых) в настоящее время ма­териальных явлений характе­ризуется очень широким диапазоном простран­ственных и временных областей (рисунок 1.1).

 

                                       микромир              макромир

 

                   10^-18                 10^-12               10^-6                   1                      10⁶                       10¹²              10²⁶         r, м

         Элементарные                      размер             размер        радиус                     размер   видимой

         частицы                                 атома              человека     Земли                   части вселенной

 

                                       t, с                                                                     

                                                       10^-23                               10¹⁸  (десятки млрд.  лет)                    

                                       

Рисунок 1.1 – Границы изучаемых явлений в физике

 

Принципиально важно то, что количественные изменения физических объ­ектов и областей пространства, в которых происходят физические явле­ния, со­провождаются качественными изменениями характера законов, их описывающих. Поэтому важно знать характерные значения соответствующих физических вели­чин. Так естественным масштабом скоростей в природе является скорость рас­пространения света в вакууме с = 3∙10⁸ м/с. С ней связано качественное отличие нерелятивистских движений (v<<c) от релятивистских ( v~с). С постоянной Планка ħ = 1,054∙10^-34 Дж·с свя­зано разграничение законов физики на квантовые и классические.

         Физика – наука экспериментальная и, одновременно, всесторонне теоретизи­рованная. Она выработала эффективные методы «свертывания» инфор­мации (огромный фактический материал) благодаря четкой иерархии физических законов: от небольшого числа основных законов и фундаментальных принципов – к частным, имеющим конкретную практическую значимость в той или иной об­ласти профессиональной деятельности специалиста.

 

1.1             Механическое движение. Пространство и время. Система отсчета

 

Предметом механики является изучение механического движения тел и свя­занных с этим движением взаимодействий между телами. Под механическим движением понимают изменение взаимного положения тел или их частей в про­странстве со временем.

         Понятия пространства и времени есть тот фундамент, на котором строится физическая теория. Пространство и время не существуют отдельно от материи, это формы существования материи, органически связанные между собой. Про­странство выражает порядок сосуществования материальных объектов, время – порядок смены явлений.

         Абстрактные математические модели пространства и времени (например, эвклидово пространство) в большей или меньшей степени отражают свойства ре­альных пространства и времени, изучение которых является одной из основных задач вузовской физики.

         Всякое движение относительно. Для описания механического движения необ­ходимо выбрать систему отсчета: совокупность тела отсчета, системы коор­динат и часов.

 

1.2        Основная задача механики. Уравнение движения твердого тела

 

Основной задачей механики является определение состояния изучаемой системы (материальная точка, совокупность материальных точек, твердое тело) в любой момент времени, если известно состояние этой системы в начальный мо­мент.

         В классической механике состояние частицы полностью характеризуется заданием в данный момент времени трех её (координат (x,y,z) и трех проекций   (р_x, р_y, р_z) импульса).

         Твердое тело может совершать разнообразные сложные движения (примеры из техники). Все они, вообще говоря, могут рассматриваться как сложение двух простых: поступательного и вращательного. Поступательное движение твердого тела эквивалентно движению частицы с массой, равной массе тела, и помещенной в его центр инерции. При вращательном движении твердого тела вокруг закреп­ленной оси все точки тела движутся по окружностям, центры которых лежат на этой оси. В этом случае состояние тела может быть задано углом поворота вокруг оси и угловой скоростью.

        

1.3            Основные понятия динамики вращательного движения: момент       им­пульса, момент силы, момент инерции

 

Рисунок 1.2

 

Момент импульса частицы относительно точки О называется вектор,  равный

,                                                                     (1.1)

 

где  – радиус вектор частицы в данный   момент времени,

                – ее импульс ().

Вектор момента импульса перпендикулярен плоскости, в которой лежат векторы  и  (рисунок 1.2).

         Момент импульса системы частиц равен векторной сумме моментов импуль­сов всех частиц системы

 

   (аналогично: ).                      (1.2)

 

Моментом силы относительно точки О называется вектор  равный

 

,                                                         (1.3)

 

где   –  радиус–вектор точки приложения силы .

Момент силы характеризует способность силы вызывать вращение тела во­круг точки, относительно которой он берется. Тело, закрепленное в точке О, под действием силы  повернется вокруг оси, совпадающей с направлением момента  (рисунок 1.3).

 

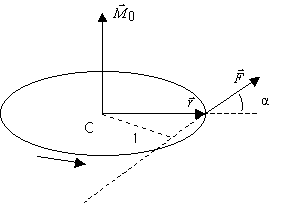
Рисунок 1.3

 

Взяв производную по времени от (1.1), можно показать, что скорость изме­нения момента импульса частицы определяется моментом силы

.                                                                 (1.4)

Соотношение (1.4) есть уравнение моментов.

Пусть твердое тело может вращаться вокруг закрепленной оси Oz. К телу приложена сила . Моментом силы относительно оси Oz называется проек­ция М_z момента силы  относительно точки О. Он характеризует способность данной силы вызвать вращение вокруг данной оси и равен

 

,                                   (1.5)

  

где   l –  плечо силы , равное R sin   

– радиус-вектор, проведенный от оси в точку приложения силы в плос­кости, перпендикулярной оси;

– проекция силы  на эту плоскость.

Чтобы определить момент импульса тела относительно оси, надо взять проек­цию на эту ось суммарного момента импульса относительно точки О всех частиц этого тела (рисунок 1.4)

                                       .                                           (1.6)

Легко убедиться в том, что это выражение (1.6) можно преобразовать к ввиду

 

 .                                   (1.7)

Величина

           .                                              (1.8)

 

называется моментом инерции тела относительно оси. Момент инерции зависит от распределения массы тела вокруг оси и характеризует инертные свойства тела при вращательном движении. Таким образом, имеем

 

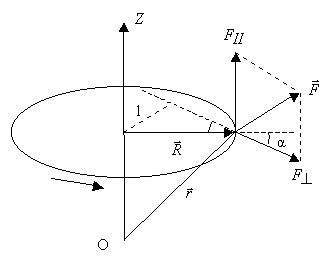
Рисунок 1.4

 

, или  .                                 (1.9)

        

Из (1.4) и (1.5) с учётом (1.9) получим

 

,                                                   (1.10)

 

где   – момент всех сил, приложенных к телу, относительно оси Z;

 – момент инерции тела относительно данной оси;

 – угловое ускорение вращающегося тела.     

Выражение (1.10) представляет собой основной закон динамики вращатель­ного движения твердого тела вокруг неподвижной оси.

        

2 Лекция 2. Энергия, работа, мощность

 

     Цели лекции:

- усвоить понятия: энергия, работа, мощность;

- овладеть методом расчета различных видов энергии.

 

2.1 Энергия как общая мера различных форм движения материи

 

Существует много форм движения материи. Механическое движение – про­стейшая из них.  Для его количественного описания мы использовали понятие импульса  . Количественной характеристикой теплового движения служит температура Т, электрического поля – и т.д. Все эти величины отражают качест­венные особенности различных форм движения материи. Но различные формы движения обнаруживают взаимную превращаемость.  Следовательно, необходимо введение такой физической величины, которая относится ко всем формам движе­ния материи и отражает их взаимную превращаемость. Такой физической вели­чиной является энергия – одно из наиболее общих понятий в физике.

Энергия есть единая мера различных форм движения материи.

(Следует заметить: понятие энергии не «открыто», а именно введено в физику. Это продукт мыслительной деятельности человека.)

Так как движение есть неотъемлемое свойство материи, то всякая система обладает энергией. Энергия системы количественно характеризует эту систему с точки зрения  возможных в ней изменений (количественных и качественных). Энергия - функция состояния.

В природе непрерывно идут процессы, в которых механическое движение и энергия передаются от одних тел к другим. Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно охарактеризовать процесс обмена энергиями между взаимодейст­вующими телами, в механике рассматривают работу силы, приложенной к дан­ному телу. Работа есть мера изменения энергии в процессах силового взаимодей­ствия.

 

2.2 Кинетическая энергия и работа силы

 

Рассмотрим некоторую частицу массы m. Подействуем на неё силой . Урав­нение второго закона Ньютона для этой частицы:

 

  .                                                                 (2.1)

                                                                                                                                                 

Умножим скалярно уравнение (2.1) на вектор бесконечно малого переме­щения частицы  (учтем, что = )

 

.                                                           (2.2)

 

Из рисунка 2.1 видно, что скалярное произведение  равно

 

                                       .

 

                                                                                       

Рисунок 2.1

 

Следовательно, 

                            .                                                                   (2.3)

     

Величина в правой части уравнения (2.3) называется работой dA силы

                           

,                                                       (2.4)                                                                            

 

где α – угол между силой  и перемещением  . 

Формула (2.4) выражает элементарную работу силы . При перемещение тела на конечное расстояние полная работа выражается криволинейным интегра­лом вдоль траектории движения

 

         .                                                       (2.5)                                                                                              

 

Работа силы – величина алгебраическая, она может быть положительной, отрицательной и равна нулю. Графическое представление работы показан на ри­сунке 2.2:

Рисунок 2.2

 

Рассмотрим левую часть уравнения (2.3). Она представляет собой полный дифференциал некоторой функции

 

  .                                                            (2.6)                                                                                                         

                                                                                     

Величина W_k называется кинетической энергией частицы. Кинетическая энергия – это часть полной энергии частицы, связанная с её движением. Естест­венно предположить, что покоившееся тело (V=0) не обладает кинетической энер­гией, тогда из (2.6) следует что

 .                                                              (2.7)                                                                                     

 

При вращательном движение твердого тела вокруг неподвижной оси  его кинетическая энергия равна

 

                   .                                                             (2.8)

         Выражения (2.7) и (2.8) справедливы только для нерелятивистских частиц (v<<c). Уравнение (2.7) справедливо и в случае, когда на частицу действует несколько сил. Тогда А₁₂ – сумма работ всех сил. Таким образом,  изменение кинетической энергии частицы равно работе всех сил, действующих на эту частицу.

 

А₁₂=W_k2-W_k1 .                                                                 (2.9)   

 

Физическая величина, равная работе, отнесенной к единице времени, назы­вается мощностью

 .                                                                      (2.10)

 

2.3 Консервативные и неконсервативные силы. Потенциальное поле сил

 

Все силы, независимо от их физической природы, принято делить на два класса: консервативные и неконсервативные. Сила называется консерватив­ной, если её работа не зависит от того, по какой траектории  перемещается час­тица из начальной точки в конечную.

 

 .                                                           (2.11)          

                                                                                                                                        

Если перемещение происходит по замкнутому пути, работа консервативной силы равна нулю

 

                   .                                                      (2.12)

                                                                                                                                             

Консервативными являются центральные силы (гравитационные, кулонов­ские), сила тяжести, сила упругости.

Работа неконсервативной силы зависит от пути, по которому происходит перемещение. Примером таких сил являются сила трения, сила сопротивления среды. Работа силы трения всегда отрицательна. Такие силы называются диссипа­тивными.

Полем сил называют область пространства, в каждой точке которого на по­мещенную туда частицу действует сила, закономерно меняющаяся от точки к точке . Силовые поля являются векторными. Силовое поле может быть однород­ным (поле силы тяжести), центральным (гравитационное поле). Поля консервативных сил обладают рядом характерных свойств, они образуют класс потенциальных полей. Такое поле в каждой точке можно охарактеризовать неко­торой функцией W_p(), зависящей от положения точки в пространстве и харак­тера силы таким образом, что работа консервативной силы  при перемеще­нии частицы между точками 1 и 2 будет равна убыли функции W_p

 

 A₁₂ =W_p1 –W_p2 =-∆W_p .                                                 (2.13)                                                                                         

 

Функция W_p называется потенциальной энергией частицы во внешнем кон­сервативном поле. Из (2.13) следует, что работа в таком поле совершается за счет потенциальной энергии.

Потенциальная энергия частицы W_p() всегда имеет смысл энергии взаимо­действия с объектами, создающими поле. Формула (2.13) позволяет в каж­дом конкретном случае получить выражения для W_p  (с точностью до произволь­ной постоянной).

Получим связь между силой и энергией частицы, находящейся в потенци­альном поле. Для этого запишем элементарную работу

 

.                                      (2.14)

 

Проекция силы на произвольное направление l:

 

                   .                                                                      (2.15)

 

Взяв в качестве направления перемещения направления вдоль осей коорди­нат  x, y, z, получим

 

                    ,                                           (2.16)

 

 или           

          .                                                        (2.17)

Формула (2.17) выражает связь между энергией и силой в потенциальном поле.

        

 

3 Лекция 3. Законы сохранения в механике

 

Цели лекции:

-        уяснить смысл законов сохранения как фундаментальных законов при­роды;

-        усвоить их формулировки и границы применения.

 

Законы сохранения импульса, момента импульса и энергии выделяются среди других законов своей всеобщностью. Это фундаментальные законы при­роды, которые выполняются не только в классической, но и в релятивистской  физике и квантовой механике.

Все законы сохранения были открыты вначале опытным путем как обобще­ние огромного количества экспериментальных фактов. Позже пришло понимание глубокой взаимосвязи этих законов, позволившее не только осмыслить их все­общность, но и предсказать в каких условиях тот или иной закон сохранения мо­жет видоизменять свою форму.

 

         3.1 Закон сохранения импульса

 

Закон сохранения импульса есть общий закон природы, в основе которого лежит однородность пространства, т.е. одинаковость свойств пространства во всех ее точках.

Закон сохранения импульса соблюдается только для изолированных систем. Действительно, если система помещена во внешнее поле сил, то для нее разные области пространства уже не будут эквивалентны.

         Изолированной, или замкнутой, системой называется система (совокуп­ность взаимодействующих между собой тел), на которую не действуют внешние силы.

Полный импульс замкнутой системы материальных точек (тел) не изменя­ется с течением времени

                            .                                                (3.1)

 

3.2 Закон сохранения момента импульса

 

При выводе основного закона динамики вращательного движения мы рас­сматривали твердое тело как систему материальных точек и пришли к соотноше­нию    

                                      ,                                                                     (3.2)

где – момент импульса системы;

       – суммарный момент внешних сил, действующих на систему.

Сумма моментов внутренних сил всегда для любой системы равна нулю.

Если внешние силы отсутствуют (система замкнута), то ,                         следовательно .             

Момент импульса замкнутой системы материальных точек (тел) оста­ется постоянным

                                             .                                                      (3.3)

 

Если тело вращается вокруг неподвижной оси и , то .                      Учитывая , что , получаем

 

                                            .                                                              (3.4)

 

         Закон сохранения момента импульса подобно закону сохранения импульса является фундаментальным законом природы. В основе его лежит свойство изо­тропности пространства, т.е. поворот замкнутой системы как целого не отража­ется на ее механических свойствах.

 

3.3 Закон сохранения энергии в механике

 

Закон сохранения и превращения энергии является одним из фундаменталь­ных законов природы. В основе сохранения энергии лежит однородность вре­мени, т.е. равнозначность всех моментов времени. Разные моменты времени экви­валентны в том смысле, что любой физический процесс протекает одинаковым образом независимо от того, когда он начался. Закон сохранения и превращения энергии имеет глубокий физический смысл. Он подтверждает положение о том, что движение является неотъемлемым свойством материи, оно несотворимо и не­уничтожимо, а лишь преобразуется из одних форм в другие.

Рассмотрим полную механическую энергию частицы и системы частиц.

Вернемся к формуле (2.9). Пусть на частицу действуют консервативные силы  и неконсервативные. Тогда

 

                                                      W_k2–W_k1=A₁₂^*+A₁₂ .

 

Так как  A₁₂^*=W_p1–W_p2 ,  получим

 

                                       (W_k2+W_p2)–(W_k1+W_p1)=A_{12 . .}                                                                 (3.5)

 

Полная механическая энергия частицы  W есть сумма её кинетической и по­тенциальной энергий. Изменение полной механической энергии частицы, нахо­дящейся в поле консервативных сил, равно работе неконсервативных сил, дейст­вующих на частицу

                            W₂–W₁=A₁₂  .                                                                                                  (3.6)

                                                                                                                                         

Энергия системы N невзаимодействующих частиц определяется как сумма всех энергий частиц, составляющих данную систему

                   .                                                        (3.7)                                                                                                                      

 

Если частицы взаимодействуют между собой, следует учесть энергию их взаимодействия, которая уже не является аддитивной величиной  

 

                   .                                                           (3.8)                                                                                                                               

        

Если между частицами системы действуют только консервативные силы (такая система называется консервативной), а внешние силы отсутствуют (A₁₂ =0), то ее полная механическая энергия сохраняется, как это следует из формулы (3.6). Это утверждение и есть закон сохранения полной механической энергии. Оче­видно, что полная механическая энергия сохраняется лишь для замкнутой консер­вативной системы тел.

         Законы сохранения импульса, момента импульса и энергии стали весьма мощ­ным и эффективным инструментом исследования. Эта важная роль законов сохранения обусловлена рядом причин:

-          законы сохранения не зависят ни от траекторий частиц, ни от харак­тера действующих сил. Поэтому они позволяют получить ряд весьма общих и существенных заключений о свойствах различных механических процессов, не вникая их детальное рассмотрение с помощью уравнений движения;

-         этот факт позволяет использовать законы сохранения даже тогда, когда силы вообще неизвестны (столкновения тел, молекул).

 

4 Лекция 4. Принцип относительности. Элементы релятивистской механики

 

Цель лекции:

- уяснить сущность механического принципа относительности и основных принципов специальной теории относительности, а так же следствий из них.

 

4.1 Принцип относительности Галилея

 

Принцип относительности Галилея (механический принцип относительно­сти) отражает фундаментальное свойство природы: никакими механическими опытами, проводимыми в инерциальной системе отсчета, нельзя установить, движется ли эта система отсчета прямолинейно и равномерно или покоится.

 

 

 

Принципу относительности Галилея соответствуют преобразования коор­динат Галилея. Если оси двух инерциальных систем отсчета параллельны и отно­сительное движение происходит вдоль одной из них (например, вдоль оси х) (рисунок 4.1), пре­образования Галилея (прямые и обратные) имеют вид:

 

                                                             

 

 

 

 

 

 

Рисунок 4.1

      

 (4.1)

 

 

 

 

где – скорость системы К` относительно условно неподвижной    сис­темы К.

         Физические величины, которые при преобразованиях Галилея остаются неиз­менными, называются инвариантами преобразований Галилея.

         Одной из таких величин является ускорение

                                           

                                                                                                                                (4.2)

                                                                                            ,

 

что обеспечивает и инвариантность всего второго закона Ньютона

                                                                                                                                                                                                                                                                                                                             

                                             

        

Среди основных инвариантов классической механики отметим пространст­венный интервал  (т .е. расстояние между двумя пространственными точками)

 

,               (4.3)

 

а так же временной интервал

                                                                                         .                                                      (4.4)

 

         К неинвариантным величинам в классической механике относится скорость. Классический закон сложения скоростей:

                                                                                       .                                                        (4.5)                                        

          Принцип относительности и преобразования Галилея отражают представ­ления об абсолютном пространстве и абсолютном времени, которые лежат в основе классической механики.

 

4.2 Постулаты Эйнштейна. Специальная теория относительности

 

         Специальная теория относительности (СТО) – это физическая теория про­странства и времени, в которой предполагается, что пространство однородно и изотропно, время – однородно.

         В основе специальной теории относительности Эйнштейна лежат два посту­лата: обобщенный принцип относительности и принцип постоянства скорости света в вакууме:

- все физические явления в инерциальных системах отсчета протекают оди­наково.

         - скорость света в вакууме одинакова во всех инерциальных системах от­счета и не зависит от движения источников и приемников света, т.е. яв­ляется универсальной постоянной. Она равна

                                                 м/с.

         Следствия из основных постулатов Эйнштейна:

          - время течет по-разному в разных инерциальных системах отсчета. Утвер­ждение о том, что между двумя данными событиями прошел оп­ределенный промежуток времени, приобретает смысл только тогда, ко­гда указано, к какой системе отсчета это утверждение относится; собы­тия, одновременные в некоторой системе отсчета, могут быть неодно­временными в другой системе;

- относительность временных интервалов одного и того же события в систе­мах отсчета К и К` :

                                               

                                                        .                                                        (4.6)

 

Время, отсчитываемое по часам, движущимся вместе с объектом, называ­ется  собственным временем этого объекта. Обозначим его , тогда

                                                                                                                  (4.7)

 

 

        

         Движущиеся часы идут медленнее неподвижных. Замедление хода времени в  системе, где часы покоятся, не является кажущимся и не связано с влиянием движения часов на их работу, а отражает относительный характер времени. Итак, не существует единого мирового времени. Время, его течение, понятия одновре­менности событий – относительны.

Относительность пространственных интервалов

 

                                                                                                          (4.8)

 

          Длина стержня , измеренная в системе отсчета, в которой стержень непод­вижен, называется собственной. Как видно из (4.8), эта длина является мак­симальной, т.е. во всех системах отсчета длина тел уменьшается по сравнению с собственной. Это явление называется лоренцевым сокращением размеров тел в направлении движения. Лоренцево сокращение геометрических размеров тел не является кажущимся и не связано с физическим воздействием движения на размеры тела. Оно отражает неабсолютность пространственных интервалов, их зависимость от выбора системы отсчета.

 

4.3 Преобразования Лоренца

 

         Релятивист­ские преобразования координат и времени, отражающие свойства пространства и времени в специальной теории относительности, называются преобразованиями Лоренца. Согласно этим преобразованиям переход от системы К` к системе К осуществляется по формулам (4.9), а от К к системе К` – по формулам (4.10)

                      .                (4.9)

        

                                                                               (4.10)

                             

 

 

 

На основе полученных преобразований координат и времени можно дать еще одну формулировку принципа относительности: физические законы инвари­антны относительно преобразований Лоренца.

         Рассмотрим некоторые следствия из преобразований Лоренца. Во-первых, преобразования Лоренца наглядно демонстрируют неразрывную взаимосвязь пространственных и временных свойств нашего мира. Таким обра­зом, нельзя говорить отдельно о пространстве и отдельно о времени, правильно будет говорить о пространстве – времени, в котором существует наш мир. Иными словами, наш мир четырехмерен.

         Во-вторых, на основе преобразований Лоренца можно описать относитель­ность одновременности, о которой мы ранее говорили на качественном уровне.

         В-третьих, оказывается, что выражаемый формулой (4.5) классический за­кон сложения скоростей несправедлив при движении тел со скоростями, близ­кими скорости света. Релятивистский закон сложения скоростей для случая, когда частица движется вдоль оси Х

 

                                                                     (4.11)                                                        

 

4.4 Инварианты специальной теории относительности

 

         Из преобразований Лоренца следует, что скорость света одна и та же в раз­личных инерциальных системах отсчета. Этот вывод соответствует принципу по­стоянства скорости света. Из формул преобразований Лоренца следует также, что скорость света является максимальной .

         В релятивистской механике инвариантность пространственных и времен­ных интервалов относительно преобразований Лоренца не имеет места. Возни­кает вопрос, нельзя ли в специальной теории относительности указать величину, свя­занную с пространственными и временными интервалами между двумя собы­тиями, которая была бы инвариантна преобразованиям Лоренца? Этот вопрос ре­шается положительно. Таким инвариантом в специальной теории относительно­сти является величина , определяемая соотношением

        

   .                 (4.12)

        

Эта величина называется пространственно – временным интервалом (или просто интервалом) между событиями.

 

4.5 Элементы релятивистской динамики

 

         Релятивистский импульс выражается формулой

                                                    .                                              (4.13)

         С учетом выражения (4.13) основной закон динамики, представленный соот­ношением

будет справедлив и для релятивистских движений.

         В релятивистском законе динамики в общем случае направления векторов и не совпадают; нарушается и пропорциональность между величинами ускорения и силы.

Введем в рассмотрение величину , называемую полной энергией тела

         

         .                                             (4.14)

        

Полная энергия тела величина сугубо положительная, причем и в состоянии по­коя она не равна нулю. При  полная энергия называется энергией покоя

                                                              

                                                            .                                                   (4.15)                             

        

Формула (4.15) устанавливает взаимосвязь энергии покоя тела и его массы и показывает, что масса и энергия представлены в любом теле в пропорциональных количествах. Каждое изменение энергии покоя тела неизбежно сопровождается пропорциональным изменением его массы.

         Полная энергия включает и энергию движения, т.е. кинетическую энергию. Поэтому кинетическая энергия тела определяется как разность между полной энергией и энергией покоя

                                                    .                              (4.16)                                      

        

         Взятые раздельно друг от друга энергия W и импульс р относительны, то есть, различны в разных системах отсчета. Однако взятые совместно в виде ком­бинации  они образуют абсолютную характеристику состояния частицы, инвариантную относительно преобразовании Лоренца. Из инвариантности этой величины вытекает релятивистская взаимосвязь между импульсом и энергией – при переходе из одной инерциальной системы в другую, импульс и энергия час­тицы изменяются так, что комбинация  остается неизменной.

        

5 Лекция 5. Статистические распределения

 

         Цели лекции:

-        уяснить сущность статистического и термодинамического методов иссле­дования, предмет данной науки;

-          изучить основные законы классической статистической физики.

 

5.1 Статистический и термодинамический методы исследования

 

Статистическая физика и термодинамика – два взаимосвязанных раздела физики, изучающих наиболее общие свойства макроскопических физических сис­тем, включая и такие системы, которые непосредственно связаны с нашим жизне­обеспечением.

         Задачей термодинамики является изучение свойств материальных тел, харак­теризуемых непосредственно измеряемыми в опытах величинами (макро­скопическими параметрами: объемом, температурой, давлением и т.д.), на основе наиболее об­щих абсолютно верных принципов – начал термодинамики. При этом не привле­каются никакие модельные представления о строении вещества. Сила термодина­мики в том, что её выводы верны в такой же степени, в какой верны начала тер­модинамики.

          Статистическая физика основана на модельных атомо-молекулярных пред­ставлениях о строении макротел (например, модель идеального газа) и мате­матической статике. Свойства макросистем, в конечном счете, определяются свойствами частиц системы, особенностями их движения и усреднёнными значе­ниями динамических характеристик этих частиц (энергии, скорости и т.д.). Стати­стическая физика дает способы вычисления подобных средних и с их помощью определяет макропараметры систем. Так было получено основное уравнение мо­лекулярно-кинетической теории

                             ,                                                         (5.1)

где  p – давление газа,

n – число молекул газа в единице объёма (концентрация молекул),        – средняя энергия поступательного движения молекул.

         Оба метода – термодинамический и статистический, обладают своими досто­инствами и недостатками. Их согласованное применение даёт наиболее пол­ный и надёжный результат.

 

5.2 Закон равномерного распределения энергии по степеням свободы

 

         Основные понятия: число степеней свободы молекулы i, поступательные, вращательные и колебательные степени свободы.

         Одним из важнейших законов статистической физики, применимым к класси­ческим системам, является закон равномерного распределения энергии по степеням свободы:

в состоянии теплового равновесия на каждую степень свободы молекулы приходится в среднем одинаковая кинетическая энергия, равная . Здесь  – постоянная Больцмана.

         При хаотическом движении ни один из видов движения не имеет преиму­ществ перед другим, но следует иметь в виду, что колебательное движение свя­зано  с переходом кинетической энергии в потенциальную и обратно. При учёте энергии колебаний атомов в молекуле нужно принимать во внимание среднюю кинетическую и среднюю потенциальную энергии. Полная энергия молекулы:

  ,                                                     (5.2)

 

           ,                                      (5.3)

 

где i – число степеней свободы молекулы.

 

 

 

5.3 Закон Максвелла для распределения молекул по скоростям

 

         Рассмотрим газ в состоянии термодинамического равновесия. Движение его частиц подчиняется законам классической механики. Пусть газ содержит N моле­кул, масса каждой молекулы m. Тепловое хаотическое движение характеризуется тем, что распределение молекул по направлениям движения равномерно (все на­правления равновероятны). Но числовые значения скоростей молекул не могут быть одинаковыми, в результате столкновений должно установится некоторое распределение по скоростям молекул, которое не будет зависеть от времени.

         Если скорость молекулы газа может принимать значения , то имеет смысл постановка вопроса: сколько молекул dN из общего числа N обладает ско­ростями, лежащими в некотором интервале  около заданной скорости ? Оче­видно:

                                                .                                                      (5.4)

 

Функция                                                                                                      (5.5)

 

называется функцией распределения молекул по скоростям. Она имеет следую­щий смысл:  определяет долю молекул, скорости которых заключены в единич­ном интервале около заданного значения . Функция  удовлетворяет условию нормировки .

         Задача о распределении молекул газа по скоростям была сформулирована и решена Дж. К. Максвеллом в 1859 – 1860 гг. Функция распределения Максвелла имеет вид, представленной на рисунке 5.1 и выражается формулой

                               .                                            (5.6)

 

Вероятность того, что значение скорости произвольно выбранной молекулы ле­жит в интервале  равна   .    

 

 

 

 

 

 

                                                          

 

            Рисунок 5.1

Основные свойства распределения Максвелла:

-        лишь малый процент молекул обладает очень малыми и очень боль­шими скоростями;

-        существует значение скорости (вероятнейшая), соответствующее мак­симуму функции , так что значительная часть молекул обладает ско­ростями близкими к . Легко показать, что

;                                                   (5.7)

-          из асимметрии кривой распределения следует, что доля молекул, скоро­сти которых превышают , всегда больше, чем доля молекул со скоро­стями . Эта диспропорция увеличивается с возрастанием темпера­туры (кривые для  и  на графике функции  >).

Зная функцию распределения, можно найти среднее значение любой физи­ческой величины, зависящей от скорости. Среднеарифметическая скорость равна

      .                                    (5.8)

Среднеквадратичная скорость                 

  

      ;         ;           .                       (5.9)

 

Вид распределения  не зависит от того, как частицы взаимодейст­вуют друг с другом. Он определяется лишь способностью частиц обмениваться энергией в процессе установления равновесного состояния. В законе Максвелла температура является параметром, от которого зависит вид кривой. Говорить о температуре системы можно лишь в том случае, когда  в системе установилось тепловое (хаотическое) движение частиц, скорости которых распределены по за­кону Максвелла.

 

5.4 Закон Больцмана для распределения частиц во внешнем потенциальном поле

 

         При тепловом движении все направления движения частицы равноверо­ятны, а изменения в положении каждой частицы носят случайный характер. По­этому можно говорить о вероятности обнаружения частицы в том, или ином месте.

         Пусть идеальный газ занимает объём V и находится в равновесном состоя­нии с температурой T. При отсутствии внешнего поля все положения любой мо­лекулы равновероятны. Именно поэтому газ распределяется по всему объёму с одинаковой концентрацией .

         Если газ находится во внешнем силовом поле, частицы газа испытывают дей­ствие этого поля, и картина меняется. Плотность и давление газа оказываются в различных местах разными. Рассмотрим случай, когда силы внешнего поля яв­ляются потенциальными и действуют только в одном направлении z. Обозначим потенциальную энергию частицы . Можно показать, что в состоянии тепло­вого равновесия концентрация частиц газа, подверженного действию внешнего поля, измеряется по закону

                                               .                                              (5.10)

Это соотношение называется законом Больцмана.

         Рассмотрим поле земного тяготения. Вблизи земной поверхности потенциаль­ная энергия молекулы  . Учитывая, что , получим дав­ление газа на высоте z над поверхностью земли

                                        .                                      (5.11)

 

Эта формула называется барометрической. Её можно применить и для достаточно разряженной смеси газов (воздух).

         Оба рассмотренные распределения можно объединить в один закон Мак­свелла – Больцмана. Для реальных газов он применим до тех пор, пока можно пренебрегать взаимодействием молекул на расстоянии. Кроме того, при очень низких температурах движение молекул уже не подчиняется классическим зако­нам – возникает отступление от закона Максвелла – Больцмана (область вырож­денного газа).

 

6 Лекция  6. Основы термодинамики

 

         Цели лекции:

-        изучить основные законы (начала) термодинамики;

-        освоить методы их использования при анализе процессов, происходя­щих в макросистемах.

 

6.1 Теплота и работа как формы обмена энергией в термодинамике.   Первое начало термодинамики

 

         Внутренняя энергия U макроскопических тел качественно отличается от меха­нической энергии системы частиц. Это отличие проявляется в существовании лишь двух форм изменения внутренней энергии – работы и теплоты.

         Работа А есть мера изменения внутренней энергии системы при силовых взаимодействиях её с окружающей средой. Совершение работы всегда связано с возникновением какого-либо упорядоченного движения, с изменением внешних параметров системы (например, объема V).

         Теплота Q есть мера измерения внутренней энергии системы в процессах теплопередачи и не сопровождается изменением внешних параметров. Меха­низмы теплопередачи: теплопроводность, излучение, конвекция.

         Теплота и работа – не виды энергии, а формы её обмена.

         Закон сохранения энергии, сформированный с учетом того, что в термодина­мике возможны лишь два способа обмена энергией между системой и окружающей средой, является фундаментальным законом физики:

теплота, переданная системе, и работа, совершенная над системой, идут на из­менение внутренней энергии системы.

                                    , или ,                                            (6.1)

 

где – работа, совершенная над системой,

      – работа системы над  внеш­ними силами.

         Внутренняя энергия является функцией состояния системы. Ее изменение зависит только от начального и конечного состояний и не зависит от способа пе­рехода между состояниями.

         Теплота и работа зависят не только от этих состояний, но и от вида про­цесса; они являются функциями процесса.

 

6.2          Второе начало термодинамики

 

6.2.1 Круговые процессы. КПД тепловых машин

Первое начало термодинамики указывает на возможность совершать работу за счет тепла, получаемого системой от внешних тел. Например, при изотермиче­ском расширении идеального газа между состояниями 1–2: .

 

 

 

 

 

 

                   

                                               Рисунок 6.1

 

Однако, действие тепловых машин основано на круговых (циклических) процессах, в которых система (рабочее тело) после ряда изменений возвращается в исходное состояние. При этом некоторое количество теплоты будет отдано среде.

В принципиальном отношении работа тепловой машины может быть све­дена к следующему: рабочее тело получает от нагревателя теплоту , отдает холо­дильнику  и разность этих теплот преобразует в полезную работу  (рисунок 6.1).  – своеобразный «налог», который необходимо заплатить природе за возможность преобразования некоторого количества теплоты в работу. Эффективность теплового двигателя характеризуется его коэффициентом полезного действия 

                                         .                                            (6.2)

          Выражение (6.2) показывает, что КПД тепловых машин принципиально меньше единицы. Этот результат не является следствием первого начала термо­динамики, а выражает содержание другого фундаментального закона – второго начала термодинамики. Другие формулировки этого закона:

- невозможен циклический процесс, единственным результатом которого яв­ляется производство работы и обмен энергией с одним тепловым ре­зервуаром (У.Томсон);

-       невозможен вечный двигатель второго рода (В.Оствальд);

-  невозможен циклический процесс, единственным результатом которого была бы передача теплоты от менее нагретого тела к более нагретому (Р.Клаузиус).

          Эмпирические формулировки второго начала не выражаются в математиче­ской форме. Будучи внешне разнообразны, они имеют внутреннее единство, по су­ществу, они эквивалентны друг другу.

          6.2.2 Цикл Карно. Теорема Карно и теорема Клаузиуса

          Среди всех циклических процессов особое место принадлежит циклу Карно, с изучением которого связано открытие второго начала термодинамики. Это единственный цикл, который при наличии одного нагревателя и одного холо­дильника может быть выполнен обратимым образом. Цикл Карно состоит из двух изотерм и двух адиабат. Предположив, что рабочим телом является идеаль­ный газ, получим КПД обратимого цикла Карно

                                                ,

                                  

                                                               .                                                   (6.3)

               Теорема Карно:

-     КПД обратимого цикла Карно не зависит от природы рабочего тела и уст­ройства системы, выполняющей этот цикл, а определяется только температурой нагревателя  и холодильника ;

-     КПД необратимых машин (работающих по необратимому циклу), меньше КПД обратимых машин, т.е. . Следовательно,

 

                                             .                                             (6.4)

 

          Строго обратимые процессы в макросистемах невозможны, поэтому выраже­ние (6.3) носит асимптотический характер – к нему можно приближаться, но точного значения нельзя достичь.

          Теорема Карно (6.4) является математическим выражением второго начала термодинамики, применительно к замкнутым процессам с одним нагревателем и одним холодильником. Знак равенства в (6.4) имеет место для обратимых процес­сов, а знак неравенства – для необратимых.

          Обобщением теоремы Карно на случай произвольных циклов является нера­венство Клаузиуса (теорема Клаузиуса):  

                                                                       .                                                (6.5)

 

6.2.3 Энтропия. Второе начало термодинамики как закон возрастания энтро­пии

          Все рассмотренные формулировки второго начала термодинамики указы­вают на то, что одного лишь учета и сохранения количества энергии недостаточно для того, чтобы судить о возможности того или иного процесса. Энергия должна характеризоваться не только количественно, но и качественно. Величиной, опре­деляющей качество энергии и позволяющей количественно описать ограничения, налагаемые вторым началом термодинамики, является энтропия  S.

          Запишем теорему Клаузиуса (6.5) для произвольного обратимого цикла

                                                           .                                                        (6.6)

Из равенства нулю интеграла (6.6) следует, что величина  представляет со­бой полный дифференциал некоторой функции состояния S, так что    

                                                 и        .                                   (6.7)

 

          Формулы (6.7) следует рассматривать как определенные понятия энтропии в термодинамике.

          Некоторые свойства энтропии, вытекающие из ее определения (6.7):

-  энтропия системы есть величина аддитивная ;

- при обратимом процессе без теплообмена – адиабатный   процесс - энтропия остается постоянной;

- энтропия процесса может быть определена лишь с точностью до произволь­ной постоянной.

          Изменение энтропии в обратимых процессах рассчитывается на основании соотношений (6.7) и (6.1)

 

                                                           .                                                 (6.8)

         

          Для анализа тепловых процессов используется TS – диаграмма, где в каче­стве осей координат выбраны функции состояния T и S.

          Глубокий физический смысл энтропии раскрывается в статистической фи­зике. Л.Больцманом было показано, что энтропия S определяется логарифмом числа микросостояний , посредством которых реализуется рассматриваемое мак­росостояние:

                                                                 ,                                                    (6.9)

           

          где k – постоянная Больц­мана,

                 – статистический вес данного макросостояния.

           Формула (6.9) называется формулой Больцмана. Она позволяет дать энтропии наглядное толкование.

          Допустим, что все атомы жестко закреплены в определенных местах. Тогда существует только одно микросостояние,  и . Передача системе некото­рого количества теплоты увеличивает неупорядоченность внутренней структуры и хаотичность движения образующих ее частиц ( растет). Поэтому можно ска­зать, что энтропия является мерой беспорядка.

          С понятием энтропии связана наиболее общая формулировка второго на­чала термодинамики:

          в изолированной системе энтропия не убывает

 

                                                     ,     .                                              (6.10)

 

          Знак равенства в (6.10) соответствует случаю, когда в системе идут только обратимые процессы, энтропия остается неизменной. Все реальные процессы, как правило, необратимые, значит энтропия изолированной системы всегда растет. Рост энтропии означает переход системы от менее вероятных состояний к более вероятному, т.е. равновесному состоянию.

          Однако, возможны и флуктуации. Закон возрастания энтропии в изолирован­ной системе носит статистический характер.

          Второе начало термодинамики, выраженное математически в (6.10), нахо­дится в соответствии со всеми раннее рассмотренными формулировками.

          Из анализа работы тепловых машин следует, что доступной для превраще­ния в работу dA является не вся энергия, переданная системе в форме тепла dQ, а только её часть , и тем меньшая, чем больше будет энтропия. Это обстоятельство позволяет охарактеризовать энтропию и как меру работоспособности. Возрастание энтропии системы является характерным признаком естественных процессов и соответствует понижению качества энергии. Изолированная система всегда переходит в состояние термодинамического рав­новесия, в котором энтропия достигает своего максимального значения, а энергия «обесценивается».

          Понятие энтропии относится  не только к изолированным системам, но и к открытым. Связь между энергией, энтропией и возможностью системой совер­шать работу необходимо принимать во внимание при создании различных техни­ческих устройств и технологий.

 

7 Лекция 7. Явления переноса

 

Цели лекции:

-       ознакомиться с явлениями переноса;

-       уяснить общие закономерности, механизмы и индивидуальные характери­стики явлений переноса.

 

         7.1 Общая характеристика явлений переноса

 

В состоянии термодинамического равновесия параметры системы (темпера­тура , давление , концентрация молекул  и т.д.) одинаковы во всех частях сис­темы. В этих условиях самопроизвольное возникновение каких-либо макро­процессов в системе невозможно.

         При нарушении равновесия система становится физически неоднородной, параметры состояния, характеризующие эту систему, могут оказаться различ­ными в разных частях системы. Если такую систему предоставить самой себе, то она неизбежно снова самопроизвольно возвратится в наиболее вероятное состоя­ние – состояние равновесия.

         Процессы пространственного выравнивания макроскопических параметров, характеризующих систему, связаны с переносом от точки к точке внутри системы некоторых микроскопических характеристик и обеспечиваются тепловым движе­нием. Подобные процессы называются явлениями переноса.

         Явления переноса могут быть связаны не только с процессами, возвращаю­щими систему в состояние равновесия, но и с воздействием извне, связанным с поддержанием неравновесного состояния системы в течение неограниченного времени. В этом случае они становятся стационарными (т.е. не зависящими от времени).

         Интенсивность процесса переноса характеризуется потоком соответствую­щей величины.

         Потоком какой-либо величины называется количество этой величины, прохо­дящей в единицу времени через некоторую воображаемую поверхность (на­пример, поток массы , поток импульса  и т.д.)

         Поток – скалярная алгебраическая величина, знак которой определяется выбо­ром направления, вдоль которого поток считается положительным.

         Диффузией называется обусловленный тепловым движением процесс пере­носа вещества из областей среды, где его плотность выше, в области, где она ниже.

         Рассмотрим некоторую среду, в которой имеется неоднородное распределе­ние концентрации  какого-либо компонента, например, вдоль оси . Быстрота изменения концентрации  характеризуется производной  ( – проекция на ось  градиента концентрации данного компонента). Температура, суммарная концентрация  (равновесная) и давление всюду одинаковы.

         В этом случае возникает поток молекул  и следовательно, массы  данного компонента в направлении убывания его концентрации. Экспериментально установлено, что поток массы через перпендикулярную к оси  поверхность  равен

 

                                                     ,                                             (7.1)

где – парциальная плотность -того  компонента,

       – масса молекулы данного компонента,

       – коэффициент пропорциональности, называемый диффузией.

         Уравнение (7.1) называется законом Фика. Знак минус обусловлен тем, что поток направлен в сторону убывания плотности (концентрации) данного компо­нента среды.

         Если в системе имеется неоднородное распределение температуры (), то возникает поток тепла  в сторону убывания температуры

                                                        ,                                                        (7.2)

где – коэффициент пропорциональности, зависящий от свойств среды и назы­ваемый теплопроводностью.

Соотношение (7.2) называется законом Фурье и описывает теплопровод­ность – процесс теплопередачи за счет хаотического движения частиц среды.

         Если в газообразной среде  неодинаковы скорости соседних слоев, то от слоя к слою (поперек направления движения слоев) будет переда­ваться импульс молекул. Поток импульса  через поверхность , перпендикуляр­ную оси , будет

                                                  .                                      (7.3)

        

Уравнение (7.3) называется законом Ньютона и описывает перенос им­пульса – вязкость, или внутреннее течение. Величина , являющаяся коэффициент­ом пропорциональности, называется динамической вязкостью среды.

         Итак, при диффузии от слоя к слою среды передается масса, при теплопровод­ности – энергия, при вязкости – импульс. Законы Фика, Фурье и Ньютона являются эмпирическими. Их теоретическое обоснование дает молеку­лярная физика.

         7.2 Элементы молекулярно–кинетической теории явлений переноса

 

         Для количественного анализа явлений переноса необходимо усвоить кинема­тические характеристики молекулярного движения:

-        эффективный диаметр молекулы d и эффективное сечение  столк­новений;

-        среднее число соударений, испытываемых одной молекулой газа в еди­ницу времени ;

-          среднюю длину свободного пробега молекулы   

 

.                                                     (7.4)

 

         Пусть величина  характеризует некоторое молекулярное свойство, отнесен­ное к одной молекуле (это может быть энергия, импульс, концентрация, заряд и т.д.) Предположим, что в среде имеется градиент этой величины вдоль оси .    

                                              

Рисунок 7.1

 

Выделим перпендикулярную оси  площадку  (рисунок 7.1) и подсчитаем суммарный по­ток  величины  через эту площадку, обусловленный тепловым движением молекул. При этом надо учесть, что площадку  непосредственно пересекают лишь те молекулы, которые в момент последнего столкновения находились от площадки на расстоянии, не более средней длины свободного пробега, и получим поток, направленный вдоль (или против) оси

 

             .               (7.5)    

  

         Уравнение (7.5) является основным уравнением процессов переноса, опреде­ляющим поток величины  через площадку . Получим из (7.5) уравне­ния Фика, Фурье и Ньютона.

         Пусть молекулы равномерно заполняют некоторый объем, и все они мало отличаются друг от друга по своим механическим параметрам. Концентрация не­которого сорта молекул . Учитывая, что в (7.5) величина  есть характери­стика, отнесенная к одной молекуле, имеем     

 

      ,                                                         (7.6)

 

где – равновесная концентрация молекул.

 

                           ,                                       (7.7)

 

где                                 .                                                     (7.8)

 

         Мы не только пришли к уравнению (7.1), но и получили выражение для вели­чины  – диффузии.

         В случае теплопроводности  есть средняя энергия теплового движения мо­лекулы

                   .                                     (7.9)

 

Тогда уравнение переноса принимает вид

 

        ,                      (7.10)

 

                                       ,                                                        (7.11)

 

         Здесь – теплопроводность,

   – плотность,

   – изохорная удельная теплоемкость среды.

В случае вязкости . Следовательно,

 

                 ,                                     (7.12)  

 

                                               .                                                   (7.13)

 

Из выражений (7.8), (7.11) и (7.13) следует, что ,   .

         Наличие этой связи между коэффициентами в уравнениях переноса обуслов­лено одинаковостью физической природы процессов переноса и тем, что все они описываются одинаковыми уравнениями вида (7.5).

 

8 Лекция 8. Электростатическое поле в вакууме

 

Цели лекции:

-       изучение свойств и характеристик электростатического поля;

         -  определение основной задачи электростатики и освоение методов ее реше­ния.

 

8.1 Электростатическое поле и его характеристики

 

Электрический заряд частицы является одной из основных ее ха­рактеристик, определяющей_ интенсивность_ электромагнитных взаимодействий. Ему присущи_следующие_свойства:

-        электрический заряд существует в двух видах: положительный и отрица­тельный. Так, в атомах отрицательным зарядом обладают электроны, а положительным – ядра;

-        электрический заряд является релятивистски–инвариантным: он не изме­няется при движении носителя заряда, т.е. его величина не зависит от системы отсчета;

-  электрический заряд аддитивен: заряд любой системы всегда равен алгеб­раической сумме зарядов составляющих систему частиц;

-        электрический заряд дискретен, т.е. любой заряд кратен элементарному за­ряду е: q=±Ne, где е=1,6×10^–19 Кл. Это свойство называется квантованностью электрических зарядов. Электрон и протон являются но­сителями элементарных соответственно отрицательного и положи­тельного зарядов;

-        суммарный заряд электрически изолированной системы не изменяется. Это свойство называется законом сохранения электрического заряда.

Перечисленные свойства являются фундаментальными законами, они не вы­водятся из каких-либо других законов, и не обнаружено ни одного явления, кото­рое противоречило бы этим свойствам.

 

8.2 Электростатическое поле. Характеристики электростатического  поля

 

Взаимодействие между электрически заряженными частицами и телами, со­гласно современным представлениям, осуществляется_через_поле. Электрическое поле неподвижных электрических зарядов называется электростатическим полем. Силы, дейст­вующие на заряженные частицы со стороны электростатического поля, называ­ются электростатическими. В электростатике используется модель (физическая абстракция), подобная материальной точке, это – точечный заряд. Точечным зарядом называется заряженное тело, размерами которого можно пре­небречь по сравнению с расстояниями от этого тела до других заряженных тел, отсчитываемыми от их центров.

Напряженность электростатического поля в данной точке есть физиче­ская величина, определяемая силой, действующей на единичный положительный заряд, помещенный в данную точку поля

 

.                                                        (8.1)

Направление вектора напряженности совпадает с направлением силы, дей­ствующей на положительный пробный заряд.

         Опыт показывает, что к кулоновским силам применим принцип независимо­сти действия сил, рассмотренный в механике. Следовательно, результирующая сила, действующая на пробный заряд Q₀, в любой точке поля, равна векторной сумме сил, приложенных к нему со стороны каждого из зарядов Q_i  системы

 

.                                                 (8.2)

 С учетом (8.1) для напряженности поля , созданного системой зарядов,  получим

                                                        .                                                               (8.3)

Уравнение (8.3) выражает принцип суперпозиции (наложения) электриче­ских полей.

         Если в электростатическом поле, создаваемом неподвижным зарядом Q, вдоль произвольной траектории из точки 1 в точку 2 перемещается точечный пробный заряд Q₀ (рисунок 8.1), то сила, приложенная к нему со стороны поля,

 

Рисунок 8.1

совершает работу

                            ,                          

 

где_–угол_между_векторами силы_с_и перемещения .

Используя закон Кулона и соотношение , получим

 

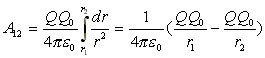                                                                   (8.4)

 

Из (8.4) следует, что работа не зависит от траектории перемещения (или пути), а определяется только начальным 1 и конеч­ным 2 положениями заряда Q₀. Поэтому электростатическое поле является потен­циальным, а электростати­ческие силы – консервативными.
         Следовательно, работа сил электростатического поля равна убыли потенци­альной энергии и может быть записана в виде

 

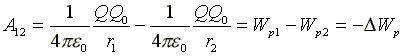                                      (8.5)

 

Потенциал электростатического поля есть физическая величина, равная отношению потенциальной энергии W_р  пробного точечного заряда, помещенного в рассматриваемую точку поля, к этому заряду Q₀ (или равная потенциальной энергии единичного положительного заряда в данной точке поля)

                                               .                                                       (8.6)

 

Работа, совершаемая силами поля при перемещении заряда Q₀ из точки 1 с потенциалом   в точку 2 с потенциалом   равна

 

                                         .                                                  (8.7)

 

Между напряженностью поля – его силовой характеристикой, и потенциа­лом – энергетической характеристикой поля, существует взаимосвязь, обуслов­ленная потенциальностью электростатического поля. В поле потенциальных сил потенциальная энергия и сила взаимосвязаны

 

   .

 

где  – оператор набла (или просто набла), который имеет вид

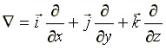
                                                                                   (8.8)

Знак "минус " свидетельствует о направлении вектора , он всегда направлен в сторону уменьшения потенциала.

8.3 Основная задача электростатики

 

Основная задача электростатики заключается в нахождении характеристик поля: напряженности поля  и потенциала  – по заданным величинам и распределению зарядов в пространстве. Решить эту задачу можно двумя способами, используя принцип суперпозиции и теорему Га­усса.

Потоком напряженности электрического поля сквозь поверхность , находя­щуюся в этом поле, называется величина

 

                 ,                                         (8.9)

где – проекция вектора  на нормаль  к элементарной  площадке  .

         Эта величина алгебраическая: она зависит не только от конфигурации поля, но и от выбора направления нормали n к площадке S. В случае замкнутых по­верхностей принято нормаль n направлять наружу области, охватываемой этой поверх­ностью.

         Поток вектора  сквозь произвольную замкнутую поверхность  зависит только от алгебраической суммы зарядов, охватываемых этой поверхностью

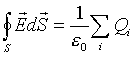                                              .                                                 (8.10)

Формула (8.10) выражает теорему Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме за­ключенных внутри этой поверхности зарядов, деленной на электрическую посто­янную .

Теорема Гаусса удобна для расчета электростатических полей симметрич­ных систем зарядов. Для этой цели необходимо установить характер поля (на­правление силовых линий), выбрать замкнутую гауссову поверхность, проходя­щую через рассматриваемую точку так, чтобы поток напряженности поля сквозь эту поверхность легко выражался через искомое значение напряженности. В каче­стве примеров применения теоремы Гаусса к расчету электростатических полей рассматриваются поля бесконечной однородно заряженной плоскости, двух па­раллельных плоскостей, заряженной сферической или цилиндрической поверхно­стей с различным распределением зарядов (линейным, поверхностным, объем­ным)

 

8.4 Основные теоремы электростатики в вакууме

 

Теорема о циркуляции вектора . Электростатическое поле представляет со­бой поле неподвижных зарядов. Оно является консервативным, т.е. работа сил этого поля не зависит от пути, а зависит от начального и конечного положений заряда. Если в качестве пробного заряда взять единичный положительный заряд, то работа сил при его перемещении из точки 1 в точку 2 будет равна  .

Если осуществляется работа по произвольному замкнутому пути, то она равна нулю

.                                                          (8.11)

Интеграл  называют циркуляцией вектора напряженности . Таким об­разом,  циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Утверждение (8.11) называют теоремой о циркуляции вектора . Силовое поле, обладающее свойством (8.11) называется потенциальным. Формула (8.11) справедлива для электростатического поля.

Из обращения в нуль циркуляции вектора напряженности  следует, что ли­нии напряженности электростатического поля не могут быть замкнутыми.

Вторая тео­рема - теорема Гаусса -  свидетельствует о том, что источниками электростатического поля являются электрические заряды. По аналогии с гидростатикой источниками называют положительные заряды, а стоками – отрицательные заряды. Линии век­тора электростатического поля начинаются в местах источников поля, а в местах стоков они заканчиваются.

 

9 Лекция 9. Электростатическое поле в веществе

 

Цели лекции:

-       изучение явления поляризации диэлектриков и теоремы Гаусса для поля в веществе;

-       ознакомление с поведением векторов  и  на границе диэлектриков.

 

9.1 Диэлектрики. Поляризация диэлектриков

 

Диэлектриками называются вещества, практически не проводящие электри­ческий ток в обычных условиях.

Согласно классическим представлениям в диэлектриках, в отличие от про­водников, нет свободных носителей зарядов, которые под действием электриче­ского поля могли бы прийти в упорядоченное движение и образовать электриче­ский ток проводимости. Электроны атомов диэлектрика связаны с ядром атома, и нужны сильные внешние факторы, чтобы нарушить эту связь.

Молекулы диэлектрика электрически нейтральны, представляют собой сис­темы с суммарным зарядом, равным нулю. Несмотря на это молекулы обладают электрическими свойствами, и в первом приближении молекулу можно рассмат­ривать как электрический диполь.

Положительный заряд такого диполя равен суммарному заряду ядер, поме­щен в «центр тяжести» положительных зарядов; отрицательный заряд равен сум­марному заряду электронов и помещен в «центр тяжести» отрицательных зарядов. Электрический момент такого диполя , (– суммарный положитель­ный заряд всех атомных ядер в молекуле, – вектор, проведенный из «цен­тра тяжести» электронов в «центр тяжести» положительных зарядов атомных ядер).

Внесение диэлектриков во внешнее электрическое поле приводит к возник­новению электрического момента диэлектрика, отличного от нуля, диэлектрик поляризуется.

Поляризацией диэлектрика называется процесс появления под воздействием внешнего электрического поля ориентированных по полю диполей, в результате чего электрический момент некоторого объема диэлектрика становится отличным от нуля.

Диэлектрики делятся на три группы: полярные, неполярные и кристалличе­ские. Соответственно трем группам диэлектриков различают три вида поляриза­ции: электронная (деформационная) у неполярных диэлектриков, ориентационная (дипольная) у полярных, ионная у диэлектриков с ионными кристаллическими решетками.

 

9.2  Поляризованность. Объемные и поверхностные связанные заряды

 

Количественной мерой поляризации диэлектрика является вектор , называе­мый поляризованностью (вектором поляризации) и равный отношению электрического дипольного момента физически бесконечно малого объема ди­электрика к этому объему:

                                     ,                                                       (9.1)

где – дипольный момент одной молекулы.

Физический смысл вектора поляризации состоит в том, что его модуль оп­ределяет степень поляризованности диэлектрика, а его направление совпадает с направлением поляризации. Поляризованность – макроскопическая характери­стика, она определяется напряженностью внешнего электрического поля, вызы­вающего поляризацию.

У изотропных диэлектриков любого типа поляризованность связана с на­пряженностью поля в той же точке простым соотношением

                                      ,                                                              (9.2)

где   – диэлектрическая восприимчивость диэлектрика, безразмерная вели­чина, характеризующая способность диэлектрика к поляризации.

В пределах малого объема все молекулы неполярного диэлектрика приобре­тают в электрическом поле (рисунок 9.1а) одинаковые электрические моменты , поэтому поляризованность равна   (– концентрация молекул).

 

а)                                                       б)

                                                     

 

                                                       

 

 

 

   Рисунок 9.1 -Поляризация неполярных (а) и полярных (б) диэлектриков

 

Диэлектрическая восприимчивость такого диэлектрика не зависит явно от температуры. Температура может влиять лишь косвенно – через концентрацию молекул.

В случае полярных диэлектриков ориентирующему действию внешнего поля (рисунок 9.1б) препятствует тепловое движение молекул, стремящееся раз­бросать их дипольные моменты по всем направлениям. В результате устанавлива­ется некоторая преимущественная ориентация дипольных моментов молекул в направлении поля, расчет и опыты приводят к  формуле (9.2).

Диэлектрическая проницаемость полярных диэлектриков обратно пропор­циональна температуре.

Поляризованность кристаллических диэлектриков тоже связана с напря­женностью поля соотношением (9.2). Следует отметить, что линейная зависи­мость между  и  выполняется лишь в не слишком сильных полях. Сущест­вуют и диэлектрики для которых формула (9.2) неприемлема, это некоторые кри­сталлы электриты, сегнетоэлектрики. У сегнетоэлектриков связь между   и   нелинейная и зависит от предшествующих значений  (это явление называется гистерезисом).

Из рисунка 9.1 следует, что при внесении диэлектрика во внешнее поле происходит его поляризация, т.е. положительные заряды смещаются по полю, от­рицательные – против поля, в результате на гранях пластины из диэлектрика воз­никают избыточные положительные заряды с поверхностной плотностью  (справа) и отрицательные с поверхностной плотностью  (слева). Эти заряды называются поверхностными связанными (поляризационными), они входят в со­став атомов и молекул диэлектрика, покидать пределы которых не могут.

Между поляризованностью  и поверхностной плотностью связанных заря­дов  имеется простая связь 

                                  .                                                         (9.3)

 

С учетом (9.2) придем к формуле

 

                                       ,                                                                (9.4)

 

где  – проекция поляризованности на внешнюю нормаль к данной точки поверхности;

        – проекции напряженности поля на ту же нормаль.

Связанные заряды отличаются от сторонних лишь тем, что не могут поки­нуть пределы молекул, в состав которых входят, в остальном они имеют такие же свойства, как и прочие, в частности, они являются источниками электрического поля.

 

9.3 Вектор электрического смещения. Теорема Гаусса для электростатиче­ского поля в диэлектрике

 

Выше было отмечено, что источниками поля служат не только сторонние, но и связанные заряды, поэтому теорему Гаусса для поля  можно записать

                            ,                                                   (9.5)

где   – алгебраическая сумма сторонних и связанных  зарядов, охватываемых поверхностью S. 

Формула (9.5) малопригодна для нахождения вектора , т.к. заранее не из­вестно распределение связанных зарядов, которое зависит от поля .

Вычисление полей во многих случаях упрощается введением вспомогатель­ной величины, источниками которой являются только сторонние заряды, и назы­ваемой электрическим смещением или электрической индукцией

                                              

 .                                                (9.6)

Следует отметить, что вектор  представляет собой сумму двух совер­шенно различных величин:  и , поэтому он действительно вспомога­тельный вектор, не имеющий какого–либо физического смысла, но во многих случаях введение его упрощает изучение поля в диэлектриках.

Поток вектора  через произвольную замкнутую поверхность равен алгеб­раической сумме сторонних зарядов, охватываемых этой поверхностью,

 

                                         .                                                    (9.7)

Это и есть теорема Гаусса для вектора .

Подставив выражение (9.2) для  в (9.6), получим

 

                                    

или

                                                ,                                                    (9.8)

где  – диэлектрическая проницаемость вещества, являющаяся основ­ной электрической характеристикой диэлектрика.

9.4  Условия на границе двух диэлектриков

 

Поведение векторов  и  на границе раздела двух однородных изотроп­ных диэлектриков определяется с помощью основных теорем электростатики: теоремы о циркуляции вектора  (8.11) и теоремы Гаусса для вектора  (9.7)

 

                                 ,                 .

Согласно теореме о циркуляции вектора

                                ,                  ,                                          (9.9)

 

т.е. тангенциальная составляющая вектора  одинакова по обе стороны вблизи границы раздела, не претерпевает скачка, тангенциальные составляющие вектора  претерпевают скачок при переходе границы раздела.

Из теоремы Гаусса получаются соотношения

 

                                ,                 .                                                 (9.10)

 

Из соотношений (9.10) следует, что при переходе через границу раздела нормальная составляющая  не изменяется, а нормальная составляющая  претер­певает разрыв.

Полученные условия для составляющих векторов  и  на границе раздела двух диэлектриков (9.9) и (9.10) означают, что линии этих векторов преломляются, вследствие чего угол  между нормалью к поверхности раздела и линией  изменяется (рису­нок 9.2).

 

                                                                                               

                                                                                

                                                                          

 

                                                                

 

Рисунок 9.2 – Преломление векторов  и на границе двух диэлектриков ()

 

С учетом полученных условий закон преломления линий напряженности электростатического поля на поверхности раздела двух диэлектрических сред при отсутствии на той поверхности свободных зарядов выражается формулой

 

                                       .                                                          (9.11)

 

10 Лекция 10. Энергия электрического поля

 

Цели лекции:

-       изучение энергии взаимодействия системы зарядов;

-       изучение энергии уединенного проводника и конденсатора;

-       изучение энергии электростатического поля.

 

10.1 Энергия взаимодействия системы зарядов

 

Энергия взаимодействия присуща системе  взаимодействующих частиц, за счет ее совершается работа при взаимных перемещениях этих частиц. Она зависит от закона взаимодействия между частицами и от их взаимного расположения. В количественном отношении эта энергия равна работе, совершаемой силами  взаи­модействия при перемещении всех частиц системы на бесконечные расстояния друг от друга. Если в системе частицы, энергия каждой в поле другой соответст­венно W₁₂ и W₂₁, то очевидно, что W₁₂=W₂₁=W_р. поэтому потенциальную энергию взаимодействия двух частиц можно представить равной

Следовательно, для энергии взаимодействия системы  многих частиц можно записать

где – потенциальная энергия i-й частицы в полях всех остальных частиц системы.

Для системы взаимодействующих точечных зарядов с учетом определения потенциала (8.6) получим

                                                      (10.1)

 

где – полный потенциал, создаваемый в точке расположения заряда Q_i всеми остальными зарядами системы.

Если заряд распределен непрерывно по объему V с объемной плотностью , то, разлагая систему зарядов на совокупность элементарных зарядов  и переходя от суммирования в (10.1) к интегрированию, получим

,                                                    (10.2)

 

где  – потенциал, создаваемый всеми зарядами системы  в элементе объе­мом .

 Аналогично можно перейти к энергии заряда, распределенного по поверх­ности.

 

10.2 Энергия уединенного проводника и конденсатора

 

Пусть проводник имеет заряд Q и потенциал . Т.к. поверхность проводника эквипотенциальна,  можно вынести из-под знака интеграла в фор­муле (10.2). Оставшийся интеграл есть заряд Q на проводнике и, следовательно, энергия заряженного проводника равна

                                           (10.3)

 

Энергия заряженного проводника равна работа внешних сил при его за­рядке.

Для энергии заряженного конденса­тора справедлива формула

                                                    (10.4)

 

10.3 Энергия электрического поля

 

Рассмотрим заряженный плоский конденсатор. Его энергия определяется формулами (10.4), а электроемкость – формулой

 

                                             .                                                               (10.5)

 Если расстояние  между обкладками значительно меньше их размеров, то электрическое поле в конденсаторе можно считать однородным. Тогда  , подставляя это выражение и (10.5) в (10.4), получим

 

                                                       (10.6)

 

где  объем, в котором сосредоточено электрическое поле               плоского конденсатора.

Формула (10.6) показывает, что энергия конденсатора выражается через на­пряженность , характеризующую электростатическое поле. При таком подходе в роли носителя энергии выступает поле, по объему которого и распределена эта  энергия. Этот вывод подтверждается в области переменных во времени полей, т.к. именно они могут распространяться в пространстве от возбудивших их электри­ческих зарядов в виде электромагнитных волн, способных переносить энергию. (В частности, энергия, за счет которой существуют жизнь на Земле, доставляется от Солнца электромагнитными волнами).

С учетом (10.6) можно получить формулы плотности энергии электриче­ского поля

 

     .                                            (10.7)

 

В изотропном диэлектрике направления векторов  и  совпадают, по­этому формуле (10.7) можно придать следующий вид, заменив  его значением

.                                         (10.8)

Первое слагаемое в этом выражении совпадает с плотностью энергии поля в вакууме, второе представляет собой энергию, затрачиваемую на поляризацию ди­электрика.

Зная плотность энергии поля в каждой точке, можно найти энергию поля, заключенную в любом объеме V, вычислив интеграл

 

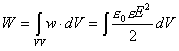  .                                                     (10.9)

 

Формула (10.9) является универсальной, применима для расчета однород­ного и неоднородного электростатического поля, а так же переменных непотен­циальных полей.

 

11 Лекция 11. Постоянный электрический ток

 

Цели лекции:

-       изучить основные характеристики постоянного тока;

-       усвоить основные положения классической теории электропроводности ме­таллов и вывод из неё основных законов электрического тока.

 

11.1       Общие характеристики и условия существования тока

 

Электрическим током  называется упорядоченное движение заряженных частиц или заряженных макроскопических тел.

Электрический ток проводимости –  упорядоченное движение в веществе или в вакууме свободных заряженных частиц – носителей тока.

Конвекционный электрический ток  – электрический ток, осуществляемый движением в пространстве заряженного макроскопического тела.

Условия существования тока: наличие в среде носителей тока, наличие в ней электрического поля.

Для поддержания тока необходим источник электрической энергии, в кото­ром осуществляется преобразование какого-либо вида энергии в энергию элек­трического тока.

Количественной мерой электрического тока служит  сила тока – ска­лярная физическая величина, определяемая зарядом, переносимым через рас­сматриваемую поверхность в единицу времени

                                                   .                                                            (11.1)

Если сила тока и его направление не изменяются во времени, то такой ток называется  постоянным   и     .

Для постоянства электрического тока необходима неизменность напряжён­ности электрического поля во всех точках проводника, по которому течёт ток. Следовательно, заряды не должны накапливаться или убывать где-либо в этом проводнике. Это условие означает, что цепь постоянного тока должна быть замк­нутой, а сила тока – одинаковой во всех поперечных сечениях цепи.

Для характеристики направления электрического тока в разных точках рас­сматриваемой поверхности и распределения силы тока по ней вводится вектор плотности тока.

Плотностью тока  называется физическая величина, определяемая силой тока, проходящего через единицу площади поверхности, перпендикулярной на­правлению тока

                                                 .                                                            (11.2)

Из  (11.2) следует, что сила тока через произвольную поверхность  равна по­току через эту поверхность  вектора плотности тока                                       

                                                  .                                                     (11.3)

         Плотность тока можно выразить через скорость        упорядоченного движения зарядов в проводнике, концентрацию носителей тока      и элементар­ный заряд     носителя      

                                                  .                                              (11.4)

 

11.2 Уравнение непрерывности. Условие стационарности электрического тока

       Если в проводящей среде, где протекает ток, представить замкнутую по­верхность , то согласно (11.3) поток вектора плотности тока сквозь эту поверх­ность равен току, идущему из области, ограниченной этой поверхностью. В силу закона сохранения заряда этот интеграл равен убыли заряда в единицу времени внутри ограниченного объёма

                                                       .                                           (11.5)

         Соотношение (11.5) называют уравнением непрерывности.

         В случае стационарного (постоянного) тока распределение зарядов в про­странстве неизменно, поэтому   что свидетельствует о том, что в случае постоянного тока линии вектора  нигде не начинаются и нигде не заканчива­ются, они замкнуты, т.е. поле вектора  не имеет источников.

 

11.3 Классическая электронная теория электропроводности металлов

  

В опытах К. Рикке (1901), С.Л. Мандельштама и Н.Д. Папалекси (1913),     Р. Толмена и  Б. Стюарта (1916) было показано, что носителями тока в металлах яв­ляются свободные электроны, т. е. электроны, слабо связанные с ионами кристал­лической решётки  металла. Концентрация свободных электронов имеет значения порядка .

Исходя из представлений о свободных электронах, П. Друде и Х. Лоренц создали классическую теорию металлов. В теории Друде–Лоренца пред­полагается:

-   электроны проводимости ведут себя подобно молекулам идеального газа;

-   средняя скорость теплового движения электронов может быть опреде­лена по формуле   ;

-   электроны сталкиваются преимущественно не между собой, а с ионами, образующими кристаллическую решётку металла, что приводит к уста­новлению теплового равновесия между электронным газом и кристалли­ческой решёткой;

-   ввиду малости средней скорости упорядоченного движения   элек­тронов по сравнению со средней скоростью  теплового движения , среднее время свободного пробега   электронов опре­деляется по формуле     

        ,                                                          (11.6)

где    –  средняя длина свободного пробега электронов;

-        при соударениях с ионами электроны полностью теряют скорость упоря­доченного движения, передавая приобретённую энергию решётке, уве­личивая внутреннюю  энергию металла, последний нагревается;

-        электрическое сопротивление металлов обусловлено соударениями сво­бодных электронов с ионами.

         Исходя из выше указанного, можно вывести законы Ома и Джоуля–Ленца в дифференциальной форме.

Закон Ома. Свободный электрон ускоряется электрическим полем в про­воднике. Уравнение его движения имеет вид

                                                              ,

          где m – масса электрона;

        а – ускорение электрона;

        е – заряд электрона.

         Поскольку  движение электрона равноускоренное, то средняя скорость упорядоченного движения электронов запишется в виде            

                                                         ,                                                    (11.7)

 а  плотность тока  – 

                                                   ,                                                   (11.8)

 

Величину                     

                                                                                                       (11.9) 

называют удельной электрической проводимостью, а обратную ей величину    – удельным электрическим сопротивлением  проводника.  Следовательно,

                                                                          

                                                                                                                         (11.10)

 

Уравнение (11.10) выражает закон Ома в дифференциальной форме.

          Закон Джоуля–Ленца. При каждом столкновении электрон передаёт иону решётки среднюю энергию, сообщённую ему электрическим полем,

 

                                                                                  (11.11)

 

         Частота столкновений каждого электрона с атомами равна  , а  n элек­тронов   ­–    .   Поэтому  объёмная плотность тепловой мощности тока   определяется выражением

       

                                                   (11.12)

  

           или                                       

                                                         .                                                    (11.13)

 

Уравнение (11.13) выражает  закон Джоуля–Ленца в дифференциальной форме.

Несмотря на наглядность и верность зависимости плотности тока и количе­ства выделяемой теплоты от напряжённости поля, классическая теория электро­проводности не приводит к правильным количественным результатам. Главные расхождения теории с экспериментом состоят в следующем:

– эксперимент для зависимости удельной проводимости   от температуры приводит к закону  , а из формулы (11.9) следует     , т. к. по кинетической теории газов  ;

-       по теореме о равнораспределении энергии по степеням свободы следует ожидать от свободных электронов большого вклада в теплоёмкость про­водников, что не наблюдается в экспериментах. 

 Указанные трудности преодолены в квантовой теории, учитывающей вол­новые  свойства микрочастиц.

 

12 Лекция 12. Магнитное поле в вакууме

   

         Цели лекции:

-          ознакомиться с основными характеристиками магнитного поля;

-          уяснить основные методы расчета магнитных полей.

 

12.1     Магнитное поле. Вектор магнитной индукции

 

         Силовое поле, создаваемое магнитами, называется магнитным полем. Источ­ником постоянного магнитного поля являются стационарные электриче­ские токи. Поле постоянных магнитов также создается токами –  микроскопиче­скими токами (молекулярными токами). В общем случае можно утверждать, что вокруг всякого движущегося заряда должно существовать магнитное поле. Маг­нитных зарядов в природе не существует.

         Силовой характеристикой магнитного поля является вектор , называе­мый магнитной индукцией поля. По определению, магнитная индукция  чис­ленно равна отношению силы, действующей на заряженную частицу со стороны магнитного поля, к произведению абсолютного значения заряда и скорости час­тицы, если направление скорости частицы таково, что эта сила максимальна

                                                          ,                                                           (12.1)

 

при этом векторы   образуют правую тройку (рисунок 12.1).

                  

 

 

 

 

 

 

Рисунок 12.1

 

Магнитное поле называется однородным, если во всех его точках  векторы магнитной индукции одинаковы как по модулю, так и по направлению. В про­тивном случае магнитное поле называется неоднородным.

         Для графического изображения стационарного магнитного поля пользу­ются методом линий магнитной индукции. Силовыми линиями магнитного поля (линиями магнитной индукции) называются линии, проведенные в магнитном поле так, что в каждой точке поля касательная к линии магнитной индукции совпадает с направлением вектора  в этой точке поля.

 

12.2 Принцип суперпозиции. Закон Био–Савара–Лапласа

 

          Принцип суперпозиции. Результаты экспериментов показывают, что для магнитного поля, как и для электрического, выполняется принцип суперпози­ции: магнитное поле, создаваемое несколькими зарядами или токами, равно век­торной сумме магнитных полей, создаваемых каждым зарядом или током в от­дельности

                                                .                                                             (12.2)

 

           Закон Био–Савара–Лапласа позволяет вычислить магнитную индукцию в каждой точке поля, создаваемого током, текущим в проводнике любой формы. Согласно этому закону магнитная индукция постоянного электрического тока I  в вакууме должна удовлетворять уравнению

 

                                      ,                                                 (12.3)

                        

где – магнитная индукция магнитного поля, созданного элементом тока;

  - элемент тока, направление которого совпадает с направлением вектора плотности тока;

   – радиус-вектор, проведенный из этого элемента в рассмат­риваемую точку С поля (рисунок 12.2);

          Гн/м – магнитная постоянная;

          I – сила тока в провод­нике.

Вектор   направлен в точке С  перпендикулярно плоскости векторов  и  по правилу буравчика.

 

 

 

 

 

 

 

                                                                        

                                                                 

 

 

 

                                                        Рисунок 12.2

 

12.3Магнитный поток. Основные законы магнитного поля

 

         Магнитное поле обладает, как и электрическое, двумя важнейшими свойст­вами. Эти свойства, связанные с потоком и циркуляцией векторного поля , выра­жают основные законы магнитного поля.

         Магнитным потоком сквозь малую поверхность площадью dS называется физическая величина

 

                                      ,                              (12.4)

 

где   d = d ;

         – единичный вектор нормали к  площадке  dS ;

         В_n – проекция вектора   на направление нормали.

          Магнитный поток через произвольную поверхность

 

                                               .                                                       (12.5)

 

Теорема Гаусса для поля : поток вектора магнитной индукции через замкну­тую поверхность равен нулю. Этот закон выражает тот факт, что магнит­ных зарядов в природе нет. Магнитное поле источников не имеет

 

         .                                                        (12.6)

 

Циркуляции вектора   по произвольному контуру для магнитного поля по­стоянных токов равна произведению     на алгебраическую сумму токов, охваты­ваемых этим контуром

 

.                                                     (12.7)

Из (12.7) следует, что в отличие от электростатического поля магнитное поле является вихревым. Практический аспект теоремы о циркуляции магнитной индукции состоит в том, что с помощью (12.7) можно рассчитывать магнитные поля, создаваемые некоторыми конфигурациями электрических токов.

 

12.4  Работа перемещения проводника с током в постоянном магнитном поле

 

         Элементарная работа, совершаемая силами магнитного поля при перемеще­нии замкнутого контура с током в магнитном поле равна произведению силы тока на изменение магнитного потока через поверхность, ограниченную контуром

 

                                                    .                                                          (12.8)

Полная работа сил магнитного поля при перемещении контура с током от на­чального положения 1 до конечного 2 может быть определена по формуле

 

                                                        .                                                     (12.9)

В случае постоянного тока

 

                                               .                                                     (12.10)

 

12.5 Эффект Холла

 

Эффект Холла – это возникновение в металле с током плотностью  , поме­щенном в магнитное поле , электрического поля  в направлении перпендикуляр­ном  и , что схематически показано на рисунке 12.3. Величина возникающего электрического поля может быть определена через разность потен­циалов . Экспериментально показано, что 

 

.                                            (12.11)

Данное выражение представляет собой холловскую поперечную разность по­тенциалов.

 

 

                                                                                                              

 

           

 

 

                           Рисунок 12.3

 

         Появление поперечной разности потенциалов  обусловлено тем, что на упорядоченно движущиеся носители тока в проводнике (на рисунке 12.3 это элек­троны) действуют со стороны магнитного поля с силой Лоренца, в результате чего частицы отклоняются.

 Используя электронную теорию проводимости можно показать, что посто­янная Холла  в формуле (12.12) равна

                                                      ,                                                                                   (12.12)

  где е – заряд электрона;

                  n – концентрация носителей тока (электронов) в веществе.                         

 

13 Лекция 13. Магнитное поле в веществе

 

         Цели лекции:

-   ознакомиться с характеристиками магнитного поля в веще­стве;

-   уяснить основные методы расчета магнитных полей в веществе.

 

13.1 Намагничивание вещества. Намагниченность

 

        Всякое вещество является магнетиком, т.е. способно под действием магнит­ного поля намагничиваться и создавать свое магнитное поле. Результирующие поле в веществе

 

                                               ,                                                             (13.1)

         где  – индукция внешнего поля (поля токов проводимости);

       – индукция собственного (внутреннего) поля, создаваемого намагничен­ным веществом.

         Намагничивание вещества обусловлено преимущественной ориентацией или индуцированием магнитных моментов отдельных молекул в одном направлении. Следует подчеркнуть, что вещества, молекулы которых в отсутствии поля не имеют магнитного момента, намагничиваются за счет индуцирования элементар­ных круговых токов молекул, в результате чего молекулы и всё вещество приобретают магнитный момент.

        Степень намагничивания магнетика характеризуется магнитным момен­том единицы объема - вектором , который называется намагниченностью

                                               ,                                                        (13.2)

 

где   – бесконечно малый объем в окрестностях рассматриваемой точки магнетика; 

        – магнитный момент отдельной молекулы.

Суммирование проводится по всем молекулам в объеме   .

           Намагниченность любого элемента объема создается внешним магнитным полем, поэтому  зависит от . В то же время, намагниченное вещество создает поле , следовательно величина  зависит от .

         Рассмотрим в намагниченном веществе малый элемент объема в форме длин­ного цилиндра, ось которого параллельна направлению вектора намагничен­ности (рисунок 13.1а).

 

 

                                                     

   

 

 

 

Рисунок 13.1

 

Элементарные токи представлены на сечении цилиндра (рисунок 13.1б). Действие совокупности этих магнитных моментов можно формально заме­нить действием тока , называемого током намагничивания, обтекающим поверх­ность данного цилиндра. Магнитный момент выбранного нами элемента объема можно представить двумя способами

 

                                               .                                             (13.3)

Тогда

                                                   .                                                        (13.4)

 

         В общем случае можно показать, что суммарное действие всех микротоков можно характеризовать циркуляцией вектора  .

 

                                               .                                                          (13.5)

        

13.2 Основные теоремы магнитостатики для поля в веществе

 

         Теорема  Гаусса. Поле намагниченного вещества, так же как и поле токов проводимости источников не имеет, поэтому теорема Гаусса записывается без изменений, как и для поля в вакууме

 

                                               .                                                         (13.6)

 

Следовательно, линии вектора   остаются всюду непрерывными.

Теорема о циркуляции вектора .  В магнетиках циркуляция вектора  опреде­ляется как токами проводимости , так и токами намагничивания ,   а именно

 

                                               .                                              (13.7)

         С учетом формулы (13.5) получим

 

                                               .                                               (13.8)

 

Величина, стоящая под интегралом

 

                                                                                                                 (13.9)

называется напряженностью магнитного поля. Она не имеет непосредственного физического смысла, но с её помощью в удобной форме записываются уравнения для магнитных полей в неоднородных средах.

Теорема о циркуляции вектора : циркуляция вектора  по произволь­ному замкнутому контуру в произвольной среде равна алгебраической сумме то­ков проводимости, охватываемых этим контуром

 

                                               .                                                    (13.10)

         Полученное соотношение называют законом полного тока. Этот закон ши­роко используется для расчета магнитных полей в неоднородных средах.

Между   и    существует линейная зависимость

 

                                                                                                          (13.11)

 

где     – магнитная восприимчивость среды, характерная для каждого магне­тика.

Величина    может различной как положительной, так и отрицательной.

Магнетики, которые подчиняются зависимости (13.11), подразделяют на па­рамагнетики ( и диамагнетики ( . У  парамагнетиков , а у диамаг­нетиков . Для ферромагнетиков зависимость  от  имеет слож­ный характер: она нелинейная и, кроме того, наблюдается гистерезис, т.е. за­висимость     от предыстории магнетика.

Принимая во внимание (13.11) можно получить следующее выражение для связи векторов   и :

 

                                               ,                                                            (13.12)

 

где  – магнитная проницаемость среды.

У парамагнетиков ,   диамагнетиков , причем  для диа- и парамаг­нетиков мало отличаются от единицы, т.е  магнитные свойства этих магне­тиков выражены слабо.

К парамагнетикам можно отнести такие вещества, которые намагничива­ются во внешнем магнитном поле в направлении вектора . Атомы (молекулы или ионы) парамагнетика обладают собственным магнитным моментом . К ним относятся (щелочные и щелочно-земельные металлы, кислород, хлорное же­лезо и др.). В отсутствии магнитного поля парамагнетик не намагничен, т.к. сум­марный магнитный момент молекул равен нулю.

К диамагнетикам можно отнести такие вещества, которые намагничиваются во внешнем магнитном поле в направлении, противоположном направлению век­тора магнитной индукций . Магнитные моменты атомов, молекул или ионов в отсутствие внешнего магнитного поля равны нулю. Диамагнетиками являются инертные газы, медь, золото, вода (жидкая), серебро и другие вещества. В магнит­ном поле атомы (молекулы вещества) приобретают наведенные магнитные мо­менты.

Ферромагнетиками являются твердые вещества, обладающие самопроиз­вольной (спонтанной) намагниченностью, которая сильно изменяется под влия­нием внешних воздействий – магнитного поля, деформации, изменения темпера­туры. Внутреннее магнитное поле в ферромагнетиках  может в сотни и тысячи раз превосходить внешнее поле. Такими свойствами обладают кристаллы переходных металлов (железо, кобальт, никель), некоторых редкоземельных элементов и ряда сплавов, ферриты, а так же некоторые металлические стекла.       

 

13.3 Граничные условия для магнитного поля. Расчет магнитных полей в не­однородных средах

 

На границе раздела сред обе векторные характеристики магнитного поля  и  скачкообразно изменяются по величине и направлению. Граничные условия для векторов  и  выводятся по аналогии с электрическим полем (лекция 9) и выражаются формулами

 

         .                                                      (13.13)

 

Полученные условия для составляющих векторов  и  на границе раздела двух диэлектриков означают, что линии этих векторов преломляются, вследствие чего угол  изменяется (рисунок 13.2)

 

 

                                                                                             

                                                                                

                                                                          

                                

 

Рисунок 13.2 – Преломление векторов  и  на границе двух диэлектриков ()

 

Расчет магнитных полей в неоднородных средах осуществляется с помощью закона полного тока и граничных условий.

                  

 

 

 

 

 

Св.план 2006 г., поз. 135

 

 

 

 

 

Лариса Васильевна Завадская,

Ляйля Хамитовна Мажитова,

Людмила Айзиковна Тонконогая

 

Физика1. Конспект лекций 

(для студентов очной формы обучения специальностей 

050718- Электроэнергетика, 050717 -Теплоэнергетика)

 

 

 

 

 

 

 

Редактор Ж.М. Сыздыкова

 

 

 

 

 

Подписано к печати                                                  Формат 60´84 1/16

Тираж  __ экз.                                                            Бумага типографская № 1

Объем  3,6  уч.  изд.л.                                               Заказ ___ цена __  тенге.

 

 

 

 

 

 

 

 

Копировально-множительное бюро

Алматинского института энергетики и связи

050013, Алматы, Байтурсынова, 126