Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра физики
ФИЗИКА
Конспект лекций
для студентов специальностей
5В074600 – Космическая техника и технологии
Алматы 2013
СОСТАВИТЕЛИ: Т.Д. Дауменов, Т.С. Байпакбаев, М.Ш. Карсыбаев Физика. Конспект лекций для студентов специальности 5В074600 ––Космическая техника и технологии - Алматы: АУЭС, 2013 59 с.
Излагается краткое содержание лекций по дисциплине «Физика» для студентов бакалавриата специальности 5В074600 ––Космическая техника и технологии.
Конспект лекций «Физика» представляет собой еще один элемент системы методического обеспечения учебного процесса по дисциплине и может быть использован в качестве раздаточного материала на лекционных занятиях, а также в самостоятельной работе над теоретическим материалом при подготовке к практическим, лабораторным занятиям и экзаменам.
Ил. -14 , библиогр. -16 назв.
Рецензент: Член УМК: ст. преп. каф. ТКС Шахматова Г.А.
Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2012 г.
Ó НАО «Алматинский университет энергетики и связи», 2013 г.
Содержание
Введение 4
1 Лекция. Электростатическое поле в вакууме 5
2 Лекция. Диэлектрики в электростатическом поле 9
3 Лекция. Проводники в электрическом поле 12
4 Лекция. Законы постоянного тока 14
5 Лекция. Магнитное поле токов. 21
6 Лекция. Силы в магнитном поле 24
7 Лекция Магнитные свойства вещества 27
8 Лекция. Явление электромагнитной индукция 31
9 Лекция. Уравнения Максвелла 35
10 Лекция. Статистические распределения 39
11 Лекция. Первое начало термодинамики 42
12 Лекция. Второе начало термодинамики 46
13 Лекция. Явления переноса 51
14 Лекция. Элементы механики сплошных сред 55
15 Лекция. Элементы механики жидкости 58
Список литературы 62
Введение
Курс физики совместно с курсом высшей математики составляет основу теоретической подготовки бакалавра и играет роль фундаментальной базы будущей деятельности выпускников высшей технической школы. любой специальности, в том числе для специальности 5В074600 – Космическая техника и технологии.
Задачи курса физики состоят в том, чтобы:
-раскрыть сущность основных законов, теорий классической и современной физики в их внутренней взаимосвязи и целостности, так как для будущего бакалавра важно усвоение иерархии физических законов и понятий, границ их применимости, позволяющих эффективно использовать их в конкретных ситуациях;
-формировать у студентов умение и навыки решения обобщённых типовых задач дисциплины как основы умения решать профессиональные задачи;
-формировать у студентов умение оценивать степень достоверности результатов, полученных экспериментальными или теоретическими методами. способствовать развитию у студентов творческого мышления, навыков самостоятельной познавательной деятельности, умения моделировать физические ситуации с использованием компьютера;
-ознакомить студентов с современной измерительной аппаратурой, выработать умение и навыки проведения экспериментальных исследований и обработки их результатов, умение выделить конкретное физическое содержание в прикладных задачах будущей специальности.
Курс физики представляет собой единое целое. Содержание материала и логика его изложения должны быть подчинены перечисленным целям и задачам.
Данный конспект лекций составлен согласно ГОСО РК 6.08.028-2009 и типовой учебной программе, утвержденной приказом № 514 МОиН РК от 11 ноября 2009 года для специальности 5В074600 Космическая техника и технологии и может служить основой для учебной деятельности студента и призван помочь ему для более глубокого изучения учебного материала, а также при подготовке к практическим и лабораторным занятиям.
1 Лекция. Электростатическое поле в вакууме
Цель лекции:
-ознакомление с силовой и энергетической характеристиками электростатического поля;
-введение понятия потока вектора напряженности электрического поля через поверхность.
1.1 Введение. Основная задача электростатики. Напряженность электрического поля
В природе существуют четыре фундаментальных взаимодействия между элементарными частицами - сильное, электромагнитное, слабое и гравитационное. Каждое из них связано с определенной характеристикой частицы. Гравитационное взаимодействие зависит от массы частиц, а электромагнитное - от электрических зарядов. Основные свойства зарядов:
1) Электрические заряды бывают двух типов: положительные и отрицательные.
2) Закон сохранения заряда: алгебраическая сумма электрических зарядов замкнутой системы остается неизменной.
3) Электрический заряд – релятивистски инвариантная величина.
По современным представлениям (теория близкодействия) взаимодействие между зарядами осуществляется через электрическое поле с конечной скоростью. Основные свойства электростатического поля:
1) электростатическое поле создается вокруг всякого электрического заряда,
2) на всякий другой заряд, помещенный в это поле, действует сила.
Основной задачей электростатики является определение характеристик электростатического поля по известному распределению зарядов.
Закон Кулона: сила ![]() взаимодействия
между двумя неподвижными точечными зарядами пропорциональна произведению
величин зарядов
взаимодействия
между двумя неподвижными точечными зарядами пропорциональна произведению
величин зарядов ![]() и
и
![]() и обратно
пропорциональна квадрату расстояния
и обратно
пропорциональна квадрату расстояния ![]() между ними:
между ними:
![]() или
или 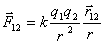 , (1.1)
, (1.1)
где
![]() - сила,
действующая на заряд
- сила,
действующая на заряд ![]() со
стороны заряда
со
стороны заряда ![]() ,
,
![]() -
радиус-вектор, соединяющий заряд
-
радиус-вектор, соединяющий заряд ![]() с зарядом
с зарядом ![]() .
.
В
СИ коэффициент пропорциональности равен ![]() = 9.109,
= 9.109, ![]() Ф/м – электрическая
постоянная.
Ф/м – электрическая
постоянная.
Тогда
![]() .
.
Силовой характеристикой электростатического поля служит вектор напряженности электрического поля в данной точке:
![]() , (1.2)
, (1.2)
где
![]() - сила,
действующая на пробный заряд
- сила,
действующая на пробный заряд ![]() , помещенный в эту точку поля.
, помещенный в эту точку поля.
Напряженность поля точечного заряда в вакууме:
![]() или
или ![]() . (1.3)
. (1.3)
Линии напряженности – это линии, касательные к которым
в каждой точке направлены так же, как и вектор напряженности ![]() в данной точке поля.
Линии напряженности проводят с такой густотой, чтобы число линий, проходящих через
единицу поверхности, перпендикулярной к ним, было равно (или пропорционально)
модулю вектора напряженности поля
в данной точке поля.
Линии напряженности проводят с такой густотой, чтобы число линий, проходящих через
единицу поверхности, перпендикулярной к ним, было равно (или пропорционально)
модулю вектора напряженности поля ![]() в данном месте. Линии напряженности
электростатического поля, начавшись на заряде, уходят на бесконечность
(положительный заряд), либо, приходя из бесконечности, заканчиваются на заряде
(отрицательный заряд).
в данном месте. Линии напряженности
электростатического поля, начавшись на заряде, уходят на бесконечность
(положительный заряд), либо, приходя из бесконечности, заканчиваются на заряде
(отрицательный заряд).
Электрическое поле называется однородным, если вектор
напряженности в любой точке поля постоянен по модулю и направлению ![]() . Линии напряженности
однородного поля имеют вид параллельных линий, проведенных с одинаковой
густотой.
. Линии напряженности
однородного поля имеют вид параллельных линий, проведенных с одинаковой
густотой.
1.2 Поток вектора напряженности электрического поля. Теорема Гаусса
Потоком вектора напряженности ![]() однородного поля через плоскую поверхность
однородного поля через плоскую поверхность
![]() называется
величина:
называется
величина:
![]() , (1.5)
, (1.5)
где
![]() - угол между
вектором
- угол между
вектором ![]() и
нормалью
и
нормалью ![]() к
поверхности
к
поверхности ![]() ,
,
![]() - проекция
вектора
- проекция
вектора ![]() на
нормаль
на
нормаль ![]() .
.
Для неоднородного поля и произвольной поверхности поток вектора напряженности через эту поверхность
![]() .
.
При рассмотрении макроскопических зарядов отвлекаются от их дискретной (прерывистой) структуры и считают их распределенными всюду в пространстве непрерывным образом с конечной плотностью.
Теорема Гаусса для электростатического
поля в вакууме: - поток вектора напряженности электростатического поля в
вакууме через произвольную замкнутую поверхность равен алгебраической сумме
заключенных внутри этой поверхности зарядов, деленной на ![]() :
:
![]() . (1.6)
. (1.6)
Пример. Поле равномерно заряженной бесконечной плоскости
![]() . (1.7)
. (1.7)
Тогда поле в центре плоского конденсатора Е = σ/ε0 или Е = σ/ε0ε (при наличии диэлектрика с диэлектрической проницаемостью ε).
1.3 Работа сил электростатического поля по перемещению заряда. Потенциал электростатического поля
Если в электростатическом поле точечного заряда ![]() из точки 1 в точку 2
вдоль силовой линии перемещается другой точечный заряд
из точки 1 в точку 2
вдоль силовой линии перемещается другой точечный заряд ![]() , то сила, приложенная к
заряду, совершает работу. Работа силы
, то сила, приложенная к
заряду, совершает работу. Работа силы ![]() на элементарном перемещении
на элементарном перемещении ![]() равна
равна
![]() . (1.8)
. (1.8)
Работа при перемещении заряда ![]() из точки 1 в точку 2
из точки 1 в точку 2
 (1.9)
(1.9)
не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной 2 точек. Этот вывод справедлив для любого электростатического поля. Следовательно, электростатическое поле является потенциальным.
Работа сил поля равна убыли потенциальной энергии:
![]() . (1.10)
. (1.10)
Следовательно, заряд ![]() в поле заряда
в поле заряда ![]() обладает потенциальной энергией:
обладает потенциальной энергией:
![]() . (1.11)
. (1.11)
Значение константы выбирается таким образом,
чтобы при удалении заряда на бесконечность (т.е. при ![]() ) потенциальная энергия
обращалась в ноль.
) потенциальная энергия
обращалась в ноль.
Величина ![]() называется потенциалом поля в данной
точке и используется, наряду с напряженностью
называется потенциалом поля в данной
точке и используется, наряду с напряженностью ![]() , для описания электрических полей.
, для описания электрических полей.
Работа, совершаемая силами
электростатического поля при перемещении заряда ![]() из точки 1 в точку 2,
может быть представлена как
из точки 1 в точку 2,
может быть представлена как
![]() .
.![]() (1.12)
(1.12)
Разность потенциалов двух точек 1 и 2 электростатического поля равна работе, совершаемой силами поля, при перемещении единичного положительного заряда из точки 1 в точку 2:
![]() . (1.13)
. (1.13)
Единица потенциала – вольт (В): 1В есть потенциал такой точки поля, в которой заряд в 1Кл обладает потенциальной энергией 1Дж.
Потенциал поля системы зарядов равен алгебраической сумме потенциалов полей, создаваемых каждым из зарядов в отдельности:
![]() . (1.14)
. (1.14)
Работа, совершаемая при перемещении
электрического заряда в электростатическом поле по любому замкнутому контуру![]() , равна нулю:
, равна нулю:
![]() . (1.15)
. (1.15)
Циркуляция вектора напряженности электростатического поля вдоль любого контура равна нулю. Следовательно, согласно математической теореме Стока, ротор напряженности электростатического поля также равен нулю:
rotE = 0. (1.16)
Связь между напряженностью электростатического поля и потенциалом выражается формулой:
![]() или
или ![]() . (1.17)
. (1.17)
Поверхности, во всех точках которых потенциал имеет одно и то же значение, называется эквипотенциальными поверхностями. Линии напряженности всегда нормальны эквипотенциальным поверхностям.
Установленная связь между напряженностью поля и потенциалом позволяет по известной напряженности поля найти разность потенциалов между двумя произвольными точками поля. Например, разность потенциалов между двумя бесконечными параллельными заряженными плоскостями (плоский конденсатор):
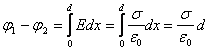 , (1.18)
, (1.18)
где
![]() - расстояние
между плоскостями.
- расстояние
между плоскостями.
2 Лекция. Диэлектрики в электростатическом поле
Цель лекции:
-ознакомление с особенностями изменения электрического поля при внесении диэлектриков;
-введение новых величин для изучения свойств электрического поля при наличии диэлектриков.
2.1 Поляризация диэлектриков. Поляризованность. Напряженность поля в диэлектрике
Диэлектриками являются вещества, практически не проводящие электрического тока, так как в них нет свободных зарядов.
При внесении диэлектрика в электрическое поле изменяются свойства как самого поля, так и диэлектрика. Диэлектрики делятся на следующие типы:
1)
Неполярные диэлектрики – это вещества, молекулы которых в отсутствии внешнего
электрического поля не обладают электрическим моментом ![]() . Молекулы приобретают такой
момент во внешнем электрическом поле (упругий диполь). К неполярным диэлектрикам
относятся Н2, О2, N2 и др.
. Молекулы приобретают такой
момент во внешнем электрическом поле (упругий диполь). К неполярным диэлектрикам
относятся Н2, О2, N2 и др.
2)
Полярные диэлектрики – это вещества, молекулы которых имеют электрический
момент ![]() при
отсутствии внешнего электрического поля, т.к. центры «тяжести» положительных и
отрицательных зарядов молекулы не совпадают (жесткий диполь). Во внешнем
электрическом поле диполи повернутся вдоль поля, и диэлектрик приобретает
отличный от нуля результирующий момент. К полярным диэлектрикам относятся H2O, NH3, CO и др.
при
отсутствии внешнего электрического поля, т.к. центры «тяжести» положительных и
отрицательных зарядов молекулы не совпадают (жесткий диполь). Во внешнем
электрическом поле диполи повернутся вдоль поля, и диэлектрик приобретает
отличный от нуля результирующий момент. К полярным диэлектрикам относятся H2O, NH3, CO и др.
3) Кристаллические диэлектрики с ионной решеткой – вещества, внутренняя структура которых представляет собой пространственную решетку с правильным чередованием ионов разных знаков. Молекулы в таких кристаллах можно рассматривать как систему двух вдвинутых одна в другую ионных подрешеток. Под действием внешнего электрического поля происходит относительное смещение подрешеток, приводящее к возникновению дипольных моментов.
Поляризацией диэлектрика называют процесс, в результате которого диэлектрик приобретает электрический момент под воздействием внешнего электрического поля.
Соответственно трем группам диэлектриков различают три механизма поляризации:
1) электронная поляризация смещения;
2) ориентационная, или дипольная, поляризация;
3) ионная поляризация.
В результате поляризации на диэлектрике возникают заряды, называемые связанными.
Для количественной характеристики поляризации диэлектрика используется векторная величина – поляризованность, определяемая как электрический момент единицы объема диэлектрика:
![]() . (2.1)
. (2.1)
Поляризованность связана с поверхностной плотностью
связанных зарядов ![]() соотношением
соотношением
![]() . (2.2)
. (2.2)
Появление связанных зарядов приводит к возникновению дополнительного
электрического поля ![]() ,
которое направлено против внешнего поля
,
которое направлено против внешнего поля ![]() и ослабляет его. Результирующее поле
внутри диэлектрика
и ослабляет его. Результирующее поле
внутри диэлектрика
![]() . (2.3)
. (2.3)
Для большого класса диэлектриков поляризованность ![]() линейно зависит от напряженности поля
линейно зависит от напряженности поля ![]() внутри диэлектрика и
если диэлектрик изотропный, то
внутри диэлектрика и
если диэлектрик изотропный, то
![]() , (2.4)
, (2.4)
где ![]() - диэлектрическая
восприимчивость вещества.
- диэлектрическая
восприимчивость вещества.
Тогда поле внутри диэлектрика
![]() или
или ![]() , (2.5)
, (2.5)
где
![]() -
диэлектрическая проницаемость среды. Она показывает, во сколько раз поле в
вакууме больше поля в диэлектрической среде.
-
диэлектрическая проницаемость среды. Она показывает, во сколько раз поле в
вакууме больше поля в диэлектрической среде.
2.2 Электрическое смещение. Диэлектрическая восприимчивость вещества. Теорема Гаусса для вектора электрического смещения
На границе раздела двух диэлектриков линии напряженности прерываются, т.к.
вектор ![]() претерпевает
скачок. Поэтому для описания электрического поля в неоднородных диэлектриках
гораздо удобнее пользоваться вектором электрического смещения (индукции)
претерпевает
скачок. Поэтому для описания электрического поля в неоднородных диэлектриках
гораздо удобнее пользоваться вектором электрического смещения (индукции)![]() вместо напряженности
поля
вместо напряженности
поля ![]() .
.
![]() . (2.6)
. (2.6)
Для изотропного диэлектрика векторы ![]() и
и ![]() параллельны, поэтому параллельны и
параллельны, поэтому параллельны и ![]() и
и ![]() :
:
![]() . (2.7)
. (2.7)
В анизотропных диэлектриках направления ![]() и
и ![]() , вообще говоря, не совпадают, и поэтому
направления
, вообще говоря, не совпадают, и поэтому
направления ![]() и
и
![]() также
различны.
также
различны.
Теорема Гаусса для вектора электрического смещения: поток вектора смещения D электрического поля в диэлектрике через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов:
![]() . (2.8)
. (2.8)
2.3 Условия на границе двух диэлектриков
На границе раздела двух изотропных диэлектриков с диэлектрическими
проницаемостями![]() и
и ![]() выполняются
следующие условия:
выполняются
следующие условия:
![]() ,
, ![]() , (2.9)
, (2.9)
![]() ,
, ![]() , (2.10)
, (2.10)
где ![]() и
и ![]() - углы между нормалью к границе раздела и
вектором
- углы между нормалью к границе раздела и
вектором ![]() (или
(или![]() ) в первой и второй средах.
) в первой и второй средах.
3 Лекция. Проводники в электрическом поле
Цель лекции:
-изучение явления при внесении проводника во внешнее электрическое поле;
-введение понятия электростатической индукции.
3.1 Равновесие зарядов на проводнике. Напряженность поля вблизи поверхности проводника
Носители заряда в проводнике способны перемещаться под действием сколь угодно малой силы. Поэтому для равновесия зарядов на проводнике необходимо выполнение следующих условий:
1) Напряженность поля всюду внутри проводника должна быть равна нулю
![]() . (3.1)
. (3.1)
2) Напряженность поля на поверхности проводника должна быть в каждой точке направлена по нормали к поверхности
![]() . (3.2)
. (3.2)
Следовательно, в случае равновесия зарядов поверхность проводника будет эквипотенциальной,
а сообщенный ему заряд распределится по поверхности проводника с некоторой
плотностью ![]() .
.
Напряженность поля в вакууме вблизи поверхности проводника равна
![]() . (3.3)
. (3.3)
Для получения этого соотношения используем теорему Гаусса для вектора D. Внутри проводника Е и D равны нулю. Поток вектора D через боковую поверхность цилиндра равен нулю, отличен от нуля только поток через внешнее основание DdS, равный σdS. Тогда D = σ и Е = σ/ε0.
3.2 Проводник во внешнем электрическом поле. Электростатическая индукция
При внесении незаряженного проводника в электрическое поле носители заряда
приходят в движение: положительные в направлении вектора ![]() , отрицательные – в
противоположную сторону. В результате у концов проводника возникают заряды
противоположного знака, называемые индуцированными зарядами. Явление
перераспределения зарядов на проводнике во внешнем электростатическом поле
называется электростатической индукцией. Процесс будет происходить до тех пор,
пока не будут выполнены условия (1,2) равновесия зарядов на проводнике.
, отрицательные – в
противоположную сторону. В результате у концов проводника возникают заряды
противоположного знака, называемые индуцированными зарядами. Явление
перераспределения зарядов на проводнике во внешнем электростатическом поле
называется электростатической индукцией. Процесс будет происходить до тех пор,
пока не будут выполнены условия (1,2) равновесия зарядов на проводнике.
3.3 Энергия взаимодействия системы зарядов. Энергия заряженного проводника конденсатора
Взаимную потенциальную энергию
точечных зарядов ![]() и
и
![]() , находящихся на расстоянии
, находящихся на расстоянии ![]() друг от друга, можно рассматривать как
потенциальную энергию заряда
друг от друга, можно рассматривать как
потенциальную энергию заряда ![]() , находящегося в поле заряда
, находящегося в поле заряда ![]() , либо как потенциальную энергию заряда
, либо как потенциальную энергию заряда ![]() , находящегося в поле заряда
, находящегося в поле заряда ![]() :
:
![]() , (3.5)
, (3.5)
где
![]() и
и ![]() - соответственно
потенциалы, создаваемые зарядом
- соответственно
потенциалы, создаваемые зарядом ![]() в точке нахождения заряда
в точке нахождения заряда ![]() и
зарядом
и
зарядом ![]() в точке нахождения
в точке нахождения ![]() .
.
В случае ![]() неподвижных
зарядов энергия взаимодействия системы точечных зарядов равна
неподвижных
зарядов энергия взаимодействия системы точечных зарядов равна
![]() , (3.6)
, (3.6)
где
![]() - потенциал,
создаваемый в той точке, где находится заряд
- потенциал,
создаваемый в той точке, где находится заряд ![]() , всеми зарядами, кроме
, всеми зарядами, кроме ![]() - го:
- го:
![]() . (3.7)
. (3.7)
Поверхность уединенного проводника является
эквипотенциальной, т.е. ![]() . Заряд
. Заряд ![]() , находящийся на проводнике, можно
рассматривать как систему точечных зарядов
, находящийся на проводнике, можно
рассматривать как систему точечных зарядов ![]() . Тогда
. Тогда
![]() . (3.8)
. (3.8)
Приняв во внимание связь между зарядом на проводнике и его потенциалом, можно записать следующие выражения для энергии заряженного проводника:
![]() . (3.9)
. (3.9)
Пусть потенциал обкладки конденсатора, на которой находится заряд +![]() , равен
, равен ![]() , а потенциал обкладки,
на которой находится заряд -
, а потенциал обкладки,
на которой находится заряд -![]() , равен
, равен ![]() . Тогда
. Тогда
![]() . (3.10)
. (3.10)
Приняв во внимание связь между зарядом на обкладках конденсатора и разностью потенциалов между его обкладками, можно записать следующие выражения для энергии заряженного конденсатора:
![]() . (3.11)
. (3.11)
3.4 Энергия электростатического поля
Энергия заряженного конденсатора сосредоточена в его электрическом поле, т.е. в пространстве между обкладками. Энергию конденсатора можно выразить через величины, характеризующие электрическое поле в зазоре между обкладками. Для плоского конденсатора имеет место выражение
![]() , (3.12)
, (3.12)
где
![]() - объем,
занимаемый полем.
- объем,
занимаемый полем.
Если поле однородно, заключенная в нем энергия
распределяется в пространстве с постоянной плотностью ![]() .
.
![]() . (3.13)
. (3.13)
Зная плотность энергии электрического поля в каждой
точке, можно найти энергию электрического поля, заключенную в любом объеме ![]() :
:
![]() . (3.14)
. (3.14)
4 Лекция. Законы постоянного тока
Цель лекции:
- ознакомление с законами постоянного тока для различных цепей;
- введение понятия электродвижущей силы в цепи постоянного тока.
4.1. Условия существования электрического тока Характеристики электрического тока
Электрическим током называется упорядоченное (направленное) движение электрических зарядов. Для возникновения и существования электрического тока необходимо выполнение двух условий:
1) наличие в данном теле свободных носителей тока – заряженных частиц, способных перемещаться в пределах всего тела;
2) наличие электрического поля внутри тела.
За направление тока условно принимают направление движения положительных зарядов.
Для количественной характеристики электрического тока служат две величины: сила тока и плотность тока.
Сила тока ![]() – физическая величина, определяемая
электрическим зарядом, проходящим через поперечное сечение проводника в единицу
времени:
– физическая величина, определяемая
электрическим зарядом, проходящим через поперечное сечение проводника в единицу
времени:
![]() . (4.1)
. (4.1)
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. Для постоянного тока
![]() . (4.2)
. (4.2)
Единица силы тока – ампер (А).
Физическая величина, определяемая зарядом, проходящим в единицу времени через единицу поверхности, перпендикулярной направлению тока, называется плотностью тока:
![]() . (4.3)
. (4.3)
Плотность тока связана со скоростью ![]() упорядоченного движения зарядов (дрейфа):
упорядоченного движения зарядов (дрейфа):
![]() , (4.4)
, (4.4)
где
![]() и
и ![]() - концентрация и заряд
носителей тока.
- концентрация и заряд
носителей тока.
Зная вектор плотности тока ![]() в каждой точке проводника, можно
определить силу тока:
в каждой точке проводника, можно
определить силу тока:
![]() , (4.5)
, (4.5)
где
интегрирование производится по всей поверхности ![]() - сечения проводника.
- сечения проводника.
Уравнение непрерывности выражает закон сохранения заряда:
![]() . (4.6)
. (4.6)
4.2 Закон Ома. Сопротивление проводника
Если состояние проводника остается неизменным, то для
каждого проводника существует однозначная зависимость между разностью
потенциалов на его концах и силой тока в нем:![]() . Она называется вольтамперной характеристикой
проводника.
. Она называется вольтамперной характеристикой
проводника.
Для металлов эту зависимость впервые экспериментально установил немецкий физик Г.Ом. Сила тока согласно закону Ома для участка цепи пропорциональна приложенному напряжению, т.е.
![]() , (4.7)
, (4.7)
где![]() – электрическое
сопротивление проводника.
– электрическое
сопротивление проводника.
Единица сопротивления – ом (Ом): 1 Ом – сопротивление такого проводника, в котором при напряжении 1 В течет постоянный ток силой 1 А.
Сопротивление проводников зависит от его размеров и формы, а также от материала, из которого проводник изготовлен. Эта зависимость особенно проста для проводника цилиндрической формы:
![]() , (4.8)
, (4.8)
где
![]() - длина
проводника,
- длина
проводника,
![]() - площадь его
поперечного сечения,
- площадь его
поперечного сечения,
![]() - удельное
сопротивление, зависящее только от рода вещества и его состояния.
- удельное
сопротивление, зависящее только от рода вещества и его состояния.
Единица удельного сопротивления - Ом·м. Сопротивление металлов увеличивается с ростом температуры:
![]() , (4.9)
, (4.9)
где
![]() - удельное
сопротивление металла при 0˚С,
- удельное
сопротивление металла при 0˚С,
![]() - температурный коэффициент
сопротивления металла.
- температурный коэффициент
сопротивления металла.
Для многих металлов ![]() практически не зависит от температуры и
близок к 1/273 °С-1.
практически не зависит от температуры и
близок к 1/273 °С-1.
При очень низких температурах в некоторых веществах
наблюдается явление сверхпроводимости, при котором сопротивление скачком
обращается в ноль. Впервые сверхпроводимость была обнаружена в 1911 году у
ртути голландским физиком Х.Камерлинг-Оннесом. Позже сверхпроводимость была
установлена у свинца, олова, ниобия и у других металлов, а также у ряда
сплавов. Температура, при которой исчезает сопротивление, называется
критической температурой ![]() . В 1933 году немецким физиком
В.Мейсснером было открыто второе фундаментальное свойство сверхпроводников:
при температуре ниже
. В 1933 году немецким физиком
В.Мейсснером было открыто второе фундаментальное свойство сверхпроводников:
при температуре ниже ![]() магнитное
поле выталкивается из толщи образца (эффект Мейсснера).
магнитное
поле выталкивается из толщи образца (эффект Мейсснера).
В 1986 году были открыты металлоксидные
высокотемпературные сверхпроводники (ВТСП) с критическими температурами ![]() , превышающими температуру
кипения жидкого азота при нормальном атмосферном давлении (77К).
, превышающими температуру
кипения жидкого азота при нормальном атмосферном давлении (77К).
4.3 Электродвижущая сила. Работа и мощность постоянного тока. Закон Джоуля - Ленца
Если в проводнике создать электрическое поле и не принять мер для его поддержания, то перемещение носителей тока очень быстро приведет к выравниванию потенциалов на концах проводника и ток прекратится. Для того чтобы поддерживать ток достаточно длительное время, нужно от конца проводника с меньшим потенциалом (для положительных носителей тока) непрерывно отводить приносимые сюда током заряды, а к концу с большим потенциалом непрерывно их подводить. Силы электростатического поля не способны осуществить такое перемещение зарядов. Для этого необходимы сторонние силы.
Сторонние силы характеризуются работой,
которую они совершают над перемещающимися по цепи зарядами. Величина, равная
работе сторонних сил по перемещению единичного положительного заряда,
называется электродвижущей силой (э.д.с.)![]() , действующей
в цепи или на ее участке.
, действующей
в цепи или на ее участке.
![]() . (4.10)
. (4.10)
Единица измерения э.д.с. – вольт (В).
Стороннюю силу ![]() , действующую на заряд
, действующую на заряд ![]() , можно представить в виде
, можно представить в виде
![]() , (4.11)
, (4.11)
где
![]() -
напряженность поля сторонних сил.
-
напряженность поля сторонних сил.
Работа сторонних сил над зарядом ![]() на участке цепи 1-2 равна
на участке цепи 1-2 равна
![]() . (4.12)
. (4.12)
Тогда э.д.с., действующая на участке 1-2:
![]() . (4.13)
. (4.13)
Э.д.с., действующая в замкнутой цепи:
![]() , (4.14)
, (4.14)
т.е. э.д.с., действующая в замкнутой цепи, может быть определена как циркуляция вектора напряженности сторонних сил.
Результирующая сила, действующая в каждой точке цепи
на заряд ![]() , равна
, равна
![]() , (4.15)
, (4.15)
где
![]() - силы
электростатического поля.
- силы
электростатического поля.
Работа, совершаемая результирующей силой над зарядом на участке 1-2, определяется выражением
![]() . (4.16)
. (4.16)
Величина, численно равная работе, совершаемой
электростатическими и сторонними силами при перемещении единичного
положительного заряда, называется напряжением ![]() на данном участке цепи:
на данном участке цепи:
![]() . (4.17)
. (4.17)
Участок цепи, на котором не действуют сторонние силы, называется однородным. Участок, на котором на носители тока действуют сторонние силы, называется неоднородным. Для однородного участка цепи напряжение совпадает с разностью потенциалов:
![]() . (4.18)
. (4.18)
Закон Ома для неоднородного участка цепи имеет вид:
![]() . (4.19)
. (4.19)
Для замкнутой цепи ![]() , поэтому закон Ома для замкнутой цепи
будет иметь вид:
, поэтому закон Ома для замкнутой цепи
будет иметь вид:
![]() , (4.20)
, (4.20)
где![]() – суммарное
сопротивление всей цепи.
– суммарное
сопротивление всей цепи.
Работа тока, совершаемая постоянным током в
проводнике, имеющем сопротивление ![]() и находящемся под напряжением
и находящемся под напряжением ![]() , рассчитывается по
формулам:
, рассчитывается по
формулам:
![]() . (4.21)
. (4.21)
Мощность постоянного тока равна
![]() . (4.22)
. (4.22)
Если ток проходит по неподвижному металлическому проводнику, то вся работа тока идет на его нагревание и, по закону сохранения энергии,
![]() . (4.23)
. (4.23)
Таким образом, количество теплоты, выделяющееся в проводнике:
![]() . (4.24)
. (4.24)
Данные соотношения выражают закон Джоуля-Ленца, экспериментально установленный независимо друг от друга Дж. Джоулем и Э.Х. Ленцем.
4.4 Классическая электронная теория электропроводности металлов
Исходя из представлений о свободных электронах, немецкий физик П. Друде создал классическую электронную теорию металлов, которая затем была усовершенствована голландским физиком Х. Лоренцем. Эта теория основана на предположении, что электроны проводимости ведут себя подобно молекулам идеального газа. При своем движении они сталкиваются с ионами, расположенными в узлах кристаллической решетки, в результате чего устанавливается термодинамическое равновесие между электронным газом и решеткой. Классическая электронная теория хорошо объясняет существование электрического сопротивления металлов, законы Ома и Джоуля-Ленца.
Закон Ома в дифференциальной форме:
![]() , (4.25)
, (4.25)
где
величина ![]() ,
обратная удельному сопротивлению
,
обратная удельному сопротивлению ![]() , называется удельной проводимостью
вещества.
, называется удельной проводимостью
вещества.
Закон Джоуля-Ленца в дифференциальной форме:
![]() , (4.26)
, (4.26)
где
![]() - удельная
тепловая мощность, определяемая как количество теплоты, выделяющееся за единицу
времени в единице объема проводника.
- удельная
тепловая мощность, определяемая как количество теплоты, выделяющееся за единицу
времени в единице объема проводника.
Согласно теории Друде, электрон во время свободного
пробега движется равноускоренно под действием силы ![]() , действующей на него со стороны
электрического поля. К концу свободного пробега скорость электрона достигнет
, действующей на него со стороны
электрического поля. К концу свободного пробега скорость электрона достигнет
![]() , (4.27)
, (4.27)
где
![]() - среднее
время между двумя последовательными соударениями электрона с ионами решетки.
- среднее
время между двумя последовательными соударениями электрона с ионами решетки.
Средняя скорость направленного движения (дрейфа) электронов
![]() . (4.28)
. (4.28)
Тогда плотность тока в металлическом проводнике пропорциональна напряженности поля (закон Ома в дифференциальной форме):
![]() . (4.29)
. (4.29)
Коэффициент пропорциональности между ![]() и
и ![]() есть не что иное, как удельная проводимость
материала:
есть не что иное, как удельная проводимость
материала:
![]() . (4.30)
. (4.30)
К концу свободного пробега электрон приобретает кинетическую энергию:
![]() . (4.31)
. (4.31)
При соударении с ионом эта энергия полностью передается решетке и идет на
увеличение внутренней энергии металла, т.е. на его нагревание. В единицу
времени каждый электрон испытывает ![]() соударений. Следовательно, за единицу
времени решетке в единице объема проводника передается энергия, равная удельной
тепловой мощности
соударений. Следовательно, за единицу
времени решетке в единице объема проводника передается энергия, равная удельной
тепловой мощности ![]() :
:
![]() . (4.32)
. (4.32)
Коэффициент пропорциональности между ![]() и
и ![]() есть удельная проводимость материала
есть удельная проводимость материала ![]() . Следовательно, последняя формула выражает закон Джоуля-Ленца в
дифференциальной форме.
. Следовательно, последняя формула выражает закон Джоуля-Ленца в
дифференциальной форме.
Несмотря на очевидные достоинства классической электронной теории проводимости металлов, она имеет и ряд существенных недостатков, проявляющихся в противоречиях некоторых выводов теории с опытом. Наиболее яркими примерами несостоятельности классической электронной теории электропроводности металлов являются сверхпроводимость и теория теплоемкости металлов.
Согласно классической электронной теории электрическое сопротивление есть результат соударений электронов проводимости с ионами кристаллической решетки. С этих позиций невозможно объяснить полное отсутствие электрического сопротивления у некоторых металлов и сплавов в сверхпроводящем состоянии.
Теплоемкость металла слагается из теплоемкости его
кристаллической решетки и теплоемкости электронного газа. Согласно классической
электронной теории молярная теплоемкость одноатомного электронного газа равна ![]() . В таком случае
. В таком случае
![]() . (4.33)
. (4.33)
Опыт, однако, показывает, что молярные теплоемкости всех химически простых
твердых тел, в том числе металлов, одинаковы и равны ![]() . Таким образом, вопреки
представлениям электронной теории проводимости металлов электронный газ
практически не обладает теплоемкостью.
. Таким образом, вопреки
представлениям электронной теории проводимости металлов электронный газ
практически не обладает теплоемкостью.
Эти и некоторые другие противоречия теории с опытом успешно разрешены квантовой теорией проводимости.
5 Лекция. Магнитное поле токов
Цель лекции:
-ознакомление с экспериментальными законами магнитных полей постоянных токов;
-введение дифференциальных законов для магнитных полей постоянных токов.
5.1 Магнитное взаимодействие токов. Вектор магнитной индукции
В 1820 г. датский физик Х. Эрстед обнаружил
ориентирующее действие электрического тока на магнитную стрелку. Практически
одновременно с этим французский физик А.М. Ампер открыл и подробно исследовал
взаимодействие двух проводников с током. Было установлено, что магнитное
взаимодействие свойственно только движущимся электрическим зарядам (токам).
Магнитное взаимодействие токов осуществляется посредством особой формы материи
– магнитного поля. Основное свойство магнитного поля заключается в том, что на
проводники с током, находящиеся в нем, действуют силы. Для изучения свойств
магнитного поля используется рамка с током. За направление магнитного поля в
данной точке принимается направление, вдоль которого располагается
положительная нормаль к рамке![]() . Вращающий момент пары сил, действующей
на рамку с током равен
. Вращающий момент пары сил, действующей
на рамку с током равен
![]() , (5.1)
, (5.1)
где
![]() - магнитный
момент рамки с током,
- магнитный
момент рамки с током,
![]() - количественная
характеристика магнитного поля, называемая вектором магнитной индукции.
- количественная
характеристика магнитного поля, называемая вектором магнитной индукции.
Магнитная индукция в данной точке однородного магнитного поля определяется максимальным вращающим моментом, действующим на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна направлению поля. Единица измерения магнитной индукции – тесла (Тл).
5.2 Закон Био-Савара-Лапласа. Магнитное поле прямого тока. Магнитное поле в центре кругового проводника
Закон Био-Савара-Лапласа для проводника с током ![]() , элемент
, элемент ![]() которого создает в
некоторой точке поля индукцию
которого создает в
некоторой точке поля индукцию ![]() , записывается в виде
, записывается в виде
![]() , (5.2)
, (5.2)
где
![]() -
радиус-вектор, проведенный из элемента тока
-
радиус-вектор, проведенный из элемента тока ![]() в рассматриваемую точку поля,
в рассматриваемую точку поля,
![]() = 4π·10-7
Гн/м - магнитная постоянная.
= 4π·10-7
Гн/м - магнитная постоянная.
Направление ![]() перпендикулярно
перпендикулярно
![]() и
и ![]() , т.е. перпендикулярно
плоскости, в которой они лежат. Это направление может быть найдено по правилу
правого винта: направление вращения головки винта дает направление
, т.е. перпендикулярно
плоскости, в которой они лежат. Это направление может быть найдено по правилу
правого винта: направление вращения головки винта дает направление ![]() , если поступательное
движение винта соответствует направлению тока в элементе.
, если поступательное
движение винта соответствует направлению тока в элементе.
Модуль вектора определяется выражением
![]() , (5.3)
, (5.3)
где
![]() - угол между
векторами
- угол между
векторами ![]() и
и ![]() .
.
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами, равна векторной сумме магнитных индукций полей, создаваемых каждым током в отдельности:
![]() . (5.4)
. (5.4)
Применение закона Био-Савара-Лапласа совместно с принципом суперпозиции позволяет рассчитать магнитные поля некоторых токов.
1. Магнитное поле прямого тока
![]() , (5.5)
, (5.5)
где
![]() - расстояние
от тока до рассматриваемой точки.
- расстояние
от тока до рассматриваемой точки.
2. Магнитное поле в центре кругового тока
![]() , (5.6)
, (5.6)
где
![]() - радиус
кругового тока.
- радиус
кругового тока.
5.3 Линии индукции магнитного поля. Вихревой характер магнитного поля. Напряженность магнитного поля. Закон полного тока
Линии, касательная к которым в каждой точке совпадают
с направлением вектора ![]() , называются линиями магнитной индукции.
Линии магнитной индукции прочерчивают с такой густотой, чтобы число линий,
пересекающих единицу поверхности, перпендикулярной к ним, было равно (или
пропорционально) модулю вектора
, называются линиями магнитной индукции.
Линии магнитной индукции прочерчивают с такой густотой, чтобы число линий,
пересекающих единицу поверхности, перпендикулярной к ним, было равно (или
пропорционально) модулю вектора ![]() в данном месте.
в данном месте.
Линии магнитной индукции всегда замкнуты и охватывают проводники с током. Векторные поля, обладающие непрерывными линиями, называются вихревыми. Магнитное поле – вихревое поле.
Для описания магнитного поля наряду с магнитной
индукцией используют другую физическую величину – напряженность магнитного поля
![]() . В вакууме
она связана с вектором магнитной индукции соотношением
. В вакууме
она связана с вектором магнитной индукции соотношением
![]() . (5.7)
. (5.7)
Единица измерения напряженности магнитного поля – А/м.
Введем понятие магнитного напряжения:
![]() . (5.8)
. (5.8)
Магнитное напряжение зависит от формы контура ![]() и не определяется только положением точек
начала и конца этого контура. Магнитное напряжение по любому замкнутому
контуру (циркуляция вектора
и не определяется только положением точек
начала и конца этого контура. Магнитное напряжение по любому замкнутому
контуру (циркуляция вектора ![]() ) отлично от нуля. Циркуляция вектора
) отлично от нуля. Циркуляция вектора ![]() по произвольному
замкнутому контуру равна алгебраической сумме токов, охватываемых этим
контуром:
по произвольному
замкнутому контуру равна алгебраической сумме токов, охватываемых этим
контуром:
![]() , (5.9)
, (5.9)
где
![]() - число
проводников с токами, охватываемых контуром
- число
проводников с токами, охватываемых контуром ![]() произвольной формы.
произвольной формы.
Это теорема о циркуляции вектора ![]() называется также законом полного тока для
магнитного поля в любой среде.
называется также законом полного тока для
магнитного поля в любой среде.
Применяя теорему о циркуляции вектора ![]() , можно рассчитать напряженность
магнитного поля внутри соленоида и тороида.
, можно рассчитать напряженность
магнитного поля внутри соленоида и тороида.
1.
Поле соленоида длиной ![]() ,
имеющей
,
имеющей ![]() витков,
витков,
![]() . (5.10)
. (5.10)
2.
Поле тороида – кольцевой катушки, витки которой намотаны сердечник, имеющей
форму тора радиуса ![]() ,
,
![]() , (5.11)
, (5.11)
где
![]() - число
витков.
- число
витков.
6 Лекция. Силы в магнитном поле
Цель лекции:
- ознакомление с силами, действующими на проводники с током во внешнем магнитном поле, а также с силой Лоренца.
6.1 Закон Ампера. Взаимодействие параллельных токов
Сила ![]() , с которой магнитное поле действует на
элемент тока
, с которой магнитное поле действует на
элемент тока ![]() ,
помещенный в это поле,
,
помещенный в это поле,
![]() . (6.1)
. (6.1)
Направление вектора ![]() может
быть найдено по правилу левой руки: если ладонь левой руки расположить так,
чтобы в нее входил вектор
может
быть найдено по правилу левой руки: если ладонь левой руки расположить так,
чтобы в нее входил вектор ![]() , а четыре вытянутых пальца расположить по
направлению тока в проводнике, то отогнутый большой палец покажет направление
силы, действующей на ток. Модуль силы Ампера вычисляется по формуле
, а четыре вытянутых пальца расположить по
направлению тока в проводнике, то отогнутый большой палец покажет направление
силы, действующей на ток. Модуль силы Ампера вычисляется по формуле
![]() , (6.2)
, (6.2)
где
![]() - угол между
векторами
- угол между
векторами ![]() и
и ![]() .
.
Два параллельных проводника с токами ![]() и
и ![]() , расстояние между которыми
равно
, расстояние между которыми
равно ![]() ,
притягиваются друг к другу, если токи текут в одном направлении и отталкиваются
друг от друга, если токи имеют противоположные направления.
,
притягиваются друг к другу, если токи текут в одном направлении и отталкиваются
друг от друга, если токи имеют противоположные направления.
![]() . (6.3)
. (6.3)
6.2 Сила Лоренца. Движение заряженных частиц в магнитном поле
Сила, действующая на электрический заряд ![]() , движущийся в
магнитном поле со скоростью
, движущийся в
магнитном поле со скоростью ![]() , называется силой Лоренца:
, называется силой Лоренца:
![]() . (6.4)
. (6.4)
Направление силы Лоренца находится с помощью правила левой руки: если ладонь
левой руки расположить так, чтобы в нее входил вектор ![]() , а четыре вытянутых пальца
направить вдоль вектора
, а четыре вытянутых пальца
направить вдоль вектора ![]() , то отогнутый большой палец покажет
направление силы, действующей на положительный заряд. Модуль силы Лоренца равен
, то отогнутый большой палец покажет
направление силы, действующей на положительный заряд. Модуль силы Лоренца равен
![]() , (6.5)
, (6.5)
где
![]() - угол между
векторами
- угол между
векторами ![]() и
и ![]() .
.
Если частица движется в однородном магнитном поле со скоростью![]() , то сила Лоренца
постоянна по модулю и нормальна к траектории частицы. Согласно второму закону
Ньютона, эта сила создает центростремительное ускорение. Следовательно, частица
будет двигаться по окружности, радиус которой определяется из условия
, то сила Лоренца
постоянна по модулю и нормальна к траектории частицы. Согласно второму закону
Ньютона, эта сила создает центростремительное ускорение. Следовательно, частица
будет двигаться по окружности, радиус которой определяется из условия ![]() , откуда
, откуда
![]() . (6.6)
. (6.6)
Период вращения частицы
![]() , (6.7)
, (6.7)
т.е.
период вращения частицы в однородном магнитном поле определяется только
величиной, обратной удельному заряду ![]() частицы, и магнитной индукции поля
частицы, и магнитной индукции поля ![]() , но не зависит от ее
скорости. На этом основано действие циклических ускорителей заряженных частиц.
, но не зависит от ее
скорости. На этом основано действие циклических ускорителей заряженных частиц.
6.3 Магнитный поток
Магнитным потоком через плоскую поверхность ![]() , расположенную в однородном
магнитном поле с индукцией
, расположенную в однородном
магнитном поле с индукцией ![]() , называется скалярная величина, равная
, называется скалярная величина, равная
![]() , (6.8)
, (6.8)
где
![]() - угол между
вектором
- угол между
вектором ![]() и нормалью
и нормалью
![]() к поверхности.
к поверхности.
Единица измерения магнитного потока – вебер (Вб): 1 Вб – магнитный поток, проходящий через плоскую поверхность площадью 1 м2, расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл.
Магнитный поток через произвольную поверхность ![]() , расположенную в неоднородном
магнитном поле равен
, расположенную в неоднородном
магнитном поле равен
![]() . (6.9)
. (6.9)
Магнитный поток через любую замкнутую поверхность равен нулю:
![]() . (6.10)
. (6.10)
Эта теорема, называемая теоремой Гаусса для вектора магнитной индукции отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.
6.4 Механическая работа в магнитном поле
На проводник с током в магнитном поле действует сила Ампера. Если проводник не закреплен, то под действием силы Ампера он будет перемещаться.
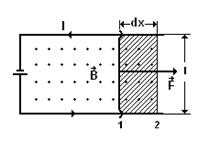
Рисунок 6.1
При этом магнитное поле совершает работу:
![]() , (6.11)
, (6.11)
где
![]() - магнитный
поток через поверхность
- магнитный
поток через поверхность ![]() .
.
Таким образом, работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником.
Для замкнутого контура с постоянным током работа магнитного поля при конечном перемещении контура равна
![]() . (6.12)
. (6.12)
На контур с током в магнитном поле действует пара сил
с моментом ![]() ,
стремящаяся повернуть рамку так, чтобы его плоскость стала перпендикулярна к
,
стремящаяся повернуть рамку так, чтобы его плоскость стала перпендикулярна к ![]() .
.
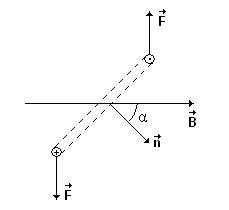
Рисунок 6.2
Момент пары сил определяется по формуле
![]() , (6.13)
, (6.13)
где
![]() - магнитный
момент контура.
- магнитный
момент контура.
Модуль момента пары сил равен
![]() , (6.14)
, (6.14)
где
![]() - угол между
направлением нормали
- угол между
направлением нормали ![]() к
плоскости рамки и направлением вектора магнитной индукции
к
плоскости рамки и направлением вектора магнитной индукции ![]() .
.
7 Лекция. Магнитные свойства вещества
Цель лекции:
-ознакомление с особенностями поведения магнитного поля при внесении в него магнетиков;
-введение новых величин, для объяснения явления намагничивания магнетиков.
7.1 Магнитные моменты электронов и атомов
Все вещества, помещенные в магнитное поле, намагничиваются.
Причину этого явления объяснил А.Ампер, выдвинув гипотезу о том, что в любом
теле существуют микроскопические токи, обусловленные движением электронов в
атомах и молекулах. Электрон, движущийся по круговой орбите, эквивалентен
круговому току, поэтому он обладает орбитальным магнитным моментом ![]() , модуль которого
, модуль которого
![]() , (7.1)
, (7.1)
где
![]() - сила тока;
- сила тока;
![]() - частота вращения
электрона по орбите;
- частота вращения
электрона по орбите;
![]() - площадь орбиты.
- площадь орбиты.
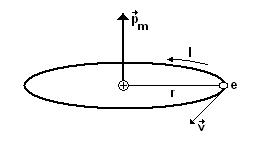
Рисунок 7.1
Впоследствии было установлено, что, кроме орбитального магнитного
момента, электрон обладает собственным (спиновым) магнитным моментом ![]() , который связан с
собственным механическим моментом, называемым спином. Спин является неотъемлемым
свойством электрона, подобно его заряду и массе.
, который связан с
собственным механическим моментом, называемым спином. Спин является неотъемлемым
свойством электрона, подобно его заряду и массе.
Следовательно, магнитный момент электрона складывается из орбитального и спинового магнитных моментов. Пренебрегая магнитными моментами ядер, можно рассматривать магнитный момент атома как векторную сумму магнитных моментов (орбитальных и спиновых) входящих в атом электронов:
![]() . (7.2)
. (7.2)
7.2 Диамагнетики и парамагнетики
Во внешнем магнитном поле орбита электрона, ориентированная
относительно
вектора ![]() произвольным
образом, совершает прецессию. Прецессионное движение электронных орбит
эквивалентно круговому току, порождающему магнитное поле атома. Наведенные
таким образом магнитные поля атомов направлены противоположно внешнему полю и,
складываясь, образуют магнитное поле вещества, ослабляющее внешнее магнитное
поле. Этот эффект называется диамагнитным, а вещества, намагничивающиеся во
внешнем магнитном поле против направления поля, называются диамагнетиками (Bi, Ag, Au, Cu, C,
многие органические соединения и др.).
произвольным
образом, совершает прецессию. Прецессионное движение электронных орбит
эквивалентно круговому току, порождающему магнитное поле атома. Наведенные
таким образом магнитные поля атомов направлены противоположно внешнему полю и,
складываясь, образуют магнитное поле вещества, ослабляющее внешнее магнитное
поле. Этот эффект называется диамагнитным, а вещества, намагничивающиеся во
внешнем магнитном поле против направления поля, называются диамагнетиками (Bi, Ag, Au, Cu, C,
многие органические соединения и др.).
Диамагнетизм присутствует во всех веществам (редкоземельные элементы, Pt, Al и т.д.), однако, в некоторых из них он подавляется парамагнитным эффектом. Атомы парамагнитных веществ при отсутствии внешнего магнитного поля обладают магнитными моментами. Однако вследствие теплового движения молекул их магнитные моменты ориентированы беспорядочно и взаимно компенсируются. При внесении парамагнетика во внешнее магнитное поле устанавливается преимущественная ориентация магнитных моментов атомов по полю. Таким образом, парамагнетик намагничивается, создавая собственное магнитное поле, совпадающее по направлению с внешним полем и усиливающее его. Этот эффект называется парамагнитным.
7.3 Намагниченность. Магнитное поле в веществе. Магнитная восприимчивость вещества
Для количественного описания намагничения вводят векторную величину – намагниченность, определяемую магнитным моментом единицы объема вещества:
![]() . (7.3)
. (7.3)
Магнитное поле в веществе складывается из двух полей: внешнего поля, создаваемого
намагничивающим током в вакууме ![]() , и поля
, и поля ![]() , создаваемого молекулярными токами в
намагниченном веществе:
, создаваемого молекулярными токами в
намагниченном веществе:
![]() . (7.4)
. (7.4)
Поле, создаваемое молекулярными токами ![]() , связано с намагниченностью
, связано с намагниченностью ![]() соотношением
соотношением
![]() . (7.5)
. (7.5)
Тогда
![]() . (7.6)
. (7.6)
В несильных полях, как показывает опыт, намагниченность прямо пропорциональна напряженности поля, вызывающего намагничение, т.е.
![]() , (7.7)
, (7.7)
где
![]() –
безразмерная величина, называемая магнитной восприимчивостью вещества.
–
безразмерная величина, называемая магнитной восприимчивостью вещества.
Тогда магнитную индукцию поля в веществе можно записать в виде
![]() , (7.8)
, (7.8)
где
безразмерная величина ![]() представляет собой магнитную
проницаемость вещества.
представляет собой магнитную
проницаемость вещества.
Закон полного тока для магнитного поля в веществе:
![]() , (7.9)
, (7.9)
где
![]() и
и ![]() - соответственно алгебраические
токи макротоков (токов проводимости) и микротоков (молекулярных токов),
охватываемых произвольным замкнутым контуром
- соответственно алгебраические
токи макротоков (токов проводимости) и микротоков (молекулярных токов),
охватываемых произвольным замкнутым контуром ![]()
![]() .
.
7.4 Условия на границе двух магнетиков
На границе раздела двух веществ 1 и 2 выполняются
следующие условия для векторов ![]() и
и ![]() :
:
![]() ,
, ![]() , (7.10)
, (7.10)
![]() ,
, ![]() . (7.11)
. (7.11)
Помимо рассмотренных двух классов веществ – диа- и парамагнетиков, существуют еще сильномагнитные вещества – ферромагнетики. Ферромагнетики обладают спонтанной намагниченностью, т.е. они намагничены даже в отсутствии внешнего магнитного поля.
7.5 Основные свойства ферромагнетиков
1.
магнитная проницаемость ![]() достигает очень больших значений (до 106);
достигает очень больших значений (до 106);
2.
зависимость магнитной проницаемости ![]() от напряженности внешнего магнитного поля
от напряженности внешнего магнитного поля
![]() , т.е. связь
между векторами намагниченности
, т.е. связь
между векторами намагниченности ![]() и напряженности магнитного поля
и напряженности магнитного поля ![]() не линейна;
не линейна;
3. магнитный гистерезис;
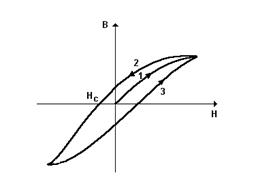
Рисунок 7.2
4. наличие характерной температуры (точка Кюри), при которой ферромагнетик теряет свои свойства.
8 Лекция. Явление электромагнитной индукции
Цель лекции:
- ознакомление появления ЭДС индукции в неподвижных и движущихся проводниках во внешнем магнитном поле;
-введение закона электромагнитной индукции в дифференциальной форме.
8.1 Электромагнитная индукция
Электромагнитная индукция была открыта Фарадеем в 1831 г. Электромагнитной индукцией называется возникновение электродвижущих сил под действием магнитных полей. Для демонстрации этого явления берут неподвижный магнит и проволочную катушку, концы которой соединены с гальванометром. При движении катушки в постоянном магнитном поле в ней возбуждается электрический ток, прекращающийся, когда катушка останавливается. Этот ток называется индукционным током, а само явление – электромагнитной индукцией. В частности, когда катушка равномерно вращается в постоянном магнитном поле, индукционный ток периодически меняет свою силу и направление. Возбуждение электрического тока при движении проводника в магнитном поле объясняется действием силы Лоренца, возникающей при движении проводника. Рассмотрим случай, когда два параллельных провода АВ и СD помещены в постоянное однородное магнитное поле, перпендикулярное к плоскости рисунка и направленное к читателю (см.рисунок 8.1). Слева провода АВ и СD замкнуты, справа разомкнуты. Вдоль проводов может свободно скользить проводящий мостик ВС. Когда мостик движется вправо со скоростью v, вместе с ним движутся и электроны. На каждый движущийся заряд е в магнитном поле действует сила Лоренца
![]() . (8.1)
. (8.1)
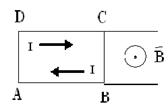 В результате электроны начнут перемещаться по мостику вверх, т.е. по
нему потечет ток, направленный вниз. Это и есть индукционный ток. Сила Лоренца
в описанном опыте играет роль сторонней силы, возбуждающей электрический ток.
В результате электроны начнут перемещаться по мостику вверх, т.е. по
нему потечет ток, направленный вниз. Это и есть индукционный ток. Сила Лоренца
в описанном опыте играет роль сторонней силы, возбуждающей электрический ток.
Соответствующая напряженность стороннего поля равна Рисунок 8.1
![]() . (8.2)
. (8.2)
Электродвижущая сила, создаваемая этим полем,
называется электродвижущей силой индукции и обозначается ![]() . В рассматриваемом случае
. В рассматриваемом случае
![]() . (8.3)
. (8.3)
Знак
минус поставлен потому, что стороннее поле направлено против положительного обхода
контура, определяемого вектором ![]() по правилу правого винта. Величина
по правилу правого винта. Величина ![]() есть приращение
площади контура ABCD в единицу времени, или скорость приращения этой
площади. Поэтому величина
есть приращение
площади контура ABCD в единицу времени, или скорость приращения этой
площади. Поэтому величина ![]() равна
равна ![]() т.е. скорости приращения магнитного потока,
пронизывающего площадь контура ABCD. Таким образом,
т.е. скорости приращения магнитного потока,
пронизывающего площадь контура ABCD. Таким образом,
![]() . (8.4)
. (8.4)
Единица измерения э.д.с. индукции – вольт (В), действительно:
![]() .
.
Результат
(8.4) справедлив и в том случае, когда однородное магнитное поле ![]() направлено под любым
углом к плоскости контура ABCD. Тогда не составляет труда распространить формулу (8.4)
на случай любого замкнутого провода, движущегося произвольным образом в
постоянном неоднородном магнитном поле.
направлено под любым
углом к плоскости контура ABCD. Тогда не составляет труда распространить формулу (8.4)
на случай любого замкнутого провода, движущегося произвольным образом в
постоянном неоднородном магнитном поле.
8.2 Закон электромагнитной индукции как следствие закона сохранения энергии
К формуле (8.4) можно прийти также с помощью закона
сохранения энергии, как это впервые сделал Гельмгольц (1821-1894).
Рассматривается замкнутый виток провода, в которой включен гальванический
элемент с электродвижущей силой ![]() . Виток движется в постоянном магнитном
поле. За время dt амперовы силы совершают над витком работу
. Виток движется в постоянном магнитном
поле. За время dt амперовы силы совершают над витком работу ![]() . Кроме того, в витке
выделяется джоулево тепло
. Кроме того, в витке
выделяется джоулево тепло ![]() . Сумма этих работ должна равняться работе
гальванического элемента
. Сумма этих работ должна равняться работе
гальванического элемента ![]() т.е.
т.е.
![]() , (8.5)
, (8.5)
отсюда
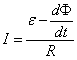 . (8.6)
. (8.6)
Таким
образом, движущемся витке ток определяется не только электродвижущей силой
гальванического элемента, к ней добавляется слагаемое -![]() которое и есть электродвижущая
сила индукции.
которое и есть электродвижущая
сила индукции.
8.3 Индукционные токи
Индукционные токи могут возникать и в неподвижных проводниках. Возьмем замкнутый провод и постоянный магнит. При движении провода возникает индукционный ток. Что произойдет, если, оставляя провод неподвижным, двигать магнит? Покой и движение – понятия относительные. Явление индукции должно зависеть только от относительного движения провода и магнита. Отсюда следует, что при движении магнита будет возбуждаться такой же индукционный ток, что и при соответствующем движении провода. Опыт подтверждает это заключение. Таким образом, для возбуждения индукционного тока существенно изменение магнитного потока через контур проводника, а не способ, каким это изменение достигается. Всякий раз, когда меняется магнитный поток, пронизывающий контур неподвижного или движущегося замкнутого провода, в проводе возникает индукционный ток, причем во всех случаях электродвижущая сила индукции определяется формулой (8.4). Эта формула определяет не только величину, но и направление индукционного тока, которое определяется правилом Ленца: индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток.
8.4 Зависимость э.д.с. индукции от индуктивности
Электрический ток, текущий в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, по закону Био-Савара-Лапласа, пропорционально току. Сцепленный с контуром магнитный поток Ф, поэтому пропорционален току I в контуре:
![]() , (8.7)
, (8.7)
где коэффициент пропорциональности L называется индуктивностью контура.
При изменении силы тока в контуре будет изменяться также и сцепленный с ним магнитный поток; следовательно, в контуре будет индуцироваться э.д.с. Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией.
Единица измерения индуктивности - генри (Гн):
1 Гн=1 Вб/А=1 В с/А.
Используя
формулу (8.7), можно получить выражение для индуктивности соленоида, которая
зависит от числа витков соленоида N, его длины ![]() , площади S и
магнитной проницаемости
, площади S и
магнитной проницаемости![]() вещества, из которого изготовлен сердечник
соленоида:
вещества, из которого изготовлен сердечник
соленоида:
![]() . (8.8)
. (8.8)
Применяя к явлению самоиндукции закон Фарадея, при условии, что контур не деформируется и магнитная проницаемость не изменяется, получим
![]() . (8.9)
. (8.9)
8.5 Коэффициент взаимной индукции
Рассмотрим два неподвижных контура (1 и 2), расположенных
достаточно близко друг от друга. Пусть в контуре 1 течет ток ![]() , а в контуре 2 -
, а в контуре 2 - ![]() . Пусть
. Пусть ![]() - часть магнитного
потока, создаваемого первым током, который пронизывает контур второго тока.
Тогда
- часть магнитного
потока, создаваемого первым током, который пронизывает контур второго тока.
Тогда
![]() . (8.10)
. (8.10)
Если
ток в первом контуре изменяется, то в контуре индуцируется э.д.с ![]() :
:
![]() . (8.11)
. (8.11)
Если изменяется ток во втором контуре, то э.д.с., индуцируемая в первом контуре, аналогично может быть записана в виде
![]() . (8.12)
. (8.12)
Явление
возникновения э.д.с. в одном из контуров при изменении силы тока в другом
называется взаимной индукцией. Коэффициенты пропорциональности ![]() называются взаимной
индуктивностью контуров. Расчеты, подтверждаемые опытом, показывают, что
называются взаимной
индуктивностью контуров. Расчеты, подтверждаемые опытом, показывают, что
![]() . (8.13)
. (8.13)
Можно
показать, что взаимная индуктивность двух катушек с количествами витков ![]() , намотанных на общий
тороидальный сердечник имеет вид:
, намотанных на общий
тороидальный сердечник имеет вид:
![]() . (8.14)
. (8.14)
8.6 Магнитная энергия тока. Энергия магнитного поля
Магнитное поле является носителем энергии. Выражение
для магнитной энергии тока можно получить через работу, которая затрачивается
током на создание магнитного поля. Для изменения магнитного потока на величину
![]() необходимо
совершить работу
необходимо
совершить работу ![]() .
Тогда работа по созданию магнитного потока будет равна
.
Тогда работа по созданию магнитного потока будет равна
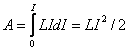 .
.
Следовательно, магнитная энергия тока может быть определена этой работой
![]() . (8.15)
. (8.15)
Энергию магнитного поля можно представить как функцию величин, характеризующих это поле в окружающем пространстве. Можно показать, что формула (8.15) может быть преобразована к виду
![]() , (8.16)
, (8.16)
где V - объем пространства, занятого магнитным полем.
Исследование свойств переменных полей, в частности, распространения электромагнитных волн, явилось доказательством того, что энергия магнитного поля (16) локализована в пространстве, причем в единице объема пространства заключена энергия с объемной плотностью, равной
![]() . (8.17)
. (8.17)
Формула (8.17) справедлива как для однородного, так и для неоднородного полей. Она справедлива также и для переменных полей. Отметим, что это выражение справедливо только для сред, для которых зависимость В от Н линейная, т.е. оно относится только к пара- и диамагнетикам.
9 Лекция. Уравнения Максвелла
Цель лекции:
-объяснение связей уравнений Максвелла с экспериментальными законами электродинамики;
-ознакомление с уравнениями Максвелла в интегральной и дифференциальной формах.
9.1 Максвеллова трактовка закона индукции
Когда проводник движется в постоянном магнитном поле,
индукционный ток вызывается магнитной составляющей силы Лоренца (1). Какая же
сила возбуждает индукционный ток в неподвижном проводнике, находящемся в
переменном магнитном поле? Ответ был дан Максвеллом. Согласно Максвеллу, всякое
изменение магнитного поля во времени возбуждает в окружающем пространстве
электрическое поле. Циркуляция вектора напряженности ![]() этого поля по любому
неподвижному замкнутому контуру
этого поля по любому
неподвижному замкнутому контуру ![]() определяется выражением
определяется выражением
![]() . (9.1)
. (9.1)
Между
максвелловым и фарадеевым пониманием явления электромагнитной индукции имеется
существенное различие. Согласно Фарадею, электромагнитная индукция состоит в
возбуждении электрического тока. Для ее наблюдения необходимо наличие
замкнутого проводника. Максвелл, напротив, видит сущность электромагнитной
индукции, прежде всего в возбуждении электрического поля, а не тока.
Электромагнитная индукция может наблюдаться и тогда, когда в пространстве
вообще нет никаких проводников. Появление индукционного тока в замкнутом
проводнике при внесении последнего в переменное магнитное поле есть лишь одно
из проявлений электрического поля![]() , возникшего в результате изменения поля
магнитного. Но поле
, возникшего в результате изменения поля
магнитного. Но поле ![]() может
производить и другие действия, например, поляризовать диэлектрик, вызвать
пробой конденсатора, ускорять и тормозить заряженные частицы и т. п. Оно может
вызвать электрический ток и в незамкнутом проводнике.
может
производить и другие действия, например, поляризовать диэлектрик, вызвать
пробой конденсатора, ускорять и тормозить заряженные частицы и т. п. Оно может
вызвать электрический ток и в незамкнутом проводнике.
Максвеллова формулировка закона индукции более общая, чем формулировка Фарадея. Она принадлежит к числу наиболее важных обобщений электродинамики.
9.2 Дифференциальная форма записи закона электромагнитной индукции
Математически закон индукции в понимании Максвелла
выражается формулой (9.1), где интеграл берется по замкнутому контуру, который
может быть проведен и в диэлектрике, а не обязательно в проводнике, как было у
Фарадея. Магнитный поток ![]() определяется интегралом
определяется интегралом
![]() , (9.2)
, (9.2)
взятым
по произвольной поверхности S, натянутой на контур ![]() . Поэтому формулу (9.1) можно представить
в виде
. Поэтому формулу (9.1) можно представить
в виде
![]() . (9.3)
. (9.3)
Применив к последнему выражению теорему Стокса, получим
![]() . (9.4)
. (9.4)
Это - дифференциальная форма закона электромагнитной индукции. Уравнение (9.3) или эквивалентное ему уравнение (9.4) – одно из основных соотношений теории электромагнитного поля. Оно входит в систему уравнений Максвелла.
9.3 Токи смещения
Основные уравнения электромагнитного поля в неподвижных средах, применимые не только к постоянным, но и к переменным электромагнитным полям, были установлены Максвеллом. К уравнениям Максвелла можно прийти путем последовательного обобщения опытных фактов. Надо решить, какие из полученных ранее уравнений могут быть сохранены, какие должны быть отброшены и какие надо обобщить. Можно сохранить только такие уравнения, которые не противоречат представлениям теории поля.
К основным уравнениям электродинамики присоединим закон сохранения электрического заряда:
![]() . (9.5)
. (9.5)
Если электромагнитное поле стационарно, то это уравнение переходит в
![]() . (9.6)
. (9.6)
Известная теорема о циркуляции напряженности магнитного поля
![]() (9.7)
(9.7)
также может быть преобразована в дифференциальную форму
![]() , (9.8)
, (9.8)
а
потому удовлетворяет требованиям теории поля. Однако она не может входить в
число основных уравнений электродинамики, потому что уравнение (9.8)
противоречит закону сохранения электрического заряда (9.5). Чтобы устранить это
противоречие, продифференцируем по времени соотношение ![]() :
:
![]()
или ввиду условия замкнутости токов
![]() . (9.9)
. (9.9)
Величину
![]() (9.10)
(9.10)
Максвелл
назвал током смещения, а сумму ![]() - полным током (точнее -
плотностью полного тока). А условие замкнутости тока должно быть записано для
полного тока
- полным током (точнее -
плотностью полного тока). А условие замкнутости тока должно быть записано для
полного тока
![]() , (9.11)
, (9.11)
т.е.
полный ток всегда соленоидален. Поэтому противоречие с уравнением (9.5)
устранится, если в уравнении (9.8) ток проводимости ![]() заменить полным током, т.е. написать
заменить полным током, т.е. написать
![]() . (9.12)
. (9.12)
9.4 Система уравнений Максвелла
Дополнив основные факты из области электромагнетизма установлением магнитных действий токов смещения, Максвелл мог написать систему фундаментальных уравнений электродинамики. Таких уравнений четыре.
В интегральной форме они имеют вид
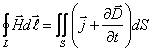 , (I)
, (I)
![]() , (II)
, (II)
![]() , (III)
, (III)
![]()
![]() . (IV)
. (IV)
В дифференциальной форме
![]() , (Iа)
, (Iа)
![]() , (IIа)
, (IIа)
![]() , (IIIа)
, (IIIа)
![]() . (IVа)
. (IVа)
Уравнения Максвелла показывают, что источниками электрического поля могут быть либо электрические заряды, либо магнитные поля, меняющиеся во времени. Магнитные же поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Максвелла в интегральной форме справедливы и в тех случаях, когда существуют поверхности разрыва, на которых свойства среды или напряженности электрического и магнитного полей меняются скачкообразно. Поэтому в этой форме уравнения Максвелла обладают большей общностью, чем в дифференциальной форме, которая предполагает, что все величины в пространстве и во времени меняются непрерывно. Поэтому дифференциальные уравнения Максвелла должны быть дополнены граничными условиями:
![]() (9.13)
(9.13)
Здесь
![]() -
поверхностная плотность электрических зарядов, а
-
поверхностная плотность электрических зарядов, а ![]() - поверхностная плотность тока
проводимости на рассматриваемой границе раздела.
- поверхностная плотность тока
проводимости на рассматриваемой границе раздела.
В случаях, когда поверхностные заряды и токи отсутствуют, граничные условия (9.13) преобразуются к виду
![]() (9.14)
(9.14)
Отметим, что уравнения Максвелла не могут быть выведены. На них следует смотреть как на основные аксиомы классической электродинамики, полученные путем обобщения опытных фактов.
9.5 Относительность электрического и магнитного полей
К электромагнитному полю применим только принцип относительности Эйнштейна, так как факт распространения электромагнитных волн в вакууме во всех системах отсчета с одинаковой скоростью не совместим с принципом относительности Галилея.
Из принципа относительности вытекает, что отдельное рассмотрение электрического и магнитного полей имеет относительный смысл. Так, если электрическое поле создается системой неподвижных зарядов, то эти заряды, являясь неподвижными относительно одной инерциальной системы отсчета, движутся относительно другой и, следовательно, будут порождать не только электрическое, но и магнитное поле. Аналогично, неподвижный относительно одной инерциальной системы отсчета проводник с постоянным током, возбуждая в каждой точке пространства постоянное магнитное поле, движется относительно других инерциальных систем, и создаваемое им переменное магнитное поле возбуждает вихревое электрическое поле.
10 Лекция. Статистические распределения
Цель лекции:
- ознакомление со статистическими и термодинамическими методами исследования систем, состоящих из большого количества частиц;
-ознакомление с классическими распределениями частиц Максвелла-Больцмана.
10.1 Статистический и термодинамический методы исследования
Для исследования свойств макроскопических тел, т.е. систем из огромного количества молекул, используются два метода исследования: статистический и термодинамический.
Описать состояние таких систем с помощью уравнений движения молекул не представляется возможным из-за очень большого их числа. Даже при гипотетическом решении этой задачи невозможно было бы получить представление о состоянии и свойствах газа как целого, хотя состояние газа можно описать с помощью трех макропараметров таких, как давление, объем и температура. Причина этого заключается в том, что в системах с огромным числом частиц возникают качественно новые статистические закономерности, которые перестают быть справедливыми в системах с малым числом частиц.
Поэтому для описания свойств таких систем используется статистический метод, в котором свойства тел, характеризуемые такими макропараметрами, как давление и температура, рассматриваются как усредненный результат действия отдельных молекул.
При термодинамическом методе исследования свойств макроскопических тел и происходящих в них процессах не учитывается их микроскопическая структура. Описание систем производится с помощью макропараметров на основе нескольких эмпирических начал термодинамики. При научном исследовании свойств систем и происходящих в них процессов используются оба метода, которые дополняют друг друга и позволяют решать общую задачу.
10.2 Распределение Максвелла
Как показывает теория и опыт, распределение молекул по скоростям оказывается не случайным, а вполне определенным. И это не только не противоречит представлению о хаотичности молекулярных движений, но именно ею и обусловлено.
Будем искать число молекул ![]() в единице объема газа, скорости
которых лежат в определенном интервале скорости от
в единице объема газа, скорости
которых лежат в определенном интервале скорости от ![]() до
до ![]()
![]() . (10.1)
. (10.1)
Здесь ![]() доля молекул в единице объема
газа, скорости которых лежат в интервале от
доля молекул в единице объема
газа, скорости которых лежат в интервале от ![]() до
до ![]()
Таким образом, функция распределения – это вероятность того, что любая из молекул газа, содержащихся в единице его объема, обладает скоростью, лежащей в интервале dv вблизи скорости v
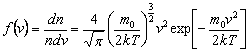 . (10.2)
. (10.2)
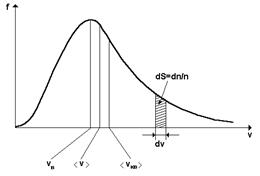
Рисунок 10.1
Функция
![]() удовлетворяет
условию нормировки:
удовлетворяет
условию нормировки:
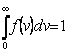 . (10.3)
. (10.3)
Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью.
![]() . (10.4)
. (10.4)
Средняя арифметическая скорость определяется по формуле:
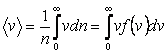 , (10.5)
, (10.5)
![]() . (10.6)
. (10.6)
Средняя квадратичная скорость молекул определяется по формуле:
 , (10.7)
, (10.7)
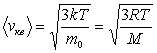 . (10.8)
. (10.8)
При повышении температуры максимум функции распределения молекул по скоростям сместится вправо. Однако площадь, ограниченная кривой, остается неизменной.
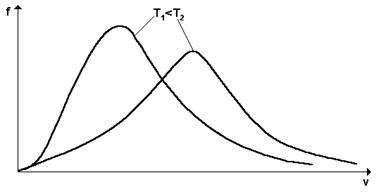
Рисунок 10.2
Экспериментально распределение Максвелла было подтверждено опытами Штерна (1920 г.) и других исследователей.
10.3 Барометрическая формула. Распределение Больцмана
Молекулы любого газа находятся в поле тяготения Земли. Тяготение, с
одной стороны, и тепловое движение молекул – с другой, приводят к некоторому стационарному состоянию газа, при котором давление газа с высотой убывает.
Пусть ![]() , т.е. не зависят от
высоты. Тогда, если на высоте
, т.е. не зависят от
высоты. Тогда, если на высоте ![]() атмосферное давление равно
атмосферное давление равно ![]() , то на высоте
, то на высоте ![]() , оно равно
, оно равно ![]() :
:
![]() , (10.9)
, (10.9)
где
![]() - плотность
газа на высоте
- плотность
газа на высоте ![]() .
.
Следовательно,![]() .
.
Используя уравнение Клапейрона – Менделеева, приводим
к виду ![]() . Интегрируя,
получим
. Интегрируя,
получим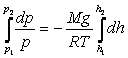 или
или ![]() , откуда путем
потенцирования имеем:
, откуда путем
потенцирования имеем:
![]() или
или 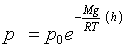 (10.10)
(10.10)
Это уравнение, устанавливающее закон убывания давления с высотой, называется барометрической формулой (используется для определения высоты над Землей путем измерения давления на данной высоте).
Учитывая,
что ![]() , можно
записать
, можно
записать
![]() , или
, или 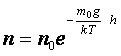 . (10.11)
. (10.11)
Здесь
![]() -
потенциальная энергия молекулы в поле силы тяжести. Если газ находится в
каком-нибудь другом силовом поле, так что его молекулы обладают некоторой
потенциальной энергией, то число частиц, обладающих заданной энергией
-
потенциальная энергия молекулы в поле силы тяжести. Если газ находится в
каком-нибудь другом силовом поле, так что его молекулы обладают некоторой
потенциальной энергией, то число частиц, обладающих заданной энергией ![]() , определяется формулой
, определяется формулой
![]() . (10.11)
. (10.11)
Эта функция носит название распределения Больцмана и справедлива для потенциального силового поля любой природы для системы одинаковых частиц.
11 Лекция. Первое начало термодинамики
-Цель лекции:
- ознакомление с законом сохранения энергии в термодинамике;
- введение интегральных и дифференциальных формах записи первого начала термодинамики.
11.1 Закон равнораспределения энергии по степеням свободы
Из сравнения выражений для давления газа
p = nkT и p = (2/3)n <Ek>
следует
<Ek> = (3/2)kT, (11.1)
т.е. средняя кинетическая энергия поступательного движения молекул прямо пропорциональна термодинамической температуре.
Только поступательно движутся одноатомные молекулы (например, инертных газов). Двух - и более атомные молекулы могут также совершать вращательные и колебательные движения.
В статистической физике имеет место закон равнораспределения энергии по степеням свободы. Числом степеней свободы системы называется число независимых координат, определяющих ее положение в пространстве. Тогда одноатомные молекулы имеют только три поступательные степени свободы, двухатомные - три поступательные и две вращательные, многоатомные и абсолютно твердое тело - три поступательные и три вращательные степени свободы.
Итак, возвращаясь к одноатомным молекулам, можно утверждать, что согласно закону равнораспределения на каждую степень свободы приходится в среднем одинаковая кинетическая энергия, равная kT/2.
Тогда средняя энергия молекулы равна
<E> = (i /2)kT, (11.2)
где i - сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы.
11.2 МКТ теплоемкости идеальных газов и ее ограниченность
Теплоемкостью тела называется величина, равная количеству тепла, которое нужно сообщить телу, чтобы повысить его температуру на 1К.
Удельная теплоемкость – это теплоемкость 1кг вещества.
![]() . (11.3)
. (11.3)
Молярная теплоемкость – это теплоемкость 1 моля вещества.
![]() . (11.4)
. (11.4)
Газ можно нагревать при постоянном объеме или при постоянном давлении.
Соответственно у газа различают две теплоемкости: ![]() и
и ![]() .
.
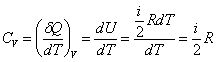 , (11.5)
, (11.5)
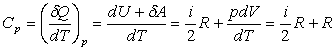 , (11.6)
, (11.6)
![]() . (11.7)
. (11.7)
Это выражение называется формулой Майера.
Таким образом, ![]() и
и ![]() определяются числом степеней
свободы молекул идеального газа и должны быть кратны R/2. Однако опыт показывает отклонения значений
теплоемкости от теоретических. Более того, теплоемкость проявляет зависимость
от температуры, объяснение чему можно дать лишь с помощью квантовой теории
теплоемкости газов.
определяются числом степеней
свободы молекул идеального газа и должны быть кратны R/2. Однако опыт показывает отклонения значений
теплоемкости от теоретических. Более того, теплоемкость проявляет зависимость
от температуры, объяснение чему можно дать лишь с помощью квантовой теории
теплоемкости газов.
11.3 Внутренняя энергия. Первое начало термодинамики
Важной характеристикой термодинамической системы является ее внутренняя энергия U - энергия хаотического (теплового) движения микрочастиц системы и энергия взаимодействия этих частиц. Внутренняя энергия – однозначная функция термодинамического состояния системы, т.е. в каждом состоянии система обладает вполне определенной внутренней энергией. Это означает, что при переходе системы из одного состояния в другое изменение внутренней энергии определяется только разностью значений внутренней энергии этих состояний и не зависит от пути перехода.
Так
как в идеальном газе взаимная потенциальная энергия молекул равна нулю, то
внутренняя энергия, отнесенная к одному молю газа, будет равна сумме
кинетических энергий ![]() молекул:
молекул:
![]() . (11.8)
. (11.8)
Внутренняя энергия для произвольной массы ![]() газа
газа
![]() , (11.9)
, (11.9)
где
![]() молярная
масса;
молярная
масса;
![]() количество вещества.
количество вещества.
Внутренняя энергия системы может изменяться в результате различных процессов, например, совершения над системой работы или сообщения ей теплоты. Можно говорить о двух формах передачи энергии от одних тел к другим: работе и теплоте. Энергия механического движения может превращаться в энергию теплового движения, и наоборот. При этих превращениях соблюдается закон сохранения и превращения энергии; применительно к термодинамическим процессам этим законом и является первое начало термодинамики, установленное в результате обобщения многовековых опытных данных.
![]() . (11.10)
. (11.10)
Уравнение (11.10) выражает первое начало термодинамики: теплота, сообщаемая системе, расходится на изменения ее внутренней энергии и на совершение ею работы протии внешних сил. В дифференциальной форме оно будет иметь вид
![]() . (11.11)
. (11.11)
где
![]() бесконечно
малое изменение внутренней энергии системы;
бесконечно
малое изменение внутренней энергии системы;
![]() - элементарная
работа,
- элементарная
работа,
![]() - бесконечно малое
количество теплоты.
- бесконечно малое
количество теплоты.
В этом выражении ![]() полный
дифференциал, а
полный
дифференциал, а ![]() и
и
![]() таковыми не
являются. Из формулы (11.10) видно, что количество теплоты выражается в тех же
единицах, что работа и энергия, т.е. в джоулях (Дж).
таковыми не
являются. Из формулы (11.10) видно, что количество теплоты выражается в тех же
единицах, что работа и энергия, т.е. в джоулях (Дж).
Если система периодически возвращается в первоначальное состояние, то
изменение ее внутренней энергии ![]() . Тогда согласно первому началу
термодинамики,
. Тогда согласно первому началу
термодинамики,
![]() , (11.12)
, (11.12)
т.е. вечный двигатель первого рода – периодически действующий двигатель, который совершал бы большую работу, чем сообщенная ему извне энергия, - невозможен.
Работа газа при изменении его объема (например, газ, находящийся под поршнем в цилиндре), вычисляется по формуле
![]() , (11.13)
, (11.13)
где S - площадь поршня,
Sdl = dV – изменение объема системы.
Таким образом,
![]() . (11.14)
. (11.14)
Полную работу А, совершаемую газом при изменении его объема от начального до конечного объема, найдем интегрированием формулы (11.14)
 . (11.15)
. (11.15)
12 Лекция. Второе начало термодинамики
Цель лекции:
- ознакомление с понятием о направлении термодинамических процессов;
- введение понятия энтропии.
12.1 Обратимые и необратимые процессы
Система находится в термодинамическом равновесии, если макроскопические величины, определяющие ее состояние (давление, температура), остаются постоянными. В состоянии термодинамического равновесия в системе не могут происходить такие явления, как теплопроводность, диффузия, химические реакции, фазовые переходы.
Если система выведена из состояния равновесия и после этого предоставлена самой себе, то, как показывает опыт, сам собой происходит переход к равновесному состоянию. Но когда равновесие уже установлено, то система не может сама собой возвратиться к первоначальному неравновесному состоянию (например, выравнивание температуры двух соприкасающихся тел, расширение газа в пустоту). Это указывает на важную особенность процессов, происходящих в молекулярных системах, - на их необратимость. Этим молекулярные процессы отличаются от механических, для которых характерна строгая обратимость.
Термодинамический процесс называется обратимым, если он, будучи проведен в обратном направлении, возвращает систему в исходное состояние так, чтобы система прошла через те же промежуточные состояния, что и в прямом процессе, но в обратной последовательности, а состояние тел вне системы осталось неизменным.
Обратимый процесс – понятие идеализированное. Однако их изучение представляет интерес по двум причинам:
1) многие процессы в природе и технике практически обратимы;
2) обратимые процессы являются наиболее экономичными: имеют максимальный КПД, что позволяет указать пути повышения КПД реальных тепловых двигателей.
12.2 Тепловые и холодильные машины. Цикл Карно. КПД. Теоремы Карно
Если тепло передается телу, которое при этом может расширяться, то оно может совершить работу. Согласно первому началу термодинамики:
![]() . (12.1)
. (12.1)
Наибольшая работа совершается при изотермическом процессе, когда внутренняя энергия не изменяется.
![]() . (12.2)
. (12.2)
Но это относится к однократному акту передачи теплоты телу, совершающему работу. Но для техники представляют интерес не такие единичные акты преобразования теплоты в работу. Реально существующие устройства (паровые машины, ДВС) действуют циклически.
Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное.
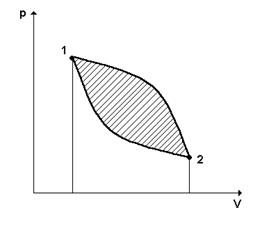
Рисунок 12.1
Если за цикл совершается положительная работа (цикл протекает по часовой стрелке), то он называется прямым. Если же за цикл совершается отрицательная работа (цикл протекает против часовой стрелки), то он называется обратным.
Принцип Кельвина: невозможно осуществить циклический процесс, единственным результатом которого было бы превращение в механическую работу теплоты, отнятой у какого-нибудь тела, без того, чтобы произошли какие-либо изменения в другом теле. Таким образом, для совершения работы в циклической машине необходимо участие двух тел с различной температурой – нагревателя и холодильника. Согласно закону сохранения энергии
![]() . (12.3)
. (12.3)
Коэффициентом полезного действия (КПД) тепловой машины называется отношение
совершаемой ею работы ![]() к количеству теплоты
к количеству теплоты ![]() ,
получаемой машиной от нагревателя:
,
получаемой машиной от нагревателя:
![]() . (12.4)
. (12.4)
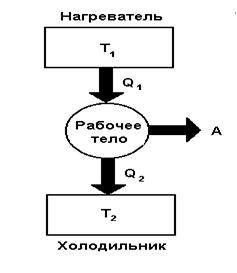
Рисунок 12.2
Рассмотрим круговой процесс, при котором тепло, отнятое у нагревателя, можно превратить в работу наилучшим образом, т.е. так, чтобы полученная работа была максимально возможной. Этот цикл называется циклом Карно.
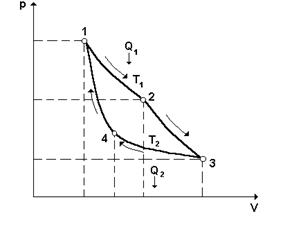
Рисунок 12.3
![]() , (12.5)
, (12.5)
![]() ,
, ![]() ,
, ![]() , (12.6)
, (12.6)
![]() . (12.7)
. (12.7)
Для адиабатных процессов имеем
![]() ,
, ![]() , (12.8)
, (12.8)
или
![]() . (12.9)
. (12.9)
Тогда КПД можно определить как
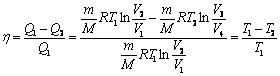 . (12.10)
. (12.10)
Теоремы Карно:
1)Тепловая машина, работающая при данных значениях температур нагревателя и холодильника, не может иметь КПД больший, чем машина, работающая по обратимому циклу Карно при тех же значениях температур нагревателя и холодильника.
2)КПД цикла Карно не зависит от рода рабочего тела, а только от температур нагревателя и холодильника.
12.4 Энтропия и ее свойства
Понятие энтропии введено в 1865 г. Р. Клаузиусом. Для выяснения физического смысла энтропии рассматривают отношение теплоты ![]() ,
полученной телом в изотермическом процессе, к температуре
,
полученной телом в изотермическом процессе, к температуре ![]() теплоотдающего
тела, называемое приведенным количеством теплоты
теплоотдающего
тела, называемое приведенным количеством теплоты ![]() .
Приведенное количество теплоты, сообщаемое телу на бесконечно малом участке
процесса, равно
.
Приведенное количество теплоты, сообщаемое телу на бесконечно малом участке
процесса, равно ![]() . Приведенное количество теплоты, сообщаемое телу в любом
обратимом круговом процессе, равно нулю:
. Приведенное количество теплоты, сообщаемое телу в любом
обратимом круговом процессе, равно нулю:
![]() . (12.11)
. (12.11)
Из этого равенства следует, что подынтегральное
выражение ![]() есть
полный дифференциал некоторой функции, которая определяется только состоянием
системы и не зависит от пути, каким система пришла в это состояние, т.е. является
функцией состояния. Таким образом,
есть
полный дифференциал некоторой функции, которая определяется только состоянием
системы и не зависит от пути, каким система пришла в это состояние, т.е. является
функцией состояния. Таким образом,
![]() . (12.12)
. (12.12)
Функция состояния, дифференциал которой равен ![]() ,
называется энтропией.
,
называется энтропией.
Для обратимых процессов в замкнутой системе ![]() ,
для необратимых процессов энтропия замкнутой системы возрастает
,
для необратимых процессов энтропия замкнутой системы возрастает ![]() >
>![]() .
.
Неравенство Клаузиуса: энтропия замкнутой системы может либо возрастать, либо оставаться постоянной.
Энтропия системы равна сумме энтропий тел, входящих в систему.
Если система совершает равновесный переход из состояния 1 в состояние 2, то изменение энтропии вычисляется по формуле:
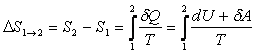 . (12.13)
. (12.13)
Найдем изменение энтропии в процессах идеального газа:
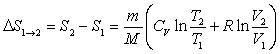 . (12.14)
. (12.14)
При изотермическом процессе:
![]() . (12.15)
. (12.15)
При изохорном процессе:
![]() . (12.16)
. (12.16)
Физический смысл энтропии вскрывается в статистической
физике: энтропия связывается с термодинамической вероятностью.
Термодинамическая вероятность ![]() состояния системы – это число способов, которыми
может быть реализовано данное состояние макроскопической системы, или число
микросостояний, осуществляющих данное макросостояние.
состояния системы – это число способов, которыми
может быть реализовано данное состояние макроскопической системы, или число
микросостояний, осуществляющих данное макросостояние.
Согласно Больцману:
![]() . (12.17)
. (12.17)
Энтропия является мерой неупорядоченности системы.
12.5 Второе начало термодинамики и неосуществимость вечного двигателя второго рода
Некоторые формулировки второго начала термодинамики:
1) любой необратимый процесс в замкнутой системе происходит так, что энтропия системы возрастает
2) невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу (Кельвин)
3) невозможен процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому (Клаузиус).
Третье начало термодинамики (теорема Нернста).
Энтропия всех тел стремится к нулю при стремлении к нулю температуры:
![]() (12.18)
(12.18)
13 Лекция. Явления переноса
Цель лекции:
- ознакомление с явлениями диффузии, теплопроводности и внутреннего трения в термодинамически неравновесных процессах.
13.1 Силы межмолекулярного взаимодействия
Согласно экспериментальным и теоретическим
исследованиям, межмолекулярные силы взаимодействия ![]() обратно пропорциональны n–ой
степени расстояния между молекулами:
обратно пропорциональны n–ой
степени расстояния между молекулами:
![]() ~
~![]() , (13.1)
, (13.1)
где
для сил притяжения ![]() ,
а для сил отталкивания
,
а для сил отталкивания ![]() .
.
Таким образом, эти силы очень быстро убывают с увеличением расстояния между молекулами, причем особенно быстро убывают силы отталкивания.
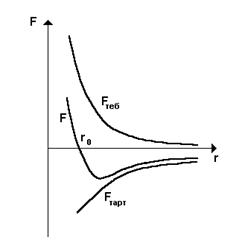
Рисунок 13.1
13.2 Кинетические характеристики молекулярного движения
Молекулы газа, находясь в состоянии хаотического движения, непрерывно сталкиваются друг с другом. Вследствие этого траектория молекул представляет собой ломаную линию, похожую на траекторию броуновской частицы. Изобразим путь, пройденный некоторой молекулой, за 1с.
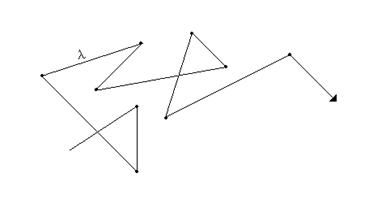
Рисунок 13.2
Длиной свободного пробега молекулы называется путь, проходимый ею между двумя последовательными столкновениями.
Длина свободного пробега все время меняется. Поэтому следует говорить о средней длине свободного
пробега ![]() . Для определения
. Для определения ![]() разделим путь, пройденный молекулой за 1с и численно
равный
разделим путь, пройденный молекулой за 1с и численно
равный ![]() , на среднее число столкновений
, на среднее число столкновений ![]() ,
испытываемых молекулой за 1с.
,
испытываемых молекулой за 1с.
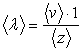 . (13.2)
. (13.2)
Для определения ![]() будем считать молекулы шариками диаметра
будем считать молекулы шариками диаметра ![]() . Изобразим путь,
пройденный одной из молекул за 1с. Допустим, что остальные молекулы неподвижны.
Движущаяся молекула столкнется только с теми молекулами, центры которых лежат
внутри ломаного цилиндра радиусом
. Изобразим путь,
пройденный одной из молекул за 1с. Допустим, что остальные молекулы неподвижны.
Движущаяся молекула столкнется только с теми молекулами, центры которых лежат
внутри ломаного цилиндра радиусом ![]() .
.
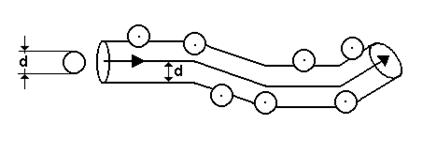
Рисунок 13.3
Следовательно, среднее число столкновений ![]() за 1с равно числу молекул
в объеме ломаного цилиндра. Такой объем можно рассчитать как объем спрямленного
цилиндра высотой
за 1с равно числу молекул
в объеме ломаного цилиндра. Такой объем можно рассчитать как объем спрямленного
цилиндра высотой ![]() и площадью основания
и площадью основания ![]() .
Тогда
.
Тогда
![]() (13.4)
(13.4)
Если же учесть движение остальных молекул, то, как показывает более строгий расчет, число столкновений будет равно
![]() . (13.5)
. (13.5)
Следовательно, средняя длина свободного пробега молекул рассчитывается так
![]() . (13.6)
. (13.6)
Так как ![]() , то средняя длина свободного пробега молекул обратно
пропорциональна давлению. По мере понижения давления газа средняя длина
свободного пробега его молекул возрастает и при сильном разрежении становится
равной размеру сосуда
, то средняя длина свободного пробега молекул обратно
пропорциональна давлению. По мере понижения давления газа средняя длина
свободного пробега его молекул возрастает и при сильном разрежении становится
равной размеру сосуда ![]() . Это состояние газа называется вакуумом.
В зависимости от соотношения
. Это состояние газа называется вакуумом.
В зависимости от соотношения ![]() и
и ![]() различают: средний вакуум
различают: средний вакуум ![]() ;
высокий
;
высокий ![]() >
>![]() ; сверхвысокий вакуум
; сверхвысокий вакуум ![]() >>
>>![]() .
.
В настоящее время достигнуты давления ![]() мм.рт.ст.
мм.рт.ст.
13.3 Феноменологические уравнения явлений переноса в газах
В термодинамически неравновесных системах возникают особые необратимые процессы, называемые явлениями переноса, в результате которых происходит пространственный перенос массы, импульса, энергии. К явлениям переноса относятся диффузия (перенос массы), внутреннее трение (перенос импульса) и теплопроводность (перенос энергии).
Общее уравнение переноса выводится на основе молекулярно-кинетической теории идеального газа.
Ограничимся одномерным случаем. Систему отсчета
выберем так, чтобы ось ![]() была ориентирована в направлении
переноса. Тогда
была ориентирована в направлении
переноса. Тогда
![]() , (13.7)
, (13.7)
где
![]() - переносимая
физическая характеристика;
- переносимая
физическая характеристика;
![]() -
количество физической характеристики, перенесенное молекулами в направлении
-
количество физической характеристики, перенесенное молекулами в направлении ![]() за
время
за
время ![]() через площадку
через площадку ![]() .
.
Отношение ![]() называется градиентом физической величины
называется градиентом физической величины ![]() и
характеризует быстроту ее изменения в направлении наибольшего возрастания физической
величины.
и
характеризует быстроту ее изменения в направлении наибольшего возрастания физической
величины.
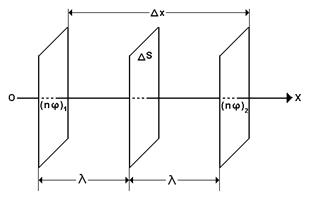
Рисунок 13.4
13.4 Диффузия, вязкость, теплопроводность
В явлении диффузии переносимой физической
характеристикой является масса молекулы ![]() . В
таком случае
. В
таком случае ![]() , а
, а
![]() . (13.8)
. (13.8)
Тогда
![]() . (13.9)
. (13.9)
Обозначив
![]() ,
, ![]() . (13.10)
. (13.10)
получим уравнение диффузии или закон Фика.
![]() . (13.11)
. (13.11)
Коэффициент пропорциональности ![]() называется коэффициентом диффузии. Коэффициент
диффузии обратно пропорционален давлению (т.к.
называется коэффициентом диффузии. Коэффициент
диффузии обратно пропорционален давлению (т.к. ![]() ~
~ ![]() ) и пропорционален квадратному корню из
температуры (т.к.
) и пропорционален квадратному корню из
температуры (т.к.![]() ~
~ ![]() ).
).
В случае внутреннего трения (вязкости) переносимой физической характеристикой является импульс молекулы
![]() ,
,
где
![]() - скорость
слоя газа.
- скорость
слоя газа.
В таком случае ![]() .
.
Тогда
![]() , (13.12)
, (13.12)
где
![]() -
изменение импульса одного слоя относительно другого, происходящее за время
-
изменение импульса одного слоя относительно другого, происходящее за время ![]() на
пограничной площадке
на
пограничной площадке ![]() .
.
Тогда
![]() . (13.13)
. (13.13)
Обозначив
![]() , Па·с, (13.14)
, Па·с, (13.14)
получим уравнение внутреннего трения или закон Ньютона.
Коэффициент пропорциональности ![]() называется коэффициентом внутреннего
трения. Коэффициент внутреннего трения не зависит от давления, т.к.
называется коэффициентом внутреннего
трения. Коэффициент внутреннего трения не зависит от давления, т.к. ![]() ~
~ ![]() , а
, а ![]() ~ p. Однако для разреженного газа
~ p. Однако для разреженного газа ![]() не зависит от давления, поэтому
не зависит от давления, поэтому
![]() ~
~ ![]() . Коэффициент
внутреннего трения
. Коэффициент
внутреннего трения ![]() прямо пропорционален
прямо пропорционален ![]() .
.
В этом случае переносимой физической характеристикой является энергия молекулы <φ> = (i/2)kT. В таком случае
![]() , (13.15)
, (13.15)
![]() , (13.16)
, (13.16)
где ΔQ - количество теплоты, переносимое за время Δt сквозь площадку ΔS, перпендикулярную направлению убывания температуры. Тогда
![]() , (13.17)
, (13.17)
обозначив
![]() ,
,![]() ,
,
получим уравнение теплопроводности или закон Фурье:
![]() . (13.18)
. (13.18)
Коэффициент пропорциональности χ
называется коэффициентом теплопроводности. Коэффициент теплопроводности не зависит от давления, т.к. ![]() ~
~ ![]() , а
, а ![]() ~ p.
Однако для сильно разреженного газа
~ p.
Однако для сильно разреженного газа ![]() не зависит от давления, поэтому χ
~ p.
Зависимость теплопроводности от давления
в разреженном газе используется в устройстве термоса (сосуда Дьюара).
не зависит от давления, поэтому χ
~ p.
Зависимость теплопроводности от давления
в разреженном газе используется в устройстве термоса (сосуда Дьюара).
Коэффициент теплопроводности χ прямо пропорционален <v>, λ и теплоемкости единицы объема.
Соотношения между коэффициентами переноса: η ≈ Dρ; χ ≈ ηcv ≈ Dρcv.
Внешнее сходство математических выражений явлений переноса обусловлено общностью лежащего в основе теплопроводности, диффузии и внутреннего трения молекулярного механизма перемешивания молекул в процесс их хаотического движения столкновений друг с другом.
14 Лекция. Элементы механики сплошных сред
Цель лекции:
- ознакомление с действием сил, изменяющих форму и размеры реального тела;
-введение величин, объясняющих явление деформации твердого тела.
14.1 Упрощенные модели реальных систем
В классической механике широко используются три основных модели: 1) материальная точка;
2) абсолютно твердое тело;
3) сплошная среда.
В первой модели пренебрегают размерами, формой и внутренним строением макротела; во второй учитывают размеры и форму, но пренебрегают деформацией и внутренним строением тела; в третьей учитывают размеры, форму и деформацию тела , но пренебрегают его атомно-молекулярным строением. Плодотворность перечисленных моделей доказывается совпадением с высокой, хотя и не абсолютной, точностью выводов механики с экспериментом для очень широкого круга задач.
14.2 Деформация твердого тела
Деформация называется упругой, если после прекращения действия внешних сил тело принимает первоначальные размеры и форму. Деформации, которые сохраняются в теле после прекращения действия внешних сил, называются пластическими или остаточными. Деформации реального тела всегда пластические, так как они после прекращения действия внешних сил никогда полностью не исчезают. Если остаточные деформации малы, то ими можно пренебречь и рассматривать упругие деформации.
14.3 Напряжение. Относительная деформация. Модуль Юнга. Закон Гука
В теории упругости доказывается, что все виды деформаций (растяжение, или сжатие, сдвиг, изгиб, кручение) могут быть сведены к одновременно происходящим деформациям растяжения или сжатия и сдвига.
Рассмотрим
однородный стержень длиной ![]() и площадью сечения S, к
концам которого приложены направленные вдоль его оси силы
и площадью сечения S, к
концам которого приложены направленные вдоль его оси силы ![]() , в результате чего длина
стержня меняется на величину
, в результате чего длина
стержня меняется на величину ![]() . При растяжении
. При растяжении ![]() положительно, а при сжатии
отрицательно.
положительно, а при сжатии
отрицательно.
Сила, действующая на единицу площади поперечного сечения, называется напряжением:
![]() .
(14.1)
.
(14.1)
Если сила направлена по нормали к поверхности, напряжение называется нормальным, если же по касательной к поверхности – тангенциальным.
Количественной мерой, характеризующей степень деформации, испытываемой телом, является его относительная деформация. Так, относительное изменение длины стержня(продольная деформация)
![]() .
(14.2)
.
(14.2)
Относительное поперечное растяжение (сжатие)
![]() ,
(14.3)
,
(14.3)
где d – диаметр стержня.
Деформации
![]() и
и ![]() всегда имеют разные
знаки (при растяжении
всегда имеют разные
знаки (при растяжении ![]() положительно, а
положительно, а ![]() отрицательно и наоборот). Из
опыта вытекает взаимосвязь:
отрицательно и наоборот). Из
опыта вытекает взаимосвязь:
![]() ,
(14.4)
,
(14.4)
где
![]() -
положительный коэффициент, зависящий от свойств материала и называемый
коэффициентом Пуассона.
-
положительный коэффициент, зависящий от свойств материала и называемый
коэффициентом Пуассона.
Английский физик Р. Гук экспериментально установил, что для малых деформаций справедливо
![]() ,
(14.5)
,
(14.5)
где коэффициент пропорциональности Е называется модулем Юнга.
Из выражения (14.5) видно, что модуль Юнга определяется напряжением, вызывающем относительное удлинение, равное единице.
Из формул (14.2), (14.3) и (14.1) вытекает, что
![]()
или
![]() ,
(14.6)
,
(14.6)
где k - коэффициент упругости.
Выражение (14.6) также задает закон Гука, согласно которому удлинение стержня при упругой деформации пропорционально действующей на стержень силе.
14.4 Потенциальная энергия растяжения (сжатия)
Потенциальная энергия упругорастянутого (сжатого) стержня равна работе, совершаемой внешними силами пр деформации:
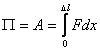 ,
,
где x - абсолютное удлинение стержня, в процессе деформации.
Используя закон Гука (14.6) и интегрируя имеем:
![]() ,
(14.7)
,
(14.7)
т.е. потенциальная энергия растянутого (сжатого) стержня пропорциональна квадрату деформации.
Деформацию сжвига можно осуществить, если взять брусок, имеющий форму прямоугольного параллелепипеда, и приложить силу, касательную к его поверхности, при этом относительная деформация сдвига определяется из формулы
![]() .
(14.8)
.
(14.8)
где
![]() -
абсолютный сдвиг параллельных слоев тела относительно друг друга, h расстояние
между слоями (для малых углов
-
абсолютный сдвиг параллельных слоев тела относительно друг друга, h расстояние
между слоями (для малых углов ![]() ).
).
15 Лекция. Элементы механики жидкости
Цель лекции:
-ознакомление с единым подходом к изучению движения жидкостей и газов;
-объяснение уравнения Бернулли и следствий из него.
15.1 Давление в жидкости и газе
Гидроаэродинамика – раздел механики, изучающий равновесие и движение жидкостей и газов, их взаимодействие между собой и обтекаемыми ими твердыми телами, - использует единый подход к изучению жидкостей и газов.
В механике с большой степенью точности жидкости и газы рассматриваются как сплошные, непрерывно распределенные в занятой ими части пространства. Плотность же газов от давления зависит существенно. Сжимаемостью жидкости и газа во многих задачах можно пренебречь и пользоваться единым понятием несжимаемой жидкости - жидкости, плотность которой всюду одинакова и не меняется со временем.
Если
в покоящуюся жидкость поместить тонкую пластинку, то части жидкости,
находящиеся по разные стороны от нее, будут действовать на каждый ее элемент ![]() с силами
с силами ![]() , которые независимо
от того, как пластинка ориентирована, будут равны по модулю и направлены
перпендикулярно площадке
, которые независимо
от того, как пластинка ориентирована, будут равны по модулю и направлены
перпендикулярно площадке ![]() , так как наличие касательных сил привело
бы частицы жидкости в движение.
, так как наличие касательных сил привело
бы частицы жидкости в движение.
Физическая величина, определяемая нормальной силой, действующей со стороны жидкости на единицу площади, называется давлением p жидкости:
![]() . (15.1)
. (15.1)
Единица
давления – паскаль (1 Па = 1 Н/![]() ).
).
Давление при равновесии жидкостей (газов) подчиняется закону Паскаля: давление в любом месте покоящейся жидкости одинаково по всем направлениям, причем давление одинаково передается по всему объему, занятому покоящейся жидкостью
Рассмотрим,
как влияет вес жидкости на распределения давления внутри покоящейся несжимаемой
жидкости. При равновесии жидкости давление по горизонтали всегда одинаково,
иначе не было бы равновесия. Поэтому свободная поверхность покоящейся жидкости
всегда горизонтальна вдали от стенок сосуда. Тогда при поперечном сечении S столба
жидкости, его высоте h и плотности ![]() весе
весе ![]() , а давление на нижнее основание
, а давление на нижнее основание
![]() ,
(15.2)
,
(15.2)
т.е. давление изменяется линейно с высотой. Давление, определяемое формулой (15.2), называется гидростатическим давлением. Согласно формуле (15.2), сила давления на нижние слои жидкости будет больше, чем на верхние, поэтому на тело, погруженное в жидкость, действует сила, определяемая законом Архимеда: на тело, погруженное в жидкость (газ), действует со стороны этой жидкости направленная вверх выталкивающая сила, равная весу вытесненной телом жидкости (газа):
![]() ,
(15.3)
,
(15.3)
где![]() - плотность жидкости,
V объем погруженного в жидкость тела.
- плотность жидкости,
V объем погруженного в жидкость тела.
15.2 Уравнение неразрывности
Движение жидкостей называется течением, а совокупность частиц движущейся жидкости – потоком. Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, чтобы густота их, характеризуемая отношением числа линий к площади, перпендикулярной им площадки, через которую они проходят, была больше, где больше скорость течения жидкости, и меньше там, где жидкость течет медленнее.
Часть жидкости, ограниченную линиями тока, называют трубкой тока. Течение жидкости, называется установившимся (или стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются
Рассмотрим
какую-либо трубку тока. Выберем два ее сечения ![]() и
и ![]() , перпендикулярные направлению скорости.
За время
, перпендикулярные направлению скорости.
За время ![]() через
сечение S проходит объем жидкости
через
сечение S проходит объем жидкости ![]() ; следовательно, за 1 с через
; следовательно, за 1 с через ![]() пройдет объем
жидкости
пройдет объем
жидкости ![]() ,
через сечение
,
через сечение ![]() за
1 с -
за
1 с - ![]() .
Если жидкость несжимаема (
.
Если жидкость несжимаема (![]() ), то выполняется соотношение:
), то выполняется соотношение:
![]() . (15.4)
. (15.4)
Соотношение (15.4) называется уравнением неразрывности для несжимаемой жидкости.
15.3 Уравнение Бернулли
Выделим в стационарно текущей идеальной жидкости трубку тока,
ограниченную
сечениями ![]() и
и
![]() , по которой
слева направо течет жидкость. За малый промежуток времени
, по которой
слева направо течет жидкость. За малый промежуток времени ![]() жидкость перемещается от
сечения
жидкость перемещается от
сечения ![]() к
сечению
к
сечению ![]() ,
от
,
от ![]() к
к ![]()
Согласно
закону сохранения энергии, изменение полной энергии ![]() идеальной несжимаемой жидкости
должно быть равно работе А внешних сил по перемещению массы
идеальной несжимаемой жидкости
должно быть равно работе А внешних сил по перемещению массы ![]() жидкости:
жидкости:
![]() . (15.5)
. (15.5)
С
другой стороны, А - это работа, совершаемая при перемещении всей жидкости,
заключенной между сечениями ![]() и
и ![]() за рассматриваемый малый промежуток
времени
за рассматриваемый малый промежуток
времени ![]() .
Для перенесения массы
.
Для перенесения массы ![]() от
от ![]() до
до ![]() жидкость должна переместиться на
расстояние
жидкость должна переместиться на
расстояние ![]() и
от
и
от ![]() до
до ![]() - на расстояние
- на расстояние ![]() .
.![]()
![]() и
и ![]() настолько малы, что всем точкам
соответствующих объемов приписывают постоянные значения скорости
настолько малы, что всем точкам
соответствующих объемов приписывают постоянные значения скорости ![]() , давления
, давления ![]() и высоты
и высоты ![]() . Следовательно,
. Следовательно,
![]() , (15.6)
, (15.6)
где
![]() и
и ![]() (отрицательна, так как
направлена в сторону, противоположную течению жидкости).
(отрицательна, так как
направлена в сторону, противоположную течению жидкости).
Полные
энергии будут складываться из кинетической и потенциальной энергии массы ![]() жидкости:
жидкости:
![]() , (15.7)
, (15.7)
![]() . (15.8)
. (15.8)
Используя (15.5) - (15.8) , получим
![]() . (15.9)
. (15.9)
Согласно уравнению неразрывности для несжимаемой жидкости (15.4), объем, занимаемый несжимаемой жидкостью, остается постоянным, т.е.
![]() . (1510)
. (1510)
Разделив выражение (15.9) на (15.10), получим
![]() , (15.11)
, (15.11)
где
![]() плотность
жидкости.
плотность
жидкости.
Так как сечения выбирались произвольно, можно записать
![]() . (15.12)
. (15.12)
Выражение (15.12) выведено швейцарским физиком Д.Бернулли и называется уравнением Бернулли. Как видно из его вывода, уравнение Бернулли – выражение закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Оно хорошо выполняется и для реальных жидкостей, внутренне трение которых, не очень велико.
Величина
![]() в формуле
(15.12) называется статическим давлением, величина
в формуле
(15.12) называется статическим давлением, величина ![]() динамическим давлением,
динамическим давлением, ![]() гидростатическое
давление.
гидростатическое
давление.
Для
горизонтальной трубки тока (![]() ) выражение (15.12) принимает вид:
) выражение (15.12) принимает вид:
![]() , (15.13)
, (15.13)
которое называется полным давлением.
Отметим, что данный конспект лекции по дисциплине «Физика» даст возможность обеспечить необходимый минимум знаний студента согласно государственному общеобразовательному стандарту высшего образования (ГОСО РК 6.08.06802009) для специальности 5В074600 – Космическая техника и технологии.
Список литературы
1 Савельев И.В. Курс физики: в 3-х т. -М., 1989.
2 Трофимова Т.И. Курс физики. -М., 1998.
3. Детлаф А.А., Яворский Б.М. Курс физики. -М.: Высш. шк., 2004.
4. Трофимова Т.И. Курс физики. - М.: Высш. шк., 2006.
5. Матвеев А.Н. Электричество и магнетизм. - М.: Высш.шк., 1983.
6. Курс физики. Под ред. Лозовского В.Н. – СПб.: Лань, 2001. – т. 1.
7. Курс физики. Под ред. Лозовского В.Н. – СПб.: Лань, 2001. – т. 2.
8. Иродов И.Е. Основные законы механики.- М.: Высш. шк., 1997.
9. Иродов И.Е. Электромагнетизм. Основные законы. - М.: Физматлит., 2000.
10. Джанколи Дж. Физика. - М.: Мир, 1989, т.1-2.
Сборники задач:
11. Чертов А.Г., Воробьев А.А. Задачник по физике.- М.: Высш. шк., 1981/ 2007.
12. Иродов И.Е. Задачи по общей физике.- М.: Физматлит., 2006.
13. Физика. Задания к практическим занятиям/ под ред. Лагутиной Ж.П. – Минск: Вышэйшая школа, 1989.
14. Савельев И.В. Сборник вопросов и задач по общей физике. - М.: Наука, 1988.
15. Трофимова Т.И. Сборник задач по курсу физики для втузов. - М.: Оникс 21 век, 2003.
16. Волькенштейн В.С. Сборник задач по общему курсу физики.– СПб.: Книжный мир, 2003.
Св.план 2012 г., поз. 312