Некоммерческое акционерное общество

АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра физики

ФИЗИКА ЭЛЕКТРОМАГНИТНЫХ ВОЛН И АТОМА

Конспект лекций

для студентов всех форм обучения специальностей

5В074600 – Космическая техника и технологии

Алматы 2012

СОСТАВИТЕЛИ: Т.Д. Дауменов, М.Ш. Карсыбаев, А.И. Кенжебекова. Физика электромагнитных волн и атома. Конспект лекций для студентов всех форм обучения специальности 5В074600 ––Космическая техника и технологии - Алматы: АУЭС, 2012 – с.

Излагается краткое содержание лекций по дисциплине «Физика электромагнитных волн и атома» для студентов бакалавриата специальности 5В074600 ––Космическая техника и технологии.

Конспект лекций «Физика электромагнитных волн и атома» представляет собой еще один элемент системы методического обеспечения учебного процесса по дисциплине и может быть использован в качестве раздаточного материала на лекционных занятиях, а также в самостоятельной работе над теоретическим материалом при подготовке к практическим, лабораторным занятиям и экзаменам.

Ил. , табл. , библиогр. – назв.

Рецензент: канд. физ.-мат. наук, доц.

Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2012 г.

Ó НАО «Алматинский университет энергетики и связи», 2012 г.

Содержание

Содержание
Введение
1 Лекция. Система уравнений Максвелла
1.1 Несовместимость закона сохранения зарядов с уравнением непрерывности. Токи смещения
1.2 Максвеллова трактовка закона электромагнитной индукции
1.3 Дифференциальная форма записи закона электромагнитной индукции
1.4 Система уравнений Максвелла
1.5 Относительность электрического и магнитного полей
2 Лекция. Система уравнений Максвелла для квазистационарной области электромагнитного поля
2.1 Условие квазистационарности электромагнитного поля
2.2 Уравнения Максвелла для квазистационарной области электромагнитного поля
2.3 Скин –эффект
3 Лекция. Электромагнитные волны
3.1 Уравнения Максвелла для электромагнитных волн. Волновое уравнение
3.2 Решения волновых уравнений. Свойства плоских электромагнитных волн
4 Лекция. Закон сохранения электромагнитных волн. Излучение электромагнитных волн
4.1 Закон сохранения электромагнитных волн. Теорема Пойнтинга
5 Лекция. Свет как электромагнитная волна. Отражение и преломление плоских электромагнитных волн в диэлектриках
5.1 Неизменность частоты электромагнитной волны при отражении и преломлении
5.2 Закон Снеллиуса
5.3 Связь между интенсивностями падающей, отраженной и преломленной волн
6 Лекция. Интерференция света
6.1 Принцип суперпозиции волн. Интерференционный член
6.2 Временная и пространственная когерентность
6.3 Методы наблюдения интерференции света
6.4 Излучение диполя
7 Лекция. Дифракция волн 7.1 Принцип Гюйгенса-Френеля
7.2 Метод зон Френеля
7.3 Дифракция на одной и многих щелях
7.4 Спектральное разложение
7.5 Временная и пространственная когерентность
7.6 Методы наблюдения интерференции света
8 Лекция. Дисперсия света
8.1 Волновой пакет. Групповая скорость. Связь между фазовой и групповой скоростями
8.2 Вынужденное колебание связанного электрона в электрическом поле
8.3 Диэлектрическая проницаемость среды
8.4 Показатель преломления среды 8.5 Поглощение (абсорбция) света
9 Лекция. Поляризация света
9.1 Естественный и поляризованный свет
9.2 Закон Малюса
9.3 Закон Брюстера
10 Лекция. Корпускулярно-волновой дуализм вещества как универсальное свойство материи. Уравнение Шредингера
10.1 Гипотеза де Бройля и ее экспериментальное подтверждение Корпускулярные свойства электромагнитного излучения
10.2 Волновые свойства микрочастиц и соотношение неопределенностей Гейзенберга
10.3 Уравнение Шредингера. Состояние частицы в квантовой механике. Пси-функция. Временное и стационарное уравнения Шредингера
11 Лекция. Решение уравнения Шредингера для простейших квантовых систем. Задача о частице в одномерной прямоугольной яме
11.1 Уравнение Шредингера для бесконечно глубокой ямы
11.2 Собственные значения задачи
11.3 Собственные функции задачи
11.4 Принцип соответствия Бора
12 Лекция. Атом водорода. Энергетический спектр атома водорода
12.1 Потенциальная энергия взаимодействия. Уравнение Шредингера
12.2 Квантовые числа
12.3 Спин электрона
13 Лекция. Принцип Паули. Распределение электронов в атоме по состояниям
13.1 Принцип тождественности одинаковых частиц
13.2 Принцип Паули
13.3 Распределение электронов в атоме по состояниям
13.4 Полный момент импульса электрона в атоме
13.5 Формула тонкой структуры термов
14 Лекция. Спектр гелия. Парагелий и ортогелий
14.1 Гипотеза об орто – и парагелиев
14.2 Синглетные и триплетные состояния гелия
14.3 Вентильный фотоэффект
15 Лекция. Теория периодической системы Д.И. Менделеева
15.1 Квантовые числа
15.2 Принцип Паули и идеальная система элементов
Список литературы

Введение

«Физика электромагнитных волн и атома. Конспект лекций» представляет собой изложение содержания материала лекций по этой дисциплине и предназначен для студентов 5В074600 ––Космическая техника и технологии, которые обучаются по программам бакалавриата на факультете ФРТиС.

Курс «Физика электромагнитных волн и атома» включает в себя некоторые разделы классической и современной физики. Ясная физическая и мировоззренческая интерпретация представлений классической и современной физики формирует у студентов способность перестраивать свое мышление к восприятию неизбежных трансформаций старых научных и технических представлений в принципиально новые.

В каждой лекции отражены основные вопросы темы в их логической связи и структурной целостности, но без детальной проработки математических выкладок или примеров. Поэтому данная учебно-методическая разработка может и должна служить лишь ориентировочной основой для учебной деятельности студента при подготовке к практическим занятиям, рубежному и итоговому контролю.

1 Лекция. Система уравнений Максвелла

1.1 Несовместимость закона сохранения зарядов с уравнением непрерывности. Токи смещения

Закон сохранения электрического заряда в дифференциальной форме имеет вид

, (1.1)

а уравнение непрерывности, выражающее условие замкнутости постоянного тока записывается следующим образом

. (1.2)

Видно, что уравнение (1.2) противоречит закону сохранения электрического заряда (1.1). Чтобы устранить это противоречие, Максвелл предположил, уравнение непрерывности (1.2) должен быть записан для полного тока:

, (1.3)

где

(1.4)

Продифференцируем по времени соотношение

или ввиду уравнения (1.1):

. (1.5)

Из сравнения формул (1.3), (1.4) и (1.5) получим выражение для плотности токов смещения введенной Максвеллом в следующем виде:

(1.6)

Известная теорема о циркуляции напряженности магнитного поля

может быть преобразована в дифференциальную форму

в которой вместо плотности тока проводимости должен быть записан плотность полного тока, тогда теорема о циркуляции магнитного поля примет вид:

. (1.7)

Последняя формула является обобщенным законом Био-Савара-Лапласа в дифференциальной форме.

1.2 Максвеллова трактовка закона электромагнитной индукции

Когда проводник движется в постоянном магнитном поле, индукционный ток вызывается магнитной составляющей силы Лоренца. Какая же сила возбуждает индукционный ток в неподвижном проводнике, находящемся в переменном магнитном поле? Ответ был дан Максвеллом. Согласно Максвеллу, всякое изменение магнитного поля во времени возбуждает в окружающем пространстве электрическое поле. Циркуляция вектора напряженности этого поля по любому неподвижному замкнутому контуру определяется выражением

. (1.8)

Между максвелловым и фарадеевым пониманием явления электромагнитной индукции имеется существенное различие. Согласно Фарадею, электромагнитная индукция состоит в возбуждении электрического тока. Для ее наблюдения необходимо наличие замкнутого проводника. Максвелл, напротив, видит сущность электромагнитной индукции, прежде всего в возбуждении электрического поля, а не тока. Электромагнитная индукция может наблюдаться и тогда, когда в пространстве вообще нет никаких проводников. Появление индукционного тока в замкнутом проводнике при внесении последнего в переменное магнитное поле есть лишь одно из проявлений электрического поля, возникшего в результате изменения поля магнитного. Но поле может производить и другие действия, например, поляризовать диэлектрик, вызвать пробой конденсатора, ускорять и тормозить заряженные частицы и т. п. Оно может вызвать электрический ток и в незамкнутом проводнике.

Максвеллова формулировка закона индукции более общая, чем формулировка Фарадея. Она принадлежит к числу наиболее важных обобщений электродинамики.

1.3 Дифференциальная форма записи закона электромагнитной индукции

Математически закон индукции в понимании Максвелла выражается формулой (1.8), где интеграл берется по замкнутому контуру, который может быть проведен и в диэлектрике, а не обязательно в проводнике, как было у Фарадея. Магнитный поток определяется интегралом

, (1.9)

взятым по произвольной поверхности S, натянутой на контур . Поэтому формулу (1.8) можно представить в виде

. (1.10)

Применив к последнему выражению теорему Стокса, получим

. (1.11)

Это - дифференциальная форма закона электромагнитной индукции. Уравнение (1.10) или эквивалентное ему уравнение (1.11) – одно из основных соотношений теории электромагнитного поля. Оно входит в систему уравнений Максвелла.

1.4 Система уравнений Максвелла

Дополнив основные факты из области электромагнетизма установлением магнитных действий токов смещения, Максвелл мог написать систему фундаментальных уравнений электродинамики. Таких уравнений четыре.

В интегральной форме они имеют вид

, (I)

, (II)

, (III)

. (IV)

В дифференциальной форме

, (Iа)

, (IIа)

, (IIIа)

. (IVа)

Уравнения Максвелла показывают, что источниками электрического поля могут быть либо электрические заряды, либо магнитные поля, меняющиеся во времени. Магнитные же поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Максвелла в интегральной форме справедливы и в тех случаях, когда существуют поверхности разрыва, на которых свойства среды или напряженности электрического и магнитного полей меняются скачкообразно. Поэтому в этой форме уравнения Максвелла обладают большей общностью, чем в дифференциальной форме, которая предполагает, что все величины в пространстве и во времени меняются непрерывно. Поэтому дифференциальные уравнения Максвелла должны быть дополнены граничными условиями

(1.12)

Здесь - поверхностная плотность электрических зарядов, а - поверхностная плотность тока проводимости на рассматриваемой границе раздела.

В случаях, когда поверхностные заряды и токи отсутствуют, граничные условия (1.12) преобразуются к виду

(1.13)

Отметим, что уравнения Максвелла не могут быть выведены. На них следует смотреть как на основные аксиомы классической электродинамики, полученные путем обобщения опытных фактов.

1.5 Относительность электрического и магнитного полей

К электромагнитному полю применим только принцип относительности Эйнштейна, так как факт распространения электромагнитных волн в вакууме во всех системах отсчета с одинаковой скоростью не совместим с принципом относительности Галилея.

Из принципа относительности вытекает, что отдельное рассмотрение электрического и магнитного полей имеет относительный смысл. Так, если электрическое поле создается системой неподвижных зарядов, то эти заряды, являясь неподвижными относительно одной инерциальной системы отсчета, движутся относительно другой и, следовательно, будут порождать не только электрическое, но и магнитное поле. Аналогично, неподвижный относительно одной инерциальной системы отсчета проводник с постоянным током, возбуждая в каждой точке пространства постоянное магнитное поле, движется относительно других инерциальных систем, и создаваемое им переменное магнитное поле возбуждает вихревое электрическое поле.

2 Лекция. Система уравнений Максвелла для квазистационарной области электромагнитного поля

2.1 Условие квазистационарности электромагнитного поля

А) Заметим, что внутри проводников, в частности внутри металлов, плотность токов смещения обычно настолько мала по сравнению с плотностью токов проводимости:

. (2.1)

что без ущерба для точности вычислений можно ими вообще пренебречь.

Предположим, например, что мы имеем дело с периодическим током частоты

. (2.2)

Токи смещения определяются по формуле

. (2.3)

А ток проводимости в отсутствии сторонних сил записывается в виде

. (2.4)

При этом выполняются соотношения

(2.5)

Чтобы выполнялось условие (2.1), необходимо выполнения следующего выражения

. (2.6)

Если рассматриваемая среда является металлом, тогда из-за условие (2.6) оценивается следующим образом

. (2.7)

Условие (2.7) выполняется в металлах для всех частот, применяемых в технике (в том числе и радиотехнике), и нарушается лишь в области частот, соответствующих инфракрасной части спектра.

Б) Изменение электромагнитного поля происходит так медленно, что можно пренебречь эффектом запаздывания, который обусловлен конечностью распространения электромагнитных волн. Это условие может быть выражено математически рассмотрением распространения плоских электромагнитных волн в направлении оси со скоростью . Электрический вектор может быть записан в виде:

. (2.8)

Поскольку линейные размеры рассматриваемой области жстаточно малы, множитель может быть разложен в ряд:

. (2.9)

Согласно последнего равенства, если его правая часть независима от координаты , только при этом эффектом запаздывания можно пренебречь, т.е.:

. (2.10)

Тогда условие квазистационарности электромагнитного поля записывается в виде:

. (2.11)

Таким образом, при достаточной малости рассматриваемой области эффектом запаздывания можно пренебречь. Например, для технической частоты 50 Гц длина волны равна 6000 км., значит для такой частоты размеры области квазистационарности составляет несколько тысяч километров.

2.2 Уравнения Максвелла для квазистационарной области электромагнитного поля

В квазистационарной области электромагнитного поля уравнения Максвелла в произвольнй среде записываются следующим образом:

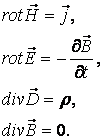(2.12)

Здесь

В квазистационарной области электромагнитного поля связь между электрическими и магнитными полями осуществляется законом электромагнитной индукции Фарадея, поэтому эти поля не могут быть рассмотрены отдельно друг от друга. Согласно условиям (2.6), (2.11) связью, обусловленной токами смещения можно пренебречь.

2.3 Скин –эффект

В отличие от постоянного тока переменный ток не распределяется равномерно по сечению проводника, а концентрируется на его поверхности. Это явление получившее название скин-эффекта (английское слово - кожа), ток концентрируется на «коже» проводника.

Рассмотрим элементарную теорию этого эффекта. На протяжении однородного проводника величины будем считать постоянными. Считая, что сторонние силы отсутствуют, используя уравнения Максвелла

(2.13)

(2.14)

подставляя закон Ома

(2.15)

в правую часть уравнения (2.13), а также образовав операцию ротор с обеих частей и воспользовавшись уравнением (2.14), получим для вектора дифференциальное уравнение в частных производных:

(2.16)

Здесь использованы выражения и учтена возможность замены местами дифференцие по координатам и времени.

Аналогичным путем можно получить такое же уравнение для вектора напряженности электрического поля

(2.17)

Обе величины удовлетворяют одному и тому же дифференциальному уравнению, поэтому ограничимся рассмотрением решения (2.17). Для простоты предположим, что однородный проводник занимает полупространство , а поверхность проводника совпадает с плоскостью (см.рисунок 2.1).

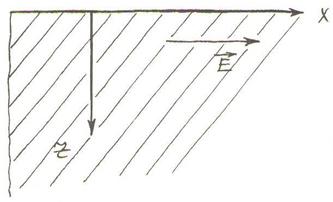
Рисунок 2.1

Пусть переменный ток частоты идет по оси :

(2.18)

Тогда по закону Ома будут справедливы следующие соотношения:

(2.19)

При этом уравнение (2.17) упрощается:

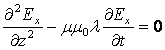(2.20)

Чтобы переменный ток протекал с частотой , необходимо изменение электрического поля со временем с такой же частотой. Следовательно, решение уравнения (2.20) будем искать в следующем виде:

(2.21)

Подстановка этого решения в уравнение (2.20) дает

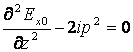(2.22)

для удобства введено обозначение

(2.23)

- вещественное число. Известно, что решение уравнения (2.22) ищется в виде

(2.24)

и - произвольные постоянные, а

(2.25)

или

(2.26)

С помощью последних соотношений выражение (2.24) примет вид:

(2.27)

Отметим, что произвольная постоянная должна быть равна нулю. Действительно, совпадает с поверхностью проводника, с ростом этой координаты электрическое поле должен расти бесконечно, что лишено физического смысла. Искомое решение уравнения (2.20) окончательно может быть представлено выражением:

(2.28)

Действительная часть которого можно записать в виде:

(2.29)

А плотность тока выражается следующим образом:

(2.30)

Здесь обозначает плотность тока на поверхности проводника. Согласно последним соотношениям с углублением во внутрь проводника фазы электрического вектора и плотности тока меняются по линейному закону, а их амплитуды падают по экспоненциальному закону . Практически плотность переменного тока на расстоянии от поверхности проводника, равном

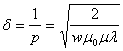(2.31)

уменьшается раз (примерно 2,7 раз). Это расстояние может быть названо толщиной проникновения поля, соответственно переменного тока. Чтобы оценить величину рассмотрим следующий пример, для металлов ,

тогда

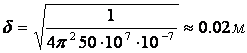
А при , примерно.

Приведенные оценки показывают, что при высоких частотах скин-эффект значительно влияет на распределение переменного тока по сечению проводника. Для постоянного тока , поэтому плотность тока и напряженность поля по толщине проводника сохраняет свое постоянное значение. Приведенная элементарная теория может быть применена проводникам цилиндрической формы. Можно показать, что и в этом случае с повышением частоты ток концентрируется на тонкой поверхности проводника, при этом сопротивление провода должно стать равным сопротивлению полого цилиндра, обладающего стенками соответствующей толщины, т.е. сопротивление переменному току будет увеличиваться.

Практическое значение скин-эффекта велико, он позволяет принимать выгодное с точки зрения экономики и технологии решение, например, для внутренней части проводника использовать недорогие металлы и напылением их дорогими металлами с малыми сопротивлениями, где будут протекать токи высокой частоты. Кроме того, во внутренней области провода отсутствует магнитное поле, поэтому из-за уменьшения энергии магнитного поля, при неизменной силе тока, уменьшается индуктивность проводника.

3 Лекция. Электромагнитные волны

3.1 Уравнения Максвелла для электромагнитных волн. Волновое уравнение

Электромагнитные волны – это оторванные от своих источников электромагнитные поля (), поэтому уравнения Максвелла примут следующий вид:

, (3.1)

, (3.2)

, (3.3)

. (3.4)

При распространении электромагнитных волн в непроводящей среде (), эти уравнения запишутся следующим образом:

, (3.1а)

, (3.2а)

, (3.3а)

. (3.4а)

Образуем операцию rot с обеих сторон выражения (3.2а) и учитывая формулу (3.1а) можно записать

тогда из-за уравнения (3.3а) получим для вектора напряженности электрического поля следующее дифференциальное уравнение в частных производных второго порядка:

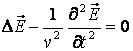. (3.5)

Здесь скорость распространения электромагнитных волн в непроводящей среде (в диэлектриках).

Аналогичным образом можно получить такое же уравнение для вектора напряженности магнитного поля

. (3.6)

Из последних формул следует, что как электрический вектор, так и магнитный вектор удовлетворяют одному и тому же дифференциальному уравнению. Эти уравнения принято назвать волновыми уравнениями.

3.2 Решения волновых уравнений. Свойства плоских электромагнитных волн

Можно показать, что решениями волновых уравнений (3.5), (3.6) плоские электромагнитные волны распространяющиеся в произвольном направлении

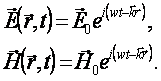(3.7)

или сферические волны

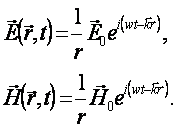(3.8)

Здесь амплитуды волн, - частота, - волновой вектор, показывающий направление распространения волны.

Чтобы исследовать свойства плоских волн, выражения (3.7) нужно подставить в уравнения (3.5), (3.6) соответственно, при этом надо учесть, что для произвольного вектора операции rot, div можно представить в виде:

Применение к векторам операции равносиьно умножению этих векторов на величину –, это видно из следующего примера:

т.е.

аналогично

Равенство нулю скалярного произведения векторов:

(3.9)

Означает, что каждый из векторов перпендикулярен вектору , т.е. как электрический вектор, так и магнитный вектор лежат в плоскости, перпендикулярной к направлению распространения волны.

Теперь, перепишем уравнение Максвелла (3.2а), используя выше описанную методику:

Последнее соотношение можно привести к следующему виду:

. (3.10)

где -единичный вектор, в направлении распространения волны .

Видно, что векторы взаимно перпендикулярны и они оба перпендикулярны вектору . Тогда можно констатировать тот факт, что , образуют взаимно перпендикулярную правовинтовую систему векторов (рисунок 3.1):

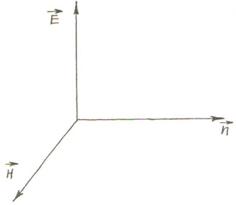
Рисунок 3.1

Рассмотрение модуля обеих сторон равенства (3.10)

. (3.11)

Дает возможность заключить, что векторы и меняются со временем синхронно и синфазно.

4 Лекция. Закон сохранения электромагнитных волн. Излучение электромагнитных волн

4.1 Закон сохранения электромагнитных волн. Теорема Пойнтинга

Уравнения электромагнитных волн (3.1) – (3.4) показывают изменения векторов электромагнитного поля со временем, однако эти уравнения не могут быть экспериментаьно проверены каждое в отдельности. Эти уравнения приобретут определенное физическое содержание лишь в том случае, если будет точно указано, в каких явлениях, доступных наблюдению и изучению на опыте, и каким именно образом проявляется существование электромагнитных волн. Руководствуясь принципом сохранения энергии, мы заключаем, что возникновение или исчезновение известных нам форм энергии должно происходить за счет преобразования некоторой иной формы энергии, которую мы называем энергией электромагнитного поля W:

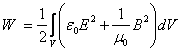. (4.1)

Выразив энергию электромагнитной волны в форме объемного интеграла (4.1), мы тем самым получаем возможность истолковать это выражение в том смысле, что энергия волны вполне опеделенным образом локализована в пространстве, причем объемная плотность энергии в произвольном месте определяется выражением:

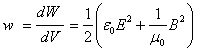. (4.2)

Рассмотрим изменение во времени количества энергии W, находящегося внутри объема , ограниченного некоторой неподвижной замкнутой поверхностью и предположим, что в этой области отсутствуют заряды и токи (электромагнитная волна – это электромагнитное поле, оторванное от своих источников):

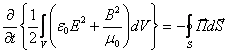. (4.3)

Здесь использованы следующие формулы из векторного анализа

а также известные соотношения

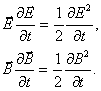
Причем введено обозначение:

(4.4)

Исходя из представленияо локализации электромагнитной энергии в пространстве, мы должны на основании этого обстоятельства заключить, что электромагнитная энергия вытекает через поверхность S из рассматриваемого объема V наружу и притом в количестве единиц энергии в секунду. Это положение носит название теоремы Поинтинга, а вектор называется вектором Пойнтинга. Таким образом, уравнение (4.3) выражает собой закон сохранения энергии электромагнитных волн. Используем уравнение ()

. (4.5)

Откуда следует, что отношение численных значений векторов и от времени не зависит, т.е. векторы эти обладают одинаковыми фазами и изменяются синхронно. Согласно уравнению (4.5) также следует, что плотность магнитной энергии в поле волны оказывается равной плотности энергии электрической. При этом абсолютное значение вектора Пойнтинга может быть представлено следующим образом:

. (4.6)

Таким образом, количество энергии протекающее в единицу времени через единичную площадку, перпендикулярную к вектору Пойнтинга (т.е. перпендикулярную к направлению волны), количеству энергии за единицу времени, это значит, что скорость течения энергии совпадает с фазовой скоростью волны.

4.2 Осциллятор. Излучение осциллятора

Известно, что произвольно сложной, но в целом нейтральной системы зарядов на больших расстояниях от этой системы просто выражается с помощью вектора электрического (дипольного) момента p. Если дипольный момент системы меняется со временем ее принято назвать осциллятором.

Согласно представлениям классической электродинамики электромагнитные волны возбуждаются электрическими зарядами, движущимися с ускорением. Простейшей излучающей системой является электрический диполь, момент которого изменяется периодически.

Рассмотрим излучение гармонического осциллятора – элементарного диполя, размер ℓ которого много меньше длины волны ℓ<<λ, а электрический момент изменяется со временем по гармоническому закону

p=p_mcosωt . (4.7)

Примером такой системы служит неподвижный точечный заряд +q и колеблющийся около него точечный заряд – q. Вблизи диполя картина электромагнитного поля очень сложная. Она упрощается в так называемой волновой зоне диполя, то есть на расстояниях r, значительно превышающих длину волны r>>λ. Если волна распространяется в однородной и изотропной среде, то волновые поверхности в волновой зоне имеют сферическую форму. Направление векторов E и H в каждой точке перпендикулярно к лучу; при этом E направлен по касательной к «меридиану», а H – по касательной к «параллели» (см.рисунок 4.1).

В каждой точке векторы E и H колеблются по закону cos(ωt-kr), иначе говоря, заряд, совершающий гармонические колебания с частотой ω, излучает монохроматическую волну той же частоты. Амплитуды E_mи H_m зависят от расстояния r до излучателя и от угла между направлением радиус-вектора и осью диполя, для вакуума эта зависимость имеет вид:

E_m ~H_m~. (4.8)

Рисунок 4.1

Интенсивность волны равна:

I~. (4.9)

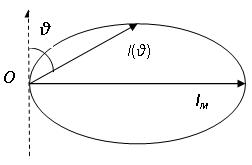
Из (4.9) следует, что интенсивность волны изменяется вдоль луча обратно пропорционально квадрату расстояния r. Кроме того, она сильно зависит от угла . На рисунке 4.2 приведена полярная диаграмма направленности излучения. Вдоль оси диполя излучение отсутствует (I=0), а в направлениях, перпендикулярных к оси, интенсивность излучения максимальна.

Теоретические расчеты показывают, что мощность излучения диполя (энергия, излучаемая в единицу времени) пропорциональна квадрату второй производной дипольного момента по

Рисунок 4.2

времени: P~, (4.10)

для гармонически осциллирующего диполя:

P~ p_m²ω⁴cos²ωt. (4.11)

Усреднение за период колебания T=2π/ω дает:

<P>~ p_m²ω⁴. (4.12)

Таким образом, средняя мощность излучения диполя пропорциональна квадрату амплитуды его дипольного момента и четвертой степени частоты.

При решении некоторых проблем в оптике (дисперсия, поглощение в средах, поляризация) атом рассматривают как излучающий диполь, в котором оптический электрон совершает колебания около ядра. Также, всякая реальная передающая антенна может быть представлена как совокупность точечных диполей.

5 Лекция. Свет как электромагнитная волна. Отражение и преломление плоских электромагнитных волн в диэлектриках

Согласно теории Максвелла свет – электромагнитное излучение, длины волн которого лежат в пределах от 0,001 мкм до 100 мкм, то есть свет, в широком смысле слова, включает ультрафиолетовую, видимую и инфракрасную области спектра. Длины волн видимого света лежат в интервале от 380 нм до 770 нм (в вакууме), а частоты занимают диапазон ν=(0,39 . Белый свет – составной, он представляет собой наложение волн, длины λ которых охватывают весь диапазон воспринимаемых глазом электромагнитных волн.

5.1 Неизменность частоты электромагнитной волны при отражении и преломлении

Рассмотрим преломление и отражение плоских монохроматических электромагнитных волн на поверхности раздела двух однородных диэлектриков 1 и 2, используя граничные условия для векторов электромагнитной волны.

Пусть на плоскую границу раздела падает плоская волна, часть которой преломляется во вторую среду, а другая часть отражается (Рисунок 5.1). Обозначим все величины, относящиеся падающей волне индексами 10, отраженной – 11, а преломленной – 12, и запишем напряженности электрического поля для каждой из этих волн, аналогичные выражения для напряженностей магнитного поля записывать не будем.

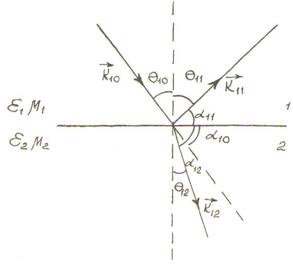
Рисунок 5.1

. (5.1)

. (5.2)

. (5.3)

Используем непрерывность тангенциальной составляющей электрического поля в следующем виде:

. (5.4)

Это условие удобно представить следующим образом:

. (5.5)

Величины и не зависят от времени. Производные по времени с обеих частей последнего выражения выглядят так:

. (5.6)

Теперь, заменим величину в правой части равенства , используя формулу (5.5):

. (5.7)

Последнее равенство должно выполняться для любого момента времени , это возможно при выполнении следующего равенства:

. (5.8)

Аналогичным образом, заменяя , можем получить

(5.8)

Это значит, что при отражении и преломлении частота электромагнитной волны не меняется:

. (5.10)

5.2 Закон Снеллиуса

Предположим, что радиус – вектор лежит на поверхности раздела между диэлектриками, это возможно , если в качестве начала координат выберем точку лежащую на этой поверхности. При этом условие (5.4) запишется в виде:

. (5.11)

Величины и –независимые. К обеим частям (5.11) применим операцию:

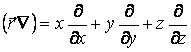
и учтем, что

Тогда:

. (5.12)

Величину в правой части этого выражения заменим с помощью (5.11):

. (5.13)

Поскольку величина лежит на границе раздела произвольным образом, равенство (5.13) выполняется при условии:

. (5.14)

Аналогичным образом, в формуле (5.12) заменяя величину с помощью (5.11), получим:

. (5.15)

Тогда

. (5.16)

Последнее равенство может быть переписано в виде:

. (5.17)

Скорости падающей, отраженной и преломленной волн обозначим соответственно через и . Они с учетом (5.10) связаны с волновыми числами следующими соотношениями:

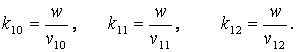(5.18)

Падающая и отраженная волны расположены в первой среде, поэтому:

Из-за (5.17) следует, что или , тогда выполняется равенство

. (5.19)

Т.е., угол падения равен углу отражения. Из выражений (5.18), (5.17) следует также равенство:

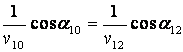Из-за , последнее равенство примет вид

(5.20)

С учетом выражений для скоростей падающей и преломленной волн , окончательно получим, что

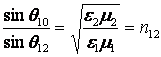. (5.21)

Отношение синусов углов падения и преломления равно относительному показателю преломления второй среды относительно первой. В оптике этот закон называют законом Снеллиуса.

5.3 Связь между интенсивностями падающей, отраженной и преломленной волн

Можно показать, что усредненная за период интенсивности волн могут быть представлены в виде:

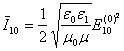, (5.22)

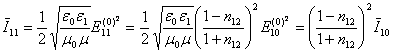, (5.23)

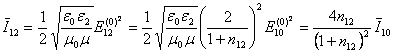. (5.24)

Формулы (5.22) – (5.24) называются формулами Френеля.

Они показывают связь между интенсивностями падающей, отраженной и преломленной волн:

(5.25)

Выражения (522) – (5.25) удовлетворяют закону сохранения, т.е. что средний за период поток энергии в падающей волне равен сумме средних потоков энергии в преломленной и отраженной волнах

6 Лекция. Интерференция света

6.1 Принцип суперпозиции волн. Интерференционный член

Пусть в некоторой области перекрываются две световые, то есть электромагнитные волны. В линейных средах и в вакууме взаимодействие между полями отсутствует. Поэтому волны распространяются независимо друг от друга и в области перекрытия имеет место суперпозиция полей

E=E₁+E₂ . (6.1)

В области, в которой перекрываются две световые волны, интенсивность волн запишется в виде

I=<(E₁+E₂ )²>= I₁ + I₂+2<E₁E₂>. (6.2)

Последнее слагаемое в выражении (6.2) называется интерференционным членом. Его величина может быть выражена в виде

<cosδ>, (6.3)

где δ – разность фаз складываемых колебаний.

Результаты сложения волн определяются тем, являются ли волны когерентными или нет:

а) если две волны излучаются двумя независимыми источниками, то разность фаз таких волн в каждой точке (например, экрана) непрерывно изменяется случайным образом, принимая с равной вероятностью любые значения от 0 до 2π, тогда <cos δ> = 0, І₁₂ = 0 и

I = I₁ + I₂ . (6.4)

Таким образом, при наложении некогерентных волн наблюдаемая интенсивность равна сумме интенсивностей каждой из волн в отдельности;

б) если разность фаз δ, возбуждаемых волнами колебаний, остается постоянной во времени, то волны называются когерентными и в этом случае

I=I₁ + I₂+2. (6.5)

Рассмотрим случай, когда обе волны строго монохроматичны и имеют одну и ту же частоту ω. Монохроматическая волна – это строго синусоидальная волна с постоянными во времени частотой ω, амплитудой A и начальной фазой φ; при этом амплитуда и начальная фаза могут меняться от одной точки пространства к другой, а частота одна и та же везде.

В точках пространства, где выполняется условие cos δ = 1, или

δ=0, 2π, 4π, 6π,…, (6.6)

при разности фаз, равной четному числу π, возникают максимумы интенсивности I_max =I₁ + I₂+2.

Минимумы возникают в таких точках, в которых cos δ = -1, значит, условие образования интерференционного минимума имеет вид:

δ=π, 3π, 5π,…, (6.7)

то есть, разность фаз должна быть равна нечетному числу π. При этом

I_min =I₁ + I₂- 2 .

Таким образом, при наложении когерентных волн происходит перераспределение потока в пространстве, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности. Это явление называется интерференцией волн.

Частным случаем интерференции является образование стоячей волны. Стоячая волна образуется при наложении двух когерентных волн, распространяющихся в противоположных направлениях.

Пусть вдоль оси OX распространяются во встречных направлениях две монохроматические с частотой ω и одинаковой амплитудой A₀ волны

E₁=A₀cos(ωtkx) и E₂=A₀cos(ωt+kx).

В результате их наложения образуется волна

E =E₁ + E₂ = 2 A₀coskx·cosωt. (6.8)

Амплитуда полученной волны определяется выражением

‌. (6.9)

В отличие от бегущей волны амплитуда стоячей волны зависит от координаты x. В точках, в которых │coskx‌│= 1, амплитуда удваивается (максимальна) и равна 2A₀, а в точках, где │coskx‌│= 0, амплитуда равна нулю (минимальна). Эти точки называют соответственно пучностями и узлами стоячей волны.

6.2 Временная и пространственная когерентность

Излучение обычных источников (не лазеров) некогерентно; это обусловлено тем, что оно складывается из волн, излучаемых громадными совокупностями его атомов. Процесс излучения атома продолжается в течение времени, длительностью порядка 10^-8 с. За это время успевает образоваться цуг волн длиной примерно 3 м. Свет от обычного источника представляет хаотичную последовательность отдельных цугов. Поэтому при наложении световых волн от разных источников фазовые соотношения между колебаниями многократно изменяются случайным образом, и устойчивой интерференционной картины не возникает.

Тем не менее, когерентные световые волны можно получить даже от обычных источников. Общий метод таков: волну, излучаемую одним источником света, разделяют каким–либо способом на две части, которые затем в некоторой области пространства перекрываются. В области перекрытия происходит наложение интерференция расщепленных «половинок» элементарных волновых цугов, излученных отдельными атомами.

Оптическая длина пути L – это произведение расстояния ℓ, которое проходит волна в некоторой среде, на показатель n преломления в данной среде . Разность оптических длин проходимых волнами путей от точки расщепления до точки их наложения называют оптической разностью хода:

. (6.10)

Связь между разностью фаз двух волн и оптической разностью хода

. (6.11)

Тогда условие образования интерференционных максимумов:

, m=0, 1, 2, 3,… (6.12)

Интерференционные минимумы наблюдаются, если волны приходят в противофазе, при этом оптическая разность хода равна нечетному числу полуволн:

, m=0, 1, 2, 3,… (6.13)

Когерентностью называется согласованное протекание нескольких колебательных или волновых процессов.

Согласованное протекание волновых процессов, происходящих в одной и той же точке, но в разные моменты времени, называют временной когерентностью. Промежуток времени τ_ког, в течение которого случайные изменения начальной фазы волны в данной точке достигают значения порядка π, называется временем когерентности. За это время колебание становится некогерентным по отношению к самому себе. Расстояние, на которое перемещается волна за время τ_ког, называют длиной когерентности . Следовательно, расщепленные волны, приходящие в точку наблюдения с разностью хода, равной или превышающей ℓ_ког, не образуют интерференционной картины, т.к. некогерентны.

Соответствующий расчет дает, что время когерентности обратно пропорционально интервалу частот , представленных в данной световой волне: . Это означает, что чем уже интервал частот, представленных в данной световой волне, тем больше время когерентности этой волны. Для монохроматической волны и время когерентности .

Длину когерентности можно оценить с помощью соотношения . Для солнечного света λ=0,50 мкм (зеленая часть спектра) и Δλ=0,40 мкм, тогда

ℓ_ког≈(0,50)²/0,40 мкм ≈0,6 мкм=0,6·10^{-3 мм.}

Пространственная когерентность – это согласованное протекание колебательных процессов, которые совершаются в один и тот же момент времени в разных точках поверхности, перпендикулярной направлению распространения волны (так называемой квазиволновой поверхности). Пространственная когерентность зависит от условий излучения и формирования световых волн. В реальной световой волне, излучаемой множеством независимых атомов протяженного источника света, разность фаз колебаний в двух точках квазиволновой поверхности Q, - случайная функция времени.

Радиусом когерентности ρ_ког называют расстояние между двумя точками поверхности Q, случайные изменения разности фаз δ, в которых достигают порядка π. Если источник имеет форму диска, диаметр которого виден из данной точки под углом φ, то. Для Солнца φ≈0,01 рад, λ≈0,50 мкм, ρ_ког≈0,05 мм.

6.3 Методы наблюдения интерференции света

6.3.1 Опыт Юнга. В опыте Юнга пучок яркого солнечного света пропускался через узкую щель S. Прошедшим светом освещались две узкие параллельные и близко расположенные щели S₁ и S₂ во втором непрозрачном экране. На экране в области перекрытия пучков наблюдались параллельные чередующиеся темные и светлые интерференционные полосы.

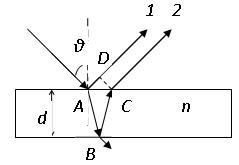Расстояние между двумя соседними максимумами интенсивности называют расстоянием между интерференционными полосами, а расстояние между соседними минимумами интенсивности – шириной интерференционной полосы. Расстояние между полосами и ширина полосы имеют одинаковое значение, равное

Рисунок 6.1 . (6.14)

Где d – расстояние между щелями, l – расстояние от щелей до экрана, - длина волны.

6.3.2 Интерференция в тонких пленках. Пусть на плоскопараллельную пленку толщины d с показателем преломления n падает параллельный пучок монохроматического света с длиной волны λ₀.При отражении от обеих поверхностей пленки разность хода между волнами 1 и 2 (см. рисунок 6.1) равна

«Потеря» полуволны обусловлена тем, что при отражении от оптически более плотной среды (с бóльшим показателем преломления n) фаза отраженной волны скачком изменяется на , а при отражении от оптически менее плотной среды – не изменяется.

После геометрических преобразований и с учетом закона преломления света:

. (6.15)

6.3.3 Кольца Ньютона. При отражении света от поверхностей зазора между стеклянной пластиной и прижатой к ней плоско-выпуклой линзой наблюдаются кольца Ньютона. При нормальном падении света интерференционная картина имеет вид чередующихся темных и светлых концентрических колец. В отраженном свете в центре картины - темное пятно; радиусы темных колец:

, (6.16)

где m - номер кольца, m=1, 2, 3, …;

R – радиус кривизны линзы.

7 Лекция. Дифракция волн

7.1 Принцип Гюйгенса-Френеля

В однородных и изотропных средах распространение волн происходит прямолинейно и подчиняется законам геометрической оптики.

В средах с резкими неоднородностями, например, вблизи краев непрозрачного экрана или отверстия, наблюдается дифракция - огибание волнами препятствий (соизмеримыми с длиной волны падающего света) и проникновение в область геометрической тени.

Рисунок 7.1

Для объяснения и расчета дифракционных явлений в теории волн применяется принцип Гюйгенса-Френеля.

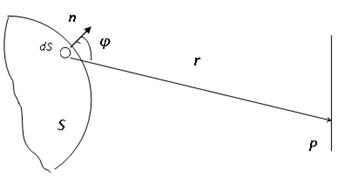
Согласно принципу Гюйгенса-Френеля каждый элемент волновой поверхности (в общем случае - любой вспомогательной поверхности, до которой доходит излучение) dS можно рассматривать как источник вторичной сферической волны. Поскольку эти вторичные волны являются составными частями единой исходной волны, они когерентны между собой, поэтому в произвольной точке наблюдения P, в которую приходят вторичные волны, будет происходить их наложение (интерференция), в результате чего волны либо усиливают друг друга, либо гасят.

Амплитуда вторичной волны пропорциональна площади элемента волновой поверхности dS, на расстоянии r от него она убывает по закону 1/r. Следовательно, от каждого элемента волновой поверхности в точку наблюдения P (см.рисунок 8.1) приходит колебание светового вектора

dE=K(φ)cos(ωt-kr+α), (7.1)

где (ωt+α) – фаза колебания в месте расположения поверхности S;

r – расстояние от элемента dS поверхности до точки P;

A – множитель, определяемый амплитудой световой волны в том месте, где находится площадка dS;

K(φ) – коэффициент, зависящий от угла φ между нормалью n к площадке dS и направлением от нее к точке P. При φ =0 этот коэффициент максимален, при φ = π/2 он обращается в нуль.

Результирующее колебание в точке P представляет собой суперпозицию колебаний (8.1), взятых по той части волновой поверхности S, которая открыта для точки наблюдения P:

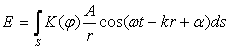. (7.2)

Формула (7.2) - аналитическое выражение принципа Гюйгенса – Френеля.

7.2 Метод зон Френеля

В тех случаях, когда источники света имеют симметричную форму и соответственной симметрией обладают волновые поверхности излучаемых ими волн, амплитуду результирующего колебания можно найти простым алгебраическим или геометрическим суммированием.

Этот простой и эффективный метод носит название метода зон Френеля и заключается в следующем. В качестве вспомогательной поверхности выбирается одна из волновых поверхностей (во всех точках которой фазы волны одинаковы). Эта поверхность разбивается на участки, называемые зонами Френеля, таким образом, чтобы разность хода волн от внутреннего и внешнего краев каждого участка до точки наблюдения была равна половине длины волны λ/2. В некоторых случаях вместо точки наблюдения задается некоторое направление в пространстве, тогда половине длины волны должна равняться разность хода волн от краев участка в данном направлении.

Рассмотрим метод зон Френеля на примере точечного источника света S, волновые поверхности которого представляю собой (в однородной и изотропной среде) концентрические сферы. Рассмотрим одну из этих сфер, удаленную от точки наблюдения на расстоянии b. Разобьем эту волновую поверхность на кольцевые зоны таким образом, что расстояния от краев (внутреннего и внешнего) каждой зоны отличались на λ/2. Ясно, что расстояние от края первой (центральной) зоны до точки P, равно (b+λ/2), а от внешнего края m–ой зоны – (b+mλ/2).

Колебания, приходящие в точку P от аналогичных участков (например, лежащих в середине зон, или у внешних краев) двух соседних зон, приходят в противофазе. Поэтому и результирующие колебания, создаваемые каждой из зон в целом, будут для соседних зон отличаться по фазе на π. Следовательно, вторичные волны двух соседних зон будут приходить в точку наблюдения в противофазе и при наложении друг друга гасить.

Точный расчет дает, что площади кольцевых зон при не слишком больших m примерно одинаковы. Расстояние b_m от зоны до точки P медленно растет с ростом номера m. Все это приводит к тому, что амплитуда A_m колебания, возбуждаемого m–ой зоной в рассматриваемой точке P, монотонно убывает с ростом m, так что

A₁> A₂>A₃>A₄> … > A_m-1>A_m>A_m+1> …

Вследствие монотонного убывания амплитуд оказывается, что амплитуда A_m колебания от некоторой m–й зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон

A_m=. (7.3)

Фазы колебаний, возбуждаемых соседними зонами, отличаются на π, поэтому амплитуда A результирующего колебания в точке P может быть представлена в виде знакопеременного ряда

A= A₁– A₂ + A₃ – A₄+ A₅- … (7.4)

Перепишем выражение (6.4) следующим образом

(7.5)

С учетом соотношения (7.3) при m→ ∞ (на пути от источника S до экрана P нет никаких препятствий) выражение (7.5) упрощается

A= A₁/2. (7.6)

Полученное соотношение означает, что амплитуда, создаваемая в некоторой точке P всей сферической волновой поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной.

Рисунок 7.2

Если на пути волны поставить непрозрачную преграду с вырезанным в ней круглым отверстием, оставляющим открытой лишь одну центральную зону, то амплитуда в точке P будет равна A₁, то есть в два раза будет больше, чем A. Соответственно интенсивность света в этом случае будет в четыре раза больше, чем в отсутствие преград между источником и экраном (между точками S и P).

Внешний радиус m–ой кольцевой зоны можно определить по формуле

. (7.7)

Из соотношения (7.4) следует, что если между источником S и экраном P находится круглая диафрагма (отверстие в непрозрачной преграде), то интенсивность света в точке наблюдения P – центре дифракционной картины - будет зависеть от того, сколько зон укладываться в этом отверстии.

Минимумы интенсивности будут наблюдаться при четном числе зон m =2,4,6,… (поскольку колебания от каждой пары соседних зон взаимно гасят друг друга), а максимумы – при нечетном числе зон m =1,3,5,… В целом, дифракционная картина от круглого отверстия имеет вид чередующихся светлых и темных колец

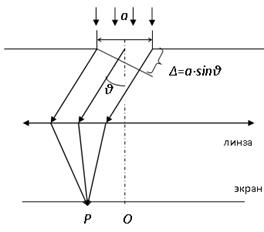
Рисунок 7.3

7.3 Дифракция на одной и многих щелях

Пусть на узкую длинную щель шириной a падает по нормали к ней плоская световая волна. Поместим за щелью собирающую линзу, а в фокальной плоскости линзы - экран (см.рисунок 7.3).

Дифракционная картина на экране при освещении узкой щели монохроматическим светом от лазера представляет собой систему симметрически расположенных вдоль прямой линии светлых (того же цвета, что и лазерное излучение) пятен, при этом в центре картины располагается максимум, по интенсивности значительно превосходящий остальные максимумы. Максимумы разделены минимумами.

Дифракционные минимумы наблюдаются при таких углах дифракции θ, для которых в щели укладывается четное число зон Френеля:

, (7.8)

где m – порядок минимума, принимает значения 1, 2, 3, …

Дифракционная решетка представляет собой совокупность большого числа расположенных в одной плоскости, отстоящих друг от друга на одно и то же расстояние, одинаковых параллельных щелей.

Расстояние d между серединами соседних щелей называется периодом (или постоянной) решетки. Период решетки равен сумме ширины щели a и непрозрачного промежутка между щелями: d=a+b.

Для получения более четкой дифракционной картины между дифракционной решеткой и экраном располагают собирающую линзу так, что экран находится в ее фокальной плоскости (см.рисунок 7.4).

При прохождении через дифракционную решетку имеет место, во-первых, интерференции световых волн, дифрагировавших на каждой щели в отдельности; во-вторых, интерференция волн, дифрагировавших от разных щелей. При этом положение минимумов (7.8), соответствующих дифракции на одной щели, остается неизменным и при дифракции на N щелях.

Положение главных дифракционных максимумов при нормальном падении параллельного пучка монохроматического света длиной волны λ на дифракционную решетку определяется из формулы:

dsinθ = mλ , m=0, 1, 2, 3, …, m_пред , (7.9) где m_пред– наибольший порядок наблюдаемого максимума, равный целому числу , ближайшему к отношению d/λ с меньшей стороны.

7.4 Спектральное разложение

Положение дифракционных максимумов (кроме центрального) зависит от длины волны λ. Поэтому при падении на решетку немонохроматического (например, белого) света разным длинам волн будут соответствовать сдвинутые относительно друг друга максимумы, то есть все максимумы ненулевого порядка (m=1, 2,…) разложатся в спектр.

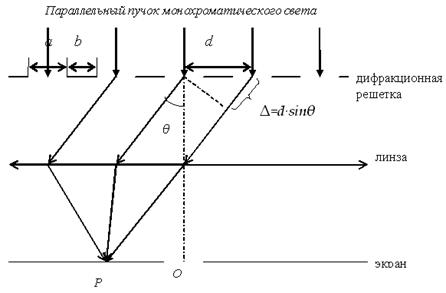
Рисунок 7.4

Таким образом, дифракционная решетка позволяет установить спектральный состав направленного на нее излучения и потому представляет собой спектральный прибор. Если излучение состоит из нескольких монохроматических волн, например, λ₁ и λ₂, то и каждый из максимумов (кроме центрального) будет состоять из отдельных (двух - в нашем примере) спектральных линий; причем очень важно, что максимумы для каждой длины волны (при большом числе N щелей в дифракционной решетке) получаются очень узкими. Поэтому решетка – это спектральный прибор высокого разрешения.

В отличие от стеклянной призмы дифракционная решетка:

а) сильнее отклоняет не фиолетовые, а наоборот, красные лучи – с большей длиной волны λ;

б) равномерно растягивает спектр, в то время как призма – неравномерно, т. к. длинноволновая (красная) часть ее спектра сжата, а коротковолновая (фиолетовая) более растянута.

8 Лекция. Дисперсия света

8.1 Волновой пакет. Групповая скорость. Связь между фазовой и групповой скоростями

Фазовая скорость волны определяется как

(8.1)

Волновой пакет – это группа близких по волновым числам и по частотам монохроматических волн, амплитуды и фазы которых таковы, что в любой момент времени их сложение дает локализованный в некотором объеме пространства одиночный волновой импульс.

Волновой пакет характеризуется средними значениями волнового числа k₀ и частоты ω₀, и интервалами ∆k и ∆ω в спектральных разложениях волнового пакета по волновым числам и частотам:

(k₀- ∆k) ≤ k ≥ (k₀+ ∆k), ∆k<< k₀, (ω₀- ∆ω) ≤ ω ≥ (ω₀+∆ω), ∆ω<< ω₀.

Установлено, что чем меньше временная длительность ∆t пакета, тем больше интервал частот ∆ω в его спектральном разложении; и - чем короче его пространственная протяженность Δx, тем больше интервал волновых чисел ∆k.

Пусть в одном направлении с одной и той же скоростью v распространяются две плоские гармонические волны с одинаковыми амплитудами A₀ и близкими по значению частотами (ω и ω+dω) и волновыми числами (k и k+dk).

Согласно принципу суперпозиции:

Формально полученное выражение можно рассматривать как уравнение квазигармонической волны с медленно периодически изменяющейся амплитудой:

. (8.2)

За скорость u распространения этой несинусоидальной волны принимают скорость перемещения точки M, в которой амплитуда имеет максимальное значение. Следовательно, точка M движется по закону (tdω-xdk)=const. Величина

(8.3)

называется групповой скоростью (скоростью группы волн). Поскольку в этой точке максимальна и плотность энергии, то групповая скорость и есть скорость перемещения энергии волны.

Связь между групповой и фазовой скоростями волны имеет вид:

. (8.4)

Явление дисперсии характеризуется зависимостью показателя преломления среды от частоты электромагнитных волн:

. (8.5)

Согласно теории Максвелла показатель преломления определяется как , поэтому при распространении электромагнитных волн в диэлектриках дисперсия отсутствует. Однако с точки зрения классической электронной теории (микроэлектродинамики) явление дисперсии может быть объяснено решением соответствующего дифференциального уравнения.

8.2 Вынужденное колебание связанного электрона в электрическом поле

Вынужденное колебание электрона во внешнем электрическом поле с амплитудой и частотой описывается уравнением:

, (8.6)

- коэффициент радиационного трения, – частота свободного колебания электрона. Это неоднородное дифференциальное уравнение второго порядка. Решение (8.6) (без сдвига фазы) может быть представлено в виде:

. (8.7)

Переменный дипольный момент колеблющегося электрона выражается формулой:

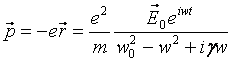. (8.8)

Предположим, что в единице объема вещества находятся независимых дру то друга электронов. Тогда вектор поляризованности можно записать в виде:

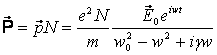. (8.9)

С одной стороны, вектор электрического смещения , напряженность электрического поля и вектор поляризованности связаны соотношением:

с другой стороны

8.3 Диэлектрическая проницаемость среды

Из последних формул найдем выражение для диэлектрической проницаемости среды :

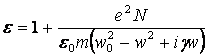. (8.10)

Видно, что диэлектрическая проницаемость зависит от частоты падающей волны, причем она оказалась комплексной величиной. Соответственно этому факту волновое число также будет комплексным:

Запишем комплексное волновое число в виде:

(8.11)

при этом электрический вектор падающей волны

с учетом (8.11) можно представить следующим образом:

. (8.12)

Т.е., вещественная часть комплексного вектора будет волновым вектором, а мнимая часть характеризует ослабление волны при поглощении ее средой, или усиление волны активной средой.

8.4 Показатель преломления среды

Из формулы (8.10) найдем выражение для показателя преломления среды . В разряженных газах и средах с малой концентрацией электронов справедливо неравенство:

. (8.13)

поэтому:

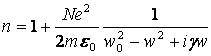, (8.14)

Представим комплексную проницаемость , выделяя ее вещественную и мнимую части:

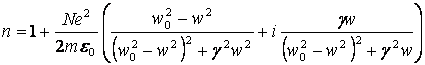. (8.15)

Ее вещественная часть характеризует показатель преломления диспегирущей среды ( рисунок 8.1).

Рисунок 8.1

Несмотря на простоту рассмотренной модели формула (8.16) достаточно полно характеризует диспергирующие свойства разряженных газов и некоторых растворов.

Особенностью явления дисперсии является то обстоятельство, что в окрестности частоты показатель преломления испытывает быстрое возрастание (нормальная дисперсия), затем уменьшение скачком (область аномальной дисперсии) с последующим его возрастанием (снова нормальная дисперсия). Если в веществе имеются различные заряды, совершающие вынужденные колебания с различными собственными частотами , то

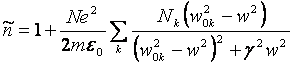. (8.17)

8.5 Поглощение (абсорбция) света

Поглощением ( абсорбцией) света называется явление уменьшения энергии световой волны при ее распространении в веществе вследствие преобразования энергии волны в другие виды энергии. В результате поглощения интенсивность света при прохождении через вещество уменьшается.

Поглощение света в веществе описывается законом Бугера:

, (8.18)

где и - интенсивности плоской монохроматической световой волны на входе и выходе слоя поглощающего вещества толщиной - коэффициент поглощения, зависящий от длины волны света, химической природы и состояния вещества и не зависящий от интенсивности света. При интенсивность света на выходе уменьшается в e раз.

Явление поглощения широко используются в абсорбционном спектральном анализе смеси газов, основанном на измерениях спектров частот и интенсивностей линий поглощения. Структура спектров поглощения определяется составом и строением молекул, поэтому изучение спектров поглощения является одним из основных методов количественного и качественного исследования веществ.

9 Лекция. Поляризация света

Следствием теории Максвелла является поперечность световых волн: векторы напряженностей электрического Е и магнитного Н полей волны взаимно перпендикулярны и колеблются перпендикулярно вектору скорости v распространения волны. Поэтому для описания закономерностей поляризации света достаточно знать поведение лишь одного из векторов. Обычно все рассуждения ведутся относительно светового вектора – вектора напряженности Е электрического поля.

9.1 Естественный и поляризованный свет

Свет представляет собой суммарное электромагнитное излучение множества атомов. Атомы же излучают световые волны независимо друг от друга, поэтому световая волна, излучаемая в целом, характеризуется всевозможными равновероятными колебаниями светового вектора (рисунок 9.1 а; луч перпендикулярен плоскости рисунка). В данном случае равномерное распределение векторов Е объясняется большим числом атомарных излучателей, а равенство амплитудных значений векторов Е – одинаковой интенсивностью излучения каждого из атомов. Свет со всевозможными равновероятными ориентациями вектора Е (также и Н) называется естественным.

Свет, в котором направления колебаний светового вектора каким-то образом упорядочены, называется поляризованным. Так, если в результате каких-либо внешних воздействий появляется преимущественное направление колебаний векторов Е (рисунок 9.1 б), то имеем дело с частично поляризованным светом. Свет, в котором вектор Е колеблется только в одном направлении, перпендикулярном лучу (рисунок 9.1 в), называется плоскополяризованным.

Степенью поляризации называется величина

(9.1)

где - соответственно максимальная и минимальная интенсивности частично поляризованного света, пропускаемого анализатором. Для естественного света = и Р = 0, для плоскополяризованного = 0 и Р = 1.

9.2 Закон Малюса

Естественный свет можно преобразовать в плоскополяризованный, используя так называемые поляризаторы, пропускающие колебания только определенного направления. В качестве поляризаторов могут быть использованы среды, анизотропные в отношений колебаний вектора Е, например природный кристалл – турмалин. Если направить естественный свет перпендикулярно турмалина (рисунок 9.2), вырезанный параллельно его оптической оси, то при вращении этого турмалина вокруг направления луча, никаких изменений интенсивности прошедшего через турмалин света не наблюдаем. Если на пути луча поставить вторую пластинку турмалина и вращать ее вокруг направления луча, то интенсивность света, прошедшего через пластинки, меняется в зависимости от угла между оптическими осями кристаллов по закону Малюса:

, (9.2)

где и - соответственно интенсивности света, падающего на второй кристалл и вышедшего из него. Следовательно, интенсивность прошедшего через пластинки света изменяется от минимума (полное гашение света) при (оптические оси пластинок перпендикулярны) до максимума при (оптические оси пластинок параллельны).

Если пропустить естественный свет через два поляризатора, главные плоскости которых образуют угол , то из первого выйдет плоскополяризованный свет, интенсивность которого ,. Тогда интенсивность света, прошедшего через два поляризатора равна:

. (9.3)

9.3 Закон Брюстера

Если естественный свет падает на границу раздела двух диэлектриков, то часть его отражается, а часть преломляется. Исследования показали, что в отраженном луче преобладают колебания, перпендикулярные плоскости падения, в преломленном – колебания, параллельные плоскости падения.

Степень поляризации зависит от угла падения лучей и показателя преломления. Шотландский физик Д. Брюстер установил закон, согласно которому при угле падения (угол Брюстера), определяемого соотношением

(9.4)

( - показатель преломления второй среды относительно первой), отраженный луч является плоскополяризованным (содержит только колебания, перпендикулярные плоскости падения). Преломленный же луч при угле падения Брюстера поляризуется максимально, но не полностью. Если свет падает на границу раздела под углом Брюстера, то отраженный и преломленный лучи взаимно перпендикулярны.

10 Лекция. Корпускулярно-волновой дуализм вещества как универсальное свойство материи. Уравнение Шредингера

10.1 Гипотеза де Бройля и ее экспериментальное подтверждение

Гипотеза де Бройля (1924 г.) – дуализм не является особенностью одних только оптических явлений, но имеет универсальное значение. Фотон обладает энергией

и импульсом

По идее де Бройля движение электрона или какой-либо другой частицы связано с волновым процессом, длина волны которого равна

, (10.1)

а частота

. (10.2)

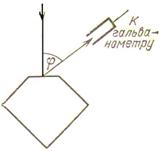Опыт Дэвиссон – Джермер (1927 г.) – отражение электронов от монокристалла никеля (кубическая система) (см.рисунок 10.1). Рассеяние оказалось особенно интенсивным при определенном значений угла рассеяния j, который соответствовал отражению от атомных плоскостей, расстояние между которыми d было известно из рентгенографических исследований (см.рисунок 10.2). Рисунок 10.1

Рисунок 10.2

Вычисленная по формуле (11.1) длина волны для максимального тока (U) равна 1,67 А. Брэгговская длина волны, отвечающая условию

2dSin,

равнялась 1,65 А. Опыты Дэвиссона – Джермера подтвердили идеи де Бройля.

В 1927 г. Г.П. Томсон и независимо от него П.С. Тартаковский получили дифракционную картину при прохождении электронного пучка через металлическую фольгу.

Было обнаружено, что дифракционные явления обнаруживаются также у атомных и молекулярных пучков.

Л.М. Биберман, Н.Г. Сушков, В.А. Фабрикант (1949 г.) – опыт со слабым электронным пучком.

10.2 Волновые свойства микрочастиц и соотношение неопределенностей Гейзенберга

В классической механике состояние материальной точки определяется заданием динамических переменных (координата, импульс, энергия и т.д.).

Своеобразие микрочастиц - при измерениях не для всех переменных получаются определенные значения:

. (10.3)

Любая микрочастица не может иметь одновременно точных значений координаты x и компоненты импульса р. Если одна из переменных имеет точное значение, другая переменная при этом оказывается совершенно неопределенной.

В.Гейзенберг (1927 г.): Произведение неопределенностей значений двух сопряженных переменных не может быть по порядку величины меньше постоянной Планка . (Принцип неопределенности Гейзенберга). Энергия Е и время t - также канонически сопряженные величины, поэтому

. (10.4)

10.3 Уравнение Шредингера. Состояние частицы в квантовой механике. Пси-функция. Временное и стационарное уравнения Шредингера

Э. Шредингер (1926 г.) – в развитие идеи де Бройля о волновых свойствах вещества получил свое временное уравнение

. (10.5)

- комплексная функция (пси- функция) координат и времени, характеризует состояние микрочастицы. Это основное уравнение нерелятивистской квантовой механики. Для стационарных состояний оно имеет вид:

. (10.6)

В квантовой механике большую роль играет понятие оператора. Под оператором подразумевают правило, посредством которого одной функции сопоставляется другая функция:

Здесь - символическое обозначение оператора. Под символом оператора скрывается совокупность действий, с помощью которых исходная функция (j) превращается в другую функцию (f). Оператор может, в частности, представлять собой умножение исходной функции на некоторую функцию U. Тогда = U и, следовательно, . Если рассматривать функцию U в уравнении (10.6) как оператор, действие которого на пси-функцию сводится к умножению на U, то уравнению (10.6) можно придать вид

. (10.7)

В этом уравнении символом обозначен оператор энергии Е, его называют оператором Гамильтона или гамильтонианом:

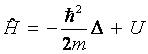. (10.8)

По Борну (1926 г.) квадрат модуля функции определяет вероятность dP того, что частица будет обнаружена в пределах объема dV

. (10.9)

А - коэффициент пропорциональности, для пси-функции выполняется следующее условие нормировки:

. (10.10)

Из смысла функции вытекает, что квантовая механика имеет статистический характер. Уравнение Шредингера позволяет найти пси – функцию данного состояния и, следовательно, определить вероятность нахождения частицы в различных точках пространства. Из уравнения (11.6) и условий, налагаемых на пси – функцию, непосредственно вытекают правила квантования энергии.

Пси – функция должна быть однозначной, непрерывной и конечной, кроме того она должна иметь непрерывную и конечную производную – стандартные условия.

В уравнение Шредингера входит в качестве параметра полная энергия частицы Е. В теории дифференциальных уравнений доказывается, что уравнения вида (10.6) имеют решения, удовлетворяющие стандартным условиям, не при любых значениях энергии Е, а лишь при некоторых избранных значениях. Эти избранные значения называются собственными значениями соответствующей величины, т.е. энергии. Решения, соответствующие собственным значениям Е, называются собственными функциями задачи. Совокупность собственных значений называется спектром величины. Если эта совокупность образует дискретную последовательность, спектр называется дискретным. Если собственные значения образуют непрерывную последовательность, спектр называют непрерывным или сплошным.

11. Лекция Решение уравнения Шредингера для простейших квантовых систем. Задача о частице в одномерной прямоугольной яме

Найдем собственные значения энергии и соответствующие им собственные функции для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме. Предположим, что частица может двигаться только вдоль оси x. Пусть движение ограничено непроницаемыми для частицы стенками: x = 0 и x =l. Потенциальная энергия в этом случае равна нулю при и обращается в бесконечность при x < 0 и x > l (см.рисунок 11.3а).

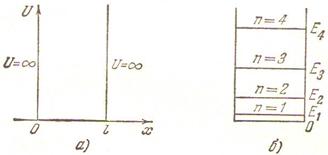
Рисунок 11.3

11.1 Уравнение Шредингера для бесконечно глубокой ямы

Уравнение Шредингера для такой задачи упрощается:

, (11.11)

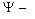функция удовлетворяет условию

, (11.12)

l - ширина ямы.

11.2 Собственные значения задачи

Можно показать, что собственные значения энергии частицы являются дискретными:

(n = 1, 2, 3, . . .). (11.13)

Таким образом, энергия частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т. е. квантуется (см.рисунок 11.3 б). Квантованные значения энергии называются уровнями энергии, а число n, определяющее энергетические уровни частицы, называется главным квантовым числом.

11.3 Собственные функции задачи

Собственные функции имеют вид:

(n =1, 2, 3, . . .). (11.14)

Рассмотрение плотности вероятности обнаружения частицы на различных расстояниях от «стенок» ямы показывает, что поведение микрочастицы указывает на то, что представления о траекториях в квантовой механике несостоятельны (см.рисунок 11.4 а,б).

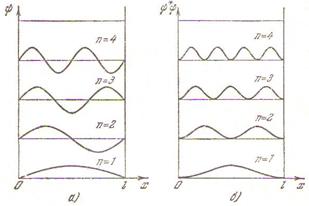
Рисунок 11.4

Из выражения (11.13) вытекает, что энергетический интервал между соседними уровнями равен

. (11.15)

11.4 Принцип соответствия Бора

Если рассмотреть относительное расстояние между уровнями DЕ_n/E_n~1/n,то будет иметь место сближение уровней с ростом n. Этот результат является частным случаем принципа соответствия Бора (1923 г.), согласно которому законы квантовой механики должны при больших значениях квантовых чисел переходить в законы классической физики. Более общая трактовка принципа соответствия: всякая новая, более общая теория, являющаяся развитием классической, не отвергает её полностью, а включает в себя классическую теорию, указывая границы её применения, причем в определенных случаях новая теория переходит в старую.

12 Лекция. Атом водорода. Энергетический спектр атома водорода.

Эта задача сводится к задаче о движении электрона в кулоновском поле ядра.

12.1 Потенциальная энергия взаимодействия. Уравнение Шредингера

Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze (для атома водорода Z = 1),

, (12.1)

где r - расстояние между электроном и ядром (рисунок 12.1). U(r) с уменьшением r (при приближении электрона к ядру) неограниченно убывает.

Рисунок 12.1

С учетом (10.6) стационарное уравнение Шредингера примет следующий вид:

(12.2)

где m – масса электрона;

Е – полная энергия электрона в атоме.

Поле, в котором движется электрон, является центрально -симметричным. Поэтому нужно воспользоваться сферической системе координат: r,

Можно показать, что уравнение (12.2), в сферической системе координат, имеет требуемые (т.е. однозначные, конечные и непрерывные) решения в следующих случаях:

1) при любых положительных значениях Е;

2) при дискретных отрицательных значениях энергии, равных:

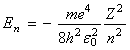(n = 1, 2, 3, …). (12.3)

Самый нижний уровень отвечающий минимальной возможной энергии, - основной, все остальные (n = 2,3, …) – возбужденные. При отрицательных энергиях движение электрона является связанным – он находится внутри гиперболической «потенциальной ямы». По мере роста главного квантового числа n энергетические уровни располагаются теснее и при n = При Е движение электрона является свободным, эта область непрерывного спектра соответствует ионизованному атому. Энергия ионизации атома водорода равна

Выражение (12.3) совпадает с аналогичной формулой, полученной Бором для энергии атома водорода. Однако если Бору пришлось вводить свои постулаты, то в квантовой механике дискретные значения энергии, являясь следствием самой теории, вытекают из решения уравнения Шредингера.

12.2 Квантовые числа

В квантовой механике доказывается, что уравнению Шредингера (12.2) удовлетворяют собственные функции , определяемые тремя квантовыми числами: главным n, орбитальным l , и магнитным .

Главное квантовое число n определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения, начиная с единицы:

n = 1,2,3, …

Из решения уравнения Шредингера вытекает, что момент импульса (механический орбитальный момент) электрона квантуется, т.е. не может быть произвольным, а принимает дискретные значения, определяемые формулой:

(12.4)

где l – орбитальное квантовое число, которое при заданном n принимает значения

l = 0,1, …, (n – 1),

т.е. всего n значений, и определяет момент импульса электрона в атоме.

Из решения уравнения Шредингера следует также, что вектор момента импульса электрона может иметь лишь такие ориентации в пространстве, при которых его проекция на направление z внешнего магнитного поля принимает квантованные значения, кратные :

(12.5)

где - магнитное квантовое число, которое при заданном l может принимать значения

(12.6)

т.е. всего 2l + 1 значений. Таким образом, магнитное квантовое число определяет проекцию момента импульса электрона на заданное направление, причем вектор момента импульса электрона в атоме может иметь в пространстве 2l + 1 ориентаций. Число различных состояний, соответствующих данному n, равно

(12.7)

Вероятность обнаружения электрона в различных частях атома различна. Электрон при своем движении как бы «размазан» по всему объему, образуя электронное облако, плотность которого характеризует вероятность нахождения электрона в различных точках объема атома. Квантовые числа n и l характеризуют размер и форму электронного облака в пространстве.

В атомной физике, по аналогии со спектроскопией, состояние электрона, характеризующееся квантовыми числами l = 0, называют s- состоянием, l = 1 – p- состоянием, l = 2 – d- состоянием, l = 3 – f- состоянием и т.д. Значение главного квантового числа указывается перед условным обозначением орбитального квантового числа. Например, электроны в состояниях с n = 2 и l = 0 и 1 обозначаются соответственно символами 2s и 2p.

Квантовые числа n, l, и позволяют более полно описать спектр испускания (поглощения) атома водорода, полученный в теории Бора.

В квантовой механике вводятся правила отбора, ограничивающие число возможных переходов электронов в атоме, связанных с испусканием и поглощением света:

1) изменение орбитального квантового числа удовлетворяет условию

(12.8)

2) изменение магнитного квантового числа удовлетворяет условию

(12.9)

12.3 Спин электрона

Опыты О. Штерна и В. Герлаха по прямым измерениям магнитных моментов в неоднородном магнитном поле (1922 г.).

Для объяснения тонкой структуры спектральных линий, а также ряда других трудностей в атомной физике американские физики Д. Уленбек и С. Гаудсмит предположили, что электрон обладает собственным неуничтожимым механическим моментом импульса, не связанным с движением электрона в пространстве, - спином.

Спин электрона (и всех других микрочастиц) – квантовая величина, у неё нет классического аналога; это внутреннее неотъемлемое свойство электрона, подобное его заряду и массе.

Если электрону приписывается собственный механический момент импульса (спин) , то ему соответствует собственный магнитный момент . Спин квантуется по закону

(12.10)

где s – спиновое квантовое число.

По аналогии с орбитальным моментом импульса, проекция спина квантуется так, что вектор может принимать 2s + 1 ориентаций. Так как в опытах Штерна и Герлаха наблюдались только две ориентаций, то 2s + 1 = 2, откуда S=1/2. Проекция спина на направление внешнего магнитного поля, являясь квантованной величиной, определяется выражением, аналогичным (12.5):

, (12.11)

где - магнитное квантовое число; оно может иметь только два значения:

Таким образом, опытные данные привели к необходимости характеризовать электроны (и микрочастицы вообще) добавочной внутренней степенью свободы. Поэтому для полного описания состояния электрона в атоме необходимо наряду с главным, орбитальным и магнитным квантовыми числами задавать ещё магнитное спиновое квантовое число.

13 Лекция Принцип Паули. Распределение электронов в атоме по состояниям

13.1 Принцип тождественности одинаковых частиц

В классической механике считается, что частицы, обладающие одинаковыми свойствами, принципиально различимы или индивидуализированы по местонахождению в пространстве. Это связано с тем, что их движение происходит по определенным траекториям, что дает принципиальную возможность проследить за движением каждой частицы.

Совсем иначе обстоит дело в квантовой механике, доказавшей неприменимость для микрочастиц классических представлений о движении частиц по траекториям. Состояние системы частиц описывается волнлвой функцией, которая имеет вероятностный смысл. Если две одинаковые микрочастицы поменять местами, то результат такого обмена никак нельзя обнаружить экспериментально. Одинаковые частицы в квантовой механике принципиально неразличимы.

Пусть для определенности система состоит из двух электронов и ее состояние в некоторый момент времени описывается функцией , причем через обозначена совокупность всех координат одной частицы, а через - совокупность координат другой частицы. Введем оператор перестановки P, действие которого состоит в том, что он меняет местами частицы. Подействовав этим оператором на функцию , мы получим функцию . В силу принципа тождественности одинаковых частиц мы не можем отличить получаемую систему от исходной. Другими словами, для невырожденных состояний волновая функция может отличаться от функции только постоянным множителем. Итак

(13.1)

Действуя оператором P второй раз мы, очевидно, придем к исходному состоянию

, (13.2)

откуда собственное значение оператора суть , а собственное значение оператора P суть . Следовательно,

(13.3)

мы теперь видим, что принцип тождественности одинаковых частиц ведет к определенному свойству симметрии волновой функции. Действительно, из (13.3) следует, что при перестановке частиц волновая функция не меняется, либо меняет знак. Волновая функция, которая не меняется при перестановке частиц, называется симметричной относительно этих частиц, волновая функция, которая при перестановке частиц меняет только свой знак, называется антисимметричной. Изменение знака волновой функции не означает изменения состояния, так как физический смысл имеет лишь квадрат модуля волновой функции. Установлено, что симметрия или антисимметрия волновых функций определяется спином частиц. В зависимости от характера симметрии все элементарные частицы и построенные из них системы (атомы, молекулы) делятся на два класса. Частицы с полуцелым спином (электроны, протоны, нейтроны) описываются антисимметричными волновыми функциями и подчиняются статистике Ферми-Дирака; эти частицы называются фермионами. Частицы с нулевым или целочисленным спином (мезоны, фотоны) описываются симметричными волновыми функциями и подчиняются статистике Бозе-Эйнштейна; эти частицы называются бозонами.

13.2 Принцип Паули

Если тождественные частицы имеют одинаковые квантовые числа, то их волновая функция симметрична относительно перестановки частиц. Для одинаковых фермионов, входящих в одну систему, не могут находиться в одинаковых состояниях, так как для фермионов волновая функция должна быть антисимметричной. Обобщая опытные данные, В. Паули сформулировал принцип, согласно которому системы фермионов встречаются только в состояниях, описываемых антисимметричными волновыми функциями. Другими словами, в системе одинаковых фермионов любые два из них не могут одноаременно находиться в одном и том же состоянии. Число однотипных бозонов, находящихся в одном и том же состоянии, не лимитируется.

13.3 Распределение электронов в атоме по состояниям

Состояние электронов в атоме определяется выбором четырех квантовых чисел:

главного n (n=1,2,3, …),

орбитального ,

магнитного ,

магнитного спинового

Распределение электронов в атоме подчиняется принципу Паули, который может быть использован в его простей шей формулировке: в одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых чисел , т.е.

или 1, (13.4)

где - число электронов, находящихся в квантовом состоянии, описываемым набором четырех квантовых чисел. Таким образом, принцип Паули утверждает, что два электрона, связанные в одном и том же атоме, различаются значениями по крайней мере одного квантового числа. Максимальное число электронов, находящихся в состояниях, определяемых данным квантовым числом, равно

. (13.5)

Совокупность электронов в многоэлектронном атоме, имеющих одно и то же главное квантовое число n, называют электронной оболочкой. В каждой из оболочек электроны распределяются по подоболочкам, соответствующим данному . Поскольку орбитальное квантовое число принимает значения от 0 до n-1, число подоболочек равно порядковому номеру n оболочки. Количество электронов в подоболочке определяется магнитным и магнитным спиновым квантовыми числами: максимальное число электронов в подоболочке с данным равно .

13.4 Полный момент импульса электрона в атоме

Отметим, что четверка квантовых чисел пригодна для описания состояния электрона лишь в том случае, когда все физические величины, связанные с ними, не меняются со временем. Однако орбитальное движение электрона создает магнитное поле H, с которым взаимодействует собственный магнитный момент электрона. Это взаимодействие называется спин-орбитальным. Мы ограничимся качественным рассмотрением этого взаимодействия, используя векторную модель атома.

Можно пользоваться полуклассическим методом рассуждения, при котором с квантомеханическими векторами моментов можно оперировать, как с обычными векторами, но с учетом квантования их абсолютных величин и проекций. Например, можно складывать векторы l и S по обычному правилу параллелограмма, суммарный вектор j = l+S есть полный момент импульса электрона. Но так как векторы l и S связаны через посредство соответствующих магнитных полей (спин-орбитальное взаимодействие), то они прецессируют относительно j, как два механических гироскопа, связанных упругой нитью прецессируют относительно направления своего неизменяемого полного момента импульса. В это чисто классическое рассуждение вносятся следующие поправки, характерные для евантовой механики. Во-первых, углы между l и S не могут быть произвольными, а ограничиваются требованиями пространственного квантования l и S , а именно вектор l (численно равный ) может располагаться относительно направления поля только под такими углами, чтобы проекция его была равна , а вектор S – под такими углами, чтобы проекция его равнялась . Тем самым угол между ограничивается дискретным рябом избранных значений. Во-вторых, полный момент импульса численно равен

(13.6)

Причем , т.е. для электрона . Таким образом, j есть квантовое число полного момента импульса. Проекция вектора j на направление поля равна

(13.7)

где может принимать 2j+1 значений j,j-1,…,-j.

13.5 Формула тонкой структуры термов

В спектроскопии принято обозначать различные энергетические состояния отдельных электронов и всего атома специальными символами, по которым сразу можно указать все квантовые числа. Для отдельных электронов главное квантовое число обозначается числовым коэффициентом, а квантовое число орбитального момента – следующей за ним буквой s , p, d, f хорошоизвестной нам схеме, наконец, квантовое число j дается в виде индекса справа внизу. Символ означает состояние электрона, в котором n = 3, l = 0, j = ½. Для атомов с одним излучающим электроном, т.е. для водородоподобных атомов и атомов первой группы периодической системы, энергетические состояния излучающего электрона и атома совпадают. Тем не менее принято обозначать термы атома вместо малых большими буквами S, P, D, F; кантовое число j дается, как у отдельного электрона, индексом справа внизу. Наконец, малой цифрой слева вверху обозначается кратность терма; например (читается «дублет Р»).

Из анализа спектров было установлено, что переходы происходят только между такими состояниями, у которых j имеет либо одно и то же значение, либо изменяется на :

. (13.8)

14 Лекция Спектр гелия. Парагелий и ортогелий

14.1 Гипотеза об орто – и парагелиев

Рассмотрим конкретные системы, состоящие из нескольких одинаковых частиц. Простейшим примером таких систем являются атомы или ионы, электронная оболочка которых состоит из двух электронов. Это – атом гелия и аналогичные ему ионы: и т. п.

Наиболее известная из спектральных линий гелия желтая линия - именно та линия, благодаря которой гелий был открыт впервые в спектре солнечных протуберанцев (18 августа 1866 г.), - на самом деле является триплетом с длинами волн в ангстремах:

Длины волн Относительная интенсивность

5875,963 1

5875,643 3

5875,601 5

Как видно, расстояние в шкале длин волн между двумя последними линиями составляет всего 0, 042 ангстрема, ввиду чего долгое время эти линии принимались за одну, и характерная линия считалась дублетом. Главная серия триплетов гелия лежат в инфракрасной части спектра. Напротив, соответствующие серии синглетов лежат преимущественно в ультрафиолетовой части спектра.

Ввиду такого резкого различия в характере спектральных серий и их дублирования первоначально была высказана гипотеза, что гелий на самом деле является смесью двух элементов, из которых один – именно тот, который дает триплетные серии и, в частности, линию - был назван ортогелием, а другой – дающий синглетные серии – парагелием.

Гипотеза эта оказалась, однако, неправильной. Дело в том, что возникновение двух сильно смещенных относительно друг друга замкнутых серий термов является следствием свойств симметрии системы двух электронов гелия, связанным с неразличимостью электронов, а причиной замкнутости серий является особое правило отбора _ так называемый запрет интеркомбинаций, в силу которого триплетные уровни комбинируются только с триплетными, а синглетные – только с синглетными.

14.2 Синглетные и триплетные состояния гелия

Рассмотрим атом гелия с точки зрения принципа Паули. Отметим, что, полная собственная функция является произведением координатных (орбитальных) и спиновых функций. В случае двух электронов мы имеем четыре возможности ориентации проекции спинов, причем каждый электрон в отношении спина может находиться в двух состояниях: с проекцией параллельной полю, со спиновой функцией , антипараллельной полю, со спиновой функцией . Для двух электронов можно составить четыре комбинации, удовлетворяющие требованию симметрии (значок С) или антисимметрии (значок А): . Орбитальные функции обозначим через . Тогда полных собственных функций , отличающихся симметрией будет восемь комбинаций: , . Из них 1-3 и 8 симметричные функции, 4-7 – антисимметричные. Нас будут интересовать только антисимметричные функции. Функции 5 соответствует параллельная комбинация спинов, для нее сумма проекций равна 1, для функции 7 сумма проекций -1. Можно убедиться в том, что у комбинации 6 полное квантовое число также равна единице. Три состояния 5, 6, 7 образуют одну группу, характеризуемую полным квантовым числом S = 1; это триплетное состояние. Что касается состояния 4, то для него только одна возможность, его полное квантовое число спина равна нулю; состояние 4 - синглетное. Мультиплетность определяется как 2S+1.

15 Лекция Теория периодической системы Д.И. Менделеева

15.1 Квантовые числа

Энергетическое состояние электрона в атоме характеризуется четырьмя квантовыми числами. В системе, состоящей из ядра и электронов, взаимодействующих по закону Кулона, в отсутствие поля все состояния с одинаковыми квантовыми числами и различными между собой совпадают (вырождение). Это вырождение исчезает в магнитном поле, причем в слабом поле каждый уровень с данным значением j распадается на 2j+1 подуровней. Сильное поле разрывает связь между векторами l и S, так что квантовое число j теряет смысл, и состояние характеризуется

системой квантовых чисел .

15.2 Принцип Паули и идеальная система элементов

Этот принцип для интересующего нас случая сформулируем следующим образом: в атоме может существовать только один электрон в состоянии, характеризуемом данными значениями четырех квантовых чисел, т.е. два электрона, связанные в одном и том же атоме, должны различаться значениями по крайней мере одного квантового числа. Максимальное число электронов с одинаковым квантовым числом выразится суммой, определяемой формулой (13.5).

Для того чтобы лучше уяснить себе это, полезно разобрать следующую таблицу:

Таблица 15.1

l = 0 1 2 3 4

s p d f g

Максимальное число электронов

2 +6

2 + 6 +10

2 + 6 +10 +14

2 + 6 +10 +14 + 18

Совокупность электронов, оьладающих одинаковым главным квантовым числом, образует слой. Совокупность электроновЮ имеющих одинаковые n и l, образуют оболочку. Для различных значений n слои имеют названия, связанные, с терминологией, принятой в спектроскопии рентгеновских лучей, а именно:

n 1 2 3 4 5

слой K L M N O

Из сказанного видно, что принцип Паули дает следующую картину построения электронной оболочки атомов, объясняющую периодичность системы элементов. Каждый вновь присоединяющийся электрон связывается в состоянии с наименьшими возможными квантовыми числами. Эти электроны постепенно заполняют слой с одним и тем же главным квантовым числом n.. Когда число их достигает максимальной для данного n величины, т.е. , построение слоя заканчивается, причем получается устойчивая структура (благородный газ). Следующий электрон начинает заполнение уже нового слоя и т. д.

Список рекомендуемой литературы:

Учебники:

1. Савельев И.В. Курс физики.- М.: Наука, 1989. - т. 2.

2. Савельев И.В. Курс физики.- М.: Наука, 1989. - т. 3.

3. Детлаф А.А., Яворский Б.М. Курс физики. -М.: Высш. шк., 2004.

4. Трофимова Т.И. Курс физики. - М.: Высш. шк., 2004.

5. Курс физики. Под ред. Лозовского В.Н. – СПб.: Лань, 2001. – т. 1.

6. Курс физики. Под ред. Лозовского В.Н. – СПб.: Лань, 2001. – т. 2.

7. Джанколи Дж. Физика. М.: Мир, 1989, т.1-2.

Сборники задач:

8. Чертов А.Г., Воробьев А.А. Задачник по физике.- М.: Высш. шк., 2006.

9. Иродов И.Е. Задачи по общей физике.- М.: Физматлит., 2006.

10. Физика. Задания к практическим занятиям/ под ред. Лагутиной Ж.П. – Минск: Вышэйшая школа, 1989.

11. Савельев И.В. Сборник вопросов и задач по общей физике. - М.: Наука, 1988.

12. Трофимова Т.И. Сборник задач по курсу физики для втузов. - М.: Оникс 21 век, 2003.

13. Волькенштейн В.С. Сборник задач по общему курсу физики. – СПб.: Книжный мир, 2003.

Методические руководства:

14. Физика 2. Конспект лекций (для студентов очной формы обучения специальности 050717 – Теплоэнергетика и 050718 - Электроэнергетика). Завадская Л.В., Тонконогая Л.А. – Алматы: АИЭС, 2010. – 64 с.

15. Физика 2. Методическое руководство по освоению курса для студентов специальностей 050719 – Радиотехника, электроника и телекоммуникации, 050704 – Вычислительная техника и программное обеспечение/ Сост.М.Ш., Кулымбаева М.Ш., Саламатина А.М., Семененя В.А., Бергалиев Е.Ш. – Алматы: АИЭС, 2006. – 40 с.

16. Электромагнетизм. Методические указания к выполнению лабораторных работ/ Сост. Байпакбаев Т.С., Завадская Л.В., Тонконогая Л.А. - Алматы: АИЭС, 2009 г.-35 с.

17. Колебания. Методические указания к выполнению лабораторных работ/ Сост. Завадская Л.В., Тонконогая Л.А., Семененя В.А., Калыкпаева Р.С. - Алматы: АИЭС, 2008 г.-27 с.

18. Волновая оптика. Методические указания к выполнению лабораторных работ для студентов всех форм обучения всех специальностей /Сост. Карсыбаев М.Ш., Дауменов Т.Д., Мухтарова М.Н.- Алматы: АИЭС, 2010 г.- 40 с.

19. Квантовая физика. Методические указания к выполнению лабораторных работ для студентов всех форм обучения всех специальностей /Сост. Карсыбаев М.Ш., Манабаев Х.Х..- Алматы: АИЭС, 2006 г.- 39 с.

20. Физика 2. Тестовые вопросы для студентов всех форм обучения всех специальностей. /Карсыбаев М.Ш., Наурызбаева Г.К., Кунелбаев М.М.– Алматы: АИЭС, 2010. – 55 с.

Дополнительная литература:

21. Тамм И.Е. Основы теории электричества.-М.: Физматлит., 1966.

22. Шпольский Э.В. Атомная физика. Т. 1,2. – М.: Физматлит., 1974.

Св.план 2012 г., поз. 314