АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ ИСВЯЗИ
Кафедра Инженерной Кибернетики
Прикладная теория информации
Методические указания к выполнению лабораторных работ
для студентов всех форм обучения специальности
050702 - «Автоматизация и управление»
Алматы 2008
СОСТАВИТЕЛИ: Ю. В. Шевяков. Ш.М. Байматаева. Прикладная теория информации. Методические указания к выполнению лабораторных работ для студентов всех форм обучения специальности 050702 - Автоматизация и управление.- Алматы: АИЭС, 2008.-36 с.
Методы цифровой обработки сигналов в системах связи, управления и контроля приобретают большую важность и в значительной мере заменяют классические аналоговые методы. Данные методические указания к лабораторным работам по дисциплине «Прикладная теория информации» включают материалы по основным разделам курса и базируются на моделировании с помощью пакета проектирования систем передачи дискретных сигналов «SystemView». Программа «SystemView» весьма полезна именно в том плане, что она позволяет представить системы связи, цифровую обработку сигналов (ЦОС) и средства их анализа в интуитивно понятном для практического применения виде.
1 Лабораторная работа № 1. Исследование спектров дискретных сигналов
При выполнении лабораторных работ используется пакет «SystemView» Пакет «SystemView» представляет собой мощную интегрированную среду проектирования с почти неограниченными возможностями:
- построения моделей широкополосных систем связи, использующих
сложные цифровые сигналы;
- анализа их поведения в различной помеховой и шумовой обстановке;
- отработки алгоритмов работы цифровых адаптивных фильтров.
Пользовательский интерфейс программы прост в обращении и интуитивен. Основу пакета составляет базовый модуль, к которому подключаются различные специализированные библиотеки, обеспечивающие проектировщиков моделями почти всех необходимых функциональных блоков. На рисунке 1.1 показано окно моделирования «SystemView». Основными элементами окна проектирования являются панель инструментов, строка состояния, и панель моделей. Строка меню имеет выпадающее меню, показывающее основные функции: File (Файл), Edit (Правка), View (Вид), Preferences (Свойства), NotePads (Блокноты), Connections (Соединения), Compiler (Компилятор), System (Система), Tokens (Модели), Tools (Инструменты), и Help (Справка).
Панель инструментов состоит из кнопок, которые выполняют следующие функции:
- управление над моделями или группами моделей в окне
проектирования;
- пуск и останов моделирования;
- обеспечение доступа к окну анализа и другим сервисным функциям.
Панель библиотек используется для выполнения различных действий с моделями или группой моделей. Для перемещения выбранной модели необходимо:
- дважды быстро нажать мышкой на нужную кнопку;
- либо, нажав мышкой и удерживая ее в нажатом состоянии, переместить курсор с выделенной моделью на рабочее поле окна проектирования.
Для каждой кнопки панели инструментов и панели библиотек доступна краткая информация. Чтобы увидеть информацию, необходимо подвести указатель к нужной кнопке, после чего в выпадающем окне появится информация о соответствующей кнопке.

Рисунок 1.1
Все схемы, используемые в лабораторных работах, по умолчанию установлены в каталоге C:\ПТИ\...
Для того, чтобы запустить процесс моделирования, необходимо создать новый проект, объединяя определенные модели, либо открыть уже существующий проект. Для открытия существующего проекта необходимо щелкнуть по меню “File“ (Файл) и выбрать строку “Open Existing System“(Открыть существующий проект). На экране должна появиться схема выбранного устройства или системы.
Для запуска процесса моделирования необходимо нажать в панели инструментов на кнопку Run (Пуск). В ходе моделирования в левом нижнем углу строки состояния появляется перемещающаяся полоса, которая показывает, на каком этапе находится процесс моделирования.
Результаты моделирования отображаются в окне анализа. Для перехода в Окно анализа необходимо нажать кнопку Analysis Window (Окно анализа) на панели инструментов. Окно Analysis Window (Окно анализа) является основным инструментом для исследования и анализа полученных данных. В «SystemView» имеется большое количество различных функций, позволяющих выполнить подробное изучение исследуемой системы. Окно анализа показано на рисунке 1.2.
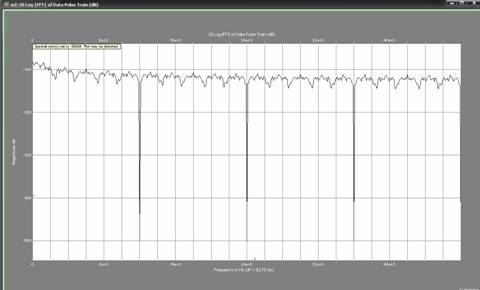
Рисунок 1.2
Одной из особенностей Окна анализа является возможность простого изменения (увеличения) любого графика. Для рассмотрения какой-либо области достаточно выделить требуемую с помощью мыши . Это свойство очень полезно для исследования отдельных деталей исследуемого процесса. Для возврата изображения в исходное состояние достаточно нажать кнопку Reset Scale на инструментальной панели или, вызвав контекстное меню правой кнопкой мыши, выбрать операцию Rescale. При этом графическое изображение будет возращено в исходное состояние. Управление режимом отображения координат осуществляется с помощью кнопок LogY и LogX. При этом одна из осей координат графика или обе оси отображаются в логарифмическом масштабе.
Размещение окон можно менять с помощью кнопок Tile Vertical(Разместить вертикально), Tile Horizontal (Разместить горизонтально) и Tile cascade (Разместить каскадом). Имеется возможность экспорта графических изображений в виде метафайлов или точечных рисунков в другие приложения Windows.
Для анализа результатов «SystemView» имеет мощный встроенный калькулятор. Вызов калькулятора осуществляется с помощью кнопки Sink Calculator, размещенной в правой нижней части Окна анализа. Более подробные сведения о пакете моделирования телекоммуникационных систем «SystemView» можно почерпнуть из [1].
Цель работы: ознакомление со способами получения сигналов и приобретение практических навыков в определении спектрального состава дискретных сигналов.
1.1 Домашняя подготовка
1.1.1 Предварительно, до выполнения лабораторной работы, изучить по рекомендованной литературе теоретические сведения по спектрам и спектральной характеристике сигналов.
1.1.2 Изучить задание на лабораторную работу и методические указания к нему.
1.1.3 Ответить на контрольные вопросы.
1.2 Методика проведения работы
1.2.1 Формирование последовательностей прямоугольных, треугольных и гауссовых импульсов
Окно System View содержит функциональные элементы, включенные в стандартные библиотеки Source, Sink, Function, Operator, Adder, Multiplier, MetaSystem I/O. В библиотеке Source имеется разнообразный набор источников детерминированных и случайных сигналов (группы periodic, Noise/PN, Aperiodic и Import). Выбор группы, в которой находится нужный сигнал, производится щелчком по ее имени на панели диалогового окна SystemView Library, после чего в окне отображается перечень источников сигналов выбранной группы.
Генерация периодической последовательности видеоимпульсов прямоуольной формы осуществляется с помощью источника Pulse Train. Он имеет следующие параметры:
Amplitude – амплитуда, В;
Frequency – частота, Гц;
Pulse width – длительность импулсьа, с;
Offset – смещение, В;
Phase (deg) – начальная фаза, град.
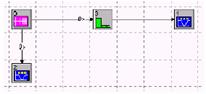
Пример использования Pulse Train показан на рисунке 1.3
Рисунок 1.3- Применение pulse Train
Генерация периодической последовательности пилообразных импульсов осуществляется с помощью Sawtooth. Этот источник имеет следующие параметры
Amplitude – амплитуда, В;
Frequency – частота, Гц;
Offset – смещение, В;
Phase (deg) – начальная фаза, град.
Генерация
двух гармонических напряжений: ![]()
![]() осуществляется с помощью источника Sinusoid. Он имеет следующие параметры:
осуществляется с помощью источника Sinusoid. Он имеет следующие параметры:
Amplitude – амплитуда, В;
Frequency – частота, Гц;
Phase (deg) – начальная фаза, град.
1.2.2 Пример спектрального анализа
1.2.3 Спектры строятся при помощи прямого и обратного преобразований Фурье
Формирование прямоугольных импульсных сигналов для передачи по линиям связи
Для уменьшения полосы пропускания необходимо уменьшить уровень высокочастотных гармоник в спектре импульсов данных. Следовательно, необходимо использовать формирующий фильтр, посредством которого до передачи данные (импульсы) преобразуются в прямоугольную форму. Спектр прямоугольной последовательности импульсов описывается таким выражением [2]

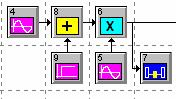
Формирование импульсной последовательности может быть выполнено с помощью цифрового фильтра, имеющего прямоугольную импульсную передаточную функцию длительностью 1/2400 секунды. Откройте систему squ_pulse.svu (см. рисунок 1.4).
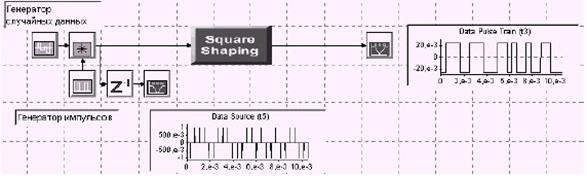
Рисунок 1.4
В этой системе представлено выбранное изображение для фильтра, формирующего прямоугольный импульс. Модуль Square Shaping является обыкновенным линейным системным модулем SystemView. SystemView позволяет изменять внешний вид иконки любого модуля по вашему выбору. Замена осуществляется выбором строки Custom Picture... контекстного меню нажатием правой кнопки мыши на символе модуля:
а) рассмотрите импульсную передаточную функцию и вес фильтра (все установки при 1/40 = 0.025) фильтра, формирующего прямоугольный импульс, и убедитесь в том, что он является фильтром, имеющим 40 весовых элементов. Частота дискретизации выбрана равной 96 000 Гц. Длительность импульсной передаточной характеристики этого фильтра равна
![]()
Убедитесь, что частотная характеристика фильтра, имеет линейную характеристику. Оцените ширину полосы, занимаемой импульсной последовательностью;
б) запустите процесс моделирования и перейдите в окно анализа. Рассмотрите переданные импульсы и также изучите полосу пропускания последовательности прямоугольных импульсов, просматривая амплитудно-частотную характеристику (спектр) последовательности прямоугольных импульсов;
в) увеличьте число выборок до 8192 и запустите систему снова, а затем перейдите в окно анализа.
Примечание. Спектральная характеристика сигнала должна носить более сглаженный вид по сравнению с предыдущим запуском.
1.3 Задание к выполнению работы
1.3.1 Сформировать последовательность прямоугольных, пилообразных, и синусоидальных сигналов.
1.3.2 Варианты заданий (по указанию преподавателя) приведены в таблице 1.
Т а б л и ц а 1
|
№ варианта |
T, c |
А, мм |
Ts, с |
|
1 |
5 |
0,5 |
0,01 |
|
2 |
6 |
0,65 |
0,02 |
|
3 |
4 |
0,5 |
0,01 |
|
4 |
5 |
0,65 |
0,04 |
|
5 |
6 |
0,55 |
0,03 |
|
6 |
4 |
0,6 |
0,04 |
|
7 |
5 |
0,5 |
0,02 |
|
8 |
7 |
0,7 |
0,03 |
Продолжение таблицы 1
|
9 |
3 |
0,6 |
0,04 |
|
10 |
4 |
0,6 |
0,05 |
|
11 |
5 |
0,65 |
0,01 |
|
12 |
6 |
0,5 |
0,02 |
|
13 |
5 |
0,5 |
0,03 |
|
14 |
4 |
0,7 |
0,04 |
|
15 |
6 |
0,5 |
0,01 |
|
16 |
5 |
0,55 |
0,02 |
|
17 |
3 |
0,6 |
0,03 |
|
18 |
4 |
0,5 |
0,04 |
|
19 |
3 |
0,65 |
0,01 |
|
20 |
7 |
0,6 |
0,02 |
|
21 |
6 |
0,7 |
0,03 |
|
22 |
5 |
0,6 |
0,04 |
|
23 |
4 |
0,5 |
0,01 |
|
24 |
5 |
0,65 |
0,02 |
|
25 |
4 |
0,55 |
0,01 |
1.4 Контрольные вопросы
1.4.1 Что такое "сигнал"?
1.4.2 Детерминированный и случайный сигналы, обоснуйте их различие.
1.4.3 В какой зависимости друг от друга частота повторения сигнала f и период Т? Как зависит круговая частота ω от частоты повторения сигнала f?
1.4.4 Дайте определение амплитудному и фазовому спектрам.
1.4.5 Что такое эффективная ширина спектра?
1.4.6 Что такое база сигнала?
1.4.7 Может ли база сигнала быть меньше единицы? Почему?
1.4.8 Какой сигнал называют широкополосным?
2 Лабораторная работа №2 Проектирование конечной передаточной импульсной функции (FIR)
Цель работы: ознакомление с методами создания фильтров с конечной передаточной импульсной функцией
2.1 Задания по работе
2.1.1 По рекомендуемым литературным источникам ознакомиться с методами синтеза фильтров с конечной импульсной характеристикой различных типов.
2.1.2 Изучить задание на лабораторную работу и методические указания к нему.
2.1.3 Ответить на контрольные вопросы.
2.2 Методические указания к выполнению работы
Цифровая фильтрация, по существу, ключевая операция в передаче информации. Фильтрация сигнала в полосе частоты - фундаментальная операция, используемая фактически во всех системах связи. Простой пример - отделение высокого шума частоты от речевого сигнала, или более сложный пример - цифровая фильтрация полученных символов данных от спутника в целях уравнивания канала.
Цифровые фильтры могут быть легко разработаны с помощью SystemView. В первой части этого раздела мы опишем несколько действий, чтобы спроектировать простой низкочастотный фильтр с band-pass, номиналом от 0 до 1000 Гц, для частоты дискретизации, как показано на рисунке 2.1.
|
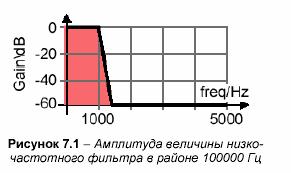
Увеличение полосы пропускания band-pass установлено в 0 дБ. Это означает, что понижение частот в этой области – 0 дБ, т. е., зависимость является линейной:
20log10GAIN = 20log101 = 0 дБ.
|

Для band-stop – линейная зависимость от 0.01:
20log100.01 = 20log1010-2 = -40 дБ.
2.2.1 Линейные системы и фильтры
Выбирая  «Универсальный Оператор», выберите
кнопку
«Универсальный Оператор», выберите
кнопку ![]() и затем маркер
и затем маркер ![]() «Линейные системные фильтры».
Должно появиться диалоговое окно, показанное на
рисунке 2.2. При использовании диалогового окна, показанного на рисунке 2.2 мы
можем проектировать стандартные, низкочастотные, высокочастотные, полосовые и
полосно-заграждающие band-stop FIR фильтры, и IIR фильтры (при выборе кнопки
«Линейные системные фильтры».
Должно появиться диалоговое окно, показанное на
рисунке 2.2. При использовании диалогового окна, показанного на рисунке 2.2 мы
можем проектировать стандартные, низкочастотные, высокочастотные, полосовые и
полосно-заграждающие band-stop FIR фильтры, и IIR фильтры (при выборе кнопки ![]() ). Также могут быть
разработаны и другие фильтры, если выбрать кнопку CUSTOM
). Также могут быть
разработаны и другие фильтры, если выбрать кнопку CUSTOM ![]() .
.
2.2.2 Проектирование фильтра
От открытого окна диалога (рисунок
2.2) выберите «Проектирование FIR фильтра», используя кнопку ![]() и выберите кнопку
и выберите кнопку ![]() . Частоты полосы перехода фильтра
определены как дробные величины осуществления выборки (так называемые
нормализованные частоты). Определите фильтр (для частоты осуществления
выборки), который начнет отрезать полосу в 1000 Гц, с шириной полосы частот
перехода в 400 Гц и band-stop, понижая до
–40 дБ.
. Частоты полосы перехода фильтра
определены как дробные величины осуществления выборки (так называемые
нормализованные частоты). Определите фильтр (для частоты осуществления
выборки), который начнет отрезать полосу в 1000 Гц, с шириной полосы частот
перехода в 400 Гц и band-stop, понижая до
–40 дБ.
Обратите внимание, что параметры частоты введены как дроби осуществления выборки. Как только Вы ввели эти значения, должно появиться диалоговое окно, как указано ниже :
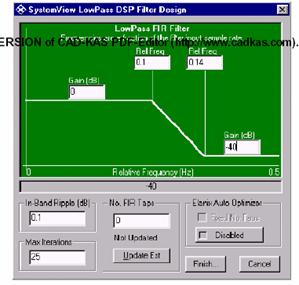
Рисунок 2.3 - Линейные системные фильтры
При использовании кнопки, ![]() оцените требуемое количество
весов, чтобы выполнить необходимые требования к фильтру. Вы, вероятно, получите
ответ, около 51, который появится в окне параметров
оцените требуемое количество
весов, чтобы выполнить необходимые требования к фильтру. Вы, вероятно, получите
ответ, около 51, который появится в окне параметров![]() С помощью левой кнопки мыши, выберите кнопку
С помощью левой кнопки мыши, выберите кнопку ![]() в диалоговом окне. Теперь вы увидите значения
веса фильтра (в формате с плавающей запятой) перечисленный вверху
в диалоговом окне. Теперь вы увидите значения
веса фильтра (в формате с плавающей запятой) перечисленный вверху ![]() полосы прокрутки
(ScrollBox).
полосы прокрутки
(ScrollBox).
Обратите внимание, что, пока
Вы не нажали кнопку, ![]() проектирование
не было начато. SystemView
делает “оценку” по количеству
проектирование
не было начато. SystemView
делает “оценку” по количеству ![]() weights так, чтобы мы могли задать фактический
алгоритм проектирования фильтра. Эта оценка не может быть оптимальной, и
следовательно имеется опция Авто Оптимизатор, использующая
weights так, чтобы мы могли задать фактический
алгоритм проектирования фильтра. Эта оценка не может быть оптимальной, и
следовательно имеется опция Авто Оптимизатор, использующая ![]() , которое выполняет итерации, чтобы
найти оптимальное (минимальное) число весов.
, которое выполняет итерации, чтобы
найти оптимальное (минимальное) число весов.
2.2.3 Фильтр Усиления
Для просмотра
амплитудно-частотного отклика FIR-фильтра нажмите один раз левой кнопкой мыши
на кнопке, ![]() расположенной
на нижней правой стороне диалогового окна
расположенной
на нижней правой стороне диалогового окна ![]() (как показано на рисунке 2.2). Кнопка
(как показано на рисунке 2.2). Кнопка ![]() отобразит импульсную
передаточную функцию. Обратите внимание, что при нажатии Ctrl+Левая кнопка
мыши Вы увеличите диалоговое окно, а при нажатии Ctrl+Правая кнопка мыши
появятся опции включения/отключения панелей. Также обратите внимание, что,
используя меню диалогового окна,
отобразит импульсную
передаточную функцию. Обратите внимание, что при нажатии Ctrl+Левая кнопка
мыши Вы увеличите диалоговое окно, а при нажатии Ctrl+Правая кнопка мыши
появятся опции включения/отключения панелей. Также обратите внимание, что,
используя меню диалогового окна, ![]() Вы можете сохранять коэффициенты в файл.
Вы можете сохранять коэффициенты в файл.
Используя фильтр, разработанный в предыдущих действиях, мы можем теперь моделировать в SystemView, чтобы демонстрировать различие частоты и общей цифровой фильтрации. Обратите внимание, что, если Вы используете студенческую версию SystemView, все ваши проекты ограничены максимальным количеством weights 64.
2.2.4 Низкочастотная цифровая фильтрация
В этом примере мы произведем вышеупомянутую простую низкочастотную систему фильтрации (см. рисунок 2.4).
|
Рисунок 2.4
а) установите источник качающейся частоты с начальной частотой
50Hz и конечной частотой 4800Hz в интервале 0.8192 с;
б) убедитесь, что Вы
определили параметры системного времени ![]()
как частоту дискретизации![]() 10 000Hz и количество выборок, равным
10 000Hz и количество выборок, равным![]() 8192, то есть время
моделирования - 0.8191 секунд. Таким образом, качание частоты сигнала
фактически полностью охватывает полосу Найквиста от 0 до 5000Hz;
8192, то есть время
моделирования - 0.8191 секунд. Таким образом, качание частоты сигнала
фактически полностью охватывает полосу Найквиста от 0 до 5000Hz;
в) используйте качающуюся частоту как входной сигнал FIR- фильтра, который Вы разработали, и выведите выходы обоих устройств (генератора качающейся частоты и фильтра) на модули вывода (sink) SystemView как показано на диаграмме выше;
г) запустите систему и просмотрите амплитуды спектра в окне анализа. Удалены ли все частоты выше 1200 Гц?;
д) спроектируйте новый фильтр с band-stop понижением ( -60 дБ и 500 Гц ).
2.2.5 Фильтрация Гауссова Шума
Повторите пункт 2.2.4, используя в качестве источника входного сигнала генератор Гауссовского шума вместо ранее использованного источника линейно качающейся частоты. Выбранный Гауссов белый шум содержит “все” частоты. Используйте инструментальные средства System-View для анализа в частотной области, чтобы убедиться в правильности функционирования фильтра.
2.2.6 Полосовая фильтрация
Спроектируйте полосовой фильтр, чтобы передать полосу частот между 900 и 1200 Гц. Тщательно выберите ширину полосы частот перехода, которая позволит Вам проектировать фильтр с “разумным” количеством весов.
Если Вы используете студенческую версию, тогда Вам придется установить подавление в полосе заграждения (band-stop) примерно равным минус 40 дБ и переходную полосу с обеих сторон около 400 Гц.
Чтобы убедиться, что система функционирует правильно, используйте в качестве входного сигнала фильтра также Гауссов шум или однородный шум.
|

2.3 Задание к выполнению работы. Выполнить синтез фильтра с конечной импульсной характеристикой. Частота дискретизации в системе System Rate=100 Гц. Варианты заданий указаны в таблице 2:
Т а б л и ц а 2
|
№ п.п. |
Тип фильтра |
Верхняя относительная частота полосы пропускания |
Нижняя относи-тельная граничная частота полосы задержи-вания |
Коэффи-циент передачи в полосе пропус-кания, дБ |
Коэффициент передачи в полосе задержива-ния, дБ |
Неравно-мерность в полосе пропус-кания |
|
1 |
ФНЧ |
0,2 |
0,25 |
0 |
-60 |
0,1 |
|
2 |
ФНЧ |
0,05 |
0,055 |
0 |
-60 |
0,5 |
|
3 |
ФНЧ |
0,3 |
0,32 |
0 |
-60 |
0,1 |
|
4 |
ФНЧ |
0,25 |
0,28 |
0 |
-40 |
0,2 |
|
5 |
ФВЧ |
0,215 |
0,2 |
0 |
-40 |
0,1 |
|
6 |
ФВЧ |
0,35 |
0,3 |
0 |
-60 |
0,2 |
|
7 |
ФВЧ |
0,12 |
0,1 |
0 |
-60 |
0,3 |
|
8 |
ФВЧ |
0,06 |
0,05 |
0 |
-40 |
0,4 |
|
9 |
ФНЧ |
0,15 |
0,18 |
0 |
-40 |
0,3 |
|
10 |
ФНЧ |
0,1 |
0,13 |
0 |
-40 |
0,4 |
|
11 |
ФНЧ |
0,1 |
0,13 |
0 |
-60 |
0,5 |
|
12 |
ФНЧ |
0,3 |
0,32 |
0 |
-40 |
0,1 |
|
13 |
ФВЧ |
0,19 |
0,17 |
0 |
-40 |
0,5 |
|
14 |
ФВЧ |
0,17 |
0,15 |
0 |
-60 |
0,1 |
|
15 |
ФВЧ |
0,22 |
0,2 |
0 |
-60 |
0,2 |
|
16 |
ФВЧ |
0,42 |
0,4 |
0 |
-40 |
0,3 |
|
17 |
ФВЧ |
0,45 |
0,42 |
0 |
-40 |
0,4 |
|
18 |
ФВЧ |
0,215 |
0,2 |
0 |
-40 |
0,5 |
|
19 |
ФВЧ |
0,27 |
0,25 |
0 |
-40 |
0,1 |
|
20 |
ФВЧ |
0,37 |
0,35 |
0 |
-40 |
0,2 |
|
21 |
ФНЧ |
0,12 |
0,14 |
0 |
-40 |
0,1 |
|
22 |
ФВЧ |
0,33 |
0,3 |
0 |
-40 |
0,1 |
|
23 |
ФНЧ |
0,1 |
0,2 |
0 |
-40 |
0,5 |
|
24 |
ФВЧ |
0,2 |
0,18 |
0 |
-40 |
0,2 |
|
25 |
ФВЧ |
0,37 |
0,35 |
0 |
-40 |
0,5 |
2.4 Содержание отчета
2.4. 1 Краткие сведения из теории.
2.4.2 Экранные изображения фильтров с конечной импульсной характеристикой.
2.4.3 Частотные характеристики фильтров с конечной импульсной характеристикой.
2.4.4 Выводы по работе.
2.5 Контрольные вопросы
2.5.1 Что такое фильтрация?
2.5.3 Что такое полоса задерживания и полоса пропускания фильтра низких частот?
2.5.4 Какие предъявляются требования к фильтрам во временной области?
3 Лабораторная работа №3. Изучение видов аналоговой модуляции
Цель работы: изучение аналоговых видов модуляции и способов получения модулированных сигналов.
3.1 Задания по работе
3.1.1 По данному описанию и рекомендуемым литературным источникам изучить виды модуляции: амплитудной, фазовой, частотной, способы получения модулированных сигналов.
3.1.2 Получить и зарисовать временные диаграммы модулированных сигналов.
3.2. Сведения из теории
Передающее устройство осуществляет преобразование непрерывных сообщений или знаков в сигналы, удобные для прохождения по конкретной линии связи (либо для хранения в некотором запоминающем устройстве). При этом один или несколько параметров выбранного носителя изменяются в соответствии с передаваемой информацией. Такой процесс называют модуляцией. Он осуществляется модулятором. Обратное преобразование сигналов в символы производится демодулятором.
Модулированный сигнал можно представить как произведение двух функций:
![]() ,
,
где ![]() – функция представляющая несущее колебание
(переносчик);
– функция представляющая несущее колебание
(переносчик);
![]() –
модуляционная функция, выражающая воздействие предаваемого сообщения U(t) на
несущий параметр.
–
модуляционная функция, выражающая воздействие предаваемого сообщения U(t) на
несущий параметр.
В зависимости от того, какой из параметров изменяется – амплитуда А или угол q - различают два основных вида модуляции: амплитудную и угловую. Угловая модуляция, в свою очередь, подразделяется на два вида: частотную (ЧМ) и фазовую (ФМ). Эти два вида тесно связаны между собой, и различие между ними проявляется лишь в характере изменения во времени угла y при одной и той же модулирующей функции.
Амплитудная модуляция – изменение амплитуды колебаний с частотой значительно меньшей, чем частота самих колебаний.
![]()
![]()
где ![]() коэффициент
модуляции
коэффициент
модуляции
![]()
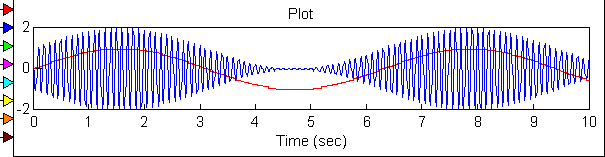
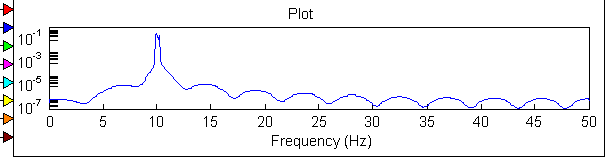
Осциллограмма и спектрограмма АМ модулированного сигнала
Угловая модуляция (фазовая и частотная) – изменение фазы медленно по сравнению с периодом колебаний.
![]()
![]()
![]()
Фазовая модуляция
![]()
![]()
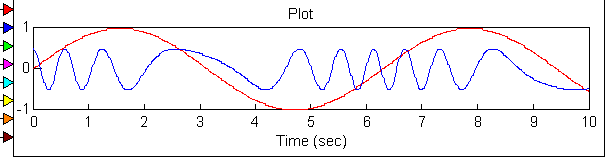
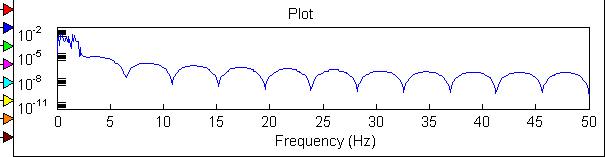
Осциллограмма и спектрограмма ФМ модулированного сигнала
Частотная модуляция
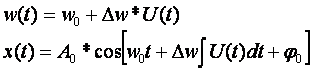
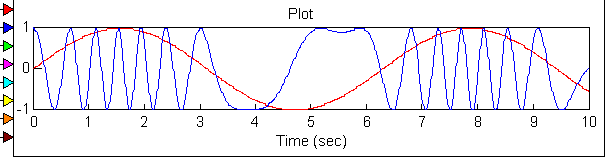
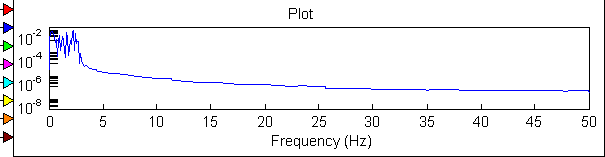
Осциллограмма и спектрограмма ЧМ модулированного сигнала
3.3 Порядок выполнения работы
3.3.1 Составить структурные схемы АМ, ЧМ, ФМ модуляций.
3.3.2 Модулировать синусоидальный сигнал (параметры источника сигнала и модулятора согласно варианту). Варианты заданий приведены в таблице 3.
3.3.3 С помощью сумматора получить сигнал сложной формы, модулировать его (настроить модулятор и источник самостоятельно).
3.3.4 Зарисовать полученные осциллограммы и спектрограммы.
Т а б л и ц а 3
|
№
|
Параметры АМ |
Параметры ЧМ |
Параметры ФМ |
Параметры источника |
|
|||||||||||||||
|
|
Амплитуда, В |
Часто-та |
Амплитуда, В |
Частота |
Шаг, Гц/В |
Ампли-туда, В |
Частота, Гц |
Шаг, Гц/В |
Ампли- туда, В |
Частота, Г |
|
|||||||||
|
1 |
1 |
5 |
1,9 |
2 |
1,2, |
2,9 |
2,9 |
10 |
1 |
0,2 |
|
|||||||||
|
2 |
1,1 |
6 |
1,8 |
2,1 |
1,3 |
2,8 |
2,8 |
9 |
1,1 |
0,3 |
|
|||||||||
|
3 |
1,2 |
7 |
1,7 |
2,2 |
1,4 |
2,7 |
2,7 |
8 |
1,2 |
0,4 |
|
|||||||||
|
4 |
1,3 |
8 |
1,6 |
2,3 |
1,5 |
2,6 |
2,6 |
7 |
1,3 |
0,5 |
|
|||||||||
|
5 |
1,4 |
9 |
1,5 |
2,4 |
1,6 |
2,5 |
2,5 |
6 |
1,4 |
0,6 |
|
|||||||||
|
6 |
1,5 |
10 |
1,4 |
2,5 |
1,7 |
2,4 |
2,4 |
5 |
1,5 |
0,7 |
|
|||||||||
|
7 |
1,6 |
11 |
1,3 |
2,6 |
1,8 |
2,3 |
2,3 |
4 |
1,6 |
0,8 |
|
|||||||||
|
8 |
1,7 |
12 |
1,2 |
2,7 |
1,9 |
2,2 |
2,2 |
3 |
1,7 |
0,9 |
|
|||||||||
|
9 |
1,8 |
13 |
1,1 |
2,8 |
2 |
2,1 |
2,1 |
2 |
1,8 |
1 |
|
|||||||||
|
10 |
1,9 |
14 |
1 |
2,9 |
2,1 |
2 |
2 |
1 |
1,9 |
1,1 |
|
|||||||||
|
11 |
2 |
15 |
2 |
3 |
2,2 |
1,9 |
1,9 |
11 |
2 |
1,2 |
|
|||||||||
|
12 |
2,1 |
16 |
2,1 |
3,1 |
2,3 |
1,8 |
1,8 |
12 |
2,1 |
1,3 |
||||||||||
|
13 |
2,2 |
17 |
2,2 |
3,2 |
2,4 |
1,7 |
1,7 |
13 |
2,2 |
1,4 |
||||||||||
|
14 |
2,3 |
18 |
2,3 |
3,3 |
2,5 |
1,6 |
1,6 |
14 |
2,3 |
1,5 |
||||||||||
|
15 |
2,4 |
19 |
2,4 |
3,4 |
2,6 |
1,5 |
1,5 |
15 |
2,4 |
1,6 |
||||||||||
|
16 |
2,5 |
20 |
2,5 |
3,5 |
2,7 |
1,4 |
1,4 |
16 |
2,5 |
1,7 |
||||||||||
|
17 |
2,6 |
21 |
2,6 |
3,6 |
2,8 |
1,3 |
1,3 |
17 |
2,6 |
1,8 |
||||||||||
|
18 |
2,7 |
22 |
2,7 |
3,7 |
2,9 |
1,2 |
1,2 |
18 |
2,7 |
1,9 |
||||||||||
|
19 |
2,8 |
23 |
2,8 |
3,8 |
3 |
1,1 |
1,1 |
19 |
2,8 |
2 |
||||||||||
|
20 |
2,9 |
24 |
2,9 |
3,9 |
3,1 |
1,2 |
1,2 |
20 |
2,9 |
2,1 |
||||||||||
|
21 |
2,5 |
14 |
2,1 |
3 |
3 |
1,1 |
1,2 |
15 |
2 |
2 |
||||||||||
|
22 |
2 |
15 |
2 |
3 |
3,1 |
1,5 |
1,2 |
16 |
2,1 |
2,2 |
||||||||||
|
23 |
2 |
16 |
2,1 |
2,3 |
3 |
1,6 |
1,4 |
10 |
2 |
2,1 |
||||||||||
|
24 |
2,1 |
17 |
2,2 |
2,4 |
3,2 |
1,6 |
1,5 |
15 |
2,2 |
2,3 |
||||||||||
|
25 |
2,3 |
15 |
2,2 |
2,4 |
2,3 |
1,6 |
1,5 |
14 |
2,1 |
2,4 |
||||||||||
3.4 Задание к выполнению работы
Исследование схем амплитудной модуляции с ДБП
- собрать схему амплитудного модулятора с двумя боковыми полосами (см. рисунок 3.1), установить параметры, снять экранные изображения выходного модулированного сигнала и его спектра. Варианты заданий приведены в таблице 4.
Т а б л и ц а 4
|
№ варианта |
Частота fсигн, Гц |
Частота fмод, Гц |
Коэффициент модуляции |
|
1 |
20 |
200 |
0.2 |
|
2 |
30 |
250 |
0,4 |
|
3 |
50 |
500 |
0,4 |
|
4 |
80 |
800 |
0,5 |
|
5 |
100 |
1000 |
0,5 |
|
6 |
40 |
300 |
0,2 |
|
7 |
55 |
500 |
0,4 |
Продолжение таблицы 4
|
8 |
60 |
600 |
0,4 |
|
9 |
70 |
700 |
0,2 |
|
10 |
90 |
900 |
0,5 |
|
11 |
60 |
500 |
0,2 |
|
12 |
70 |
700 |
0,5 |
|
13 |
80 |
800 |
0,2 |
|
14 |
90 |
900 |
0,2 |
|
15 |
100 |
1100 |
0,2 |
|
16 |
70 |
800 |
0,4 |
|
17 |
100 |
1200 |
0,5 |
|
18 |
90 |
800 |
0,5 |
|
19 |
50 |
600 |
0,2 |
|
20 |
60 |
700 |
0,4 |
|
21 |
50 |
500 |
0,2 |
|
22 |
60 |
400 |
0,5 |
|
23 |
70 |
300 |
0,3 |
|
24 |
80 |
500 |
0,5 |
|
25 |
100 |
400 |
0,2 |
|
Рисунок 3.1 |
Рисунок 3.2 |
- собрать схему амплитудного демодулятора с двумя боковыми полосами (см. рисунок 3.2), рассчитать параметры ФНЧ и установить параметры, снять экранные изображения выходного демодулированного сигнала.
Исследование схем балансной амплитудной модуляции
- собрать схему балансного амплитудного модулятора (см. рисунок 3.3), установить параметры (таблица 4), снять экранные изображения выходного модулированного сигнала и его спектра.
|
Рисунок 3.3 |
Рисунок 3.4 |
- собрать схему балансного амплитудного демодулятора (см. рисунок 3.4), рассчитать параметры ФНЧ и установить параметры, снять экранные изображения выходного демодулированного сигнала
- изменить частоту синхронного детектирования на 10% и объяснить полученные результаты.
Исследование схем синхронного детектирования
- собрать схему амплитудного демодулятора с синхронным детектором (см. рисунок 3.5), установить параметры (таблица 4), снять экранные изображения выходного демодулированного сигнала
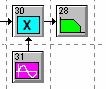
Рисунок 3.5
- изменить частоту синхронного детектирования на 10% и объяснить, полученные результаты.
Исследование схем амплитудной модуляции с ОБП
- собрать схему амплитудного модулятора и демодулятора с ОБП (см. рисунок 3.6), установить параметры (таблица 4), снять экранные изображения выходного модулированного сигнала

Рисунок 3.6
- изменить частоту синхронного детектирования на 10% и объяснить, полученные результаты.
- ввести в канал связи между модулятором и демодулятором источник гауссовского (нормального шума). Исследовать влияние помех на искажения сигнала. Снять экранные изображения.
3.5 Содержание отчета
1. Краткие сведения из теории.
2. Модуляционные характеристики.
3. Осциллограммы и спектрограммы сигналов.
4. Выводы о сделанной работе.
3.6 Контрольные вопросы
1. Какие виды переносчиков сигналов используются для аналоговой модуляции?
2. Как можно получить АМ, ЧМ, ФМ сигналы?
3. В чем отличие между ФМ и ЧМ и в чем их сходство?
4. Зависимость формы сигнала на выходе модулятора от напряжения модулируемого сигнала.
4 Лабораторная работа. № 4 Формирование дискретных сигналов
4.1 Цель работы: изучение методов формирования и передачи дискретных сообщений.
4.2 Предварительная подготовка
Изучить методы формирования дискретных сообщений, методы построения линейных кодов.
4.3 Рабочее задание
4.3.1 Исследовать характеристики системы связи при передаче импульсными сигналами малой длительности.
4.3.2 Исследовать методы формирования прямоугольных импульсных сигналов для передачи по линиям связи.
4.3.3 Провести исследование формирования двуполярного кода с возвращением к нулю
4.3.4 Провести исследование методов формирования линейных кодов RZ, ЧПИ, «МанчестерII» и сравнить спектральные характеристики сообщений при передаче короткими импульсами, прямоугольными импульсами, с помощью кодов RZ, ЧПИ, «МанчестерII».
4.4 Методические указания по выполнению работы
4.4.1 Передача импульсными сигналами малой длительности
Если мы должны передать данные в двоичном коде (то есть 0 и 1), возможна передача короткими импульсами, имеющими уровень +1 В при двоичной "1" и 1 В при двоичном "0". Цифровая система связи (DSP), передает данные со скоростью 1/T символов в секунду. Однако ширина полосы, требуемая для передачи этих данных, значительно выше, чем скорость передачи, так как каждый бит представлен импульсным сигналом, имеющим очень короткую длительность.
Как известно, спектр одиночного импульса описывается выражением [2]
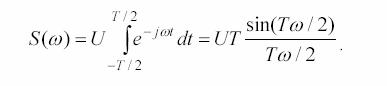
Спектр одиночного импульса затухает в общем случае лишь при бесконечно больших значениях аргумента (имеет бесконечный спектр). Откройте систему impulse_data.svu (см. рисунок 4.1).
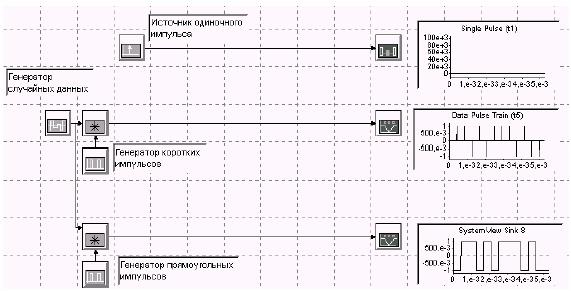
Рисунок 4.1
Скорость передачи данных всегда установлена равной 2400 бит/с. Следовательно, период повторения импульсов будет равен
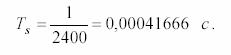
Частота выборок моделирования установлена на более высоком уровне 96 000 Гц (40×2400) для моделирования «аналогового» выходного сигнала. Запустите систему и в Окне анализа обратите внимание на то, что импульсные данные требуют для передачи бесконечной полосы пропускания, в чем можно убедиться по форме БПФ последовательности данных.
4.4.3 Формирование двуполярного кода с возвращением к нулю
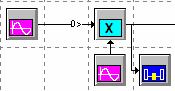
Изменяя фильтр, формирующий импульс, получите длительность 1/4800с. Эта последовательность прямоугольных импульсов имеет название двуполярного кода с возвращением к нулю (return to zero). Это преобразование осуществляется с помощью цифрового фильтра с прямоугольной импульсной передаточной характеристикой длительностью 1/4800 с. Откройте систему squ_pulse_rz.svu (см. рисунок 4.2)
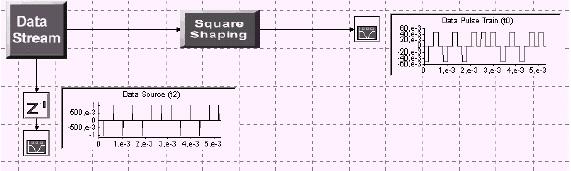
Рисунок 4.2
а) изучите импульсную передаточную характеристику и убедитесь, что весовые коэффициенты фильтра, формирующего прямоугольный импульс, соответствуют 1/20 = 0.05 и частота дискретизации выбрана равной 96 000 Гц, длительность импульсной передаточной функции этого фильтра 1/4800-ая секунды. Убедитесь, что частотная характеристика величины фильтра соответствует рисунку (график показан только до частоты 10000 Гц) и что фильтр имеет линейную характеристику;
б) запустите систему и перейдите в окно анализа. Изучите переданные импульсы и определите полосу пропускания последовательности прямоугольных импульсов с помощью спектра сигнала из последовательности прямоугольных импульсов;
в) увеличьте число выборок до 8192 для получения более сглаженной (более усредненной) частотной характеристики фильтра, запустите систему снова и в окне анализа обратите на амплитудно-частотную характеристику. Форма характеристики должна теперь быть более гладкой чем, в предыдущем случае.
4.4.4 Коды линии
Формы цифровых сигналов, предназначенных для передачи по линии связи, получили наименование линейных кодов (ПК). ЛК применяются для передачи данных без модуляции в первичной полосе частот, начинающейся с нуля. Иначе говоря, данные, представляющие собой обычные двоичные последовательности, перед подачей в линию связи подвергаются соответствующему преобразованию в линейном кодере. Наиболее широкое применение в аппаратуре связи получили такие линейные коды, как код без возвращения к нулю (Non Return to Zero NRZ), код с чередующейся полярностью импульсов (ЧПИ) (Alternate Mark Inversion AMI), корреляционные коды («Манчестер II»).
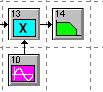
В файле binary_signalling.svu (см. рисунок 4.3) показаны примеры построения устройств формирования вышеуказанных кодов. Кодеры ЧПИ и манчестерского кода формируются с помощью метасистем, структура которых приведена на рисунках 4.4 и 4.5.
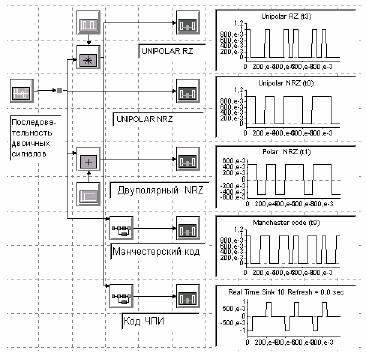
Рисунок 4.3
а) сигнальная продолжительность импульса – 0,1 с, следовательно, скорость передачи данных - 10 бит/с. Частота дискретизации –100 Гц, следовательно один бит представлен 10 выборками. Источник данных - текстовый файл из единиц и нулей, который имеет начальную последовательность 0101011100100101000000....;
б) запустите процесс моделирования и сравните различные сигнальные последовательности в Окне анализа;
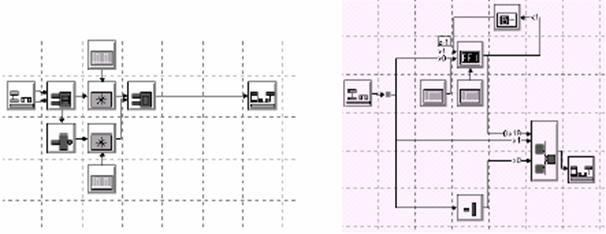
Рисунок 4.4 Рисунок 4.5
в) увеличьте число выборок до 10000 и запустите систему снова. В Окне анализа рассмотрите величину частоты спектра, которая была сгенерирована. Зарисуйте спектры исследуемых сигналов.
4.5 Контрольные вопросы
4.5.1Объясните различие в спектральном составе сигналов, передаваемых короткими импульсами (τи << Tп) и сигналов прямоугольной формы.
4.5.2 Объясните принцип формирования прямоугольного сигнала в схеме, приведенной на рисунке 4.2.
4.5.3 Объясните принципы построения устройств формирования кодов RZ, ЧПИ, «Манчестер II».
5 Лабораторная работа №5. Квантование и дискретизация
Цель работы: изучение методов квантования и дискретизации сигналов.
5.1 Задания по работе
5.1.1 По рекомендуемой литературе изучить теоретические материалы по квантованию и дискретизации сигналов.
5.1.2 Изучить задание на лабораторную работу и методические указания к нему.
5.1.3 Ответить на контрольные вопросы.
5.2 Методические указания к выполнению работы
В этом разделе мы будем использовать квантователь из библиотеки функциональных значков SystemView, чтобы квантовать входной сигнал на фиксированное количество битов. Моделирование в предыдущих случаях, входные сигналы различных лексем были с точностью плавающей точки, поэтому для большинства целей мы можем предположить, что заметного квантования нет.
5.2.1 Квантование сигнала
Соберите схему, приведенную на рисунке 5.1.
Установите следующие параметры в системе (таблица 5).
Т а б л и ц а 5

Система берет (с точностью плавающей точки) квантованный выходной сигнал генератора пилообразного сигнала с амплитудой напряжения 1,875 В и преобразует его в целое квантованное число. Все источники выходных сигналов в SystemView, по умолчанию установлены на точность с плавающей точкой (исключая, конечно, источники, которые считываются из файла, которые могут быть установлены на точность с фиксированной точкой).
|
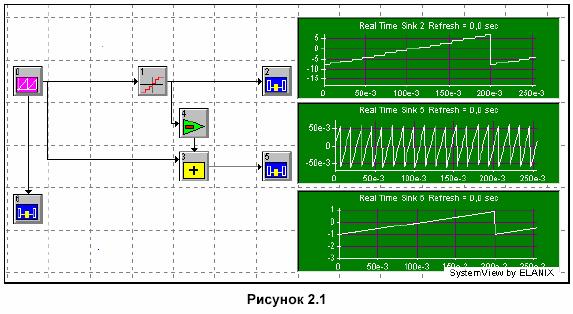
|
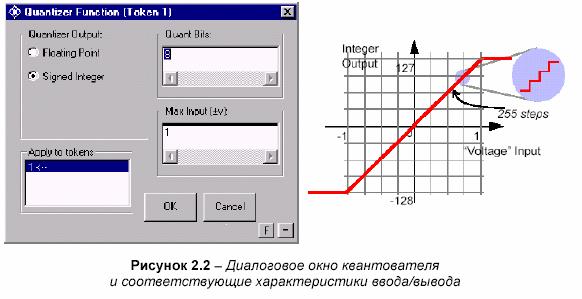
а) просмотрите параметры значка 4-х битного квантователя и убедитесь, что он имеет входные/выходные характеристики, показанные на рисунке 5.2. Обратите внимание, входной квантователь является восьмибитным, поэтому вторичная амплитуда дополнения находится в пределах от -23 до 23, например, -8 до +7;
б) Запустите систему и затем в окне анализа убедитесь, что значения
выборок такие, как
предполагались на выходе квантователя рассмотренного выше. (Не забудьте нажать мерцающую синим цветом кнопку «Загрузить обновленные
данные блока», ![]() чтобы
увидеть обработанные данные только
прошедшего процесса моделирования);
чтобы
увидеть обработанные данные только
прошедшего процесса моделирования);
в) определите погрешность квантования, вычисление которой осуществляется модулями 3, 4 и 5. Объясните полученные результаты;
г) модифицируйте
параметры квантователя![]() так, чтобы обеспечить трехбитное
квантование (8 уровней как показано на рисунке 5.3) с таким же ±1 колебанием напряжения как раньше.
Запустите систему
и убедитесь,
что результаты такие, как предполагалось, и совпадают с данными таблицами, показанными
на рисунке 5.3;
так, чтобы обеспечить трехбитное
квантование (8 уровней как показано на рисунке 5.3) с таким же ±1 колебанием напряжения как раньше.
Запустите систему
и убедитесь,
что результаты такие, как предполагалось, и совпадают с данными таблицами, показанными
на рисунке 5.3;
д) модифицируйте систему так, чтобы амплитуда пилообразного сигнала на входе была равна 2 В. Запустите систему и обратите внимание на эффект «сжимания» ADC. Это происходит потому, что присутствует проблема нелинейности, которая появляется тогда, когда входное напряжение на ADC слишком высокое;
е) обратите внимание, что в диалоговом окне параметров квантователя можно настроить вывод так, что он будет выводиться в форме с плавающей точкой или как целое число. Произвести такую настройку можно при помощи радио-кнопок, показанных на рисунке 5.2. Теперь установите форму вывода «с плавающей точкой», запустите процесс моделирования и объясните то, что теперь показывается на выходе.
|
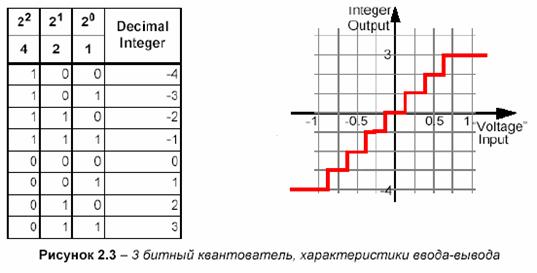
ж) измените модуль генератора прямоугольных импульсов на генератор синусоидальных сигналов (ГСН), запустите систему повторно при значении выходных напряжений ГСН, равных 1,75, 1,875 и 2,0 В. Объясните полученные результаты.
5.3 Дискретизация и наложение спектров (aliasing)
В этом разделе мы продемонстрируем явление элайзинга. Если частотные составляющие сигнала больше чем fs/2 , то проявляется элайзинг. Элайзинг проявится в искажении сигнала. Например, если тон в 6000 Гц является входным сигналом для системы ЦОС (без анти-элайзинга и фильтров восстановления) и произведена выборка в 10000 Гц, то сигнал будет интерпретироваться как тон в 4000 Гц. Одним из простейших способов тестирования линейности системы по особенностям частоты является подача на вход чистого тона или синусоидального сигнала. Если при этом на выходе мы получаем не чистый тон или не синусоидальную волну с той же частотой, то тогда можно сделать вывод, что система является нелинейной.
|
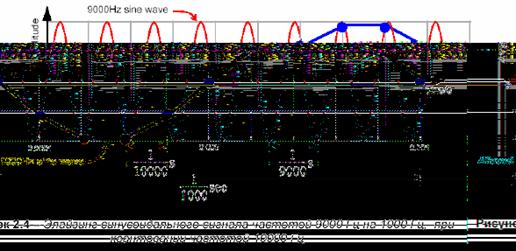
Чтобы увидеть, как выглядит сигнал, подвергнутый элайзингу, рассмотрим рисунок, для которого производится выборка тона в 9000 Гц для fs=10000 Гц. Судя по рисунку 5.4, ясно, что f s /2 = 5000Гц и 9000 Гц будет псевдонимизироваться. По диаграмме видно, что когда мы восстанавливаем сигнал, то получаем 1000 Гц синусоидальную волну.
5.4 Простой элайзинг
Соберите схему, приведенную на рисунке 5.5.
|

Установите следующие параметры в системе (таблица 6).
Т а б л и ц а 6
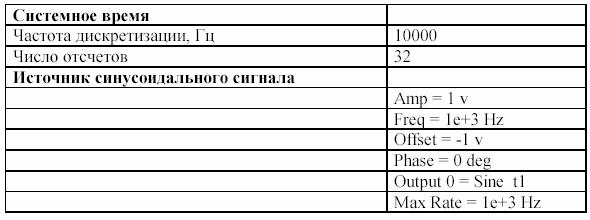
Убедитесь, что все параметры обоих генераторов синусоидальных
волн (в первом примере) абсолютно идентичны:
а) запустите процесс моделирования и затем в Окне анализа проверьте выходные сигналы обоих генераторов синусоидальных сигналов: они должны быть идентичны. Обратите внимание на разные названия двух блоков. Включая и выключая, убедитесь, что когда осуществляется выборка в 1000 Гц, в синусоидальном сигнале в 10000 Гц, присутствуют 10 выборок на период;
б) измените частоту верхнего генератора синусоидальных волн на 2000 Гц. Запустите систему и убедитесь в том, что сигнал на выходе совпадает с тем, который вы предполагаете;
в) теперь измените частоту верхнего генератора синусоидальных волн на 4500 Гц. Это частота приближается к половине частоты выборки fs/2 = 5000 Гц. Убедитесь, просмотрев результаты в Окне анализа, что сигнал на выходе такой, как предполагался;
Обратите внимание, что теперь более двух выборок на период и, следовательно, когда окно SystemView объединяет выборки между собой прямыми линиями (интерполяция первого порядка). Тем не менее, квантование сигнала осуществляется в соответствии с критерием Найквиста, и поэтому вся информация о синусоидальном сигнале (амплитуда, фаза и частота) сохраняется;
г) в этот раз мы изменяем частоту верхнего генератора синусоидального сигнала на верхнюю границу половины частоты выборки fs/2 = 5000 Гц, т.е. на значение 9000 Гц. Пронаблюдайте, что выходной сигнал, когда выборка производится для 10 000 Гц, подвергнулся элайзингу и выглядит как синусоидальный сигнал частотой 1000 Гц;
д) увеличьте частоту верхнего генератора синусоидальных волн до более чем 11000 Гц. Обратите внимание, что на выходе мы опять видим синусоидальный сигнал частотой 1000 Гц.
5.5 Восстановление дискретизированных сигналов
Соберите систему (см. рисунок 5.6):
|
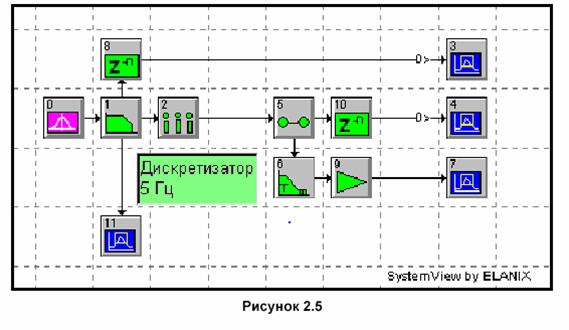
Установите следующие параметры в системе (таблица 7).
Т а б л и ц а 7
|
![]()
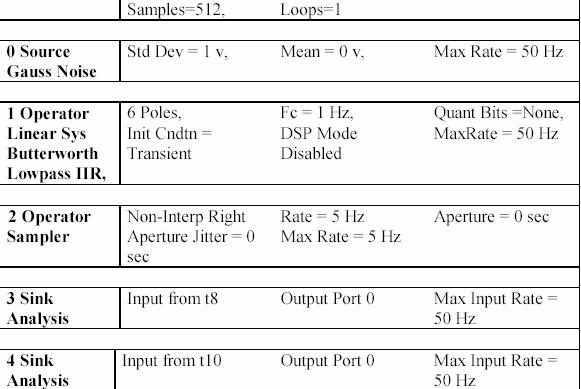
Продолжение таблицы 7

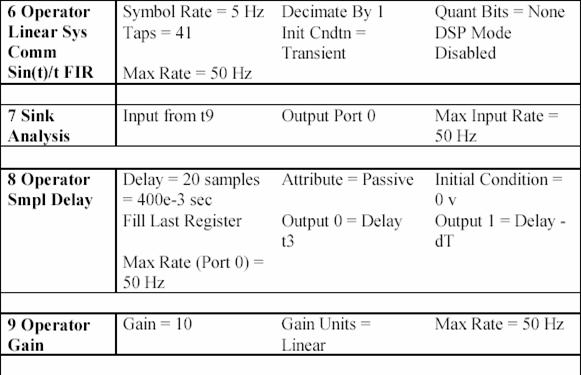

Это упражнение иллюстрирует источник случайных помех с ограниченной полосой пропускания 1 Гц (односторонние). Над этим сигналом была произведена выборка с частотой в 5 Гц, а затем он был восстановлен, используя функцию sinc (sin x/x). Спектр Xs(f) дискретизированного сигнала определяется как:
|
|
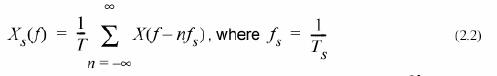
где X(f) - спектр оригинала недискретизированного сигнала. Наиболее качественное восстановление исходного сигнала x(t) из его отсчетов xs(t) определяется как
|
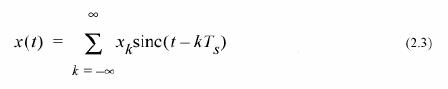
Принимая во внимание формулу 5.2 для числа отсчетов K в модели, мы
имеем
|
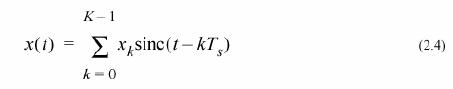
a) выполните
моделирование для проверки основных описанных операций. В Окне анализа ![]() посмотрите на спектр
выбранного сигнала и обратите внимание на повторение (копию) спектра, который
представлен формулой 5.1.
посмотрите на спектр
выбранного сигнала и обратите внимание на повторение (копию) спектра, который
представлен формулой 5.1.
в) посмотрите на входной сигнал (с ограниченной полосой шума), дискретизированный сигнал и восстановленный сигнал. Являются ли исходный и восстановленный сигналы эквивалентными?
|
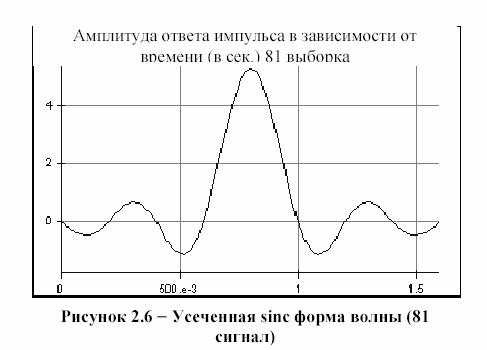
Амплитуда ответа импульса в зависимости от времени (в сек.) 81 выборка:
c) обратите внимание, что для идеального восстановления дискретизированного сигнала, как показано в формуле 5.2 требуется идеальная функция sinc, т.е. с бесконечным числом сигналов (taps). Посмотрите на импульсную характеристику функции sinc, используя открывающееся диалоговое окно параметра маркера sinc (маркер 6), и обратите внимание, что конечное число сигналов, это - усеченная sinc форма волны, так как импульсная характеристика полностью не спадает до нуля. ) Чтобы получать более точное представление о sinc сигнале, число выборок (taps) фильтра sinc должно быть увеличено.
|
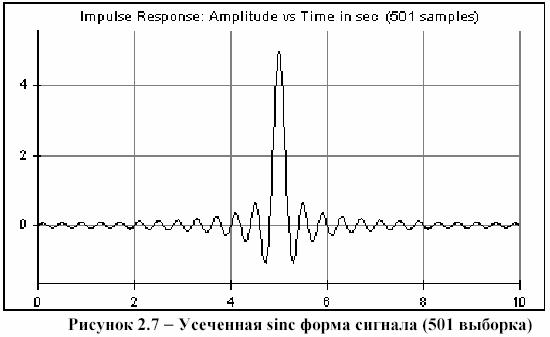
5.6 Задание к выполнению работы. Исследовать схему, показанную на рисунке 5.6. Установите параметры функционального модуля 6 следующими (таблица 8):
Т а б л и ц а 8
|
№ варианта |
Число выборок (taps) |
Частота (Symbol Rate) |
Максимальная частота (Max Rate) |
|
1 |
50 |
5 |
50 |
|
2 |
60 |
5 |
50 |
|
3 |
70 |
5 |
50 |
|
4 |
80 |
5 |
50 |
|
5 |
90 |
5 |
50 |
|
6 |
100 |
5 |
50 |
|
7 |
120 |
5 |
50 |
|
8 |
150 |
5 |
50 |
|
9 |
200 |
5 |
50 |
|
10 |
230 |
5 |
50 |
|
11 |
250 |
5 |
50 |
|
12 |
260 |
5 |
50 |
|
13 |
280 |
5 |
50 |
|
14 |
300 |
5 |
50 |
|
15 |
320 |
5 |
50 |
|
16 |
350 |
5 |
50 |
Продолжение таблицы 8
|
17 |
360 |
5 |
50 |
|
18 |
370 |
5 |
50 |
|
19 |
380 |
5 |
50 |
|
20 |
400 |
5 |
50 |
|
21 |
420 |
5 |
50 |
|
22 |
450 |
5 |
50 |
|
23 |
460 |
5 |
50 |
|
24 |
480 |
5 |
50 |
|
25 |
500 |
5 |
50 |
5.6 Содержание отчета
5.6.1 Краткие сведения из теории.
5.6.2 Схемы исследований.
5.6.3 Экранные изображения сигналов и их спектры.
5.6.4 Анализ полученных результатов.
5.7 Контрольные вопросы
5.7.1 Что такое квантование?
5.7.2 Что означает шум квантования? Какие есть источники квантования?
5.7.3 В каких случаях появляется элайзинг?
5.7.4 Что такое дискретизация?
5.7.5 Способы восстановления дискретных сигналов
Литература
1. Куприянов М.С. Техническое обеспечение цифровой обработки сигналов: Справочник. – СПб.: Наука и техника, 2000.
2. Гаранин М.В., Журавлев В.И., Кунегин С.В. Системы и сети передачи информации. М.: Радио и связь, 2000.
3. Телекоммуникационные системы и сети: Учебное пособие.-Под ред. В.П. Шувалова: М.: Горячая линия-Телеком, 2003.
4. Передача дискретных сообщений: Учебник/Под ред. В.П. Шувалова.
М.: Радио и связь, 1990.
5. Солонина А.И. и др. Основы цифровой обработки сигналов.: 2-е издание. – СПб.: БХВ-Петербург, 2005.-768с.
6. Назаров М.В. и др. Теория передачи сигналов. – М.: Связь, 1980.
7. Зюко А.Г. Теория передачи сигналов. – М.: Радио и связь, 1986.
8. Разевиг В.Д., Лаврентьев Г.В., Златин И.Л. SystemView средство системного проектирования радиоэлектронных устройств. – М.: Горячая линия-Телеком, 2002.
9. Скляр Б. Цифровая связь: Теоретические основы и практическое
применение. - М.: Вильямс, 2003.
Содержание
1 Лабораторная работа №1. Исследование спектров дискретных сигналов 3
2 Лабораторная работа №2. Проектирование конечной передаточной импульсной функции (FIR) 9
3 Лабораторная работа №3. Изучение видов аналоговой модуляции 15
4 Лабораторная работа №4. Формирование дискретных сигналов 21
5 Лабораторная работа №5. Квантование и дискретизация 25
Список литературы 35