Алматы энергетика және байланыс институты
Инженерлік кибернетика кафдрасы
БАСҚАРУ ОБЪЕКТТЕРДІ МОДЕЛЬДЕУ ЖӘНЕ ИДЕНТИФИКАЦИЯЛАУ
050702 - «Автоматтандыру және басқару» мамандығының студенттеріне арналған дәрістер жинағы
Алматы 2009
ҚҰРАСТЫРУШЫ: Ибраева Л.К. «Басқару объекттерді модельдеу және идентификациялау» пәні бойынша 050702 - «Автоматтандыру және басқару» мамандығының студенттеріне арналған дәрістер жинағы.– Алматы: АЭжБИ, 2009. – 84 б.
Дәрістер жинағы «Басқару объекттерді модельдеу және идентификациялау» пәні бойынша типтік жұмыс бағдарлама негізінде «Автоматтандыру және басқару» мамандығының студенттеріне құрастырылған. Жинақ 20 тақырыптан тұрады және теориялық материалды оқығанда, емтихан мен зертханалық жұмыстарға дайындалғанда, курстық және өзіндік жұмыстарды орындағанда студенттерге көмек ретінде негізделген.
Мазмұны
|
|
б |
|
Кіріспе |
5 |
|
1 дәріс. Модельдеудің түсініктемелері. Модельдеу мақсаты |
6 |
|
2 дәріс. Математикалық модельдеудің негізгі терминдері. Математикалық модельдердің түрлері 2.1 Математикалық модельдеудегі негізгі терминдер 2.2. Математикалық модельдердің негізгі түрлері |
10 10 11 |
|
3 дәріс. Модельдеу процесінің қадамдары. Модельдерді құрастырудың негізгі принциптері 3.1 Модельдеу процесінің қадамдары 3.2 Модельдерді құрастырудың негізгі принциптері |
14 14 15 |
|
4 дәріс. Объектілердің динамикалық сипаттамаларын анықтаудың аналитикалық әдістері 4.1 Динамиканың негізгі теңдеулері 4.2 Динамика теңдеулерін қарапайымдау 4.3 Теңдеулерді сызықтандыру |
18 18 20 21 |
|
5 дәріс. Жинақталған параметрлері бар объектілерді аналитикалық әдістермен модельдеу |
22 |
|
6 дәріс. Жинақталған параметрлері бар объектілерді модельдеудің мысалдары |
26 |
|
7 дәріс. Жинақталған параметрлері бар модельдер. Жылу алмастыру процестерді модельдеу |
29 |
|
8 дәріс. Жылулық объектілерінің сипаттамаларын аналитикалық әдістермен анықтау |
33 |
|
9 дәріс. Таратылған параметрлері бар объектілерді модельдеу |
37 |
|
10 дәріс. Идентификация мәселесі туралы жалпы мәліметтер 10.1 Негізгі түсініктемелер 10.2 Идентификациялау әдістерін классификациялау |
41 41 42 |
|
11 дәріс. Идентификациялау есебінің қойылуы 11.1 Идентификациялау объектісі 11.2 Идентификациялау есебінің қойылуы |
45 45 46 |
|
12 дәріс. Сызықты динамикалық объектілерді идентификациялау. Тура әдістері 12.1 Динамикалық сипаттамаларды тура әдістермен анықтау 12.2 Өтпелі функция бойынша идентификациялау |
49 49 50 |
|
13 дәріс. Сызықты динамикалық объектілерді идентификациялау. Тура әдістері 13.1 Екінші ретті процестердің өтпелі функциясы көмегімен графикалық идентификациялау 13.2 Импульсті өтпелі функция көмегімен графикалық идентификациялау 13.3 Жиілік сипаттама көмегімен идентификациялау |
53 53 54 54 |
|
14 дәріс Сызықты объектілерді параметрлік идентификациялау 14.1 Статикалық детерминерленген сызықты модельдер 14.2 Динамикалық детерминерленген модельдер |
57 57 59 |
|
15 дәріс. Сызықты динамикалық объектілерді параметрлі емес идентификациялау. Корреляциялық функциялар 15.1 Параметрлі емес модельді анықтаудың жалпы амалдары 15.2 Сигналдардың корреляциялық функцияларын анықтау |
61 61 62 |
|
16 дәріс. Сызықты динамикалық объектілерді параметрлі емес идентификациялау. Винер-Хопф теңдеуі 16.1 Импульсті өтпелі функцияны анықтау 16.2 Винер-Хопф теңдеуін алгебралық әдісімен шешу |
65 65 66 |
|
17 дәріс. Объектілердің сипаттамалары мен сигналдарын аппроксимациялауда негізделген идентификациялау әдістері 17.1 Функцияларды аппроксимациялау туралы қысқаша мәліметтер 17.2 Импульсті өтпелі функцияның дискретті мәндерін тегістеу 17.3 Импульсті өтпелі функцияны алдын-ала аппроксимациялауда негізделген идентификациялау әдісі |
68 68 69
71 |
|
18 дәріс. Объектілер мен сигналдардың динамикалық сипатта-маларын аппроксимациялауда негізделген идентификациялау әдістері 18.1 Импульсті өтпелі және корреляциялық функцияларды бірге аппроксимациялауда негізделген идентификациялау әдісі 18.2 Сигналдарды аппроксимациялауда негізделген идентификациялау әдісі |
72
72 73 |
|
19 дәріс. Сызықты емес объектілерді идентификациялау 19.1 Сызықты емес динамикалық объектілерді идентификациялаудың ерекшеліктері 19.2 Объектілердің сипаттамаларын сызықтандыруда негізделген әдістер 19.3 Априорлы белгілі түрлері бар сызықты емес функцияларын идентификациялау 19.4 Жалпы түрдегі сызықты емес объектілерді идентификациялау 19.4.1 Функционалдық модельдер 19.4.2 Бағаланатын параметрлері бойынша сызықты болып табылатын модельдер. |
76 76 77 77 78 78 79 |
|
20 дәріс. Алдынала өңдеу алгоритмдерді және сәйкестікті бағалау 20.1 Объектінің стационарлығы мен сызықтығын бағалау алгоритмдері 20.2 Модельдің нақты объектіге ұқсастық дәрежесін санды бағалау Әдебиеттер тізімі |
80 80 81 |
Кіріспе
Инженерлік қызмет алдымен техникалық объектілерді жобалаумен байланысқан. Жобалау дегеніміз - өнімді жасаудың бейнелеуін алу процесі. Техниканың әртүрлі салаларында жобалану объект ретінде өнімдер немесе процестер болуы мүмкін. Ғылым және техника прогресі күрделі техникалық объектілердің, яғни өзара байланысқан элементтерінің көп санынан тұратын күрделі жүйелердің пайда болуына себеп болады.
Күрделі жүйелерді (осындай жүйелерге басқару объектілер да жатады) өңдеп, жобалап жасаған кезде қарастырып отырған объектілердің сандық және сапалық қасиеттерін білу қажет. Көп деген жағдайлар себебінен әдетте күрделі объектілердегі осындай заңдылықтарын практикалық тексеру мүмкін емес. Сонымен бірге осындай тексеру көп материалдар шығындарын және көп уақытты талап етеді. Осы себептерден қарастырып отырған күрделі объектілердің қасиеттері мен заңдылықтарын модельдеу әдістері негізінде зерттеудің өте көп мағынасы бар.
Қоршаған орта туралы біздің тәжірибелеріміз біздің қабылдауымызда негізделген. Бұл мәлімет бірақ тікелей қолданылмайды. Әдетте ол объектіні бейнелеп зерттеуге қолданылатын қарапайым қасиеттер жиынына түрленеді. Сапа жағынан қасиеттер жақсы, жаман, ауыр, т.б. болуы мүмкін, бірақ модельдеу үшін біз көбінесе өлшенетін сандық қасиеттерін қолданамыз. Зерттелетін шамалар объекттегі нақты шамалардан қарапайым болған кезде ғана зерттеулерді өткізуге болады. Сонымен бірге барлық қасиеттер бір уақытта қарастырылмайды. Әдетте қасиеттер жиынынан бізге бірсыпыра қасиеттері керек. Мысалы, бір құжаттың ксерокопиясын қарастырайық. Көшірімін жасаған кезде құжаттың көп деген қасиеттері өзгереді: қағаз, оның форматы басқа болуы мүмкін. Бірақ бізге тек қана құжаттың мазмұны керек болса, біз көшірмеге қанағаттанамыз. Тек қана қажетті қасиеттердің минимал санын қарастыру мақсатымен модель әдейі қарапайымдалады.
Модель ешқашан да жеткілікті толық болмайтынын түсіну қажет. Ол әрқашан да шектелген және модельдеу мақсаттарына сай болуы керек, берілген объекттің қажетті қасиеттер сандары мен олардың толықтығы анықталған зерттеуге қажетті болатындай бейнеленеді.
Модельді зерттеу қадамында модельдеудің уақыт интервалында модель параметрлерінің белгіленген мәндерінде модельденетін жүйенің жүріс-тұрысы, яғни модельді «орындау» («execution») жаңадан өндіріледі. Әдетте ізделінген нәтижеге жету үшін модельді бір рет орындау жеткілікті болмайды. Зерттеу табысы көбінесе есептеу тәжірибені автоматтандыру мүмкіндіктерден тәуелді болады. Қазіргі кездегі компьютерлік модельдеу пакеттері есептеу тәжірибелерді ұйымдастырғанға виртуалды стенд концепциясын қолданады.
1 дәріс. Модельдеудің түсініктемелері. Модельдеу мақсаты
Дәрістің мазмұны:
- модельдеудің түсініктемелері; модельдер түрлері; модельдеудің мақсаттары.
Дәрістің мақсаты:
- модельдеудің негізгі түсініктемелері мен модельдер түрлерін оқу.
Ғылыми зерттеулерде бақылаудан немесе тәжірибелерден алынған мәліметтердің аз сандарында негізделген болжамдардың - гипотезалардың көп мағынасы бар. Ұсынылған гипотезаларды тез және толық тексеру арнайы тәжірибелер арқылы орындалады. Гипотезаларды тұжырымдап, олардың дұрыс екенін тексеру үшін аналогиялар, яғни екі объекттің дербес ұқсастығы туралы пікірлер қолданылады. Гипотезалар әдетте практикада тексерілетін ғылыми пікірлерге ұқсастығы бойынша жасалады. Сонымен, аналогиялар гипотезалары тәжірибемен байланыстырады. Нақты ортаны суреттейтін гипотезалар мен аналогиялар көрнекілік болып, сонымен бірге зерттеуге ыңғайлы логикалық сұлбалар түрде көрсетілуі керек. Пікірлер мен логикалық құрастыруларды жеңілдетіп, құбылыстар табиғатын анықтайтын тәжірибелерді өткізуге мүмкіндік беретін логикалық сұлбалар модельдер деп аталады. Басқа сөзбен айтқанда, модель дегеніміз нақты объектті орынбасатын объект. Осындай объект моделін құрастыру процесін модельдеу деп атайды. Модельдеу нақты объекттің қасиеттерін орынбасар объект көмегімен зерттеуге мүмкіндік береді.
Модельдеу - әртүрлі процестер мен құбылыстарды зерттеуге қолданатын көп тараған әдіс. Процестердің күрделілігі процестің өтуін анықтайтын параметрлерінің көп санымен, параметрлер арасындағы әртүрлі өзара байланыстар және өзара әсерлермен анықталады. Біздер зерттеулерді жеңілдету мақсатымен осындай ақпараттар көлемін азайтуға, таңдалынатын мүмкіншіліктер санын шектеуге тырысамыз. Бұл мақсатқа жету үшін процестерді зерттеуге модельді яғни зерттелетін процестің қажетті бағытта шектелген бөлек сипаттамаларын бейнелейтін қарапайымдалған жүйені қолданамыз. Берілген құбылыс, процесс немесе техникалық жүйені тікелей зерттеу орнына модель деп аталатын басқа құбылысқа, процеске немесе техникалық жүйеге көшу модельдеудің мәнісі болып табылады. Осындай көшудің негізгі мақсаты – зерттеуді жеңілдету, біздерге керекті шамаларды анықтауға қол жеткізу, зерттелетін құбылыстарды жасанды жаңадан өңдеу.
Сонымен, берілген объекттің барлық немесе кейбір қасиеттерімен сәйкес келетін қасиеттері бар кез келген объектті берілген объекттің моделі деп атаймыз. Нақты объектте өткізуге қиын немесе ыңғайсыз қымбат болатын зерттеулерді өткізу үшін модель жасалады.
Модельді жасаудың кейбір мақсаттары мен негізгі зерттеу түрлерін белгілеуге болады:
- мәнін түсіну құралы ретінде модель айнымалылардың өзара байланыстарын, олардың уақыт бойынша өзгеру айырмашылықтарын, маңызды заңдарын анықтауға мүмкіндік береді. Модельді жасаған кезде зерттелетін объекттің құрамы түсінікті болады, маңызды себеп-салдар байланыстары анықталады. Модельді құрастырған кезде бірте-бірте модельге қойылатын талаптар қөзқарасы жағынан бастапқы объекттің қасиеттері маңызды және маңызды емес деп бөлінеді. Бастапқы объект жұмысының біздерге қажетті қасиеттеріне қатыс болатын ерекшеліктері ізделінеді. Белгілі мағына жағынан ғылыми қызмет табиғат құбылыстарының модельдерін құрастырудан және зерттеулерден тұрады;
- болжау құралы ретінде модель объекттің жүріс-тұрысын болжауды үйреніп, әртүрлі модель басқару нұсқаларын сынап, оны басқаруға мүмкіндік береді. Әдетте нақты объектілермен тәжірибе өткізу ыңғайсыз, кейбір кезде қауіпті немесе кейбір себептерден - тәжірибе ұзақтығы, объекттің бүлінуі немесе жойылу қауіп-қатерінен, нақты объекттің жоқтығынан (мысалы, ол әлі жобалануда) мүмкін емес;
- құрастырылған модельдерді параметрлердің оптималды қатынастарын табуға, кейбір ерекше режимдерін зерттеуге қолдануға болады;
- кейбір кезде модель бастапқы объектіні оқыту мақсатымен орын басады, мысалы, персоналды нақты жағдайдағы жұмысқа дайындағанда тренажер ретінде немесе виртуалды зертханада зерттелетін объект ретінде қолдануда. Орындалатын модульдер түрінде жасалған модельдер басқару жүйелерді стендтерде зерттегенде басқару объектілердің имитаторлары ретінде қолданылады, жобалаудың бастапқы кезеңдерінде болашақ аппаратты жасалатын басқару жүйелердің өзінің орнын басады.
Модельдерді жағдайға байланысты екі топқа бөлуге болады: материалды және идеалды; сондықтан заттық және абстрактты модельдеуді қарастыруға болады. Заттық модельдеудің негізгі түрлері физикалық және аналогты модельдеу болып табылады. Нақты объектке оның үлкейтілген немесе кішірейтілген көшірмесі сәйкес қойылса, модельдеуді (макеттеуді) физикалық деп атайды. Бұл көшірме ұқсастық теориясы негізінде зерттелетін құбылысты сипаттайтын негізгі саңдардан алынған ұқсастық критерийлер бойынша жасалады, сондықтан модельде қажетті қасиеттер сақталынды деуге болады. Физикалық модельдерде белгілі зерттеуге қажетті бастапқы объекттің геометриялық пропорцияларынан басқа да қасиеттері сақталынады (мысалы, объект материалы немесе бояу гаммасы). Мысалы, ұшақты жобалаған кезде аэродинамикалық қасиеттері бірдей болатын оның макеті жасалады. Физикалық модельді жасағанда келесіні есепке алу керек: нақты жүйеге қарағанда талдаудың қуатты әдістерін қолдануға мүмкіндік беретіндей модельмен жұмыс істеу қарапайым және қауіпсіз болуы керек, Қарапайым жүйелер үшін (мысалы, гидравликалық немесе бірфазалы жылулық жүйелер) ұқсастық принципі және физикалық модельдеу өзін дәлелдейді, себебі критерийлер сандары шектелген болады. Физикалық модельдеудің негізгі кемшілігі – объекттің әр нұсқасына өзінің моделін жасау керек, бұл жағдай материалды ресурстарын және жұмыстың көп көлемін талап етеді. Сонымен физикалық модельдеуді қолданудың аймағы шектелген, сондықтан күрделі жүйелерді зерттеудің негізгі әдісі математикалық модельдеу болып табылады.
Аналогты модельдеу бастапқы объектті басқа физикалық табиғаты бар, бірақ жүріс-тұрысы бастапқы объектісімен бірдей болатын объектпен алмастыруда негізделген. Мысалы, тербелістер мен резонансты зерттегенде механикалық жүйелер заңдылықтарын, сонымен бірге электр тізбектерін қолдануға болады. Аналогты модельдеуде орынбасу объектте керекті ерекшеліктерін көріп, оларды дұрыс түсіну өте маңызды. Физикалық және аналогты модельдеу зерттеудің негізгі әдісі ретінде модельмен тәжірибе жасауды талап етеді, бірақ бұл тәжірибе бастапқы объекттегі тәжірибеден тартымды болады. Кезінде аналогты есептеу машиналары кең қолданылған. Олардың көмегімен модельдеу өткізу электр құбылыстарының басқа физикалық табиғаты бар құбылыстармен ұқсас болуында негізделген. Мысалы, электр тізбектегі тербелістер ракетаның бұрыш тербелістеріне ұқсас, ал электр тізбекпен тәжірибелерді өткізу арзан және қауіпсіз (ұшып баражатқан ракетаға қарағанда). Аналогты машиналарда жаңадан өңделетін электр тербелістерді арнайы аспаптармен – осцилографтармен бақылап, модельдің жүріс-тұрысын «көруге» болады.
Идеалды модель дегеніміз - нақты немесе елестететін объектілердің абстрактты бейнелері. Идеалды модельдеуді екі түрге бөледі: интуитивті және таңбалы. Қолданатын модель болғанымен, оны бейнелей алмай, бірақ оның көмегімен қоршаған ортаны болжап немесе түсініктіру өткізсе, интуитивті модель туралы әңгімелегеніміз. Осы мағынада әр адамның өмірлік тәжірибесі оның қоршаған ортасының моделі деп есептеуге болады. Әртүрлі жағдайда адам миы шешім қабылдау есебін қалай шешетінін біз әлі білмейміз.
Модель ретінде белгілерді немесе символдарды: сұлбалар, графиктер, сызбалар, әртүрлі тілдердегі мәтіндер, сонымен бірге формалды, математикалық формулалар және теорияларды қолданатын модельдеу таңбалы модельдеу деп аталады. Таңбалы модельдеуге міндетті түрде қатынасатын интерпретаторы болуы керек (әдетте адам болады). Сызбалар, мәтіндер, формулалардың өз бетінше ешқандай мағынасы жоқ, оларды түсінетін және күнделікті қызметінде қолданатын біреу болуы керек. Таңбалы модельдеудің маңызды түрі математикалық модельдеу болып табылады. Объекттердің физикалық табиғатынан дерексіздендіріп, математика идеалды объекттерді оқиды. Математикалық модельдеу табиғат заңдарының саны шектеулігінде және ұқсастық принциптерінде негізделген. Яғни басқа сөзбен айтқанда әртүрлі физикалық табиғаты бар құбылыстар бірдей математикалық тәуелділіктермен бейнеленулері мүмкін. Мысалы, дифференциалдық теория көмегімен аталып кеткен электр немесе механикалық тербелістерді жалпы түрде оқуға, сонан соң алынған білімдерді белгілі физикалық табиғаты бар объектті зерттеуге қолдануға болады.
Математикалық өрнектермен немесе алгоритмдермен формалданған жүйе бейнеленуі математикалық модельдеу деп аталады. Кез келген физикалық шамалардан тұратын математикалық өрнекті процестің математикалық моделі ретінде қарастыруға болады. Физикалық модельдеуге қарағанда математикалық модельдеу оригиналдың тек қана математикалық бейнелеуі бар және математикалық өрнектермен байланысқан параметрлерін зерттеуге болады. Сонымен бірге зерттелетін процестің физикасы сақталмайды, бір теңдеулер табиғаты жағынан әртүрлі құбылыстарды бейнелеуге мүмкіндік беріп, объекттің жүріс-тұрысын толық бейнелемей, оның бөлек функционалды байланыстарын табуға мүмкіндік береді. Сонымен, нақты объекттің математикалық моделі деген берілген физикалық объектке сәйкес қойылған математикалық объект деуге болады. Әрине, нақты физикалық байланыстарды көрсететін математикалық тәуелділіктерді анықтайтын өрнектер белгілі болу керек. Келешекте біздер тек қана математикалық модельдер туралы әңгімелейміз.
Математикалық модельдеудің маңызды түрі – компьютерлік модельдеу. Әртүрлі қызмет бағдарламаларды қосындылап (мысалы, уақыт бойынша сурет немесе графиктерді салатын), математикалық модельдің бағдарламалық іске асырылуы компьютерлік модель деп аталады. Компьютермен қабылданып, онымен интерпретацияланса, компьютерлік модель физикалық модельдің қасиеттерін білдіреді. Компьютерлік модель физикалық құрылғы ретінде сынақ стендтер, тренажерлар, виртуалды зертханалар құрамына кіруі мүмкін. Бұл модельдің арнайы түрі, өзінде абстрактты және физикалық қасиетттерін қабылдайтын, көп деген пайдалы мүмкіндіктері бар. Солардың ішіндегі бастысы – модельді жасау және өзгерту өте қарапайым процесс болып табылады. Сонымен бірге алынатын нәтижелерінің дәлдіктері өте жоғары және модельдердің функционалды қүрделі болатынын атап кету керек. Сондықтан, қазірде модельдеу деп әдетте компьютерлік модельдеуді атайды.
Математикалық модельді құрастыру физика, химия, биология пәндерінен белгілі заңдарды қолданумен орындалады. Алынған модельді аналитикалық жолмен зерттеуге болады, бірақ көбінесе оны орындайтын бағдарлама дайындалады. Компьютерлік модельдеудің бастапқы қадамдарында осы бағдарламалар жоғарғы деңгейлі бағдарламалау тілдерде жасалған, ол кезде қолданылатын бағдарламалау технологиялар модельдерді жасауға өте көп уақытты талап ететін. Қазірде математикалық модельді модельдеу бағдарламаға түрлендіру процесін автоматтандыратын модельдеуге арналған көп деген жүйелер, модельдеу пакеттер өңделген. Қазіргі пакеттерді қолданушының көзқарасы жағынан компьютерлік модельді құрастыру негізінде модельдің математика тіліндегі бейнелеуін қолданылатын жүйенің тіліне көшіруге және ұсынылған сандық әдістердің ішінен керектісін таңдауда тұрады.
Математикалық модельдерге қойылатын талаптар: дәлдік – бұл қасиет модель көмегімен болжанған объекттің параметрлерінің мәндері ақиқат мәндермен сәйкестігінің дәрежесін көрсетеді; компьютер уақытының шығындарының тиімділігі; универсалдық яғни біртекті объектілер топтарына анализдеуге қолдануға болатындығы.
2 дәріс. Математикалық модельдеудің негізгі терминдері. Математикалық модельдердің түрлері
Дәрістің мазмұны:
- математикалық модельдеудің негізгі түсініктемелері; математикалық модельдердің түрлері.
Дәрістің мақсаты:
- математикалық модельдеудің негізгі түсініктемелерін және математикалық модельдердің түрлерін оқу.
2.1 Математикалық модельдеудегі негізгі терминдер
Кез келген математикалық модель келесі: компоненттер, айнымалылар, параметрлер, функционалдық тәуелділіктер, шектеулер деп аталатын құрастырушылардың реттелген комбинациясы болып табылады.
Сәйкес ұйымдастыру амалымен жүйені құрастыратын құрамдастыру бөліктерді модель компонеттері деп түсінеді. Компоненттер бөлінбейтін құрамдастырушылар (модель "элементтері") немесе "ішкі жүйе" болып табылатын құрамдастырушылар болуы мүмкін. Әдетте жүйенің кірістері мен шығыстары айнымалылар деп, ал басқа шамалар – параметрлер деп аталады. Мұндай келісім шарт бойынша алынады. Қосымша келісімдер болмаса қайсысы айнымалы, қайсысы параметр деген сұраққа жауап табылмайды. Осындай келісім ретінде, мысалы, функциялар класы алынуы мүмкін. Айнымалыларды кірістегі және шығыстағы айнымалы деп бөлгеніміз де абсолютты болмайды. Мұндай бөлу тек қана анықталған жүйеге қолданылады. Зерттелетін жүйенің анықталған қасиеттеріне сүйену керек. Жүйе кірістері (экзогендік айнымалылар) жүйеден тыс пайда болады және сыртқы себептер әрекеттері нәтижесінен туады; жүйе шығыстары (эндогендік айнымалылар) экзогендік айнымалылар жүйеге әсер еткен себебінен жүйеде пайда болады. Математикалық модельдердің бас құрастырушылары – функционалдық тәуелділіктер. Олар жүйенің немесе компоненттің айнымалыларының және параметрлерінің жүріс-тұрысын бейнелейді. Әдетте олар экзогендік (х) және эндогендік (у) айнымалылар немесе айнымалылар және олардан тәуелді параметрлер (р) арасындағы ішкі қатынастарды орнатады:
а) y = φ(p,x),
б) р = ψ(x,y).
φ функциясы көбінесе операторлық (немесе оператор), ал ψ функциясы – параметрлік деп аталады. Жүйенің жұмысының заңы аналитикалық, графикалық, кестелік, т.б. түрде берілуі мүмкін. Модельдердің соңғы құрамдастырушысы – шектеулер. Қарапайым кезде шектеулер деп модель аргументтерінің векторының өзгеру аймағын түсінеді xÎDx. Модель параметрлері де кейбір рұқсат етілген аймақта берілуі мүмкін pÎDp. Көбінесе модельденетін жүйе қоршаған ортаға әсер етпейді деп белгіленеді. Қоршаған ортаның әсерін есепке алмау негізделген болуы керек.
2.2 Математикалық модельдердің негізгі түрлері
Қолданудың әртүрлі аспектілерін қанағаттандыратын жалпы универсалды модельді жасау мүмкін емес. Басқарылатын объекттің кейбір қасиеттерін қамтып көрсететін ақпаратты алу үшін модельдерді классификациялау қажет.
Классификациялаудың негізінде φ оператордың ерекшеліктері жатады. Уақыттық және кеңістіктік белгілері бойынша басқару объекттердің барлық түрлерін келесі кластарға бөлуге болады: статикалық немесе динамикалық; сызықты немесе сызықты емес; уақыт бойынша үздіксіз немесе дискретті; стационарлы немесе стационарлы емес; параметрлері кеңістік бойынша өзгеретін процестер және параметрлі кеңістік бойынша өзгермейтін процестер. Математикалық модельдер сәйкес объектілерді суреттейтін болғандықтан, оларға да осы кластарды қолдануға болады. Модельдің толық атауына айтылған белгілердің барлығы кіруі мүмкін. Осы белгілер модельдердің сәйкес типтер атауларының негізі болып табылды.
Жүйеде зерттелетін процестер сипаттарына сәйкес модельдердің барлығын келесі түрлерге бөлуге болады.
Процесте кез келген кездейсоқ әсерлер жоқ деп есептелсе, процесс детерминерленген (анықталған) деп аталады; осындай процестерді бейнелейтін модельдер – детерминерленген модель болады.
Ықтималдық процестер мен оқиғаларды бейнелейтін модельдер стохастикалық модель деп аталады; бұл кезде кездейсоқ процестің бірсыпыра іске асырылуы болжанып, орта сипаттамалары бағаланады.
Стационарлы және стационарлы емес модельдер. Егер де φ оператордың түрі және оның p параметрлері уақыт бойынша өзгермесе, яғни келесі орындалса
φ[p(t),x]= φ[p(t+τ),x], яғни y= φ(p,x)
онда модель стационарлы болып табылады.
Егер де модель параметрлері уақыт бойынша өзгеретін болса
y= φ[p(t),x]
модель параметрлік стационарлы емес.
Уақыттан функция түрі де тәуелді болса, бұл жағдай стационарлы еместіктің ең жалпы түрі болады. Бұл кезде функцияға тағы бір аргумент қосылады:
y= φ(p,t,x)
Статикалық және динамикалық модельдер. Модель түрлерін осылай бөлгеннің негізінде зерттелетін объекттің материалды жүйе ретінде қозғалысының ерекшеліктері жатады.
Басқару есептер көзқарасы жағынан модельдер туралы әңгімелесек, кеңістік деп геометриялық кеңістікті атамайтынымызды еске алу қажет. Бұл кезде кеңістік деп күй кеңістігін, яғни шығудағы у айнымалыларының күй координаталарын түсінеміз. у векторының элементтері ретінде әдетте бақыланатын технологиялық параметрлер (шығын, қысым, температура, ылғалдық, тұтқырлық, ж.б.) болады. у векторының элементтерінің құрамы объекттің өзі үшін (модельге қарағанда) толығырақ болуы мүмкін, себебі модельдеу кезде нақты объекттің қасиеттерінің тек қана бір бөлігін оқу қажет. Күй кеңістігінде және уақыт бойынша басқару объекттің қозғалысы y(t) векторлық процесс көмегімен бағаланады.
Егер де жүйе күйі өзгермесе, яғни жүйеде тепе-теңдік орындалса, жүйе моделі статикалық деп аталады, бірақ қозғалыс тепе-теңдіктегі объекттің статикалық күйімен байланысқан. Статикалық модельдердің математикалық бейнелеуіне айнымалы ретінде уақыт кірмейді, бұл бейнелеу алгебралық теңдеулерден немесе объект таратылған параметрлері бар объект болса, дифференциалдық теңдеулерден тұрады.
Статикалық модельдер әдетте сызықты емес болады. Олар объекттің бір режимнен басқа режимге көшу себебінен пайда болатын тепе-теңдік жағдайын тура бейнелейді.
Динамикалық модель объекттің күйінің уақыт бойынша өзгеруін бейнелейді. Осындай модельдердің математикалық бейнелеуіне міндетті түрде уақыт бойынша туынды кіреді. Динамикалық модельдер дифференциалды теңдеулерді қолданады. Бұл теңдеулердің дәл шешімдері дифференциалдық теңдеулердің тек қана бірсыпыра кластарына белгілі. Көбінесе жуықты болатын сандық әдістерді қолдану керек болады.
Басқару мақсаттарымен көбінесе динамикалық модельді кірудегі және шығудағы айнымалыларды байланыстыратын беріліс функция ретінде көрсетеді.
Сызықты және сызықты емес модельдер. Математикадағы анықтама бойынша келесі L(λ1x1+λ2x2)=λ1L(x1)+λ2L(x2) шарт орындалса L(x) функциясы сызықты болады.
Сол сияқты көп өлшемді функциялар үшін сызықты функцияда тек қана алгебралық қосу және айнымалыны тұрақты коэффициентке көбейту операциялары қолданылады. Егер де модель операторының өрнегінде сызықты емес операциялар болса, модель сызықты емес болады, кері жағдайда – сызықты.
Жинақталған және таратылған параметрлері бар модельдер. Біздер кіргізген терминология бойынша модель атауында “параметрлер” сөздің орнына ”күй координатасы” түсініктемесін қолдану дұрыс болар еді. Бірақ бұл технологиялық процестерді модельдеу тақырыбы бойынша жұмыстардың бәрінде кездесетін қалыптасқан атау.
Егер де процесс айнымалылары уақыт бойынша, сонымен бірге кеңістік бойынша да (немесе тек кеңістік бойынша) өзгеретін болса, онда осындай процестерді бейнелейтін модельдер таратылған параметрлері бар модельдер деп аталады. Бұл кезде z=(z1,z2,z3) геометриялық кеңістігі еңгізіледі және теңдеулердің түрі келесідей болады:
y(z)=φ[p(z),z,x)], p(z)=ψ[y(z),z,x].
Олардың математикалық бейнелеуі әдетте дербес туындылары бар дифференциалдық теңдеулерден немесе қарапайым дифференциалдық теңдеулерден (жалғыз кеңістік координатасы бар стационарлы процестерде) тұрады.
Егер де объекттің күй координаталар
мәндерінің кеңістік бойынша біркелкі еместігін есепке
алмауға болса, яғни келесі градиент ![]() болса, сәйкес модель – жинақталған параметрлері бар модель
болады. Олар үшін масса мен энергия бір нүктеде
жинақталған сияқты.
болса, сәйкес модель – жинақталған параметрлері бар модель
болады. Олар үшін масса мен энергия бір нүктеде
жинақталған сияқты.
Кеңістіктің өлшемі міндетті түрде 3-ке тең болмауы мүмкін. Мысалы, жылытылатын жұмыс ортасы бар және жұқа бүйірлі сырты бар құбырдың моделі әдетте объекттің бір өлшемділігін қолданады – тек қана құбыр ұзындығы есептелінеді. Сонымен бірге, қалың бүйір арқылы жұмыс ортаның шектелген көлемге жылы тасымалдау процесі де тек қана бүйір жуандығын есепке алатын бір өлшемді модельмен бейнелене алады, т.б. Белгілі объекттер үшін сәйкес теңдеулердің түрі негізделуі керек.
Уақыт бойынша үздіксіз және дискретті модельдер. Үздіксіз модельдер жүйелердегі үздіксіз процестерді бейнелейді. Уақыт үздіксіз аргумент ретінде қарастырылатын объект күйін бейнелейтін модельдер уақыт бойынша үздіксіз модель болады:
y(t)=φ[p(t),x(t)], p(t)=ψ[y(t),x(t)].
Дискретті модельдер дискретті болып табылатын процестерді
бейнелеуге қолданылады. Дискретті модель объект жүріс-тұрысын
дискретті уақыттың аралықтарында болжай алмайды. Егер де
уақыт бойынша ∆t
қадамымен кванттауды еңгізсек, онда
![]() шкала қарастырылады, мұнда i=0,1,2…
дискретті уақыт мағынасы болады. Сонда дискретті модель келесі
түрде болады:
шкала қарастырылады, мұнда i=0,1,2…
дискретті уақыт мағынасы болады. Сонда дискретті модель келесі
түрде болады:
y(i)=φ[p(i),x(i),∆t]; p(i)=ψ[x(i),y(i),∆t].
∆t қадамы дұрыс таңдалынса, дискретті модельден алдын ала берілген дәлдікпен нәтижені алуға болады. ∆t өзгерсе, айырымдық теңдеудің де коэффициенттері қайта есептелінуі керек.
Дискретті-үздіксіз модельдер. Егер де үздіксіз процестермен бірге объектте дискретті процестер бар екендігін көрсету керек болса, дискретті-үздіксіз модельдер қолданылады.
3 дәріс. Модельдеу процесінің қадамдары. Модельдерді құрастырудың негізгі принциптері
Дәрістің мазмұны:
- модельдеу процесінің қадамдары; модельдерді құрастырудың негізгі принциптері.
Дәрістің мақсаты:
- модельдеу процесінің қадамдары мен модельдерді құрастырудың негізгі принциптерін оқу.
3.1 Модельдеу процесінің қадамдары
Жалпы кезде модельдеу процесі келесі қадамдардан тұрады:
1. Модельденетін объектті бейнелеу. Ол үшін нақты процесті құратын құбылыстардың құрамы зерттеледі. Осы зерттеу нәтижесінде процестің мағыналы бейнелеуі пайда болады, бұл бейнелеуде мүмкіндік болса, барлық заңдарды дәл көрсету қажет. Осы бейнелеуден қолданбалы есептің қойылуы шығады. Есеп қойылуы модельдеудің мақсаттарын, ізделінетін шамалардың тізімін, қажетті дәлдікті анықтайды. Сонымен бірге есеп қойылуының математикалық формулировкасы болмауы мүмкін.
Маңызды бейнелеу формалданған сұлбаны құрастырудың негізі болып табылады. Формалданған сұлба маңызды бейнелеу мен математикалық модель арасындағы өзара түйін болып табылады. Бұл сұлба міндетті түрде өңделмейді. Тек қана зерттелетін процесс күрделі болғандықтан, маңызды бейнелеуден тікелей математикалық модельге көшу қиын болған кезде. Бұл арада да материалды көрсету түрі мәтіндік болуы мүмкін, бірақ зерттеу есептің процесс сипаттамаларының, параметрлер жүйесінің, сипаттамалар мен параметрлер арасындағы байланыстарының анық математикалық формулировкасы болуы керек.
2. Оригиналдың маңызды қасиеттерін жақсы көрсететін және зерттеуге ыңғайлы модельді таңдау. Формалданған сұлбаны математикалық модельге түрлендіру математикалық әдістерімен қосымша ақпаратты қолданбай орындалады. Бұл қадамда барлық ара қатынастар аналитикалық түрде, логикалық шарттар – теңсіздіктер түрінде жазылады, барлық мағлұматтар мүмкіндік болса аналитикалық түрге келтіріледі. Математикалық бейнелеуді құрастырғанда әртүрлі теңдеулер қолданылады: алгебралық (стационарлы режимдерге), қарапайым дифференциалды теңдеулер (стационарлы емес режимдерге), таратылған параметрлері бар объекттердің динамикасын математикалық бейнелеуге дербес туындылы дифференциалдық теңдеулер қолданылады. Егер де объектте детерминерленген қасиеттер мен бірге стохастикалық та қасиеттері болса, интегро-дифференциалдық теңдеулер қолданылады.
3. Модельді зерттеу. Бұл қадамда барлық әрекеттер модельге қолданылады және олар объект туралы білімдерді алуға, оның дамуының заңдарын орнатуға бағытталған. Модельді зерттеудің маңызды артықшылығы - әртүрлі бастапқы шарттар үшін және олардың өзгеру тәртіптері әртүрлі болғанда көптеген оқиғаларды қайталау мүмкіншілігі.
4. Нәтижелерге талдау беру. Математикалық модельде алынған мәндерді нақты зерттелетін объектке көшіру сұрақтары осы қадамда қарастырылады. Зерттеушіге модельмен орын басқан объекттің қасиеттері керек. Осындай көшірудің мүмкіншілігі модельмен оригиналдың элементтерімен қатынастарының сәйкес болғанында негізделген. Бұл қатынастар модельдеу процесінде орнатылған болатын. Математикалық модельді қолданғанда нәтижелердің дәлдігін, яғни объекттің бейнеленуінің адекваттылық дәрежесін еске алу керек.
Математикалық модельдеуді қолдану жетістіктері модельдің сәтті жасалғанына, адекваттылығына, модельді оқып білу дәрежесіне, оны қолданудың ыңғайлылығына тәуелді болады. Математикалық модельдеуде компьютерлерді қолдану параметрлер және сыртқы факторлардың мәндерінің өзгеруінің кез келген жағдайларында, сонымен бірге нақты тәжірибелерде жасалынбайтын шарттарда зерттеулерді өткізуге мүмкіндік береді. Сондықтан объектті өңдеу және жобалау қадамдарында туатын көп деген сұрақтарға басқа күрделі әдістерді қолданбай жауап алуға мүмкіндік пайда болады.
3.2 Модельдерді құрастырудың негізгі принциптері
Басқару жүйенің өмірлік циклы келесі негізгі периодтардан тұрады: жобалау, пайдалану және модернизациялау.
Технологиялық агрегатты жобалау процесі бір уақытта оны өңдеу мен жасау процестерімен бірдей өтеді. Бұл жағдай басқару жүйелерді жобалау процесінің ерекше өзгешелігі болып табылады. Сонда әлі жасалынбаған техникалық құрылғының қасиеттері туралы ақпаратты алудың жалғыз жолы бар осындай жүйелердің элементтерін сипаттайтын процестерді аналитикалық бейнелеу.
Зерттелетін объекттің белгілі ерекшеліктеріне физиканың (кей кезде химияның да) теориялық заңдылықтар жиындарын қолдану аналитикалық әдістердің негізі болып табылады. Сондықтан аналитикалық модельдерде априорлық қасиеттері бар деп есептеуге болады.
Басқару жүйелерді жобалау процесіне қолданғанда математикалық модельдер өздерінің негізгі міндетін қанағаттандыру керек, басқару жүйенің құрамы туралы шешім қабылдау процесін ақпаратпен қамтамасыздандыру. Осындай жүйелердің элементтерінің параметрлерін оптималдау сұрағы жобалаудың соңғы қадамында туады - бұл енгізу процесі болады. Өзінің ерекше қасиеттеріне қарай (модельдеу көзқарасы жағынан) енгізуді қолданудың басталуы деп есептеуге болады. Технологиялық агрегаттарды жобалаған кезде модельдерге қойылатын талаптар объекттің тек қана құрамы туралы шешім қабылдауда емес, сонымен бірге оның элементтерінің параметрлері туралы (мысалы, құбырлардың ұзындығы сияқты) шешім қабылдау қажеттілігімен байланысты.
Басқару жүйелерді қолдану процесі объекттің математикалық модельдеріне өзінің шарттарын қояды, олар өзінің міндетіне қарай келесідей:
- технологиялық процестің өлшеу аспаптармен бақыланбайтын координаталары туралы;
- әртүрлі режимді факторлар себебінен уақыт бойынша өзгеретін технологиялық процестің кейбір бөлімдерінің қасиеттері туралы ағынды (оперативті) ақпаратты алуға қажет болады.
. Модельдердің бөлінген кластарының екеуі де агрегаттарды қолданудың қажетті дәлдігімен жүйе реакциясын болжауы керек.
Сонымен, математикалық модельдерді құрудың екі принципиалды әртүрлі амалдары бар.
Модельді таңдағанда зерттелетін процестің жүріс-тұрысын анықтайтын физика-химия заңдылықтарды есепке алуда бірінші амал негізделген. Осындай модельдер аналитикалық модельдер деп аталады. Басқа сөзбен айтқанда, модель теңдеулерін алу үшін зат пен энергияны сақтау фундаменталды заңдылықтары қолданылады, объектте өтетін физикалық және химиялық процестерді теориялық анализдеп модель теңдеулері шығарылады. Мұнда тәжірибелерді өткізу керек емес, сондықтан процестері жақсы оқылған объекттері жобалау қадамында олардың статикалық және динамикалық сипаттамаларын анықтау үшін осы әдістерді қолдануға болады. Объектті толығымен бейнелеген кезде алынған жүйенің есебін табу өте қиын.
Екінші амал "қара жәшік" концепциясында негізделген, яғни объекттің ішкі құрамы белгісіз, одан да зор, зерттеушіге керек те емес деп есептелінеді. Барлық ақпарат объектті пассивті және активті тәжірибелерде бақылаудан алынады, басқа сөзбен айтқанда процесс қасиеттерін "кіріс -шығыс" қатынас арқылы бейнелеген жеткілікті деп есептелінеді. Әдетте рұқсат етілген модельдер кластары ізделінетін параметрлер арқылы сызықты болатын белгілі функциялар жүйесі бойынша жіктеу қатарлары ретінде таңдалынады. Осындай жолмен алынған модельдер эмпирикалық (тәжірибелік) деп аталады. Тәжірибелік модельдердің артықшылығы параметрлердің өзгеру диапазонының кіші аралығында объект қасиеттері дәл бейнелетіндігі және математикалық бейнелеудің қарапайымдылығы. Бұл модельдердің негізгі кемшілігі – теңдеуге кіретін параметрлер мен объект сипаттамалары арасындағы функционалдық байланысты анықтауға мүмкін емес.. Сонымен бірге, осындай модельдерді басқа біртектес объекттерге қолдануға болмайды.
Аналитикалық және тәжірибелік әдістер арасында ақпараттық жағынан және қолдану аймағы жағынан принципиалды айырмашылықтары бар. Аналитикалық әдістер екі сұраққа жауап бере алады: объекттің жүріс-тұрысы қандай және неге олай? Екінші түрдегі модельдер тек қана "қандай?" деген сұраққа жауап бере алады. Эмпирикалық әдістер тек қана белгілі жұмыс істейтін қондырғыларды автоматтандыру және оптимизациялауға лайықты.
Аналитикалық әдістер эмпирикалық әдістерге қарағанда жалпы болып табылады және олардың көмегімен алынған нәтижелер фундаменталды болады. Бірақ бұл жеңіл берілмейді. Олар эмпирикалық әдістерге қарағанда күрделі және қиындықтар аналитикалық модельді құру кезінен бастап туады. Егер де объектті "қара жәшік" ретінде бейнелеу үшін статистика мен автоматты реттеу теориясынан білімдер жеткілікті болса, аналитикалық модельдерді құру үшін физика, химия, гидродинамика, т.б. пәндердің әртүрлі салаларынан білімдері мен түрлі-түрлі математикалық аппараты қажет. Сонымен бірге бұл қиындықтар аналитикалық модельдердің үлкен ақпараттық сыйымдылығымен орнын толтырады.
Эмпирикалық модельдердің бір түрі – имитациялық модельдер. Процестерді модельдегенде математикалық модельді ізделу шамалар арқылы арнайы теңдеулер жүйесіне түрлендіру міндетті түрде орындалуы кейкезде керек емес. Математикалық модельмен бейнеленетін құбылыстарды олардың логикалық құрамын, уақытта кезектесуін сақтап арнайы модельдеу қондырғылармен немесе есептеу техникамен қайтадан өңдеуді имитациялық модельдеу деп атайды. Аналитикалық әдіске қарсы имитациялық модельдеу кезінде орындалатын әрекеттер мағынасы ізделінетін болып таңдалынған шамалардан әлсіз тәуелді. Ізделінетін шамаларды бағалау үшін модельде айналып жүрген кез келген тіркелген және кейіннен өңдеуге қол жететін лайықты ақпарат қолданылуы мүмкін.
Аппараттық модельдеуде процесті зерттеу үшін арнайы модельдеу қондырғылар қолданылады; олардың жұмыс принциптері механикалық, электр, гидравликалық, жылулық және т.б. құбылыстардың аналогияларында негізделген.
Компьютерде модельдеу аппараттық модельдеудің арнайы түрі болып табылады. Процесті компьютерде модельдеу үшін оның математикалық моделін арнайы модельдеу алгоритмге түрлендіру керек. Осы алгоритмге сәйкес компьютерде зерттелетін процестің элементарлы құбылыстарын (олардың байланыстары мен өзара тәуелділіктерін есепке алып) бейнелейтін ақпарат тудырылады. Бұл ақпараттың кейбір бөлігі модельдеу нәтижесінде алу керекті процестің сипаттамаларын анықтауға қолданылады.
«Имитациялық модель» деген атау процесс-оригинал мен компьютердегі процесс арасында физикалық сәйкестік бар екенін білдірмейді. Бұл екі процесс нақты жүйенің жүріс-тұрысын бейнелейтін ақпарат құрамы мен оның сипаттамалары және модельдеу кезіндегі компьютермен өңделетін ақпарат жағынан сәйкес болады.
Имитациялық модельдер өзінің шешімдерін аналитикалық модельдер сияқты түрде көрсете алмайды, олар тек қана тәжірибемен анықталатын жағдайлардағы жүйе жүріс-тұрысын анализдеуге қолданатын құрал ретінде қолданылады.
4 дәріс. Объектілердің динамикалық сипаттамаларын анықтаудың аналитикалық әдістері
Дәрістің мазмұны:
- динамиканың негізгі теңдеулері.
Дәрістің мақсаты:
- динамиканың негізгі теңдеулерін, теңдеулерді қарапайымдау жолдарын оқып білу; модельдерді сызықтандыру процедурасын қолдануды үйрену.
4.1 Динамиканың негізгі теңдеулері
Аналитикалық модельдер танып білетін модельдер болады. Құбылыс механизмдерін, яғни объектте бар барлық себеп-салдарлық байланыстарды модель операторының құрамында қамтып көрсету осындай модельдердің ерекшелігі.
Кез келген математикалық модельді құрастыру модельденетін объектті физикалық бейнелеуден басталады. Сонымен бірге модельде көрсететін және оларды бейнелеу кезде қабылданатын негізгі келісімдерді орнататын объектте өтіп жатқан "элементарлы" болатын процестерді бөледі. Бұл арада "элементарлы" деген "қарапайым" дегенді білдірмейді, тек қана ол процестер басқа күрделі процестердің құрастырушысы болатынын білдіреді. Әдетте "элементарлы" деп бір құбылыстар класының процестерін есептейді, мысалы, масса алмасу, жылу тасымалдау, т.б. Әдетте келесі "элементарлы" процестер есепке алынады: фазалар ағындарының қозғалысы, фазалар арасында масса алмасу, жылу беру, агрегаттық күйді өзгерту, химиялық түрлендіру. Есепке алынатын элементарлы процестердің тізімін объектті бейнелейтін математикалық модельге енгізілетін құбылыстардың жиыны анықтайды.
Жылу энергетика өндірісінің негізгі технологиясы келесі элементарлы құрастырушылары бар физикалық процестерде негізделген:
- механикалық процестер – қатты материалдарды механикалық өңдеу;
- гидродинамикалық процестер (сұйықтық пен газды тасымалдау);
- жылу процестері (жылыту және суыту);
- масса алмасу процестері (булану және конденсациялану).
Осы барлық процестерінің өту заңдылықтары олар өтетін ортаның қозғалу шарттарымен байланысты, ол шарттар гидро және газодинамика заңдарымен анықталады. Сонымен бірге олардың барлығы (біріншісінен басқа) жүйенің бөлек бөліктері арасында зат пен энергияны тасымалдау элементарлы процестерінде негізделген. Осындай тасымалдау процестердің заңдылықтарын термодинамика оқиды. (Механикалық процестерді оқу серпімділік теориясының және қатты зат механикасының заңдарында негізделген). Сондықтан көп деген технологиялық процестерін модельдеудің теориялық негізі гидро және газодинамика болып табылады.
Технологиялық процестердің элементарлы қадамдарындағы ғылым негізі жалпы болғандықтан, оларды анализдеу және олардың модельдерінің рұқсат етілген кластарын құрастыру принциптері де жалпы болады. Жалпы кезде объекттің математикалық моделін құрастыру кірудегі шаманың кез келген өзгерісінде шығудағы шаманың өзгеруін анықтауға мүмкіндік беретін жүйенің операторын анықтауға саяды. Реттеу объекттердің сипаттамаларын аналитикалық жолмен анықтау олардың дифференциалдық теңдеулерін құрастыруда негізделген. Дифференциалдық теңдеулерді құру негізгі физикалық заңдарда: масса, энергия және қозғалыс мөлшерін сақтау заңдарында негізделген.
Жүйенің күйін әдетте термодинамика заңдарымен өрнектейді. Термодинамиканың бірінші заңының келесідей математикалық және физикалық формулировкасы бар: элементарлы көлемдегі субстанцияның өзгеруі көлем бетінен кіру ағындар мен шығу ағындар шығындарының алгебралық қосындысына тең. Бұл заң материя мен оның қозғалысының жоғалмайтынын бейнелейді және масса, энергия мен қозғалыс мөлшерін сақтау заңдар арқылы жазылады.
Массаны сақтау заң. Бұл заң классикалық механиканың негізгі заңы болып табылады: қозғалыстағы материалды жүйенің кез келген бөлігінің массасы уақыттан тәуелсіз және тұрақты шама болады.
Қозғалыс мөлшерін сақтау заңы: қозғалыстағы материалды жүйенің кез келген бөлігінің қозғалыс мөлшерінің өзгеру жылдамдығы сыртқы күштердің қосындысына тең.
Энергияны сақтау заңы: Оқшау жүйесіне жылудың шексіз кіші δQ шамасы беріліп, жүйемен шексіз кіші δA шамадай жұмыс жасалса, жүйе энергиясы de = δQ – δA шамаға өзгереді.
Бұл заңдардың барлығын дифференциалды теңдеулермен бейнелеуге болады. Олар тағы да F(p, v, T)=0 күй теңдеуімен толтырылуы керек. Шектеу шарттарымен бірге осы теңдеулер толығымен динамикалық жүйенің кез келген уақыттағы жүріс-тұрысын бейнелейді. Математикалық бейнелеуге кіретін теңдеулер саны міндетті түрде модельдеу процесінде ізделінетін айнымалылар санына тең болуы керек.
Қарапайым дифференциалдық теңдеулерден тұратын математикалық бейнелеудің ерекшелігі болып табылатын бастапқы шарттарды қажетті түрде анықтаудың қажеттілігі. Дербес туындылары бар теңдеулерде бастапқы шарттармен бірге шектегі шарттарды да анықтау қажет (себебі параметрлер бірнеше координаттар бойынша таратылған), олар жалпы кезде уақыттан тәуелді функциялар болады. Кей кезде объектті дифференциалдық теңдеумен бейнелеу орнына айырымдық теңдеулер қолданылады. Осындай түрлендіруде қателік пайда болады, модельдеу нәтижесін бағалағанда, осы қателікті есепке алу керек.
Математикалық модельдерді құрастырғанда блоктық принципі кең қолданылады. Бұл кезде модель бөлек қарастырып отырған процестің бір жағын қамтып көрсететін логикалық тұтас блоктардан құрастырылады. Осы принципке сәйкес тұтас процестің және оның түйіндерінің – элементарлы процестердің физикалық негіздері анализденеді. Әуелі математикалық бейнелеу құрамының негізі болып процестің гидродинамикалық моделі зерттеледі. Содан кейін химиялық процестердің, масса және жылу тасымалдаудың кинетикасы зерттеледі, содан кейін осы әрбір процестің математикалық бейнелеуі жасалады. Соңғы қадамда барлық зерттелген элементарлы процестердің бейнелеулері тұтас бір теңдеулер жүйесіне ұйымдасады.
4.2 Динамика теңдеулерін қарапайымдау
Динамика теңдеулер жүйесі әдетте сызықты емес болғандықтан, оларды аналитикалық жолмен шешу жалпы кезде мүмкін емес. Сондықтан есеп спецификасына қарай теңдеулер және шектеулермен анықталатын кейбір байланыстарды жою үшін әртүрлі қарапайымдау әрекеттері орындалады. Сонымен бірге процестің маңызды қасиеттері сақталу керек.
Ең қарапайым (математикалық шешу жағынан) статикалық есеп болады. Уақыт және координаттар бойынша туындылар нөлге тең, сондықтан дифференциалдық теңдеулер орнына алгебралық теңдеулерді аламыз (жинақталған параметрлері бар объекттердің стационарлы режимдері).
Қарапайымдылық жағынан келесі стационарлық есеп болады. Теңдеулерде уақыт бойынша туындалар нөлге тең болады, сондықтан тәуелсіз координаттар саны азаяды (біздер осындай есептерді қарастырмаймыз). Стационарлы емес есептердің математикалық түрін қарапайымдау үшін өзара байланысқан жүйелер санын азайту, теңдеулер санын азайту жолымен, бөлек теңдеулердегі кейбір байланыстарды жою жолымен, кеңістік координаттар санын азайту және теңдеулерді сызықтандыру жолдарымен орындалады. Әрине, кейбір теңдеулерді жою жүйе дәрежесін төмендетеді. Математикалық көзқарас жағынан жүйе бекітілмеген болады. Жойылған теңдеулерді процестің жүріс-тұрысын жуықтап көрсететін алгебралық тәуелділіктермен алмастыру керек. Мысалы, сәйкес параметрлері тұрақты деп есептелінуі мүмкін.
Көптеген практикалық жағдайларда нақты ағынның қозғалу заңдары тәжірибелік мәліметтер негізінде табылады. Тәжірибелік зерттеулерден ағынның нақты құрамын қамтып көрсететін кейбір коэффициенттері анықталады, мысалы, жылдамдық, температура, тығыздылықтың кеңістік бойынша өзгеретінін есепке алатын тәуелділіктер. Осындай коэффициенттері үйкелу, жылу беру, екі компоненттік қоспаларда фазалардың бір-бірі арқылы қозғалу жылдамдықтар, т.б. болып табылады. Олардың барлығы ағынның интегралдық сипаттамалары болады, олар анықталған жуықтаумен нақты ағындағы қозғалыс мөлшерімен, жылулықпен, затпен алмасуды қамтып көрсетеді. Аталған коэффициенттер көмегімен және ағын кесіндісі бойынша параметрлердің орта мәндерімен жылу беру, гидравликалық кедергі, фазалар таратылуы көрсетіледі. Олар арасындағы байланыстар да тәжірибеден табылады.
Эмпирикалық коэффициенттерді және аталған тәуелділіктерді қолдану ағынның нақты үш өлшемдігін қарастырмауға мүмкіндік береді. Сонда кейбір теңдеулер қарапайымдалады, кейбіреулерін жоюға болады. Осындай қарапайымдауды өткізуге болады, себебі эмпирикалық тәуелділіктер ағынның нақты үш өлшемділігін қамтып көрсетеді деп есептеуге болады. Кей кезде жоғарыда айтылған қорытындылар негізінде динамикалық сипаттамаларды есептеу үшін бір өлшемді модельді қолдануға болады, ал кейбір кезде жинақталған параметрлері бар модельді. Бір өлшемді модельдерде параметрлер тек қана ағын осімен бағытталған бір координата бойынша өзгереді. Канал кесіндісі бойынша параметрлер тұрақты болып орта мәнге тең деп есептелінеді.
Жинақталған параметрлері бар модельдерде жүйенің барлық параметрлері кеңістік координаталардан тәуелді емес, тек қана уақыт функциясы болады деп есептелінеді. Кеңістік координата бойынша туындылар функцияның кірудегі және шығудағы мәндерінің айырмашылығының канал ұзындығына қатынасымен алмасады.
Тұрақты жүйелерде өтпелі процестер барлық біртекті параллелді қосылған элементтерінде бірдей өтеді. Сондықтан өтпелі процестерді зерттегенде толық жүйені қарастырмай, тек қана жүйенің бір элементін қарастыруға болады.
4.3 Теңдеулерді сызықтандыру
Модельдерді қарапайымдаудың бір әдісі алынған теңдеуді сызықтандыру болады, басқа сөзбен айтқанда сызықты математикалық модельге көшу.
Процестердің динамикасын модельдеудің соңғы мақсаты динамикалық сипаттамаларын анықтау үшін алған модельдерді басқару жүйелерде қолдану болып табылады. Сондықтан міндетті түрде теңдеулердің шешімін табу керек. Сызықты дифференциалдық теңдеулер жеңіл шешіледі. Бірақ объекттің жүріс-тұрысын әр кезде сызықты теңдеумен бейнелеу мүмкін емес. Сондықтан сызықты емес тәуелділіктер аргументтердің берілген диапазонында сызықты өрнектермен жуықталады. Басқа сөзбен айтқанда, кірудегі аргументтердің берілген диапазонында сызықты емес теңдеулер сызықты теңдеулермен алмастырылады, сызықтандырылады. Сызықты объектілерде кірудегі және шығудағы сигналдар арасындағы байланыс беріліс функциямен жеңіл бейнеленеді. Сызықтандыру әдетте сызықты емес теңдеулерді бастапқы стационарлы режим аймағында Тейлор қатарына жіктеу жолымен орындалады. Жіктеудің тек қана сызықты мүшелерін қалдырып, соңынан теңдеулерден статика теңдеулерін алып тастаймыз. Осы жолмен алынған объект моделі бастапқы стационарлы режимнен кіші ауытқуларда орындалады.
5 дәріс. Жинақталған параметрлері бар объектілерді аналитикалық әдістермен модельдеу
Дәрістің мазмұны:
- жинақталған параметрлері бар объекттерді модельдеудің аналитикалық әдістері.
Дәрістің мақсаты:
- жинақталған параметрлері бар объекттерді модельдеудің негізгі аналитикалық әдістерін мысалдарда оқып білу.
Жинақталған параметрлері бар объекттердің дифференциалдық теңдеулерін құрастырғанда әдетте материалды және жылулық баланс теңдеулерін қолданады.
Материалды баланс заңы бойынша бекітілген кеңістікте зат массасының уақыт бірлігінің өзгеруі кірудегі және шығудағы ағындардың алгебралық қосындысына тең:
![]() (5.1)
(5.1)
мұнда: Di (i=1,k) – i-ші кірудегі ағынның массалық шығыны, Dj (j=1,r) - j-ші шығудағы ағынның массалық шығыны, G – қарастырылып отырған көлемдегі зат массасы,, t -уақыт.
Сол сияқты уақыт бірлігінде заттың энтальпиясының өзгеруі қарастырылып отырған затқа жылуды әкелетін (немесе алып кететін) жылулық ағындардың алгебралық қосындысына тең:
![]() ,
(5.2)
,
(5.2)
мұндағы Qi (i=1,k) – i-ші кірудегі жылу ағыны, Qj (j=1,r) - j-ші шығудағы жылу ағыны, I – дене энтальпиясы.
Әртүрлі процестердің олардың әртүрлі жүріс-тұрысындағы жалпы модельдеу теориясын орнату мүмкін емес. Сондықтан негізгі масса, энергия, қозғалыс мөлшерін сақтау заңдарын қолдануды көрнекі көрсету үшін бірсыпыра мысалдарды қарастырамыз.
5.1 мысалы. Резервуардағы сұйықтық деңгейін реттеу моделі.
Тәуелсіз кірудегі Gк(t) ағыны және шығудағы тәуелді Gш(t) ағыны бар ағу резервуар біздің зерттеу объектіміз болып табылады. Шығудағы ағын көлемі саңылаудан жоғары орнатылған сұйықтықтың H деңгейінен және саңылаудың fc кесіндісінен тәуелді.
Объекттің математикалық моделін жасағанда келесі теңдеулер қолданылады.
Жүйенің материалды баланс теңдеуі (М – жинақтағы сұйықтық қоры):
![]() (5.3)
(5.3)
Бірақ Gс тәуелсіз айнымалы болып табылмайды, ол М шамасының функциясы. Гидродинамика заңына сәйкес саңылаудан шыққан ағын қозғалысты сақтау заңдылығына бағынды. Ол келесі теңдеумен көрсетіледі:
![]() (5.4)
(5.4)
мұнда μ – шығын коэффициенті, fc –саңылау қимасының ауданы, g - еркін құлау үдеуі, H - резервуардағы сұйықтық деңгейі.
Бірнеше жағдайларды қарастырайық.
а) Жүйенің тепе-теңдік
жағдайдағы жүріс-тұрысын зерттейік. Тепе-теңдік
деп уақыт бойынша күй координаттарының (бұл арада Н және
Gш) өзгермеуін түсінеміз. Тепе-теңдік
жағдайда резервуарда зат мөлшері өзгермейді, сондықтан
![]()
Сонымен материалдық баланс теңдеуі келесі анық өрнекпен көрсетіледі:
![]()
Басқа жақтан қарасақ, математикалық көзқарасы бойынша тепе-теңдік жағдайда барлық күй координаттарының туындылары нөлге тең болады
![]() сондықтан
сондықтан
![]()
Осыдан келесі шығады
![]() немесе
немесе
![]()
Нәтижесінде келесіні аламыз
![]() (5.5)
(5.5)
(5.4) өрнегін (5.5) теңдеуіне қойып резервуардағы сұйықтық деңгейін есептеуге келесіні аламыз
![]() .
.
Сонымен, тепе-теңдікте болатын жүйенің математикалық моделін келесі түрде жаза аламыз
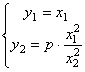 немесе
немесе 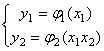
мұндағы x1 = Gк, x2 = fc; y1 = Gш, y2 = H - модель айнымалылары,
p =
![]() -
параметрі.
-
параметрі.
Бұл модель статикалық болып табылады, модельдің атауы объекттің тепе-теңдік жағдайдағы статикалық күйімен байланысты.
б) Сұйықтығы бар резервуардың тепе-теңдікті орнатпай, жалпы кездегі жүріс-тұрысын зерттеу керек.
Резервуардағы саңылаудан жоғары орнатылған сұйықтық мөлшері келесі өрнектен анықталады:
![]() ,
,
мұнда F – резервуар қимасының ауданы, ρ – тығыздылық.
F пен ρ шамалары тұрақты яғни F= F0,
ρ=
ρ0 деп есептеп және
![]() орнына (5.4) өрнекті
қолданып, келесі дифференциалды теңдеуді аламыз
орнына (5.4) өрнекті
қолданып, келесі дифференциалды теңдеуді аламыз
![]() (5.6)
(5.6)
Бұл теңдеуді жалпы түрде келесідей жазуға болады
![]()
(5.4) өрнекті де келесі жалпы түрге келтіруге болады
![]()
Сонымен, екі белгісіз айнымалысы бар екі теңдеуден тұратын жүйе
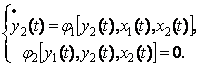 (5.7)
(5.7)
сұйықтығы бар резервуардың динамикалық моделі болады. Динамика жүйе күйінің өзгеруімен байланысты.
Бұл мысалда статикалық модель динамикалық модельдің жеке түрі болады. Мұндай жағдай міндетті түрде орындалмайды. Әдетте, модельдердің осындай екі түрі бір-бірін толықтырады.
в) Сұйықтығы бар резервуардың сызықтандырылған динамикалық моделін алайық. Бастапқы тепе-теңдік жағдай t0 уақытына сәйкес деп есептейміз.
Бастапқы тепе-теңдік жағдайдағы жүйе күйінің координаттарын статикалық модельден аламыз. Сонда
![]()
![]() .
.
Теңдеулер жүйесінде негізгі сызықсыздықты орнататын (5.4) өрнегі. Оны Тейлор қатарына жіктеп, жіктеудің тек қана сызықты мүшелерін қалдырамыз
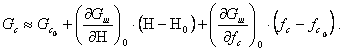 (5.8)
(5.8)
Қатардың коэффициенттерін анықтаймыз
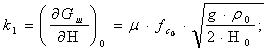
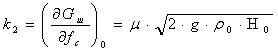
Бастапқы тепе-теңдік күйді есепке алып, модельде тек қана айнымалылардың өзінің бастапқы мәндерінен ауытқуын зерттейміз
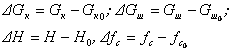 (5.9)
(5.9)
Сонда:
![]()
Бұл теңдеу сызықтандырылған модельдің бірінші теңдеуі болады. Келесілерді есепке алып
![]() және
және ![]() ,
,
сызықтандыру (5.8) нәтижесін (5.5) –ке қойып, келесіні аламыз
![]() .
.
Келесі
y1 = ΔGш, y2 = ΔΗ, x1 = ΔGк және x2 = Δfc,
белгілеулерді қолданып, сұйықтығы бар резервуардың сызықтандырылған динамикалық моделін келесі теңдеулер жүйесімен көрсетуге болады
 (5.10)
(5.10)
Мұнда
![]()
Модельдің жалпы (5.7) түрі толығымен (5.10) теңдеумен сәйкес, тек қана φ1 және φ2 функциялары өзгереді.
ki және T -
теңдеулер коэффициенттері, сызықтандырылған модельдің
параметрлері болып табылады және өтпелі процесс алдындағы
тепе-теңдік жағдайдан тәуелді. Сондықтан, модельденетін
объекттің бастапқы күйлері ![]() өзгерсе, модель параметрлерінде
қайтадан табу керек болады.
өзгерсе, модель параметрлерінде
қайтадан табу керек болады.
Режимдердің кең диапазонында сипаттамаларының шұғыл өзгеретін жағдайларында объектті модельдеу қажет болса, сипаттамаларды координаттар өзгеретін бөлек бөліктерде сызықтандырады. Сонда сызықты емес объект сызықты тәуелділіктер жиынтығымен бірге олардың орындалатын диапазонын білдіретін логикалық өрнектермен белгіленеді.
6 дәріс. Жинақталған параметрлері бар объекттерді модельдеудің мысалдары
Дәрістің мазмұны:
- жинақталған параметрлері бар объекттерді модельдеудің мысалдары.
Дәрістің мақсаты:
- жинақталған параметрлері бар объекттерді модельдеудің негізгі аналитикалық әдістерін мысалдарда оқып білу.
6.1 мысалы. Алдыңғы дәрісте сұйықтығы бар резервуардың моделі қарастырылған еді. Енді екі резервуардан тұратын каскадты жүйенің теңдеулерін жазайық.
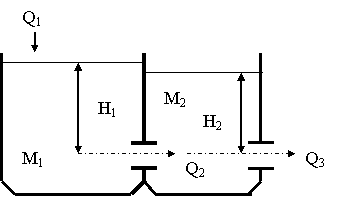 |
6.1 Сурет – Резервуарлар каскады
Мұндағы М1 және М2 – қорлар, Q1, Q2, Q3 - сұйықтық ағындары, F1 және F2 – резервуарлар қималарының аудандары, f1, f2 – резервуарлардың саңылаулар қималарының аудандары, μ1, μ2 –шығын коэффициенттері, H1, H2 - сұйықтық деңгейлері, ρ – зат тығыздылығы.
Бұл жағдайда келесі баланстық қатынастарымен қатар:
![]() ,
(6.1)
,
(6.1)
![]() (6.2)
(6.2)
келесі қосымша тәуелділіктер де орындалады:
![]() (6.3)
(6.3)
![]() (6.4)
(6.4)
![]() (6.5)
(6.5)
![]() (6.6)
(6.6)
Жазылған теңдеулер жиынтық каскадының теңдеулері болып табылады. Бірақ, жиі жағдайда, белгілі айнымалылар арасындағы тәуелділікті табу қажет болады.
Мысалы, Q3 шығыс және Q1 кіріс арасындағы тәуелділікті табу керек болсын. Ол үшін Q2, M1, M2, H1, H2 айнымалыларды алып тастап, теңдеулерде тек қана Q1 және Q3 қалдыру керек.
(6.3) және (6.6) теңдеулерден мынаны аламыз
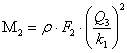 (6.7)
(6.7)
ал (6.4) және (6.5), (6.6) теңдеулерінен келесіні
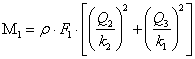 (6.8)
(6.8)
(6.7)-ні есепке алып, (6.2) теңдеуінен келесіні аламыз
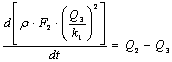
немесе
![]() (6.9)
(6.9)
(6.1) теңдеуіне (6.8), (6.9) теңдеулеріндегі М1 және Q2 өрнектерін қойып, келесіні аламыз
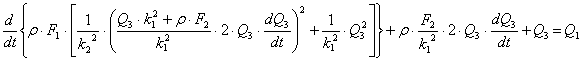
Бұл екінші ретті сызықтық емес теңдеу, Q1 және Q2 - уақыт функциялары, қалғандары – тұрақтылар.
Теңдеу реті қаскадтағы жинақтар санына тең.
Егер резервуардан сұйықты итеретін
ауыртпалық күшіне қосымша герметикалық
резервуардағы Р сыртқы қысымды есепке алса не өзгереді?
Бұл жадайда ![]() өрнегі орнына, бастапқы қатынас
болып
өрнегі орнына, бастапқы қатынас
болып ![]() қолданылады, бұнда
ρ – сұйықтықтың
тығыздылығы.
қолданылады, бұнда
ρ – сұйықтықтың
тығыздылығы.
6.2 мысалы. Екі жинақтан
құралған сусымалы материалдарға арналған
жүйе берілген болсын. Бірінші жинақтағы ағын конвейер
немесе насоспен екінші жинаққа келіп түседі. Жүйе
күйі келесі айнымалылармен сипатталады: бірінші жинаққа
келтірілетін ағын Q1, бірінші жинақтан шығарылатын
ағын ![]() ,
екінші жинаққа
келтірілетін ағын
,
екінші жинаққа
келтірілетін ағын
![]() , жүйенің шығарылатын ағыны Q2
және жинақтардағы материал қорлары M1 мен М2
(6.2 суреті)..
, жүйенің шығарылатын ағыны Q2
және жинақтардағы материал қорлары M1 мен М2
(6.2 суреті)..
Осы жүйенің теңдеулерін құрастырайық. Әр жинақтың күйі жоғарыда анықталған теңдеумен суреттеледі:
![]()
![]()
Осы теңдеулердің байланысын анықтау
үшін, ![]() және
және ![]() ағындардың байланыстарының теңдеулерін алу
қажет.
ағындардың байланыстарының теңдеулерін алу
қажет.
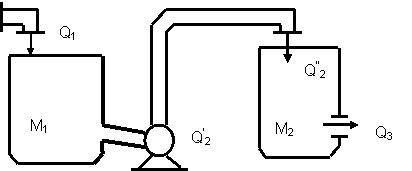 |
2 Сурет - Екі жинақтан құралған жүйенің динамика теңдеуін анықтау
Егер тасымалдау тұрақты өнімділікті
насосымен немесе конвейерімен жүзеге асырылса, онда бірінші
жинақтан шығатын барлық ![]() ағыны кешігумен екінші жинаққа
түседі. Кешігу τ
уақыты жинақтар
арасындағы қашықтықпен және конвейердің
лента бойымен немесе құбыр бойымен материал
қозғалысының жылдамдылығымен анықталады.
ағыны кешігумен екінші жинаққа
түседі. Кешігу τ
уақыты жинақтар
арасындағы қашықтықпен және конвейердің
лента бойымен немесе құбыр бойымен материал
қозғалысының жылдамдылығымен анықталады.
![]() шамасы
τ уақыты кезінде, t – τ уақыт кезіндегі
шамасы
τ уақыты кезінде, t – τ уақыт кезіндегі
![]() ағынның
шамасына тең, яғни: Q2''(t) = Q2'
(t – τ). Осыны есепке ала отырып,
жинақ жүйесінің теңдеуі мына түрге енеді:
ағынның
шамасына тең, яғни: Q2''(t) = Q2'
(t – τ). Осыны есепке ала отырып,
жинақ жүйесінің теңдеуі мына түрге енеді:
![]()
![]() .
.
Бұл теңдеулер қарастырып отырған объект моделінің жалпы түрі болып табылады. Егер де модельмен тәжірибелерді немесе анықталған есептеулерді өткізу қажет болса, әрине, кірудегі және шығудағы ағындардың өзгеру заңдылықтарын анықтап алу керек. Мысалы, сандық түрде бункер-конвейер жүйесінің теңдеуін алу керек болсын. Бункерді заттан босату ұзындығы l=50 м конвейермен орындалады, конвейер лентасының жылдамдылығы
θ=1
м/с =3600м/сағ, кірудегі ағын Q1 = 100т/сағ = const.
Бункер теңдеуі: ![]() (М- бункердегі зат массасы). Конвейер теңдеуі
(М- бункердегі зат массасы). Конвейер теңдеуі
Q3 (t)= Q2 (t – τ) = Q2 (t – 50/3600) немесе Q2 (t)= Q3(t + 50/3600).
Аралық Q2 айнымалыны жойып, келесі теңдеуді аламыз
![]() .
.
7 дәріс. Жинақталған параметрлері бар объекттер. Жылуалмастыру процестерді модельдеу
Дәрістің мазмұны:
- жинақталған параметрлері бар объекттерді модельдеудің аналитикалық әдістері.
Дәрістің мақсаты:
- жылу алмастырғыштағы процестерді модельдеу мысалында жылу баланс теңдеуін және эмпирикалық тәуелділіктерді қолдануды үйрену.
Алдында айтылып кеткендей, көптеген практикалық жағдайларда нақты ағынның қозғалу заңдары тәжірибелік мәліметтер негізінде табылады. Эмпирикалық коэффициенттерді және аталған тәуелділіктерді қолдану ағынның нақты үш өлшемдігін қарастырмауға мүмкіндік береді. Сонда кейбір теңдеулер қарапайымдалады, кейбіреулерін жоюға болады. Осындай қарапайымдауды өткізуге болады, себебі эмпирикалық тәуелділіктер ағынның нақты үш өлшемділігін қамтып көрсетеді деп есептеуге болады. Кей кезде жоғарыда айтылған қорытындалар негізінде динамикалық сипаттамаларды есептеу үшін бір өлшемді модельді, ал кейбір кезде жинақталған параметрлері бар модельді қолдануға болады, Айтылған пікірді көрнекі көрсету үшін жылуалмастырғыштағы процестердің динамикасын қарастырайық.
7.1 мысалы. Интенсивті араластыруы бар жылу айырбастағышқа температурасы θ1-ге тең сұйықтықтың Q1 ағыны келіп түседі (7.1 сурет).
Жылу айырбастағышта ұсталып тұратын материалдың орташа көлемі V-ға тең. Жылу айырбастағыштан θ2 температураға ие Q2 ағыны әкетіледі.
Жылу айырбастағыштағы материал қоры тұрақталған: жылу айырбаста-ғыш герметика түрде жабық немесе материалдың шығуы үстіндегі ашық жерден төгілу арқылы жүзеге асырылады немесе егер материал астындағы бөліктен кәдімгі күш пен шығарылса, жинақтағы деңгей бөлек автоматты жүйемен тұрақталған.
V=const болғандықтан, онда Q1= Q2= Qорта.
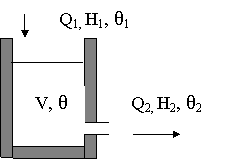
7.1 Сурет – Жылу айырбастағыш
Материалды араластыру соншалықты интенсивті болғандықтан, көлеміндегі θ температура және әкетілетін ағындағы θ2 температура өзара тең, яғни θ = θ2.
Кіріс шамасы H1 – жылудың келтірілетін ағыны, ал шығыс шамасы – шығарылатын ағынның температуасы θ2 болатын теңдеулерді құрамыз. H1 кіріс шаманың өзгерісі, ағынның Q1 өзгерісіне, сонымен қатар, оның температурасының өзгерісінен тәуелді болуы мүмкін. Осыған байланысты, біртіндеп күрделенетін жағдайларды қарастырайық.
а) Жылу айырбастағыш идеалды жылу изоляциясына ие, яғни сыртқы ортаға жылу ауыстыру жоқ.
Интенсивті араластыру жағдайында, объектті жинақталған деп санап, жылу балансының келесі теңдеуін қолдануға болады::
![]() (7.1)
(7.1)
Мұнда ρ – материал тығыздылығы;
С – материалдың жылу сыйымдылығы;
Hi - уақыт бірлігінде жылу айырбастағышқа келтірілетін (оң саны) немесе әкетілетін (теріс саны) жылу мөлшері.
Q1 кірудегі ағынымен жылуа йырбастағышқа
H1= ρ·с ·θ1 ·Q1. (7.2)
жылуы келеді.
Q2 шығудағы ағынымен
H2= ρ·с ·θ2 ·Q2. (7.3)
жылу мөлшері шығарылады.
H1 және H2 жылулық балансының теңдеуіне қойып, келесіні аламыз
![]() (7.4)
(7.4)
немесе
![]() ,
,
![]()
θ = θ2 есепке алып, мынаны аламыз
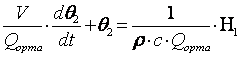
немесе
![]()
Мұндағы
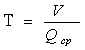 -
уақыт тұрақтылығы;
-
уақыт тұрақтылығы; ![]() - беріліс коэффициенті.
- беріліс коэффициенті.
б) Қоршаған ортаға келесі заңына сәйкес жылу ауыстыру бар
H2 = h·S· (θ – θc), (7.5)
мұнда h – жылу беру коэффициенті, S - жылу айырбастағыш бетінің ауданы, θc - сыртқы ортаның температурасы..
Бұл жағдайда жылу балансы теңдеуі келесі түрде жазылады
![]() (7.6)
(7.6)
Түрлендіргеннен кейін:
![]() (7.7)
(7.7)
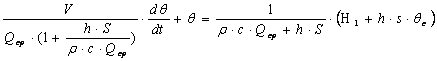
Соңында келесіні аламыз
![]() (7.8)
(7.8)
Мұнда 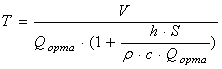 ,
, 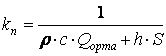 .
.
Бұл жағдайда Т тұрақтысы
азайды, себебі ![]() мүшесі әрқашан да оң
таңбалы.
мүшесі әрқашан да оң
таңбалы.
Егер де қоршаған ортаның температурасы
тұрақты болса, онда температураның координаттар басын
θc нүктесіне
орнатып, ![]() мүшесін
алып тастауға болады, кері жағдайда
θc-ты сыртқы әсері деп
қарастыруға болады.
мүшесін
алып тастауға болады, кері жағдайда
θc-ты сыртқы әсері деп
қарастыруға болады.
в) Жылу айырбастағыш қабырғаларының қалыңдығын, яғни олардың жылу сыйымдылығын есепке алу керек.
V көлемінен қабырғаға жылулық ағыны
H31 =hм ·S· (θ – θм),
мұнда hм – ағыннан қабырғаларға жылу беру коэффициенті,
θм – қабырға температурасы.
Қабырғадан сыртқы ортаға жылу ағыны
H4= hc·S·(θM - θ2),
мұнда hc – қабырғадан сыртқы ортаға жылу беру коэффициенті.
Жылу айырбастағыш қабырғалары жылу сыйымдылығына ие болғандықтан, ағын және қабырғалардың жылулық балансының екі теңдеуін жазамыз
![]() (7.9)
(7.9)
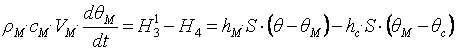 (7.10)
(7.10)
Аралық θм айнымалыны алып тастайық.
Ол үшін θ = θ2, Q2 = Qорта болатынын ескере отырып, бірінші теңдеуден θм табып
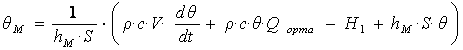 (7.11)
(7.11)
оны екінші теңдеуге қоямыз
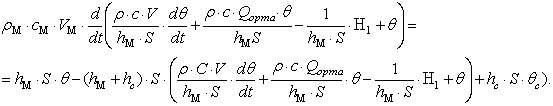 (7.12)
(7.12)
Түрлендіргеннен кейін келесіні аламыз
 (7.13)
(7.13)
Шығудағы шама - θ1, кірудегі - H и θс.
Егер де θс = const болса, онда θс нүктесіне температура координаттар басын ауыстырып, θс бар мүшені шығарып тастауға болады. Онда Q және H1 айнымалылары қалады, сондықтан теңдеуді келесі түрде жазуға болады
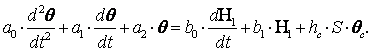 (7.14)
(7.14)
мұнда ai және bi модель коэффициенттерін анықтайды.
Екінші ретті теңдеуді алдық, өйткені объектте екі жинақталған параметрлері бар сыйымдылықтар бар: жылу айырбастағыш және ағын кеңістіктері.
8 дәріс. Жылулық объектілердің сипаттамаларын аналитикалық әдістерімен анықтау
Дәрістің мазмұны:
- жинақталған параметрлері бар жылулық объекттерді модельдеудің аналитикалық әдістері.
Дәрістің мақсаты:
- жинақталған параметрлері бар жылулық объекттерді модельдеудің негізгі аналитикалық әдістерін мысалдарда оқу.
Анықталған жылуэнергетикалық объекттерді қарастырайық. Жоғарыда аталған материалда және жылу баланс теңдеулері бастапқы теңдеулер болып табылады.
8.1 мысалы. Бу генераторының қыздырылмайтын бөлігі (коллектор, қосу бу құбыры). Кірудегі шама – бөлік кірісіндегі жұмыс ортаның температурасы, шығудағы - бөлік шығуындағы жұмыс ортаның температурасы. Бөліктегі жұмыс ортаның қысымы тұрақты, қоршаған ортаға жылу берілмейді деп есептелінеді.
Келесі белгілерді қолданамыз: Dc – жұмыс
орта шығыны; ![]() – жұмыс ортаның кірудегі және
шығудағы энтальпиясы; Qм – металлдың
бөлігіне әсер ететін жылулық ағын; Ic – бөліктегі
жұмыс ортасының энтальпиясы; Iм – бөліктегі металл
энтпльпиясы; Gc және Gм –бөліктегі жұмыс
орта және металл массалары; iм – металл энтальпиясы;
α2 –
бөліктің ішкі H2 бетіне
жылуберу коэффициенті;
Θ’c және
Θ’’c –бөліктің кірісімен шығысындағы жұмыс
ортаның температурасы;
Θм
– металл
температурасы; ср және см – металл және жұмыс
ортаның меншікті жылу сыйымдылығы.
– жұмыс ортаның кірудегі және
шығудағы энтальпиясы; Qм – металлдың
бөлігіне әсер ететін жылулық ағын; Ic – бөліктегі
жұмыс ортасының энтальпиясы; Iм – бөліктегі металл
энтпльпиясы; Gc және Gм –бөліктегі жұмыс
орта және металл массалары; iм – металл энтальпиясы;
α2 –
бөліктің ішкі H2 бетіне
жылуберу коэффициенті;
Θ’c және
Θ’’c –бөліктің кірісімен шығысындағы жұмыс
ортаның температурасы;
Θм
– металл
температурасы; ср және см – металл және жұмыс
ортаның меншікті жылу сыйымдылығы.
Жұмыс ортаның жылулық баланс теңдеуі
![]()
Металл үшін жылулық баланс теңдеуі
![]()
Келесі өрнектерді Ic = i’’c· Gc, Iм = iм· Gм, Qм = α2·H2· (Θ’’c - Θм),
∆i = с·∆ Θ, есепке алып, айнымалылырдың ауытқуына көшіп, стационарлы режимнің теңдеулерін қарастырып отырған теңдеулерден алып тастап, бөліктің сызықты моделінің дифференциалды теңдеулерін аламыз
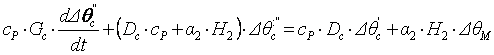 (8.1)
(8.1)
 (8.2)
(8.2)
(8.1), (8.2) теңдеулеріне Лаплас түрлендіруін қолданайық. Ол үшін теңдеулердің екі жағын да e-st өрнекке көбейтіп, 0-дан ∞-ке дейін интегралдаймыз, сонымен бірге функция мен оның туындысының бейнелері келесідей
y(t)÷Y(s), y'(t)÷sY(s) байланысатынын есепке аламыз.
Келесідей белгілеулерді. ∆Θ’’c ÷ Z(s), ∆Θ’c ÷Y(s), ∆Qм ÷X(s) қолданайық. Сонда
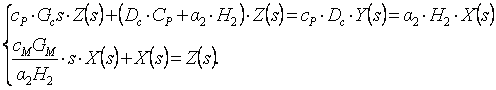
Екінші
теңдеуден  .
.
Бірінші теңдеуден
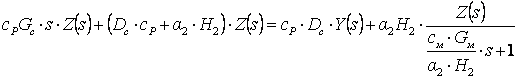 .
.
Dcсp шамасына бөліп, келесіні аламыз
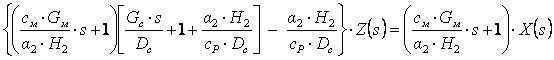
Осыдан
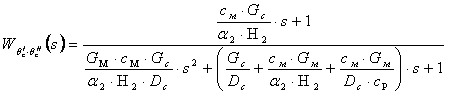
Уақыт тұрақтысы
![]() физикалық
жұмыс ортаның берілген шығынында бөлікті жұмыс
ортамен толтыру уақытына сәйкес болып табылады және де шамасы
кішкене болады. Практикалық есептеулерде оны нөлге тең деп
алады, сонда беріліс функциясы келесі түрге түрленеді
физикалық
жұмыс ортаның берілген шығынында бөлікті жұмыс
ортамен толтыру уақытына сәйкес болып табылады және де шамасы
кішкене болады. Практикалық есептеулерде оны нөлге тең деп
алады, сонда беріліс функциясы келесі түрге түрленеді
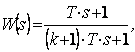 мұнда
мұнда
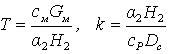 .
.
8.2 мысалы. Араластыру жылу алмастырғыш (шашырату коллекторы). Кірудегі шамалар коллектор кірісіндегі жұмыс ортаның шығыны мен температурасы болып табылады, шығудағы шама – жұмыс ортаның коллектор шығысындағы температурасы. Жұмыс ортаның шығудағы шығыны ортаның кірудегі және шашыратуға шығындарының қосындысына тең, шашыратылатын ортаның температурасы тұрақты деп есептелінеді.
Жұмыс орта үшін жылулық баланс теңдеуі
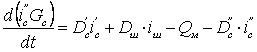
мұндағы ![]() - коллектордың кірісіндегі және
шығыстағы жұмыс орта шығындары,
- коллектордың кірісіндегі және
шығыстағы жұмыс орта шығындары,
![]() -
судың шашыратылуға шығыны,
-
судың шашыратылуға шығыны, ![]() - шашыратылатын судың
энтальпиясы.
- шашыратылатын судың
энтальпиясы.
Алындағы мысалдағыдай, айнымалылардың ауытқуларына көшіп, стационарлы режимдегі теңдеулерді алып тастап, жұмыс орта үшін сызықты дифференциалды теңдеуді аламыз
 (8.3)
(8.3)
мұндағы ![]() - стационарлы режимдегі коллектордың
кірісіндегі және шығыстағы жұмыс орта шығындары,
- стационарлы режимдегі коллектордың
кірісіндегі және шығыстағы жұмыс орта шығындары,
![]() – стационарлы режимдегі жұмыс
ортаның бөлік кірісіндегі энтальпиясы,
– стационарлы режимдегі жұмыс
ортаның бөлік кірісіндегі энтальпиясы,
![]() -
стационарлы режимдегі шашыратылатын судың энтальпиясы. Металл үшін (8.2)
теңдеуі қалады.
-
стационарлы режимдегі шашыратылатын судың энтальпиясы. Металл үшін (8.2)
теңдеуі қалады.
Лаплас түрлендіруін қолданып (8.2), (8.3) теңдеулерден, алдындағыдай қарапайымдылардан кейін әртүрлі каналдар бойынша беріліс функцияларды табуға болады
а) ![]() каналы бойынша беріліс функциясын табайық:
каналы бойынша беріліс функциясын табайық:
 Осыдан
Осыдан
![]() мұндағы
мұндағы
![]() .
.
![]() шамасына бөліп, уақыт
тұрақтысының
шамасына бөліп, уақыт
тұрақтысының ![]() шамасы азғантай деп есептеп, келесіні аламыз
шамасы азғантай деп есептеп, келесіні аламыз
![]() мұнда
мұнда ![]()
б) ![]() канал бойынша
канал бойынша
 мұнда
мұнда
 ;
;
в)
![]() канал бойынша
канал бойынша  мұнда
мұнда 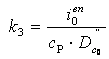 .
.
8.3 мысалы. Бу сыйымдылығы. Сыйымдылық кедергісі оның шығысында жинақталған және жұмыс ортаның энтальпиясы өтпелі процесс кезінде өзгермейді деп есептелінеді. Жұмыс ортаның қысымы сыйымдылықтан кейін реттегіш көмегімен тұрақты болып орнатылады. Сыйымдылық ішіндегі жұмыс ортаның қысымы әкелінетін ортаның шығынына әсер етпейді деп есептелінеді. Кірудегі шамалар кірістегі жұмыс ортаның шығыны мен қысымы болады, шығудағы шамалар – жұмыс ортаның шығыстағы шамасы мен сыйымдылықтағы қысым. Жұмыс орта үшін материалды баланс теңдеуі
![]()
Жинақталған кедергі арқылы жұмыс ортаның шығыны келесі өрнекпен анықталады
![]()
мұнда ![]() -
жұмыс ортаның кедергі алдында
және оның кейінгі қысымдары. Айнымалылар ауытқуларына
көшіп, сызықтандыруды өткізгеннен кейін келесілерді
Gc
=ρc ·V және
-
жұмыс ортаның кедергі алдында
және оның кейінгі қысымдары. Айнымалылар ауытқуларына
көшіп, сызықтандыруды өткізгеннен кейін келесілерді
Gc
=ρc ·V және
 есепке алып, жүйенің сызықты моделінің
теңдеулерін аламыз
есепке алып, жүйенің сызықты моделінің
теңдеулерін аламыз
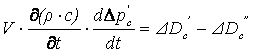 ;
(8.6)
;
(8.6)
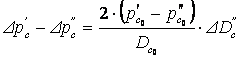 (8.7)
(8.7)
мұндағы V – бөліктегі
жұмыс ортаның көлемі, ρc – ортаның тығыздылығы,
![]() -
стационар режиміндегі жұмыс ортаның кедергі алдында және
оның кейінгі қысымы,
-
стационар режиміндегі жұмыс ортаның кедергі алдында және
оның кейінгі қысымы, ![]() - стационар режиміндегі жұмыс ортаның
шығыны. (9.4-9.5) теңдеулерге Лаплас түрлендіруін
қолданғаннан кейін келесі каналдар арқылы
- стационар режиміндегі жұмыс ортаның
шығыны. (9.4-9.5) теңдеулерге Лаплас түрлендіруін
қолданғаннан кейін келесі каналдар арқылы
![]() ,
,
![]() ,
,
![]()
![]() беріліс функцияларды аламыз. Студенттер осыны
өздері орындауы керек.
беріліс функцияларды аламыз. Студенттер осыны
өздері орындауы керек.
9 дәріс. Таратылған параметрлері бар объекттерді модельдеу
Дәрістің мазмұны:
- таратылған параметрлері бар объекттерді аналитикалық әдістерімен модельдеу.
Дәрістің мақсаты:
- таратылған параметрлері бар объекттерді аналитикалық әдістермен модельдеуді мысалдарда қарастыру.
Кейбір күй координаталары (технологиялық параметрлері) геометриялық кеңістік бойынша өзгеретін объекттер болады. Мысалы, факелдің температурасы жану кеңістіктің әртүрлі нүктелерінде әртүрлі болады. Осындай объекттердің модельдері кеңістік бойынша таратылған немесе параметрлері таратылған модельдер болып табылады да, модель операторына геометриялық z = (z1, z2, z3) координаталарын енгізу қажет болады.
Параметрлері таратылған маңызды жылу энергетикалық объекттер жалғыз фазалық және екі фазалық жылу тасымалдаушысы бар жылу алмастырғыштар болып табылады. Таратылған жылу алмастырғыштардың динамикалық сипаттамаларын зерттегенде жұмыс орта ағыны әдетте бір өлшемді, яғни құбыр қимасы бойынша жұмыс ортаның параметрлері тұрақты деп есептелінеді. Сонымен бірге қозғалып тұрған ортаның кинетикалық және потенциалды энергияларының өзгеруін есепке алмайды, себебі бұл шамалар өтпелі процесс кезіндегі жылу энергияның өзгеруіне қарағанда өте аз шама болып табылады.
Осы ескертулерді есепке алып параметрлері таратылған жылуалмастырғыштарды аналитикалық жолмен зерттегенде бастапқы болып алынатын жұмыс ортаның негізгі теңдеулері кәдімгідей қарапайымдалады.
9 - мысал. Ұзындығы L, қимасы f тұрақты құбыр берілген болсын. Осы құбыр бойынша қысылмайтын ағын (сұйықтық) қозғалады, құбырдың әр қимасында ағынның келесідей сипаттамалары бар: G - шығын, Р – қысым және температура q (10.1 суретті қараңыз). Құбыр изоляцияланбаған, яғни процесс изотермиялық болады. Құбыр кірісіндегі (1) және шығысындағы (2) қималарында ағынның физикалық сипаттамаларының байланыстарын зерттейік.
Зерттелетін объект ұзындығы (z) бойынша таратылған жұмыс ортаның параметрлері қима бойынша бірдей деп есептелінеді (бір өлшемді объект).
Негізгі теңдеулерді жазамыз.
- зат мөлшерін сақтау теңдеуі
![]()
![]() (9.1)
(9.1)
- қозғалыс мөлшерін сақтау теңдеуі
![]()
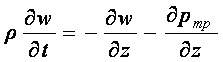 ,
(9.2)
,
(9.2)
- жұмыс ортаның күй теңдеуі (r үшін):
![]() . (9.3)
. (9.3)
Бұл жүйе құбыр моделінің бастапқы түрі. Осы жүйені аналитикалық жолмен шешу тек қана карапайым келісулерді қолданып өткізуге болады. Осындай келісім ретінде келесі шартты алуға болады: құбырды бірнеше элементарлы кесінділерге бөлеміз, кесінділердің әрқайсысы жинақталған объект болып табылады. Элементтердің саны көп болса, нақты жүйеге жуықтау жақсы болады. Жүйені жалғыз элементпен алмастырып, бірінші жуықтауды аламыз және жинақталған объект үшін теңдеулерді жазамыз.
а) Келесілерді орнатамыз. Қысым мен шығынның динамикаларын кез келген қимада (яғни барлық z үшін) қарастырмаймыз, тек қана кірудегі және шығудағы қималар байланысын қарастырамыз (есептің бастапқы қойылуы да осындай). Сонда құбұрдың бастапқы сұлбасы орнына оның эквивалентін аламыз, бұл эквивалент жинақталған V = L*f көлеммен және төмендегі өрнекпен анықталатын шығудағы қимадағы гидравликалық кедергімен сипатталады:
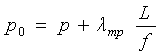
мұндағы p – құбырдың
жергілікті кедергілерінің қосынды коэффициенті;
![]() -
жұмыс ортаның құбыр қабырғаларына
үйкелу коэффициенті.
-
жұмыс ортаның құбыр қабырғаларына
үйкелу коэффициенті.
Сонымен бірге құбыр ұзындығы бойынша қысымның өзгеруінен пайда болатын ағын үдеуін есепке алмаймыз, яғни
![]()
деп есептейміз.
Сонда (9.2) келесідей түрленеді
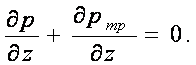 (9.4)
(9.4)
Жұмыс ортаның массасының барлығы V эквиваленттік көлемде орнатылған, ал ол көлемге Р1 қысымы әсер етеді, сондықтан (9.2) орнына келесіні қолданамыз
r1 = r (p1, q). (9.5)
(9.1) сақтау теңдеуін құбыр ұзындығын есепке алып, келесідей түрлендіреміз
![]()
немесе
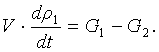 (9.6)
(9.6)
Сол сияқты (9.4) орнына
![]() немесе
немесе ![]() (9.7)
(9.7)
Гидравликадан белгілі үйкелуге кететін шамасын анықтайтын өрнегін қолданамыз
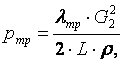 (9.8)
(9.8)
Осыдан G2 тауып және (10.6) қолданып қозғалыс мөлшерін сақтау теңдеуін аламыз
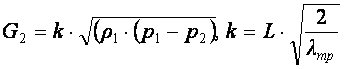 (9.9)
(9.9)
Сонымен, (9.5), (9.6), (9.9)) – ағынның алты G1, G2, P1, P2, r1, q физикалық сипаттамалары арқылы жүйесі.
Әрі қарай түрлендіру жолы сипаттамаларды экзогендік және эндогендік айнымалыларына бөлуге тәуелді. Ең көп тараған бөлу келесі болады: тәуелсіз - G1, P2, q болсын, сонда жүйе G2, P1, r1 айнымалылары арқылы шешілуі керек. Әдетте объект күйінің өлшенетін координаталарының, яғни G2, P1 өзгеруін зерттеуді қарастырады. Онда (2.4) күй теңдеуі r1 жоюға қолданылады
![]() ;
;
![]() (9.10)
(9.10)
Осы жүйе құбырдың жинақталған сызықты емес динамикалық стационарлы моделі болып табылады.
б) Сызықты емес өрнектерге Тейлор қатарын қолдану жолымен алынатын сызықтандырылған модельді қарастырайық. Теңдеулер жүйесін айнымалылардың бастапқы күй (оның координаталарының қосымша «0» индексі бар) бойынша ауытқулары арқылы жазып, келесіні аламыз


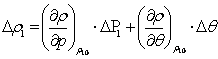
Соңында
![]()
![]()
мұндағы

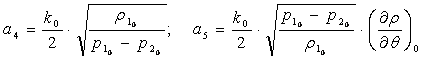 .
.
Қажет болса алты «кіріс-шығыс» каналдары жиынымен құрастырылған эквивалентті модельді алуға болады. Автоматты басқару жүйелері теориясынан белгілі эквиваленттеу ережелері бойынша әр каналдың сипаттамаларын анықтауға болады.
в) Есеп шарты қарастырған мысалға ұқсайды. Айырмашылығы тек құбыр бойынша қозғалатын ағын қысылатын ағын болатынында. Бұл арада негізгі есепке алатын шарт келесіде: қысылатын ағынның қасиеттері идеалды газ қасиеттеріне жақын. Сондықтан қысылатын ортаның қасиеттерін анықтауға термодинамикадан белгілі өрнектерді қолдануға болады. Мысалы, изотермиялық процесс үшін
![]()
Онда (10.7) теңдеуге r1 орнына анық өрнекті қоюға болады:
![]() .
.
10 дәріс. Идентификация мәселесі туралы жалпы мәліметтер
Дәрістің мазмұны:
- идентификация түсініктемесі; идентификация түрлері; идентификациялау әдісетерін классификациялау.
Дәрістің мақсаты:
- идентификациялау теориясының жалпы мәліметтерін оқу.
10.1 Негізгі түсініктемелер
Алдында қарастырған әдістер оқып білу әдістері болып табылады. Объект немесе құбылыс механизмін, яғни объектте бар барлық себеп-салдар байланыстарды модель операторының құрылымында көрсету осындай модельдердің ерекшелігі болып табылады. Айтылған байланыстарды есептемесе, модельдің біліп тану қасиеті жойылар еді, себебі білу үшін жалғыз «қалай» деген сұраққа емес, сонымен бірге «неге» деген сұраққа да жауап алу керек.
Енді біз басқару есебін шешуге қолдану мақсатына негізделген модельдер класын оқимыз). Дұрыс құрастырылған басқару сигналы объектті белгілі бастапқы күйден қажетті күйге көшіру үшін мақсатымен басқаруды орындау үшін басқару объекттің сипаттамаларын білу қажет.
Идентификациялау деп аталатын автоматты басқару теориясының маңызды бағыттарының бірі кірудегі және шығудағы сигналдар өлшеулер нәтижелерінің негізінде объекттің сипаттамаларын анықтау есебін шешеді. Біліп тану модельдерге қажетті осындай модельдер құбылыстың ішкі механизмдерін бейнелемеуі мүмкін. Олар объект кірістері мен шығыстары арасындағы тек қана кейбір формалды байланыстарды орнатады. Осы байланыстың сипаттары мен ерекшеліктері басқару объектті идентификациялау процесінде алынған модельдің негізі болып табылады.
Идентификациялау (лат.identifico – ұқсату) деген белгілі критерий дәлдігімен объектке адекватты (лат. adaeguatus – теңескен) болатын оның математикалық моделін құрастыру процесі. Тағы бір анықтамасы: идентификация – объект мен модель арасындағы өзара бір мәнді сәйкестікті орнату процесі. Басқару теориясында көбінесе келесі анықтаманы қолданады: идентификация – тәжірибелік зерттеулер мәліметтері негізінде объект сипаттамаларын анықтау.
Идентификацияның ерекшелігі басқару мақсаттарымен анықталады. Кез келген басқару алгоритмінде қойылған есеп көзқарасы жағынан объектке ең тиімді әсерді анықтауға мүмкіндік беретін объект моделі орнатылады. Әр нақты объекттегі модель сипаттамаларының ауытқулары кей кезде оның параметрлері мен құрылымын өзгертеді. Сондықтан модельді түзету қажет болады. Басқаруды синтездеу алдында модельді түзету қажет, басқа сөзбен айтқанда , объектті қайтадан идентификациялау. Сонымен, басқару екі қадамға бөлінеді: бірінші қадамда объекттің адекватты моделін синтездеу керек, екіншісінде – осы модель негізінде басқаруды синтездеу. Сондықтан идентификация бөлек есеп болмайды, ол басқару мақсаттарына бағынышты болып басқару есебінің құрылымдасқан бөлігі болады. Бірақ, көбінесе методологиялық көзқарас жағынан идентифициялау өздігінше мақсат ретінде қарастырылады, себебі модельдерді синтездеу әдістері басқаруды синтездеу әдістерінен өзгеше болып табылады. Осы жағдай себебінен идентификациялау басқару теориясының бөлек бөлімі болып орнатылды.
Жүйе туралы априорлық ақпарат көлеміне қарай идентификациялау кең мағынадағы және тар мағынадағы деп бөлінеді. Модель операторының құрылымын анықтау процесі кең мағынадағы (немесе құрылымдық) идентификациялау деп аталады. "Құрылым" деген түсініктеменің анық анықтамасы жоқ және әртүрлі авторлар бұл түсініктемені әртүрлі талқылайды. Берілген коэффициентеріне дейінгі дәлдікпен алынған модель операторын модель құрылымы деп атаймыз. Кірудегі және шығудағы сигналдарды өлшеу нәтижелері негізінде математикалық модельдің құрылымы анық болған кезде оның параметрлерін бағалау тар мағынадағы идентификация болады. Кең мағынадағы идентификация кезінде жүйе туралы априорлы ақпарат өте аз немесе жоқ болады. Тар мағынадағы идентификация кезінде жүйе туралы априорлы ақпарат жеткілікті болады.
Егер де модель операторы оның параметрлеріне дейінгі дәлдікпен берілсе, параметрлік идентификациялау есебін аламыз.
Бұл есептің қойылуы келесідей: тәжірибелік мәліметтер негізінде модель анықталған мағынада ең тиімді (немесе жеткілікті дәлдікпен) объект операторын аппроксимациялайтындай параметрлер векторының мәндерін анықтау.
Егер де модель операторында белгісіз функциялары бар болса, осындай операторлар терминдерінде идентификация параметрлі емес деп аталады.
Әрқашан келесіні есепке алу керек:
- талқыланып отырған идентификациялау әдістерінің біреуі де жүйелердің барлық түрлерін идентификациялауға жарамайды, олардың әрқайсысының өзінің қолдану аймағы бар;
- зерттелетін процестің математикалық моделін құрастыру мақсатын әрқашанда біліп отыру керек; осыдан әдісті таңдауда және соңғы нәтижелерді дұрыс интерпретациялауда болады;
- жүйенің жаңадан өңделген математикалық моделін қолданудың шектелген аймағын белгілеу керек.
10.2 Идентификациялау әдістерін классификациялау
Негізіне қандай негізгі қасиет салынғанына қарай идентификациялау әдістерін классификациялау әртүрлі жолдармен орындалуы мүмкін. Сондықтан әр классификация салыстырмалы болып табылады.
Зерттелетін жүйе қандай класқа жататынына қарай идентификациялау әдістері келесідей бөлінеді:
- сызықты немесе сызықсыз жүйелерді идентификациялау әдістері; сонымен бірге сызықты жүйелерді идентификациялау жеңілдеу болады, себебі олардың суперпозифиялық қасеттері бар;
- стационарлы немесе стационарлы емес жүйелерді идентификациялау әдістері. Егер де дәл идентификациялауға қажетті уақытқа қарағанда жүйе параметрлері баяу өзгеретін болса, жүйелер стационарлы болып есептелінуі мүмкін;
- дискретті және үздіксіз жүйелерді идентификациялау әдістері;
- жалғыз немесе бірнеше кіріс әсерлері бар жүйелерді идентификациялау әдістері;
- детерминерленген немесе стохастикалық процестерді иден-тификациялау әдістері. Стохастикалық процестерді идентификациялағанда әдетте жүйе күйі туралы ықтималдық пікірлерге негізделеді. Практикада өлшеу нәтижелерінің барлығы бөгеттер себебінен дәл болмайды, сондықтан дәл идентификациялау үшін фильтрацияны немесе тегістеу операцияларын қолдану қажет болады. Детерминерленген жүйелерді идентификациялағанда әдетте фильтрация өткізілген деп есептелінеді.
Айтылған классификациялау тәсілдерінің негізінде идентификациялау күрделілігі қойылған. Модель құрылымын таңдау процесінде қиындықтарды ескере отырып, модельді «төмендетуге» болатынына, яғни оны объекттің әлде- қайда қарапайымдалатынына көңіл бөлу керек. Мысалы, егер де объект динамикасы өте жоғары болмаса, динамикалық объекттің жүріс-тұрысын статикалық модельмен бейнелеуге болады; сызықты емес объектті сызықтымен аппроксимациялау, т.б. Әрине, осындай модельдер негізінде құрастырылған басқарудың тиімділігі төмендейді. Бірақ осы төмендеуі көп білінбесе, ал идентификациялаудан ұтатын табысты болса, осындай таңдауды оптималды деп есептеуге болады.
Идентификациялау есебі объект моделінің құрылымын анықтап, оның параметрлерін қайтадан өңдеуге саятын болғандықтан, идентификациялау есептері мен әдістерін классификациялау негізіне объекттің алдын ала зерттеп тану дәрежесін таңдауға болады. Бұл ең маңызды, бірақ қолдануға қиын нұсқасы – жүйе туралы априорлы ақпараттың бар болуына қарай идентификациялау әдістерін клаасификациялау. Мұнда барлық объекттерді келесі топтарға бөлуге болады:
- коэффициенттерінің жуықтаған мәндеріне дейін оларды бейнелейтін теңдеулері белгілі болатын объекттер; осындай объекттер үшін идентификациялау есебі жоқ болады, бұл есеп параметрлерінің жуықтаған мәндерін дәлелдеуге келтіріледі;
- оларды бейнелейтін теңдеулер белгілі, бірақ коэффициенттерінің сандық мәндері белгісіз болатын объекттер; осы объекттер үшін идентификациялау процесі белгілі құрылымы бар модельдердің белгісіз параметрлерін қалпына келтіруге саяды;
- оларды бейнелейтін теңдеулерінің анықталған түрі және параметрлерінің сандық мәндері белгісіз болатын объекттер, бірақ объект туралы априорлы ақпарат бар, мысалы, объект сызықты, ондағы өтпелі процестер монотонды болып табылады, т.б. Модель құрылымы бұл кезде осы белгілі априорлы ақпарат негізінде таңдалынып, тәжірибелер өткізу кезде дәлелденуі мүмкін, содан кейін параметрлерін қалпына келтіру есебі шешіледі;
- олар туралы ешқандай априорлы ақпараты жоқ объекттер («қара жәшік»).
Кез келген шектес топтарының арасында анық шекті орнату қиын болып табылады.
Процестер динамикасын зерттеудің тәжірибелік әдістері оның кіріс және шығыс координаттарындағы орнатылған ақпаратты өңдеуде негізделген. Объектте тәжірибені өткізу әдісіне қарай идентификациялау әдістерін активті, пассивті және аралас деп бөлуге болады.
Егер де зерттелетін объект кірісіне алдын ала анықталған сыналатын ісерлер беріліп, шығудағы сигнал зерттелсе, идентификациялау әдістері активті болып табылады. Сыналатын әсерлер импульсті, периодтық немесе кездейсоқ уақыттан тәуелді функциялары болуы мүмкін.
Көбінесе объекттің әдеттегі жұмысын жасанды сыналатын әсерлермен бұзуға рұқсат берілмейді. Осындай жағдайда идентификациялаудың пассивті әдістері қолданылады, әдетте, статистикалық (мысалы, корреляциялық). Бұл кезде кірістегі сигналдың кездейсоқ табиғилық тербелістері қолданылады.
Осындай әдістерді тиімді қолдану үшін бақылаудың үлкен интервалын алу керек, сондықтан компьютерлерді міндетті түрде пайдаланады. Жасанды сыналатын әсерлерді қолданбағандықтан, басқару процесіне идентификациялау жабдықтарының қажет емес әсерлерін жояды, бірақ идентификациялау дәлдігі төмендейді, әсіресе басқару шаманың кіші деңгейлерінде. Сондықтан ең болмаса осындай жағдайда активті тәжірибені өткізу немесе пассивті тәжірибедегі бақылау интервалын үлкейту ұсынылады. Кірудегі сигналдар объекттің барлық сипаттайтын жиіліктерінен тұруы керек.
Қай әдісті қолдану дұрыс болатынын шешу жеңіл сұрақ емес. Ол анықталған объекттің қасиеттерінен, идентификациялаудың қажетті дәлдігінен және сыналатын сигналдың түріне тәуелді.
Идентификациялау әдістері ұсынылған классификациядан басқа келесі белгілер бойынша бөлінуі мүмкін:
- объект сипаттамаларын көрсету әдісі бойынша (уақыт немесе жиілік кеңістігінде);
- объект мен модельдің ұқсастығын орнататын критерийі бойынша;
- модельдің белгісіз параметрлерін қалпына келтіру әдістері бойынша (итерациялық немесе итерациялық емес).
Алынған математикалық бейнелеу нақты объекттегі бар болатын заңдылықтарды шешілетін басқару есебінің талап ететін дәлдігімен көрсетуі керек. Одан басқарудың сапасы тәуелді болады.
11 дәріс. Идентификациялау есебінің қойылуы
Дәрістің мазмұны:
- идентификациялау есебінің қойылуы; сәйкессіздік функционалы.
Дәрістің мақсаты:
- идентификациялау есебінің қойылуымен танысу; сәйкессіздік функционалын минимумдау әдісін оқып білу.
11.1 Идентификациялау объектісі
 Кез
келген нақты объектте шығудағы айнымалыларға
әртүрлі факторлардың көп саны әсер етеді.
Бұл факторлар бөгеттер (шулар) немесе біз танымайтын параметрлер
болуы мүмкін. Идентификациялау объекттің келесі түрде
көрсетеміз:
Кез
келген нақты объектте шығудағы айнымалыларға
әртүрлі факторлардың көп саны әсер етеді.
Бұл факторлар бөгеттер (шулар) немесе біз танымайтын параметрлер
болуы мүмкін. Идентификациялау объекттің келесі түрде
көрсетеміз:
11.1 Сурет – Идентификациялау объекті
Мұндағы: Х = (x1…хn) – объекттің бақыланатын кірістері;
Е = ( e1…ek) – оның бақыланбайтын кірістері;
У = (y1…ym) – объекттің бақыланатын шығыстары.
Динамикалық объекттерді идентификациялауға объекттің кірісіндегі және шығыстарындағы сигналдар ақпарат көзі болып табылады. Е бөгет туралы мәліметтер, әдетте, жоқ. Объекттің барлық кірістері сыртқы ортаның объектке әсерлері және сыртқы ортаның күйлерінен және уақыттан тәуелді анықталған функциялар әсерлері болып табылады. Жиі жағдайда объект кірістері уақыттан тәуелді кездейсоқ функциялар болып табылады; олардың статистикалық қасиеттері жалпы кезде белгісіз, бірақ Х(t) және Y(t) функцияларының үздіксіз немесе дискретті түрдегі іске асырулары бар.
Таза бөгеттер, өлшенетін сигналдармен корреляцияланатын өлшенбейтін сигналдар, өлшеулер және түрлендірулердің қателіктері, т.б. болатын объекттегі шулардың себебінен де идентификациялау қиындалады. Бақыланбайтын E(t) кіріс туралы оның құрылымы, яғни осы кездейсоқ функцияның сипаттамасы белгілі деп есептелінеді. Әдетте E(t) нормалды кездейсоқ процесс, бірақ оны тікелей бақылау мүмкін емес деп алынады. Жалпы көзқарасты жоймай, осындай барлық шуларды шығыста орнатуға болады (11.2 сурет).
Идентификация процедурасын бастау үшін қажетті объект туралы барлық ақпараттар екі түрге бөлінеді: априорлы және апостериорлы ақпарат.
Объекттің кірістері мен шығыстарын бақылау алдында белгілі априорлы ақпарат идентификацияланатын объекттің құрылымын анықтайды.
11.2 Сурет – Динамикалық жүйенің классикалық көрсетілуі
Мысалы, келесі төрт белгілерді (бірақ, құрылым тек олармен анықталмайды) атауға болады: динамикалық, стохастикалық, сызықсыз, дискреттілік қасиеттер. Әрине, объект туралы пікірлер апостериорлы ақпаратты талқылағаннан кейін, яғни объекттің кірістері мен шығыстарының жүріс-тұрысын бақылағаннан кейін өзгеруі мүмкін.
Апостериорлы ақпарат сандық түрде көрсетіледі, яғни бұл объекттің кірісі мен шығысын бақылау нәтижелері (протокол). Үздіксіз объекттер үшін үздіксіз мәліметтердің тіркелулерін аламыз: бір бақылау периодындағы (0<=t<=T) объект кірісінің барлық өлшеулері X(t) және оның шығыстарының өлшеу нәтижелері Y(t). Протокол келесі түрде жазылады: (<X(t), Y(t)>, 0<=t<=T). Мұның мағынасы келесідей: объект жүріс-тұрысы n+m әртүрлі қисықтар x1(t),…, xn(t); y1(t),…, ym(t) түрінде осы интервалда тіркелген.
Дискретті түрде X = (X1,…, XN), Y = (Y1, …, YN) және де протокол келесі (<Xi Yj>, i=1,…, N; j = 1,…,N) түрде жазылады, мұнда Xi = (x1i,…,xni), Yi = (y1i ,…, ymi). Осы протокол n+m тік жолдары және N жәй жолдары бар кесте болып табылады
|
х11 |
х21 |
… |
xn1 |
y11 |
y21 |
… |
ym1 |
|
х12 |
х22 |
… |
xn2 |
y12 |
y22 |
… |
ym2 |
|
|
|
|
|
|
|
|
|
|
х1N |
х2N |
… |
xnN |
y1N |
y2N |
… |
ymN |
11.2 Идентификациялау есебінің қойылуы
Объект берілген болсын, оның әдеттегідей жұмыс кезінде бір уақытта оның кірісіндегі x(t) және шығысындағы y(t) функцияларын өлшеуге мүмкіндік бар болсын. Жалпы кезде бұл функциялар кездейсоқ болып табылады. Осы x(t) және y(t) өлшеу нәтижелерін қолданып, берілген объекттің моделін құрастыру қажет болсын, яғни кірісіндегі x(t) және шығысындағы y(t) функцияларды бір-біріне сәйкестендіретін операторды табу. Дәлірек айтқанда, модель операторының өзін емес, оның жуықтаған мәнін, яғни бағасын табу есебі қойылады. Басқа сөзбен айтқанда, объект операторына белгілі мағынада жақын болатын модель операторын құрастырамыз.
Объект сипаттамаларын көрсететін операторын А0 деп белгілейік, ол кірістегі еркін x(t) сигналына шығудағы y(t) сигналын сәйкестіреді
y(t)=A0{x(t)}
А0 операторының жуықтамасы ретінде қолданылатын кейбір А операторды табу идентификациялау есебінің мағынасы болады, яғни
yм(t) = A{x(t)},
мұнда A0 – объект сипаттамасы, A – модель сипаттамасы.
Оператордың А бағасы белгілі мағынада оның нақты мәніне жақын болса, тек қана сонда модель мен объект арасындағы сәйкестік туралы әңгімелеуге болады. Жақындығын дәлелдеу өте қиын, себебі А және А0 операторларының құрылымы, олардың кірістер саны әртүрлі болуы мүмкін және А0 операторы белгісіз. Осыған байланысты операторлардың жақындығын олардың бірдей кірудегі x(t) әсеріне y(t) және yм(t) реакциялары бойынша бағалауға болады.
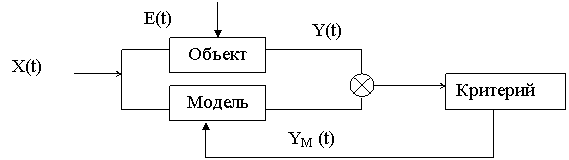
11.3 Сурет – Идентификациялау процедурасының сұлбасы
Жалпы кезде ρ(y,yм) функциясы орнатылады, ол y, yм тәуелді, бірақ А-дан тәуелсіз болады және жоғалту функциясы немесе невязка (сәйкессіздік) функциясы деп аталады. Бұл функцияның келесідей қасиеттері бар:
1) ρ(y,yм)>=0 кез келген y,yм үшін;
2) тек қана y=yм болғанда ρ(y,yм)= 0;
3) ρ(y,yм) – үздіксіз және төмен қарай ойылған, яғни бұл функция әрқашанда екі кез келген y,yм нүктелерін байланыстыратын түзу кесіндісінен жоғары жатпайды.
Егер де y,yм әр нүктеде емес, барлық бақылау интервалында жақын болуы керек болса, онда барлық интервалда жақындық өлшемін енгізу керек. Осындай өлшем ретінде келесі функционалды қолдануға болады:
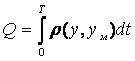 (11.1)
(11.1)
Егер де физикалық мағынасы бойынша ақпараттың маңызы уақыттың әртүрлі моменттерінде бірдей болмаса, онда келесідей нормалау шартымен
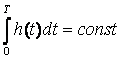 (11.2)
(11.2)
h(t)>0 салмақ функциясы енгізіледі.
Сонда
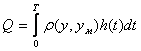 (11.3)
(11.3)
h(t) функциясын таңдау ақпараттың маңыздылығымен анықталады.
Дискретті жағдайда Q функционалы келесі түрде жазылады
![]() (11.4)
(11.4)
мұнда hi >0 (i=1,…,N, ∑ hi =N) – i моментіндегі ақпарат салмағы.
Q функционалы сәйкессіздік (невязка) функционалы деп аталады, ол А-дан тәуелді. Сонымен невязка дәрежесін (сәйкессіздік дәрежесін) модель А операторынан ашық түрде тәуелді (11.3) немесе (11.4) функционалдар түрінде көрсетуге болады. Әрине, идентификациялау процесін осы функционалды минимумдауға тырысып құрастырамыз, яғни Q функционалын А операторлар бойынша минимумдау есебін шешеміз
![]()
Бұл функционалды минимумдағанда, А операторын еркін таңдамаймыз, оларды белгілі операторлар класынан Ω таңдаймыз. Нәтижесінде А* операторын аламыз (жалғыз болмауы мүмкін), оның келесідей қасиеті бар
![]() (11.5)
(11.5)
Басқа сөзбен айтқанда, невязка осы операторда минималды. Идентификациялау есебін шешуге минимумдау процедурасын қолдану өте маңызды болып табылады. Идентификациялаудың сапасының критерийі орта жоғалтуларды көрсетеді. Орта жоғалтулар неғұрлым кіші болса, соғұрлым идентификациялау сапасы жоғары болады. Идентификациялау сапасының жақсаруы икемделетін модельдің құрылымын таңдап6 оның параметрлерін өзгерту арқылы орындалады. Өзгертулер идентификациялау алгоритмдерімен орындалады. Идентификациялау алгоритмі жоғалтулар функциясымен және күйіне келтірілетін модельдің құрылымымен анықталады. Объект пен күйіне келтірілетін модельдің кірудегі әсерлері мен шығудағы шамаларын бақылап, n мәні өскен сайын орта жоғалтулары минимумдалатындай, идентификациялау алгоритмі модельдің параметрлерін өзгертеді.
Идентификациялаудың қиындықтары. Идентификациялау есебінің шешімі ізделінетін операторлардың Ω класын анықтауда бірінші қиындығы болады. Бұл қиындықты формалды жолмен жеңу қазіргі кезде мүмкін емес. Әзірше Ω оператор класы туралы шешімді тек қана адам қабылдай алады. Сонымен бірге келесілерді есепке алу керек: басқару объект ретіндегі объекттің құрылымын; объект жұмысының механизмін (басқару мақсаттарына әсер ететін); басқару мақсаттарын; басқару алгоритмін. Соңғы екі пункттері Ω класын болашақ басқарумен байланысырады, сол басқару үшін объект идентификацияланады. Екінші қиындық минимумдау есебін ыңғайлы және тез шешуде болады. Идентификациялау алгоритмі қойылған есепті белгілі мағынада тиімді шешу керек. Басқа сөзбен айтқанда идентификациялау есебінің тиімділігінің критерийі анықталуы керек.
12 дәріс. Сызықты динамикалық объекттерді идентификациялау. Тура әдістері
Дәрістің мазмұны:
- сызықты объекттерді идентификациялау әдістері; арнайы түрдегі сигналдар көмегімен идентификациялау.
Дәрістің мақсаты:
- өтпелі функция көмегімен сызықты объекттерді идентификациялау әдістерін оқып білу.
Сызықты болатын немесе жеткілікті дәлдікпен сызықты модельдермен аппроксимацияланатын объекттерді идентификациялау әдістерін қарастырамыз.
Сызықты объекттің динамикалық сипаттамаларын тәжірибелі жолмен анықтау әдістерін үш негізгі топтарға бөлуге болады.
Тура әдістер деп аталатын әдістері бірінші топты құрастырады. Бұл топтың әдістерімен келесідей сипаттамалар анықталады: жиілік аймағында – амплитудалық және фазалық сипаттамалары, уақыт аймағында – импульсті өтпелі және өтпелі функциялары. Бұл топтың әдістері объект кірісіне арнайы сигналдарды беруді талап етеді, кей кезде оны жасау мүмкін емес немесе рұқсат етілмейді.
Белгілі құрылымы бар модельдердің параметрлерін қалпына келтіру әдістері екінші топты құрастырады.
Объекттің белгісіз динамикалық сипаттамаларын объект туралы бар болатын априорлы ақпарат негізінде таңдалынатын аналитикалық өрнектермен аппроксимациялауда негізделген әдістері үшінші топтың әдістері болып табылады.
12.1 Динамикалық сипаттамаларды тура әдістермен анықтау
Тура әдістерде идентификациялау арнайы түрдегі сигналдар көмегімен орындалады. Басқару жүйелерде іске асырылған бірінші әдістері жиілік, сатылық және импульсті әсерлерді қолданумен орындалды. Осы әдістердің көбісі тек қана сызықты жүйелерге қолданылады. Егер сигналдар деңгейлері кішкене шамалар болса, олар сызықтандырылған жүйелерге де қолдануы мүмкін. Бұл әдістер арнайы сигналдарды талап етеді: өтпелі функция (сатылы өтпелі функция) бойынша идентификациялау үшін сатылы сигналдарды, импульсті өтпелі функциямен идентификациялау үшін кірісте импульсты сигналдарды және жиілік сипаттамаларды анықтау үшін әртүрлі жиіліктердегі синустық кірістегі сигналдарды.
Объекттің әдеттегідей кірістегі сигналдардың орнына айтылған арнайы сигналдары қолданылатын болғандықтан, бұл әдістер идентификацияны, әрине, басқару процесінен тыс кезде өткізілетінін талап етеді. Сондықтан бұл әдістер тек қана сызықты стационарлы жүйелерге қолданылады, себебі осындай жүйелерде кіріс сигналдардың бір түріне алынған кіріс/шығыс қатынасы басқа түрдегі кіріс сигналдарына да сақталады.
Аталған кіріс сигналдарының үшеуінің ішінде сатылы кіріс сигналы қолдануға ең қарапайым болып табылады, ал синусоидалдық сигналдарды кіріске беру синусоидалдық әсерлерді жасап, жиілікті сәйкес диапазонда өзгерту керек. Импульсті әсер бойынша идентификациялау үшін импульсті кіріс сигналын жасап, қолдануымен байланысты техникалық қиындықтар пайда болады. Бұл әдісті сызықтандырылған жүйелерге қолдануға болмайды, себебі анықтама бойынша импулс амплитудасы кіші шама бола алмайды.
12.2 Өтпелі функция бойынша идентификациялау
Идентификациялау кезде қолданылатын қарапайым кіріс сигналы сатылы сигнал болып табылады. Осындай сигнал жүйе кірісінде, мысалы, кіріс клапанды кенет ашу (жабу), басқару кернеуді қосу (өшіру), т.б. жолдарымен орнатылады, сонымен бірге олардың барлығын арнайы аппаратураны қолданбай орнатуға болады. Идеалды сатылы сигналдың өсу уақыты нөлге тең, бірақ мұны физикалық іске асыру мүмкін емес, себебі ол кезде өсу жылдамдылығы шексіз үлкен шама болуы керек. Сондықтан кез келген нақты сатылы сигнал идеалды сатылы сигналының тек қана аппроксимациясы болады. Бірақ, егер де сигналдың өсу уақыты жоғарғы гармониканың периодынан әлдеқандай кіші болса, идентификациялау қателігі кіші шама болады. Бөгеттері бар процестерде немесе өлшеулерге шулар әсер еткен болса, шуларға фильтрлеу процедурасын қолдану қажет.
Өтпелі процесс көмегімен идентификациялау басқару процесінен тыс автономды орындалады, сондықтан тек қана стационарлы процестерге қолданылады. Бірақ сатылы әсерлер жүйелерді жұмысқа қосқанда және де олардың әдеттегідей жұмыс кезінде де көп деген жүйелерге әсер ететін болғандықтан, жүйе жұмысын бұзбай өтпелі функцияларды жазып алуға болады. Осында қарастырып отырған әдістің артықшылығы болады. Сонымен бірге, жүйе стационарлы деп есептеу керек, себебі идентификациялау нәтижелері сатылы сигналды қолданғаннан да кейін дәл болады деп есептелінеді. Сонымен бірге сатылы сигналдың амплитудалары диапазонында жүйе сызықты деп есептелінеді.
Сонымен, жүйенің беріліс функциясын анықтау үшін оның өтпелі функциясының графигін қолданамыз. Осындай әдісті сызықты жүйелердің көбісіне (1 және 2 ретті және жоғарғы дәрежелі апериодтық жүйелерге) қолдануға болады. Өтпелі функциялар көмегімен графикалық идентификациялау әдісті бірінші ретті процестерге қолданғанда дәлдігі жоғарырақ болады.
Өтпелі процестің графигі берілген болсын. t0=0 уақыт моментінде x шамасы секіру жолымен а шамасына өзгереді. Объект теңдеуін жазу керек. Ізделінетін теңдеудің түрі бірінші ретті объект үшін келесідей болады
![]() немесе
немесе ![]() .
(12.1)
.
(12.1)
Теңдеудің T және k параметрлерін анықтау керек.
Осы параметрлерді анықтаудың бірнеше әдісін қарастырайық:
а) біріншіден берілген бастапқы шарттарда теңдеудің аналитикалық шешімін табамыз. Осы шешімге T және k параметрлері кіреді. Графикалық және аналитикалық шешімдерді салыстырып, шешімнің аналитикалық өрнегінің парметрлерін табамыз. Бастапқы шарттар: t=0 болғанда y=0 және t>0 болғанда x=a үшін теңдеудің жалпы шешімінің өрнегі келесі түрде жазылады:
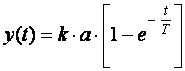 (12.2)
(12.2)
Графикте екі нүктені алайық (бұл жеткілікті). Осы нүктелердің координаттарын шешім өрнегіне қойып, екі T және k белгісіздерді анықтау үшін екі теңдеуді аламыз:
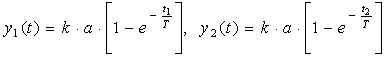
Бірақ бұл теңдеулер трансцендентті, сондықтан олардан T және k мәндерін есептеу өте қиын. Алынған шешімнің дәлдігі төмен, себебі графиктің тек қана екі нүктесі қолданылды;
б) дәлдігі жоғарырақ шешімді алу үшін графикті ∆t қадамымен y1, y2 , y3,…ординаталарға бөлеміз. Алынған нүктелер үшін, жалпы шешімді қолданып, келесіні жазуға болады
![]()
![]()
т.с.
Келесіні есептейміз
![]() т.с.
т.с.
e
![]() деп белгіліп, келесіні жазамыз
деп белгіліп, келесіні жазамыз
![]() ,
,
![]()
![]() , т.с.
, т.с.
Сонымен бірге
![]()
![]()
![]() және
т.с.
және
т.с.
q мәндеріндегі
айырмашылықтар тәжірибе және y(t) мәндерін
анықтаудың қателіктерімен байланысты. Алынған qi
мәндерінің орта арифметикалық ![]() мәнін
есептеп, уақыт тұрақтысын келесі өрнектен
мәнін
есептеп, уақыт тұрақтысын келесі өрнектен
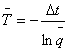 нақтылауымызға болады:
нақтылауымызға болады:
Сол сияқты, келесілерді есептеп
![]()
![]()
![]() және т.с.,
және т.с.,
нақтыланған kорта мәнін анықтаймыз;
в) практикада жиі қолданылатын келесі қарапайым әдіс.
![]() t ∞-ке
ұмтылған жағдайда y(t) = k*a болады, яғни асимптота
ординатасы бойынша (асимптота ординатасы K=ka) k мәнін
анықтауға болады. k коэффициенті шығудағы
сигналдың тұрақталған мәнімен кірудегі
сигналдың амплитудасы арасындағы қатынасты көрсетеді.
t ∞-ке
ұмтылған жағдайда y(t) = k*a болады, яғни асимптота
ординатасы бойынша (асимптота ординатасы K=ka) k мәнін
анықтауға болады. k коэффициенті шығудағы
сигналдың тұрақталған мәнімен кірудегі
сигналдың амплитудасы арасындағы қатынасты көрсетеді.
t = T болғанда, функция
y (t)=b·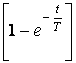 = b· (1-e-1) = b· (1-0.37) =
0.63·b.
= b· (1-e-1) = b· (1-0.37) =
0.63·b.
Сонымен, бірінші ретті жүйенің өтпелі функциясы өзінің тұрақталған мәнінің 63% жеткендегі уақыт бөлігі жүйенің T уақыт тұрақтысы болады. Графикте өтпелі процестің тұрақтанған шамасының 63% белгілеп, осы нүктенің абсциссаның табамыз (Т параметрін).
г) Т тұрақтыны келесі жолмен де анықтауға болады. Шешімді дифференциалдап, t мәнін 0-ге ұмтылдырамыз, сонда
![]() ,
,
![]() (12.6)
(12.6)
мұнда α
шамасы t = 0 болған кездегі функция
графигіне жанаманың көлбеу бұрышы. Сонда T=![]() .
Сонымен, T шамасы - координаттар
басынан жанама асимптотамен қиылысатын нүктеге дейінгі уақыт
өсінің кесіндісі.
.
Сонымен, T шамасы - координаттар
басынан жанама асимптотамен қиылысатын нүктеге дейінгі уақыт
өсінің кесіндісі.
Бұл ең қарапайым, бірақ дәлдігі төмен шешім. Себебі жанаманы дәл өткізу және асимптотаның b ординатасын дәл анықтау өте қиын. Сонымен бірге, шешім графиктің тек қана бастапқы және соңғы нүктелерін қолданады.
Егер де өтпелі функция τ уақытысына кешіксе, яғни сатылы әсерді бергеннен кейін τ уақытысы бойынша нөлге тең болса, онда жүйенің уақыттық кешігуі бар, ол үшін Лаплас түрлендіруі e-τs шамасы болады.
Сонда өтпелі функция келесі өрнектермен жазылады
 (12.7)
(12.7)
Ал беріліс функцияны келесі түрде
аламыз 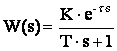 .
.
13 дәріс. Сызықты динамикалық объекттерді идентификациялау. Тура әдістері
Дәрістің мазмұны:
- Арнайы түрлі сигналдар көмегімен идентификациялау.
Дәрістің мақсаты:
- импульсті өтпелі функция және жиілік сипаттамалар көмегімен сызықты объектті идентификациялау әдістерін оқу.
13.1 Екінші ретті процестердің өтпелі функциясы көмегімен графикалық идентификациялау
Екінші ретті объект келесі теңдеумен бейнеленеді
![]() (13.1)
(13.1)
Кірістегі әсер х = а. t>0 болғанда кірудегі әсер бірлік функция
x=a=1 болатын шартында T1, T2 және k-ны есептейік.
Алдындағыдай (бірінші ретті объект) басында теңдеудің жалпы шешімін жазамыз
![]() (13.2)
(13.2)
t=0
болғанда y=0, ![]() осы бастапқы шарттары
үшін интегралдау тұрақтыларын табамыз
осы бастапқы шарттары
үшін интегралдау тұрақтыларын табамыз
![]()

Осыдан ![]()
![]()
Сонда ізделінетін дербес шешім
 (13.3)
(13.3)
Осы өрнекке графиктің үш нүктесінің координаттарын қойып, ізделінетін шамаларға үш теңдеуді алуға болады. Бірақ бұл теңдеулер трансцендентті болғандықтан, шешімін табу оңай емес. Осы орайда бірінші ретті объектке қолданған әдісті пайдалануға болады.
13.2 Импульсті өтпелі функциясы көмегімен графикалық идентификациялау
Импульсті өтпелі функциялары көмегімен сызықты жүйелерді идентификациялау процедурасы өтпелі функциямен идентификациялауға ұқсас. Осындай идентификациялау үшін идентификацияланатын жүйе кірісіне импульсті әсерді (делта-функцияны) беру керек. Сондықтан идентификациялау басқару процесінен тыс орындалады.
Бірлік импульс үшін Лаплас түрлендіруі бірге тең: X(s) = 1. Сонда шығудағы сигнал үшін Лаплас түрлендіруі Y(s) = W(s) және Y(t) = L-1[Y(s)] = L-1[W(s)]= g(t). Басқа сөзбен айтқанда, сызықты жүйе үшін импульсті өтпелі функциясы оның беріліс функциясының кері Лаплас түрлендіруіне сәйкес. Бұл нәтиже идентификациялау үшін өте маңызды.
Бірінші ретті жүйелер келесі беріліс функциясымен сипатталады
![]()
Онда импульсты өтпелі функция келесі түрде жазылады
![]() .
(13.4)
.
(13.4)
T және K параметрлері графиктен анықталады:
бастапқы нүктеде
![]() , ал g(t) функциясы
, ал g(t) функциясы ![]() мәніне
жететін уақыт T-ға тең:
мәніне
жететін уақыт T-ға тең:
![]() .
(13.5)
.
(13.5)
Т
тұрақтысын келесі жолмен де табуға болады: g(t)
графигінің басынан жанаманы өткізіп, оның уақыт осімен
қиылысқан нүктесін аламыз, себебі ![]() теңдеуіне
сәйкес келесіні жазуға болады
теңдеуіне
сәйкес келесіні жазуға болады ![]() және
t = T болғанда келесіні аламыз
және
t = T болғанда келесіні аламыз ![]() ( жанама теңдеуінен)
( жанама теңдеуінен)
Практика
жүзінде жүйенің кіріс сигналы импульске жуықтау болады
және g(t) ешқашанда ![]() шамасынан басталмайды.
Бұл жағдайда t=0 аймағындағы максималды еңкею t=0
шамасының кері бағытынан
шамасынан басталмайды.
Бұл жағдайда t=0 аймағындағы максималды еңкею t=0
шамасының кері бағытынан ![]() шамасына жететіндей
жалғастырылады.
шамасына жететіндей
жалғастырылады.
13.3 Жиілік сипаттама көмегімен идентификациялау
Реттеу жүйелерді анализдеу және синтездеу үшін жиілік сипаттамалар кең қолданылады. Бірақ оларды объект теңдеулерін анықтауға да пайдалануға болады. Жиілік әдіс амплитуда-фазалық сипаттамаларды қолданады. Жиілік сипаттама көмегімен идентификациялау синустық немесе жиіліктері қарастырылып отырған интервалда өзгеретін синустық сигналдарды жуықтайтын сигналдарды қолдануда негізделген.
Бұл әдістердің көп артықшылықтары бар: гармоникалық кіріс сигналдары өлшеулердің әртүрлі нүктелерінде ортогоналды болып табылады, сондықтан жиілік сипаттамалардың әр нүктесі басқалардан тәуелсіз анықталады; осы жағдайға байланысты әдістің үлкен дәлдігі бар; өңдеудің қарапайымдылығы; өлшеулерді бекітілген жүйеде орындауға болады; бөгеттер әсерлерінің төмен деңгейлері.
Кемшіліктері: күрделілігі және төменгі жиілікте өлшеу жүргізу үшін құрылғылардың көп мөлшерде болуы; өлшеу уақытының үлкен болуы; сигналдарды түрлендірудің қажеттілігі; өлшеу шарттары және зерттелетін объекттің параметрлері бақылау кезінде өзгеріп кетуі.
Фурье түрлендіруін қолданғанда кірістегі және шығыстағы сигналдар келесідей байланысады:
Y(jω) = W(jω)·X(jω),
мұндағы W(jω) – ω жиілігіндегі жүйенің беріліс функциясы. Бұл комплексті шама
W(jω) = α(ω) + j·β(ω);
│W(jω)│= ![]() ;
;
φ(ω) =
arg[W(jω)]=
![]()
Егер де объект кірісіне синустық A0sin(ωt) әсер берілсе, онда тұрақтанған шығудағы сигналдың өлшенген мәні келесідей болады
y(t) = A1sin[ωt + φ(ω)] + n(t),
мұнда n(t) - өлшеу қателігі, ![]() =│W(jω)│, φ = Arg[W(jω)].
=│W(jω)│, φ = Arg[W(jω)].
W(jω) жиілік сипаттаманы анықтау үшін әртүрлі ω жиіліктерде A0sin(ωt) синусоидалды кіріс сигналдар беріліп, оларға сәйкес шығудағы A1sin[ωt + φ. сигналдар жазылады. Қажетті жиілік сипаттаманы алу үшін A1/A0 және φ шамалары қарастырып отырған ω әр мәні үшін анықталады. Басқа сөзбен айтқанда кірудегі және шығудағы сигналдардың жазулары бойынша ωi жиіліктегі амплитудалардың қатынастары қарастырылып, |W(jωi)| анықталады. Фазалық φ(ωi) ығысуды x(t) және y(t) қисықтардың максимумдарын салыстырып табады. Алынған жиілік сипаттамалар объекттің теңдеуін анықтауға мүмкіндік береді.
Объектті идентификациялау процедурасын мысалда қарастырайық. Тәжірибеден алынған жиілік сипаттамалар негізінде жүйенің беріліс функциясын анықтаймыз. Тәжірибелерді өткізіп, кірудегі және шығудағы сигналдарды өлшеп, содан кейін жоғарыда айтылғандай объекттің амплитудалық А(ω) және фазалық φ(ω) сипаттамаларын анықтап, жиіліктің қарастырып отырған әр мәні үшін келесіні жаза аламыз
P(ωi) = A(ωi)·cosφ(ωi),
Q(ωi) = A(ωi)·sinφ(ωi)
Модельдің құрылымдық параметрлері (бұл арада теңдеу реті) құрылымдық идентификациялау қадамында анықталатынын еске салайық. Теңдеудің белгілі ретін (болжанатын) алайық. Анық болуы үшін объект үшінші ретті деп есептейік. Онда
![]() (13.6)
(13.6)
Беріліс функцияның коэффициенттерін анықтау керек. Алмастырып, беріліс функцияны оның нақты және жорамал бөліктерінің қосындысы ретінде жазамыз
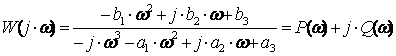
Осыдан
![]()
Комплексті өрнектердің нақты және жорамал бөліктерінің коэффициенттерін теңестіріп, келесіні аламыз
![]()
![]()
Бұл теңдеулер ω-ның барлық мәндері үшін орындалады.
Осы теңдеулерге жиіліктердің әртүрлі ωi және оларға сәйкес P(ωi), Q(ωi) мәндерін қойып, беріліс функциясының белгісіз коэффициенттерін анықтауға алгебралық теңдеулер жүйесін аламыз. Тәжірибелік өлшеулерде, сонымен бірге осы өлшеулер негізінде есептелінген P(ωi), Q(ωi) функцияларында қателіктер бар болады, сондықтан есептелген коэффициенттері нақты коэффициенттері-мен сәйкес келмейді. Коэффициенттер мәндерін нақтылау үшін есептеулер басқа жиіліктермен қайталанады және екі есептеулердің орта мәні алынады.
Егер де объект реті болжанатын реттен жоғары болса, қате есептеулердегі коэффициенттер мәні бірінші мәндерден көп өзгеше болады. Басқа сөзбен айтқанда, коэффициенттерде өте үлкен айырмашылық болса, объект реті төмен алынған (бұл айырмашылық тәжірибе қателігі емес).
Полигармоникалық кірістегі сигналдарды қолданғанда бөгеттерге тұрақтылық көбейеді. Кірістегі сигналдардың жиілік спектрі белгілі болғандықтан, кірудегі және шығудағы сигналдардың өлшеу нәтижелері негізінде барлық қажетті гармоникалар үшін Фурье коэффициенттерін табуға болады.
14 дәріс. Сызықты объекттерді параметрлік идентификациялау
Дәрістің мазмұны:
- сызықты объекттерді параметрлік идентификациялау
Дәрістің мақсаты:
- сызықты объекттерді параметрлік идентификациялау әдістерін оқу (статикалық және динамикалық детерминерленген объекттер).
Сызықты немесе белгілі дәлдікпен сызықты деп есептеуге болатын объекттерді қарастырамыз. Параметрлік жағдайда модель өзінің параметрлерімен анықталады, идентификациялау процесінде оларды бағалау керек. Бағалау үшін сәйкессіздік функционалын минимумдау процедурасы қолданылады. Осы процедураны түсіну үшін әуелі статикалық детерминерленген жағдайды қарастырамыз.
14.1 Статикалық детерминерленген сызықты модельдер
n кірісі және m шығысы бар сызықты объекттің моделінің құрылымы жалғыз болады және сызықты алгебралық теңдеулер жүйесімен бейнеленеді
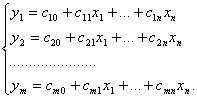
cij, i =1,..., m; j = 0,…,n коэффициенттері m(n+1) идентификацияланады
Векторлық түрде ![]()
мұнда X = (x1, x2,,…, xn)
– кіріс; Y = (y1, y2,,…, yn) –
шығыс; C0 = (c10, …,cm0);
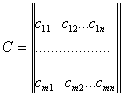
Объект туралы ақпаратты келесі түрде көрсетуге болады {Xj, Yj k}, k =1,…,m. C0 және C идентификацияланады.
n>1, m=1 жағдайды қарастырайық. m>1 жағдайы қарастырылатын жағдайды m рет қайталауға келтіріледі.
Сонымен, 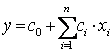 немесе
немесе ![]()
(n+1) белгісіз коэффициенттерді {Xj, Yj}, j =1,…,N, ақпарат негізінде анықтау керек, мұндағы Xj=(x1j, x2j, …, xnj) - кірістің j-ші күйі, Yj – осы кіріске жүйе реакциясы.
Бұл есепті шешудің әдеттегі амалы – объект мен модельдің шығыстарын теңестіру
![]() (14.1)
(14.1)
(n+1) белгісіздері бар N теңдеуді алдық (идентификациялау теңдеулерінің жүйесін). Бұл жүйенің жалғыз шешімі болуы үшін келесі матрицаның
|
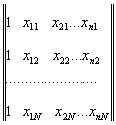 (14.2)
(14.2)
Бұл орындалуы үшін осы матрицаның (n+1) сызықты-тәуелсіз жолын табу керек. Сондықтан N жұптардан (n+1)
![]()
сызықты-тәуелсіз жолдарын таңдау керек.
Сонда (14.1) жүйенің шешімі идентификацияланатын параметрлерінің дәл мәндерін анықтайды (егер де объект нақты сызықты болса).
Бірақ біздер ақпараттың барлығын қолданған жоқпыз. Оны қолдану үшін келесі сәйкессіздік функцияны кіргізейік:
![]() (14.3)
(14.3)
мұндағы ![]() - жергілікті сәйкессіздік функция (i-ші
жұпта).
- жергілікті сәйкессіздік функция (i-ші
жұпта).
Енді С параметрлерді бағалау есебін (14.3) функциясын минимумдау есебі ретінде қарастыруға болады немесе келесі алгебралық сызықты жүйеге келтіруге
 (14.4)
(14.4)
Егер де (14.2) жүйесінің рангы (n+1)-ге тең болса, жүйенің детерминанты нөльге тең емес болады.
(14.1) және (14.4) жүйелердің шешімдері бірдей. Не үшін осы күрделі әдісті қолданамыз және де (14.1) тек қана (n+1) нүктені талап етеді? Қалған N – (n+1) не үшін керек? Егер де объект нақты дереминерленген және сызықты болса, онда екінші әдісті қолданбауға да болады. Бірақ объект сызықтыға жақын болуы мүмкін. Онда екі нүкте бойынша құрастырылған модель өрескел болады. Екінші әдіс объектті «тегістейді».
Егер де (14.4) жүйенің рангы (n+1)-ден кіші болса? Бұл жағдайда келесі амалдарды қолдануға болады
1) Өлшеулерді қайталау керек. Мүмкін жүйе күйлері бірінші тәжірибелерде әртүрлі болмады. Бұл амал көмектеспесе, модель құрылымын өзгерту керек.
2) Идентификацияланатын параметрлер санын азайту, яғни кірістің біреуін қарастырмау керек, мысалы, аз өзгеретін кірістің біреуін. (14.2) рангы оның өлшемімен бірдей болғанша осы амалды қайталау керек.
14.2 Динамикалық детерминерленген модельдер
Бір өлшемді жағдайда кірістегі x = x(t) және шығыстағы y = y(t) арасындағы байланыс қарапайым дифференциалды теңдеумен көрсетіледі
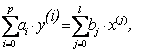 мұнда
мұнда
![]() (14.5)
(14.5)
бастапқы diy(0)/dti, i = 0,1,…, n-1 шарттарымен бірге.
Модель (p+l+1) параметрлерімен c= (a0,…,ap-1,b0,…,bl) анықталады.
Кірістегі және шығыстағы сигналдары дискретті түрде берілген болса, объект динамикасын сипаттау үшін дифференциалды теңдеулер орнына айырымдық теңдеулер қолданылады. Кірістегі және шығыстағы сигналдары дискретті мәндерін xk-I = x[(k-j)] және yk-j = y[(k-j)] деп белгілеп, айырымдық теңдеуді (дифференциалды теңдеудің аналогы) келесі түрде жазамыз
![]() (14.6)
(14.6)
Сонымен бірге бастапқы шарттарды да орнату қажет.
Модельдің құрылымдық параметрлері p және l болып табылады, олар құрылымдық идентификациялау процесінде таңдалынады.
(14.5) модельді жиі жағдайда дифференциалдық теңдеулер жүйесі ретінде көрсеткен ыңғайлы. y1 = y, y2 = y(1), y3 = y(2). … , yk = y(k-1) белгілейік. Онда (14.1) жүйе түрінде келесідей жазылады
![]() (14.7)
(14.7)
(14.5) жүйесі (14.7) түрге келтіріледі, бірақ (14.7) жалпы жағдайда (14.5)-ке келтірілмейді.
Жалпы түрде

Онда жүйенің
векторлық түрі
![]()
Y = (y1,…, yp) – күй векторы, X’=(x, x(1), …, x(l)) – әсерлер векторы, A – коэффициенттердің квадратты матрицасы, B – коэффициенттердің төртбұрышты матрицасы. Сонымен, идентификациялау процедурасын құру үшін бастапқы ақпарат болып идентификацияланатын модельдің (14.5) түрі және [0,T] аралығындағы (Xt, Yt) бақылаулар болып табылады.
ai, bj параметрлерді анықтау керек. Жалпы кезде бақылаулар нәтижелерін (14.5) модель теңдеуіне қойғанда ол теңдеуде теңдік орындалмайды. Сонымен, (14.5) теңдеуінде оң жақ және сол жақтағы бөліктерінің айырмашылығы минималданатындай ai, bj мәндерін іздейміз.
Сәйкессіздік функцияны келесідей құрастырамыз: (14.5) теңдеуге объекттің бақылаулары - Xt, Yt функцияларын қойғанда, теңдеудің оң және сол жақ бөліктерінің айырмашылығының орта квадраты ретінде:
 (14.8) (14.8)-ді
ai мен bj бойынша минимумдаймыз. Минимумдау
нәтижесі – с* идентификацияланатын параметрлер мәні болып табылады.
(14.8) (14.8)-ді
ai мен bj бойынша минимумдаймыз. Минимумдау
нәтижесі – с* идентификацияланатын параметрлер мәні болып табылады.
(14.8) функциясының барлық белгісіз параметрлері бойынша туындыларын тауып (функция тегіс болғандықтан), сызықты теңдеулер жүйесін аламыз, осы жүйенің шешімі минимумдау есебінің шешімі болады.
Алынған жүйені стандартты есептеу әдістерімен шешуге болады. Бірақ жүйе коэффициенттерін есептеу үшін объекттің кірудегі xt және шығудағы yt сигналдарының туындыларын білу керек. Егер де осы сигналдар аналитикалық түрде берілген болса, ешқандай қиыншылық жоқ. Кері туындыларды алу әдісін таңдау керек, бұл таңдау анықталған шарттардан тәуелді байланысты және есеп үшін бөлек анықталады:
1) сандық дифференциалдауды қолдану, яғни туындылардың жуықтаған нүктелік бағаларын
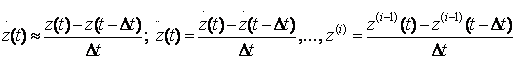 (14.9)
(14.9)
∆t - бағалаудың негізін орнататын интервал. Бұл әдістің екі кемшілігі бар. Біріншіден, туындылар бағаларының дәлдігі олардың реті жоғарыланғанмен бірге төмендейді. Практикада екінші реттен жоғары туындыларды жақсы бағалау мүмкін емес. Екіншіден, t=0 болғанда i-ші туындыны бағалау үшін функцияның t<0 интервалындағы мәндерін білу қажет, яғни z(-∆t), z(-2∆t), …, z(-i∆t). Бұл мәндер өлшеулерде жоқ, сондықтан (4)-те интегрелдау шектерін [0, T] емес, [i∆t, T] деп аламыз, мұнда i – максималды туындының нөмірі.
2) функцияны ρ(t) салмағымен тегістеу аппаратын қолдануға болады.
3) функцияны белгілі функциялар жүйесі бойынша қатарға жіктеуді қолдануға болады (тегістеу операциялар болғандықтан, туындыларды анықтаудың қателіктері аз болады).
Идентификациялау есебінің шешімі болу үшін минимумдау есебін шешу нәтижесінде алынған жүйенің анықтауышы нөлге тең болмауы керек. Егер де осы шарт орындалмаса, объекттің кірістері мен шығыстарының басқа іске асыруларын қолдану қажет немесе модель ретін төмендету (идентификацияланатын параметрлер p және l санын азайту) керек. Бірінші амал мақсатқа жеткізбеуі мүмкін, ал екіншісі тізбектеліп қолданғанда түбінде мақсатқа жеткізеді.
15 дәріс. Сызықты динамикалық объекттерді параметрлі емес идентификациялау. Корреляциялық функциялар
Дәрістің мазмұны:
- сызықты динамикалық объекттерді параметрлі емес идентификациялау
Дәрістің мақсаты:
- сызықты динамикалық объекттерді параметрлі емес идентификациялау проблемаларымен танысу; сигналдардың корреляциялық функцияларын анықтау әдістерін оқу.
15.1 Параметрлі емес модельді анықтаудың жалпы амалдары
Параметрлі жағдайда модель өзінің параметрлерінің жиынымен анықталатыны және олар идентификациялау процесінде бағаланатыны алдында айтфлды. Параметрлі емес модель жалпы кезде үздіксіз функциямен анықталады, бірақ ол нүктелермен немесе белгілі функциялар жүйесі бойынша қатарға жіктеумен берілуі мүмкін, сонда біздер параметрлі жағдайды қарастырамыз. Сызықты динамикалық объекттің спецификасы оның бірлік импульсті әсерге реакциясымен анықталады. Осы жағдай импульсті өтпелі («салмақты») функциямен сипатталатын параметрлі емес модельді анықтаудың негізінде болады.
Өтпелі функцияны анықтаудың артықшылықтары: өлшеулердің қарапайымдылығы, өлшеудің аз уақыты, сигналдарды өңдеудің қарапайымдылығы, сынап көруге арналған сигналдың қарапайымдылығы. Кемшілігі: дәлдігі төмен.
Практика жүзінде импульсті өтпелі функция жиі қолданылады. Біз қарастырып отырған стационарлы жағдайда бұл функция тек қана бір айнымалыдан, яғни уақыттан тәуелді:
g = g(t), 0 <= t <∞.
Жүйеге x(t) әсер берілгенде сызықты жүйенің y(t) сипаттамасы осы функция көмегімен біртекті келесідей анықталады
 (15.1)
(15.1)
мұнда t < 0 болғанда x(t) = 0 болады. (Бұл өрнек жийма интегралы деп аталады).
g(t) импульсты өтпелі функцияны анықтау үшін объекттің x(t) кірістерінің өлшеулерін оның бар болуының барлық уақытында, яғни t=0 –ден t=∞-ке дейін өзгергенде алуымыз керек екендігін (15.1) формуласынан көреміз. Бірақ тұрақты жүйелердің (әрине, біздер осындай жүйелерді қарастырамыз) салмақты функциясының келесідей қасиеті бар
lim g(t) = 0.
![]() t ∞
t ∞
Физикалық бұл шарт тұрақты жүйенің импульсті әсерден кейін өзінің бастапқы қалпына қайта оралатынын көрсетеді. Сондықтан, (15.1) өрнегінде жоғарғы интегралдау шегін шексіздік демей, Tg деп алуға болады; оның мәні келесі шарттан анықталады
t>Tg болғанда
![]() ,
,
яғни Tg уақыт моментінен бастап, салмақты функция 100α-пайызды диапазоннан шықпайды (әдетте α = 0.05).
Енді жийма интегралын келесі түрде жаза аламыз
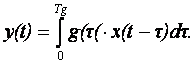
Алдыңғы дәрістерде зерттелетін объекттің динамикалық сипаттамаларын анықтаудың әдістері ретінде объект кірісіне арнайы түрдегі (импульсты, сатылы, гармоникалық) жасанды әсерлерді беріп, жүйе реакциясын өлшеп, осы бақылаулар нәтижесін қолдануды қарастырдық.
Келесі себептерден бұл әдістерді жиі жағдайларда қолдану мүмкін болмайды:
- объекттегі процестердің қалыпты тәртібінің бұзылу себебінен объект кірісіне арнайы түрдегі әсерлерді беру мүмкін емес немесе қолайлы емес;
- жиі жағдайларда осы әсерлерге бақыланбайтын бөгеттер қосылады, сондықтан объекттің динамикалық сипаттамаларын типтік кіріс сигналдары бойынша анықтау мүмкін болмайды.
Осы себептерді еске алып, статистикалық амалды қолданатын әдісті қарастырайық. Статистикалық әдісте ақпарат көзі ретінде идентификацияланатын объекттің табиғи кездейсоқ сигналдарын қолданады. Кездейсоқ сигналдарының жиілік спектр қажетті болатынының ықтималдағы өте төмен, сондықтан кездейсоқ сигналдармен бірге кейбір қателіктер пайда болуы мүмкін. Осы қателіктерді азайту мақсатымен статистикалық әдісті қолданғанда есептеу көлемі өте көп болады, сондықтан компьютерлерді қолдануға тура келеді.
Идентификациялаудың статистикалық әдісін қолданғанда корреляциялық және спектрлік функциялар кең қолданылатын функциялар болып табылады. Кездейсоқ функциялардың сипаттамаларын бейнелейтін басқа да функциялар бар (мысалы, ықтималдық таратылу заңдары), бірақ оларды идентификациялау есебіне қолдану шектелген.
15.2 Сигналдардың корреляциялық функцияларын анықтау
Корреляциялық функцияларын бағалау үшін тәжірибелерді көп мөлшерде өткізіп, оның әрқайсысында кездейсоқ функциялардың жүзеге асыруларын жазып, содан кейін әр t кесіндісінде кездейсоқ функцияның орта мәнін анықтау керек. Басқа сөзбен айтқанда, жүзеге асырулар бойынша орта мәнді анықтау қажет.
Кездейсоқ сигналдардың статистикалық сипаттамаларын бірнеше емес, жалғыз тәжірибеден анықтаған, басқа сөзбен айтқанда, [0, T] уақыт аралығындағы орта мәнін табу ыңғайлы болар еді.
Уақыт бойынша орта мәні жиынтық бойынша орта мәнімен бірдей болатын қасиеті бар стационарлы кездейсоқ функция эргодикалық функция деп аталады (математикалық күтім немесе корреляция функциясы бойынша). Эргодикалық гипотезасы ансамбль бойынша орталандыруды уақыт бойынша алынған жалғыз іске асыру бойынша орталандырумен алмастыруға мүмкіндік береді.
Уақыттың екі t1 және t2 = t1 + τ моменттеріндегі кездейсоқ процестің екі мәнінің орта шамасы корреляциялық (кей-кезде автокоррреляциялық) функция деп аталады. Стационарлы кездейсоқ процесс үшін корреляциялық функция тек қана τ = t2 - t1 шамасынан тәуелді болады
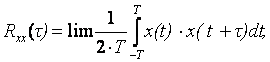 (15.2)
(15.2)
сонымен бірге Rxx(τ) = Rxx(-τ) .
Корреляциялық функция кездейсоқ процестің әртүрлі уақыт моменттеріндегі мәндерінің арасындағы байланысты сипаттайды. Уақыт интервалы τ өскен сайын корреляциялық функция кемиді – кездейсоқ процестің бір-бірінен уақыт бойынша алыс орнатылған мәндері арасындағы байланыс кемиді. τ = 0 (t1 = t2) болғанда орталықтанған кездейсоқ процесс үшін корреляциялық функцияның мәні дисперсиясына тең.
Уақыттың екі t1 және t2 = t1 + τ моменттеріндегі екі кездейсоқ процестерінің мәндерінің орта шамасы өзара корреляциялық функция деп аталады. Стационарлы кездейсоқ процесс үшін корреляциялық функция тек қана τ = t2 - t1 шамасынан тәуелді болады
 (15.3)
(15.3)
Өзара корреляциялық функция екі кездейсоқ процестерінің әртүрлі уақыт моменттеріндегі мәндерінің арасындағы байланысты сипаттайды. Уақыт интервалы τ өскен сайын өзара корреляциялық функциясының да мәндері кемиді.
Өлшеулердің көлемі шектелген болғандықтан, бұл функциялардың орнына олардың келесідей бағалары қолданылады
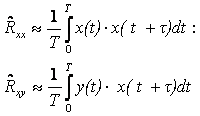 (15.4)
(15.4)
мұнда 0≤τ≤TR, уақыт периоды TR келесі шарттан анықталады: τ > TR болғанда корреляциялық функция берілген диапазоннан (әдетте 5%) шықпайды:
│R(τ )│ ≤ 0.05Rmax (5% кем корреляцияны есепке алмауға болады).
Әрине, TR мәні Rxx(τ) мен Rxy(τ)
үшін әртүрлі болады. Бірақ бізге объекттің
динамикалық сипаттамалары керек, ал олар Rxy(τ) функциясында көрсетіледі, сондықтан TR
=TRxy деп алуға болады. Сонымен, бастапқы
ақпарат келесі корреляциялық функцияларына түрленеді: <
![]() ,
, ![]() , 0≤τ≤TR>.
, 0≤τ≤TR>.
Компьютерлер көмегімен есептеулерді өткізгенде T интервалы ұзындығы ∆t болатын N тең бөлшектерге бөлінеді, τ және t дискретті мәндерді (∆t-ға еселі) қабылдайды
τ = k·∆t ![]() k = 0,1,2,3…, t = kt ·∆, kt
=1,2,3…
k = 0,1,2,3…, t = kt ·∆, kt
=1,2,3…
Онда интегралды келесі жуықтаған қосындымен алмастыруға болады
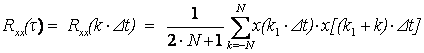
Келесі формула жиі қолданылады
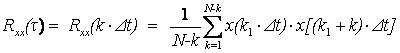 (15.5)
(15.5)
k=0,1,…,
N,
![]() –
ығысу интервалы (k=0,
…, N-1),
N –
корреляциялық
функцияның өлшенетін координаталар саны,
x – интервалдағы
x-тің орта мәні.
–
ығысу интервалы (k=0,
…, N-1),
N –
корреляциялық
функцияның өлшенетін координаталар саны,
x – интервалдағы
x-тің орта мәні.
(15.5) бойынша корреляциялық функцияны анықтаудың дәлдігі бақылау T интервалының ұзындығымен, корреляцияның τmax максималды уақыт мәнімен, уақыт бойынша дискреттеудің ∆t қадамымен, 0<=τ<=τmax интервалында анықталатын корреляциялық функцияның ординаталары санымен анықталады. Корреляцияның максималды уақыт мәні деп келесі шартты |R(τ)|<= 0,05·Rmax қанағаттыратын τ мәнін түсінеміз.
Корреляциялық функцияны анықтаудың жалпы сұлбасы:
1. Зерттелетін кездейсоқ процестердің іске асырулары орталықтанады.
2. Алдын ала жиілік анализ өткізіледі. Оның нәтижесінде зерттелетін сигналдардағы жоғарғы fmax және төменгі fmin гармоникалары бағаланады.
3. Сигналдың корреляциялануының максималды уақыты анықталады:
τmax=![]()
Корреляциялық функцияны қажетті дәлдікпен есептеу интервалы таңдалынады. Мысалы, кездейсоқ процестің орталықтанған іске асырулары үшін корреляциялық функцияны 2% дәлдігімен анықтау үшін T ≈16· τmax деп аламыз.
Котельников теоремасы негізінде уақыт бойынша дискреттеу
қадамы таңдалынады: ∆t <=
![]() .
Дискреттеудің деңгейлер саны
таңдалынады. 2% дәлдік үшін - 14 деңгей.
.
Дискреттеудің деңгейлер саны
таңдалынады. 2% дәлдік үшін - 14 деңгей.
4.
Есептелінетін координаттар
саны анықталады: N=![]() .
.
5. (15.5) алгоритмі бойынша есептеулер өткізіледі.
16 дәріс. Сызықты динамикалық объекттерді параметрлі емес идентификациялау. Винер-Хопф теңдеуі
Дәрістің мазмұны:
- сызықты динамикалық объекттерді параметрлі емес идентификациялау әдістері
Дәрістің мақсаты:
- сызықты динамикалық объекттерді параметрлі емес идентификациялау әдістерін оқу
16.1 Импульсті өтпелі функцияны анықтау
Тұрақты коэффициенттері бар сызықты теңдеумен бейнеленетін жалғыз кірісі мен жалғыз шығысы бар объект үшін кірудегі x(t) және оған y(t) реакциясы жийма интегралымен байланысқан
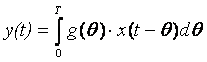 (16.1)
(16.1)
t<0 болғанда x(t)=0 болады, y(t)=v(t)+εy(t), x(t)=u(t)+ εx(t), v(t) және u(t) – сигналдардың ақтиқат мәндері, εx(t), εy(t) - тәжірибелерде пайда болатын бөгеттер.
Келесі себептерге байланысты импульсті беріліс функцияны тікелей жийма интегралынан табу қажетсіз немесе мүмкіндігінше болмайтын болады: (16.1) түріндегі интегралдық теңдеулер Вольтерра теңдеулері болып табылады (бірінші немесе екінші ретті), олар нашар шартталған немесе төмен деңгейде шартталған, сондықтан дұрыс шешімді табу үшін арнайы әдістерді қолдану қажет болады. Сонымен бірге, өлшеу нәтижесінде объекттің кірісі мен шығысындағы кездейсоқ процестердің мәндері үлкен қателіктермен алынады, оларды тегістеу қажет.
Объектке стационарлы кездейсоқ әсер берілгенде импульсті өтпелі функцияны статистикалық әдісімен анықтау үшін осы теңдеуге ұқсас, бірақ корреляциялық функцияларды байланыстыратын теңдеу болады. Осы теңдеуді шығарайық.
Кірістің автокорреляциялық функциясы келесі
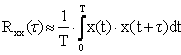 (16.2)
(16.2)
Кіріс пен шығыстың өзара корреляциялық функциясы
 (16.3)
(16.3)
Кірістегі және шығыстағы бөгеттердің корреляциясы жоқ, ал εx(t), εy(t) бөгеттер тәуелсіз және ақ шу болады деп есептейміз. Сонда өлшеулердің қателіктерін есепке алмауға болады, яғни Rxx(τ) ≈ Ruu(τ), Rxy(τ) ≈ Ruv(τ).
Осы қорытынды үшін бөгеттердің әсерін минимумдайтын корреляциялық амал қолданылады. Біздер объект операторын орта квадраттар ауытқудың минимумы бойынша іздейтінімізді еске салайық. Ал, осы орта квадрат ауытқу жоғалту (сәйкессіздік) функцияның математикалық күтімі болады. Корреляциялық функцияда – екінші орта момент.
(16.3) теңдеуіміз бар, бірақ y(t) пен x(t) келесі (16.1) теңдеумен байланысқан
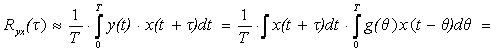
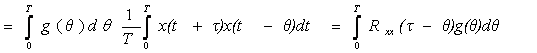
Осыдан
![]() (16.4)
(16.4)
Винер-Хопф теңдеуі деп аталатын теңдеуін аламыз.
Бұл теңдеуді (16.1) теңдеуі ретінде қарастыруға болады, егер де Rxx(t) кіріс әсері деп, ал Ryx(t) – оған реакциясы деп есептесек. Идентификация осы (16.4) теңдеуін [0,T] аралығында шешуге келтіріледі. Бірақ g(t) өшетін функция болғандықтан, яғни t→∞ болғанда lim g(t) = 0, кейбір Tg уақыттан бастап оның мәндерін есепке алмауға болады. Әдетте Tg шамасын идентификациялау алдында анықтайды. Мысалы, |R(τ)|<= 0.05Rmax болатын TR уақытын анықтауға болады. TR шамасы Rxx(t) және Ryx(t) үшін әртүрлі болады. Бізге объекттің динамикалық қасиеттері керек, ал олар Ryx(t) бейнеленеді, сондықтан TR шамасы Ryx(t) бойынша анықталады.
Сонымен, динамикалық сипаттамаларды анықтау есебі келесі қадамдарға бөлінеді:
1. Объект кірісі және шығысындағы кездейсоқ процестерді жазып алу.
2. Кіріс сигналының автокорреляциялық және кіріс пен шығыс сигналдарының өзара корреляциялық функцияларын есептеу.
3. TR параметрді анықтау.
4. (16.4) интегралдық теңдеуді шешу.
Сонымен, импульсті өтпелі функцияны анықтау есебін Винер-Хопф теңдеуін шешуге келтірдік. Винер-Хопф теңдеуін шешу әдістерін қарастырайық.
16.2 Винер-Хопф теңдеуін алгебралық әдісімен шешу
(16.4) теңдеуді шешудің әдістерінің біреуі – алгебралық әдіс. (16.4) теңдеуін сызықты алгебралық теңдеулер жүйесі ретінде көрсетеміз. Ол үшін дискретті уақытқа көшіп, интегралды қосынды ретінде жазамыз. Бастапқы интервал m тең интервалдарға t, 2t, …, mt бөлінеді және жуықтап интегралды келесі қосынды ретінде жаза аламыз:
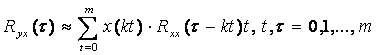 (16.5)
(16.5)
gi = g(it) белгілеп, τ = t, 2t,..., mt деп есептеп келесі жүйені аламыз
Rx·G=Q (16.6)
мұндағы
G = [g1,
g2,…,gm]T, Q= [q1, q2…,
qm]T, qi=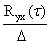 ,
,
Rx – квадратты симметриялық mхm матрицасы:
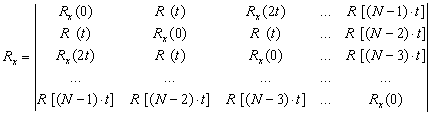
Сонымен, g(τ) импульсті өтпелі функцияның ординаталарының m мәнін t, 2t,…, mt нүктелерде анықтау үшін m сызықты теңдеулерден тұратын жүйені алдық.
Нақты объекттерде әдетте g(0) = 0,
сондықтан (16.5) теңдеулердің оң жағындағы
бірінші қосындыларын қиыстырып алып тастауға болады. Сонымен
бірге, жүйе анықтауышының диагоналды симметриялылығын
сақтау үшін көбінесе ![]() бір қадамға ығыстырылады,
яғни (5) жүйесін бірінші жолдан емес, екінші жолдан
қарастырады. Егер де ∆
аралығы жеткілікті кіші болса, қателік аз шамада болады.
бір қадамға ығыстырылады,
яғни (5) жүйесін бірінші жолдан емес, екінші жолдан
қарастырады. Егер де ∆
аралығы жеткілікті кіші болса, қателік аз шамада болады.
Винер-Хопф теңдеуі нашар шартталған болады: корреляциялық функциялардың бастапқы мәндерінің кіші шамаға өзгеруі шешімдерін үлкен шамаға өзгертеді және корреляциялық функцияларының ақиқат мәндерінің орнына олардың бағалары қолданылған болатын. Сондықтан Винер-Хопф теңдеуінің шешімдерінің қателіктері өте үлкен. Осы жолмен алынған импульсті өтпелі функциялардың орта квадраттар қателігінің шамасы өте аз, минимумға жақын болғанымен, олардың құндылығы немесе бағалылығы төмен, себебі бұл функциялар объекттегі процестердің физикалық мағынасына сәйкес болмайды. Физикалық мағына тек қана тегістелген шешімдерде бар.
Нашар шартталған теңдеулерді жөндеудің әдісінің бірі келесіде негізделген: шешім интегралды операторлардың (интегралды теңдеулер болса) немесе сызықты операторлардың (сызықты алгебралық теңдеулер болса) өздік фунцияларының сызықты комбинациялары болып ізделінеді. Идентификациялау есебін шешкенде әдетте жийма операторының өздік функциялары әдетте белгісіз болады. Бірақ, мысалы, Винер-Хопф теңдеуінің шешімдерін белгілі тегіс жұмыр функциялары бойынша (идентификацияланатын объекттегі процестердің нақты орындалурына сәйкес) жіктеу, тегістеу есебін жақсы шешеді. Бұл амалды Винер-Хопф теңдеуіне кіретін корреляциялық функцияларға да қолдануға болады. Сондықтан идентификациялау әдістерін практикада іске асырғанда аппроксимациялау және тегістеу процедуралары кең қолданылады.
17 дәріс. Объекттер сипаттамалары мен сигналдарын аппроксимациялауда негізделген идентификациялау әдістері
Дәрістің мазмұны:
- импульсті өтпелі функияны тегістеу әдістері
Дәрістің мақсаты:
- Белгісіз объекттер сипаттамалары мен сигналдарды аппроксимациялауды қолданып, параметрлі емес идентификациялауды өткізетін әдістерін оқу.
Идентификациялау әдістерін практикалық іске асырғанда, тегістеу қасиеттері бар аппроксимациялау процедуралар кең тараған.
17.1 Функцияларды аппроксимациялау туралы қысқаша мәліметтер
Аппроксимациялау есебі – функцияны белгілі функциялар жүйесімен жуықтау. Қарастырылып отырған f(t) функциясы [0,T] интервалында абсолютты интегралданатын болсын. Практикада әдетте бұл талап орындалады. Берілген функция осы интервалда абсолютты интегралданатын кейбір аппроксимациялайтын функциялардың φ(t)} жүйесі бойынша жіктеледі
![]() (17.1)
(17.1)
Аппроксимациялайтын функциялардың түрі аппрроксимацияланатын функция туралы априолы ақпараты негізінде ізделінеді. Аппроксимациялау коэффициенттері кейбір алдын ала таңдалынған жуықтау критерийді минимумдайтындай таңдалынады. Келесі жуықтауларды қолдануға болады: тепе-теңдік, интерполяциялық, квадраттық. Алғашқы екі жуықтауды қолданып, есептің дәл шешімін алу үшін шексіз интервалда (идентификациялау алгоритмдеріне жиі кіретін) жіктеудің коэффициенттерін есептеу үшін шектелген алгоритм жоқ. Осы жағдай және іске асырудың алгоритмдік қарапайымдылығы квадраттық жуықтаудың кең тарауына себеп болған. Жіктеу коэффициенттері бұл кезде алгебралық теңдеулер жүйесінен табылады. Скалярлы көбейтінділерді келесідей белгілеп
 (17.2)
(17.2)
ізделінетін жүйені аламыз:
a0(φ0, φ0) + a1(φ0, φ1) + … + aN(φ0, φN) = (φ0, f);
………………………………………………… (17.3)
a0(φ0, φN) + a1(φ1, φN) + … + aN(φN, φN) = (φN, f).
(17.3) жүйенің шешімі жалғыз болуы үшін оның анықтауышы нөлге тең болмауы керек. Таңдалынған аппроксимациялайтын функциялар жүйесі сызықты-тәуелсіз болса, тек қана сол жағдайда ғана анықтауыш нөлге тең болмайды.
Егер де аппроксимациялайтын функциялар жүйесіне басқа талаптар (абсолютты интегралданытннан басқа) қойылмаса, (17.3) жүйе бірлесе шешіледі. Және N кесіндінің ұзындығы өзгергенде қайтадан барлық an коэффициенттерді есептеу керек болады. Сонымен бірге, жүйені шешу үшін (17.2) интегралдардың N(N+1)/2 санын есептеу керек. Аппроксимациялау an коэффициенттерін тәуелсіз табу үшін және (17.3) жүйе шешімін қарапайымдау үшін {φ(t)} функцияларын [0,T] интервалында ортогоналды функциялар ретінде таңдаған жөн, яғни келесі қасиеттері бар:
![]()
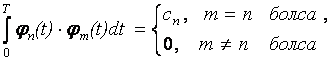 (17.4)
(17.4)
мұндағы cn - кейбір тұрақты.
Егер де {φ(t)} функциялар ортогоналды болса, (17.3) жүйенің анықтаушысы диагоналды болады да, коэффициенттерді есептейтін формулалар келесі түрге қарапайымдалынады:
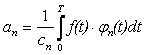
Егер тұрақтылар cn=1 болса, {φ(t)} функциялар жүйесі ортонормалданған болып табылады, формулалардың өрнектері белгілі Фурье формулаларға келтіріледі, ал коэффициенттер Фурье коэффициенттері деп аталады (мүшелері [0,T] интервалында ортонормаланған функциялар болатын Фурье қатарларымен сәйкес). Кей кезде белгілі w(t) салмақпен ортогоналды болатын функциялар таңдалынады:
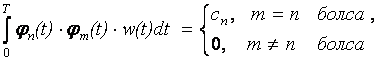 (17.5)
(17.5)
Салмақ функциясын таңдағанда, интервалдағы тәуелсіз айнымалының өзгеруінің қателігін айқындау талабы орындалуы керек.
Алдында қарастырылған алгебралық әдістің кемшілігі – Винер-Хопф жүйесін шешу. Бастапқы интегралды теңдеудің қате болуы жүйенің нашар шартталғандығына келтіреді. Объект туралы априорлы ақпарат негізінде таңдалынатын тегіс импульсті өтпелі функцияны табудың бірнеше әдістері бар.
17.2 Импульсті өтпелі функцияның дискретті мәндерін тегістеу
Тегістеудің ең қарапайым және бірінші пайда болған түрінің бірі Винер-Хопф теңдеуіне эквивалентті алгебралық жүйенің алынған шешімдерін аппроксимациялау болып табылады.
(16.5) теңдеулер жүйесін сандық әдісімен шешкен нәтижесінде g(t) импульсті өтпелі функцияның қадамы тұрақты 0, 1,…, n нүктелеріндегі дискретті g0, g1,…, gm мәндерін аламыз. Дискретті шамалардың алынған тізбегін кейбір аппроксимациялау полином көмегімен көрсетеміз
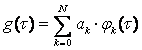 (17.6)
(17.6)
мұнадғы {φk(τ)} – кейбір ортогоналды аппроксиациялау функциялар жүйесі.
Аппроксимациялау коэффициенттері келесідей анықталады
![]() (17.7)
(17.7)
Аппроксимациялау функциялар жүйесіне қойылатын негізгі талаптар:
- {φk(τ)} функциялары абсолютты интегралданатын болуы керек;
- идентификациялау теңдеуінің шешімін жөндеу үшін {φk(τ)} жеткілікті тегіс болуы керек;
- {φk(τ)}функциялар жүйесі сызықты-тәуелсіз болуы керек;
- {φk(τ)} функциялар жүйесі ортогоналды болуы керек;
- {φk(τ)} функциялар жүйесі полиномның N дәрежесі өскен сайын аппроксимациялау жылдамдалуын қамту керек;
- {φk(τ)} функциялар күрделі емес есептеулер көмегімен қарапайым іске асырылуы керек.
Аппроксимациялайтын полиномның N дәрежесін таңдау сұрағы пайда болады. Бұл өте күрделі сұрақ және қазіргі кезде аяғына дейін шешілмеген. Осы есепті шешкен кезде келесідей амалдарды қолдануға болады:
1. Кей кезде импульсті өтпелі функцияның сипаттамасы белгілі. Онда аппроксимациялау {φk(τ)}функциялардың анықталған түрін есепке алып, аппроксимациялайтын полиномның N дәрежесін анықтауға болады.
2. Егер де өзара-корреляциялық Rxy функциясының өлшеуінің қателіктерінің дисперсиясы белгілі болса, N мәнін математикалық статистикада кең қолданылатын χ2 критерийдің көмегімен анықтауға болады.
3. Егер де өзара-корреляциялық Rxy функциясының өлшеуінің қателіктерінің дисперсиясы белгілі болмаса, N мәнін математикалық статистикадан белгілі Фишер критерийі көмегімен анықтауға болады
Бірақ та, N-нің үлкен мәндерінде есептеулерінің қателіктерінің себебінен Пирсон және Фишер критерийлердің сенімділігі төмендейді.
4. Аппроксимациялайтын полиномның N дәрежесін таңдаудың жалпы амалы Гаусс принципінде негізделген. N мәні келесі функционалдың N бойынша минимумдалу шартынан табылады
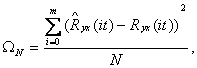 (17.8)
(17.8)
мұнда
![]() -
(17.7) полиномды (17.6 ) теңдеулер жүйесіне импульсті өтпелі
функциясы орнына қойған нәтижесі. Басқа сөзбен
айтқанда, Ryх-тің дисперсиясы минимумдалады.
-
(17.7) полиномды (17.6 ) теңдеулер жүйесіне импульсті өтпелі
функциясы орнына қойған нәтижесі. Басқа сөзбен
айтқанда, Ryх-тің дисперсиясы минимумдалады.
17.3 Импульсті өтпелі функцияны алдын ала аппроксимациялауда негізделген идентификациялау әдісі
Идентификациялау есебін тиімділеу әдісі
объекттің g(t) импульсты өтпелі функциясын алдын ала аппроксимациялап,
содан кейін осы жіктеудің Фурье коэффициенттерін кірістегі және
шығыстағы сигналдарды бақылау негізінде анықтауда
болады. Импульсті өтпелі функцияны (17.1) қосындымен
аппроксимациялаймыз, мұнда {φk(τ)}- ортогоналды функциялар. Объекттің y(t) және
![]() модельдің
шығу сигналдарының ауытқуларын минимумдаймыз, мұнда
модельдің
шығу сигналдарының ауытқуларын минимумдаймыз, мұнда
![]() жийма
интегралынан анықталады
жийма
интегралынан анықталады
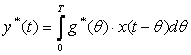 (17.9)
(17.9)
Осы теңдеуге импульсті өтпелі функцияның (17.2) өрнегін қойып, келесіні аламыз
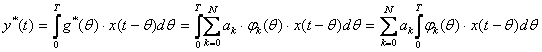 (17.10)
(17.10)
Идентификацитялау критерийдің түрі
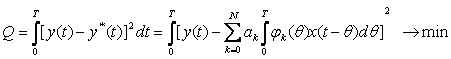 (17.6)
(17.6)
Осыдан
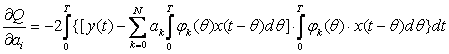 (17.12)
(17.12)
![]() болғанда ең жақсы таңдау
орындалады.
болғанда ең жақсы таңдау
орындалады.
Жіктеудің белгісіз коэффициенттерін анықтау үшін нәтижесінде келесі жүйені аламыз
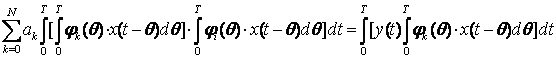 17.13)
17.13)
Әдетте практикада N<<m, яғни (16.5 )-ке қарағанда, (17.13) жүйенің реті неғұрлым кіші және де {φk(τ)} функциялар тегіс болғандықтан, осы жүйе жақсы шартталған. Бірақ аппроксимациялау полиномның N дәрежесін таңдау проблемасы жойылмайды.
18 дәріс. Объекттер және сигналдардың динамикалық сипаттамаларын аппроксимациялауда негізделген идентификациялау әдістері
Дәрістің мазмұны:
- импульсті өтпелі функцияны тегістеу әдістері
Дәрістің мақсаты:
- объекттер және сигналдардың белгісіз динамикалық сипаттамаларын аналитикалық өрнектермен аппроксимациялауда негізделген идентифи-кациялау әдістерін оқу
Тегістелген импульсті өтпелі функцияны анықтау әдістерін қарастыруды жалғастырамыз.
18.1 Импульсті өтпелі және корреляциялық функцияларды бірге аппроксимациялауда негізделген идентификациялау әдісі
Объект сигналдарының корреляциялық функцияларын кейбір аппроксимациялау полиноммен алдын-ала тегістеп, жөндеу эффектісін алуға болады. Осы әдіс бойынша импульсті өтпелі функция (17.1) өрнегімен аппроксимацияланады, мұнда коэффициенттері (17.2) бойынша табылады. Сонымен бірге, Винер-Хопф теңдеуіне эквивалентті (16.5) алгебралық теңдеулер жүйесінің оң жағы да осы функциялармен аппроксимацияланады.
![]() (18.1)
(18.1)
Теңдеулер саны белгісіздер санына тең болу үшін (17.1) және (18.1) өрнектерде аппроксимациялау функциялардың N саны бірдей болуы керек (сонда алынған жүйе квадратты болады).
(17.1)-ден өзгеше (18.1) өрнегінің
![]() (18.2)
(18.2)
коэффициенттері берілген деп есептейміз, себебі өзара-корреляциялық Ryx(t) функцияның мәндері түйіндерде берілген, ал {φ(τ)} функциялары белгілі.
Винер-Хопф теңдеуіне эквивалентті (16.5) алгебралық теңдеулер жүйесіне импульсті өтпелі функцияның (17.1) және өзара-корреляциялық функцияның (18.1) өрнектерін қоямыз; екі жағында φj(τ) көбейтіп, τ=0-ден τ=m-ға дейін қосындылаймыз
![]() (18.3)
(18.3)
{φj(τ)} ортогонормалданған болғандықтан белгісіз ak коэффициенттері бойынша сызықты алгебралық теңдеулер жүйесін аламыз
![]() (18.4)
(18.4)
мұнда ![]() (18.5)
(18.5)
Осы жүйені есептеп, (17.1) өрнек бойынша импульсті өтпелі функциясының бағасын анықтаймыз.
Бастапқы жүйеге қарағанда (18.4) жүйенің реті неғұрлым кіші және {φj(τ)} тегіс және реттері кіші функциялар болғандықтан, жүйе жақсы шартталған. Сондықтан қарапайым есептеулер көмегімен импульсті өтпелі функцияның бағаларын жеткілікті дәлдікпен анықтауға болады. Есептеу процесінде аппроксимациялайтын функциялардың санын таңдау алдында айтылып кеткен қиындықтары кездеседі.
18.2 Сигналдарды аппроксимациялауда негізделген
идентификациялау әдісі
Егер де объекттің кірістегі және шығыстағы сигналдары кейбір аналитикалық өрнектермен аппроксимацияланатын болса, импульсті өтпелі функцияныда жийма интегралынан немесе Винер-Хопф теңдеуінен аналитикалық түрде алуға болады. Осы амалды іске асыруын қарастырайық. Объекттің кірістегі және шығыстағы сигналдары бақылау интервалында кейбір функцияларының сызықты комбинациясымен аппроксимацияланған. Ізделінетін импульсті өтпелі функцияны да осы функциялар жүйесімен аппроксимациялаймыз. Мысалы, сигналдар {pi(t)}ортогоналды полиномдар қатарларына жіктелген болсын
![]()
![]() (18.6)
(18.6)
мұнда ![]() , ал pij - полином коэффициенттері.
, ал pij - полином коэффициенттері.
Басқа сөзбен айтқанда сигналдар дәрежелі қатарлар түрінде көрсетіледі
![]() (18.7)
(18.7)
мұнда коэффициенттері жіктеу коэффициенттерімен келесідей
байланысқан
![]()
Импульсті өтпелі функцияны да дәрежелі қатар ретінде іздейміз
![]() (18.8)
(18.8)
(18.7) бен (18.8)-ды жийма интегралына қойып, келесіні аламыз
![]() (18.9)
(18.9)
Бірдей дәрежедегі коэффициенттерін теңестіріп, (18.10)-ғы gi коэффициенттерін анықтауға алгебралық теңдеулер жүйесін аламыз. Нәтижесінде:

Комплексті кеңістікте аппроксимациялау есебі, яғни Лаплас бойынша жеңіл түрленетін ортогоналды функциялар қатарларымен көрсету қызық болып табылады. Осындай функциялар болып, мысалы, L(t) Лагерр функциялары табылады. Бұл кезде келесі бар
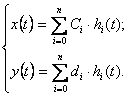 (18.10)
(18.10)
(18.10) өрнектер комплексті кеңістікте келесідей жазылады
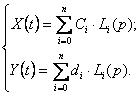
ал объекттің беріліс функциясының түрі
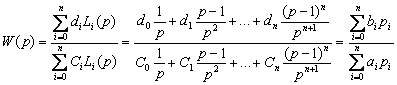
{an} және {ck} коэффициенттері арасында келесідей байланыстар бар
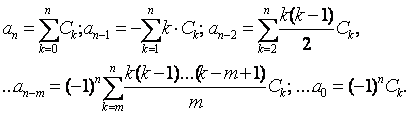
{bi} мен {di} арасындағы осы сияқты қатынастарды да алуға болады.
Егер де объект кірісіне берілетін сигнал үзікті–тұрақты сипат немесе функциясымен жеткілікті дәлдікпен аппроксимацияланатын болса, идентификациялау алгоритмі қарапайымдалады. Тұрақты мәні бар кірістегі сигналдың j-ші интервалы үшін келесіні жазуға болады
![]() , мұнда h(t) - өтпелі функция.
, мұнда h(t) - өтпелі функция.
Белгілі ортнормалданған функциялар жүйесі бойынша осы функцияны жіктейік
![]()
Бұл кезде шығудағы сигналды да осы функциялар жүйесімен жіктеп, келесіні жазуға болады
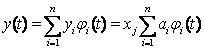 , осыдан аламыз:
, осыдан аламыз: ![]()
Егер де кірістегі сигнал үзік-сызықты функциямен аппроксимацияланатын болса, осы амалды қолдануға болады.
Әдетте аппроксимациялайтын функцияларды таңдағанда олардың аз санында жақсы жуықтауды алу талабына сүйемелденеді. Идентификациялау есебін шешкенде кең қолданылатын кейбір полиномдарды атап кетейік.
Бастапқы Лагерр полиномдары (0, ∞) интервалында ω(t) = e-t салмағымен ортонормалды болып табылады. n-ші ретті Лагерр полиномының түрі
![]() (18.11)
(18.11)
бірінші үш полиномдар үшін өрнектері келесі болады
![]()
Келесі шарт орындалатындай
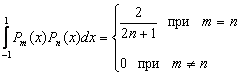
Лагерр полиномдары ортогоналды болады.
Нормалдыралғаннан кейін (18.21) өрнегі келесідей жазылады:
![]()
Аппроксимациялау функциялардың тағы да маңызды түрі [-1,1] интервалында ортогоналды болатын Лежандр полиномдары болады. n–ші Лежандр полиномы келесі өрнекпен бейнеленеді
![]() Лежандрдың бірінші полиномдарының түрі
Лежандрдың бірінші полиномдарының түрі
![]()
Чебышев полиномдары [-1,1] интервалында
![]() салмағымен ортогоналды. n -ші ретті Чебышев
полиномының түрі
салмағымен ортогоналды. n -ші ретті Чебышев
полиномының түрі
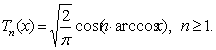
Бірінші полиномдары үшін өрнектер
![]()
f(x) функцияны Чебышев полиномдары жүйесі бойынша жіктегендегі коэффициенттері
![]() .
.
Кез келген функцияны Чебышев полиномдарымен аппроксимациялап, қателіктің біртекті таратылуына және оның интервал соңғы шегінде жиналмауына қол жеткізуге болады.
19 дәріс. Сызықты емес объекттерді идентификациялау
Дәрістің мазмұны:
- сызықты емес объекттерді идентификациялаудың ерекшеліктері; сызықты емес объекттерді идентификациялаудың есептерін шешу әдістері.
Дәрістің мақсаты:
- сызықты емес объекттерді идентификациялаудың әдістерін оқу.
19.1 Сызықты емес динамикалық объекттерді идентификациялаудың ерекшеліктері
Статикалық та, динамикалық та процестердің міндетті түрде есепке алынатын сызықты емес сипаттамалары болуы мүмкін. Алдында қарастырғаннан сызықты болатын динамикалық объекттерді идентификациялау өте күрделі есеп екеніне көзіміз жетті. Ал, сызықты емес динамикалық объекттерді идентификациялағанда қиыншылықтар одан да зор болады.
Қиыншылықтарының негізгісі келесіде болады: сызықты емес объекттің өтпелі процесі кірістегі сигналдың тек қана түрінен емес, сонымен бірге амплитудасынан да тәуелді; активті идентификацияны өткізгенде бұл жағдай сынап көруге арналған сигналды таңдауға күрделі және қайшылық талаптарын орнатады.
Екінші кедергі – объекттерді бейнелейтін сызықты емес операторларының түрлерінің шексіздік саны.
Қазіргі кезде ұсынған сызықты емес динамикалық объекттерді идентификациялау әдістері осы және тағы да басқа жағдайлар себебінен әзірше практикалық қолданудан алыс болады.
19.2 Объекттердің сипаттамаларын сызықтандыруда негізделген әдістер
Сызықты емес объекттерді идентификациялау әдістері ішінде сызықтандыру әдістері ең дамыған әдістер болып табылады. Осы курста біз бірнеше рет осындай есептермен кездестік. Әдістің идеясын еске салайық: сызықты емес тәуелділіктер сызықты тәуелділіктермен алмасады.
Объект теңдеуі жалпы кезде келесі түрде болады:
L[y(t)] = f[x(t)],
мұнда L – сызықты дифференциалдық оператор.
f(x) функциясын x0 жұмыс нүкте аймағында дәрежелік қатарға жіктейміз
f(x) = a0 + a1(x - x0) + a 2 (x - x0)2 + …
Айнымалылардың өсімшелерін
![]() және
y0=f(х0)
деп белгілеп (1) операторын
өсімшелер арқылы келесідей аламыз
және
y0=f(х0)
деп белгілеп (1) операторын
өсімшелер арқылы келесідей аламыз
![]() сонымен
бірге сызықтандыру коэффициенті
K=a1.
сонымен
бірге сызықтандыру коэффициенті
K=a1.
Қарапайымдылық және кейбір кезде жеткілікті дәлдік осындай әдістердің дамуына себеп болды. Бірақ көбінесе объектті сызықты жуықтау жеткілікті болмауы мүмкін.
19.3 Априорлы белгілі түрлері бар сызықты емес функцияларын идентификациялау
Егер де сызықты емес түрі туралы априорлы ақпарат болса, «ақиқат» сызықты емес функциялардың параметрлерін идентификациялауға болады. Осындай жағдайда келесі амалдардың біреуін қолдануға болады.
а) Бастапқы аналитикалық өрнекте айнымалыларды алмастырып, содан кейін сызықтандырып, объекттің сызықты моделін алуға болады.
Келесі өрнекпен бейнелетін процесті қарастырайық
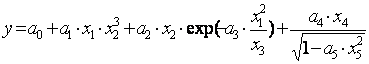 (19.1)
(19.1)
Бұл процесті идентификациялау үшін әуелі келесідей жаңа айнымалыларды кіргізейік:
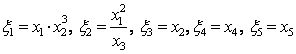 (19.2)
(19.2)
Нәтижесінде аламыз
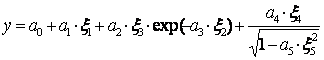 (19.3)
(19.3)
Енді оның айнымалыларының өсімшелері өте аз деп есептеп, (3) теңдеуді сызықтандырамыз
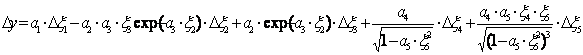 (19.4)
(19.4)
Келісідей белгілерді енгізіп
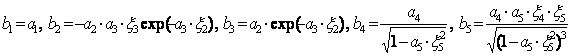 (19.5)
(19.5)
аламыз
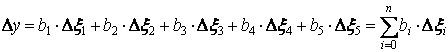 (19.6)
(19.6)
b1,b2,…,bs коэффициенттерін
сызықты регрессия әдісімен идентификациялауға болады.. Келесіні
![]() есепке алып, а5 –ті анықтауға
болады, себебі
есепке алып, а5 –ті анықтауға
болады, себебі ![]() және
және
![]() өлшеулері бар. а5 өрнегін
(19.5) формуласына қойып,
өлшеулері бар. а5 өрнегін
(19.5) формуласына қойып, ![]() аламыз.
аламыз. ![]() ,
,![]() мүшелерін
мүшелерін
![]() ,
,![]() үшін (19.5) өрнектерден келесі түрде табуға
болады.
үшін (19.5) өрнектерден келесі түрде табуға
болады. ![]() шамасын
шамасын ![]()
![]() өрнегінен табамыз,
өрнегінен табамыз,
![]() -ті (1 9.5)-ке
қойып
-ті (1 9.5)-ке
қойып ![]() тікелей анықталады.
тікелей анықталады.
Осы бейнеленген (19.1) процесті идентификациялау нұсқасы бойынша сызықты емес тәуелділіктердің көп деген түрлерін идентификациялауға болады.
б) Келесі түрдегідей
![]() экспоненциалды өрнектермен берілетін
экспоненциалды өрнектермен берілетін
процестерді идентификациялау үшін, оларды логарифмдеу
жолымен келесі түрдегі байланыстарға түрлендіреміз
![]() .
.
Келесідей ![]() белгілеп,
белгілеп, ![]() аламыз.
Мұнда А және В – орта квадраттар қателігін минимумдау
әдісімен жеңіл есептеледі.
аламыз.
Мұнда А және В – орта квадраттар қателігін минимумдау
әдісімен жеңіл есептеледі.
Сол сияқты келесі түрдегі процестерде
![]() логарифмдеуді қолданып, келесі өрнекті
аламыз
логарифмдеуді қолданып, келесі өрнекті
аламыз ![]() . Одан а
және b (19.7) теңдеудегі сияқты есептелінеді.
. Одан а
және b (19.7) теңдеудегі сияқты есептелінеді.
Бірақ кей кезде мұндай әдіс жарамайды, сондықтан оны қолдану үшін кейбір қосымша ақпарат керек. Мысалы, бұл әдісті келесі жүйеге
![]() ,
,
қолдана алмаймыз. Мұнда
![]() идентификациялау керек.
идентификациялау керек.
Кіші ауытқулар әдісін қолданып,
келесіні аламыз: ![]() . Мұнда
b коэффициентін орта квадраттар критерий
көмегімен идентифи-кациялауға болады6
. Мұнда
b коэффициентін орта квадраттар критерий
көмегімен идентифи-кациялауға болады6
![]() бірақ
бірақ
![]() үшін
шешімді ала алмаймыз. Әрине, екінші және одан жоғары дербес
туындыларды қолдануға болады (немесе екінші және келесі ретті
ауытқуларды), бірақ практикада оның мәні жоқ,
себебі туындылардың маңыздылығы төмен, әсіресе
өлшеулердің шуы болса.
үшін
шешімді ала алмаймыз. Әрине, екінші және одан жоғары дербес
туындыларды қолдануға болады (немесе екінші және келесі ретті
ауытқуларды), бірақ практикада оның мәні жоқ,
себебі туындылардың маңыздылығы төмен, әсіресе
өлшеулердің шуы болса.
19.4 Жалпы түрдегі сызықты емес объекттерді идентификациялау
Қарапайым бір өлшемді кезде модель сызықты емес дифференциалды теңдеумен көрсетіледі
![]()
-сызықты емес ![]() аргументтердің скалярлы функциясы, бақылаулар негізінде оны
идентификациялау керек. Векторлы түрде бұл теңдеу келесідей
жазылады:
аргументтердің скалярлы функциясы, бақылаулар негізінде оны
идентификациялау керек. Векторлы түрде бұл теңдеу келесідей
жазылады: ![]() мұнда
мұнда
![]() ,
F - екі аргументтің векторлы
функциясы.
,
F - екі аргументтің векторлы
функциясы.
![]() бақылауларды келесі түрге келтіреміз
(бастапқы функцияларды дифференциалдап, ол үшін тегістеу аппаратын
қолданамыз).
бақылауларды келесі түрге келтіреміз
(бастапқы функцияларды дифференциалдап, ол үшін тегістеу аппаратын
қолданамыз).
![]()
19.4.1 Функционалдық модельдер
Белгісіз параметрлері бар белгілі функция болсын. Бұл кезде
![]()
теңдеулер жүйесі берілген бастапқы шарттарда және идентификацияланатын параметрлердің белгілі мәндерінде сандық әдістерімен интегралданады (мысалы, Рунге-Кутта әдістерімен)
Алынған шешім ![]() бақылаулармен салыстырылады және сәйкессіздік
функциясы алынады
бақылаулармен салыстырылады және сәйкессіздік
функциясы алынады

Осы функцияны минимумдау есебі идентификациялау есебін шешеді.
Егер де модель құрылымы дифференциалданатын функциялар класынан таңдалынған болса, бұл есепті трансценденттік теңдеулер жүйесі шешеді (мұндай жүйелерді де шешу оңай емес):
![]() ,
,
мұнда [,] – скалярлы көбейтінді.
Кері жағдайда минимумдаудың ізденіс әдістерін қолдануға болады. Ол үшін келесі рекурренттік процедура құрылады
![]()
мұнда ![]() - іздеу
алгоритмімен анықталатын қадам.
- іздеу
алгоритмімен анықталатын қадам.
Ізденісті іске асыру үшін біздерге
әртүрлі ![]() -ларда
F функциясының тек қана мәндері керек, сондықтан модельді
аналитикалық бейнелеу класынан басқа кластарда да
құруға болады (сондықтан осы амал функционалды деп
аталады).
-ларда
F функциясының тек қана мәндері керек, сондықтан модельді
аналитикалық бейнелеу класынан басқа кластарда да
құруға болады (сондықтан осы амал функционалды деп
аталады).
19.4.2 Бағаланатын параметрлері бойынша сызықты болып табылатын модельдер
Олар функционалдық модельдердің жеке түрі және ізделінетін функцияны берілген функциялар жүйесі бойынша жіктеу нәтижесінде құрастырылады
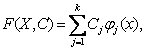
мұнда ![]() - берілген
функциялар жүйесі, құрылымдық идентификация
қадамында анықталады. Аппроксимацияны, мысалы, полиномдар
көмегімен өткізуге болады. Бірақ барлық кезде де
параметрлері анықталатын сызықты емес идентификацияланатын
функцияның тек қана кейбір спецификалық түрін
болжап, идентификацияны өткізуге болады.
- берілген
функциялар жүйесі, құрылымдық идентификация
қадамында анықталады. Аппроксимацияны, мысалы, полиномдар
көмегімен өткізуге болады. Бірақ барлық кезде де
параметрлері анықталатын сызықты емес идентификацияланатын
функцияның тек қана кейбір спецификалық түрін
болжап, идентификацияны өткізуге болады.
Коэффициенттерді іздеу есебі белгілі әдістермен шешіледі.
20 дәріс. Алдын ала өңдеу алгоритмдері және сәйкестікті бағалау
Дәрістің мазмұны:
- зерттелетін объекттің қасиеттерін бағалау; модельдің нақты объектке сәйкестік дәрежесін бағалау.
Дәрістің мақсаты:
- объекттің стационарлық пен сызықтығын бағалау алгоритмдерін игеру; модельдің нақты объектке сәйкестік дәрежесін бағалауды үйрену.
20.1 Объекттің стационарлығы мен сызықтығын бағалау алгоритмдері
Идентификациялау алгоритмдерді дұрыс қолдану үшін объекттің келесідей – стационарлық/стационарлы еместік, сызықтық/бейсызықтық сияқты қасиеттерін алдын ала бағалау қажет болады. Бұл есептер мәліметтерді алдын ала өңдеу алгоритмдері көмегімен шешіледі. Уақыттың белгілі интервалдарында өлшенген объекттің кірісіндегі және шығысындағы сигналдарының квантталған мәндерінің массивтері жалпы кезде бастапқы мәліметтер болып табылады. Мүмкін болатын тренд (стационарлық емес) пайда болатындай стационарлыққа тексерілетін іске асырудың ұзындығы жеткілікті болуы керек.
Зерттелу объекттің кірісіндегі стационарлы
кездейсоқ сигналына оның шығысында стационарлы сигнал
сәйкес болса, объект стационарлы деп есептелінеді. Егер де кез келген t1,…,tn
және τ
үшін (x[t1+τ],…,x[tn+τ])
кездейсоқ векторының таратылуы τ
–дан тәуелсіз болса,
![]() кездейсоқ
процесі қатал стационарлы болады. Нақты
қолданбалылардың көбісі үшін процестің әлсіз
стационарлығын, яғни оның орта мәндері мен
автокорреляциялық функциясы уақыттан тәуелсіздігін тексеру
жеткілікті.
кездейсоқ
процесі қатал стационарлы болады. Нақты
қолданбалылардың көбісі үшін процестің әлсіз
стационарлығын, яғни оның орта мәндері мен
автокорреляциялық функциясы уақыттан тәуелсіздігін тексеру
жеткілікті.
Стационарлықты тексеру алгоритмі:
1. Процестің стационарлығын бағалау үшін процестің іске асыруын бірдей ұзындығы бар n интервалға бөледі. Әр n-ші интервал үшін орта мәндері мен орта квадратын есептейді, алынған мәндерді интервалдар нөмірлерінің өсуі бойынша орнатады
<1x>, <2x>, … , <nx>, <1x2>, <2x2>, … , <nx2>,
мұндағы < > - уақыт бойынша орталықтандыру.
2. Осы тізбектердің әр қайсысын белгілі сериялар және трендтер әдістерімен немесе функционалды қатарларға жіктеу жолымен трендке сынайды.
3. Осы әдістерді қолданғанда алынған нәтижелерді болжау негізінде маңыздылықтың 5%-дық деңгейінде объекттің стационарлығы туралы шешім қабылданады.
Әуелі стационарлыққа кірістегі сигналдың іске асырулығы тексеріледі. Егер де ол стационарлы емес болса, әрі қарай статистикалық өңдеу жалғастырылмайды. Кері жағдайда стационарлыққа шығыстағы сигналдың іске асырулығы тексеріліп, объекттің стационарлығы немесе стационарлы еместігі туралы пікір ұсынылады.
Объекттің сызықтығы туралы пікір іске асырулардың таратылу заңдарын бағалау негізінде төмендегі ережелер бойынша жасалады:
- егер де кірудегі сигнал нормалды заң бойынша таратылған болса, онда шығудағы сигналдыңда заңы нормалды болатыны сигналдың сызықты жүйеден өту теориясынан белгілі;
- егер де кірістегі сигналдың таратылу заңы нормалды болмаса, онда сызықты динамикалық объекттің шығудағы сигналды нормаландыратын қасиеті бар;
- сызықты емес жүйеден өткенде нормал заңы бойынша таратылған сигнал өзгереді.
Аталған оқиғалар келесі кестеде көрсетілген:
|
Сигналдың таратылу заңы |
Объект типі |
|
|
Кірістегі сигнал |
Шығыстағы сигнал |
|
|
Нормалды |
Нормалды |
Сызықтық |
|
Нормалды |
Нормалды емес |
Сызықтық емес |
|
Нормалды емес |
Нормалды |
Сызықтық |
Сонымен, объекттің сызықтығын бағалау есебі бастапқы іске асырулардың таратылу заңдарының нормалды екендігін тексеруге келтіріледі. Егер де объекттің кірісіндегі және шығысындағы сигналдардың таратылу заңдары нормалды болмаса, объекттің сызықтығы немесе сызықты еместігі туралы шешім қабылдай алмаймыз. Бұл кезде объекттің сызықтығын бағалау идентификациялау қадамында өткізіледі.
Таратылу заңының нормалды болатыны математикалық статистиканың стандартты әдістері көмегімен өткізіледі.
20.2 Модельдің нақты объектке ұқсастық дәрежесін санды бағалау
Математикалық модельді құрастырғанда тек қана негізгі маңызды факторларды есепке алып, басқаларын алып тастаймыз. Негізгі факторлар деп шығудағы айнымалыға басымдылық әсер ететін кірістерді есептейді. Әрине, алынған математикалық бейнелеу әр кезде де нақты объекттен төмен болады, ол объекттің тек қана белгілі есепті шешуге қажетті болатын негізгі заңдылықтарын көрсетеді. Сонымен бірге, бір объекттің әртүрлі есептерін шешу үшін әртүрлі математикалық бейнелеулерін құрастыруға болады.
Сонымен бірге, объекттердің физикалық табиғаттары әртүрлі болғанымен, әртүрлі процестердің де математикалық бейнелеулері бірдей болуы мүмкін. Мысалы, әртүрлі физикалық, механикалық, химиялық, т.б. жүйелер бірдей дифференциалдық теңдеулермен сипатталуы мүмкін. Сонда модельдің объектке изоморфтылығы (сәйкестігі, ұқсастығы, адекваттылығы) туралы айтуға болады. Біздер идентификациялау әдістері көмегімен құрастырылған модельдерді қарастырғандықтан, «идентификациялау дәрежесі» деген терминді қолданамыз.
Нақты процестер көп өзара байланысқан айнымалылары бар күрделі объекттер болып табылады және ол байланыстардың барлығын есепке алу мүмкін емес. Сондықтан қандай және неше айнымалыларды модельге енгізу керек, ал қайсысын есепке алмауға болады деген сұрақ туады. Әр факторды модельге енгізу олардың іске асыруларын алып, статистикалық өңдеу зерттеулерінің үлкен көлемімен байланысты, бұл жұмыс уақыт пен құралдардың көп шығынын талап етеді. Идентификациялау дәрежесі белгілі есепті шешуін қамту керек. Басқа сөзбен айтқанда, объекттің мүмкін болатын бейнелеулерінің барлық түрлерінен бір жағынан, оны іске асыру жағынан максималды қарапайым, екінші жағынан қойылған есепті шешуге мүмкіндік беретін түрін таңдау керек. Мысалы, егер де шығудағы айнымалылардың дисперсиясымен сипатталатын бір өндірілетін өнімнің сапасы туралы әңгімелесек, әрине, идентификациялау есебінің шешімі ретінде алынған модель шығудағы айнымалыны осы дисперсияның сипаттайтын дәлдігімен есептеуге мүмкіншілік беруі керек.
Шығудағы айнымалыны анықтау дәлдігін шартты математикалық күтімнің дисперсиясы бойынша анықтайды, яғни шартты дисперсияның (қалдық дисперсияның) математикалық күтімі бойынша. Сондықтан, бұл сипаттаманы объектілердің модельдерінің сәйкестіктер дәрежесінің сипаттамасы ретінде қолдануға болады. Бірақ, дисперсия нөлден шексіздікке дейін мәндерді қабылдайды, ол практикалық еспетеулерге ыңғайсыз. Осы жағдайды есепке алып, сәйкестік дәрежесінің сандық мөлшері 0-ден 1-ге дейін мәндерді қабылдау талабын қоямыз (0 - толығымен сәйкес емес, 1 - толығымен сәйкес, яғни функционалдық тәуелділік). Сондықтан, сәйкестік дәрежесінің мөлшері ретінде шығудағы y(t) айнымалының кірудегі x(t) айнымалы бойынша шартты математикалық күтімінің дисперсиясының шығудағы y(t) айнымалының дисперсиясына қатынасты алады.
Бір өлшемді жағдайда y(t)-тің x(t) мәндерінің жиындары бойынша шартты математикалық күтімі орта квадраттар ауытқуды минимумдайтын критерийі бойынша оптималды оператор болады
![]() (20.1)
(20.1)
Онда (20.1) модельдің
![]()
объектке сәйкестігінің бағасы ретінде келесі қатынасты алады
![]() ,
(20.2)
,
(20.2)
мұнда ![]() - t аргументінің сәйкес
мәндеріндегі, яғни барлық s
- t аргументінің сәйкес
мәндеріндегі, яғни барлық s![]() T аргументтеріндегі х мәндері
бойынша, шығудағы y(t) айнымалының x(t) кірудегі
айнымалының мәндері бойынша шартты математикалық
күтімі; D{y(t)} – шығудағы y(t) айнымалының
дисперсиясы.
T аргументтеріндегі х мәндері
бойынша, шығудағы y(t) айнымалының x(t) кірудегі
айнымалының мәндері бойынша шартты математикалық
күтімі; D{y(t)} – шығудағы y(t) айнымалының
дисперсиясы.
(20.2)-де анықтама бойынша
![]()
яғни t уақытындағы шығудағы y(t) айнымалының барлық s үшін кірудегі x(s) функциясының мәндерінің жиыны бойынша регрессия бетінің y(t) математикалық күтімінен ауытқуының квадратының математикалық күтімі.
Шартты математикалық күтімнің
дисперсиясы y(t) барлық s![]() T үшін x(s) кірістің
мәндерінің барлық жиынының әсерінен пайда болатын
шығудың жалпы дисперсиясының бөлігі.
T үшін x(s) кірістің
мәндерінің барлық жиынының әсерінен пайда болатын
шығудың жалпы дисперсиясының бөлігі.
Жалпы дисперсияны келесідей көрсетуге болады
![]() (20.3)
(20.3)
Сонда
![]()
(20.3) есепке алып, (20.2) -ден жазамыз
![]() .
.
Сонда
![]() (20.4)
(20.4)
- модельдің объектке сәйкессіздік дәрежесінің сандық сипаттамасы.
(20.2), (20.4 ) анықтамалардан, (20.3) есепке алып, келесіні жазамыз
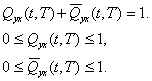
Шынында да, егер модель y(t)-пен байланыспаған
немесе әлсіз байланысқан есепке алынатын x(t) ақпарат
негізінде құрастырылса, (бұл жағдайда D{M{y/x}}
мәніне қарағанда ![]() мәндері өте үлкен болады), онда
сәйкестік дәрежесі өте кіші немесе нөл болады, ал
сәйкессіздік дәрежесі өте үлкен немесе 1-ге тең
болады.
мәндері өте үлкен болады), онда
сәйкестік дәрежесі өте кіші немесе нөл болады, ал
сәйкессіздік дәрежесі өте үлкен немесе 1-ге тең
болады.
Сонымен, сәйкестік дәрежесінің мөлшері объект туралы біздің біліміміздің дәрежесін, оны формалдау дәрежесін бағалайды.
Әдебиеттер тізімі
1. Дейч А.М. Методы идентификации динамических объектов. – М.:
Энергия, 1979.
2. Гроп Д. Методы идентификации систем управления. – М.: Мир, 1979.
3. Сейдж А., Мелса Дж. Идентификация систем. – М.: Наука, 1974.
4. Хемминг Р.В. Цифровые фильтры.- М.: Сов. Радио, 1980.
5. Рабинер Л., Голд Б. Теория и применение цифровой обработки сигналов – М., Мир,1978.
6. Эйкхофф П. Основы идентификации систем управления. – М.: Мир, 1983
7. Цыпкин Я.З. Основы информационной теории идентификации. – М.: Наука, 1984.
8. Химмельблау Д, Анализ процессов статистическими методами. – М., Мир, 1973.
9. Дрейпер Н., Смит Г. Прикладной регрессионный анализ. – М., Мир, 1986.
10. Хартман К., Лецкий Э., Шефер В. и др. Планирование эксперимента в исследовании технологических процессов. – М., Мир, 1977.
11. Серов, Е.П., Корольков Б.П. Динамика парогенератора. - М., Энергия, 1977.
12. Плютинский В.И., Погорелов В.И. Автоматическое управление и защита теплоэнергетических установок АЭС. - М., Энергоатомиздат, 1983.
13. Кафаров В.В., Перов В.А., Мешалкин В.П. Принципы математического моделирования химико-технологических систем. - М., Химия, 1976.
14. Профос П. Регулирование паросиловых установок.
15. Лазарев Ю. MatLAB 5.x – К.: Изд.группа ВHV, 2000.
16. Бенькович Е., Колесов Ю., Сениченков Ю. Практическое моделирование динамических систем. – СПб.: БХВ_Петербург, 2002.
17. MATLAB 6.5 SP1/7.06 Simulink 5/6 в математике и моделировании. – М7: СОЛОН-Пресс6 2005.
18. Ибраева Л.К. Основные приемы работы в среде MatLab. Методический практикум – Алматы;АИЭС, 2004.
19. Ибраева Л.К. Моделирование и идентификация объектов управления. Методические указания к выполнению курсовой работы для студентов специальности «Автоматизация и информатизация систем управления» - Алматы: АИЭС, 2005.
20. Ибраева Л.К. Моделирование и идентификация объектов управления.
Методические указания к выполнению лабораторных работ для студентов специальности «Автоматизация и управление» - Алматы: АИЭС, 2007.
21. Солодовников В.В. Статистическая динамика линейных систем автоматического управления. – М.: Физматгиз, 1960.