Алматинский институт энергетики и связи
Кафедра инженерной кибернетики
МОДЕЛИРОВАНИЕ И ИДЕНТИФИКАЦИЯ ОБЪЕКТОВ УПРАВЛЕНИЯ
Методические указания к выполнению лабораторных работ
для студентов специальности
«Автоматизация и информатизация систем управления»
Алматы 2005
СОСТАВИТЕЛЬ: Ибраева Л.К. Моделирование и
идентификация объектов управления. Методические указания к выполнению
лабораторных работ (для студентов специальности 360140 – Автоматизация и
информатизация в системах управления). – Алматы: АИЭС, 2005. – 22 с.
Методические указания предназначены для выполнения
лабораторных работ по дисциплине «Моделирование и идентификация объектов
управления».
В первой и второй лабораторных работах построение
моделей объектов проводится на базе аналитических методов моделирования.
Исследование процесса в первой работе проводится на основе полученных
дифференциальных уравнений модели, во второй работе полученная модель
преобразуется в передаточную функцию объекта. Для имитационного моделирования
поведения рассматриваемых систем используется пакет моделирования динамических
систем Simuink системы MatLab.
При проектировании систем управления широко
используется идентификация систем. Вторая и третья лабораторные работы
посвящены вопросам параметрической (третья работа) и непараметрической
(четвертая работа) идентификации систем. Для решения задач используется
графическая оболочка идентификации и
другие средства системы MatLab.
Рецензент: канд. техн. наук, профессор Б.Д.Хисаров.
Печатается по плану издания Алматинского института
энергетики и связи на 2005 г.
© Алматинский институт энергетики и связи, 2005 г.
Содержание
|
|
|
|
Введение |
4 |
|
1 Лабораторная работа № 1.
Моделирование процессов в мельнице |
5 |
|
1.1 Описание процесса. |
5 |
|
1.2 Пакет Simulink системы MatLAB |
5 |
|
1.3. Задание на выполнение лабораторной работы |
6 |
|
1.4 Требования к отчету |
6 |
|
1.5 Варианты заданий |
6 |
|
1.6 Контрольные вопросы |
7 |
|
2
Лабораторная работа № 2. Динамика газожидкостного сепаратора |
7 |
|
2.1 Описание объекта |
7 |
|
2.2 Математическая модель газожидкостного
сепаратора |
9 |
|
2.3. Задание на выполнение работы |
10 |
|
2.4.
Содержание отчета |
11 |
|
2.5 Варианты заданий |
11 |
|
2.6 Контрольные вопросы |
11 |
|
3
Лабораторная работа № 3. Параметрическая идентификация линейных систем |
12 |
|
3.1 Постановка задачи |
12 |
|
3.2
Дискретные модели линейных систем |
12 |
|
3.3 Реализация модели линейной системы |
13 |
|
3.4
Идентификация параметров |
14 |
|
3.5
Верификация модели |
16 |
|
3.6
Преобразование модели |
16 |
|
3.7 Задание на выполнение работы |
16 |
|
3.8
Содержание отчета |
17 |
|
3.9 Варианты заданий |
17 |
|
3.10 Контрольные вопросы |
17 |
|
4
Лабораторная работа № 4. Непараметрическая идентификация динамических
объектов |
18 |
|
4.1 Постановка задачи |
19 |
|
4.2 Задание на выполнение работы |
20 |
|
4.3
Содержание отчета |
20 |
|
4.4 Варианты заданий |
21 |
|
4.5 Контрольные вопросы |
21 |
|
Список литературы |
21 |
Введение
Существует два принципиально различных подхода к
построению математических моделей.
Первый подход основан на выборе моделей с учетом
основных физико-химических закономерностей, определяющих течение исследуемого
процесса. Такие модели называются аналитическими
моделями процесса.
Второй базируется на концепции "черного
ящика", то есть постулируется, что внутренняя структура объекта неизвестна
да и не должна интересовать исследователя. Вся информация получается только в
результате наблюдений за объектом при пассивном и активном эксперименте, то
есть считается достаточным описание свойств процесса через отношения
"вход-выход". Полученные таким образом модели называются эмпирическими (экспериментальными).
Аналитические методы определения характеристик
объектов регулирования основаны на составлении их дифференциальных уравнений.
Составление дифференциального уравнения базируется на использовании основных
физических законов: сохранения массы, энергии и количества движения. В
лабораторной работе 1 исследование процесса проводится на основе
дифференциальных уравнений модели.
Как правило, аналитическим методом удается получить
нелинейное уравнение объекта, аналитическое решение которого в общем случае не
может быть получено. Следующим шагом является линеаризация полученного уравнения, то есть переход к линейной
математической модели объекта. Линеаризация обычно проводится путем разложения
нелинейных зависимостей в ряд Тейлора в окрестности исходного стационарного
режима с сохранением только линейных частей разложения и последующим вычитанием
уравнений статики. Полученная таким образом линейная модель объекта справедлива
лишь при малых отклонениях от исходного стационарного режима. Решение
часто проводится в области изображений
Лапласа или Фурье. В этом случае получают соответственно передаточные функции
или АФХ. В лабораторной работе 2 модель в виде системы дифференциальных
уравнений линеаризуется и преобразуется в передаточные функции, исследование
проводится в области изображений.
При построении эмпирических моделей используются
реализации входных и выходных переменных объекта (в пассивном или активном
эксперименте). Задачи восстановления таких моделей изучаются в теории идентификации. В лабораторной работе 3
рассматривается задача параметрической идентификации, в лабораторной работе 4 –
задача непараметрической идентификации.
Во всех лабораторных работах используются различные
инструментарии системы MatLab –
командное окно системы, пакет Simulink, графическая оболочка для идентификации систем.
1 Лабораторная
работа № 1. Моделирование
процессов в мельнице
Цель работы: привитие
навыков получения математической модели объекта управления, анализа
динамических характеристик объекта, анализа переходной функции объекта при
возмущении его по различным каналам, навыков моделирования объекта управления
на ЭВМ.
1.1 Описание процесса
В мельницу поступает
входной поток исходного перерабатываемого материала Ф0, содержащего
крупные фракции. Выходной поток из мельницы Фвых, пропорционален
массе материала в мельнице М
Фвых
= aМ,
где a = 0.5 (1/час) -
константа пропорциональности.
В мельнице происходит
измельчение крупной фракции со скоростью W, пропорциональной
массе крупной фракции
W = k(M) (1-C) M,
где С = Мм/М;
k(M) = k0 (2M+ - M)/M+.
Здесь
С - доля мелкой фракции (Мм
- масса мелкой фракции в мельнице;
k0 - константа скорости
измельчения,
М+ - характерная
масса, соответствующая максимальной скорости измельчения (максимальной
производительности мельницы). Значение М+ = 10 т; k0 = 1,5 (1/час).
Математическая модель объектов в виде системы
дифференциальных уравнений выводится на основе аналитических методов
моделирования.
При составлении уравнений математической модели объекта
используются следующие уравнения баланса:
а) баланс общей массы в
мельнице
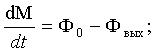
б) баланс массы мелких
фракций (готового продукта) в мельнице

1.2 Пакет Simulink системы MatLAB
Для имитационного моделирования поведения
рассматриваемого объекта и управления им применяются пакеты Simulink и Stateflow
системы MatLAB.
Пакет моделирования динамических систем Simulink предназначен для математического моделирования
линейных и нелинейных динамических систем и устройств, представленных своей
функциональной блок-схемой, именуемой моделью.
Для построения функциональной блок-схемы моделируемых
устройств Simulink имеет обширную библиотеку
блочных компонентов и удобный редактор блок-схем. Используя палитры компонентов
(наборы) блок-схем, пользователь с помощью мыши переносит нужные компоненты на
рабочий стол пакета и соединяет линиями входы и выходы блоков. Таким образом
создается блок-схема модели.
Simulink автоматизирует следующий наиболее трудоемкий этап
моделирования: он составляет и решает сложные системы алгебраических и
дифференциальных уравнений, описывающих заданную функциональную схему (модель),
обеспечивая удобный и наглядный визуальный контроль за поведением созданного
пользователем виртуального устройства.
1.3. Задание на выполнение
лабораторной работы
1.3.1 Используя уравнения
баланса вещества в мельнице, построить математическую модель процесса.
1.3.2 В пакете Simulink
системы MatLab
построить блок-диаграмму динамической модели объекта.
1.3.3 Провести
имитационные эксперименты на модели (по варианту).
1.4 Содержание
отчета
Отчет по
лабораторной работе должен содержать:
1.4.1
Вывод уравнений
математических моделей процессов.
1.4.2
Блок-диаграммы моделей с поясняющими комментариями.
1.4.3
Результаты проведенных исследований.
1.5 Варианты заданий
1.5.1 Исследовать производительность мельницы Р=СФвых
как функцию входного потока Ф0(t). Найти наиболее
производительные режимы.
1.5.2 Исследовать влияние на производительность мельницы
амплитуды А периодически изменяющегося входного потока
Ф0 = Ф0*
+ Аcos(0.2t),
где t задается в часах, Ф0* = 5
т/час.
Требуется найти амплитуды
наиболее «опасных» колебаний входного потока.
1.5.3 Исследовать влияние на производительность мельницы частоты w периодически изменяющегося входного потока
Ф0(t) = Ф0*
+ 2.5cos(wt),
где Ф0*
= 5 т/час; t задается в часах.
Требуется найти наиболее
«опасные» частоты колебаний входного
потока.
1.5.4 Исследовать влияние на
производительность мельницы частоты w периодически изменяющегося коэффициента a
a= a0 + a1cos(wt),
где a0 = 0.5 (1/час); a1 = 0.25 (1/час).
Выбрать оптимальный режим изменения a.
1.6 Контрольные
вопросы
1.6.1 Каковы основные типы математических моделей?
1.6.2 В чем отличие аналитических методов моделирования от
экспериментальных?
1.6.3 Какие законы сохранения используются для вывода
уравнений модели рассматриваемого процесса?
1.6.4 Как по виду модели определить, является ли она
динамической?
2 Лабораторная работа № 2 Динамика газожидкостного
сепаратора
Цель работы:
привитие навыков составления математической модели объекта управления на основе
аналитического подхода, линеаризации модели и преобразования к передаточным
функциям, анализа переходной функции объекта при возмущении его по различным
каналам.
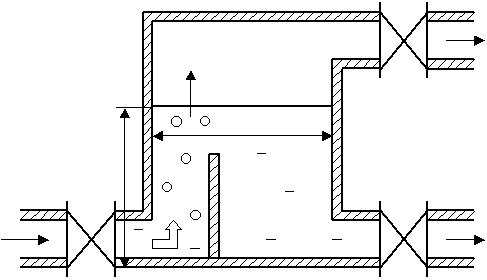
2.1 Описание объекта
Сепаратор состоит из гидроемкости, где необходимо
поддерживать постоянным уровень жидкости H, и газовой полости, где необходимо поддерживать в
заданных пределах давление Р. Ввод эмульсии производится в нижние горизонты
гидроемкости (рисунок 2.1).
 Vn
Vn
n
ρГ QР вых
 барботажная
зона QГвх
барботажная
зона QГвх
P4=const
S
отстойник
![]()
 Н VC
Н VC
QЭ QГвх ρЖ
m L
P2Л Р2n QЖвых
![]() QЖВХ
QЖВХ
Р1=const P3=const
![]() разделительная стенка
разделительная стенка
Рисунок
2.1 - Принципиальная схема сепаратора с вводом эмульсии в гидроемкость
В свою очередь гидроемкость состоит из двух частей:
барботажной зоны и отстойника. Это достигается с помощью разделительной стенки.
Суммарный объем сепаратора - VC,
сечение – S, объем газовой полости - VП, объем
гидроемкости – SH. Остальные обозначения на
рисунке и в тексте.
Газожидкостный сепаратор – объект с двумя
регулируемыми параметрами H и Р. В
качестве независимых переменных (на уровне объекта) выступают степени открытия
вентилей на стороне газожидкостной эмульсии, газа и чистой жидкости.
Из условия функционирования сепаратора должны
выполняться следующие неравенства
![]() ,
, ![]()
Газонасыщенность ε определяется отношением объема
газовой фазы к объему эмульсии “газ-жидкость” и изменяется в пределах ε
< 1. Давления в нижнем сечении сепаратора различны для барботажной зоны (![]() ) и для отстойника (
) и для отстойника (![]() )
)
![]()
![]() ,
,
![]() (1.1)
(1.1)
Полагаем, что вентили m и n осуществляют
регулирующее воздействие для поддержания давления газа Р и уровня жидкости Н в
сепараторе, а вентиль L установлен со
стороны нагрузки. В дальнейшем индексами m, n, L обозначается степень открытия соответствующего
клапана (меняются от 0 до 1). Степень открытия вентилей m, n, l определяет объемный расход эмульсии QЭ, газа QГ и
жидкости QЖ соответственно.
Объемные расходы указанных компонентов определяются с
учетом турбулентного режима истечения
![]() (1.2)
(1.2)
![]() (1.3)
(1.3)
Расход газа на клапане m определяется равенством
![]() (1.4а)
(1.4а)
Объемный расход газа у поверхности раздела “жидкость –
газовая полость” с учетом изотермического расширения пузырей при их всплывании
определяется равенством
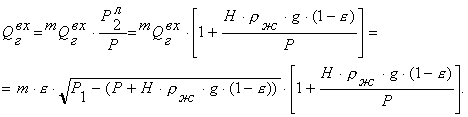 (1.4б)
(1.4б)
Истечение газа из газовой полости сепаратора
определяется равенством:
![]() . (1.5)
. (1.5)
При анализе динамики сепаратора пренебрегаем
изменением степени растворения газа в жидкости под действием изменчивости
давления газа над жидкостью. То есть полагаем, что в отстойнике наблюдается
стационарная концентрация газа в жидкости, которая не оказывает существенного
влияния на плотность жидкости в отстойнике.
2.2
Математическая модель газожидкостного сепаратора
Для вывода математической модели используются условия
материального баланса в несжимаемой жидкости:
-
уравнение статики:
![]() , (
, (![]()
![]() );
(2.1)
);
(2.1)
-
уравнение динамики:
![]() . (2.2)
. (2.2)
Для вывода уравнения динамики гидроемкости с проточной
газовой полостью с произвольным давлением запишем уравнение (2.2) в приращениях
(∆):
![]() . (2.2а)
. (2.2а)
Выражения для Qжвх и Qжвых имеют
нелинейности, поэтому для линеаризации уравнений применим разложение этих
выражений в ряд Тейлора и оставим только линейные члены ряда:
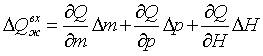 , (2.3)
, (2.3)
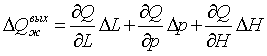 (2.4)
(2.4)
Определив коэффициенты ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
, ![]() этих разложений
из соотношений (1.2), (1.3), подставив их в уравнение (2.2а), получим уравнение
динамики гидроемкости относительно переменных ∆Р и ∆Н (∆m и ∆L –
независимые переменные)
этих разложений
из соотношений (1.2), (1.3), подставив их в уравнение (2.2а), получим уравнение
динамики гидроемкости относительно переменных ∆Р и ∆Н (∆m и ∆L –
независимые переменные)
![]() (2.5)
(2.5)
Выражения для коэффициентов при переменных B,C, D, F студенты
определяют самостоятельно.
Чтобы записать уравнение (2.5) в безразмерной форме,
введем обозначения:
![]()
![]() ,
, ![]()
![]()
![]()
(индекс
“0” означает базовые значения параметров). В уравнении (2.5) выполним следующие
преобразования
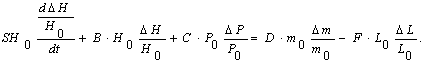 (2.5а)
(2.5а)
Так как в статике H = const, P = const, имеем
![]()
Получив выражения для ![]() и
и ![]() из уравнений (1.2) и
(1.3) соответственно, приравняем их
из уравнений (1.2) и
(1.3) соответственно, приравняем их ![]() . Разделим уравнение (2.5а) на
. Разделим уравнение (2.5а) на ![]() и, используя для
упрощения этого уравнения полученные выражения, получим уравнение динамики
гидроемкости
и, используя для
упрощения этого уравнения полученные выражения, получим уравнение динамики
гидроемкости
![]() (2.6)
(2.6)
Коэффициенты уравнения определяются студентами.
Для вывода уравнения динамики проточной газовой
полости при произвольном изменении уровня жидкости Н полагаем, что процесс
сжатия газа является изотермическим (Т = const) и может быть описан уравнением состояния идеального
газа:
![]() (2.7)
(2.7)
где М – масса газа в полости с объемом Vn;
R – универсальная газовая постоянная. Отсюда
![]()
![]()
Так
как ![]() то
то ![]()
Элементарное приращение ∆М находим как небаланс
между изменениями прихода ![]() и расхода
и расхода ![]() газа в полость Vn за промежуток времени dt:
газа в полость Vn за промежуток времени dt:
![]() (2.8)
(2.8)
В (2.8) выражения для ![]() и
и ![]() получаем как
результат линеаризации функций
получаем как
результат линеаризации функций ![]() и
и ![]() из (1.4б) и (1.5).
Окончательно уравнение динамики газовой полости в приращениях в линеаризованном
виде:
из (1.4б) и (1.5).
Окончательно уравнение динамики газовой полости в приращениях в линеаризованном
виде:
![]() (2.9)
(2.9)
где E, C1, B1, D1, F1 –
коэффициенты уравнения (определяются студентами).
Уравнение динамики газовой полости сепаратора безразмерной форме:
![]() (2.10)
(2.10)
Коэффициенты
уравнения определяются студентами.
2.3
Задание на выполнение работы
Заданы следующие
конструктивные и технологические параметры газожидкостного сепаратора:
V0 = 6.75 м2; S = 1.14 м2; H0 =
2.1 м; P0 = 6 кгс/см2; ρж = 860 кг/м3; ε1= 0.2; ε2=
0.4; ![]() м3/сут;
м3/сут; ![]() м3/сут; P1 = 8
кгс/см2; P3 = 4
кгс/см2; ; P4 = 1
кгс/см2; 1кгс/см2 =
м3/сут; P1 = 8
кгс/см2; P3 = 4
кгс/см2; ; P4 = 1
кгс/см2; 1кгс/см2 = ![]() Па; 1м3/сут =
Па; 1м3/сут = ![]() м3/с.
м3/с.
2.3.1 Выведите уравнения динамики гидроемкости и
газовой полости сепаратора.
2.3.2 Определите коэффициенты уравнений (2.6), (2.10).
2.3.3 Запишите эти уравнения в операторной форме.
2.3.4 Запишите передаточные функции, описывающие
динамику сепаратора по различным каналам (пл варианту).
2.3.5 Используя пакет
имитационного моделирования Simulink системы
Matlab, получить переходные процессы объекта в цифровом виде
и в виде графика.
2.4 Содержание отчета
Отчет должен содержать:
2.4.1 Подробный
вывод уравнений динамики с комментариями.
2.4.2 Подробное
описание процедуры линеаризации.
2.4.3 Расчет
коэффициентов модели.
2.4.4 Процедуру
преобразования дифференциальной модели в передаточную функцию.
2.4.5 Блок-диаграмму модели в пакете Matlab.
2.4.6 Графики переходных функций.
2.4.7
Сравнительный анализ переходных функций с учетом свойств саморегулирования
газожидкостного сепаратора.
2.5
Варианты заданий
|
№ |
Выходная переменная |
Входная переменная |
|
1 |
Уровень жидкости φ1 |
Степень открытия клапана m |
|
2 |
Уровень жидкости φ1 |
Степень открытия клапана L |
|
3 |
Уровень жидкости φ1 |
Степень открытия клапана m |
|
4 |
Давление газа φ2 |
Степень открытия клапана m |
|
5 |
Давление газа φ2 |
Степень открытия клапана L |
|
6 |
Давление газа φ2 |
Степень открытия клапана m |
2.6.
Контрольные вопросы
2.6.1 Указать, существуют ли взаимные соотношения
между числом регулируемых величин, количеством регулирующих воздействий и
числом нагрузок на объект?
2.6.2 Объяснить физическую и математическую природу
саморегулирования газожидкостного сепаратора по различным каналам.
2.6.3 Показать, каким образом знак постоянного
коэффициента при переменной в управлении влияет на вид переходной функции.
2.6.4 В каком случае газожидкостный сепаратор может
превратиться в неустойчивый объект?
2.6.5 Какие параметры газожидкостного сепаратора
оказывают существенное влияние на вид переходной функции объекта?
3 Лабораторная работа № 3. Параметрическая идентификация
линейных систем
Цель работы: освоить методы
параметрической идентификации систем, применить для процедуры идентификации
возможности командного окна и графического пользовательского интерфейса системы
MatLAB.
3.1 Постановка задачи
Построение модели объекта по наблюдаемым данным
называется идентификацией и включает
определение его структуры и параметров. Объектом идентификации может быть
устройство, явление или процесс.
Построение
модели начинается с выбора структуры модели, определяющей взаимосвязь
наблюдаемых данных через совокупность параметров. После этого формируются входные воздействия и подаются
на объект, и измеряются отклики на эти воздействия (выходные сигналы). Затем
входные и выходные сигналы и выбранная структура используются для оценки
значений параметров в соответствии с принятым критерием качества. Критерий
качества идентификации характеризует степень адекватности модели объекту в
рамках согласованных допущений и ограничений. Очень часто используется
среднеквадратичный критерий, в соответствии с которым ищутся такие оценки
параметров, которые обеспечивают минимальный средний квадрат разности выходных
сигналов модели и объекта при одном и том же входном воздействии. Оценивание
параметров выполняется на основе алгоритма идентификации, определяющего правила
поиска оценок. Наконец, для того, чтобы проверить, насколько точно построенная
модель имитирует или предсказывает данные наблюдений, необходимо сравнить их
при одинаковых воздействиях. Эта процедура называется верификацией модели.
3.2 Дискретные модели линейных систем
Описание дискретных линейных систем основывается на
разностных уравнениях вида
y(n) = b1u(n-1)
+ … +bnbu(n-nb) – a1y(n-1) - … - anay(n-na),
(1)
где последовательности u(n) и y(n) представляют собой
входной и выходной сигналы, соответственно; n — индекс времени.
В некоторых приложениях (например, в
теории систем управления) разностные уравнения записывают в компактном виде с
помощью оператора сдвига q.
Тогда уравнение (1) можно записать в операторном виде следующим
образом
A(q)y(n)
= B(q)u(n). (2)
В реальных условиях система подвержена влиянию внешних
помех v, однако часто полагают, что действие этих помех можно отобразить
аддитивной случайной составляющей сигнала y и являющейся результатом
прохождения белого шума e через фильтр с неизвестной передаточной функцией H.
Детерминированная же составляющая выходного сигнала формируется с помощью
передаточной функции G, определяющей динамические свойства системы. Тогда в
общем виде модель системы можно описать с помощью уравнения
y(n) = G(q)u(n) + H(q)e(n). (3)
Одна из
наиболее простых и часто используемых моделей определяет связь между сигналами
системы с помощью уравнения
y(n) = b1u(n-1) + … +bku(n-nnb)
– a1y(n-1) - … - anay(n-na) + e(n)
или
в операторном виде
A(q)y(n) = B(q)u(n) + e(n) (4)
и
называется ARX-моделью, где сочетание AR относится к авторегрессионной
(AvtoRegressive) части A(q)y(n), а X показывает наличие внешнего (eXternal)
входа, на который поступает сигнал u(n).
Если помеха v(n) моделируется как скользящее среднее
белого шума, то получаем ARMAX-модель:
y(n) = b1u(n-1) + …
+bnbu(n-nb) – a1y(n-1) - … - anay(n-na)
+
+ e(n) + c1e(n-1)
+ … +cnce(n- nc) (5)
или
A(q)y(n) = B(q)u(n) + C(q)e(n). (6)
MA-часть (Moving Average) в названии модели указывает
на скользящее усреднение C(q)e(n).
3.3 Реализация модели линейной системы
Вначале необходимо реализовать
«измерительный стенд», на котором получим экспериментальные данные (по
варианту).
Модель системы легко построить, используя блоки
Simulink системы Matlab. Для построения модели нужны сумматоры, умножители на
константу, элементы задержки (1/z), входные (Input и Noise) и выходной (Output)
порты.
Перед тем, как к входам построенной модели подключить
источники сигналов, а к выходу — регистрирующие блоки, представьте модель
объекта в виде подсистемы с подключенными входными и выходными портами. Для
завершения процедуры построения полной модели подключите к подсистеме
необходимые блоки источников и приёмников сигналов.
В результате вы получите модель измерительного стенда,
с которого будете получать данные для идентификации системы. Заметим, что
данные модели автоматически не помещаются в рабочую область Matlab. Чтобы применить к ним команды Matlab, вначале экспортируйте их в рабочую область,
используя блок To Workspace.
Следующий шаг заключается в определении параметров входных и выходных блоков модели. Эти параметры пользователь может
выбирать по своему усмотрению и устанавливать в соответствующем окне. При
выборе вида и параметров входных сигналов можно руководствоваться простым
практическим соображением: в рабочей полосе частот амплитудный спектр сигнала
должен быть достаточно насыщенным, то есть иметь как можно больше ненулевых
спектральных составляющих.
После определения параметров блоков в меню “Simulation” - “Parameters…” вводятся данные, необходимые для
моделирования работы системы
Результатами работы построенной модели являются
входной и выходной сигналы, записанные в массивы. Значения этих сигналов
загружены в рабочую область программы.
3.4 Идентификация параметров
В лабораторной работе для идентификации линейной
системы, подверженной действию внешнего шума и описываемой разностным
уравнением, используется графическая интерактивная программа ident (GUI — graphic user interface),
входящая в состав инструментария ident пакета Matlab
Загрузите графическую программу идентификации, для
чего в командном окне необходимо набрать ident.
В результате загрузки на экране появится панель (главное окно) программы ident
(рисунок 3.1).
Последовательность ваших действий:
а) Для загрузки данных эксперимента выберите
раскрывающееся меню Data-Import…; в
появившемся диалоговом окне введите имена входных и выходных переменных модели;
введите любое имя для данных в соответствующее поле; также можно ввести
интервал времени, текст комментария. Затем нажмите кнопку Import и
данные отобразятся в иконке графической оболочки. Закройте окно импорта данных.
Обратите внимание, что данные также появятся в полях Working Data и Validation Data.
б) Флажок Time Plot позволяет отразить
окно с графиками входов и выходов. Это окно имеет меню для управления. Вы
можете выделить мышью прямоугольную область на графике для увеличения фрагмента
графика, щелчком левой кнопки мыши можно увеличить/уменьшить масштаб, двойной
щелчок возвращает исходный масштаб. Чтобы очистить окно графиков щелкните на
иконке с данными. В дальнейшем, чтобы работать с новыми данными надо
переместить их мышью в область Working Data.
Двойной
щелчок на иконке данных вызывает еще одно окно, где можно изменить название
массива данных.
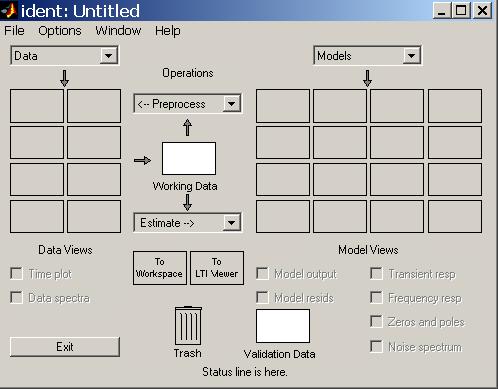
Рисунок 3.1 – Графическое
окно идентификации
в) Команда Select Range
раскрывающегося меню Preprocess позволяет выбрать подмножество из массива данных. Это
можно сделать через редактируемые текстовые поля появившегося окна или, выделяя
мышью прямоугольную область на графиках сигналов. Нажатие на Insert
размещает выбранные данные в новой иконке. Для верификации модели обычно
используются данные, которые не использовались для идентификации параметров.
Можно разделить исходные массивы x и y на две
половины, одна из которых используется для идентификации, а вторая - для
подтверждения модели. В реальной работе, особенно если приходится иметь дело со
сложными объектами, для верификации используются несколько наборов различных
данных. Для идентификации выбранные данные переносятся в область Working Data, для верификации модели соответствующие данные переносятся
в область Validation Data
(перетаскиванием с помощью мыши).
г) Для оценивания параметрической модели в раскрывающемся
меню Estimate выберите Parametric model, задайте структуру
модели в появившемся окне (поле Structure); откройте окно для редактирования
порядка модели (кнопка Order
Editor), установите значения констант, затем щелкните на кнопку Estimate. Результатом выполнения последнего пункта являются
оценки a, b и c соответствующих параметров модели. Для того, чтобы эти оценки
отобразить в командном окне Matlab, надо дважды щёлкнуть правой клавишей мыши
по пиктограмме модели и в открывшемся окне нажать клавишу “Present”.
В раскрывающемся меню Estimate можно выбрать другие виды
модели.
д) Существуют и другие
возможности просмотра характеристик моделей, они выбираются из списка Model Views с помощью соответствующего флажка и обычно: для
корреляционной модели просмотр результата – Transient Response; для спектральной модели – Frequency Response.
3.5 Верификация модели
Для того, чтобы убедиться, насколько точно построенная
модель описывает объект, необходимо проанализировать её поведение. Эта
процедура называется подтверждением или верификацией модели.
Программа
ident предоставляет пользователю широкий набор средств для анализа и
подтверждения модели. Эти процедуры выполняются с помощью установки флажков в
окнах, расположенных в правой нижней части панели.
Для сравнения наблюдаемых и
моделируемых выходных сигналов установите флажок “Model output”. В открывшемся
окне представлены графики измеренного (линия чёрного цвета) и рассчитанного по
модели выходных сигналов. Для рассмотрения отдельных фрагментов необходимо,
удерживая в нажатом положении левую клавишу мыши, выделить на графике
прямоугольную область, которая будет отображена на всё графическое окно.
Установка флажков “Transient resp” и “Frequency resp”
приводит к построению соответственно реакции на единичное ступенчатое
воздействие и частотной характеристики модели, а флажка “Zeros and poles” — к
отображению полюсов и нулей её передаточной функции.
3.6 Преобразование модели
В пакете MatLAB в
инструментарии идентификации систем одним из основных форматов является theta-формат. Этот формат может быть преобразован во
множество других представлений модели.
Например, не используя графическую оболочку, можно
оценить параметры ARMAX модели следующим образом:
th = armax (z, nn),
где z = [y x] – вектор входных и выходных данных, nn = [na nb nc nk] – размерность модели.
В дальнейшем из этого формата можно
получить все другие: преобразовать непрерывную модель в дискретную и наоборот,
получить ARX-модель, получить параметры
модели, преобразовать в модель пространства состояний, получить передаточную
функцию.
Например, преобразование theta-формата
к передаточной функции получается следующим образом:
[num den] = th2tf(th).
3.7 Задание на лабораторную работу
3.7.1 В пакете Simulink собрать модель «измерительного» стенда (по варианту).
3.7.2 Определить входные сигналы и подать их на вход
объекта; рассчитать реакцию (выходные
сигналы).
3.7.3
Результаты эксперимента передать в рабочую область программы.
3.7.4 Провести параметрическую идентификацию объекта,
то есть, полагая, что нам неизвестны параметры объекта, оценить их по имеющимся
реализациям входных и выходных сигналов. Для этого:
- вызвать функцию ident;
- загрузить данные эксперимента из рабочей области;
- выделить некоторый диапазон экспериментальных данных
для идентификации объекта;
- задайте структуру и порядок модели, получите оценки
параметров модели;
- проведите верификацию модели, используя другой
диапазон экспериментальных данных.
- проведите анализ полученных результатов.
3.7.5 Получите эту же модель, используя командное окно
MatLab, преобразуйте ее в передаточную функцию объекта.
3.8 Содержание отчета
Отчет по работе должен содержать:
- блок-диаграмму «измерительного» стенда с поясняющими
комментариями;
- результаты экспериментов на стенде;
- результаты идентификации: выбранную структуру и
порядок модели (с обоснованием выбора), искомые параметры модели, сравнительные
графики выходов объекта и модели;
- анализ полученных результатов;
- передаточную функцию объекта.
3.9 Варианты заданий
3.9.1 y(n) = 0,12u(n – 1) + 0,055752u(n – 2) + 2,0549y(n – 1) –
1,756677y(n – 2) +
0,576335y(n – 3) + e(n) – e(n – 1) + 0,2e(n – 2).
3.9.2 y(n) = 0,44u(n – 1) + 0,07u(n – 2) +
1,049y(n – 1) – 1,677y(n – 2) +
+ 0,76335y(n – 3) + e(n) – 0,2e(n – 1) + 0,1e(n – 2).
3.9.3. y(n) = 0,35u(n – 1) -
0,05u(n – 2) + 0,052y(n – 1) + 1,25y(n – 2)+
e(n) – 0,4e(n – 1) + 0,2e(n –
2).
3.9.4 y(n) = 0,12u(n – 1) +
2,0549y(n – 1) – 1,756677y(n – 2) +
+ e(n) – e(n – 1) + 0,2e(n – 2).
3.9.5
y(n) = 0,42u(n – 1) + 0, 055752u(n – 2) + 1,049y(n – 1) – 1,756677y (n – 2) +
e(n) – 0,2e(n – 1).
3.9.6 y(n) = 0,15u(n – 1) + 0,05u(n – 2) + 1,49y(n
– 1) – 0,7577y(n – 2) +
+ 1,4535y(n – 3) + e(n) – e(n – 1) + 0,1e(n – 2).
3.9.7 y(n) = 0,44u(n – 1) + 0.549y(n – 1) –
1,457y(n – 2) + e(n) – e(n – 1)
3.9.8 y(n) = 0,48u(n – 1) + 0,17u(n – 2) +
0,054y(n – 1) – 1,382(n – 2) +
+1,463y(n – 3) + e(n) +0,1e(n – 1) + 0,1e(n – 2).
3.9.9 y(n) =1,12u(n – 1)
+1,152u(n – 2) +05689y(n – 1) – 1,8677y(n – 2) +
+ 0,46335y(n – 3) + e(n) – e(n – 1).
3.9. 10 y(n) = 0,13u(n – 1) + 0,044587u(n – 2) +
2,1023y(n – 1) – 1,8012y(n – 2) + 0,6102y(n – 3) + e(n) – e(n – 1) + 0,2e(n – 2).
3.10 Контрольные
вопросы
3.10.1 Что такое идентификация?
3.10.2 В чем отличие параметрической идентификации от
непараметрической?
3.10.3 Для чего предназначена графическая оболочка ident?
3.10.4 Как можно определить порядок линейной
дискретной модели?
3.10.5 Что такое оценка параметра?
3.10.6 Какой критерий используется для оценивания
параметров линейной модели?
3.10.7 Какие виды модели могут быть оценены средствами
пакета Matlab?
4 Лабораторная работа № 4. Непараметрическая
идентификация
динамических объектов
Цель работы: освоить методы непараметрической
идентификации систем, применить для идентификации возможности командного окна и
встроенные процедуры системы MatLAB.
4.1 Постановка задачи
При идентификации
линейного стационарного динамического объекта статистическими методами
весовая функция определяется из уравнения Винера-Хопфа:
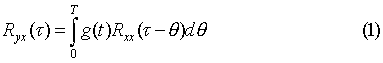
Один из способов его решения – численный. Суть численного
метода заключается в возможности представления этого уравнения системой
линейных алгебраических уравнений:
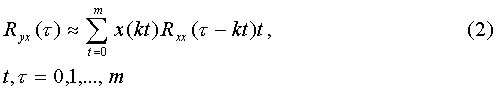
Решение
этой системы позволяет определить
дискретные значения ординат весовой функции g(τ) в точках t, 2t,…, mt.
Эти решения получаются с большими погрешностями, так как вместо истинных
значений корреляционных функций используются их оценки, сама система плохо
обусловлена. Хотя полученные значения импульсных переходных функций имеют малую
СКО, близкую к минимуму, ценность их невелика, так как эти функции не
соответствуют физическому смыслу процессов в объекте. Физический смысл имеют
гладкие решения. Поэтому используются различные процедуры сглаживания
импульсной переходной функции.
4.2 Задание на лабораторную работу:
Зарегистрированы входные и выходные переменные исследуемого объекта в
течение определенного интервала времени. По результатам этих измерений
вычислены автокорреляционная и взаимнокорреляционная функции (см. таблицу
вариантов). Требуется определить численным методом из уравнения Винера-Хопфа
импульсную переходную функцию. Затем полученные дискретные значения этой
функции следует аппроксимировать полиномами различных порядков и выбрать
наилучшую степень аппроксимации.
Порядок выполнения работы
4.2.1 Записать систему
линейных алгебраических уравнений (2) для своего варианта. Представить эту
систему в матричном виде:
Ax = b (3)
4.2.2
Для решения системы (3) использовать командное
окно системы Matlab. Ввести в этом окне значения элементов матрицы A и
вектора b.
Решение
системы получается в виде:
x = inv(A)*b
4.2.3
Отразить
на графике полученные дискретные значения импульсной переходной функции –
функция plot(t,u).
4.2.4
Полученные дискретные значения аппроксимировать с
помощью
аппроксимирующих
полиномов разного порядка и выбрать наилучшую степень аппроксимации. Отразите
на графике аппроксимирующие
полиномы и дискретные значения весовой функции. Для этого в командное
окно вводятся нижеописанные команды. Рекомендуется для сохранения этих команд
создать М-файл:
- вначале введите вектора значений
аргументов и функции;
- для аппроксимации данных примените
процедуру
Р =
polifit (X,Y,n),
здесь n – порядок полинома, X,Y –
вектора аргументов и значений функций; результат – вектор коэффициентов
полинома длиной (n+1);
эта процедура используется несколько раз (для разных степеней полинома);
-
для представления графика дискретной функции в виде отдельных вертикальных
линий используется процедура stem(x,y), а также для отражения графика дискретной функции на той
же фигуре, что и полиномы, введите hold;
- определите
диапазон изменения аргумента полиномов, например, в виде
х=0:0.05:6;
-
рассчитайте значения полиномов, используя процедуру y = polyval (P,x);
-
затем процедурой plot(x,y1, х, у2,…) постройте графики
полиномов;
-
для нанесения сетки на фигуру используется функция grid.
4.2.5 Выберите полином, который
наилучшим образом аппроксимирует импульсную весовую функцию (если бал
сформирован М-файл, надо запустить его на выполнение).
4.3 Содержание
отчета
Отчет по работе должен содержать:
-
систему алгебраических уравнений для определения дискретных значений импульсной
переходной функции;
-
результат решения этой системы;
-
текст М-файла для аппроксимации дискретных значений импульсной переходной
функции;
-
результат выполнения программы;
-
обоснованный выбора наилучшего аппроксимирующего полнинома.
4.4 Варианты
заданий
|
Вариант 1 |
t, мин |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
∞ |
|
|
Rx(t) |
1 |
0,37 |
0,16 |
0,05 |
0,02 |
0,01 |
0,005 |
0 |
|
|
Rxy(t) |
0,1788 |
0,4729 |
0,3866 |
0,2565 |
0,1454 |
0,06 |
0,03 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 2 |
t, мин |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
∞ |
|
|
Rx(t) |
1 |
0,47 |
0,2 |
0,1 |
0,05 |
0,01 |
0,005 |
0 |
|
|
Rxy(t) |
0,2376 |
0,5128 |
0,1343 |
0,2848 |
0,155 |
0,003 |
0,003 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 3 |
t, мин |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
∞ |
|
|
Rx(t) |
1 |
0,53 |
0,26 |
0,15 |
0,1 |
0,02 |
0,003 |
0 |
|
|
Rxy(t) |
0.3049 |
0.5792 |
0.5575 |
0.4152 |
0.2176 |
0,002 |
0,002 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 4 |
t, мин |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
∞ |
|
|
Rx(t) |
1 |
0,5 |
0,3 |
0,2 |
0,09 |
0,03 |
0,003 |
0 |
|
|
Rxy(t) |
0.3978 |
0.7428 |
0.7030 |
0.5960 |
0.3200 |
0,001 |
0,001 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 5 |
t, мин |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
∞ |
|
|
Rx(t) |
1 |
0,52 |
0,28 |
0,18 |
0,1 |
0,02 |
0,005 |
0 |
|
|
Rxy(t) |
0.4872 |
0.9122 |
0.8998 |
0.7320 |
0.4088 |
0,002 |
0,002 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 6 |
t, мин |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
∞ |
|
|
Rx(t) |
1 |
0,46 |
0,22 |
0,12 |
0,1 |
0,03 |
0,004 |
0 |
|
|
Rxy(t) |
0.3825 |
0.8008 |
0.7846 |
0.6214 |
0.3794 |
0,001 |
0,002 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 7 |
t, мин |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
∞ |
|
|
Rx(t) |
1 |
0,38 |
0,19 |
0,04 |
0,02 |
0,01 |
0,005 |
0 |
|
|
Rxy(t) |
0.1735 |
0.4398 |
0.3637 |
0.2415 |
0.1026 |
0,003 |
0,002 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 8 |
t, мин |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
∞ |
|
|
Rx(t) |
1 |
0,45 |
0,2 |
0,1 |
0,05 |
0,01 |
0,004 |
0 |
|
|
Rxy(t) |
0.2531 |
0.5655 |
0.5020 |
0.3365 |
0.1445 |
0,003 |
0,002 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 9 |
t, мин |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
∞ |
|
|
Rx(t) |
1 |
0,39 |
0,19 |
0,06 |
0,01 |
0,001 |
0,0001 |
0 |
|
|
Rxy(t) |
0.2428 |
0.6008 |
0.5659 |
0.4181 |
0.1166 |
0,0005 |
0,003 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 10 |
t, мин |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
∞ |
|
|
Rx(t) |
1 |
0,35 |
0,18 |
0,05 |
0,02 |
0,01 |
0,005 |
0 |
|
|
Rxy(t) |
0.2495 |
0.6569 |
0.5835 |
0.3389 |
0.1058 |
0,002 |
0,003 |
0 |
4.5 Контрольные вопросы
4.5.1
В чем суть непараметрической идентификации?
4.5.2 Какие объекты описывает уравнение
Винера-Хопфа,
4.5.3
Почему возможно представить уравнение Винера-Хопфа системой
алгебраических уравнений?
4.5.4
Дайте определение корреляционных функций.
4.5.5
Обоснуйте выбор аппроксимирующих полиномов.
Список литературы
1.
Дейч А.М Методы
идентификации динамических объектов.- М.: Энергия, 1979.
2.
Советов Б.Я., Яковлев
С.А. Моделирование систем. _М.: Высшая школа, 1990.
3 Дьяконов В. П. MatLab 6/6.1/6.5 + Simulink 4/5. Основы применения. – М.: Солон-ПРЕСС, 2004.
4 Дьяконов В.П. Simulink 4. – М.: Солон-ПРЕСС, 2004.
Доп. план 2005 г., поз. 2
Лида Куандыковна Ибраева
МОДЕЛИРОВАНИЕ И ИДЕНТИФИКАЦИЯ ОБЪЕКТОВ ИССЛЕДОВАНИЯ
Методические указания к выполнению лабораторных работ
(для студентов специальности 360140 -
Автоматизация и информатизация систем управления)
Редактор
Ж.М.Сыздыкова
Подписано
к печати Формат 60Х84 1/16
Тираж 50
экз. Бумага типографская №1
Объем
1.5 уч.-печ. л. Заказ Цена 44 тг.
Копировально-множительное бюро
Алматинского института энергетики и связи
480013 Алматы, ул. Байтурсынова, 126