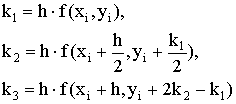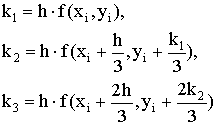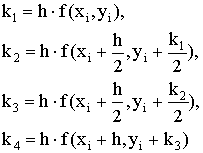АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ

 

Кафедра инженерной кибернетики

 

 

 

 

 

 

 

 

 

МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ИНЖЕНЕРНЫХ РАСЧЁТАХ НА ЭВМ

 

Методические указания к выполнению лабораторных работ

(для студентов специальности 360140-«Автоматизация и информатизация в системах управления»)

 

 

 

 

 

 

 

 

 

Алматы 2005

 

СОСТАВИТЕЛИ: М.У. Зияханов, А.А. Аманбаев. Методические указания к выполнению лабораторных работ (для студентов очной формы обучения специальности 360140-Автоматизация и информатизация в системах управления). – Алматы: АИЭС,2005. -37 с.

 

 

 

 

 

Методические указания разработаны в соответствии с рабочей программой дисциплины «Математические модели в инженерных расчётах на ЭВМ» для студентов специальности «Автоматизация и информатизация в системах управления» и содержат рекомендации по выполнению лабораторных работ, по оформлению и защите отчетов; в них приведены цель и порядок выполнения каждой лабораторной работы, перечень рекомендуемой литературы и контрольные вопросы.

Выполнение лабораторных заданий предусматривает работу на персональных компьютерах с использованием табличного процессора и алгоритмического языка высокого уровня.

Методические указания предназначены для студентов инженерно-технических специальностей всех форм обучения, в рабочие планы которых включена дисциплина   «Математические модели в инженерных расчётах на ЭВМ»,  они также могут быть рекомендованы аспирантам и магистрантам, не являющимся специалистами в этой области.

Ил.7, табл.8, библиогр.  -   9 назв.

 

 

 

 

 

 

 

Рецензент: кандидат технических  наук, доцент Л.К.Ибраева.

 

 

 

 

Печатается по плану издания Алматинского института энергетики и связи на 2005 год.

 

 

 

 

Ó       Алматинский институт энергетики и связи, 2006 г.

Содержание                                                                                                                   

Введение  …………………………………………………………………..

5

1 Лабораторная работа  № 1. Решение алгебраических и трансцендентных уравнений ..……………………..………………………..……

 

6

1.1 Теоретические сведения ……………………………………………

6

1.2 Общие теоретические сведения  ...…………………………………..

6

1.3 Метод деления пополам ………..…………………………………….

7

1.4 Метод касательных (Ньютона) .…….….…………………………….

7

1.5 Задание ……………… ..………………………………………………

9

1.6 Методика расчета к выполнению индивидуального задания………

9

1.7 Требования к отчету ………………………………………………….

10

2 Лабораторная работа  № 2. Решение системы линейных алгебраических уравнений …………………….....………………………………

 

11

2.1 Теоретические сведения ……………………………………………

11

2.2 Общие сведения о методах решений……………………………..….

11

2.3 Алгоритм метода  Гаусса ……….………………………...………….

11

2.4 Задание ……………….………………………………………………

13

2.5 Методика расчета к выполнению индивидуального задания………

13

2.6 Требования к отчету ………………………………………………….

13
3 Лабораторная работа № 3. Метод наименьших квадратов ….……..

15

3.1 Теоретические сведения …..…………………………………………

15

3.2 Общие сведения о проблеме аппроксимации функций……………

15

3.3  Метод наименьших квадратов  ………….....………………………

16

3.4  Задание……………….....……………………………………………

17

3.5 Методика расчета к выполнению индивидуального задания………

17

3.6  Требования к отчету……………………………………….…………

17

4 Лабораторная работа № 4. Методы численного интегрирования …

19

4.1 Теоретические сведения ……………………………………………

19

4.2  Общие теоретические сведения о методах интегрирования

19

4.3  Метод прямоугольников  ..…………………………………………

19

4.4  Метод трапеций  .…………………………………………………….

20

4.5  Задание ………………....……………………………………………

21

4.6 Методика расчета к выполнению индивидуального задания………

21

4.7  Требования к  отчету ………………………………………………

21
5 Лабораторная работа №5. Решение задачи Коши для обыкновенных дифференциальных уравнений ………………………………….……….

 

22

5.1 Теоретические сведения …..…………………………………………

22

5.2  Общие понятия и постановка задачи Коши для обыкновенных

дифференциальных уравнений   ..………………………………………

 

22

5.3 Решение задачи Коши для дифференциального уравнения первого порядка методом Эйлера. ……..…………………………………………

 

23

5.4 Решение задачи Коши для дифференциального уравнения первого порядка методом Рунге-Кутта ………………………………………

 

24

5.5 Приближенное решение задачи Коши для систем дифференциальных уравнений методом Рунге-Кутта.…………………………………

 

25

5.6 Задание ………………..……………………………………………….

26

5.7 Методика расчета к выполнению индивидуального задания………

26

5.8 Требования к отчету ………………………………………………….

26

6 Лабораторная работа № 6. Конечно-разностный метод решения краевой задачи для дифференциального уравнения второго порядка .

 

27

6.1Теоретические сведения .…………………………………………

27

6.2 Постановка краевой задачи для дифференциального уравнения

второго порядка  .………………………………………………………

 

27

6.3 Конечно-разностный метод решения задачи ..……………………

28

6.4 Метод прогонки решения системы алгебраических уравнений с трехдиагональной матрицей  .……………………………………………

 

28

6.5 Алгоритм решения краевой задачи …..……………………………

29

6.6 Задание ..……………… ..…………………………………………

30

6.7 Методика расчета к выполнению индивидуального задания ……

30

6.8 Требования к отчету .…………………………………………………

31

7 Лабораторная работа № 7. Метод сеток для решения уравнения теплопроводности ...………………………………………………………

 

32

7.1 Теоретические сведения  .……………………………………………

32

7.2 Постановка задачи о теплопроводности ...…………………………

32

7.3 Метод сеток для решения  уравнения теплопроводности …..……

33

7.3.1 Явная расчетная схема и ее алгоритм ..…….……………………

34

7.3.2 Неявная расчетная схема и ее алгоритм .………………………….

34

7.4 Задание ………………..……………………………………………….

36

7.5 Методика расчета к выполнению индивидуального задания………

36

7.6 Требования к отчету ………………………………………………….

36
Список литературы ……………………………………………………….

37

 

 

 

 

Введение

Математические модели процессов и явлений в различных областях науки и техники являются одним из основных способов получения новых знаний и технологических решений. Рассматриваются различные типовые математические задачи, получаемые в процессе математического моделирования инженерных задач и задач автоматизированного управления. Для осуществления моделирования студент независимо от его специальности должен знать определённый минимальный набор алгоритмов вычислительной математики, а также владеть способами их программной реализации на персональном компьютере. Требование классификаций компьютера зависит от использования языка программирования; например, если студент использует язык Delphi, тогда нужен минимум Pentium II.

Изучение дисциплины «Математические модели в инженерных расчётах на ЭВМ» базируется на знаниях студентов, полученных при изучении физики, математики и информатики, она является дисциплиной, связывающей вышеназванные фундаментальные дисциплины с дисциплинами общепрофессионального (ОПД) и специального (СД) циклов.

В каждой лабораторной работе указана цель работы, приведены краткие теоретические сведения, методические указания, контрольные вопросы, пример выполнения работы, листинг программы и индивидуальные задания.

Порядок выполнения всех лабораторных работ следующий:

-изучить теоретический материал по теме и ознакомиться с методическими указаниями к лабораторной работе;

-выполнить пример, приведенный в данных методических указаниях;

-ответить на контрольные вопросы;

-выполнить индивидуальное задание: составить собственную программу решения задачи на языке высокого уровня, а также решить задачу с использованием табличного процессора Excel;

-сдать отчет по лабораторной работе.

Отчет по лабораторной работе должен включать следующие обязательные разделы:

-титульный лист;

-постановку задачи;

-метод  и алгоритм решения задачи;

-листинг программы;

-результаты решения задачи, полученные с помощью программы на языке высокого уровня и на EXCEL;

-анализ полученных решений.

По желанию студента и по усмотрению преподавателя студенту может быть предложена более сложная задача из области, выбранной им специальности, где могут быть использованы некоторые из рассматриваемых здесь численных методов и компьютерных программ. Такая задача может иметь научно-исследовательский характер и рассматриваться как научно-исследовательская работа студента (НИРС).

1 Лабораторная работа №1. Решение алгебраических и трансцендентных уравнений

Цель работы – научить студентов  применять вычислительные методы для решения алгебраических и трансцендентных уравнений, часто встречающихся в инженерной практике.

 

1.1 Теоретические сведения

1.2 Общие теоретические сведения

 

Во многих научных и инженерных задачах возникает необходимость решения уравнений вида

                                    ¦(x) = 0 ,                                                               (1.1)

 

где x – неизвестная величина;

¦(x) - заданная и непрерывная в некотором промежутке функция.

Так, например, в электродинамике при математическом моделировании электромагнитных волновых колебательных процессов в линиях передачи и резонаторах получают так называемое дисперсионное уравнение (1.1). Требуется решить данное уравнение, т.е. найти такое значение неизвестной величины x, которое обращает заданное уравнение в тождество. Такое значение неизвестной величины называют корнем уравнения (1.1).

Если уравнение (1.1) имеет следующий вид

A 0 + A 1 x  + A 2 x 2 +  .  .  .  + A n x n = 0,

где  A i   -известные коэффициенты, то оно называется алгебраическим уравнением  n-ой степени. Во всех других случаях уравнение (1.1) называется трансцендентным.

Процесс решения уравнения (1.1) состоит из двух этапов:

-отделение корня, т.е. определение такого малого промежутка [a,b], где имеется единственный корень уравнения;

-уточнение значения корня с заданной точностью e.

Для отделения корня уравнения (1.1) существуют определенные правила; они основаны на следующих утверждениях:

-на концах некоторого промежутка [a,b] функция ¦(x) имеет различные знаки;

-функция ¦(x) в данном промежутке [a,b] является монотонной.

Отделение корня может быть выполнено с помощью табличного процессора EXCEL. Рассмотрим пример, где требуется решить уравнение

                    2 sin 2 x + 3 x  3  - 7 =0 .

Задавая разные значения  аргументу x, находят значения функции

                   ¦( x )= 2 sin 2 x + 3 x  3  - 7.

Например, при x=0, ¦( 0 )=-7, при x=1, ¦( 1 ) < 0, при x=2, ¦( 2 ) > 0. Отсюда видно, что в промежутке [1,2] заданное уравнение может иметь решение. Для доказательства единственности этого решения необходимо проверить монотонность функции ¦(x) в данном промежутке, она должна быть здесь монотонно возрастающей функцией, т.е. ее первая производная должна быть положительной ¦¢(x)>0. Убедимся в этом, для этого определяем ее первую производную ¦¢(x)=2 sin2x + 9x2,   и здесь легко можно показать, что она в промежутке [1,2] принимает только положительные значения. Итак, выполняются оба условия единственности корня уравнения (1.1) в данном промежутке.

Уточнение значения корня уравнения (1.1) осуществляется одним из существующих методов, в частности, метод деления пополам, метод касательных (Ньютона), метод хорд и другие. Все эти методы являются итерационными, где используются рекуррентные формулы, и заданная точность, вычисления корня определяет условия завершения итерационного процесса. Рассмотрим здесь процесс решения уравнения (1.1) двумя методами: деление пополам и касательных. После изучения этих методов другие методы могут быть легко изучены студентами самостоятельно.

 

1.3  Метод  деления пополам

Допустим, что корень уравнения (1.1) отделен, т.е. найден промежуток [a,b], где имеется единственный корень. Теперь необходимо найти его приближенное значение с заданной точностью e. Алгоритм вычисления корня будет следующий:

а) определяется середина промежутка [a,b]: c=(a+b)/2;

б) проверяется условие¦(с)=0, если это условие выполняется, то искомое решение найдено и выводится значение c;

в) если условие ¦(с)=0 не выполняется, то проверяется условие

¦(с) ¦(a)<0;

если это выполняется, то b=c ,  в противном случае  a= c;

г) проверяется условие |a-b|<e, если это условие выполняется, то процесс решения уравнения завершается и выводится значение c в качестве искомого решения; если это условие не выполняется, т.е. заданная точность не достигнута, то осуществляется переход к п.1.2.1 для продолжения вычислений.

Каждое повторение этих операций называется итерацией; количество итераций зависит от самого уравнения, заданной точности вычисления e и выбранного вначале промежутка [a,b].

Блок-схема алгоритма нахождения корня методом деления пополам приведена на рисунке 1.1.

 

1.4 Метод касательных (Ньютона)

 

Метод касательных также является итерационным методом, где используется следующая рекуррентная формула для определения любого (k-го) приближения корня заданного уравнения (1.1)

 

                     x k = x k-1 - ¦(x k-1 ) /¦¢(x k-1),                                              (1.2)

 

где x k-1 - предыдущее приближение искомого корня,

x k - вычисляемое приближение искомого корня.

Если будет задано первоначальное приближение корня, то по формуле (1.2) могут быть найдены любые приближения искомого корня, следовательно, можно получить бесконечный ряд чисел x i ,  i=1,2,3, . . .. Если этот ряд сходится, то его предел должен быть истинным значением искомого корня. Однако для достижения этого значения корня необходимо выполнить бесконечное количество итераций. Поэтому для завершения такого вычислительного процесса должно быть задано условие, определяемое заданной точностью решения уравнения; оно имеет вид

                                 | x k   -x k-1| <  e                                                        (1.3)

    

При выборе начального приближения корня необходимо руководствоваться следующим правилом: за исходную точку следует выбирать тот конец отрезка [a,b], в котором знак функции совпадает со знаком второй производной. В ОДНОМ случае f(b) · f"(х) > 0 и начальная точка х=b, во втором  f(а) · f"(х) > 0 и в качестве начального приближения берем х=a.

Обозначим xk-1 = x0, xk = x для удобства записи в дальнейшем. Тогда формула (1.2) будет иметь вид

                                      x   =  x0 - ¦( x0) / ¦¢( x0) ,                                    (1.4)                                                  

 а формула (1.3) –

                                                 | x    - x0 | <  e .                                                  (1.5)

 

Алгоритм решения уравнения (1.1) методом касательных будет иметь следующий вид:

а) вводится в память компьютера значение первоначального приближения корня x;

б) x0  принимает значения x;

в) по формуле (1.4) определяется новое приближение корня;

г) проверяется условие (1.5); если оно выполняется, то вычислительный процесс завершается,  а если условие (1.5) не выполняется, то продолжается процесс вычисления;

        д) вывод значения корня.

 

Блок-схема алгоритма нахождения корня методом касательных приведена на рисунке 1.2.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


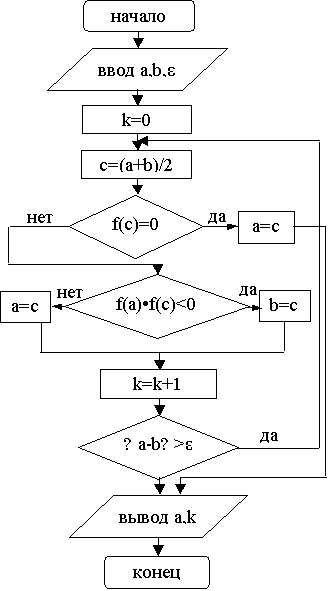
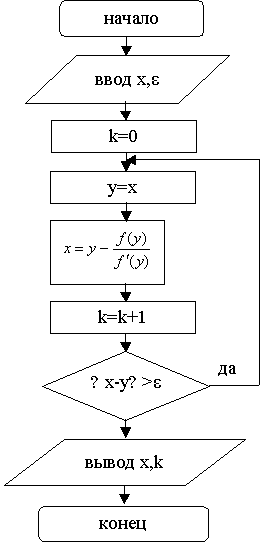
Рисунок 1.1 - Блок-схема метода деления        Рисунок 1.2 - Блок-схема метода

                       пополам                                                                касательных

 

1.5 Задание

1.5.1 Каждый студент должен выбрать вариант задания из таблицы 1, согласно указаниям преподавателя.

1.5.2 Найти интервал [a,b] в котором имеется единственное решение уравнения f(x).

1.5.2 Используя методы касательных и деления пополам, составить программу для решения выбранного варианта в интервале [a,b] с точностью e.

1.5.3 Ввести исходные данные и получить результат счета на ПЭВМ.

1.5.4 Составить необходимый отчет о ходе выполнения работы.

 

1.6 Методика расчета к выполнению индивидуального задания

1.6.1 Изучите данные методы, алгоритмы и блок-схемы.

1.6.2 Для метода касательных определите начальное приближение корня. Выбор начального приближения корня подробно написано в пункте 1.4

1.6.3 Используя алгоритмы или блок-схемы (рисунок 1.1 и рисунок 1.2),  составить необходимые программы.

 

1.7 Требования к отчету

Отчет по лабораторной работе должен содержать:

1.7.1 Запись или распечатку программы с результатами.

1.7.2 Сравнительный анализ двух методов по количеству итерации и точности конечного результата при заданном e.

1.7.3 Ответы на контрольные вопросы.

1.7.3.1 Какие уравнения называются трансцендентными?

1.7.3.2 Какие вычислительные процессы считаются итерационными?

1.7.3.3 Что такое отделение корня уравнения?

1.7.3.4 Какое условие является условием существования корня уравнения в заданном промежутке ?

1.7.3.5 Почему монотонность функции f(x) является необходимым условием единственности для решения уравнения  f(x)=0 ?

1.7.3.6 Что такое точность вычисления корня уравнения ?

1.7.3.7 Можно ли использовать вышеприведенные программы для решения других уравнений?

 

Таблица 1 - Индивидуальные задания

Вариант

 Функция f(x)

Точность e

       1

  3 cos 2 (x) + 4 x 3 – 9   = 0

0.0001

       2

   e x  -  10 x  + 7 = 0

0.0001

       3

   e-x  + 3 x – 9 = 0

0.001

       4

   x5 – 3 x2  + 5 x – 2,5 = 0 

0.001

       5

  2 x3 + 5 x2  +  4 x –13 = 0

0.001

       6

  5 x  + e-x – 3 = 0

0.001

       7

  5 sin 2x  + 3 x  - 1,5  = 0

0.001

       8

  2  ln x2 + 5 x  - 9  = 0      

0.0001

       9

   6 e-x – 3 x2  + 13 = 0

0.001

      10

  3 x5 + 4 x 3 + 2 x – 2,3 = 0

0.001

11

  tg1.2618x-0.16433x=0

0.0001

12

  tg3.47x-0.50691x=0

0.0001

13

  ln4x-3.8125x+3.25=0

0.0001

14

  6.5476e-0.6462x-x=0

0.0001

15

  7sin5.5857x-2.55x=0

0.0001

 

2 Лабораторная работа  № 2. Решение системы линейных алгебраических уравнений

 

Цель работы – научить студентов решать систему n - линейных алгебраических уравнений, к которым часто приводятся математические модели инженерных задач.

2.1 Теоретические сведения

2.2 Общие сведения о методах решения

Многие практические задачи механики, электротехники, автоматизированного управления и других часто приводят к системе линейных алгебраических уравнений, и решение её рассматривают как важное прикладное значение при разрешении различных проблем науки и техники. Общий вид такой системы может быть представлен так

 

  ,                                                               (2.1)

 

где a ij - заданные коэффициенты и свободные члены системы уравнений,

x i -неизвестные величины, значения которых должны быть определены,

 i=1,2,3, . . . ,n  , j=1,2,3,  . . . , n+1 .

В настоящее время хорошо разработан арсенал численных методов решения линейных алгебраических уравнений на ЭВМ. Многообразие численных методов решения линейных алгебраических систем можно разделить на прямые (точные) и итерационные.

Прямые методы характеризуются тем, что дают решение системы за конечное число арифметических операций. К прямым методам относятся метод Крамера, методы последовательного исключения неизвестных (метод Гаусса и его модификации, метод главного элемента, метод квадратного корня и другие).

Итерационные методы являются приближенными. Они дают решения системы как предел последовательных приближений, вычисляемых по единообразной схеме. К итерационным методам относятся метод простой итерации, метод Зейделя, метод релаксации, градиентные методы и их модификации.

2.3 Алгоритм метода Гаусса

Подвергнем систему (2.1) следующему  преобразованию, называемую схемой единственного деления. Считая a11  ¹ 0 (ведущий элемент), разделим на a11    коэффициенты первого уравнения. Выполнения условия a11  = 0 можно добиться всегда путем перестановки уравнений системы

x 1+ a 12( 1) x 2+ a 13 ( 1) x 3+ .  .  .  + a 1n( 1) x n = a 1n+1( 1)  .                          (2.2)

 

Пользуясь уравнением (2.2), легко исключить неизвестное x1 из остальных уравнений системы для этого достаточно из каждого уравнения вычесть уравнение (2.2), предварительно умноженное на соответствующий коэффициент при x1.  Система уравнений будет иметь следующий вид:

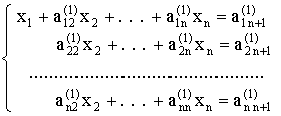,                                                    (2.3)

где a ij( 1)    -новые коэффициенты , полученные после преобразования. Повторяя этот процесс, вместо системы (2.1) получим равносильную ей систему с треугольной матрицей. Из треугольной матрицы последовательно  находятся значения всех неизвестных xn ,  xn-1, . . . , x1.

Таким образом, процесс решения системы (2.1) по методу Гаусса распадается на два этапа. Первый этап, состоящий в последовательном исключении неизвестных, называют прямым ходом. Второй – нахождение значений неизвестных  принято называть обратным ходом.

Формулы, которые приводят систему (2.1) к треугольной матрице, в общем виде для любого k – го шага  записываются

 

                 a kj(k)   =  a  kj (k-1)/ a kk(k-1)  ,               i = 1,2,3, . . . , n,                                     

                  a ij(k)    = a ij(k-1) – a ik(k-1) a kj(k)    ,  i = 1,2,3, . . . , n,                              (2.4)

                                                                 j = 1,2,3, . . . , n+1, (i ¹k) ,

                                                                                                      k = 1,2,3, . . . , n.

 

Формулы (2.4) называются формулами преобразования Гаусса. Эти формулы определяют алгоритм решения системы уравнений (2.1).

2.3.1 Ввод матрицы  A, составленной из коэффициентов и свободных членов заданной системы уравнений.

2.3.2      Начало цикла по счетчику k = 1.

2.3.3 Предполагается, что a kk ¹ 0; если это условие не выполняется, то осуществляется замена k- го уравнения другим уравнением (одним из последующих).

2.3.4 Составляется цикл по счетчику i = 1,2,3,  .  .  .  n, где вычисляются значения коэффициентов k- го уравнения по первой формуле Гаусса (2.4).

2.3.5 Начало цикла по счетчику i =1.

2.3.6 Проверка условия i ¹ k если это условие не выполняется, то  i=i+1.

2.3.7 Цикл по счетчику j = 1,2,3, . . . , n+1 ,  где  вычисляются коэффициенты любого уравнения, кроме k- го, по второй формуле Гаусса (2.4).

2.3.8 Переход к следующему шагу,  k= k+ 1.

2.3.9 Если k £ n, то управление передается в п. 2.2.3 для продолжения вычислений.

2.3.10 Вывод полученного решения системы уравнений xi,  i =1,2,3, . . . , n.

Алгоритм замены одним уравнением другого определяется как цикл по счетчику j=1,2,3, . . . , n+1 и имеет следующий вид:

2.3.11  начало цикла по счетчику j=1;

2.3.12 вспомогательной переменной b присваивается значение коэффициента k –го уравнения b = a kj;

2.3.13 коэффициенту k – го уравнения присваивается значение  коэффициента k+1 – го уравнения a kj = a k+1j;

       2.3.14 коэффициенту k+1 –го уравнения присваивается значение a k+1j = b;

2.3.15 конец цикла по счетчику j.

Используя данный алгоритм, напишите  программу на любом языке высокого уровня для решения своего варианта задания.

 

2.4 Задание

2.4.1 Каждый студент должен выбрать вариант задания из таблицы 2, согласно указаниям преподавателя.

2.4.2 Используя метод Гаусса составить программу для решения выбранного варианта.

2.4.3 Ввести исходные данные и получить результат счета на ПЭВМ.

2.4.4 Решить систему с помощью табличного процессора Excel.

2.4.5 Составить необходимый отчет о ходе выполнения работы.

 

2.5 Методика расчета к выполнению индивидуального задания

2.5.1 Изучить данный метод и алгоритм.

2.5.2 Используя алгоритм,  составьте необходимую программу на языке высокого уровня.

2.5.3 При отладке программы на каждом шаге выводить матрицу коэффициентов А на экран монитора для проверки правильности хода вычислений.

2.5.4 Решить систему трех уравнений с тремя неизвестными с помощью табличного процессора Excel.

2.5.5 Составить программу для проверки.

 

2.6 Требования к отчету

Отчет по лабораторной работе должен содержать:

2.6.1 Запись или распечатку программы с результатами.

2.6.2 Вывод формул метода Гаусса по лекциям и учебникам для понимания сущности метода.

2.6.3 Сравнительный анализ двух полученных результатов.

2.6.4 Ответы на контрольные вопросы.

2.6.4.1 Какое условие является условием существования   единственного решения системы линейных алгебраических уравнений (2.1)?

2.6.4.2 Сколько шагов должно быть выполнено для решения рассматриваемой системы?

2.6.4.3 Как осуществляется исключение неизвестной величины в каждом шаге ?

2.6.4.4 Каким образом происходит замена одного уравнения другим ?

2.6.4.5 Почему в каждом шаге коэффициент при k –ой неизвестной считается отличной от нуля ?

2.6.4.6 Что получится, если на каком – то k – ом шаге не будет уравнения с ненулевым коэффициентом при k –ой неизвестной ?

2.6.4.7 Для чего используется первая формула Гаусса ?

2.6.4.8 Для чего используется вторая формула Гаусса ?

2.6.4.9 От чего зависит точность данного метода ?

 

Таблица 2 - Индивидуальные задания

№ варианта

Матрица коэффициентов системы А

Столбец свободных членов

I

II

III

1

1.84

2.32

1.83

2.25

2.60

2.06

2.53

2.82

2.24

-6.09

-6.98

-5.52

2

2.58

1.32

2

2.93

1.55

2.25

3.13

1.58

2.34

-6.66

-3.58

-5.01

3

2.36

2.51

2.59

2.37

2.4

2.41

2.13

2.10

2.06

1.48

1.92

2.16

4

3.43

4.17

4.3

3.38

4

4.1

3.09

3.65

3.67

5.52

6.93

7.29

5

3.88

3

2.67

3.78

2.79

2.37

3.45

2.39

1.96

10.41

8.36

7.62

6

2.53

3.95

2.78

2.36

4.11

2.43

1.98

3.66

1.94

12.66

21.97

13.93

7

2.69

2.73

2.93

2.47

2.39

2.52

2.07

1.92

2.02

19.37

19.43

20.80

8

4.07

2.84

4.99

3.79

2.44

4.50

3.37

1.95

3.97

40.77

27.68

49.37

9

3.19

4.43

3.40

2.89

4.02

2.92

1.48

3.53

2.40

33.91

47.21

32.92

10

2.95

5.11

4.38

2.58

4.62

3.82

2.16

4.14

3.30

44.16

46.68

65.34

11

2.93

3.47

4.78

2.55

2.98

4.22

2.14

2.50

3.70

46.41

54.78

75.81

12

3.74

4.02

4.18

3.36

3.51

3.61

2.94

3.04

3.09

63.26

67.51

70.03

13

1.54

3.65

2.45

2.44

2.31

3.22

2.49

2.45

3.17

-4.34

-3.91

-5.27

14

3.75

4.18

3.43

3.59

3.70

3.88

2.97

3.22

3.36

53.38

59.28

62.62

15

1.53

2.35

3.83

1.61

2.31

3.73

1.43

2.07

3.45

-5.13

-3.69

-5.98

 

3 Лабораторная работа № 3. Метод наименьших квадратов

Цель работы – изучение методов математико-статистической и компьютерной обработки результатов экспериментов, испытаний и статистических наблюдений.

3.1 Теоретические сведения

3.2 Общие сведения о проблеме аппроксимации функций

Для установления закономерностей при изучении многих природных явлений проводятся эксперименты или осуществляют сбор статистических данных об объекте исследования. Если набор экспериментальных данных получен со значительной погрешностью, то не имеет смысла использовать интерполяцию Лагранжа полиномами и сплайнами для обработки результатов. В этом случае необходимо провести аппроксимирующую кривую, которая не проходит через экспериментальные точки, но в то же время отражает исследуемую зависимость, сглаживает возможные выбросы за счёт погрешности эксперимента. Такую операцию называют аппроксимацией, полученную при этом функцию называют аппроксимирующей функцией, а ее график  аппроксимирующей линией.

Пусть изучается связь между двумя переменными x и y; для этого рассматривается таблица значений этих переменных, полученных из эксперимента или в результате сбора данных:

 

        X

        X 1

        X 2

        X3

      .  .  .

       X n

        Y

        Y1

        Y2

        Y3

        .  .  .

       Yn

 

В дальнейшем эти табличные данные называются статистическими (экспериментальными) и на основе этих данных должна быть получена функция, связывающая переменных x и y:

                                       y = f(x).

Для определения такой функции необходимо решить две задачи, называемые двумя основными задачами статистики:

- определение общего вида аппроксимирующей функции y = f(x) может включать в себя неизвестные параметры, например, общий вид линейной функции y = a x + b зависит от двух параметров, а общий вид квадратичной функции y = a x 2 + b x + c - от трех параметров и т.д. ;

- определение конкретного вида функции, когда определены значения неизвестных параметров a и b или a, b, c.

Первая задача решается феноменологическим методом, исходя из интуиции исследователя и заданной таблицы значений аргумента x и функции y. Для решения второй задачи используется метод наименьших квадратов.

 

3.3 Метод наименьших квадратов

Сущность метода заключается в следующем. Рассматривается выражение

U =  å ( y i –  f( x i ))2 Þ min,

которое является суммой квадратов отклонений статистических точек от линии аппроксимации. Минимум этого выражения означает, что линия аппроксимации располагается очень близко от статистических точек. Если рассматривается конкретная функция y = f(x), то выражение U может быть рассмотрено как функция от  неизвестных параметров, входящих в общий ее вид. Поэтому условие минимума функции U является условием определения неизвестных параметров.

Здесь рассматривается самый простой случай аппроксимации, когда в качестве  аппроксимирующей функции рассматривается линейная функция          y = a x + b. Этот случай называется линейной аппроксимацией. Тогда функция U  имеет следующий вид

U =  å ( y i –  a x i  -b)2 Þ min,

где a и b – неизвестные параметры, а условие минимума

U ¤ a = - 2  å (y i – a x i –b) x i = 0,

U ¤ b= - 2  å ( y i – a x i –b)   = 0.

После простых преобразований можно получить систему двух уравнений с двумя неизвестными a и b

                                         a å x i 2+  b å x i=  å x i y i,                                  (3.1)

                                 a å x i   +  b n     =  å y i .

Решая эту систему, можно получить значения неизвестных параметров a и b

                   a= (s4 n  -  s1s2) ¤ (ns3 – s12),    b = (s3 s2 – s4 s1) ¤ (n s3 – s12),        ( 3.2 )

где

           s1=å x i, ,  s2= å y i  ,  s3= å x i 2  ,  s4 = å xi yi  .                                           ( 3.3 ) 

Алгоритм данного метода имеет следующий вид:

- ввод исходных данных - одномерных массивов X, Y;

- простой цикл для вычисления сумм по формулам (3.3);

- вычисление искомых коэффициентов по формулам (3.2).

Если аппроксимирующая функция имеет следующий вид y = a x 2 + b x + c, то этот случай называется квадратичной аппроксимацией. В этом случае для определения трех неизвестных параметров a , b , c будет получена из условия минимума функции U система трех алгебраических уравнений. Решение этой системы уравнений предлагается студентам выполнять самостоятельно.

3.4 Задание

3.4.1 Каждый студент должен выбрать вариант задания из таблицы 3, согласно указаниям преподавателя.

3.4.2 Повторить теоретический материал лекции и вывести формулу метода наименьшего квадрата для функций

 y = a x 2 + b x + c.

3.4.3 Определить аппроксимирующую функцию при  заданной таблице значений.

3.4.4 Используя метод наименьшего квадрата, составить программу для решения линейного и квадратичного типа уравнения.

3.4.5 Ввести исходные данные и получить результат счета на ПЭВМ.

3.4.6 Решить данный вариант двумя способами: с помощью языка программирования и с помощью табличного процессора Excel.

3.4.7 Составить необходимый отчет о ходе выполнения работы.

3.5 Методика расчета к выполнению индивидуального задания

3.5.1 Изучить данный метод и алгоритм.

3.5.2 Используя алгоритм, составить необходимую программу на языке высокого уровня.

3.5.3 Решить индивидуальное задание с помощью:

а)  табличного процессора Excel;

б) алгоритмического языка высокого уровня.

3.5.4 Сравнить полученные значения искомых параметров.

3.5.5 При отладке программы на каждом шаге выводить матрицу коэффициентов А на экран монитора для проверки правильности хода вычислений.

3.5.6 Составить программу для проверки.

3.6 Требования к отчету

Отчет по лабораторной работе должен содержать:

3.6.1 Запись или распечатку программы с результатами.

3.6.2 Вывод формул метода наименьшего квадрата для уравнения линейного и квадратичного типа по лекциям и учебникам для понимания сущности метода.  

3.6.3 Сравнительный анализ двух полученных результатов.

3.6.4 Ответы на контрольные вопросы.

3.6.4.1 Что такое аппроксимация функций ?

3.6.4.2 Какую функцию называют аппроксимирующей ?

3.6.4.3 Что такое линейная аппроксимация ?

3.6.4.4 Какой вид имеет аппроксимирующая линия при линейной аппроксимации ?

3.6.4.5 Почему рассматривают  минимум суммы квадратов отклонений статистических точек от аппроксимирующей линии ?

3.6.4.6 Какой результат будет получен после аппроксимации ?

3.6.4.7 Что такое квадратичная аппроксимация ?

3.6.4.8 Можно ли использовать в качестве аппроксимации другие виды функций ?

3.6.4.9 Почему коэффициент при b во втором уравнении системы (3.1)  равен n ?

3.6.4.10 Если используется в качестве аппроксимирующей функции полином степени k , то какую систему уравнений приходится решать для определения неизвестных коэффициентов полинома ?

 

Таблица 3 - Индивидуальные задания

№1

x

10.5

11

11.5

12

12.5

13

13.5

y

4

6

10

40

20

12

8

№2

x

12.5

13

13.5

14

14.5

15

15.5

y

5

15

40

25

8

4

1

№3

x

10

11

12

13

14

15

16

y

8

10

60

12

5

3

2

№4

x

45

50

55

60

65

70

75

y

4

6

8

10

35

20

12

№5

x

11

11.5

12

12.5

13

13.5

14

y

5

10

30

25

15

10

5

№6

x

12

13

14

15

16

17

18

y

5

15

10

25

8

4

3

№7

x

30

32

34

36

38

40

42

y

5

15

40

25

8

4

3

№8

x

10

11

12

13

14

15

16

y

4

6

10

40

30

12

8

№9

X

13

14

15

16

17

18

19

Y

5

10

30

25

15

10

5

№10

x

25

30

35

40

45

50

55

y

6

7

13

11

22

20

16

№11

x

7

8

9

10

11

12

13

y

4

6

11

14

21

18

16

№12

x

5

10

15

20

25

30

35

y

4

10

9

23

8

5

2

№13

x

6

8

10

12

14

16

18

y

7

12

15

23

11

9

4

№14

x

7

8

9

10

11

12

13

y

5

8

11

20

17

9

2

№15

x

5

7

9

11

13

15

17

y

7

10

14

24

16

8

3

 

4 Лабораторная работа №4. Методы численного интегрирования

Цель работы – изучение методов вычисления определенных интегралов на компьютере.

4.1 Теоретические сведения

4.2 Общие теоретические сведения о методах интегрирования

В инженерной практике часто возникает проблема вычисления определенного интеграла следующего вида

                                      S =,                                                        (4.1)

где f ( x ) – заданная функция;

a – нижний;

b – верхний пределы.

К понятию определённого интеграла приводят самые разнообразные задачи: определение площади фигуры, объём тела вращения, длина дуги плоской кривой, отыскание работы переменной скорости и многие другие.

Основным недостатком численных методов является то, что результат получается в виде приближенного числового значения. Точность этих методов зависит от выбранного шага h, чем меньше шаг, тем точнее результат. Очевидно, что для достижения большой точности необходимо производить большой объем вычислительной работы.

По определению определенный интеграл (4.1) численно равен площади фигуры, ограниченной прямыми x=a, х=b, осью абсцисс, графиком подынтегральной функции f( x ) .

Поэтому вычисляют площадь этой фигуры различными приближенными методами и определяют значение интеграла. Для вычисления площади данной фигуры ее делят на n частей. Для этого выбирают шаг h и делят отрезок на n равных частей длины h. Тогда фигура будет разделена на n криволинейных трапеций. Для вычисления площади каждой из этих криволинейных трапеций разными способами заменяют криволинейную сторону другой линией, а затем их вычисляют. Здесь рассматриваются популярные и очень простые методы вычисления определенного интеграла: метод прямоугольников и трапеций. Другие методы могут быть изучены студентами самостоятельно.

4.3 Метод прямоугольников

В этом случае криволинейный участок каждой криволинейной трапеции заменяется прямым отрезком, параллельным оси абсцисс. Тогда будут получены n прямоугольников; стороны каждого прямоугольника равны h и f(xi) , x i = a + ih , i = 1,2,3, . . . , n. Следовательно, площадь каждого прямоугольника определяется формулой s i  = h f ( x i ), а их сумма определяет приближенное значение площади рассматриваемой фигуры или приближенное значение интеграла

     S » h (f ( x 1 ) + f ( x 2 ) + f ( x 3 ) + . . . + f ( x n) )                             (4.2)

Эту формулу называют формулой прямоугольников для вычисления определенного интеграла (4.1). Алгоритм данного метода очень простой; требуется составить простой цикл для вычисления суммы.

Блок-схема алгоритма нахождения решения методом прямоугольников  приведена на рисунке 4.1.

4.4 Метод трапеций

В данном случае криволинейная сторона каждой криволинейной трапеции будет заменена прямым отрезком, соединяющим точки с координатами ( x i –1, f ( x i – 1)) и ( x i, f ( x i)), i =1,2,3, . . . , n. Тогда будут получены n трапеции, высота каждой из них равна h, а основания равны f( x i – 1) , f ( x i) . Площадь каждой из полученных трапеций равна s i  = h ( f ( x i ) + f ( x i – 1)) / 2 , а их сумма определяет приближенное значение рассматриваемого интеграла

S » h{[f (x 0) + f (x n)]/2+f (x1)+f (x2)+f (x3) + . . . +f(x n –1)}.                 (4.3)

Эту формулу называют формулой трапеций.

Блок-схема алгоритма нахождения решения методом трапеций приведена на рисунке 4.2.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


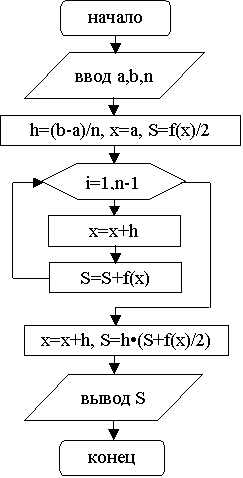
Рисунок 4.1- Блок-схема метода                     Рисунок 4.2 - Блок-схема метода

               прямоугольников                                              трапеций

 

 

 

4.5 Задание

4.5.1 Каждый студент должен выбрать вариант задания из таблицы 4, согласно указаниям преподавателя.

4.5.2 Для решения определенного интеграла методом прямоугольника и трапеции составить программу.

4.5.3 Решить данный вариант двумя способами: с помощью языка программирования и с помощью табличного процессора Excel.

4.5.4 Ввести исходные данные и получить результат счета на ПЭВМ.

4.5.5Составить необходимый отчет о ходе выполнения работы.

4.6 Методика расчета к выполнению индивидуального задания

4.6.1 Изучить данные методы, алгоритмы и блок-схемы.

4.6.2 Используя алгоритмы или блок-схемы (рисунок 4.1 и рисунок 4.2),  составить необходимые программы.

4.6.3 Решение определенного интеграла методом прямоугольника и трапеции с помощью:

а)  табличного процессора Excel;

б) алгоритмического языка высокого уровня.

4.7 Требования к отчету

Отчет по лабораторной работе должен содержать:

4.7.1 Запись или распечатку программы с результатами.

4.7.2 Сравнительный анализ двух методов по точности результатов, в зависимости от изменения шага h.

4.7.3 Ответы на контрольные вопросы.

4.7.3.1 Каковы преимущества численных методов интегрирования ?

4.7.3.2 Каковы недостатки численных методов интегрирования?

4.7.3.3 Какова точность вычисления определенного интеграла методом трапеций?

4.7.3.4 По Вашему мнению, какой из двух предложенных выше методов более точный ?

4.7.3.5 В каких случаях целесообразно применение численных методов интегрирования ?

4.7.3.6 Если верхний предел интеграла переменная величина  z, то как будет организован цикл для вычисления значений интеграла для c£z£d ?

Вычислить 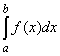  для заданного числа n разбиений отрезка [a,b] методом трапеции и прямоугольника.

Таблица 4 - Индивидуальные задания

№

Подынтегральная функция

a

b

n

I

II

III

IV

V

1

Cos(x+x3)

0

50

2

Sin(x4+2x3+x2)

0

50

3

esinx

0

1

50

4

Sinx·

0

1

50

5

ecosx

0

1

50

6

Chx2

0

1

50

7

Cosx2

0

50

8

Sin(x+x2)

0

50

9

Ln(sinx)

50

10

Cosx3

0

50

11

0

1

50

12

Sin2x·

0

1

50

13

Sin3x

0

1

50

14

Cos2x

0

1

50

15

Sin22x

0

1

50

 

5 Лабораторная работа № 5. Решение задачи Коши для обыкновенных дифференциальных уравнений

Цель работы – изучение численных методов решения обыкновенных дифференциальных уравнений, к которым приводятся инженерные задачи.

 

5.1 Теоретические сведения

5.2 Общие понятия и постановка задачи Коши для обыкновенных дифференциальных уравнений

Дифференциальное уравнение, полученное в результате исследования какого – либо реального явления или процесса, называют дифференциальной моделью этого явления или процесса. В процессе построения дифференциальных моделей важное, а подчас и первенствующее значение имеет знание законов той области науки, с которой связана природа изучаемой задачи. Так, например, в механике это могут быть законы Ньютона, в теории электрических цепей – законы Кирхгофа, в теории скоростей химических реакций – законы действия масс и т.д. Понятно, что дифференциальные модели – это частный случай того множества математических моделей, которые могут быть построены при изучении окружающего нас мира.

Уравнения, связывающие независимую переменную x, функцию y, производных этой функции y¢, y¢¢, y¢¢¢ ,  .  .  . y ( n ), называются обыкновенными дифференциальными уравнениями, и общий вид таких уравнений следующий

 

            F ( x , y, y¢, y¢¢,  y¢¢¢ ,  .  .  .  , y( n)  ) = 0.                                      (5.1)   

Порядок дифференциального уравнения определяется порядком наибольшей производной функции, входящей в уравнение. Решением данного уравнения является любая функция, которая удовлетворяет его.

 В большинстве случаях для дифференциальных уравнений рассматриваются две задачи: задача Коши (или задача с начальными условиями) и краевая задача  (или задача с граничными условиями).

Задача Коши для дифференциального уравнения (5.1) ставится так: найти такую функцию y = y ( x ), удовлетворяющую  дифференциальному уравнению (5.1) и начальным условиям при x = a , 

      y (a) = c1,  y¢(a) = c2 ,  y¢¢(a) = c3,  . . . , y( n-1) (a) = cn ,                       (5.2)

где    a ,  c1, c2 , c3 , . . . , cn  - заданные числа.

Аналитическое решение задачи (5.1) – (5.2) возможно только для самых простейших уравнений. Для уравнений, часто возникающих при решении реальных практических задач, аналитические методы бессильны. Поэтому такие задачи решаются численными методами.

В настоящее время существуют различные численные методы для решения задачи Коши (5.1) – (5.2). Ниже будут рассмотрены простые в применении методы – метод Эйлера и метод Рунге-Кутта. Другие методы без особого труда могут быть изучены студентами самостоятельно по рекомендованным источникам, так как многие численные методы решения задачи Коши основаны на той же идее, по которой разработан метод Эйлера. Ниже будут рассмотрены некоторые задачи, для решения которых будут использованы метод Эйлера и метод Рунге-Кутта.

 

5.3 Решение задачи Коши для дифференциального уравнения первого порядка методом Эйлера

Пусть рассматривается задача Коши для дифференциального уравнения первого порядка, т.е. задано уравнение

                                 y ¢ = F ( x , y )                                                         ( 5.3 )       

и начальное условие  при   x = a,

                                 y (a) = c .                                                                 ( 5.4 )

Требуется найти такую функцию  y = y ( x ) в некотором промежутке[a, b], удовлетворяющую уравнению (5.3 ) и начальному условию ( 5.4 ).

Для решения этой задачи выбирают маленький шаг h, и промежуток [a, b]  делится на n=(b–a)/h  участков, длина каждого из которых равна шагу  h;  точки деления обозначаются xi=a+ih,   где i=0,1,2, . . . , n.  Значения искомой функции  в этих точках обозначаются yi=y(xi).  Основной идеей метода Эйлера является замена производной искомой функции конечно-разностным соотношением, вытекающим из определения производной функции

                               y ¢(x i) = (y (x i+1) – y (x i)) /h .                                 ( 5.5 )

Если использовать формулу ( 5.5 ) для уравнения ( 5.3 ), то для любой точки рассматриваемого промежутка [a, b] можно записать следующую рекуррентную формулу

                               yi+1 = yi+hF(xi,yi ),                                                    ( 5.6 )

где i=0,1,2, . . . , n–1, а из начального условия (5.4)  следует

                               y 0 =  c ,  x 0 = a.                                                        (5.7)     

Итак, применение метода Эйлера привело задачу (5.3) – (5.4) к рекуррентным формулам (5.6) – (5.7). Алгоритм этих формул очень простой.

5.3.1 x = a,  y = c, i = 1  (начальные условия).

5.3.2 z = y (переход к новой итерации).

5.3.3 y = z + h F( x, z) (вычисление значения искомой функции в новой точке).

5.3.4  x = x + h,  i = i + 1 (переход к следующей точке).

5.3.5  Вывод вычисленных значений  x,y.

5.3.6  Если   i £ n , то осуществляется переход в п. 5.3.2.

Здесь введены обозначения yi + 1 = y,   y i  =z,   x i  = x  для удобства записи.

После изучения предложенного выше теоретического материала студент должен написать программу решения задачи Коши для конкретного дифференциального уравнения. Такая программа может быть использована для любого уравнения; единственным отличием в ней будет вид функции F( x, z) и значения a, c и h.

 

5.4 Решение задачи Коши для дифференциального уравнения первого порядка методом Рунге-Кутта

Существуют другие явные (т.е. значение yi+1 явно вычисляется по k предыдущим значениям yi,yi-1,…,yi-k+1) и одношаговые (k=1) методы. Наиболее распространенным из них является метод Рунге-Кутта. На его основе могут  быть построены разностные схемы разного порядка точности (таблица 5.1). Наиболее употребительной схемой метода Рунге-Кутта является схема 3.

Таблица 5.1.

№

Формула

вспомогательные переменные

порядок ошибки

1

2

3

Метод Рунге-Кутта требует большого объема вычислений, однако обладает значительной точностью, что дает возможность проводить счет с большим шагом. Кроме того, важным преимуществом этого метода (например: перед методами Адамса и типа Адамса) является возможность применения «переменного шага», т.е. он допускает расчеты на неравномерных сетках.

5.5. Приближенное решение задачи Коши для систем  дифференциальных уравнений методом Рунге-Кутта

Рассмотренные методы могут быть использованы также для решения систем дифференциальных уравнений.

Покажем это для случая систем двух уравнений вида.

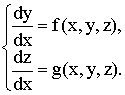                                                                                                                     (5.8)

Используя схему 3, формулы Рунге-Кутта запишем в следующем виде

 

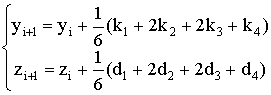                                                     (5.9)

         

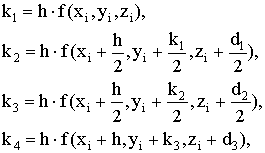
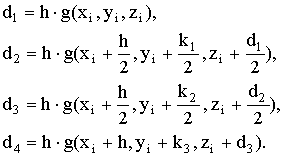
Если рассматривается задача Коши для обыкновенных дифференциаль-ных уравнений высшего порядка (5.1) - (5.2), то она приводится к системе дифференциальных уравнений обычном способом, понижением порядка уравнения.

 Пусть необходимо решить задачу Коши для дифференциального уравнения второго порядка.

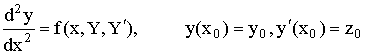.                                (5.10)

Введем вторую неизвестную функцию . Тогда сформулированная задача Коши заменяется следующей:

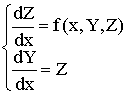                                                                                    (5.11)

Y(x0)=y0,  Z(x0)=z0.

В заключение еще раз отметим особенность одношаговых методов, состоящую в том, что для получения решения в каждом новом расчетном узле достаточно иметь значение функции лишь в предыдущем узле. Это позволяет, непосредственно вести счет, начиная с i=0 по известным начальным значениям. Кроме того, указанная особенность допускает изменение шага в любой точке в процессе счета, что позволяет строить численные алгоритмы с автоматическим выбором шага.

 

5.6 Задание

5.6.1 Каждый студент должен выбрать вариант задания из таблицы 5, согласно указаниям преподавателя.

5.6.2 Для решения дифференциального уравнения, составить программу используя метод Эйлера и метод Рунге-Кутта.

5.6.3 Решить данный вариант двумя способами: с помощью языка программирования и табличного процессора Excel.

5.6.4 Ввести исходные данные и получить результат счета на ПЭВМ.

5.6.5 Составить необходимый отчет о ходе выполнения работы.

5.7 Методика расчета к выполнению индивидуального задания

5.7.1 Изучить данные методы, алгоритмы и блок-схемы.

5.7.2 Используя алгоритмы, составить необходимые программы.

5.7.3 Решить дифференциальное уравнение методом Эйлера и методом Рунге-Кутта с помощью:

а)  табличного процессора Excel;

б) алгоритмического языка высокого уровня.

5.8 Требования к отчету

Отчет по лабораторной работе должен содержать:

5.8.1 Запись или распечатку программы с результатами.

5.8.2 Сравнительный анализ влияния на результат точности при изменения шага h.

5.8.3. Результаты проведенных исследований.

5.8.4 Ответы на контрольные вопросы.

5.8.4.1 Какие уравнения называются дифференциальными?

5.8.4.2 Что является решением дифференциального уравнения?

5.8.4.3 Что такое общее решение дифференциального уравнения?

5.8.4.4 Какое решение дифференциального уравнения называется частным?

5.8.4.5 При каких случаях возможна замена первой производной функции конечно-разностным соотношением?

5.8.4.6 Каковы погрешности метода Эйлера и метода Рунге-Кутта?

5.8.4.7 Если рассматривается система трех дифференциальных уравнений, то сколько будет неизвестных функций?

 

Решить на отрезке [a,b] с шагом h задачу Коши для следующих дифференциальных уравнений.

Таблица 5 - Индивидуальные задания

№

Уравнение

a

b

h

y0

I

II

III

IV

V

VI

1

y'-e-4x(2y)=0

0

1

0.02

0.2

2

4y'-x2(arctgx+y2)=0

1

2

0.05

1

3

5y'-xln2x+ex=0

2

3

0.02

1

4

y2-y'-arctgх=0

1

3

0.04

2

5

8xy3+yy'-ex=0

0

2

0.04

5

6

-3xey-4y'+5y=0

0

1

0.05

3

7

y2-y'+8yesinx=0

1

2

0.02

2

8

3xlny-5y'+4y=0

1

1.6

0.02

2

9

2 y'- y'ctgx+cos2x=0

0.5

1

0.01

1

10

y'-y3+sin2x=0

0

0.2

0.01

1

11

y'-e-6x(y)=0

0

1

0.02

0.5

12

6y'-x3(cosx+y2)=0

0

2

0.02

1

13

7y'-xlnx+ex=0

2

3

0.02

1

14

5xy3+2y'-e2x=0

0

2

0.04

1

15

-3xeyx-7y'+9y=0

0

1

0.05

4

 

6 Лабораторная работа № 6. Конечно-разностный метод решения краевой задачи для дифференциального уравнения второго порядка

Цель работы – изучение  метода решения краевой задачи, для дифференциальных уравнений второго порядка.

 

6.1 Теоретические сведения

6.2 Постановка краевой задачи для обыкновенного дифференциального уравнения второго порядка

В инженерной практике и при решении многих задач механики, физики, теории колебаний и других часто возникает  необходимость решения краевой задачи для обыкновенных дифференциальных уравнений следующего вида

 

                             y ¢¢+ p (x) y ¢+ g (x) y = f(x),                                       (6.1),

 

где p (x), g (x) , f(x) – заданные, непрерывные и определенные в некотором промежутке   [a,b] функции, а  x – независимая переменная, y – искомая функция. На границах промежутка[a,b] заданы краевые условия:

                              при  x= a , y ( a ) = c,                                                  (6.2)

                              при  x=b ,  y ( b) = d ,                                                 (6.3)

 где  a, b, c, d – известные постоянные величины.

Требуется найти  функцию y = y(x) в промежутке [a,b], удовлетворяющую дифференциальному уравнению (6.1) и граничным условиям (6.2) и (6.3).

 

6.3 Конечно-разностный метод решения задачи

 

Сущность конечно-разностного метода заключается в следующем, промежуток [a,b] делим на  n равных частей с шагом h и получаем точки разбиения отрезка x i = a + i h, где i = 0, 1, 2, . . . , n. При этом y i = y(x i) – значение искомой функции в точках разбиения. Затем производные искомой функции, вошедшие в исходное дифференциальное уравнение и граничные условия, заменяются конечно-разностными соотношениями.

             yi¢ =  (yi+1 – yi-1)/2h,         y¢¢i = (yi+1 –2yi + yi-1)/h.                      (6.4) 

Тогда исходное дифференциальное уравнение (6.1) будет записано в виде дискретных формул относительно дискретных значений искомой функции y i

                          A i y i - 1 - B i y i   + C i y i + 1 = D i,                                     (6.5)

где                    A i =1-

                          B i  = 2-gih2

                         C i   = 1+

                            D i   =  h2fi.

А из граничных условий (6.2) и (6.3)  -

                         y 0     = c , y n = d.                                                               (6.6)

Формулы (6.5) представляют собой систему линейных алгебраических уравнений относительно неизвестных значений искомой функции в точках разбиения, причем эта система имеет особенность, ее основная матрица является трехдиагональной. Итак, вместо дифференциального уравнения (6.1) необходимо решить систему линейных алгебраических уравнений (6.5).

 

6.4 Метод прогонки решения системы алгебраических уравнений с трехдиагональной матрицей

 

Особенность матрицы системы уравнений позволяет использовать метод прогонки, сущность которого заключается в следующем: решение системы (6.5) находят в виде следующей рекуррентной формулы

                           y i  = a i+ 1 y i+1   + b i+1,                                                ( 6.7 )

где a i ,   bi  - неизвестные пока коэффициенты, называемые коэффициентами прогонки; они будут определены в дальнейшем. Из этой формулы, очевидно, следует следующая формула

                                                 yi -1    =  a i yi   + bi                                                                             (6.8)

 Подставляя формулу (6.8) в систему уравнений (6.5), получим

                              y i = -    y i+1  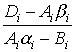 + ,                       (6.9)    

Сравнение формул ( 6.7 ) и ( 6.9) позволяет получить формулы для вычисления коэффициентов прогонки

                           a i+ 1 = - 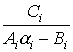  ,   b i+1  =.                     (6.10) 

Эти формулы являются рекуррентными и для вычисления значений неизвестных коэффициентов прогонки необходимо вначале определить первоначальные коэффициенты, для чего используется граничное условие на левой границе рассматриваемого промежутка [a,b]

                                          a1 = 0  ,  b1  =  c .                                                                   (6.11)

Вычисление значений коэффициентов прогонки по формулам (6.11) и (6.10) называется прямой прогонкой. После вычисления коэффициентов прогонки вычисляются значения искомой функции y i, для чего используется граничное условие на правой границе промежутка [a,b]

                                          y n = d .                                                           (6.12) 

и рекуррентная формула (6.7). Процесс вычисления значений искомой функции по формулам (6.12) и (6.7) называется обратной прогонкой.

Блок-схема алгоритма нахождения решения методом прогонки приведена на рисунке 6.1.

 

6.5 Алгоритм решения краевой задачи

 

Алгоритм решения краевой задачи для дифференциального уравнения конечно-разностным методом имеет следующий вид:

6.5.1 Ввод исходных данных a, b, c, d.

6.5.2 Цикл для вычисления значений заданных функций p(x), g(x), f(x)  для x=xi , i =0,1,2, . . . , n.

6.5.3 Цикл для вычисления коэффициентов системы уравнений (6.5) Ai ,  Bi , C i , Di.

6.5.4 Вычисление первоначальных коэффициентов прогонки по формулам (6.11).

6.5.5 Цикл для вычисления коэффициентов прогонки по формулам (6.10).

6.5.6 Определение значения искомой функции на правой границе по формуле (6.12).

6.5.7 Цикл для вычисления значений искомой функции по формуле (6.7).

6.5.8 Вывод значений аргумента x и функции y.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


                 Рисунок 6.1 Блок-схема метода прогонки

6.6 Задание

6.6.1 Каждый студент должен выбрать вариант задания из таблицы 6, согласно указаниям преподавателя.

6.6.2 Преобразовать дифференциальное уравнение в конечно-разностный вид, используя граничные условия.

6.6.3 Используя метод прогонки, составить программу для решения выбранного варианта.

6.6.4 Ввести исходные данные и получить результат счета на ПЭВМ.

6.6.5 Составить необходимый отчет о ходе выполнения работы.

6.7 Методика расчета к выполнению индивидуального задания

6.7.1 Изучите данный метод, алгоритм и блок-схему.

6.7.2 Преобразуйте дифференциальное уравнение второго порядка с помощью соответствующей  конечно-разностной схемы к трехдиагональному виду.

6.7.3 Используя алгоритм  составьте программу на языке высокого уровня.

6.8 Требования к отчету

Отчет по лабораторной работе должен содержать:

6.8.1 Запись или распечатку программы с результатами.

6.8.2 Вывод формул метода прогонки по лекциям и учебникам для понимания сущности метода.

6.8.3 Ответы на контрольные вопросы.

6.8.3.1 Какая задача называется краевой?

6.8.3.2 Определите физическую сущность каждого члена уравнения (6.1), если оно описывает колебательное движение какого-либо объекта.

6.8.3.3 От какого параметра зависит точность метода ?

6.8.3.4 Почему производные искомой функции заменены формулами (6.4)?

6.8.3.5 Какая система алгебраических уравнений является системой с трехдиагональной матрицей ?

6.8.3.6 Почему процесс вычисления коэффициентов прогонки называется прямой прогонкой ?

6.8.3.7 Почему процесс вычисления значений искомой функции называется обратной прогонкой ?

 

Найти решения следующих дифференциальных уравнений при заданных граничных условиях:

Таблица 6 - Индивидуальные задания

№

Уравнение

Граничные условия

h

1

y ¢¢ + x y ¢  - e - x y  =  sin (px)

y (0) = 0,  y (1) = 0

0.01

2

y ¢¢ +  x 2 y ¢  + x y  =  cos (px)

y (1) = 1,  y (2) = 1

0.01

3

y ¢¢ +  x -2 y ¢ + x 3 y = e x

y (1) =1,  y (2) = 0

0.01

4

y ¢¢ + sin(x)y¢+cos(x)y=ex sin(x)

y(0) = 1,  y(1) = 0

0.01

5

y ¢¢ + x -2 y ¢ +x 3 y = e x

y (1) = 0,  y (2) = 0

0.01

6

y ¢¢ - x 2 y ¢ + x y = sin (x)

y (0) =1,  y (1) = 0

0.01

7

y ¢¢ + arctg(x) y¢ + xy = cos (x)

y (0) =1,  y (1) = 0

0.01

8

y ¢¢ +(1–x)y¢ + y = x cos(x)

y (0) =0,  y (1) =1

0.01

9

y ¢¢ +(1-x )y¢ +y =  e -x

y (0) = 0,  y (1) =1

0.01

10

y ¢¢ + x 2y ¢ + 2y  = 2x - 1

y (0) = 0,  y (1) = 1

0.01

11

y ¢¢ + 2xy ¢ - e - x y  =  sin (px)

y (0) = 0,  y (1) =0

0.01

12

y ¢¢ + x y ¢  + x y  =  sin (px)

y (0) = 0,  y (1) = 0

0.01

13

y ¢¢ - x 2 y ¢ + 2xy = sin (x/2)

y (0) = 1,  y (1) = 0

0.01

14

y ¢¢ +(2–x)y¢ + 2y = cos(x)

y (0) = 0,  y (1) =1

0.01

15

y ¢¢ +2x 2y ¢ + y2  = 2x - 3

y (0) = 0,  y (1) = 1

0.01

 

7 Лабораторная работа № 7. Метод сеток для решения уравнения теплопроводности

 

Цель работы – изучение одного из популярных методов – метод сеток для решения уравнений математической физики на примере задачи о теплопроводности.

 

7.1 Теоретические сведения

7.2 Постановка задачи о распространении тепла в стержне

 

Рассматривается однородный стержень длины l, теплоизолированный с боков и достаточно тонкий, чтобы в любой момент времени  температуру во всех точках поперечного сечения можно было считать одинаковой. Если на концах стержня поддерживается определенная температура, то происходит «перетекание» тепла от более нагретого к менее нагретому участку стержня. Требуется рассматривать процесс распространения тепла в стержне и определить температуру в любом сечении стержня в любой момент времени.

Для решения этой задачи необходимо вначале создать ее математическую модель, т.е. найти совокупность математических зависимостей, определяющих связь между основными параметрами задачи. Поэтому  вводятся следующие обозначения:

t  - время, x  - координата сечения стержня;

u = u ( x.t ) – температура сечения  x в момент времени t;

        k  - коэффициент теплопроводности, зависящий от материала стержня;

 c -  удельная теплоемкость;      

 s -  площадь сечения;

 r -  плотность материала стержня.

По закону Фурье количество тепла, перетекающее через сечения   x за промежуток времени [t, t +Dt], равно

                          Q 1 = - k s Dt u ( x, t ) ¤ x ,                                           (7.1)                      

 а через сечения  x+Dx   -

                          Q 2 =  - k s Dt u ( x + Dx, t ) ¤ x .                                 (7.2)

Разность Q 1 – Q 2   определяет количество тепла, которое повышает температуру элементарного участка стержня [x, x+Dx] на Du

                          Q1 – Q2  = c r s Dx Du                                                    (7.3)

После простых преобразований из формул (7.1), (7.2) и (7.3) можно получить следующую формулу

k s Dt [u ( x + Dx, t ) ¤  x - u ( x, t ) ¤ x] = c r s Dx Du.

Если обе части этого равенства разделить на c r s Dx Dt и при D x ® 0,  Dt®0 можно получить следующее уравнение

                                    u ¤ t =    a 2  2u  ¤  x 2 ,                                                                (7.4) 

где  a 2 = k/c r - коэффициент температуропроводности. Уравнение (7.4) называется уравнением теплопроводности; оно относится к уравнениям параболического типа. Для решения этого уравнения должны быть заданы условия: начальное и граничные. Начальное условие характеризует начальный температурный режим стержня, т.е. при

                                        t = 0 , u (x,0 ) = f ( x ),                                           (7.5)

 где f( x )  - заданная функция, определяющая температуру в сечении x стержня.

На концах стержня должны быть заданы изменения температуры

                              при x=0 ,  u (0,t) = p (t ) ,                                        (7.6)     

                              при x= l,     u (l,t) = q (t),                                         (7.7)

где p ( t ) , q ( t ) – заданные функции.

Итак, получены формулы (7.4 ) – (7.7), которые описывают рассматриваемый процесс распространения тепла в стержне. Совокупность этих формул является математической моделью задачи о распространении тепла в стержне. На основании этой модели можно сформулировать математическую постановку задачи: найти такую функцию u = u ( x, t ) в прямоугольнике [ 0 £ x £ l ,   0 £ t £ T], удовлетворяющую уравнению (7.4), начальному условию (7.5), граничным условиям (7.6) и (7.7).  Здесь T – промежуток времени, для которого рассматривается данный процесс.

 

7.3 Метод сеток для решения уравнения теплопроводности

Самым эффективным для решения задач уравнений математической физики является метод сеток. Выбираются шаги:

h –шаг по координате x;

t- шаг по времени t.

После этого область интегрирования делится на маленькие прямоугольники с помощью взаимноперпендикулярных семейств  параллельных прямых           x=xi =ih,  i=0,1,2, . . . , n=l / h; t=tj , j= 0,1,2, . . . , m=T/t,  т.е. на область интегрирования наносится сетка. Точки пересечения    ( x  i , t j ) прямых называются узловыми. Значения искомой функции в узловых точках обозначаются u i j   =  u ( x i  , t j ) . Производные искомой функции заменяются конечно-разностными соотношениями, в частности, вторая производная по координате x

                              2u  ¤ x2    = ( ui +1j –2uij+ ui -1j) / h2                                                 (7.8)

а первая производная по времени может быть заменена различными способами. Самыми распространенными являются два способа:

                              u ¤ t =(u i j  - u i j - 1 ) ¤ t,                                                    (7.9)

                              u ¤t =(u i j + 1 - u i j ) ¤t.                                                      (7.10)

Использование формулы (7.9) приводит к неявной расчетной схеме, а формулы (7.10) – к явной расчетной схеме. Эти расчетные схемы имеют принципиальное отличие друг от друга. Преимуществом явной схемы является ее простота, а недостатком является то, что для устойчивости таких схем требуется выполнение некоторых дополнительных условий. Неявная схема всегда устойчива, однако она сложнее, чем явная схема. На практике преимущественно используют неявную схему для решения уравнения теплопроводности.

 

7.3.1 Явная расчетная схема и ее алгоритм

Используя формулы (7.8) и (7.10), из формулы (7.4) можно получить следующую

                     u i j+1 = u i j + t (ui j + 1 -2ui j + ui-1 j)/ h 2,                               (7.11)   

где i=1, 2, 3, . . . , n–1, j= 0,1,2, . . . , m -1 ; эта формула справедлива только для внутренних узловых точек области интегрирования. К ним необходимо присоединить начальное и граничные условия. Они будут записаны в следующем виде

                           ui 0 = f i , i = 0,1,2, . . . , n,                                           (7.12)

                           u0 j = p j , j = 1,2,3, . . . , m,                                                                  (7.13)

                           un j  = G j , j =1,2,3, . . . , m.                                         (7.14)

Явная разностная схема называется условно устойчивой при ограничениях на τ и h и удовлетворяет следующему условию:

Формулы (7.11) – (7.14) будут определять алгоритм явной расчетной схемы:

7.3.1.1 Цикл для вычисления значений искомой функции в начальный момент времени определяется по формуле (7.12).

7.3.1.2  Начало внешнего цикла по времени или по счетчику цикла j.

7.3.1.3  Вычисление значений искомой функции на границах по формулам (7.13) и (7.14).

7.3.1.4  Внутренний цикл по счетчику цикла i для вычисления значений искомой функции для внутренних точек по формуле (7.11).

7.3.1.5  Вывод значений искомой функции.

7.3.1.6  Конец внешнего цикла по j.

Блок-схема решения уравнения теплопроводности (явная схема) приведена на рисунке 7.1.

7.3.2 Неявная расчетная схема и ее алгоритм

Используя формулы (7.9) и (7.8), из (7.4) можно получить следующую формулу

         lui – 1 j  - (1-l) ui j  +lui + 1 j  = -u i  j-1 - tf i j,                                      (7.15)

         i=1,2,3, . . . , n-1,   j=1,2,3, . . . , m,    где l = t/h2.

Абсолютно устойчива при любом соотношении шага τ и h.

К ним должны быть присоединены формулы (7.12) – (7.14). Таким образом, формулы  (7.12) – (7.15) будут определять неявную расчетную схему. Здесь для каждого шага по времени необходимо решить систему алгебраических уравнений с трехдиагональной матрицей. Такая система ранее (в предыдущей лабораторной работе №6) рассматривалась при решении краевой задачи для обыкновенных дифференциальных уравнений, для решения которой был использован метод прогонки.

Студенту рекомендуется самостоятельно составить алгоритм для данной расчетной схемы и разработать программу решения задачи.

Блок-схема решения уравнения теплопроводности (неявная схема) приведена на рисунке 7.2.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


                                                                                                                                     

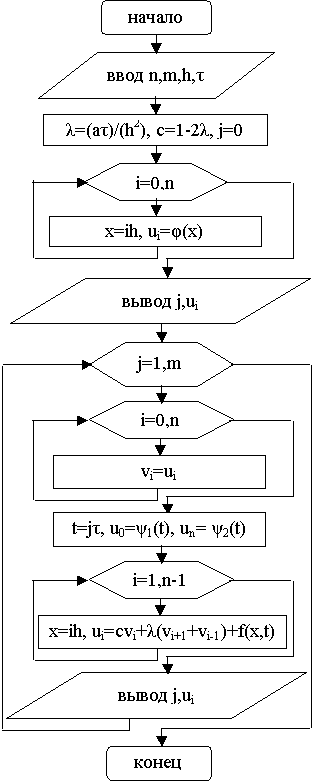
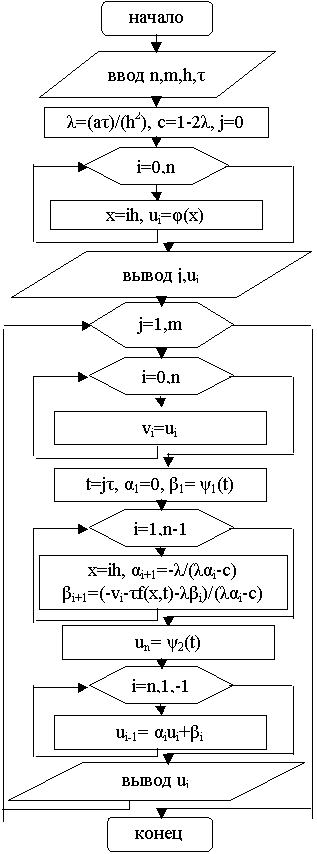
Рисунок 7.1-Блок-схема решения урав- Рисунок 7.2-Блок-схема решения уравнения теплопроводности(явная схема)  нения теплопроводности(неявная схема)

7.4 Задание

7.4.1 Каждый студент должен выбрать вариант задания из таблицы 7, согласно указаниям преподавателя.

7.4.2 Преобразовать дифференциальное уравнение в конечно-разностный вид, используя граничные условия.

7.4.3 Используя метод сеток, составить программу для явной и неявной разностной схемы.

7.4.4 Ввести исходные данные и получить результат счета на ПЭВМ.

7.4.5 Составить необходимый отчет о ходе выполнения работы.

 

7.5 Методика расчета к выполнению индивидуального задания

7.5.1 Изучите данный метод, алгоритм и блок-схему.

7.5.2 Преобразуйте дифференциальное уравнение второго порядка с помощью соответствующей  конечно-разностной схемы.

7.5.3 Решить уравнение теплопроводности двумя схемами: явной и неявной с использованием алгоритмического языка высокого уровня.

7.5.4 Используя алгоритмы или блок-схемы (рисунок 7.1 и рисунок 7.2),  составить необходимые программы.

7.6 Требования к отчету

Отчет по лабораторной работе должен содержать:

7.6.1 Запись или распечатку программы с результатами.

7.6.2 Вывод формул метода сеток по лекциям и учебникам для понимания сущности метода.

7.6.3 Сравнительный анализ двух схем на устойчивость в зависимости от t и h, точность результата и количество итерации.

7.6.3 Ответы на контрольные вопросы.

7.6.3.1  Какие уравнения называются уравнениями математической физики?

7.6.3.2 Назовите типы уравнений математической физики.

7.6.3.3 Какому типу относится уравнение теплопроводности?

7.6.3.4 Какие задачи могут быть приведены к уравнениям эллиптического типа ?

7.6.3.5 Какие уравнения относятся к уравнениям гиперболического типа?

7.6.3.6 В чем отличие конечно-разностного метода от метода сеток?

7.6.3.7 От какого параметра зависит точность метода сеток?

7.6.3.8 При выполнении какого условия явная расчетная схема устойчива?

7.6.3.9 Почему система (7.15) является системой с трехдиагональной матрицей ?

7.6.3.10 Почему формула (7.11) является явной ?

7.6.3.11 Почему формулу (7.15) называют неявной ?

7.6.3.12 Назовите другие методы решения задач математической физики.

 

Решить смешанную задачу для уравнения теплопроводности

                +f(x,t),                  где а =1,  f(x,t)= 0

с начальным условием            U(x,0) = j(x)

и граничными условиями      U(0,t) = y1(t),   U(L,t) = y2(t)

Таблица 7 - Индивидуальные задания

№

j(x)

y1

y2

I

II

III

IV

1

x(x + 1)

0

2t + 1

2

(x + 1)2

2t

0

3

x2 - 2x + 0,5

2t

2

4

t + 1

0

5

x sinpx

2t

0

6

1 + 2x(1 - x)

-6t + 1

1,5

7

Cos(x + 0,8)

6t + 0,9

0,5

8

x(x-1) + 0,5

0,2

2(t – 0,2)

9

Lg(1,5 + 2x)

0,2

3(t + 0,2)

10

Cos(2x + 0,2)

1

0,2t

11

2x(x+2)

0

2t

12

(x+1)3

2t

1

13

Sin(x+0,6)

5t+0,7

0,3

14

2+x(1-x)

-5t

2

15

x2+2x

2

3t

 

Список литературы

1.   Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.:  Изд-во «Наука», 1972 .

2.   Турчак Л.И. Основы численных методов: Учеб. пособие. – М.: Наука. Гл. ред. физ.-мат. лит., 1987. – 320 с.

3.   Сливина Н.С. Лабораторный практикум по высшей математике: Учеб. пособие для втузов. –М.: Высш. шк. 1983. – 203 с.

4.   Cамарский А.А., Гулин А.В. Математические модели в инженерных расчётах на ЭВМ, - М.: Наука, 1989. - 432 с.

5.   Cамарский А.А. Теория разностных схем. – М.: Наука, 1977.

6.   Марчук Г.И. Методы вычислительной математики. – М.: Наука, 1980.

7.  Вержбицкий В.М. Основы численных методов: Учебник для вузов – М.: Высш. шк., 2002.- 840 с.

8.  Вержбицкий В.М. Численные методы. Математический анализ и обыкновенные дифференциальные уравнения, - М.: Высшая школа, 2001.-382 с.

9.  Бахвалов Н.С.,Жидков Н.П., Кобельков Г.М. Численные методы.- М.: Лаборатория базовых знаний, 2002. – 632 с.

 

 

Св.план 2003 г., поз.20

 

 

 

 

 

 

 

 

Зияханов Мухтар Умирзакович
Аманбаев Абдирахман Абдиханович

 

 

МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ИНЖЕНЕРНЫХ РАСЧЁТАХ НА ЭВМ

 

Методические указания к выполнению лабораторных работ

(для студентов очной формы обучения специальности 360140-Автоматизация и информатизация в системах управления)

 

 

 

 

 

 

Редактор Сыздыкова Ж.М.

 

 

Подписано к печати _______                                           Формат  60х84   1/16

Тираж       50      экз.                                                           Типографская бумага №1

Объем               уч.-изд.л                                                    Заказ ______ цена _____                                                                

 

 

 

 

 

 

 

 

 

 

Копировально - множительное бюро

Алматинского института энергетики и связи

050013, Алматы, Байтурсынова, 126.