АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра инженерной кибернетики
Основы сбора и передачи информации
Методические указания к выполнению расчетно-графических работ
для специальности 050702 – Автоматизация и управление
Алматы 2007
СОСТАВИТЕЛИ: Ю.В. Шевяков, Ш.М. Байматаева. Основы сбора и передачи информации. Методические указания к выполнению расчетно-графических работ для студентов очной формы обучения специальности 0500702 – Автоматизация и управления. – Алматы: АИЭС, 2007. – 11с.
Рассмотрены методы исправления одиночных ошибок и нахождения двойных ошибок при построении циклических кодов, построение кодирующих устройств для заданного циклического кода. Построение кодирующих устройств для заданного циклического кода осуществляется в среде программной системы System View.
Методические указания предназначены для студентов специальности 0500702 – Автоматизация и управления.
1 Расчетно-графическая работа №1. Построение циклических кодов
Согласно определению циклического кода все многочлены, соответствующие его разрешённым кодовым комбинациям, должны делиться на образующий многочлен g(x) без остатка. Для этого достаточно, чтобы на g(x) делились без остатка многочлены, составляющие образующую матрицу кода. Последние получаются циклическим сдвигом, что соответствует последовательному умножению g(x) на x с приведением по модулю xn+1.
Следовательно, в общем случае многочлен gi(x) является остатком от деления произведения g(x)*xi на многочлен xn+1 и может быть записан так
![]()
где с=1, если степень g(x)xi превышает n-1, С=0, в противном случае.
Отсюда следует, что все многочлены кода будут делиться на g(x) без остатка в том случае, если на g(x) будет делиться без остатка многочлен xn+1.
Таким образом, чтобы g(x) мог породить циклический код, он должен быть делителем многочлена xn+1.
Групповой код способен исправить столько разновидностей ошибок, сколько различных классов насчитывается в приведенном приложении. Следовательно, корректирующая способность циклического кода будет тем выше, чем больше остатков может быть образовано при делении многочлена, соответствующего искаженной кодовой комбинации, на образующий многочлен кода.
Наибольшее число остатков, равное 2m-1, может обеспечить только неприводимый многочлен, который делится сам на себя и не делиться ни на какой другой многочлен.
Исправление одиночных или обнаружение двойных ошибок. Прежде чем исправить одиночную ошибку в принятой комбинации из n разрядов, необходимо определить какой из разрядов был искажен. Это можно сделать только в том случае, если каждой одиночной ошибке в определенной разряде соответствуют свой класс вычетов или опознаватель. Так как в циклическом коде опознавателями ошибок являются остатки от деления многочленов на образующий многочлен кода g(x), то g(x) должно обеспечить требуемое число различных остатков при делении векторов ошибок с единицей в искаженном разряде. Как отмечалось, наибольшее число остатков дает неприводимый многочлен. При степени многочлена m=n-k он может дать 2n-k-1 ненулевых остатков (нулевой остаток является опознавателем безошибочной передачи).
Следовательно, необходимым условием исправления любой одиночной ошибки является выполнение неравенства
![]()
где Сn – общее число разновидностей одиночных ошибок в кодовой комбинации из n символов; отсюда находим степень образующего многочлена кода
![]()
и общее число символов в кодовой комбинации. Наибольшие значения k и n для различных m можно найти пользуясь таблицей:
Т а б л и ц а 1.1
|
m |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
n |
1 |
3 |
7 |
15 |
31 |
63 |
127 |
255 |
511 |
1023 |
|
k |
0 |
1 |
4 |
11 |
26 |
57 |
120 |
27 |
502 |
1013 |
Доказано, что любой двучлен типа x2m-1+1=xn+1 может быть представлен произведением всех неприводимых многочленов, степени которых являются делителями числа m (от 1 до m включительно). Следовательно, для любого m существует по крайней мере один неприводимый многочлен степени m, входящий сомножителем в разложение двучлена xn+1.
Пример - Выберем образующий многочлен для случая n=15 и m=4.
Двучлен x15+1 можно записать в виде произведения всех неприводимых многочленов, степени которых являются делителями числа 4. Последнее делится на 1 ,2,4.
В таблице неприводимых многочленов находим один многочлен первой степени, а именно x+1, один многочлен второй степени x2+x+1 и три многочлен четвертой степени: х4+х+1, х4+х3+1, х4+х3+х2+х+1. перемножив все многочлены, убедимся в справедливости соотношения (х+1) x2+x+1)(х4+х+1)(х4+х3+1)(х4+х3+х2+х+1)=х15+1.
Один из сомножителей четвертой степени может быть принят за образующий многочлен кода. Возьмем, например, многочлен х4+х3+1, или в виде двоичной последовательности 11001.
Чтобы убедиться, что каждому вектору ошибки соответствует отличный от других остаток, необходимо поделить каждый из этих векторов на 11001.
Векторы ошибок m младших разрядов имеют вид:
00…0001, 00…0010, 00…0100, 00…1000.
Степени соответствующих им многочленов меньше степени образующего многочлена g(x). Поэтому они сами являются остатками при нулевой целой части. Остаток, соответствующий вектору ошибки в следующем старшем разряде, получаем при делении 00…10000 на 11001,т.е.:
10000
11001
1001
Аналогично могут быть найдены и остальные остатки. Однако их можно получить проще, деля на g(x) комбинацию в виде единицы рядом с нулями и выписывая все промежуточные остатки:
 10000000000… 11001 Остатки
10000000000… 11001 Остатки
11001 1001
10010 1011
11001 1111
10110 0111
11001 1110
11110 0101
11001 1010
011100 1101
11001 0011
010100 0110
11001 1100
11010 0001
11001 0010
0011000 0100
11001 1000
0001000
При последующем делении остатки повторяются.
Таким образом, мы убедились в том, что число различных остатков при выбранном g(x) равно n=15, и следовательно, код, образованный таким g(x), способен исправить любую одиночную ошибку. С тем же успехом за образующий многочлен кода мог бы принят и многочлен х4+х+1. При этом был бы получен код, эквивалентный выбранному.
Однако, использовать для тех же целей многочлен (х4+х3+х2+х+1) нельзя. При проверке числа различных остатков обнаруживается, что их у него не 15, а только 5. Действительно,
 |
10000000000… 11111 Остатки
11111 1111
11110 0001
11111 0010
00010000 0100
1000
Это объясняется тем, что многочлен х4+х3+х2+х+1 входит в разложение не только двучлена х15+1, но и двучлена х5+1.
Задание 1. Проверить обеспечивает ли заданный многочлен требуемое число остатков. Варианты заданий выбираются по порядковому номеру студента в списке группы.
Т а б л и ц а 1.2
|
№ варианта |
Двучлен |
Образующий многочлен |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
Х3+1 x7+1 x7+1 x15+1 x15+1 x15+1 x31+1 x31+1 x31+1 x31+1 x31+1 x31+1 x63+1 x63+1 x63+1 x63+1 x63+1 x63+1 x63+1 x63+1 x63+1 х127+1 х127+1 х127+1 х127+1 |
х2+х+1 x3+x+1 x3+x2+1 x4+x+1 x4+x3+1 x4+x3+x2+x+1 x5+x2+1 x5+x3+1 x5+x3+x2+x+1 x5+x4+x2+x+1 x5+x4+x3+x+1 x5+x4+x3+x2+1 x6+x+1 x6+x3+1 x6+x4+x2+x+1 x6+x4+x3+x+1 x6+x5+1 x6+x5+x2|+x+1 x6+x5+x3+x2+1 x6+x5+x4+x+1 x6+x5+x4+x2+1 x7+x+1 x7+x3+1 x7+x3+х2+х+1 x7+x4+1 |
Задание 2
Для заданного образующего многочлена построить циклический код с обнаружением одиночной ошибки. Вариант образующего многочлена такой же как и в первом задании.
2 Расчётно-графическая работа №2. Построение кодирующих устройств для заданного циклического кода
Все известные кодирующие устройства для любых типов циклических кодов, выполненные на регистрах сдвига, можно свести к двум типам схем. Схемы первого типа вычисляют значения проверочных символов путем непосредственного деления многочлена а(х)хm на образующий многочлен g(x). Это делается с помощью регистра сдвига, содержащего n-k разрядов (рисунок 2.1). В данной схеме коэффициенты кодируемого многочлена участвуют в обратной связи не через n-k сдвигов, а сразу с первого такта. Это позволяет устранить разрыв между информационными и проверочными символами. В исходном состоянии ключ K1 находится в положении 1.
Информационные символы одновременно поступают как в линию связи, так и в регистр сдвига, где за k тактов образуется остаток. Затем ключ К1 переходит в положение 2 и остаток поступает в линию связи.
|

Рассмотрим процесс деления многочлена а(х)хm= (x+1)x на многочлен
g(x) = x3+x2+ 1 за k тактов.
|

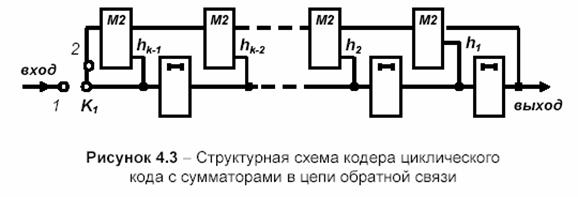
Схема кодирующего устройства для заданного g(x) приведена на рисунке 2.2. Процесс формирования кодовой комбинации шаг за шагом представлен в таблице 2.1, где черточками отмечены освобождающиеся ячейки, занимаемые новыми информационными символами. С помощью схем второго типа вычисляют значения проверочных символов как линейную комбинацию информационных символов, т. е. они построены на использовании основного свойства систематических кодов. Кодирующее устройство строится на основе k-разрядного регистра сдвига (рисунок 2.3). Выходы ячеек памяти подключаются к сумматору в цепи обратной связи в соответствии с видом генераторного многочлена
![]()
В исходном положении ключ K1 находится в положении 1. За первые k тактов поступающие на вход информационные символы заполняют все ячейки регистра. После этого ключ переводят в положение 2. На каждом из последующих тактов один из информационных символов выдается в канал связи и одновременно формируется проверочный символ, который записывается в последнюю ячейку регистра. Через n-k тактов процесс формирования проверочных символов заканчивается, и ключ K1 снова переводится в положение 1.
|
|
В течение последующих k тактов
содержимое регистра выдается в канал связи с одновременным заполнением ячеек
новой последовательности информационных символов. Рассмотрим процесс
формирования кодовой комбинации с использованием генераторного многочлена для
случая![]()
![]() Определяем генераторный многочлен
Определяем генераторный многочлен
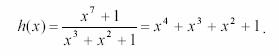
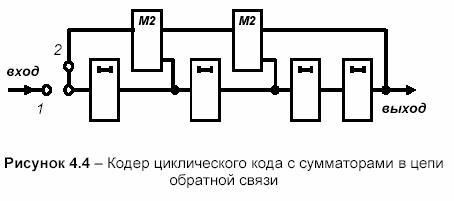
Соответствующая h(x) схема кодирующего устройства приведена на рисунке 2.4.
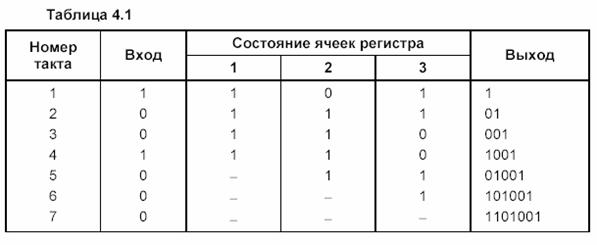
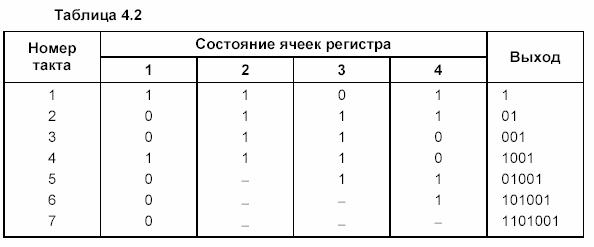
Формирование кодовой комбинации поясняется в таблице 2.2. Оно начинается после заполнения регистра информационными символами.
|
|
Задание:
а) вариант образующего многочлена остаётся таким же как и в РГР№1;
б) в среде программной системы System Veiw построить кодирующее устройство на основе формирования кодовой комбинации с использованием генераторного многочлена;
в) использовать схему crc_encoder.svu для модификации при построении кодирующего устройства;
г) сравнить код (РГР№1) с полученным на модели.
Литература
1. Гоноровский И.С. Радиотехнические цепи и сигналы. – М.: Радио и связь, 1994.
2. Дмитриев В.И. Прикладная теория информации. – М.: Высшая школа, 1989.
3. Назаров М.В. и др. Теория передачи сигналов. – М.: Связь, 1980.
4. Зюко А.Г. Теория передачи сигналов. – М.: Радио и связь, 1986.
5. Баскаков С.И. Радиотехнические цепи и сигналы. – М.: Высшая школа, 2000.
6. Разевиг В.Д., Лаврентьев Г.В., Златин И.Л. SystemView средство системного проектирования радиоэлектронных устройств - М.: Горячая линия-Телеком, 2002.
7. Гаранин М.В., Журавлев В.И., Кунегин С.В. Системы и сети передачи информации. - М.: Радио и связь, 2000.
8. Телекоммуникационные системы и сети: Учебное пособие.-Под. ред. В.П. Шувалова.-М.: Горячая линия -Телеком, 2003.
9. Передача дискретных сообщений: Учебник/Под ред. В.П. Шувалова. - М.: Радио и связь, 1990.