Некоммерческое акционерное общество

АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра инженерной кибернетики 

 

ОСНОВЫ СБОРА И ПЕРЕДАЧИ ИНФОРМАЦИИ

Конспект лекций

Для студентов всех форм обучения специальности 050702 –

Автоматизация и управление 

 

Алматы 2008

        

СОСТАВИТЕЛЬ: Ю.В. Шевяков. Основы сбора и передачи информации. Конспект лекций для студентов всех  форм обучения специальности 050702-Автоматизация управления.- Алматы: АИЭС, 2008.-61  с. 

 

В конспекте лекций изложены основы организации, принципы построения, методы и алгоритмы систем сбора и передачи информации. Указанные объекты рассмотрения входят в состав как подсистемы АСУТП, так и могут носить автономный характер и выполнять основное функциональное назначение в SCADA – системах. Конспект лекций предназначен для студентов, обучающихся по специальности 050702 – Автоматизация управления.

  

Содержание 

Введение                                                                                                                     5

1 Лекция 1 Организация систем сбора и обработки цифровой информации

ТОУ                                                                                                                            5

1.1 Назначение и общие принципы организации АСУТП                                     5   

1.2 Критерии управления                                                                                          6

1.3 Виды подсистем.                                                                                                  6

1.3.1 Сбор и первичная обработка информации                                                      6

1.3.2  Контроль состояния объекта                                                                          6

 1.3.3 Автоматическое регулирование и оптимальное управление                       6

1.3.4  Расчет технико-экономических показателей                                                      6

1.3.5 Связь с MES – системой (АСУ предприятия)                                            6

1.4 Состав АСУ ТП                                                                                                   6

1.5 Структурная организация АСУ ТП.                                                                  7

1.5.1 Централизованные АСУ ТП.                                                                           7

1.5.2 Распределенные АСУ ТП                                                                                8

2 Лекция 2 SCADA-системы. Функциональная организация сбора

информации в системах реального времени                                                          9

2.1. Функциональная организация сбора информации в SCADA –

системах                                                                                                                    10  

2.2 Системы реального времени                                                                            10

2.2.1 Режим реального времени [real time processing]                                         11                 

3 Лекция 3  SCADA-системы.  Алгоритмы первичной обработки информа-

ции                                                                                                                             13

3.1 Алгоритмы сбора и первичной обработка информации                                13

3.2 Первичная обработка информации                                                                  14

3.2.1 Контроль достоверности информации                                                         15

3.2.2 Интерполяция и экстраполяция                                                                    15

3.2.3 Фильтрация сигналов измерительной информации                                    16

4 Лекция 4  SCADA-системы. Пути интеграции  АСУП (MES –системы) и     

 АСУТП (SCADA и DCS)                                                                                       17

4.1 Уровни информационного взаимодействия систем управления                  17

4.2 Реляционные БД и БД реального времени                                                      18                                                

5 Лекция 5  Основы теории кодирования и коды. Помехоустойчивое

кодирование                                                                                                             21

5.1 Помехоустойчивое кодирование                                                                     21

5.1.1 Классификация помехоустойчивых кодов                                               21

5.1.2 Блоковый код. Общие принципы использования избыточности           22

6 Лекция 6  Помехоустойчивое кодирование. Блоковый код                               24

6.1 Связь корректирующей способности кода с кодовым расстоянием            25   

6.2 Показатели качества корректирующего кода                                                 27

7 Лекция 7  Линейные коды. Математическое введение к линейным кодам    29

7.1 Линейные коды                                                                                                  29

7.2 Математическое введение к линейным кодам                                              30

8 Лекция 8  Коды с исправлением искажений. Групповые коды                      34

8.1 Линейный код как подпространство линейного век­торного                         

пространства                                                                                                           34

8.2 Построение двоичного группового кода                                                        35

9 Лекция 9  Групповые коды. Определение проверочных равенств                 38

9.1 Случай исправления одиночных и двойных независимых ошибок            38

9.2 Определение проверочных равенств                                                              40

10 Лекция 10  Матричное представление линейных кодов                                43

10.1 Матричное представление линейных кодов                                                 43

10.2 Образующая матрица линейного кода                                                          44

11 Лекция 11 Циклические коды. Математические основы для построения

 циклических кодов                                                                                                 47

11.1 Построение циклических кодов                                                                     48

11.2 Математическое введение к циклическим кодам                                         50

12 Лекция 12 Циклические коды. Определение образующего многочлена      51

12.1 Требования, предъявляемые к образующему многочлену                          51

12.2 Выбор образующего многочлена по заданному объёму кода и заданной корректирующей способности                                                                               52

12.2.1 Обнаружение одиночных ошибок                                                              53

12.2.2 Исправление одиночных или обнаружение двойных ошибок                 53

13 Лекция 13 Циклические коды. Математические основы для построения

 циклических кодов                                                                                                55

13.1 Выбор неприводимого много­члена g(x)                                                       55

13.2 Обнаружение и исправление независимых ошибок произвольной

         кратности                                                                                                         56

13.2.1 Обнаружение и исправление пачек ошибок                                              57

13.3 Методы образования циклического кода                                                      57

13.4 Матричная запись циклического кода                                                          58

13.5 Укороченные циклические коды                                                                   59

Список литературы                                                                                                 61

               

Введение 

SCADA-системы ответственны лишь за уровень промышленной автоматизации, связанный с получением данных от различных датчиков и устройств  ввода/вывода, с визуализацией собранной информации и её архивацией. Доступ же к этой информации со стороны руководителя предприятия, а также руководителей экономических подразделений до недавнего времени был лишь опосредованным. Для анализа производства в целом, для моделирования его отдельных этапов, для выявления критических участков и слабых звеньев важна организация доступа к данным, отражающим весь процесс производства, с возможностью воздействия на него, в том числе и в реальном времени.

Для реализации подобных задач автоматизации промышленных предприятий в целом попытки создания интегрированных систем автоматизации, реализующих функции SCADA-систем, ERP-систем и, в целом,  MES-систем, основным направлением определяется создание единого информационного пространства базирующегося на технологической информации в цифровой форме  собранной и обработанной в реальном времени.

В распределённых микропроцессорных системах управления алгоритмы первичной обработки информации реализуются в виде стандартных модулей базового программного обеспечения микропроцессорных контроллеров.

Наряду с традиционной формой рассмотрения методов и алгоритмов построения коммутируемых линий связи подсистем сбора, первичной обработки и передачи информации, рассматриваются способы передачи информации во времени с использованием баз данных реального времени.

 

1 Лекция 1  Организация систем сбора и обработки цифровой информации ТОУ

Цель лекции: определение основных функций информационных подсистем в системах управления разного уровня.

 

Содержание лекции: классификация систем управления технологическими объектами управления. Подсистемы АСУТП. Основные функции SCADA – систем.

 

1.1  Назначение и общие принципы организации АСУТП

 

         АСУТП - человеко-машинная система, в которой человек принимает содержательное участие в выработке решения.

         АСУТП осуществляет воздействие на объект в том же, что и протекающие в нем процессы, т.е. АСУТП работает в режиме реального времени. В АСУТП в качестве объекта выступает ТОУ (технологический объект управления).

            ТОУ представляет собой совокупность технологического оборудования и реализуемого на нем по соответствующим инструкциям и регламентам технологического процесса производства целевого продукта.В качестве ТОУ в АСУТП рассматриваются технологические установки, отдельные производства и технологические процессы всего предприятия.

            При создании АСУТП необходимо определить цель этой системы.

Степень достижения поставленной цели принято характеризовать с помощью

 критериев управления.

 

            1.2 Критерии управления

 

         Критерий управления должен быть обязательно выражен количественно и зависеть от выбранных управляющих воздействий.

 

            1.3 Виды подсистем

 

АСУТП реализует свои функции с помощью следующих подсистем.

1.3.1 Сбор и первичная обработка информации:

- сбор информации  с ТОУ;

- проверка достоверности информации ;

- фильтрация сигналов измерительной информации ;

- расчет действительных значений параметров;

- усреднение и интегрирование значений параметров.

          1.3.2  Контроль состояния объекта:

- отображение информации ;

- контроль и регистрация отклонения параметров от заданных значений;

- анализ срабатывания блокировок и защит.

1.3.3                         Автоматическое регулирование и оптимальное управление:

- стабилизация технологических параметров;

- каскадное и связанное регулирование;

- логическое управление;

- дискретное, программное управление задвижками;

- статическая оптимизация.

1.3.4     Расчет технико-экономических показателей:

- расчет себестоимости продукции;

- расчет материального баланса.

       1.3.5 Связь с MES – системой (АСУ предприятия):

- передача сообщений на верхний уровень;

- прием сообщений с верхнего уровня.

        

1.4 Состав АСУ ТП

 

 

                                           Рисунок 1.1- Составные части АСУ

 

Оперативный персонал состоит из операторов технологов, осуществляющих контроль и управление объектом, и эксплуатационного персонала, обеспечивающего функционирование технических средств систем.

Организационное обеспечение представляет собой совокупность документов, устанавливающих порядок и правила функционирования оперативного персонала.

          Сюда входят:

1) технологические инструкции и регламенты, определяющие ведение процесса в нормальной, предаварийной и аварийной ситуации;

          2) инструкции по эксплуатации системы.

          В состав программного обеспечения входят:

1)     операционная система;

2)     система управления базовых данных (СУБД);

3)     специализированное программное обеспечение.

 

          1.5 Структурная организация АСУ ТП

 

          1.5.1 Централизованные АСУ ТП

 

 

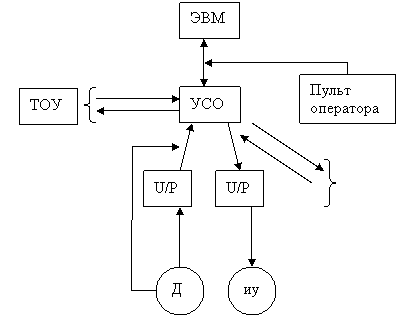
 Рисунок 1.2 - Централизованная система управления ТОУ

 

         УСО - устройство связи с объектом.

В состав УСО входят :

         - АЦП ( аналого-цифровой преобразователь);

         - ЦАП (цифро - аналоговый преобразователь);

         - коммутатор.

Минусы:

          - многочисленные кабели,связывающие датчики с объектом;

          - поломка ЭВМ (много резервов).

 

1.5.2 Распределенные АСУ ТП

 

                                                                                

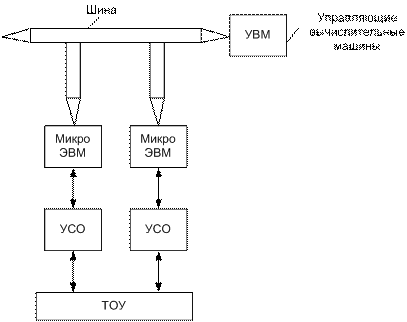
    Рисунок 1.3 - Распределённая система управления ТОУ

 

С появлением цифровых датчиков появилась возможность не только обрабатывать информацию в цифровой форме, но и передавать эту информацию в цифровой форме. Цифровая передача данных между отдельными устройствами сделала основой построения АСУ вычислительную сеть. Такая вычислительная сеть используется для создания резервов для пользователей, расположенных на небольшой территории, поэтому такая сеть называется локальной.

         В настоящее время различают 2 типа распределения систем управления:

         1- SCADA – системы;

         2- DCS – системы.

         SCADA – Supervisory Control and Data Acquisition – система сбора данных и управления.

         DCS – Distributed Control System – децентрализованные системы управле-ния.

 

 

 

 

 

 

 

 

 

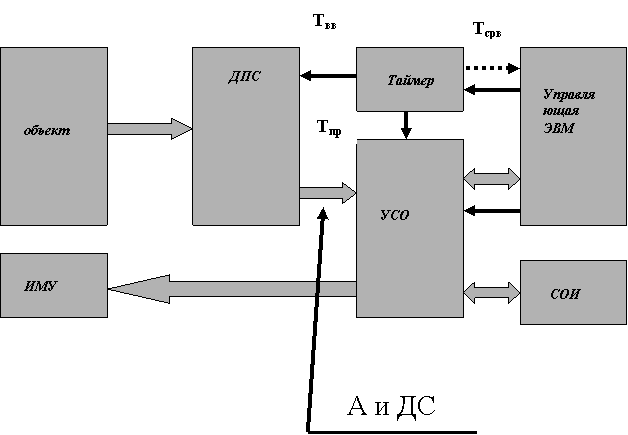
          Рисунок 1.4 -Функционально - структурная схема SCADA - системы

 

2 Лекция 2  SCADA-системы.  Функциональная организация сбора информации в системах реального времени

Цель лекции: определения и  основные функции информационных подсистем в системах управления реального времени.

Содержание лекции: определение систем реального времени. Временная организация  SCADA – систем.

 

2.1 Функциональная организация сбора информации в SCADA – системах

 

SCADA-системы это уровень промышленной автоматизации, связанный с получением данных от различных датчиков и устройств  ввода/вывода, с визуализацией собранной информации и её архивацией. Для анализа производства в целом, для моделирования его отдельных этапов, для выявления критических участков и слабых звеньев важна организация доступа к данным, отражающим весь процесс производства, с возможностью воздействия на него, в том числе и в реальном времени. Для реализации подобных задач автоматизации промышленных предприятий в целом попытки создания интегрированных систем автоматизации, реализующих функции SCADA-систем, ERP-систем и, в целом,  MES-систем, основным направлением определяется создание единого информационного пространства базирующегося на технологической информации в цифровой форме  собранной и обработанной в реальном времени.

 

      

 

 

 

 

 

 

 

 

 

 

 

Рисунок 2.1 - Обобщенная структура систем типа SCADA

2.2 Системы реального времени

 

Real-time system система реального времени (СРВ) это любая система, в которой существенную роль играет время генерации выходного сигнала. Это обычно связано с тем, что входной сигнал соответствует каким-то изменениям в физическом процессе, и выходной сигнал должен быть связан с этими же изменениями. Временная задержка от получения входного сигнала до выдачи выходного сигнала должна быть небольшой, чтобы обеспечить приемлемое время реакции. Время реакции является системной характеристикой: при управлении ракетой требуется реакция в течении нескольких миллисекунд, тогда как для диспетчерского управления движением пароходов требуется время реакции, измеряемое днями.

Системы обычно считаются системами реального времени, если время их реакции имеет порядок миллисекунд; диалоговыми считаются системы с временем реакции порядка нескольких секунд, а в системах пакетной обработки время реакции измеряется часами или днями. Примерами систем реального времени являются системы управления физическими процессами с применением вычислительных машин, системы торговых автоматов, автоматизированные системы контроля и автоматизированные испытательные комплексы.

2.2.1 Режим реального времени [real time processing].

Режим обработки данных, при котором обеспечивается взаимодействие вычислительной системы с внешними по отношению к ней процессами в темпе, соизмеримом со скоростью протекания этих процессов.

Пример – цикл управления самолетом, летящим на автопилоте. Датчики самолета должны постоянно передавать измеренные данные в управляющий компьютер. Если данные измерений теряются, то качество управления самолетом падает, возможно вместе с самолетом.

Пример – выделение самостоятельных программно-технических комплексов с функциями сбора, первичной обработки и передачи информации  (PI System ). PI System предоставляет информацию о технологических процессах в реальном масштабе времени на уровень управления производством и бизнес-систем для специалистов среднего и верхнего звеньев предприятия.

PI System - это инструмент построения информационной системы производства реального времени для промышленного предприятия. PI System наилучшим образом обеспечивает сбор, хранение и представление в едином формате данных от различных SCADA-систем, DCS, ПЛК, устройств ручного ввода, заводских лабораторий и т. п.

          Рисунок 2.2- Функциональный состав системы реального времени

 

На рисунке 2.3 представлена циклограмма функционирования системы реального времени. Из циклограммы видно, что организация реального времени обеспечивается функционированием подсистемы сбор и первичной обработки информации

 

 

 

 

 

 

 

 

 

 

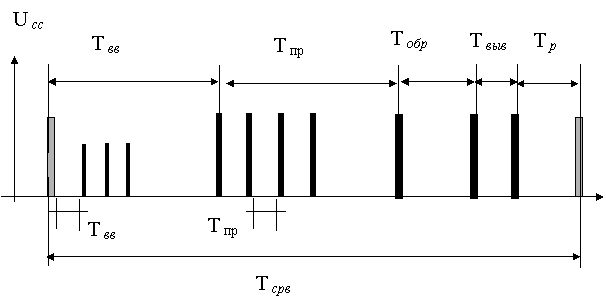
   Рисунок 2.3 - Циклограмма функционирования системы реального времени.

 

3 Лекция 3  SCADA-системы.  Алгоритмы первичной обработки

информации

Цель лекции: определение и изучение   алгоритмов первичной обработки информации информационных подсистем  реального времени.

 

Содержание лекции: алгоритмы сбора и первичной обработки информации. Алгоритмы контроля достоверности информации. Интерполяция и экстраполяция. Фильтрация сигналов измерительной информации.

 

3.1 Алгоритмы сбора и первичной обработки информации

 

Организация сбора информации в автоматизированных системах управления (SCADA-системах) определяет получение информации от датчиков технологических переменных ТОУ в цифровой форме в соответствии с алгоритмом общего функционирования (циклограмма СРВ, лекция 2)

 

 

           

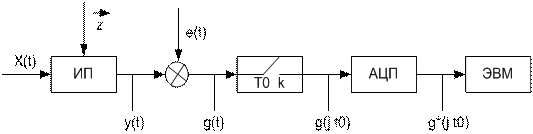
Рисунок 3.1- Информации от датчиков технологических переменных ТОУ в цифровой форме

 

 

                Рисунок 3.2- Схема организации сбора информации

 

x(t) – сигнал измерительной информации

g(t) – выходная величина преобразователя (полезный сигнал)

z – влияющие факторы

g(t) – смесь полезного сигнала и помехи

к – коммутатор

 

Пример реализации переменной Х при измерении температуры термопарой:

                 

где:

t – температура горячего спая – x

t0 – температура холодного спая  z0

  

Если  z0    - номинальная статическая характеристика

 

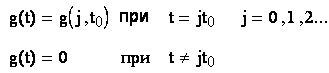
Далее идет квантование по уровню, в результате чего получаем  y*(j t0).

 

         3.2 Первичная обработка информации

Группа алгоритмов, хранящейся в ЭВМ в числовом значении параметра, называется алгоритмами первичной обработки информации. Основные алгоритмы первичной обработки информации:

1.     Контроль достоверности информации

2.     Интерполяция и экстраполяция

3.     Фильтрация сигналов измерительной информации

4.     Аналитическая градуировка датчиков

5.     Коррекция восстановленных значений.

         3.2.1 Контроль достоверности информации

Наиболее часто встречающимися причинами недостоверности информации являются:

1) неисправности датчиков и преобразователей;

2)     влияние помех в линиях связи;

3)     ухудшение метрологических характеристик ИП.

 

     Контроль достоверности информации осуществляется путем сравнения:

  - контроль по верхним и нижним пределам

 

                            

 

                                  

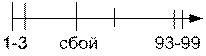
         - контроль по скорости изменения значений.

 

Если скорость изменяется по температуре => сбой

 

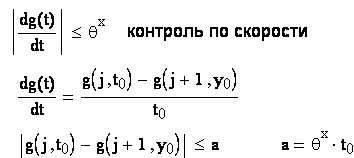
         3.2.2 Интерполяция и экстраполяция

 

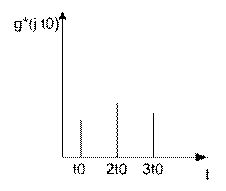
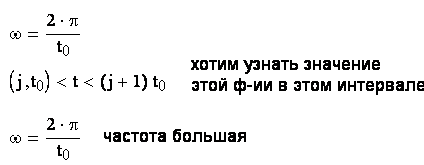
применяют ступенчатую интерполяцию (интерполяцию нулевого порядка). Поскольку интервалы очень малы, то

.

 

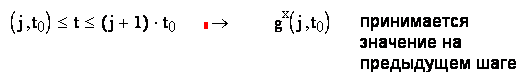3.2.3 Фильтрация сигналов измерительной информации

 

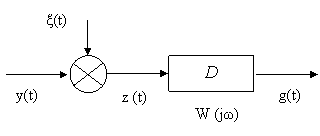          Рисунок 3.3- Фильтрация сигналов измерительной информации

 

Входной сигнал представляет собой случайный процесс z (t) при -∞ < t < ∞  и пусть z (t) представляет собой смесь ( не обязательно аддитивную ) полезного сигнала y(t) и помехи ξ(t). Требуется построить систему (фильтр Ф) такой обработки входного сигнала, которая позволила бы получить на выходе желаемый сигнал g(t), являющийся результатом определённой операции D над одним лишь полезным сигналом:

На практике применяют следующие частные случаи, когда:

а) g(t) = y(t) (-α) – задача фильтрации и сглаживания;

    б) g(t) = y(t) - задача фильтрации;

    в) g(t) = y(t) (+α) - задача фильтрации и упреждения;

где α >0.

С точки зрения требований к объёму вычислений выгодно использовать для (α) фильтр экспоненциального сглаживания:

 

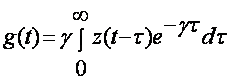            ,                                                         (3.1)

где - параметр фильтра.

Дискретный вариант фильтра (3.1) применяется в подсистемах сбора и передачи информации, а также в системах SCADA :

,                  (3.2)

где z[n] – значение входного сигнала в момент времени nΔt

(Δt – интервал дискретизации);

- параметр фильтра (0 < <1).

Кроме этого, в системах  часто применяются фильтры - статистический фильтр и фильтр скользящего среднего.

 

4 Лекция 4  SCADA-системы. Пути интеграции  АСУП (MES –системы)  и АСУТП (SCADA и DCS)

 

Цель лекции:  определение и  основные проблемы создания единого информационного пространства в системах управления реального времени и АСУП (MES –системы).

 

Содержание лекции: уровни информационного взаимодействия систем управления. Реляционные БД и БД реального времени

 

4.1 Уровни информационного взаимодействия систем управления

 

Две подсистемы автоматизации промышленных предприятий АСУП, включающая системы автоматизации управленческой и финансово-хозяйственной деятельности и системы планирования ресурсов предприятия, и АСУТП (системы автоматизации технологических и производственных процессов) развивались обособленно и независимо друг от друга (см. рисунок 4.1). Это сложившееся разделение и отражено на рисунке 4.1, где уровень управления процессом производства целиком отнесён к подсистеме АСУП. Однако в реальности чёткой границы между уровнем управления производством и АСУТП нет, а напротив, есть  их некое перекрывание, в силу взаимной неразрывности выполняемых функций. 

 

 

 

 

Рисунок 4.1- Уровни информационного взаимодействия систем управления

 

         В подсистемах АСУТП принципиально важной является работа в реальном времени. Негарантированное время реакции на событие в технологическом процессе недопустимо. Различные каналы обмена (а соответственно, и протоколы) характеризуются соответствующими приоритетами, которые зависят от степени ответственности выполняемых задач (алармы, архивы, работа с таблицами РБД).

Наличие общих свойств программного обеспечения обеих подсистем позволяет говорить о том, что объективные возможности для интеграции созрели. Благодаря уже существующим единым сетевым протоколам и современным информационным технологиям есть все необходимые предпосылки для успешного решения этих задач. Рассмотрим следующие способы интеграции подсистем уровней АСУП и АСУТП:

 

Ø     использование баз данных, в том числе в качестве буфера между различными подсистемами, позволяет обеспечивать оперативный обмен данными между подсистемами. Причем БД являются как основой функционирования самих подсистем, так и средством, используемым для хранения функциональных данных. Именно БД, скорее всего, могут стать основным средством интеграции двух подсистем;

 

Ø      применение класса продуктов, главным назначением которых является импортирование объектов из одной подсистемы и экспортирование их в другую подсистему.

 

4.2 Реляционные БД и БД реального времени

 

С помощью СУБД решаются проблемы, связанные с огромными объемами дублированной и иногда противоречивой информации в системах управления технологическими процессами, предоставляемой различными и, зачастую, несовместимыми друг с другом способами. Использование традиционных реляционных баз данных, ориентированных на MES - системы , не всегда возможно в системах управления технологическими процессами. Этому препятствуют несколько основных ограничений:

 

Ø     производственные процессы генерируют данные очень быстро. Чтобы хранить производственный архив системы, например, с 7500 рабочими переменными, в БД каждую секунду необходимо вставлять 7500 строк. Обычные БД не могут выдержать подобную нагрузку;

 

Ø     объёмы производственной информации настолько велики, что она просто не вмещается в традиционную БД. Например, многомесячный архив завода с 7500 рабочими переменными требует под БД около 1 Терабайта дисковой памяти. Сегодняшние технологии такими объемами манипулировать не могут;

 

Ø     SQL как язык не подходит для обработки временных или периодических данных, типичных для производственных систем. В частности, чрезвычайно трудно указать в запросе периодичность выборки возвращаемых данных.

 

Результатом преодоления этих ограничений стало появление класса продуктов, называемых базами данных реального времени (БДРВ). Отмечаются две концепции создания БДРВ: новая независимая разработка БД или разработка БДРВ на основе известных реляционных БД, например, MS SQL Server. Более перспективным представляется второй способ, поскольку, во-первых, он дешевле, а во-вторых, технологичнее . В качестве примера реализации БДРВ отметим, например, IndustrialSQL Server (компания Wonderware) и Plant2SQL (Ci Technologies). Основные функции БДРВ, построенные на основе MS SQL Server заключаются в следующем:

 

Ø     сохранение некритичной во времени информации в БД Microsoft SQL Server, в то время как вся технологическая информация сохраняется в специальном формате;

 

Ø     поддержание высокой пропускной способности, что обеспечивает сохранение огромных потоков информации с высокой разрешающей способностью;

 

Ø     поддержание целостности данных, что обеспечивает запись больших объемов информации без потерь;

 

Ø     добавление в Microsoft SQL Server свойств сервера реального времени.

 

В настоящее время БДРВ являются продуктами, ориентированными на хранение технологической информации, на обеспечение связи с управленческими данными, на использование уже ставших стандартными в подсистемах АСУП интерфейсов OLE DB, Internet. На рисунке 4.2 показаны информационные потоки. С одной стороны это данные, поступающие из различных технологических источников для сохранения в БД, с другой данные, запрашиваемые потребителями через интерфейс SQL-сервера.

  

 

 

 

 

 

 

 

 

 

 

 

 

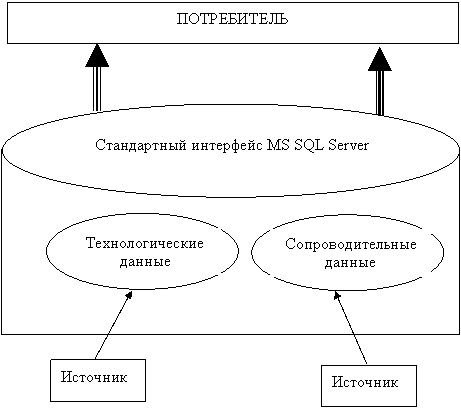 Рисунок 4.2 - БДРВ на основе MS SQL Server

 

Используемая в БДРВ архитектура клиент-сервер позволяет заполнить промежуток между промышленными системами контроля и управления реального времени, для которых характерны большие объемы информации, и открытыми гибкими управленческими информационными системами.

 Следует подчеркнуть, что в зависимости от требований создаваемой системы возможны следующие варианты решений:

 

a)     использование только РБД, в таблицы которой подсистема АСУТП по SQL-запросам записывает технологические данные; в дальнейшем последние могут быть использованы обеими подсистемами;

 

b)    использование БДРВ, которые обеспечивают более высокие характеристики регистрации данных и упрощают (без использования SQL) процесс внесения данных в таблицы;

 

c)     построение комбинированного решения, предполагающего использование БДРВ для технологических первичных данных и таблиц РБД для вторичной информации.

 

5 Лекция 5  Основы теории кодирования и коды. Помехоустойчивое

                  кодирование

 

Цель лекции: определение и изучение методов теории кодирования, применяемых в информационных подсистемах АСУ.

 

Содержание лекции: принципы помехоустойчивого кодирования. Определение и классификация корректирующих кодов. Блоковый код.

5.1 Помехоустойчивое кодирование

Бурный рост теории и практики помехоустойчивого кодирования в последнее десятилетие связан, в первую очередь, с созданием средств телеобработки данных, вычислительных систем и сетей, региональных автомати­зированных систем управления, систем автоматизации научных исследований. Высокие требования к достовер­ности передачи, обработки и хранения информации в указанных системах диктовали необходимость такого кодирования информации, которое обеспечивало бы воз­можность обнаружения и исправления ошибки.

В этом случае кодирование должно осуществляться так, чтобы сигнал, соответствующий принятой последо­вательности символов, после воздействия на него пред­полагаемой в канале помехи оставался ближе к сигналу, соответствующему конкретной переданной последователь­ности символов, чем к сигналам, соответствующим дру­гим возможным последовательностям. Степень близости обычно определяется по числу разрядов, в которых последовательности отличаются друг от друга.

Это достигается ценой введения при кодировании избыточности, которая позволяет так выбрать передавае­мые последовательности символов, чтобы они удовлет­воряли дополнительным условиям, проверка которых на приемной стороне дает возможность обнаружить и испра­вить ошибки.

Коды, обладающие таким свойством, называют поме­хоустойчивыми. Они используются как для исправления ошибок (корректирующие коды), так и для их обнаруже­ния.

 

5.1.1 Классификация помехоустойчивых кодов

 

У подавляющего большинства существующих в нас­тоящее время помехоустойчивых кодов указанные усло­вия являются следствием их алгебраической структуры. В связи с этим их называют алгебраическими кодами. (В отличие, например, от кодов Вагнера, корректирующее действие которых базируется на оценке вероятности искажения каждого символа).

Алгебраические коды можно подразделить на два больших класса: блоковые и непрерывные.

В случае блоковых кодов процедура кодирования заключается в сопоставлении каждой букве сообщения (или последовательности из k символов, соответствую­щей этой букве) блока из п символов. В операциях по преобразованию принимают участие только указан­ные k символов, и выходная последовательность не за­висит от других символов в передаваемом сообщении.

Блоковый код называют равномерным, если п остается постоянным для всех букв сообщения.

Различают разделимые и неразделимые блоковые коды. При кодировании разделимыми кодами выходные последовательности состоят из символов, роль которых может быть отчетливо разграничена. Это инфор­мационные символы, совпадающие с символами после­довательности, поступающей на вход кодера канала, и избыточные (проверочные) символы, вводимые в исход­ную последовательность кодером канала и служащие для обнаружения и исправления ошибок.

При кодировании неразделимыми кодами раз­делить символы выходной последовательности на инфор­мационные и проверочные невозможно.

Непрерывными (древовидными) называют такие ко­ды, в которых введение избыточных символов в коди­руемую последовательность информационных символов осуществляется непрерывно, без разделения ее на неза­висимые блоки. Непрерывные коды также могут быть разделимыми и неразделимыми.

Наиболее простыми в отношении технической реали­зации кодами этого класса являются сверточные (рекуррентные) коды.

 

5.1.2 Блоковый код. Общие принципы использования избыточности

 

Спо­собность кода обнаруживать и исправлять ошибки обус­ловлена наличием избыточных символов. На вход коди­рующего устройства поступает последовательность из k информационных двоичных символов. На выходе ей соот­ветствует последовательность из п двоичных символов, причем n>k.

Всего может быть 2^k различных входных и 2ⁿ различных выходных последовательностей. Из общего числа 2 ⁿ выходных последовательностей только 2^k по­следовательностей соответствуют входным. Назовем их разрешен­ными кодовыми комбинациями.

 Остальные 2ⁿ — 2^k возможных вы­ходных последовательностей для пе­редачи не используются. Назовем их запрещенными комбинациями.

                                                                                                                               

 

 

 

 

 

 

 

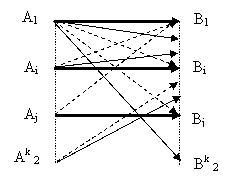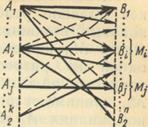
                       Рисунок 5.1-  Варианты передачи информации с помехами

 

Искажение информации в про­цессе передачи сводится к тому, что некоторые из передан­ных символов заменяются другими - неверными. Так как каждая из 2^k разрешенных комбинаций в результате дей­ствия помех может трансформироваться в любую другую, то всего имеется 2^k• 2ⁿ возможных случаев передачи (см. рисунок 5.1). В это число входят:

2^k случаев безошибочной передачи (на рисунке 5.1 обо­значены жирными линиями);

2 ^k (2 ^k -1) случаев перехода в другие разрешенные комбинации, что соответствует не обнаруживаемым ошиб­кам (на рисунке 5.1 обозначены пунктирными линиями);

2^k(2ⁿ - 2^k) случаев перехода в неразрешенные комби­нации, которые могут быть обнаружены (на рисунке 5.1 обозначены тонкими сплошными линиями).

Следовательно, часть обнаруживаемых ошибочных кодовых комбинаций от общего числа возможных слу­чаев передачи составляет:

2^k(2ⁿ - 2^k) / 2^k • 2ⁿ = 1 — 2^k / 2ⁿ .                                    (5.1)              

Пример

Определим обнаруживающую способность кода, каждая комбинация которого содержит всего один избыточный сим­вол ( n = k+1 ). Общее число выходных последовательностей составляет 2^k+1, т. е. вдвое больше общего числа кодируемых входных после­довательностей. За подмножество разрешенных кодовых комбинаций можно принять, например, подмножество 2^k комбинаций, содержащих четное число единиц (или нулей).

При кодировании к каждой последовательности из k инфор­мационных символов добавляется один символ (0 или 1) такой, чтобы число единиц в кодовой комбинации было четным. Искажение любого нечетного числа символов переводит разрешенную кодовую комбинацию в подмножество запрещенных комбинаций, что обнаруживается на приемной стороне по нечетности числа единиц. Часть опознанных ошибок составляет

                    1 -  2^k / 2^k+1 = 1/2.                                                                  (5.2)

 

Рассмотрим случай исправления ошибок.

Любой метод декодирования можно рассматривать как правило разбиения всего множества запрещенных кодовых комбинаций на 2^k  непересекающихся подмно­жеств Mi, каждое из которых ставится в соответствие одной из разрешенных комбинаций. При получении запрещенной комбинации, принадлежащей подмножеству Mi, принимают решение, что передавалась разрешенная комбинация Ai. Ошибка будет исправлена в тех слу­чаях, когда полученная комбинация действительно обра­зовалась из A_it,  т.е. 2ⁿ —2^k случаях.

Всего случаев перехода в неразрешенные комбинации 2^k(2ⁿ - 2^k). Таким образом, при наличии избыточности любой код способен исправлять ошибки. Отношение числа исправляемых кодом ошибочных кодовых комбина­ций к числу обнаруживаемых ошибочных комбинаций равно

                             (2ⁿ -2^k )/ [2^k(2ⁿ -2^k)] = 1 / 2^k .                                       (5.3)

Способ разбиения на подмножества зависит от того, какие ошибки должны исправляться данным конкретным кодом.

Большинство разработанных до настоящего времени кодов предназначено для корректирования взаимно независимых ошибок определенной кратности и пачек (пакетов) ошибок.

Взаимно независимыми ошибками будем называть такие искажения в передаваемой последовательности символов, при которых вероятность появления любой комбинации искаженных символов зависит только от числа искаженных символов r и вероятности искажения одного символа р.

Кратностью ошибки называют количество искажен­ных символов в кодовой комбинации.

При взаимно независимых ошибках вероятность искажения любых r символов в  n-разрядной кодовой комбинации

                                                                           _{Pr= C} ^r _{n  P} ^r_{(1 – P)} ^{n -r}                                                                          (5.4)  

Если учесть, что p<<1, то в этом случае наиболее вероятны ошибки низшей кратности. Их и следует обна­руживать и исправлять в первую очередь.

 

6 Лекция 6  Помехоустойчивое кодирование. Блоковый код

Цель лекции: определение и изучение методов теории кодирования, применяемых в информационных подсистемах АСУ.

 

Содержание лекции: принципы помехоустойчивого кодирования. Характеристики корректирующего кода.

 

6.1 Связь корректирующей способности кода с кодовым расстоянием

 

Как было рассмотрено ранее,  при взаимно независимых ошибках наиболее вероятен переход в кодовую комбинацию, отличающуюся от данной в наимень­шем числе символов.

Степень отличия любых двух кодовых комбинаций характеризуется расстоянием между ними в смысле Хэмминга или просто кодовым расстоянием. Оно выра­жается числом символов, в которых комбинации отли­чаются одна от другой, и обозначается через d.

Чтобы получить кодовое расстояние между двумя комбинациями двоичного кода, достаточно подсчитать число единиц в сумме этих комбинаций по модулю 2. Например:

                                               1001111101

                                           1100001010

                                                 0101110111, d = 7.

Минимальное расстояние, взятое по всем парам кодовых разрешенных комбинаций кода, называют мини­мальным кодовым расстоянием.

Декодирование после приема может производиться таким образом, что принятая кодовая комбинация отождествляется с той разрешенной, которая находится от нее на наименьшем кодовом расстоянии.

Такое декодирование называется декодированием по методу максимального правдоподобия.

Очевидно, что при d = 1 все кодовые комбинации являются разрешенными.

Например, при п = 3 разрешенные комбинации обра­зуют следующее множество: 000, 001, 010, 011, 100, 101, 110, 111.

Любая одиночная ошибка трансформирует данную комбинацию в другую разрешенную комбинацию. Это случай безызбыточного кода, не обладающего корректи­рующей способностью.

Если d = 2, то ни одна из разрешенных кодовых комбинаций при одиночной ошибке не переходит в дру­гую разрешенную комбинацию. Например, подмножество разрешенных кодовых комбинаций может быть образо­вано по принципу четности в них числа единиц, как это приведено ниже для п = 3:

 

 

000,   011, 101, 110 - разрешенные комбинации

001,  010, 100, 111    - запрещенные комбинации

 

Код обнаруживает одиночные ошибки, а также другие ошибки нечетной кратности (при п = 3 тройные). В об­щем случае при необходимости обнаруживать ошибки кратности до r включительно минимальное хэммингово расстояние между разрешенными кодовыми комбинация­ми должно быть по крайней мере на единицу больше r, т. е.

                                d_{0 min} ≥ r +l.                                                                          (6.1)

Действительно, в этом случае ошибка, кратность кото­рой не превышает r, не в состоянии перевести одну разрешенную кодовую комбинацию в другую.

Для исправления одиночной ошибки каждой разре­шенной кодовой комбинации необходимо сопоставить подмножество запрещенных кодовых комбинаций. Чтобы эти подмножества не пересекались, хэммингово расстоя­ние между разрешенными кодовыми комбинациями должно быть не менее трех. При п = 3 за разрешенные комбинации можно, например, принять 000 или 111. Тог­да разрешенной комбинации 000 необходимо приписать подмножество запрещенных кодовых комбинаций 001, 010, 100, образующихся в результате возникновения единичной ошибки в комбинации 000.

Подобным же образом разрешенной комбинации 111 необходимо приписать подмножество запрещенных кодо­вых комбинаций: 110, 011, 101, образующихся в резуль­тате возникновения единичной ошибки в комбинации 111:

 

                                                 001

                                                 010

Разрешённые    000                100            Запрещённые

комбинации      111                011            комбинации

                                                 101

                                                 110

В общем случае для обеспечения возможности исправления всех ошибок кратности до s включительно при декодировании по методу максимального правдопо­добия каждая из ошибок должна приводить к запре­щенной комбинации, относящейся к подмножеству исход­ной разрешенной кодовой комбинации.

Подмножество каждой из разрешенных n - разрядных комбинаций Bi (см. рисунок 6.1) складывается из запрещенных комбинаций, являющихся следствием воздействия:

единичных ошибок (они располагаются на сфере радиусом d=1, и их число равно ,

 

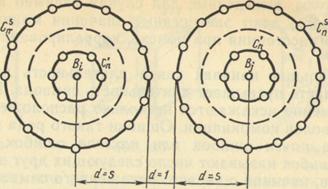
                   Рисунок 6.1- Разрешающая способность кодов

двойных ошибок (они располагаются на сфере радиу­сом d = 2, и их число равно) и т. д.

Внешняя сфера подмножества имеет радиус d = s и содержит  запрещенных кодовых комбинаций.

Поскольку указанные подмножества не должны пере­секаться, минимальное хэммингово расстояние между разрешенными комбинациями должно удовлетворять соотношению

                                           d_{n min} ≥ 2s + l.                                                            (6.1)

Нетрудно убедиться в том , что для исправ­ления всех ошибок кратности s и одновременного обна­ружения всех ошибок кратности r(r≥s) минимальное хэммингово расстояние нужно выбирать из условия

                                       d _{n 0  min} ≥ r +s+l.                                                      (6.2)

        

Формулы, выведенные для случая взаимно независи­мых ошибок, дают завышенные значения минимального кодового расстояния при помехе, коррелированной с сиг­налом.

В реальных каналах связи длительность импульсов помехи часто превышает длительность символа. При этом одновременно искажаются несколько расположенных ря­дом символов комбинации. Ошибки такого рода получили название пачек ошибок или пакетов ошибок. Длиной пачки ошибок называют число следующих друг за другом символов, начиная с первого искаженного символа и кон­чая искаженным символом, за которым следует не менее ρ неискаженных символов. Основой для выбора ρ служат статистические данные об ошибках. Если, например, ко­довая комбинация 00000000000000000 трансформирова­лась в комбинацию 01001000010101000 и ρ принято равным трем, то в комбинации имеется два пакета длиной 4 и 5 символов.

Применение корректирующего кода не может гарантировать безошибочного приема, но дает возмож­ность повысить вероятность получения на выходе пра­вильного результата.

 

6.2 Показатели качества корректирующего кода

 

 Одной из основных характеристик корректирующего кода явля­ется избыточность кода, указывающая степень удлинения кодовой комбинации для достижения определенной корректирующей способности. Если на каждые п симво­лов выходной последовательности кодера канала прихо­дится k информационных и п — k проверочных, то отно­сительная избыточность кода может быть выражена одним из соотношений

                              R_n= (n – k ) / n                                     (6.3)

   или

                              R_n= (n – k ) / k                                     (6.4)

 

Величина R_k, изменяющаяся от 0 до ∞, предпочтитель­нее, так как лучше отвечает смыслу понятия избыточ­ности. Коды, обеспечивающие заданную корректирую­щую способность при минимально возможной избы­точности, называют оптимальными.

В связи с нахождением оптимальных кодов оценим, например, наибольшее возможное число Q разрешенных комбинаций n-значного двоичного кода, обладающего способностью исправлять взаимно независимые ошибки кратности до s включительно. Это равносильно отыска­нию числа комбинаций, кодовое расстояние между кото­рыми не менее d = 2s +1.

Общее число различных исправляемых ошибок для каждой разрешенной комбинации составляет   .

Каждая из таких ошибок должна приводить к запре­щенной комбинации, относящейся к подмножеству дан­ной разрешенной комбинации. Совместно с этой комбинацией подмножество включает 1 +    комбинаций.

Как отмечалось, однозначное декодирование возможно только в том случае, когда названные подмножества не пересекаются. Так как общее число различных комбинаций n-значного двоичного кода составляет 2ⁿ , число разрешённых комбинаций не может превышать

                                  

или

                                    Q ≤ 2ⁿ  / .

Эта верхняя оценка найдена Хэммингом. Для некото­рых конкретных значений кодового расстояния d соот­ветствующие Q указаны в таблице 6.1

 

          Т а б л и ц а 6.1 

                  

d	Q	d	Q
1	2n	5
2	≤2 n -1	…
3		…
4		2k + 1

 

 

Коды, для которых в приведенном соотношении дости­гается равенство, называют также плотноупакованными.

Однако не всегда целесообразно стремиться к исполь­зованию кодов, близких к оптимальным. Необходимо учитывать другой, не менее важный показатель качества корректирующего кода - сложность технической реализа­ции процессов кодирования и декодирования.

Если информация должна передаваться по медленно действующей, ненадежной и дорогостоящей линии связи, а кодирующее и декодирующее устройства предполага­ется выполнить на высоконадежных и быстродействую­щих элементах, то сложность этих устройств не играет существенной роли. Решающим фактором в таком слу­чае является повышение эффективности использования линии связи и поэтому желательно применение коррек­тирующих кодов с минимальной избыточностью.

Если же корректирующий код должен быть применен в системе, выполненной на элементах, надежность и быстродействие которых равны или близки надежности и быстродействию элементов кодирующей и декодирую­щей аппаратуры (например, для повышения достовер­ности воспроизведения информации с запоминающего устройства цифровой вычислительной машины), то кри­терием качества корректирующего кода является надеж­ность системы в целом, т. е. с учетом возможных иска­жений и отказов в устройствах кодирования и деко­дирования. В этом случае часто более целесообразны коды с большей избыточностью, но обладающие преиму­ществом простоты технической реализации.

 

7 Лекция 7  Линейные коды. Математическое введение к

линейным кодам

Цель лекции: определение и изучение методов теории кодирования, применяемых в информационных подсистемах АСУ.

 

Содержание лекции: принципы помехоустойчивого кодирования. Линейные коды. Описание линейных кодов с использованием представлений линейной алгебры.

 

7.1 Линейные коды

 

Самый большой класс разделимых кодов составляют линейные коды, у которых значения проверочных символов определяются в результате

проведения линейных операций над определенными инфор­мационными символами. Для случая двоичных кодов каждый проверочный символ выбирают таким, чтобы его сумма с определенными информационными символами была равна нулю. Символ проверочной позиции имеет значение 1, если число единиц информационных разря­дов, входящих в данное проверочное равенство, нечетно, и 0, если оно четно. Число проверочных равенств (а следовательно, и число проверочных символов) и но­мера конкретных информационных разрядов, входящих в каждое из равенств, определяется тем, какие и сколько ошибок должен исправлять или обнаруживать данный код. Проверочные символы могут располагаться на любом месте кодовой комбинации.

При декодировании определяется справедливость про­верочных равенств. В случае двоичных кодов такое определение сводится к проверкам на четность числа единиц среди символов, входящих в каждое из равенств (включая проверочный). Совокупность проверок дает информацию о том, имеется ли ошибка, а в случае необ­ходимости и о том, на каких позициях символы иска­жены.

Любой двоичный линейный код является групповым, так как совокупность входящих в него кодовых комбина­ций образует группу. Уточнение понятий линейного и группового кода требует ознакомления с основами линейной алгебры.

 

7.2 Математическое введение к линейным кодам

 

 Осно­вой математического описания линейных кодов является линейная алгебра (теория векторных пространств, теория матриц, теория групп). Кодовые комбинации рассматри­вают как элементы множества, например, кодовые ком­бинации двоичного кода принадлежат множеству поло­жительных двоичных чисел.

Множества, для которых определены некоторые ал­гебраические операции, называют алгебраическими сис­темами. Под алгебраической операцией понимают одно­значное сопоставление двум элементам некоторого треть­его элемента по определенным правилам. Обычно основ­ную операцию называют сложением (обозначают а+b = с) или умножением (обозначают а∙b = с), а обрат­ную ей - вычитанием или делением, даже если эти операции проводятся не над числами и неидентичны соответствующим арифметическим операциям.

Рассмотрим кратко основные алгебраические системы, широко используемые в теории корректирующих кодов. Группой называют множество элементов, в котором определена одна основная операция и выполняются сле­дующие аксиомы:

1.     В результате применения операции к любым двум элементам группы образуется элемент этой же группы (требование замкнутости).

2.     Для любых трех элементов группы a, b и с удов­летворяется равенство (а+b)+c = а+(b+c) (если ос­новная операция - сложение) и равенство a∙(bc) = (ab)∙c (если основная операция - умножение).

3.     В любой группе G_n существует однозначно опре­деленный элемент, удовлетворяющий при  всех значе­ниях а из G_n условию a+0=0 + a = a (если основная операция - сложение) или условно a • 1 = 1 • а = а (если основная операция - умножение).

В первом случае, этот элемент называют нулем и обо­значают символом 0, а во втором - единицей и обозна­чают символом 1.

4.  Всякий элемент  а  группы  обладает  элементом, однозначно определенным уравнением а + (— а) = — а+ а = 0 (если основная операция сложение) или уравне­нием

a • a^-1  =  a^-1• a= 1 (если основная операция - умно­жение).

В первом случае, этот элемент называют противопо­ложным и обозначают (-а), а во втором - обратным и обозначают a^-1.

Если операция, определенная в группе, коммутативна, т. е. справедливо равенство a + 6 = b + a (для группы по сложению) или равенство a •  b = b • a (для группы по умно­жению), то группу называют коммутативной или абелевой.

Группу, состоящую из конечного числа элементов, называют конечной. Число элементов в группе называют порядком группы.

Чтобы рассматриваемое нами множество n-разрядных кодовых комбинаций было конечной группой, при выпол­нении основной операции число разрядов в результирую­щей кодовой комбинации не должно увеличиваться. Этому условию удовлетворяет операция символического поразрядного сложения по заданному модулю q (q -простое число), при которой цифры одинаковых разрядов элементов группы складываются обычным порядком, а результатом сложения считается остаток от деления полученного числа на модуль q.

При рассмотрении двоичных кодов используется опе­рация сложения по модулю 2. Результатом сложения цифр данного разряда является 0, если сумма единиц в нем четна, и 1, если сумма единиц в нем нечетна, например:

1 0 1 1 1 0 1

                                     0 1 1 1 1 0 1

                                         0 0 0 1 1 1 0

                                         1 1 0 1 1 1 0

Выбранная нами операция коммутативна, поэтому рассматриваемые группы будут абелевыми.

Нулевым элементом является комбинация, состоящая из одних нулей. Противоположным элементом при сло­жении по модулю 2 будет сам заданный элемент. Сле­довательно, операция вычитания по модулю 2 тождест­венна операции сложения.

 

Пример 6.1

Определить, являются ли группами следующие множества кодовых комбинаций:

1)0001, 0110, 0111, 0011;

2)0000, 1101, 1110, 0111;

3)   000, 001, 010, 011, 100, 101, 110, 111.

Первое множество не является группой, так как не содержит нулевого элемента.

Второе множество не является группой, так как не выполняется условие   замкнутости, например сумма по модулю 2 комбинаций 1101 и 1110 дает комбинацию 0011, не принадлежащему исходному множе­ству.

Третье множество удовлетворяет всем перечисленным условиям и является группой.

Подмножества группы, являющиеся сами по себе группами относительно операции, определенной в группе, называют подгруппами. Например, подмножество трех­разрядных кодовых комбинаций: 000, 001, 010, 011 обра­зуют подгруппу указанной в примере группы трехразряд­ных кодовых комбинаций.

Пусть в абелевой группе G_n задана определенная подгруппа А. Если В - любой не входящий в А элемент из G_n, то суммы (по модулю 2) элементов В с каждым из элементов подгруппы А образуют смежный класс группы G_n по подгруппе А, порождаемый элементом В.

Элемент В, естественно, содержится в этом смежном классе, так как любая подгруппа содержит нулевой эле­мент. Взяв последовательно некоторые элементы В_j, груп­пы, не вошедшие в уже образованные смежные классы, можно разложить всю группу на смежные классы по подгруппе А.

Элементы В_j  называют образующими элементами смежных классов подгруппы.

В таблице разложения, иногда называемой групповой таблицей, образующие элементы обычно располагают в крайнем левом столбце, причем крайним левым эле­ментом подгруппы является нулевой элемент.

Пример 6.2. Разложим группу трехразрядных двоичных кодовых комбинаций по подгруппе двухразрядных кодовых комбинаций. Разложение выполняем в соответствии с табицей 6.2.

 

                     Т а б л и ц а  6.2

Пример 6.3. Разложим группу четырехразрядных двоичных кодо­вых комбинаций по подгруппе двухразрядных кодовых комбинаций.

Существуют много вариантов разложения в зависимости от того, какие элементы выбраны в качестве образующих смежных классов. Один из вариантов представлен в таблице 6.3.

 

 

 

                    Т а б л и ц а  6.3

Кольцом называют множество элементов R, на кото­ром определены две операции (сложения и умножения), такие, что:

1) множество R является коммутативной группой по сложению;

2)      произведение элементов aR и bR есть эле­мент R (замкнутость по отношению к умножению);

3)      для любых трех элементов a, b и с из R справед­ливо равенство a∙(bc) = (ab) ∙c (ассоциативный закон для умножения);

4)      для любых трех элементов а, b и с из R выпол­няются соотношения

a(b + c) = ab + ac и ( b+c)a = ba+ca (дистрибутивные законы).

Если для любых двух элементов кольца справедливо соотношение ab = bа, кольцо называют коммутативным. Кольцо может не иметь единичного элемента по умноже­нию и обратных элементов.

Примером кольца может служить множество действи­тельных четных целых чисел относительно обычных операций сложения и умножения.

Полем F называют множество по крайней мере двух элементов, в котором определены две операции - сложе­ние и умножение, и выполняются следующие аксиомы:

1)      множество   элементов   образует   коммутативную группу по сложению;

2)      множество ненулевых элементов образует комму­тативную группу по умножению;

3)      для любых трех элементов множества а, b, с вы­полняется соотношение (дистрибутивный закон)

a(b+c) = ab+ac.

Поле F является, следовательно, коммутативным кольцом с единичным элементом по умножению, в кото­ром каждый ненулевой элемент обладает обратным элементом. Примером поля может служить множество всех действительных чисел.

Поле GF(P), состоящее из конечного числа элемен­тов Р, называют конечным полем или полем Галуа. Для любого числа Р, являющегося степенью простого числа q существует поле, насчитывающее Р элементов. Напри­мер, совокупность чисел по модулю q, если q-простое число, является полем.

Поле не может содержать менее двух элементов, поскольку в нем должны быть по крайней мере единич­ный элемент относительно операции сложения (0) и еди­ничный элемент относительно операции умножения (1). Поле, включающее только 0 и 1, обозначим GF (2). Правила сложения и умножения в поле с двумя элемен­тами следующие:

 

+	0	1			0	1
0	0	1		0	0	0
1	1	0		1	0	1

         

Двоичные кодовые комбинации, являющиеся упоря­доченными последовательностями из п элементов поля GF (2), рассматриваются в теории кодирования как частный случай последовательностей из п элементов поля GF(P). Такой подход позволяет строить и анализировать коды с основанием, равным степени простого числа.

В общем случае суммой кодовых комбинаций A_j и A_i называют комбинацию A_f  = A_j + A_i . в которой любой символ  A_k (k=1, 2, ..., п) представляет собой сумму k-x символов исходных комбинаций, причем суммиро­вание производится по правилам поля GF(P). При этом вся совокупность n-разрядных кодовых комбинаций ока­зывается абелевой группой.

В частном случае, когда основанием кода является простое число q, правило сложения в поле GF(q) совпа­дает с правилом сложения по заданному модулю q.

 

8 Лекция 8  Коды с исправлением искажений. Групповые коды

Цель лекции: определение и изучение методов помехоустойчивого кодирования , применяемых в информационных подсистемах АСУ.

 

Содержание лекции: принципы помехоустойчивого кодирования. Групповые коды. Построение двоичного группового кода.

 

8.1 Линейный код как подпространство линейного век­торного

      пространства

 

В рассмотренных алгебраических системах (группа, кольцо, поле) операции относились к одному классу математических объектов (элементов). Такие операции называют внутренними законами компо­зиции элементов.

В теории кодирования широко используются модели, охватывающие два класса математических объектов (например, L и Ω). Помимо внутренних законов композации в них задаются внешние законы композиции элементов, по которым любым элементам  и aL ставится в соответствие элемент cL.

Линейным векторным пространством над полем эле­ментов F (скаляров) называют множество элементов V (векторов), если для него выполняются следующие аксиомы:

1)      множество   V  является   коммутативной  группой относительно операции сложения;

2)      для любого вектора v из V и любого скаляра сиз F определено произведение cv которое содержится в V (замкнутость по отношению умножения на скаляр);

если u и v из V векторы, а с и d из F скаляры, то справедливо c(c + v) = cu + cv, (с + d) = cv + dv (дис­трибутивные законы);

3) если v- вектор, а с и d - скаляры, то (cd)v = = c(dv) и 1 • v = v (ассоциативный закон для умножения на скаляр).

Выше было определено правило поразрядного сложе­ния кодовых комбинаций, при котором вся их совокуп­ность образует абелеву группу. Определим теперь опера­цию умножения последовательности из п элементов поля GF(P) (кодовой комбинации) на элемент поля а, из GF(P] аналогично правилу умножения вектора на ска­ляр:

a_i (a₁,a₂, …, a_n) =(a_i a₁,a_i a₂, …, a_i a_n)                                      

[умножение элементов производится по правилам поля GF(P)].

Поскольку при выбранных операциях дистрибутивные законы и ассоциативный закон (п. 3, 4) выполняются, все множество n-азрядных кодовых комбинаций можно рассматривать как векторное линейное пространство над полем GF(P), а кодовые комбинации - как его векторы.

В частности, при двоичном кодировании векторы состоят из элементов поля GF (2),  (т. е. 0 и 1). Сложение проводят поразрядно по модулю 2. При умножении век­тора на один элемент поля (1) он не изменяется, а умно­жение на другой (0) превращает его в единичный эле­мент векторного пространства, обозначаемый символом 0= (0 0...0).

Если в линейном пространстве последовательностей из п элементов поля GF(P) дополнительно задать опера­цию умножения векторов, удовлетворяющую определен­ным условиям (ассоциативности, замкнутости, билиней­ности по отношению к умножению на скаляры), то вся совокупность n-разрядных кодовых комбинаций превра­щается в линейную коммутативную алгебру над полем коэффициентов GF(P].

Подмножество элементов векторного пространства, которое удовлетворяет аксиомам векторного простран­ства, называют подпространством.

Линейным кодом называют множество векторов, обра­зующих подпространство векторного пространства всех n-разрядных кодовых комбинаций над полем GF(P).

В случае двоичного кодирования такого подпро­странство комбинаций над полем GF (2) образует любая совокупность двоичных кодовых комбинаций, являющаяся подгруппой группы всех n-разрядных двоичных кодо­вых комбинаций. Поэтому любой двоичный линейный код является групповым.

8.2 Построение двоичного группового кода

Построение конкретного корректирующего кода про­изводят, исходя из требуемого объема кода Q, т. е. необ­ходимого числа передаваемых команд или дискретных значений измеряемой величины и статистических данных о наиболее вероятных векторах ошибок в используемом канале связи. Вектором ошибки называют n-разрядную двоичную последовательность, имеющую единицы в раз­рядах, подвергшихся искажению, и нули во всех осталь­ных разрядах. Любую искаженную кодовую комбинацию можно рассматривать теперь как сумму (или разность) по модулю 2 исходной разрешенной кодовой комбинации и вектора ошибки.

Исходя из неравенства 2^k-1≥ Q (нулевая комбина­ция часто не используется, так как не меняет состояния канала связи), определяем число информационных раз­рядов q, необходимое для передачи заданного числа команд обычным двоичным кодом.

Каждой из 2^k-1 ненулевых комбинаций q-разрядного безызбыточного кода нам необходимо поставить в соот­ветствие комбинацию из п символов. Значения символов в п - k проверочных разрядах такой комбинации уста­навливаются в результате суммирования по модулю 2 значений символов в определенных информационных раз­рядах.

Поскольку множество 2^k комбинаций информацион­ных символов (включая нулевую) образует подгруппу группы всех n-разрядных комбинаций, то и множество 2^q n-разрядных комбинаций, полученных по указанному правилу, тоже является подгруппой группы «-разрядных кодовых комбинаций. Это множество разрешенных кодо­вых комбинаций и будет групповым кодом.

Нам надлежит определить число проверочных разря­дов и номера информационных разрядов, входящих в каждое из равенств для определения символов в про­верочных разрядах.

Разложим группу 2ⁿ всех n-разрядных комбинаций на смежные классы по подгруппе 2^k разрешенных n-раз­рядных кодовых комбинаций, проверочные разряды в которых еще не заполнены. Помимо самой подгруппы кода в разложении насчитывается 2^п-k - 1 смежных классов. Элементы каждого класса представляют собой суммы по модулю 2 комбинаций кода и образующих элементов данного класса. Если за образующие элементы каждого класса принять те наиболее вероятные для заданного канала связи вектора ошибок, которые долж­ны быть исправлены, то в каждом смежном классе сгруппируются кодовые комбинации, получающиеся в ре­зультате воздействия на все разрешенные комбинации определенного вектора ошибки. Для исправления любой полученной на выходе канала связи кодовой комбинации теперь достаточно определить, к какому классу смежно­сти она относится. Складывая ее затем (по модулю 2) с образующим элементом этого смежного класса, полу­чаем истинную комбинацию кода.

Ясно, что из общего числа 2ⁿ—1 возможных ошибок групповой код может исправить всего 2^n-k -1 разно­видностей ошибок по числу смежных классов.

Чтобы иметь возможность получить информацию о том, к какому смежному классу относится полученная комбинация, каждому смежному классу должна быть поставлена в соответствие некоторая контрольная после­довательность символов, называемая опознавателем (синдромом).

Каждый символ опознавателя определяют в результа­те проверки на приемной стороне справедливости одного из равенств, которые мы составим для определения зна­чений проверочных символов при кодировании.

Ранее указывалось, что в двоичном линейном коде значения проверочных символов подбирают так, чтобы сумма по модулю 2 всех символов (включая провероч­ный), входящих в каждое из равенств, равнялась нулю. В таком случае число единиц среди этих символов четное. Поэтому операции определения символов опознавателя называют проверками на четность. При отсутствии ошибок в результате всех проверок на четность образу­ется опознаватель, состоящий из одних нулей. Если про­верочное равенство не удовлетворяется, то в соответст­вующем разряде опознавателя появляется единица. Исправление ошибок возможно лишь при наличии взаимно однозначного соответствия между множеством опознавателей и множеством смежных классов, а следо­вательно, и множеством подлежащих исправлению век­торов ошибок.

Таким образом, количество подлежащих исправлению ошибок является определяющим для выбора числа избыточных символов п - k. Их должно быть достаточно для того, чтобы обеспечить необходимое число опознава­телей.

Если, например, необходимо исправить все одиночные независимые ошибки, то исправлению подлежат п оши­бок:

000...01

000...10

                      ………

010...00

100...00

Различных ненулевых опознавателей должно быть не менее п. Необходимое число проверочных разрядов, следовательно, должно определяться из соотношения

                                      2^n-k – 1 ≥ n                                                                    (8.1)

или

                                       2^n-k – 1 ≥                                                               (8.2)

Если необходимо исправить не только все единичные, но и все двойные независимые ошибки, соответствующее неравенство принимает вид

2^n-k – 1 ≥ ++                                                        (8.3)

В общем случае, для исправления всех независимых ошибок кратности до 5 включительно получаем

                                          2^n-k – 1 ≥ +++  …  +                                    (8.4)

Стоит подчеркнуть, что в приведенных соотношениях указывается теоретический предел минимально возмож­ного числа проверочных символов, который далеко не во всех случаях можно реализовать практически. Часто проверочных символов требуется больше, чем следует из соответствующего равенства.

Одна из причин этого выяснится при рассмотрении процесса сопоставления каждой подлежащей исправле­нию ошибки с ее опознавателем.

Составление таблицы опознавателей

Начнем для простоты с установления опознавателей для случая исправления одиночных ошибок. Допустим, что необхо­димо закодировать 15 команд. Тогда требуемое число информационных разрядов равно четырем. Пользуясь соотношением 2^n-k – 1 = п, определяем общее число раз рядов кода, а следовательно, и число ошибок, подле­жащих исправлению (n =7). Три избыточных разряда позволяют использовать в качестве опознавателей трех­разрядные двоичные последовательности.

В данном случае ненулевые последовательности в принципе могут быть сопоставлены с подлежащими исправлению ошибками в любом порядке. Однако более целесообразно сопоставлять их с ошибками в разрядах, начиная с младшего, в порядке возрастания двоичных чисел (таблица 8.1).

                     Т а б л и ц а  8.1

При таком сопоставлении каждый опознаватель пред­ставляет собой двоичное число, указывающее номер раз­ряда, в котором произошла ошибка.

Коды, в которых опознаватели устанавливаются по указанному принципу, известны как коды Хэмминга.

 

9 Лекция 9  Групповые коды. Определение проверочных равенств

 

Цель лекции: определение и изучение методов помехоустойчивого кодирования , применяемых в информационных подсистемах АСУ.

 

Содержание лекции: принципы помехоустойчивого кодирования. Построение двоичного группового кода. Составление таблицы опознавателей и проверочных равенств.

 

9.1 Случай исправления одиночных и двойных независимых ошибок

 

В качестве опознавателей одиночных ошибок в первом и втором разрядах можно принять, как и ранее, комбинации 0...001 и 0...010.

Однако, в качестве опознавателя одиночной ошибки в третьем разряде комбинацию 0...011 взять нельзя. Та­кая комбинация соответствует ошибке одновременно в первом и во втором разрядах, а она также подлежит исправлению и, следовательно, ей должен соответство­вать свой опознаватель 0...011.

В качестве опознавателя одиночной ошибки в третьем разряде можно взять только трехразрядную комбинацию 0...0100, так как множество двухразрядных комбинаций уже исчерпано. Подлежащий исправлению вектор ошиб­ки 0...0101 также можно рассматривать как результат суммарного воздействия двух векторов ошибок 0...0100 и 0...001 и, следовательно, ему должен быть поставлен в соответствие опознаватель, представляющий собой сумму по модулю 2 опознавателей этих ошибок, т. е. 0...0101.

Аналогично находим, что опознавателем вектора ошибки 0...0110 является комбинация 0...0110.

Определяя опознаватель для одиночной ошибки в чет­вертом разряде, замечаем, что еще не использована одна из трехразрядных комбинаций, а именно 0...0111. Однако, выбирая в качестве опознавателя единичной ошибки в i-м разряде комбинацию с числом разрядов, меньшим i, необходимо убедиться в том, что для всех остальных подлежащих исправлению векторов ошибок, имеющих единицы в i-м и более младших разрядах, получатся опознаватели, отличные от уже использован­ных. В нашем случае, подлежащими исправлению век­торами ошибок с единицами в четвертом и более младших разрядах являются:

                         0...01001, 0...01010, 0...01100.

Если одиночной ошибке в четвертом разряде поста­вить в соответствие опознаватель 0...0111, то для указан­ных векторов опознавателями должны были бы быть со­ответственно

    0...0111              0...0111              0...0111

0...0001           0...0001          0...0100

    0...0110               0...0110              0…0011   .

   

Однако эти комбинации уже использованы в качестве опознавателей других векторов ошибок, а именно:

0...0110, 0...0101, 0...0011.

Следовательно, во избежание неоднозначности при декодировании в качестве опознавателя одиночной ошиб­ки в четвертом разряде следует взять четырехразрядную комбинацию 1000. Тогда для векторов ошибок

0...01001, 0...01010, 0...01100

опознавателями соответственно будут:

0...01001, 0...01010, 0...01100.

Аналогично можно установить, что в качестве опозна­вателя одиночной ошибки в пятом разряде может быть выбрана не использованная ранее четырехразрядная ком­бинация 01111.

Действительно, для всех остальных подлежащих исправлению векторов ошибок с единицей в пятом и более  младших  разрядах  получаем  опознаватели,  отли­чающиеся от ранее установленных:

Векторы ошибок          Опознаватели

0...010001                      0…01110

0...010010                      0…01101

                        0...010100                      0…01011

0...011000                       0…00111.

Продолжая сопоставление, можно получить таблицу опознавателей для векторов ошибок данного типа с лю­бым числом разрядов. Так как опознаватели векторов ошибок с единицами в нескольких разрядах устанавли­ваются как суммы по модулю 2 опознавателей одиночных ошибок в этих разрядах, то для определения правил построения кода и составления проверочных равенств достаточно знать только опознаватели одиночных оши­бок в каждом из разрядов. Для построения кодов, исправляющих двойные независимые ошибки, "таблица таких опознавателей определена с помощью вычис­лительной машины вплоть до 29-го разряда. Опозна­ватели одиночных ошибок в первых пятнадцати раз­рядах приведены в таблице 9.1

По тому же принципу аналогичные таблицы опре­делены и для ошибок других типов, например для трой­ных независимых ошибок, пачек ошибок в два и три символа.

 

   9.2 Определение проверочных равенств

 

Итак, для любого кода, имеющего целью исправлять наиболее вероятные векторы ошибок заданного канала связи (взаимно не­зависимые ошибки или пачки ошибок), можно составить таблицу опознавателей одиночных ошибок в каждом из разрядов. Пользуясь этой таблицей, нетрудно опреде­лить, символы каких разрядов должны входить в каждую из проверок на четность.

 

 

 

 

 

                     Т а б л и ц а  9.1

 

Рассмотрим в качестве примера опознаватели для ко­дов, предназначенных исправлять единичные ошибки (таблица 9.2).

 

          Т а б л и ц а  9.2

В принципе можно построить код, усекая эту табли­цу на любом уровне. Однако из таблицы видно, что оптимальными будут коды (7, 4), (15, 11), где первое число равно n, а второе k, и другие, которые среди кодов, имеющих одно и то же число проверочных символов, допускают наибольшее число информационных символов.

Усечем эту таблицу на седьмом разряде и найдем номера разрядов, символы которых должны войти в каж­дое из проверочных равенств.

Предположим, что в результате первой проверки на четность для младшего разряда опознавателя будет получена единица. Очевидно, это может быть следствием ошибки в одном из разрядов, опознаватели которых в младшем разряде имеют единицу. Следовательно, первое проверочное равенство должно включать символы 1, 3, 5 и 7-го разрядов:

a₁  a₃  a₅ a₇ = 0.

Единица во втором разряде опознавателя может быть следствием ошибки в разрядах, опознаватели которых имеют единицу во втором разряде. Отсюда второе про­верочное равенство должно иметь вид

a₂  a₃  a₆  a₇ = 0.

Аналогично находим и третье равенство:

a₄ a₅  a₆  a₇ = 0.

Чтобы эти равенства при отсутствии ошибок удов­летворялись для любых значений информационных сим­волов в кодовой комбинации, в нашем распоряжении имеется три проверочных разряда. Мы должны так выбрать номера этих разрядов, чтобы каждый из них вхо­дил только в одно из равенств. Это обеспечит одно­значное определение значений символов в проверочных разрядах при кодировании. Указанному условию удовлет­воряют разряды, опознаватели которых имеют по одной единице. В нашем случае это будут первый, второй и четвертый разряды.

Таким образом, для кода (7, 4), исправляющего одиночные ошибки, искомые правила построения кода, т. е. соотношения, реализуемые в процессе кодирования, принимают вид:

a_{1 =} a₃  a₅ a₇

                                                 a_{2 =} a₃  a₆  a₇                                                               (9.1)

a₄₌ a₅  a₆  a₇

 

Поскольку построенный код имеет минимальное хэммингово расстояние

d _min = 3, он в соответствии с (6.1) может использоваться с целью обнаружения еди­ничных и двойных ошибок. Обращаясь к таблице 9.2, легко убедиться, что сумма любых двух опознавателей еди­ничных ошибок дает ненулевой опознаватель, что и явля­ется признаком наличия ошибки.

Пример 9.1. Построим групповой код объемом 15 слов, способный исправлять единичные и обнаруживать двойные ошибки.

В соответствии с (6.17) код должен обладать минимальным хэмминговым расстоянием, равным 4. Такой код можно построить в два этапа. Сначала строим код заданного объема, способный исправлять единичные ошибки. Это код Хэмминга (7, 4). Затем добавляем еще один проверочный разряд, который обеспечивает четность числа еди­ниц в разрешенных комбинациях.

Таким образом, получаем код (8, 4). В процессе кодирования реализуются соотношения:

a_{1 =} a₃  a₅ a₇

 a_{2 =} a₃  a₆  a₇                

a₄₌ a₅  a₆  a₇

a₈₌ a₁ a₂a₃  a₄a₅ a₆ a₇

Обозначив синдром кода (7, 4) через S₁, результат общей проверки на четность — через S₂() и пренебрегая возможностью возникновения ошибок кратности 3 и выше, запишем алгоритм декоди­рования:

при S₁ = 0  и       S₂ = 0         ошибок нет;

при S₁ = 0  и       S₂ = 1         ошибка в восьмом разряде;

при S₁ ≠ 0  и       S₂ = 0         двойная ошибка ( коррекция блокируется,

                                               посылается запрос повторной передачи);

при S₁ ≠ 0  и       S₂ = 1         одиночная ошибка (осуществляется её исправление).

Пример 9.2. Используя табл. 9.2, составим правила построения кода (8,2), исправляющего все одиночные и двойные ошибки.

Усекая табл. 9.1 на восьмом разряде, найдем следующие прове­рочные равенства:

a₁  a₅  a₈ = 0                                                 a₃₄ a₅ = 0

a₂  a₅  a₈ = 0                                                 a₆  a₈ = 0

    a₃  a₅ = 0                                                          a₇  a₈ = 0

Соответственно правила построения кода выразим соотношениями

   a_{1 =} a₅  a₈                                                                                            a₄₌ a₅

   a_{2 =} a₅  a₈                                                                                             a_{6 =} a₈

     a_{3 =} a₅                                                                                                          a_{7 =} a₈

Отметим, что для построенного кода d_min = 5, и, следовательно, он может использоваться для обнаружения ошибок кратности от 1 до 4.

Соотношения, отражающие процессы кодирования и декодирования двоичных линейных кодов, могут быть реализованы непосредственно с использованием сумма­торов по модулю два. Однако декодирующие устройства, построенные таким путем для кодов, предназначенных исправлять многократные ошибки, чрезвычайно гро­моздки. В этом случае более эффективны другие прин­ципы декодирования.

 

10 Лекция 10  Матричное представление линейных кодов

 

Цель лекции: определение и изучение методов помехоустойчивого кодирования, с использованием матричного представления.

 

Содержание лекции: принципы помехоустойчивого кодирования. Использование матричного представления для построения двоичного группового кода.

 

         10.1 Матричное представление линейных кодов

 

   В теории кодирования элементами матрицы являются элементы некоторого поля GF(P), а строки и столбцы матрицы рассматриваются как векторы. Сложение и ум­ножение элементов матриц осуществляется по правилам поля GF(P).

Пример10.1 Вычислим произведение матриц с элементами из поля

 GF (2):

 

         

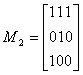
Элементы c_ik матрицы произведения М = М₁ М₂  будут равны:

                                    с₁₁ = (011) (101) = 0+0+1 = 1

                                    с₁₂ = (011) (110) = 0+1+0 = 1

                                    с₁₃ = (011) (100) = 0+0+0 = 0

                                    с₂₁ = (100) (110) = 1+0+0 = 1

                                    с₂₂ = (100) (110) = 1+0+0 = 1

                                    с₂₃ = (100) (100) = 1+0+0 = 1

                                    с₃₁ = (001) (101) = 0+0+1 = 1

                                    с₃₂ = (001) (110) = 0+0+0 = 0

                                    с₃₃ = (001) (100) = 0+0+0 = 0

Следовательно,

 

10.2 Образующая матрица линейного кода

 

Зная закон построения кода, определим все множество разрешенных кодовых комбинаций. Расположив их друг под другом, получим матрицу, совокупность строк кото­рой является подпространством векторного пространства n-разрядных кодовых комбинаций (векторов) из элемен­тов поля GF(P). В случае двоичного (п, k)-кода матрица насчитывает п столбцов и 2^k — 1 строк (исключая нуле­вую). Например, для рассмотренного ранее кода (8,2), исправляющего все одиночные и двойные ошибки, мат­рица имеет вид

a₅ a₈ a₁ a₂ a₃ a₄ a₆ a₇

       0  1   1  1  0   0   1   1

       1  0   1  1  1   1   0   0

          1  1   0  0  1   1   1   1

При больших п и k матрица, включающая все векторы кода, слишком громоздка. Однако совокупность векторов, составляющих линейное пространство разрешенных кодо­вых комбинаций, является линейно зависимой, так как часть векторов может быть представлена в виде линей­ной комбинации некоторой ограниченной совокупности векторов, называемой базисом пространства.

Совокупность векторов Vj, Vo, Va, ..., V_n называют линейно зависимой, когда существуют скаляры с₁...с_п (не все равные нулю), при которых

c₁ V₁ + c₁ V₁ + … + c₁ V₁  = 0.

В приведенной матрице, например, третья строка представляет собой суммы по модулю два первых двух строк.

Для полного определения пространства разрешенных кодовых комбинаций линейного кода достаточно записать в виде матрицы только совокупность линейно независимых векторов. Их число называют размерностью векторного пространства.

Среди 2^k-1 ненулевых двоичных кодовых комбина­ций — векторов их только k. Например, для кода (8,2)

 

                         а₁ а₂ а₃ а₄ а₅ а₆ а₇ а₈

           М _8,2 =  1  1  0  0  0  1  1  1

                         1  1  1  1  1  0  0  0.

 

Матрицу, составленную из любой совокупности век­торов линейного кода, образующей базис пространства, называют порождающей (образующей) матрицей кода.

Если порождающая матрица содержит k строк по п элементов поля GF(q), то код называют (n,k)-кодом. В каждой комбинации (n,k)-кода k информационных символов и п — k проверочных. Общее число разрешен­ных кодовых комбинаций (исключая нулевую)

                                          Q = q^k.-1.

Зная порождающую матрицу кода, легко найти раз­решенную кодовую комбинацию, соответствующую любой последовательности A_ki из k информационных символов. Она получается в результате умножения вектора A_ki на порождающую матрицу M_n,k:

                          A_ni = A_ki ∙ M_n,k .

Найдем, например, разрешенную комбинацию кода (8,2), соответствующую   информационным   символам   а₅=1, а₈=1.

             [11] M_8,2 = [11] = 00111111

Пространство строк матрицы остается неизменным при выполнении следующих элементарных операций над строками: 1) перестановка любых двух строк; 2) умно­жение любой строки на ненулевой элемент поля; 3) сло­жение какой-либо строки с произведением другой строки на ненулевой элемент поля, а также при перестановке столбцов.

Если образующая матрица кода М₂ получена из образующей матрицы кода  М₁с помощью элементарных операций над строками, то обе матрицы порождают один и тот же код. Перестановка столбцов образующей матрицы кода приводит к образующей матрице эквива­лентного кода. Эквивалентные коды весьма близки по своим свойствам. Корректирующая способность таких ко­дов одинакова.

Для анализа возможностей линейного (n,k)-кода, а также для упрощения процесса кодирования удобно, чтобы порождающая матрица (M_n,k) состояла из двух матриц: единичной матрицы размерности k×k и дописы­ваемой справа матрицы-дополнения (контрольной под­матрицы) размерности k • (п — k), которая соответствует п — k проверочным разрядам:

 

                    M_n,k = [ I_k P_k,n-k ] =                                     (10.1)

 

Разрешенные кодовые комбинации кода с такой порождающей матрицей отличаются тем, что первые k символов в них совпадают с исходными информационны­ми, а проверочными оказываются (n — k) последних сим­волов.

Действительно, если умножим вектор-строку A_ki =  матрицу

M_n,k = [ I_k P_k,n-k ], получим вектор A_n,i =,

где проверочные символы  являются линейными комбинациями информационных

                                                                                                        (10.2)

Коды, удовлетворяющие этому условию, называют сис­тематическими. Для каждого линейного кода существует эквивалентный систематический код.

B свою очередь, по заданной матрице-дополнению P _k,n-k  можно определить равенства, задающие правила построения кода. Единица в первой строке каждого столбца указывает на то, что в образовании соответ­ствующего столбцу проверочного разряда участвовал первый информационный разряд. Единица в следующей строке любого столбца говорит об участии в образовании проверочного разряда второго информационного разря­да и т. д.

Так как матрица-дополнение содержит всю информа­цию о правилах построения кода, то систематический код с заданными свойствами можно синтезировать путем построения соответствующей матрицы-дополнения.

Так как минимальное кодовое расстояние d для ли­нейного кода равно минимальному весу его ненулевых векторов, то в матрицу-дополнение должны быть включе­ны такие k строк, которые удовлетворяли бы следующе­му общему условию: вектор-строка образующей матри­цы, получающаяся при суммировании любых l(1≤l≤k) строк, должна содержать не менее d — l отличных от нуля символов.

Действительно, при выполнении указанного условия любая разрешенная кодовая комбинация, полученная суммированием l строк образующей матрицы, имеет не менее d ненулевых символов, так как l  ненулевых символов она всегда содержит в результате сумми­рования строк единичной матрицы.

Синтезируем таким путем образующую матрицу дво­ичного систематического кода (7,4) с минимальным кодовым расстоянием d = 3.

В каждой вектор-строке матрицы-дополнения соглас­но сформулированному условию (при l = 1) должно быть не менее двух единиц. Среди трехразрядных векторов таких имеется четыре: 011, 110, 101, 111.

Эти векторы могут быть сопоставлены со строками единичной матрицы в любом порядке. В результате получим матрицы систематических кодов, эквивалентных коду Хэмминга, например:

                               M_7,4   =

Нетрудно убедиться, что при суммировании несколь­ких строк такой матрицы (l>1) получим вектор-строку, содержащую не менее d = 3 ненулевых символов.

Имея образующую матрицу систематического кода M_n,k = [ I_k P_k,n-k ], можно построить так называемую про­верочную (контрольную) матрицу Н размерности (n-k) × n:

 

                     H =  =  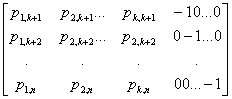                    (6.29)

При умножении неискаженного кодового вектора A_ni на матрицу, транспонированную к матрице Н, получим вектор, все компоненты которого равны нулю:

 

A_ni Н^T=│,,…,,...,│∙=│S_k+1, S_k+2,…,S_j,… S_n│=│0,0,…0,…0│.

 

Каждая компонента S_j является результатом проверки справедливости соответствующего уравнения декодиро­вания:

                                   

 

11 Лекция 11 Циклические коды. Математические основы для построения циклических кодов

 

Цель лекции: определение и изучение методов помехоустойчивого кодирования.

Понятие об образующем многочлене.

 

Содержание лекции: циклические коды. Общие понятия и определения.  Идеал и порождающий многочлен. Требования к образующему  многочлену.

 

11.1 Построение циклических кодов

Общие понятия и определения. Любой групповой код (п, k) может быть записан в виде матрицы, включающей k линейно независимых строк по п символов и, наоборот, любая совокупность k линейно независимых п-разрядных кодовых комбинаций может рассматриваться как обра­зующая матрица некоторого группового кода. Среди все­го многообразия таких кодов можно выделить коды, у которых строки образующих матриц связаны дополни­тельным условием цикличности. Все строки образующей матрицы такого кода могут быть получены циклическим сдвигом одной комбинации, называемой образующей для данного кода. Коды, удовлетворяющие этому условию, получили название цикли­ческих кодов.

Сдвиг осуществляется справа налево, причем крайний левый символ каждый раз переносится в конец комбина­ции. Запишем, например, совокупность кодовых комбина­ций, получающихся циклическим сдвигом комбинации 001011:

                                        G =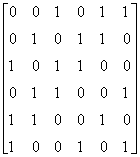  

 

Число возможных циклических ( п ,k )-кодов значи­тельно меньше числа различных групповых (п, k)-кодов.

При описании циклических кодов n-разрядные кодо­вые комбинации представляются в виде многочленов фиктивной переменной х. Показатели степени у х соот­ветствуют номерам разрядов (начиная с нулевого), а коэффициентами при х в общем случае являются элементы поля GF(q). При этом наименьшему разряду числа соответствует фиктивная переменная

 х°= 1. Мно­гочлен с коэффициентами из поля GF(q] называют многочленом над полем GF(q). Так как мы ограничиваем­ся рассмотрением только двоичных кодов, то коэффи­циентами при х будут только цифры 0 и 1. Иначе говоря, будем оперировать с многочленами над полем GF(2).

Запишем, например, в виде многочлена образующую кодовую комбинацию 01011:

G(x) = 0 • х⁴ + 1 • х³ + 0 • х² + 1 . х + 1 .

Поскольку члены с нулевыми коэффициентами при записи многочлена опускаются, образующий многочлен:

                                            G(x) = x³ + x+1.                                             (11.1)

Наибольшую степень х в слагаемом с ненулевым ко­эффициентом называют степенью многочлена. Теперь действия над кодовыми комбинациями сводятся к дей­ствиям над многочленами. Суммирование многочленов осуществляется с приведением коэффициентов по модулю два.

Указанный циклический сдвиг некоторого образующе­го многочлена степени п — k без переноса единицы в конец кодовой комбинации соответствует простому умножению на х. Умножив, например, первую строку матрицы (001011), соответствующую многочлену  g_o(x) =x³+х+1, на х, получим вторую строку матрицы (010110), соответствующую многочлену x∙g_o(x).

Нетрудно убедиться, что кодовая комбинация, полу­чающаяся при сложении этих двух комбинаций, также будет соответствовать результату умножения многочлена х³ + х+1 на многочлен х+1. Действительно,

            0 0 1 0 1 1                                 х³ + 0 + х +1

        0 1 0 1 1 0                                               x +1

            0 1 1 1 0 1                                 х³ + 0 + х + 1

                                                          х⁴ + 0 + х² + x

                                                              х⁴ +  х³ + х² + 0 +1

Циклический сдвиг строки матрицы с единицей в старшем (n-м) разряде (слева) равносилен умножению соответствующего строке многочлена на х с одновремен­ным вычитанием из результата многочлена х^п +1 =  х^п— 1, т. е. с приведением по модулю х^п + 1.

Отсюда ясно, что любая разрешенная кодовая комби­нация циклического кода может быть получена в резуль­тате умножения образующего многочлена на некоторый другой многочлен с приведением результата по модулю х^п + 1. Иными словами, при соответствующем выборе образующего многочлена любой многочлен циклического кода будет делиться на него без остатка.

Ни один многочлен, соответствующий запрещенной кодовой комбинации, на образующий многочлен без остатка не делится. Это свойство позволяет обнаружить ошибку. По виду остатка можно определить и вектор ошибки.

Умножение и деление многочленов весьма просто осу­ществляется на регистрах сдвига с обратными связями, что и явилось причиной широкого применения цикличе­ских кодов.

 

11.2 Математическое введение к циклическим кодам

 

 Так как каждая разрешенная комбинация n-разрядного циклического кода есть произведение двух многочленов, один из которых является образующим, то эти комби­нации можно рассматривать как подмножества всех произведений многочленов степени не выше n—1. Это наталкивает на мысль использовать для построения этих кодов еще одну ветвь теории алгебраических сис­тем, а именно — теорию колец.

Как следует из приведенного ранее определения (Л. 7), для образования кольца на множестве n-разрядных кодовых комбинаций необходимо задать две опе­рации: сложение и умножение.

Операция сложения многочленов уже выбрана нами с приведением коэффициентов по модулю два.

Определим теперь операцию умножения. Нетрудно ви­деть, что операция умножения многочленов по обычным правилам с приведением подобных членов по модулю два может привести к нарушению условия замкнутости.    Действительно, в результате умножения могут быть полу­чены многочлены более высокой степени, чем п—1, вплоть до 2(п— 1), а соответствующие им кодовые комби­нации будут иметь число разрядов, превышающее п и, следовательно, не относятся к рассматриваемому множе­ству. Поэтому операция символического умножения за­дается так:

1)      многочлены перемножаются по обычным прави­лам, но с приведением подобных членов по модулю два;

2)      если старшая степень произведения не превышает n—1, то оно и явля-ется результатом символического умножения;

3)      если старшая степень произведения больше или равна п, то многочлен произведения делится на заранее определенный многочлен степени п и результатом символического умножения считается остаток от деления.

Степень остатка не превышает n—1, и следователь­но, этот многочлен принадлежит к рассматриваемому множеству n - разрядных кодовых комбинаций. При анализе циклического сдвига с перенесением единицы в конец кодовой комбинации установлено, что таким многочленом n-й степени является многочлен х^п+1.

Действительно, в результате умножения многочлена степени п — 1 на х получим

                G(x) = (x^{n- 1}+ x^{n- 2}+…+ x+1)∙x = xⁿ+ x^{n- 1}+…+ x                      (11.2)

 

 

Следовательно, чтобы результат умножения и теперь соответствовал кодовой комбинации, образующейся пу­тем циклического сдвига исходной кодовой комбинации, в нем необходимо заменить х^п на 1. Такая замена эквивалентна делению полученного при умножении много­члена на хⁿ+1с записью в качестве результата остатка от деления, что обычно называют взятием остатка или приведением по модулю х^п+1 (сам остаток при этом называют вычетом).

Выделим теперь в нашем кольце подмножество всех многочленов, кратных некоторому многочлену g(x). Такое подмножество называют идеалом, а многочлен g(x) — по­рождающим многочленом идеала.

Количество различных элементов в идеале определя­ется видом его порождающего многочлена. Если на по­рождающий многочлен взять 0, то весь идеал будет составлять только этот многочлен, так как умножение его на любой другой многочлен дает 0.

Если за порождающий многочлен принять 1[g(x) =1], то в идеал войдут все многочлены кольца. В общем слу­чае число элементов идеала, порожденного простым мно­гочленом степени n—k, составляет 2^k.

Теперь становится понятным, что циклический двоич­ный код в построенном нами кольце n-разрядных двоич­ных кодовых комбинаций является идеалом.

Остается выяснить, как выбрать многочлен g(x), способный породить циклический код с заданными свой­ствами.

 

12 Лекция 12 Циклические коды. Определение образующего многочлена

 

Цель лекции: определение и изучение методов помехоустойчивого кодирования. Определение образующего многочлена.

 

Содержание лекции: циклические коды. Общие понятия и определения.  Идеал и порождающий многочлен. Выбор образующего многочлена по заданному объёму кода и заданной корректирующей способности.

 

12.1 Требования, предъявляемые к образующему многочлену

 

Согласно определению циклического кода все мно­гочлены, соответствующие его кодовым  комбинациям, должны делиться на g(x) без остатка. Для этого доста­точно, чтобы на g(x] делились без остатка многочлены, составляющие образующую матрицу кода.  Последние получаются циклическим сдвигом, что соответствует по­следовательному умножению g(x] на х с приведением по модулю х^п+1.

Следовательно, в общем случае многочлен g_i(x) является остатком от деления произведения g(x) • хⁱ на многочлен х^п+ 1 и может быть записан так:

       g_i(x} = g(x}xⁱ + c(xⁿ+1),                                                                 (12.1)

где с = 1, если степень g(x)xⁱ превышает п - 1; с = О, если степень g(x)xⁱ не превышает п—1.

Отсюда следует, что все многочлены матрицы, а по­этому и все многочлены кода будут делиться на g(x) без остатка только в том случае, если на g(x) будет делиться без остатка многочлен х^п+1.

 Таким образом, чтобы g(x) мог породить идеал, а следовательно, и циклический код, он должен быть дели­телем многочлена  х^п+1.

Поскольку для кольца справедливы все свойства группы, а для идеала - все свойства подгруппы, кольцо можно разложить на смежные классы, называемые в этом случае классами вычетов по идеалу.

Первую строку разложения образует идеал, причем нулевой элемент располагается крайним слева. В качест­ве образующего первого класса вычетов можно выбрать любой многочлен, не принадлежащий идеалу. Остальные элементы данного класса вычетов образуются путем суммирования образующего многочлена с каждым многочленом идеала.

Если многочлен g(x) степени m = п — k является дели­телем х^п+1, то любой элемент кольца либо делится на g(x) без остатка (тогда он является элементом идеала), либо в результате деления появляется остаток r(х), представляющий собой многочлен степени не выше m-1.

Элементы кольца, дающие в остатке один и тот же многочлен r_i(x), относятся к одному классу вычетов. Приняв многочлены r(х) за образующие элементы клас­сов вычетов, разложение кольца по идеалу с образую­щим многочленом g(x) степени m можно представить таблице 12.1, где f(x) — произвольный многочлен степени не выше п - m -1.

         Т а б л и ц а  12.1

0	g(x)	xg(x)	(x+1)g(x)	…	f(x)g(x)
r1(x)	g(x)+ r1(x)	xg(x)+ r1(x)	(x+1)g(x) + r1(x)	…	f(x)g(x) + r1(x)
r2(x)	g(x)+ r2(x)	xg(x)+ r2(x)	(x+1)g(x) + r2(x)	…	f(x)g(x) + r2(x)
…	…	…	…	…	…
…	…	…	…	…	…
rz(x)	g(x)+ rz(x)	xg(x) + rz(x)	(x+1)g(x) + rz(x)	…	f(x)g(x) + rz(x)

 

Как отмечалось, групповой код способен исправить столько разновидностей ошибок, сколько различных классов насчитывается в приведенном разложении. Сле­довательно, корректирующая способность циклического кода будет тем выше, чем больше остатков может быть образовано при делении многочлена, соответствующего искаженной кодовой комбинации, на образующий многочлен кода.

Наибольшее число остатков, равное 2^m-1 (исключая нулевой), может обеспечить только неприводимый (прос­той) многочлен, который делится сам на себя и не делит­ся ни на какой другой многочлен (кроме 1).

 

12.2 Выбор образующего многочлена по заданному объёму кода и заданной корректирующей способности

 

По заданному объему кода однозначно определяется число информационных разрядов k. Далее необходимо найти наименьшее п, обеспечивающее обнаружение или исправление ошибок заданной кратности. В случае циклического кода эта проблема сводится к нахождению нужного многочлена g(x).

Начнем рассмотрение с простейшего циклического кода, обнаруживающего все одиночные ошибки.

   12.2.1 Обнаружение одиночных ошибок

   Любая принятая по каналу связи кодовая комбинация h(x), возможно содер­жащая ошибку, может быть представлена в виде суммы по модулю два неискаженной комбинации кода f(x) и вектора ошибки ξ(x):

                                  h(x) = f(x) ξ(x)                                                 ( 12.1)

При делении h(x) на образующий многочлен g(x) остаток, указывающий на наличие ошибки, обнаружи­вается только в том случае, если многочлен, соответ­ствующий вектору ошибки, не делится на g(x): f(x) — неискаженная комбинация кода и, следовательно, на g(x) делится без остатка.

Вектор одиночной ошибки имеет единицу в искажен­ном разряде и нули во всех остальных разрядах. Ему соответствует многочлен ξ(x) = xⁱ. Последний не должен делиться на g(x). Среди неприводимых многочленов, входящих в разложении х^п+1, многочленом наименьшей степени, удовлетворяющим указанному условию, являет­ся х+1. Остаток от деления любого многочлена на x+1 представляет собой многочлен нулевой степени и может принимать только два значения: 0 или 1. Все коль­цо в данном случае состоит из идеала, содержащего многочлены с четным числом членов, и одного класса вычетов, соответствующего единственному остатку, равному 1. Таким образом, при любом числе информацион­ных разрядов необходим только один проверочный раз­ряд. Значение символа этого разряда как раз и обеспе­чивает четность числа единиц в любой разрешенной кодовой комбинации, а следовательно, и делимость ее на  x+ 1.

Полученный циклический код с проверкой на чет­ность способен обнаруживать не только одиночные ошиб­ки в отдельных разрядах, но и ошибки в любом не­четном числе разрядов.

 12.2.2 Исправление одиночных или обнаружение двойных ошибок

 Прежде чем исправить одиночную ошибку в при­нятой комбинации из п разрядов, необходимо определить, какой из разрядов был искажен. Это можно сделать только в том случае, если каждой одиночной ошибке в определенном разряде соответствуют свой класс выче­тов и свой опознаватель. Так как в циклическом коде опознавателями ошибок являются остатки от деления многочленов ошибок на образующий многочлен кода g(x), то g(x) должно обеспечить требуемое число раз­личных остатков при делении векторов ошибок с едини­цей в искаженном разряде. Как отмечалось, наибольшее число остатков дает неприводимый многочлен. При степе­ни многочлена т = п - k он может дать 2^{n- k}- 1 нену­левых остатков (нулевой остаток является опознавателем безошибочной передачи).

Следовательно, необходимым условием исправления любой одиночной ошибки является выполнение неравен­ства

                                                                                                        (12.2)

где С_п — общее число разновидностей одиночных ошибок в кодовой комбинации из п символов; отсюда находим степень образующего многочлена кода

                                         т = п — k ≥ log₂(n+l)                                            (12.3)

и общее число символов в кодовой комбинации. Наиболь­шие значения k и п для различных т можно найти, поль­зуясь таблицей 12.1.

Как указывалось, образующий многочлен g(x) должен быть делителем двучлена х^п+1. Доказано [20], что лю­бой двучлен типа x^2m-1+1 = х^п+1 может быть пред­ставлен произведением всех неприводимых многочленов, степени которых являются делителями числа т (от 1 до m включительно).

 

                       Т а б л и ц а  12.1

Следовательно, для любого т существует по крайней мере один неприводимый многочлен степени т, входящий сомножителем в разложение дву­члена х^п+ 1.

Пользуясь этим свойством, а также имеющимися [20] таблицами многочленов, неприводимых при двоичных коэффициентах, выбрать образующий мно­гочлен при известных п и т несложно. Определив образующий многочлен, необходимо убедиться в том, что он обеспечивает заданное число остатков.

Пример 12.1 Выберем образующий многочлен для случая п = 15 и m = 4.

Двучлен x¹⁵+l можно записать в виде произведения всех не­приводимых многочленов, степени которых являются делителями числа 4. Последнее делится на 1, 2, 4. В таблице неприводимых многочленов находим один многочлен первой степени, а именно х+1, один многочлен второй степени х² + х+1 и три многочлена четвертой степени: х⁴+ х+1, х⁴ + х³+1, х⁴ + х³+ х² + х+ 1. Перемножив все многочлены, убедимся в справед­ливости соотношения (х+ 1)(х² + х + 1)( х⁴+ х+1)( х⁴ + х³+ х² + х+ 1) = x¹⁵+l.

Один из сомножителей четвертой степени может быть принят за обра­зующий многочлен кода. Возьмем, например х⁴ + х³+1, многочлен, или в виде двоичной последовательности 11001.

Степени соответствующих им многочленов меньше степени обра­зующего многочлена g(x). Поэтому они сами являются остатками при нулевой целой части. Остаток, соответствующий вектору ошибки в следующем старшем разряде, получаем при делении 00.. .10000 на 11001, т.е.

1 0000 | 11001

                                             1 1001

    1001

Аналогично могут быть найдены и остальные остатки. Однако их можно получить проще, деля на g(x) комбинацию в виде единицы с рядом нулей и выписывая все промежуточные остатки:

    1 000000000… | 11001                            Остатки 

 1 1001

        10010                                              1001                                     1101

    11001                                               1011                                     0011

          1011                                               1111                                     0110

        …                                                     0111                                     1100

 …                                                      1110                                      0001

        …                                                      0101                                     0010

 …                                                       1010                                     0100

…                                                                                                     1000

                                                                                                                                                                         

   При последующем делении остатки повторяются.

   С тем же успехом за образующий многочлен кода мог быть принят и многочлен х⁴ + х+1. При этом был бы получен код, эквивалентный выбранному. Однако использовать для тех же целей многочлен х⁴ + х³ + х² + x+1 нельзя. При проверке числа различных остатков обнаружи­вается, что их у него не 15, а только 5. Это объясняется тем, что многочлен х⁴ + х³ + х² + х + 1 входит в разложение не только двучлена x¹⁵+ 1, но и двучлена х⁵+ 1.

 

13 Лекция 13 Циклические коды. Математические основы для построения циклических кодов

 

Цель лекции: определение и изучение методов помехоустойчивого кодирования. Определение образующего многочлена.

 

Содержание лекции: циклические коды. Общие понятия и определения.  Идеал и порождающий многочлен. Выбор образующего многочлена по заданному объёму кода и заданной корректирующей способности.

 

13.1 Выбор неприводимого много­члена g(x)

 

В качестве об­разующего следует выбирать такой неприводимый много­член g(x) (или произведение таких многочленов), кото­рый, являясь делителем двучлена х^п+ 1, не входит в раз­ложение ни одного двучлена типа x^λ+1, степень которо­го К меньше п. В этом случае говорят, что многочлен g(x) принадлежит показателю степени п. В таблице 13.1 приведены основные характеристики некоторых кодов, способных исправлять одиночные ошибки или обнаруживать все одиночные и двойные ошибки.

 

 

 

 

          Т а б л и ц а  13.1

Эти коды могут быть использованы для обнаружения любых двойных ошибок. Многочлен, соответствующий вектору двойной ошибки, имеет вид (x) = xⁱ+x^j, или (x) =  xⁱ(x^j-i+1) при j>i. Так как j-i<n, a g(x) не кратен х и принадлежит показателю степени п, то(x)  не делится на g(x), что и позволяет обнаружить двойные ошибки.

Обнаружение ошибок кратности три и ниже. Обра­зующие многочлены кодов, способных обнаруживать одиночные, двойные и тройные ошибки можно опреде­лить, базируясь на следующем указании Хэмминга. Если известен образующий многочлен р(х^т} кода длины п, позволяющего обнаруживать ошибки некоторой крат­ности 2, то образующий многочлен g(x) кода, способного обнаруживать ошибки следующей кратности (z+1), мо­жет быть получен умножением многочлена р(х^т) на мно­гочлен х+1, что соответствует введению дополнительной проверки на четность. При этом число символов в ком­бинациях кода за счет добавления еще одного проверочно­го символа увеличивается до n+1.

В таблице 13.2 приведены основные характеристики не­которых кодов, способных обнаруживать ошибки кратно­сти три и менее.

 

                      Т а б л и ц а  13.2

 

13.2 Обнаружение и исправление независимых ошибок произвольной кратности

 

Важнейшим классом кодов, используемых в каналах, где ошибки в последователь­ностях символов возникают независимо, являются коды Боуза — Чоудхури — Хоквингема. Доказано, что для любых целых положительных чисел т и s<n/2 суще­ствует двоичный код этого класса длины п = 2^т—1 с числом проверочных символов не более ms, который способен обнаруживать ошибки кратности 2s или исправ­лять ошибки кратности s. Для понимания теоретических аспектов этих кодов необходимо ознакомиться с рядом новых понятий высшей алгебры.

13.2.1 Обнаружение и исправление пачек ошибок. Для про­извольного линейного блокового (п, k)-кода, рассчитан­ного на исправление пакетов ошибок длины b или менее, основным соотношением, устанавливающим связь кор­ректирующей способности с числом избыточных симво­лов, является граница Рейджера:

                                            n - k ≥ 2b.                                                           (13.1)

При исправлении линейным кодом пакетов длины b или менее с одновременным обнаружением пакетов длины l≥b или менее требуется по крайней мере b+l проверочных символов.

Из циклических кодов, предназначенных для исправ­ления пакетов ошибок, широко известны коды Бартона, Файра и Рида — Соломона.

Первые две разновидности кодов служат для исправ­ления одного пакета ошибок в блоке. Коды Рида — Соломона способны исправлять несколько пачек ошибок.

 

13.3 Методы образования циклического кода

 

Существует несколько различных способов кодирования. Принципиально наиболее просто комбинации циклического кода можно получить, умножая многочлены а(х), соответст­вующие комбинациям безызбыточного кода (информаци­онным символам), на образующий многочлен кода g(x). Такой способ легко реализуется. Однако он имеет тот существенный недостаток, что получающиеся в резуль­тате умножения комбинации кода не содержат инфор­мационные символы в явном виде. После исправления ошибок такие комбинации для выделения информацион­ных символов приходится делить на образующий много­член кода.

Применительно к циклическим кодам принято (хотя это и не обязательно) отводить под информационные k символов, соответствующих старшим степеням много­члена кода, а под проверочные n — k символов низших разрядов.

Чтобы получить такой систематический код, применя­ется следующая процедура кодирования.

Многочлен а(х), соответствующий k-разрядной ком­бинации безизбыточного кода, умножаем на х^т, где т = п — k. Степень каждого одночлена, входящего в а(х), увеличивается, что по отношению к комбинации кода означает необходимость приписать со стороны младших разрядов m нулей. Произведение а(х)х^т делим на обра­зующий многочлен g(x). В общем случае при этом полу­чаем некоторое частное q(x) той же степени, что и а(х) и остаток r(х). Последний прибавляем к а(х)х^т. В резуль­тате получаем многочлен

f(x) = a(x)x^m + r(x).                                                     (13.2)

Поскольку степень g(x) выбираем равной т, степень остатка r(х) не превышает m—1. В комбинации, соответствующей многочлену а(х)х^т, т младших разря­дов нулевые, и, следовательно, указанная операция сло­жения равносильна приписыванию r(х) к а(х) со стороны младших разрядов.

Покажем, что f(x) делится на g(x) без остатка, т. е. является многочленом, соответствующим комбинации кода. Действительно, запишем многочлен а(х)х^т в виде

                                a(x)x^m=q(x)g(x) + r(x).                                                     (13.3)

Так  как операции сложения и вычитания по модулю два идентичны, r(х) можно перенести влево, тогда

                                а(х)х^т + r(x) = f(x) = q(x)g(x)                                    (13.4)

что и требовалась доказать.

Таким образом, циклический код можно строить, приписывая к каждой комбинации безизбыточного кода остаток от деления соответствующего этой комбинации многочлена на образующий многочлен кода. Для кодов, число информационных символов в которых больше чис­ла проверочных, рассмотренный способ реализуется наи­более просто.

Следует указать еще на один способ кодирования. Так как циклический код является разновидностью груп­пового кода, то его проверочные символы должны выра­жаться через суммы по модулю два определенных инфор­мационных символов.

Равенства для определения проверочных символов могут быть получены путем решения рекуррентных соот­ношений

                                                                                                 (13.5)

 

где h— двоичные коэффициенты так называемого гене­раторного многочлена h(х), определяемого так

            h(x) = (xⁿ + 1)/g(x) = h₀ + h₁ x +... + h_k x.                                          (13.6)

Соотношение (13.6) позволяет по заданной последо­вательности информационных сигналов a₀, a₁ ..., a_k-1 вычислить п — k проверочных символов a_k,, a_k+1, …, a_n-1  роверочные символы, как и ранее, размещают­ся на местах младших разрядов.

 

13.4 Матричная запись циклического кода

 

Полная обра­зующая матрица циклического кода M_n,k составляется из двух матриц: единичной I_k (соответствующей k инфор­мационным разрядам) и дополнительной Ck,n-k (соот­ветствующей проверочным разрядам):

                                         M_n,k= ||I_kС._k,n-k ||.                                                          (13.7)

Построение матрицы I_k трудностей не представляет.

Если образование циклического кода производится на основе решения рекуррентных соотношений, то его дополнительную матрицу можно определить, восполь­зовавшись правилами, указанными ранее. Однако, обычно строки дополнительной матрицы циклического кода C_k,n-k определяются путем вычисления многочленов r(х). Для каждой строки матрицы I_k соответствующий r(х) находят делением информационного многочлена а(х)х^т этой строки на образующий многочлен кода g(x).

Пример 13.1 Запишем образующую матрицу для циклического кода (15,11) с порождающим многочленом g(x) = х⁴ + х³ + 1.

Воспользовавшись результатами ранее проведенного деления, полу­чим

M_15,11 =

Существует другой способ построения образующей матрицы, бази­рующийся на основной особенности циклического (п, k)-кода (Л.№11). Он проще описанного, но получающаяся матрица менее удобна.

Матричная запись кодов достаточно широко распространена.

 

13.5 Укороченные циклические коды

 

 Корректирующие возможности циклических кодов определяются степенью т образующего многочлена. В то время как необходимое число информационных символов может быть любым целым числом, возможности в выборе разрядности кода весьма ограничены. Однако можно построить код минимальной разряд­ности, заменив в (п, k) -коде j первых информационных символов нулями и исключив их из кодовых комбинаций. Код уже не будет циклическим, поскольку циклический сдвиг одной разрешенной кодовой комбинации не всегда приводит к другой разрешенной комбинации того же кода. Получаемый таким путем линейный (п-j, k -j)-код называют укороченным циклическим кодом. Мини­мальное расстояние этого кода не менее, чем минималь­ное кодовое расстояние (п, k)-кода, из которого он полу­чен. Матрица укороченного кода получается из образую­щей матрицы (п, k)-кода исключением j строк и столб­цов, соответствующих старшим разрядам. Например, образующая матрица кода (9,5), полученная из матри­цы кода (15,11), имеет вид

                                M_9,5 =   

 

Список литературы 

1.     Сергиенко А.Б. Цифровая обработка сигналов. – СПб.: Питер, 2002.

2.     Гультяев А.К. MATLAB 5.2. Имитационное моделирование в среде Windows: Практическое пособие. – СПб.: КОРОНА принт, 1999.

3.      Гоноровский И.С.  Радиотехнические цепи и сигналы. – М.: Радио и связь, 1994.

4.     Дмитриев В.И. Прикладная теория информации. – М.: Высшая школа, 1989.

5.     Зюко А.Г. Теория передачи сигналов. – М.: Радио и связь, 1986.

6.     Баскаков С.И. Радиотехнические цепи и сигналы. – М.: Высшая школа, 2000.

7.     Баранов А.А. Квантование по уровню и временная дискретизация в цифровых системах управления. – М., 1990.

8.     Баричев С.Г. Основы современной криптографии: Учебный курс. – М.: 2001.

9.     Куприянов М.С. Техническое обеспечение цифровой обработки сигналов: Справочник. – СПб.: Наука и техника, 2000.

10. Разевиг В.Д., Лаврентьев Г.В., Златин И.Л. SystemView средство системного проектирования радиоэлектронных устройств - М.:Горячая линия-Телеком, 2002.

11. Скляр Б. Цифровая связь: Теоретические основы и практическое применениею - М.: Вильямс, 2003.

12. Гаранин М.В., Журавлев В.И., Кунегин С.В. Системы и сети передачи

Информацию - М.: Радио и связь, 2000.

13. Передача дискретных сообщений: Учебник/Под ред. В.П. Шувалова. -

М.: Радио и связь, 1990.