Алматинский институт энергетики и связи
Кафедра инженерной кибернетики
ТЕОРИЯ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Методические указания к выполнению лабораторных работ для студентов специальности 5В0702 – Автоматизация и управление
Алматы 2010
СОСТАВИТЕЛИ: Хисаров Б.Д., Аталыкова А.К. Теория нелинейных систем автоматического управления. Методические указания к выполнению лабораторных работ для студентов специальности 5В0702 – Автоматизация и управление. – Алматы: АИЭС, 2010 – 18 с.
Рассматриваются вопросы изучения фазовых портретов линейных систем второго порядка, исследование систем с переменной структурой, исследование автоколебаний в нелинейных системах автоматического управления.
1 Лабораторная работа №1. Изучение фазовых портретов линейных систем второго порядка
Цель работы: знакомство с одним из методов исследования нелинейных систем - методом фазовой плоскости; исследование взаимосвязей между корнями характеристического уравнения переходного процесса и фазовыми портретами линейных систем второго порядка.
1.1 Общие сведения
Метод фазового пространства применим для исследования как линейных, так и нелинейных систем. Наиболее наглядное представление дает рассмотрение линейной системы, описываемой дифференциальным уравнением второго порядка.
![]() (1.1)
(1.1)
где х - отклонение регулируемой (выходной) координаты системы от состояния равновесия.
Введем фазовые координаты ![]() и перепишем уравнение (1.1) в
следующем виде:
и перепишем уравнение (1.1) в
следующем виде:
 (1.2)
(1.2)
Очевидно, что в плоскости (х1, х2) состоянию равновесия системы будет соответствовать начало координат.
Интегрирование уравнений (1.2) дает уравнения кривых, по которым строят фазовые траектории.
![]() . (1.3)
. (1.3)
Конкретный вид функции зависит от коэффициентов ![]() . Но так как эти же
коэффициенты определяют и корни характеристического уравнения данной системы
. Но так как эти же
коэффициенты определяют и корни характеристического уравнения данной системы
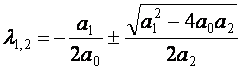 ,
(1.4)
,
(1.4)
то существует однозначная
зависимость между корнями ![]() и типом фазового портрета линейной системы
2-го порядка.
и типом фазового портрета линейной системы
2-го порядка.
При этом возможны шесть различных случаев:
1) корни вещественные и отрицательные
![]() -
-
система устойчивая;
2) корни комплексные и имеют отрицательные вещественные части
![]()
- система устойчивая;
3) корни чисто мнимые
![]()
- колебательная граница устойчивости линейной системы;
4) корни комплексные и имеют положительные вещественные части
![]()
- неустойчивая линейная система;
5) корни вещественные положительные
![]()
- неустойчивая линейная система;
6) корни вещественные и имеют разные знаки
![]()
- система неустойчивая.
Рассмотрим эти ситуации:
1) в системе есть апериодический затухающий переходной процесс и уравнение (1.1) имеет решение
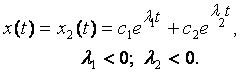 (1.5)
(1.5)
Вторая фазовая координата по времени будет иметь вид
![]() . (1.6)
. (1.6)
На фазоворй плоскости все координаты пересекаются в начале координат и имеются следующие две асимптоты
![]() и
и ![]() ;
(1.7)
;
(1.7)
2) имеется затухающий колебательный процесс
![]() , (1.8)
, (1.8)
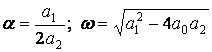 , (1.9)
, (1.9)
![]() , (1.10)
, (1.10)
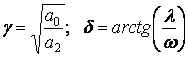 . (1.11)
. (1.11)
Уравнения (1.8), (1.10) на фазовой плоскости дают семейство спиралей.
3) имеется следующее решение
![]() ,
(1.12)
,
(1.12)
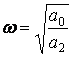 ,
то есть присутствуют незатухающие колебания
,
то есть присутствуют незатухающие колебания
Вторая фазовая координата будет иметь вид
![]() .
(1.13)
.
(1.13)
Для фазовой траектории уравнение будет иметь вид
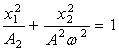 ,
(1.14)
,
(1.14)
то есть фазовые плоскости являются эллипсами.
4) решение уравнения имеет вид:
![]() ,
(1.15)
,
(1.15)
![]() ,
,
то есть имеют место колебания с бесконечно возрастающей амплитудой. Фазовая траектория – плоская расходящаяся спираль;
5) решение уравнения имеет вид:
![]() ,
(1.16)
,
(1.16)
![]() ,
(1.17)
,
(1.17)
то есть имеет место бесконечное возрастание выходной величины. На фазовой плоскости появятся две асимптоты
![]() и
и ![]() (1.18)
(1.18)
6) переходная характеристика будет апериордической, но фазовая траектория другая. Например, а1=0. Тогда уравнение (1.2) запишется в следующем виде
![]() (1.19)
(1.19)
или
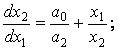 (1.20)
(1.20)
Если проинтегрируем уравнение (1.20), получим фазовые траектории в виде гипербол
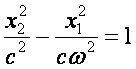 .
(1.21)
.
(1.21)
Асимптотами гипербол являются прямые ![]() ,
здесь
,
здесь ![]() .
.
1.2 Задание на лабораторную работу
1.2.1 Подберите значенеия параметров системы для различных вариантов корней храктеристического уравнения (для приведенных случаев).
1.2.2 Для различных начальных значений х0 и х00 определите переходные характеристики и фазовые траектории.
1.2.3 Выполните следующие задания в среде VisSim:
- для уравнений (1.1), (1.2) постройте структурную схема решения;
- выберите значения a 0, a1,
a2 для первого случая, определите ![]() и
и ![]() , установите на схеме оэффициенты k1
жәине k2;
, установите на схеме оэффициенты k1
жәине k2;
- для различных начальных условий получите переходные процессы х1 и определите значение коэффициента для времени tпп переходного процесса;
- используя координаты х1 и х2=х1, определите фазовые траектории системы;
1.2.4 Выполните задания предыдущих пунктов для всех (2, 3, 4, 5, 6) случаев.
1.3 Требования к отчету по работе
Отчет по работе должен содержать:
- схему системы;
- выбранные значения коэффициентов;
- корни характеристического уравнения;
- график переходного процесса;
- график фазовой траектории.
1.4 Контрольные вопросы
1.4.1 Объсните суть фазового метода.
1.4.2 Какая существует взаимосвязь между корнями характеристического уравнения и фазовыми портретами линейных систем второго порядка?
1.4.3 Как будет выглядеть фазовая координата устойчивой системы?
1.4.4 Как будет выглядеть фазовая координата, если в системе есть затухающий колебательный процесс?
1.4.5 Как будет выглядеть фазовая координата, если в системе есть незатухающие колебания?
1.4.6 Как будет выглядеть фазовая координата, если имеет место бесконечное возрастание выходной величины?
2 Лабораторная работа №2 Исследование систем с переменной структурой
Цель работы: построение и исследование фазовых портретов нелинейных систем 2-го порядка с переменной структурой.
Исследование переходных характеристик и фазовых портретов систем второго порядка в предыдущей лабораторной работе показывает, что имеются решения с неустойчивым движением. На практике могут оказаться случаи, когда невозможно получить устойчивую систему при определенных значениях параметров объекта управления. В то же время можно исследовать метод припасовывания для построения фазовых портретов нелинейных систем, допускающих кусочно-линейную аппроксимацию характеристик. Согласно этому методу, фазовую траекторию строят по частям, каждой из которых соответствуют линейные участки характеристик, причем значения фазовых координат в конце каждого участка фазовой траектории являются начальными условиями для решения уравнения на следующем участке. Общий фазовый портрет системы получают «сшиванием» фазовых траекторий, найденных на отдельных участках.
В данной работе требуется построить фазовый портрет замкнутой нелинейной системы состоящей из линейной части и нелинейного элемента, осуществляющего переключения структуры при заданном алгоритме управления (см.рисунок 2.1).
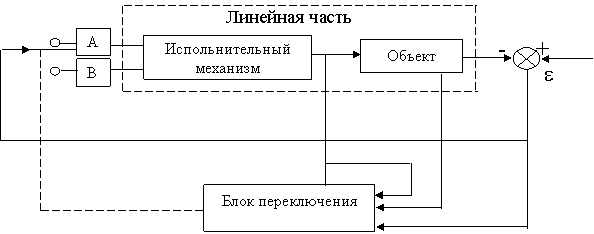 |
Рисунок 2.1 – Схема замкнутой нелинейной системы
Метод припасовывания лежит в основе построения систем с переменной структурой, дает дополнительную возможность получения различных желаемых процессов автоматического регулирования.
Рассмотрим переходной процесс системы, где исполнительный механизм вместе с регулируемым объектом описываются передаточной функцией
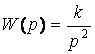 . (2.1)
. (2.1)
Первое и второе звенья характеризуется коэффициентами усиления k1 и k2 соответственно. Тогда уравнения динамики замкнутой системы будут
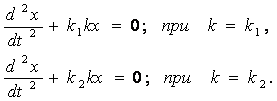
 Каждое из
этих уравнений является уравнением неустойчивой системы (незатухающие
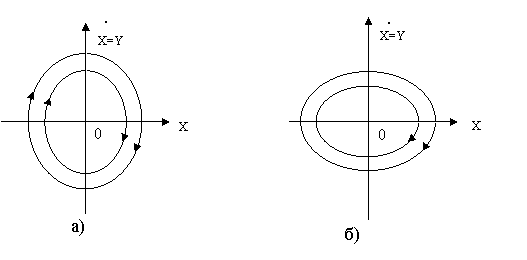
колебания). Фазовые портреты системы будут как на рисунках (2.2а) и (2.3б).
Каждое из
этих уравнений является уравнением неустойчивой системы (незатухающие
колебания). Фазовые портреты системы будут как на рисунках (2.2а) и (2.3б).
![]()
Обозначим
![]() .
.
Ведем следующий закон переключений:
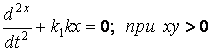 ,
(2.4)
,
(2.4)
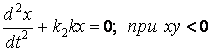 . (2.5)
. (2.5)
Если следовать законам переключения (2.4) и (2.5) и использовать метод припасовывания, то получим затухающий колебательный процесс, т.е. за счет переменности структуры система становится устойчивой (см.рисунок 2.3).
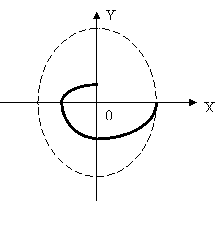
Рисунок 2.3 – Устойчивая система
Рассмотрим следующее уравнение системы второго порядка
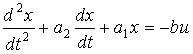 , (2.6)
, (2.6)
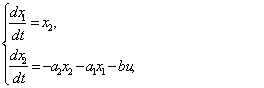 |
(2.7)
(2.8)
![]() ,
,
![]() ,
(2.9)
,
(2.9)
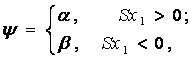 (2.10)
(2.10)
![]() и
и 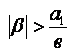 .
.
Тогда фазовые траектории будут как на рисунке 2.4а и 2.4б.
Из следующего соотношения
![]() , (2.11)
, (2.11)
здесь λ1,2 – корни уравнения (2.8), получим
S=x2-cx1 , (2.12)
S – одна из линий переключения. Из уравнения (2.10) видно, что линиями переключения является прямая S и ось абсцисс х1=0.
В работе надо исследовать три разлияных режима:
1) режим преключений (с>λ); здесь фазовый портрет будет выглядеть как на рисунке 2.5;
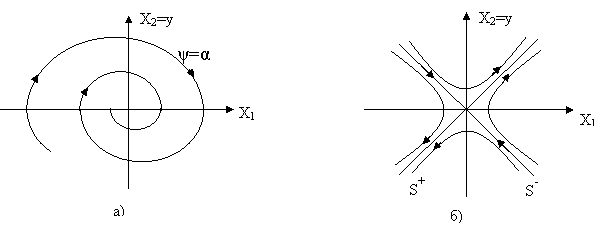
Рисунок 2.4– Фазовые траектории системы второго порядка
2) режим движения по вырожденным траекториям; в данном случае линия переключения S совпадает совпадает с асимптотой (устойчивой) S1 .
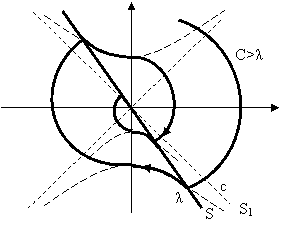 |
Рисунок 2.5– Фазовые портреты режима переключения
Изображающая, начинаясь с любой точки фазовой плоскости, попадает на линию переключения S, затем продолжает движение к началу координат по устойчивой асимптоте. При этом получаем переходной процесс максимум с одним перерегулированием (рисунок 2.6);
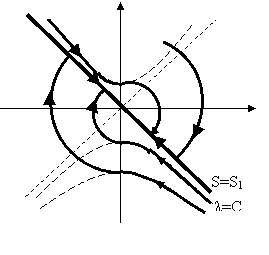
Рисунок 2.6 – Режим движения по заданной траектории
3) режим «скольжения» - наиболее интересный и полезный случай, когда с<λ. Особенностью является то, что фазовые портреты направлены навстречу друг другу на линии переключения S. В идеальном варианте изображаемая точка на пути S переключается с бесконечной частотой. И так как регулирующий вектор направлен в сторону начала координат, она устремляется к нулю вдоль линии переключения (см.рисунок 2.7).
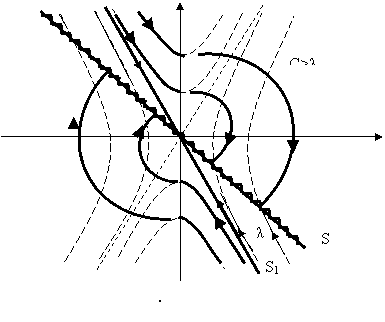
Рисунок 2.7 - Реализация устойчивых движений с помощью системы с переменной структурой
2.2 Задание на лабораторную работу
2.2.1 Постройте структурные схемы систем (2.1) и (2.2) в среде VisSim.
2.2.2 Придавая различные значения k1 и k2 для системы (2.1), получите переходные характеристики (во времени) x1(t) и фазовые портреты y=x2=f(x1).
2.2.3 Исследуйте зависимость tпп=t(k1,k2, k1/k2).
2.2.4 Для системы (2.2) сформируйте закон переключения (2.10).
2.2.5 Исследуйте режимы с>λ, с=λ и с<λ; получите переходные процессы и фазовые портреты.
2.2.6 Для «скользящего» режима исследуйте процесс при изменении параметров а1, а2, в.
2.3 Требования к отчету
Отчет по работе должен содержать:
- структурные схемы;
- фазовые траектории при выбранных коэффициентах;
- переходные процессы;
- выводы по выполненным исследованиям.
3 Лабораторная работа №3. Исследования автоколебаний в нелинейной системе методом гармонического баланса
Цель работы: изучение метода гармонического баланса и приобретение навыков расчета параметров автоколебаний и моделирования нелинейных систем.
3.1 Общие сведения
Для приближенного определения автоколебаний в нелинейной системе можно применить метод гармонического баланса. Он основан на использовании частотных характеристик нелинейных систем, получаемых при гармонической линеаризации нелинейностей.
Основная идея заключается в том, что линеаризация нелинейностей систем производится на режиме автоколебаний, которые предполагаются близкими к синусоидальным. Это предложение оказывается близким для большинства автоматических систем, линейная часть которых является хорошим низкочастотным фильтром.
Если на вход статического нелинейного элемента с характеристикой y=f(x) подать гармонический сигнал x(t)=Asinωt, то на выходе устанавливаются периодические колебания, которые можно представить как сумму гармонических составляющих с помощью ряда Фурье.
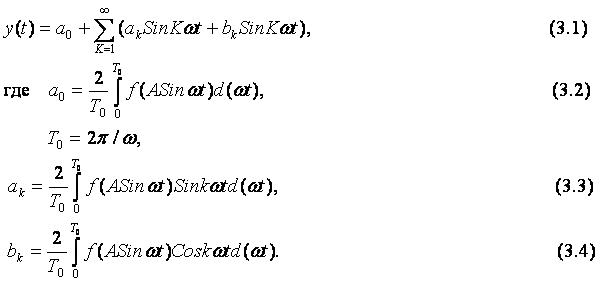
Предположим, что все гармоники, начиная со второй, имеют достаточно малую амплитуду по сравнению с первой, и ими можно пренебречь.
Тогда уравнение вынужденных колебаний напишется в виде:
![]() или
или
 где
где
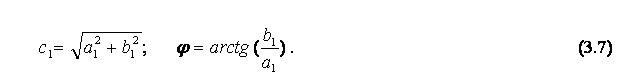 Для симметричных нелинейностей а0=0,
то тогда
Для симметричных нелинейностей а0=0,
то тогда
![]() (3.8)
(3.8)
Сравнивая y(t) с x(t), можно ввести характеристики, аналогичные частотным характеристикам линейных систем (3.9) и инверсную АФХ (3.10)
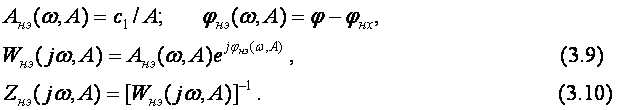
 Нелинейная система в виде замкнутой
системы может быть представлена в виде (см. рисунок 3.1).
Нелинейная система в виде замкнутой
системы может быть представлена в виде (см. рисунок 3.1).
Рисунок 3.1 – Нелинейная система
Если на вход нелинейного элемента подают гармонический сигнал с частотой ω1, то, с учетом свойства фильтра линейной части, в замкнутой системе возникнут незатухающие колебания.
Это означает, что система находится на границе устойчивости, которой соответствует условие:

Если уравнения (2.13) и (2.14) имеют действительное положительное решение (ωа, Аа), то в системе возможны автоколебания с частотой ωа и амплитудой Аа.
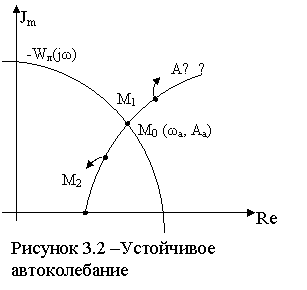
Систему (2.13) и (2.14) можно решать графически. Для этого в плоскости комплексного переменного строят АФХ линейной части Wл(jω) и инверсную АФХ нелинейного элемента Zнэ(А). Точка пересечения годографов Wл(jω) и Zнэ(А) определяют амплитуду Аа и частоту ωа. Если годографы не пересекаются, то автоколебания в системе невозможны. Метод гармонического баланса позволяет также ответить на вопрос, будут ли автоколебания устойчивы.
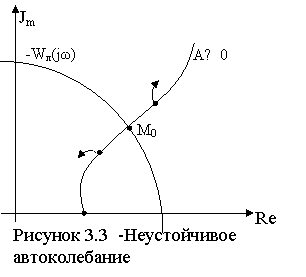
Пусть взаимное расположение кривых Wл(jω) и Zнэ(А) таково, что увеличение амплитуды колебаний соответствует движению по кривой Zнэ(А) вправо (см. рисунок 3.2). Тогда точки Wл(jω) и Zнэ(А) соответствуют автоколебаниям. Если под воздействием возмущения амплитуда колебаний возрастает (Аа+ΔАа), то новому состоянию нелинейного элемента будет соответствовать точка М1, которая находится вне АФХ линейной части. При этом Wл(jω) < Zнэ(А), значит, Wраз (jω, А)<1, и, следовательно, в этом состоянии система будет вести себя как устойчивая, т.е. амплитуда колебаний будет уменьшаться и через некоторое время станет равной исходной Аа.
 |
|||
 |
|||
Если под действием возмущения амплитуда автоколебаний станет меньше Аа, то новому состоянию системы будет соответствовать точка М2, в которой система ведет себя как неустойчивая. Следовательно, амплитуда будет возрастать и вернется к исходному значению Аа.
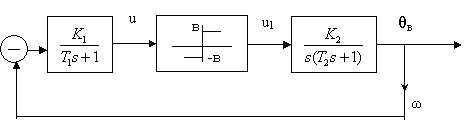
Рисунок 3. 4 - Устойчивость состояния равновесия следящей системы
В качестве примера рассмотрим исследование устойчивости состояния равновесия следящей системы, структурная схема которой изображена на рисунке 3.4, если ее параметры В=1 В; k1 k2 =10 c-1; T1=10 c; T2=1 c.
Для решения по структурной схеме запишем уравнение линейной части системы в виде
![]() . (3.15)
. (3.15)
Для нелинейного элемента имеем
u1(t)=q(A)u(t) (3.16)
где
![]() . (3.17)
. (3.17)
Подставляя выражения (3.16) и (3.17) в уравнение (3.15), получим
![]() . (3.18)
. (3.18)
Применяя к уравнению (3.18) преобразование Лапласа при нулевых начальных условиях, запишем
![]() . (3.19)
. (3.19)
Из уравнений (3.19) найдем характеристическое уравнение
![]() . (3.20)
. (3.20)
Возможность существования периодического решения уравнения проанализируем с помощью критерия устойчивости Михайлова. Для этого в уравнение (3.20) подставим s=jω; тогда найдем
![]() . (3.21)
. (3.21)
Откуда, приравнивая действительную и мнимую часть нулю, получаем
 (3.22)
(3.22)
Из второго уравнения определяем частоту периодического решения
![]() ,
,
а из первого при этом получаем
![]() . (3.23)
. (3.23)
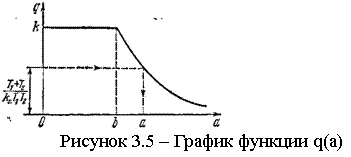
Используя готовый график
q(а)= ![]() (рисунок
3.5), находим амплитуду периодического решения а.
(рисунок
3.5), находим амплитуду периодического решения а.
 |
Для определения устойчивости решения, согласно критерию, надо найти производные выражений (3.22):

Критерий удовлетворяется. Следовательно, имеют место автоколебания.
Если учесть, что q(а)=<k (см.рисунок 3.5), из уравнения (3.23) вытекают условия существования автоколебаний
![]() или
или ![]() (3.24)
(3.24)
где К = k1k2k— общий коэффициент усиления разомкнутой цепи данной системы в линейном плане. Легко видеть, что (3.24) представляет собой условие неустойчивости этой системы как линейной согласно критерию Гурвица. Граница устойчивости
![]()
является в то же время границей автоколебаний.
3.2 Задание на выполнение лабораторной работы
3.2.1 Рассчитать и построить зависимость амплитуды и частоты автоколебаний на выходе САУ от коэффициента усиления линейной части системы.
3.2.2.Проверить выполнение условий применимости гармонической линеаризации.
3.2.3 Составить в Vissim или MathLab математическую модель, приведенную на рисунке 3.4.
Характеристики нелинейных элементов выдаются преподавателем, параметры звеньев сведены в таблицу 3.1.
3.2.4 Провести эксперименты
и снять характеристики на выходе и
статическую характеристику НЭ.
ТаблицаЗ.1 - Параметры звеньев
|
№ в. |
Т1 |
Т2 |
ТЗ |
ВидНЭ |
В |
в |
tg а |
|
1 |
1 |
0.1 |
0.1 |
Рис 2а |
50 |
- |
- |
|
2 |
1 |
1 |
0.1 |
Рис 2а |
70 |
- |
- |
|
3 |
0.2 |
0.1 |
0.1 |
Рис 2а |
60 |
- |
- |
|
4 |
1 |
0.1 |
0.1 |
Рис 26 |
50 |
10 |
- |
|
5 |
1 |
1 |
0.1 |
Рис 2в |
80 |
8 |
- |
|
6 |
1 |
0.5 |
0.1 |
Рис 2в |
50 |
5 |
- |
|
7 |
1 |
0.5 |
0.1 |
Рис 2г |
- |
10 |
1 |
|
8 |
1 |
1 |
0.1 |
??? |
60 |
10 |
- |
3.3 Требования к отчету
Отчет по лабораторной работе должен содержать:
- структурную схему модели;
- экспериментальные данные;
- выполненные расчеты;
- выводы по работе.
4. Список литературы
1. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. - «Наука», 1975, 2005г.
2. Методы классической современной теории автоматического управления. Под ред. К.А. Пупкова. В 5 ти – томах. М., 2004.
3. Цыпкин Я.З., Попков Ю.С. Теория нелинейных импульсных систем. - М., 1974.
4. Душин С.Е. Теория систем автоматического управления. – М.: Высшая школа, 2003.
|
Содержание |
с |
|
1 Лабораторная работа №1. Изучение фазовых портретов линейных систем второго порядка |
3 |
|
2 Лабораторная работа №2 Исследование систем с переменной структурой |
7 |
|
3 Лабораторная работа №3. Исследования автоколебаний в нелинейной системе методом гармонического баланса |
12 |
|
Список литературы |
17 |