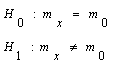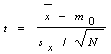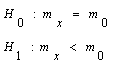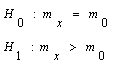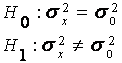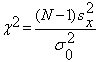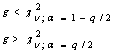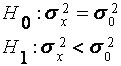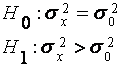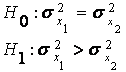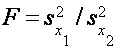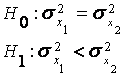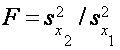Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра инженерной кибернетики
Теория и техника инженерного эксперимента
Методические указания к выполнению лабораторных работ
Для магистрантов специальности 6М070200 –
Автоматизация и управление
Алматы 2010
СОСТАВИТЕЛЬ: Ибраева Л,К. Теория и техника инженерного эксперимента. Методические указания к выполнению лабораторных работ для магистрантов специальности 6M070200 - Автоматизация и управление.- Алматы: АУЭС, 2010 - 36 с.
Методические указания содержат описания к 7 лабораторным работам и предполагают выполнение этих работ на виртуальном лабораторном стенде, разработанном на кафедре «Инженерная кибернетика».
Методические указания используются при выполнении лабораторных работ по дисциплине «Теория и техника инженерного эксперимента».
Содержание
Введение. Описание виртуальной лабораторной установки |
3 |
|
1 Лабораторная работа. Основные характеристики и экспериментальный анализ случайных величин 1.1 Экспериментальный анализ одномерной случайной величины 1.2 Экспериментальный анализ двумерной случайной величины 1.3 Задание и порядок выполнения работы 1.4 Содержание отчета 1.5 Контрольные вопросы |
6 6 7 7 8 9 |
|
2 Лабораторная работа. Статистическое оценивание 2.1 Точечные и интервальные оценки параметров 2.2 Планирование эксперимента при построении интервальных оценок 2.3 Задание и порядок выполнения работы 2.4 Содержание отчета 2.5 Контрольные вопросы |
1010 11 11 12 13 |
|
3 Лабораторная работа. Проверка статистических гипотез 3.1 Планирование эксперимента при проверке гипотез с помощью критериев значимости 3.2 Задание и порядок выполнения работы 3.3 Содержание отчета 3.4 Контрольные вопросы |
13
13 15 17 17 |
|
4 Лабораторная работа. Полный факторный эксперимент 4.1 Построение математической модели объекта методом полного факторного эксперимента 4.2 Задание и порядок выполнения работы 4.3 Содержание отчета 4.4 Контрольные вопросы |
19
19 20 23 23 |
|
5 Лабораторная работа. Дробный факторный эксперимент 5.1 Построение статистической модели объекта методом дробного факторного эксперимента 5.2 Задание и порядок выполнения работы 5.3 Содержание отчета 5.5 Контрольные вопросы |
24
24 25 26 26 |
|
6 Лабораторная работа. Планирование экстремальных поисковых экспериментов 6.1 Постановка задачи оптимизации 6.2 Задание и порядок выполнения лабораторной работы 6.3 Содержание отчета 6.4 Контрольные вопросы |
27 27 28 30 30 |
|
7 Лабораторная работа. Планирование второго порядка 7.1 Общие сведения 7.2 Центральное композиционное планирование 7.3 Нахождение экстремальной точки с помощью полиномов второго порядка 7.4 Задание и порядок выполнения лабораторной работы 7.5 Содержание отчета 7.6 Контрольные вопросы |
3131 31 32
32 33 34 |
|
Список литературы |
35 |
Введение. Описание виртуальной лабораторной установки
Современные компьютерные технологии позволяют значительно упростить и удешевить проведение лабораторных работ по планированию экспериментов. Это достигается за счет использования моделирования реальных систем на компьютере. То есть программа в соответствии с заданной легендой и функцией отклика имитирует поведение реального объекта и предоставляет органы работы с ним. На кафедре «Инженерная кибернетика» АУЭС разработано виртуальное моделирующее устройство, построенное по этому принципу. Моделирующее устройство используется для проведения лабораторных занятий по дисциплине магистратуры «Теория и техника инженерного эксперимента» специальности «Автоматизация и управление». Основа проекта – использование среды графического программирования LabView фирмы National Instruments. National Instruments LabVIEW (Laboratory Virtual Instrument Engineering Workbench) представляет собой высокоэффективную среду графического программирования, в которой можно создавать гибкие и масштабируемые приложения измерений, управления и тестирования с минимальными временными и денежными затратами. Несомненным достоинством графических систем программирования является то, что разработчиком приложения может быть сам постановщик задачи. В отличие от текстовых языков в LabVIEW программы создаются в виде графических диаграмм, подобных обычным блок-схемам. Технология LabVIEW вносит принципиальные изменения в создание прикладного программного обеспечения, поскольку эта система позволяет реализовать произвольный набор методов измерения, анализа, отображения и управления в автоматизированных системах различного профиля на базе обычного персонального компьютера [1].
Рассматриваемое виртуальное моделирующее устройство предназначено для моделирования сложных объектов управления, описываемых статистическими уравнениями в виде полиномов не выше второго порядка с несколькими входными и выходными величинами и подверженных воздействию случайных помех и временных дрейфов. На этой модели можно изучать влияние четырех факторов и их парных взаимодействий на два отклика системы. Моделирование объектов управления производится с целью исследования различных экспериментально-статистических методов идентификации (получения математического описания) и оптимизации [2]. Лабораторный стенд состоит из следующих функциональных узлов (см. рисунок 1): модели объекта, генератора шума (ГШ), генератора дрейфа параметров объекта (ГД), полей ввода входных сигналов (х1,х2, х3, х4) и блока измерения откликов (у1, у2).
Моделирующее устройство представляет собой программную реализацию математической модели сложного объекта управления, задаваемой в виде системы уравнений:
![]()
где ![]() — векторная выходная величина;
— векторная выходная величина; ![]() — вектор факторов;
ε – случайная помеха,
a(t) —
временной дрейф.
— вектор факторов;
ε – случайная помеха,
a(t) —
временной дрейф.
На данный момент для реализации функциональной зависимости используется квадратичный полином вида
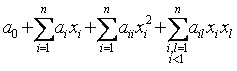 .
.
Для моделирования случайной помехи и временного дрейфа служат генератор шума и генератор дрейфа параметров. Случайная помеха моделируется по нормальному закону распределения вероятностей с нулевым математическим ожиданием и постоянной дисперсией; временной дрейф может быть представлен в виде дискретного процесса либо некоторой непрерывной функции времени.
Моделирующее устройство предназначено для измерения значений входных и выходных величин в условных единицах (в цифровом виде).
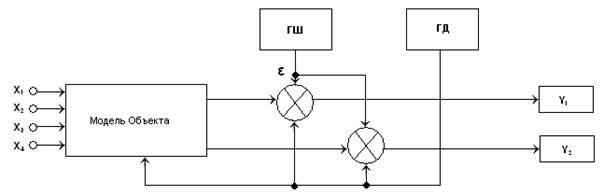
Рисунок 1 – Схема моделирующего устройства
В процессе эксплуатации моделирующего устройства исследователь выполняет такие же операции, как и при работе с реальным объектом, а именно:
1) подготовка к работе: выбор параметров объекта; задание характеристик генераторов дрейфа и шума; выбор метода исследования;
2) проведение экспериментов, включающее варьирование (установление и измерение) факторов, измерение выходных переменных и обработку результатов измерения.
В ходе лабораторной работы характеристики моделей объектов задаются пользователем. Этим самым можно изменять число и степень влияния основных факторов и их взаимодействий на первый или второй отклик объекта. В устройстве предусмотрена возможность введения аддитивного шума различной интенсивности, а также временного дрейфа с различными характеристиками. Перед обучающимися могут быть поставлены исследовательские задачи различной сложности, требующие для своего решения широкого набора статистических методов. Для имитации экспериментов и снятия характеристик объекта разработан пользовательский интерфейс. В основном окне этого приложения выбирается тема исследования (нажатием на соответствующую кнопку), дальнейшая работа проходит в режиме диалога с пользователем, в котором моделирующее устройство отражает на определенных формах «реакцию» объекта на действия пользователя. Пользователю необходимо предпринять те или иные действия в соответствии с алгоритмом решаемой задачи. То есть пользователь до проведения экспериментов на модели должен изучить рассматриваемые методы исследования.
На данный момент виртуальное моделирующее устройство включает следующие темы по исследованию сложных систем, подверженных случайным помехам:
- тема 1 «Статистические процедуры», в которую входят задачи экспериментального анализа одномерных и двумерных случайных величин; изучение методов статистического оценивания характеристик случайных величин и методов планирования эксперимента при построении интервальных оценок; овладение методикой применения статистических критериев для проверки гипотез относительно оценок характеристик случайных величин;
- тема 2 «Полный факторный эксперимент» и тема 3 «Дробный факторный эксперимент» предназначены для изучения методов планирования экспериментов для получения линейной и неполной степенной математических моделей статики сложных объектов;
- тема 4 – «Планирование экстремальных поисковых экспериментов» предназначена для изучения методов поисковой оптимизации статистических объектов при наличии случайных помех и включает решение задач оптимизации двумя методами: градиентным и методом Гаусса-Зейделя;
- тема 5 «Планирование второго порядка»; в этой теме изучаются методы планирования эксперимента для получения математического описания в виде полинома второго порядка и использование этого описания для предсказания координат оптимума; рассматриваются два вида центрального композиционного планирования: ортогональное и ротатабельное планирование.
В процессе выполнения лабораторных работ приобретаются и закрепляются навыки по применению теории планирования эксперимента на практике.
1 Лабораторная работа. Основные характеристики и экспериментальный анализ случайных величин
Цель работы – изучить способы экспериментального определения основных характеристик случайных величин.
1.1 Экспериментальный анализ одномерной случайной величины
Пусть имеется выборка экспериментальных
данных ![]() .
Обработку этих данных для получения эмпирических характеристик одномерной
случайной величины проводят в следующей последовательности:
.
Обработку этих данных для получения эмпирических характеристик одномерной
случайной величины проводят в следующей последовательности:
1 Построение вариационного ряда (ряда распределения).
Вариационный ряд ![]() получают
из исходных данных путем расположения
получают
из исходных данных путем расположения ![]() в порядке возрастания.
в порядке возрастания.
2 Построение диаграммы накопленных частот ![]() . Эта функция является эмпирическим
аналогом интегрального закона распределения и вычисляется по формуле
. Эта функция является эмпирическим
аналогом интегрального закона распределения и вычисляется по формуле
![]()
где ![]() - число элементов выборки, для которых
xj <x.
- число элементов выборки, для которых
xj <x.
Ступенчатая функция, соответствующая функции ![]() , называется диаграммой
(полигоном) накопленных частот.
, называется диаграммой
(полигоном) накопленных частот.
3 Построение
гистограммы выборки. Гистограмма ![]() является эмпирическим аналогом функции
плотности распределения f(x). Ее строят следующим образом:
является эмпирическим аналогом функции
плотности распределения f(x). Ее строят следующим образом:
- определяют по формуле ![]() количество интервалов, на
которое должна быть разбита ось Ох (найденное значение округляют до
ближайшего целого числа);
количество интервалов, на
которое должна быть разбита ось Ох (найденное значение округляют до
ближайшего целого числа);
- определяют длину интервала
![]() ,
,
для удобства величину
![]() можно
округлить;
можно
округлить;
- середину области изменения выборки (центр
распределения) ![]() принимают
за центр некоторого интервала, после чего легко находят границы и окончательное
количество указанных интервалов так, чтобы в совокупности они перекрывали всю
область от
принимают
за центр некоторого интервала, после чего легко находят границы и окончательное
количество указанных интервалов так, чтобы в совокупности они перекрывали всю
область от ![]() до
до ![]() ;
;
- подсчитывают количество наблюдений Nm, попавшее в каждый интервал; оно равно числу членов вариационного ряда, для которых справедливо неравенство
![]() ,
,
здесь ![]() и
и ![]() - границы m-го интервала. Значение
zi, попавшее на границу между (m-1)-м и
m-м интервалом, относят к
m-му
интервалу;
- границы m-го интервала. Значение
zi, попавшее на границу между (m-1)-м и
m-м интервалом, относят к
m-му
интервалу;
- подсчитывают относительную частоту
наблюдений ![]() ,
попавших в данный интервал;
,
попавших в данный интервал;
- строят гистограмму, представляющую собой
ступенчатую кривую, значение которой на
m-м
интервале (![]() ,
,![]() ), m=1,2,…, k постоянно
и равно
), m=1,2,…, k постоянно
и равно ![]() .
.
1.2 Экспериментальный анализ двумерной случайной величины
Обработка результатов наблюдений над двумерной совокупностью выполняется по следующей схеме:
1) построение поля рассеяния: на плоскости с координатами x,y отмечают экспериментальные точки;
2) составление таблицы двумерного
распределения. Оси Ox и Oy разбивают на отдельные интервалы
длиной ![]() и
и ![]() . Величины
. Величины
![]() ,
, ![]() , количество интервалов k и размещение этих
интервалов для каждой из переменных X и Y находят по правилам,
изложенных для одномерного случая. Соответствующие границы наносят на диаграмму
рассеяния и подсчитывают количество (частоты) точек
, количество интервалов k и размещение этих
интервалов для каждой из переменных X и Y находят по правилам,
изложенных для одномерного случая. Соответствующие границы наносят на диаграмму
рассеяния и подсчитывают количество (частоты) точек ![]() , попавших в каждый из
образовавшихся прямоугольников (точку, попавшую на границу, относят или к
правому или к верхнему прямоугольнику). Далее составляют таблицу следующей
структуры (см.таблицу 1.1). В каждой клетке таблицы в числителе отмечают
величину
, попавших в каждый из
образовавшихся прямоугольников (точку, попавшую на границу, относят или к
правому или к верхнему прямоугольнику). Далее составляют таблицу следующей
структуры (см.таблицу 1.1). В каждой клетке таблицы в числителе отмечают
величину ![]() , а в
знаменателе – относительные частоты
, а в
знаменателе – относительные частоты 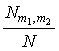 . Эту таблицу можно использовать как
исходную для построения гистограмм и диаграмм накопленных частот в трехмерном
пространстве, которые являются эмпирическими аналогами интегрального закона и
двумерной функции распределения.
. Эту таблицу можно использовать как
исходную для построения гистограмм и диаграмм накопленных частот в трехмерном
пространстве, которые являются эмпирическими аналогами интегрального закона и
двумерной функции распределения.
1.3 Задание и порядок выполнения работы
1.3.1 Ознакомиться с теоретическим материалом, методикой
экспериментального анализа одномерных и двумерных случайных величин.
1.3.2 Изучить назначение и принципы работы виртуального
лабораторного стенда для экспериментального исследования сложных систем.
Провести исследование свойств одномерной случайной величины Х.
1.3.3 Используя виртуальный лабораторный стенд, провести эксперименты на «объекте» исследования:
- загрузить программу ttip.exe;
- в списке тем выбрать строку «Статистические процедуры; вкладка 1- «Анализ одномерной случайной величины»;
- в появившемся окне в поле «Ввести номер исследуемого канала» введите цифру 1.
- введите объем выборки N=30 и
значение среднего квадратического отклонения ![]() =15;
=15;
- снять выборку, состоящую из N
значений случайной величины Х, при заданном ![]() .
.
1.3.4 Обработать результаты экспериментов:
- построить вариационный ряд;
- с помощью вариационного ряда построить диаграмму накопленных частот;
- построить гистограмму выборки;
Провести исследование свойств двумерной совокупности
случайных величин ![]() .
.
1.3.5 Провести эксперименты:
- загрузить программу ttip.exe;
- в списке тем выбрать строку «Статистические процедуры; вкладка 2- «Анализ двумерной случайной величины»;
- в появившемся поле «Ввести номер исследуемого канала» введите цифру 1;
- введите объем выборки N=30, значение
коэффициента ![]() =5
и значение среднего квадратического отклонения
=5
и значение среднего квадратического отклонения ![]() =20;
=20;
- установить значение х1, полученное в 1.3.3, снять значение y1; установить следующее значение х2, снять y2 и т.д. до yN;
- повторить эксперименты еще два раза
при других значениях a1 и
σy:
![]()
1.3.6 Обработать результаты экспериментов:
- по полученным данным построить три поля рассеяния;
- составить таблицы двумерных распределений.
1.4 Содержание отчета
Отчет по работе должен содержать:
- описание методики проведения экспериментов на виртуальном стенде для формирования одномерной выборки;
- результаты проведенных экспериментов;
- вариационный ряд;
- диаграмму накопленных частот;
- гистограмму выборки;
- описание методики проведения экспериментов на виртуальном стенде для формирования двумерной выборки;
- результаты проведенных экспериментов;
- три поля рассеяния;
- таблицы двумерных распределений.
1.5 Контрольные вопросы
1.5.1 Дайте частотное определение вероятности.
1.5.2 Что такое случайная величина?
1.5.3 Дайте определение интегральной функции распределения. Что она характеризует?
1.5.4 Дайте определение дифференциальной функции распределения. Что она характеризует?
1.5.5 Что является эмпирическим аналогом интегрального закона распределения. Как его находят?
1.5.6 Что является эмпирическим аналогом дифференциального закона распределения. Как его находят?
1.5.7 Дайте определение двумерной случайной величины.
1.5.8 Что такое поле рассеяния?
1.5.9 Что оценивает коэффициент корреляции?
1.5.10 Для чего используется таблица двумерных распределений?
Т а б л и ц а 1.1 – Таблица двумерного распределения
|
для y Интер- валы для x |
|
|
... |
|
… |
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
||
|
… |
|
|
… |
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
||
|
… |
|
|
… |
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
2 Лабораторная работа. Статистическое оценивание
Цель работы – изучение методов точечного и интервального оценивания характеристик случайных величин; ознакомление со способами планирования эксперимента при построении интервальных оценок.
2.1 Точечные и интервальные оценки параметров
Точечные
оценки – это оценки некоторых неизвестных числовых параметров распределения. Они
представляют собой числа, полученные путем подстановки выборочных значений ![]() в формулу для
оценивания искомого параметра. Именно для таких оценок используются понятия
состоятельности, несмещенности, эффективности.
в формулу для
оценивания искомого параметра. Именно для таких оценок используются понятия
состоятельности, несмещенности, эффективности.
Различные вероятностные утверждения относительно значений точечных оценок могут быть сформулированы с помощью выборочных распределений. Эти распределения являются табулированными функциями. Среди них можно отметить:
- распределение выборочного среднего при
известной дисперсии – нормированное нормальное распределение (U-распределение).
Таблицу этого распределения используют, чтобы предсказать до извлечения выборки
вероятность того, что выборочное среднее окажется в некотором интервале с
фиксированными границами, если только известны ![]() и
и ![]() исходного распределения; можно также
решить другую задачу: определить интервал, содержащий с заданной вероятностью
выборочное среднее;
исходного распределения; можно также
решить другую задачу: определить интервал, содержащий с заданной вероятностью
выборочное среднее;
- выборочное распределение оценки среднего (![]() - распределение)
применяется для описания вероятностных свойств выборочных дисперсий (нахождение
интервала с заданной вероятностью р содержащего конкретное выборочное
значение
- распределение)
применяется для описания вероятностных свойств выборочных дисперсий (нахождение
интервала с заданной вероятностью р содержащего конкретное выборочное
значение ![]() ,
если только известна
,
если только известна ![]() ;
;
- распределение выборочного среднего в случае
неизвестной дисперсии (t-распределение Стьюдента) применяется для
выяснения вероятностных свойств выборочного математического ожидания, когда
дисперсия генеральной совокупности неизвестна (например, для построения
интервала, в который с веротностью р попадает ![]() ;
;
- распределение отношения двух выборочных дисперсий (F-распределение Фишера) служит для сравнения оценок дисперсий, полученных по двум независимым выборкам различных объемов. Это распределение может применяться для высказывания тех или иных вероятностных утверждений об отношении выборочных дисперсий до извлечения выборки (например, для определения интервала, в котором с заданной вероятностью р будет заключено данное отношение).
Точечные оценки не дают информации о степени
близости ![]() к
соответствующему теоретическому параметру
к
соответствующему теоретическому параметру ![]() . Поэтому более информативный способ
оценивания неизвестных параметров заключается не в определении единичного
точечного значения, а в построении интервала, где с заданной степенью достоверности
будет находиться оцениваемый параметр, то есть в построении интервальной
оценки параметра
. Поэтому более информативный способ
оценивания неизвестных параметров заключается не в определении единичного
точечного значения, а в построении интервала, где с заданной степенью достоверности
будет находиться оцениваемый параметр, то есть в построении интервальной
оценки параметра ![]() .
.
2.2 Планирование эксперимента при построении интервальных оценок
При построении интервальных оценок планирование
эксперимента сводится к определению необходимого объема выборки с тем, чтобы
при фиксированной доверительной вероятности р была бы достигнута
заданная точность оценивания параметров. В качестве характеристики этой
точности будем использовать относительную величину 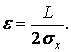
Рассмотрим решение задачи планирования для
оценивания ![]() и
и ![]() . Доверительные
интервалы для основных параметров нормального распределения приведены в
литературе [2,3]. На основании этих формул при определении математического
ожидания имеем
. Доверительные
интервалы для основных параметров нормального распределения приведены в
литературе [2,3]. На основании этих формул при определении математического
ожидания имеем
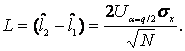
Отсюда
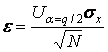 и задаваясь
предельно допустимой относительной погрешностью
и задаваясь
предельно допустимой относительной погрешностью ![]() , получим
, получим
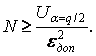
При
оценивании среднеквадратического отклонения используется уравнение для
определения ![]() (доверительный
интервал для σх - оценивает среднеквадратическое отклонение с
относительной погрешностью, не превышающей 100ε%):
(доверительный
интервал для σх - оценивает среднеквадратическое отклонение с
относительной погрешностью, не превышающей 100ε%):
![]()
Из этого уравнения методом подбора с помощью таблицы ![]() -распределения находится
-распределения находится
![]() , а затем
, а затем
![]()
2.3 Задание и порядок выполнения работы
2.3.1 Рассчитать необходимые объемы выборок для получения оценок математического ожидания (N1) и среднего квадратического отклонения (N2) с заданной точностью (доверительная вероятность р = 0,95; при оценивании тх допустимая относительная погрешность ε1доп; при оценивании σx погрешность ε2 доп).
2.3.2 Провести эксперименты с одномерной случайной величиной:
- загрузить программу ttip.exe;
- в списке тем выбрать строку «Статистические процедуры; вкладка 1- «Анализ одномерной случайной величины»;
- для канала Х1 снять две выборки необходимых объемов N1 и N2 при заданном среднем квадратическом отклонении σ (по варианту).
2.3.3 Обработать результаты эксперимента:
- для каждой выборки
рассчитать оценки математического ожидания, дисперсии
и среднего квадратического ![]() отклонения случайной
величины Х двумя способами: а) по известным формулам; б) используя
стандартную процедуру normfit командного
окна системы Matlab; сравнить полученные результаты;
отклонения случайной
величины Х двумя способами: а) по известным формулам; б) используя
стандартную процедуру normfit командного
окна системы Matlab; сравнить полученные результаты;
- по первой выборке найти интервальную оценку тх (с доверительной вероятностью р = 0,95);
- по второй выборке
найти интервальные оценки ![]() (с доверительной вероятностью р
= 0,95);
(с доверительной вероятностью р
= 0,95);
2.3.4 Провести эксперименты с двумерной случайной величиной:
- в программе ttip в списке тем выбрать строку ««Статистические процедуры; вкладка 2 - «Анализ двумерной случайной величины»;
- используя в качестве входных значений
случайной величины Х первую выборку (из п.2.3.2), получить значения
случайной величины Y; повторить эти эксперименты для второй выборки (коэффициент
![]() и значение
среднего квадратического отклонения
и значение
среднего квадратического отклонения ![]() - по варианту первой лабораторной работы);
- по варианту первой лабораторной работы);
2.3.5 Обработать результаты эксперимента:
- вычислить для обоих случаев оценки коэффициента корреляции двумя способами: а) по известным формулам; б) используя стандартную процедуру canoncorr командного окна системы Matlab; сравнить полученные результаты.
Варианты заданий
|
Вар-ты |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
ε1доп |
0,6 |
0,62 |
0,65 |
0,7 |
0,73 |
0,75 |
0,8 |
0,84 |
0,85 |
0.9 |
|
ε2 доп |
0,15 |
0,155 |
0,16 |
0,165 |
0,17 |
0,175 |
0,18 |
0,19 |
0,20 |
0,25 |
2.4 Содержание отчета
Отчет по работе должен содержать:
- расчеты необходимого объема выборок для получения оценок математического ожидания и среднего квадратического отклонения;
- результаты проведенных экспериментов с одномерной случайной величиной (две выборки необходимых объемов);
- расчеты оценок математического ожидания, дисперсии и среднего квадратического отклонения по известным формулам и с помощью стандартных процедур;
- интервальные оценки математического ожидания, дисперсии и среднеквадратического отклонения;
- результаты экспериментов для формирования двумерной выборки;
- расчет оценки коэффициента корреляции по известной формуле и с помощью стандартных процедур.
2.5 Контрольные вопросы
2.5.1 Дать определение генеральной совокупности и выборки.
2.5.2 В чем состоит различие между оцениваемым параметром
генеральной совокупности и его оценкой?
2.5.3 Какие оценки параметров распределения называются
состоятельными, несмещенными и эффективными?
2.5.4 Что такое точечные оценки параметров?
2.5.5 Как находятся оценки математического ожидания и дисперсии и каковы их свойства?
2.5.6. Какими свойствами обладает оценка коэффициента корреляции?
2.5.7 Какие выборочные распределения вы знаете?
2.5.8 Для решения каких задач применяется выборочные распределения?
2.5.9 Как определяются
доверительные интервалы для mx, ![]() ,
, ![]() ?
?
2.5.10 В чем состоит планирование эксперимента при построении
интервальных оценок?
3 Лабораторная работа. Проверка статистических гипотез
Цель работы – ознакомление с простейшими способами планирования экспериментов для проверки гипотез.
3.1 Планирование эксперимента при проверке гипотез с помощью критериев значимости
Статистическая гипотеза – определенное предположение относительно свойств генеральной совокупности, из которой извлекается выборка.
Критерии значимости – это критерии, с помощью которых проверяются гипотезы об абсолютных значениях параметров или о соотношениях между ними для генеральных совокупностей с известной (с точностью до параметров) функцией распределения вероятностей.
Планирование эксперимента при проверке гипотез с
помощью критериев значимости состоит в определении объема
N
выборки, гарантирующего обнаружение заданного отклонения исследуемого параметра
![]() от
гипотетического
от
гипотетического ![]() при
фиксированных вероятностях первого и второго рода (
при
фиксированных вероятностях первого и второго рода (![]() и
и ![]() ).
).
Если проверяются гипотезы для математического ожидания (см. таблицу 3.1, критерии 1-3), то необходимое число наблюдений определяют из формулы:

где 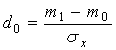 ,
, ![]() - возможные значения математического
ожидания.
- возможные значения математического
ожидания.
Для критериев 4-6 (см. таблицу 3.1) необходимое число
наблюдений определяется при d0<1 следующим образом: с помощью таблицы ![]() распределения находят
такое число степеней свободы
распределения находят
такое число степеней свободы ![]() , для которого
, для которого
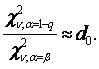
Для критериев 7-9 из таблицы 3.1 используют таблицы
F-
распределения. Необходимые объемы выборок ![]() Значения
Значения ![]() находят с помощью приближенного
соотношения
находят с помощью приближенного
соотношения
![]()
Если ![]() то эта формула упрощается
то эта формула упрощается
![]()
Критерием согласия называется критерий гипотезы о том, что генеральная совокупность имеет
распределение предполагаемого типа (будем говорить о нормальном распределении).
Среди различных критериев согласия наиболее употребителен универсальный
критерий согласия Пирсона ![]() .
.
3.2 Задание и порядок выполнения работы
3.2.1 Используя результаты экспериментов, проведенных в лабораторной работе 2 (для одномерной выборки), проверить гипотезы с уровнем значимости q, используя стандартные критерии из таблицы 3.1:
- по первой выборке q = 0,01 ÷ 0,05;
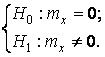 или
или
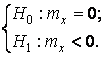 или
или 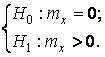
- по второй выборке q = 0,01÷ 0,1;
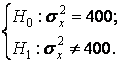 или
или
 или
или
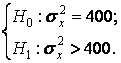
- по двум полученным выборкам q = 0,01÷ 0,1
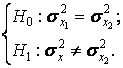
3.2.2 Выполнить проверку гипотез о
значении математического ожидания выборки ![]() , используя встроенные функции ttest и ztest системы
MatLab.
Сравнить результаты.
, используя встроенные функции ttest и ztest системы
MatLab.
Сравнить результаты.
3.2.3 Для критерия проверки гипотезы относительно значения математического ожидания определить объем выборки N, необходимый для обнаружения заданного расхождения d0 между гипотетическим и фактическим значениями mx (d0=0,4; β =0,05).
3.2.4 Снять экспериментально необходимую выборку (эксперименты проводить как в лабораторной работе 2).
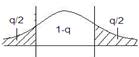
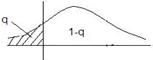
3.2.5 По выборке построить гистограмму. Если в каком-либо j-ом интервале число наблюдений nj окажется меньше пяти, то его объединяют с соседним интервалом (или интервалами) так, чтобы число наблюдений в таком объединенном интервале оказалось большим или равным пяти. Пусть Kr – окончательное число интервалов группирования:
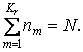
3.2.6 С помощью критерия согласия
![]() проверить гипотезу о нормальности
распределения (q =0,05).
Для этого:
проверить гипотезу о нормальности
распределения (q =0,05).
Для этого:
- определить теоретическую вероятность ![]() попадания в каждый из
Kr интервалов случайной величины с нормальным распределением.
попадания в каждый из
Kr интервалов случайной величины с нормальным распределением.
Значения ![]() находятся с помощью таблиц интегрального
нормального закона распределения F(х) по формулам
находятся с помощью таблиц интегрального
нормального закона распределения F(х) по формулам

- вычислить число
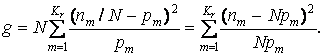
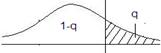
Задавшись уровнем значимости
q,
по таблице ![]() -
распределения найти критическое значение
gкр, причем критическая область определяется
неравенством
-
распределения найти критическое значение
gкр, причем критическая область определяется
неравенством ![]() ;
;
- сравнить значения g и gкр и вынести решение о принятии (если g≤ gкр) или отклонении (g>gкр) рассматриваемой гипотезы о виде функции распределения.
3.3 Содержание отчета
Отчет по работе должен содержать:
- результаты экспериментов, используемые для проверки гипотез;
- проверяемые гипотезы;
- выбранные статистические критерии для проверки гипотез;
- результат проверки;
- расчет необходимого объема выборки для проверки гипотезы
относительно значения математического ожидания;
- гистограмму выборки;
- расчет теоретической вероятности ![]() и числа
g;
и числа
g;
- определение критического значения
gкр по таблице ![]() - распределения;
- распределения;
- вывод о виде функции распределения.
3.4 Контрольные вопросы
3.4.1 Дайте определение статистической гипотезы.
3.4.2 Что такое нулевая гипотеза? Альтернативная гипотеза?
3.4.3 Что такое уровень значимости?
3.4.4 Какова общая процедура проверки статистических гипотез?
3.4.5 Что такое критерий значимости?
3.4.6 Какого рода гипотезы проверяются с помощью критериев значимости?
3.4.7 Перечислите стандартные критерии для проверки гипотез.
3.4.8 Как проверяются гипотезы относительно значений математических ожиданий и дисперсий нормальных генеральных совокупностей?
3.4.9 Как определить необходимый объем выборки для проверки гипотез?
3.4.10 Что такое критерий согласия?
Т а б л и ц а 3.1 – Стандартные критерии для проверки гипотез
|
№ |
Проверяемая ги-потеза Н0 и аль-тернативная ги-потеза Н1 |
Информа-ция о па-раметрах распреде-ления |
Статистика g и ее обозначение для каждого критерия |
Распределе-ние статисти-ки g при справедлив. гипотезе H0 |
Критическая область |
|
1 |
|
|
|
t-распреде-ление с
степенями свободы |
|
|
2 |
|
||||
|
3 |
|
||||
|
4 |
|
|
|
степенями свободы
|
|
|
5 |
|
||||
|
6 |
|
П р о д о л ж е н и е т а б л и ц ы 3.1
|
№ |
Проверяемая гипотеза Н0 и альтернативная гипотеза Н1 |
Информа-ция о па-раметрах распреде-ления |
Статистика g и ее обозначение для каждого критерия |
Распреде-ление статистики g при спра-ведливой гипотезе H0 |
Критическая область |
|
7 |
|
|
|
F-распределение с
|
|
|
8 |
|
|
|||
|
9 |
|
|
4 Лабораторная работа. Полный факторный эксперимент
Цель работы — изучение методов планирования экспериментов для получения линейной и неполной степенной математических моделей статики сложных объектов.
4.1 Построение математической модели объекта методом полного факторного эксперимента
Для построения линейных и
неполных степенных математических моделей применяют полный факторный
эксперимент, обладающий ортогональной матрицей планирования. Математическое описание
поверхности отклика объекта в окрестности точки базового режима
![]() можно получить варьированием каждого из
факторов
можно получить варьированием каждого из
факторов ![]() на
двух уровнях, отличающихся от базового уровня на величину интервала
варьирования
на
двух уровнях, отличающихся от базового уровня на величину интервала
варьирования ![]() .
.
Эксперимент, реализующий все возможные неповторяющиеся комбинации уровней n независимых управляемых факторов, каждый из которых варьируют на двух уровнях, называется полным факторным экспериментом (ПФЭ). Число таких комбинаций N=2n определяет тип планирования (ПФЭ 2n).
Матрица планирования представляется в виде таблицы, составленной по следующим правилам:
- каждая g-я строка
матрицы содержит набор координат ![]() точки, в которой проводится g-й
опыт (i=1,2,…,n;
g=1,2,…,N);
точки, в которой проводится g-й
опыт (i=1,2,…,n;
g=1,2,…,N);
- вводится фиктивная переменная x0=+1;
- в первой строке (g=1) все управляемые факторы выбирают на
нижнем уровне, то есть xi=-1. Последующие g-е варианты варьирования при
составлении матрицы плана выбираются следующим образом: при построчном переборе
всех вариантов частота смены знака факторов для каждого последующего фактора ![]() вдвое меньше, чем для
предыдущего
вдвое меньше, чем для
предыдущего ![]() Столбцы
управляемых факторов образуют собственно план эксперимента, а остальные
столбцы матрицы получаются перемножением соответствующих значений управляемых
факторов и необходимы для расчета соответствующих коэффициентов при
взаимодействиях.
Столбцы
управляемых факторов образуют собственно план эксперимента, а остальные
столбцы матрицы получаются перемножением соответствующих значений управляемых
факторов и необходимы для расчета соответствующих коэффициентов при
взаимодействиях.
Нахождение модели методом ПФЭ состоит из следующих этапов:
- планирование эксперимента;
- проведение эксперимента;
- проверка воспроизводимости (однородности выборочных дисперсий
![]()
- получение математической модели объекта с проверкой статистической значимости выборочных коэффициентов регрессии;
- проверка адекватности математического описания.
4.2 Задание и порядок выполнения работы
4.2.1 Построить матрицу планирования ПФЭ для двух независимых факторов, варьируемых на двух уровнях.
4.2.2 Провести эксперименты в соответствии с составленным планом ПФЭ 22:
- загрузить программу ttip.exe;
- в списке работ выбрать строку «Тема 4. Полный факторный эксперимент»;
- задать модель объекта с двумя факторами х1, х2, установив следующие значения коэффициентов: ao = 4; a1 = 4; a2 = - 3; a12 = 3.
- установить координаты
базовой точки ![]() :
x10 = 50;
x20 = 60;
:
x10 = 50;
x20 = 60;
- установить интервалы варьирования ![]() ;
;
- средняя квадратическая ошибка воспроизводимости эксперимента
![]() .
.
Провести три серии параллельных опытов (m = 3).
Результаты занести в протокол. Результаты наблюдений усреднить.
4.2.3 Построить матрицу планирования ПФЭ для трех независимых факторов, варьируемых на двух уровнях.
4.2.4 Провести эксперименты в соответствии с составленным планом ПФЭ 23:
- задать модель объекта с тремя факторами х1 x2, х3, установив следующие значения коэффициентов: ao = 4; a1 = 4; a2 = - 3; a2 = - 4; a12 = 3, a13 = 0; a23 = -2;
- установить координаты базовой точки ![]() :
x10 = 50;
x20 = 60;
x30 = 50;
:
x10 = 50;
x20 = 60;
x30 = 50;
- установить интервалы варьирования ![]() ;
;
- средняя квадратическая ошибка воспроизводимости
эксперимента ![]() .
.
Провести три серии параллельных опытов (m = 3).
Результаты занести в протокол. Результаты наблюдений усреднить.
4.2.5 Обработать результаты наблюдений экспериментов п.4.2.2 и 4.2.4:
а) провести проверку воспроизводимости эксперимента:
- вычислить оценки дисперсии по формуле
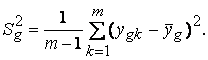
Для проверки гипотезы об однородности оценок
дисперсий ![]() использовать
критерий Кохрена:
использовать
критерий Кохрена:
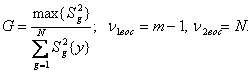
Если значения критерия G, вычисленное по
данным эксперимента, меньше критического значения, полученного по таблице (при
числе степеней свободы числителя ![]() , знаменателя -
, знаменателя - ![]() и уровне значимости, например, q=5%),
то гипотеза об однородности отвечает результатам эксперимента и наилучшая
оценка генеральной дисперсии воспроизводимости
и уровне значимости, например, q=5%),
то гипотеза об однородности отвечает результатам эксперимента и наилучшая
оценка генеральной дисперсии воспроизводимости ![]() равна
равна
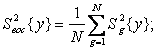
б) рассчитать оценки коэффициентов регрессии. При ПФЭ получаются независимые оценки коэффициентов регрессионной модели. Эти оценки находятся по формулам
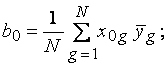
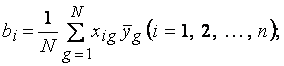
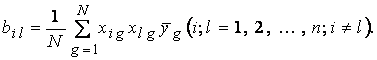
в) определить дисперсии оценок
коэффициентов ![]() по формуле:
по формуле:
![]()
где N - число точек факторного пространства, в которых проводится эксперимент; m - число серий дублирующих опытов в этих точках;
г) проверить гипотезы о значимости оценок коэффициентов регрессии (проверка нуль-гипотезы) с помощью критерия Стьюдента

Если найденная величина параметра
tj
превышает
значение tкр,
определенное из таблицы t –
распределения для числа степеней свободы ![]() , при заданном уровне значимости q
%, то нуль-гипотеза отвергается и соответствующую оценку
bj
коэффициента
признают статистически значимой; коэффициент должен быть сохранен. В противном
случае нулевую гипотезу не отвергают и оценку
bj
считают
статистически незначимой;
, при заданном уровне значимости q
%, то нуль-гипотеза отвергается и соответствующую оценку
bj
коэффициента
признают статистически значимой; коэффициент должен быть сохранен. В противном
случае нулевую гипотезу не отвергают и оценку
bj
считают
статистически незначимой;
д) проверить адекватность полученного
математического описания помощью
дисперсии адекватности ![]() , оценка которой находится по формуле
, оценка которой находится по формуле
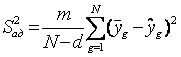
где d – число членов аппроксимирующего
полинома. Дисперсия адекватности определяется числом степеней свободы ![]()
Проверка гипотезы об адекватности проводится с использование F-критерия Фишера:
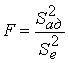 .
.
Если вычисленное значение критерия
F
меньше критического (F≤Fкр), найденного по таблицами критерия Фишера, для
соответствующих степеней свободы ![]() при заданном уровне значимости qад
, то нуль-гипотеза принимается. В противном случае гипотезу отвергают и
математическое описание признается неадекватным.
при заданном уровне значимости qад
, то нуль-гипотеза принимается. В противном случае гипотезу отвергают и
математическое описание признается неадекватным.
4.2.6 Рассчитать по адекватным моделям значения функции отклика в 4 точках (отличных от тех, в которых проводились опыты).
Провести в этих же точках эксперименты на объекте. Сравнить результаты. Сделать выводы.
4.3 Содержание отчета
Отчет по работе должен содержать:
- матрицу планирования ПФЭ для двух независимых факторов,
варьируемых на двух уровнях;
- описание методики проведения экспериментов на виртуальном
лабораторном стенде;
- протокол экспериментов и усредненные значения откликов в каждой точке факторного пространства (заносятся в матрицы, добавленные к матрице планирования);
- статистический анализ результатов наблюдений:
а) проверка воспроизводимости эксперимента; вывод;
б) оценки коэффициентов регрессии, дисперсии оценок коэффициентов, проверка их значимости; выводы;
в) полученное уравнение регрессии;
г) проверка адекватности полученного математического описания;
вывод;
- расчет по модели значения функции отклика в 4 точках, отличных от тех, в которых проводились опыты. Результаты эксперименты в этих же точках на объекте, Сравнение результатов. Выводы;
- матрицу планирования ПФЭ для трех независимых факторов,
варьируемых на двух уровнях;
- описание методики проведения экспериментов на виртуальном
лабораторном стенде;
- протокол экспериментов и усредненные значения откликов в каждой точке факторного пространства (заносятся в матрицы, добавленные к матрице планирования);
- статистический анализ результатов наблюдений (проводится также,
как и для двухфакторной модели).
4.4 Контрольные вопросы
4.4.1 Что называется полным факторным экспериментом?
4.4.2 Как выбираются факторы планирования, их основные (базовые)
уровни и интервалы варьирования?
4.4.3 Указать порядок проведения эксперимента методом ПФЭ.
4.4.4 Как составляется матрица планирования ПФЭ?
4.4.5 Как проверить воспроизводимость вариантов варьирования ПФЭ?
4.4.6 При каких условиях не соблюдается требование
воспроизводимости эксперимента и как следует поступить в этом случае?
4.4.7 Как проверяется значимость оценок коэффициентов регрессии?
4.4.8 При каких условиях оценки коэффициентов регрессии незначимы и как эти условия устранить?
4.4.9 Как проверить адекватность математической модели?
4.4.10 При каких условиях не соблюдается требование адекватности математической модели и как следует поступить в этом случае?
5 Лабораторная работа. Дробный факторный эксперимент
Цель работы — изучение методов планирования экспериментов для получения линейной и неполной степенной математических моделей статики сложных объектов.
5.1 Построение статистической модели объекта методом дробного факторного эксперимента
При решении ряда задач парные взаимодействия и взаимодействия высших порядков отсутствуют или пренебрежимо малы. В других задачах, кроме основных факторов, необходимо учитывать лишь некоторые парные взаимодействия из множества возможных взаимодействий, входящих в планы ПФЭ. Кроме того, на первых этапах исследования часто нужно получить в первом приближении лишь линейную аппроксимацию изучаемого уравнения связи при минимальном количестве опытов. В таких случаях для построения статистической модели объекта используют дробный факторный эксперимент (ДФЭ), в процессе проведения которого реализуется часть ПФЭ (дробная реплика). При построении ДФЭ должна учитываться априорная информация о влиянии на отклик различных взаимодействий факторов. Если влияние некоторого взаимодействия пренебрежимо мало, то соответствующий этому взаимодействию столбец в матрице ПФЭ может быть использован для варьирования нового фактора, не вошедшего ранее в число основных.
Для правильного планирования ДФЭ необходимо использовать все полученные ранее сведения теоретического и интуитивного характера об объекте и выделить те факторы и произведения факторов, влияние которых на отклик существенно. Способ образования каждого из дополнительных столбцов матрицы дробного факторного плана задается генератором плана. Генератор плана служит для построения дробной реплики. При построении дробных планов значимые взаимодействия рассматриваются как самостоятельные факторы, а незначимые – как потенциально возможные генераторы плана. Выбор генератора не может быть произвольным, так как оценки коэффициентов модели в дробном факторном эксперимента получаются смешанными с различными взаимодействиями.
Для получения правила
смешения оценок коэффициентов модели вводится понятие контраста
(определяющего соотношения). Под контрастом плана понимают соотношение, полученное
на основе генератора плана, с помощью которого задается элемент первого столбца
матрицы планирования для фиктивной переменной, то есть элемент, равный единице.
Например, если генератор плана задается соотношением ![]() , то, умножив обе части этого
соотношения на
, то, умножив обе части этого
соотношения на ![]() ,
получим
,
получим ![]() , так
как всегда
, так
как всегда ![]() .
Знание контраста позволяет найти всю систему смешивания оценок без анализа
матрицы ДФЭ. Для этого достаточно по очереди умножить факторы, входящие в
модель, на контраст. Получаем
d+1 равенство, каждое из которых содержит
2p
переменных
(факторов и их взаимодействий). Действия всех переменных, входящих в
определенное равенство, смешаны между собой.
.
Знание контраста позволяет найти всю систему смешивания оценок без анализа
матрицы ДФЭ. Для этого достаточно по очереди умножить факторы, входящие в
модель, на контраст. Получаем
d+1 равенство, каждое из которых содержит
2p
переменных
(факторов и их взаимодействий). Действия всех переменных, входящих в
определенное равенство, смешаны между собой.
Таким образом, для определения пригодности найденного плана ДФЭ требуется установить, не содержат ли какие-либо из указанных равенств хотя бы двух переменных из списка существенных переменных. Если нет, то план пригоден для экспериментирования, если содержит, то он не позволяет оценить коэффициенты регрессионной модели и должен быть изменен.
5.2 Задание и порядок выполнения работы
5.2.1 Найти определяющие соотношения полуреплик планирования типа 24-1 с генерирующими соотношениями:
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
5) ![]() 6)
6)
![]() 7)
7)
![]() 8)
8)
![]()
Выбрать из этих полуреплик одно соотношение для реализации ДФЭ, если априори известно, что на отклик могут оказывать влияние только три парных взаимодействия x1x2, x2x3, х2х4 и линейные члены. Выбор производить из условия получения несмешанных оценок линейных коэффициентов и коэффициентов трех указанных парных взаимодействий.
5.2.2 Построить матрицу планирования ДФЭ 24 -1.
5.2.3 Провести эксперименты в соответствии с планом выбранной полуреплики типа 24-1:
- загрузить программу ttip.exe;
- в списке работ выбрать строку «Тема 5. Дробный факторный
эксперимент»;
- задать модель объекта с четырьмя факторами х1, х2, х3, x4, установив следующие значения: коэффициентов aо =- 4; a1 = 4; a2 = -3; a3 = - 4; a4 =4; a12 = 3; a12= - 3; a23= - 2; a24 = -4;
- установить координаты
базовой точки ![]() x10 = 50;
x20 = 60; х30 - = 50;
x40 = 40;
x10 = 50;
x20 = 60; х30 - = 50;
x40 = 40;
- установить интервалы варьирования
![]() ;
;
- среднеквадратическая ошибка
воспроизводимости эксперимента
![]() .
.
Провести три серии параллельных опытов (m = 3).
Результаты занести в протокол.
5.2.4 Обработать результаты наблюдений:
- выполнить проверку воспроизводимости эксперимента. Проверка однородности оценок дисперсии отклика в различных точках факторного пространства проводится в полном соответствии с методикой, изложенной для ПФЭ, различие состоит лишь в числе точек плана;
- получить математическую модель объекта. Процедура определения оценок коэффициентов регрессии и проверки их значимости полностью совпадает с процедурой, применяемой для исследования объекта методом полного факторного эксперимента;
- проверить адекватность математического описания. Адекватность математического описания функции отклика проверяют теми же методами, что и для ПФЭ.
5.2.5 Рассчитать по адекватной модели значения функции отклика в 4 точках (отличных от тех, в которых проводились опыты). Провести в этих же точках эксперименты на объекте. Сравнить результаты. Сделать выводы.
5.3 Содержание отчета
Отчет по работе должен содержать:
- обоснованный выбор генерирующего соотношения;
- матрицу планирования ДФЭ 24 -1;
- описание методики проведения экспериментов в соответствии с
планом выбранной полуреплики типа 24-1;
- протокол экспериментов и усредненные значения откликов в каждой точке факторного пространства;
- статистический анализ результатов наблюдений.
5.4 Контрольные вопросы
5.4.1 Что называется дробным факторным экспериментом?
5.4.2 Что такое дробная реплика?
5.4.3 Что такое генерирующее соотношение и как оно выбирается?
5.4.4 Как составляется матрица планирования ДФЭ?
5.4.5 Что такое определяющее соотношение и как с его помощью
составляется система совместных оценок?
5.4.6 От чего зависит разрешающая способность дробных реплик?
5.4.7 Какие процедуры включает статистический анализ результатов
эксперимента?
5.4.8 Назовите выборочное распределение, используемое для проверки
воспроизводимости эксперимента.
5.4.9 Назовите выборочное распределение, используемое для проверки
значимости оценок коэффициентов регрессии.
5.4.10 Назовите выборочное распределение, используемое для проверки
адекватности математической модели.
6 Лабораторная работа. Планирование экстремальных поисковых экспериментов
Цель работы – ознакомление с методами поисковой оптимизации статистических объектов при наличии случайных помех.
6.1 Постановка задачи оптимизации
Главной задачей и конечной целью решения большого числа разнообразных исследовательских проблем управления, проектирования и планирования обычно является достижение и поддерживание экстремальных (наилучших) показателей. Процесс нахождения и поддержания наилучших (в определенном смысле) значений целевой функции объекта называется оптимизацией. Критерий оптимизации (целевая функция) y обычно задается, иногда исследователь выбирает его сам. Этот критерий должен удовлетворять следующим основным условиям: 1) нести в себе существенную информацию об объекте, о качестве процесса; 2) измеряться с достаточной точностью; 3) носить обобщенный характер, то есть отражать свойства и качества процесса в целом – часто это интегральный показатель.
Будем исходить из задачи нахождения максимума. Тогда задача оптимизации сводится к отысканию таких значений факторов
![]()
при которых целевая функция y достигает своего максимума. Напомним, что на объект воздействуют аддитивные помехи, поэтому функция отклика выражает не функциональную, а регрессионную зависимость.
Для решения задачи оптимизации можно применить два принципиально различных подхода: 1) если известна или есть возможность найти n-факторную математическую модель для той части факторного пространства, где расположен экстремум функции отклика, то задачу оптимизации решают аналитическим или численным методом; 2) если математическое описание не получено по каким-либо причинам, то осуществляют экспериментальный поиск точки экстремума.
В первом случае используют известное из математического анализа свойство функций, имеющих экстремум: в точке экстремума первая производная этой функции обращается в нуль. Приравнивая нулю все частные производные функции отклика по каждому из n факторов, получают систему уравнений, которую можно решить аналитически или численно.
Во многих практических случаях аналитическая зависимость функции отклика неизвестна или ее нахождение представляет собой сложную задачу. Тогда задачу оптимизации проще решать с помощью второго подхода, то есть с помощью экспериментального анализа. Для этого сначала с помощью специально спланированных пробных опытов изучают характер поверхности отклика в районе первоначально выбранной (базовой, основной) точки факторного пространства. Затем совершают «рабочее» движение в сторону экстремума, причем направление движения определяют по результатам пробных опытов. Такое движение может осуществляться путем ряда этапов, которые могут объединяться в «циклы» (последовательная процедура).
Методы поисковой оптимизации различаются способами постановки пробных опытов в окрестности начальной (базовой) точки и определения направления движения к экстремуму, а также способами организации самого рабочего движения к экстремуму. Например, метод Гаусса-Зейделя предусматривает поочередное нахождение частных экстремумов целевой функции по каждому фактору xi (i=1,2,..,n). При этом на каждом i-м этапе стабилизируют n-1 факторов и варьируют только один i-й фактор. Градиентные методы имеют несколько разновидностей, различающихся правилами выбора ступеней варьирования и рабочих шагов на каждом этапе движения к экстремуму. Сущность стратегии всех этих разновидностей состоит в том, что на каждом этапе вокруг очередной базовой точки организуют пробные эксперименты, по результатам которых оценивают новое направление градиента, после чего в этом направлении совершают один рабочий шаг.
Выбор базовой точки является отдельной задачей. Обычно
базовая точка соответствует номинальному режиму ведения технологического
процесса ![]() Иногда
эту точку выбирают в центре области, которую желательно исследовать, либо в центре
области ограничений, если они имеются (при таком выборе базовой точки все
направления являются равноправными, а это важно в случае, когда заведомо ничего
неизвестно о том, где, хотя бы примерно, расположен экстремум).
Иногда
эту точку выбирают в центре области, которую желательно исследовать, либо в центре
области ограничений, если они имеются (при таком выборе базовой точки все
направления являются равноправными, а это важно в случае, когда заведомо ничего
неизвестно о том, где, хотя бы примерно, расположен экстремум).
Для повышения надежности результатов в каждой запланированной точке факторного пространства выполняют по нескольку параллельных опытов.
Разные поисковые методы в разных условиях обладают различной помехоустойчивостью. Под помехоустойчивостью метода понимается его способность правильно оценивать направление рабочего движения, а также способность быстро и точно приводить рабочую точку в область экстремума, несмотря на наличие помех.
6.2 Задание и порядок выполнения лабораторной работы
6.2.1 Загрузить программу
ttip.exe.
В списке работ выбрать
строку «Планирование экстремальных поисковых экспериментов». Задать модель объекта с двумя факторами ![]() и
и ![]() , установив следующие значения
коэффициентов:
, установив следующие значения
коэффициентов:
![]()
6.2.2 Установить начальные параметры:
- координаты базовой точки:![]() ;
;
- средняя квадратическая ошибка воспроизводимости
отклика ![]() ;
;
- интервалы варьирования
![]() .
.
6.2.3 Провести поиск точки максимума оптимизируемой целевой функции методом Гаусса-Зейделя:
- определить координаты пробных точек
![]()
для первого фактора;
- снять с объекта в этих пробных точках значения
отклика ![]() ;
;
- сравнить полученные отклики, и если
![]() ,
,
то
совершить рабочее движение на один рабочий шаг ![]() по
направлению
по
направлению ![]() в
точку М3;
в
точку М3;
- повторять описанные действия в том же направлении до тех пор, пока на каком-то k-ом шаге не окажется, что
![]() .
.
За частный экстремум принимают (k-1)-ю точку с откликом ![]() ;
;
- аналогично провести поиск частного экстремума по
второму фактору: стабилизируют все факторы, кроме ![]() . За новую базовую точку принимают точку с
координатами
. За новую базовую точку принимают точку с
координатами
![]() ,
,
а
фактор х2 варьируют на выбранную величину интервала
варьирования ![]() .
По достижении частного экстремума по фактору х2 точку нового частного
экстремума принимают за новую базовую точку;
.
По достижении частного экстремума по фактору х2 точку нового частного
экстремума принимают за новую базовую точку;
- если экстремум не найден начать следующий цикл поиска экстремума.
Поисковое движение к экстремуму заканчивают по достижении такой точки факторного пространства, при движении из которой в любую сторону по всем факторным осям в положительном и отрицательном направлениях, значения отклика оказываются меньшими. Такую точку принимают за экстремум (максимум).
6.2.4
Весь ход поисковых экспериментов изобразить графически на плоскости факторов ![]() и
и ![]() . Возле каждой пробной и рабочей
точки записать значения
. Возле каждой пробной и рабочей
точки записать значения ![]() , полученные в них опытным путем.
, полученные в них опытным путем.
6.2.5 Провести поиск точки максимума оптимизируемой целевой функции методом простого градиента:
- принять рабочий шаг ![]()
- определить координаты пробных точек
![]()
![]()
- снять с объекта значения отклика в этих пробных точках; -
- вычислить оценки составляющих вектор-градиента в точке ![]() для каждого
i-го
фактора:
для каждого
i-го
фактора:
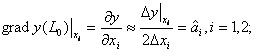
- найти координаты рабочей точки на направлении градиента:
![]()
- проверить условие
![]() .
.
Если по результатам пробных опытов в (k+1)-й рабочей точке выполняется это условие, то движение к экстремуму прекращают и эту рабочую точку принимают за точку экстремума; в противном случае перейти к следующему шагу;
- очередную рабочую точку принять за новую базовую точку и вокруг нее организовать новые пробные опыты, совершить новый рабочий шаг.
6.2.6 Весь ход поисковых экспериментов изобразить графически на плоскости
факторов ![]() и
и ![]() . Возле каждой пробной и
рабочей точки записать значения
. Возле каждой пробной и
рабочей точки записать значения ![]() , полученные в них опытным путем.
, полученные в них опытным путем.
6.3 Содержание отчета
Отчет по работе должен содержать:
1) результаты выполнения поисковых экспериментов методом Гаусса-Зейделя:
- координаты пробных точек, а также значения откликов в этих точках;
- координаты рабочих точек;
- значение экстремума;
- графическое изображение поиска на плоскости факторов
![]() и
и ![]() ;
;
2) результаты выполнения поисковых экспериментов градиентным методом:
- координаты пробных точек, а также значения откликов в этих точках;
- оценки компонент вектор-градиента в текущей базовой точке;
- координаты рабочей точки на направлении градиента;
- найденное значение экстремума;
- графическое изображение поиска на плоскости факторов
![]() и
и ![]() .
.
6.4 Контрольные вопросы
6.4.1 Как формулируется задача оптимизации?
6.4.2 Какими подходами можно решить задачу оптимизации?
6.4.3 Что общего у всех методов экспериментального поиска экстремума?
6.4.4 В чем заключается основная идея и процедура метода Гаусса-Зейделя?
6.4.5 В чем заключается основная идея и процедура обычного метода градиента?
6.4.6 Что служит критерием достижения экстремума в этих методах?
6.4.7 Дайте определение помехоустойчивости метода.
6.4.8 Как можно повысить надежность результатов в поисковых методах?
6.4.9 В чем отличие базовой и рабочей точек в методах поиска экстремума?
6.4.10 Для чего нужны пробные опыты в этих методах?
7 Лабораторная работа. Планирование второго порядка
Цель работы – изучение методов планирования эксперимента для получения математического описания в виде полинома второго порядка и использование этого описания для предсказания координат оптимума
7.1 Общие сведения
Для оптимизации статических объектов управления широко используют математические модели в виде полиномов второго порядка, с достаточной точностью описывающие поведение объекта в окрестности экстремальной точки. Для получения квадратичных моделей пользуются результатами эксперимента, проведенного по плану второго порядка.
Планы второго порядка отличаются от линейных тем, что факторы варьируют на нескольких уровнях, минимум на трех. Наиболее широкое применение получили ортогональные, ротатабельные и D-оптимальные планы.
При ортогональном планировании коэффициенты уравнения регрессии оцениваются независимо с минимальными дисперсиями, причем факторы с незначимыми коэффициентами можно сразу отбрасывать, без пересчета оставшихся значимых коэффициентов, как это необходимо при неортогональных планах.
Ротатабельные планы позволяют получать уравнения регрессии, предсказывающие значения выходной величины объекта с одинаковой точностью во всех направлениях на одинаковом расстоянии от центра плана.
7.2 Центральное композиционное планирование
В случае ортогонального центрального композиционного планирования (ОЦКП) критерием оптимальности плана является ортогональность столбцов матрицы планирования. В силу ортогональности все оценки коэффициентов определяются независимо друг от друга. После выполнения попарной ортогонализации столбцов, отвечающих свободному члену β0 и квадратичным коэффициентам βii, i=1,…, n, а также столбцов, отвечающих квадратичным членам между собой, регрессионная модель ищется в виде
![]()
При ротатабельном центральном композиционном планировании (РЦКП) с равномерным расположением точек на сфере получаются вырожденные матрицы. Для устранения этого применяют ротатабельные планы с комбинированием точек, лежащих на сферах различного радиуса. На практике удобно использовать сферу нулевого радиуса, что сводится к добавлению экспериментальных точек в центре плана. При РЦКП точки плана располагаются на трех сферах: центральные точки (сфера нулевого радиус), точки куба и звездные точки.
7.3 Нахождение экстремальной точки с помощью полиномов второго порядка
Адекватные полиномы второго порядка используют для предсказания оптимальной точки (точки экстремуму), так как градиентные методы оптимального поиска вблизи оптимума иногда непригодны из-за ограничений точности определения градиента (ограничен пробный шаг, ограничена точность измерения выходной величины). Для нахождения оптимальной точки приравнивают нулю значения компонент градиента, вычисленных по формуле:
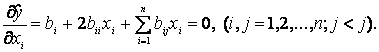
Решая систему
n
линейных уравнений по числу n
факторов, получают n координат оптимальной точки в относительных величинах
(начало координат находится в центре эксперимента, а уровни
xi нормированы). Затем, используя формулу (7.2) для
дисперсии ![]() ,
оценивают точность предсказания функции
,
оценивают точность предсказания функции ![]() .
.
7.4 Задание и порядок выполнения лабораторной работы
7.4.1 Составить ортогональный план второго порядка для двухфакторного эксперимента.
7.4.2 Загрузить
программу ttip.exe.
В списке
работ выбрать строку «Планирование второго порядка». Задать
модель объекта с двумя факторами ![]() и
и ![]() , установив следующие значения
коэффициентов:
, установив следующие значения
коэффициентов:
![]()
7.4.3
Провести эксперимент по составленному плану с центром в точке с координатами ![]() и интервалом
варьирования
и интервалом
варьирования ![]() при
заданной средней квадратической ошибке воспроизводимости эксперимента
при
заданной средней квадратической ошибке воспроизводимости эксперимента ![]() . Провести три
параллельные серии опытов (m=3).
. Провести три
параллельные серии опытов (m=3).
7.4.4 Обработать результаты эксперимента:
- провести проверку воспроизводимости;
- получить математическую модель объекта. Вычисление оценок коэффициентов регрессии, как обычно, производится методом наименьших квадратов:

![]() ;
;
- вычислить дисперсии оценок коэффициентов

- с помощью t-критерия Стьюдента проверить значимость коэффициентов;
- с помощью F-критерия Фишера проверить адекватность полученного математического описания;
- найти точку экстремума.
7.4.5 Составить ортогональный и ротатабельный планы второго порядка для трехфакторного эксперимента.
7.4.6
Провести эксперименты по составленным планам с центром в точке с координатами ![]() и интервалами
варьирования
и интервалами
варьирования ![]() при
заданной средней квадратической ошибке воспроизводимости эксперимента
при
заданной средней квадратической ошибке воспроизводимости эксперимента ![]() . Провести три
параллельные серии опытов (m=3). Рассчитать среднее значение отклика, полученного
в экспериментах в каждой точке матрицы планирования.
. Провести три
параллельные серии опытов (m=3). Рассчитать среднее значение отклика, полученного
в экспериментах в каждой точке матрицы планирования.
7.4 Содержание отчета
Отчет по работе должен содержать:
- матрицу планирования ОЦКП для двухфакторного эксперимента;
- описание методики проведения экспериментов на виртуальном лабораторном стенде;
- протокол экспериментов и усредненные значения откликов в каждой точке факторного пространства;
- статистический анализ результатов наблюдений:
а) процедуру проверки воспроизводимости эксперимента; вывод;
б) оценки коэффициентов регрессии, дисперсии оценок коэффициентов, проверка их значимости; выводы;
в) полученное уравнение регрессии;
г) процедуру проверки адекватности полученного математического описания;
- найденная точка экстремума;
- матрицы ОЦКП и РЦКП для трехфакторного эксперимента;
- результаты трех серий экспериментов, проведенных по этим планам; среднее значение отклика.
7.5 Контрольные вопросы
7.5.1 Когда и для чего используется ЦКП и в чем его отличие от планирования ПФЭ и ДФЭ?
7.5.2 Что является критерием оптимальности плана при ОЦКП и РЦКП?
7.5.3 Как достигается ортогональность матрицы планирования при ОЦКП?
7.5.4 Как с помощью полученного математического описания находится точка экстремума?
7.5.5 Приведите матрицу планирования для произвольного симметричного ЦКП.
7.5.6 Как определяется общее число точек ЦКП?
7.5.7 Как оценивается точность предсказания значения выходной величины в заданной точке факторного пространства?
7.5.8 Для чего необходимо проделывать параллельные опыты в одних и тех же точках факторного пространства?
7.5.9 Приведите матрицу планирования ОЦКП для двух и трехфакторного эксперимента.
7.5.10 Приведите матрицу планирования РЦКП для двух и трехфакторного эксперимента
Список литературы
1. Джеффри Тревис. LabVIEW для всех. – М.:ДМК Пресс, 2005.
2. Красовский Г.И., Филаретов Г.Ф. Планирование эксперимента. – Минск: изд. БГУ, 1982.
3. Дрейпер Н., Смит Г. Прикладной регрессионный анализ. – М.: Мир, 1987.
4. Ибраева Л.К. Теория и техника инженерного эксперимента. Конспект лекций для магистрантов специальности 6N0702 – Автоматизация и управление. – Алматы: АУЭС,2010.