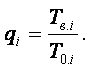АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра тепловых энергетических установок
ЭКСПЛУАТАЦИОННАЯ НАДЕЖНОСТЬ И БЕЗОПАСНОСТЬ ТЭС
Методические указания к выполнению лабораторных работ
для магистрантов специальности 050717 - Теплоэнергетика
Алматы 2009
СОСТАВИТЕЛЬ: А.И. Соколов. Эксплуатационная надежность и безопасность ТЭС. Методические указания к выполнению лабораторных работ для магистрантов специальности 05071 – Теплоэнергетика. – Алматы: АИЭС, 2009. – 23 с.
Методические указания содержат четыре лабораторные работы по курсу "Эксплуатационная надежность и безопасность ТЭС" для магистрантов. В лабораторных работах более углубленно, чем на практических занятиях и в расчетно-графической работе рассматриваются вопросы, связанные с расчетом вероятности отказа или снижения мощности энергоблока, рассчитывается время простоя блока, связанное с полным отказом и со снижением мощности в связи с отказом составляющих блок элементов. В третьей работе рассчитывается вероятное время простоя энергоблока на основе времени безотказной работы составляющего оборудования. В четвертой работе на примере простейшей схемы дается задание решить систему уравнений Колмогорова-Чепмена и построить зависимость безотказной работы от времени для этой схемы.
Введение
Лабораторные работы по курсу "Эксплуатационная надежность и безопасность ТЭС" носят расчетный характер.
Предлагаемые лабораторные работы являются дополнением к "Методическим указаниям и заданиям к расчетно-графическим работам для студентов магистрантов специальности 050717 – Теплоэнергетика [2]. Для полного охвата лекционного материала в данном пособии предлагаются две работы по расчету вероятности отказа и снижению мощности энергоблока вследствие отказа отдельных элементов блока аналитическим методом с использованием логических схем – метода дерева отказов. Одна работа посвящена расчету времени простоя или частичного снижения мощности на основе расчета коэффициентов готовности подсистем блока. В четвертой работе на примере простейшей схемы предлагается найти решение системы дифференциальных уравнений Колмогорова-Чепмена применяя прямое и обратное преобразование Лапласа. Этот метод довольно трудоемкий и более подробно описан в учебном пособии [1].
Исходные данные для заданий к лабораторным работам, такие как средняя наработка до отказа и среднее время восстановления отдельных элементов оборудования взяты из оперативных журналов электростанций и из экспертных оценок.
Таким образом, данные методические указания, включающие четыре расчетные лабораторные работы, вместе с пособием [2], являются практическим дополнением лекционного материала, изложенного в учебном пособии [1].
В дальнейшем предполагается данные задачи после некоторой переработки сделать для работы на компьютере.
1 Лабораторная работа № 1
Логико-вероятностный метод определения надёжности технологической части электростанции
Цель работы: Приобретение навыков вычисления длительности аварийного останова энергоблока, вероятности состояния отказов, коэффициента простоя и коэффициента готовности энергоблока на основе дерева отказов по известным наработкам на отказ и времени восстановления отдельных элементов.
1.1 Теоретическая часть
Условием применимости логико-вероятностных методов определения надежности технологической системы является существование логической схемы и независимость отказа элементов. Одним из таких методов является метод построения дерева отказов.
Деревом отказов называется логическая иерархическая схема, представляющая собой связь событий отказа системы с отказами элементов. Вершины дерева представляют логические операции "И" (логическое произведение) и "ИЛИ" (логическая сумма). Дерево отказов начинается с конечного события, в качестве которого понимается полный отказ системы. На более низком уровне обозначаются события, которые вызывают конечное событие в соответствии с логической операцией, связывающей эти события. На нижнем уровне располагаются события отказа элементов. Пример построения дерева отказов показан на рисунке 1.1. Здесь дерево отказов построено для максимально упрощенной тепловой схемы энергоблока.
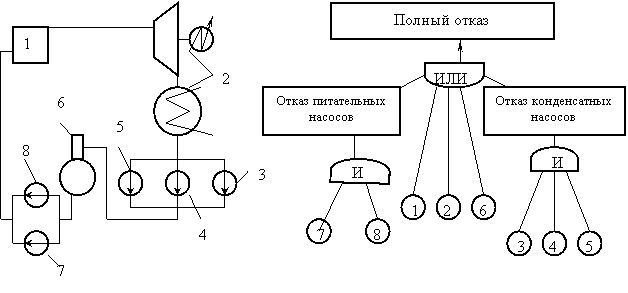
Рисунок 1.1
Анализ дерева отказов заключается в определении такой комбинации элементов, одновременный отказ которых приводит к вершине дерева – отказу энергоблока. Для рассмотренного примера (см. рисунок 1.1) множество элементов, отказ которых приводит к отказу системы, составит {1}, {2}, {6}, {7,8}, {3,4,5}. Это множество элементов называется сечением. Минимальное сечение – такое множество, из которого нельзя удалить ни одного элемента, иначе оно перестанет быть сечением. Если анализ дерева отказов начинать от конечного события, то при прохождении через вершину "И" увеличивается число элементов в сечении, а при прохождении через вершину "ИЛИ" – число сечений. Рассмотренное дерево отказов содержит пять минимальных сечений 1, 2, 6, (7,8), (3, 4, 5). Если определено множество минимальных сечений, то можно рассчитать вероятность отказа всей системы по интенсивностям отказов составляющих элементов.
Для проведения анализа надежности схемы она представляется логической схемой, т.е. совокупностью элементов, имеющих последовательное или параллельное соединение. Параллельное соединение понимается в том смысле, что имеется резервирование, например, питательных, бустерных, конденсатных насосов и других элементов схемы. Затем строится дерево отказов. Паропровод, состоящий из двух ниток, не считается резервированным.
Математическое описание дерева отказов, представленного в логической форме, осуществляется с помощью действий, заменяющих логические операции "ИЛИ" на знак "+", "И" – на знак "х".
Вероятность аварийного останова энергоблока вследствие отказа элементов рассчитывается по выражению
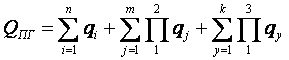. (1.1) Вероятность
отказа отдельного элемента равна
|
|
(1.2) |
Коэффициент готовности системы
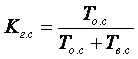. (1.3)
Противоположный показатель – коэффициент простоя
. (1.4)
В случае экспоненциального закона распределения случайной величины время наработки до отказа системы равно
(1.5)
где T0.nj – время наработки до отказа подсистем с параллельно включёнными элементами.
Время восстановления системы
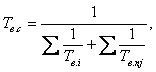(1.6)
где Tв.пi – время восстановления подсистем с параллельно включёнными элементами.
В формулах (1.5) и (1.6) первое слагаемое представляет собой сумму интенсивностей отказа и интенсивностей восстановления последовательно соединенных элементов без резерва. Второе слагаемое – сумма интенсивностей отказа и интенсивностей восстановления последовательно соединенных блоков однотипных элементов с резервированием.
Если два параллельно включенных элемента не однотипны, то среднее время наработки на отказ и среднее время восстановления этой подсистемы вычисляется по формулам
, 
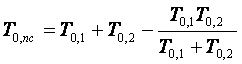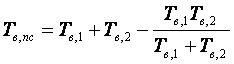. (1.7)
1.2 Задание
Рассматривается аварийный останов энергоблока вследствие отказов оборудования. Принципиальная схема тепловой части показана на рисунке 1.2. Схема состоит из 1- парогенератора (ПК); 2- турбины (Т); 3- конденсатора (К); 4, 5- двойной нитки паропровода (ПП); 6,7- резервированной системы дутьевых вентиляторов (ДВ); 8, 9- резервированной системы дымососов (Д); 10, 11- резервированной системы циркуляционных насосов (ЦН); 12, 13, 14- двойного резервирования конденсатных насосов (КН); 15, 16, 17- системы подогревателей низкого давления (ПНД); 18- деаэратора (Др); 19 20, 21- двойного резервирования бустерных насосов (БН); 22- питательного электронасоса (ПЭН); 23- питательного турбонасоса (ТН); 24- трубопроводов питательной воды (ПТ); 25- системы топливоподачи (ТП); 26- электрогенератора.
Составные системы и подсистемы общего технологического цикла следующие
1. Паровой тракт, в котором происходит основной цикл преобразования энергии. Его основные элементы – ПК, Т, Г, К, ПП, ЦН.
2. Питательный тракт. Его основные элементы – КН, ПНД, Др, БН, ПЭН, ПТН, ПТ.
3. Система топливоподачи (показана условно – ТП).
4. Газовоздушный тракт, включающий в себя тягодутьевые механизмы котла – ДВ и Д, служит для обеспечения сгорания топлива в топке котла и последующего удаления продуктов горения.
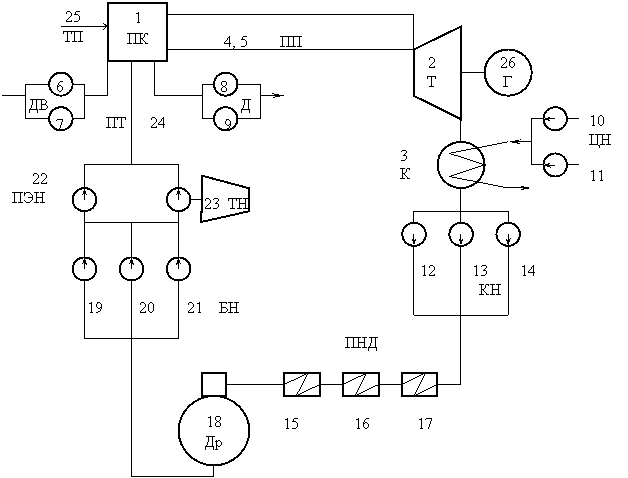
Рисунок 1.2
На основании данных эксплуатации и ремонтов конкретных электростанций, взятых из оперативных журналов электростанций, и ремонтов электрооборудования и на основании экспертных оценок получены данные по средней наработке на отказ и по среднему времени восстановления отдельных элементов тепловой схемы электростанций. Эти данные сведены в таблицу 1.1.
В работе необходимо рассчитать вероятность аварийного останова блока, время наработки на отказ, время восстановления, коэффициент готовности и коэффициент простоя блока.
1.3 Порядок выполнения работы
1. В соответствии с принципиальной тепловой схемой энергоблока (см. рисунок 1.2) определить системы и подсистемы схемы, построить логическую схему и соответствующее дерево отказов.
2. Определить вероятности отказов отдельных элементов схемы qi и вероятности отказов блоков однотипных элементов qin.
3. Вычислить вероятность отказа и вероятность безотказной работы энергоблока в целом.
4. Вычислить коэффициенты надежности энергоблока: коэффициент готовности системы Кг, коэффициент простоя Кп.
Т а б л и ц а 1.1 – Показатели надежности теплосилового оборудования (получены из статистических данных)
|
№ элемента |
Оборудование |
Обозначе-ние |
Показатели надежности |
Вероятности отказа элементов |
|
|
То, ч |
Тв, ч |
qi |
|||
|
1 |
Парогенератор |
ПК |
4200 |
70 |
|
|
2 |
Паровая турбина |
Т |
8600 |
68 |
|
|
3 |
Конденсатор |
К |
14000 |
25 |
|
|
4, 5 |
Паропроводы (один гиб)*) |
ПП |
105 |
1,6 |
|
|
6, 7 |
Дутьевые вентиляторы |
ДВ |
30500 |
45 |
|
|
8, 9 |
Дымососы |
Д |
23000 |
30 |
|
|
10, 11 |
Циркуляционные насосы |
ЦН |
55000 |
33 |
|
|
12, 13, 14 |
Конденсатные насосы |
КН |
40000 |
20 |
|
|
15, 16, 17 |
ПНД |
ПНД |
14000 |
10 |
|
|
18 |
Деаэратор |
Др |
45000 |
25 |
|
|
19, 20, 21 |
Бустерные насосы |
БН |
30200 |
20 |
|
|
22 |
Питательный электронасос |
ПЭН |
19500 |
31 |
|
|
23 |
Турбонасос |
ПТН |
3000 |
45 |
|
|
24 |
Трубопровод питательной воды **) |
ПТ |
6 задвижек |
|
|
|
25 |
Система топливоподачи (мазутный насос) |
ТП |
12000 |
35 |
|
|
26 |
Электрогенератор |
Г |
15000 |
55 |
|
*) Наработка на отказ одного гиба составляет То = 105 ч. Среднее количество гибов на одном паропроводе равно 12. Следовательно вероятность отказа паропровода
|
|
(1.8) |
**) Вероятность состояния отказа трубопроводов питательной воды зависит от количества задвижек на трубопроводе. Наработка на отказ одной задвижки То =16500 ч, время восстановления Тв = 10 ч.
2 Лабораторная работа № 2
Логико-вероятностный метод определения вероятности снижения нагрузки энергоблока
Цель работы: Приобретение навыков расчета вероятности снижения мощности энергоблока в зависимости от режимных отказов на основе построения дерева отказов, по известным наработкам на отказ и времени восстановления отдельных элементов блока.
2.1 Теоретические сведения
Теоретические сведения о построении дерева отказов приведены в первом пункте лабораторной работы № 1. Кроме построения дерева отказов можно построить дерево снижения нагрузки и рассматривать только снижение нагрузки энергоблока. В этом случае не учитываются полные отказы блока. В данной работе рассматривается только снижение нагрузки. При построении дерева отказов в этом случае вершинным событием является снижение нагрузки. На более низком уровне обозначаются события, которые вызывают конечное событие в соответствии с логической операцией, связывающей эти события. На нижнем уровне располагаются события отказа элементов, приводящие к снижению нагрузки. Пример построения дерева отказов для события снижения нагрузки блока показан на рисунке 2.1. Здесь дерево отказов построено для максимально упрощенной тепловой схемы энергоблока.
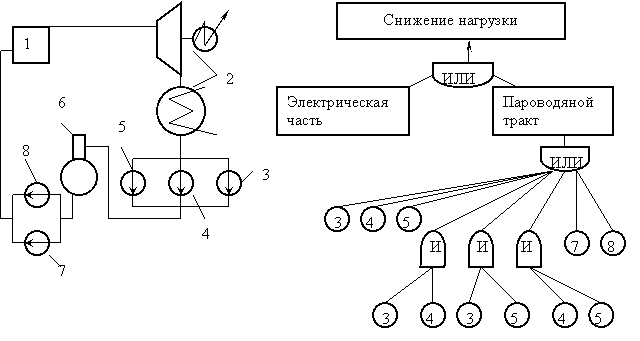
Рисунок 2.1
Анализ дерева отказов заключается в определении такой комбинации элементов, одновременный отказ которых приводит к вершине дерева – снижению нагрузки. Для рассмотренного примера (см. рисунок 2.1) множество элементов, отказ которых приводит к снижению нагрузки, составит {3}, {4}, {5}, {7}, {8}, {3,4}, {3,5}, {4,5}. Это множество элементов называется сечением. Минимальное сечение – такое множество, из которого нельзя удалить ни одного элемента, иначе оно перестанет быть сечением. Если анализ дерева отказов начинать от конечного события, то при прохождении через вершину "И" увеличивается число элементов в сечении, а при прохождении через вершину "ИЛИ" – число сечений. Это дерево отказов содержит восемь минимальных сечений 3, 4, 5, 7, 8, (3,4), (3,5), (4,5). Если определено множество минимальных сечений, то вероятность снижения нагрузки энергоблока можно рассчитать по интенсивности отказов элементов.
Для проведения анализа надежности схемы все системы представляются совокупностью элементов, имеющих последовательное или параллельное соединение. Параллельное соединение понимается в том смысле, что имеется резервирование, например, питательных, бустерных, конденсатных насосов и других элементов схемы.
Математическое описание дерева отказов, представленного в логической форме, осуществляется с помощью действий, заменяющих логические операции "ИЛИ" на знак "+", а "И" – на знак "х".
Суммарная интенсивность отказа элементов, приводящая к снижению нагрузки системы вычисляется по формуле
. (2.1)
2.2 Задание
Рассматривается снижение нагрузки энергоблока вследствие отказов теплотехнического оборудования. Принципиальная схема тепловой части и ее состав показана на рисунке 1.2 в лабораторной работе № 1. Средняя наработка на отказ отдельных элементов схемы дана в таблице 1.1 в лабораторной работе № 1.
В данной работе необходимо с использованием метода дерева отказов рассчитать вероятность состояния сниженной нагрузки рассматриваемого блока электростанции.
2.3 Порядок выполнения работы
1. В соответствии с принципиальной тепловой схемой энергоблока (см. рисунок 1.2) определить системы и подсистемы схемы и построить соответствующее дерево отказов для снижения нагрузки.
2. Из таблицы (1.1) выбрать элементы, ведущие к снижению номинальной мощности и определить вероятности отказов этих элементов схемы qi.
3. Вычислить вероятность снижения нагрузки энергоблока в целом.
4. Сравнить с результатами работы № 1 и сделать выводы.
3 Лабораторная работа № 3
Комплексная оценка показателей надёжности энергоблока
Цель работы: Ознакомить с методами расчета таких показателей, как годовой расчетный период времени работы блока, времени частичных вынужденных отказов, времени полных вынужденных отказов, времени планово-профилактического обслуживания и др. на основе среднестатистических данных по времени наработки до отказа, времени восстановления отдельных элементов блока и принципиальной схемы блока.
3.1 Теоретическая часть
В данной работе проводится расчет упрощенной схемы блока, рассматриваемого как систему, и включающего в себя отдельные элементы: парогенератор, турбину, электрогенератор и вспомогательное оборудование.
Методика комплексной оценки показателей надежности энергоблока проводится в следующей последовательности.
1. Разрабатывается принципиальная и логическая схемы системы.
2. Делается оценка показателей Т0 и Тв отдельных элементов системы.
3. Определяются подсистемы логической схемы.
4. Рассчитываются показатели готовности подсистем.
5. Определяется мощность состояний подсистем.
6. Определяется сочетание состояний в подсистемах и оценка их
готовности.
7. Оцениваются основные показатели готовности системы.
8. Анализируется влияние показателей на готовность системы.
3.1.1 Разработка принципиальной и логической схемы системы
Выбирается принципиальная схема системы, в которую включаются все те элементы, влияние которых на готовность системы рассматривается в расчете. Из схемы исключаются те элементы, влияние которых на готовность системы в расчете не рассматривается или оно ничтожно мало по сравнению с влиянием рассматриваемых элементов.
При построении логической схемы системы местоположение элементов должно соответствовать их влиянию на показатели надежности системы и может не соответствовать требованиям физических связей на принципиальной схеме.
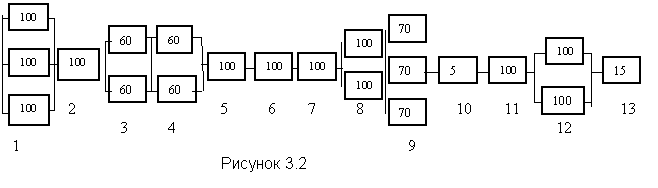
Для каждого элемента указывается его мощность (производительность) в %, влияющая на итоговую мощность системы. Эта величина определяется на основе данных завода изготовителя. Пример упрощенной принципиальной схемы энергоблока дан на рисунке 3.1, а соответствующая ей логическая схема с указанием мощности элементов приведена на рисунке 3.2.
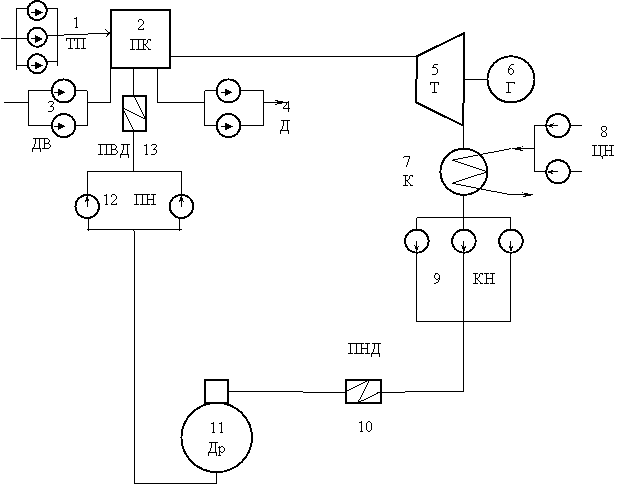
Рисунок 3.1
3.1.2 Оценка наработки на отказ и времени восстановления элементов
Такая оценка делается на основании данных эксплуатации и ремонтов на электростанциях или на основании экспертных оценок. Эти показатели приведены в таблице 3.1. Там же дана мощность (производительность) отдельных элементов блока.
Т а б л и ц а 3.1
|
№ в схеме |
Элемент |
Т0 |
Тв |
Мощность |
|
1 |
Мазутный насос |
12000 |
35 |
100 |
|
2 |
Парогенератор |
4200 |
70 |
100 |
|
3 |
Дутьевой вентилятор |
30500 |
45 |
60 |
|
4 |
Дымосос |
23000 |
30 |
60 |
|
5 |
Паровая турбина |
8600 |
60 |
100 |
|
6 |
Электрогенератор |
15000 |
55 |
100 |
|
7 |
Конденсатор |
14000 |
25 |
100 |
|
8 |
Циркуляционный насос |
55000 |
30 |
100 |
|
9 |
Конденсатный насос |
40000 |
15 |
70 |
|
10 |
ПНД |
14000 |
10 |
5 |
|
11 |
Деаэратор |
45000 |
25 |
100 |
|
12 |
Питательный насос |
2000 |
45 |
100 |
|
13 |
ПВД |
6500 |
25 |
15 |
3.1.3 Разбивка системы на подсистемы
Исходная логическая схема состоит из 21 элементов. Количество сочетаний возможных состояний составляет 221 = 2097152. Для сокращения вычислительной работы вводится понятие подсистем. Каждый элемент может принадлежать только одной подсистеме. При разбивке логической схемы энергоблока на подсистемы нужно учитывать мощность элемента и проводить объединение в подсистемы по элементам с одинаковой единичной мощностью и с учетом их технологических связей. Так, например, в состав первой подсистемы ПС-1 в рассматриваемом примере выделяются элементы со 100 % единичной производительностью
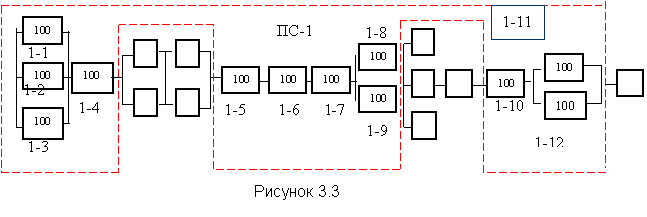
Точно также выделяются другие подсистемы, включающие элементы одинаковой единичной производительности независимо от последовательности их соединений в принципиальной схеме. Учитывая технологически связи, дутьевые вентиляторы и дымососы целесообразно включить в две различные подсистемы.
Подсистема ПС-5 состоит только из одной компоненты – группы ПНД, отказ которой приведет к снижению мощности на 5 % (обеспечивает мощность 95 % от номинала). ПС-6 также состоит из одной компоненты (группа ПВД), отказ которой приведет к снижению мощности блока на 15 % (обеспечивается 85 % от номинальной мощности блока). В результате энергоблок как группа подсистем разбивается на 6 подсистем. Количество состояний подсистем в анализе блока сократилось до 27 = 128. Задача сводится к исследованию соединенных последовательно подсистем (см. рисунок 3.4).
 |
3.1.4 Расчет показателей готовности подсистем
Показатель готовности подсистем определяется по формуле (1.3), где Т0,с и Тв,с определяются по формулам (1.5) и (1.6). Коэффициент готовности определяется для каждой подсистемы.
3.1.5 Определение мощности состояния подсистем
На основании анализа мощностей (производительностей) компонент, входящих в подсистемы, определяется характерная возможная или частичная мощность подсистем, и результат вписывается в таблицу, пример которой приведен ниже.
Т а б л и ц а 3.2
|
Подсистема |
Кол-во элементов в подсистеме |
Возможная или частичная мощность одной подсистемы, % |
|
ПС-1 |
12 |
100 |
Для подсистем ПС-5 и ПС-6 в таблицу вписывается мощность системы при выходе этих подсистем из строя, т.е. 95 и 85 %, соответственно.
3.1.6 Определение сочетаний в подсистемах и оценка их готовности
Количество состояний компонент равно 2п, где п – количество элементов в подсистеме, однако, для подсистемы ПС-1, в состав которой входят 13 элементов и количество состояний подсистемы равно 213 = 8192, рассматривать все состояния нецелесообразно, т.к. интересны лишь состояния, приводящие к полному отказу блока, а это только характеризуется найденной в п. 4 величиной коэффициента готовности подсистемы ПС-1 Кг. Противоположный показатель, коэффициент аварийности, равен Кпс = 1 – Кг. Эти величины вписываются в таблицу 3.3, которая дополняется всеми остальными подсистемами.
Т а б л и ц а 3.3
|
Подсистема |
Элементы и мощности их состояний в % |
Мощность подсистемы, % |
Готовность состояния подсистемы |
||
|
ПС-1 с элементами мощностью по 100 % |
Сочетания из 12 элементов |
100
|
|
||
|
0 |
|
||||
|
ПС-2 (дутьевые вентиляторы) |
Э 2-1 |
Э 2-2 |
- |
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В ПС-2 4 сочетания работающих и неработающих элементов Мощность ПС-2 при двух работающих элементах (вентиляторах) равна 100 %, при одном неработающем элементе – 60 % (таких состояния 2) и обоих неработающих элементах – 0 %.
При состоянии работоспособности обоих вентиляторов готовность ПС-2 по закону умножения вероятностей будет равна произведению вероятностей (значений готовности) обоих элементов, т.е. КгКг. При одном работающем вентиляторе готовность ПС-2 равна Кг(1 – Кг) – два состояния. При обоих неработающих вентиляторах готовность ПС-2 равна (1 – Кг)(1 – Кг). Готовность всех четырех состояний записывается в таблицу 3.3, в последний столбец. Точно также делается анализ всех остальных подсистем. Результаты записываются в таблицу 3.3.
Полная группа подсистем является интерпретацией всего блока. Это отражается в таблице 3.4, которая строится из данных таблицы 3.3.
Т а б л и ц а 3.4
|
Группа подсистем |
Состояния мощности подсистем, % |
Мощность состояния блока, % |
Готовность состояния блока |
|||||
|
ПС-1 |
ПС-2 |
ПС-3 |
ПС-4 |
ПС-5 |
ПС-6 |
|||
По горизонтали указаны номера семи подсистем, составляющих энергоблок. Под ними даны мощности состояний соответствующих подсистем. Правее в колонке указана соответствующая состояниям подсистем мощность энергоблока. Количество состояний всей системы равно 27 = 128, однако часть состояний из этого количества можно исключить и ограничиться только рассмотрением состояний, отвечающим полной работоспособности (100 %), одной из одинаковых частичных работоспособностей, или нулевой работоспособностью. Такое количество рассматриваемых вариантов обосновывается тем, что часть из них совмещается по результирующей мощности. Состояния системы в таблице удобно располагать в порядке убывания мощности от 100 % до нуля. В последний столбец вписывается готовность состояния системы в целом. Данные для этого берутся из таблицы 3.3. Готовность блока определяется перемножением готовностей состояний подсистем для заданных мощностей при состоянии подсистем в соответствии с таблицей 3.4. Сумма всех чисел в последнем столбце должна равняться единице.
3.1.7 Определение основных показателей готовности энергоблока
Предварительно рассмотрим схему анализа показателей готовности для энергоблока (см. рисунок 3.5). На этом рисунке даны следующие обозначения:
Т – расчетный период времени (обычно 1 год или 8760 часов);
Тэ – период для анализа эффективности, ч;
Тг – период для анализа готовности, ч;
Тчв – время частичных вынужденных отказов, ч;
Тпв – время полных вынужденных отказов, ч;
Тпл – время планово-профилактического обслуживания, ч.
 |
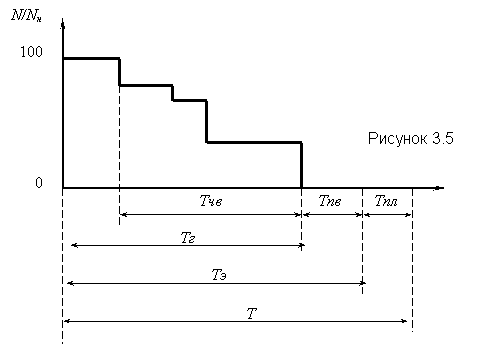В течение времени (Тг - Тчв) энергоблок несет полную электрическую нагрузку. Частичные вынужденные отказы энергоблока вызываются полными вынужденными отказами элементов энергоблока, но в связи с их резервированием располагаемая мощность может находиться в пределах 100% ³ N/Nн > 0. В течение времени Тпв в результате полных вынужденных отказов нагрузка блока падает до нуля. Коэффициент готовности может быть представлен выражением
. (3.1)
Этот показатель не учитывает частичные снижения нагрузки по причине частичных отказов. Для учета частичных отказов энергоблока используется эквивалентный коэффициент готовности
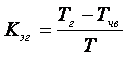. (3.2)
В этом показателе время Тчв выражается эквивалентно с учетом недоотпуска электроэнергии во время частичных отказов
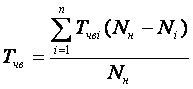, (3.3)
где Тчвi – время i-го частичного вынужденного отказа;
(Nн – Ni) – снижение мощности энергоблока в результате i-го частичного отказа;
Nн – номинальная мощности блока;
Ni – мощность при i-м частичном отказе.
В расчетах также используется коэффициент полных вынужденных отказов
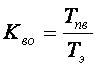(3.4)
и эквивалентный коэффициент вынужденных отказов
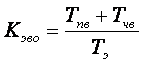. (3.5)
Для дальнейших расчетов принимается, что в течение года простой энергоблока в планово-предупредительных ремонтах составляет 30 суток, откуда период для анализа эффективности Тэ = 365 – 30 = 335 суток. Этот период приходится на работоспособное состояние, а также на полные (N =0) и частичные (0 < N < 100 %) отказы.
Для определения основных показателей готовности энергоблока необходимо перестроить таблицу 3.4 в следующем виде:
Т а б л и ц а 3.5
|
Номер состояния |
Готовность состояния |
Мощность состояния, % |
Продолжительность состояния, сут |
|
1 |
|
|
|
Для состояний одинаковой мощности блока (60 % и 0 %) готовность суммируется. Продолжительность состояний определяется умножением готовности блока на продолжительность Тэ периода для анализа (335 сут) и результат записывается в четвертую колонку. Подставляя полученные результаты в формулы (3.1) – (3.5), получаем основные показатели готовности блока.
3.2 Задание
Рассчитать время работы энергоблока на номинальной мощности, время работы на пониженной мощности вследствие частичных вынужденных отказов, время простоя блока вследствие полного отказа оборудования и на основании полученных данных определить основные показатели готовности энергоблока. Принципиальная схема блока и ее состав показана на рисунке 3.1, а в таблице 3.1 дано время наработки на отказ, время восстановления и мощность отдельных элементов приведенной схемы, полученные на основании статистических данных.
Проанализировать полученные данные и дать предложения по увеличению надежности блока.
3.3 Порядок выполнения работы
1. Изучить принципиальную схему энергоблока на рисунке 3.1 и сравнить с соответствующей логической схемой.
2. В соответствии с рисунком 3.3 начертить логическую схему блока и выделить на ней остальные подсистемы блока (ПС-2 – ПС-6).
3. Построить дерево отказов для подсистемы ПС-1.
4. Рассчитать время наработки до отказа, время восстановления, коэффициент готовности и коэффициент простоя для каждой подсистемы.
5. Определить мощности состояний подсистем и внести в таблицу 3.2.
6. Определить значения готовности для состояний подсистем и внести в таблицу 3.3.
7. Определить готовность всех состояний для энергоблока и полученные данные внести в таблицу 3.4.
8. Вычислить продолжительность различных состояний энергоблока, данные внести в таблицу 3.5 и на их основании рассчитать основные показатели готовности энергоблока: Коэффициент вынужденных отказов Кво, эквивалентный коэффициент вынужденных отказов Кэво, эквивалентное время частичных вынужденных отказов Тчв, коэффициент готовности за календарный год с учетом плановых ремонтов и полных отказов Кгг, эквивалентный коэффициент готовности за календарный год с учетом плановых ремонтов, полных и частичных отказов.
9. Проанализировать полученные данные, сделать вывод о надежности данного энергоблока и дать рекомендации о ее повышении.
4 Лабораторная работа № 4
Расчёт показателей надёжности системы с использованием марковских процессов
Цель работы: На базе простейшей схемы дать полное представление о расчете вероятности безотказной работы системы с использованием марковских процессов, получить кривую закона надежности в зависимости от времени работы системы.
4.1 Теоретическая часть
В основе метода расчета надежности с использованием марковских процессов лежит описание функционирования систем с дисперсным множеством состояний, каждое из которых определяется состоянием составляющих систему элементов, и непрерывным временем. Такое описание состояния систем возможно только в том случае, если для каждого момента времени вероятность любого состояния в будущем зависит только от состояния системы в настоящем и не зависит от того, каким путем система пришла в это состояние. Предполагается, что время работы и восстановления элементов и системы распределяется по экспоненциальному закону.
Методика расчета строится следующим образом [1]. Для соответствующей физической системы строится логическая схема, в которой последовательно соединятся блоки однотипных элементов. На базе логической схемы строится граф состояний системы, в котором отдельные состояния изображаются вершинами с соответствующими номерами. Вершины соединяются ребрами, характеризующими интенсивность возможных переходов системы. Прямые ребра соответствуют событиям отказа элемента, обратные – его восстановлению.
Интенсивность прямых переходов из i-го состояния в j-е, обусловленная отказом элементов, рассчитывается как произведение интенсивности перехода элемента l-го блока на число работоспособных элементов этого блока в i-м состоянии.
. (4.1)
Интенсивность обратного перехода из j-го состояния в i-е определяется восстановлением или заменой отказавшего элемента и рассчитывается как произведение интенсивности восстановления элемента l-го блока на число отказавших элементов этого блока в j-м состоянии.
(4.2)
После построения графа состояний и определения всех возможных переходов и их интенсивностей записывается квадратная матрица интенсивностей переходов. Размер матрицы соответствует количеству вершин графа
. (4.3)
После построения матрицы интенсивностей переходов записывается система дифференциальных уравнений Колмогорова-Чепмена и условие нормировки
,
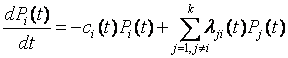i = 1, 2, …, k, (4.4)
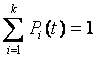. (4.5)
На практике наиболее часто встречаются однородные марковские процессы. В этом случае коэффициенты дифференциальных уравнений Колмогорова-Чепмена не зависят от времени, т.е. получается система обыкновенных дифференциальных уравнений с постоянными коэффициентами. Для решения такой системы уравнений удобнее всего воспользоваться методом преобразований Лапласа. В преобразованном виде система (4.4) будет иметь вид
, (4.6)
где s – комплексная переменная Лапласа;
Р(s) – изображение вектор-функции 
.
Таким образом получается система алгебраических уравнений для изображений Р(s), которая решается обычными методами линейной алгебры. Затем, применяя обратное преобразование Лапласа к изображению Р(s) с учетом начальных условий Pi(t0) = P 0i, i = 1, 2, …, k (P0i – заданные вероятностные реализации состояний процесса в момент t = t0), находятся решения P(t) исходной системы.
4.2 Задание
Рассматривается простейшая схема, состоящая из одного блока двух однотипных элементов или система из двух блоков по одному элементу в каждом блоке (см. рисунок 4.1).
 |
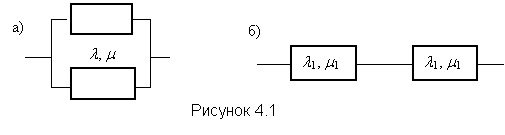Интенсивность отказа и восстановления элементов на рисунке 4.1 (а) равна l и m, на рисунке 4.1 (б) – l1, m1 и l2, m2. Конкретные значения этих параметров приведены в таблице 4.1. Необходимо написать для этой системы уравнения Колмогорова-Чепмена, решить их методом преобразования Лапласа и для вероятностей безотказной работы в основном состоянии Р1(t) построить кривую зависимости от времени, начиная с момента t = 0 до финальной вероятности.
4.3 Порядок выполнения работы
1. Для одной из систем (по заданию преподавателя) строится граф достижимых состояний и определяется интенсивность прямых и обратных переходов.
2. В соответствии
с графом состояний записывается матрица интенсивностей переходов 
и система
дифференциальных уравнений Колмогорова-Чепмена вместе с условием нормировки.
Одно из уравнений заменяется условием нормировки.
3. Полученная система дифференциальных уравнений преобразуется с помощью оператора Лапласа в систему алгебраических уравнений.
4. Так как работоспособным состоянием является только первое, то полученную систему необходимо решать только относительно P1(s). Записывается решение P1(s) по правилу Крамера.
5. Определяются корни знаменателя.
6. Выражение для P1(s) записывается в общем виде и затем разлагается на простые дроби
, (4.7)
где si – корни знаменателя. Число простых дробей в правой части равно
числу корней знаменателя i.
D1 – определитель системы в котором первый столбец заменен на
столбец, составленный из свободных членов системы.
Преобразование этого равенства приведет к системе алгебраических уравнений относительно неопределенных коэффициентов А, В, С, … . Полученная система решается относительно этих коэффициентов в общем виде. Полученные решения подставляются в (4.7).
7. Путем обратного преобразования Лапласа из полученного выражения находится оригинал P1(t). В это выражение подставляются заданные значения интенсивностей отказов и восстановлений и найденные значения si. Подстановка значений t от 0 до получения финального значения вероятности P1(t) даст возможность построить кривую изменения P1(t).
Т а б л и ц а 4.1
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
l×104 |
1,0 |
1,25 |
0,9 |
1.5 |
0,9 |
1,7 |
0,8 |
2,0 |
1,6 |
1,8 |
|
m |
0,1 |
0,09 |
0,15 |
0,15 |
0,09 |
0,06 |
0,14 |
0,12 |
0,1 |
0,12 |
|
l1×104 |
2,0 |
2,1 |
2,2 |
2,3 |
2,4 |
2,5 |
2,6 |
2,7 |
2,8 |
2,9 |
|
l2×104 |
2,3 |
2,2 |
2,1 |
2,0 |
1,9 |
1,8 |
1,7 |
1,6 |
1,5 |
1,4 |
|
m1 |
0,1 |
0,1 |
0,05 |
0,11 |
0,12 |
0,13 |
0,14 |
0,18 |
0,15 |
0,2 |
|
m2 |
0,12 |
0,13 |
0,14 |
0,15 |
0,14 |
0,13 |
0,12 |
0,11 |
0,1 |
0,09 |
Список литературы
1. Соколов А.И. Эксплуатационная надежность ТЭС: Учебное пособие. – Алматы: АИЭС, 2009. – 127 с.
2. Соколов А.И. Эксплуатационная надежность ТЭС и АЭС: Метод. указания и задания для расчетно-графических работ. – Алматы: АИЭС, 2009. – 20 с.
3. Соколов А.И. Эксплуатационная надежность ТЭС и АЭС: Учебное пособие. – Алматы: АИЭС, 2006. – 106 с.
4. Соколов А.И. Эксплуатационная надежность ТЭС и АЭС: Конспект лекций. – Алматы: АИЭС, 2003. – 85 с.