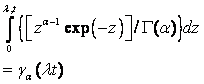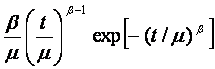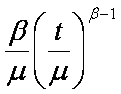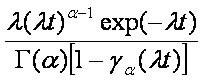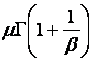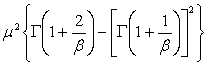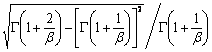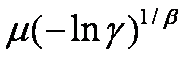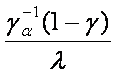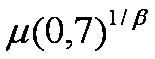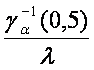МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
Алматинский институт энергетики и связи
А.И. Соколов
ЭКСПЛУАТАЦИОННАЯ НАДЁЖНОСТЬ И БЕЗОПАСНОСТЬ ТЭС
Учебное пособие
Алматы 2009
В учебном пособии с точки зрения общих принципов теории надёжности рассмотрена надёжность тепловых схем ТЭС и их отдельных узлов. Даны особенности обеспечения надёжности на каждой из трёх стадий жизни объекта – на стадии проектирования, изготовления и эксплуатации. Надёжность объектов определяется через их единичные и комплексные показатели надёжности. Рассмотрены особенности расчёта на внезапные и постепенные отказы, а также параметрическая надёжность технических систем, когда выходные параметры рассматриваемого объекта выходят за допустимые пределы. Предварительно вводятся основные понятия теории надёжности. В учебное пособие включены аналитические методы расчета надёжности. Приведенный материал сопровождается иллюстрациями. Учебное пособие предназначено для магистрантов, обучающихся по специальности направления – Тепловые электрические станции.
Современное развитие техники характеризуется непрерывным ростом показателей мощности, скорости, точности. Ограничиваясь только проблемами энергетики, можно отметить рост единичной мощности энергоблоков, использование пара критических и сверхкритических параметров. Мощность энергетических ядерных реакторов достигла 1500 МВт. Аварийный отказ в работе мощного оборудования ТЭС сопровождается крупными затратами на восстановление этого оборудования, а в случае аварии на АЭС – заражением больших площадей долгоживущими радиоактивными материалами и рассеиванием радиоактивной пыли на тысячи километров.
Вместе с тем для современных технических объектов характерно внедрение электроники, автоматизации отдельных операций и циклов, что обеспечивает более широкие возможности по управлению, адаптации к внешним воздействиям, регулированию различных функций.
Для эффективного использования технических систем необходимо, чтобы они обладали высокими показателями качества и надёжности. Под качеством технического устройства понимается обычно совокупность свойств, определяющих его пригодность для использования по назначению. Стандарт ISO даёт следующее определение качества: "Качество – совокупность свойств и характеристик продукции или услуг, которые придают им способность удовлетворять обусловленные или предполагаемые потребности". С другой стороны, "надёжность – это свойство технического объекта сохранять требуемые показатели качества в течение всего периода его использования".
С течением времени технические характеристики объекта меняются. Это происходит за счёт того, что он находится во взаимодействии с окружающей средой, с человеком, управляющим этим объектом. Накопление количества различных воздействий на объект меняет его качественные показатели. Это изменение может быть как абсолютным, так и относительным.
Абсолютное изменение качества связано с различными процессами, действующими на объект, за счёт которых изменяются характеристики объекта и происходит его физическое старение. Износ энергетического оборудования приводит к снижению мощности энергоблока.
Относительное изменение качества объекта связано с его моральным старением. Относительное изменение качества в теории надёжности не рассматривается.
Наука о надёжности изучает изменение показателей качества технических объектов и их выход из строя под влиянием тех причин, которые приводят к абсолютным изменениям свойств объектов.
Основной движущей силой при создании новых и использовании существующих изделий является стремление обеспечить высокий уровень качества и надёжности. Мероприятия, проводимые в этой области, затрагивают все стадии создания и реализации технических объектов, включая этапы проектирования, изготовления, испытания, хранения и эксплуатации.
При проектировании объекта устанавливаются и обосновываются необходимые требования к надёжности. На этой стадии выбираются применяемые материалы, разрабатывается конструкция и методы защиты от вредных воздействий, рассматривается возможность автоматически восстанавливать утраченную работоспособность, оценивается приспособленность объекта к ремонту и техническому обслуживанию. Например, при проектировании энергоблоков большой мощности пришлось отказаться от латунных трубок в подогревателях низкого давления и заменить их трубками из нержавеющей стали, что обеспечило надёжность работы котла. Для предотвращения недогрева конденсата, что особенно сильно влияет на работу тепловой схемы турбины большой мощности, были разработаны подогреватели низкого давления смешивающего типа. Установка таких подогревателей вместо поверхностных ПНД 1, 2, работающих под вакуумом, полностью устранила недогрев конденсата на этом участке, снизила перерасход пара из отборов турбины в последующие ПНД и в целом стабилизировала работу тепловой схемы турбины.
При изготовлении объекта обеспечивается и контролируется его надёжность, так как она зависит от качества изготовленных узлов и деталей, методов контроля выпускаемой продукции, возможности управления ходом технологического процесса, от качества сборки, методов испытания, доводки и от других показателей технологического процесса. На этой стадии особенно важна обкатка оборудования, например, паровых турбин, в заводских условиях.
При эксплуатации объекта реализуется его надёжность, которая зависит от методов и условий эксплуатации, принятой системы ремонта, методов технического обслуживания, применяемых режимов работы и других эксплуатационных факторов. Энергоблоки, особенно атомные, спроектированные и изготовленные для работы в базовом режиме, резко снижают свою надёжность и долговечность, если их использовать в пиковом режиме или часто изменять выходную мощность.
Уровень надёжности объекта должен быть таким, чтобы при его использовании в любых, оговоренных в технических условиях ситуациях, не возникали отказы, то есть не нарушалась его работоспособность. Кроме того, объект должен иметь запас надёжности для повышения сопротивляемости экстремальным воздействиям, когда объект попадает в обстоятельства, не предусмотренные техническими условиями.
Запас надёжности также необходим для обеспечения работоспособности объекта при его износе. Износ приводит к постепенному ухудшению технических характеристик объекта. Поэтому, чем выше запас надёжности, тем дольше объект будет находиться в работоспособном состоянии.
Недостаточный уровень надёжности объекта может привести к различным последствиям при нарушении его работоспособности, основными из которых являются следующие.
Гибель объекта, когда он перестаёт функционировать в результате поломки, деформации, заклинивания механизмов, возникновения катастрофических процессов (разрушения конструкции, пожара, радиации и др.). Например, разрушение подшипника турбины приводит к выходу из строя всего блока.
Снижение эффективности работы объекта. Объект способен функционировать, но с меньшим к.п.д., производительностью, точностью и другими техническими характеристиками, которые были достигнуты для нового неизношенного объекта. Шлаковые или ванадиевые отложения на экранных трубках котла снижают его паропроизводительность, что в итоге снижает выходную мощность блока. Отложения золы на поверхностях теплообмена в воздухоподогревателе снижают температуру воздуха, подаваемого в топку, что ведёт к перерасходу топлива.
Первая категория последствий является недопустимой, так как она часто связана не только с уровнем надёжности объекта, но и с проблемами безопасности. Вторая категория последствий характерна для нормального функционирования большинства машин и технических объектов.
В учебном пособии рассматривается надёжность, связанная с возможными отказами различной природы, и надёжность, связанная с изменением выходных параметров объекта.
1 Надёжность и общечеловеческие проблемы
Надёжность технических объектов является неотъемлемой частью всей жизнедеятельности человеческого общества. Обеспечение и увеличение надёжности технических устройств по своей значимости выдвигается на первый план, наряду с такими вопросами, как образование и проблемы здоровья.
С надёжностью машин связаны такие проблемы, как содержание ремонтных предприятий и заводов по изготовлению запасных частей, служб по техническому обслуживанию и профилактике. На ремонт и техническое обслуживание различных машин и объектов за всё время их эксплуатации затрачивается в 5-10 раз больше средств, чем на изготовление новых. Только на износ, трение и коррозию подвижных соединений машин в индустриально развитых странах тратится приблизительно 4,5 % валового национального дохода. Это приводит к потерям сырьевых материалов и энергии общей стоимостью в несколько сотен миллиардов долларов ежегодно во всём мире.
Особенно велики потери от недостаточной надёжности уникального оборудования, при выходе из строя которого по непредвиденным обстоятельствам велика опасность трагических последствий для людей и окружающей среды. Достаточно вспомнить аварию на Чернобыльской АЭС и гибель космического корабля "Челленджер".
По прогнозам специалистов ожидается, что в XXI веке по большинству отраслей промышленности в сфере эксплуатации и ремонта будет занято до 80-90 % всех трудовых ресурсов.
При простое объекта, связанном с его отказом, он не выполняет своих функций. Это связано с простоем других агрегатов, находящихся с ним в единой технологической цепочке. Например, отказ котла или турбины приводит к остановке всего энергоблока.
Ненадёжность объекта может приводить не только к большим экономическим потерям, но и к гибели людей и катастрофическим изменениям в окружающей среде. Это уже упоминавшаяся авария на Чернобыльской АЭС, возникновение парникового эффекта от чрезмерных выбросов СО2 и метана, кислотные дожди, возникающие от присутствия окислов серы и азота в воздухе, сжигающие растительность и уничтожающие памятники культуры в городах.
2 Основные определения, используемые в теории надежности
2.1 Понятие надежности
В условиях современного развития промышленности непрерывно растут показатели мощности, скорости, точности. Вместе с этим необходима и гарантия того, чтобы промышленные объекты и технические устройства были надежными, гарантировали безотказность в работе и сохранение заложенных в них технических характеристик достаточно длительное время. Что же такое "надежность"?
Определение надежности дается Государственным стандартом следующим образом: "Надежность – свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонтов, хранения и транспортировки".
К параметрам, характеризующим способность выполнять требуемые функции, относят кинематические и динамические параметры, показатели конструкционной прочности, показатели точности функционирования, производительность, скорость.
Основным выходным параметром ТЭС и АЭС является располагаемая электрическая мощность, теплопроизводительность, паропроизводительность, содержание летучей золы и вредных веществ в дымовом газе (ТЭС) и радиационный фон на станции и вне её (АЭС). Первые три параметра должны быть не ниже установленных, два последних – не выше допустимых.
Приведенная формулировка надежности относится к любому техническому устройству. Электрические станции обладают той особенностью, что в любой момент времени количество вырабатываемой энергии должно равняться спросу на нее. Для АЭС к этой особенности налагается еще и требование обеспечения радиационной безопасности. Поэтому формулировка надежности для АЭС должна быть следующей: "Свойство АЭС сохранять во времени способность вырабатывать электрическую (и/или тепловую) энергию определенных параметров по требуемому графику нагрузки в допустимых для нормальной эксплуатации радиационных условиях при заданной системе технического обслуживания и ремонтах оборудования".
В определение надежности входят три основные положения:
- выполнения заданных функций;
- время их выполнения;
- условия эксплуатации.
Выполнение заданных функций объектом может быть лучшим или худшим. В данном случае необходимо определить границы выполнения функций, при которых объект сохраняет требуемый уровень надежности. Например, в парогенераторе перегорела лампочка подсветки уровнемера воды в барабане. Можно ли считать, что парогенератор перестал выполнять заданные функции?
Прежде чем ответить на этот вопрос, необходимо ввести два понятия, тесно связанных с надежностью – работоспособность и исправность.
Работоспособность – это состояние изделия или системы, при котором оно способно выполнять заданные функции, сохраняя заданные параметры, установленные требованиями технической документации.
С другой стороны, исправность изделия – это его соответствие абсолютно всем требованиям технической документации, в том числе и требованиям второстепенных параметров, характеризующих удобство эксплуатации, внешний вид и т.д.
Таким образом, в вышеприведенном примере парогенератор работоспособен, но неисправен. Он был бы неработоспособен, если бы снизилась температура или увеличилась влажность пара. Итак, если изделие исправно, то оно обязательно и работоспособно, но работоспособное изделие может быть неисправным.
Работоспособность системы связана не только со способностью работать, т.е. выполнять необходимые функции, но и с тем, чтобы при этом её параметры находились в допустимых пределах. Например, парогенератор должен вырабатывать пар определённых параметров – определённой температуры и давления.
Событие, которое заключается в нарушении работоспособности системы, называется отказом. Различные отказы имеют и разные последствия от незначительных отклонений в работе объекта до аварийных ситуаций.
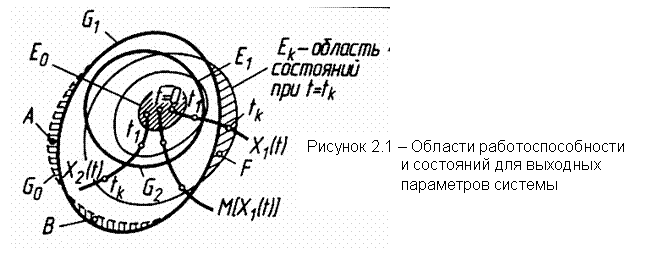
В общем виде модель изменения работоспособности системы во времени при трансформации её параметров за счёт процессов старения показана на рисунке 2.1. Состояние системы можно характеризовать некоторым набором установленных параметров Х1, Х2, …, Хп, которые изменяются с течением времени и являются случайными функциями времени Xi(t).
Все параметры системы можно рассматривать как составляющие общего вектора X(t), который изменяется в процессе функционирования системы в п-мерном пространстве, так называемом фазовом пространстве. Поэтому изменение состояния системы можно характеризовать некоторой траекторией случайного процесса X(t) в фазовом пространстве.
 |
Причины изменения состояния системы связаны с воздействием на неё различных видов энергии, приводящих к возникновению процессов, изменяющих (как правило, ухудшающих) начальные параметры системы. На характер реализации случайных функций, описывающих в фазовом пространстве траекторию изменения состояния системы, решающее влияние оказывает физика процессов старения и конструктивные особенности системы.
В п-мерном фазовом пространстве можно выделить две области. Область состояний Е, в которой с заданной вероятностью находятся выходные параметры системы в рассматриваемый период времени, т.е. область, в которой находятся реализации случайного процесса X(t). Область работоспособности G, которая ограничивает допустимые значения Х1тах, Х2тах, …, Хп тах.
Область состояния системы изменяется с течением времени, а область работоспособности задана в соответствии с установленными требованиями к системе. Если область состояний находится внутри области работоспособности, т.е. является её подмножеством E Ì G, то система функционирует нормально, и все её параметры находятся в допустимых пределах. Выход области состояний за пределы области работоспособности означает возрастание вероятности перехода системы в такое состояние, когда его отдельные параметры примут недопустимые значения, т.е. произойдёт отказ.
Эти области и состояния условно показаны на рисунке 2.1 в двухмерном фазовом пространстве. Границы области состояний Е с течением времени изменяются от Е0 (при t = 0) до Ek (при t = tk), т.е. E(t) является функцией времени – длительности эксплуатации системы. На рисунке приведены также две реализации процесса изменения параметров X1(t) и X2(t), математическое ожидание этого процесса M[X(t)] и границы областей работоспособности G1 и G2 для разных требований к точности функционирования системы (G2 – более жёсткие требования).
Из схемы видно, что через промежуток времени t = tk область состояний Ek приняла такие размеры, что её часть F вышла за пределы области G1, и, следовательно, имеется вероятность нарушения условия нахождения всех параметров в допустимых пределах. К нарушению работоспособности системы привело, например, её функционирование, описываемое реализацией X1(t).
Если область работоспособности ограничена более строгими условиями G2, то период возможного выхода параметра за установленные пределы наступит раньше.
Рассматривая область работоспособности систем, следует различать действительную область (G0), которая определяет требуемую работоспособность системы, и назначенную – (G1), которая диктуется требованиями технических условий к отдельным параметрам. Между этими областями, как правило, имеется большее или меньшее различие, так как в силу сложности процессов изменения состояния трудно точно назначить предельное значение отдельных параметров, определяющих её работоспособность.
Область A как разница между областями G0 и G1 является областью неиспользованных возможностей, когда по техническим условиям система считается потерявшей работоспособность, хотя она ещё может правильно функционировать, а область B является областью неучтённых параметров, когда согласно техническим условиям систему можно эксплуатировать, хотя она в действительности уже стала неработоспособной.
Время выполнения заданных функций неразрывно связано с надежностью, так как изделие должно сохранять свои технические характеристики во времени. Вне времени понятие надежности полностью теряет смысл. Сравнивая надежность двух систем, необходимо рассматривать вероятность безотказной работы каждой из них за один и тот же промежуток времени. Так, система № 1 будет более надежна, чем система № 2, если Р1(t) > Р2(t), где t – один и тот же промежуток времени от начала их работы, Р – вероятность безотказной работы.
Условия эксплуатации. Сроки до первого отказа у одинакового оборудования, но работающего в разных условиях могут существенно отличаться. Оборудование, которое испытывается в лабораторных условиях, отказывает позже, чем аналогичное оборудование, работающее в полевых условиях. Для определения надежности оборудования, работающего в различных условиях, рекомендуется вводить коэффициенты для среднего значения интенсивности отказов элементов. Величины этих коэффициентов могут меняться от 1 для условий работы в лаборатории до 50-60 для условий судовой аппаратуры и до 1000-2000 для современных ракетных и спутниковых установок. Долговечность турбины, работающей на судовой электростанции, будет меньше, чем на стационарной ТЭС.
Факторы, влияющие на надёжность объекта, работающего в полевых условиях, могут быть следующими.
Механическая энергия передаётся по всем звеньям механизмов объекта в процессе работы и воздействует на машину в виде статических и динамических нагрузок от взаимодействия с внешней средой.
Тепловая энергия действует на объект и его узлы при колебаниях температуры окружающей среды, при осуществлении рабочего процесса, при работе приводных механизмов, электротехнических и гидравлических устройств. Работа оборудования в условиях сильных морозов приводит к снижению прочностных свойств материалов. Переменный режим работы турбины приводит к циклическому изменению температуры паропроводов. В материале паропровода, особенно в местах гибов и сварки, возникает усталостное разрушение, что, в конце концов, приводит к образованию трещины и разрушению паропровода.
Химическая энергия выражается в коррозии отдельных узлов механизмов во влажном воздухе, особенно в тропическом климате. Химическое оборудование работает в условиях агрессивных сред, разрушающих отдельные узлы и механизмы объекта. Например, избыточное статическое давление в дымовой трубе, если не приняты специальные конструкторские меры на стадии проектирования и изготовления, приводят к проникновению окислов серы в стенки трубы. Образующаяся сернистая кислота разъедает бетон, и труба, рассчитанная на долгие годы эксплуатации, начинает разрушаться. Это хорошо видно по влажным подтёкам на внешней поверхности трубы, а в зимний период – по довольно значительным наледям.
Радиоактивное излучение образуется в процессе ядерных реакций и присутствует в космосе. Оно может воздействовать на материалы, изменяя их свойства. Циркониевый сплав, из которого изготавливают корпуса тепловыделяющих элементов ядерных энергетических реакторов, под действием радиоактивного излучения становится хрупким, в корпусе элемента образуются трещины, через которые может происходить утечка радиоактивных веществ в воду первого контура. На реакторе устанавливают специальные приборы анализа воды на наличие радиоактивных изотопов. Появление в воде определённого типа изотопов сигнализирует о необходимости проведения профилактических работ по замене тепловыделяющих элементов.
Электромагнитная энергия в виде радиоволн пронизывает всё пространство вокруг машины и может оказывать влияние на работу электронной аппаратуры.
Биологические факторы могут влиять на работоспособность объекта и вызывать биоповреждения, например, в виде биокоррозии металлов, когда на его поверхности развиваются микроорганизмы – водородные бактерии. Особенно интенсивно эти процессы протекают в тропическом климате, где микроорганизмы разрушают не только пластмассы, но и металлы.
Готовое оборудование определенный срок своей жизни находится на хранении. Сохранность – это свойство изделия находиться в исправном состоянии в процессе хранения. Если хранение рассматривать как неотъемлемую часть эксплуатации, то сохранность – это та же надежность в специфических условиях. Сохранность системы зависит от большого числа факторов, имеющих случайный характер. Поэтому этот параметр оценивается вероятностными методами. Критериями сохранности могут быть все критерии надежности. Особенностью сохранности является преобладание постоянных отказов из-за ухудшения характеристик элементов вследствие старения. Однако в процессе хранения старение одних элементов не приводит к старению или отказу других, и постепенные отказы элементов можно считать событиями независимыми, а их параметры не коррелированными, в отличие от отказов одних элементов, обусловленных отказами других при работе оборудования.
2.2 Составные свойства понятия надежности
Надежность – сложное свойство, включающее в себя безотказность, долговечность и ремонтопригодность, которые в свою очередь зависят от качества, живучести и безопасности.
Безотказность – свойство оборудования непрерывно сохранять работоспособное состояние в течение заданного времени и определенных режимах эксплуатации. Безотказность является основным свойством неремонтируемых изделий. В основном она рассматривается применительно к их использованию по назначению, но во многих случаях необходима оценка безотказности при хранении и транспортировке объекта. Показатели безотказности, которые будут рассматриваться ниже, могут вводиться по отношению ко всем возможным отказам объекта либо по отношению к какому-нибудь одному или нескольким типам отказов. В теории надежности также существует понятие долговечности.
Долговечность – это способность оборудования к длительной эксплуатации при необходимом техническом обслуживании, включая и различные виды ремонта. Долговечность характеризуется сроком службы (предельным состоянием), в конце которого изделие, оставаясь работоспособным, претерпевает такие изменения, связанные с износом и старением, устранение которых становится невозможным или экономически невыгодным. Срок службы может выражаться в единицах времени, количестве циклов нагружения или в других единицах.
Разница между безотказностью и долговечностью заключается в том, что безотказность – это свойство объекта непрерывно сохранять работоспособность в течение какого-то ограниченного времени, а долговечность – длительно сохранять работоспособность с возможными перерывами на ремонт.
Безотказность особенно важна для таких объектов, как самолеты, космические аппараты, железнодорожный транспорт. Недопустим отказ двигателя в полете или отказ аппаратуры железнодорожной блокировки. Повышение безотказности системы всегда оправдано, если оно не требует несообразно больших затрат. С другой стороны, нет смысла стремиться к долговечности, так как чрезмерная долговечность большинства изделий ведет к их моральному старению. Например, телевизор, изготовленный из деталей и узлов, предназначенных для космической техники, мог бы проработать несколько тысяч лет. Срок службы ТЭС при проектировании определяется в 30-50 лет. Тем не менее в летний период, когда отсутствует потребность в тепле и снижается требуемая электрическая мощность, отдельные системы станции выводятся из работы для профилактического и капитального ремонта. В зимний период от всех систем станции требуется безотказная работа для бесперебойного снабжения теплом и электроэнергией. В случае внезапного отказа какой-либо системы электростанция должна иметь резервное оборудование.
Предельное состояние для ТЭС и АЭС – это состояние, при котором ее дальнейшее применение для выработки энергии недопустимо по условиям безопасности или экономически нецелесообразно, либо восстановление ее работоспособного состояния технически невозможно или экономически невыгодно.
Переход объекта в предельное состояние влечет за собой временное или окончательное прекращение эксплуатации объекта. При достижении предельного состояния объект должен быть снят с эксплуатации, направлен в средний или капитальный ремонт, списан, уничтожен или передан для применения не по назначению.
Для неремонтируемых объектов имеет место предельное состояние двух видов. Первый вид совпадает с неработоспособным состоянием. Второй вид предельного состояния обусловлен тем обстоятельством, что, начиная с некоторого момента времени, дальнейшая эксплуатация еще работоспособного объекта оказывается недопустимой в связи с опасностью или вредностью эксплуатации. Переход неремонтируемого объекта в предельное состояние второго вида происходит до потери объектом работоспособности.
Для ремонтируемых объектов выделяют два или более видов предельных состояний. Например, для двух видов предельных состояний требуется отправка объекта в средний или капитальный ремонт, то есть временное прекращение применения объекта по назначению. Третий вид предельного состояния предполагает окончательное прекращение применения объекта по назначению. Критерии предельного состояния каждого вида устанавливаются нормативно-технической, конструкторской и/или эксплуатационной документацией.
Кроме понятия долговечности, вводятся еще такие понятия, как средний ресурс и срок службы. Средний ресурс – это суммарная наработка объекта за период его эксплуатации до разрушения или другого предельного состояния. Срок службы – это календарная продолжительность эксплуатации объекта до разрушения или другого предельного состояния.
Сложные системы, к которым относятся тепловые и атомные электростанции, в процессе эксплуатации требуют профилактических и внеплановых ремонтов. Это приводит к вынужденным простоям. Длительность вынужденного простоя не входит в понятие надежности и сохранности, а такие характеристики надежности, как вероятность и среднее время безотказной работы, частота и интенсивность отказов, не полностью характеризуют эксплуатационные качества изделий. Для более полного описания процесса эксплуатации вводится понятие ремонтопригодности.
Ремонтопригодность изделия – это его приспособленность к обнаружению и устранению отказов, а также к их предупреждению, т.е. это степень трудности или простоты выполнения ремонта. Другими словами, ремонтопригодность – это приспособленность объекта к техническому обслуживанию, к обнаружению и предупреждению отказов и повреждений, а также причины, их вызывающие. Ремонтопригодность является одним из важнейших свойств, составляющих понятие надежности, для ремонтируемых изделий. С вероятностной точки зрения ремонтопригодность характеризуется ремонтоспособностью изделия.
Ремонтоспособность – это вероятность того, что отказавший элемент оборудования будет доведен до рабочего состояния за время ремонта, не превышающее заданное, при выполнении ремонта в определенных условиях.
Ремонтируемым изделием (восстанавливаемым) называется такое, которое можно восстановить в данных условиях эксплуатации путем ремонта, выполняемого подручными средствами. Эти изделия могут иметь более одного отказа, многократно ремонтироваться и после каждого ремонта восстанавливать свою работоспособность.
Примерами ремонтируемых изделий могут служить отдельные элементы парогенератора, паропроводы, барабаны, каркас и обмуровка, запорная арматура, насосы и др.
Неремонтируемыми (невосстанавливаемыми) изделиями называются изделия, работоспособность которых в случае возникновения отказа либо не поддается восстановлению в данных условиях эксплуатации, либо не подлежит такому восстановлению. Такие изделия после первого же отказа подлежат замене.
Примерами неремонтируемых изделий могут служить сигнальные и осветительные лампы, многие электронные детали и узлы приборов автоматического управления, полупроводниковые приборы, трубы поверхностей нагрева парогенераторов, тепловыделяющие сборки и твэлы ядерного реактора. Для неремонтируемых приборов понятия безотказности и долговечности совпадают.
С экономической точки зрения ремонтопригодность может быть выражена следующей зависимостью
Сэ = Сэ1 + Сотк× п ,
где Сэ1 – стоимость эксплуатации, не зависящая от возникновения
отказов;
Сотк – средняя стоимость устранения одного отказа;
п – число отказов за данный промежуток времени;
Сэ – эксплуатационная стоимость изделия или системы за этот
промежуток времени.
Зачастую проще снизить Сотк, чем уменьшить п, а это значит, что повышение ремонтопригодности изделия может быть эффективным способом уменьшения эксплуатационных затрат. С другой стороны, ремонтопригодность в значительной мере определяет эффективность изделия.
Например, если при сравнении двух одинаковых блоков окажется, что первый ремонтируется один раз в год, а второй – три, но на ремонт первого уходит тридцать часов, а на ремонт второго – пять, то второй блок будет более эффективным. Однако частые ремонты, связанные с остановкой основного оборудования (котлов, турбин), недопустимы, так как стоимость таких остановок очень высока.
Для повышения надежности сложных систем, особенно в случаях, когда их отказы связаны с риском для жизни людей или большим убытком, при проектировании приходится выбирать более качественные элементы, обладающие большей надежностью, или облегчать режим работы элементов, или вводить резервную аппаратуру. Все это требует увеличения веса, стоимости, габаритов и приводит к некоторой избыточности по указанным характеристикам.
Избыточность – это превышение веса, габаритов либо стоимости изделия или системы по сравнению с минимально необходимыми для заданных параметров и структуры, связанных с обеспечением заданной надежности.
Избыточность нельзя отождествлять с резервированием, т.к. резервирование – только один из вариантов избыточности.
Избыточность, гарантируя высокую надёжность системы, в то же время увеличивает вес и размеры системы, что во многих случаях является недопустимым. Когда требуется высокая надёжность, но габариты и вес ограничены, перспективной является функциональная избыточность. Функциональная избыточность – способность системы (особенно биологической) при выходе из строя тех или иных его элементов возлагать выполнение их функций на другие элементы. В этом случае огромную роль играет способность системы к самоперераспределению функций элементами системы. Создание самонастраивающихся и саморегулируемых систем, которые могут приспосабливаться к изменяющимся условиям работы и восстанавливать утраченную работоспособность, гарантирует выполнение заданной работы в течение длительного времени при достаточно сильных внешних воздействиях и процессах, происходящих внутри самой системы.
Избыточность в некоторых случаях подразумевает установку более качественных элементов и деталей. Определение понятия качества было дано во введении. Качество устройства часто зависит также от способа его использования. Например, если паротурбинный энергоблок, спроектированный для несения базовых нагрузок, использовать в переменных режимах с частыми остановками и пусками, то это окажет существенное влияние на его состояние, на готовность к работе и, в конечном счете, на его надежность и живучесть.
В комплексе требований надежности, предъявляемых к электростанциям, входит и обеспечение безопасности, в том числе и радиационной, для людей и окружающей среды. Безопасность – это свойство объекта при изготовлении, эксплуатации и в случае нарушения работоспособного состояния не создавать угрозу для жизни и здоровья людей и окружающей среды.
Живучесть – это способность технического устройства противостоять крупным возмущениям, исключающая процесс развития аварий и поломку оборудования или сохранять ограниченную работоспособность при наличии дефектов или повреждений определенного вида, а также при отказе некоторых компонентов. Понятие живучесть занимает пограничное место между понятиями надежности и безопасности. Особенно жёсткие требования к живучести и безопасности применяются для атомных электростанций. При сильном землетрясении или других экстремальных условиях реактор не должен разрушиться с выбросом радиоактивных элементов в окружающую среду.
Ранее часто упоминались такие понятия, как объект, система, элемент, устройство. Под техническим объектом или системой понимается какое-то целое, включающее в себя функционально взаимосвязанные элементы или устройства. Система предназначается для выполнения заданной целостной программы. Элементами или устройствами называются отдельные части системы, способные самостоятельно выполнять определенные задачи. При этом каждый элемент, в свою очередь, может состоять из целого ряда других подэлементов, по отношению к которым он выступает уже как система. В соответствии с этим различают различные иерархические уровни образования систем и элементов. Так, единая энергетическая система включает в себя в качестве элементов электростанции тепловые, атомные, гидро, линии электропередачи и т.д. Если электростанцию рассматривать как систему, то ее элементами являются котел, турбогенераторная установка, система топливоприготовления, газовоздушный тракт, реактор и т.д. В свою очередь элементами турбогенераторной установки являются сама турбина, электрогенератор, конденсатор, конденсатные и питательные насосы, деаэратор, регенеративные подогреватели. Таким образом, разделение оборудования на системы и элементы зависит от того уровня, на котором осуществляется решение поставленной задачи. Понятие системы и ее уровня формулируется на основе поставленной цели. Элементами в данном случае считается любое техническое устройство, не подлежащее дальнейшему расчленению.
Объектом называется какое-либо устройство системы или ее элемента, принятое для изучения определенных его свойств вне всякой связи с другими элементами. Например, можно изучать работу деаэратора при различных режимах и концентрациях газа в воде. На более низком иерархическом уровне можно рассматривать работу барботажного листа, расположенного на дне бака деаэратора.
2.3 Классификация отказов и области возможных состояний ТЭС
Говоря о надежности и ее составляющих, подразумевается, что в какой-то момент времени отдельный элемент системы в целом может потерять способность частично или полностью воспроизводить эксплуатационные рабочие характеристики и параметры. Таким образом, с понятием надежности неразрывно связано другое фундаментальное понятие теории надежности – отказ. Полная или частичная потеря системой или элементом их функциональных свойств называется отказом. Условием нормальной работы электростанции, атомной или тепловой, является выполнение следующих условий.
|
Nр(t) ³ Nтр; А(t) £ Адоп, |
(2.1) |
где Nр(t) – располагаемая мощность станции по производимой электроэнергии, теплу или пару, которая при нормальной эксплуатации должна превышать или равняться требуемой в любой момент времени мощности Nтр(t);
A(t) – уровень радиации на рабочих местах, в цехах и окружающей станцию территории для АЭС или уровень химического загрязнения для ТЭС, который в любой момент не должен превышать допустимый уровень радиации или нормы ПДК.
Нарушение любого из неравенств (2.1) является необходимым и достаточным условием отказа.
Понимание физики отказов и способов борьбы с ними – важнейшее условие успешного развития всех практических вопросов обеспечения надежности.
Классификация отказов по их последствиям приводит к понятию критичности отказа. Критерием для классификации могут служить прямые и косвенные потери, вызванные отказом, затраты труда и времени по устранению последствий отказов, возможность и целесообразность ремонта силами потребителя, изготовителя или другой организации, продолжительность простоев, вызванных отказами, степень снижения производительности и т.д.
Моменты отказов в сложных системах, к которым принадлежат и электрические станции, обычно случайное событие. Тем не менее иногда отказ можно предсказать. Это возможно при систематических отказах одних и тех же элементов. Такие отказы называются закономерными, в отличие от случайных отказов. Систематические отказы, возникающие из-за ошибок проектирования или технологии обработки, устраняются, поэтому нет смысла вносить их в классификацию отказов.
Кроме закономерных отказов, можно также предсказать постепенный отказ, которому предшествует непрерывное и монотонное изменение одного или нескольких параметров, характеризующих способность объекта выполнять заданные функции. Постепенные (износовые) отказы возникают в результате протекания того или иного процесса старения, ухудшающего начальные параметры изделия.
Основным признаком постепенного отказа является то, что вероятность его возникновения F(t) в течение заданного периода времени от t1 до t2 зависит от длительности предыдущей работы изделия t1. Чем дольше использовалось изделие, тем выше вероятность возникновения отказа, т.е. F2(Dt) > F1(Dt), если t2 > t1, где Fi(Dt) – вероятность отказа за период от ti до (ti + Dt).
К этому виду относится большинство отказов машин. Они связаны с изнашиванием, коррозией, усталостью, ползучестью и другими процессами старения материала, из которого сделано изделие.
Внезапные отказы – это те, причиной которых являются процессы, возникшие в результате сочетания неблагоприятных факторов и случайных внешних воздействий, превышающих возможности изделия к их восприятию.
Основным признаком внезапного отказа является то, что вероятность его возникновения F(t) в течение заданного периода времени от t1 до t2 не зависит от длительности предыдущей работы изделия.
Примером таких отказов могут служить тепловые трещины, возникающие в детали вследствие прекращения подачи смазки; поломки детали из-за неправильных методов эксплуатации системы или возникновения перегрузок; деформация или поломка деталей, попавших в непредусмотренные условия работы. Отказ при этом происходит, как правило, внезапно, без предшествующих симптомов разрушения и не зависит от степени изношенности изделия.
Например, причиной отказа автомобильной покрышки может быть как износ протектора в результате длительной эксплуатации, так и прокол, возникший вследствие езды по плохой дороге и неблагоприятного сочетания случайных факторов.
Вероятность отказа покрышки из-за износа протектора у старой покрышки во много раз больше, чем у новой. В противоположность этому прокол – внезапный отказ – не связан с длительностью работы покрышки до данного события. Вероятность его возникновения одинакова как для новых покрышек, так и для изношенных.
Критерием принадлежности отказа к категории постепенного или внезапного служит наличие или отсутствие зависимости вероятности безотказной работы от времени предыдущей работы изделия.
Для постепенного отказа процесс потери работоспособности X(t) начинается сразу при эксплуатации изделия, а его скорость g либо постоянна, либо является функцией времени g(t).
Для внезапного отказа время его возникновения Тв является случайной величиной и подчиняется некоторому закону распределения f(Tв), не зависящему от состояния изделия. Скорость процесса при его возникновении протекает весьма быстро g ® ¥, и не она, а функция f(Tв) определяет вероятность безотказной работы. Может быть, и третий вид отказов, который включает особенности двух предыдущих и называется сложным отказом. Здесь время начала возникновения отказа – случайная величина, не зависящая от состояния изделия, а скорость процесса потери работоспособности изделия g(t) зависит от физики процесса старения.
Например, внешние ударные воздействия на машину от посторонних предметов (редкое случайное событие) могут явиться источником возникновения усталостной трещины из-за первичного повреждения поверхности детали. Постепенное развитие трещины будет происходить по мере дальнейшей эксплуатации машины, т.е. здесь имеет место схема возникновения сложно отказа.
Отказы функционирования и параметрические отказы. Последствия отказов весьма разнообразны. Отказы функционирования приводят к тому, что изделие не может выполнять возложенные на него функции. Например, в результате отказа редуктор не передаёт движения, двигатель внутреннего сгорания не запускается, насос не подаёт масла и т.п. Часто отказ функционирования связан с поломками или заклиниванием отдельных элементов изделия.
Параметрический отказ, который наиболее характерен для современных машин и систем, возникает при выходе параметров (характеристик) системы за допустимые пределы. Здесь система становится неработоспособной с точки зрения требований, установленных техническими условиями.
Продолжение использования изделия, имеющего параметрический отказ, может привести к весьма тяжёлым экономическим и иным последствиям. Например, к выпуску некачественной продукции, которая может быть причиной отказов функционирования в сфере её эксплуатации, к невыполнению изделием поставленных задач, к большим дополнительным затратам времени и средств. Но роль параметрического отказа важна ещё и потому, что в сложных системах параметрические отказы элементов могут привести к отказу функционирования.
Отказы функционирования и параметрические отказы могут быть как постепенными, так и внезапными, так как эти классификации отказов проводятся по различным признакам. Например, отказ измерительного прибора из-за недопустимых внешних воздействий будет параметрическим, если потеряна его точность из-за нагрева от внешних источников тепла, и отказом функционирования, если произошло заклинивание его механизма из-за запылённости атмосферы.
Фактические и потенциальные отказы. При эксплуатации изделий рано или поздно наступит его первый, а затем и последующие отказы. Если эти отказы предотвращаются заблаговременно выполнением ремонта и регулировок, то они воспринимаются не как фактические, а как потенциально возможные события. Такие отказы называются потенциальными. Для изготовителей и эксплуатационников характерно постоянное стремление к недопущению любых отказов при работе системы. Это может быть достигнуто не только за счёт совершенства конструкции, но и путём предотвращения возможных отказов при правильной организации системы ремонта и технического обслуживания, строгого выполнения правил эксплуатации.
Однако отсутствие физических отказов ещё не свидетельствует о высокой надёжности системы. Она может вообще не иметь отказов при эксплуатации, тем не менее уровень её надёжности не будет удовлетворительным, если это достигнуто за счёт большого объёма профилактических и ремонтных работ. Поэтому когда речь идёт об отказах изделия, то имеется в виду главным образом потенциально возможные, а не только фактические отказы. Статистическая информация из сферы эксплуатации, когда учитываются лишь фактические отказы, часто даёт неверное представление об уровне надёжности системы.
Допустимые и недопустимые отказы. Все возникающие при работе системы отказы можно разделить на две группы. К первой группе относятся отказы, появление которых неизбежно, так как система имеет ограниченные возможности по восприятию различных воздействий. Ко второй – относятся отказы, которые являются следствием нарушения методов и правил проектирования, изготовления и эксплуатации системы и которые возможно и необходимо избежать.
Допустимые отказы связаны обычно с процессами старения, которые нельзя предотвратить и которые приводят к постепенному ухудшению выходных параметров изделия. Сюда же следует отнести и внезапные отказы, которые вызваны неблагоприятным сочетанием факторов, если последние находятся в пределах, указанных в технических условиях. Конструктор может сознательно допустить небольшую вероятность возникновения отказа, чтобы облегчить и удешевить конструкцию. Это допустимо лишь в тех случаях, когда отказ не вызовет катастрофических последствий. Например, даже в самолётных конструкциях допускается развитие усталостных трещин в некоторых элементах и панелях крыльев.
Недопустимые отказы связаны с нарушением условий производства и эксплуатации и с неучтёнными факторами. Во-первых, это отказы из-за нарушения технических условий при изготовлении и сборке изделий. Во-вторых, отказы могут наступить при нарушении правил и условий эксплуатации и ремонта – повышение режимов работы системы выше допустимых, нарушение правил ремонта, ошибки людей, управляющих системой и др. Кроме этого, существуют и скрытые причины возникновения недопустимых отказов – это неучтённые в технических условиях и нормативах параметры, влияющие на надёжность. Изделие может быть выполнено в строгом соответствии с техническими условиями, однако сами технические условия не учитывают всех тех объективно существующих факторов, которые влияют на надёжность и проявляются в процессе эксплуатации. Анализ принадлежности каждого отказа к той или иной категории классификации позволяет выбрать показатели надёжности и модель расчёта, правильно отражающие реальную ситуацию, в которой используется изделие.
Отказ нельзя отождествлять с неисправностью, так как неисправность связана с нарушением любого параметра изделия (например, уже упоминавшаяся перегоревшая лампочка подсветки водомерной системы парогенератора). Отказ, ведущий к частичной или полной утрате работоспособности, связан с нарушением только основных параметров, характеризующих нормальную работу изделия.
Событие полной потери работоспособности станции, когда либо ее располагаемая мощность становится ниже минимального (Nmin) уровня, при котором еще допустима передача энергии потребителю, либо параметр радиационной (химической) обстановки A(t) превышает допустимое значение Aдоп, называется полным отказом:
|
0 £ Nр(t) < Nmin; A(t) > Адоп. |
(2.2) |
Обычно минимальная мощность Nmin находится на уровне или немного превосходит мощность, необходимую для покрытия собственных нужд станции Nсн.
В отличие от полного отказа, частичный отказ – такое нарушение работоспособности станции, при котором располагаемая мощность становится меньше требуемой, но не менее уровня Nmin, т.е. достаточной для частичного обеспечения требуемого графика нагрузки, при этом параметр радиационной (химической) обстановки А лежит в допустимых пределах
|
Nmin £ Nр(t)< Nтр(t); A(t) £ Aдоп. |
(2.3) |
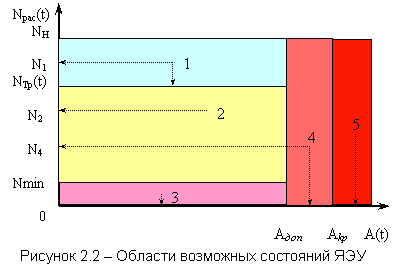 Перечисленные состояния
станции удобно изобразить на графике в координатах мощность (N)
- радиационная обстановка (А). Каждая точка плоскости с координатами [Np(t),
A(t)] характеризует конкретное состояние станции с точки
зрения ее работоспособности. Область (1), лежащая между номинальной
мощностью и требуемой и левее Адоп, является областью полной
работоспособности станции. Область (2), лежащая в границах между
требуемой мощностью и минимальной и левее Адоп, – область
частичной работоспособности. Эта область включает нижнюю горизонтальную
границу, но не включает верхнюю. Область (3), когда располагаемая
мощность ниже минимальной, – область неработоспособного состояния станции. В области
(2) и (3) станция неработоспособна по причине технической
неисправности. В области (4) правее Адоп АЭС
неработоспособна по причине недопустимого по условиям безопасности нарушения
радиационной обстановки. В этом случае станция должна снижать мощность и
выводить реактор из работы, с учетом возможности потребителей прервать
технологический производственный цикл. При попадании станции в область (5),
когда радиоактивный фон превышает критическую норму, ни при каких условиях
дальнейшая работа станции недопустима, необходимо ее немедленное отключение.
Перечисленные состояния
станции удобно изобразить на графике в координатах мощность (N)
- радиационная обстановка (А). Каждая точка плоскости с координатами [Np(t),
A(t)] характеризует конкретное состояние станции с точки
зрения ее работоспособности. Область (1), лежащая между номинальной
мощностью и требуемой и левее Адоп, является областью полной
работоспособности станции. Область (2), лежащая в границах между
требуемой мощностью и минимальной и левее Адоп, – область
частичной работоспособности. Эта область включает нижнюю горизонтальную
границу, но не включает верхнюю. Область (3), когда располагаемая
мощность ниже минимальной, – область неработоспособного состояния станции. В области
(2) и (3) станция неработоспособна по причине технической
неисправности. В области (4) правее Адоп АЭС
неработоспособна по причине недопустимого по условиям безопасности нарушения
радиационной обстановки. В этом случае станция должна снижать мощность и
выводить реактор из работы, с учетом возможности потребителей прервать
технологический производственный цикл. При попадании станции в область (5),
когда радиоактивный фон превышает критическую норму, ни при каких условиях
дальнейшая работа станции недопустима, необходимо ее немедленное отключение.
Из приведенного графика видно, что частичный отказ по техническим причинам может происходить двумя путями. При отказе какого-либо элемента мощность станции становится ниже требуемой, и она переходит из области (1) в область (2). Такой отказ называется отказом первого рода. С другой стороны, при наличии отказа оборудования располагаемая мощность станции может быть выше требуемой. Но в какой-то момент требуемая нагрузка повышается и становится выше располагаемой мощности, т.е. граница между зонами (1) и (2) передвигается выше точки 1, и станция перестает выдавать требуемую мощность. Такой отказ называется отказом второго рода. Соответственно отказам первого и второго рода существуют восстановления первого и второго рода, соответствующие либо восстановлению оборудования, либо снижению требуемой мощности без восстановления оборудования.
Вообще для любого объекта все отказы можно классифицировать следующим образом. При частичном отказе объект перестает выполнять какую-либо одну или несколько из своих основных функций, продолжая в то же время работать и нормально выполнять остальные функции, или частично снижает свой выходной эффект. При полном отказе объект перестает выполнять все свои основные функции.
3 Управление надёжностью
Для создания и эксплуатации объектов, в том числе электрических станций, отвечающих заданным требованиям надёжности, необходима её строгая количественная оценка. Только измеряя и контролируя различные показатели, характеризующие надёжность, можно добиться безотказной работы оборудования в течение назначенного срока.
Жизненный цикл любого объекта состоит из трёх этапов – проектирования, изготовления и эксплуатации.
Надёжность объекта закладывается на этапе его проектирования. На этапе изготовления и эксплуатации должна обеспечиваться надёжность, заложенная на этапе проектирования.
Управление надёжностью осуществляется точно таким же образом, как в системах автоматического управления осуществляется управление объектом или процессом. Например, рассмотрим процесс, в котором необходимо поддерживать постоянную температуру в системе. На рисунке 3.1 объектом управления является котёл, в трубной системе которого датчики температуры периодически, через определённые промежутки времени, измеряют температуру (звено 1).
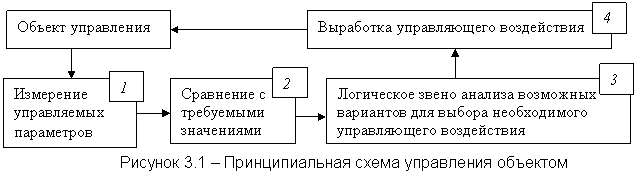
Полученные данные передаются в блок сравнения 2, где происходит сравнение измеренной температуры с заданной. Если измеренная температура лежит вне заданного диапазона, то вырабатывается сигнал рассогласования, который передаётся в блок 3 выработки управляющего решения. В блоке 3 вырабатывается решение, каким образом привести температуру в заданный диапазон – изменить подачу топлива, воздуха или изменить расход нагреваемой воды. После выработки решения сигнал подаётся в блок 4 выработки управляющего воздействия. В блоке 4 формируется управляющий сигнал, который передаётся на объект управления, на соответствующий исполнительный механизм, который изменяет расход топлива, воздуха или нагреваемой воды.
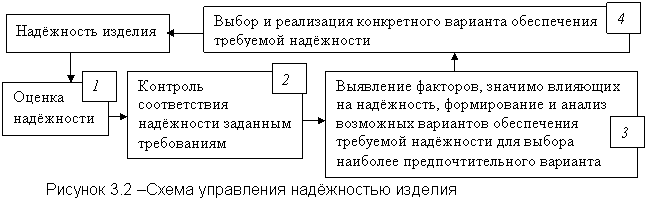
По такой же схеме осуществляется управление надёжностью объекта (рисунок 3.2). На этапе 1 оценивается надёжность существующего объекта. На этапе 2 проводится сравнение с требуемой надёжностью по всем параметрам. Если надёжность объекта не соответствует заданной надёжности, то на этапе 3 выявляются факторы, влияющие на надёжность системы, и анализируются варианты, которые обеспечили бы требуемую надёжность. На этапе 4 из всех рассмотренных вариантов выбираются наиболее рациональные и реализуются на объекте.
Конкретное приложение данной схемы требует решения следующих основных задач.
На этапе проектирования – расчёт сроков службы основных элементов объекта (по износу, усталостной прочности), прогнозирование надёжности объекта по его выходным параметрам, анализ вариантов и выбор рациональной конструкции по показателям надёжности, оценка оптимальных режимов работы и области применения объекта с учётом заданного периода сохранения работоспособности. Более наглядно это можно отразить на диаграмме, изображённой на рисунке 3.3.
Специфика этапа проектирования заключается в том, что объекта ещё не существует, есть лишь проект, и требуется, чтобы он отвечал предъявляемым требованиям по надёжности.
Звено 1 представляет собой проведение прогнозного расчёта надёжности объекта. В этом звене выполняются последовательно три типа задач: 1.1 выбор номенклатуры показателей надёжности; 1.2 сбор необходимых исходных данных для их прогнозной оценки, в частности, по надёжности составляющих элементов аналогов объекта и его составных частей; 1.3 собственно оценка надёжности в результате структурного количественного анализа надёжности объекта при заданных показателях надёжности составляющих элементов, их функциональных связях, режимах использования системы, технического обслуживания и ремонтов.
На этапе 2 реализуется специальная математическая процедура проверки соответствия прогнозируемой оценки надёжности изделия предъявляемым количественным требованиям с учётом того, что оценка объективно неточная. Это звено имеет смысл только в том случае, если предварительно решена задача 2.1, установлены комплексные требования к надёжности объекта. На этапе 2.2 проводится проверка установленных показателей надёжности на макетах и опытных образцах.
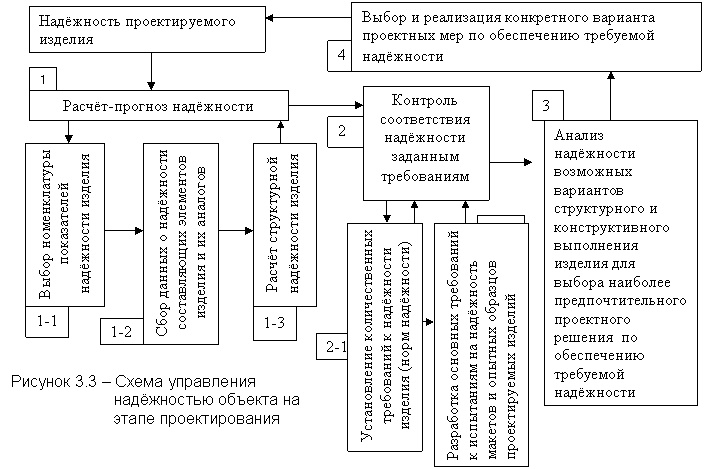
На этапе 3 анализируются факторы, пути целенаправленного изменения надёжности. В частности, выполняется количественный анализ надёжности возможных вариантов изделия, отличающихся от исходного структурными или конструктивными изменениями. Для этого сначала выявляется и формируется предпочтительный ряд таких вариантов. Результаты данного этапа 3 служат основной выходной информацией для этапа 4.
На этапе создания нового образца – создание системы управления качеством и надёжностью, обеспечение надёжности технологического процесса изготовления деталей и узлов объекта, разработка методов испытания образцов элементов по параметрам качества и надёжности, обеспечение необходимой культуры производства.
Блок-схема управления надёжностью объекта на этапе создания будет иметь такой же вид, как и на этапе проектирования, за исключением этапа 2.2 и 3. На этапе 2.2 должна быть разработка основных требований к испытаниям на надёжность опытной партии и серийных образцов. Основным содержанием этапа 3 должен быть количественный анализ влияния факторов изготовления на надёжность изделия.
На этапе эксплуатации – разработка рациональной системы технического обслуживания и ремонта, создание методов и средств для диагностирования состояния отдельных узлов объекта в процессе эксплуатации, создание информационной базы данных о надёжности объекта и его элементов.
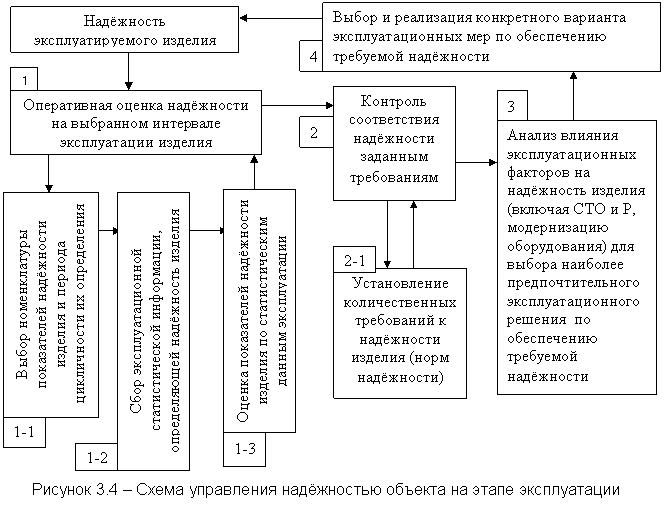
Блок-схема управления надёжностью на этапе эксплуатации приведена на рисунке 3.4.
4. Основные теоремы теории вероятностей
Основная задача теории надежности – установление закономерностей возникновения отказов, изучение влияния внешних и внутренних факторов на надежность, установление количественных характеристик, методов оценки и расчета надежности, определение методов обеспечения надежности при проектировании, изготовлении и эксплуатации объектов.
Для решения этих задач в настоящее время наиболее разработана статистическая, вероятностная теория надежности. Это обусловлено достаточной доступностью исследования суммарного влияния различных факторов, таких, как свойства материалов, конструкции элементов, технологических процессов, внешних воздействий и режимов работы на состояние элементов и устройств.
Для понимания излагаемого в данном курсе материала в этом разделе приводятся основные определения и теоремы теории вероятностей.
Одним из основных понятий теории вероятностей является понятие случайной величины или случайного события. Эта величина в результате каких-либо испытаний может принимать то или иное значение, которое заранее не известно. При анализе надежности энергетического оборудования могут встречаться дискретные и непрерывные случайные величины. Дискретные случайные величины принимают лишь отдельные друг от друга значения. К таким величинам относится, например, число единиц отказавшего оборудования из общего его числа. Непрерывные случайные величины непрерывно заполняют некоторое пространство на числовой оси. К таким величинам относится время работы оборудования до его отказа.
Любое случайное событие
может возникнуть в результате испытаний. Если при п испытаниях
(явлениях, событиях) некоторое случайное событие А появлялось
k
раз, то отношение ![]() называют
частотой случайного события А. При безграничном увеличении числа п
испытаний это отношение стремится к некоторому положительному пределу р,
который называется вероятностью события А
называют
частотой случайного события А. При безграничном увеличении числа п
испытаний это отношение стремится к некоторому положительному пределу р,
который называется вероятностью события А
|
|
(4.1) |
Отсюда следует, что событие А
произойдет примерно пр раз и не произойдет 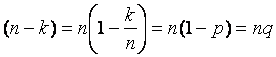 раз. Величина вероятности
события А лежит в пределах 0 ≤ р(А) ≤ 1.
раз. Величина вероятности
события А лежит в пределах 0 ≤ р(А) ≤ 1.
Кроме определения вероятности одиночного события, часто необходимо определить вероятность более сложных событий, состоящих из появления одного любого события из нескольких возможных попарно несовместных событий. В этом случае вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей событий.
|
Р(А1 + А2 + …+ Ап) = Р(А1) +Р(А2) + … +Р(Ап). |
(4.2) |
Полной группой называется совокупность единственно возможных событий испытания. Сумма вероятностей А1, … Ап, образующих полную группу, равна единице:
|
Р(А1) + Р(А2) + …+ Р(Ап) = 1. |
(4.3) |
Если события совместны, то вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления
|
Р(А1 + А2) = Р(А1) + Р(А2) – Р(А1А2). |
(4.4) |
Вероятность совместного появления нескольких независимых событий одновременно равна произведению вероятностей этих событий
|
|
(4.5) |
Если появление одного события зависит от появления другого события, то такие события называются зависимыми. В этом случае вводится понятие условной вероятности РА(В), т.е. вероятности события В, вычисленной в предположении, что событие А уже наступило.
При вычислении одновременного появления двух зависимых событий применяется теорема умножения вероятностей зависимых событий. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило.
|
Р(АВ) = Р(А)×РА(В). |
(4.6) |
Если зависимых событий несколько, то вероятность появления нескольких зависимых событий равна произведению вероятности появления одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже совершились
|
Р(А1А2 … Ап) = Р(А1)×РА1(А2)×РА1А2(А3)× … ×РА1А2…Ап-1(Ап). |
(4.7) |
Если событие А может наступить при появлении одного из несовместных событий В1, В2, … Вп, которые образуют полную группу, то вероятность события А вычисляется следующим образом
|
Р(А) = Р(В1)×РВ1(А) + Р(В2)×РВ2(А) + … + Р(Вп)×РВп(А) = ∑Р(Вi)×PBi(A), |
(4.8) |
то есть вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий В1, В2, … , Вп, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А. Соотношение (4.8) носит название формулы полной вероятности события.
Следствием теоремы умножения и формулы полной вероятности события является теорема гипотез. Пусть имеется полная группа несовместных гипотез Н1, Н2, …, Нп, вероятности которых до опыта известны и равны соответственно Р(Н1), Р(Н2), …, Р(Нп). Произведен опыт, в результате которого наблюдалось появление некоторого события А. В связи с появлением этого события А, вероятности гипотез изменятся и станут равными
|
|
(4.9) |
Формула (4.9) называется формулой Байеса или теоремой гипотез.
При практическом применении теории вероятностей часто приходится встречаться с задачами, в которых один и тот же опыт повторяется неоднократно. В результате каждого опыта может появиться или не появиться некоторое событие А (например, появление трещины при испытании серии гибов паропровода). В случае независимости опытов вероятность появления события А во всех опытах одинакова. Пусть производится п независимых опытов, в каждом из которых вероятность появления события А равна р, тогда вероятность того, что событие А появится ровно т раз, выражается формулой
|
|
(4.10) |
где Спт – число сочетаний из п по т;
q = 1 – p есть вероятность невыполнения события А в опыте. Так как выражение (4.10) по своей форме представляет собой разложение бинома (q+p)m, распределение вероятностей типа (4.10) называется биномиальным.
4.1 Дифференциальная, интегральная и условная плотность распределения и их характеристики
Любая случайная величина, и непрерывная, и дискретная, полностью описывается интегральной функцией распределения, т.е. вероятностью того, что случайная величина Х примет значение, меньшее некоторого фиксированного значения х
|
F(x) = P(X < x). |
(4.11) |
Для случайных дискретных величин F(x) есть неубывающая случайная функция; для непрерывных случайных величин F(x) – монотонно возрастающая непрерывная функция (рисунок 4.1).
Из определения интегральной функции распределения следует, что F(0)=0; F(∞) = 1. Согласно теореме сложения вероятностей для непрерывной случайной величины можно записать
|
Р(Х < а) + Р(а £ Х < b) = Р(Х < b) Р(а ≤ Х < b) = F(b) – F(а). |
(4.12) |
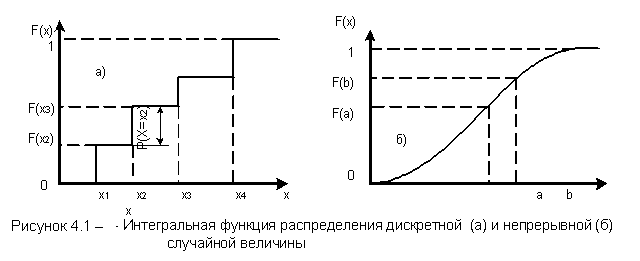
Аналогично для дискретной случайной величины:
|
Р(Х < х2) + Р(Х=х2) = Р(Х < х3) Р(Х = х2) = F(х3) – F(х2). |
(4.13) |
Из (4.12) очевидно, что для непрерывной случайной величины вероятность принять конкретное значение равно нулю, но есть смысл говорить о вероятности попадания случайной величины в бесконечно малый интервал х+dx
|
Р(х ≤ Х <х + dх) = F(х + dх) – F(х). |
(4.14) |
Умножая и деля правую часть на dx и устремляя dx к нулю, получаем
|
Р(х ≤ Х < х + dх) = F'(х)dх. |
(4.15) |
Производная от интегральной функции распределения называется дифференциальной функцией распределения вероятностной случайной величины или плотностью распределения
|
|
(4.16) |
Из определения функции распределения следует, что f(x) ≥ 0 при х ≥ 0, f(∞) = 0,
|
|
(4.17)
(4.18)
(4.19) |
Другой важной характеристикой непрерывной случайной величины является условная плотность распределения или условный дифференциальный закон распределения λ(х), представляющий собой условную вероятность того, что случайная величина Х примет значение в сколько угодно малом единичном интервале около точки х, при условии, что левее этой точки значение случайной величины не реализовывалось, т.е. Х ≥ х
|
λ(х) = РХ≥х(х ≤ Х < х + dх). |
(4.20) |
Из теоремы умножения вероятностей зависимых событий
|
Р(х ≤ Х < х + dх) = Р(Х ≥ х)·РХ≥х(х ≤ Х < х + dх), |
(4.21) |
 т.е. вероятность попадания Х в интервал (х,
х +dx) равняется произведению вероятности не попадания Х
в область Х < х на условную вероятность попадания Х в
интервал (х, х + dх) при условии Х ≥ х.
т.е. вероятность попадания Х в интервал (х,
х +dx) равняется произведению вероятности не попадания Х
в область Х < х на условную вероятность попадания Х в
интервал (х, х + dх) при условии Х ≥ х.
Основной величиной, характеризующей дифференциальную функцию распределения, является математическое ожидание (среднее значение). Эмпирически математическое ожидание определяется как среднее арифметическое от эмпирических выборочных значений рассматриваемой случайной величины
|
|
(4.22) |
Для непрерывной случайной величины математическое ожидание выражается интегралом
|
|
(4.23) |
для дискретной случайной величины математическое ожидание вычисляется в виде суммы
|
|
(4.24) |
где хi – значение случайной величины Х;
рi – вероятность реализации этих значений.
Математическое ожидание обладает следующими свойствами:
а) математическое ожидание постоянной величины равно самой постоянной
|
М(С) = С; |
(4.25) |
б) постоянный множитель можно выносить за знак математического ожидания
|
М(СХ) = СМ(Х); |
(4.26) |
в) математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий
|
М(ХУ … Z) = M(X)M(Y) … M(Z); |
(4.27) |
г) математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин
|
М(Х + У + … Z) = M(X) + M(Y) + … + M(Z); |
(4.28) |
д) математическое ожидание М(Х) числа появления события А в п независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании
|
М(Х) = пр. |
(4.29) |
С другой стороны, дифференциальная функция распределения характеризуется дисперсией D(х), определяющей степень рассеяния возможных значений случайной величины около ее среднего значения – математического ожидания. Математически дисперсия непрерывной случайной величины определяется интегралом
|
|
(4.30) |
Дисперсия дискретной случайной величины представляет собой математическое ожидание квадрата отклонения случайной величины от ее математического ожидания
|
|
(4.31) |
Из этого определения легко выводится другая, более удобная для вычислений формула
|
|
|
Для практического вычисления дисперсии дискретной случайной величины удобнее пользоваться другим определением дисперсии – разностью между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания
|
D(X) = M(Х2) – [M(X)]2 . |
(4.32) |
Свойства дисперсии:
а) дисперсия постоянной величины равна нулю
|
D(C) = 0; |
(4.33) |
б) постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат
|
D(CX) = C2D(X); |
(4.34) |
в) дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин
|
D(X + Y + … + Z) = D(X) + D(Y) + … + D(Z); |
(4.35) |
г) дисперсия разности двух независимых случайных величин равна сумме их дисперсий
|
D(X – Y) = D(X) + D(Y); |
(4.36) |
д) дисперсия числа появления события А в п независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятность появления и не появления события в одном испытании
|
D(X) = npq. |
(4.37) |
Дисперсия имеет размерность квадрата случайной величины. Поэтому для удобства расчетов обычно рассматривают ее аналог – среднее квадратичное отклонение, имеющее размерность случайной величины
|
|
(4.38) |
Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратичных отклонений этих величин
|
|
(4.39) |
В теории надежности также рассматривается относительное рассеяние случайной величины около ее математического ожидания, которое называется коэффициентом вариации
|
|
(4.40) |
Наиболее вероятное значение случайной величины называется модой Мо. Для непрерывных случайных величин, имеющих один или несколько максимумов плотности распределения, Мо – это значение случайной величины, отвечающее максимуму функции f(x) (рисунок 4.2).
В теории надежности часто используется числовая характеристика случайной величины, называемая гамма-процентным значением. Обычно применяется для описания непрерывных случайных величин. По физическому смыслу это такое значение случайной величины Тg, вероятность принять или превысить которое для случайной величины равно g
|
Р(Х ³ Тg) = g; Р(Х < Тg) = 1 – g. |
(4.41) |
Значение Тg, отвечающее g = 0,5 (50 %), называется медианой случайной величины Ме. Вероятности для случайной величины принять значение большее Ме, и меньшее Ме равны между собой
|
Р(Х < Ме) = Р(Х ³ Ме) = 0,5. |
|
Для случайных величин, имеющих симметричную относительно математического ожидания плотность распределения f(x), математическое ожидание и медиана совпадают
|
М(Х) = Тср = Ме(Х). |
|
Соотношения между интегральной функцией распределения, дифференциальной функцией распределения, условной дифференциальной функцией распределения и вероятностью безотказной работы приведены в таблице 4.1.
Таблица 4.1 – Связь между функциями F(t), f(t), P(t), l(t)
|
Функция |
F(t) |
f(t) |
P(t) |
l(t) |
|
F(t) |
- |
|
1 – P(t) |
|
|
f(t) |
|
- |
|
|
|
P(t) |
1 – F(t) |
|
- |
|
|
l(t) |
|
|
|
- |
Так как понятие надежности неразрывно связано с понятием времени, то в дальнейшем аргументом всех рассматриваемых непрерывных функций будет время t. Поэтому в таблице 4.1 во всех функциях х заменено на t.
5 О математических моделях
5.1 Математические модели описания поведения технических систем
Для оценки надежности какого-либо объекта необходимо иметь информацию в виде исходных данных. Использование такой информации зависит от математической модели, выбранной для описания поведения системы.
Данные в виде успехов или отказов, не доставляющие никакой информации, кроме факта выполнения или невыполнения критерия удачи, называются качественными данными.
Данные, дающие дополнительную информацию, например, время безотказной работы объекта, называются количественными данными. Когда в результате анализа данных количественные характеристики можно подчинить известному математическому закону, то эти данные можно с успехом использовать при оценке надежности. Такая модель позволяет получить более точные оценки. Рассмотрение количественных данных ведет к более эффективному использованию информации. Это особенно существенно в случае дорогостоящего эксперимента и ограниченного объема исходных данных. Однако если с исходными данными невозможно сопоставить какую-либо математическую модель, то в этом случае оценку надежности необходимо проводить, основываясь на качественных данных.
По виду исходных данных обычно можно заключить, какой из двух классов распределений вероятностей должен использоваться для оценки надежности. Этими классами являются дискретные и непрерывные распределения. Если надежность рассматривать как параметр, то, как правило, этот параметр не будет явно входить в распределение. В общем случае надежность следует рассматривать как некоторую функцию параметров математической модели, и перед тем, как производить какую-либо статистическую оценку надежности, необходимо пройти несколько предварительных этапов. Первый этап – установление типа распределения вероятностей, описывающих явление отказа. Второй этап – оценка параметров, однозначно определяющих закон распределения. Последний этап – совместное использование данных о распределении вероятностей и полученных оценок параметров этого распределения с целью получения оценки надежности.
Первый этап состоит в определении вида модели, т.е. в установлении общего закона возникновения отказов. Например, при построении некоторой функции всей совокупности наблюдений или очень большой выборки можно получить кривые надежности, описывающие поведение устройства. Кривые надежности можно составить для большого количества функций: например, число отказов в зависимости от времени использования устройства, число отказов в зависимости от числа циклов или от величины напряжения. Существует также много способов получения выборочных данных. Так, наблюдаемыми данными могут быть наработки между отказами, количество отказов в фиксированном количестве опытов, количество успехов до первого отказа, общая наработка на отказ и т.д.
Важно отметить, что, кроме истинных характеристик отказов устройств, модель отказов также определяется методом получения выборочных данных. Примером действия характеристик отказов может служить тот факт, что так называемые "случайные отказы" часто следуют показательному распределению, в то время как "постепенные отказы" часто можно характеризовать нормальным распределением.
Примером влияния метода получения выборочных данных служит то, что для оценки надежности по такой информации, как "один отказ в п испытаниях", можно пользоваться биномиальным распределением. Это распределение становится неприменимым, если известно, что испытания велись до первого отказа.
Модели такого рода могут быть построены из общих соображений, т.е. при помощи математического определения вероятности событий, которые наблюдаются, или эмпирически. В последнем случае наблюдаемой картине отказов для устройства конкретного типа приписывается тот же характер, что и в ранее наблюдавшихся случаях. Тем не менее, как в случае теоретической, так и в случае эмпирической модели используемые модели следует проверять на соответствие с выбранной моделью.
В результате проверок наблюдений может оказаться, что в данных имеются искажения или изменился характер выборочного плана. В последнем случае также может потребоваться изменение модели для получения более точного соответствия с имеющимися данными или для более правильного описания изменившегося закона, связанного с событием, которое должно наблюдаться.
В тех случаях, когда из общих соображений модель получить нельзя, или нет уверенности, что наблюдения следуют определенному закону, можно построить модель лишь в процессе проб и ошибок. Эта задача иногда облегчается различными приемами, но следует иметь в виду, что только полная информация может доказать представительность выбранной модели.
Большинство используемых распределений вероятностей содержит один, два, а иногда три параметра, полностью определяющих вид кривой распределения, ее расположение и другие характеристики. Поскольку свойства таких распределений общеизвестны и многие из них табулированы, можно делать выводы относительно наблюдаемых данных, основываясь на нашем знании этих распределений. Выражения характеристик некоторых распределений приведены в приложении В.
После установления общего вида модели, т.е. когда принято конкретное распределение, приступают к следующей задаче однозначного определения распределения при помощи параметров. Это связано с задачей оценки и связанными с ней статистическими методами.
5.2 Временные характеристики отказов
Модели такого вида используются для оценки таких событий, как, например, "время безотказной работы больше Т", где Т – требуемое или ожидаемое время работы системы, или "выходной параметр лежит в заданных пределах". Вероятность любого такого события можно назвать надежностью системы.
Прежде чем определить тип математической модели функции распределения, необходимо рассмотреть интенсивность отказов, которая дает общий подход к определению распределения времени безотказной работы.
Интенсивность отказов l(t) определяется по заданному распределению времени безотказной работы как условная плотность вероятности времени до отказа при условии, что устройство не отказывало до момента t. Если f(t) – безусловная плотность вероятности, то f(t)dt представляет долю устройств, включенных в момент t = 0, которые отказали в интервале (t, t + dt). Но l(t)dt представляет долю тех же устройств, которые не отказали до момента t, но отказали в том же интервале (t, t + dt). Отсюда видно, что l(t) и f(t) связаны соотношением
|
|
(5.1) |
Понятие интенсивности отказов вводится для невосстанавливаемых объектов. Для восстанавливаемых объектов понятие интенсивности отказов теряет смысл, т.к. само условие, что "отказа до момента t не было", не выполняется, т.е. после отказов объекты восстанавливались и продолжали работать. Однако если восстанавливаемый объект условно рассматривать как невосстанавливаемый, например, в период только до первого отказа или между восстановлением и следующим отказом, то использование понятия интенсивности отказов возможно и в некоторых случаях даже полезно.
Временные характеристики отказов связываются с отказами трех типов. Графически поведение интенсивности отказов показано на рисунке 5.1. Если устройство вводится в действие в момент t = 0, то оно уже при этом может быть в состоянии отказа. Такие отказы называются начальными. Вероятность начального отказа устройства можно оценить долей дефектных устройств в момент включения. Возможен случай, когда начальные отказы проявляются вскоре после момента t = 0, в период приработки. В этот период отбраковываются дефектные изделия. Обычно приработочные отказы связаны с качеством проектирования, технологии изготовления, сборки, монтажа, выходного и входного контроля. Приработочные отказы устраняются во время пуско-наладочных испытаний объекта, его опытной эксплуатации и в принципе должны быть выявлены и устранены перед сдачей объекта в эксплуатацию. Одним из средств уменьшения пуско-наладочного периода являются предварительные испытания отдельных элементов в условиях, близких к реальным условиям эксплуатации изделия, и отбраковка дефектных элементов перед сборкой. Поэтому при количественном анализе надежности объекта на этапе его проектирования считают, что приработочные отказы объекта будут устранены до начала его эксплуатации и в качестве l(t) принимают зависимость рисунка 5.1 с усеченным периодом I, полагая, что началом эксплуатации объекта является момент t1.
Пройдя начальный период, устройства, оставшиеся после отбраковки, входят в режим постоянной интенсивности отказов l(t) = const, которая гораздо меньше, чем в начальный период. Этот период называется периодом нормальной эксплуатации или периодом случайных отказов. Длительность этого периода намного больше приработочного периода и отличается для различных устройств и изделий, но в любом случае заданное время безотказной работы любого устройства никогда не может превосходить продолжительность периода нормальной эксплуатации данного устройства. В этот период уровень интенсивности отказов будет минимальным, а надёжность изделия остаётся примерно одинаковой. Увеличение надёжности изделия можно добиться только путём снижения интенсивности отказов используемых элементов.
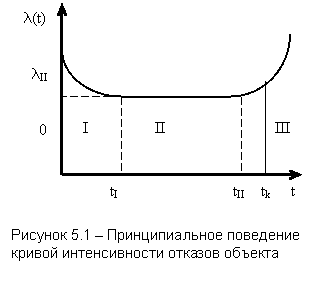 Совершенство, качество объекта с
точки зрения надежности определяется протяженностью (tII –
tI)
II
периода, когда процессы старения в нем еще существенно не проявляются. В этот
период отказы обуславливаются действием необычно жестких, непредвиденных и/или
непредотвратимых внешних обстоятельств, возникающих в процессе работы объекта. При
этом в объекте увеличивается концентрация нагрузок, превышающих расчётную
нагрузку. Физический смысл случайного отказа сводится к тому, что после
некоторого сравнительно быстрого количественного изменения какого-либо параметра
в элементе происходят качественные изменения, в результате которых он теряет
свои важнейшие свойства, необходимые для нормальной работы. Примером таких
отказов может служить перегорание предохранителя или пробой изоляции в
электрических устройствах, неожиданная поломка в механических изделиях без
предварительных симптомов разрушения.
Совершенство, качество объекта с
точки зрения надежности определяется протяженностью (tII –
tI)
II
периода, когда процессы старения в нем еще существенно не проявляются. В этот
период отказы обуславливаются действием необычно жестких, непредвиденных и/или
непредотвратимых внешних обстоятельств, возникающих в процессе работы объекта. При
этом в объекте увеличивается концентрация нагрузок, превышающих расчётную
нагрузку. Физический смысл случайного отказа сводится к тому, что после
некоторого сравнительно быстрого количественного изменения какого-либо параметра
в элементе происходят качественные изменения, в результате которых он теряет
свои важнейшие свойства, необходимые для нормальной работы. Примером таких
отказов может служить перегорание предохранителя или пробой изоляции в
электрических устройствах, неожиданная поломка в механических изделиях без
предварительных симптомов разрушения.
Последний период, третий, называется периодом поздних отказов, когда начинается резкое возрастание l(t), а следовательно, и вероятность отказа объекта. Этот период связан с постепенным изнашиванием материала, накапливаемым разрушением, усталостью. Продолжать эксплуатацию объекта в этом периоде нецелесообразно. Рационально снять его с эксплуатации, не доводя до износового отказа, например, в момент tk. Выбрать момент tk > tII надо из соображений экономики и безопасности в целом.
Если интенсивному износу подвергается не весь объект целиком, а только отдельные его элементы, то момент tк нужно определять именно для этих элементов и производить их профилактическую замену. Своевременная замена изношенных элементов даёт возможность почти полностью исключить влияние отказов из-за износа на надёжность работы объекта и увеличить таким образом продолжительность периода его нормальной эксплуатации. Особенно целесообразна такая профилактическая замена элементов при эксплуатации сложных и ответственных технических систем длительного пользования.
Таким образом, задача обеспечения высокого уровня надёжности заключается, во-первых, в исключении приработочных отказов путем наблюдения их распределения, определения продолжительности периода приработки и осуществления этой приработки до начала эксплуатации изделия; во-вторых, предупреждении износовых отказов путём определения сроков профилактической замены различных элементов и деталей и, в-третьих, предупреждении, уменьшении или полном устранении внезапных отказов при помощи специальных мер при проектировании, изготовлении и эксплуатации объекта.
6 Законы распределения случайных величин
6.1 Экспоненциальный закон распределения вероятностей
 Это однопараметрический закон,
которому подчиняется наработка до отказа невосстанавливаемых объектов в том
случае, если отказы не связаны со старением, усталостью материала или
постепенным ухудшением его характеристик, а зависят от внешних случайных факторов,
например, от резкого увеличения нагрузки любого вида. Экспоненциальному закону
распределения подчиняется наработка восстанавливаемого объекта между соседними
отказами до окончания периода приработки. Иногда время восстановления объектов
в первом приближении тоже подчиняется экспоненциальному закону. Вероятность
безотказной работы на заданном интервале не зависит от предшествующего времени
работы t, а лишь от длины интервала
t, т.е. поведение системы не зависит от прошлого. В терминах надежности
это означает, что система, проработавшая в течение любого времени и еще не
отказавшая, в смысле надежности совершенно эквивалентна по своим вероятностным
свойствам новой идентичной системе. Таким образом, при экспоненциальном
распределении времени работы до отказа не имеет смысла проводить
предупредительные профилактические замены долго проработавших элементов, так
как подобные замены не приводят к улучшению показателей надежности.
Это однопараметрический закон,
которому подчиняется наработка до отказа невосстанавливаемых объектов в том
случае, если отказы не связаны со старением, усталостью материала или
постепенным ухудшением его характеристик, а зависят от внешних случайных факторов,
например, от резкого увеличения нагрузки любого вида. Экспоненциальному закону
распределения подчиняется наработка восстанавливаемого объекта между соседними
отказами до окончания периода приработки. Иногда время восстановления объектов
в первом приближении тоже подчиняется экспоненциальному закону. Вероятность
безотказной работы на заданном интервале не зависит от предшествующего времени
работы t, а лишь от длины интервала
t, т.е. поведение системы не зависит от прошлого. В терминах надежности
это означает, что система, проработавшая в течение любого времени и еще не
отказавшая, в смысле надежности совершенно эквивалентна по своим вероятностным
свойствам новой идентичной системе. Таким образом, при экспоненциальном
распределении времени работы до отказа не имеет смысла проводить
предупредительные профилактические замены долго проработавших элементов, так
как подобные замены не приводят к улучшению показателей надежности.
При экспоненциальном распределении случайной величины условная плотность вероятности постоянна и является параметром закона: l(х) = l = const и равна интенсивности отказа. Интегральная функция распределения имеет вид
|
F(t) = 1 – e-lt. |
(6.1) |
Отсюда, плотность распределения равна
|
f(t) = le-lt. |
(6.2) |
Соответственно, математическое ожидание и дисперсия принимают вид
|
М(Т) = 1/l, D(T) = 1/l2, |
(6.3) |
а коэффициент вариации равен единице: u = 1. Графически функциональные характеристики экспоненциального распределения представлены на рисунке 6.1. Вероятность попадания в заданный интервал (a, b) непрерывной случайной величины t находится следующим образом. Так как P(a< t< b) = F(a) – F(b), a F(a) = 1 – e-la, F(b) = 1 – e-lb, то
|
P(a< t< b) = e-la – e-lb. |
(6.4) |
6.2 Распределение Вейбулла
Распределение Вейбулла – двухпараметрический закон, являющийся достаточно универсальным законом, охватывающим широкий спектр распределения случайных величин. По этому закону обычно распределяются наработки до отказа, связанные со старением или усталостью конструкционных материалов. Для этого закона интегральная функция распределения имеет вид
|
|
(6.5) |
а дифференциальная функция распределения и условная плотность принимают значения
|
|
(6.6)
(6.7) |
Параметрами распределения являются m > 0 и b > 0. m играет роль параметра масштаба, его изменение просто сжимает или растягивает кривую. b – параметр формы (рисунок 6.4). При b = 1 распределение Вейбулла переходит в экспоненциальное распределение. Таким образом, экспоненциальное распределение является частным случаем распределения Вейбулла. При b > 1 условная плотность распределения l(t) возрастает, при b < 1 – убывает.
6.3 Нормальный закон распределения (закон Гаусса)
Одномерная случайная величина x называется нормально распределенной со среднем значением m (математическое ожидание) и среднеквадратичным отклонением s, если ее плотность распределения вероятности дается выражением
|
|
(6.8) |
Соответственно, интегральная функция распределения будет иметь вид
|
|
(6.9) |
При параметрах m = 0 и s = 1 x называется нормированной нормальной случайной величиной с нормированной нормальной плотностью и функцией распределения. Эти функции имеют специальное обозначение и табулированы:
|
|
(6.10)
(6.11) |
Графически плотность распределения f(x) представляет собой колоколообразную кривую, симметричную относительно прямой t = m и показана на рисунке 6.2. Там же приведен график условной плотности распределения l(t). Значения m – s, m + s и m соответствуют точкам перегиба этих кривых. На рисунке 6.3 показано влияние параметра s на форму кривой f(t). Для этих кривых среднее квадратичное отклонение будет наименьшим для кривой 1 и наибольшим для кривой 3: s1 < s2 < s3. Параметр m определяет положение этих кривых на оси t.
Нормальный закон распределения наиболее часто встречается на практике. Он является предельным законом, к которому приближаются все другие законы распределения. При помощи нормального распределения хорошо описываются различные случайные величины, которые формируются под воздействием большого числа различных факторов, примерно эквивалентных по степени своего влияния. В частности, этому закону подчиняются ошибки измерений. Время восстановления ремонтируемых изделий в ряде случаев приближенно распределено по нормальному закону. Иногда приближенно определяется по этому же закону наработка до отказа восстанавливаемых изделий. Нормальное распределение часто используется для приближенных расчетов в тех случаях, когда имеет место биномиальное распределение или распределение Пуассона. Также оно хорошо служит для описания случайного дрейфа различных параметров.
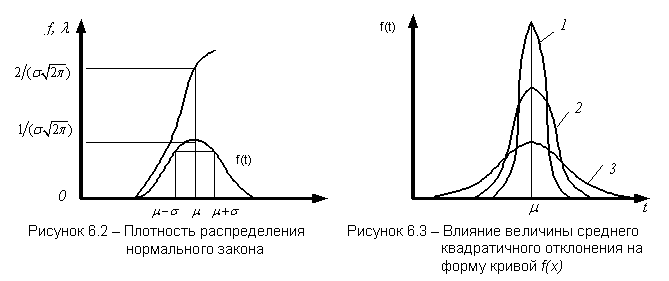
|
Широкое использование нормального закона распределения обусловлено теоремой Ляпунова: "Если случайная величина Х может быть представлена суммой очень большого числа взаимно независимых (или слабо зависимых) случайных величин (Х = åХi), влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному, с параметрами m = åmi, s = åsi, причем результат не зависит от законов распределения Xi".
Если же известно, что Хi распределены по нормальным законам, то даже в случае зависимости Хi между собой, закон распределения величины Х будет нормальным при любом п и любых mi и si, причем
|
m =
åmi;
|
(6.12) |
где rij – коэффициент корреляции случайных величин Хi и Хj.
Отсюда следует, что нормальный закон обладает свойством устойчивости, которое состоит в том, что композиция нормальных законов распределяется также нормально.
В случае, если по нормальному закону распределяется не сама величина, а ее логарифм, то такой закон распределения называется логарифмически нормальным законом. Наработка до отказа у многих невосстанавливаемых элементов имеет логарифмически нормальное распределение, если отказ наступает вследствие усталостного разрушения. В ряде случаев этому закону подчиняется время восстановления.
6.4 Закон гамма-распределения (распределение Пирсона)
Гамма распределением описывается время работы объекта между т-м и (т + к)-м отказами при условии, что наработка между соседними отказами распределена по экспоненциальному закону. Этот закон так же, как и закон Вейбулла, универсален в смысле многообразия форм распределения, которые он описывает. Его также используют для описания распределения времени работы объекта до отказа, связанного с ухудшением прочностных свойств материалов. Основные характеристики гамма-распределения приведены в приложении В. Параметрами закона являются l > 0 и a > 0. При a = 1 гамма распределение переходит в экспоненциальное. Условная плотность l(t) при a > 1 возрастает, а при a < 1 – убывает. Вид плотности гамма распределения при l = 1 показан на рисунке 6.5.
В некоторые характеристики закона Вейбулла и гамма распределения входит гамма-функция, которая имеет вид
|
|
(6.13) |

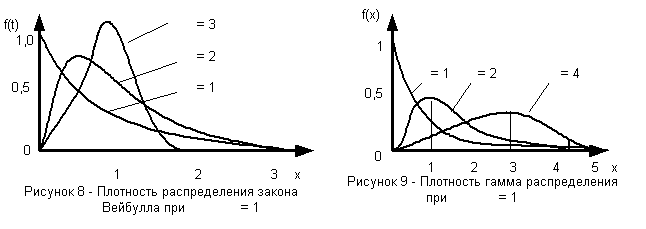
Эта функция табулирована. ga(и) – неполная гамма функция (табулирована);
ga-1 – обратная функция для ga(и).
В приложении В в качестве итога приведены выражения характеристик рассмотренных распределений непрерывных случайных величин.
6.5 Законы распределения дискретных случайных величин
Одним из наиболее важных дискретных распределений является биномиальное распределение. Это двухпараметрическое распределение с параметрами п и р, где п – любое натуральное число, р – любое вещественное число от 0 до 1. К биномиальному распределению приводит следующая математическая модель: п объектов одновременно или по очереди участвуют в испытании. По окончании испытания каждый объект может либо попасть в состояние А, либо нет, причем вероятность р попасть в состояние А для всех объектов постоянна и одинакова. В этих условиях случайная величина т – число элементов из п, которые в результате испытания оказались в состоянии А, распределена по биномиальному закону. Вероятность того, что т примет конкретное значение из ряда 0 … 1, определяется по формуле Бернулли
|
Рп(т) = Сптртqn – m , |
(6.14) |
где q
– вероятность события, противоположного событию А. При п
®
¥ биномиальный закон сходится к нормальному с
параметрами m =
пр и ![]() . Среднее значение
числа благоприятных событий (математическое ожидание)
M(n,m)
= pn, а дисперсия
D(n,
m) =
npq. Биномиальное
распределение используется при исследовании нагруженного резервирования.
. Среднее значение
числа благоприятных событий (математическое ожидание)
M(n,m)
= pn, а дисперсия
D(n,
m) =
npq. Биномиальное
распределение используется при исследовании нагруженного резервирования.
Те же самые математические модели приводят к закону Пуассона при больших п и малых р, т.е. при п ® ¥ и р ® 0. Параметром служит a = пр. Кроме того, закон Пуассона может описывать распределение большого числа случайных событий за некоторый произвольный интервал Dх (времени t, пространства S и др.), если известно среднее число событий на единицу этого интервала u. В этом случае параметром закона будет a = uDх, где a – среднее число событий за (или на) Dх, т – случайная величина с областью возможных значений от 0 до ¥. Аналитическое выражение закона
|
|
(6.15) |
При больших значениях (a > 9) закон Пуассона приближается к нормальному с параметрами m = a, s = Öa. Закон Пуассона является устойчивым распределением, т.е. композиция распределений Пуассона есть также распределение Пуассона.
7 Классификация и характеристики показателей надежности
Показателем надежности объекта называется количественная характеристика одного или нескольких свойств, составляющих его надежность.
Если показатель, которым характеризуется надежность объекта, связан с одним единичным свойством надежности, то такой показатель называется единичным показателем надежности. Если он связан с несколькими единичными свойствами надежности, то такой показатель является комплексным. Система показателей надежности в целом должна обеспечить возможность численной характеристики каждого из единичных свойств надежности. Надежность сложных объектов, к которым относятся и объекты энергетики, характеризуется несколькими единичными свойствами, следовательно, ее численная оценка должна быть осуществлена комплексом показателей надежности.
Любые объекты можно разделить на простые и сложные. Различие между этими объектами с точки зрения надежности можно трактовать следующим образом. Простой объект может быть охарактеризован двумя состояниями: полной работоспособностью и неработоспособностью, т.е. его надежность, измеряемая любым показателем, изменяющимся в относительных единицах в пределах от 1 до 0, соответствует в одном случае единице, а во втором – нулю. В таких объектах отказ соответствует скачкообразному переходу от состояния полной работоспособности к состоянию неработоспособности, а восстановление – обратному переходу.
Сложный объект характеризуется частично неработоспособными состояниями, возникающими вследствие частичных отказов. Значение какого-либо показателя надежности, измеряемого в относительных единицах, для сложного объекта может быть любым в диапазоне от 1 до 0. Обычно такой объект никогда не находится ни в состоянии полной работоспособности, ни в состоянии полной неработоспособности. Для системы, состоящей из п элементов, возможно 2п различных состояний. Все множество состояний системы называется фазовым пространством состояний, которое в общем случае не обязательно является дискретным.
Деление системы на элементы является делом условным и зависит от таких факторов, как цели исследования, наличие исходных данных, уровня качественного представления объекта исследования и т.д. В каждом конкретном случае элементом считается часть системы, дальнейшая детализация которой нецелесообразна. Например, в единой энергетической системе за элемент можно принимать электростанцию, линию электропередачи и т.д. При более детальном исследовании станция, например, рассматривается как система, а элементами являются ее подразделения и т.д.
7.1 Единичные показатели надежности
Закон надежности Р(t) представляет собой вероятность безотказной работы объекта в течение заданного времени t при определенных условиях эксплуатации. Если известен интегральный закон распределения случайной величины – наработки объекта до отказа F(t), то по определению
|
Р(t) = 1 – F(t). |
(7.1) |
Действительно, поскольку F(t) есть вероятность того, что отказ наступит до момента t, то 1 – F(t) есть вероятность того, что в пределах заданной наработки t отказ объекта не возникнет. Типичный вид закона надежности показан на рисунке 7.1, его очевидные свойства
|
P(0) = 1; P(¥) = 0. |
(7.2) |
Т.о., вероятность безотказной работы P(t) и вероятность отказа образуют полную группу событий
|
|
|
Вероятность того, что отказ объекта наступит в заданном интервале времени [a, b), равна P(a £ t < b) = P(a) – P(b).
Зная выражение F(t) через безусловную f(t) и условную l(t) плотность распределения наработки объекта до отказа, можно написать выражения для закона надежности через эти плотности
|
|
(7.3) |
Здесь плотность f(t) представляет собой вероятность того, что отказ объекта произойдет в малом единичном интервале около момента наработки t.
Численные значения F(t) и P(t) равны соответственно площади под кривой распределения f(t) до и после значения t =T.
При статистической выборке можно воспользоваться следующей оценкой надежности для невосстанавливаемых объектов
|
|
(7.4) |
где п – число изделий, поставляемых на испытание;
т(t) – число изделий, отказавших к моменту времени t.
Черта сверху означает, что параметр является статистической оценкой.
Закон надежности в качестве количественной характеристики очень удобен при расчетах вследствие того, что он характеризует изменение надежности во времени; достаточно полно характеризует надежность, так как охватывает большинство факторов, влияющих на надежность; значение Р(t) может быть сравнительно легко получено для сложных систем; Р(t) является удобной характеристикой как простейших элементов, так и сложных систем и даже комплексов. Вместе с тем его недостатком является то, что он характеризует надежность восстанавливаемых систем только до первого отказа и является достаточно полной характеристикой надежности только для систем разового использования.
При оценке безотказности высоконадёжных систем, когда в течение данного периода работы должно быть обеспечено значение P(t), близкое к единице или равное ей, непосредственное применение P(t) довольно затруднительно. Создание высоконадёжных систем с P(t) = 1 возможно за счёт большой избыточности, т.е. при наличии запаса надёжности. Этот запас может быть определён, если оцениваются физические процессы, приводящие к отказу изделия, и для данных условий эксплуатации определяется максимально возможная скорость данного процесса.
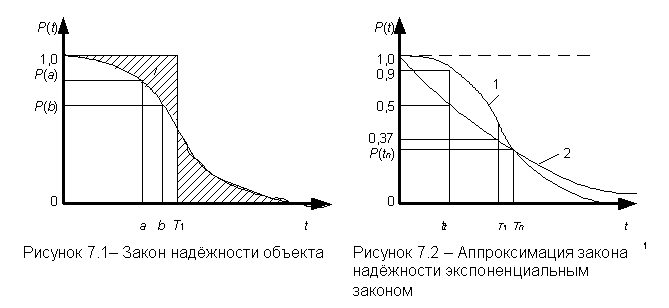 |
Пусть известно, что за данный период времени t = T0 параметр системы X может принимать различные значения (так как является случайной величиной), но его экстремальная величина за данный период времени t = T0 будет Xэк. Это значение определено, например, из оценки скорости изнашивания сопряжения для наиболее неблагоприятных (но допустимых или возможных) условий эксплуатации (максимальные режимы, недостаточная смазка и т.п.). Тогда, если значение параметра, при котором наступит отказ системы, будет Xmax > Xэк, запас надёжности X2 = gcp можно подсчитать как
|
|
(7.5) |
Запас надёжности может подсчитываться так же, как отношение Хтах к такому значению параметра Хg, при котором с вероятностью g параметр не выйдет за данные пределы, т.е.
|
|
(7.6) |
Период времени, в течение которого обеспечивается Кн ³ 1, называется гарантированным периодом безотказной работы системы Тr.
Запас надёжности характеризует устойчивость системы к отказам, а скорость его изменения определяет период допустимой эксплуатации высоконадёжного изделия. Создание запаса надёжности так же, как и запаса прочности, гарантирует системе сохранение работоспособности.
Однако по сравнению с прочностными расчётами здесь, во-первых, запас устанавливается по отношению к разнообразным выходным параметрам системы (а не только к прочностным характеристикам), и, во-вторых, он изменяется во времени и имеет вероятностную природу.
Таким образом, полной характеристикой процесса потери системой работоспособности является закон распределения сроков службы (наработки) до отказа (закон надёжности). Если он известен и выражается в дифференциальной f(t) или интегральной P(t) форме, то получение всех характеристик безотказности не представляет трудностей.
Противоположным и несовместным событием с вероятностью безотказной работы является вероятность отказа, то есть вероятность того, что при определённых условиях эксплуатации в заданном интервале времени возникнет хотя бы один отказ
|
|
(7.7) |
По статистическим данным вероятность отказа за время t равна отношению числа отказавших элементов к числу элементов, поставленных на испытания
|
|
(7.8) |
Если рассматривать вероятность отказа в единицу времени на любом заданном интервале времени, то приходим к понятию частоты отказов. Частотой отказов называется отношение числа отказавших элементов в единицу времени к первоначальному числу испытываемых элементов при условии, что все вышедшие из строя элементы не восстанавливаются
|
|
(7.9) |
где m(Dt)
– число отказавших элементов в интервале времени от  .
.
Частота отказов есть закон распределения времени работы элемента до первого отказа. Поэтому
|
|
(7.10)
(7.11) |
В разделе о непрерывных распределениях вероятностей был введен единичный показатель надежности – интенсивность отказов l(t). Принимая во внимание закон надежности, приведенное выражение (5.1) для l(t) можно переписать в виде
|
|
(7.12) |
Для самого простого однопараметрического экспоненциального закона распределения закон надежности принимает вид
|
|
(7.13) |
С помощью интенсивности отказов можно численно определять другие показатели надежности: вероятность безотказной работы, среднее время безотказной работы и др. Интенсивность отказов весьма полезна для качественной классификации основных распределений: распределения с возрастающей интенсивностью отказов соответствуют процессам старения элементов, т.е. ухудшению вероятностных характеристик надежности со временем. Распределения с убывающей интенсивностью отказов соответствуют ситуациям, когда имеет место закалка, приработка деталей, т.е. "выжившие" в результате первоначальной работы объекты обладают в среднем лучшими характеристиками надежности, чем те, которые еще не работали.
По статистической оценке интенсивность отказов – отношение числа отказавших элементов в единицу времени к среднему числу элементов, исправно работающих в данный отрезок времени
|
|
(7.14) |
где 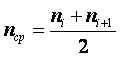 – среднее число исправно
работающих элементов в
– среднее число исправно
работающих элементов в
интервале Dti;
ni – число элементов, исправно работавших в начале интервала Dt;
ni+1 – число элементов, исправно работавших в конце интервала Dt.
По вероятностной оценке связь между интенсивностью отказов и частотой отказов находится из выражения
|
|
(7.15) |
Средняя наработка до отказа – это математическое ожидание или среднее значение случайной величины t – времени наработки объекта до первого отказа
|
|
(7.16) |
где f(t) = dF(t)/dt.
Зная закон надежности, можно получить значение для средней наработки до отказа, интегрируя предыдущее выражение по частям
|
|
|
|
|
(7.17) |
На рисунке 7.1 показана геометрическая иллюстрация вычисления величины Т1. Величина Т1 есть такое значение t, при котором площадь прямоугольника с высотой 1 и основанием Т1 равняется площади под кривой закона надежности Р(t) – интегралу (7.17). Для этого площади заштрихованных на рисунке областей должны совпадать.
В частном случае экспоненциального закона надежности объекта средняя наработка до отказа равна
|
|
(7.18) |
где l - параметр закона.
По статистическим данным средняя наработка до первого отказа вычисляется по формуле
|
|
(7.19) |
где ti – время безотказной работы i-го образца.
Для определения средней
наработки до первого отказа необходимо знать моменты выхода из строя всех
испытуемых элементов. Поэтому для вычисления ![]() пользоваться (7.19) неудобно. На практике
удобнее пользоваться другим выражением, где вместо времени
ti учитывается количество вышедших из строя элементов
ni в каждом
i-м интервале времени
пользоваться (7.19) неудобно. На практике
удобнее пользоваться другим выражением, где вместо времени
ti учитывается количество вышедших из строя элементов
ni в каждом
i-м интервале времени
|
|
(7.20) |
где 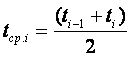 ;
; 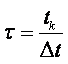 ;
;
ti-1 – время начала i-го интервала;
ti – время конца i-го интервала;
tk – время, в течение которого вышли из строя все элементы;
Dt = ti-1– ti – интервал времени.
Если опыт прекращают до того, как откажут все элементы, то п – количество отказавших элементов.
Произвольный закон надежности с возрастающей интенсивностью отказов l(t) ¹ const можно аппроксимировать экспоненциальным законом с параметром l = 1/Т1, где Т1 – средняя наработка (7.17) для указанного закона Р(t). Тогда в области 0 £ t < Тп всегда будет
|
Р(t) > ехр(– t/Т1), |
(7.21) |
где Тп > Т1 – наработка, отвечающая точке пересечения двух рассматриваемых законов (рисунок 7.2).
В этой области вероятность безотказной работы объекта, полученная по экспоненциальному приближению, будет всегда ниже, чем истинная P(t). Оценка безотказности, полученная с такой аппроксимацией, будет выше, чем оцененная в запас. Поскольку в рассматриваемой области P(t) изменяется от 1 до 0,37 и ниже, т.е. охватывает всю реально интересную область значений P(t), то экспоненциальная аппроксимация является вполне допустимой. С другой стороны, такая аппроксимация может дать чрезмерный запас (время tt на рисунке 7.2), где Pэксп(t) = 0,5, а реальная вероятность P(t) = 0,9. В таких случаях необходимо делать более точные оценки.
Гамма-процентная наработка до отказа. Применение параметра безотказной работы P(t) без указания периода времени t = T, в течение которого рассматривается работа объекта, смысла не имеет, поскольку они связаны зависимостью (7.3) и любое требуемое значение P(t) можно обеспечить выбором длительности периода Т. Чем ниже требования безотказности, тем большую длительность работы объекта можно допустить.
При высоких требованиях к надёжности объекта задаются допустимым значением P(t) = g % и определяют время работы объекта t = Tg, соответствующее данной регламентируемой вероятности безотказной работы. Значение Тg называется гамма-процентным ресурсом (неслучайная величина), и по его значению судят о большей или меньшей безотказности объектов. При g = 50 % получается значение среднего ресурса Т50 = Тт. Следовательно, определение гамма-процентной наработки на отказ – это наработка, в течение которой отказ объекта не возникает с вероятностью g.
Если известна плотность распределения наработки объекта до отказа f(t), то для вычисления Тg можно записать уравнения
|
|
(7.22) |
Медианная наработка объекта до отказа определяется по (7.22) при g = 0,5.
Параметр потока отказов w(t) является аналогом интенсивности отказов для восстанавливаемых объектов. При определении w(t) предполагается следующая эксплуатация восстанавливаемого объекта. С момента t = 0 объект эксплуатируется по назначению и работает до отказа, после отказа происходит мгновенное восстановление его работоспособности, и он опять начинает работать до очередного отказа и т.д. Моменты отказов восстанавливаемого объекта на оси суммарной наработки образуют поток отказов.
Параметром потока отказов w(t) называется среднее число отказов восстанавливаемого объекта в малом единичном интервале наработки D(t) ® 0 около момента t
|
|
(7.23) |
где M[m(t)], M[m(Dt)] – математические ожидания числа отказов m
объекта за наработки t и Dt соответственно.
Непосредственно из определения w(t) следует, что среднее число отказов восстанавливаемого объекта за произвольную наработку t
|
|
(7.24) |
Величина w(t)dt есть условная вероятность того, что отказ восстанавливаемого объекта произойдет в интервале [t, t + dt] при условии, что в момент t его не было.
Последовательные отказы рассматриваемых восстанавливаемых объектов, как правило, независимы и таковы, что не происходят одновременно в момент t по два, три и т.д., т.е. поток ординарный. Поэтому в общем случае, когда w(t) ¹ const, поток отказов восстанавливаемого объекта будет пуассоновским с переменным параметром w(t). Вероятность безотказной работы такого объекта описывается формулой
|
|
(7.25) |
Сравнивая это выражение с (7.12), можно сделать вывод: в области 0 £ t £ t1 до первого отказа восстанавливаемого объекта, где для него имеет смысл понятие интенсивности отказов l1(t), w(t) = l1(t), где индекс "1" означает интенсивность отказов на интервале 0 £ t £ t1 до первого отказа.
Если на последующих интервалах t2, …, tп объект полностью восстанавливает свою исходную надежность, то среднее значение этих случайных величин ti совпадает и равно T1 – средней наработке до первого отказа. В этом случае для партии однотипных объектов при t ® ¥ (t >> Т1)
|
w(t) = 1/Т1 = const. |
(7.26) |
Очевидно, что если закон надежности восстанавливаемого объекта экспоненциальный (7.13), (7.21) с постоянным для любого t параметром l, то для такого объекта при любых 0 £ t < ¥ w(t) = w = l и среднее число отказов за наработку t тср(t) = wt = lt.
При статистической оценке параметр потока отказов можно рассматривать как отношение числа отказавших элементов в единицу времени к числу испытываемых элементов при условии, что все вышедшие из строя элементы заменяются исправными
|
|
(7.27) |
где m(Dt) – число отказавших элементов в интервале времени от
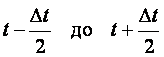 ;
;
п – число испытываемых образцов;
Dt – интервал времени.
Средняя наработка на отказ. Это показатель безотказности восстанавливаемого объекта, численно равный отношению наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки. С учетом (7.24)
|
|
(7.28) |
где ![]() –
среднее на интервале t значение
w(t).
Для случая (7.26) средняя
–
среднее на интервале t значение
w(t).
Для случая (7.26) средняя
наработка на отказ по формуле (7.28)
|
ТО = Т1 , |
(7.29) |
где Т1 – средняя наработка до отказа объекта при произвольном законе
надежности Р(t).
Для случая экспоненциального закона надежности средняя наработка на отказ
|
|
(7.30) |
Согласно статистической точки зрения, наработка на отказ – это среднее значение времени между соседними отказами
|
|
(7.31) |
где ti – время непрерывной работы образца между (i – 1)-м и i-м
отказами;
m – число отказов за некоторое время t.
(7.31) определяет наработку на отказ по данным испытания одного образца. Если на испытании находится n образцов в течение времени t, наработка на отказ вычисляется по формуле
|
|
(7.32) |
где tij – время исправной работы j-го образца между (i – 1)-м и i-м
отказами;
mj – число отказов j-го образца за время t.
Параметр потока отказов и наработка на отказ характеризуют надёжность ремонтируемого изделия и не учитывают времени, потребного на его восстановление, поэтому они не характеризуют готовности изделия к выполнению своих функций в нужное время, как коэффициент готовности и коэффициент вынужденного простоя, которые будут рассмотрены в следующем разделе.
Закон восстановления объекта. Этот закон представляет собой вероятность того, что время восстановления работоспособного состояния объекта не превышает заданного t. Следовательно,
|
Рв(t) = Fв(t) , |
(7.33) |
где Fв(t) – функция распределения случайной величины – времени восстановления работоспособного состояния объекта после отказа.
Если известна плотность распределения времени восстановления объекта fв(t), то
|
|
(7.34) |
Здесь fв(t) - вероятность того, что восстановление работоспособного состояния объекта будет закончено в малом единичном интервале времени около момента t. Это дифференциальная форма закона восстановления объекта.
Основные теоретические формы законов Fв(t) и fв(t) те же, что приведены в таблице В1 для F(t) и f(t). Чаще других в качестве закона восстановления используется экспоненциальный закон
|
Pв(t) = 1 – exp(–mt); fв(t) = m×exp(– mt), |
(7.35) |
где m - параметр закона.
Интенсивность восстановления – это условная плотность распределения случайной величины – времени восстановления работоспособного состояния объекта m(t). Она аналогична интенсивности отказов l(t). Физически m(t) есть условная вероятность того, что восстановление работоспособного состояния объекта будет закончено в малом единичном интервале около момента t при условии, что до этого момента восстановление не завершилось. Математически ее можно записать в виде
|
|
(7.36 |
где ![]() – функция распределения времени
восстановления;
– функция распределения времени
восстановления;
fв(t) – плотность распределения Fв(t).
Если интенсивность отказов l(t) вводится как характеристика невосстанавливаемых объектов, то m(t) является характеристикой восстанавливаемых объектов, для которых проведение восстановления работоспособного состояния предусмотрено в нормативно-технической документации. Основные теоретические законы изменения m(t) те же, что и приведенные в таблице приложения для условной плотности l(t). На практике чаще других находит применение экспоненциальный закон восстановления, для которого m(t) = m = const – интенсивность восстановления постоянна и равна параметру закона.
Среднее время восстановления (среднее время простоя), вызванное отказом. Это математическое ожидание случайной величины – времени восстановления работоспособного состояния объекта. Среднее время восстановления
|
|
(7.37) |
В процессе восстановления работоспособности отказавшего объекта можно выделить два основных случая: ремонт производится на месте; отказавший элемент заменяется исправным, а затем ремонтируется.
В математических моделях надежности сложных объектов предполагается непрерывный контроль работоспособности, т.е. отказ обнаруживается мгновенно. Локализация отказа тоже мгновенная. Т.о., время простоя объекта делится на два основных периода: время ожидания ремонта (при наличии очереди) и собственно время ремонта. Такая детализация на фазы очень важна при анализе надежности восстанавливаемых объектов при различных режимах эксплуатации и ремонта.
В ядерной энергетике специфика восстановления работоспособного состояния оборудования после отказов заключается еще в наличии фактора ионизирующего излучения для определенных групп оборудования. Поэтому для таких объектов время восстановления работоспособного состояния, кроме чистого времени восстановительного ремонта, включает в себя еще время, связанное с необходимостью выдержки оборудования или его дезактивации для снижения интенсивности ионизирующего излучения до допустимого уровня. В этом случае употребляется термин среднее время простоя, вызванного отказом.
Для экспоненциального закона Тв = 1/m, где m - параметр экспоненциального закона, являющийся интенсивностью восстановления объекта.
Закон долговечности объекта – это вероятность Рд(t) того, что предельное состояние объекта наступит не ранее момента t. По аналогии с законом надежности он определяется законом распределения F(t) случайной величины, характеризующей долговечность объекта, т.е. либо его ресурса, либо срока службы.
Для невосстанавливаемого объекта закон долговечности совпадает с законом надежности: Pд(t) ≡ P(t). Поэтому все, что было сказано о законе P(t) и его характеристиках, полностью относится и к Pд(t).
Для восстанавливаемых объектов формальное математическое определение всех рассмотренных функциональных и числовых характеристик долговечности объектов полностью сохраняется, но теперь будем иметь дело с более сложными и достаточно редко реализующимися случайными величинами: с ресурсом восстанавливаемого объекта и с его сроком службы
|
|
(7.38) |
где ti и tiкал – соответственно наработка и календарное время эксплуатации
объекта между (i – 1)-м и i-м отказами;
i = 1,2, …, j (при j = 1 получаем случай невосстанавливаемого
объекта);
j – номер последнего отказа, за которым следует снятие его с
эксплуатации.
В соответствии с центральной предельной теоремой Ляпунова для случайных величин tp и tc при условии, что они являются суммами многих случайных величин, следует ожидать, что закон распределения будет близок к нормальному, а в случае j = 1 у них будут другие законы. Обозначим эти законы долговечности
|
Р(tp) = 1 – F(tp), P(tc) = 1 – F(tc), |
(7.39) |
где F(tp) и F(tc) – функции распределения случайных величин tp и tc
соответственно;
P(tp) и P(tc) – вероятности того, что ресурс и срок службы объекта
окажутся не меньше заданных значений tp и tc. Законы P(tp) и P(tc),
помимо того, что при j >> 1 будут близки к нормальному, будут,
как правило, иметь малые коэффициенты вариации.
Средний ресурс и средний срок службы при известных законах P(tp) и P(tc) вычисляются по формулам (7.17), где под отказом надо понимать предельное состояние
|
|
(7.40) |
– это математическое ожидание случайных величин tp и tc. Если законы P(tp) и P(tc) неизвестны, то Tp и Tc оцениваются эмпирически.
Вероятность восстановления за заданное время. В ряде задач надежности оказывается необходимым знать вероятность того, что восстановление элемента или системы будет завершено в течение времени t0. При известной функции распределения Fв(t) случайной величины h эта вероятность равна 1 – Fв(t).
7.2 Комплексные показатели надежности
Для оценки долговечности системы необходимо рассматривать весь период её эксплуатации вплоть до прекращения использования по назначению и учитывать мероприятия, проводимые для поддержания её работоспособности. При этом объектом рассмотрения должна быть система, а не отдельные её узлы и элементы, поскольку методы и стратегия ремонта и технического обслуживания системы связаны с анализом её функционирования как единой сложной системы.
При назначении показателей долговечности системы следует иметь в виду следующее:
- продолжительность эксплуатации системы (т.е. работа её до предельного состояния) определяется её моральным износом и затратами, связанными с физическим износом, а также требованиями безопасности эксплуатации;
- должны быть оценены суммарные затраты времени и средств, необходимые для поддержания работоспособного состояния изделия. Эти затраты, как правило, связаны в основном с методами ремонта и технического обслуживания системы;
- основанием для проведения ремонтных операций служат изменение выходных параметров системы и вероятность отказа её отдельных узлов и элементов;
- должна быть оценена вероятность безотказной работы системы в период её работы между остановками для ремонта и технического обслуживания.
Поэтому для оценки долговечности системы применяют следующие три основных показателя:
Тр – установленный ресурс (срок службы) всей системы, который определяет период её работы до предельного состояния с учётом требований безопасности и экономической эффективности;
Кти – коэффициент технического использования, который характеризует затраты времени (и соответственно средств) на восстановление работоспособности системы;
Кг – коэффициент готовности, который оценивает безотказность системы в период её функционирования.
Коэффициент готовности объекта – это комплексный показатель надежности, характеризующий готовность объекта к работе на интервале времени между плановыми остановками объекта, в течение которых применение объекта по назначению не предусматривается, например, остановки на плановый ремонт, модернизацию. Количественно коэффициент готовности есть вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых его применение по назначению не предусмотрено. Коэффициент готовности Кг оценивает непредусмотренные остановки системы, наличие которых свидетельствует о том, что плановые ремонты и мероприятия по техническому обслуживанию не полностью выполняют свою роль.
Режим работы станции характеризуется чередованием периодов работы с периодами простоя для восстановления работоспособности объекта после его отказа. Плановые остановки сюда не включаются. Для такого режима коэффициент готовности объекта
|
|
(7.41) |
где tраб – суммарное время работы объекта за некоторый период
эксплуатации, на котором определяется Кг;
tвосст – суммарное время восстановления работоспособности объекта
после отказов за тот же интервал эксплуатации;
dв – доля времени эксплуатации (включающего периоды работы и
восстановления), приходящаяся на восстановление
работоспособности объекта после отказов.
Можно показать, что в период нормальной эксплуатации объекта, когда его средняя наработка на отказ То = const, коэффициент готовности для простого режима работы
|
|
(7.42) |
Статистически коэффициент готовности можно определить и как отношение числа работоспособных объектов к общему числу объектов, наблюдаемых в некоторый случайно выбранный удаленный момент времени.
Физический смысл коэффициента готовности заключается в следующем. В простейшем случае, когда l = const и m = const, и, предполагая, что при t = 0 система находится в исправном состоянии (P(0) = 1), вероятность работоспособности системы определяется из выражений
|
|
(7.43) |
где 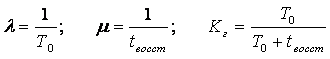 .
.
Из (7.43) видно, что Рг(t) ® Кг при t ® ¥, т.е. коэффициент готовности имеет смысл вероятности нахождения системы в работоспособном состоянии при установившемся процессе эксплуатации.
Для невосстанавливаемых на интервале t объектов коэффициент готовности в соответствии с определением численно равен вероятности безотказной работы P(t).
С коэффициентом готовности тесно связан противоположный ему коэффициент вынужденного простоя – отношение времени вынужденного простоя к сумме времен исправной работы и вынужденных простоев объекта, взятых за один и тот же календарный срок
|
|
(7.44) |
Коэффициент готовности и коэффициент вынужденного простоя связаны между собой зависимостью
|
Кп = 1 – Кг. |
Коэффициент оперативной готовности. Этот коэффициент вводится для технических объектов, предназначенных для выполнения некоторых функций в течение интервала времени [t, t + t0]. По ГОСТу коэффициент оперативной готовности определяется как вероятность того, что объект, находясь в режиме ожидания, окажется в работоспособном состоянии в произвольный момент времени и, начиная с этого момента, будет работать безотказно в течение заданного интервала времени.
|
|
(7.45) |
где R(t0) – вероятность того, что объект работоспособен в произвольный достаточно удаленный момент времени t и проработает безотказно в течение интервала длительностью t0.
Объектами с такими характеристиками являются, например, системы предотвращения развития аварий на ядерных реакторах, которые должны немедленно включиться в работу при отказах основного оборудования реактора; системы регулирования, когда регулируемый параметр процесса выходит за заданные пределы и др.
Коэффициент технического использования объекта. Обычно используется для восстанавливаемых объектов в качестве показателя надежности, характеризующего долю времени пребывания объекта в работоспособном состоянии по отношению ко всему рассматриваемому календарному периоду эксплуатации, включающему периоды работоспособности и простоев, связанных как с плановыми ремонтами (ППР) или техническим обслуживанием, так и с неплановыми ремонтами с целью ликвидации отказов объекта.
Для объектов с простым режимом работы коэффициент технического использования
|
|
(7.46) |
где tраб – суммарное время работы объекта за рассматриваемый интервал
календарного времени tкал, на котором определяется Ктм;
tвосст – суммарное время восстановления работоспособного состояния
объекта после полных отказов при работе (неплановых ремонтов) за
тот же календарный период tкал;
tппр – суммарное время проведения ППР объекта (включая техническое
обслуживание) за тот же календарный период tкал;
dв, dп – доли календарного времени tкал, связанные с восстановлением
работоспособности объекта после полных отказов и с планово-
предупредительными ремонтами, соответственно.
Коэффициент Кти численно равен вероятности того, что в данный, произвольно взятый момент времени система работает, а не ремонтируется и не находится в техническом обслуживании. Следует подчеркнуть, что коэффициент технического использования не будет полноценной характеристикой, если рассматривается ограниченный промежуток времени, так как малые затраты на ремонт за это время ещё не означают малые суммарные затраты за весь период эксплуатации. Возможен вариант, когда недостаточное внимание к профилактическим работам и техническому обслуживанию в процессе эксплуатации системы (то есть незначительные затраты на ремонт в рассматриваемый период) приведет к повышенным затратам времени и средств при последующих ремонтах.
Поэтому при определении Кти необходимо брать весь период эксплуатации системы или, как минимум, период до её капитального ремонта.
Для определения Кти необходимо установить его зависимость от срока службы элементов системы.
Время простоя из-за данной i-й детали или узла системы будет
|
|
(7.47) |
где Тi – длительность работы i-й детали системы до очередного ремонта;
ti – время (трудоёмкость) ремонта i-й детали (узла), включая разборку,
сборку и выверку.
Отношение Tраб/Ti показывает, сколько раз в течение периода, равного Tраб, ремонтировалась данная деталь.
Подставляя Ti.рем в формулу (7.46), получим коэффициент технического использования, выраженный через продолжительность работы и трудоёмкость ремонта отдельных деталей и узлов системы
|
|
(7.48) |
При периодических ремонтах, когда одновременно ремонтируется группа деталей, под Тi понимается время до очередного ремонта, а под ti – его трудоёмкость.
Из (7.48) следует, что основным методом повышения долговечности системы является сокращение времени , затрачиваемого на ремонт и повышение срока службы её деталей.
Как видно из (7.48), коэффициент Кти зависит от суммы, которая называется относительными ремонтными потерями
|
|
(7.49) |
Относительные ремонтные потери z могут применяться в качестве самостоятельного критерия, заменяющего Кти при оценке долговечности системы.
Время, которое затрачивается на ремонт и техническое
обслуживание, зависит не только от методов и технологии ремонта, но и от
конструкции изделия, которая характеризуется ремонтопригодностью.
Следовательно, ремонтопригодность, которая определяет затраты времени ![]() в (7.46), является
составной частью долговечности.
в (7.46), является
составной частью долговечности.
Коэффициент использования мощности Ким характеризует относительную энерговыработку за рассматриваемый интервал эксплуатации по отношению к максимально возможной. Ким равен отношению выработанной станцией энергии за заданное календарное время эксплуатации tкал к количеству энергии, которую станция выработала бы за этот же период, работая непрерывно на номинальной мощности Nн
|
|
(7.50) |
В общем случае
|
|
(7.51) |
Можно записать формулу для Ким и через среднюю фактическую мощность станции
|
|
(7.52) |
где Nф – средняя фактическая мощность станции на интервале
эксплуатации tэ = tраб + tвосст
|
|
(7.53) |
Очевидно, что во время tвосст Nф(t) = 0.
7.3 Общая модель изменения работоспособности изделия
Основные показатели надёжности непосредственно связаны с общей моделью изменения работоспособности изделия во времени. Если область состояний Е в течение времени t = T является частью области работоспособности G, то есть его подмножеством E Ì G, то изделие будет устойчиво по отношению к отказам, так как вероятность их возникновения F(t) = 0. Это условие можно записать как
|
X(t = T) Ì G. |
(7.54) |
В этот период показателем надёжности изделия будет являться его запас надёжности Kн. Вероятность возникновения отказа может наступить лишь после того момента времени, когда условие (7.5) нарушится и будет пересечение множеств Е и G. До этого периода времени работа изделия будет протекать в устойчивой зоне по отношению к отказам, и запас этой устойчивости может характеризоваться значением Kн > 1. Поскольку Kн(t) является функцией времени, то происходит расход запаса надёжности и необходимо определение периода времени, в течение которого его значение Kн = 1 и области E и G будут соприкасаться.
Значение t = Tr, при котором Kн = 1, будет являться гарантированным периодом безотказной работы изделия по данному параметру или по их совокупности, если рассматривается вся вектор-функция X(x1, x2, … xn).
Период времени t = Tg, при котором вероятность безотказной работы задана значением g = P(t) %, будет являться гамма-процентным ресурсом.
Коэффициент технического использования Кти характеризует затраты, позволяющие сократить область состояний Е и улучшить показатели качества и параметрической надёжности изделия.
При определении показателей параметрической надёжности системы большое значение имеет установление границ области работоспособности Хтах. Даже небольшое изменение Хтах может существенно повлиять на численное значение показателей надёжности, особенно если границы областей Е и G находятся в непосредственной близости.
Критериями предельного состояния системы и её элементов могут служить ситуации, при которых:
- выход параметра за установленные пределы нарушает качество функционирования системы, например, точность обработки на станке;
- наибольшее допустимое значение параметра диктуется требованиями безопасности, например, попадание системы в зону повышенной вибрации, тепловыделения;
- возрастание параметра приводит к снижению эффективности работы системы, например, возрастает расход топлива, снижается выходная мощность;
- выходной параметр связан с воздействием на окружающую среду, которая регламентирована (превышение ПДК, шум, превышение радиационного фона);
- достижение параметром значения, при котором возможна интенсификация процесса потери системой работоспособности.
Предельно допустимое значение выходного параметра Хтах, которое установлено техническими условиями, определяет границу области работоспособности. Но в некоторых случаях сам ход процесса изменения выходных параметров и наличие зон их резкого возрастания может наложить дополнительные ограничения на размеры области работоспособности. Кроме того, надо учитывать, что требования к выходным параметрам различны в зависимости от сферы применения системы и могут изменяться.
Типичные области работоспособности показаны на рисунке 7.3. Наиболее распространен случай, когда установленное значение не зависит от времени и область работоспособности сохраняет свои границы постоянными на протяжении всего периода эксплуатации системы (рисунок 7.3 а). Однако если требования к параметрам системы устанавливаются потребителем, то границы этой области Хтах будут занимать в определённом интервале случайное положение со своим законом распределения и область работоспособности является размытым множеством (рисунок 7.3 б).
Производитель может осуществлять отбор своих изделий в зависимости от требований, поставленных потребителем. Если с течением времени требования к данному типу изделий повышаются, например, из-за конкуренции, то по мере эксплуатации системы будет происходить не только её физический износ, но и будут сужаться границы области допустимых значений её выходных параметров (рисунок 7.3 в).
 |
Иногда допускается расширение области работоспособности для возможного дальнейшего использования изношенного изделия в других сферах, где требования к параметрам изделия могут быть ниже (рисунок 7.3 г). Перевод изделия в другую категорию качества производится обычно после того, как оно отработало свой ресурс, и его ремонт не может полностью восстановить выходные параметры, или это нецелесообразно делать по экономическим соображениям. Примером может служить применение отработавшего свой ресурс авиационного двигателя для стационарных установок.
В ряде случаев при установлении предельно допустимого значения параметра Хтах следует учитывать не только требования к данной технической характеристике системы, но и возможность интенсивного изменения параметра при приближении к значению Хтах.
Вероятность попадания системы в зону интенсивного выхода из строя может послужить основанием для ограничения области работоспособности значениями меньшими Хтах, начиная с некоторого периода t = T0 (рисунок 7.3 д).
Ещё большую опасность представляет возможность резкого возрастания реализации X(t) после некоторого периода работы системы (рисунок 7.3 е). Тогда область работоспособности должна быть ограничена значением Ттах, которое гарантирует нахождение параметра в зоне нормального протекания процесса X(t), а значение Хтах носит в известной степени формальный характер.
Таким образом, область работоспособности в координатах x – t ограничена как значением Хтах, связанным с требованиями, предъявляемыми к параметрам системы, так и в ряде случаев значениями t = Tmax.
Установление границ области работоспособности для каждого типа изделий является одним из основных этапов при разработке математических моделей расчёта и прогнозирования их параметрической надёжности.
8 Параметрическая надёжность
8.1 Классификация процессов старения
Старение различных объектов и изделий происходит под действием необратимых физических и химических процессов на поверхности и в объёме материала, в результате чего происходит его повреждение, т.е. отклонение его контролируемых свойств от их обычных значений.
Внешнее проявление процесса старения может быть довольно разнообразным. При объёмном старении может происходить разрушение детали, её деформация или изменение свойств материала.
Разрушение материала изделия приводит, как правило, к недопустимым отказам, поскольку оно носит лавинообразный характер и протекает с большой скоростью. Разрушение материала может произойти как в результате возникновения недопустимых статических или динамических нагрузок, так и при длительном действии переменных нагрузок, приводящих к усталостным разрушениям. В первом случае будут иметь место внезапные отказы, если превышение допустимых значений нагрузок не связано с длительностью предшествующей эксплуатации изделия.
Усталостные разрушения относятся к постепенным отказам, так как при работе элемента происходит изменение несущей способности материала и время предшествующей эксплуатации влияет на возможность возникновения отказа – усталостной поломки. Характерным проявлением процесса старения материала является необратимая деформация детали, когда отказ может наступить значительно раньше, чем будет исчерпана его несущая способность. Это связано с возникновением на отдельных участках детали пластических деформаций. При снятии внешних нагрузок упругие деформации исчезают, а в областях, претерпевших пластическое деформирование, возникают остаточные деформации.
Изменение пластических деформаций во времени – ползучесть – может привести к нарушению нормальной работы элемента. Например, вследствие ползучести диска и лопаток газовой турбины перекрываются зазоры, предусмотренные между лопаткой и корпусом, что приводит к поломке лопаток.
К объёмным явлениям также можно отнести изменение свойств материала, когда изменяются механические, магнитные и другие свойства, возникают процессы газопроницаемости или просачивания жидкости через стенку резервуара. К этой же категории относятся процессы засорения или изменения свойств жидкости и газа, например, засорение масла в системе смазки подшипников турбины.
К поверхностным явлениям процесса старения относится либо потеря материала поверхности, либо присоединение нового материала из окружающей среды. Это происходит в тех случаях, когда поверхность подвергается температурным, химическим, механическим или другим воздействиям.
При потере материала происходит разрушение поверхности в результате коррозии, эрозии, кавитации и других процессов. Коррозия материала – это его разрушение в результате химического или электрохимического действия среды. Различают атмосферную, электрохимическую и газовую коррозию.
Коррозия в сочетании с действием переменного напряжения приводит к коррозионной усталости материала. Наиболее часто коррозионной усталости подвергаются рабочие колёса насосов, гребные винты судов, рессоры, тросы.
При действии на поверхность детали потока газа или жидкости при определённых условиях может возникать эрозия. Процессы эрозионного разрушения характерны для деталей насосов, перекачивающих суспензию или нефть, шнеков для перемещения твёрдых материалов, мельниц и др. Сильному эрозионному разрушению подвергаются поверхности, на которых возникает кавитация. При определённых условиях процессы кавитации могут протекать весьма интенсивно, особенно если они сопровождаются коррозионными явлениями. Обычно кавитация наблюдается в гидронасосах, гребных винтах, трубопроводах.
К процессам, приводящим к потере материала, относится также прогар, характерный для деталей, работающих в условиях высоких температур и соприкасающихся с горячей струёй газа. Этот вид повреждения характерен для деталей камер сгорания и лопаток газовых турбин, выхлопных труб двигателей внутреннего сгорания.
Многие поверхности деталей машин, взаимодействуя с окружающей средой, претерпевают такие изменения, в результате которых происходит присоединение – нарост материала, и поверхность изменяет свою форму и свойства.
Налипание на поверхность посторонних частиц происходит в результате адгезии, когезии, адсорбции, диффузии, проявлении различных химических связей и действия сил электрического происхождения. В качестве примера можно привести покрытие зольными отложениями экранных труб в пылеугольных топках, ванадиевую коррозию экранных труб в топках мазутных котлов.
Для гидравлических систем, имеющих малые проходные сечения, часто происходит процесс заращивания каналов – облитерация. Этот процесс связан с соударением и слипанием твёрдых частиц и примесей в жидкости и их налипание на стенки каналов. В результате изменяется проходное сечение канала, следовательно, расход жидкости и давление.
При взаимодействии поверхности с окружающей средой часто происходят процессы, которые только изменяют геометрические и физические свойства поверхности: её шероховатость, твёрдость, отражающую способность.
Если поверхность не свободна, а находится в контакте с другой поверхностью, то в этом случае происходит изнашивание поверхностей. Износ – это результат процесса постепенного изменения размеров детали по её поверхности при трении. Кроме того, может быть смятие, когда имеет место перемещение материала под действием сил трения и усталость поверхностных слоёв, когда под действием контактных нагрузок возникают локальные очаги разрушения поверхности. При взаимном перемещении соприкасающихся поверхностей обычно происходит изнашивание, смятие, если соприкасающиеся поверхности взаимно неподвижны (шпоночные и шлицевые соединения, упоры). Усталость поверхностных слоёв обычно бывает при трении без скольжения (шариковые подшипники). Качение с относительным скольжением вызывает усталость и изнашивание, а в ряде случаев и смятие поверхности. В наибольшей степени это проявляется в зубчатых передачах.
У сопряжённых поверхностей может произойти изменение условий контакта, т.е. изменение площади контактирующих поверхностей, глубины взаимного внедрения микровыступов, разрыв масляной плёнки, что в свою очередь изменяет выходные параметры сопряжения – коэффициент трения, контактную жёсткость.
8.2 Методы оценки износа
Для количественной оценки износа существуют два метода. С помощью первого метода выбирают критерии для непосредственного измерения величины повреждения изделия, это может быть степень деформации изделия, линейный или весовой износ поверхности, глубина и размеры каверны и т.д.
Второй метод оценки применяют тогда, когда о повреждении судят косвенно, по изменению выходного параметра. Например, по содержанию масла в сжатом воздухе можно судить о степени изношенности уплотняющих колец на поршне компрессора.
Повреждение поверхности может быть полным или локальным. Полное повреждение обычно неравномерно распределено по поверхности детали. Поэтому оценка степени повреждения поверхности может проводиться интегральным методом, когда оценивается суммарный эффект повреждения, и дифференциальным, когда оценивается степень повреждения в каждой точке или области данной поверхности.
В интегральном методе оценкой степени повреждения может быть потеря веса Ug, мг, объёма поверхности Uv, мм3 – объём повреждённого или удалённого материала, или среднее значение линейного износа поверхности Ucp. Аналогичные показатели могут применяться при явлениях нароста, когда оценивается количество прибавившегося материала.
В дифференциальных методах оценивается линейный износ поверхности U, мкм – изменение размера детали при её изнашивании в направлении, перпендикулярном поверхности трения. При коррозии применяется глубинный показатель, оценивающий уменьшение толщины металла в каждой точке поверхности. Эти показатели являются функцией координат данной точки поверхности – U = f(x, y).
Необходимо, чтобы показатели степени повреждения были непосредственно связаны с выходными параметрами: прочностью, жёсткостью, газопроницаемостью, отражательной способностью, коэффициентом трения и др.
Изменение выходных параметров изделия во времени зависит от природы протекания процесса старения: X(t) = F[U(t)]. F является неслучайной функцией. Для F наиболее типична линейная зависимость, когда U и X связаны передаточным коэффициентом. Например, при изнашивании сопряжения зазор D непосредственно увеличивается при возрастании износа U, т.е. D = D0 + U, где D0 – начальный зазор.
Нелинейная зависимость между X и U характерна для динамических нагрузок Рд при росте зазоров в изнашиваемых сопряжениях (зубчатые передачи, многозвенные механизмы).
В ряде случаев зависимость выходного параметра от степени повреждения может иметь зону нечувствительности с последующим резким изменением значения Х. Например, коррозия стенки резервуара не влияет на давление в нём, но после любого локального повреждения стенки на глубину U = d резервуар вообще теряет способность содержать жидкость.
Во многих случаях выходной параметр зависит от нескольких повреждений U1, U2, …, Un, которые могут иметь различные законы изменения во времени, например, несущая способность конструкции зависит от коррозии, усталости и износа её элементов. В этом случае
|
|
(8.1) |
При линейных зависимостях
U
= kt удобнее пользоваться значением скорости протекания
процесса 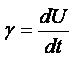 :
:
|
|
(8.2) |
Сложные изменения характеризуются не одним, а несколькими выходными параметрами Х1, Х2, … Хп. В этом случае конкретный вид повреждения может оказывать влияние на изменение разных выходных параметров, и эти зависимости записываются системой уравнений.
|
|
(8.3) |
При наличии образования связей, когда скорость процесса зависит от величины повреждения, эти уравнения должны быть записаны в дифференциальной форме.
При старении протекают необратимые процессы повреждения, поэтому зависимость U(t) является, как правило, монотонной неубывающей функцией.
Наиболее стабильно протекают стационарные процессы, когда скорость протекания процесса g постоянна или колеблется около среднего значения. Это происходит в том случае, если все факторы, влияющие на скорость процесса, стабилизировались.
Если при старении возникают факторы, которые интенсифицируют или замедляют скорость его протекания, т.е. скорость процесса g изменяется монотонно, то функция U(t) будет нелинейной. Такой ход процесса связан с тем, что его скорость зависит не только от внешних факторов, но и от степени повреждения U, которая в свою очередь влияет на интенсивность дальнейшего протекания процесса повреждения. Например, увеличение износа сопряжения приводит к повышению динамических нагрузок, которые увеличивают процесс износа. Это условие можно записать в виде
|
|
(8.4) |
При линейной зависимости g от U, т.е. при
|
|
(8.5) |
интегрированием этого уравнения получим экспоненциальную зависимость для величины повреждения как функции времени.
При положительном k
|
|
(8.6) |
При отрицательном k
|
|
(8.7) |
В некоторых случаях, когда на скорость процесса действует одновременно ряд равноценных факторов, которые претерпевают изменения во времени, зависимость g(t) может иметь экстремум, что характерно для некоторых видов коррозии. В этих случаях функция U(t) имеет точку перегиба.
В некоторых процессах сначала происходит накопление каких-то внутренних повреждений, а затем с некоторым запаздыванием, начинается процесс старения. Несмотря на то, что физический процесс начинается сразу, характеристики, принятые для оценки его результатов, проявляются позже. Например, при усталостных разрушениях материала трещины зарождаются лишь после определённого числа циклов нагружения.
Если рассматривать совокупность элементов, то исходные свойства материала и начальные параметры имеют рассеяние, так как являются продуктом некоторого технологического процесса, который функционирует с определённой точностью.
С другой стороны, процесс старения связан с широкой вариацией режимов работы и условий эксплуатации изделий. Поэтому зависимости, описывающие процессы старения, становятся функциями случайных аргументов – нагрузок, температур, скоростей и т.д.
Для оценки степени повреждения с учётом вариации начальных свойств можно записать выражение
|
|
(8.8) |
где U0 – случайная величина, оценивающая начальные свойства;
U(t) – случайный процесс старения.
В ряде случаев процесс старения может быть описан в виде элементарной случайной функции
|
|
(8.9) |
где А – случайная величина;
j(t) – математическое ожидание процесса.
Это наиболее простой тип случайной функции, так как здесь случайная природа явления заключена лишь в коэффициенте А. Более полное описание процесса можно представить, выделив стационарный случайный процесс A(t)
|
|
(8.10) |
Данная функция описывает широкий круг процессов. В наиболее общем виде случайную функцию можно представить, используя метод канонического разложения
|
|
(8.11) |
где mg(t) – математическое ожидание функции g(t);
Ai – случайные коэффициенты с математическим ожиданием, равным
нулю;
ji(t) – неслучайные функции (координатные функции).
Это разложение удобно тем, что при линейном преобразовании случайной функции коэффициенты разложения остаются неизменными, а математическое ожидание и координатные функции подвергаются тому же линейному преобразованию.
8.3 Схема формирования параметрического отказа
Структура физико-вероятностной модели параметрического отказа может быть представлена в виде блок-схемы. Этапы такой блок-схемы являются общими для различных по своему характеру и содержанию параметрических отказов.
При эксплуатации системы на неё действуют все виды энергии. Однако процессы старения могут возникать лишь при определённом энергетическом уровне. Если этот уровень не превзойдён, то предпосылки для возникновения отказа будут устранены в самом начале.
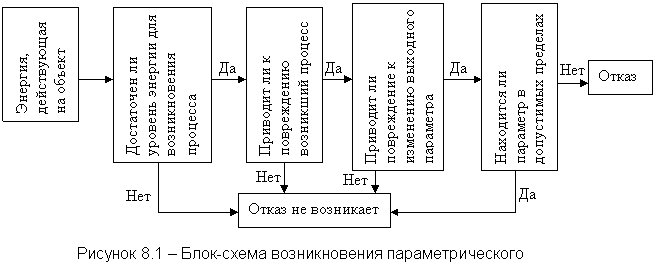
Малая энергетическая нагруженность элементов системы – один из главных путей повышения их безотказности, которая приводит, однако, к увеличению габаритов изделия.
Если же процесс старения возник, то он будет изменять начальные свойства или состояние материалов, из которого выполнена любая система (включая не только элементы и детали, но и смазочные материалы, топливо и т.д.). Под действием различных видов энергии могут появляться и развиваться во времени такие процессы, как деформация, изнашивание, коррозия и другие, которые могут привести к изменению регламентированных характеристик системы, т.е. к её повреждению. Полученное повреждение может влиять или не влиять на выходные параметры системы.
Если данное повреждение не влияет на выходной параметр системы, то отказ не возникает. Например, изменение шероховатости поверхности турбинной лопатки газовой турбины, которое происходит в первые часы её работы, хотя и изменяет начальные контролируемые параметры лопатки, но, как правило, не влияет на мощность, к.п.д. и другие характеристики турбины. Поэтому из-за изменения шероховатости поверхности лопаток отказа турбины не происходит.
Параметрический отказ возникает в том случае, если повреждение приводит к изменению выходного параметра, а значение этого параметра выйдет за установленные пределы.
8.4 Линейная модель параметрического отказа
Часто встречается случай, когда рассеивание выходного параметра Х подчиняется нормальному распределению, а его изменение во времени – линейному закону
|
|
(8.12) |
где а – начальное значение параметра Х;
gх – скорость изменения параметра при эксплуатации системы.
Из этой формулы следует, что срок службы (наработка) до отказа, который определяет время t = T достижения параметром значения X = Xmax, будет
|
|
(8.13) |
Значение Т является функцией двух случайных аргументов а и gх, которые при нормальном законе распределения характеризуются математическим ожиданием (соответственно а0 и gхср) и средним квадратичным отклонением (sа и sх). В этом случае для каждого фиксированного значения t = T параметр X также будет распределён по нормальному закону f(X) с характеристиками:
математическое ожидание –
|
|
(8.14) |
среднее квадратичное отклонение –
|
|
(8.15) |
В этой модели нормальному распределению подчиняются начальное значение параметра а и скорость процесса gх, т.е. разные по размерности величины.
Оценивается именно скорость процесса, потому что она зависит от большого числа факторов, характеризующих режимы и условия работы системы и не связанных с длительностью её эксплуатации. Если рассеивание данной величины является результатом суммирования от воздействия ряда независимых случайных факторов, сравнимых по своему значению, то, согласно центральной предельной теореме теории вероятностей, результирующее распределение будет приближаться к нормальному.
Полученные зависимости для Хср и s определяют область состояний параметра Х в функции времени t и позволяет получить характеристики параметрической надёжности системы.
Вероятность отказа F(t) определяется вероятностью выхода параметра X за пределы Xmax, а вероятность безотказной работы P(t) может быть подсчитана с помощью функции Лапласа Ф(Х) при 0,5 £ Ф £ 1
|
|
(8.16) |
Закон надёжности ![]() не подчиняется в
данном случае нормальному распределению, он асимметричен, находится в области
положительных значений t, а показатель
не подчиняется в
данном случае нормальному распределению, он асимметричен, находится в области
положительных значений t, а показатель
|
|
(8.17) |
является его медианой.
При выделении наибольших возможных значений ан и gн можно подсчитать запас надёжности
|
|
(8.18) |
Запас надёжности уменьшается по мере эксплуатации системы, и гарантированный период безотказной работы Тг может быть подсчитан по (8.18) при условии t = Tг при Кн = 1, откуда
|
|
(8.19) |
(8.16) и полученные из неё формулы (8.18) и (8.19) могут быть использованы для оценки надёжности системы по данному выходному параметру на стадии проектирования или для новой машины до начала её эксплуатации. Для расчёта необходимо определить следующие величины:
Хтах – предельно допустимое значение выходного параметра, которое устанавливается техническими требованиями к системе;
а0 и sа – характеристики распределения начального параметра системы, которые зависят от точности изготовления системы и от возможного их изменения при действии сил, температур, параметров окружающей среды и других факторов, связанных с работой системы. Допустимые значения этих показателей также должны быть установлены техническими требованиями. При наличии опытного образца или новой машины они могут быть определены экспериментально;
gхср и sх – характеристики скорости процесса изменения выходных параметров системы в результате её старения. Их оценка связана с использованием закономерностей, описывающих физику процессов старения, и с расчётом того влияния, которое оказывает данный процесс на выходные параметры.
Если изменение выходного параметра в исследуемом промежутке времени не наблюдается, т.е. gх ® 0, то из (8.16) получим, что
|
|
(8.20) |
т.е. вероятность отказа от времени не зависит. Это значение P(t) оценивает вероятность применения годного или негодного изделия, которое либо будет безотказно работать весь рассматриваемый период эксплуатации, либо параметры нового изделия могут быть за пределами допустимых значений.
Во многих случаях изменение параметра ограничивается двумя пределами Хтах и Xmin. Вероятность безотказной работы системы P(t) в данном случае равна
|
|
(8.21) |
8.5 Нелинейная модель параметрического отказа
Во многих случаях изменение выходного параметра во времени может иметь нелинейный характер (gх ¹ const), что связано в первую очередь с физикой процесса старения. Такие процессы, как коробление корпусных деталей, тепловые деформации, изнашивание в процессе приработки и другие нелинейно зависят от времени.
Ещё большая нелинейность выходного параметра во времени будет в том случае, если это изменение связано с несколькими разнохарактерными процессами старения или с обратимыми процессами.
В общем случае, если известны математическое ожидание выходного параметра Х во времени Mx(t) и его дисперсия Dx(t), то вероятность безотказной работы системы при рассеивании параметра по нормальному закону в данный момент времени t = T может быть определена как
|
|
(8.22) |
Например, если изменение параметра во времени подчиняется экспоненциальному закону (тепловые процессы, коробление изделия)
|
|
(8.23) |
где А – установившееся значение параметра (при t ® ¥) и a – тепловая постоянная узла, зависящая от его конструкции и материалов, тогда математическое ожидание
|
|
(8.24) |
где ![]() – математическое ожидание
параметра А, который имеет рассеивание по нормальному закону.
– математическое ожидание
параметра А, который имеет рассеивание по нормальному закону.
Если среднее квадратичное отклонение параметра sх также изменяется во времени по экспоненциальному закону с параметрами sх и a0, т.е.
|
|
(8.25) |
то вероятность безотказной работы будет
|
|
(8.26) |
8.6 Одновременное проявление постепенных и внезапных отказов
В ряде случаев для изделий существует опасность возникновения как постепенных, так и внезапных отказов. Если они проявляются как независимые события и вероятность безотказной работы для постепенного и внезапного отказов известны (соответственно Рп(t) и Рв(t)), то значение Р(t) для сложного события может быть подсчитано по теореме умножения вероятностей
|
|
(8.27) |
Например, если постепенные отказы подчиняются закону распределения (8.16), а внезапные – экспоненциальному, получим
|
|
(8.28) |
В этом случае в начальный период работы системы основное влияние на Р(t) оказывают внезапные отказы, а затем всё большее значение приобретают постепенные отказы.
9 Структурная надёжность
9.1 Сложные системы
Любая техническая система представляет собой совокупность подсистем и элементов, объединенных вспомогательными технологическими связями. Примером такой системы может служить совокупность всего оборудования электростанции, или на более низком иерархическом уровне системой могут выступать воздушно-газовый тракт, паротурбинная установка с регенерацией тепла, электрогенератор со всей электрической схемой, энергетический реактор вместе с первым контуром и системой защиты.
Для выбора и оптимизации основных параметров устанавливаемого оборудования и расходов рабочих тел разрабатывается, в соответствии с термодинамическими циклами энергетических установок, принципиальная тепловая схема электростанции.
В отличие от принципиальной тепловой схемы, развернутая или функциональная схема содержит все тепловое оборудование электростанции, включая рабочее и резервное, и соединяющие его трубопроводы со всей необходимой арматурой. В развернутую схему включаются трубопроводы, объединяющие различное оборудование в соответствии с последовательностью основного технологического процесса, а также трубопроводы, соединяющие однородное оборудование и служащие для перетока теплоносителя и обеспечения нормальной работы электростанции и резервирования оборудования. Функциональные тепловые схемы электростанции характеризуют надежность осуществления основного технологического процесса для данного оборудования, позволяют определить возможные режимы, объем и последовательность операций включения и выключения теплового оборудования при его пуске, остановке и изменении электрической нагрузки.
По функциональному назначению и влиянию на надежность работы энергоблока или электростанции в целом все элементы и системы функциональной схемы можно разделить на четыре группы.
К первой группе относятся элементы и системы, отказ которых приводит к полному отказу всего блока. Такими элементами являются реактор, парогенератор, турбина, главные паропроводы с их арматурой, конденсатор.
Ко второй группе относятся элементы и системы, отказ которых приводит к частичному отказу энергоблока, т.е. к пропорциональному уменьшению электрической мощности и отпускаемой теплоты. К таким элементам можно отнести тягодутьевые машины, питательные, конденсатные и циркуляционные насосы, котлы в дубль-блочных схемах.
В третью группу включают элементы, отказ которых приводит к понижению экономичности энергоблока без ущерба выработки электрической и тепловой энергии. К этой группе можно отнести ПВД.
К четвертой группе относятся элементы и системы, обеспечивающие предотвращение и локализацию аварий и радиационную безопасность на АЭС. Это оборудование системы циркуляции теплоносителя для отвода остаточного тепловыделения в реакторе после его остановки, оборудование систем управления и аварийной защиты. Так, например, аварийное отключение турбин в одноконтурных схемах АЭС может сопровождаться подъемом давления в контуре теплоносителя, срабатыванием предохранительных клапанов и, как следствие, выбросом радиоактивных веществ в окружающую среду. Резкое снижение мощности блока с реактором типа ВВЭР, например, из-за остановки главного циркуляционного насоса, вызывает не только термическую усталость парогенератора, но и может привести к режиму обратной циркуляции. Все аварийные остановы энергоблоков или резкие снижения мощности приводят к появлению термоусталостных напряжений в оболочках твэлов и их разгерметизации.
С точки зрения надёжности сложная техническая система обладает как отрицательными, так и положительными свойствами.
Факторы, отрицательно влияющие на надёжность сложных систем, следующие.
Большое число узлов, агрегатов, элементов, отказ каждого из которых может привести к отказу всей системы.
Сложные системы часто бывают уникальными или имеются в нескольких экземплярах, и статистические данные не могут быть использованы для оценки их работоспособности. Это усугубляется тем, что даже одинаковые системы могут работать в различных условиях эксплуатации и выполнять неодинаковые функции.
У систем и машин одинакового конструктивного выполнения каждый экземпляр имеет индивидуальные черты. Незначительные вариации свойств отдельных элементов сказываются на выходных параметрах системы. Чем сложнее система, тем большими индивидуальными особенностями она обладает.
Свойства сложных систем, положительно влияющие на надёжность, следующие.
Сложным системам в той или иной мере свойственно саморегулирование или самоприспособление, когда система способна найти наиболее устойчивое для своего функционирования состояние.
Для сложной системы, как правило, возможно восстановление работоспособности по частям, без прекращения её функционирования. Например, на электростанции с параллельными связями при выходе из строя котла или турбины возможно подключение резервного оборудования на время ремонта.
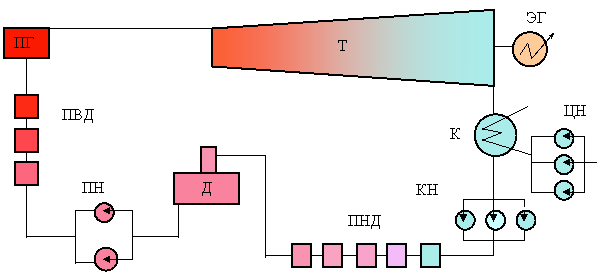 |
||||||
 |
||||||
|
||||||
Не все элементы одинаково влияют на надёжность сложной системы, и можно выделить ограниченное число тех элементов, которые, в основном, определяют её работоспособность.
Уровень надежности системы закладывается на этапе проектирования. На последующих этапах изготовления, сборки, пусконаладочных работ и эксплуатации практически невозможно повысить этот уровень. Выбранная на этапе проектирования структура системы определяет уровень ее надежности и затраты, необходимые для достижения этого уровня. Следовательно, предварительный анализ надежности так же, как и анализ других конструктивных параметров, необходимо проводить на этапе проектирования.
Расчет количественных показателей надежности сложных технических систем, какими являются ТЭС и АЭС, требует составления структурных (логических) схем, которые, в отличие от функциональных, отражают логические, а не физические связи. Структурные схемы позволяют определить такое количество или такую комбинацию отказавших элементов схемы, которые приводят к отказу всей системы. Построение логической схемы показано на рисунке 9.1.
Все элементы, отказ любого из которых приводит к остановке всего блока, соединяются последовательно. К ним на схеме относятся парогенератор, турбина, электрогенератор, конденсатор и деаэратор. Элементы, отказ которых приводит к пропорциональному снижению мощности (выходного эффекта), соединяются параллельно. К ним относятся циркуляционные, конденсатные и питательные насосы, группа подогревателей низкого давления. Хотя подогреватели низкого давления на функциональной схеме соединены последовательно, на структурной схеме они соединяются между собой параллельно, т.к. выход из строя отдельного подогревателя только снижает выходную мощность (если нет перерасхода топлива). Выход всех ПНД в конечном итоге приводит к отказу блока. Подогреватели высокого давления на логической схеме отсутствуют, т.к. их отключение не приводит к отказу блока, а только к перерасходу топлива. Параллельное соединение также называется резервированием. Так как отказ всех элементов, соединенных параллельно, приводит к отказу всего блока, то такие узлы параллельно соединенных элементов к общей цепи подключаются последовательно. Таким образом, любую функциональную схему, отражающую физические и технологические связи между составляющими ее элементами, можно преобразовать в логическую схему с параллельным и последовательным соединением элементов.
Параллельное или последовательное соединение элементов на структурной схеме зависит также от характера их повреждения. Это можно рассмотреть на примере двух масляных фильтров в системе смазки подшипников турбины (рисунок 9.2). Эти фильтры конструктивно могут быть установлены параллельно или последовательно.
Отказ фильтра может произойти в результате засорения сетки или её разрыва.
|
Конструктивная схема |
Структурная схема |
|
|
Засорение сетки |
Разрыв сетки |
|

В случае засорения сетки структурная схема соответствует конструктивной, т.к. параллельное соединение фильтров в этом случае только снизит надёжность системы, а при последовательном соединении отказ любого из фильтров приведёт к отказу системы (необходимый поток масла не будет проходить через фильтр).
При отказе фильтра из-за разрыва сетки структурная схема противоположна конструктивной. При параллельном выполнении отказ любого фильтра будет означать отказ системы, так как при разрыве сетки неочищенный поток масла пойдёт через данный фильтр. Поэтому структурная схема изображена в виде последовательных элементов. При последовательном включении фильтров разрыв сетки одного из них не будет означать отказа, так как дублирующий фильтр продолжает выполнять свои функции. Поэтому структурная схема изображена в виде параллельного соединения.
Точка соединения элементов на структурной схеме называется вершиной. Точки входа и выхода схемы называются полюсами.
9.2 Надежность сложных систем
Структурной надежностью системы называется результирующая надежность системы, вычисленная при условии задания ее структурной схемы и известных значений надежности всех входящих в нее элементов. Так как значение надежности отдельных элементов изменяется в зависимости от режима и условий их работы и во времени, то это необходимо учитывать при расчете надежности всей системы. Однако рассматривать формирование показателей надёжности сложных систем, таких, как, например, тепловая или атомная электростанция, состоящих из механических подсистем и машин, в виде расчленённых структур можно в большинстве случаев весьма условно и, как правило, лишь тогда, когда к их выходным параметрам не предъявляются жёсткие требования, а необходимо обеспечить лишь функционирование отдельных узлов и механических систем.
Чем выше требования к параметрам системы, тем в большей взаимосвязи находятся все её элементы. Разбивать систему на независимые элементы и вести расчёт вероятности безотказной работы расчленённых систем можно для механических подсистем и машин в следующих случаях:
- при рассмотрении больших систем, состоящих из отдельных машин, самостоятельных агрегатов и подсистем (к таким системам относятся ТЭС, АЭС, энергетические системы, технологические комплексы);
- при рассмотрении нескольких независимых выходных параметров подсистемы;
- при анализе надёжности подсистем или машин, состоящих из отдельных агрегатов, особенно в тех случаях, когда их принцип работы и особенности функционирования представляют самостоятельную конструктивную единицу (например, турбина со всеми вспомогательными подсистемами и механизмами).
9.2.1 Последовательное соединение
Последовательным называется такое соединение элементов, при котором отказ хотя бы одного элемента приводит к отказу всей системы. Такое соединение также называется основным. Если у последовательно соединенных элементов значения надежности независимы друг от друга, т.е. выход из строя одного элемента не меняет надежности других, то надежность системы в этом случае определяется как произведение значений надежности отдельных элементов
|
|
(9.1) |
В случае экспоненциального закона распределения ![]() , надежность системы
будет равняться
, надежность системы
будет равняться
|
|
|
или
|
|
(9.2) |
где 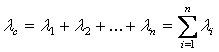 – интенсивность отказа системы равна сумме
интенсивностей отказа ее элементов. Соответствующее значение времени наработки
до отказа
– интенсивность отказа системы равна сумме
интенсивностей отказа ее элементов. Соответствующее значение времени наработки
до отказа
|
|
(9.3) |
По аналогии время восстановления системы при ремонте
|
|
(9.4) |
Если все элементы схемы идентичны, т.е. имеют одно и то же значение надежности, то
|
|
(9.5) |
В том случае когда надежность системы, определенная
как  , имеет
для значений надежности отдельных элементов различные законы распределения,
например, экспоненциальный
, имеет
для значений надежности отдельных элементов различные законы распределения,
например, экспоненциальный
|
|
|
и Вейбулла
|
|
|
то, подставляя значения pi в рс и логарифмируя, получим
|
|
(9.6) |
Для решения обратной задачи, когда задано значение р0с и нужно найти срок службы, отвечающий значениям рс ³ р0с, необходимо вычислить и построить графики функций (рисунок 9.3)
|
|
(9.7) |
Точка пересечения кривых y1 = f1(t) и y2 = f2(t) определит искомое значение t.
9.2.2 Параллельное соединение (резервирование)
Параллельной называется такая система, работоспособность хотя бы одного элемента которой обеспечивает работоспособность всей системы. Параллельное соединение, состоящее из т элементов, надежность каждого из которых не зависит от отказа любого другого, показано на рисунке 9.4.
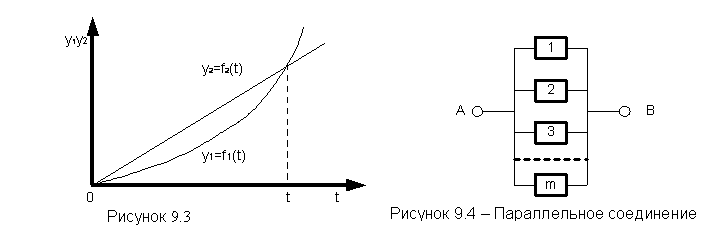
Резервированным соединением элементов называется такое соединение, при котором отказ наступает только после отказа основного элемента и всех резервных элементов. Основным параметром резервирования является его кратность.
Под кратностью резервирования (т – 1) понимается отношение числа резервных элементов к числу резервируемых (основных). Резервирование бывает с целой и дробной кратностью. Обозначение на схеме у них одинаковое, и для их различия на схеме указывается кратность резервирования (т – 1). При резервировании с целой кратностью величина (т – 1) есть целое число, при резервировании с дробной кратностью (т – 1) – дробное несокращаемое число. Например: (т – 1) = 4/2 означает резервирование с дробной кратностью, при котором число резервных элементов равно 4, число основных – 2, а общее число элементов – шести. Сокращать дробь нельзя, т.к. если (т – 1) = 4/2 = 2, то это значит, что имеет место резервирование с целой кратностью, при котором число резервных элементов равно 2, а общее число элементов равно трем.
Рассмотрим случай резервирования с постоянно включенным резервом и с целой кратностью. Расчет надежности такой системы ведется с использованием противоположного показателя – вероятности отказа qi. В этом случае вероятность отказа системы равна
|
|
(9.8) |
Надежность работы такой системы будет противоположной величиной вероятности отказа
|
|
(9.9) |
Если все элементы имеют одинаковую вероятность отказа q1=q2= … =qm, то qc = qm = (1 – p)m и
|
|
(9.10) |
Следует отметить, что если закон надежности элементов подчиняется экспоненциальному закону распределения, то результирующая надежность уже не будет экспоненциальной. Действительно, если
|
|
|
то
|
|
(9.11) |
В случае двух параллельно включенных элементов
|
|
(9.12) |
Если интенсивности отказов этих элементов одинаковы, l1 = l2 = l, то
|
|
(9.13) |
Вероятное (среднее) время безотказной работы такой системы и время восстановления равны
|
|
(9.14) |
Для трех параллельно включенных одинаковых элементов
|
|
(9.15) |
Вероятная наработка до отказа и вероятное время восстановления
|
|
(9.16) |
Вообще, для одинаковых элементов, соединенных параллельно и подчиняющихся экспоненциальному закону распределения,
|
|
(9.17) |
Последовательно-параллельная структура представляет совокупность последовательных подсистем, соединенных параллельно (общее постоянное резервирование с целой кратностью, рисунок 9.5а). Она состоит из т параллельно включенных последовательных цепочек по пj элементов в каждой. Вероятность безотказной работы системы с общим резервированием и целой кратностью составляет
|
|
(9.18) |
В этой формуле  – вероятность безотказной
работы каждой последовательной цепи. Если все элементы одинаковые, то (9.18)
можно упростить следующим образом. Вероятность безотказной работы каждой
последовательной цепочки р¢
= рп, следовательно, q¢ = 1 – pn, а надежность всей системы
– вероятность безотказной
работы каждой последовательной цепи. Если все элементы одинаковые, то (9.18)
можно упростить следующим образом. Вероятность безотказной работы каждой
последовательной цепочки р¢
= рп, следовательно, q¢ = 1 – pn, а надежность всей системы
|
|
|
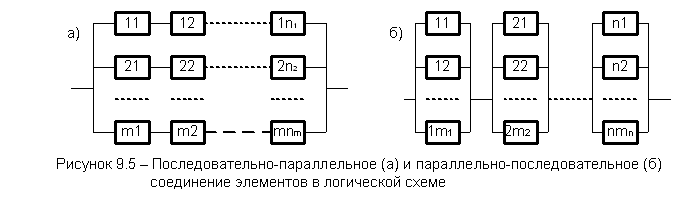
Если т ® ¥, то рс ® 1, т.е. параллельное соединение цепочек из одинаковых элементов увеличивает надежность системы. Если п ® ¥, то рс ® 0, и если п ® ¥ и т ® ¥, то рс ® 0.
Параллельно-последовательная структура представляет собой совокупность параллельных подсистем, соединенных последовательно (раздельное постоянное резервирование с целой кратностью, рисунок 9.5б). В этом случае последовательно соединено п групп из т параллельно соединенных элементов. Вероятность отказа любого блока
|
|
|
а значение надежности этого блока
|
|
|
Результирующая надежность всей схемы
|
|
(9.19) |
В случае, если все элементы одинаковы, формула (9.19) приводится к виду
|
рс = [1 – (1 – р)т]п. |
|
Если т ® ¥, то рс ® 1; если п ® ¥, рс® 0; если т ® ¥ и п ® ¥, то рс ® 1.
В случае общего резервирования с дробной кратностью и постоянно включенным резервом закон надежности и средняя наработка до отказа будут иметь вид
|
|
(9.20)
(9.21) |
где р0(t) – вероятность безотказной работы основного или любого
резервного элемента;
l – общее число основных и резервных систем;
h – число систем, необходимое для нормальной работы
резервированной системы. В данном случае кратность
резервирования m = (l – h)/h.
Пример. Дана система, логическая схема которой показана на рисунке 9.6. Найти вероятность безотказной работы системы при известных вероятностях безотказной работы ее элементов, значения которых указаны на рисунке.
Решение. Система состоит из двух неравнонадёжных устройств (I и II). Устройство I состоит из четырех узлов, устройство II представляет собой нерезервированное устройство, надежность которого известна. Так как оба устройства неравнонадежны, то на основании (9.9) имеем
|
|
|
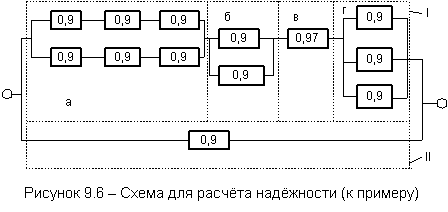
Найдем вероятность ![]() . Вероятность безотказной работы
устройства I равна произведению вероятностей
безотказной работы всех узлов, т.е. рI
= рарбрврг . В узле а
число элементов основной и резервной цепи п = 3, а кратность
резервирования т = 1. Тогда
. Вероятность безотказной работы
устройства I равна произведению вероятностей
безотказной работы всех узлов, т.е. рI
= рарбрврг . В узле а
число элементов основной и резервной цепи п = 3, а кратность
резервирования т = 1. Тогда
|
|
|
В узле б кратность общего резервирования т = 1. Тогда на основании (9.18)
|
|
|
В узле г применено резервирование с дробной кратностью, когда общее число основных и резервных систем = 3, число систем, необходимых для нормальной работы, = 2. Тогда на основании (9.20)
|
|
Вероятность безотказной работы устройства I будет
|
РI = рарбрврг = 0.93×0,99×0,97×0,972 » 0,868. |
|
Тогда вероятность безотказной работы всей системы будет
|
|
|
9.3 Системы с приводимой структурой
К таким системам относятся системы, структура которых может быть получена при помощи следующей регулярной процедуры: рассматривается одиночный двухполюсный элемент, затем элемент заменяется простейшей структурой (последовательной или параллельной). Далее элемент в структуре, полученной на первом шаге, заменяется соответствующей последовательной или параллельной структурой и т.д. В результате через некоторое число шагов может быть получена довольно сложная структура, которая путем соответствующих обратных трансформаций (т.е. путем замены отдельных чисто последовательных или чисто параллельных подсистем в этой системе некоторыми эквивалентными подсистемами) может быть опять сведена к простейшей двухполюсной системе, т.е. к элементу. Такие системы носят название систем с приводимой структурой.
|
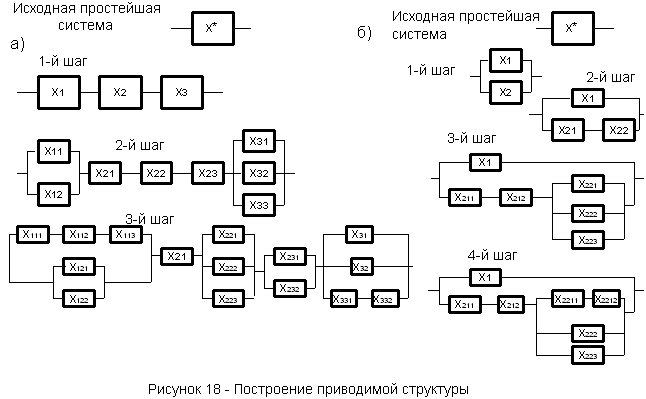
На рисунке 9.7 показан для иллюстрации простой пример возможного построения приводимой структуры, начиная с эквивалентного элемента х*. Исходная система на первом шаге представляется в виде последовательной системы, состоящей в данном случае из трех последовательных элементов х1, х2, х3. Далее элемент х1, например, представляется в виде параллельного соединения двух элементов х11 и х12, т.е. каждому элементу приписывается второй индекс, соответствующий его номеру в подсистеме, которая характеризуется первым индексом. Процедура продолжается, как это показано на рисунке 9.7а. Второй пример возможного построения системы с приведенной структурой показан на рисунке 9.7б.
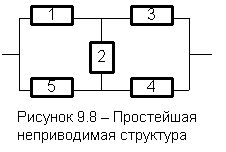 На рисунке 9.8 показан
пример структуры, которая не может быть получена с помощью указанной регулярной
процедуры и которая, в то же время с помощью той же процедуры (но в обратном
порядке) не может быть никак упрощена. Эта схема представляет собой пример
простейшей неприводимой структуры – это так называемая мостиковая
схема. Следует отметить, что для двухполюсной схемы, имеющей менее пяти
элементов, не удается построить ни одной неприводимой структуры. Для схемы из
пяти элементов можно построить всего одну такую структуру. С ростом размерности
схемы доля неприводимых структур в общем числе возможных структур резко
возрастает. Вообще говоря, с ростом числа элементов в логической двухполюсной
схеме доля таких структур стремится к единице.
На рисунке 9.8 показан
пример структуры, которая не может быть получена с помощью указанной регулярной
процедуры и которая, в то же время с помощью той же процедуры (но в обратном
порядке) не может быть никак упрощена. Эта схема представляет собой пример
простейшей неприводимой структуры – это так называемая мостиковая
схема. Следует отметить, что для двухполюсной схемы, имеющей менее пяти
элементов, не удается построить ни одной неприводимой структуры. Для схемы из
пяти элементов можно построить всего одну такую структуру. С ростом размерности
схемы доля неприводимых структур в общем числе возможных структур резко
возрастает. Вообще говоря, с ростом числа элементов в логической двухполюсной
схеме доля таких структур стремится к единице.
Для неприводимых структур не удается построить структурных функций так же просто, как для схем с приводимой структурой. Для неприводимых структур структурную функцию удобно записывать, вводя понятие путей и сечений.
9.4 Связь между стоимостью и надежностью
Если система состоит из п последовательно соединенных элементов, имеющих надежности р1, р2, … , рп, стоимости с1, с2, … , сп, веса Q1, Q2, … , Qп, то результирующая надежность определяется
|
|
|
результирующая стоимость
определится как 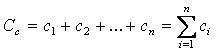 ,
а результирующий вес –
,
а результирующий вес –
|
|
|
Если надежность одного элемента равна р0, а стоимость с0, то для получения требуемой надежности р необходимо параллельное соединение т элементов, при котором
|
1 – р = (1 – ро)т. |
|
Полная стоимость будет
|
|
|
Если в системе имеется п групп, содержащих по т1, т2, … , тп параллельно соединенных элементов, имеющих стоимости со1, со2, … , соп, то общая стоимость будет
|
|
(9.22) |
10 Классификация методов и общие принципы расчета надежности
структурных схем
Количественные методы оценки надежности технических систем можно разбить на два класса:
а) прямые, заключающиеся в непосредственной оценке показателей надежности объекта (ТЭС, АЭС) в результате статистической обработки данных его эксплуатации;
б) косвенные, заключающиеся, например, в оценке показателей надежности объекта, исходя из его структурной схемы и надежности составляющих его элементов.
Очевидно, что первые методы применимы только на этапе эксплуатации объекта. В свою очередь, вторые являются единственно возможными для использования на этапе его проектирования.
Косвенные методы структурной надежности подразделяются на аналитические методы и метод статистического моделирования (Монте-Карло). В энергетике, в частности, ядерной, наибольшее распространение нашли аналитические методы вследствие их оперативности при достаточной точности. Эти методы основаны на изучении функционального назначения объектов, разработке их функционально-структурных схем и моделировании процессов изменения состояний. Для этого структурная схема представляется в виде совокупности элементов с определенными связями и выходным эффектом. Выходным эффектом конденсационных ТЭС и АЭС является располагаемая электрическая мощность, для ТЭЦ – располагаемая электрическая мощность и производительность по отпуску теплоты (технологического пара и горячей воды).
Расчет структурной надежности ТЭС и АЭС включает в себя следующие этапы:
- представление ТЭС и АЭС в виде функционально-структурной схемы с определением взаимосвязей между элементами;
- формирование исходных данных по надежности элементов структурных схем;
- выявление множества состояний системы с разделением их на работоспособные и неработоспособные;
- расчет вероятностей возможных состояний системы;
- определение вероятностных характеристик изменения требуемой мощности или производительности;
- расчет комплексных показателей надежности.
В зависимости от используемого метода расчета надежности состояния сложной системы представляют в виде графов состояний и переходов или в виде функций алгебры и логики. При этом система представляется совокупностью п восстанавливаемых элементов, каждый из которых в любой момент времени может находиться в одном из двух состояний: полной работоспособности и неработоспособности. Состояние системы определяется состояниями ее элементов и может быть представлено вектором X(t) = {x1(t), …, xn(t)}, где xi(t) – двоичная переменная, принимающая значение 1, если элемент работоспособен, и 0, если неработоспособен. Если система состоит из п элементов, то число возможных состояний составит 2п. Состояние полной работоспособности обозначается как X(t) = 1, т.е. X(t) = {1, …, 1}. Состоянию полной неработоспособности всех элементов соответствует X(t) = {0, …, 0}. Система, для которой отказ элементов сопровождается уменьшением ее выходного эффекта, называется системой с монотонной структурой.
Расчеты надежности структурных схем проводятся при условии, что показатели надежности входящих элементов заданы. Если элементы восстанавливаемые, то необходимо иметь два (обычно в дифференциальной форме) показателя: наработку на отказ f(t) и время восстановления g(t). В случае экспоненциальных законов распределения безотказности и восстановления в качестве исходных данных, задаются интенсивности отказа l и восстановления m. Экспоненциальный закон распределения времени безотказной работы f(t) = lе-lt и времени восстановления g(t) = μе-μt элементов задаётся тогда, когда он является таковым в результате статистической обработки эксплуатационных данных. Его можно определить также по средним значениям времени безотказной работы Т0 и времени восстановления Тв. Для невосстанавливаемых элементов под временем восстановления Тв понимается время, необходимое для замены отказавшего элемента. Для элементов схемы, эксплуатация которых осуществляется до назначенного ресурса, должны быть заданы дифференциальные законы распределения наработки и время замены элемента на новый.
В основу аналитических методов расчета надежности энергетических установок положены два подхода. Один из них основан на использовании логических схем (метод дерева отказов и метод минимальных путей и минимальных сечений), а другой – на использовании моделей пространства состояний (метод перебора состояний и марковская модель).
Условием применимости первого подхода является существование логической схемы и независимости отказов элементов. Эти методы позволяют получить только стационарные вероятности работы или отказы системы за длительный период. Кроме того, логические схемы можно построить только для относительно простых систем.
Вторая группа методов расчета надежности основана на вычислении вероятностей и частот состояний, выборе критериев и условий отказа системы. Эти методы требуют более сложного математического аппарата и позволяют получать нестационарные значения показателей надежности. При их использовании законы распределения вероятностей отказов и восстановлений элементов, как правило, принимаются экспоненциальными. Представление элементов в двух состояниях (работа – отказ) в этом случае необязательно.
10.1 Расчет надежности методом минимальных путей и минимальных
сечений
Этот метод применяется только для систем с монотонной структурой, свойства которых формулируются следующим образом:
- система работоспособна, если все элементы работоспособны, т.е. Х(1, …,1) = 1;
- система находится в отказовом состоянии, если все элементы отказали, т.е. Х(0, …, 0) = 0;
- при отказе элемента состояние системы только ухудшается, т.е. Ф(х1, …, хп) ³ Ф(х1¢, …, хп¢), если хi > хi¢.
Путем в структурной схеме называется такое подмножество ее элементов, которое позволяет, переходя от одного элемента к другому через общую им вершину, пройти от одного полюса схемы до другого. Путей в двухполюсной схеме может быть достаточно много, причем путь может включать и петли, т.е. путь может более одного раза проходить через одну и ту же вершину. Один путь имеется только в последовательной системе, причем подмножество элементов, образующих путь, совпадает со всем множеством элементов. В параллельной системе путем является все множество элементов и любое его непустое подмножество.
Минимальным путем двухполюсной структурной схемы называется такое подмножество его элементов, которое позволяет, переходя от одного элемента к другому через общую их вершину, пройти от входного полюса к выходному, но исключение хотя бы одного любого элемента из этого подмножества приводит к тому, что оставшееся подмножество элементов уже не является путем.
Из этого определения следует, что минимальный путь представляет последовательное соединение некоторых элементов структурной схемы, причем крайние элементы этого соединения связаны соответственно с входным и выходным полюсом. В последовательной схеме минимальным путем является множество всех ее элементов, а в параллельной системе каждый минимальный путь состоит только из одного элемента, а число таких минимальных путей равно числу элементов в системе.
Сечением двухполюсной структурной схемы называется такое подмножество ее элементов, удаление которых из схемы разрывает все пути этой схемы. В этом случае, как и в случае с путями, различных сечений в схеме может быть много. Единственное сечение имеется только в параллельной схеме, причем подмножество элементов, образующих это сечение, совпадает со всем множеством элементов схемы. В последовательной схеме сечением является любое подмножество элементов, в том числе и все множество элементов схемы.
Минимальным сечением двухполюсной структурной схемы называется такое подмножество ее элементов, удаление которых из схемы разрывает все пути схемы, но введение хотя бы одного любого из элементов этого подмножества приводит к образованию хотя бы одного пути. Из этого определения следует, что минимальное сечение есть параллельное соединение некоторых элементов схемы. В параллельной системе минимальным сечением является множество всех ее элементов, а в последовательной системе каждое минимальное сечение состоит всего из одного элемента, а число таких минимальных сечений равно числу элементов в системе.
Для примера можно рассмотреть двухполюсную неприводимую мостиковую структурную схему, показанную на рисунке 9.8. Всеми путями этой схемы будут следующие: 13, 54, 124, 523, 134, 543, 153, 154, 524, 123, 1524, 1523, 1234, 5234, 15234. Как видно, некоторые пути включают "висячие" элементы. Например, в 134 висячим элементом является 4, а в 524 – 2. Из всех этих путей минимальными являются 13, 54, 124, 523. Их количество r = 4.
Сечениями мостиковой схемы будут следующие: 15, 34, 124, 152, 523, 153, 154, 543, 134, 234, 1524, 1523, 1534, 1234, 5234, 15234. Согласно определению, минимальными являются сечения 15, 34, 124, 523. Количество их равняется s=4.
Теперь исходную структурную мостиковую схему можно представить в виде параллельной схемы минимальных путей и в виде последовательной схемы минимальных сечений (рисунок 10.1).
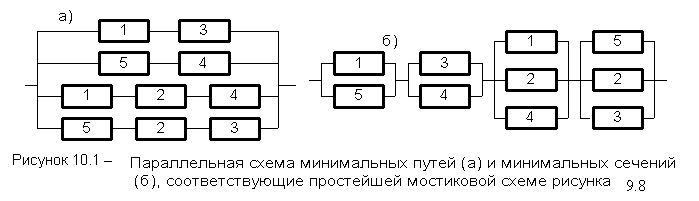
Таким образом, структурная схема рисунка 9.8 приведена к двум структурным схемам – последовательно-параллельной и параллельно-последовательной, которые были рассмотрены ранее.
Из определения пути видно, что связанность двухполюсной структуры обеспечивается наличием хотя бы одного пути (или минимального пути) в схеме. Согласно (9.1), надежность последовательной структуры равна произведению надежностей составляющих ее элементов. Для последовательно-параллельной структуры, к которой относится параллельная схема минимальных путей, при одинаковой надежности элементов справедливо равенство (9.17). В общем случае, когда надежность составляющих элементов различна, вероятность безотказной работы двухполюсной системы можно выразить через вероятность безотказной работы параллельной схемы минимальных путей
|
|
(10.1) |
В этой формуле Е{X(t)} – логическая функция работоспособности системы; nj – количество последовательных элементов в каждом j-м минимальном пути, общее число которых m.
Из определения сечения и минимального сечения следует, что для нарушения связности двухполюсной системы достаточно исключения элементов, принадлежащих хотя бы одному минимальному сечению. Последовательная структура минимальных сечений есть не что иное, как параллельно-последовательное соединение в общем виде (сравните рисунки 9.5б и 10.1б). Вероятность безотказной работы последовательной структуры минимальных сечений может быть выражена в виде
|
|
(10.2) |
В этой формуле количество параллельно включенных элементов в каждом минимальном сечении равно mi, а количество таких сечений равно n (i = 1, …, n). В формулах (10.1), (10.2) знак равенства ставится, когда все минимальные пути и минимальные сечения независимы, т.е. реализуется в чистом виде рассмотренные ранее последовательно-параллельное и параллельно-последовательное соединение. Знак неравенства ставится в том случае, если минимальные пути и минимальные сечения являются зависимыми, т.е. один и тот же элемент может принадлежать нескольким путям или нескольким сечениям. В приведенном примере такими элементами являются 2, который принадлежит 3 и 4 минимальным путям, 1, принадлежащий 1 и 3 путям, 3, принадлежащий 1 и 4 путям, 5, принадлежащий 2 и 4 путям, и 4, принадлежащий 2 и 3 путям, т.е. каждый элемент схемы принадлежит двум путям. То же самое относится к последовательной схеме минимальных сечений, в которой каждый элемент принадлежит двум сечениям.
Таким образом, (10.1) и (10.2) определяют граничные значения вероятности безотказной работы для любой двухполюсной системы, приведенной к параллельной схеме минимальных путей и последовательной схеме минимальных сечений. С помощью этих граничных значений можно сделать интервальную оценку вероятности безотказной работы исследуемой системы:
|
|
(10.3) |
10.2 Метод дерева отказов
10.2.1 Определение метода дерева отказов
Деревом отказов называется логическая графологическая иерархическая схема, представляющая собой связь событий отказа системы с отказами элементов. Вершины дерева представляют логические операции типа "И" и "ИЛИ", обозначающие соответственно произведение и сумму событий. Дерево отказов начинается с конечного события, в качестве которого понимается полный отказ системы. На более низком уровне обозначаются события, которые вызывают конечное событие в соответствии с логической операцией, связывающей эти события. На нижнем уровне располагаются события отказа элементов. Анализ дерева отказов заключается в определении такой комбинации элементов, одновременный отказ которых приводит к вершине дерева – отказу системы. Это множество элементов называется сечением. Минимальное сечение – такое множество, из которого нельзя удалить ни одного элемента, иначе оно перестанет быть сечением. Если анализ дерева отказов начинать от конечного события, то при прохождении через вершину "И" увеличивается число элементов в сечении, а при прохождении через вершину "ИЛИ" – число сечений.
При анализе дерева отказов используются следующие стандартные логические символы:
![]() – событие, включающее
компоненты или системы, вершинное событие, а также все полученные события,
которые дальше разрабатываются при построении дерева отказов;
– событие, включающее
компоненты или системы, вершинное событие, а также все полученные события,
которые дальше разрабатываются при построении дерева отказов;
È, V (ИЛИ) – логическая операция "ИЛИ", определяющая возникновение любого события на данном уровне, расположенном ниже вышестоящего уровня, и заканчивающаяся отказом на вышестоящем уровне;
![]() Ç, Λ
(И) – логическая операция "И", определяющая одновременное
возникновение всех находящихся под этим знаком событий на данном уровне,
расположенном ниже вышестоящего уровня, и заканчивающаяся отказом на
вышестоящем уровне, обводятся прямоугольной рамкой, первичные отказы обводятся
кружком .
Ç, Λ
(И) – логическая операция "И", определяющая одновременное
возникновение всех находящихся под этим знаком событий на данном уровне,
расположенном ниже вышестоящего уровня, и заканчивающаяся отказом на
вышестоящем уровне, обводятся прямоугольной рамкой, первичные отказы обводятся
кружком .
Необходимым условием для построения дерева отказов для элемента или подсистемы является наличие показателей наработки на отказ и времени восстановления работоспособного состояния и возможности только двух состояний: полного отказа или полной работоспособности.
10.2.2 Построение дерева отказов
Последовательная система. Эта система работоспособна, когда работоспособны все ее элементы. Если вместо работоспособности рассматривать отказ, то последовательная система отказывает, если отказывает хотя бы один ее элемент.
Построение дерева отказов начинается с вершинного события, к которому можно отнести полный отказ системы, уменьшение выходного эффекта и т.д. и затем это событие сводится к отказам элементов, т.е. базисным событиям. Логические связи между базисными событиями, которые порождают вершинное событие, отображаются в направленном графе – дереве отказов. Дерево отказов для последовательной системы показано на рисунке 10.2б. Базисные события элементов 1, 2, …, п связаны между собой логическими звеньями "ИЛИ" (V). Менее употребительным является построение деревьев работоспособности. Для примера последовательной схемы дерево работоспособности имеет вид, показанный на рисунке 10.2в. Для получения вершинного события – работоспособности системы, базовые события, т.е. работоспособность элементов, соединяются логическими звеньями "И" (Λ).
|

Параллельная система. Эта система работоспособна, если работоспособен хотя бы один ее элемент. Иными словами, параллельная система отказывает тогда, когда отказывают все ее элементы. Вершинное событие – отказ системы, связан с базовыми событиями – отказами элементов, через логическое звено "И" (Λ) (рисунок 10.3).
|
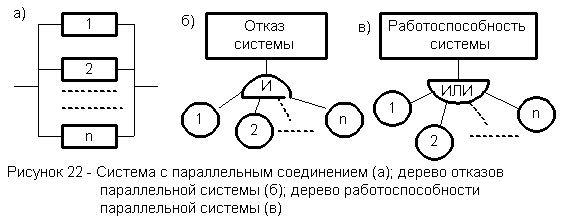
На дереве работоспособности вершинное событие – работоспособность системы, связано с базовым событием – работоспособностью элементов, через логическую операцию "ИЛИ" (V).
Комбинация параллельных и последовательных систем. Обычно используются технические системы, представляющие собой комбинацию двух основных типов соединений – параллельную и последовательную. Однако во многих случаях системы произвольного вида не сводятся к такой комбинации, если они включают в себя неприводимые подсистемы, например, мостиковые схемы. Но для практических целей любую произвольную систему всегда можно свести к комбинации последовательных и параллельных систем. Это возможно в любом случае, если допустить, что один и тот же реально существующий элемент может занимать несколько позиций в схеме расчета надежности. Сведение схемы расчета надежности произвольного вида к комбинации из параллельных и последовательных систем можно осуществить с помощью уже рассмотренного метода минимальных путей и минимальных сечений. Построение дерева отказов для простой комбинации параллельного и последовательного соединения элементов показано на рисунке 10.4.
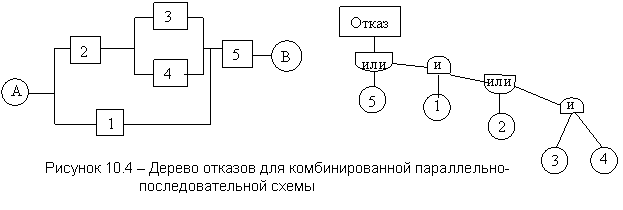 |
При построении дерева отказов исходят из определенного нежелательного события (вершинного события) и анализируют возможные причины его возникновения. При этом необходимо обеспечить разумную степень детализации. Готовое дерево отказов представляет в виде логической диаграммы все последовательности событий, которые могут привести к основному событию.
С помощью метода дерева отказов получают:
- систематизированное представление всех возможных причин вершинного события и их взаимодействие;
- обозримый и доступный для изучения материал анализа причин отказа;
- параметры надежности системы, полученные в результате количественного анализа деревьев.
Построение дерева отказов предполагает детальный анализ процесса функционирования системы. После установления вершинного события исследуется, можно ли представить вершинное событие как отказ одного из элементов системы. Если можно, то такое событие соединяется звеном "ИЛИ". Если это не так, то пытаются свести вершинное событие к таким отказам, которые сами по себе или совместно порождают основное событие.
Необходимо следить, чтобы список причин был полным, так как упущение возможных событий, приводящих к отказам, является основным источником погрешностей при построении дерева отказов.
Установленные события-отказы, как и вершинное событие, подвергаются дальнейшей детализации. Из каждого такого события развивается ветвь дерева. Первичные отказы не подвергаются дальнейшей разработке. Алгоритм построения деревьев отказов показан на рисунке 10.5.
Построение деревьев отказов для сложных технических систем может представлять большие трудности, но такое построение может быть настолько формализовано, что его можно выполнить на ЭВМ.
Пример построения дерева отказов показан на рисунке 10.6. За вершинное событие принимается полный отказ схемы, т.е. невозможность прохождения от одного полюса к другому. К этому приводит отказ элемента 1 или 12. К вершинному событию отказы этих элементов присоединяются через логический оператор ИЛИ. Затем рассматривается возможность отказа системы (вершинного события) при отказе любого элемента в подсистеме I, заключенной

между элементами 1 и 12. Отказ одного любого элемента в этой подсистеме не может привести к вершинному событию. Поэтому из блока 3 рисунка 24 сразу переходим к блоку 6. В подсистеме I к вершинному событию может привести одновременный отказ элемента 11 и оставшейся части подсистемы I. Эти два события через оператор И присоединяются к верхнему оператору ИЛИ и далее проводится анализ подсистемы II, состоящей из элементов 2 – 10. В этой подсистеме к вершинному событию может привести одновременный отказ элементов 2 и 3, которые соединяются между собой логическим оператором И или к одновременному отказу элемента 7 и подсистемы III. Оба события соединяются между собой тоже логическим оператором И. Оба логических оператора И присоединяются к верхнему оператору ИЛИ. Затем идет анализ подсистемы III и далее алгоритм анализа продолжается, пока не будет достигнут самый нижний уровень дерева.
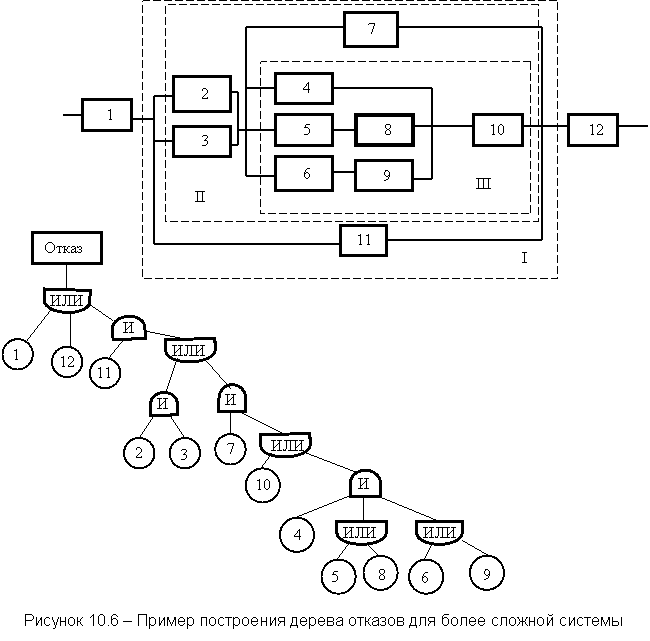 |
11 Марковские процессы
11.1 Определение марковского процесса
Марковские процессы являются наиболее изученным классом случайных процессов и часто используются в практических приложениях. С помощью марковских процессов можно адекватным образом описывать поведение многих реальных физических систем, а с другой стороны, для них хорошо разработан математический аппарат, позволяющий решать многие прикладные задачи.
Марковский процесс
Случайный процесс, протекающий в системе G с дискретными состояниями Х1, Х2, … Хi, …, называется марковским, если для любого момента времени t0 вероятность каждого из состояний системы в будущем (при t > t0) зависит только от её состояния в настоящем (при t = t0) и не зависит от того, когда и как она пришла в это состояние (при t < t0).
Марковские процессы называют также процессами без последействия, так как для них поведение процесса в будущем определяется настоящим состоянием и не зависит от предыстории.
Марковские процессы можно разделить на несколько основных видов: Марковская цепь – дискретный марковский процесс с дискретным временем; Марковская последовательность – непрерывный марковский процесс с дискретным временем; разрывный марковский процесс – дискретный марковский процесс с непрерывным временем; непрерывный марковский процесс – непрерывный марковский процесс с непрерывным временем; дискретный марковский процесс – дискретно-непрерывный марковский процесс. В этом случае при непрерывном изменении времени t случайный марковский процесс G(t) в некоторые моменты времени имеет скачки, а на интервалах времени между скачками ведет себя как непрерывный марковский процесс.
При анализе надежности ТЭС и АЭС их функционирование рассматривается как случайный процесс перехода станции из состояния в состояние, обусловленный отказами и восстановлениями ее составляющих элементов, который при определенных условиях может быть достаточно строго описан дискретным марковским процессом. Отдельную реализацию дискретного марковского процесса можно представить в виде ступенчатой функции. Процесс G(t) может принимать только дискретные значения X1, X2, …, Xn. Смена этих значений – состояний процесса – происходит в некоторые случайные моменты времени tn.
Марковский "процесс гибели". Марковский процесс G(t) = Xi (i = 1, 2, …, k) называется "процессом гибели", если вероятность перехода из состояния Xi в состояние Xi+1 за время t равна lit + o(t), где li > 0, а вероятности всех прочих переходов равны o(t), т.е. имеют более высокие порядки малости, чем t.
Процесс "гибели и размножения". Пусть марковский процесс G(t) может изменять свое состояние, лишь переходя в ближайшие соседние состояния, из Xi в Xi+1 или в Xi–1 при i ³ 2, а из X1 только в X2. Если, во-первых, вероятность того, что за время t осуществиться переход Xi ® Xi+1, равна lit + o(t) (l = const > 0), во-вторых, вероятность перехода Xi ® Xi–1 (при i ³ 2) равна mit + o(t), (mi = const > 0), а вероятности всех прочих переходов имеют более высокие порядки малости, чем t, то процесс G(t) представляет собой "процесс гибели и размножения".
Процесс гибели может быть применен для описания функционирования резервированной системы однотипных невосстанавливаемых элементов, а процесс гибели и размножения – для резервированной системы однотипных восстанавливаемых элементов.
Вероятность перехода между состояниями процесса. Вероятность того, что система за период времени от момента ts до t (t > ts) перейдет из состояния Xi в состояние Xj, можно записать следующим образом
|
pij(ts, t) = P(ts, Xi; t, Xj) = P{G(t) = Xj|G(ts) = Xi}. |
(11.1) |
Это есть условная вероятность того, что система в момент времени t будет находиться в состоянии Xj, если в предшествующий момент времени ts она находилась в состоянии Xi.
Очевидно, что
|
pij(ts,
t)
³ 0.
pij(ts, ts) =
dij = |
(11.2) |
где k – полное число состояний процесса G(t);
dij – символ Кроникера.
11.2 Классификация состояний процесса
Состояние Xi называется несущественным, если из состояния Xi возможен переход в Xj, в то время как возвращение в состояние Xi невозможно. Все остальные состояния называются существенными. Например, для технической системы с невосстанавливаемыми элементами все состояния марковского процесса, описывающего его функционирование, будут несущественными. Если же техническая система состоит из восстанавливаемых элементов, то состояние соответствующего марковского процесса будет существенным.
Существенные состояния Xi и Xj называются сообщающимися, если существуют такие интервалы времени tо и t, что pij (to, to + to) > 0 и pji(to + to, to + to + t) > 0, т.е. вероятности переходов между ними положительны.
Существенные состояния можно разбить на классы так, что состояния, принадлежащие одному классу, будут сообщаться, принадлежащие разным классам – не будут сообщаться. Можно выделить класс поглощающих состояний. Состояние Xi называется поглощающим, если система, попав однажды в это состояние, уже никогда не сможет из него выйти. Для системы, находящейся в поглощающем состоянии Xi в момент времени to: pij (to, t) = 0 для любого j и при любом t > to.
11.3 Свойства марковских процессов
Однородность. Если вероятности переходов марковского процесса G(t) для всех возможных состояний Xi и Xj не зависят от значений ts и t, а зависят лишь от их разности t = t – ts, т.е. pij(ts, t) = pij(t), i, j = 1, 2, …, k, то марковский процесс G(t) называется однородным.
Регулярность. Марковский процесс G(t) с дискретным множеством состояний {Xi, i = 1, 2, …, k} называется регулярным, если:
- его вероятности перехода pij(t, t) удовлетворяют фундаментальному уравнению
|
|
(11.3) |
- для каждого состояния Xi существует предел
|
|
(11.4) |
- для каждой пары состояний Xi и Xj имеется непрерывная по времени плотность вероятности перехода lij(t), определяемая равенством
|
|
(11.5) |
где предел существует равномерно по t, а при фиксированном j – равномерно по i.
С учетом (11.2) можно получить следующее соотношение
|
|
(11.6) |
Из формул (11.4) и (11.5), в частности, следует, что для однородного регулярного марковского процесса величины ci(t) и lij(t) (i, j = 1, 2, …, k) не зависят от времени: ci(t) = ci = const и lij(t) = lij = const.
Ординарность. Процесс называется ординарным, если за малый промежуток времени t невозможно более чем одно изменение состояния процесса. Ординарность означает, что вероятность более чем однократного изменения состояния процесса за малый промежуток времени t есть величина более высокого порядка малости, чем t.
Требование ординарности марковского процесса, описывающего эволюцию технической системы при изменении ее надежности, означает, что за малый промежуток времени t невозможны отказ или восстановление более чем одного элемента технической системы, т.е. вероятность события, заключающегося в появлении двух и более отказов или восстановлений за малый промежуток времени t, имеет более высокий порядок малости, чем t.
Эргодичность. Марковский процесс эргодичен, если для вероятностей переходов из произвольного состояния Xi в любое состояние Xj существуют пределы
|
|
|
Для технической системы, функционирование которой описывается марковским процессом, эргодичность последнего означает, что при больших временах t система переходит в некоторое стационарное состояние, вероятность реализации которого перестает зависеть от времени. При этом вероятности любых переходов pij(t) также перестают зависеть от времени и становятся равными вероятностям реализации стационарных состояний системы P¥j, которые называются финальными вероятностями. Другими словами, за длительный промежуток времени, когда система многократно может переходить из состояния в состояние, вероятность нахождения системы в заданном состоянии (или множестве состояний) перестает зависеть от исходного состояния (при t = 0).
Теорема. Если марковский процесс однородный, имеет лишь конечное число состояний для любых i и j, вероятности pij положительны, то марковский процесс эргодичен.
Теорема доказывается, исходя из вида решения дифференциальных уравнений Колмогорова-Чепмена для вероятностей состояний марковского процесса.
11.4 Вывод уравнений Колмогорова-Чепмена
Система дифференциальных уравнений для вероятностей реализации возможных состояний Pi(t) ординарного дискретного марковского процесса выводится из общих физических соображений. Эта система уравнений представляет собой систему уравнений баланса вероятностей.
Вероятность для процесса перейти из состояния Xi в любое другое возможное состояние за малое время Dt: Q1 = [1 – pii(t, t + Dt)]Pi(t) = ci(t)DtPi(t), где pii(t, t + Dt) – вероятность того, что процесс не изменит своего состояния за время от t до t + Dt. В то же время вероятность того, что процесс попадет в состояние Xi из какого-либо другого состояния за время Dt,
|
|
|
где pji(t, t + Dt) – вероятность того, что система, находясь в момент времени t в состоянии Xj, в момент времени t + Dt окажется в состоянии Xi. Тогда по соображениям баланса можно написать
|
Pi(t + Dt) – Pi(t) = Q2 – Q1. |
|
Переходя к пределу при Dt ® 0, получаем систему дифференциальных уравнений Колмогорова-Чепмена
|
|
(11.7) |
где Pi(t) = P(t; Xi)– вероятность того, что в момент времени t > t0 процесс будет находиться в состоянии Xi. Вероятность Pi(t) удовлетворяет условию нормировки
|
|
(11.8) |
где k – полное число состояний рассматриваемого марковского процесса. Для доказательства этого достаточно сложить уравнения системы (11.7). Соотношение (11.8) является выражением того факта, что с вероятностью, равной единице, процесс находится в каком-то одном из состояний {Xi, i= 1, 2, …, k}.
Ранее были введены величины ci(t) (11.4), lij(t) (11.5). Первая из них представляет собой интенсивность ухода из состояния Xi, а вторая – интенсивность перехода между состояниями Xi и Xj.
Уравнения (11.7) в матричной форме записываются в следующем виде
|
|
(11.9) |
где вектор 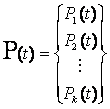 – вектор- столбец, а
матрица
– вектор- столбец, а
матрица ![]() имеет
вид
имеет
вид
|
|
(11.10) |
Из системы
уравнений (11.7) легко получить систему уравнений для вероятностей реализации
состояний "процесса гибели". Если учитывать, что в "процессе
гибели" возможны лишь переходы Xk ® Xk+1, матрица ![]() принимает вид
принимает вид
|
|
|
Отсюда и из соотношения (11.6) следует, что в данном случае систему уравнений (11.7) можно записать в следующей форме
|
|
(11.11) |
Эти уравнения называются системой уравнений "процесса гибели".
Аналогично получаются уравнения "процесса гибели и размножения". Матрица интенсивностей переходов для этого процесса с учетом того, что возможны только переходы Xk ® Xk+1 и Xk ® Xk–1, выглядит следующим образом
|
|
|
Соответственно этой матрице ![]() можно записать систему
уравнений. С учетом соотношения (11.6) система примет вид:
можно записать систему
уравнений. С учетом соотношения (11.6) система примет вид:
|
|
(11.12) |
Эта система уравнений называется уравнениями "процесса гибели и размножения".
Системы уравнений (11.7), (11.11) и (11.12) следует интегрировать при начальных условиях
|
Pi(t0) = P0i, i = 1, 2, …, k, |
(11.13) |
где P0i – заданные вероятности реализации состояний процесса в момент t = t0.
Очевидно, что для "процесса гибели" условия (11.13) вырождаются в
|
P1(t0) = 1, P2(t0) = P3(t0) = … = Pk(t0) = 0. |
(11.14) |
Рассматриваемые системы обыкновенных дифференциальных уравнений (11.7), (11.11) и (11.12) с начальными условиями вида (11.13) представляют собой классическую задачу Коши. Решение задачи Коши на конечном отрезке временной оси [a, b] существует и единственно при непрерывных коэффициентах соответствующих уравнений. В силу линейности этих уравнений данное положение справедливо и для неограниченного промежутка времени.
В приложениях теории надежности коэффициенты уравнений, как правило, определяются линейными комбинациями интенсивностей отказов или восстановлений отдельных элементов рассматриваемой технической системы и являются непрерывными и ограниченными функциями времени. Следовательно, везде в дальнейшем выполняются условия теорем существования и единственности решений соответствующих задач Коши.
11.5 Методы решений уравнений Колмогорова-Чепмена
Методы решений системы уравнений Колмогорова-Чепмена довольно разнообразны. Эти уравнения можно решать как аналитически, так и численными методами. К последним можно отнести метод последовательных приближений, метод Эйлера, метод Рунге-Кутта и др.
К аналитическим методам относится метод исключения, в котором систему уравнений первого порядка сводят к одному уравнению более высокого порядка. Метод исключения накладывает определенные ограничения на коэффициенты уравнений, требуя существования для них k – 1 непрерывных производных.
Метод неопределенных коэффициентов Лагранжа позволяет с помощью нормировки (11.8) исходную систему уравнений свести к системе k – 1 дифференциальных уравнений.
Существуют методы для решения частных случаев системы уравнений Колмогорова-Чепмена, например, для случая "процесса гибели".
На практике часто приходится иметь дело с однородными марковскими процессами. В этом случае коэффициенты дифференциальных уравнений Колмогорова-Чепмена не зависят от времени, т.е. получается система обыкновенных дифференциальных уравнений с постоянными коэффициентами. При решении этих уравнений можно использовать упомянутые выше методы, но в данном случае удобнее использовать метод преобразования Лапласа.
11.5.1 Метод преобразования Лапласа
Преобразование Лапласа сводит проблему решения дифференциальных уравнений к решению алгебраических уравнений. Метод удобен еще и тем, что процедура решения поддается счету на ЭВМ.
При применении преобразования Лапласа исходные интегро-дифференциальные зависимости переводятся в зависимости алгебраические, а исходные функции (оригиналы) – в функции изображения. Для полученных алгебраических уравнений решения находятся в виде функций-изображений. Найденное решение преобразуется обратно в пространство функций-оригиналов.
Преобразованием Лапласа для кусочно-непрерывной функции f(t), определенной при t ³ 0, растущей не быстрее некоторой показательной
| f(t)| < Ceat (a > 0, C > 0), называется интеграл
|
|
(11.15) |
Это преобразование ставит в соответствие каждой функции f(t), для которой несобственный интеграл сходится, единственную функцию j(s) комплексной переменной s = s + iw .
Обратное преобразование Лапласа
|
|
(11.16) |
в каждом открытом интервале t > 0, где f(t) ограничена и непрерывна.
Для преобразования Лапласа справедливы следующие соотношения:
|
|
|
|
|
|
|
|
(11.17) |
|
|
|
где f(0), f¢(0), f¢¢(0), …, fk-1(0) – значения f(t) и ее производных при t = 0.
В таблице 11.1 приведены некоторые функции и соответствующие им изображения, которые могут встретиться при решении уравнений Колмогорова-Чепмена.
Таблица 11.1 – Преобразования Лапласа для некоторых, наиболее часто
встречающихся функций
|
f(t) |
j(s) |
f(t) |
j(s) |
|
d(1) |
1 |
cos (b t) |
|
|
1(t) |
1/s |
|
|
|
f(t) |
j(s) |
f(t) |
j(s) |
|
|
1/(s + a) |
ln t |
(g = 0,57721 – постоян. Эйлера |
|
|
1/(s – a) |
||
|
sin (b t) |
|
|
|
11.6 Стационарные уравнения марковского процесса
Если все состояния марковского процесса сообщающиеся, то за достаточно большой промежуток времени процесс может попасть в каждое из них. Естественно предположить, что вероятности реализации состояний процесса Pi(t) при достаточно большом t перестают зависеть от времени и от начального распределения
|
|
(11.18) |
Величины ![]() называются финальными
вероятностями марковского процесса, а их вычисления – стационарной задачей.
называются финальными
вероятностями марковского процесса, а их вычисления – стационарной задачей.
Для уравнений Колмогорова-Чепмена с постоянными коэффициентами при выполнении условий (11.4) и (11.5) всегда будут существовать финальные вероятности.
Учитывая независимость от времени величин ci и lij, i, j = 1, 2, …, k, и явный вид уравнений (11.7), легко получить уравнения для определения финальных вероятностей Рi¥. Предположим существование предела (11.18) и рассмотрим пределы правой и левой части уравнений (11.7) при t ® ¥
|
|
|
Нетрудно убедиться, что
|
|
(11.19) |
Действительно, если бы предел правой части был больше нуля, то функции Pi(t) при t ® ¥ неограниченно возрастали бы; если же он был бы отрицательным, то они неограниченно убывали бы при t ® ¥, что противоречит условию (11.18), что и доказывает справедливость утверждения (11.19), т.е. существование решения стационарной задачи.
Таким образом, финальные (стационарные) вероятности реализации состояний марковского процесса удовлетворяют следующей системе линейных алгебраических уравнений
|
|
(11.20) |
Условие нормировки (11.8) в данном случае позволяет однозначно разрешить линейно-зависимую систему однородных уравнений (11.20). Система (11.20) просто получается из системы (11.7), если приравнять нулю ее левые части.
Как видно из (11.20) и (11.8), для определения k неизвестных финальных вероятностей имеется k + 1 линейное уравнение. Однако k уравнений (11.20) линейно зависимы. В этом нетрудно убедиться, суммируя левые части и принимая во внимание (11.6). В результате получится тождество. Поэтому k финальных вероятностей следует определять из k – 1 уравнений (11.20) и уравнения (11.8).
Если размерность
системы уравнений (11.20) достаточно велика, то явное выражение Рi¥
можно получить и через главные миноры (k –
1)-го порядка матрицы ![]() . В этом случае система уравнений может
быть записана в виде
. В этом случае система уравнений может
быть записана в виде
|
|
(11.21) |
где аji – алгебраическое дополнение элемента,
находящегося на пересечении i-й строки и j-го столбца матрицы ![]() . Можно показать, что аji = аij.
. Можно показать, что аji = аij.
Тогда, если положить
|
|
(11.22) |
то можно убедиться, что это выражение является решением уравнений (11.20) и (11.8).
11.7 Состояния технических систем и их эволюция
При описании функционирования технической системы с помощью марковского процесса с дискретным множеством состояний и непрерывным временем необходимо определить показатели надежности системы. Эти показатели вычисляются через вероятности состояний технической системы – вероятности состояний марковского процесса, описывающего ее эволюцию во времени. Для вероятности реализации k состояний существует система (11.7) k обыкновенных линейных дифференциальных уравнений первого порядка в общем случае с коэффициентами, зависящими от времени. Иногда вероятности состояний могут быть определены из системы k линейных алгебраических уравнений (11.20).
Таким образом, анализ надежности сводится к решению системы k уравнений, где число уравнений равно количеству рассматриваемых состояний процесса.
11.7.1 Состояния системы и их признаки
Признак состояния – число отказавших элементов. Состояние системы может определяться числом отказавших элементов, составляющих техническую систему. В этом случае один и тот же уровень мощности для электростанции может реализовываться в нескольких различных состояниях. Отдельное состояние технической системы характеризуется т-мерным вектором е = {е1, е2, …, ет}, где т – число единиц оборудования в рассматриваемой технической системе; еi = 1, если i-я единица оборудования работоспособна, и еi = 0, если i-я единица оборудования отказала.
Пусть Е – пространство состояний, задаваемое вектором е.
При таком подходе к определению состояний процесса интенсивности переходов между ними представляют собой величины, кратные интенсивностям отказов или восстановлений отдельных элементов анализируемой системы. Данный метод описания состояний процесса можно применить для технических систем, состоящих из небольшого числа компонентов ввиду сложностей, возникающих при решении больших систем уравнений. Число состояний системы в этом случае равно 2т.
Признак состояния – уровень мощности. В этом случае под состоянием технической системы понимается такое состояние ее оборудования, при котором располагаемая мощность системы Np равняется некоторому фиксированному значению Np = Ni из заданного ограниченного набора {Ni}, i = 1, 2, …, n.
По сравнению с предыдущим подходом в данном случае п – число состояний системы (набор значений располагаемой мощности) намного меньше т – числа состояний системы, соответствующего числу состояний всех ее элементов: п << 2m. Но для определения интенсивностей переходов между состояниями процесса требуется детальное изучение структурно-функциональной схемы рассматриваемой системы, возможных сочетаний отказов и восстановлений и их последствий для различных единиц оборудования. В настоящее время не существует универсальной методики определения интенсивностей переходов между состояниями процесса при таком их определении. Следовательно, данный подход можно использовать только в случае достаточно простых структурно-функциональных схем, когда ясна картина отказов и восстановлений и их последствий для любого сочетания состояний отдельных единиц оборудования
Признак состояния – число отказавших элементов в блоке. Подавляющее большинство технических систем, особенно таких, как ядерные энергетические установки, обладает свойством блочности, заключающимся в наличии среди составляющего оборудования совокупностей (блоков) однотипных элементов. Такие совокупности представляют собой структуры типа т из п. Система типа т из п – это система элементов, неразличимых по их влиянию на надежность системы более высокого уровня иерархии, отказ которой наступает при отказе т элементов из полного числа п.
Свойство блочности дает возможность сократить число состояний пространства Е марковского процесса. Принимая во внимание неразличимость элементов в блоке, можно описывать множество его состояний с помощью дискретной переменной xj, равной числу неработоспособных элементов в j-м блоке. Очевидно, что xj принимает значения 0, 1, 2, …, rj, где rj – число элементов в j-м блоке.
Пусть система состоит из L блоков. Состояние системы, а значит, процесса, описывающего ее функционирование, может быть описано L-мерным вектором
х = (х1, х2, …, хL) = {xj}, j = 1, 2, …, L.
При расчетах надежности блочной системы такая форма записи векторов состояний позволяет процесс функционирования системы рассматривать в пространстве Е*, в котором каждое состояние есть комбинация состояний блоков. В этом пространстве число состояний в общем случае порядка
|
|
(11.23) |
что будет меньше, чем в пространстве Е, где каждое состояние есть комбинация различных состояний отдельных единиц оборудования.
Однако не все
состояния являются достижимыми. В каждом блоке существует максимальное
количество отказавших элементов lj, называемое
критической группой, при котором наступает отказ системы. Таким образом,
недостижимыми будут такие состояния системы ![]() , для которых выполняется условие lj £ xj £ nj.
, для которых выполняется условие lj £ xj £ nj.
Интенсивность переходов между состояниями пространства Е* определяется как некие линейные комбинации интенсивностей отказов и восстановлений отдельных элементов, входящих в различные блоки. Оба пространства Е* и Е могут быть представлены в виде графов состояний.
11.7.2 Графическое представление состояний системы. Граф
состояний
Граф состояний – это графическое представление состояний системы и возможных переходов между состояниями с указанием интенсивностей этих переходов и уровня мощности системы, реализующегося в каждом из состояний. Отдельное состояние изображается точкой, называемой вершиной графа. Вершины соединяются между собой ребрами, изображающими возможные переходы между состояниями. При этом переход (и соответствующее ему ребро) называется прямым, если он порожден отказом отдельного элемента рассматриваемой технической системы, и обратным, если он порожден восстановлением элемента.
Построение графа состояний любой системы начинается с составления полного набора ее состояний или полного набора вершин графа
|
|
|
где k – полное число состояний технической системы (вершин графа);
xij – число отказавших элементов в j-м блоке и в i-м состоянии системы.
Полный набор векторов{Xi} определяется числом возможных сочетаний всех допустимых значений их координат xij, j =1, 2, …, L. Вершины графа можно разделить на три типа, которые соответствуют работоспособным состояниям технической системы; состояниям ее полного отказа, после которых допустимо восстановление работоспособности системы; и, наконец, состояниям полного отказа технической системы, после которых восстановление работоспособности на рассматриваемом промежутке времени невозможно. Эти вершины называются, соответственно, вершинами первого, второго и третьего типов. Вершины третьего типа допускают объединение в одну вершину без потери информации.
Прямые ребра графа состояний строятся в соответствии с отказами элементов рассматриваемой системы, а обратные – в зависимости от применяемой стратегии ее ремонтного обслуживания, в частности, с учетом того, одновременно или в какой определенной последовательности восстанавливаются отказавшие элементы. Выбор определенной стратегии ремонтного обслуживания особенно существенен при построении обратных ребер, выходящих из тех вершин графа состояний, которые определяются состояниями системы с более чем одним отказавшим элементом оборудования. Ребрами соединяются i-я и k-я вершины графа состояний, если для какой-либо компоненты из радиус-векторов Xi и Xk выполняется условие |xij – xkj| = 1 и при этом для всех прочих компонент радиус-векторов Xi и Xk: xil = xkl, l ¹ j. Если xij – xkj = –1, то ребро по отношению к вершине i будет прямым, если же xij – xkj = +1, то по отношению к i-й вершине ребро будет обратным. Максимально возможное число прямых ребер, выходящих из отдельной вершины графа состояний, равно числу блоков L в рассматриваемой системе.
Вершины графа нумеруются в определенном порядке. Нумерация вершин начинается с вершины, соответствующей состоянию, в котором все оборудование технической системы работоспособно. Радиус-вектор этой вершины Хi = {0, 0, …, 0}. Затем нумеруются остальные вершины первого типа, далее, в порядке возрастания, присваиваются номера вершинам второго типа. Множество вершин третьего типа после объединения соответствующих им состояний в одно вырождается в множество, содержащее только одну вершину. Этой вершине присваивается последний номер, например, k. Таким образом, граф состояний системы будет содержать k вершин.
11.8 Интенсивность перехода между состояниями
При составлении системы дифференциальных уравнений Колмогорова-Чепмена очень важно правильное определение коэффициентов уравнений – интенсивности переходов между состояниями lij(t). В пространстве Е* интенсивность переходов lij(t) легко определяется после построения графа состояний марковского процесса, описывающего эволюцию состояний рассматриваемой технической системы. Интенсивность переходов определяется по известным интенсивностям отказов ll и интенсивностям восстановления ml отдельных элементов технической системы.
Интенсивность перехода из состояния с ml работоспособными элементами l-го блока в состояние с ml – 1 работоспособным элементом при одинаковом числе работоспособных элементов во всех прочих блоках равна тlll. Это связано с независимостью отказов каждого из таких элементов. В свою очередь интенсивность переходов из состояния с pl отказавшими элементами l-го блока в состояние с pl –1 отказавшими элементами того же блока, т.е. интенсивность перехода, обусловленного восстановлением отказавшего элемента системы, равна plml, что определяется независимостью восстановления каждого из отказавших элементов.
Пример. Техническая система, изображенная на рисунке 11.1, состоит из двух типов элементов, фильтра и двух насосов, у которых интенсивности отказов равны l1 и l2, а интенсивности восстановлений – m1 и m2 соответственно. Предполагается, что восстановление начинается сразу после отказа элемента и что восстанавливаться может сразу несколько элементов. В соответствии с данными условиями строится граф состояний.
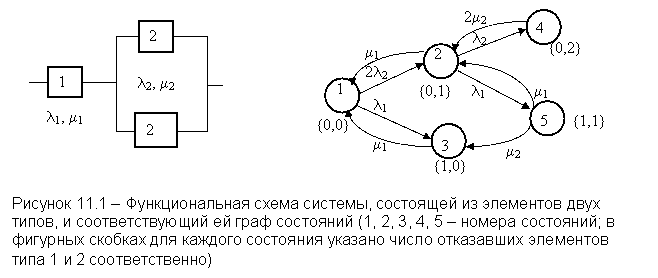
Из состояния 1 с полностью работоспособным оборудованием возможны переходы в состояния 2 и 3, обусловленные отказами соответственно элементов первого и второго типов. Переход 1 ® 2 реализуется при отказе одного из двух элементов второго типа, поэтому интенсивность этого перехода равна 2l2. Переход 1 ® 3 осуществляется при отказе элемента первого типа, и его интенсивность равна просто интенсивности отказа этого элемента. Соответственно определяется интенсивность других прямых переходов. В частности, из состояния 2 возможны переходы при отказах элементов первого и второго типов, это переходы 2 ® 4 и 2 ® 5. Интенсивности этих переходов равны l2 и l1 соответственно.
Обратные переходы. В состоянии 4 оба элемента второго типа неработоспособны. Состояние 4 является отказовым состоянием системы. Из него возможен лишь переход, обусловленный восстановлением одного из двух отказавших элементов – переход в состояние 2. Интенсивность такого перехода в силу одновременности и независимости восстановления отказавших элементов равна 2m2. Из состояния 5 возможны обратные переходы в состояния 2 и 3 при восстановлении соответственно элементов второго и первого типов. Интенсивности этих переходов равны m1 и m2. Из состояния 2 и 3 также возможны переходы, обусловленные восстановлением элементов. Это переходы 2 ® 1 и 3 ® 1. В этих состояниях неработоспособными являются один элемент второго типа и один элемент первого типа. Поэтому интенсивности обратных переходов равны m2 и m1.
11.9 Общий случай
Система состоит из L блоков оборудования, каждый из которых состоит из ni однотипных элементов. После определения радиус-векторов всех вершин графа состояний такой системы и построения прямых и обратных ребер переходят к определению интенсивностей переходов между состояниями. Интенсивность прямого перехода из состояния с номером i в состояние с номером j (если такой переход возможен) будет равна (ni – xil)ll, где ll – интенсивность отказа элемента l-го блока, отказ которого приводит к данному переходу i ® j. Если же такой переход невозможен, то интенсивности lij приписывается нулевое значение. Здесь nl – xil – число работоспособных элементов блока l в i-м состоянии пространства E*. Таким образом, для любого i и j
|
|
(11.24) |
Интенсивность обратного перехода равна интенсивности восстановления соответствующего элемента, умноженной на число отказавших элементов данного типа в рассматриваемом состоянии, т.е. xjlml, при условии, что возможно одновременное проведение восстановительных работ на всех отказавших единицах оборудования. Если же обратный переход невозможен, то интенсивности приписывается нулевое значение. Таким образом, для любых возможных номеров состояний j и i можно записать
|
|
(11.25) |
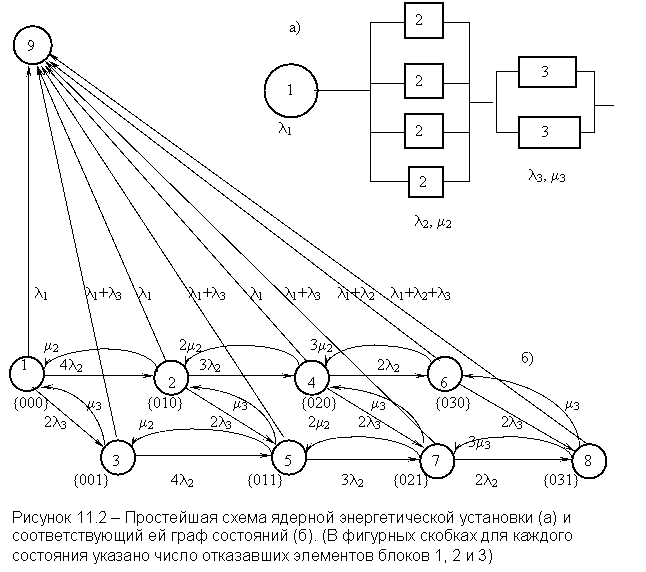
Так определяются интенсивности всех возможных переходов между состояниями марковского процесса, описывающего функционирование технической системы в пространстве Е*, т.е. задаются коэффициенты дифференциальных уравнений Колмогорова-Чепмена.
Пример. На рисунке 11.2 приведен простейшей пример функциональной схемы ЯЭУ и граф состояний марковского процесса, описывающий ее функционирование в фазовом пространстве Е*. Схема состоит из реактора 1, четырех главных циркуляционных насосов (ГЦН) 2 и двух сепараторов 3. При построении графа было принято, что реактор 1 не восстанавливаем на рассматриваемом интервале времени, а ГЦН и сепараторы допускают восстановление при работе ЯЭУ на сниженных по отношению к номинальному
уровню мощности. Полный отказ установки (уменьшение ее мощности до нуля) происходит при отказе реактора или всех ГЦН, или всех сепараторов. На рисунке этому состоянию ЯЭУ соответствует состояние с номером 9. Это поглощающее состояние.
11.10 Пример расчёта показателя надёжности методом,
использующим марковскую модель
|

Решение. Число состояний блока согласно (11.23)
GL = 2×2
= 4. Число достижимых состояний G = 3. Граф состояний приведён на рисунке 25б. Состояние 4
(1,1) является недостижимым. Матрица ![]() для этой системы имеет вид
для этой системы имеет вид
|
|
|
В соответствии с этой матрицей система уравнений Колмогорова-Чепмена принимает вид
|
|
|
|
|
(11.26) |
|
|
|
Условие нормировки записывается в виде
|
|
(11.27) |
Для решения системы дифференциальных уравнений воспользуемся преобразованием Лапласа ((11.15), (11.17) и таблица 11.1). Условие нормировки, прежде чем применить преобразование Лапласа, запишем в дифференциальной форме
|
|
(11.28) |
Последнее уравнение системы заменим на уравнение нормировки. В итоге, после преобразования Лапласа, получим
|
|
(11.29) |
Так как работоспособным является только первое состояние, то необходимо решить систему относительно j1(s) и обратить значение j1(s) по формуле обратного преобразования Лапласа (формула (11.16) и таблица 11.1). Решение системы (11.29) относительно j1(s) по правилу Крамера принимает вид
|
|
(11.30) |
Определим корни знаменателя
|
|
Подставляя значения
|
|
в (11.30) и проведя вычисления, получим s1 = – 0,01019; s2 = – 0,01261; s3 = 0.
Выражение для j1(s) имеет вид
|
|
|
Разложим его на простые дроби
|
|
(11.31) |
Приводя к общему знаменателю среднюю часть этого равенства и складывая, получим
|
|
(11.32) |
Для нахождения неизвестных коэффициентов А, В и С сравним коэффициенты при одинаковых степенях s в числителях средней и правой части (11.32) и составим систему алгебраических уравнений
|
|
(11.33) |
Отсюда сразу находим 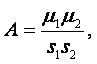 а система (11.33) принимает вид
а система (11.33) принимает вид
|
|
|
Решая совместно эти два уравнения, получим неизвестные коэффициенты
|
|
|
Делая обратное преобразование Лапласа для выражения (11.31), получим
|
|
(11.34) |
Подставляя сюда найденные выражения для коэффициентов А, В и С и проведя соответствующие преобразования, получаем окончательное выражение для вероятности безотказной работы заданной системы в зависимости от времени
|
|
(11.35) |
Из полученного решения следует, что при t = 0 P1(t) = 1, а при 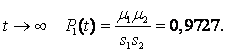
Для определения стационарного значения вероятности безотказной работы система алгебраических уравнений имеет вид (из (11.26) и (11.27))
|
|
|
Решение этой системы по правилу Крамера будет
|
|
|
Подставляя исходные данные, получаем Р1 = 0,9727, что согласуется с Р1(t) при t ® ¥, т.е. стационарный коэффициент готовности
|
|
|
Решение для системы (11.26), (11.27) показано на рисунке 11.4.
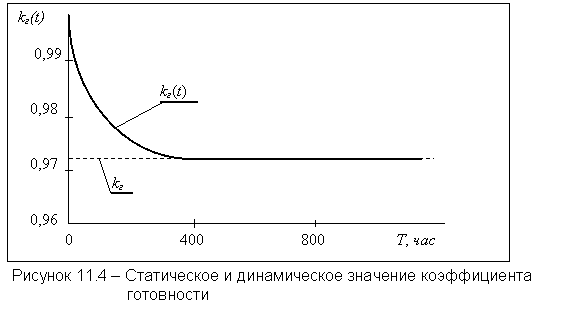 |
11.11 Общий порядок вычисления показателей надежности
Использование марковских процессов для оценки надежности технических систем позволяет получать все показатели надежности в виде функций времени. В такой форме показатели более информативны и удобны в инженерных приложениях, чем отдельные значения показателей в некоторые фиксированные моменты времени.
Ниже приводится общий порядок вычисления показателей надежности сложной технической системы в рамках марковской модели.
Анализ системы. Анализ надежности любой системы начинается с построения на основе инженерного анализа структурно-функциональной схемы системы и выбора способа описания пространства ее состояния.
Построение графа состояний. Затем строится
граф состояний марковского процесса, описывающий эволюцию рассматриваемой
системы и в нем все состояния разбиваются на два класса: работоспособные и
неработоспособные. После построения графа состояний и определения
интенсивностей всех возможных переходов, выписывается матрица ![]() . В ней выделяются
блоки, соответствующие работоспособным состояниям, отказовым состояниям, из
которых возможно восстановление работоспособности системы на интервале времени
[0, T], и, наконец, отказовым состояниям, из которых
невозможно восстановление работоспособности на интервале [0, T].
Последние состояния могут быть объединены в одно. Чтобы выделить такие блоки,
необходимо разумно пронумеровать вершины графа. Для этого сначала нумеруются
работоспособные состояния, затем отказовые состояния, из которых возможно
восстановление работоспособности и в последнюю очередь – отказовые состояния,
из которых невозможно восстановление работоспособности
. В ней выделяются
блоки, соответствующие работоспособным состояниям, отказовым состояниям, из
которых возможно восстановление работоспособности системы на интервале времени
[0, T], и, наконец, отказовым состояниям, из которых
невозможно восстановление работоспособности на интервале [0, T].
Последние состояния могут быть объединены в одно. Чтобы выделить такие блоки,
необходимо разумно пронумеровать вершины графа. Для этого сначала нумеруются
работоспособные состояния, затем отказовые состояния, из которых возможно
восстановление работоспособности и в последнюю очередь – отказовые состояния,
из которых невозможно восстановление работоспособности
Определение вероятностей состояния. После
определения матрицы ![]() составляется
и решается система дифференциальных уравнений Колмогорова-Чепмена. Решение
системы дифференциальных уравнений дает вероятности реализации всех возможных
состояний системы в виде функции времени Pi(t). Знание этих вероятностей и матрицы
составляется
и решается система дифференциальных уравнений Колмогорова-Чепмена. Решение
системы дифференциальных уравнений дает вероятности реализации всех возможных
состояний системы в виде функции времени Pi(t). Знание этих вероятностей и матрицы ![]() является достаточным
для определения основных показателей надежности технической системы.
является достаточным
для определения основных показателей надежности технической системы.
12 Расчет комплексных показателей надежности
В каждый фиксированный момент времени техническая система может находиться лишь в каком-то одном состоянии. Это говорит о несовместимости событий нахождения системы в i-м состоянии в момент времени t.
Коэффициент готовности Kг(t) есть вероятность того, что в момент времени t техническая система работоспособна. В соответствии с этим определением можно записать
|
|
(12.1) |
где Рi(t) – вероятность i-го состояния в момент времени t;
S+ – множество работоспособных состояний.
Выбирая произвольные моменты времени t и используя соотношение (12.1), можно определить Kг(t) в виде функции времени для всего рассматриваемого временного диапазона.
Параметр потока отказов – среднее число отказов (переходов в отказовое состояние) в единицу времени. Этот показатель может быть рассчитан по формуле
|
|
(12.2) |
где S– – множество отказовых состояний системы.
Каждое слагаемое такой двойной суммы lij(t)Pi(t) представляет собой среднее число переходов из работоспособного состояния Xi в неработоспособное состояние Xj в единицу времени около момента времени t. Такое среднее число переходов определяется как произведение вероятности того, что в момент времени t реализуется состояние Xi, на интенсивность перехода из этого состояния в отказовое состояние Xj. Рассматривая все возможные переходы из работоспособного состояния в отказовые, определяется параметр потока отказов технической системы.
Полученный параметр потока отказов W(t) отнесен к времени эксплуатации, включающему периоды работы системы и периоды восстановления ее работоспособности после отказов. Время эксплуатации не включает в себя плановые простои системы.
Наряду с этим параметром можно рассматривать параметр потока отказов, отнесенный к чистому времени работы технической системы Wo(t). В случае независимости от времени обоих параметров W(t) = W и Wo(t) = Wo они связаны между собой простой зависимостью
|
W = WoKг и Wo = W/Kг . |
|
Средняя наработка технической системы на отказ представляет собой отношение суммарной наработки системы за время эксплуатации к математическому ожиданию числа ее отказов. Отсюда,
|
|
(12.3) |
Действительно, 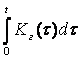 представляет собой время на периоде
эксплуатации от 0 до t, в течение которого
система находилась во множестве работоспособных состояний, а
представляет собой время на периоде
эксплуатации от 0 до t, в течение которого
система находилась во множестве работоспособных состояний, а 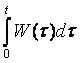 – среднее число
отказов системы за время [0, t].
– среднее число
отказов системы за время [0, t].
Среднее время восстановления технической системы может быть вычислено по формуле
|
|
(12.4) |
Здесь  – время в интервале от 0 до t, в течение которого система находится в
неработоспособном состоянии. При достаточно большом времени эксплуатации можно
считать, что среднее число восстановлений равно среднему числу отказов. Поэтому
среднее время восстановлений системы, равное времени пребывания системы в
отказовом состоянии, отнесенному к среднему числу восстановлений после отказов,
может быть рассчитано по формуле (12.4).
– время в интервале от 0 до t, в течение которого система находится в
неработоспособном состоянии. При достаточно большом времени эксплуатации можно
считать, что среднее число восстановлений равно среднему числу отказов. Поэтому
среднее время восстановлений системы, равное времени пребывания системы в
отказовом состоянии, отнесенному к среднему числу восстановлений после отказов,
может быть рассчитано по формуле (12.4).
Если рассматриваемая система состоит только из невосстанавливаемых элементов, то тот факт, что в момент времени t система работоспособна, равносилен тому, что до этого момента отказов не было. Поэтому вероятность безотказной работы в данном случае будет совпадать с коэффициентом готовности R(t) = Kг(t) и может быть рассчитана по формуле (12.1).
Если же в составе системы есть оборудование, которое
может быть восстановлено на рассматриваемом периоде времени [0, T], то для определения вероятности безотказной работы системы
R(t) требуются
дополнительные расчеты. С этой целью все неработоспособные состояния
рассматриваются как поглощающие, для чего приравниваются нулю все интенсивности
переходов из состояний, принадлежащих множеству S–
. При проведении этой операции получается новая матрица ![]() меньшей размерности по
сравнению с матрицей
меньшей размерности по
сравнению с матрицей ![]() .
Уменьшение размерности достигается за счет объединения всех отказовых состояний
в одно. Решая затем систему дифференциальных уравнений (11.20) с матрицей
.
Уменьшение размерности достигается за счет объединения всех отказовых состояний
в одно. Решая затем систему дифференциальных уравнений (11.20) с матрицей ![]() , получаем вероятности
реализации работоспособных состояний Pi(t), i = 1, 2, …, NR – 1, и вероятность отказового состояния PNR(t).
Очевидно, что искомая вероятность безотказной работы системы R(t) будет равна
, получаем вероятности
реализации работоспособных состояний Pi(t), i = 1, 2, …, NR – 1, и вероятность отказового состояния PNR(t).
Очевидно, что искомая вероятность безотказной работы системы R(t) будет равна
|
|
(12.5) |
Итак, для определения показателей надежности в виде функций времени необходимо найти решение системы дифференциальных уравнений Колмогорова-Чепмена, а затем на их основе по формулам (12.1)-(12.5) определить искомые показатели.
Если системы дифференциальных уравнений оказываются слишком большими и очевидно, что их решение займет слишком много времени, то используют упрощающие приемы, например, метод декомпозиции – разбиение системы на части, вычисления для них показателей надежности и уже на их основе показателей надежности системы в целом.
Приложение А
Основные понятия и определения
Безопасность (Safety) – свойство объекта не допускать ситуаций, опасных для объекта и окружающей среды.
Безотказность (Reliability; Failure-free operation) – свойство объекта непрерывно сохранять работоспособное состояние в течение некоторого времени или наработки.
Внезапный отказ (Sudden failure) – отказ, характеризующийся скачкообразным изменением значений одного или нескольких параметров объекта.
Долговечность (Durability; longevity) – свойство объекта сохранять работоспособное состояние до наступления предельного состояния при установленной системе технического обслуживания и ремонта.
Живучесть (Resistibility) – свойство объекта противостоять крупным возмущениям, исключающее процесс развития аварий и поломку оборудования, или сохранять ограниченную работоспособность при наличии дефектов или повреждений определённого вида, а также при отказе некоторых компонентов.
Избыточность (Redundancy) – превышение веса, габаритов либо стоимости объекта по сравнению с минимально необходимыми для заданных параметров и структуры, связанных с обеспечением заданной надёжности.
Исправность (Good state) – состояние объекта, при котором он соответствует всем требованиям нормативно-технической и/или проектной документации.
Качество (Quality) – совокупность свойств, определяющих степень пригодности объекта для его использования по назначению.
Критерий отказа (Failure criterion) – признак или совокупность признаков нарушения работоспособного состояния объекта, установленные в нормативно-технической и/или проектной документации.
Критичность отказа (Failure criticality) – совокупность признаков, характеризующих последствия отказа.
Надёжность (Reliability; dependability) – свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность, выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонта, хранения и транспортировки.
Надёжность АЭС (ТЭС) – свойство АЭС (ТЭС) сохранять во времени способность вырабатывать электрическую и/или тепловую энергию определенных параметров по требуемому графику нагрузки в допустимых для нормальной эксплуатации радиационных (пылегазовых) условиях при заданной системе технического обслуживания и ремонта оборудования.
Неисправность (Fault; faulty state) – состояние объекта, при котором он не соответствует хотя бы одному из требований нормативно-технической и/или проектной документации.
Неработоспособность (Down state) – состояние объекта, при котором значение хотя бы одного параметра, характеризующего способность выполнять заданные функции, не соответствует требованиям нормативно-технической и/или проектной документации.
Неремонтируемый объект (Nonrepairable item) – объект, ремонт которого невозможен или не предусмотрен нормативно-технической, ремонтной и/или проектной документацией.
Отказ (Failure) – событие, заключающееся в нарушении работоспособного состояния объекта.
Параметрическая надёжность (Parametric reliability) – надёжность, связанная не с отказом функционирования объекта, а с изменением его выходных параметров.
Последствия отказа (Failure effect) – явления, процессы, события и состояния, обусловленные возникновением отказа объекта.
Постепенный отказ (Gradual failure) – отказ, возникающий в результате постепенного изменения значений одного или нескольких параметров объекта.
Предельное состояние (Limiting state) – состояние объекта, при котором его дальнейшая эксплуатация недопустима или нецелесообразна, либо восстановление его работоспособного состояния невозможно или нецелесообразно.
Причина отказа (Failure cause) – явления, процессы, события и состояния, вызывающие возникновение отказа объекта.
Работоспособность (Up state) – состояние объекта, при котором значения всех параметров, характеризующих способность выполнять заданные функции, соответствует требованиям нормативно-технической и конструкторской документации.
Ремонт (Repair) – восстановление утраченной объектом работоспособности путём замены или реновации (обновления) повреждённых элементов конструкции.
Ремонтируемый объект (Repairable item) – объект, ремонт которого возможен и предусмотрен нормативно-технической, ремонтной и/или проектной документацией.
Ремонтопригодность (Maintainability) – свойство объекта, заключающееся в приспособленности к поддержанию и восстановлению работоспособного состояния путём технического обслуживания и ремонта.
Ресурс (Useful life; life) – суммарная наработка объекта от начала его эксплуатации или её возобновления после ремонта до перехода в предельное состояние.
Сохранность (Storability) – свойство объекта сохранять в заданных пределах значения параметров, характеризующих способности объекта выполнять требуемые функции, в течение и после хранения и/или транспортирования.
Срок службы (Useful lifetime; lifetime) – календарная продолжительность эксплуатации от начала эксплуатации объекта или её возобновления после ремонта до перехода в предельное состояние.
Приложение Б
Основные показатели надёжности
Таблица Б1
|
Обозначение |
Показатель |
Определение |
Область применения |
|
P(t) |
Вероятность безотказной работы |
Вероятность того, что в пределах заданной наработки или времени работы отказ объекта не возникает |
Основной показатель для оценки надёжной работы изделия |
|
Tg |
Гамма-процентный ресурс, ч |
Наработка (срок службы) до отказа при заданной вероятности безотказной работы g, выраженной в процентах. |
Допустимая продолжительность работы изделия при заданных требованиях к его безотказности |
|
Tm |
Средний ресурс, ч |
Гамма-процентный ресурс при g = 50 % |
Для характеристики средней продолжительности работы изделия |
|
Tp(Tсл) |
Установленный ресурс (срок службы) |
Установленная продолжительность работы изделия до ремонта или технического обслуживания. Тр = Тк – ресурс до капитального ремонта |
Для назначения параметров системы ремонта и технического обслуживания |
|
Кн |
Запас надёжности |
Отношение предельно допустимого значения заданного параметра к его экстремальному фактическому значению при данном состоянии объекта |
Для изделий с высокими требованиями к надёжности |
|
Tr |
Гарантированный период безотказной работы |
Наработка (время работы), в течение которой обеспечивается значение Кп³1 |
Для характеристики безотказной и безопасной работы изделия |
|
|
Параметр потока отказов, 1/ч |
Среднее число отказов изделия в единицу времени, Тср наработка на отказ |
Для изделий, допускающих отказы данного вида в период функционирования |
|
l |
Интенсивность отказов, 1/ч |
Условная плотность вероятности возникновения отказа объекта, которая определяется для рассматриваемого момента времени при условии, что до этого момента времени отказ не возник |
Может применяться вместо показателя Р(t), особенно если l = const |
продолжение таблицы Б1
|
Tn |
Ресурс (срок службы) до предельного состояния, ч |
Установленная продолжительность работы объекта до предельного состояния |
Использование объекта по назначению в течение Тп допустимо и целесообразно |
|
Кти |
Коэффициент технического использования |
Отношение времени выполнения объектом своих функций к сумме этого времени и времени его нахождения в ремонте или техническом обслуживании за весь период эксплуатации |
Характеризует затраты времени, необходимые для восстановления утраченной работоспособности |
|
Kг |
Коэффициент готовности |
Вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается |
Оценивает безотказную работу изделия в периоды его функционирования (между ремонтами и ТО) |
|
Xmax |
Предельно допустимое значение выходного параметра |
Граница области работоспособности, при выходе за пределы которой происходит отказ |
Для фиксации параметрических отказов |
Приложение В
Характеристики основных законов распределения
Таблица В1
|
Обозначение |
Аналитическое выражение закона |
||
|
Экспоненциаль-ный |
Вейбулла |
Гамма-распределение |
|
|
F(t) |
|
|
|
|
f(t) |
|
|
|
|
l(t) |
l |
|
|
|
M(Т) |
1/l |
|
a¤l |
|
D(Т) |
1/l2 |
|
a¤l2 |
|
u |
1 |
|
|
|
Tg |
– (ln g)/l |
|
|
|
Me(Т) |
0,7/l |
|
|
|
Мo(Т) |
0 |
|
|
Закон надежности объекта |
|||
|
Р(t) |
exp(-lt) |
|
|
продолжение таблицы В1
|
Обозначе-ние |
Аналитическое выражение закона |
|||
Нормальный |
Усеченный нормальный |
Логарифмически нормальный |
||
|
F(t) |
|
|
|
|
|
f(t) |
|
|
|
|
|
l(t) |
|
|
|
|
|
M(Т) |
m |
|
|
|
|
D(Т) |
s2
|
|
|
|
|
u |
s¤m
|
|
|
|
|
Tg |
|
|
|
|
|
Me(Т) |
m |
|
|
|
|
Мo(Т) |
m |
m - при усечении левее моды исходного нормального закона; 0 – при усечении по моде или правее моды исходного закона |
|
|
Закон надежности объекта |
||||
|
Р(t) |
при m > 3 |
|
|
|
Список литературы
1. Соколов А.И. Эксплуатационная надёжность и безопасность ТЭС и АЭС. – Алматы: АИЭС, 2003. – 85 с.
2. Соколов А.И. Эксплуатационная надёжность и безопасность ТЭС и АЭС. Учебное пособие. – Алматы: АИЭС, 2006. – 106 с.
3. Гмурман В.Е. Теория вероятности и математическая статистика. – М.: Высшая школа, 1998. – 368 с.*)
4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 1979. – 400 с.*)
5. Кремер Н.Ш. Теория вероятностей и математическая статистика. – М.: ЮНИТИ-ДАНА, 2000. – 544 с.*)
6. Шостак Р.Я. Операционное исчисление. – М.: Высшая школа, 1972. – 280 с.*)
7. Проников А.С. Параметрическая надёжность машин. – М.: Издательство МГТУ имени Н.Э. Баумана, 2002. – 560 с.
8. Надежность теплоэнергетического оборудования ТЭС и АЭС / Под ред. д-ра. техн. наук., проф. А.И. Андрющенко. – М.: Высшая школа, 1991. – 304 с.
9. Руденко Ю.Н., Ушаков И.А. Надежность систем энергетики. – Новосибирск: Наука, Сибирское отд., 1989. – 328 с.
10. Клемин А.И. Надежность ядерных энергетических установок. Основы расчета. – М.: Энергоатомиздат, 1987. – 344 с.
11. Клемин А.И., Емельянов В.С., Морозов В.Б. Расчет надежности ядерных энергетических установок. Марковская модель. – М.: Энергоиздат, 1982. – 208 с..
12. Райншке К., Ушаков И.А. Оценка надежности систем с использованием графов. – М.: Радио и связь, 1988. – 206 с.
13. Певзнер Л.Д. Введение в теорию надежности. – М.: Московский горный институт, 1970. – 112 с.
14. Сотсков Б.С. Основы теории и расчета надежности. – М.: МАИ, 1966. – 126 с.
15. Соколов А.И. Эксплуатационная надежность ТЭС: Метод. указания и задания для расчетно-графических работ. - Алматы: АИЭС, 2009. – 21 с.
16. Сборник задач по теории надежности. / Под ред. А.М. Половко и И.М. Маликова. – М.: Советское радио, 1972. – 408 с.
Примечание – Кроме книг, отмеченных *), можно пользоваться любыми учебниками и задачниками по теории вероятностей, математической статистике и операционному исчислению.
Содержание
|
Введение |
3 |
|
1 Надёжность и общечеловеческие проблемы |
5 |
|
2 Основные определения, используемые в теории надежности |
6 |
|
2.1 Понятие надёжности |
6 |
|
2.2 Составные свойства понятия надежности |
11 |
|
2.3 Классификация отказов и области возможных состояний ТЭС |
15 |
|
3 Управление надёжностью |
21 |
|
4 Основные теоремы теории вероятностей |
24 |
|
4.1 Дифференциальная, интегральная и условная плотности распределения и их характеристики |
27 |
|
5 О математических моделях |
32 |
|
5.1 Математические модели описания поведения технических систем |
32 |
|
5.2 Временные характеристики отказов |
34 |
|
6 Законы распределения случайных величин |
36 |
|
6.1 Экспоненциальный закон распределения вероятностей |
36 |
|
6.2 Распределение Вейбулла |
37 |
|
6.3 Нормальный закон распределения |
38 |
|
6.4 Закон гамма распределения |
40 |
|
6.5 Законы распределения дискретных случайных величин |
41 |
|
7 Классификация и характеристики показателей надежности |
41 |
|
7.1 Единичные показатели надежности |
42 |
|
7.2 Комплексные показатели надежности |
53 |
|
7.3 Общая модель изменения работоспособности изделия |
58 |
|
8 Параметрическая надёжность |
61 |
|
8.1 Классификация процессов старения |
61 |
|
8.2 Методы оценки износа |
63 |
|
8.3 Схема формирования параметрического отказа |
66 |
|
8.4 Линейная модель параметрического отказа |
67 |
|
8.5 Нелинейная модель параметрического отказа |
70 |
|
8.6 Одновременное проявление постепенных и внезапных отказов |
71 |
|
9 Структурная надёжность |
71 |
|
9.1 Сложные системы |
71 |
|
9.2 Надежность сложных систем |
75 |
|
9.3 Системы с приводимой структурой |
80 |
|
9.4 Связь между стоимостью и надежностью |
83 |
|
10 Классификация методов и общие принципы расчета надежности структурных схем |
84 |
|
10.1 Расчет надежности методом минимальных путей и минимальных сечений |
86 |
|
10.2 Метод дерева отказов |
88 |
|
11 Марковские процессы |
93 |
|
11.1 Определение марковского процесса |
93 |
|
11.2 Классификация состояний процесса |
95 |
|
11.3 Свойства марковских процессов |
96 |
|
11.4 Вывод уравнений Колмогорова-Чепмена |
97 |
|
11.5 Методы решения уравнений Колмогорова-Чепмена |
100 |
|
11.6 Стационарные уравнения марковского процесса |
102 |
|
11.7 Состояния технических систем и их эволюция |
103 |
|
11.8 Интенсивность перехода между состояниями |
107 |
|
11.9 Общий случай |
108 |
|
11.10 Пример расчёта показателя надёжности методом, использующим Марковскую модель |
110 |
|
11.11 Общий порядок вычисления показателей надёжности |
114 |
|
12 Расчёт комплексных показателей надёжности |
114 |
|
Приложение А |
118 |
|
Приложение Б |
120 |
|
Приложение В |
122 |
|
Список литературы |
124 |
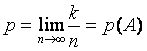
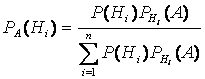 (
( ,
, .
.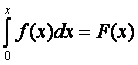 ,
,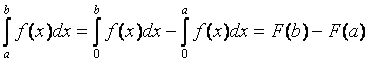 ,
,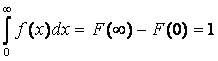 .
. .
. ,
,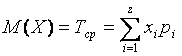 ,
,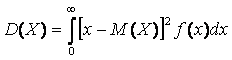
 .
.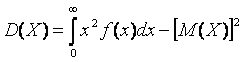 .
.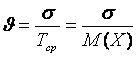 .
.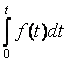
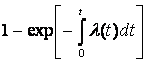
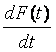
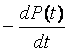
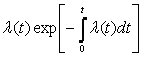
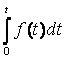
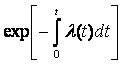
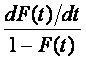
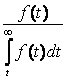
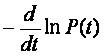
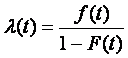 .
. ,
, ,
,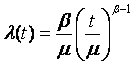 .
.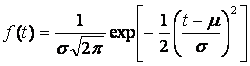 .
.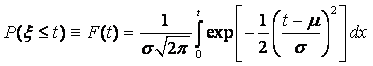 .
.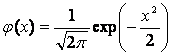 ,
,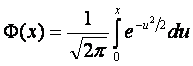 .
. ,
,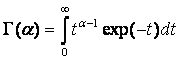 .
.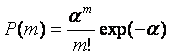 .
.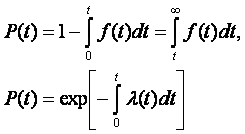 .
.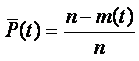 ,
,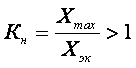 .
.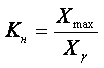 .
.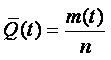 .
.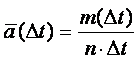 ,
,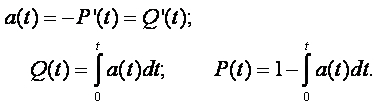
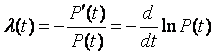 .
.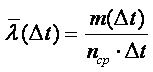 ,
,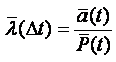 .
.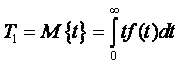 ,
,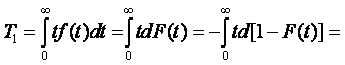
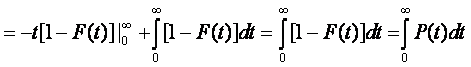 .
.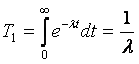 ,
,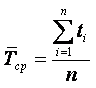 ,
,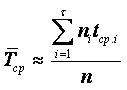 ,
,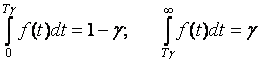 .
.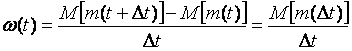 ,
,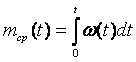 .
.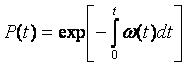
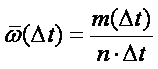 ,
,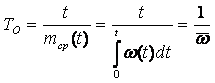 ,
,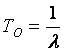 .
. 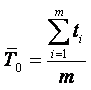 ,
,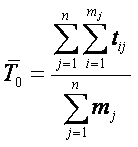 ,
, .
. ,
,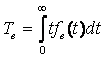 или
или 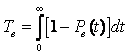 .
. ,
,
 ,
, .
.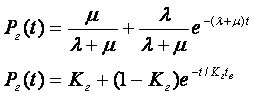 ,
,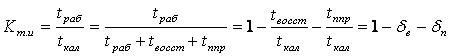 ,
,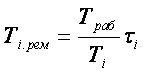 ,
,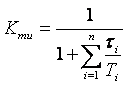 .
. .
.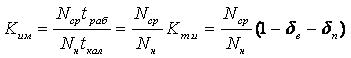 .
.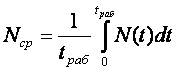 .
. ,
,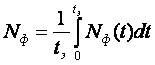 .
.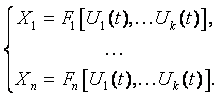
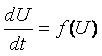 .
.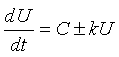 ,
,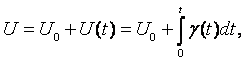
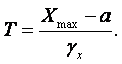



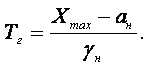
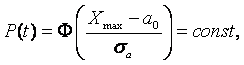
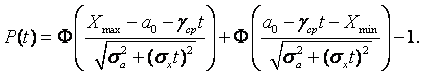
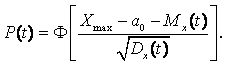
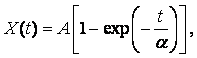
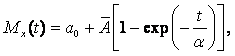
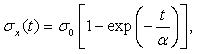
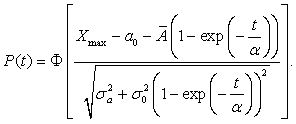
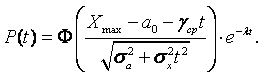
 .
.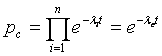 ,
,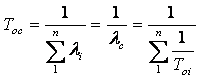 .
.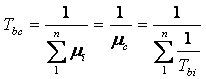 .
. ,
…,
,
…, 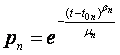 ,
,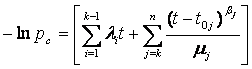 .
.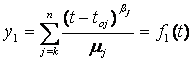 ;
; 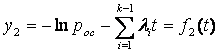 .
. .
.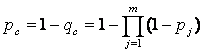 .
.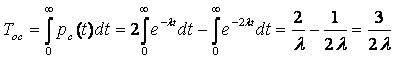 .
. 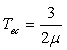 .
.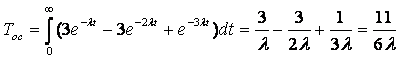 .
. 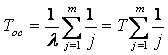 .
.
 ,
, .
. .
.
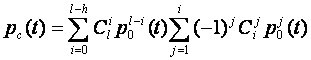 ,
,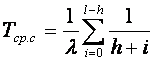 ,
,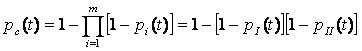 .
.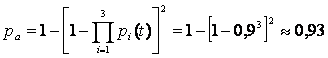 .
.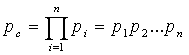 ,
, .
.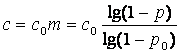 .
.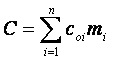 .
. .
.
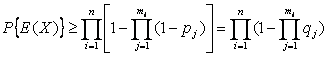 .
.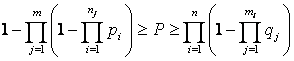 .
.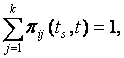
 ,
,
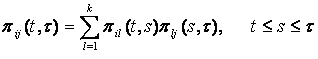 ;
;
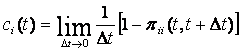
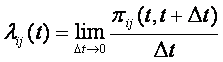 ,
,
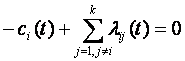 .
. ,
, 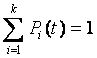 ,
,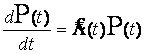 ,
,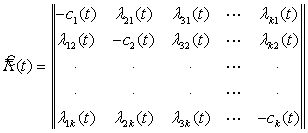 .
.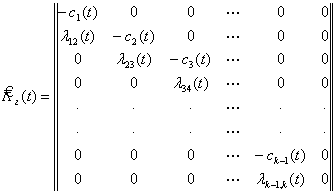 .
.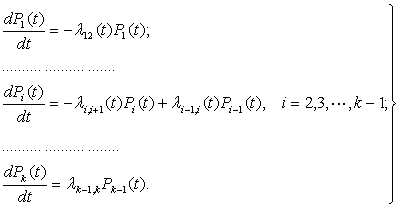
 .
.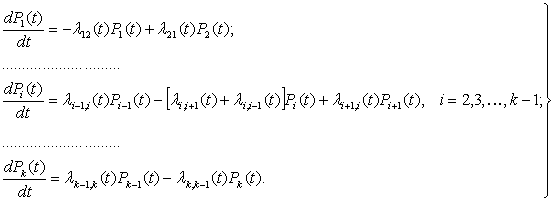
 .
.
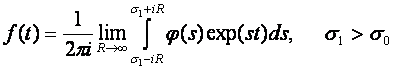
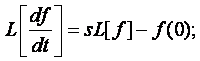



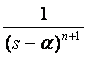
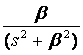

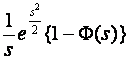
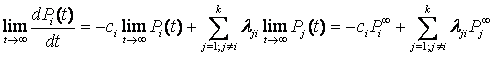 .
.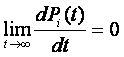 .
.
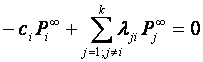 .
.
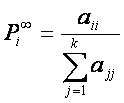 ,
,
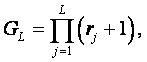 ,
,


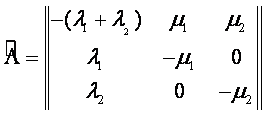 .
.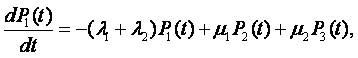
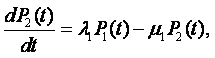
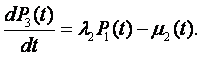
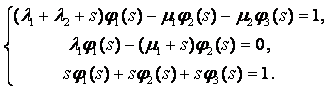
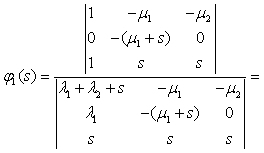
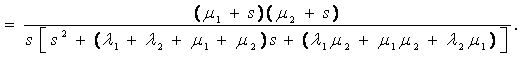
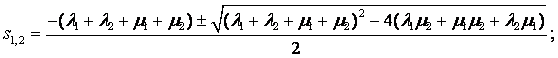

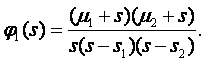
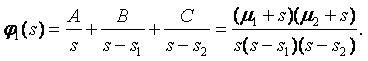
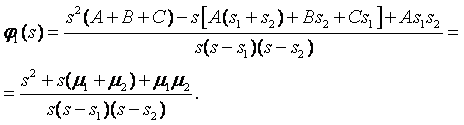
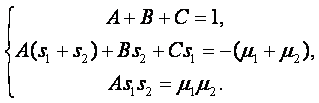
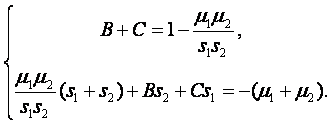
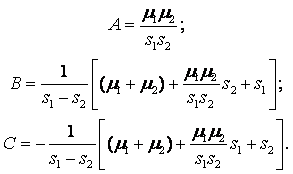

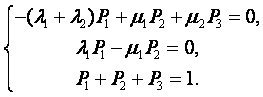
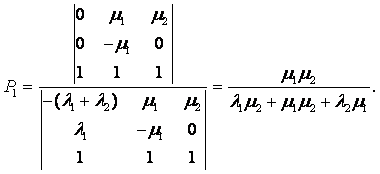

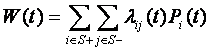 ,
,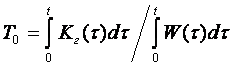 .
.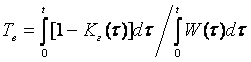 .
.
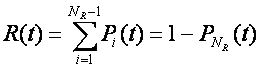 .
.