АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра тепловых энергетических установок

ЭКСПЛУАТАЦИОННАЯ НАДЕЖНОСТЬ И БЕЗОПАСНОСТЬ ТЭС

Методические указания и задания к выполнению

расчетно-графических работ для магистрантов

специальности 050717 - Теплоэнергетика

Алматы 2009

СОСТАВИТЕЛЬ: А.И. Соколов. Эксплуатационная надежность и безопасность ТЭС. Методические указания к выполнению расчетно-графических работ для магистрантов специальности 050717 - Теплоэнергетика. – Алматы: АИЭС, 2009. – 21 с.

Методические указания содержат два контрольных задания по курсу "Эксплуатационная надежность и безопасность ТЭС" для магистрантов. Расчётно-графическое задание № 1 включает 40 задач и 10 вопросов. Студент должен решить 4 задачи и ответить на 1 вопрос, связанный с обеспечением безопасности при работах на различных объектах ТЭС. Расчётно-графическое задание № 2 включает 20 задач повышенной трудности. Студент должен решить две задачи. В обоих вариантах задачи выбираются в соответствии с индивидуальным шифром студента. Общие методические указания даны в разделе 1. В разделе 2.1 даны предварительные методические указания для решения всех типов задач, данных в обоих контрольных заданиях. Более подробные теоретические сведения, связанные с темой предлагаемых задач, даны в учебном пособии [4]. Контрольные задания охватывают практически весь материал, который предусмотрен данным курсом.

Введение

Количественные показатели надежности тепловых и атомных электростанций могут быть получены путем обработки статистических данных по их эксплуатации или путем расчета по известным характеристикам надежности элементов и функционально-структурным схемам. Соответственно методы расчета надежности структурных схем ТЭС называются статистическими или аналитическими. Наиболее распространены аналитические методы вследствие их оперативности при достаточной точности. Эти методы основаны на изучении функционального назначения станций, разработке их функционально-структурных схем и моделировании процессов изменения состояний. Для этого структурная схема представляется в виде совокупности элементов с определенными связями и выходным эффектом. Выходным эффектом конденсационных ТЭС и ТЭЦ является располагаемая электрическая мощность и производительность по отпуску тепла.

В зависимости от используемого метода расчета надежности состояния сложной системы представляют в виде графов состояний и переходов или в виде функций алгебры и логики. При этом система представляется совокупностью п восстанавливаемых элементов, каждый из которых в любой момент времени может находиться в одном из двух состояний: полной работоспособности и неработоспособности.

В большинстве случаев структурную схему ТЭС можно представить в виде параллельно-последовательных структур. Если отказ хотя бы одного элемента приводит к отказу системы в целом, то такое соединение называется последовательным. Последовательное соединение элементов в смысле надежности не совпадает с их физическим соединением. Так, например, трубы радиационной части котла или пароперегревателя следует рассматривать как последовательную систему, так как разрыв одной трубы приводит к останову котла.

При параллельном соединении элементов, являющимся частным случаем резервированной системы, у которой все элементы включены постоянно, система работоспособна, если хотя бы один элемент работоспособен.

В основу аналитических методов расчета надежности энергетических установок положены два подхода. Один из них основан на использовании логических схем (метод дерева отказов и метод минимальных путей и сечений), а другой на использовании моделей пространства состояний (метод перебора состояний и марковская модель).

Условием применимости первых методов является существование логической схемы и независимости отказа элементов. Эти методы позволяют получать только стационарные вероятности работы или отказов системы за длительный период. Кроме того, логические схемы можно построить только для относительно простых систем.

Вторая группа методов расчета надежности основана на вычислении вероятностей и частот состояний, выборе критериев и условий отказа системы. Эти методы требуют более сложного математического аппарата и позволяют получить нестационарные значения показателей надежности. При их использовании законы распределения вероятностей отказов и восстановлений элементов, как правило, принимаются экспоненциальными. Представление элементов в двух состояниях (работа – отказ) в этом случае не обязательно.

1 Общие методические указания

При изучении курса "Эксплуатационная надежность и безопасность ТЭС" (ЭНиБ ТЭС) следует руководствоваться рабочей программой. Перед выполнением контрольных заданий необходимо ознакомиться по предложенной литературе с рабочей программой курса.

Контрольное задание предусматривает решение задач. Задачи необходимо решать с подробными пояснениями. Конечный результат должен быть проанализирован. После вычислений обязательно указывается размерность полученной величины. Оформление контрольных заданий должно соответствовать "Учебно-методическая документация" [1] и сопровождаться рисунками и графиками. При использовании литературы необходимо на нее ссылаться и указывать в конце работы источник информации.

Номер выполняемого варианта выбирается по первой букве фамилии, предпоследней и последней цифрам шифра студента. Работы, не соответствующие этим условиям, не рассматриваются.

2 Контрольное задание

Решить задачи, указанные в таблице 1, письменно. Задачи выбираются по первой букве фамилии студента, предпоследней и последней цифре шифра. Вопрос выбирается по последней цифре шифра.

Т а б л и ц а 1

Первая буква фамилии	А, Д	В, Г, Я	Б, Е	Ж, З, И	К, У	М, О, Ц	Н, Л	Р, Т, Ф, Х	С, Ч, Э, Ю	П, Ш, Щ
№ задачи	1, 11	2,12	3, 13	4, 14	5, 15	6,16	7, 17	8,18	9,19	10, 20
Предпоследняя цифра шифра	0	1	2	3	4	5	6	7	8	9
№ задачи	21, 31	22, 32	23, 33	24, 34	25, 35	26, 36	27, 37	28, 38	29, 39	30, 40
Последняя цифра шифра	0	1	2	3	4	5	6	7	8	9
№ задачи и вопроса	41, 51 1	42, 52 2	43, 53 3	44, 54 4	45, 55 5	46, 56 6	47, 57 7	48, 58 8	49, 59 9	50, 60 10

2.1 Методические пояснения к решению задач

2.1.1 Критерии и количественные характеристики надежности

2.1.1.1 Критерии надежности невосстанавливаемых объектов

Закон надежности или вероятность безотказной работы – это вероятность того, что в течение заданного времени t при определенных условиях эксплуатации не произойдет ни одного отказа.

По статистическим данным вероятность безотказной работы можно определить как

, (1)

где п – число изделий, поставляемых на испытание;

т(t) – число изделий, отказавших ко времени t.

На практике более удобной характеристикой является вероятность отказа Q(t).

Вероятность отказа – это вероятность того, что в заданном интервале времени при определенных условиях эксплуатации возникнет хотя бы один отказ. Отказ и безотказная работа являются событиями несовместимыми, поэтому

. (2)

Частота отказов – отношение числа отказавших элементов в единицу времени к первоначальному числу испытываемых элементов при условии, что все вышедшие из строя элементы не восстанавливаются

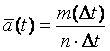, (3)

где m(Dt) – число отказавших образцов в интервале времени от t – Dt/2

до t + Dt/2.

Частота отказов есть плотность распределения времени работы объекта до первого отказа, поэтому

. (4)

Интенсивность отказов – отношение числа отказавших элементов в единицу времени к среднему числу элементов, исправно работающих в данный отрезок времени

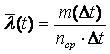, (5)

где п_ср = (n_i + n_i₊₁)/2 – среднее число исправно работающих элементов в

интервале Dt;

n_i – число элементов, исправно работающих в начале интервала Dt;

n_i₊₁ – число элементов, исправно работающих в конце интервала Dt.

Вероятностная оценка характеристики (5) находится из выражения

. (6)

Средняя наработка до первого отказа – математическое ожидание времени работы элемента до первого отказа:

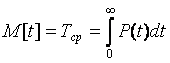Из статистической оценки

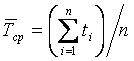, (7)

где t_i – время безотказной работы i-го образца;

n – число испытуемых образцов.

На практике удобнее пользоваться другим выражением, где вместо времени t_i учитывается количество вышедших из строя элементов n_i в каждом i-м интервале времени

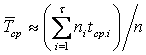, (8)

где t_cp.i = (t_i_{– 1} + t_i)/2;

t = t_k/Dt;

t_i_{– 1} – время начала i-го интервала;

t_i – время конца i-го интервала;

t_k – время, в течение которого вышли из строя все элементы;

Dt = t_i_{– 1} – t_i – интервал времени.

Если опыт прекращается до того, как откажут все образцы, то п – количество отказавших образцов.

Для оценки количественных характеристик необходимо учитывать законы распределения времени безотказной работы.

2.1.1.2 Критерии надежности восстанавливаемых изделий

Параметр потока отказов при статистических испытаниях – отношение числа отказавших элементов в единицу времени к числу испытываемых элементов при условии, что все вышедшие из строя элементы заменяются исправными

, (9)

где т(Dt) – число отказавших элементов в интервале времени от t – Dt/2

до t + Dt/2;

n – число испытываемых образцов;

Dt – интервал времени.

Наработка на отказ – среднее значение времени между соседними отказами. По статистическим данным наработку на отказ можно определить по формуле

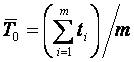, (10)

где t_i – время исправной работы элемента между (i – 1)-м и i-м

отказами;

m – число отказов за некоторое время t.

В (10) наработка на отказ определяется по данным испытаний одного образца. Если на испытании находится п образцов в течение времени t, то наработка на отказ вычисляется по формуле

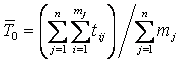, (11)

где t_ij – время исправной работы j-го образца между (i – 1)-м и i-м

отказами;

m_j – число отказов j-го образца за время t.

Для учета времени, необходимого для восстановления отказавшего элемента, вводятся такие критерии, как коэффициент готовности и коэффициент вынужденного простоя.

Коэффициент готовности – отношение времени исправной работы к сумме времен исправной работы и вынужденных простоев объекта, взятых за один и тот же календарный срок

, (12)

где t_раб – суммарное время работы объекта за некоторый период

эксплуатации, на котором определяется К_г;

t_восст – суммарное время восстановления работоспособности

объекта после отказов за тот же интервал эксплуатации;

d_в – доля времени эксплуатации (включающего периоды работы и

восстановления), приходящиеся на восстановление работоспособности объекта после отказов.

Время t_раб и t_восст вычисляется по формулам

, (13)

где t_pi – время работы объекта между (i – 1)-м и i-м отказами;

t_вi – время вынужденного простоя после i- го отказа (ремонта)

объекта.

Коэффициент вынужденного простоя – отношение времени вынужденного простоя к сумме времен исправной работы и вынужденных простоев объекта, взятых за один и тот же календарный срок

. (14)

Коэффициент готовности и коэффициент вынужденного простоя связаны между собой зависимостью

К_п = 1 – К_г.

При анализе надежности восстанавливаемых систем обычно коэффициент готовности вычисляется по формуле

К_г = Т_ср/(Т_ср + t_восст). (15)

Формула (15) верна только в том случае, если поток отказов простейший, тогда Т₀ = Т_ср.

Физический смысл коэффициента заключается в следующем. В простейшем случае, когда l = const и m = const и предполагая, что при t = 0 система находится в исправном состоянии (P(0) = 1), вероятность работоспособности системы определяется из выражений

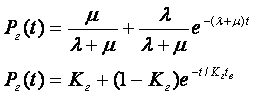, (16)

где .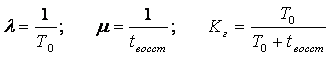

Из (16) видно, что Р_г(t) ®К_г при t® ¥, т.е. коэффициент готовности имеет смысл вероятности нахождения системы в работоспособном состоянии при установившемся процессе эксплуатации.

2.1.2 Расчет характеристик надежности невосстанавливаемых изделий при основном соединении

Основное или последовательное соединение элементов – это такое соединение, при котором отказ хотя бы одного элемента приводит к отказу всей системы. Предполагается, что отказ элемента является событием случайным и независимым.

В этом случае вероятность безотказной работы системы в течение времени t равна произведению вероятностей безотказной работы ее элементов в течение того же времени.

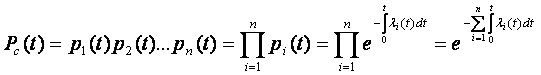(17)

Наиболее часто время возникновения отказов подчиняется экспоненциальному закону распределения, где l = const. В этом случае выражения для количественных характеристик принимают вид

. (18)

Если все элементы данного типа равнонадёжны, интенсивность отказов системы будет

, (19)

где N_i – число элементов i-го типа;

r – число типов элементов.

2.1.3 Расчет характеристик надежности невосстанавливаемых изделий при параллельном соединении

При параллельном включении элементов работоспособность всей системы обеспечивается в том случае, когда работоспособен хотя бы один элемент. Параллельное включение элементов также называется резервированием. По способу включения резервирование разделяется на постоянное и резервирование замещением.

Постоянное резервирование – это резервирование, при котором резервные элементы подключены к основным в течение всего времени работы и находятся в одинаковом с ними режиме. Резервирование замещением – резервирование, при котором резервные элементы замещают основные после их отказа. Вероятность безотказной работы при общем резервировании с постоянно включенным резервом и с целой кратностью (см. рисунок 1) находится из выражения

, (20)

где p_i(t) – вероятность безотказной работы i-го элемента в течение

времени t;

n – число элементов основной или любой резервной цепи;

m – общее число цепей (основной и резервной).

При резервировании неравнонадёжных элементов

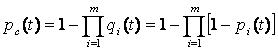, (21)

где q_i(t), p_i(t) – вероятность отказов и вероятность безотказной работы

системы в течение времени t.

При раздельном резервировании с постоянным включением и с целой кратностью (рисунок 2) вероятность безотказной работы системы находится из выражения

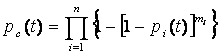, (22)

где p_i(t) – вероятность безотказной работы i-го элемента;

m_i – кратность резервирования i-го элемента;

n – число элементов основной системы.

При равнонадёжных элементах и одинаковой кратности их резервирования

. (23)

2.1.4 Интервальная оценка надежности системы методом минимальных путей и минимальных сечений

Минимальным путем двухполюсной структурной схемы называется такое подмножество его элементов, которое позволяет переходя от одного элемента к другому через общую их вершину, пройти от входного полюса к выходному, но исключение хотя бы одного любого элемента из этого подмножества приводит к тому, что оставшееся подмножество элементов уже не является путем.

Минимальным сечением двухполюсной структурной схемы называется такое подмножество ее элементов, удаление которых из схемы разрывает все пути схемы, но введение хотя бы одного любого из элементов этого подмножества приводит к образованию хотя бы одного пути.

В том случае, когда надежность составляющих элементов системы различна, верхнюю оценку вероятности безотказной работы двухполюсной системы можно сделать через вероятность безотказной работы параллельной схемы минимальных путей

. (24)

В этой формуле Е{X(t)} – логическая функция работоспособности системы; n_j – количество последовательных элементов в каждом j-м минимальном пути, общее число которых m.

Вероятность безотказной работы последовательной структуры минимальных сечений может быть выражена в виде

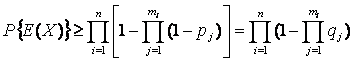. (25)

В этой формуле количество параллельно включенных элементов в каждом минимальном сечении равно m_i, а количество таких сечений равно n (i = 1, …, n). В формулах (24), (25) знак равенства ставится когда все минимальные пути и минимальные сечения независимы. Знак неравенства ставится в том случае, если минимальные пути и минимальные сечения являются зависимыми, т.е. один и тот же элемент может принадлежать нескольким путям или нескольким сечениям.

Таким образом (24) и (25) определяют граничные значения вероятности безотказной работы для любой двухполюсной системы, приведенной к параллельной схеме минимальных путей и последовательной схеме минимальных сечений. С помощью этих граничных значений можно сделать интервальную оценку вероятности безотказной работы исследуемой системы

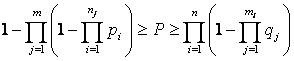. (26)

2.1.5 Марковская модель расчета надежности систем

Свойство независимости "будущего" и "прошлого" состояния объекта, или, что то же, независимость "будущего" от "прошлого" при фиксированном "настоящем" состоянии объекта называется марковским свойством, а соответствующая последовательность случайных состояний Х₁, Х₂, …, Х_п – марковской цепью. Процесс G(t), во время которого объект последовательно попадает в состояния Х₁, Х₂, …, Х_п называется марковским процессом.

Вероятность нахождения технического объекта в одном из состояний определяется системой дифференциальных уравнений Колмогорова-Чепмена

, i= 1, 2, …, k. (27)

где P_i(t) = P(t; X_i)– вероятность того, что в момент времени t > t₀

процесс будет находиться в состоянии X_i.

Вероятность P_i(t) удовлетворяет условию нормировки

(28)

где k – полное число состояний рассматриваемого марковского процесса.

Соотношение (28) является выражением того факта, что с вероятностью, равной единице, процесс находится в каком-то одном из состояний {X_i, i= 1, 2, …, k}.

Система уравнений (27) является линейно-зависимой, следовательно, для ее разрешения одно из уравнений этой системы заменяется условием нормировки (28).

Матрица системы (27) имеет вид

. (29)

Коэффициенты c_i(t) находятся из

(30)

и представляют собой интенсивность ухода из состояния Х_i.

Коэффициенты l_ij – интенсивность прямого перехода из состояния X_i в состояние X_j и определяются выражением

, (31)

где n_l – число элементов в l-м блоке;

хⁱ_l – число отказавших элементов в l-м блоке;

l_l - интенсивность отказа элемента l-го блока.

Коэффициент l_ji – интенсивность обратного перехода равна интенсивности восстановления соответствующего элемента, умноженной на число отказавших элементов данного типа в рассматриваемом состоянии:

(32)

Граф состояний – это графическое представление состояний системы и возможных переходов между состояниями с указанием интенсивностей этих переходов и уровня мощности системы, реализуемой в каждом из состояний. Отдельное состояние изображается точкой, называемой вершиной графа. Вершины соединяются между собой ребрами, изображающими возможные переходы между состояниями. При этом переход (и соответствующее ему ребро) называется прямым, если он порожден отказом отдельного элемента рассматриваемой технической системы, и обратным, если он порожден восстановлением элемента. Ребрами соединяются i-я и k-я вершины графа состояний, если для какой-либо компоненты из радиус-векторов X_i и X_k выполняется условие |xⁱ_j – x^k_j| = 1 и при этом для всех прочих компонент радиус-векторов X_i и X_k: xⁱ_l = x^k_l, l ¹ j. Если xⁱ_j – x^k_j = –1, то ребро по отношению к вершине i будет прямым, если же xⁱ_j – x^k_j = +1, то по отношению к i-й вершине ребро будет обратным. Максимально возможное число прямых ребер, выходящих из отдельной вершины графа состояний, равно числу блоков L в рассматриваемой системе.

Вершины графа нумеруются в определенном порядке. Нумерация вершин начинается с вершины, соответствующей состоянию, в котором все оборудование технической системы работоспособно. Радиус-вектор этой вершины Х_i = {0, 0, …, 0}. Затем нумеруются остальные вершины первого типа, далее, в порядке возрастания присваиваются номера вершинам второго типа. Множество вершин третьего типа после объединения соответствующих им состояний в одно вырождается в множество, содержащее только одну вершину. Этой вершине присваивается последний номер, например, k. Таким образом, граф состояний системы будет содержать k вершин.

Если коэффициенты уравнения Колмогорова-Чепмена не зависят от времени, т.е. получается система обыкновенных дифференциальных уравнений с постоянными коэффициентами, то такую систему удобно решать методом преобразования Лапласа.

При применении преобразования Лапласа исходные дифференциальные уравнения преобразуются в алгебраические, а исходные функции (оригиналы) – в функции изображения. Для преобразований Лапласа справедливы следующие соотношения:

, ,

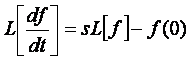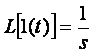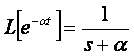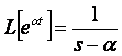, . (33)

При достаточно длительном времени эксплуатации технической системы вероятности реализации состояний процесса P_i(t) перестают зависеть от времени и от начального распределения и приходят к финальным вероятностям

В этом случае уравнения Колмогорова-Чепмена вырождаются в систему линейных алгебраических уравнений вида

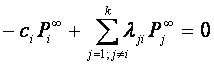, (34)

которые вместе с условиями нормировки (28) позволят однозначно найти стационарные решения для вероятности безотказной работы системы.

3 Расчётно-графическое задание № 1

3.1 Задачи 1-10

На испытания поставлено п изделий. За время t час вышло из строя m(t) изделий. За последующий интервал времени Dt вышло из строя m(Dt) изделий. Вычислить вероятность безотказной работы за время t и t + Dt, частоту отказов и интенсивность отказов на интервале Dt.

№ задачи	n	t, час	Dt, час	m(t)	m(Dt)
1	1000	3000	1000	80	50
2	100	8000	100	50	10
3	10	1000	100	3	2
4	10	1000	100	3	1
5	1000	0	1000	0	20
6	1000	1000	1000	20	25
7	1000	2000	1000	45	35
8	1000	0	100	0	50
9	45	75	5	44	1
10	45	0	10	0	19

3.2 Задачи 11-20

В течение времени Dt производилось наблюдение за восстанавливаемым изделием и было зафиксировано m(Dt) отказов. До начала наблюдения изделие проработало t₁ час, общее время наработки к концу наблюдения составило t₂ час. Найти наработку на отказ.

№ задачи	t₁, час	t₂, час	m(Dt)
11	350	1280	15
12	400	1600	3
13	1000	6400	9
14	770	4800	7
15	1200	5558	2
16	300	540	12
17	540	1200	5
18	300	3200	8
19	12	184	16
20	570	2000	27

3.3 Задачи 21-30

3.3.1 Задачи 21-25

В течение некоторого времени производилось наблюдение за работой п экземпляров восстанавливаемых изделий. Каждый из образцов проработал t час и имел т_i отказов. Требуется определить наработку на отказ по данным наблюдений за работой всех изделий.

№	m₁	t₁	m₂	t₂	m₃	t₃	m₄	t₄	m₅	t₅	m₆	t₆	m₇	t₇
21	1	300	3	600	2	400	-	-	-	-	-	-	-	-
22	3	90	6	270	4	140	5	230	3	180	-	-	-	-
23	12	960	15	1112	8	808	7	1490	-	-	-	-	-	-
24	6	144	5	125	3	80	8	176	5	150	4	112	8	216
25	8	176	5	150	4	112	8	216	-	-	-	-	-	-

3.3.2 Задачи 26-30

Изделие имеет среднюю наработку на отказ и среднее время восстановления . Определить коэффициент готовности изделия.

№ задачи
26	230	12
27	556	23
28	556	2,5
29	430	8
30	143	1,7

3.4 Задачи 31-40

3.4.1 Задачи 31-35

Объект состоит из п элементов, средняя интенсивность отказов которых l_ср. Вычислить вероятность безотказной работы в течение времени t и среднюю наработку до первого отказа. Соединение элементов основное.

№ задачи	п	l_ср, 1/час	t, час
31	5200	0,16×10^-5	200
32	3600	0,20×10^-5	50
33	2500	0,35×10^-6	100
34	2500	0,50×10^-5	100
35	1000	0,50×10^-5	100

3.4.2 Задача 36

Найти вероятность безотказной работы системы, если известны вероятности отказов элементов.

3.4.3 Задача 37

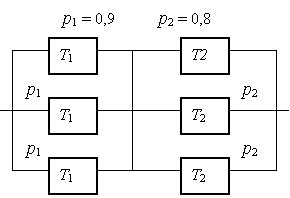
Определить вероятность безотказной работы Р_с и вероятность отказа Q_c системы, Вероятность безотказной работы элементов дана на рисунке.

3.4.4 Задача 38

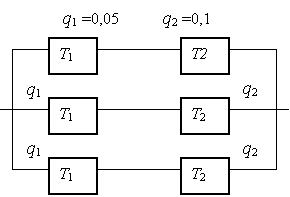
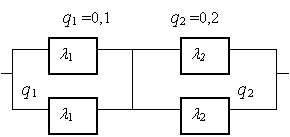
Найти по известным вероятностям отказов элементов q₁ q₂ вероятности безотказной работы системы.

3.4.5 Задача 39

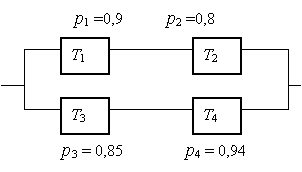
Вычислить вероятность безотказной работы системы, если известна вероятность безотказной работы элементов.

3.4.6 Задача 40

Интенсивность отказов элементов имеют следующие значения: l₁ = 0,3×10^-3 1/час, l₂ = 0,7×10^-3 1/час. Определить вероятность безотказной работы системы в течение времени t = 100 час, среднюю наработку до первого отказа, частоту отказов и интенсивность отказов в момент времени t = 100 час.

4 Расчётно-графическое задание № 2

4.1 Задачи 41-50

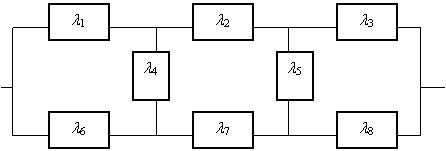Дана неприводимая схема, соответствующая системе паропроводов с поперечными связями и задвижками. Интенсивность отказов элементов схемы l₁, l₂, l₃, l₄, l₅, l₆, l₇, l₈. Определить минимальные пути и минимальные сечения для данной схемы, построить параллельную схему минимальных путей и последовательную схему минимальных сечений, сделать интервальную оценку вероятности безотказной работы всей системы и построить график вероятности безотказной работы для верхнего и нижнего предела в зависимости от времени.

№	l₁	l₂	l₃	l₄	l₅	l₆	l₇	l₈
41	8,0×10^-6	9,8×10^-6	8,0×10^-6	1,7×10^-5	7,6×10^-4	8,0×10^-5	3,6×10^-5	2,0×10^-5
42	8,2×10^-6	9,6×10^-6	7,9×10^-6	1,9×10^-5	8,0×10^-4	4,4×10^-5	3,8×10^-5	2,5×10^-5
43	8,4×10^-6	9,4×10^-6	9,5×10^-6	1,8×10^-5	9,0×10^-4	4,2×10^-5	4,2×10^-5	2,2×10^-5
44	8,6×10^-6	9,2×10^-6	7,8×10^-6	2,0×10^-5	8,5×10^-4	5,0×10^-5	5,4×10^-5	3,0×10^-5
45	8,8×10^-6	9,0×10^-6	7,5×10^-6	1,6×10^-5	5,5×10^-4	4,6×10^-5	4,9×10^-5	1,8×10^-5
46	9,0×10^-6	8,8×10^-6	7,0×10^-6	2,1×10^-5	4,3×10^-4	4,8×10^-5	4,3×10^-5	1,5×10^-5
47	9,2×10^-6	8,6×10^-6	8,6×10^-6	1,5×10^-5	5,0×10^-4	5,4×10^-5	3,5×10^-5	3,9×10^-5
48	9,4×10^-6	8,4×10^-6	8,0×10^-6	2,2×10^-5	6,1×10^-4	5,2×10^-5	3,5×10^-5	3,4×10^-5
49	9,6×10^-6	8,2×10^-6	8,2×10^-6	2,5×10^-5	5,9×10^-4	3,8×10^-5	6,0×10^-5	1,7×10^-5
50	9,8×10^-6	8,0×10^-6	8,2×10^-6	2,3×10^-5	5,2×10^-4	4,6×10^-5	5,7×10^-5	2,6×10^-5

4.2 Задачи 51-60

Для указанных структурных схем построить графы состояний марковского процесса, определить интенсивность всех возможных переходов, записать матрицу и составить систему дифференциальных уравнений Колмогорова-Чепмена. Полученную систему дифференциальных уравнений с помощью преобразования Лапласа преобразовать в систему алгебраических уравнений. Написать соответствующую систему уравнений для стационарной задачи.

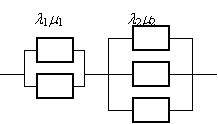51 52

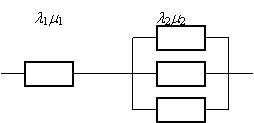
53 54

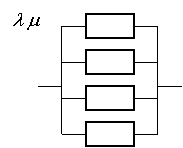55 56

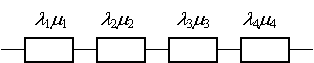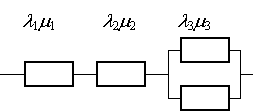57 58

59 60

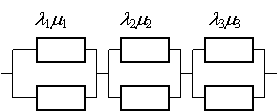4.3 Вопросы

1 Безопасное обслуживание оборудования в тепловых и химических цехах электростанций. Общие требования.

2 Обеспечение безопасности при работах в резервуарах, каналах и колодцах в тепловых и химических цехах электростанций.

3 Безопасное обслуживание и ремонт теплообменных аппаратов и трубопроводов.

4 Соблюдение техники безопасности при подготовке к ремонту и ремонте насосов, вентиляторов, дымососов, мельниц и другого оборудования, в составе которого имеются вращающиеся части.

5 Техника безопасности при теплоизоляционных и обмуровочных работах.

6 Обеспечение безопасной эксплуатации пылеприготовительных установок.

7 Как обеспечить безопасную работу персонала в топливных бункерах?

8 Обеспечение безопасности при подготовке котла к розжигу, при его эксплуатации и остановке.

9 Как обеспечить безопасное проведение ремонтных и профилактических работ в топке котла и газоходах?

10 Какие необходимо принять меры по безопасности при пуске и останове паровой турбины, при изменении режима работы?

Список литературы

1. Учебно-методическая документация. Общие требования к построению, изложению, оформлению и содержанию учебно-методической документации. СТ НАО 103521910-03-2007. – Алматы: НАО АИЭС. – 23 с.

2. Гмурман В.Е. Теория вероятности и математическая статистика. – М.: Высшая школа, 1998. – 368 с.*⁾

3. Шостак Р.Я. Операционное исчисление. – М.: Высшая школа, 1972. – 280 с.*⁾

4. Соколов А.И. Эксплуатационная надежность и безопасность ТЭС: Учебное пособие. – Алматы: АИЭС, 2009. – 127 с.

5. Справочная книга по технике безопасности в энергетике. В 2-х книгах. Кн. 1/Сост: Гаджиев Р.А. и др. – М.: Энергия, 1978. – 656 с.

6. РД.34.03.201-97. Правила техники безопасности при эксплуатации теплотехнического оборудования электростанций и тепловых сетей. – М.: 1997.

Примечание – Кроме книг, отмеченных *⁾, можно пользоваться любыми учебниками и задачниками по теории вероятностей, математической статистике и операционному исчислению.