АЛМАТИНСКИЙ ИНСТИТУТ энергетики и связи
Кафедра тепловых энергетических установок
Компьютерные технологии в теплоэнергетических
расчетах
Рабочая
программа, методические указания и задания к
контрольной работе (для студентов специальности 220140 - Тепловые электрические
станции заочной формы обучения)
Алматы 2005
СОСТАВИТЕЛИ: Н.Г. Борисова,
А.А Кибарин, А.С. Т.В. Ходанова. Компьютерные
технологии в теплоэнергетических расчетах Рабочая программа, методические
указания и задания к контрольной работе (для студентов специальности 220140 -
Тепловые электрические станции заочной формы обучения). - Алматы: АИЭС, 2005. –
21 с.
Методические указания содержат рабочую программу, методические указания и
задания к контрольным работам, перечень рекомендуемой литературы,
контрольные вопросы и требования по оформлению контрольных работ.
Ил. 1, табл. 3, библиогр.- 12 назв.
Рецензент: канд. техн. наук,
профессор Б.Д.
Хисаров
Печатается по плану издания Алматинского
института энергетики и связи на 2004 г.
Ó Алматинский институт
энергетики и связи, 2005 г.
Цели и задачи курса
Курс
«Компьютерные технологии в теплоэнергетических расчетах» является обязательным
предметом для студентов высших учебных заведений и включается в учебные планы в
качестве общепрофессиональной дисциплины.
Цель курса – формирование у
студентов знаний, умений и навыков
применения компьютерных технологий для
расчета объектов теплоэнергетики.
Задачи курса – овладение
студентами элементами численных
методов; приемами алгоритмизации; закрепления навыков использования языков
программирования; проведения вычислительного эксперимента; использования
компьютерных технологий для
исследования процессов, установок и
систем теплоэнергетики.
Дисциплина
«Компьютерные технологии в теплоэнергетических расчетах» базируется на знаниях
и умениях, приобретенных студентами при
изучении курсов «Математика»,
«Информатика», «Физика», «Химия», «Материаловедение», «Техническая
термодинамика», «Механика жидкости и газа», «Тепломассообмен». Знания, умения и
навыки, полученные студентами, используются при изучении специальных дисциплин,
в частности, курса «Методы моделирования и оптимизации теплотехнологических
установок и систем», выполнении дипломного проекта, научно-исследовательских и
инженерных работ.
В
результате изучения дисциплины студенты должны иметь представление:
-
о численных методах,
используемых при исследовании и моделировании процессов и систем теплотехники и
теплоэнергетики;
-
о
возможностях компьютерных технологий при решении прикладных задач
теплоэнергетики;
Студенты должны владеть:
-
методами
интерполяции функций;
-
численными
методами интегрирования, решения трансцендентных уравнений, систем
алгебраических уравнений, обыкновенных дифференциальных уравнений;
-
методами
решения задач оптимизации;
-
численными
методами решения задач стационарной и нестационарной теплопроводности,
конвективного теплообмена;
- способами алгоритмизации и
программирования, хранения, обработки и
представления информации;
Студенты должны
уметь:
- использовать языки высокого
уровня для составления программ расчета;
- выбрать эффективный
численный метод для решения конкретной
задачи, оценить его точность и надежность;
- использовать
текстовые и графические редакторы, мультимедийные средства и компьютерную сеть;
-
использовать готовые пакеты прикладных программ для
выполнения теплоэнергетических расчетов;
-
использовать
автоматизированные экзаменационно – обучающие компьютерные системы для самообучения и самоконтроля.
Завершающим
этапом в изучении курса является выполнение студентами контрольной работы по
составлению математической модели, алгоритма и программы расчета
теплоэнергетического объекта согласно выбранного варианта.
1 Общие
методические указания
При
изучении курса «Компьютерные технологии
в теплоэнергетических расчетах» следует руководствоваться рабочей программой курса.
Перед выполнением контрольного задания необходимо просмотреть рабочую программу и в
соответствии с основными разделами курса проработать материал, составить краткий
конспект и решить для закрепления знаний несколько задач. При изучении курса необходимо добиваться глубокого понимания
рассматриваемых вопросов, что позволит в дальнейшем использовать полученные
знания для решения практических задач.
Контрольное задание предусматривает ответы на вопросы и составление математической модели, алгоритма и программы расчета теплоэнергетического объекта согласно выбранного варианта. К выполнению контрольных работ следует приступить после того, как изучен материал курса.
2
Рабочая программа курса
Программа курса (120
часов) включает в себя самостоятельную
(100 часов) и аудиторную (20 часов) работу.
Самостоятельная
работа состоит из изучения основных разделов курса и выполнения контрольной
работы.
Аудиторная работа содержит лекционный материал (6 часов), практические занятия (4 часа) и лабораторный практикум (10 часов).
Завершающим этапом в изучении курса является выполнение студентами контрольной работы.
2.1 Содержание дисциплины
2.1.1 Введение
Цель, объем и содержание курса «Компьютерные технологии в теплоэнергетических расчетах». Основные задачи курса и место в подготовке инженера - теплоэнергетика. Основные понятия современных информационных технологий. Общая характеристика теплотехнических и теплоэнергетических расчетов [9, 11, 12].
2.1.2 Математическое
моделирование
Постановка задачи математического моделирования в теплотехнике и теплоэнергетике. Схема процесса моделирования. Классификация математических моделей [2, 4, 11, 12].
Методические указания
В этом разделе прежде всего необходимо обратить внимание на основные задачи математического моделирования в теплоэнергетике. После изучения раздела четко представлять классификацию моделей, виды моделирования и схему составления математической модели.
2.1.3 Численные методы
решения некоторых теплотехнических
задач
Интерполирование, полиномиальное интерполирование, интерполирование сплайнами, аппроксимация кривыми при решении задач приближения функций и расчета теплотехнических таблиц.
Компьютерная реализация теплового расчета теплообменного аппарата. Численное интегрирование (метод прямоугольника, трапеций, парабол, метод Гаусса) при расчете площади поверхности нагрева теплообменного аппарата.
Нахождение корней алгебраических и трансцендентных уравнений при решении критериальных уравнений тепло - и массообмена. Решение систем линейных и нелинейных алгебраических уравнений, обыкновенных дифференциальных уравнений, описывающих теплотехнические процессы.
Численные методы и их компьютерная реализация при решении задач тепломассообмена и гидродинамики. Методы интегральных соотношений, конечно - разностные методы при решении задачи вязкого течения жидкостей и газов в пограничном слое при внешнем обтекании тел. Применение метода прогонки в задачах моделирования течения в каналах. Методы математической статистики при изучении вязкого многофазного течения.
Задачи оптимизации в теплоэнергетике и теплотехнике. Методы решения задач оптимизации. Классификация методов. Применение метода прямого спуска, методов безусловной оптимизации первого порядка (метод наискорейшего спуска), методов условной оптимизации (симплекс-метод, методы штрафных функций) для решения задач оптимизации в теплоэнергетике и теплотехнике [2, 6, 9, 10, 11, 12].
Методические указания
В этом разделе следует
обратить особое внимание на численные методы решения линейных и нелинейных
уравнений, методы обработки дискретных экспериментальных данных при помощи
интерполирования и аппроксимации кривыми, методы интегрирования и решения
дифференциальных уравнений, особенно методы решения задач гидродинамики и
тепло- массообмена. Большой круг задач тепломассообмена и гидродинамики
решается при помощи методов интегральных соотношений, конечно - разностными
методами, поэтому при изучении данного раздела этим методам следует уделить
внимание.
Оптимизация теплотехнологических процессов и систем одна из важнейших задач, которая стоит перед инженером, оптимизация невозможна без знания математических методов. Поэтому при изучении раздела следует обратить внимание на методы оптимизации (одномерные, многомерные) и на то, в каких задачах применяются те или иные методы.
После изучения раздела необходимо уметь применять различные численные методы и стандартные программы при решении задач теплоэнергетики.
2.1.4 Пакеты
прикладных программ для решения теплотехнических задач
Структура и свойства пакетов прикладных программ (ППП). Разработка и тестирование ППП. Возможности ППП и управление его работой. Использование ППП для САПР. Использование системы Visio для проектирования теплотехнических схем [2, 9, 11, 12].
2.1.5
Теплотехнические
справочно-информационные системы
и банки данных
Автоматизированные системы данных и термодинамических свойств веществ. Комплексы прикладных программ для моделирования процессов гидродинамики, тепло - и массопереноса. Автоматизированные системы для моделирования теплоэнергетического оборудования [9, 12].
2.2 Содержание практических занятий
2.2.1 Определение теплофизических параметров методами интерполирования функций.
2.2.2 Расчет площади поверхности
нагрева теплообменного аппарата методами численного интегрирования.
2.3 Перечень лабораторных работ
2.3.1 Расчет теплофизических свойств рабочих тел, используемых в теплоэнергетике. Приближение функций и расчет теплотехнических таблиц.
2.3.2 Численное решение нелинейных алгебраических уравнений гидродинамики и теплообмена.
2.3.3 Численное интегрирование в тепловом расчете рекуператора.
2.3.4 Численные методы решения обыкновенных дифференциальных уравнений в теплотехнических расчетах.
2.3.5 Применение конечно - разностных методов при решении задач теплопроводности.
3. Вопросы для
самопроверки
1. Погрешность
приближенных вычислений. Влияние погрешности на конечный результат.
2. Интерполирование.
Линейная интерполяция.
3. Интерполяционный
полином Лагранжа.
4. Интерполяционный
полином Ньютона.
5. Аппроксимация
кривых.
6. Аппроксимация
кривых методом наименьших квадратов.
7. Сглаживание
кривых с помощью сплайнов.
8. Выбор
методов интерполяции, сглаживания.
9. Интервальное
оценивание параметров нормально распределенной случайной величины.
10. Линейная
регрессия.
11. Уравнения для расчета теплофизических свойств
воды и водяного пара.
12. Уравнения
для расчета теплофизических свойств газов.
17. Определение
поверхности теплообменника.
18.
Математическая модель
теплообменника для конструкторского и поверочного расчета.
19.
Численное интегрирование при расчете площади поверхности нагрева
теплообменного аппарата.
20.
Метод прямоугольника (численное интегрирование).
21.
Метод трапеций (численное интегрирование).
22.
Метод Симпсона (численное интегрирование).
23.
Численное интегрирование сплайнами.
24.
Нахождение корней алгебраических и трансцендентных уравнений при
решении критериальных уравнений тепло - и массообмена.
25.
Методы решения
нелинейных уравнений.
26.
Решение нелинейных
уравнений методом Ньютона.
27.
Решение систем линейных алгебраических уравнений.
28.
Решение систем линейных
уравнений методом Гаусса.
29.
Метод Зейделя.
30.
Решение систем нелинейных
алгебраических уравнений.
31.
Расчет равновесного
состава продуктов сгорания.
32.
Решение дифференциальных
уравнений. Задача Коши.
33.
Метод Эйлера.
34.
Метод Рунге-Кутта.
35.
Расчет процесса
образования оксидов азота в топках паровых котлов.
36.
Расчет процессов
теплообмена в трубопроводах.
37.
Дифференциальные
уравнения в частных производных. Метод сеток.
38.
Задачи
оптимизации в теплоэнергетике и теплотехнике.
39.
Методы
решения задач оптимизации. Классификация методов.
40.
Применение
метода прямого спуска, методов безусловной оптимизации первого порядка (метод
наискорейшего спуска).
41.
Применение
методов условной оптимизации (симплекс-метод, методы штрафных функций) для
решения задач оптимизации в теплоэнергетике и теплотехнике.
42.
Симплекс-метод решения
задач линейного программирования.
43.
Примеры математических
моделей энергетического оборудования.
44.
Численные методы в
теплоэнергетике.
45.
Теплотехнические справочно-информационные
системы и банки данных.
46.
Автоматизированные системы данных и термодинамических свойств
веществ.
47.
Библиотеки прикладных
программ для расчета теплообмена.
48.
Использование ППП для САПР.
49.
Разработка и тестирование ППП.
50.
Роль ЭВМ в процессе проектирования.
51.
Методы решения краевых задач.
52.
Пакеты программ для моделирования инженерных систем.
53.
Методы обработки
числовых данных.
54.
Вычислительная техника
для решения инженерных задач.
55.
Выбор метода решения
систем уравнений.
56.
Классификация
методов при решении задач оптимизации в теплоэнергетике и теплотехнике.
57.
Методы
штрафных функций.
58.
Компьютерная реализация теплового расчета теплообменного
аппарата.
59.
Типы
задач, решаемых с помощью ЭВМ.
4
Контрольное задание
4.1 Общие методические указания по выполнению контрольной работы
Контрольная работа
включает в себя ответы на вопросы и решение двух задач.
Номера
теоретических вопросов к контрольной работе приведены в таблице 1.
Работы, не соответствующие данным требованиям, не рассматриваются.
Ответы на вопросы должны
быть конкретными, краткими, написаны технически грамотно, и в то же время
полностью охватывать поставленный вопрос. Недопустимо дословное переписывание
текста из учебника. Ответы на вопросы, если требуется по заданию, необходимо
проиллюстрировать эскизами, схемами, формулами. При использовании литературы необходимо на нее ссылаться и указывать в
конце работы источник информации.
При
решении задач необходимо приводить сначала методику расчета, а затем результаты
вычислений по этой методике. При отсутствии доступа к ПК решение задач может
быть осуществлено в период экзаменационной сессии на ПК компьютерного класса кафедры
ТЭУ, результаты расчетов прилагаются.
Оформление контрольной работы должно соответствовать
«Фирменному стандарту. Работы учебные» [1] и при необходимости сопровождаться
рисунками и графиками.
При оформлении задач следует придерживаться следующего порядка:
а)
представление математической модели в общем виде;
б)
методика решения задачи в форме удобной для реализации на ЭВМ;
в)
блок-схема алгоритма задачи;
г)
программа расчета поставленной задачи на одном из алгоритмических языков и
результаты расчета в соответствии с
заданным вариантом.
Таблица 1 - Варианты
вопросов к контрольной работе
|
Сумма последних цифр шифра
зачетной книжки студента |
Номера вопросов к |
|
0 |
1,11,20,41 |
|
1 |
2,12,21,42 |
|
2 |
3,13,22,43 |
|
3 |
4,14,23,44 |
|
4 |
5,15,24,45 |
|
5 |
6,16,25,46 |
|
6 |
7,17,26,47 |
|
7 |
8,18,27,48 |
|
8 |
9,19,28,49 |
|
9 |
10,29,30,50 |
|
10 |
12,22,31,51 |
|
11 |
14,24,32,52 |
|
12 |
16,26,33,53 |
|
13 |
18,28,34,54 |
|
14 |
20,30,35,55 |
|
15 |
22,32,36,56 |
|
16 |
24,34,37,57 |
|
17 |
26,38,39,58 |
|
18 |
25,39,40,59 |
4.2 Задача №1. Методы решения алгебраических
и трансцендентных уравнений.
Цель: приобретение навыков решения алгебраических и трансцендентных уравнений итерационными методами.
Задание.
1. Для выбранной в таблице 2 функции определить область нахождения корня и принять границы интервала вычислений.
2. Разработать программу решения алгебраических и трансцендентных уравнений.
3. В качестве численного метода решения уравнения использовать метод, представленный в таблице 2.
4. Получить результаты расчета с заданной в таблице 2 точностью.
Таблица 2 - Исходные
данные для задачи №1
|
№ варианта |
Функция |
Погрешность определения
корня |
Метод решения |
|
|
0 |
|
e=0,001 |
половинного деления |
|
|
1 |
|
e=0,001 |
половинного деления |
|
|
2 |
|
e=0,01 |
Ньютона |
|
|
3 |
|
e=0,01 |
половинного деления |
|
|
4 |
|
e=0,001 |
хорд |
|
|
5 |
|
e=0,001 |
Ньютона |
|
|
6 |
|
e=0,001 |
половинного деления |
|
|
7 |
|
e=0,01 |
хорд |
|
|
8 |
|
e=0,001 |
Ньютона |
|
|
9 |
|
e=0,001 |
половинного деления |
|
|
10 |
|
e=0,005 |
Ньютона |
|
|
11 |
|
e=0,0001 |
Ньютона |
|
|
12 |
|
e=0,0005 |
половинного деления |
|
|
13 |
|
e=0,005 |
половинного деления |
|
|
14 |
|
e=0,0005 |
хорд |
|
|
15 |
|
e=0,01 |
хорд |
|
|
16 |
|
e=0,005 |
Ньютона |
|
|
17 |
|
e=0,01 |
хорд |
|
|
18 |
|
e=0,005 |
половинного деления |
Методические указания по решению
алгебраических и трансцендентных уравнений.
В научных исследованиях и инженерном проектировании часто приходится
решать алгебраические и трансцендентные уравнения. Задачи этого типа, решаемые
на компьютере, могут возникать сами по себе или же составлять часть более
сложных исследований. В любом случае скорость и эффективность, с которой
получают решение, сильно влияют на применимость соответствующего вычислительного
процесса. Выбор подходящего алгоритма для решения алгебраической системы
зависит от класса рассматриваемой задачи.
В
случае одного уравнения задачу называют линейной, алгебраической или
трансцендентной, причём первая имеет одно решение, вторая-n решений,
а в третьей число решений заранее не известно. Трансцендентными называют
нелинейные уравнения, содержащие тригонометрические функции или другие
специальные функции, например lg(x) или ex. Методы решения нелинейных уравнений такого типа делятся на прямые и
итерационные. Первые позволяют найти решение непосредственно с помощью формул и
всегда обеспечивают получение точного решения. Известным примером является формула корней квадратного
уравнения. В итерационных методах процедура решения задаётся в виде
многократного применения некоторого алгоритма. Полученное решение всегда
является приближенным, хотя может быть сколько угодно близким к точному.
Итерационные методы наиболее удобны для реализации на компьютере. Процесс решения задачи состоит в отыскании действительных
корней (нулей) уравнения f(x)=0. Хотя подобные уравнения
также могут иметь комплексные корни. Наиболее простыми и известными методами
решения нелинейных уравнений являются методы половинного деления, хорд и
Ньютона.
Метод
половинного деления состоит из следующих операций. Сначала вычисляют значение
функций в точках, расположенных через равные интервалы на оси х. Это делают до
тех пор, пока не будут найдены два последовательных значения функции f(xn) и
f(xn+1), имеющие противоположные
знаки. Затем по формуле
х ср =(х n+1+хn)/2 (1)
вычисляют середину
промежутка [xn, xn+1] и находят значение функции f(xср).
Если знак f(xср) совпадает со знаком f(xn), то в дальнейшем вместо f(xn)
используют f(xср). Если же f(xср)
имеет знак, противоположный знаку f(xn),
т.е. её знак совпадает со знаком f(xn+1), то на f(xср)
заменяют это значение функции. В результате интервал, в котором заключено
значение корня, сужается. Если значение f(xср)
достаточно близко к нулю, процесс заканчивают, в противном случае его
продолжают. Хотя метод половинного деления не обладает высокой эффективностью,
при увеличении числа итераций он обеспечивает получение всё более точного
приближённого значения корня. После того как найден первый интервал, в котором
заключён корень, его ширина после N итераций убывает в 2N раза.
В основе метода хорд лежит линейная интерполяция по двум значениям функции, имеющим противоположные знаки. При отыскании корня этот метод нередко обеспечивает более быструю сходимость, чем предыдущий.
Сначала определяют значения функции в точках,
расположенных на оси х через равные интервалы. Это делают до тех пор, пока не
будет найдена пара последовательных значений функции f(xn) и
f(xn+1), имеющих противоположные
знаки. Прямая, проведённая через эти две точки, пересекает ось х при значении
х*=(x n - f(x n))(x
n+1-x n)/f(x n+1)-f(x n). (2)
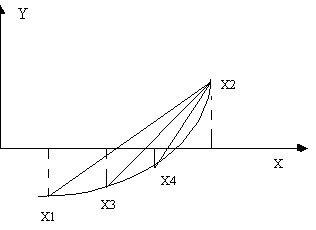Это значение аргумента
используют для определения значения функции F(x*),которое сравнивают со
значениями функций f(xn) и
f(xn+1), и в дальнейшем применяют
вместо того из них, с которым оно совпадает по знаку. Если значение f(x*) недостаточно близко к
нулю, всю процедуру повторяют до тех пор, пока не будет достигнута необходимая
степень сходимости. Процесс решения показан графически на рисунке 1.
Метод последовательных приближений,
разработанный Ньютоном, используют наиболее часто среди всех итерационных
алгоритмов. Его популярность обусловлена тем, что в отличие от двух предыдущих
методов для определения интервала, в котором заключён корень, не требуется
находить значения функции с противоположными знаками. Вместо интерполяции по
двум значениям функции экстраполяцию в методе Ньютона осуществляют с помощью
касательной к кривой в данной точке. В основе метода Ньютона лежит разложение
функции f(x) в ряд Тейлора
F(xn+h)=f(xn)+hf’(xn)+(h2/2)f”(xn)+…… (3)
Члены,
содержащие h во второй и более высоких степенях, отбрасывают;
используется соотношение
хn +h = xn +1. (4)
Предполагается,
что переход от xn к xn+1 приближает значение функции
к нулю так, что f(x n +h) = 0, тогда
хn+1=xn - f(x n )/f‘(x
n ). (5)
Значение
xn+1 соответствует точке, в
которой касательная к кривой в точке xn пересекает ось х. Так как кривая f(x) отлична от прямой, то
значение функции f(xn +1) скорее всего не будет в
точности равно нулю. Поэтому всю процедуру повторяют, причём вместо xn используют xn+1. Счёт прекращается по
достижении достаточно малого значения f(xn+1). Совершенно ясно, что быстрота сходимости в большой
мере зависит от удачного выбора исходной точки. Если в процессе итераций
тангенс f’(x) угла наклонной касательной
обращается в ноль, то применение метода усложняется. Можно также показать, что
в случае бесконечно большого f”(x) метод также не является
достаточно эффективным. Так как условие кратности корней имеет вид f(x)
= f’(x)
= 0, то в
этом случае метод Ньютона не обеспечивает сходимость.
В качестве примера составления программы расчета ниже представлены
листинги программ отыскания корня уравнения
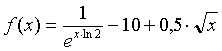
с использованием методов половинного деления (Листинг 1), хорд (Листинг 2) и
уравнения
методом
Ньютона (Листинг 3) на алгоритмическом
языке Паскаль.
Листинг 1. Метод половинного деления
program Project;
uses Crt;
Function f(x: Double): Double;
Begin
f:= 1 /(Exp(x * Ln(2))) - 10 + 0.5*Sqr(x)
End;
Var
x, Eps, a, b, c: Double;
n: Integer;
begin
Writeln('Введите значения a и b'); Read(a, b);
Writeln('Введите точность Eps'); Read(Eps);
n:= 0;
Repeat
c:= (a + b) / 2;
If (f(a) * f(c)) < 0 Then b := c
Else a := c;
Inc(n)
Until (b - a) <= Eps;
x := (a + b) / 2;
Writeln('Корень
равен x=', x:10:7);
Writeln('Количество
итераций q = ',n);
end.
Листинг 2. Метод хорд
program Project;
Uses Crt;
Var
x, Eps, a, b, c:
Double;
n: Integer;
Function f(x: Double): Double;
Begin
f := 1 / (Exp(x * Ln(2))) - 10 + 0.5*Sqr(x)
End;
Function Chord(a, b: Double): Double;
Begin
Chord := (f(b)*a - f(a)*b) / (f(b) - f(a))
End;
begin
Writeln('Введите значения a и b');
Read(a, b);
Writeln('Введите точность Eps');
Read(Eps);
n:= 0;
Repeat
C:= Chord(a, b);
If f(a)*f(C) > 0 Then a := c
Else b := c;
Inc(n)
Until Abs(Chord(a, b) - C) < Eps;
x := c;
Writeln('Корень равен x=', x:10:7);
Writeln('Количество итераций = ',n);
end.
Листинг 3. Метод Ньютона
Function
newton(start, Eps: Extended): Extended;
Var
x, prev: Extended;
{ Заданная функция }
Function F(Arg: Extended): Extended;
Begin
F:= Sqr(Arg) - 2
End;
{ Производная заданной функции }
Function Deriv(Arg: Extended): Extended;
Begin
Deriv := 2 * Arg
End;
Begin
X := start;
Repeat
prev := X;
X := prev - F(prev) / Deriv(prev);
Until Abs(X - prev) <= Eps;
newton := X
End;
Var a, Eps: Extended;
begin
Writeln('Введите начальное приближение a');
Read(a);
Writeln('Введите точность Eps');
Read(Eps);
WriteLn('Корень равен x= ', newton(a, Eps):10:7);
end.
4.3 Задача №2. Методы решения обыкновенных
дифференциальных уравнений.
Цель: приобретение навыков решения обыкновенных дифференциальных уравнений численными методами.
Задание.
1. В таблице 3 выбрать вид функции и начальные условия.
2. Разработать программу расчета дифференциального уравнения.
3. В качестве численного метода решения уравнения использовать метод, представленный в таблице 3.
4. Получить результаты расчета и сравнить полученные результаты с аналитическим методом.
Таблица 3 - Исходные
данные для задачи №2
|
№ варианта |
Функция |
t0 |
tk |
y0 |
Метод решения |
|
0 |
|
0 |
1 |
3 |
Эйлера |
|
1 |
y2t |
0 |
2 |
1 |
Модифицированный |
|
2 |
ye-2t |
0 |
1 |
1 |
Рунге-Кутта |
|
3 |
t2ye-2t |
0 |
1 |
1 |
Модифицированный |
|
4 |
y2 / t2 |
1 |
3 |
1 |
Рунге-Кутта |
|
5 |
y ln(t) / t |
1 |
3 |
1 |
Рунге-Кутта |
|
6 |
y2 ln(t) / t |
1 |
3 |
1 |
Эйлера |
|
7 |
yet/2 |
0 |
1 |
2 |
Эйлера |
|
8 |
ctg(t)/y2 |
p/4 |
p/2 |
1 |
Рунге-Кутта |
|
9 |
|
1 |
2 |
0 |
Модифицированный |
|
10 |
|
0 |
2 |
1 |
Эйлера |
|
11 |
|
1 |
2 |
0 |
Эйлера |
|
12 |
|
2 |
3 |
1 |
Модифицированный |
|
13 |
|
2 |
3 |
1 |
Рунге-Кутта |
|
14 |
|
0 |
1 |
1/e |
Рунге-Кутта |
|
15 |
|
0 |
1 |
1/e |
Модифицированный |
|
16 |
|
0 |
1 |
0 |
Модифицированный |
|
17 |
|
0 |
0.9 |
0 |
Рунге-Кутта |
|
18 |
|
0 |
1 |
3 |
Эйлера |
Методические указания по решению
обыкновенных дифференциальных уравнений.
Уравнение, содержащее одну или несколько производных, называют дифференциальным. Поскольку большинство физических законов науки и техники записано в форме дифференциальных уравнений, их решение является повседневной необходимостью. Задачи моделирования, связанные с движением массы или энергии, также неизбежно ведут к дифференциальным уравнениям. К сожалению, число уравнений, которые можно успешно решить аналитическими методами, очень ограничено. Поэтому при рассмотрении научных и инженерных задач особенно важен вопрос о решении дифференциальных уравнений с помощью персонального компьютера.
Обыкновенные дифференциальные уравнения содержат одну независимую переменную и производные по ней. Чтобы решить обыкновенное дифференциальное уравнение, необходимо знать значения зависимой переменной и (или) её производных при некоторых значениях независимой переменной. Если эти дополнительные условия заданы при одном значении независимой переменной, то такую задачу называют задачей с начальными условиями или задачей Коши. Если же условия заданы при двух значениях независимой переменной, задачу называют краевой. В задаче Коши дополнительные условия называют начальными, а в краевой задаче - граничными.
Задачу Коши можно сформулировать следующим образом. Пусть задано дифференциальное уравнение вида
(6)
и
начальное условие y(x0)=y0. Требуется найти функцию y(x), удовлетворяющую как
указанному уравнению, так и начальному условию. Обычно числовое решение этой
задачи получают, вычисляя сначала значение производной, а затем задавая малое
приращение x и переходя к новой точке x1=x0+h. Положение новой точки
определяют по наклону кривой, вычисленному с помощью дифференциального
уравнения. Таким образом, график числового решения представляет собой
последовательность коротких прямолинейных отрезков, которыми аппроксимируется
истинная кривая 
.
Сам численный метод определяет порядок действий при переходе от данной точки
кривой к следующей. Существует множество методов для численного решения задачи
Коши.
Метод Эйлера - простейший метод решения задачи Коши, позволяющий интегрировать дифференциальные уравнения первого порядка. Его точность невелика, и поэтому на практике им пользуются сравнительно редко. Однако на основе этого метода легче понять алгоритм других, более эффективных методов.
Метод Эйлера основан на
разложении y в
ряд Тейлора в
окрестности x0
y(x0+h) =
y(x0) + hy¢(x0)
+ 
2y¢¢(x0) ¼ (7)
Если
h мало, то члены, содержащие во второй или более высоких степенях,
являются малыми более
высоких порядков и ими можно
пренебречь. Тогда
y(x0+h)=y(x0)+hy¢(x0).
Значение
y¢(x0)
находим из дифференциального уравнения, подставив в него начальное условие.
Таким образом, можно получить приближенное значение зависимой переменной при
малом смещении h от начальной точки. Этот процесс можно продолжить,
используя соотношение
ym+1=yn+hf(x
n, y n ),
n=1,2,¼, (8)
и делая сколь угодно много
шагов.
Ошибка
метода имеет порядок h2, так как члены, содержащие h во
второй и более высоких степенях, отбрасываются.
В качестве примера
составления программы расчета ниже представлен листинг программы, реализующей
метод Эйлера для функции f(x,y) = - 0,1e-ax, при а = 0,6, у0 = 0,1
(Листинг 4) на алгоритмическом языке Паскаль.
Листинг 4. Метод Эйлера
Program Euler;
uses Crt;
var a, b, h, y, x, c : real;
n, i :
integer;
Function f(c, x : real) : real;
begin
f := -0.1*Exp(-c*x)
end;
begin
write('Введите левую границу промежутка '); readln(a);
write('Введите правую границу
промежутка '); readln(b);
write('Введите число точек деления '); readln(n);
write('Введите начальное условие y0 '); readln(y);
write('Введите значение коэффициента a в экспоненте ');
readln(c);
h := (b - a)/n;
x := a;
for i := 1 to n do
begin
y := y + h*f(c, x);
x := x + h;
writeln('Значение функции равно ', y, '
при x = ', x)
end
end.
Модифицированный
метод Эйлера
Хотя
тангенс угла наклона касательной к истинной кривой в исходной точке известен и
равен y¢(x0), он изменяется в соответствии с изменением независимой переменной.
Поэтому в точке x0+h наклон касательной уже не
таков, каким он был в точке x0. Следовательно, при
сохранении начального наклона касательной на всем интервале h в
результаты вычислений вносится погрешность. Точность метода Эйлера можно
существенно повысить, улучшив аппроксимацию производной. Это можно сделать,
например, используя среднее значение производной в начале и в конце интервала.
В модифицированном методе Эйлера сначала вычисляют значение функции в следующей
точке по методу Эйлера
y*n+1=yn+hf
(x n, y n ). (9)
Его используют для вычисления приближенного значения производной в конце интервала f(xn+1,y*n+1). Вычислив среднее между этим значением производной и ее значением в начале интервала, найдем более точное значение yn+1:
yn+1=yn+1/2h[f (xn, yn)+f (xn+1,y*n+1)]. (10)
Ниже
приведен пример листинга программы для решения уравнения
на
промежутке [-1, 0], с начальными условиями у0=0
(Листинг 5) на алгоритмическом языке Паскаль.
Листинг 5. Модифицированный метод Эйлера
Program Euler2;
uses Crt;
var a, b, h, y, x, eps : real;
n, I : integer;
{ Функция вычисления порядка - кол-во знаков после
запятой }
Function t(eps : real) :
integer;
var k : integer;
begin
k := -1;
repeat
eps := eps*10;
k := k + 1
until eps > 1;
t := k
end;
Function f(x, y : real) : real;
begin
f := x*x - y*y
end;
{ Вычисление шага в зависимости от заданной точности
}
Procedure Step(a, b, eps : real; var n : integer; var
h : real);
begin
n := round((b - a)/(2*eps));
h := (b - a)/n
end;
begin
write('Введите левую границу промежутка '); readln(a);
write('Введите правую границу
промежутка '); readln(b);
write('Введите начальное условие y0 '); readln(y);
write('Введите точность вычисления '); readln(eps);
Step(a, b, eps, n, h);
x := a;
writeln('Значение аргумента равно. Значение функции равно');
writeln(' ':8, x:6:6, '
':16, y:6:6);
for i := 1 to n do
begin
y := y +
h*(f (x, y) +f(x + h, y + h*(f(x,
y))))/2;
x := x + h;
writeln(' ':8, x:6:6, ' ':16, y:6:6)
end;
writeln('С точностью до ', eps:1:t(eps))
end.
Методы Рунге-Кутта
При
использовании модифицированного метода Эйлера для получения второй производной
в конечно-разностной форме достаточно было знать наклоны кривой на концах
рассматриваемого интервала. Очевидно, чем выше порядок вычисляемой производной,
тем больше дополнительных вычислений требуется внутри интервала. Метод
Рунге-Кутта дает набор формул для расчета координат внутренних точек, требуемых
для реализации этой идеи. Так как существует несколько способов расположения
внутренних точек и выбора относительных весов для найденных производных, то
метод Рунге-Кутта, в сущности, объединяет целое семейство методов решения
дифференциальных уравнений первого порядка. Наиболее распространенным является
один из них, при котором удерживаются все члены, включая h4. Это метод четвертого
порядка точности, для которого ошибка на шаге имеет порядок h5. Расчеты при использовании
этого классического метода производят по формуле
yn+1=yn+(K1+2K2+2K3+K4)/6, (11)
где
K1=hf (x n, yn), K2=hf (xn+1/2h,yn+1/2K1),
K3=hf (xn+1/2, yn+1/2K2),
K4=hf (xn+h, yn+K3)
Ниже
приведен пример листинга программы для решения уравнения
методом
Рунге-Кутта на промежутке [-1, 0], с начальными условиями у0=0 (Листинг 6) на языке Паскаль.
Листинг
6. Метод Рунге-Кутта
Program Runge_Kutte;
uses Crt;
Const nn = 100;
Type t = array[0..nn] of real;
var x : t; y : t;
a, b, h, eps : real;
n, i :
integer;
Function f(x, y : real) : real;
begin
f := x*x - y*y
end;
{ Вычисление шага в зависимости от заданной точности
}
Procedure Step(a, b, eps : real; var n : integer; var
h : real);
begin
n := round((b - a)/eps);
h := (b - a)/n
end;
Procedure Runge_Kutte(n : integer; h : real; var x : t;
var y : t);
var
k1, k2, k3, k4, ff : real;
begin
for i := 1 to n do
begin
k1 := f(x[i-1], y[i-1]);
k2 := f(x[i-1] + h/2, y[i-1] + h*k1/2);
k3 := f(x[i-1] + h/2, y[i-1] + h*k2/2);
k4 := f(x[i-1] + h, y[i-1] + h*k3);
ff := (k1 + 2*k2 + 2*k3 + k4)/6;
y[i] := y[i-1] + h*ff;
x[i] := x[i-1] + h
end
end;
Procedure Conclusion(n : integer; x : t; y : t);
begin
for i := 1 to n do writeln(x[i], y[i])
end;
begin
write('Введите левую границу промежутка '); readln(a);
write('Введите правую границу
промежутка '); readln(b);
write('Введите начальное условие y0 '); readln(y[0]);
write('Введите точность вычисления '); readln(eps);
Step(a, b, eps, n, h);
x[0] := a;
writeln('Значение аргумента равно. Значение функции равно');
writeln(x[0], y[0]);
Runge_Kutte(n, h, x, y);
Conclusion(n, x, y);
writeln('С точностью до ', h)
end.
Список рекомендуемой литературы
1.
Фирменный стандарт.
Работы учебные. Общие требования к построению, изложению, оформлению и
содержанию. – Алматы: АИЭС, 2002. – 34 с.
2. Мудров В.П. Численные методы для ПЭВМ на языках Бейсик, Фортран, Паскаль. Томск, 1991.
3. Патанкар С. Численные методы решения задач теплообмена и динамики жидкости. – М.: Энергоатомиздат, 1984.- 152 с.
4. Моисеев Н.Н. Элементы теории оптимальных систем. - М.: Наука,1975.- 526 с.
5. Методы и алгоритмы расчета тепловых сетей/Под ред. Хасилева В.Я., Меренкова А.П..- М.: Энергия, 1978.- 176 с.
6. Клима И. Оптимизация энергетических систем. - М.: ВШ, 1991.- 247 с.
7. Рыжиков Ю.И. Решение научно-технических задач на персональном компьютере. – СПб.: Корона принт, 2000.- 272 с.
8. Шуп Т.Е. Прикладные численные методы в физике и технике. - М.: ВШ, 1990.- 255 с.
9. Пакеты прикладных программ. Вычислительный эксперимент. - М.: Наука, 1983.- 148 с.
10.
Плис
А.И., Сливина Н.А. Лабораторный практикум по высшей математике. М.: Высшая
школа, 1983.
11.
Дульнев
Г.Н. и др. Применение ЭВМ для решения задач теплообмена: Учебное пособие - М.:
Высшая школа 1990. - 207 с.
12. Богатырев А.Ф., Панченко С.В., Стояк В.В., Шистер А.Г. Моделирование и оптимизация теплотехнических процессов: Учебное пособие. Алма-Ата: КазПТИ, - 1990.
Содержание
|
Цели и задачи
курса |
3 |
||||||
|
1 Общие методические
указания |
4 |
||||||
|
2 Рабочая
программа курса |
4 |
||||||
|
2.1
Содержание дисциплины |
4 |
||||||
|
2.2 Содержание практических занятий |
6 |
||||||
|
2.3 Перечень лабораторных работ |
6 |
||||||
|
3 Вопросы для
самопроверки |
6 |
||||||
|
4 Контрольное задание |
8 |
||||||
|
4.1 Общие методические указания по
выполнению контрольной работы |
8 |
||||||
|
4.2 Задача
№1 Методы решения алгебраических и трансцендентных уравнений. |
9 |
||||||
|
4.3 Задача
№2 Методы решения обыкновенных дифференциальных уравнений. |
14 |
||||||
|
Список рекомендуемой литературы |
21 |
||||||
|
План 2004 г., поз.104 Нина Гавриловна Борисова
Андрей Анатольевич Кибарин
Татьяна Викторовна
Ходанова Компьютерные
технологии в теплоэнергетических расчетах Рабочая
программа, методические указания и задания к Редактор Ж.М. Сыздыкова
Копировально-множительное
бюро Алматинского института энергетики и связи 050013
Алматы, Байтурсынова, 126 |
|