АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ

 

 

 

 

Кафедра тепловых

энергетических установок

 

 

 

 

 

Математическое моделирование и оптимизация теплоэнергетических процессов и установок

 

 

Рабочая программа, методические указания и задания к
контрольной работе (для студентов специальности 220140 «Тепловые электрические станции заочной формы обучения)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Алматы 2005

СОСТАВИТЕЛИ: А.А Кибарин, А.С. Касимов, Т.В. Ходанова. Математическое моделирование и оптимизация теплоэнергетических процессов и установок. Программа, методические указания и контрольные задания (для студентов специальности 220140 -Тепловые электрические станции заочной формы обучения). - Алматы: АИЭС, 2004. - 31 с.

 

 

 

Методические указания содержат программу, методические указания и задания к контрольным работам, перечень рекомендуемой литературы, контрольные вопросы и требования по оформлению контрольных работ.

Ил. 2, табл. 4, библиогр.- 20 назв.

 

 

 

 

 

 

 

 

Рецензент: канд. физмат. наук, доцент                                     Н.Г.Борисова

 

 

 

 

 

 

 

Печатается по плану издания Алматинского института энергетики и связи на 2004 г.

 

 

 

 

 

 

Ó Алматинский институт энергетики и связи, 2005 г.

Введение

 

Применение вычислительной техники для проведения проектных работ, оценки технико-экономических показателей работающего оборудования дает возможность значительно сократить время для решения поставленных задач, учесть большое количество вариантов расчета, проанализировать влияние множества различных факторов на эффективность работы энергетических установок.

Курс «Математическое моделирование и оптимизация теплоэнергетических процессов и установок» включает в себя знакомство с численными методами решения задач прикладного характера и направлен на освоение методов математического моделирования процессов и установок, используемых в теплоэнергетике.

Курс «Математическое моделирование и оптимизация теплоэнергетических процессов и установок» является обязательным предметом для студентов высших учебных заведений и включается в учебные планы в качестве специальной дисциплины.

 

Цель курса – формирование у студентов знаний, умений и навыков применения математических методов моделирования и оптимизации теплоэнергетических процессов и установок тепловых электрических станций и промышленных предприятий.

 

Задачи курса – овладение студентами методами и приемами аналогового, физического и математического моделирования; выработка навыков и умений: математического моделирования процессов, аппаратов и систем теплоэнергетики; проведения вычислительного эксперимента; использования вычислительной техники и компьютерных технологий для исследования и отбора оптимальных вариантов установок и систем теплоэнергетики.

Дисциплина «Математическое моделирование и оптимизация теплоэнергетических процессов и установок» базируется на знаниях и умениях, приобретенных студентами при изучении курсов: «Математика», «Информатика», «Физика», «Химия», «Техническая термодинамика», «Механика жидкости и газа», «Тепломассообмен», «Котельные установки и парогазогенераторы», «Теория и конструкция нагнетателей и тепловых двигателей», «Компьютерные технологии в теплоэнергетических расчетах».

Знания, умения и навыки, полученные студентами при изучении данной дисциплины, используются при выполнении дипломного проекта, научно- исследовательских и инженерных работ.

В результате изучения дисциплины студенты должны иметь представление:

-       об основных видах и классификации методов моделирования;

-       об общих принципах, этапах и условиях создания математических моделей для теплоэнергетических установок и систем;

-       об основах использования компьютерных технологий для реализации математических моделей.

Студенты должны владеть:

-       методами и приемами разработки математических моделей  для теплоэнергетических процессов,  установок и систем;

-       способами алгоритмизации математических моделей;

-       аналитическими и численными методами решения задач тепломассообмена;

-       численными методами расчета основных характеристик теплоносителей и тепломассообменных аппаратов;

-       методами расчета оптимальных теплоэнергетических систем.

Студенты должны уметь:

-       применять методы математического моделирования при исследовании и проектировании систем и элементов тепловых электрических станций;

-       использовать пакеты прикладных программ для моделирования и оптимизации теплоэнергетических процессов, установок и систем.

Завершающим этапом в изучении курса является выполнение студентами контрольной работы по составлению математической модели, алгоритма и программы расчета теплоэнергетического объекта согласно выбранного варианта.

 

1 Общие методические указания

 

При изучении курса «Математическое моделирование и оптимизация теплоэнергетических процессов и установок» следует руководствоваться рабочей программой курса. Перед выполнением контрольного задания необходимо просмотреть рабочую программу и в соответствии с основными разделами курса проработать материал, составить краткий конспект и решить для закрепления знаний несколько задач. При изучении курса необходимо добиваться глубокого понимания рассматриваемых вопросов, что позволит в дальнейшем использовать полученные знания для решения практических задач.

Контрольное задание предусматривает ответы на вопросы и составление математической модели, алгоритма и программы расчета теплоэнергетического объекта согласно выбранного варианта. К выполнению контрольных работ следует приступить после того, как изучен материал курса.

 

2 Рабочая программа курса

 

Программа курса (100 часов) включает в себя самостоятельную
(82 часов) и аудиторную (18 часов) работу.

Самостоятельная работа состоит из изучения основных разделов курса и выполнения контрольного задания.

Аудиторная работа содержит лекционный материал (8 часов) и лабораторный практикум (10 часов).

Завершающим этапом в изучении курса является выполнение студентами контрольного задания.

 

2.1 Содержание дисциплины

 

2.1.1 Введение

Цель, задачи и содержание курса «Математическое моделирование и оптимизация теплоэнергетических процессов и установок». Его роль в подготовке инженера-теплоэнергетика. Виды математических моделей. Этапы решения задач на ЭВМ.

 

2.1.2 Модели и виды моделирования

Аналоговое, физическое и математическое моделирование. Анализ размерностей и их примеры из курса тепломассообмена. Математическое моделирование как метод решения задач оптимальной организации теплотехнологических процессов. Основные виды и этапы разработки математических моделей. Использование блочного принципа построения математических моделей. Установление адекватности моделей.

 

Методические указания

В этом разделе прежде всего необходимо обратить внимание на основные задачи математического моделирования в теплоэнергетике. После изучения раздела четко представлять классификацию моделей, виды моделирования и схему составления математической модели.

 

2.1.3 Математическое моделирование процессов тепломассообмена

Краткий обзор развития и современное состояние моделирования процессов тепломассообмена. Математические модели, расчет теплофизических свойств водяного пара и продуктов сгорания. Используемые при этом  зависимости и полиномы и погрешность вычисления. Программа расчета теплофизических свойств воды и водяного пара. Численные методы решения стационарных и нестационарных задач теплопроводности. Моделирование задач конвективного теплообмена. Применение метода конечных разностей к уравнениям конвективного теплообмена. Методы моделирования процессов лучистого теплообмена. Детерминированные и стохастические модели массообмена.

 

Методические указания

В этом разделе следует обратить особое внимание на численные методы решения стационарных и нестационарных задач теплопроводности. Большой круг задач тепломассообмена и гидродинамики решается при помощи методов интегральных соотношений, конечно-разностными методами, поэтому при изучении данного раздела этим методам следует уделить внимание.

При решении большинства задач, связанных с расчетами теплообменников, тепловых схем КЭС и ТЭЦ необходимо использование теплофизических свойств газов, воды и водяного пара, поэтому следует обратить особое внимание на расчет теплофизических свойств водяного пара и продуктов сгорания, используемые при этом зависимости и полиномы, программы расчета теплофизических свойств воды и водяного пара.

После изучения раздела необходимо уметь применять различные численные методы и стандартные программы при решении задач тепло - массообмена.

 

2.1.4 Математическое моделирование и оптимизация тепло-  массообменных аппаратов

Моделирование и оптимизация работы рекуперативных и смесительных теплообменников. Постановка задачи расчета теплообменного аппарата. Конструкторский и поверочный расчет. Расчет поверхности теплообмена численным методом. Численный расчет теплообмена при течении несжимаемой жидкости в трубе. Решение дифференциальных уравнений в частных производных  методами сеток и прогонки.

 

Методические указания

В этом разделе следует обратить особое внимание на численные методы определения поверхности теплообмена. Особо обратить внимание на методы решения задач теплообмена при течении несжимаемой жидкости в трубе. Решение дифференциальных уравнений в частных производных методами сеток и прогонки. После изучения раздела необходимо уметь применять различные численные методы и стандартные программы при расчете теплообменных аппаратов.

 

2.1.5 Моделирование процессов в основном оборудовании ТЭС

Численный расчет процесса расширения пара в ступени турбины и в турбине в целом. Численные методы решения нелинейных уравнений. Расчет паротурбинной установки с системой регенерации. Приближенные методы решения систем линейных уравнений. Численный расчет процесса горения в котельном агрегате, равновесного состава продуктов сгорания. Решение обыкновенных дифференциальных уравнений. Методики, их точность и реализация на ЭВМ. Тепловой расчет котельных агрегатов на ЭВМ. Статическая модель расчета поверхности нагрева парового котла. Составление алгоритма и программы расчета. Расчет динамических характеристик котельных агрегатов численным методом.

Методические указания

При изучении данного раздела следует обратить внимание на методы решения нелинейных уравнений и систем линейных уравнений применительно к расчетам паротурбинной установки и котельных агрегатов в сочетании с использованием программ расчета теплофизических свойств воды и водяного пара. После изучения раздела необходимо уметь применять численные методы и стандартные программы при расчете паротурбинных установок и котельных агрегатов.

 

2.1.6 Оптимизационные задачи теплоэнергетики.

Общие методы и принципы подхода к решению задач оптимизации сложных  энергетических установок и систем. Основные задачи оптимизации СТЭПП. Задачи линейного программирования и методы их решения. Численные методы  решения задач нелинейного программирования. Градиентные методы оптимизации. Метод штрафных функций. Методы оптимизации, основанные на последовательном анализе вариантов. Задачи моделирования СТЭПП, сводящиеся к задачам дискретного программирования. Постановка задачи многокритериальной оптимизации и ее особенности. Оптимизация скорости теплоносителя и диаметра труб в теплообменнике. Оптимизация параметров газотурбинной установки. Методы одномерной оптимизации. Оптимизация распределения нагрузки между агрегатами ТЭС и энергетические характеристики паровых турбин и котельных агрегатов. Методы обработки экспериментальных данных. Интерполяция и аппроксимация. Метод наименьших квадратов. Планирование эксперимента. Уравнения для определения характеристик теплофикационных турбин. Многомерная оптимизация. Симплекс-метод, алгоритм и программа расчета. Примеры математических моделей теплоэнергетических процессов и объектов. Пакеты прикладных программ и баз данных для теплоэнергетических процессов.

 

Методические указания

Оптимизация теплотехнологических процессов и систем одна из важнейших задач, которая стоит перед инженером, оптимизация невозможна без знания математических методов. Поэтому при изучении раздела следует обратить внимание на методы оптимизации (одномерные, многомерные) и на то, в каких задачах применяются те или иные методы.

После изучения раздела необходимо уметь применять различные методы оптимизации при решении задач оптимизации параметров термодинамических циклов, оптимизации распределения нагрузки между агрегатами ТЭС.

 

2.2 Лабораторные работы

Лабораторная работа № 1. Моделирование теплообменного аппарата. Определение площади поверхности нагрева теплообменника.

Лабораторная работа № 2. Моделирование простейшей газотурбинной установки (ПГУ). Оптимизация параметров ПГУ.

Лабораторная работа № 3. Моделирование и расчет принципиальной схемы паротурбинной установки.

Лабораторная работа № 4. Моделирование и оптимизация распределения нагрузки между агрегатами ТЭЦ.

 

2.3 Тематика самостоятельной работы

2.3.1 Численные методы решения уравнений пограничного слоя и Навье - Стокса.

2.3.2 Автоматизация математического моделирования тепло-массообменных аппаратов.

2.3.3 Расчет выбросов оксидов азота.

2.3.4 Использование математических моделей для исследования и оптимизации гидравлического и теплового режимов тепловых сетей.

 

3 Вопросы для самопроверки

 

3.1        Виды математических моделей.

3.2        Этапы решения задач на ЭВМ.

3.3        Аналоговое, физическое и математическое моделирование.

3.4        Анализ размерностей и их примеры из курса тепломассообмена.

3.5        Математическое моделирование как метод решения задач оптимальной организации теплотехнологических процессов.

3.6        Основные виды и этапы разработки математических моделей.

3.7        Использование блочного принципа построения математических моделей.

3.8        Установление адекватности моделей.

3.9        Математические модели для расчета теплофизических свойств воды и водяного пара.

3.10   Математические модели для расчета теплофизических свойств продуктов сгорания

3.11   Зависимости и полиномы, используемые при моделировании  теплофизических свойств воды и водяного пара, погрешность вычисления.

3.12   Программа расчета теплофизических свойств воды и водяного пара.

3.13   Численные методы решения стационарных и нестационарных задач теплопроводности.

3.14   Моделирование задач конвективного теплообмена.

3.15   Применение метода конечных разностей к уравнениям конвективного теплообмена.

3.16   Методы моделирования процессов лучистого теплообмена.

3.17   Детерминированные и стохастические модели массообмена.

3.18   Расчет процесса образования оксидов азота в топках паровых котлов.

3.19   Расчет равновесного состава продуктов сгорания.

3.20   Моделирование и оптимизация работы рекуперативных и смесительных теплообменников.

3.21   Постановка задачи расчета теплообменного аппарата.

3.22   Конструкторский и поверочный расчет.

3.23   Расчет поверхности теплообмена численным методом.

3.24   Численный расчет теплообмена при течении несжимаемой жидкости в трубе.

3.25   Решение дифференциальных уравнений в частных производных  методами сеток и прогонки.

3.26   Численный расчет процесса расширения пара в ступени турбины и в турбине в целом.

3.27   Расчет паротурбинной установки с системой регенерации.

3.28   Приближенные методы решения систем линейных уравнений.

3.29   Численный расчет процесса горения в котельном агрегате, равновесного состава продуктов сгорания.

3.30   Решение обыкновенных дифференциальных уравнений. Методики, их точность и реализация на ЭВМ.

3.31   Тепловой расчет котельных агрегатов на ЭВМ.

3.32   Статическая модель расчета поверхности нагрева парового котла.

3.33   Составление алгоритма и программы расчета поверхности нагрева парового котла.

3.34   Расчет динамических характеристик котельных агрегатов численным методом.

3.35   Общие методы и принципы подхода к решению задач оптимизации сложных  энергетических установок и систем.

3.36   Основные задачи оптимизации СТЭПП.

3.37   Задачи линейного программирования и методы их решения.

3.38   Численные методы  решения задач нелинейного программирования.

3.39   Градиентные методы оптимизации. Метод штрафных функций.

3.40   Задачи моделирования СТЭПП, сводящиеся к задачам дискретного программирования.

3.41   Оптимизация скорости теплоносителя и диаметра труб в теплообменнике.

3.42   Оптимизация параметров газотурбинной установки.

3.43   Оптимизация температурных напоров в теплообменных аппаратах.

3.44   Оптимизация сложных трубопроводов.

3.45   Методы одномерной оптимизации.

3.46   Оптимизация распределения нагрузки между агрегатами ТЭС

3.47   Энергетические характеристики паровых турбин

3.48   Энергетические характеристики котельных агрегатов.

3.49   Методы обработки экспериментальных данных. Интерполяция и аппроксимация.

3.50   Метод наименьших квадратов.

3.51   Планирование эксперимента.

3.52   Уравнения для определения характеристик теплофикационных турбин.

3.53   Многомерная оптимизация.

3.54   Симплекс-метод, алгоритм и программа расчета.

3.55   Примеры математических моделей теплоэнергетических процессов и объектов.

3.56   Пакеты прикладных программ и баз данных для теплоэнергетических процессов. Их назначение. Возможности.

 

4 Контрольное задание

 

4.1 Общие методические указания по выполнению контрольного задания

 

Контрольное задание включает в себя ответы на вопросы и решение двух задач.

Номер выполняемого варианта теоретической части контрольного задания соответствует сумме двух последних цифр шифра зачетной книжки студента (таблица 1).

Номер выполняемого варианта задачи №1 контрольного задания - сумма двух последних цифр шифра зачетной книжки студента (таблица 2).

Номер выполняемого варианта задачи №2 контрольного задания – последняя цифра шифра зачетной книжки студента (таблица 3) и первая буква фамилии (таблица 4).

Работы, не соответствующие данным требованиям, не рассматриваются.

Ответы на вопросы должны быть конкретными, краткими, написаны технически грамотно и в то же время полностью охватывать поставленный вопрос. Недопустимо дословное переписывание текста из учебника. Ответы на вопросы, если требуется по заданию, необходимо проиллюстрировать эскизами, схемами, формулами. При использовании литературы необходимо на нее ссылаться и указывать в конце работы источник информации.

При решении задач необходимо приводить сначала методику расчета, а затем результаты вычислений по этой методике. При отсутствии доступа к ПК решение задач может быть осуществлено в период экзаменационной сессии на ПК компьютерного класса кафедры ТЭУ.

Оформление контрольного задания должно соответствовать «Фирменному стандарту. Работы учебные» [1] и при необходимости сопровождаться рисунками и графиками.

При оформлении задач следует придерживаться следующего порядка:

- описание процесса или объекта. Основные уравнения;

- представление математической модели в общем виде;

- методика решения задачи в форме удобной для реализации на ЭВМ;

- блок-схема алгоритма задачи;

- программа и результаты расчета поставленной задачи на одном из алгоритмических языков.

 

Таблица 1

Сумма последних двух цифр шифра зачетной книжки студента	Номера вопросов к контрольной работе
0	1,20,39
1	2,21,40
2	3,22,41
3	4,23,42
4	5,24,43
5	6,25,44
6	7,26,45
7	8,27,46
8	9,28,47
9	10,29,48
10	11,30,49
11	12,31,50
12	13,32,51
13	14,33,52
14	15,34,53
15	16,35,54
16	17,36,55
17	18,37,56
18	19,38,11

 

4.2 Задача №1. Изучение процессов теплообмена в трубопроводах

 

Цель: Приобретение навыков определения конвективного теплообмена для течения несжимаемой жидкости протекающей в трубе при заданном поле скоростей.

Задание.

По данным таблицы 2:

а) провести расчет конвективного теплообмена для течения несжимаемой жидкости, протекающей в трубе при заданном поле скоростей;

б) разработать программу расчета конвективного теплообмена для течения несжимаемой жидкости, протекающей в трубе при заданном поле скоростей. В качестве численного метода решения дифференциального уравнения использовать метод сеток [2];

в) для разработанной программы выполнить следующие задания:

построить в ряде сечений по длине трубы зависимость Т = f(R);

построить зависимости  a= f(Z) и Т = f(Z).

 

Таблица 2

№ варианта	Радиус трубы, R, мм	Длина трубы, L, м	Темпера-тура воды на входе, Твх, 0С	Средняя скорость, w ср, м/с	Число узлов сетки по:		Признак граничного условия на стенке
					R	L
0	50	10	70	2,0	10	100	Тw(z)=Твх+ 40 0С
1	75	10	75	2,5	10	100	qw(z)=300 Вт/м2
2	100	10	80	3,0	10	100	Тw(z)=Твх+ 45 0С
3	125	10	85	3,5	10	100	qw(z)=450 Вт/м2
4	150	10	90	4,0	10	100	Тw(z)=Твх+ 50 0С
5	175	10	100	4,5	10	100	qw(z)=500 Вт/м2
6	200	10	110	5,0	10	100	Тw(z)=Твх+ 55 0С
7	225	10	125	5,0	10	100	qw(z)=550 Вт/м2
8	250	10	150	5,5	10	100	Тw(z)=Твх+ 60 0С
9	50	10	75	2,2	10	100	qw(z)=350 Вт/м2
10	75	10	85	2,8	10	100	Тw(z)=Твх+ 45 0С
11	100	10	95	3,5	10	100	qw(z)=400 Вт/м2
12	125	10	105	3,8	10	100	Тw(z)=Твх+ 50 0С
13	150	10	115	4,2	10	100	qw(z)=500 Вт/м2
14	175	10	120	4,8	10	100	Тw(z)=Твх+ 55 0С
15	200	10	130	5,2	10	100	qw(z)=600 Вт/м2
16	225	10	140	5,5	10	100	Тw(z)=Твх+ 60 0С
17	250	10	145	6,0	10	100	qw(z)=800 Вт/м2
18	50	10	90	2,4	10	100	Тw(z)=Твх+50 0С

Примечание - Объемная теплоемкость для жидкости определяется по температуре воды на входе, теплопроводность - по материалу трубы (для всех вариантов – Сталь 20) из [6,16,18].

 

Методические указания к решению задачи №1

В качестве примера численного решения задачи конвективного теплообмена при заданном поле скоростей рассматривается задача расчета двумерного температурного поля несжимаемой жидкости Т(r,z), протекающей в трубе радиусом R и длиной L (рисунок 1). Температура жидкости на входе в трубу постоянна по поперечному сечению и равна Т_вх. На внутренней поверхности трубы заданы либо распределение по длине температуры стенки Т_w (z), либо плотности теплового потока q_w(z). Течение считается гидродинамически стабилизированным, т. е. поперечная составляющая скорости v_r=0, а продольная v_z=v_z(r) не изменяется по длине трубы. Для ламинарного стабилизированного течения профиль скорости имеет параболический вид

v_z(r)=v_о(1-r²/R²)=2v(1-r²/R²),                                         (1)

где v₀ — скорость на оси трубы;

v — средняя по сечению скорость.

Предполагая, что теплофизические свойства жидкости не зависят от температуры, и диссипация энергии за счет вязкого трения и работа сил давления пренебрежимо малы, тогда стационарное уравнение энергии, описывающее распределение темпера-туры в потоке жидкости, имеет вид

.          (2)

При решении многих практических задач переносом теплоты вдоль трубы (по направлению z) путем теплопроводности можно пренебречь по сравнению с конвективным переносом. Это допущение правомерно при числах Пекле Pe = vd/a > 1. Уравнение энергии в этом случае имеет вид

                                                (3)

Граничные условия для уравнения (3) записываются следующим образом: на оси трубы должно выполняться условие симметрии

,                                                     (4)

на стенке (r = R) задается либо распределение температуры

,                                                    (5)

либо распределение плотности теплового потока

,                                                      (6)

а во входном сечении z = 0 задается температура входящего потока

.                                                  (7)

На выходе из трубы (z = L) граничное условие ставить не надо, так как в уравнении (2) мы пренебрегли второй производной по координате z.

Определив температурное поле Т (r, z), можно найти значения локальных коэффициентов теплоотдачи а (z) в любом сечении трубы по формуле

,                                (8)

где Т (z) — среднерасходная температура жидкости в сечении z, вычисляемая по формуле

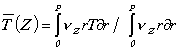.                                          (9)

Отметим, что уравнение (3) по форме аналогично нестационарному одномерному уравнению теплопроводности для неограниченного цилиндра, только вместо производной по времени записана конвективная производная v_z дТ/dz. Поэтому параболическое уравнение (3) может быть решено с помощью численных схем для одномерных нестационарных задач теплопроводности.

Введем в двумерной области [0£r£ R] * [0 £ r £ L] равномерную по r и по z пространственную сетку: r_n=(n—1)h_T, h_T=R/(N_r—1), n=1,....N_r; z_m=(m — 1)h_z,
m = 1 ..., N_z (рисунок 2) - и поставим задачу определения сеточной функции Т_п,т = Т (r_n, z_m).

Для внутренних узлов сетки запишем разностную аппроксимацию уравнения энергии, учитывая, что конвективная производная аппроксимируется разностью «против потока»

, n=2, …., Nz,      (10)

здесь v_п=v_z(r_п); r_n±1/2= r_n ± h_r/2.

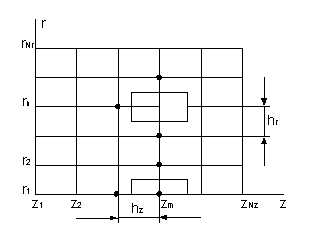Разностные уравнения для узлов, лежащих на оси трубы (n=1, m=2,..,N_z), построим методом баланса, рассматривая элементарный объем, который показан на рисунке 2. Тепловой поток Р’, поступающий в радиальном направлении через поверхность r =h_r/2, равен

.         (11)

Тепловой поток Р", выносимый из объема протекающей жидкостью, определяется выражением

.                                         (12)

В выражении (12) принято, что в элементарный объем жидкость втекает с температурой и_1,т-₁, а вытекает с температурой u_1,m, как это следует из схемы «против потока». Приравнивая потоки Р' и Р", получим

                                      (13)

Для узлов, лежащих на стенке трубы (п =N_r), разностные уравнения имеют вид:

в случае граничного условия (5)

,                                               (14)

при  простейшем варианте аппроксимации граничного условия (6)

, m=2,…,N_z..                                                                  (15)

В формуле (15) не учитывается тепловой поток, уносимый жидкостью, так как на стенке v _{n r} = v (R) = 0.

Условие (7) на входе в трубу задается точно

                                                 (16)

Разностные уравнения (10)-(15) связывают значения сеточной функции в двух соседних сечениях по оси z с номерами (т—1) и т. При известных значениях u_n,m-1 (п =1,..., N_r) эти уравнения образуют систему N_z уравнений относительно N_r значений и_п,_т сеточной функции в сечении z=z_m. Система уравнений имеет трехдиагональную матрицу и может быть решена методом прогонки, которая проводится «поперек трубы». Таким образом, построенная разностная схема аналогична неявной схеме для нестационарного одномерного уравнения теплопроводности с тем отличием, что роль временных слоев играют поперечные сечения z_m. В первом сечении (m = 1) температуры задаются граничным условием (16), а далее последовательно для каждого сечения решается методом прогонки система разностных уравнений (10)-(15) относительно неизвестных и_п,_т (п=1, ..., N_r), и определяются температуры в данном сечении.

Перепишем систему (10)-(15) в каноническом виде для системы с трехдиагональной матрицей

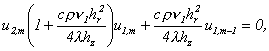                                   (17)

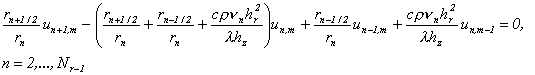(18)

 в случае условия (5)

или  в случае условия (6).

Из выражений (17) легко определить коэффициенты а_п, b_п, с_п, d_n для формы записи (22), которая используется при обращении к стандартной подпрограмме, реализующей метод прогонки [2]. Отметим, что а_п, b_п и с_п не зависят от номера поперечного сечения и рассчитываются вне основного цикла, проводимого по этим сечениям.

В приложении 1 приведен текст программы, предназначенной для расчета температурного поля жидкости по разностной схеме (10)-(16) и определения локальных коэффициентов теплоотдачи a(z_m). Распределение скорости v_z (r) в поперечном сечении, а также распределения Т_w(z) и q_w(z) могут описываться с помощью подпрограмм-функций [2] или в теле программы (приложение 1).

В каждом сечении после нахождения температур и_п,_т рассчитывается значение локального коэффициента теплоотдачи a_m= a (z_m), определяемого согласно выражению (8). При этом средняя в данном сечении температура рассчитывается с помощью квадратурной формулы трапеций

                                       (19)

а приближенное значение локального коэффициента теплоотдачи вычисляется

                                      (20)

Найденные значения a_т накапливаются в массив и выводятся на печать после окончания цикла по сечениям. Печатается таблица значений координаты z_т, коэффициента теплоотдачи a_m и локального числа Нуссельта Nu = a_m2R/l. Кроме того, в заданных сечениях выводятся значения температур и _n,m {п = 1, ..., Nr}.

 

Метод прогонки

Одним из лучших методов решения систем линейных алгебраических уравнений общего вида является метод последовательного исключения Гаусса с выбором главного элемента. Расчет по формулам этого метода требует примерно N ³ арифметических операций, поэтому при достаточно больших N потребуются значительные затраты машинного времени.

Особенность системы (17), (18) состоит в том, что в каждое уравнение для внутренних точек входят по три неизвестных, номера которых отличаются на единицу, а в первое и последнее уравнения для точек n = 1 и
п = N - по два «соседних» неизвестных. Если учесть такой специфический вид построенной нами системы разностных уравнений, то эффективность алгоритма ее решения можно существенно повысить.

Запишем систему уравнений в следующем каноническом виде

для граничной точки п= 1

                                                  (21)

для внутренних точек п= 2, ..., N - 1

                                     (22)

для граничной точки п = N

                                            (23)

Выражения для коэффициентов а_п, b_п, с_п, d_n нетрудно получить из соответствующих уравнений разностной схемы.

Систему уравнений (21) - (23) можно записать в матричной форме, причем в матрице отличны от нуля будут лишь коэффициенты, находящиеся на главной диагонали и на двух прилегающих к ней диагоналях

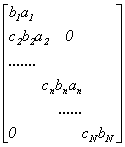
 =                                     (24)

Напомним, что N уравнений системы получаются из матричной формы записи путем умножения каждой из N строк на вектор-столбец неизвестных. При умножении строки на столбец элементы с одинаковыми номерами перемножаются, а затем все произведения складываются.

Трехдиагональный вид матрицы позволяет организовать вычисления по методу Гаусса так, чтобы не проводить операции с нулевыми элементами. Тем самым объем вычислений удается значительно уменьшить.

Модификация метода Гаусса для системы уравнений с трехдиагональной матрицей называется методом прогонки. Рассмотрим этот достаточно простой алгоритм решения системы уравнений (21)—(23). Из первого уравнения (21) для п - 1 можно выразить u₁ через u₂

;                                      (25)

здесь введены обозначения

.                                               (26)

Далее, если подставить полученное выражение для u₁ во второе уравнение (22) для п =2, то в нем останутся только неизвестные u₁ и u₃

                                       (27)

Теперь можно выразить u₂ через и₃ в виде

,                              (28)

где

                                                (29)

Если аналогичную процедуру подстановки выражений для u_n в (n + 1)-е уравнение вида (22) повторять для п = 2, ..., N - 2, то в результате получим рекуррентные соотношения, связывающие температуры в точках п и (п + 1):

                                                                     (30)

в которых коэффициенты f_n и g_n рассчитываются по формулам

.                   (31)

Начальные значения f₁ и g₁, необходимые для расчета коэффициентов f_n и g_n по формулам (31), определяются соотношениями (26).

После вычислений всех коэффициентов f_n и g_n до (N-1) – х рассмотрим последнее уравнение (30) при п=N - 1 совместно c уравнением (23) исходной системы для п = N

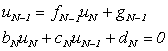                                             (32)

Из решения этой системы двух уравнений найдем температуру в последней точке

                                      (33)

Теперь, двигаясь от точки N к точкам N-1, N - 2, ... 1, можно последовательно вычислить значения и_n по рекуррентной формуле (30) и таким образом найти решение во всех точках.

Итак, алгоритм расчета по рассмотренному методу прогонки состоит из:

- вычисления коэффициентов f₁ и g₁ по (26);

- вычисления коэффициентов f_n , g_n при п=2,...,  N-1 по (31);

- определения и_N по (33);

- определения и_n по (30) в порядке убывания номера от N - 1 до 1.

Вычисление f_n и g_n часто называют прямым ходом прогонки, а вычисление u_n в порядке убывания номера п — обратным ходом.

Для решения системы (21)—(23) по методу прогонки требуется примерно 9N арифметических действий, т. е. значительно меньше, чем при использовании метода Гаусса для систем общего вида.

В приложении 1 приведена программа реализующая метод прогонки.

 

4.3 Задача № 2. Изучение влияния параметров топливно-воздушной смеси на равновесный состав продуктов сгорания и теоретическую температуру горения.

 

Цель: приобретение навыков расчетного определения влияния температуры и давления топливно-воздушной смеси на состав и температуру сгорания.

Задание.

По данным таблицы 3:

- провести расчет для заданного вида топлива равновесного состава продуктов сгорания, согласно методическим рекомендациям и определение зависимости теоретической температуры горения от температуры и давления воздуха;

- разработать программу расчета на ЭВМ для заданного вида топлива равновесного состава продуктов сгорания газообразного и жидкого углеводородного топлива, и адиабатической температуры горения.
В качестве численного метода решения нелинейного уравнения использовать метод, указанный в исходных данных для выбранного варианта;

- в качестве графического материала представить зависимость адиабатической температуры горения и концентрации компонентов в продуктах сгорания топлива от температуры и давления воздуха (таблица 4).

 

Методические указания к решению задачи №2

Для углеводородных топлив расчет ведется в предположении, что продукты сгорания состоят из девяти компонентов . Этого вполне достаточно для решения поставленной задачи. Химическое равновесие между названными компонентами описывается следующими балансовыми уравнениями:

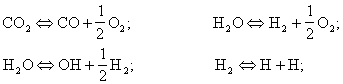                             (34)    .

Основываясь на уравнениях (34) для определения содержания отдельных компонентов можно составить систему уравнений для констант равновесия, вытекающих из закона действующих масс.

Уравнения материального баланса:

по углероду:

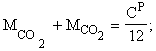                                                (35)

по водороду:

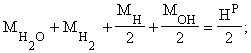                                      (36)

по кислороду:

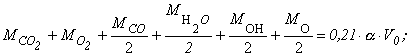       (37)

по азоту:

                                                     (38)

Уравнения для констант равновесия:

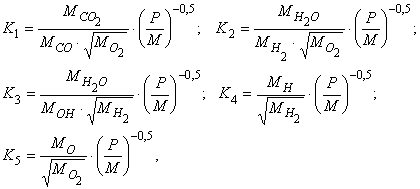
где

М_i - число киломолей  i - го компонента, образующееся при сгорании 1 кг топлива, кмоль/кг;

С^р, Н^р- массовые доли углерода и водорода в составе топлива;

М - общее количество киломолей продуктов сгорания, кмоль/кг;

V₀ - теоретически необходимое количество воздуха для сжигания
1 кг топлива, кмоль/кг;

a-коэффициент избытка воздуха;

К_i - константы равновесия химических реакций;

Р - давление, МПа.

Предложенная система уравнений (35), (39) решается численным способом, где в качестве параметра задается число М. Начальное приближение для М задается равным количеству продуктов сгорания в предположении об отсутствии диссоциации

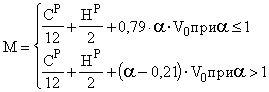                                   (40)

После расчета состава продуктов сгорания может быть определена теоретическая температура сгорания. Теоретическая температура горения зависит от ряда факторов и, в частности, от температуры воздуха (окислителя) и давления, при котором происходит процесс сгорания. Теоретическая температура горения определяется также численным способом, методом последовательных приближений с точностью до 1 К.

После расчета состава продуктов сгорания необходимо определить тепловой эффект реакции DН для случая, когда реагенты имеют температуру Т₁, а продукты сгорания – Т₂

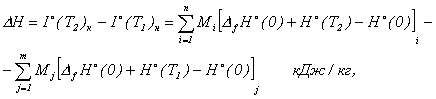                  (41)

где   - полная энтальпия продуктов сгорания при температуре Т₂, кДж/кг;

  - полная энтальпия реагентов при температуре Т₁, кДж/кг;

n – количество компонентов продуктов сгорания;

m - количество компонентов исходной смеси (реагентов);

М _i(j) - количество киломолей i – го (j– го) компонента;

- энтальпия образования вещества при стандартных условиях и Т=Т_о, кДж/кг;

- - изменение энтальпии вещества в стандартных условиях при изменении температуры от 0 до Т, кДж/кг.

Значения  и - приводятся в справочной литературе.

Формула (41) предполагает отсутствие фазовых переходов, т.е. определяет низшую теплоту сгорания топлива.

 

Расчетная схема и результаты тестового расчета

Выбирается состав топлива согласно таблицы 3. В компьютер вводятся его характеристики, а также температура воздуха и давление. На основе балансовых уравнений (34) определяется содержание отдельных компонентов входящих в состав газов. На основании уравнений материального баланса (35) и констант равновесия (36) численным методом с заданным числом М (37) рассчитывается состав равновесной смеси при заданной в таблице 3 температуре воздуха при 1 £ a > 1. Затем при заданных (таблица 4) температурах воздуха и давления, при которых происходит процесс сгорания, численным способом рассчитывается теоретическая температура горения методом последовательных приближений с точностью до 1 К. По результатам расчёта строятся следующие характеристики

.

Весь интервал изменения коэффициента избытка воздуха от 0,65 до 1,35 разбивается на 10 равных интервалов. Функциональная градуировка  по оси ординат различная. Расчёт повторяется для давлений и температур воздуха по таблице 4 и строится зависимость: . При этом весь интервал изменения температуры воздуха по оси ординат разбивается на 4 - 6 равных интервала от 300 до 800 °С.

 

Таблица  3

 

Таблица  4

№ вар.	Первая буква фамилии
0	А, М, Ц	1	2	4	10	300	400	600	800
1	Б, Н, Ч	1	3	6	12	300	400	500	700
2	В, О, Ш	1	2	6	10	350	500	700	800
3	Г, П, Щ	1	3	6	15	300	400	500	600
4	Д, Р, Э	1	4	8	12	300	350	400	600
5	Ж, С, Ю	1	2	4	8	350	500	600	800
6	З, Т, Я	1	4	8	16	400	500	600	700
7	И, У, Е	1	2	3	5	300	400	500	600
8	К, Ф, Ё	1	2	5	10	400	500	700	800
9	Л, Х	1	3	7	12	300	500	600	700

 

В приложении 2 представлен листинг программы, предназначенной для расчета состава продуктов сгорания, реализуемой на языке Паскаль.

Список литературы

1.   Фирменный стандарт. Работы учебные. Общие требования к построению, изложению, оформлению и содержанию. – Алматы: АИЭС, 2002. – 34 с.

2.   Дульнев Г.Н. и др. Применение ЭВМ для решения задач теплообмена. Учебное пособие - М.: Высшая школа 1990.  - 207 с.

3.   Богатырев А.Ф., Панченко С.В., Стояк В.В., Шистер А.Г. Моделирование и оптимизация теплотехнических процессов: Учебное пособие.- Алма-Ата: КазПТИ, 1990.

4.   Пасконов В.М., Полежаев В.И., Чудов Л.А. Численное моделирование процессов тепло- и массообмена. – М.:Наука, 1984.- 288с.

5.   Патанкар С. Численные методы решения задач теплообмена и динамики жидкости. – М.: Энергоатомиздат, 2003.- 312 с.

6.   Ривкин С.Л., Александров А.А. Термодинамические свойства воды и водяного пара. -М.: Энергия, 1975.

7.       Вульман Ф.А. Математическое моделирование тепловых схем ПТУ на ЭВМ.- М.: Машиностроение, 1985.-112 с.

8.       Математическое моделирование и оптимизация систем тепло-, водо-, нефте- и газоснабжения  / Под ред. Меренкова А.П..- Н.: Наука, 1992.- 234 с.

9.       Зайцев А.И. и др. Математическое моделирование источников энергоснабжения промышленных предприятий. - М.: Энергия, 1991.- 163 с.

10.   Злотин Г.Н., Шумский С.Н., Дульгер М.В. Методика расчета  термохимических характеристик сгорания углеводородных топлив // Энергетика. Известия вузов: -1988. - №8 - 58-63 с.

11.   Бахвалов Н.С., Жидков Н., Кобельков Г. Численные методы. –Москва: Физматлит, 2000.

12.   Попырин Л.С. Математическое моделирование и оптимизация теплоэнергетических установок. – М.: Энергия, 1978. – 416 с.

13.   Хрилев Л.С. Теплофикационные системы. - М.: Энергоатомиздат, 1988.- 272 с.

14.   Методы и алгоритмы расчета тепловых сетей / Под ред.
Хасилева В.Я., Меренкова А.П..- М.: Энергия, 1978.- 176 с.

15.   Клима И. Оптимизация энергетических систем. - М.: ВШ, 1991.- 247 с.

16.   Бажан П.И., Каневец Г.Е., Селиверстов В.М. Справочник по теплообменным аппаратам. – М.: Машиностроение, 1989. – 365 с.

17.   Плис А.И., Сливина Н.А. Лабораторный практикум по высшей математике. М.: Высшая школа, 1983.

18.   Тепловые и атомные электрические станции. Справочник под редакцией Григорьева В.А., Зорина В.М.- М.: Энергоиздат, 1989.

19.   Ю.Ю.Тарасевич. Математическое и компьютерное моделирование. Вводный курс: Учебное пособие. – М.:Эдиториал УРСС, 2001. – 144 с.

20.   Мудров В.П. Численные методы для ПЭВМ на языках Бейсик, Фортран, Паскаль. -Томск, 1991.

Приложение А

Программа расчета конвективного теплообмена для течения несжимаемой жидкости протекающей в трубе при заданном поле скоростей

 

program alfa;

{$APPTYPE CONSOLE}

uses SysUtils;

type vek=array[1..10] of real;

  const n=10;m=100;

  var

  u:array[1..n,1..m] of real;

  r,v,Tcp,alf:vek;

  a,b,c,d,g,f:vek;

  t,q,vcr,hr,hz,r0,l,cv,lam,s1,s2:real;

  i,j,k:integer;

begin

  writeln('r0,l,vcr,t,cv,lam');

  readln(r0,l,vcr,t,cv,lam);

  hr:=r0/(n-1);hz:=l/(m-1);j:=1;

  for i:=1 to n do  begin

  u[i,1]:=t;

  r[i]:=(i-1)*hr;

  v[i]:=2*vcr*(1-sqr(r[i]/r0))  end;

  a[1]:=1; c[1]:=0;

  writeln('введите гранич.усл.на стенке: 1-если задан T(z); 2-если задан q(z)');

  readln(k);

  case k of

{Программа расчета коэффициента теплоотдачи методом прогонки}

  1:begin c[10]:=0; d[10]:=t+40 end;

  2:begin write('введите q=');readln(q);c[10]:=1; d[10]:=q*hr/lam end

  end;

  a[10]:=0; b[10]:=-1;

  repeat  j:=j+1;

  b[1]:=-(1+cv*1000*v[1]*hr*hr/hz/4/lam);

  d[1]:=cv*1000*v[1]*hr*hr/hz/4/lam*u[1,j-1];

  f[1]:=-a[1]/b[1]; g[1]:=-d[1]/b[1];

  for i:=2 to n-1 do begin

     a[i]:=1+0.5/(i-1); d[i]:=cv*1000*sqr(hr)*v[i]/lam/hz*u[i,j-1];

     c[i]:=1-0.5/(i-1); b[i]:=-(2+cv*1000*sqr(hr)*v[i]/lam/hz); end;

  for i:=2 to n-1 do begin

      f[i]:=-a[i]/(b[i]+c[i]*f[i-1]);

      g[i]:=-(d[i]+c[i]*g[i-1])/(b[i]+c[i]*f[i-1]);

      end;

   u[10,j]:=-(d[10]+c[10]*g[9])/(b[n]+c[n]*f[n-1]);

   for i:=9 downto 1 do begin

   u[i,j]:=f[i]*u[i+1,j]+g[i];

   {writeln(u[i,j]);}

   end;

   until(j>=m);

    s1:=0; s2:=0;

   for j:=1 to m do  begin

     for i:=1 to n-1 do begin

       s1:=s1+v[i]*r[i]*u[i,j];

       s2:=s2+v[i]*r[i] end;

     Tcp[j]:=s1/s2;end;

     for j:=2 to m do

     alf[j]:=lam*(u[n,j]-u[n-1,j])/(hr*(u[n,j]-Tcp[j]));

   for i:=1 to n do begin

     for j:=1 to m do

     write(u[i,j*10]:6:1); writeln; readln end;

   for j:=1 to m do

     write(Tcp[j]:6:1);

   readln ;

   for j:=1 to m do

     write(alf[j*10]:8:2);

   readln

end.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приложение Б

Программа расчета равновесного состава продуктов сгорания

 

program termohim_2;

{$APPTYPE CONSOLE}

uses   SysUtils;

label 7;

const

  R=8.31; dh1=0; dh2=0; dh3=-2.839e5; dh4=3.909e4; dh5=2.16e5;

  dh6=2.4678e5; dh7=-1.138e5; dh8=-3.93e5; n=11; eps=0.01;

type

  vek=array[1..n] of real;

var

  i:integer;

  alf:vek;

  Tg,M,Mp,Cp,Hp,p,F,L0,x1,x2,x3,x4,x5,x6,x7,x8,x9,A,B:real;

  k1,k2,k3,k4,k5,f1,f2,f3,f4,f5,f6,f7,f8:real;

procedure MDOP(A,B,eps,f,Tg:real;k1,k2,k3,k4,k5:real;var x7:real);

  var

    d1,f1:real;

  function y(x7:real):real;

  begin

    y:=(-(k4/2/sqrt(F)+k2*sqrt(x7)/2/k3)+sqrt(sqr(k4/2/sqrt(f)+k2*sqrt(x7)/2/k3)+2*Hp*(1+k2*sqrt(x7*f))))/2/(1+k2*sqrt(x7*f))

  end;

function Fun(x7:real):real;

  begin

    Fun:=sqrt(x7)*(k1*Cp*sqrt(f)/24/(1+k1*sqrt(x7*f))+sqrt(x7)+k2*sqr(y(x7))*sqrt(f)/2+k2*y(x7)/2/k3+k5/2/sqrt(f))-0.21*alf[i]*L0+Cp/24

  end;

  BEGIN

    repeat

    d1:=(A+B)/2; f1:=Fun(d1);

    if (Fun(A)*f1)>0 then A:=d1 else B:=d1;

    until (abs((B-A)/d1)*100<eps);

    x7:=d1;{writeln(fun(x7)) }

  END;

begin

  alf[1]:=0.67;

  writeln('Tg,L0,Cp,Hp,p');

  readln(Tg,L0,Cp,Hp,p);

  f1:=-19.66+22.6034*ln(Tg)+4.177e5/sqr(Tg)-3.76e3/Tg+4.05e-3*Tg-2.33e-7*sqr(Tg)+8.33e-12*exp(3*ln(Tg));

  f2:=-24.695+33.55*ln(Tg)-5.113e5/sqr(Tg)+4.346e5/Tg+11.768e-4*Tg-2.34e-9*sqr(Tg)-1.284e-12*exp(3*ln(Tg));

  f3:=14.877+25.3*ln(Tg)+8.23e3/sqr(Tg)-2.2e3/Tg+9.84e-3*Tg-6.4e-7*sqr(Tg)-2.3e-11*exp(3*ln(Tg));

  f4:=29.289+23.12*ln(Tg)+3.085e5/sqr(Tg)-3.46e3/Tg+4.307e-3*Tg-2.848e-7*sqr(Tg)-1.0714e-11*exp(3*ln(Tg));

  f5:=-24.6+20.7962*ln(Tg);

  f6:=19.182+21.2419*ln(Tg)+2.034e4/sqr(Tg)-5.87e2/Tg-2.5e-4*Tg+2.558e-8*sqr(Tg)-5.31e-13*exp(3*ln(Tg));

  f7:=-4.748+29.5948*ln(Tg)-3.3e5/sqr(Tg)+2.18e3/Tg+2.74e-3*Tg-2.097e-7*sqr(Tg)+8.295e-12*exp(3*ln(Tg));

  f8:=-129.51+49.185e4/Tg+4.9e-3*Tg-4.03e-7*sqr(Tg)+1.779e-11*exp(3*ln(Tg));

  k1:=exp((f2/2+f7-f8)/R-(dh2/2+dh7-dh8)/(R*Tg));

  k2:=exp((f2/2+f1-f3)/R-(dh2/2+dh1-dh3)/(R*Tg));

  k3:=exp((f1/2+f4-f3)/R-(dh1/2+dh4-dh3)/(R*Tg));

  k4:=exp((2*f5-f1)/R-(2*dh5-dh1)/(R*Tg));

  k5:=exp((2*f6-f2)/R-(2*dh6-dh2)/(R*Tg));

  for i:=1 to n do

begin

  alf[i]:=alf[1]+(i-1)*0.068;

  if (alf[i]<=1) then

           M:=Cp/12+Hp/2+0.79*alf[i]*L0

      else  M:=Cp/12+Hp/2+(alf[i]-0.21)*L0;

 7: f:=p/M;

  A:=0; B:=0.21*alf[i]*L0;

  MDOP(A,B,eps,f,Tg,k1,k2,k3,k4,k5,x7);

  x1:=Cp/12/(1+1/k1/sqrt(x7*f));

  x2:=Cp/12-x1;

  x8:=k5*sqrt(x7/f);

  x9:=0.79*L0*alf[i];

  x4:=sqr((-(k4/2/sqrt(f)+k2*sqrt(x7)/2/k3)+sqrt(sqr(k4/2/sqrt(f)+k2*sqrt(x7)/2/k3)+2*Hp*(1+k2*sqrt(x7*f))))/2/(1+k2*sqrt(x7*f)));

  x3:=x4*k2*sqrt(x7*f);

  x5:=k4*sqrt(x4/f);

  x6:=x3/k3/sqrt(x4*f);

  Mp:=x1+x2+x3+x4+x5+x6+x7+x8+x9;

  if abs((M-Mp)/Mp)*100>0.1 then begin M:=Mp; goto 7 end;

  writeln('alfa=',alf[i]);

  writeln('x1=',x1,'  ',x2,'  ','x3=',x3,'  ',x4,'  ','x5=',x5,'  ',x6,'  ','x7=',x7,'  ',x8,'  ','x9=',x9);

  writeln('M=',M,'    ','Mp=',Mp);

  readln;

  end

end.

 

 

 

Содержание

 

Введение		3
1	Общие методические указания	4
2	Рабочая программа курса	4
	2.1 Содержание дисциплины	5
	2.2 Лабораторные работы	7
	2.3 Тематика самостоятельной работы	8
3	Вопросы для самопроверки	8
4	Контрольное задание	10
	4.1 Общие методические указания по выполнению контрольного задания	10
	4.2 Задача №1. Изучение процессов теплообмена в трубопроводах.	11
	4.3 Задача № 2. Изучение влияния параметров топливно-воздушной смеси на равновесный состав продуктов сгорания и теоретическую температуру горения.	18
Список рекомендуемой литературы		22
Приложение А		23
Приложение Б		25

 

 

 

 

 

Сводный план  2004 г., поз.105

 

 

 

Андрей Анатольевич Кибарин

Арман Салемович Касимов

Татьяна Викторовна Ходанова

 

 

 

 

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И ОПТИМИЗАЦИЯ ТЕПЛОЭНЕРГЕТИЧЕСКИХ ПРОЦЕССОВ И УСТАНОВОК

 

Программа, методические указания и контрольные задания

(для студентов специальности 220140 -Тепловые электрические станции заочной формы обучения)

 

 

Редактор               Ж.М. Сыздыкова

 

 

Подписано в печать“___”___”___”	Тираж   50   экз.
Формат 60х 84 1/16	Обьем ___________ уч. - изд.л.
Бумага типографская № 1	Заказ ________. Цена  _____ тенге

 

 

 

Копировально-множительное бюро Алматинского института энергетики и связи

 

 

 

050013, Алматы, Байтурсынова 126