ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Алматы энергетика және байланыс институты
Е. Нұрекен
СҰЙЫҚ ЖӘНЕ ГАЗ МЕХАНИКАСЫ
050717 – Жылу энергетика мамандығының студенттеріне арналған
дәрістер жинағы
Алматы 2009
ҚҰРАСТЫРУШЫ: Е. Нұрекен. Сұйық және газ механикасы. 050717 – Жылу энергетикасы мамандығының студенттеріне арналған дәрістер жинағы. Алматы: АЭжБИ, 2009.
Дәрістер жинағында қазіргі сұйық және газ механикасының негізгі бөлімдері қарастырылған. Газ бен сұйық қозғалысының теңдеулері жалпы физика, теориялық механика, техникалық жылуқозғалым және т.б. пәндермен байланыстарын ескере отырып берілген.
Сұйықтың құбырдағы қозғалысы және құбырларды сұйықағулық есептеу, қатты денелердің ағысталуы, шекаралық қабат теориясы және т.б. жалпы қозғалыс теңдеулері негізінде қарастырылған
Дәрістер жинағы 050717 – Жылу энергетикасы мамандығының студенттеріне арналған.
№1 дәріс. Кіріспе
1.1 Сұйық және газ механикасы пәні және оның әдістері
Сұйық және газ механикасы (СГМ) сұйықтар мен газдардың теңдесу қалпын және қозғалыс заңдылықтарын зерттейтін ғылым. СГМ физиканың бөлімі. Бұдан былай қысқалық үшін “сұйық” деген аталымның мағынасы тек тамшылы сұйықтар ғана емес және газдар да деп түсінілуі керек.
СГМ пәні үш
бөлімнен тұрады: сұйықтеңдесу (гидростатика),
қозғалыс кейпі (кинематика) және қозғалым
(динамика). Сұйықтеңдесу бөлімінде
сұйықтардың және оларға батырылған
денелердің теңдесуі зерттеледі. Екінші бөлімде
сұйық қозғалысының геометриялық
қасиеттерін сұйыққа әрекет етуші күштерден
бөліп алып қарастырады. Қозғалым бөлімінде
сұйықтардың қозғалысын және оған
батырылған немесе шекаралас орналасқан қатты денемен
әрекеттесуі зерттеледі. Қозғалымның екі бөлімі
бар: сұйыққозғалым және газқозғалым.
Сұйыққозғалым сығылмайтын
сұйықтың (тығыздығы
r=тұрақты)
қозғалу заңдарын зерттейді. Газқозғалым
сығылатын сұйықтардың қозғалысын (r![]() тұрақты), яғни
газдардың қозғалысын олардың тығыздығы
елеулі өзгергенде қарастырады. Сығылатын
сұйықтардың қозғалу құбылыстары
сығылмайтын сұйықтардың қозғалыс
құбылыстарына қарағанда күрделірек болады.
тұрақты), яғни
газдардың қозғалысын олардың тығыздығы
елеулі өзгергенде қарастырады. Сығылатын
сұйықтардың қозғалу құбылыстары
сығылмайтын сұйықтардың қозғалыс
құбылыстарына қарағанда күрделірек болады.
СГМ-да сұйықтардың қозғалысын зерттеу үшін маңыз (масса), қайрат (энергия) және қозғалыс мөлшерінің сақталу заңдары мен Ньютон заңдары қолданылады. Бұлардың негізінде қозғалыстың шаққылық (дифференциалдық) теңдеулері құрастырылады.
СГМ есептерін шешкенде теориялық және тәжірибелік әдістер үйлестіріледі. Көбінесе іс жүзінде пайда болған есептерді теориялық әдіспен қозғалыс теңдеулерін аумақылау (интегралдау) арқылы шешу қиынға соғады. Сондықтан көп жағдайларда тәжірибелік әдістер пайдаланады.
1.2 Сұйық ұғымының анықтамасы
Тамшылы сұйықтар мен газдардың қасиеттері әртүрлі екені белгілі. Сондықтан оларды жалпы сұйық деген ұғымымен біріктіруге мүмкіндік беретін жалпы сипаттамалық қасиеттерін тауып көрсету қажет. СГМ-ның тұрғысынан тамшылы сұйықтар мен газдардың екі жалпы сипаттамалық қасиеттері бар: жеңіл қозғалғыштық немесе аққыштық пен тұтастық.
Сонымен, сұйық дегеніміз тұтас және жеңіл қозғалғыш немесе аққыш орта.
Сұйықтың бұл қасиеттерін тереңірек түсіндірейік.
Өте аз жанама күш сұйық бөлшегіне едәуір уақыт әрекет етсе, бөлшек пішінін өзгертеді (1.1-суретті қараңыз), яғни аға бастайды. Осыны жеңіл қозғалғыштық немесе аққыштық деп атайды.
Жеңіл қозғалғыштық сұйыққа тән қасиет болса, тұтастық қасиеті-ұйғару. Шынында барлық сұйықтар молекулалардан (затшалардан) тұрады. Затшалардың ара қашықтығы болады. СГМ жеке затшалардың қозғалысын зерттемейді, сұйықты тұтас орта деп қарайды.
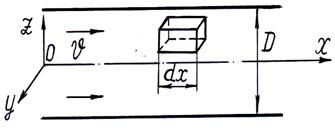
Тұтастық туралы ұйғару сұйық ағынының барлық көрсеткіштерін: жылдамдық, тығыздық жєне қысымды үзіксіз шамалар яғни кеңістік мекендіктердің (координаттарының) үзіксіз бернелері (функциялары) ретінде қарастыруға мүмкіндік береді. Егер, ағысталған денелердің сызықтық сипаттама өлшемдері (шардың диаметрі (қосөресі), қанаттың хордасы және т.б.) затшалар ара қашықтығына қарағанда өте үлкен болса, онда сұйықтар үшін тұтастық шарты орындалады. Сұйықтың кішкене (элементар) көлемінің сызықтық өлшемі затшалар ара қашықтығына қарағанда жеткілікті үлкен және ағысталған денелердің сызықтық сипаттама өлшемдерінен жеткіліткті кіші болуы керек. (1.2-суретті қараңыз).
|
|
|
|
||
|
1.1 Сурет |
|
1.2 Сурет |
||
Тұтастықты Кнудсен саны (Kn) арқылы сипаттайды
Kn=lз/L,
мұнда
lз - затшалар ара қашықтығы;
L- ағынның сипаттамалық өлшемі (құбыр үшін L=D, 1.2-сурет).
Егер, Kn<10-3 болса, сұйық ортаны тұтас деуге болады. Егер, Kn>10-3 болса, ортаны тұтас деуге болмайды.
Әуелік (атмосфералық) қысымдағы газдар үшін lз≈10-5 см, тамшылы сұйықтар үшін lз≈10-7-10-8 см, яғни өте аз шамалар. Сондықтан әдеттегі техникалық жағдайларда тұтастық шарты әрқашан да оңай орындалады. Газ қысымы азайса, lз өседі де тұтастық шарты орындалмауы мүмкін (мысалы, ғарыш құралдары үшін).
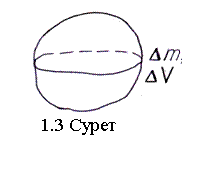
1.3 Тығыздық. Сығылғыштық
Кейбір кішкене көлемдегі сұйық тығыздығының орташа мәні сол көлемдегі маңыздың (массаның) ∆m көлемге (1.3-сурет) қатынасы ретінде анықталады.
ρор=∆m/∆V кг/м3.
Мұнда маңыз ∆m қысым мен ыстықтыққа (температураға) тәуелді емес, оларға тәуелді көлем ∆V. Көлем қысым өскенде кішірейеді, ал ыстықтық өскенде ұлғаяды.
Берілген көлемдегі заттың таралуы бірқалыпты болмаса, тығыздықтың нүктедегі мәнін былай анықтауымыз керек
![]() .
.
Сұйық тығыздығы жалпы жағдайда ыстықтық (температура) пен қысымға тәуелді
ρ=f (T,P).
Қысым мен ыстықтық өзгергенде сұйық тығыздығының (көлемінің) өзгеру қасиетін сығылғыштық деп атайды.
Тамшылы сұйықтардың газдармен салыстырғанда сығылғыштығы өте аз, сондықтан оларды көп есептерді шешкенде сығылмайтын сұйықтар деп қарауға болады. Сонымен, сұйықтарды екіге бөлуге болады: сығылмайтын (ρ=тұрақты) және сығылатын сұйық (ρ≠тұрақты).
Сығылмайтын сұйықтардың қозғалысы туралы есептерді шешу едәуір оңай. Сығылмайтын сұйық қозғалғанда көлем пішінін өзгерте алады, бірақ шамасын өзгертпейді, яғни сұйықтың тығыздығы өзгеріссіз қалады.
1.4 Тұтқырлық және сұйықтағы үйкеліс туралы Ньютонның заңы
Тұтқырлық сұйық бөлшектерінің салыстырмалы жылжуына қарсылық көрсету қасиеті.
Тұтқырлық сұйық қозғалғанда үйкеліс күші арқылы байқалады. Егер сұйық қозғалмаса не екі шектес қабаттар арасында салыстырмалы жылдамдық болмаса, онда ішкі үйкеліс нөлге тең болады.
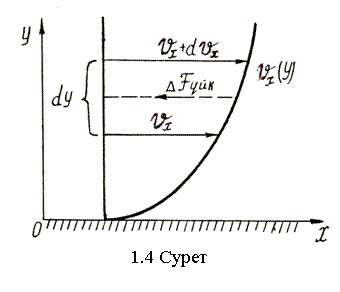 И.Ньютонның
тәжірибеден тура бағытта тақташа бойымен қозғалған
тұтқыр сұйықтың екі қабаты арасында аудан
бірлігіне әрекет ететін үйкеліс күші ағысқа тік
бағыттағы жылдамдық градиентіне сәйкес екенін тапты (1.4-сурет)
И.Ньютонның
тәжірибеден тура бағытта тақташа бойымен қозғалған
тұтқыр сұйықтың екі қабаты арасында аудан
бірлігіне әрекет ететін үйкеліс күші ағысқа тік
бағыттағы жылдамдық градиентіне сәйкес екенін тапты (1.4-сурет)
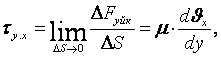 Н/м2,
(1.1)
Н/м2,
(1.1)
мұнда
∆Fүйк - үйкеліс күші;
∆S - жанасу бетінің ауданы;
μ-тұтқырлықтың қозғалымдық еселеуіші (коэффициенті);
![]() - У - жебесі бойынша
есептелген жылдамдық градиенті (тікмегземі);
- У - жебесі бойынша
есептелген жылдамдық градиенті (тікмегземі);
τyx - үйкеліс күшінің кернеуі;
μ - берілген сұйықтың физикалық сипаттамасы, ыстықтыққа (температураға) тәуелді. Тамшылы сұйықтардың тұтқырлығы ыстықтық өссе азаяды, ал газдардың тұтқырлығы өседі, бұл олардың затшалық (молекулалық) құрылымының әр түрлілігіне байланысты.
Тұтқырлықтың
қозғалымдық еселеуішінен басқа келтірілген еселеуіш
қолданылады, ол тұтқырлықтың
қозғалымдық еселеуіші мен сұйық
тығыздығының қатынасына тең ![]() =μ/ ρ, м2/с.
=μ/ ρ, м2/с.
Тұтқырлық еселеуіші тұтқырөлшер (вискозиметр) көмегімен тәжірибе арқылы анықталады.
Сұйық механикасында кейбір есептердің шешуін оңайлату үшін кейде тұтқырсыз сұйық ұғымын пайдаланады.
Тұтқырсыз сұйық табиғатта болмайды, ол теориялық ұғым. Тұтқырлығы бар сұйықтарды нақты не тұтқыр сұйық деп атайды.
1.5 Сұйықта әрекет ететін күштер. Қысым
Сұйық тыныштықта немесе қозғалғанда әр түрлі күштер әрекетінде болады. Күштерді жіктеудің әр түрлі қағидалары бар. Күш түсу аймағына қарай күштер ішкі және сыртқы болып бөлінеді. Табиғаттарына не әрекеттің сипатына қарай күштерді маңыздық және беттік деп бөлуге болады.
Маңыздық көрсеткіштер берілген сұйық көлемін құрастыратын бөлшектерге әрекет етеді. Олар берілген көлемнің маңызына сәйкесті. Маңыздық күштерге ауырлық, екпіндік, электрмагниттік күштер жатады.
Беттік күштер бөлінген көлемнің тек бетіне ғана әрекет етеді. Бұл күштерге үйкеліс, қысым және беттік керілу күштері жатады.
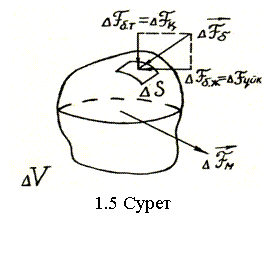
Маңыздық
күштерді сипаттау үшін олардың таралу тығыздығы
деген ұғым кіргізейік. Егер сұйықтың кішкене
көлемі ΔV-ға (1.5-сурет) маңыздық күш
![]() әрекет
етсе, онда
әрекет
етсе, онда
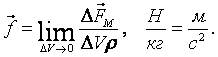
Сірә, вектор ![]() —
сұйықтың маңыз бірлігіне келетін маңыздық
күш және үдеу өлшемділігінде болады. Мысал ретінде
ауырлық күші
—
сұйықтың маңыз бірлігіне келетін маңыздық
күш және үдеу өлшемділігінде болады. Мысал ретінде
ауырлық күші ![]() үшін
үшін ![]() екенін көрсетуге болады,
мұнда g ауырлық күшінің үдеу векторы (мегземесі).
екенін көрсетуге болады,
мұнда g ауырлық күшінің үдеу векторы (мегземесі).
Беттік күштерді кернеумен сипаттауға болады. Кішкене ауданша ∆S-қа әрекет ететін беттік күш бас векторы (мегземесі) қозғалатын сұйықта екі құраушыдан: тік және жанама күштерден тұрады. Берілген ауданшаға жанама әрекет ететін үйкеліс күші, ол үшін кернеу кейіптемесі (формуласы) (1.1) жоғарыда жазылған.
Тұтқырсыз сұйықта және тыныштықтағы сұйықта жанама күш нөлге тең болады, берілген ауданшаға тек тік бағытта қысым күші ∆Fқ әрекет етеді. Қысым күші үшін кернеу былай жазылады

мұнда
p-қысым.
Сонымен, қысым дегеніміз - беттің аудан бірлігіне тік әрекет ететін күш.
Халықаралық бірліктер жүйесінде (СИ) қысымды өлшеу бірлігі 1Н/м2=1 Па.
№2 дәріс. Сұйықтеңдесу (гидростатика)
2.1 Сұйықтеңдесудің шаққылық (дифференциалдық) теңдеулері
Сұйық теңдесу
күйінде болса, онда оның бөлшектері бір-біріне және
ыдыс қабырғасына қатысты қозғалмау керек (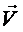 =0, p
=0, p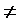 0). Бірақ ыдыспен
бірге біртұтас болып әр түрлі қозғалыстарда
(айналу, ілгерілмелі және т.б.) бола алады.
0). Бірақ ыдыспен
бірге біртұтас болып әр түрлі қозғалыстарда
(айналу, ілгерілмелі және т.б.) бола алады.
Теңдесу күйінде тұрған сұйық ішіндегі күштердің қасиеттерін қарастырайық.
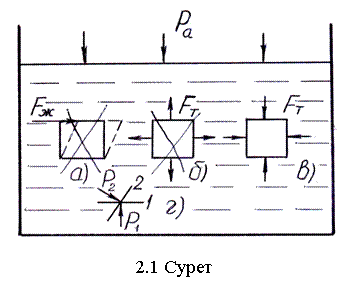 1. Тыныштық
күйдегі сұйықта беттік күштер ойша бөлінген
бөлшек бетіне тек тік бағытталады, ал жанама күштер
нөлге тең болу керек, яғни ∆Fж=0,
∆Fт
1. Тыныштық
күйдегі сұйықта беттік күштер ойша бөлінген
бөлшек бетіне тек тік бағытталады, ал жанама күштер
нөлге тең болу керек, яғни ∆Fж=0,
∆Fт![]() 0 (2.1-сурет) және ∆Fт
бөлшектің ішіне қарай бағытталады (2.1в-сурет).
0 (2.1-сурет) және ∆Fт
бөлшектің ішіне қарай бағытталады (2.1в-сурет).
Сұйық жеңіл қозғалғыш орта болғандықтан (тәжірибеден белгілі) өте аз жанама күштің әрекетінен қозғалады. Сөйтіп, жанама күштің болуы сұйық ішінде ағыс түзеді де тыныштық күйін бұзады.
2. Тыныштық күйдегі сұйықта қысым уақыт бойынша өзгермеу керек, тек нүктелер мекендіктеріне тәуелді болады
p=f(x,y,z).
Егер тыныштық күйдегі сұйықта қысым уақыт бойынша өзгерсе, онда ағыс пайда болып теңдесу бұзылады.
Сұйықта әрекет ететін маңыздық күштердің сипатынан нүктедегі қысымның тәуелділігін анықтайтын теңдеулерді қорыту үшін, тыныштықтағы сұйықтың ішінде ойша бөлектенген кішкене тік бұрышты қиықжақтың (параллепипедтің) теңдесуін қарастырамыз (2.2-суретті қараңыз).
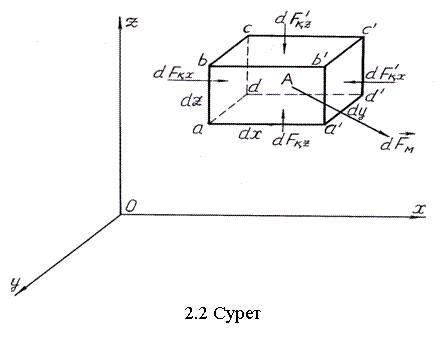
Маңыздық
күштер тығыздығыныњ ![]() құраушыларын fx ,fy
,fz , деп белгілейміз.
Қиықжақтың ортасында орналасқан А
нүктесінде қысымның шамасы Р болсын. А
нүктесінен қиыќжақтың жақтарына өткенде
қысым шамасы өзгереді, өйткені қысым мекендік бернесі
(функциясы) p=f(x,y,z). abcd және a`b`c`d`
жақтарына өткенде тек бір мекендік өте аз шамаға (
құраушыларын fx ,fy
,fz , деп белгілейміз.
Қиықжақтың ортасында орналасқан А
нүктесінде қысымның шамасы Р болсын. А
нүктесінен қиыќжақтың жақтарына өткенде
қысым шамасы өзгереді, өйткені қысым мекендік бернесі
(функциясы) p=f(x,y,z). abcd және a`b`c`d`
жақтарына өткенде тек бір мекендік өте аз шамаға (![]()
![]() -ге) өзгереді, соған
байланысты қысым шамасы да өзгереді. Қысым өсімшесі
-ге) өзгереді, соған
байланысты қысым шамасы да өзгереді. Қысым өсімшесі
![]()
![]()
![]() . (2.1)
. (2.1)
Mұнда дербес
туынды ![]() (х
жебесі бағытындағы қысым тік- мегземесі) х жебесі
бағытындағы ұзындық бірлігіне келетін қысым
шамасының өзгеруін көрсетеді.
(х
жебесі бағытындағы қысым тік- мегземесі) х жебесі
бағытындағы ұзындық бірлігіне келетін қысым
шамасының өзгеруін көрсетеді.
(2.1)-өрнек бойынша abcd жағындағы қысым
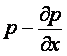
![]() ,
,
ал a`b`c`d` жағындағы қысым
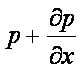
![]() , -ге
, -ге
тең болады. Aл
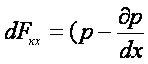
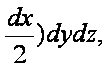 (2.2)
(2.2)
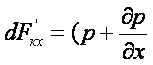
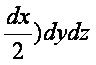 , (2.3)
, (2.3)
dFMX=fxrdxdydz. (2.4)
Осылайша ![]() жєне
жєне ![]() тікмегземелері арқылы
басқа жақтардағы қысым мен күш шамалары
өрнектеледі.
тікмегземелері арқылы
басқа жақтардағы қысым мен күш шамалары
өрнектеледі.
Қарастырылған бөлшек теңдесу күйінде болғандықтан оған түскен күштерді әрбір мекендік жебесіне проекцияласақ, онда олардың қосындысы нөлге тең болуы керек.
Алдымен барлық күштерді х жебесіне проекцияласақ
![]() (2.5)
(2.5)
теңдеуін аламыз. Оған (1.3-1.5) өрнектерін қойып, ұқсас мүшелерін келтіріп барлық мүшелерін rdxdydz-ке бөлсек, мына шаққылық (дифференциялдық) теңдеу шығады
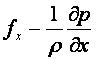 =0.
=0.
Осындай теңдеуді y жєне z жебелері үшін алуға болады. Сонда мынадай теңдеулер жүйесін жазуға болады
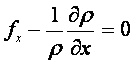 ,
,
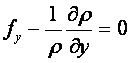 , (2.6)
, (2.6)
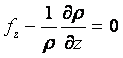 .
.
Бұл теңдеулер дербес туындылы бірінші ретті теңдеулер жүйесі. Оларды алғашқы қорытқан Л. Эйлер.
(2.6) теңдеулерді мегземелік белгілеріне сәйкес былай жазуға болады
![]() -
-![]() gradp=0.
(2.7)
gradp=0.
(2.7)
Мегземелік жазу ықшамды, талдау жүргізгенде ыңғайлы.
(2.6) теңдеулерді қысымның толық дифференциалы арқылы былай жазуға болады
dp=![]() (fxdx+fydy+fzdz).
(2.8)
(fxdx+fydy+fzdz).
(2.8)
(2.6), (2.7), (2.8)-теңдеулер баламалы (эквивалентті) теңдеулер.
Әрбір нүктесінде қысым шамасы бірдей болып келетін сұйық бетін деңгей беті (бірдей қысым беті) деп атайды. Мұндай беттің теңдеуін
(2.8) –ші өрнектен p=тұрақты, демек dp=0 дeп табуға болады
fxdx+fydy+fzdz=0. (2.9)
2.2 Сығылмайтын сұйықтың ауырлық күш өрісіндегі теңдесуі
Сұйықтеңдесу шаққылық (дифференциалдық) теңдеулерін (2.8, 2.9) қолданып, тыныштық күйдегі сұйық ішіндегі қысымның таралуын табуға болады. Қысымның таралу заңдылығын біле тұра сұйық құйылған ыдыстардың қабырғаларына және сұйыққа батырылған денелерге түсетін қысым күштерін анықтауға болады.
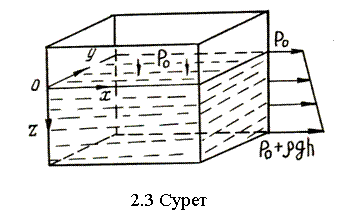 Сығылмайтын
сұйықтың күш өрісіндегі теңдесуін
қарастырайық (2.3-сурет).
Сығылмайтын
сұйықтың күш өрісіндегі теңдесуін
қарастырайық (2.3-сурет).
Егер маңыздық күштерден сұйыққа тек ауырлық күш әрекет етсе, онда оның тығыздығының проекциялары мекендік (координат) жебелеріне fx=0, fy=0 және fz=g болады.
(2.8) және (2.9) теңдеулер мына түрге келеді
dp=![]() gdz,
(2.10)
gdz,
(2.10)
gdz=0. (2.11)
(2.11) теңдеуді аумақылап (интегралдап) берілген жағдайда бірдей қысым беттері жатық (горизонталь) жазықтықтар
Z=тұрақты (2.12)
екeнін аламыз.
Сығылмайтын
сұйық жағдайында (![]() =тұрақты) (2.10)
теңдеу оңай аумақыланады (инетегралданады)
=тұрақты) (2.10)
теңдеу оңай аумақыланады (инетегралданады)
p=ρgz+C . (2.13)
Аумақылау тұрақтысы С-ны шекаралық шарттан анықтауға болады: ерікті беткe (тамшылы сұйық пен газ жанасқан бетке) сыртқы қысым p0 єрекет етеді, яѓни z=0 болғанда p=p0. Сонда (2.13)-тен аламыз демек,
p=p0+ρgz. (2.14)
Бұл қатыс
тыныштықтағы сұйықтың кез келген
нүктесіндегі қысым сыртқы қысым p0 мен
салмақ қысымының ![]() gz қосындысына тең деп
тұжырымдалған жалпы сұйықтеңдесу
заңының өрнегі (2.3-сурет).
gz қосындысына тең деп
тұжырымдалған жалпы сұйықтеңдесу
заңының өрнегі (2.3-сурет).
(2.14) теңдеу Паскаль заңының математикалық жазылуы: сұйық бетіне түскен сыртқы қысым барлық бағытта бірдей таралады.
(2.14) теңдеу арқылы анықталған қысымды толық қысым деп атайды. Егерде толық қысым ауа қысымынан үлкен болса (p>pa), онда сұйықта артық қысым дейді, ол тең болады
paрт=p-pa.
Егер сұйықтағы толық қысым ауа қысымынан кіші болса (p<pa), онда сиретулік не вакуум дейді
pc=pa-p.
№3 дәріс.
3.1 Айналған ыдыстағы сығылмайтын сұйықтың теңдесуі
Егер ыдыс айналмаса, онда сұйық бөлшектеріне тек бір ғана маңыздық күш төмен қарай бағытталған ауырлық күш түседі. Z жебесіне тік жазықтықтар бірдей қысым беттері болады. Еркін бет деңгей беті болғандықтан (p = pa), демек, ол да жазық бет болады.
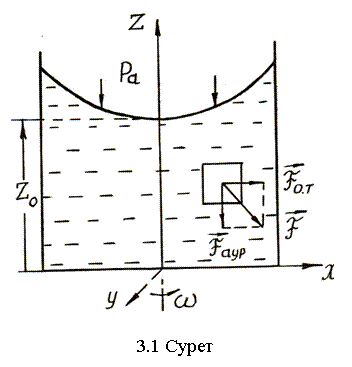 Егер ыдысты
тұрақты бұрыштық жылдамдықпен айналдыра бастаса,
онда сұйық бөлшектеріне екінші маңыздық күш
өремен (радиуспен) ыдыстың қабырғасына бағытталған
екпіндік ортадан тепкіш күш әрекет ете бастайды (3.1-сурет). Біраз
уақыттан кейін сұйық ыдыстың бұрыштық
жылдамдығына ие болады да, оның еркін беті өзгереді: орта
шенінде сұйықтың деңгейі төмендейді
қабырға жағында жоғарлайды, еркін бет айналмалы бет
болып қалыптасады, яғни теңдесудің жаңа
күйі салыстырмалық деп аталатын теңдесу орнайды.
Егер ыдысты
тұрақты бұрыштық жылдамдықпен айналдыра бастаса,
онда сұйық бөлшектеріне екінші маңыздық күш
өремен (радиуспен) ыдыстың қабырғасына бағытталған
екпіндік ортадан тепкіш күш әрекет ете бастайды (3.1-сурет). Біраз
уақыттан кейін сұйық ыдыстың бұрыштық
жылдамдығына ие болады да, оның еркін беті өзгереді: орта
шенінде сұйықтың деңгейі төмендейді
қабырға жағында жоғарлайды, еркін бет айналмалы бет
болып қалыптасады, яғни теңдесудің жаңа
күйі салыстырмалық деп аталатын теңдесу орнайды.
Маңыздық күштердің таралу тығыздығының проекциялары былай жазылады
fx=![]() 2x; fy=
2x; fy=![]() 2y; fz=-g.
(3.1)
2y; fz=-g.
(3.1)
Шекаралық шарт : x=y=0; z=z0 болғанда p=pa,
Z=![]() (x2+y2)+C,
(3.2)
(x2+y2)+C,
(3.2)
p=pa+![]() (x2+y2)+
(x2+y2)+![]() g(z0-z).
(3.3)
g(z0-z).
(3.3)
(3.2) z жебесіне қатысты айналу параболойд теңдеуі. Демек, сұйықты z жебеге қатысты айналдырған жағдайда, деңгей беті айналу параболоид түріне ие болады.
(3.3) теңдеуді біртекті емес заттарды бір-бірінен ажырататын құрылғы-центрифуганы есептеу үшін қолдануға болады. Мысалы, механикалық қоспадағы сұйықтарды бөлу (кілегейді сүттен, суды мұнайдан бөлу және т. б.) . Тығыздығы үлкен сұйық (су) ыдыстың қабырғасына қарай ал тығыздығы кіші сұйық (мұнай) ыдыстың орта шеніне жиналады.
3.2 Жазық беттегі сұйықтың қысым күші
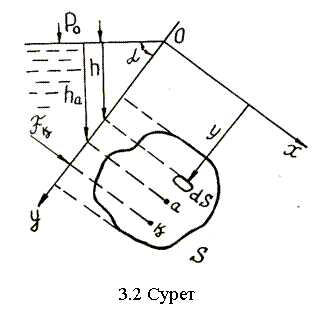 Көлбеу
жатқан жазықтықтағы S ауданына түсетін
қысым күшін анықтайық. Жазықтықта кішкене
ауданша dS-ке (3.2-сурет), түсетін қысым күші мына
кейіптемемен анықталады
Көлбеу
жатқан жазықтықтағы S ауданына түсетін
қысым күшін анықтайық. Жазықтықта кішкене
ауданша dS-ке (3.2-сурет), түсетін қысым күші мына
кейіптемемен анықталады
dFќ=pdS=(p0+![]() gh)dS. (3.4)
gh)dS. (3.4)
Сұйықтың
тереңдігі h пен кішкене ауданша мекендігінің мынандай
байланысы бар h=ysіn![]() .
.
Бүкіл S ауданына түсетін қысым күшін табу үшін (3.4) өрнекті S ауданы бойынша аумақылау (интегралдау) керек
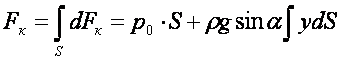
мұнда
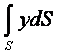 S
ауданының 0x жебесіне қатысты теңдесулік
айналдырғысы (моменті). Бұл аумақыны есептеп шықса
S
ауданының 0x жебесіне қатысты теңдесулік
айналдырғысы (моменті). Бұл аумақыны есептеп шықса
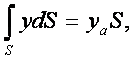
және
Fќ=p0S+![]() ghaS. (3.6)
ghaS. (3.6)
Егер p0 ауа қысымына тең болса, онда аpтық қысым күші мына кейіптемеден анықталады
![]() =
=![]() ghaS,
(3.7)
ghaS,
(3.7)
мұнда
ha-S ауданының ауырлық орталығының тік мекендігі.
Бас вектордың (қорытқы күштің) Fќ -ның түсетін нүктені қысым орталығы деп атайды. Бұл нүктенің мекендіктерін есептеп табуға болады
yќ=ya+Іa/ya×S
немесе
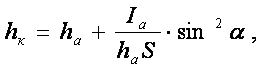 (3.8)
(3.8)
мұнда
Іa-S ауданының х жебесіне қатарлас ауырлық орталығы арқылы өтетін жебеге қатысты екпіндіктің айналдырғысы.
3.3 Архимед заңы
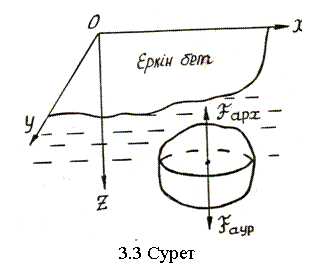
Сұйыққа батырылған денеге түсетін қысым күшін есептесе мына кейіптеме шығады
Fарх=-![]() cgVд,
(3.9)
cgVд,
(3.9)
мұнда Vд-батырылған дене көлемі;
![]() c-сұйық
тығыздығы.
c-сұйық
тығыздығы.
Fарх-cұйықтың еркін бетіне бағытталған (3.3-сурет), яғни денені сұйықтан итеріп шығаруға тырысады ол көтеруші күш немесе архимедтік күш деп аталады.
Архимед заңы: Сұйыққа батырылған денеге әрекет ететін көтеруші күш батырылған дене ығыстырып шығарған сұйықтың салмағына тең.
Егер дененің салмағы архимедтік күштен кем болса, онда дене сұйық бетіне қалқып шығады. Егер дененің салмағы архимедтік күштен артық болса, онда дене сұйыққа батады. Қалқып шығу немесе бату
Fарх= Fаур болғанда тоқтайды. Ал дененің салмағы архимедтік күшке тең болса, дене сұйық ішінде теңдесу күйінде болады.
Архимед - тұңғыш рет көтеруші күштің бар екенін тәжірибеден анықтаған ғaлым.
№4 дәріс. Сұйық қозғалысының негізгі ұғымдары мен теңдеулері
4.1 Сұйық қозғалысының түрлері
Егер мына
тәуелділіктің ![]() =f(x,y,z,
=f(x,y,z,![]() ) нақтылы түрі тауып
көрсетілсe, онда жылдамдық мегземесінің (векторының)
өрісін (таралуын) белгілі, сұйық қозғалысын
берілген деп есептеуге болады.
) нақтылы түрі тауып
көрсетілсe, онда жылдамдық мегземесінің (векторының)
өрісін (таралуын) белгілі, сұйық қозғалысын
берілген деп есептеуге болады.
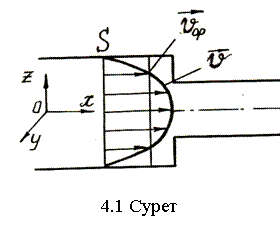
Мысал үшін құбырдың берілген қимасындағы жылдамдықтың таралуын қарастырамыз (4.1-суретті қараңыз).
S-ағынның көлденең қимасының ауданы.
Құбыр қабырғасында үйкеліс күшінің әрекетінен жылдамдық нөлге тең. Қабырғадан алшақтағанда жылдамдық өсіп құбыpдың ортасында ең үлкен мәніне жетеді.
Ағынның берілген нүктесіндегі жылдамдықты жеpгілікті жылдамдық деп атаймыз. Іс жүзінде ағынның көлденең қимасы бойынша орташаланған жылдамдықты жиі қолданады
![]() =
=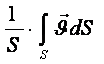 .
.
![]() -көлденең
мекендіктерге тәуелді емес, ол тек бойлық мекендігіне тєуелді
болады.
-көлденең
мекендіктерге тәуелді емес, ол тек бойлық мекендігіне тєуелді
болады.
Егер жылдамдық өрісі уақытқа байланысты өзгермесе, онда қозғалыс қалыптасқан деп аталады
![]() =f(x,y,z,).
=f(x,y,z,).
Егер ол уақытқа тәуелді болсa, онда қозғалыс қалыптаспаған болады
![]() =f(x,y,z,
=f(x,y,z,![]() ) .
) .
Жалпы жағдайда жылдамдық мегземесі үш мекендікке тәуелді, онда қозғалыс (не ағын) үш өлшемді не кеңістікті деп аталады.
Егер
жылдамдық мегзгемесі екі мекендікке тєуелді болса ![]() =f(x,y,
=f(x,y,![]() ), қозғалыс екі
өлшемді не жазықтық деп аталады.
), қозғалыс екі
өлшемді не жазықтық деп аталады.
![]() Егер жылдамдық
мегзгемесі бір мекендікке тәуелді болса
Егер жылдамдық
мегзгемесі бір мекендікке тәуелді болса ![]() =f(x,
=f(x,![]() ), қозғалыс біp өлшемді
деп аталады.
), қозғалыс біp өлшемді
деп аталады.
Енді сұйық бөлшегінің үдеуін анықтайық. Оның физикалық мағынасына сәйкес үдеу жылдамдық мегземесінің уақыт бойынша алынған толық туындысымен анықталады.
Қозғалатын
бөлшектің мекендіктері уақыт бернесі (функциясы) болады x=x(![]() ); y=y(
); y=y(![]() ); z=z(
); z=z(![]() ). Сонда
жылдамдық мегземесі уақыттың күрделі бернесі болады
). Сонда
жылдамдық мегземесі уақыттың күрделі бернесі болады
![]() .
.
Күрделі бернені шаққылау тәртібін қолдансақ
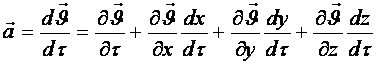 .
.
Қозғалған сұйық бөлшектер мекендіктерінің уақыт бойынша туындылары жылдамдықтың тиісті проекциялары болғандықтан, яғни
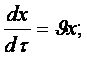
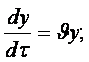
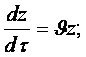
аламыз.
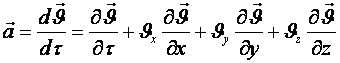 . (4.1)
. (4.1)
Мегземелік талдаудың белгілеуін пайдаланып (4.1) өрнегін былай жазуға болады
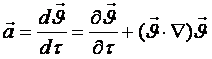 , (4.2)
, (4.2)
мұнда
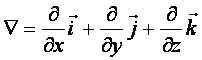 - Гамильтон
операторы (набла).
- Гамильтон
операторы (набла).
Сұйық бөлшектің толық үдеуі екі қосылғыштан тұруы мүлдем қатты дененің қозғалуынан бөлекше сұйық тұтас ортаның ерекшелігі болады. (4.2) теңдіктің оң жағындағы бірінші қосылғышы кеңістіктің кейбір белгіленген нүктесінде жылдамдықтың уақыт бойынша өзгеруін көрсетеді, яғни жергілікті өзгеруін үдеудің жергілікті құраушысы деп атайды. Екінші қосылғыш бөлшек жылдамдығының ол орын ауыстыpғандағы өзгеруін сипаттайтындықтан оны үдеудің ағындық (конвекциялық) құраушысы деп атайды.
Қалыптасқан
қозғалыста жеpгілікті үдеу әрқашан да нөлге
тең 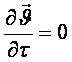 .
Ағындық үдеу қалыптасқан және қалыптаспаған
қозғалыстарда бола алады.
.
Ағындық үдеу қалыптасқан және қалыптаспаған
қозғалыстарда бола алады.
Егер
толық үдеу нөлге тең болса ![]() , қозғалыс
бірқалыпты болады. Бірқалыпты қозғалыста
сұйық бөлшектерінің жылдамдығы ағын бойында
тұрақты болады. Кері жағдайда қозғалыс
бірқалыпты болмайды.
, қозғалыс
бірқалыпты болады. Бірқалыпты қозғалыста
сұйық бөлшектерінің жылдамдығы ағын бойында
тұрақты болады. Кері жағдайда қозғалыс
бірқалыпты болмайды.
4.2 Сұйық қозғалысының тәртіптері
1883 ж. О.Рейнольдс сұйық қозғалысын тәжірибе арқылы зерттеп ретті (ламинарлық) және ретсіз (турбуленттік) деген екі қозғалыс тєртіптері болатынын анықтады.
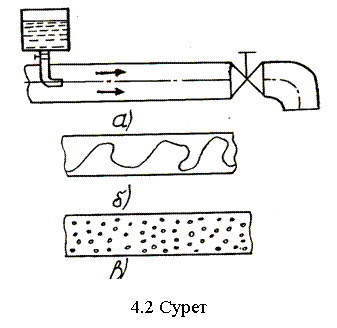
Рейнольдстің тєжіpибелік қoндырғысы 4.2а-суретте көрсетілген.
Су құйылған күбіге шыны құбыр қосылған. Реттегіштің көмегімен судың құбырдағы қозғалу жылдамдығын өзгертуге болады. Д ыдысынан жіңішке түтік бойынша құбырдың сағасына бояу келеді.
Құбырда су қозғалысының жылдамдығы аз болса боялған ағыншаны айналасындағы су таратпайды, ол құбыр қабырғасына қатарлас (параллель) қозғалады, яғни керілген жіп түріне ие болады (4.2а-сурет). Бұл жағдайда қозғалыс ретті деп аталады. Ретті тәртіпте сұйық бөлшектеpінде тек бойлық жылдамдық болады. Барлық ағыншалар бір-біріне қатар өзара макроскопиялық араласпай қозғалады.
Құбырдағы қозғалыс жылдамдығын өсірсе боялған ағынша толқын кескінін қабылдап иреңдей бастайды, тербеледі және боялған ағыншаның ішінара ағынмен араласуы байқалады, бұл ретті тәртіптен ретсіз тәртіпке ауысуын дәлелдейді. Мұндай қозғалысты ауысулық қозғалыс дейді (4.2б-сурет).
Жылдамдық одан әрі өссе, боялған ағынша кіруден біраз қашықтықта толығымен тарап, бүкіл ағын бір түске боялып, қозғалыс ретсіз, бейберекет (4.2в-сурет), яғни дамыған ретсіз тәртіп орнайды. Сұйық бөлшектері әр мезгілде өзгеріп тұратын жолсызықтар (траекториялар) бойынша қозғалады. Қабаттар арасындағы араласу негізінде әр түрлі жылдамдықтары бар жеке макроскопиялық бөлшектердің яғни сұйық көлемдердің (мольдердің) бір қабаттан екінші қабатқа өтуі арқылы жүзеге асaды. Сондықтан боялған ағынша жылдам тарап кетеді.
 Рейнольдс
сұйықтың қозғалу тәртіптерінің
көлденең қима бойынша орташа жылдамдықтан
Рейнольдс
сұйықтың қозғалу тәртіптерінің
көлденең қима бойынша орташа жылдамдықтан ![]() ,
құбырдың диаметрі d және
тұтқырлықтың келтірілген еселеуішінен
,
құбырдың диаметрі d және
тұтқырлықтың келтірілген еселеуішінен ![]() тұратын
өлшемділіксіз жиынтыққа тәуелді екенін анықталады
тұратын
өлшемділіксіз жиынтыққа тәуелді екенін анықталады
Re=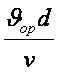 .
.
Бұл
Ұлшемділіксіз жиынтыќ Рейнольдс саны деп аталады. Ағыстың
реттіден ретсіз түріне ауысқандағы Рейнольдс санының
мәнін аумалылық саны деп атайды және Rea деп
белгіленеді. Re<Rea1![]() 2300 болса, қозғалыс
тәртібі ретті болады.
2300 болса, қозғалыс
тәртібі ретті болады.
Re>Rea1 болса-ретсіздене бастайды. Re>Rea2=104 болғанда дамыған ретсіз тәртіп болады.
Rea
шамасы құбырға кіру жағдайына,
сұйықта бастапқы ұйтқулар бар не
жоқтығына, т.б. байланысты. Кіру қимасының жиегі
өткір дөңгелек құбыр үшін Rea1![]() 2300 .
2300 .
Техникалық құбырлардағы ағыстар үшін Рейнольдс cандары Rea2-тан анағұpлым үлкен болады. Іс жүзіндегі ағындар, әдетте, дамыған ретсіз.
Сұйық
ағынының басқа жағдайлары үшін Rea
мәні басқа болады. Мысалы шардың ағысталуы үшін
Rea=(2![]() 3)×105.
3)×105.
4.3 Ағын сызығы және түтігі
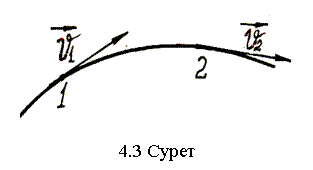 Берілген
уақыт мезетінде жылдамдық мегземесі (векторы) әрбір
нүктесінде жанама бағытталған сызықты ағын
сызығы деп атайды (4.3-сурет).
Берілген
уақыт мезетінде жылдамдық мегземесі (векторы) әрбір
нүктесінде жанама бағытталған сызықты ағын
сызығы деп атайды (4.3-сурет).
Егер сұйық бөлшегінің қозғалысын уақыт бойынша қарастырса, онда кейбір уақыт аpалығында бойымен бөлшек қозғалған сызықты жолсызық (траектория) деп атайды.
Қалыптасқан ағыста ағын сызығы жолсызықпен бірдей болады. Қалыптаспаған ағыста олаp өзара бірдей болмайды.
Егер тұйықталған контурдың барлық нүктелері арқылы ағын сызықтаpын өткізсе, онда ағын түтігін аламыз (4.4-суретті қараңыз). Ағын түтігінің ішіндегі сұйық бөлігін ағынша дейді.
Сұйық ағын түтігінің ішінде қабырғасы қатты құбырдың ішіндегідей ағады. Шынында да әрбір бөлшек оның бетінде жылдамдығы бетке жанама бағытталғандықтан онымен қиылыспайды, сол бет бойынша қозғалу керек.
 Егер
ағын түтігінің көлденең өлшемі кішкене
болса, ол кішкене түтік деп аталады. Кішкене (элементар)
түтіктің көлденең қимасында жылдамдық аз
өзгереді, оны іс жүзінде шамасы және бағыты бойынша сол
қиманың барлық нүктелерінде бірдей деуге болады,
түтіктің көлденең қимасын жазық деуге
болады.
Егер
ағын түтігінің көлденең өлшемі кішкене
болса, ол кішкене түтік деп аталады. Кішкене (элементар)
түтіктің көлденең қимасында жылдамдық аз
өзгереді, оны іс жүзінде шамасы және бағыты бойынша сол
қиманың барлық нүктелерінде бірдей деуге болады,
түтіктің көлденең қимасын жазық деуге
болады.
Кішкене
түтікте сұйық жылдамдығы оның бoйында
өзгере алады, яғни тек бір бойлық мекендікке тәуелді
болады. Сөйтіп, кішкене түтікте сұйық
қозғалысы бір өлшемді болады ![]() =f(x).
=f(x).
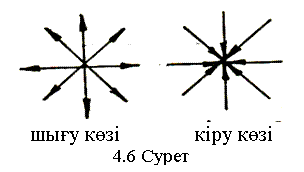
Жалпы жағдайда қозғалған ортаның кез келген нүктесі арқылы берілген уақыт мезетінде тек бір ағын сызығын жүргізуге болады, бірақта бұл ереже бұзылатын кейбір ерекше нүктелер бар (4.5, 4.6-суреттер).
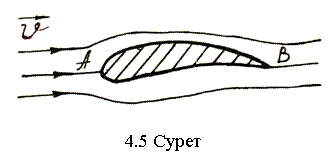
Ерекше нүктелерде ағын сызықтары қиылысады, бұл нүктелерде жылдамдық векторы әр түрлі бағытқа ие болу керек, ол жылдамдықтың шектелген мєнінде болуы мүмкін емес. Сондықтан ерекше нүктелеpде жылдамдықтың шамасы не нөлге (4.5-сурет), не шексіздікке (4.6-сурет) тең болу керек.
№5 дәріс.
5.1 Бір өлшемді ағынның қозғалыс тeңдеулері
Жоғарыда айтылғандай, бір өлшeмді ағынның көрсеткіштері (жылдамдық, қысым және т.б.) бағыты жылдамдық мегземесінің (векторының) бағытымен бірдей біp мекендікке тәуелді болады.
Шындығында, бір өлшемді ағындар болмайды, бірақ үш өлшемді қозғалысты ағын қимасы бойынша орташаланған жылдамдықтың көмегімен бір өлшемді қозғалысқа келтіруге болады (4.1-сурет). Орташаланған жылдамдық ағын бойынша өзгереді.
Бір өлшемді ағындарды сипаттау үшін, тиісті түзеткіш еселеуіштер кіргізіп кішкене ағын түтігіне алынған теңдеулерді пайдаланады. Түзеткіш еселеуіш ағын қимасындағы жергілікті жылдамдықтың таралуы біркелкі еместігін есепке алады.
5.1.1 Сұйық шығысы
Ағынның маңыздық шығысы дегеніміз ағынның көлденең қимасы арқылы уақыт бірлігінде ағып өтетін сұйық маңызы
G=r![]() S, кг/с.
(5.1)
S, кг/с.
(5.1)
Сығылмайтын сұйық үшін көлемдік шығысты қолдануға болады, ол ағынның көлденең қимасы арқылы уақыт бірлігінде ағып өтетін сұйық көлемі
Q=![]() S, м3/с.
(5.2)
S, м3/с.
(5.2)
5.1.2 Үзіксіздік теңдеуі (маңыздың сақталу заңы)
Қалыптасқан қозғалыста сұйық ішінде тұтастық үзілмесе, маңыздық шығыс ағын бойынша тұрақты болуы керек. Екі еркінше алынған ағын қималары үшін (5.1-суретті қараңыз).
r1![]() S1=r2
S1=r2![]() S2
. (5.3)
S2
. (5.3)
(5.3) теңдеу сығылатын сұйық үшін үзіксіздік теңдеуі.
Сығылмайтын
сұйық үшін ![]()
![]() S1=
S1= ![]() S2.
(5.4)
S2.
(5.4)
5.1.3 Бернулли теңдеуі (толық механикалық қайраттың сақталу заңы).
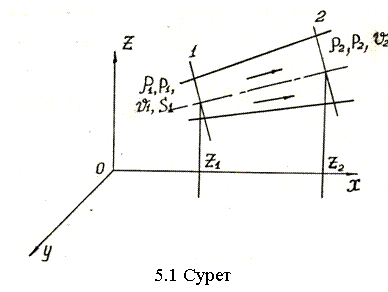
Толық механикалық қайраттың сақталу заңын пайдаланып бір өлшемді ағын үшін Бернулли теңдеуін қорытуды келтірейік (5.1-суретті қараңыз).
dt уақыт аралығындағы қалыптасқан сұйық қозғалысын қарастырсақ 1 қима арқылы бақылау көлеміне 1-2 ағып кірген сұйық маңызы және 2 қима арқылы бақылау көлемінен ағып шыққан сұйық маңызы тең болады
r1![]() S1
dt =r2
S1
dt =r2![]() S2 dt =G dt .
S2 dt =G dt .
1 қима арқылы өткен ағынның механикалық қайраты (энергиясы) келесі құраушылардан тұрады:
1)
![]() жылдамдығымен
қозғалатын Gdt маңыздың
қозғалыстық қайраты (кинетическая энергия); бұл
қайрат тең
жылдамдығымен
қозғалатын Gdt маңыздың
қозғалыстық қайраты (кинетическая энергия); бұл
қайрат тең 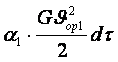 , мұнда
a1
түзету
еселеуіші;
, мұнда
a1
түзету
еселеуіші;
2) қысымның мүмкіндік (потециaлдық) қайраты, ол қысым күшінің (Fќ=P1S1) жұмысына тең яғни
p1![]() S1
dt=
S1
dt=![]() r1
r1![]() S1
dt=
S1
dt=![]() G dt,
G dt,
мұнда
![]() dt
сұйықтың
орын ауыстыруы;
dt
сұйықтың
орын ауыстыруы;
3) мүмкіндік орын қайраты (потенциaльная энергия положения)
G dtgz1.
Демек, 1-қима арқылы өткен ағынның толық қайраты үшеуінің қосындысына тең
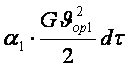 +
+![]() G dt+ G dtgz1.
G dt+ G dtgz1.
Осыған тәріздес dt уақытында 2-қима арқылы өткен ағынның толық қайраты
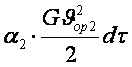 +
+![]() G dt+ G dtgz2.
G dt+ G dtgz2.
Егер
сұйықты тұтқырсыз дeсек, онда ешқандай
қайрат шығыны болмайды ![]() . 1 және 2 қималардағы
толық қайраттар өзара тең болады. Олардың
әрбір мүшесін Gdt бөлсек мына теңдеуді аламыз
. 1 және 2 қималардағы
толық қайраттар өзара тең болады. Олардың
әрбір мүшесін Gdt бөлсек мына теңдеуді аламыз
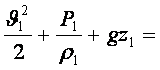
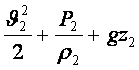 . (5.5)
. (5.5)
Қималарды бір-біріне жақындатып арасын өте аз қылса, онда (3.5) теңдеу шаққылық (дифференциялдық) түрде жазылады
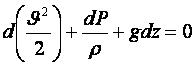 . (5.6)
. (5.6)
Сығылатын сұйық үшін Бернулли теңдеуі (5.6) теңдеуден r=f(p) екeнін есепке алып газқозғалым тарауында қорытылады.
Егер сұйық сығылмайтын болса r1=r2=r онда (5.5)-тен сығылмайтын тұтқырсыз сұйық ағыны үшін Бернулли теңдеуін аламыз
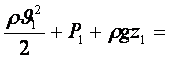
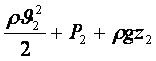 . (5.7)
. (5.7)
Шынында тұтқырлы сұйық 1-қимадан 2-қимаға дeйін қозғалғанда механикалық қайраттың біраз бөлігі тұтқырлық күш әрекетінен шығындалады (қайтымсыз жылуға айналады). Шығындалған қайратты Dқшығ-деп белгілесек сығылмайтын тұтқырлы сұйыќ ағыны үшін Бернулли теңдеуін аламыз
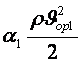 +p1+rgz1=
+p1+rgz1=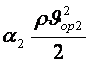 +p2+rgz2+Dқшығ
. (5.8)
+p2+rgz2+Dқшығ
. (5.8)
Тегеурінді ағындарда қысым құламасы сұйықты қозғайды, сондықтан тегеурінді ағындар үшін Dқшығ=Dpшығ. Тұтқырсыз сұйық үшін бұл мүше нөлге тең.
Егер (5.8) теңдеуді rg-ға бөлсек, онда оның барлық мүшелері сызықтық өлшемділікке ие болады
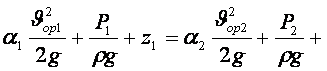 Dhшығ,
(5.9)
Dhшығ,
(5.9)
![]() мұнда
мұнда
![]() 2/2g, м-
жылдамдық тeгеуріні;
2/2g, м-
жылдамдық тeгеуріні;
p/rg, м- қысымдық (пьезометрлік) биіктік (тегеурін);
z- геометpиялық биіктік деп аталады.
Үшеуінің қосындысын толық тегеурін деп атайды.
Бернулли тeңдеуі бойынша механикалық қайраттың бір түрі екінші түріне айналады.
5.1.4 Қозғалыс мөлшерінің теңдеуі (қозғалыс мөлшерінің сақталу заңы)
Ньютонның жалпы түрдегі екінші заңы бойынша уақыт бірлігіндегі қозғалыс мөлшер мегземесінің (векторының) өзгеруі қараcтырылған денеге түсетін барлық сыртқы күштердің қорытқысына тең
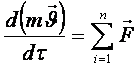 і.сырт.
(5.10)
і.сырт.
(5.10)
Бұл теңдеуді сұйық ағыны үшін жазайық (5.1-сурет). dt уақытында
1-қима
арқылы кірген қозғалыс мөлшері ![]() , ал 2-қима арқылы
шыққан қозғалыс мөлшері
, ал 2-қима арқылы
шыққан қозғалыс мөлшері ![]() , олардың айырмасын dt-ға бөліп
қозғалыс мөлшерінің теңдеуін аламыз
, олардың айырмасын dt-ға бөліп
қозғалыс мөлшерінің теңдеуін аламыз
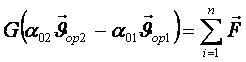 і.сырт.
(5.11)
і.сырт.
(5.11)
Ағынның бақылау бөлігіне сыртқы күштер ретінде ауырлық, қысым және үйкеліс күштері әрекет ете алады.
Қозғалыс
теңдеулеріне кірген түзеткіш еселеуіштердің мәндері іс
жүзінде бірге жуық болады. Мысалы, дөңгелек
құбырдағы ретсіз қозғалыс үшін ![]()
![]() , сондықтан оларды
көбінесе бірге тең деп алады.
, сондықтан оларды
көбінесе бірге тең деп алады.
Ағын түтігі мен тұтқырсыз сұйық ағыны үшін барлық түзеткіш еселеуіштердің мәндері бірге тең.
Үш қозғалыс теңдеулерінің көмегімен бір өлшемді ағындардың әр түрлі есептерін шешуге болады.
Бір өлшeмді ағындар үшін қозғалыс теңдеулері аумақылық (интегралдық) түрде болады, оларды бірден есептеу жүргізуге қолданамыз. Ал екі не үш өлшемді ағындар үшін қозғалыс теңдеулері шаққылық (дифференциялдық) түрде болады.
Ағындағы жылдамдық пен қысымның қалай өзгеретінін білу үшін шаққылық қозғалыс теңдеулерін аумақылау керек.
5.2 Үзіксіздіктің
шаққылық (дифференциялдық) теңдеуіҮш
өлшемді қозғалыс: ![]() =f(x,y,z,
=f(x,y,z,![]() ) үшін
маңыздың сақталу заңын жазсақ үзіксіздік
теңдеуі дифференциалдық түрде болады:
) үшін
маңыздың сақталу заңын жазсақ үзіксіздік
теңдеуі дифференциалдық түрде болады:
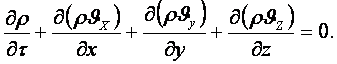 (5.12)
(5.12)
Мегземелік түрде
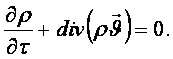 (5.13)
(5.13)
Сығылмайтын сұйық үшін
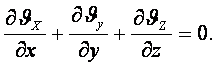 (5.14)
(5.14)
![]() (5.15)
(5.15)
5.3 Тұтқыр сұйықтың шаққылық (дифференциялдық) қозғалыс теңдеулері (Навье-Стокс теңдеулері). Бастапқы және шекаралық шарттар
Егер Ньютонның екінші заңын үш өлшемді қозғалыс үшін жазсақ сығылмайтын сұйықтың (ρ=тұрақ) қозғалыс теңдеулерін t=тұрақ болғанда векторлық (мегземелік) түрде аламыз:
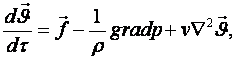 (5.16)
(5.16)
![]() (5.17)
(5.17)
 Навье-Стокс
теңдеулері 2-ретті және
Навье-Стокс
теңдеулері 2-ретті және 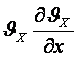 ,
, 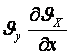 … сияқты мүшелер
болғандықтан Навьe-Стокс теңдеулері сызықты емес,
сондықтан оларды аумақылау (интегралдау) өте қиын.
Ќазіргі кезде осы теңдеулердің дєл шешуі табылған жағдайлар
көп емес. Көп жағдайларда бұл теңдеулерді
есептің шарттарына қарай ықшамдайды. Теңдеу
мүшелерін салыстырып әсері аз мүшелерді елемей қалдырып
кетеді.
… сияқты мүшелер
болғандықтан Навьe-Стокс теңдеулері сызықты емес,
сондықтан оларды аумақылау (интегралдау) өте қиын.
Ќазіргі кезде осы теңдеулердің дєл шешуі табылған жағдайлар
көп емес. Көп жағдайларда бұл теңдеулерді
есептің шарттарына қарай ықшамдайды. Теңдеу
мүшелерін салыстырып әсері аз мүшелерді елемей қалдырып
кетеді.
Қозғалыс теңдеулерінің математикалық тұрғыдан күрделенуі тек қозғалыстың екі не үш өлшемді болуына ғана байланысты екeнін тағы да ескертейік.
Қозғалыс теңдеулерін аумақылағанда бастапқы және шекаралық шарттар болу керек, олардың көмегімен аумақылау тұрақтыларын анықтайды.
Бастапқы
шаpт қалыптаспаған қозғалыста керек және
әлдеқандай уақыт мезгілінде
t=0 жылдамдық
таралуы ![]() беріледі.
Қалыптасқан қозғалыста бастапқы шарт керек
болмайды.
беріледі.
Қалыптасқан қозғалыста бастапқы шарт керек
болмайды.
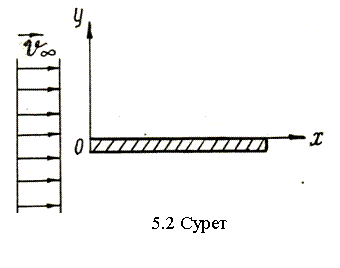
Денелеpдің ағысталуы қарастырылса шекаралық шарттар әдетте ағысталған дене бетінде және дененің бетінен шексіз қашықтықта ұйтқытылмаған сұйықта беріледі.
Мысал ретінде тақташаның ағысталуын қарастырайық (5.2-сурет).
Бастапқы
шарт: t=0
болғанда ![]() берілген.
берілген.
Шекаралыќ
шарттар: Тақташаның бетінде y=0 болғанда ![]() =0,
=0, ![]() =0,
=0, ![]() =0; тақташаның
бетінен шексіз қашықтықта:
=0; тақташаның
бетінен шексіз қашықтықта: ![]()
![]()
№6 дәріс
6.1 Ретсіз қозғалыстың негізгі сипаттамалары
Ретсіз ағында қатал ұғыныста қалыптасқан қозғалысқa жету мүмкін емес. Жылдамдық және қысым берілген нүктеде өте күрделі заңмен өзгереді. Егер ретсіз ағынның бір нүктесінде екпінсіз жылдамдық өлшеуішпен жылдамдықты өлшесе, мысалы термоанемометрмен, онда лездік жылдамдық өзінің орташа мәнініњ айналасында бейберекет толқиды (6.1-суретті қараңыз).
Егер жылдамдықты екпінді өлшеуішпен өлшесе, мысалы Пито түтігімен, онда соңғы жылдамдықтың толқуын сезбейді, уақыт бойынща орташаланған жылдамдықты көрсетеді, ол орташа жылдамдық қалыптасқан ағында уақытқа тәуелді емес
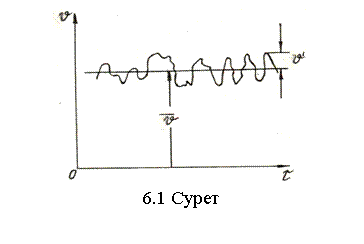
 . (6.1)
. (6.1)
Ретсіз
ағысты математикалық сипаттау үшін Рейнольдс лездік
жылдамдық пен қысымды берілген нүктеде орташаланған
жылдамдық пен қысымның және толқулық
құраушылардың ![]() және
және ![]()
![]() қосындысы деп қарастыруды
ұсынды, яғни
қосындысы деп қарастыруды
ұсынды, яғни
![]() ;
; ![]() . (6.2)
. (6.2)
Ретсіз
қозғалыста тек ![]() және
және ![]() қалыптасуы мүмкін.
Қалыптасқан қозғалыста орташаланған мәндер
мүлдем уақытқа тәуелді болмас үшін
уақыттың аpалығын
қалыптасуы мүмкін.
Қалыптасқан қозғалыста орташаланған мәндер
мүлдем уақытқа тәуелді болмас үшін
уақыттың аpалығын ![]() үлкен етіп алу керек. Онда
уақыт бойынша орташаланған жылдамдық пен қысымның
толқулық құраушыларының мәндеpі нөлге
тең болады
үлкен етіп алу керек. Онда
уақыт бойынша орташаланған жылдамдық пен қысымның
толқулық құраушыларының мәндеpі нөлге
тең болады
![]()
![]()
![]()
![]() . (6.3)
. (6.3)
Бірақта, ![]()
![]() ;
; ![]()
![]() және тағы солай. (6.4)
және тағы солай. (6.4)
Жылдамдықтың толқулық құраушылары барлық басқа кезеңдік (периодтық) өзгеретін шамалардай жиілік және амплитудамен сипатталады. Әдетте, жылдамдық толқуының амплитудасының орнына ретсіздіктің дәрежесі (қарқындылығы) деген үғым пайдаланады, ол
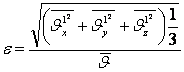 . (6.5)
. (6.5)
Жылдамдықтың толқуы үйкеліс күшінің кернеуін өсіреді. Егер ретті қoзғалыста үйкеліс күшінің кернеуі тек затшалық (молекулалық) тұтқырлықпен себептелсе
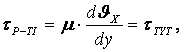 (6.6)
(6.6)
ал ретсіз ағыста
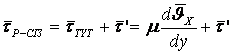 ,
(6.7)
,
(6.7)
мұнда екінші
мүше ![]() ретсіздікпен
байланысты қосымша кернеу.
ретсіздікпен
байланысты қосымша кернеу.
Екі өлшемді қозғалыс үшін мынаны көрсетуге болады
![]() (6.8)
(6.8)
6.2 Ретсіз ағынның орташаланған қозғалыс теңдеулері (Рейнольдс теңдеулері)
Іс
жүзінде ең алдымен ретсіз ағынның орташаланған
көрсеткіштерінің ![]()
![]() таралуы керек болады. Сондықтан
ретсіз ағынның орташаланған қозғалыс
теңдеулерін алу қажет. Ол үшін Рейнольдс Навье-Стокс
және үзіксіздік теңдеулеpін ретсіз қозғалысқа
да қолдануға болады деп жорамалдады, бұл теңдеулерге
қозғалыстың нақты жылдамдығын және
қысымын (6.2) қойып, орташалау амалын жасап және (6.3)
шарттарын пайдаланып орташаланған қозғалыс теңдеулерін
алды
таралуы керек болады. Сондықтан
ретсіз ағынның орташаланған қозғалыс
теңдеулерін алу қажет. Ол үшін Рейнольдс Навье-Стокс
және үзіксіздік теңдеулеpін ретсіз қозғалысқа
да қолдануға болады деп жорамалдады, бұл теңдеулерге
қозғалыстың нақты жылдамдығын және
қысымын (6.2) қойып, орташалау амалын жасап және (6.3)
шарттарын пайдаланып орташаланған қозғалыс теңдеулерін
алды
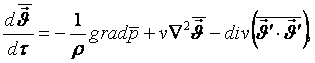 (6.9)
(6.9)
![]()
Орташаланған
қозғалыс теңдеулері Рейнольдс теңдеулері деп аталынады.
Рейнольдс теңдеулерін Навье-Стокс теңдеулерімен салыстыра отырып
Рейнольдс теңдеулерінде 9 қосымша мүшелердің 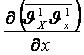 ,
, 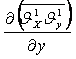
![]() және т.б. пайда болғанын
көреміз. Үзіксіздік теңдеуінің түрі
өзгермейді.
және т.б. пайда болғанын
көреміз. Үзіксіздік теңдеуінің түрі
өзгермейді.
Мына теңдіктерді оңай дәлелдеуге болады
![]()
![]()
![]()
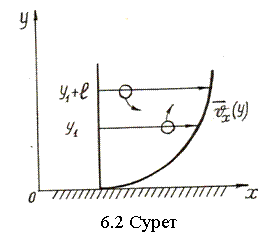 Онда белгісіз қосымша
мүшелердің саны 6 болады. Бұл мүшелер ретсіз
ағында жылдамдық толқуынан пайда болған қосымша
үйкеліс күштерін есепке алады. Рейнольдс теңдеулерінің
жүйесі тұйықталған болу үшін,
Онда белгісіз қосымша
мүшелердің саны 6 болады. Бұл мүшелер ретсіз
ағында жылдамдық толқуынан пайда болған қосымша
үйкеліс күштерін есепке алады. Рейнольдс теңдеулерінің
жүйесі тұйықталған болу үшін, ![]() және т.б. шамаларды
орташаланған жылдамдыќ құраушыларымен байланыстыратын
қосымша 6 теңдеу енгізу керек. Әрине ол үшін ретсіз
қозғалыстың табиғаты туралы қосымша болжамдар
кіргізу қажет. Бұл мәселе жалпы жағдайда шешілмей
тұр. Толқулық жылдамдықтарын орташаланған
жылдамдықпен байланыстыратын теңдеулер қарапайым
қозғалыстар үшін алынған (6.2-суретті
қараңыз). Орташаланған жылдамдыѓы х жебесімен бірдей
бағытталған, ал жылдамдық шамасы тек у мекендігіне
ғана тєуелді ағыс үшін. Демек,
және т.б. шамаларды
орташаланған жылдамдыќ құраушыларымен байланыстыратын
қосымша 6 теңдеу енгізу керек. Әрине ол үшін ретсіз
қозғалыстың табиғаты туралы қосымша болжамдар
кіргізу қажет. Бұл мәселе жалпы жағдайда шешілмей
тұр. Толқулық жылдамдықтарын орташаланған
жылдамдықпен байланыстыратын теңдеулер қарапайым
қозғалыстар үшін алынған (6.2-суретті
қараңыз). Орташаланған жылдамдыѓы х жебесімен бірдей
бағытталған, ал жылдамдық шамасы тек у мекендігіне
ғана тєуелді ағыс үшін. Демек,![]()
![]()
Л.Прандтль толқулық жылдамдықтарын орташаланған жылдамдықпен байланыстыратын теңдеуді алды.
Қосымша
мүшелерден Рейнольдс теңдеулерінде берілген жағдайда тек 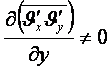 емес, онда
емес, онда ![]() -ті
-ті ![]() пен байланыстыру керек.
пен байланыстыру керек.
Cонда
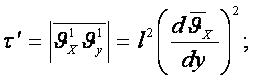 (6.10)
(6.10)
(6.10)
қатынасты еске алсақ және ![]() шамасының таңбасын
көрсету үшін былай жазуға болады
шамасының таңбасын
көрсету үшін былай жазуға болады
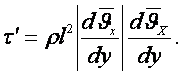 (6.11)
(6.11)
![]() -тің
таңбасы жылдамдық тікмегземесі (градиенті)
-тің
таңбасы жылдамдық тікмегземесі (градиенті) ![]() -тің таңбасымен бірдей.
-тің таңбасымен бірдей.
Араласу
қашықтығы ![]() затшалардың (молекулалардың)
еркін жол ұзындығына ұқсас, олардың
айырмашылығы мынада: біріншісі макроскопиялық ретсіздік
бөлшектерінің қозғалысы, екіншісі затшалардың микроскопиялық
қозғалысы. Араласу қашықтығы физикалық
тұрақты емес, ол ең болмағанда н‰кте бернесі
(функциясы) болады.
затшалардың (молекулалардың)
еркін жол ұзындығына ұқсас, олардың
айырмашылығы мынада: біріншісі макроскопиялық ретсіздік
бөлшектерінің қозғалысы, екіншісі затшалардың микроскопиялық
қозғалысы. Араласу қашықтығы физикалық
тұрақты емес, ол ең болмағанда н‰кте бернесі
(функциясы) болады.
Араласу қашықтығын анықтау үшін үшінші болжамды кіргізу керек. Қабырғаға жақын жерде араласу қашықтығы қабырғадан есептелген қашықтыққа сәйкес деп Прандтль болжам жасады:
l = жy, (6.12)
мұнда ж тәжірибеде анықталатын тұрақты. Сондықтан Прандтльдің ретсіздік туралы теориясы тєжірибе аралас деп аталады.
Дєл
қабырға бетінде толқу жылдамдығы нөлге тең,
демек, ![]() да
нөлге тең болады.
да
нөлге тең болады.
Прандтльдің теориясы ретсіз ағындар есептерін шешкенде көп қолданыс табуда.
6.3 Сұйыққозғалымдық ұқсастық және үлгілеу
Теориялық
зерттеудің қиындығы тұтқыр ағыстарды
тәжірибелік әдістермен зерттеуге мәжбүр етті.
Әдетте денелер ағысталуының тәжірибелік зерттеулері
табиғи нысаналарда (объекттерде) емес (дәл сол дененің
өзінде емес) геометриялық ұқсас кішкене үлгілерде
өткізіледі. Бұл жағдайларда екі ағыстың
 сұйыққозғалымдық
ұқсастығын қамтамасыз ету керек. Бұл үшін,
біріншіден, үлгімен табиғи нысананың геометриялық
ұқсастығын қамтамасыз ету керек, оны орындау үшін
екеуінің барлық сәйкесті өлшемдерінің
қатынастары бірдей болу керек, сонымен қатар сәйкесті
бұрыш тең болу керек. Мысалы, геометриялық
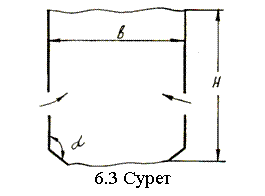
ұқсастықтың шарттарын былай жазуға болады (6.3-сурет)
сұйыққозғалымдық
ұқсастығын қамтамасыз ету керек. Бұл үшін,
біріншіден, үлгімен табиғи нысананың геометриялық
ұқсастығын қамтамасыз ету керек, оны орындау үшін
екеуінің барлық сәйкесті өлшемдерінің
қатынастары бірдей болу керек, сонымен қатар сәйкесті
бұрыш тең болу керек. Мысалы, геометриялық
ұқсастықтың шарттарын былай жазуға болады (6.3-сурет)
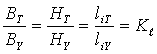 , (6.13)
, (6.13)
мұнда ![]() тұрақты,
оны тєжірибеші (экспериментатор) өзі тағайындайды.
тұрақты,
оны тєжірибеші (экспериментатор) өзі тағайындайды. ![]() -ды
үлгілеудің сызықтық масштабы деп атайды.
-ды
үлгілеудің сызықтық масштабы деп атайды.
Екіншіден үлгімен табиғаттықтың ұқсастық шарттықтарының (сандарының) бірдей болуын қамтамасыз ету керек.
Ұқсастық сандарын қозғалыс теңдеулеріне талдау жасап алуға болады. Сығылмайтын сұйық үшін:
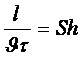 -Струхаль саны;
-Струхаль саны; 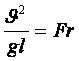 -Фруд саны;
-Фруд саны;
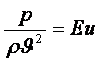 -Эйлер саны;
-Эйлер саны; 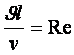 -Рейнольдс
саны. (6.14)
-Рейнольдс
саны. (6.14)
Үлгілі мен табиғи ағыстың қозғалымдық ұқсастық шарттары
![]()
![]()
![]()
![]() . (6.15)
. (6.15)
Cұйық қозғалысына әрекет ететін күштер осы төрт шарттықтармен есепке алынады: жергілікті екпін күші - Струхаль санымен, қысым күші - Эйлер санымен, ауырлық күші - Фруд санымен, тұтқырлық (үйкеліс) күші - Рейнольдс санымен.
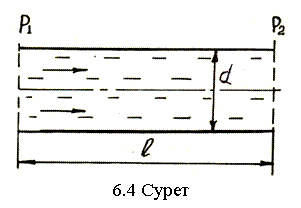 Мысал ретінде тегеурінді
құбырдағы қалыптасқан қозғалысты
үлгілеуді қарастырайық (6.4-сурет).
Мысал ретінде тегеурінді
құбырдағы қалыптасқан қозғалысты
үлгілеуді қарастырайық (6.4-сурет).
Дөңгелек құбырдың екі өлшемі: ұзындығы l және диаметрі d болғандықтан табиғи құбыр мен үлгілік құбырдың геометриялық ұқсастығын қамтамасыз ету шарты былай жазылады
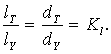
Ал ![]() -дің мәні
тәжірибе өткізу жағдайына байланысты тағайындалады.
-дің мәні
тәжірибе өткізу жағдайына байланысты тағайындалады.
Ұқсастық
сандарын қарастырайық. Қалыптасқан
қозғалыста жергілікті үдеуден болатын екпіндік күш
нөлге тең. Бұл жағдайда Струхаль шарттығы
жоқ болады. Тегеурінді ағыста p1-p2=![]() p қысым
айырмасы әрекетінен қозғалады, сұйық
құбырдың қимасын толығымен толтырады және
еркін бет түзбейді. Қозғалысқа ауырлық
күшінің әсері аз, қысым күшінің
маңызы айырықша зор болады. Сондықтан ауырлық
күшін есепке алатын Фруд санын алып тастауға болады.
p қысым
айырмасы әрекетінен қозғалады, сұйық
құбырдың қимасын толығымен толтырады және
еркін бет түзбейді. Қозғалысқа ауырлық
күшінің әсері аз, қысым күшінің
маңызы айырықша зор болады. Сондықтан ауырлық
күшін есепке алатын Фруд санын алып тастауға болады.
Ұқсастық
сандарынан екеуі: Рейнольдс және Эйлер сандары қалады.
Олардың рөлі зерттеу есебін қоюға байланысты. Біз,
мысалға, мына есепті қарастырайық: Q, d, ![]() берілген шамалар
болсын ал p1-p2=Δp=Δp‰йк-ті
анықтау керек. Бұл жағдайда
берілген шамалар
болсын ал p1-p2=Δp=Δp‰йк-ті
анықтау керек. Бұл жағдайда 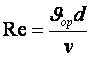 саны белгілі берілген шамалардан
құрастырылады, яғни оны тәжірибеден бұрын (есепті
шешпей тұрып) беруге болады.
саны белгілі берілген шамалардан
құрастырылады, яғни оны тәжірибеден бұрын (есепті
шешпей тұрып) беруге болады.
Эйлер санына 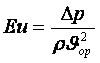 белгісіз анықталатын
шама Δp кіреді, ол тек тәжірибе өткізілгеннен кейін
(есеп шешілгеннен кейін) табылады. Сұйықтың
құбырдағы тегеурінді қозғалысында Eu саны
өлшемділіксіз кедергі шамасы болады және тек Re санына
тәуелді
белгісіз анықталатын
шама Δp кіреді, ол тек тәжірибе өткізілгеннен кейін
(есеп шешілгеннен кейін) табылады. Сұйықтың
құбырдағы тегеурінді қозғалысында Eu саны
өлшемділіксіз кедергі шамасы болады және тек Re санына
тәуелді
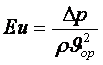 =f(Re). (6.17)
=f(Re). (6.17)
Сонымен, бұл жағдайда Re саны анықтайтын ұқсастық шарттығы болады және сол бойынша үлгілеу жүргізіледі. Тегеурінді құбырлардағы ағындар бір-біріне ұқсас болу үшін мына теңдік орындалу керек
ReT=ReY. (6.18)
Кейбіp есептерде Δp шамасы беріледі. Ондай ағындарда Eu саны басқа ұқсастық сандарына тәуелді емес және міндетті түрде орындалатын шарттық. Мысал ретінде бу шығырының ағысталатын бөлігіндегі ағынды, су шығырындағы ағысты үлгілеуді айтуға болады.
Әдетте, үлгілеу жуықша болады. Үлгілеу берілген дәлдікпен жүгізіледі.
№7 дәріс
7.1 Сұйықтың тұрақты тегеурінде кішкене тесіктен ағуы
Сұйықтың ыдыс түбінде орналасқан кішкене дөңгелек тесік арқылы ағуы туралы есепті қарастырайық. Егер тесік қосөресі (диаметрі) ыдыс қосөресімен және сұйық деңгейінің биіктігімен (7.1-сурет) салыстырғанда өте аз болса (d<0,1dы, d<0,1h), онда тесікті кішкене дейміз. Есеп шарты бойынша һ=тұрақты, p0=тұрақты, p1=тұрақты, ал ағын жылдамдығы мен шығысы анықталу керек.
һ-тұрақты шарты орындалу үшін ыдыс сыйымдылығы өте үлкен болу керек, немесе ағып шыққан сұйық мөлшеріне тең сұйық ыдысқа құйылып отыруы керек. Сонда сұйық қозғалысы қалыптасқан болады.
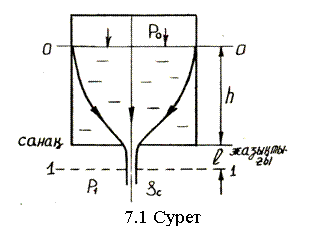 Алдымен ағыстың
жалпы көрінісін қарастырайық. Сұйық
бөлшектері екпінді болғандықтан олар тесіктен өткен
кезде бірден өздерінің қозғалу бағытын
өзгерте алмайды, тек біраз қашықтық
Алдымен ағыстың
жалпы көрінісін қарастырайық. Сұйық
бөлшектері екпінді болғандықтан олар тесіктен өткен
кезде бірден өздерінің қозғалу бағытын
өзгерте алмайды, тек біраз қашықтық ![]() жүргеннен кейін
төмен қарай тік қозғалады. Осы себептен ағынша
өзінің көлденең қимасын біртіндеп азайтып
сығылады және ыдыс түбінен белгілі
қашықтықта цилиндрлік болады. Ағыншаның (струя)
сығылуы жуықша тесік қосөресінің жартысына
тең қашықтықта бітеді
жүргеннен кейін
төмен қарай тік қозғалады. Осы себептен ағынша
өзінің көлденең қимасын біртіндеп азайтып
сығылады және ыдыс түбінен белгілі
қашықтықта цилиндрлік болады. Ағыншаның (струя)
сығылуы жуықша тесік қосөресінің жартысына
тең қашықтықта бітеді 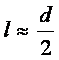 . Сығылу шамасы сығым
еселеуішімен сипатталады
. Сығылу шамасы сығым
еселеуішімен сипатталады
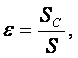
мұнда
SC-ағыншаның ең жіңішке көлденең қимасының ауданы;
S-тесік ауданы. Сығым еселеуіші әдетте тәжірибе арқылы анықталады.
Ағу жылдамдығын анықтау үшін ағынды бір өлшемді деп Бернулли теңдеуін 0-0 және 1-1 қималары үшін орташа жылдамдық белгісін түсіріп жазамыз

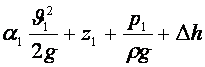 шығ.
(7.1)
шығ.
(7.1)
Сұйық аққанда жергілікті кедергіден болған қайрат (тегеурін шығыны)
Δh
шығ=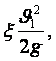 (7.2)
(7.2)
мұнда
![]() -жергілікті кедергінің
өлшемділіксіз еселеуіші.
-жергілікті кедергінің
өлшемділіксіз еселеуіші.
(7.1)
теңдеуде Δhшыѓ-ды (7.2) бойынша есепке аламыз және
қозғалыс іс жүзінде ретсіз болғандықтан ![]() деп алуға
болады. Үзіксіздік теңдеуінен
деп алуға
болады. Үзіксіздік теңдеуінен ![]() S0>>Sc
болғандықтан
S0>>Sc
болғандықтан ![]() 0<<
0<<![]() 1 болады. z0=h,
ал z1=
1 болады. z0=h,
ал z1=![]() <<h болғандықтан
оны һ-пен салыстырғанда елемеуге болады. Осыларды ескерсек (7.1)
мына түрге келеді
<<h болғандықтан
оны һ-пен салыстырғанда елемеуге болады. Осыларды ескерсек (7.1)
мына түрге келеді
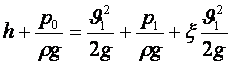 . (7.3)
. (7.3)
Бұл
теңдеуден ағу жылдамдығын анықтаймыз:![]()
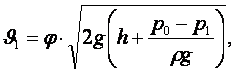 (7.4)
(7.4)
мұнда
 - жылдамдық еселеуіші.
- жылдамдық еселеуіші.
Егер p0=p1=pa болса, онда (5.4) ықшамдалады және мына түрге келеді
![]() (7.5) Сұйық шығысы тең
(7.5) Сұйық шығысы тең
Q=![]() (7.6) болғанда
(7.6) болғанда
![]() мен
мен ![]() Re-ке тәуелді
болмайды.
Re-ке тәуелді
болмайды.
мұнда
![]() шығыс еселеуіші:
шығыс еселеуіші: ![]() ,
, ![]() . Re>105
. Re>105
Егер
сұйықты тұтқырсыз десек ![]() болар еді. Судың ағуы
үшін Re>105 болғанда
болар еді. Судың ағуы
үшін Re>105 болғанда ![]() . Демек, сұйықты
тұтқырсыз десек жіберетін қате 3%-дан аспайды.
Сұйық ағынша түзіп қозғалғанда
тұтқырсыз сұйық ұғымын пайдаланып
алған тәуелділіктер тұтқыр сұйық
қозғалысын жеткілікті дәлдікпен сипаттайды.
. Демек, сұйықты
тұтқырсыз десек жіберетін қате 3%-дан аспайды.
Сұйық ағынша түзіп қозғалғанда
тұтқырсыз сұйық ұғымын пайдаланып
алған тәуелділіктер тұтқыр сұйық
қозғалысын жеткілікті дәлдікпен сипаттайды.
Сұйықтың құбырдағы қозғалысы және құбырларды сұйықағулық есептеу
7.2 Құбырлардың сұйықағулық кедергісі
Тұтқыр сұйық ағыны қозғалғанда құбырдың сұйықағулық кедергісінен механикалық қайрат шығындалады.
Жалпы жағдайда құбырдың сұйықағулық кедергісі екі құраушыдан: үйкеліс кедергісі мен жергілікті кедергілерден тұрады. Осы екі кедергінің табиғатын қарастырайық.
Сұйық қозғалғанда онымен құбыр қабырғасы арасында ағысқа қарсы бағытталған және үйкеліс кедергісінің себебі болатын үйкеліс күші пайда болады (7.2-cуретті қараңыз). Үйкеліс күшінің әрекетінен ағынның толық механикалық қайратының бөлігі жылу қайратына айналып кетеді, ол ағынның ыстықтығын жоғарлатуға не айналадағы ортаға тарайды.
Іс жүзінде құбырдың қосөресінің өзгеруі мүмкін (7.3-суретті қараңыз), ысырма шығысөлшер және т.б. болады. Бұлардың әр қайсысы ағында қосымша ұйтқуларды және құйындарды түзеді, демек, ағынның қайратын қосымша шығындайды. Бұл жағдайда қайрат шығыны қосымша кедергілердің құрылмалық ерекшеліктеріне байланысты және ағынның қысқаша ұзындығында болады. Сондықтан бұл кедергілерді жергілікті кедергілер деп атайды.
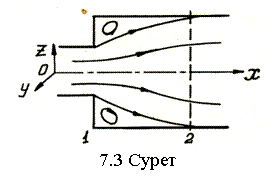 Барлық
жергілікті кедергілерде орнықты құйындар түзіледі,
оларды негізгі ағын айналдырады (7.3-суретті
қараңыз). Құйындар айналғанда үйкеліс
күшінің әрекетінен механикалық қайрат жылу
қайратына айналады.
Барлық
жергілікті кедергілерде орнықты құйындар түзіледі,
оларды негізгі ағын айналдырады (7.3-суретті
қараңыз). Құйындар айналғанда үйкеліс
күшінің әрекетінен механикалық қайрат жылу
қайратына айналады.

Тегурінді құбырларда қысым шығыны ∆ршығ жаңағы айтылған екі түрлі шығынның қосындысына тең деп алынады
![]()
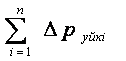 +
+ 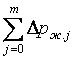 ,
,
мұнда
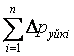 – ағынның барлық
бөліктеріндегі үйкеліс шығындарының қосындысы;
– ағынның барлық
бөліктеріндегі үйкеліс шығындарының қосындысы; 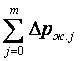 - барлық
жергілікті шығындардың қосындысы.
- барлық
жергілікті шығындардың қосындысы.
Есеп жүргізгенде Дарси-Вейсбах кейіптемелерін пайдаланады
![]()
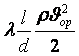 , Па (7.7)
, Па (7.7)
![]() x
x ![]() , Па. (7.8)
, Па. (7.8)
Мұнда l - үйкеліс кедергісінің өлшемділіксіз еселеуіші;
![]() және d -
құбырдың ұзындығы және
қосөресі;
және d -
құбырдың ұзындығы және
қосөресі;
r - сұйықтың тығыздығы;
![]() op -
ағынның орташа жылдамдығы;
op -
ағынның орташа жылдамдығы;
x - жергілікті кедергінің өлшемділіксіз еселеуіші.
(7.7), (7.8) кейіптемелерді тегеурін арқылы былай жазуға болады
![]()
 , м (7.9)
, м (7.9)
![]()
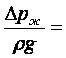
![]() , м. (7.10)
λ және ξ-дің мєндері теориялық не
тәжірибелік кейіптемелер бойынша табылады. Бұл шамалар
өлшемділіксіз болғандықтан тек өлшемділіксіз
шамаларға тәуелді болады. Жалпы жағдайда
, м. (7.10)
λ және ξ-дің мєндері теориялық не
тәжірибелік кейіптемелер бойынша табылады. Бұл шамалар
өлшемділіксіз болғандықтан тек өлшемділіксіз
шамаларға тәуелді болады. Жалпы жағдайда
l=f (Re,![]() )
; (7.11)
)
; (7.11)
l=f (Re, жерг. кедергі түрі ), (7.12)
мұнда
∆ - құбыр
қабырғасындағы бұдырлардың орташа биіктігі,
мм; ![]() =
=![]() - салыстырмалы
бұдырлық.
- салыстырмалы
бұдырлық.
(7.11) өрнектің
түрі сұйықтың қозғалыс тәртібіне
байланысты өзгереді. ξ Re санына былай тәуелді болады.
Алдымен 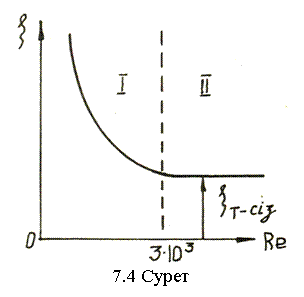 Re саны
өскен сайын ξ азаяды (7.4-сурет), содан соң ξ-дің
азаюы бәсеңдейді де Re санының кейбір мәнінен бастап ол
тұрақты болады. Бұл аймақты ІІ тәуелсізділік
аймағы деп атайды. І-ші аймақ – тәуелділік аймағы
болады. Кенет тарылу және кеңею сияқты кедергілер үшін
тәуелсізділік аймағы (автомодельная область) Re=3×103
болғанда басталады. ξ мен Re байланысын жуықша былай
жазуға болады
Re саны
өскен сайын ξ азаяды (7.4-сурет), содан соң ξ-дің
азаюы бәсеңдейді де Re санының кейбір мәнінен бастап ол
тұрақты болады. Бұл аймақты ІІ тәуелсізділік
аймағы деп атайды. І-ші аймақ – тәуелділік аймағы
болады. Кенет тарылу және кеңею сияқты кедергілер үшін
тәуелсізділік аймағы (автомодельная область) Re=3×103
болғанда басталады. ξ мен Re байланысын жуықша былай
жазуға болады
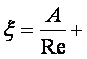
![]() ,
,
мұнда
А-әрбір жергілікті кедергі үшін әртүрлі тұрақты;
ξт-сіз - тәуелсізділік аймығындағы ξ-дің мәні.
7.3 Ағын кенет кеңейгендегі және тарылғандағы қысым шығыны
Іс жүзінде құбырдың d1 қосөресінен d2 қосөресіне дейін кеңеюі жиі кездесетін жағдай (7.3-суретті қараңыз). Сұйық бөлшектері екпінді болғандықтан жіңішке құбырдан шыққан ағын кең құбырдың көлденең қимасын біртіндеп толтыратын ағынша түзеді.
Ағынша мен құбыр қабырғасы арасында шығыршық тәрізді кеңістікте орнықты құйын түзіледі, ол негізгі ағын қайратының бөлігін тұтқырлық күш әрекетінің арқасында жылу қайратына айналдырады.
Кенет кеңейгендегі қайрат шығынын табу үшін Бернулли теңдеуін 1 және 2 қималар үшін жазамыз
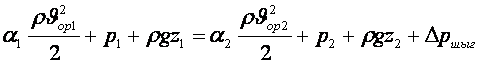 (7.13)
(7.13)
Ағынның жайылу аумағы 1-2 өте қысқа болғандықтан, үйкеліс шығыны аз, яғни шығындар негізінде кенет кеңеюден болады (∆pшығ»∆pк.к ).
Құбыр жатық болғандықтан z1=z2=0 және ретсіз қозғалыс үшін a1=a2=1 деп алуға болады. Жазуды қысқарту үшін жылдамдықтан орташа белгісін алып тастасақ, онда (7.13) теңдеуден аламыз
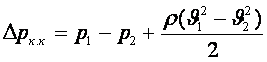 . (7.14)
. (7.14)
Қозғалыс мөлшер теңдеуінен сол қималар үшін аламыз
![]() . (7.15)
. (7.15)
Бұл теңдеу Х жебесіне проекциялап жазылған. (7.15) теңдеудің көмегімен (7.14) теңдеуден аламыз
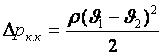 .
(7.16)
.
(7.16)
(6.10) кейіптемені Борд кейіптемесі дейді жєне оны үзіксіздік теңдеуін
![]() 1S1=
1S1=![]() 2S2
пайдаланып, мына түрге келтіруге болады
2S2
пайдаланып, мына түрге келтіруге болады
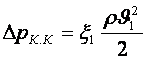 ,
(7.17)
,
(7.17)
мұнда
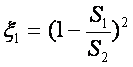 .
(7.18)
.
(7.18)
(7.17) кейіптемеде шығын жіңішке құбырдағы ағынның қозғалыс қайратының үлесі арқылы берілген.
Сұйық сыйымдылығы шектеусіз ыдысқа құбырдан ағып кірсе S2>> S1 болады, ал ξ1 1-ге ұмтылады.
Енді ағынның кенет тарылуын қарастырайық. Мұнда орнықты құйындар құбырдың екі жерінде түзіледі, олардың пайда болу себебі сұйық бөлшектерінің екпінділігі (7.5-сурет) .
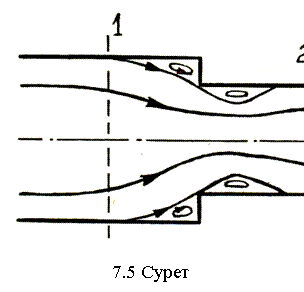 Кенет тарылу үшін де
теориялық әдіспен шығынды есептеуге кейіптеме алуға
болады.
Кенет тарылу үшін де
теориялық әдіспен шығынды есептеуге кейіптеме алуға
болады.
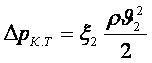 , (7.19)
, (7.19)
мұнда
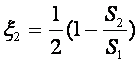 . (7.20)
. (7.20)
Толық теориялық кейіптеме орнына, есептеуге оңай тәжірибе аралас (7.20) кейіптеме келтірілген.
Егер сұйық сыйымдылығы шектеусіз ыдыстан құбырға ағып кірсе S2/S1 нөлге ұмтылады, ал ξ2 0,5-ке ұмтылады.
(7.18) және (7.20) өрнектер тәжірибе мәліметтеріне дәл келеді.
№8 дәріс
8.1 Дөңгелек құбырдағы ретті қозғалыста көрсеткіштердің таралуы және кедергі заңдылығы
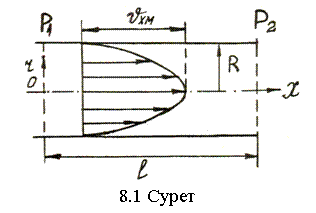
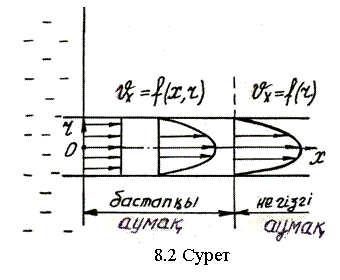
Дөңгелек ұзын құбырдағы қалыптасқан ретті қозғалысты қарастырамыз (8.1-сурет). Бұл жағдайларда кіруден біраз қашықтықта бірқалыпты қозғалыс қалыптасады, яғни жылдамдық кескіні бойлық мекендік (координата) Х-тен тәуелділігін қояды, мұндай қозғалысты тұрақтанған қозғалыс (стабилизированное движение) дейміз.
![]() x
x![]() ¹ f (x),
¹ f (x), ![]() x = f (r)
(8.1)
x = f (r)
(8.1)
Ретті қозғалыста
![]() (8.2)
(8.2)
(8.1) тұрақтану шартын және (8.2) реттілік шартын Навье-Стокс теңдеулеріне (5.16) қойса, онда олар өте ықшамдалып цилиндрлік мекендіктерде мына түрге келеді
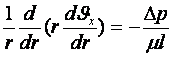 , (8.3)
, (8.3)
мұнда ![]() .
.
(8.3) шаққылық (дифференциалдық) теңдеудің шекаралық шарттары
r =
0 болғанда ![]() x =
x = ![]() xM
¹
¥
, (8.4)
xM
¹
¥
, (8.4)
r =R
болғанда ![]() x=
0.
x=
0.
(8.3) теңдеуді (8.4) шекаралық шарттарды пайдаланып оңай аумақылауға (интегралдауға) болады. Онда мына заңдылықтарды аламыз: жылдамдық таралуын
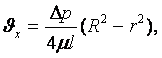 (8.5)
(8.5)
қысым таралуын
![]() . (8.6)
. (8.6)
(8.6)-дан құбыр ортасындағы ең үлкен жылдамдық
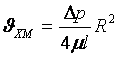 ,
(8.7)
,
(8.7)
өлшемділіксіз жылдамдық кескіні
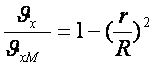 ,
(8.8)
,
(8.8)
Сұйықтың көлемдік шығысы
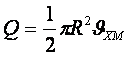 ,
(8.9)
,
(8.9)
Орташа жылдамдық
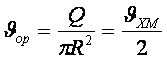 ,
(8.10)
,
(8.10)
үйкеліс кедергісінің еселеуіші
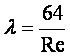 (8.11) табылады. (8.11) Пуазейль кейіптемесі деп аталады. Ретті
қозғалыста бұдырлық құбыр кедергісіне
ықпал етпейді.
(8.11) табылады. (8.11) Пуазейль кейіптемесі деп аталады. Ретті
қозғалыста бұдырлық құбыр кедергісіне
ықпал етпейді.
Ретті қозғалыста жылдамдықтың құбыр қимасы бойынша таралуы параболойд заңына бағынады, ең үлкен жылдамдық орташадан екі есе үлкен, яғни жылдамдық кескіні созылған.
 Қысым құбырдың тек
ұзындығына тәуелді, ал көлденең мекендікке
тәуелді емес. Қысым шығыны құбырда оның
ұзындығына тура сәйкес өседі. Ретті
қозғалыста құбырдың үйкеліс кедергісі
бұдырлыққа тәуелді емес.
Қысым құбырдың тек
ұзындығына тәуелді, ал көлденең мекендікке
тәуелді емес. Қысым шығыны құбырда оның
ұзындығына тура сәйкес өседі. Ретті
қозғалыста құбырдың үйкеліс кедергісі
бұдырлыққа тәуелді емес.
Дөңгелек құбырдағы тұрақтанған ағыста жылдамдықтың таралуы айналу параболоид түрінде және құбырдың барлық қималарында бірдей болады. Бұндай жылдамдық кескіні құбырға кіруден біраз қашықтықта қалыптасады. Сұйықтың ыдыстан құбырға кіру қимасында жылдамдық қима бойынша бірдей дерлік (8.2-сурет). Одан ары қарай тұтқырлық күш әрекетінен құбыр қабырғасына жанасқан сұйық қабаттары тежеледі, ал Q=тұрақты болғандықтан ағынның орталық жағында жылдамдық өседі. Осылайша құбыр ұзындығы бойынша жылдамдық кескіні біртіндеп өзгереді, ол параболоидтық болғаннан кейін өзгермейді.
Параболоидтық жылдамдық кескіні тұрақтанған құбыр бөлігін бастапқы аумақ дейміз. Бастапқы аумақта жылдамдық кескіні бойлық мекендік Х-ке тәуелді болады. Бастапқы аумақтың ұзындығын және ондағы жылдамдық кескінінің түрін анықтау күрделілеу есеп. Осы есептің шешімінен Шиллер бастапқы аумақтың ұзындығы Re санына тәуелді екенін анықтады
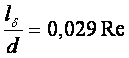 (8.12)
(8.12)
8.2 Дөңгелек құбырдағы ретсіз қозғалыста көрсеткіштердің таралуы және кедергі заңдылығы
Ретсіз ағындар үшін таза теориялық шешімдер жоқ. Барлық кейіптемелер мен заңдылықтар не тікелей тәжірибеден алынған, не тәжірибе аралас болады.
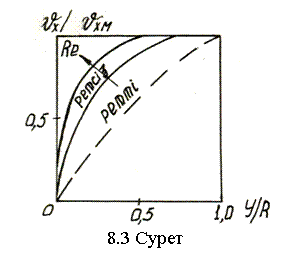
Ретті
және ретсіз қозғалыстардағы жылдамдық кескіндерін
салыстырайық (8.3-сурет). Ретті ағыста дөңгелек
құбырда максимал жылдамдықтың орташа
жылдамдыққа қатынасы 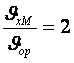 , ал ретсіз ағыста бұл
қатынас едәуір аз және Re=5×103
болғанда 1,3-тен Re = 3×106 – 1,15-ке дейін азаяды. Re®¥ үшін
көрсетілген қатынас бірге ұмтылады. Ретсіз ағында
қима бойынша жылдамдықтың біркелкі таралуы сұйық
қабаттары арасында қарқынды ретсіздік араласуынан. Ретсіздік
араласу Re саны өскен сайын қарқындай түседі.
, ал ретсіз ағыста бұл
қатынас едәуір аз және Re=5×103
болғанда 1,3-тен Re = 3×106 – 1,15-ке дейін азаяды. Re®¥ үшін
көрсетілген қатынас бірге ұмтылады. Ретсіз ағында
қима бойынша жылдамдықтың біркелкі таралуы сұйық
қабаттары арасында қарқынды ретсіздік араласуынан. Ретсіздік
араласу Re саны өскен сайын қарқындай түседі.
Ретсіз ағында
тұрақтанған қозғалыс ретті
ағындағыдай құбырдың бастапқы
аумағында қалыптасады. Никурадзенің тәжірибелік
мәліметтері бойынша 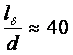 және Re санына тәуелді емес.
және Re санына тәуелді емес.
Ретсіз ағыста да
p=f(x),
Dp‰йк ~
![]() .
.
Ретсіз қозғалыста бұдырлық құбыр кедергісіне ықпал етеді және үйкеліс кедергісінің еселеуіші тәжірибелік Альтшуль кейіптемесі бойынша анықталады:
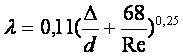 ,
(8.13)
,
(8.13)
мұнда
D–толық бұдырлық, мм құбыр сипаттамасы бойынша кестеден алынады.
8.3 Құбырдағы сұйықағулық соққы
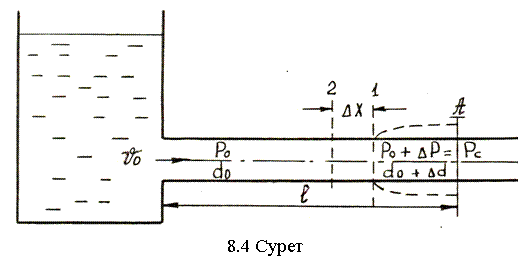
Егер тамшылы сұйық қозғалғанда ағыс жылдамдығын кенет өзгертсе (ысырманы ашса не жапса, сорғы тоқтап қалса және т.б.) қысымның қатты өзгеруінен болған сұйықағулық соққы туады. Сұйықағулық соққы кезінде қысым шамасы бірнеше рет өсіп, құбырдың қабырғасына күшті әсер етеді. Сол себептен кейде құбырлар істен шығып бұзылуы мүмкін. Сұйықағулық соққы болғанда қатты шу мен құбырдың дірілдеуі байқалады. Сұйықағулық соққыны толық зерттеп және теориялық негізін салған Н.Е. Жуковский (8.4-суретті қараңыз).
Ысырманы лезде толық жапқанда қысымның максимал өсуін Жуковский кейіптемесі бойынша анықтауға болады:
![]() .
(8.14)
.
(8.14)
мұнда
ρ–сұйық тығыздығы; ϑ0-сұйық жылдамдығы;
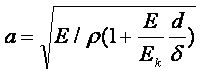 - соққы
толқынның таралу жылдамдығы,
- соққы
толқынның таралу жылдамдығы,
мұнда
E - сұйықтың серпімділік өлшемі;
Ek - құбыр жадығатының серпімділік өлшемі;
![]() - құбыр қабырғасының
салыстырмалы қалыңдығы.
- құбыр қабырғасының
салыстырмалы қалыңдығы.
Сұйықағулық соққыны азайту үшін ысырманы баяу жабу керек. Сонымен қатар сұйықағулық соққымен күресу үшін құбырларда сақтандырғыш қақпақша және ауа қалпақтарын орнатады.
№9 дәріс
9.1 Құбырларды жіктеу
Барлық құбырларды жай және күрделі деп бөлуге болады. Жай құбыр деп тармақсыз құбырды айтады, ал құбырдың жоқ дегенде бір тармағы болса күрделі құбыр деп атайды. Мысалы, ЖЭО-нан қалaға дейін ыстық су магистраль (жай) құбыр арқылы жеткізіледі, ал ыстық су қала бойынша өте күрделі құбыр жүйесі арқылы таратылады.
Құбырларды ұзын және қысқа құбыр деп бөледі.
Егер
құбырда жергілікті кедергілерден болған қысым
шығыны үйкеліс кедергісінен болған қысым
шығынынан өте аз болса (![]() -тіњ 5-10%-нaн), онда құбырды
ұзын деп есептеуге болады және толық қысым шығыны
-тіњ 5-10%-нaн), онда құбырды
ұзын деп есептеуге болады және толық қысым шығыны
![]() .
.
Егер
құбырдағы үйкеліс және жергілікті кедергілерден
болған қысым шығындары өзара шамалас болса (![]() - тіњ 5-10% - нaн),
онда құбырды қысқа деп есептеу керек және
толық қысым шығыны
- тіњ 5-10% - нaн),
онда құбырды қысқа деп есептеу керек және
толық қысым шығыны ![]() үйкеліс және жергілікті
шығындар қосындысына тең болады. Қысқа
құбырдың мысалы ретінде ортадан тепкіш сорғының
сору құбырын келтіруге болады. Ал су, газ, мұнай құбырларын
ұзын құбырлар деуге болады. Ұзын құбырлар
үшін, әдетте, жергілікті шығындарды елемейді, кейде оны
ұзындық шығынының 5-10% деп алады.
үйкеліс және жергілікті
шығындар қосындысына тең болады. Қысқа
құбырдың мысалы ретінде ортадан тепкіш сорғының
сору құбырын келтіруге болады. Ал су, газ, мұнай құбырларын
ұзын құбырлар деуге болады. Ұзын құбырлар
үшін, әдетте, жергілікті шығындарды елемейді, кейде оны
ұзындық шығынының 5-10% деп алады.
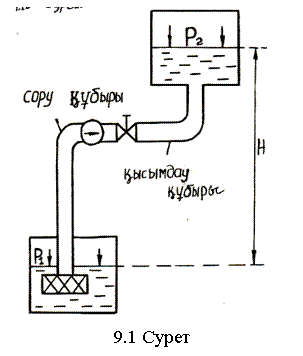
9.2 Ұзын жай құбырдың негізгі есептері
Бірінші есеп :
Құбырдың ұзындығы ![]() , қосөресі d,
, қосөресі d,
сұйық шығысы Q және
құбырдың орналасуы берілген. Осылар арқылы
сорғының қысым құламасын ![]() -ны табу керек.
-ны табу керек.
Екінші есеп: ![]() , d,
, d, ![]() берілген, ал Q=?
берілген, ал Q=?
 Үшінші есеп:
Үшінші есеп: ![]() , Q,
, Q, ![]() берілген, ал d=?
берілген, ал d=?
Бірінші есепті
шешудің әдістемесін қарастырайық. Сорғы
түзген қысым ![]() ұйкеліс
ұйкеліс ![]() , жергілікті
, жергілікті ![]() , геометриялық
, геометриялық ![]() кедергілерге
және қарсы қысымға
кедергілерге
және қарсы қысымға ![]() ќ.ќ жұмсалады (9.1-сурет).
ќ.ќ жұмсалады (9.1-сурет).
|
мұнда
![]() ,
,
![]() қ.қ.
қ.қ.![]() .
.
Егер H=0, p2=p1
және құбыр ұзын болса ![]() , онда
, онда
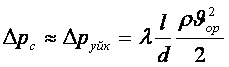 . (9.1)
. (9.1)
Мұнда 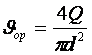 .
.
![]() еселеуішінің шамасы Re
санымен анықталатын сұйық қозғалысының
тәртібіне тәуелді .
еселеуішінің шамасы Re
санымен анықталатын сұйық қозғалысының
тәртібіне тәуелді .
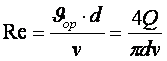 .
(9.2)
.
(9.2)
10. Егер ![]() болса, онда
қозғалыс ретті болады және
болса, онда
қозғалыс ретті болады және ![]() Пуазейль кейіптемесімен анықталады
Пуазейль кейіптемесімен анықталады
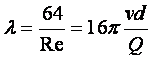 ,
(9.3)
,
(9.3)
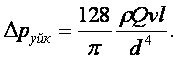 (9.4)
(9.4)
20 Егер ![]() болса, онда ағыс
ретсіз болады және сұйықағулық тегіс
құбыр үшін
болса, онда ағыс
ретсіз болады және сұйықағулық тегіс
құбыр үшін ![]() Блязиус кейіптемесімен анықталады
Блязиус кейіптемесімен анықталады
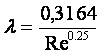 , Re < 105
,
, Re < 105
, ![]() .
(9.5)
.
(9.5)
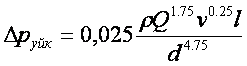 . (9.6)
. (9.6)
Екінші және үшінші есептерді шешу үшін (9.4) және (9.6) теңдеулерден Q және d - ны табу керек.
9.3 Тармақты және қатарлас құбырларды есептеу
Күрделі құбырлардың мысалы ретінде тармақты (9.2а-сурет) және қатарлас (9.2б-сурет) ұзын құбырларды қарастырайық.
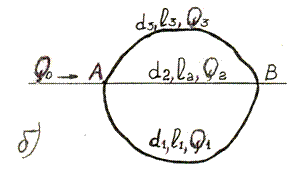
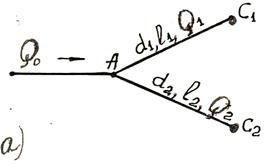
9.2 Сурет
Бұл жағдайларда есептеу әдістемелері ұқсас болғандықтан тек екінші жағдайды қарастырамыз. Қатарлас құбырларды есептегенде:
Берілгендер: Q0, d1, d2, d3(dі) і=1, 2, 3…n
![]() 1,
1, ![]() 2 ,
2 , ![]() 3 (
3 (![]() і)
і)
Анықтау керек: Q1, Q2, Q3(Qі) , DpAB .
Барлық тармақтарды
ұзын деп санаймыз, яғни ![]() .
.
Қатарлас тармақтар үшін
![]() .
.
Осыны ескере отырып мына теңдеулерді жазa аламыз
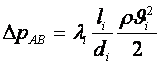 ,
,
![]() .
. ![]()
![]() 1, 2, 3 (9.7)
1, 2, 3 (9.7)
мұнда
![]() , ал
, ал 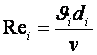 .
. ![]() белгісіз шамалар. Сондықтан
белгісіз шамалар. Сондықтан ![]() -лерді анықтау
үшін біртіндеп жуықтау әдісін қолданады.
-лерді анықтау
үшін біртіндеп жуықтау әдісін қолданады.
Іс жүзіндегі ағыстар, әдетте, ретсіз болғандықтан барлық тармақтарда қозғалыс ретсіз деп саналады және бірінші жуықтауда шаршылық (квадраттық) кедергі заңы деп ұйғарылады. Онда Альтшуль кейіптемесінен
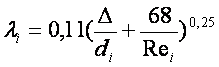 , (9.8)
, (9.8)
![]() деп кедергі еселеуіштерін бірінші
жуықтауда анықтау үшін мына кейіптемені аламыз
деп кедергі еселеуіштерін бірінші
жуықтауда анықтау үшін мына кейіптемені аламыз
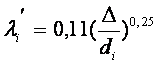 (9.9)
(9.9)
(9.9) өрнектерді пайдаланып (9.7)
теңдеулерден тармақтардағы жылдамдықтарды бірінші
жуықтауда ![]() табамыз,
олар бойынша бірінші жуықтауда Рейнольдс сандарын
табамыз,
олар бойынша бірінші жуықтауда Рейнольдс сандарын 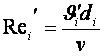 табамыз және оларды
Альтшуль кейіптемесіне қойып кедергі еселеуіштерін екінші жуықтауда
анықтаймыз
табамыз және оларды
Альтшуль кейіптемесіне қойып кедергі еселеуіштерін екінші жуықтауда
анықтаймыз
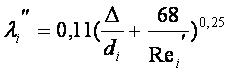 (9.10)
(9.10)
(9.10) кейіптеменің
көмегімен тармақтардағы жылдамдықтарды екінші
жуықтауда ![]() табамыз,
олар арқылы
табамыз,
олар арқылы ![]() анықталады
және тағысын-тағы.
анықталады
және тағысын-тағы.
9.4 Газ құбырларын қысым құламасы үлкен болғанда есептеу
Егер салыстырмалы
қысым құламасы 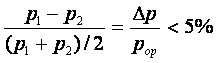
болса, (9.3-сурет), онда қысым құламасы аз деп саналады және газдың сығылғыштығын елемеуге болады (r=тұрақты). Oнда газ қозғалысының есептелуі сығылмайтын сұйықтардың қозғалысын есептеуден айырмашылығы жоқ.
Егер ![]() болса, қысым
құламасы үлкен болады және есептеу жүргізгенде
газдың сығылғыштығын есепке алу керек.
болса, қысым
құламасы үлкен болады және есептеу жүргізгенде
газдың сығылғыштығын есепке алу керек.
Газ қозғалысын талдау үшін бір өлшемді ағын деп үзіксіздік теңдеуін жазайық
![]() .
(9.11)
.
(9.11)
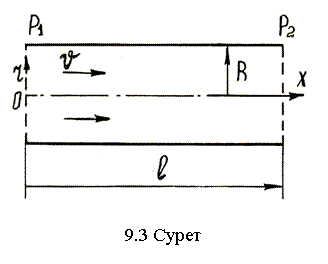 Құбыр
қосөресі тұрақты болса
Құбыр
қосөресі тұрақты болса ![]() , яғни
, яғни
![]() . (9.12)
. (9.12)
Сығылмайтын сұйық
үшін ![]() ,
онда (9.12) теңдеуден
,
онда (9.12) теңдеуден ![]() екені шығады.
екені шығады.
Сығылатын сұйық
үшін ![]() болғандықтан
болғандықтан
![]() , онда (9.12)
теңдеуден
, онда (9.12)
теңдеуден ![]() екені
шығады, яғни газдың жыдамдығы құбыр бойынша
өседі. Сонымен, қысым құламасы үлкен газ
құбырында
екені
шығады, яғни газдың жыдамдығы құбыр бойынша
өседі. Сонымен, қысым құламасы үлкен газ
құбырында
![]()
![]()
![]() . (9.13)
. (9.13)
Газ құбыры жағдайында тұрақты ыстықтықты (изотермиялық) деп санауға болады, онда l құбыр бойынша өзгермейді.
Қозғалыс теңдеулерін интегралдап, есептеу кейіптемесін аламыз:
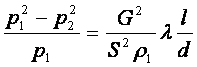 . (9.14)
. (9.14)
(6.14) теңдеудегі l Альтшуль кейіптемесі бойынша анықталады.
Газдың жылуалмаспағандағы (адиабаттық) ағысы үшін де есептеу кейіптемесін қорытуға болады.
9.5 Көлденең қимасы дөңгелек емес құбырларды есептеу
Дөңгелек құбырлар үшін алынған кейіптемелерде құбыр қосөресін сұйықағулық өре арқылы өрнектесе, онда ол кейіптемелерді қимасы дөңгелек емес құбырларды жуықша есептеу үшін қолдануға болады.
Сұйықағулық өре дегеніміз көлденең қима ауданының ылғалданған периметрге қатынасы
Rc = көлденең қима ауданы / ылғалданған периметр. (9.14)
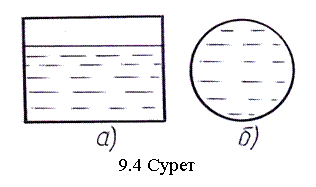 Егер құбыр
қимасын сұйық толық толтырмаса (9.4а-сурет), онда
өту қимасы ретінде қиманың тек сұйық
өтетін бөлігін алады, ал ылғалданған периметр дегеніміз
сұйықтың тек құбыр қабырғасымен
ғана жанасқан периметр (газбен жанасқан бөлігі
кірмейді).
Егер құбыр
қимасын сұйық толық толтырмаса (9.4а-сурет), онда
өту қимасы ретінде қиманың тек сұйық
өтетін бөлігін алады, ал ылғалданған периметр дегеніміз
сұйықтың тек құбыр қабырғасымен
ғана жанасқан периметр (газбен жанасқан бөлігі
кірмейді).
Енді дөңгелек құбыр үшін (9.4б-сурет) сұйық көлденең қиманы толық толтырып аққанда (9.14) бойынша сұйықағулық өрені анықтайық
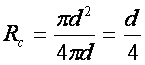 . (9.15)
. (9.15)
Сонымен дөңгелек құбыр үшін
![]() .
(9.16)
.
(9.16)
(9.16) бойынша Дарси–Вейсбах кейіптемесінде құбыр қосөресін сұйықағулық өре арқылы өрнектесек, қимасы дөңгелек емес құбырларды есептеуге жарайтын кейіптеме аламыз
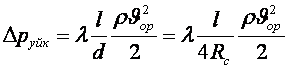 . (9.17)
. (9.17)
Үйкеліс
кедергісінің еселеуіші ![]() - ні есептеуге қажет Рейнольдс саны
да сұйықағулық өре арқылы өрнектеледі
- ні есептеуге қажет Рейнольдс саны
да сұйықағулық өре арқылы өрнектеледі
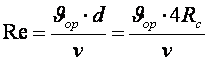 . (9.18)
. (9.18)
9.6 Көпіршіктену (кавитация)
Тамшылы
сұйықтың қайнау ыстықтығы мен қысымы
арасында тәуелділік бар екені физикадан белгілі. Сұйық
қайнайтын қысымды бу түзу қысымы ![]() -деп атайды. Сұйық
қысымы төмендегенде қайнау ыстықтығы да
төмендейді.
-деп атайды. Сұйық
қысымы төмендегенде қайнау ыстықтығы да
төмендейді.
Мысалы, су үшін
|
|
11660 |
760 |
55 |
17 |
4 |
|
t, 0С |
200 |
100 |
40 |
20 |
4 |
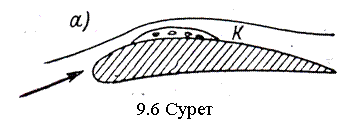
 Егер
сұйық жіңішкерген құбырда қозғалса
жылдамдық артады, ал қысым төмендейді (9.5-сурет). Берілген
ыстықтықта қысым төмендей келіп
Егер
сұйық жіңішкерген құбырда қозғалса
жылдамдық артады, ал қысым төмендейді (9.5-сурет). Берілген
ыстықтықта қысым төмендей келіп ![]() шамасына жетсе сұйық
қайнай бастайды. Ерітілген ауа мен түзілген бу көпіршіктеніп
бөліне бастайды. Сұйық ішінде бу мен ауа толған
қуыстар пайда болады. Бұл құбылысты көпіршіктену
(кавитация) деп атайды.
шамасына жетсе сұйық
қайнай бастайды. Ерітілген ауа мен түзілген бу көпіршіктеніп
бөліне бастайды. Сұйық ішінде бу мен ауа толған
қуыстар пайда болады. Бұл құбылысты көпіршіктену
(кавитация) деп атайды.
Одан әрі құбыр кеңейсе қысым жоғарлайды да көпіршіктер жарылады. Сол кезде қатты шу және діріл пайда болады.
Көпіршіктену
сұйық тек құбырда қозғалғанда
ғана емес, денелер ағысталғанда, дербес жағдайда, су
шығыры мен сорғылар қалақтарында, кеменің
еспеcінде (грeбной винт) (9.6-сурет) болады. Cу шығыры мен
сорғылардың жұмыстық доңғалағын, кеме
еспесін айналдыруды өсіргенде жылдамдықтың өсуі
қысымды кейбір аймақта бу түзу қысымына ![]() дейін төмендетуі
мүмкін және көпіршіктену пайда болады.
дейін төмендетуі
мүмкін және көпіршіктену пайда болады.
Көпіршіктену өте зиянды құбылыс, оның салдарынан қондырғының кедергісі өседі, пайдалы әрекет еселеуіші кемиді және олар мерзімінен бұрын істен шығады.
№10 дәріс. Екі текті (фазалы) ағындар қозғалысы
10.1 Екі текті ағындар туралы ұғым
Табиғатта және техникада біртекті сұйықтар ағындарымен қатар екі текті ағындар бар. Мысалы, су және су буы; су және мұз қоспасы, ауа+көмір тозаңы, ауа+мазут тамшылары, газ тәрізді жану өнімдері + күл бөлшектері, су+күл бөлшектері, су+мұнай, бұларды екі құраушылық орталар дейді. Барлық ағыстарды жуықша екі текті орталар дейді.
Егер ауа көмегімен қатты бөлшектер тасымалданса, онда ауамен тасымалдау (пневмотранспорт) деп атайды. Ағынды тозаңдалған дейді.
Егер су көмегімен
қатты бөлшектер тасымалданса, онда сумен тасымалдау
(гидротранспорт) деп атайды. Су мен ауа- тасымалдайтын орта. Көмір
тозаңы және күл бөлшектері-үзікті тек. ![]() және
және ![]() арқылы
тасымалдайтын ортаның жылдамдығы мен тығыздығын, ал
арқылы
тасымалдайтын ортаның жылдамдығы мен тығыздығын, ал ![]() арқылы
үзікті тектің жылдамдығы мен тығыздығын
белгілейді.
арқылы
үзікті тектің жылдамдығы мен тығыздығын
белгілейді.
Әдетте, ![]()
![]() (
(![]() кҰмір тозањы,
кҰмір тозањы,![]() су буы)
су буы)
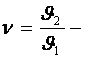 сырғанау еселеуіші деп аталынатын
нақты жылдамдықтардың қатынасы. Екі тектің
тығыздығы әртүрлі болуына байланысты бұл
еселеуіштің мәні бірден айырмашылығы болуы мүмкін,
яғни тектердің әртүрлі жылдамдықпен
қозғалуы жиі болады. Жеке жағдайларда олардың
жылдамдығы бірдей болуы мүмкін.
сырғанау еселеуіші деп аталынатын
нақты жылдамдықтардың қатынасы. Екі тектің
тығыздығы әртүрлі болуына байланысты бұл
еселеуіштің мәні бірден айырмашылығы болуы мүмкін,
яғни тектердің әртүрлі жылдамдықпен
қозғалуы жиі болады. Жеке жағдайларда олардың
жылдамдығы бірдей болуы мүмкін.
Екі текті ағындар қазандық қондырғыларда кеңінен қолданылады. Қазіргі қуатты бу қазандарының ошақтарында қатты отын тозаң түрінде қалқыған күйде жағылады. Ұнтақталған отын ошаққа ауа ағынының көмегімен жеткізіледі.
Газ тәрізді жану өнімдерімен бірге ошақ кеңістігінен күл бөлшектері шығады. Қазанның буландырғышында сумен бірге бу қозғалады.
Екі текті ағынның
негізгі сипаттамалары салыстырмалы маңыздық шығыстық
шоғыр (концентрация) 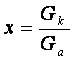 және салыстырмалы ірілік
және салыстырмалы ірілік 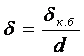 , мұнда Gқ
- қалқыған тектің маңыздық шығысы, Gа
- ағынның (қалқыған + тасымалдайтын тек)
маңыздық шығысы,
δқ.б.
-
қалқыған бөлшектердің ірілігі; d -
құбыр қосөресі (диаметрі).
, мұнда Gқ
- қалқыған тектің маңыздық шығысы, Gа
- ағынның (қалқыған + тасымалдайтын тек)
маңыздық шығысы,
δқ.б.
-
қалқыған бөлшектердің ірілігі; d -
құбыр қосөресі (диаметрі).
10.2 Қатты бөлшектерді ағынмен тасымалдау
Қалқыған қатты бөлшектер тасымалдаушы ағынның сипаттамаларына ықпал етеді. Мысалы, қалқыманың шоғыры өскенде ағынның жылдамдығы кішірейеді. Ағын берілген жағдайда қалқыманың (взвесь) тек шектелген мөлшерін алып жүре алады.
Егер x<1 болса, ағын аз тозаңдалған деп аталады. Егер x>1 болса, аѓын көп тозањдалѓан деп аталады.
x<1 болғанда қатты тектің ағын сипаттамаларына тигізетін ықпалын және бөлшектердің ағындағы өзара әрекеттесуін елемеуге болады. Бұл шартқа ошақ құбылыстарында қолданылатын тозаңдалған ағындар сәйкес келеді. Сонымен аз тозаңдалған ағындар үшін көп қателіксіз тасымалдайтын ортаның және үзікті тектің қозғалыстарын бөлек қарастыруға болады.
Көп тозаңдалған ағындардың (x>1) қозғалысын бөлшектердің ағында өзара әрекеттесуін және үзікті тектің тасымалдайтын ағын сипаттамаларына тигізетін ықпалын есепке алып қарастыру керек.
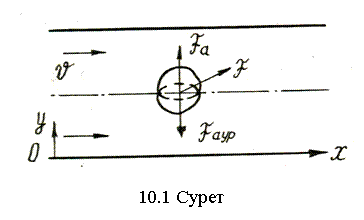 Бөлшекке сұйық
ағынында келесі күштер түседі: ауырлық күш
Бөлшекке сұйық
ағынында келесі күштер түседі: ауырлық күш ![]() , у жебесі
бағытында кері итеруші архимед күші
, у жебесі
бағытында кері итеруші архимед күші ![]() және ағынның әрекет
күші
және ағынның әрекет
күші ![]() (10.1-сурет).
Сұйыққозғалым күшін екі
құраушыға жіктеуге болады: тік
(10.1-сурет).
Сұйыққозғалым күшін екі
құраушыға жіктеуге болады: тік ![]() (көтеруші) және ағын
қозғалу бағытында
(көтеруші) және ағын
қозғалу бағытында ![]() (маңдайлық кедергі
күші).
(маңдайлық кедергі
күші). ![]() бөлшектің
ағысталуы симметриялы болмағанда және толқулық
жылдамдықтың көлденең құраушысы
бөлшектің
ағысталуы симметриялы болмағанда және толқулық
жылдамдықтың көлденең құраушысы ![]() -тің
ықпалынан пайда болады. Осы күштердің әрекетінен
қатты бөлшектер өте күрделі жолсызықтар бойынша
қозғалады және олар үзіксіз айналып отырады.
Ұсақ бөлшектер жатық (горизанталь) құбырда
тез ағын жылдамдығын қабылдайды және онда бөлшектердің
салыстырмалы жылдамдығы іс жүзінде нөлге тең болады.
-тің
ықпалынан пайда болады. Осы күштердің әрекетінен
қатты бөлшектер өте күрделі жолсызықтар бойынша
қозғалады және олар үзіксіз айналып отырады.
Ұсақ бөлшектер жатық (горизанталь) құбырда
тез ағын жылдамдығын қабылдайды және онда бөлшектердің
салыстырмалы жылдамдығы іс жүзінде нөлге тең болады.
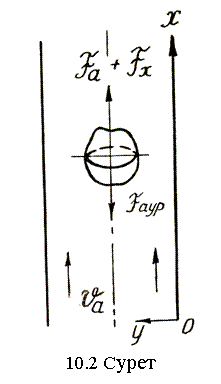 Барлық
бөлшектер қалқыған күйде болатын ағын
жылдамдығын қалқыту жылдамдығы деп атайды.
Барлық
бөлшектер қалқыған күйде болатын ағын
жылдамдығын қалқыту жылдамдығы деп атайды.
Егер ағын жылдамдығы қалқыту жылдамдығынан аз болса, онда бөлшектер құбырда шөгеді. Егер ағын жылдамдығы қалқыту жылдамдығынан едәуір асса, ол қайраттың артық шығындалуына әкеледі және құбырдың түрпілік тозуын арттырады (түрпілік тозу бөлшек жылдамдығының текшесіне (кубіне) тура сәйкес) .
Жатық құбырда қалқыту жылдамдығын тәжірибелік кейіптемемен анықтайды
![]() ќ
ќ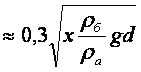 , (10.1)
, (10.1)
мұнда
![]() - сәйкесті бөлшек және
ауа тығыздықтары; g- еркін түсу үдеуі; d-
құбырдың қосөресі .
- сәйкесті бөлшек және
ауа тығыздықтары; g- еркін түсу үдеуі; d-
құбырдың қосөресі .
Тік көтерілетін ағын үшін қалқыту жылдамдығын мына шарттан оңай анықтауға болады (10.2-сурет).
![]() (10.2)
(10.2)
(10.2) теңдеуден қатты бөлшектердің ауада қозғалысы үшін қалқыту жылдамдығын анықтайтын кейіптеме алуға болады:
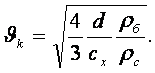 (10.3)
(10.3)
Бірақ та ![]() -ні (10.3) кейіптеме бойынша
-ні (10.3) кейіптеме бойынша ![]()
![]() -мен Re саны арқылы
байланысты болғандықтан тек біртендеп жуықтау жолымен
есептеуге болады. Бірінші жуықтауда Стокс кейіптемесін пайдалануға
болады
-мен Re саны арқылы
байланысты болғандықтан тек біртендеп жуықтау жолымен
есептеуге болады. Бірінші жуықтауда Стокс кейіптемесін пайдалануға
болады
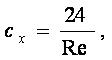 (10.4)
(10.4)
мұнда 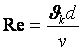 .
.
Дұрыс сфералық бөлшектерге алынған (10.3), (10.4) кейіптемелерін сфера еместігіне түзету еселеуішін кіргізіп пішіні дұрыс емес бөлшектерге қолдануға болады.
10.3 Ауамен тасымалдау құбырының кедергісі
Тәжірибе мәліметтері бойынша тозаңдалған ағындағы қайрат шығыны қғатты тектің шоғырына сәйкес. Жатық құбыр үшін мына кейіптеме қолданылады
![]() , (10.5)
, (10.5)
мұнда
![]() - сол жылдамдықпен қозғалатын
таза ағындағы қысым шығыны;
- сол жылдамдықпен қозғалатын
таза ағындағы қысым шығыны;
![]() - қалықтаманың
салыстырмалы маңыздық шығыстық шоғыры;
- қалықтаманың
салыстырмалы маңыздық шығыстық шоғыры;
![]() - тәжірибе арқылы анықталатын
өлшемділіксіз еселеуіш.
- тәжірибе арқылы анықталатын
өлшемділіксіз еселеуіш.
Егер құбыр жатық болмаса, онда ауырлық күшіне қарсы тозаңдалған ағын жұмсаған қысым шығыны тең болады
![]() ,
(10.6)
,
(10.6)
ρқ- қоспаның тығыздығы.
№11 дәріс. Қатты денелердің ағысталуы. Шекаралық қабат
11.1 Маңдайлық кедергі, көтергіш және көлденең күштер туралы ұғым
Қатты денені
сұйық ![]() жылдамдықпен
ағыстасын. Дене өлшемдерімен салыстырғанда ағын
өлшемдері шексіз (өте үлкен) болсын.
жылдамдықпен
ағыстасын. Дене өлшемдерімен салыстырғанда ағын
өлшемдері шексіз (өте үлкен) болсын.
Қатты денені
ағыстаған сұйық ағыны оған
қозғалымдық әрекет етеді, ол екі себептен болады. Егер
ағысталған дененің бетінде кішкене ауданша dS бөлінсе
(11.1-сурет), оған, біріншіден, жанама үйкеліс күші ![]() , екіншіден, тік
қысым күші
, екіншіден, тік
қысым күші ![]() әрекет етеді. Бұл кішкене
күштерді дененің барлық беті бойынша қоссақ
денеге ағын тарапынан әрекет ететін қорытқы
сұйыққозғалымдық күшті
әрекет етеді. Бұл кішкене
күштерді дененің барлық беті бойынша қоссақ
денеге ағын тарапынан әрекет ететін қорытқы
сұйыққозғалымдық күшті ![]() -ті аламыз
-ті аламыз
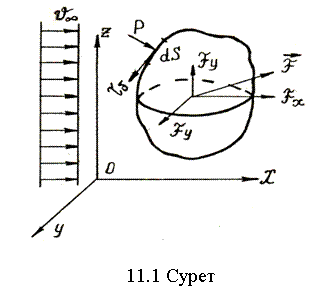
![]() .
.
Қорытқы күш
![]() -ті мекендік
(координат) жебелеріне үш құраушыға жіктеуге болады.
Денеге ағып келе жатқан ағын бағытындағы
-ті мекендік
(координат) жебелеріне үш құраушыға жіктеуге болады.
Денеге ағып келе жатқан ағын бағытындағы ![]() құраушысын
маңдайлық кедергі күші дейді.
құраушысын
маңдайлық кедергі күші дейді. ![]() көтергіш күш,
көтергіш күш, ![]() - көлденең
күш.
- көлденең
күш.
Егер ағысталған
дене XOZ және XOY жазықтықтарына қатысты симметриялы
болмаса ![]() және
және
![]() күштері
пайда болады.
күштері
пайда болады. ![]() егер
дене ZOY жазықтығына қатысты симметриялы болса да орын алады.
Қатты дене ағыстайтын ағынға
егер
дене ZOY жазықтығына қатысты симметриялы болса да орын алады.
Қатты дене ағыстайтын ағынға ![]() күшімен кедергі жасайды.
Егер дене тыныш тұрған сұйықта
күшімен кедергі жасайды.
Егер дене тыныш тұрған сұйықта ![]() жылдамдықпен
қозғалса, онда сұйық
жылдамдықпен
қозғалса, онда сұйық ![]() күшімен дене қозғалысын
тежейді.
күшімен дене қозғалысын
тежейді.
Толық маңдайлық кедергі екі құраушыдан: үйкеліс және қысым кедергілерінен тұрады.
Жазық
тақташа бойлық ағысталса, қысым тақташа бойынша
тұрақты болады (11.2а-сурет), сондықтан ![]() , ал
, ал ![]() . Сол тақташа
. Сол тақташа
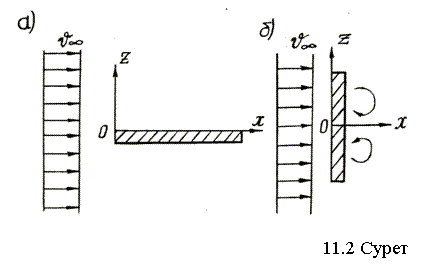
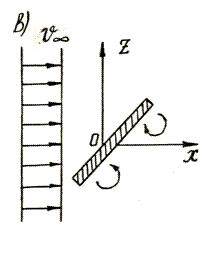 көлденең
ағысталса, онда оның артқы жағында құйындар
түзіледі, содан тақташаның артында қысым
тақташаның алдындағыдан аз болады (11.2б- сурет).
көлденең
ағысталса, онда оның артқы жағында құйындар
түзіледі, содан тақташаның артында қысым
тақташаның алдындағыдан аз болады (11.2б- сурет).
![]()
Бұдан қысым кедергісі пайда болады. Бұл жағдайда кедергінің толық күші негізінде қысым кедергісімен анықталады. Қарастырылған екі жағдай шекті жағдайлар. Жалпы жағдайда толық кедергі (11.2в-сурет) үйкеліс және қысым кедергілерінің қосындысы болады.
Үйкеліс және маңдайлық кедергі күштері келесі кейіптемемен анықталады
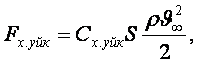 (11.1)
(11.1)
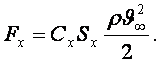 (11.2)
(11.2)
(11.1) кейіптемеге дененің нақты ағысталған бетінің ауданы қойылады. (11.2)-де Sx - ағын жылдамдығына тік жазықтыққа дене проекциясының ауданы (мидель қимасының ауданы). r -сұйық тығыздығы.
Егер денені сығылмайтын сұйықтың (r= тұрақ) шексіз ағыны ағыстаса, онда (11.1) және (11.2) кейіптемелердегі өлшемділіксіз кедергі еселеуіштері жалпы жағдайда дене пішініне және Рейнольдс санына тәуелді болады
![]() ,
,
![]() .
.
11.2 Шекаралық қабат туралы ұғым
Re саны өте кішкене болғанда (Re<<1 не Re®0) Стокс тұтқыр сұйық қозғалыс теңдеулерін оңайлатты, ол екпіндік (сызықтық емес) мүшелерді тұтқырлық мүшесімен салыстырғанда аз болғандықтан алып тастады .
Л. Прантдль Re®¥ - да шекаралық қабат ұғымын кіргізіп Навье-Стокс теңдеулерін оңайлатудың басқа әдісін ұсынды. Сонымен, қазіргі кезде Навье-Стокс теңдеулерін екі шекті жағдайларда Re®0 және Re ® ¥ -да оңайлатуға болады. Оңайланған қозғалыс теңдеулері көп маңызды жағдайларда аумақыланды (интегралданды). Жалпы жағдайда Навье-Стокс теңдеулерін олар күрделі болғандықтан аналитикалық аумақылау өте қиын. Бұл теңдеулердің күрделілігі біріншіден олардың сызықтық еместігімен байланысты.
Соңғы жылдары Навье-Стокс теңдеулерін шешудің сандық әдістері дамып келеді, бірақ та бұл жағдайда да қиыншылықтар бар. Мысалы, үлкен туындының алдында кішкене көрсеткіштің (n) болуы жеткілікті дәл сандық шешулердің табылуын қиындатады. Шекаралық қабат ұғымын қарастырайық. Нақты сұйық денені ағыстағанда тұтқырлық бар болғандықтан дене бетінде ағын жылдамдығы нөлге тең. Дене бетінен тік бағытта алыстағанда жылдамдық шамасы үлкейеді (11.3-сурет). Денеден біраз қашықтықта ол дене тұтқырсыз сұйықпен ағысталғандағыға жақын болады.
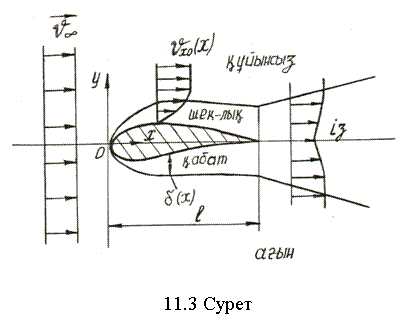 Үйкеліс
салдарынан тежелген қабаттың қалыңдығын біз
Үйкеліс
салдарынан тежелген қабаттың қалыңдығын біз ![]() деп белгілейміз, ол
дененің алдыңғы шетінен алыстағанда біртіндеп
өседі, өйткені тежелген сұйық мөлшері
дененің артқы шетіне жақындаған сайын көбейеді.
Тұтырлық ықпал ететін аймақтың
өлшемділіксіз қалыңдығын кіргізейік
деп белгілейміз, ол
дененің алдыңғы шетінен алыстағанда біртіндеп
өседі, өйткені тежелген сұйық мөлшері
дененің артқы шетіне жақындаған сайын көбейеді.
Тұтырлық ықпал ететін аймақтың
өлшемділіксіз қалыңдығын кіргізейік
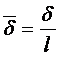 ,
,
мұнда
![]() ағысталған
дененің сипаттамалық бойлық өлшемі .
ағысталған
дененің сипаттамалық бойлық өлшемі .
Прандтль
тәжірибеден ![]() -
нің Re санына тәуелді екенін тапты
-
нің Re санына тәуелді екенін тапты
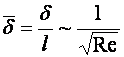 .
(11.3)
.
(11.3)
(11.3) кейіптемені талдасақ
мыналар айқын болады. Re саны кішкене болғанда ![]() болады.
болады.
Re саны
үлкен болғанда тұтқырлықтың ықпалы
дене жанындағы азғантай аймақта шоғырланады, яғни
![]() . Бұл
жағдайда Прандтль денені ағыстайтын ағынды үш
бөлікке бөлуді ұсынды. Біріншісі – ағысталған
денеге тікелей жанасады және шекаралық қабат деп аталады.
Бұл өте жұқа қабат, онда
тұтқырлықтың барлық ықпалы
шоғырланған. Екінші бөлік – ағысталған денеден
кейінгі із және үшіншісі – қалған барлық
аймақ, онда тұтқырлықтың ықпалы
білінбейді, демек, оны тұтқырсыз сұйықтың
құйынсыз ағын аймағы ретінде қарастыруға
болады.
. Бұл
жағдайда Прандтль денені ағыстайтын ағынды үш
бөлікке бөлуді ұсынды. Біріншісі – ағысталған
денеге тікелей жанасады және шекаралық қабат деп аталады.
Бұл өте жұқа қабат, онда
тұтқырлықтың барлық ықпалы
шоғырланған. Екінші бөлік – ағысталған денеден
кейінгі із және үшіншісі – қалған барлық
аймақ, онда тұтқырлықтың ықпалы
білінбейді, демек, оны тұтқырсыз сұйықтың
құйынсыз ағын аймағы ретінде қарастыруға
болады.
Жылдамдықтың сыртқы ағын жылдамдығынан айырмашылыѓы 1% болған дене бетінен саналған қашықтықты шекаралық қабат қалыңдығы деп түсінеміз
![]() болғанда
болғанда
![]()
Шекаралық қабат сұйық құбыр ішінде және ағыншаларда аққанда да түзіледі. Шекаралық қабат ретті және ретсіз болады.
Егер дене ағысталғанда шекаралық қабаттың ажырауы байқалмаса, онда мұндай денелер жақсы ағысталатын денелер деп аталынады. Ағын бойымен орналасқан тақташа, цилиндр, жұқа қанат шабуыл бұрышы аз болғанда мысал бола алады (11.4 - сурет)
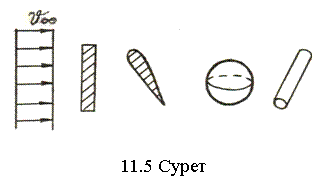 Ағысталғанда
шекаралық қабаттың ажырауы байқалса ондай денелер нашар
ағысталатындарға жатады. Нашар ағысталатын дененің
артқы жағында құйын түзіледі.
Оларға
ағында көлденең орналасқан тақташа, қанат
шабуыл бұрышы үлкен болса, шар, көлденең
ағысталған цилиндр (11.5 – сурет)
Ағысталғанда
шекаралық қабаттың ажырауы байқалса ондай денелер нашар
ағысталатындарға жатады. Нашар ағысталатын дененің
артқы жағында құйын түзіледі.
Оларға
ағында көлденең орналасқан тақташа, қанат
шабуыл бұрышы үлкен болса, шар, көлденең
ағысталған цилиндр (11.5 – сурет)

11.3 Ретті шекаралық қабаттағы қозғалыс теңдеулері
Шекаралық қабат қалыңдығының ағысталған дененің ұзындығымен (қанаттың хордасы, тақташаның ұзындығы) салыстырғанда аздығы шекаралық қабат аймағында Навье-Стокс теңдеулерін оңайлатуға мүмкіндік береді.
Навье-Стокс теңдеулерінің сығылмайтын сұйықтың жазықтық қозғалысы үшін маңыздық күштер жоқ болғанда түрі мынандай:

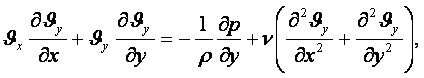 (11.4)
(11.4)
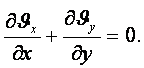
Шекаралық қабат үшін бұл теңдеулерді 1904 жылы Л.Прандтль ықшамдады. Ықшамдау үшін теңдеулерді өлшемділіксіз түрде жазып талдады. Сонда, (11.4) теңдеулер мына түрге келеді: Өлшемділіксіз шамаларды былай кіргізейік:
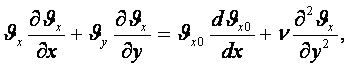
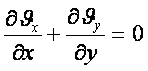 (11.5)
(11.5)
Бұл ретті шекаралық қабаттағы қозғалыс теңдеулері.
Шекаралық шарттары:
![]() болѓанда
болѓанда
![]()
![]() болѓанда
болѓанда ![]() .
.
11.4 Тақтадағы ретті шекаралық қабат
Тақта қалыптасқан жағдайда бойлық ағысталса (11.6-сурет) шекаралық қабат теңдеулері мына түрге келеді
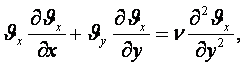 (11.6)
(11.6)
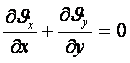 .
.
Шекаралық шарттар: Y=0
болғанда ![]() ;
;
![]()
![]() .
.
Блязиус (11.6) теңдеулерді интегралдап, жылдамдықтың таралуын, шекаралық қабаттың қалыңдығын анықтау үшін кейіптеме алды:
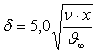 (11.7)
(11.7)
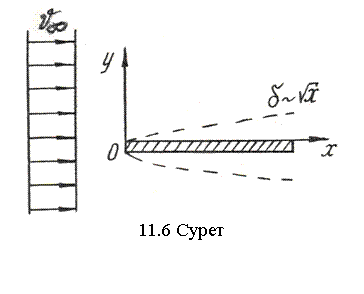 және
үйкеліс кедергісінің еселеуіші
және
үйкеліс кедергісінің еселеуіші
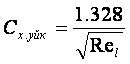 (11.8)
(11.8)
анықталады.
(11.8) кейіптемеде 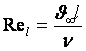 .
.
Бұл кейіптемені Re
саны ![]() мәніне
жеткенше қолдануға болады.
мәніне
жеткенше қолдануға болады.
Есептің теориялық шешімі тәжірибе арқылы мұқият тексерілді. Re<Reаум. болғанда теориялық нәтижелер тәжірибемен жақсы сәйкестенеді.
11.5 Тақтадағы ретсіз шекаралық қабат
![]() болғанда ретті
шекаралық қабат ретсіз бола бастайды. Тақтаның
алдыңғы жағында ретті шекаралық қабат орын алады
(11.7-сурет).
болғанда ретті
шекаралық қабат ретсіз бола бастайды. Тақтаның
алдыңғы жағында ретті шекаралық қабат орын алады
(11.7-сурет).
Толық дамыған ретсіз шекаралық қабат пен екі ортада әрқашан да біраз ауысулық аймақ болады, оның шамасы біріншіден, ағынның шекаралық қабаттан тысқары ретсіздік дәрежесіне, екіншіден, тақтаның бұдырлығына байланысты.
![]() болғанда
шекаралық қабат ретсіздене бастайды.
болғанда
шекаралық қабат ретсіздене бастайды. ![]() болғанда дамыған
ретсіз шекаралық қабат басталады. Есептеу жүргізгенде,
әдетте,
болғанда дамыған
ретсіз шекаралық қабат басталады. Есептеу жүргізгенде,
әдетте, ![]() деп
алады.
деп
алады.
Ретсіз шекаралық қабат қалыңдығының өсу қарқындылығы тақта ұзындығы бойынша реттіге қарағанда жоғары. Ретсіз шекаралық қабаттың құрылымы өте күрделі. Құрылымы бойынша қабатты үш аймаққа бөлуге болады: шынында ретсіз өзек (ішкі және сыртқы) 111, ретті астыңғы қабатша 1V және кезектесулік жоғарғы қабат. Аймақтар арасында ешқандай айқын шекара жоқ. Қабат қалыңдығынан 1%-дай болатын ретті астыңғы қабатша аймағы ең жұқасы. Бұл жұқа қабатта тақта бетіндегі ретті ағынның сыртқы шекарада толық ретсіздікке дейін өзгеруі болады. Әрине, кейбір ретсіз мольдер бұл қабат арқылы өтіп қабырғаға дейін жетіп қалады.
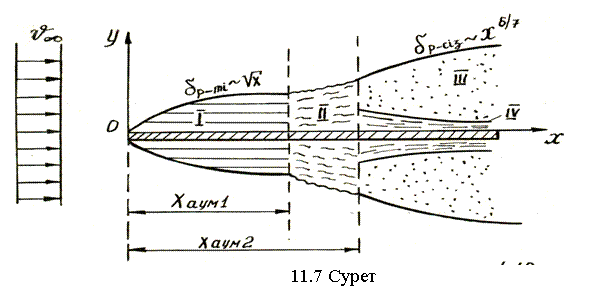 Ретсіз
шекаралық қабаттың заңдылықтары негізінен
тәжірибеден алынады.
Ретсіз
шекаралық қабаттың заңдылықтары негізінен
тәжірибеден алынады.
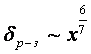 ,
(11.9)
,
(11.9)
![]() , (11.10)
, (11.10)
Мұнда 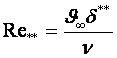 ;
; 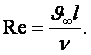
(11.10) кейіптеме шекаралық қабаттың ретті аумағы елеместей аз және Re>107 болғанда тәжірибемен дәл келеді.
№12 дәріс. Газқозғалым (газодинамика)
12.1 Үлкен жылдамдықпен қозғалғанда газдардың сығылғыштығы
Газдар үлкен жылдамдықпен
қозғалғанда олардың сығылғыштығы
біліне бастайды. Газ сығылғыштығын есепке алатын Мах саны ![]() және Пуассон
саны
және Пуассон
саны  .
.
Талдау көрсетіп отыр: ![]() болғанда
газдарды сығылмайды деп санауға болады, онда жіберілген қате
5 %-дан аспайды. Ыстықтығы 15 0C ауада дыбыстың таралу жылдамдығы
болғанда
газдарды сығылмайды деп санауға болады, онда жіберілген қате
5 %-дан аспайды. Ыстықтығы 15 0C ауада дыбыстың таралу жылдамдығы ![]() болғанда М=0,3-ке сәйкес қозғалыс
жылдамдығы
болғанда М=0,3-ке сәйкес қозғалыс
жылдамдығы ![]() -ге
тең болады.
-ге
тең болады.
Демек, егер ауа 100 м/с-ден аспайтын жылдамдықпен қозғалса оны жуықша сығылмайтын деп есептеу мүмкін. M>0,3 болғанда газдардың сығылғыштығын есептемеу едәуір қате кіргізеді.
Газ ағысының сығылғыштығын есепке алып зерттейтін сұйық механикасының бөлігі газқозғалым деп аталады.
Газда дыбыс таралу жылуалмаспайтын құбылыс. Газды дыбыс толқыны сыққанда бөлінетін жылу көрші газ қабаттарына өтіп үлгермейді, сондықтан газда дыбыс таралуы жылуалмаспайтын құбылыс деуге болады. Дыбыс жылдамдығы мына кейіптемемен анықталады
![]()
мұнда
R-
газ тұрақтысы; 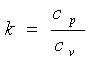 - тұрақты
қысымдағы және көлемдегі газдың меншікті
жылусыймдылықтарының қатынасы; Т - толық
ыстықтық.
- тұрақты
қысымдағы және көлемдегі газдың меншікті
жылусыймдылықтарының қатынасы; Т - толық
ыстықтық.
12.2 Газдың бір өлшемді қозғалысының негізгі теңдеулері
Бір өлшемді ағынның қозғалыс теңдеулері: үзіксіздік теңдеуі (5.3), қозғалыс мөлшерінің теңдеуі (5.11), Бернулли теңдеуінің (5.6) жалпы түрі 5 дәрісте келтірілген. (5.3), (5.11) теңдеулерін сол жазылған түрлерінде қолданамыз, ал (5.6) теңдеуді газдың сығылғыштығын есепке алып жазу керек.
Газ ағындары үшін газ тығыздығы кішкене болғандықтан мүмкіндік орын қайратының өзгеруін басқалармен салыстырғанда елемеуге болады. Осыны ескере отырып, Бернулли теңдеуін тұтқырсыз газ үшін жазайық
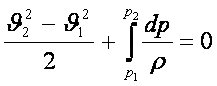 .
(12.1)
.
(12.1)
Сығылатын сұйықтар үшін аумаққыны (интегралды) алу үшін тығыздықтың ағын ыстықтығы мен қысымға тәуелді екенін есепке алу керек. Біз газ тығыздығы тек қысым бернесі (функциясы) болатын жай жағдаймен шектелеміз, яғни
![]() .
(12.2)
.
(12.2)
Мұндай сұйықтар баротроптық деп аталады. (12.2) тәуелділіктің нақты түрі газ ағынының қозғалысы қалай болатынына байланысты (мысалы, тұрақты ыстықтықта не жылуалмаспағанда). Газқозғалымда тез өтетін құбылыстар қаралғандықтан ағын қоршаған ортамен жылуалмасып үлгермейді, демек, газқозғалымда жылуалмаспайтын (адиабаттық) құбылыстардың ерекше маңызы бар. Егер жылуалмаспайтын құбылыс теңдеуін
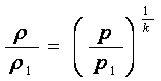
пайдалансақ, (12.1) теңдеуді интегралдасақ, Бернулли теңдеуін газ ағынының жылу алмаспаған қозғалысы үшін былай жазуға болады
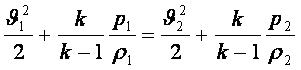 .
(12.3)
.
(12.3)
12.3 Әлсіз және әлді ұйтқулар. Тығыздалу секірмесі
Газдарда қысым
ұйтқуы (жоғарлауы не азаюы) болады. Қысым
ұйтқуы қысымның салыстырмалы өзгеруімен
сипатталады 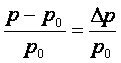 ,
мұнда p0 газдағы ұйтқуға дейінгі
қысым; p-ұйтқудан кейінгі қысымның ең
үлкен мәні.
,
мұнда p0 газдағы ұйтқуға дейінгі
қысым; p-ұйтқудан кейінгі қысымның ең
үлкен мәні.
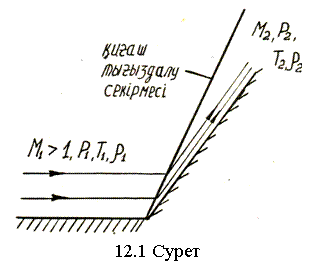 Егер
Егер
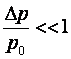 болса,
онда ұйытқуды әлсіз деп есептейді. Мысалы, дыбыс
(акустикалық) толқындары таралғанда қысымның
салыстырмалы өзгеруі өте аз. Барлық әлсіз
ұйтқулар газдарда және сұйықтықтарда
берілген ортадағы дыбыс жылдамдығына тең жылдамдықпен
таралады.
болса,
онда ұйытқуды әлсіз деп есептейді. Мысалы, дыбыс
(акустикалық) толқындары таралғанда қысымның
салыстырмалы өзгеруі өте аз. Барлық әлсіз
ұйтқулар газдарда және сұйықтықтарда
берілген ортадағы дыбыс жылдамдығына тең жылдамдықпен
таралады.
Әлді
ұйтқуда ![]() шамасы бірге шамалас және одан
едәуір үлкен бола алады. Әлді
ұйтқулардың таралу жылдамдығы берілген ортадағы
дыбыс жылдамдығынан көп артуы мүмкін. Қатты жарылыс
әлді ұйтқудың мысалы бола алады, онда
қысымның соққы толқыны пайда болады, ол газда
дыбыс жылдамдығынан жоғары жылдамдықпен таралады.
Соққы толқыны уақыт өткен сайын біртіндеп
бәсеңдеп әлсіз ұйтқуға айналады.
Ұйтқу көзі тұрақты әрекет етсе
өшпейтін соққы толқынын алуға болады.
Қарқындылығы тұрақты қалыптасқан
соққы толқын жіңішкерген арнада дыбыстан жылдам
ағынды тежегенде (12.1-сурет) және қатты дене дыбыстан жылдам
ағынмен ағысталғанда (12.2-сурет) түзіледі. Қалыптасқан
қозғалмайтын соққы толқынды тығыздалу
секірмесі
дейді.
шамасы бірге шамалас және одан
едәуір үлкен бола алады. Әлді
ұйтқулардың таралу жылдамдығы берілген ортадағы
дыбыс жылдамдығынан көп артуы мүмкін. Қатты жарылыс
әлді ұйтқудың мысалы бола алады, онда
қысымның соққы толқыны пайда болады, ол газда
дыбыс жылдамдығынан жоғары жылдамдықпен таралады.
Соққы толқыны уақыт өткен сайын біртіндеп
бәсеңдеп әлсіз ұйтқуға айналады.
Ұйтқу көзі тұрақты әрекет етсе
өшпейтін соққы толқынын алуға болады.
Қарқындылығы тұрақты қалыптасқан
соққы толқын жіңішкерген арнада дыбыстан жылдам
ағынды тежегенде (12.1-сурет) және қатты дене дыбыстан жылдам
ағынмен ағысталғанда (12.2-сурет) түзіледі. Қалыптасқан
қозғалмайтын соққы толқынды тығыздалу
секірмесі
дейді.
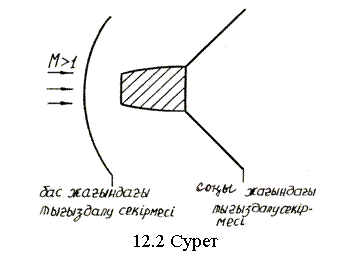 Тығыздалу
секірмесі тек дыбыстан жылдам ағындарда олар тежелгенде ғана
түзілуі мүмкін, дыбыстан жылдамдығы аз ағында ол
болмайды. Дыбыстан жылдам ағын тежелмей үдесе онда тығыздалу
секірмесі түзілмейді.
Тығыздалу
секірмесі тек дыбыстан жылдам ағындарда олар тежелгенде ғана
түзілуі мүмкін, дыбыстан жылдамдығы аз ағында ол
болмайды. Дыбыстан жылдам ағын тежелмей үдесе онда тығыздалу
секірмесі түзілмейді.
Соққы толқындарының қалыңдығы өте аз және затшалардың (молекулалардың) еркін жол ұзындығымен шамалас, сондықтан соққы толқынын газ көрсеткіштерінің үзіліс беті деуге болады.
Ұйтқудың екі түрінің негізгі айырмашылығы ағын көрсеткіштерінің (жылдамдық, қысым, тығыздық, ыстықтық) өзгеру сипатында. Әлсіз ұйтқуда ағынның барлық көрсеткіштері уақыт және мекендіктердің үзіксіз бернелері (функциялары), ал әлді ұйтқуларда ағын көрсеткіштері шекті үзіліске ұшырайды: олар соққы толқыны арқылы өткенде секіріп кенет өзгереді.
Егер тығыздалу секірмесінің беті ағын бағытына тік болса, онда тығыздалу секірмесін тік дейміз, егер ол қозғалыс бағытына көлбеу болса, онда тығыздалу секірмесін қиғаш дейміз. Қиғаш секірмелер ағысталған дененің тек бас жағында ғана емес, соңғы жағында да болады.
Ағын тығыздалу секірмесі арқылы өткенде ағынның қозғалыс қайратының бөлігі жылу қайратына қайтымсыз өтеді. Қозғалыс қайратының бұл шығыны толқындық кедергіден болады. Соққы толқынның қарқындылығы өскен сайын толқындық кедергі өседі. Жылдамдығы дыбыс жылдамдығынан аз ағында үйкеліс және қысым кедергісімен салыстырғанда толқын кедергісі аз болады.
Әдебиеттер тізімі
1. Нұрекен Е. Сұйық және газ механикасы. Сорғылар. Оқу құралы. – Алматы: АЭжБИ, 2005. – 193 б.
2. Дейли Дж, Харлеман Д. Механика жидкости. Пер. с анг.-М.: Энергия, 1971.-480с.
3. Альбом течений жидкости и газа. пер. с анг./Сост.М.Ван-Дайк,-М.: Мир, 1986.-181с.
4. Сергель О.С. Прикладная гидрогазодинамика.-М.: Машиностроение, 1981.-374с.
5. Механика жидкости и газа/Аверин С.И. и др. -М.: Металургия, 1987.-304с.
6. Абрамович Г.Н. Прикладная газовая динамика. -М.: Наука, 1969.-824с.
7. Павлов К.Ф. и др. Примеры и задачи по курсу процессов и аппаратов химической технологии. -Л.: Химия, 1987.-576с.
8. Повх И.Л. Техническая гидромеханика. -М.: Машиностроение, 1976.-502с.
9. Альтшуль А.Д. и др. Гидравлика и аэродинамика.-М.: Стройиздат, 1987.-410с.
10. Валуева Е.П., Свиридов В.Г. Введение в механику жидкости. –М.: Издательство МЭИ, 2001.-212с.
11. Нұрекен Е. Сұйық және газ механикасы. Пәндік жұмысқа әдістемелік нұсқаулар мен тапсырмалар. –Алматы: АЭжБИ, 2003.-17б.
12. Нұрекен Е. Сұйық және газ механикасы. Зерттеулік жұмыстардың сипаттамасы. –Алматы: АЭжБИ, 2003.-32б.
13. Примеры расчетов по гидравлике /под. ред. А.Д. Альтшуля.-М.: Стройиздат, 1977.-255с.
14. Тян. А.Д. Гидравлика в примерах и задачах. Алматы: Рауан, 1990.-208с.
15. Нұрекен Е. Сұйық және газ механикасы. Сорғылар. Мысалдар мен есептер. – Алматы: АЭжБИ, 2006. – 86 б.
Мазмұны
№1 дәріс. Кіріспе
1.1 Сұйық және газ механикасы пәні және әдістері................................................ 3
1.2 Сұйық ұғымының анықтамасы......................................................................... 3
1.3 Тығыздық. Сығылғыштық................................................................................ 4
1.4 Тұтқырлық және сұйықтағы үйкеліс туралы Ньютонның заңы....................... 5
1.5 Сұйықта әрекет ететін күштер. Қысым............................................................. 6
№2 дәріс. Сұйықтеңдесу (гидростатика)
2.1 Сұйықтеңдесудің шаққылық (дифференциалдық) теңдеулері........................... 7
2.2 Сығылмайтын сұйықтың ауырлық күш өрісіндегі теңдесуі............................ 10
№3 дәріс.
3.1 Айналған ыдыстағы сығылмайтын сұйық теңдесуі........................................ 11
3.2 Жазық беттегі сұйықтың қысым күші............................................................. 12
3.3 Архимед заңы................................................................................................... 13
№4 дәріс. Сұйық қозғалысының негізгі ұғымдары мен теңдеулері
4.1 Сұйық қозғалысының түрлері......................................................................... 14
4.2 Сұйық қозғалысының тәртіптері..................................................................... 15
4.3 Ағын сызығы және түтігі................................................................................. 17
№5 дәріс.
5.1 Бір өлшемді ағынның қозғалыс теңдеулері..................................................... 18
5.2 Үзіксіздіктің шаққылық (дифференциалдық) теңдеуі...................................... 22
5.3 Тұтқыр сұйықтың шаққылық (дифференциалдық) қозғалыс теңдеулері (Навье-Стокс теңдеулері). Бастапқы және шекаралық шарттар................................................... 22
№6 дәріс
6.1 Ретсіз қозғалыстың негізгі сипаттамалары...................................................... 23
6.2 Ретсіз ағынның орташаланған қозғалыс теңдеулері (Рейнольдс теңдеулері).....................................................................................................................24
6.3Сұйық қозғалымдық ұқсастық және үлгілеу........................................................26
№7 дәріс.
7.1 Сұйықтың тұрақты тегеурінде кішкене тесіктен ағуы..................................... 28
Сұйықтың құбырдағы қозғалысы және құбырларды сұйықағулық есептеу
7.2 Құбырлардың сұйықағулық кедергісі............................................................. 30
7.3 Ағынның кенет кеңейгендегі және тарылғандағы қысым шығыны............... 32
№8 дәріс.
8.1 Дөңгелек құбырдағы ретті қозғалыста көрсеткіштер таралуы және кедергі заңдылығы............................................................................................................................... 34
8.2 Дөңгелек құбырдағы ретсіз қозғалыста көрсеткіштер таралуы және кедергі заңдылығы............................................................................................................................... 36
8.3 Құбырдағы сұйықағулық соққы..................................................................... 36
№9 дәріс.
9.1 Құбырларды жіктеу......................................................................................... 37
9.2 Ұзын жай құбырдың негізгі есептері............................................................... 38
9.3 Тармақты және қатарлас құбырларды есептеу................................................ 39
9.4 Газ құбырларын қысым құламасы үлкен болғанда есептеу........................... 41
9.5 Көлденең қимасы дөңгелек емес құбырларды есептеу................................... 42
9.6 Көпіршектену (кавитация)............................................................................... 42
№10 дәріс. Екі текті (фазалы) ағындар қозғалысы
10.1 Екі текті ағындар туралы ұғым...................................................................... 43
10.2 Қатты бөлшектерді ағынмен тасымалдау...................................................... 44
10.3 Ауамен тасымалдау құбырының кедергісі..................................................... 46
№11 дәріс. Қатты денелердің ағысталуы. Шекаралық қабат
11.1 Маңдайлық кедергі, көтергіш және көлденең күштер туралы ұғым............. 46
11.2 Шекаралық қабат туралы ұғым...................................................................... 48
11.3 Ретті шекаралық қабаттағы қозғалыс теңдеулері........................................... 50
11.4 Тақтадағы ретті шекаралық қабат.................................................................. 51
11.5 Тақтадағы ретсіз шекаралық қабат................................................................. 52
№12 дәріс. Газқозғалым (газодинамика)
12.1 Үлкен жылдамдықпен қозғалғанда газдардың сығылғыштығы.................. 53
12.2 Газдың бір өлшемді қозғалысының негізгі теңдеулері.................................. 54
12.3 Әлсіз және әлді ұйтқулар. Тығыздалу секірмесі............................................ 55
Әдебиеттер тізімі.......................................................................................... 57